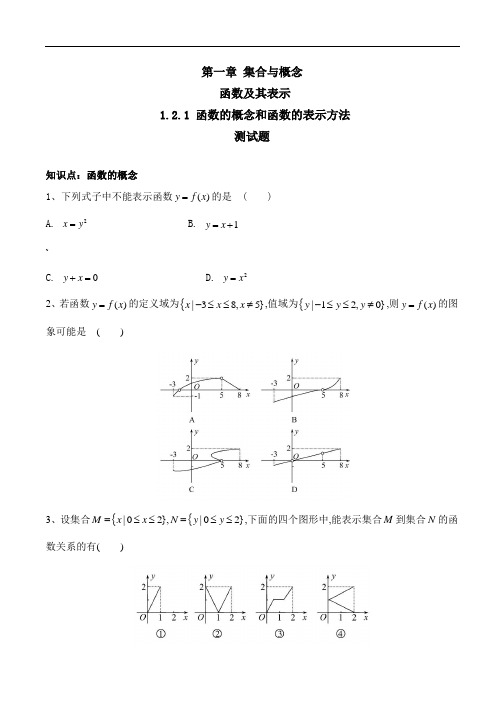
1.2.1函数的概念练习题及答案解析

1．下列说法中正确的为( )
A ．y ＝f (x )与y ＝f (t )表示同一个函数
B ．y ＝f (x )与y ＝f (x ＋1)不可能是同一函数
C ．f (x )＝1与f (x )＝x 0表示同一函数
D ．定义域和值域都相同的两个函数是同一个函数
解析：选A.两个函数是否是同一个函数与所取的字母无关，判断两个函数是否相同，主要看这两个函数的定义域和对应法则是否相同．
2．下列函数完全相同的是( )
A ．f (x )＝|x |，g (x )＝(x )2
B ．f (x )＝|x |，g (x )＝x 2
C ．f (x )＝|x |，g (x )＝x 2
x
D ．f (x )＝x 2－9x －3
，g (x )＝x ＋3 解析：选B.A 、C 、D 的定义域均不同．
3．函数y ＝1－x ＋x 的定义域是( )
A ．{x |x ≤1}
B ．{x |x ≥0}
C ．{x |x ≥1或x ≤0}
D ．{x |0≤x ≤1}
解析：选D.由⎩
⎪⎨⎪⎧
1－x ≥0x ≥0，得0≤x ≤1. 4．图中(1)(2)(3)(4)四个图象各表示两个变量x ，y 的对应关系，其中表示y 是x 的函数关系的有________．
解析：由函数定义可知，任意作一条直线x ＝a ，则与函数的图象至多有一个交点，对
于本题而言，当－1≤a ≤1时，直线x ＝a 与函数的图象仅有一个交点，当a ＞1或a ＜－1时，直线x ＝a 与函数的图象没有交点．从而表示y 是x 的函数关系的有(2)(3)．
答案：(2)(3)
1．函数y ＝1x
的定义域是( ) A ．R B ．{0}
C ．{x |x ∈R ，且x ≠0}
D ．{x |x ≠1}
解析：选C.要使1x 有意义，必有x ≠0，即y ＝1x 的定义域为{x |x ∈R ，且x ≠0}．
2．下列式子中不能表示函数y ＝f (x )的是( )
A ．x ＝y 2＋1
B ．y ＝2x 2＋1
C ．x －2y ＝6
D ．x ＝y
解析：选A.一个x 对应的y 值不唯一．
3．下列说法正确的是( )
A ．函数值域中每一个数在定义域中一定只有一个数与之对应
B ．函数的定义域和值域可以是空集
C ．函数的定义域和值域一定是数集
D ．函数的定义域和值域确定后，函数的对应关系也就确定了
解析：选C.根据从集合A 到集合B 函数的定义可知，强调A 中元素的任意性和B 中对应元素的唯一性，所以A 中的多个元素可以对应B 中的同一个元素，从而选项A 错误；同样由函数定义可知，A 、B 集合都是非空数集，故选项B 错误；选项C 正确；对于选项D ，可以举例说明，如定义域、值域均为A ＝{0,1}的函数，对应关系可以是x →x ，x ∈A ，可以是x →x ，x ∈A ，还可以是x →x 2，x ∈A .
4．下列集合A 到集合B 的对应f 是函数的是( )
A ．A ＝{－1,0,1}，
B ＝{0,1}，f ：A 中的数平方
B ．A ＝{0,1}，B ＝{－1,0,1}，f ：A 中的数开方
C ．A ＝Z ，B ＝Q ，f ：A 中的数取倒数
D ．A ＝R ，B ＝{正实数}，f ：A 中的数取绝对值
解析：选A.按照函数定义，选项B 中集合A 中的元素1对应集合B 中的元素±1，不符合函数定义中一个自变量的值对应唯一的函数值的条件；选项C 中的元素0取倒数没有意义，也不符合函数定义中集合A 中任意元素都对应唯一函数值的要求；选项D 中，集合A 中的元素0在集合B 中没有元素与其对应，也不符合函数定义，只有选项A 符合函数定义．
5．下列各组函数表示相等函数的是( )
A ．y ＝x 2－3x －3
与y ＝x ＋3(x ≠3) B ．y ＝x 2－1与y ＝x －1
C ．y ＝x 0(x ≠0)与y ＝1(x ≠0)
D ．y ＝2x ＋1，x ∈Z 与y ＝2x －1，x ∈Z X k b 1 . c o m
解析：选C.A 、B 与D 对应法则都不同．
6．设f ：x →x 2是集合A 到集合B 的函数，如果B ＝{1,2}，则A ∩B 一定是( )
A ．∅
B ．∅或{1}
C ．{1}
D ．∅或{2}
解析：选B.由f ：x →x 2是集合A 到集合B 的函数，如果B ＝{1,2}，则A ＝{－1,1，－2，2}或A ＝{－1,1，－2}或A ＝{－1,1，2}或A ＝{－1，2，－2}或A ＝{1，－2，2}或A ＝{－1，－2}或A ＝{－1，2}或A ＝{1，2}或A ＝{1，－2}．所以A ∩B ＝∅或{1}．
7．若[a,3a －1]为一确定区间，则a 的取值范围是________．
解析：由题意3a －1＞a ，则a ＞12
. 答案：(12
，＋∞) 8．函数y ＝(x ＋1)0
3－2x 的定义域是________． 解析：要使函数有意义，
需满足⎩⎪⎨⎪⎧
x ＋1≠03－2x ＞0，即x ＜32且x ≠－1. 答案：(－∞，－1)∪(－1，32
) 9．函数y ＝x 2－2的定义域是{－1,0,1,2}，则其值域是________．
解析：当x 取－1,0,1,2时，
y ＝－1，－2，－1,2，
故函数值域为{－1，－2,2}．
答案：{－1，－2,2}
10．求下列函数的定义域：
(1)y ＝－x 2x 2－3x －2；(2)y ＝34x ＋83x －2
. 解：(1)要使y ＝－x 2x 2－3x －2
有意义，则必须 ⎩⎪⎨⎪⎧
－x ≥0，2x 2－3x －2≠0，解得x ≤0且x ≠－12， 故所求函数的定义域为{x |x ≤0，且x ≠－12
}． (2)要使y ＝
3
4x ＋83x －2有意义，则必须3x －2＞0，即x ＞23， 故所求函数的定义域为{x |x ＞23
}． 11．已知f (x )＝
11＋x
(x ∈R 且x ≠－1)，g (x )＝x 2＋2(x ∈R )． (1)求f (2)，g (2)的值；
(2)求f (g (2))的值．
解：(1)∵f (x )＝11＋x
， ∴f (2)＝11＋2＝13
， 又∵g (x )＝x 2＋2，
∴g (2)＝22＋2＝6.
(2)由(1)知g (2)＝6，
∴f (g (2))＝f (6)＝11＋6＝17. 12．已知函数y ＝ax ＋1(a ＜0且a 为常数)在区间(－∞，1]上有意义，求实数a 的取值范围．
解：函数y ＝ax ＋1(a ＜0且a 为常数)．
∵ax ＋1≥0，a ＜0，∴x ≤－1a
， 即函数的定义域为(－∞，－1a
]． ∵函数在区间(－∞，1]上有意义，
∴(－∞，1]⊆(－∞，－1a
]， ∴－1a
≥1，而a ＜0，∴－1≤a ＜0. 即a 的取值范围是[－1,0)．。