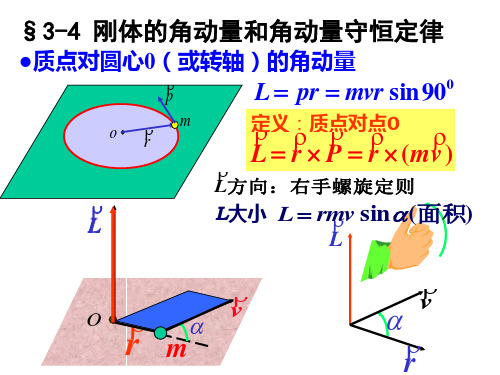
质点、刚体的角动量、角动量守恒定律
第三章 4刚体角动量和守恒
自转初每秒钟 30 - 40次 4 秒自转一次老化的 磁场地球的108~1015倍 产生脉冲波(波霎)周期 0.03~4.3秒 一亿吨/cm3 表面光滑
▲行星状星云,中间的白点可能是中子星
【例15】 一匀质细棒长为l ,质量为m,可绕通过其端点 O的水平轴转动,图示。当棒从水平位置自由释放后,它
【例13】 质量为 m1长为 l 的细杆,静止平放在粗糙的水平面上, 细杆与水平面之间的摩檫系数为 μ ,可绕通过其端点O,且与
平面垂直的固定轴转动。 另有一水平运动的质量为 m2 的滑快, 从侧面垂直与杆的方向,与杆的另一端A 碰撞。已知滑块碰撞
o 前、后的速度分别为
檫力矩。 :(2)
v1 与 v 2 求:(1)细杆转动时受到的摩 杆从开始转动到停止所需的时间.
●地球的自转角速度变化? 变慢!
问题2 水平圆盘边上,站有一人质量为m,圆盘半径为R, 转动惯量为J,以角速度ω转动,如果此人从旁边径直走 到圆盘中心,求:角速度的变化和系统动能的变化?
O
A知识点窍:相对运动和L守恒(系统受的合外力矩为零),
L Li 常量C ,转动动能 E转 J 2 2
B逻辑推理:速度对惯性参照系,行走过程中摩擦力过转轴 (Mf=0),重力矩与L垂直就是对L没有贡献,即M合=0
C解:(1)求摩擦力矩 取微元dx
dm=dx= m1 dx
x
m1 l
l
dx
对o点的力矩元 dM0 dM0 = x dmg
dM0
=
m1 l
g
x
dx
x
M0 =
l m1g x dx
0l
1 2
m1gl
【例13】 质量为 m1长为 l 的细杆,静止平放在粗糙的水平面 上,细杆与水平面之间的摩檫系数为 μ ,可绕通过其端点O,
角动量守恒定律的公式

角动量守恒定律的公式
1. 角动量守恒定律公式。
- 对于质点,角动量L = r× p(其中r是质点相对于某参考点的位矢,p = mv 是质点的动量,×表示矢量叉乘)。
- 在合外力矩M = 0时,角动量守恒,即L_1 = L_2。
- 对于定轴转动的刚体,角动量L = Iω(其中I是刚体对轴的转动惯量,ω是刚体的角速度)。
当合外力矩M = 0时,I_1ω_1=I_2ω_2。
2. 相关知识点(人教版教材相关内容补充)
- 转动惯量。
- 对于离散质点系,I=∑_im_ir_i^2,其中m_i是第i个质点的质量,r_i是该质点到转轴的垂直距离。
- 对于质量连续分布的刚体,I = ∫ r^2dm。
不同形状的刚体转动惯量有不同的计算公式,例如,对于质量为m、半径为R的均匀圆盘绕通过圆心且垂直于盘面的轴转动,其转动惯量I=(1)/(2)mR^2;对于质量为m、长为l的细棒绕通过中心且垂直于棒的轴转动,I=(1)/(12)ml^2。
- 角动量定理。
- 对于质点,M=(dL)/(dt)(M是合外力矩),这表明质点所受合外力矩等于它的角动量对时间的变化率。
- 对于刚体定轴转动,M = Iα(α是角加速度),结合L = Iω也可推导出
M=(dL)/(dt)。
4-3角动量 角动量守恒定律

M L 常量
ex
角动量守恒定律是自然界的一个基本定律.
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律 电荷守恒定律 质量守恒定律 宇称守恒定律等
许多现象都可 以用角动量守恒来 说明. 花样滑冰 跳水运动员跳水
跳水运动员
茹可夫斯基凳
例3 质量很小长度为l 的均匀细杆,可 绕过其中心 O并与纸面垂直的轴在竖直平面 内转动.当细杆静止于水平位置时,有一只 小虫以速率 v 0 垂直落在距点O为 l/4 处,并背 离点O 向细杆的端点A 爬行.设小虫与细杆 的质量均为m.问:欲使细杆以恒定的角速 度转动,小虫应以多大速率向细杆端点爬行?
解 设飞船在点 A 的速度 v 0 , 月球质 量 mM ,由万有引力和 牛顿定律
vB
R
B
vA
v0
v
O h A
u
v mM m G m 2 ( R h) Rh mM g G 2 2 R R g
2 0
v0 (
Rh
)
12
1 612 m s
1
质量 m' 在 A 点和 B 点只受有心力作用 , 角动量守恒
d r mv r F dt
所以
dL M= dt
dL M dt
t2
t1
M dt L2 L1
冲量矩
t1
t2
M dt
对同一参考点O,质点所受的冲量矩 等于质点角动量的增量.——质点的角动 量定理
3、质点的角动量守恒定律
若质点所受的合外力矩为零,即 M=0,
4-3 角动量 角动量守恒定律
力对时间累积效应: 冲量、动量、动量定理. 力矩对时间累积效应: 冲量矩、角动量、角动量定理.
《大学物理》34刚体定轴转动的角动量定理角动量守恒定律.

设子弹射入后杆起摆的角速度为ω,则有:
1 m v 0 a ( ML2 ma 2 ) 3
子弹射入后一起摆动的过程只有重力做功,故系统机 械能守恒。
1 1 L 2 2 2 ( ML ma ) mga (1 cos60 ) Mg (1 cos60 ) 2 3 2
1
2.刚体的角动量定理及守恒定律
刚体所受合外力矩与角加速度关系为
d M J J dt
利用角动量表示
dJ dL M dt dt
刚体绕定轴转动时,作用于刚体的合外力矩等于刚 体绕此轴的角动量对时间的变化率。这是刚体角动 量定理的一种形式。
当合外力矩为零时
d J dL M dt dt
如果质点所受合外力矩为零,则质点的角动量保持不变, 这就是质点的角动量守恒定律。
1. 质点角动量定理及守恒定律
例:我国第一颗人造地球卫星沿椭圆轨道绕地球运动,地心为该椭圆 的一个焦点。已知地球半径 R ,卫星的近地点到地面距离 l ,卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ,求它在远地点速率 v2 。
3.4刚体定轴转动的角动量定理 角动量守恒定律
一、冲量矩 角动量 1.冲量矩
定义:力矩与力矩作用时间的乘积称为冲量矩。
数学表达:
M dt
0
t
2.角动量
整个刚体的角动量就是刚体上每一个质元的角动 量——即每个质元的动量对转轴之矩的和。
2.1质点的角动量
o
r
v
o
L
m
L
r
m
J 恒量
如果物体所受合外力矩为零,或不受外力矩的作用, 物体的角动量保持不变,这就是角动量守恒定律。
刚体的角动量和角动量守恒定律

如图所示,刚体绕转轴 Oz 以角速度 ω 转动。 由于刚体上的每个质元都绕转轴 Oz 做圆周运动,因此都具有一定的角动量。 设第 i 个质元的质量为 mi ,它到转轴的垂直位矢为 ri ,线速度为 vi ,则该质元对转轴的角动量 Li 大 小为 Li miviri miri2
刚体的角动量和角动量守恒定律
计转轴处的摩擦力和空气阻力)。
【解】 把人和转台看作一个系统,系统不受外力矩作用,
其角动量守恒,即 mR2 1 MR2 0
2
解得 2 m
M 负号表示转台转动的方向与人跑动的方向相反。
大学物理
大学物理
刚体的角动量和角动量守恒定律 1.1 角动量
1.质点的角动量
如图所示,质量为 m 的质点相对于某一参考点 O 运动,在某一时刻,质点相对于参考点 O 的位矢为 r, 质点的速度为 v,质点的动量为 p mv ,则位矢 r 与动量 p 的矢积称为质点相对于 O 点的角动量(动量矩), 用 L 表示,即 L r p r mv
m2 Lv0
Байду номын сангаас
m2 Lv
1 3
m1L2
根据线量与角量的关系 v L ,
可解得子弹和杆一起运动时的角速度 ω 为 3m2v0
(3m2 m1)L
刚体的角动量和角动量守恒定律
, ,
,
,
例题讲解 5
如图所示,质量为 M、半径为 R 的转台,可绕过中心的竖直轴转动。质量为 m 的人站在台的边缘。最
初人和台都静止,后来人在台的边缘开始跑动。设人相对地面的角速度为 ω,求转台转动的角速度 (不
刚体的角动量和角动量守恒定律 1.1 角动量
1.质点的角动量
大学物理 第三章 角动量守恒定律 刚体汇总

解:棒下摆为加速过程,外
力矩为重力对O的力矩。在 O
棒上取质元dm,当棒处在下
摆 角时,棒 的重力矩为:
M l d(mg)
l
设 m
L
L
gl sin(
)dl
1
mgL cos
0
2
2
X dm
dmg
J 1 mL2
3
M
1 mgL cos
2
3g cos
J
1 mL2
整个刚体绕轴的角动量为所有质元角动量之和:
L Li ( miri2 )
i
i
令:J miri2 称为刚体对轴的转动惯量。
i
则刚体对轴的角动量为:L J
力对转轴的力矩
f 在转动平面内 Mz r f
Mz fr sin
Z
Mz
Or
d
P
f
转动平面
方向如图
例题P40:3-3
f 不在转动平面内,有时间可以补讲。
(2)通过棒的中点并与棒垂直的转轴的转动惯量。
解:(1) m
l
dm dx
x dx
x l
J x2dm l x2dx 1l3 1 ml2
0
33
例1、求质量为m、半径为R的均匀圆环的转动 惯量。轴与圆环平面垂直并通过圆心。
解: J R2dm R2 dm mR2
OR dm
例2、求质量为m、半径为R、厚为l 的均匀圆 盘的转动惯量。轴与盘平面垂直并通过盘心。
平行轴定理
若有任一轴与过质心的轴平行,相距
为d,刚体对其转动惯量为J,则有:
l
J=JC+md2。
z
刚体的质心: xc
刚体角动量和角动量守恒定律

• 刚体角动量介绍 • 角动量守恒定律 • 刚体角动量的应用 • 刚体角动量与现实世界的关系 • 刚体角动量与未来科技的关系
01
刚体角动量介绍
刚体的定义
刚体
在运动过程中,其内பைடு நூலகம்任意两点 间的距离始终保持不变的物体。
刚体的特性
在刚体的运动过程中,其形状和 大小不会发生变化,只改变其位 置和姿态。
刚体的角动量定义
角动量
一个物体绕固定点旋转时所具有的动 量,其大小等于物体质量、速度和旋 转半径的乘积。
刚体的角动量
当刚体绕固定点旋转时,其角动量等 于刚体质量、旋转轴上的速度和旋转 半径的乘积。
刚体的角动量的计算公式
角动量计算公式:L = mvr
其中,L表示角动量,m表示刚体的质量,v表示刚体上任意一点相对于旋转轴的速度,r表示该点到旋转 轴的距离。
证明方法一
证明方法二
证明方法三
03
刚体角动量的应用
在物理实验中的应用
陀螺仪
刚体角动量在陀螺仪中有着重要 的应用,通过测量旋转轴的角速 度,可以确定物体的方向和姿态。
摆锤实验
通过观察摆锤的摆动,可以验证 刚体角动量守恒定律,了解力矩 对刚体角动量的影响。
磁力矩实验
利用磁力矩对刚体角动量的作用, 可以研究刚体的旋转运动和磁场 的相互作用。
角动量守恒定律在设计和优化机械系 统,如电机、陀螺仪和风力发电机等 方面有广泛应用。
对体育运动的影响
在体育运动中,角动量守恒定律有助于理解旋转运动,如滑冰、花样滑冰和乒乓 球等项目的旋转动作和技巧。
运动员通过合理运用角动量守恒定律,可以调整旋转速度、方向和稳定性,提高 运动表现和竞技水平。
大学物理学教程马文蔚43角动量角动量守恒定律

解: 碰撞前M落在A点的速度
vM (2gh)1 2
碰撞后的瞬间, M、N具有相同的线速度
N
u l
B
2
M
h
C
A
l
l/
2
M、N和跷板系统,角动量守恒
mvM
l 2
J
2mu
l 2
1 12
ml 2
1 2
ml 2
第四章 刚体的转动
得
mvMl 2 ml 2 12 ml2
d
例8: 两只同重量的猴子,一只用力往上爬,另一只不爬,若滑轮重 量忽略不计,问哪一只先到达滑轮顶端?
(同时到达)
第四章 刚体的转动
例9: 如图,一质量为 m的均匀圆盘,半径为 R,放在一粗糙的 水平面上,圆盘可绕通过其中心O 的竖直光滑轴转动,开始时, 圆盘静止,有一质量为m0 的子弹以速度0 垂直打入圆盘边缘并嵌 在盘边上,求(1)子弹击中圆盘后,盘获得的角速度;(2)经多
得 3m
2Ml
m
例5 已知 M , L, m, ,求
解: 子弹与杆碰撞过程,系统角动量守恒
Lm Lm 1 ML2
23
得 3m
2ML
第四章 刚体的转动
O
Ml
ห้องสมุดไป่ตู้
/2
O
L
M
2
m
第四章 刚体的转动
例6: 人造地球卫星绕地球作椭圆轨道运动,求远地点的速度与近
地点的速度的比值
.
m1(l1 R) m2 (l2 R)
解:小虫与细杆的碰撞视为完全非弹性碰撞,碰撞前后系统角动 量守恒
大学物理第5章角动量守恒定律
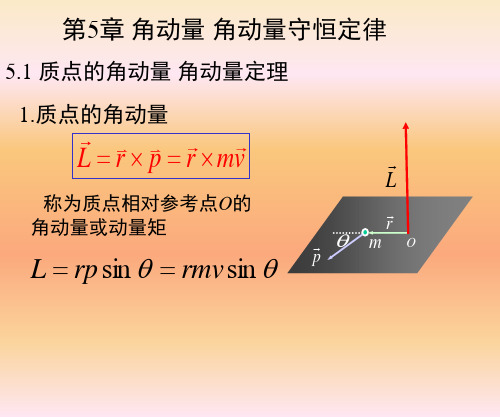
1 ml2 3
l
m
m 1.73
z2
o
l 2
G
JZ2
1 ml2 3
RGC G 不是质心
转动惯量的计算
例: 求半径为 R,总质量为 m的均匀圆盘绕垂直于盘面
通过中心轴的转动惯量 如下图:
解:
质量面密度
m R 2
J z r 2dm R r 2ds 0
Z ds
R r 2 2rdr 0
R r 2 m 2rdr
a 法向分量
an
v2 r
r 2
O
匀变速直线运动
匀变速定轴转动
v dS dt
a dv dt
v v0 at
S
v0t
1 2
at 2
v2 v02 2aS
d
dt
d
dt
0 t
0t
1t2
2
2 02 2
5.4 定轴转动刚体的角动量定理
1.刚体对转轴的力矩和角动量
z
角动量守恒
质点系的角动量定理
M J
4g
t
3 4
R
1 2
gt
2
LA
r
p
1 2
mpt3gmvg
mgt 0
orRA r源自(2) 对 O 点的角动量m
mv
r r R
LO r p (R r) p R p R mgt
Rg
LO Rmgt
2. 质点的角动量定理
角动量的时间变化率
dL
d
(r
p)
dr
p
r
dp
r 表示从O到速度矢量 v 的垂直距离, 则有
r sin s rs 2
刚体定轴转动的角动量定理 角动量守恒定律.

l 1 l 2 2 mv0 m l m( ) 4 12 4
12 v 0 7 l
12 v 0 7 l
由角动量定理
dL d ( I ) dI M dt dt dt
即
d 1 dr 2 2 mgr cos ( ml mr ) 2mr dt 12 dt
※ 刚体定轴转动的角动量定理和角动量守恒定律
刚体定轴转动对轴上一点的角动量(自学) :
结 论:
一般情况下,刚体定轴转动对轴上一点的角动 量并不一定沿角速度(即转轴)的方向,而是与其 成一定夹角;但对于质量分布与几何形状有共同对 称轴的刚体,当绕该对称轴转动时,刚体对轴上任 一点的角动量与角速度的方向相同.
4 m 2m M
[讨论] ① M>>m ② M<<m
作 业:
7.4.3. 思 考: 7.4.1.
例:
已知均匀直杆(l ,M),一端挂在光滑水平轴上,开始时静止 在竖直位置,有一子弹(m.vo)水平射入而不复出。求杆与子弹 一起运动时的角速度.
解:
子弹进入到一起运动,瞬间完成.
I
i i
i
const.
但角动量可在内部传递。
3 刚体定轴转动的角动量守恒定律 若 M 0 ,则 讨论
守 恒条件:
L I 常量
M 0
若 I 不变, 不变;若 I 变, 也变,但 L I 不变. 内力矩不改变系统的角动量. 在冲击等问题中
M in M ex L 常量
现在讨论力矩对时间的积累效应。
※ 现在讨论力矩对时间的积累效应。 质点系: dL 对点: M 外
dt
5 刚体的角动量定理和角动量守恒定律

角动量守恒定律
一.刚体的角动量定理
dL 刚体转动定理的 M dt 可以改写为 Mdt dL
对上式积分,得 式中 t
t2
1
t2
t1
t2 Mdt dL L2 L1
t1
Mdt
叫做合外力矩在
t 2 t1
时间内的冲量矩。上式表明:刚体所受合外力矩 的冲量矩,等于刚体在这段时间内刚体的角动量 的增量,这就是刚体的角动量定理。 在SI制中,冲量矩的单位式 N m s
I1 2kg m2 。 在外力推动后, 此系统开始以 n1 15 转/分转动, 转动中摩擦力矩忽略不计。
2 I 0 . 80 kg m 当人的两臂收回, 使系统的转动惯量就为 2 时, 它的转速 n2
。
光滑的水平桌面上有一长 2l、质量为 m 的匀质细杆,可绕过其中心、垂直于杆的竖直轴自 由转动。开始杆静止在桌面上。有一质量为 m 的小球沿桌面以速度 v 垂直射向杆一端,与 杆发生完全非弹性碰撞后,粘在杆端与杆一起转动。求碰撞后系统的角速度。
2 rel dt
0 T T 0
M 2m M
2M 因此,在此时间内,人相对ห้องสมุดไป่ตู้地面转过的角度为0 d t M 2m
T
M 2m M 2m T dt dt 0 M M
转台相对于地面转动的角度为
T
0
2m T 4m dt dt M 0 M 2m
2
二.角动量守恒定律 由刚体的角动量定理可见,当刚体所受的合外 力矩为零,则
L I 常量
3
上式说明,当刚体所受的合外力矩为零,或者不受外 力距的作用时,刚体的角动量保持不变,这就是角动量 守恒定律。 必须指出,这个定律不仅对一个刚体有效,对转动 惯量I会变化的物体,或者绕定轴转动的力学系统仍然 成立。如果转动过程中,转动惯量保持不变,则物体 以恒定的角速度转动;如果转动惯量发生改变,则物 体的角速度也随之改变,但两者之积保持恒定。 应用角动量守恒定律时,还应该注意的是,一个系 统内的各个刚体或质点的角动量必须是对于同一个固 定轴说的。
角动量及其守恒
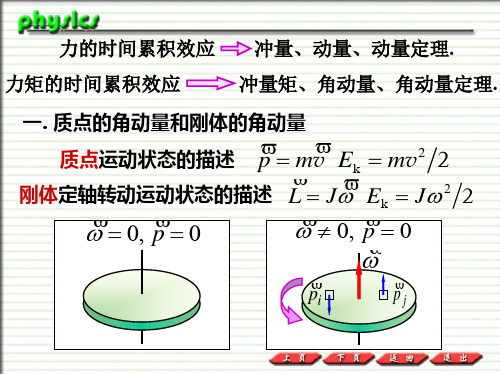
练习 关于力矩有以下几种说法:
(1)内力矩不会改变刚体对某个轴的角动量; (2)作用力和反作用力对同一轴的力矩之和必为零; (3)质量相等, 形状和大小不同的两个刚体, 在相同 力矩的作用下, 他们的角加速度一定相等; 在上述说法中
(A) 只有(2)是正确的;
(B)(1)、(2)是正确的;
(C)(2)、(3)是正确的;
(D)(1)、(2)、(3)都是正确的.
练习
人造地球卫星, 绕地球作椭圆轨道运动, 地球 在椭圆的一个焦点上, 则卫星的:
(A) 动量不守恒, 动能守恒; (B) 动量守恒, 动能不守恒; (C) 角动量守恒, 动能不守恒; (D) 角动量不守恒, 动能守恒.
力的时间累积效应 冲量、动量、动量定理.
力矩的时间累积效应
冲量矩、角动量、角动量定理.
一. 质点的角动量和刚体的角动量
刚体定质轴点转运动动运状动态状的态描的述描述pLmvJEk
mv2 2
Ek J 2
2
0, p 0
0, p 0
pi
pj
1. 质点角动量
质点在垂直于 z 轴平面上
以角速度 作半径为 的r
以子弹和沙袋为系统 以子弹和杆为系统
动量守恒;
动量不守恒;
角 .
机械能不守恒 .
圆锥摆系统 动量不守恒; 角动量守恒; 机械能守恒 .
练习 一人握有两只哑铃, 站在一可无摩擦地转动
的水平平台上, 开始时两手平握哑铃, 人、哑铃、平台 组成的系统以一角速度旋转, 后来此人将哑铃下垂于 身体两侧, 在此过程中, 系统
角动量 角动量守恒
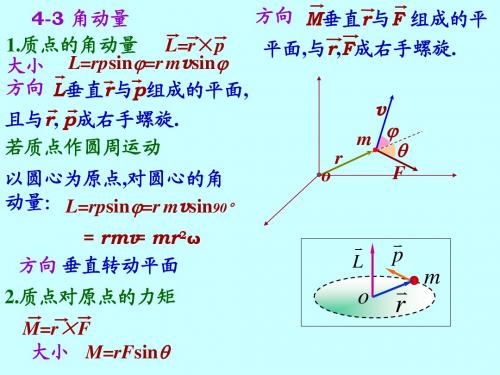
4.8
0–lgsind =vvdv
–v2/2=lg(cosθ–1)
θ
0
R 例6. 半径R, 质量M的均匀水 解: 小车与 M r m 平转台可绕中心轴自由转动, 转盘受重力 开始时静止.今有质量m的玩 与轴的支撑 具汽车静止开始在转台上作 力都平行转 半径r(r<R)的圆运动, 求汽车 轴,力矩在轴方向上无分量, 相对转台走一周时,转台转过 故小车与转盘系统对转轴角 的角度. 动量守恒.用角标0,1,2分别表 示地,转盘和小车,设u=v21,有 ω20=ω21+ω10 mvr+Iω10=0
方向:沿轴向 所有内力矩矢量和为零 所有质元的角动量方向相同 L=∑miri2 刚体所受力矩等于外力矩 L=(∑miri2) =J 的矢量和 M=∑ri×Fi L的方向:沿轴向
3.刚体的角动量定理 第i个质元 Mi=dLi/dt
4.角动量守恒定律
对于刚体定轴转动. 求和 ∑Mi=∑(dLi/dt) 条件: M外=0 结论: L=恒量 讨论: =d(∑Li)/dt (1)内力矩不改变系统的角 得 M =dL/dt 动量,角动量守恒是自然 界的一条基本定律 刚体合外力矩M 等于 (2)当M外<<M内时, L恒量; 刚体角动量L 对时间 的变化率 (3)当J=恒量时, ω=恒量 t L ω大小方向不变(如回转仪); Mdt = dL=L2–L1 t L (4)当J改变时(内力作功使质 =J2ω2–J1ω1 量重新分布),ω大小改变,但 合外力矩的冲量矩等于刚 方向不变;
7.8
L
p
o
m r
质点的角动量定理: (dr / dt ) p r (dp / dt ) 对同一参考点 ,质点 v pr F 所受的冲量矩等于质点
[理学]05-4刚体的角动量定理和角动量守恒定律
![[理学]05-4刚体的角动量定理和角动量守恒定律](https://img.taocdn.com/s3/m/eba9a1471eb91a37f0115c13.png)
双旋翼直升机不需要尾桨,它通过一对转向相反的螺 旋桨,保持系统的总角动量仍然为零
并轴双旋翼直升机通过在同轴心的内外两轴上安装 一对对转的螺旋桨来防止机身反向打转
鱼雷在其尾部也装有对转螺旋桨,其目的也是 为了消除单螺旋桨造成鱼雷自身的反转问题
为什么同手同脚地走路或 跑步会使人觉得别扭呢? 当一侧的腿向前跨出时,另 一侧的臂必须同时向前摆出, 这样躯干的上端(肩)和下 端(髋)彼此向相反方向扭 转,而躯干的中段和头部则 大体保持在原来位置上,才 可以保证整个身体对于竖直 轴的角动量保持为零 腿臂的动作正确、协调配合,对加大步长、提高步频 都有一定作用,因而对提高跑步速度有明显影响
对绕定轴转动的可变形物体而言,在不同状态下
物体对转轴的转动惯量可能不同,但是如果它所 受合外力矩为零,那么它的角动量也将保持不变
花样滑冰运动员利用四肢的伸缩改变自身的 转动惯量,可以改变绕自身竖直轴的角速度
合外力矩为零不仅是绕定轴转动刚体角动量守恒的
条件,也是任何质点系对角动量守恒的条件
l
M
m
v0
系统的角动量守恒
mv0l J
1 2 2 J ? Ml ml 3
l
M
棒的转 子弹的转 动惯量 动惯量
m
v0
mv0 M ( m)l 3
例1 一质量为M,长为l 的均质细棒,可绕过其顶端的 水平轴自由转动。当杆静止时,一质量为m的子弹以 水平速度v0射入细杆底端并穿出,穿出后子弹速度损 失3/4,求子弹穿出后棒的角速度 O 取子弹和细杆作为系统,在子弹射入 棒端并从棒中穿出的过程中,子弹与 M 细杆之间的作用力为内力,转轴上的 l 作用力和重力不产生力矩,系统所受 m 外力矩为零,系统角动量守恒
5.5 刚体定轴转动的角动量守恒定律

周期约1.19 s
脉冲星的精确周期性信号
J z const .
星体不被惯性离心力甩散,必须满足条件:
GM 4 2 3 R , ( M R ) 2 3 R
3 2 3 11 3 10 kg / m 4 G GT 2 3 3
恒星 红巨星 中子星 脉冲星是高速旋转的中子星。
5.5 刚体定轴转动的角动量定理和角动量守恒定律
一、角动量定 理 质点系 对点 对轴 刚体
M外
dL dt
Lz J z
M 外z dLz dt
d ( J z ) Mz dt
刚体的角动量定理
二、刚体定轴转动的角动量守恒定律
d ( J z ) Mz dt
M 外z 0
J z
t2 M 外z t1
d t J z 2 J z 1
——刚体定轴转动的角动量定理
【例题】一质量为 m 的子弹以水平速度射入一静止 悬于顶端长棒的下端,穿出后速度损失 3/4,求子弹穿出后棒的角速度 解:棒对子弹的阻力为 f
M
l
对子弹 fdt m( 0 ) m0 4
Fe 7.8 10 kg / m 白矮星 黑洞
三、角动量定理的另一形式 对点
M外
冲量矩
t2 M外 t1
dL dt
M外 d t d L
d t L2 L1
t2
t1
M 外 d t 力矩对时间的积累效应
刚体定轴转动
d ( J z ) Mz dt
子弹对棒的反作用力
m
f3Leabharlann 对棒的冲量矩0
3 f ldt l f dt l fdt lm0 J 4 9m0 3 lm0 4J 4Ml
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
010-质点、刚体的角动量、角动量守恒定律1. 选择题1. 一质点作匀速率圆周运动时,[ ](A) 它的动量不变,对圆心的角动量也不变. (B) 它的动量不变,对圆心的角动量不断改变. (C) 它的动量不断改变,对圆心的角动量不变.(D) 它的动量不断改变,对圆心的角动量也不断改变. 答案:(C )2. 刚体角动量守恒的充分而必要的条件是[ ](A) 刚体不受外力矩的作用. (B) 刚体所受合外力矩为零. (C) 刚体所受的合外力和合外力矩均为零.(D) 刚体的转动惯量和角速度均保持不变. 答案:(B )3. 地球绕太阳作椭圆轨道运动,太阳的中心在椭圆的一个焦点上,把地球看作一个质点,则地球的[ ](A) 动能守恒. (B) 动量守恒. (C) 对太阳中心的角动量守恒.(D) 对太阳中心的角动量守恒,动能守恒. 答案:(C )4. 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示.今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?[ ](A)角动量从小到大,角加速度从大到小. (B)角动量从小到大,角加速度从小到大. (C)角动量从大到小,角加速度从大到小. (D)角动量从大到小,角加速度从小到大. 答案:(A )5. 人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的[ ](A)动量不守恒,动能守恒. (B)动量守恒,动能不守恒.(C)对地心的角动量守恒,动能不守恒. (D)对地心的角动量不守恒,动能守恒. 答案:(C )6. 人造地球卫星绕地球作椭圆轨道运动,卫星轨道近地点和远地点分别为A 和B .用L 和E K 分别表示卫星对地心的角动量及其动能的瞬时值,则应有[ ] (A) L A >L B ,E KA >E kB . (B) L A =L B ,E KA <E KB . (C) L A =L B ,E KA >E KB . (D) L A <L B ,E KA <E KB . 答案:(C )7. 如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统[ ](A) 只有机械能守恒. (B) 只有动量守恒. (C) 只有对转轴O 的角动量守恒. (D) 机械能、动量和角动量均守恒. 答案:(C )8. 一块方板,可以绕通过其一个水平边的光滑固定轴自由转动.最初板自由下垂.今有一小团粘土,垂直板面撞击方板,并粘在板上.对粘土和方板系统,如果忽略空气阻力,在碰撞中守恒的量是[ ](A) 动能. (B) 绕木板转轴的角动量. (C) 机械能. (D) 动量. 答案:(B )9. 将一质量为m 的小球,系于轻绳的一端,绳的另一端穿过光滑水平桌面上的小孔用手拉住.先使小球以角速度ω1在桌面上做半径为r 1的圆周运动,然后缓慢将绳下拉,使半径缩小为r 2,在此过程中小球的[ ](A)速度不变. (B)速度变小. (C)速度变大. (D)速度怎么变,不能确定. 答案:(C )10. 如图所示,钢球A 和B 质量相等,正被绳牵着以角速度ω绕竖直轴转动,二球与轴的距离都为r 1.现在把轴上环C 下移,使得两球离轴的距离缩减为r 2.则钢球的角速度[ ] (A)变大. (B )变小. (C)不变.(D)角速度怎么变,不能确定. 答案:(A )11. 一个物体正在绕固定光滑轴自由转动,[ ] (A)它受热膨胀或遇冷收缩时,角速度不变. (B)它受热时角速度变大,遇冷时角速度变小. (C)它受热或遇冷时,角速度均变大. (D)它受热时角速度变小,遇冷时角速度变大. 答案:(D )12. 花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为J 0,角速度为ω0.然后她将两臂收回,使转动惯量减少为31J 0.这时她转动的角速度变为[ ] (A)31ω0. (B) ()3/1 ω0. (C) 3 ω0. (D) 3 ω0. 答案:(D )13. 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心.随后人沿半径向外跑去,在人跑向转台边缘的过程中,转台的角速度[ ](A) 不变. (B) 变小. (C) 变大. (D)不能确定角速度是否变化. 答案:(B )14. 人造地球卫星,绕地球作椭圆轨道运动,地球的中心在椭圆的一个焦点上,设地球的半径为R ,卫星的近地点高度为R ,卫星的远地点高度为2R ,卫星的近地点速度为1v ,则卫星的远地点速度2v 为[ ] (A)12v . (B) 121v . (C) 132v . (D) 123v . 答案:(C )15. 将一质量为m 的小球,系于轻绳的一端,绳的另一端穿过光滑水平桌面上的小孔用手拉住.先使小球以角速度ω1在桌面上做半径为r 1的圆周运动,然后缓慢将绳放松,使半径扩大为2 r 1 ,此时小球做圆周运动的角速度为[ ](A)1ω. (B)121ω. (C) 12ω. (D) 141ω. 答案:(D )16. 体重、身高相同的甲乙两人,分别用双手握住跨过无摩擦轻滑轮的绳子各一端.他们从同一高度由初速为零向上爬,经过一定时间,甲相对绳子的速率是乙相对绳子速率的两倍,则到达顶点的情况是[ ](A)甲先到达. (B)乙先到达. (C)同时到达. (D)谁先到达不能确定. 答案:(C )17. 光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O 自由转动,其转动惯量为31mL 2,起初杆静止.桌面上有两个质量均为m 的小球,各自在垂直于杆的方向上,正对着杆的一端,以相同速率v 相向运动,如图所示.当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为[ ] (A)L 32v . (B) L 54v . (C) L 76v . (D) L98v . 答案:(C )18. 如图所示,一水平刚性轻杆,质量不计,杆长l =20 cm ,其上穿有两个小球.初始时,两小球相对杆中心O 对称放置,与O 的距离d =5 cm ,二者之间用细线拉紧.现在让细杆绕通过中心O 的竖直固定轴作匀角速的转动,转速为ω 0,再烧断细线让两球向杆的两端滑动.不考虑转轴的和空气的摩擦,当两球都滑至杆端时,杆的角速度为[ ] (A) 2ω 0. (B)ω 0. (C)21 ω 0. (D)041ω. 答案:(D )19. 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台边缘.随后人沿半径向转台中心跑去,当人到达转台中心时,转台的角速度为[ ](A) 02ωmR J J +. (B) 02ωJ mR J +. (C) 02ωmRJ. (D) 0ω. 答案:(B )2.填空题1. 一个刚体绕轴转动,若刚体所受的合外力矩为零,则刚体的________________守恒. 答案:角动量O v俯视图2. 长为l 的杆如图悬挂.O 为水平光滑固定转轴,平衡时杆竖直下垂,一子弹水平地射入杆中.则在此过程中,由_____________组成的系统对转轴O的角动量守恒.答案:杆和子弹3. 质量为m 的质点以速度v ϖ沿一直线运动,则它对该直线上任一点的角动量为________. 答案:零4. 质量为m 的质点以速度v ϖ沿一直线运动,则它对直线外垂直距离为d 的一点的角动量大小是__________. 答案:mvd4. 一杆长l =50 cm ,可绕通过其上端的水平光滑固定轴O 在竖直平面内转动,相对于O 轴的转动惯量J =5 kg ·m 2.原来杆静止并自然下垂.若在杆的下端水平射入质量m =0.01 kg 、速率为v =400 m/s 的子弹并嵌入杆内,则杆的角速度为ω =__________________. 答案:0.4 rad/s5. 质量为0.05 kg 的小块物体,置于一光滑水平桌面上.有一绳一端连接此物,另一端穿过桌面中心的小孔(如图所示).该物体原以3 rad/s 的角速度在距孔0.2 m 的圆周上转动.今将绳从小孔缓慢往下拉,使该物体之转动半径减为0.1 m .则物体的角速度ω=_______________.答案:12 rad/s6. 如图所示,钢球A 和B 质量相等,正被绳牵着以ω0=4 rad/s 的角速度绕竖直轴转动,二球与轴的距离都为r 1=15cm .现在把轴上环C 下移,使得两球离轴的距离缩减为r 2=5 cm .则钢球的角速度ω =_ _ . 答案: 36 rad/s7. 哈雷慧星绕太阳的轨道是以太阳为一个焦点的椭圆.它离太阳最近的距离是r 1=8.75×1010 m ,此时它的速率是v 1=5.46×104 m/s .它离太阳最远时的速率是v 2=9.08×102 m/s ,这时它离太阳的距离是r 2= . 答案:5.26×1012 m8. 一质量为m 的质点沿着一条曲线运动,其位置矢量在空间直角座标系中的表达式为j t b i t a r ϖϖϖωωsin cos +=,其中a 、b 、ω 皆为常量,则此质点对原点的角动量L =________. 答案:m ω ab9. 如图所示,x 轴沿水平方向,y 轴竖直向下,在t =0时刻将质量为m 的质点由a 处静止释放,让它自由下落,则在任意时刻t ,质点对原点O的角动量L =__________________. 答案:mgbt10. 一飞轮以角速度ω0绕光滑固定轴旋转,飞轮对轴的转动惯量为J 1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍.啮合后整个系统的角速度ω=__________________. 答案:031ω11. 有一半径为R 的匀质圆形水平转台,可绕通过盘心O 且垂直于盘面的竖直固定轴OO '转动,转动惯量为J .台上有一人,质量为m .当他站在离转轴r 处时(r <R ),转台和人一起以ω1的角速度转动,如图.若转轴处摩擦可以忽略,问当人走到转台边缘时,转台和人一起转动的角速度ω2=__________________________.答案:()212mRJ mr J ++ω12. 一水平的匀质圆盘,可绕通过盘心的竖直光滑固定轴自由转动.圆盘质量为M ,半径为R ,对轴的转动惯量J =21MR 2.当圆盘以角速度ω0转动时,有一质量为m 的子弹沿盘的直径方向射入而嵌在盘的边缘上.子弹射入后,圆盘的角速度ω=______________. 答案:mM M 20+ω13. 在光滑的水平面上,一根长L =2 m 的绳子,一端固定于O 点,另一端系一质量m =0.5 kg 的物体.开始时,物体位于位置A ,OA 间距离d =0.5 m ,绳子处于松弛状态.现在使物体以初速度v A=4 m ·s -1垂直于OA 向右滑动,如图所示.设以后的运动中物体到达位置B ,此时物体速度的方向与绳垂直.则此时刻物体对O点的角动量的大小L B =_ _ _. 答案:s m N 1⋅⋅14. 在光滑的水平面上,一根长L =2 m 的绳子,一端固定于O 点,另一端系一质量m =0.5 kg 的物体.开始时,物体位于位置A ,OA 间距离d =0.5 m ,绳子处于松弛状态.现在使物体以初速度v A =4 m ·s -1垂直于OA 向右滑动,如图所示.设以后的运动中物体到达位置B ,此时物体速度的方向与绳垂直.则此时刻物体速度的大小v =_ . 答案:m/s 115. 一质量均匀分布的圆盘,质量为m ,半径为R ,放在一粗糙水平面上,圆盘可绕通过其中心O 的竖直固定光滑轴转动,圆盘和粗糙水平面之间摩擦力矩的大小为M f .开始时,圆盘的角速度为0ω,经过时间 =∆t 后,圆盘停止转动。
