刚体转动及角动量
合集下载
刚体定轴转动的角动量定理和角动量守恒定律
刚体定轴转动的角动量定理和角动量守恒定律
1、刚体定轴转动的角动量
刚体绕定轴转动的角动量等于刚体对该轴的转动惯量与角速度的乘积；方向与角速度的方向相同。
2、刚体定轴转动的角动量定理
（1）微分形式：刚体绕某定轴转动时，作用于刚体的合外力矩，等于刚体绕该定轴的角动量随时间的变化率。
（2）积分形式：当物体绕某定轴转动时，作用在物体上的冲量矩等于角动量的增量。
3、刚体定轴转动的角动量守恒定律
如果物体所受的合外力矩等于零，或者不受外力矩作用，物体的角动量保持不变。
练习：1角动量守恒的条件是 。
0=M 11222
1ωωJ J Mdt t t -=⎰刚体 ） 21J J ==ωJ 恒量
ωJ L =()ωJ dt d dt dL M ==。
§7.3 刚体定轴转动的角动量 转动惯量
a
2 a 2 h / t 自由落体公式：
r
I+I0
T m
T
mg
联系方程： a / r 2h / (rt 2 )
解得：
2 gt I mr 2 ( 1) I 0 2h
例3 已知：弧形闸门 例3 ， R，m， rc 2 3 R o(z) 2 Io 7 9 mR ，a 0.1g，
I x 2 dm x 2 dx
1 3 x 3
l 2 l 2
l 2 l 2
l/2 O
l/2 x dx
x
l3 12
m l3 m 1 将 代入, I ml 2 l 12 l 12
例2 均匀细棒绕垂直于通过左端点转轴的转动惯量。
解：任取一质元 dm dx
i i
I x mi yi2
i
I y mi xi2
i
因此， I
z
Ix Iy
特例：薄圆板 Ix =Iy=mR2/4
6、性质
转动惯量具有可加性 刚体对某轴的转动惯量
各个部分对转轴转动惯量的和
=
例
o l r
Io I杆o I盘o
1 I 杆o m l l 2 3 1 I 盘o mr r 2 mr (r l ) 2 2
T1
x T2 m2 a2 N
[解]建立坐标系，令 x 轴坚直向上， m1 取逆时针方向为正的转动方向。 a1
m1 g T1 m1a1
T2 m2 g m2a2
1 T1 R T2 R mR 2 2
T1
T2
mg
例1
a1 a2 R 由于绳子不可伸长且不打滑 ，
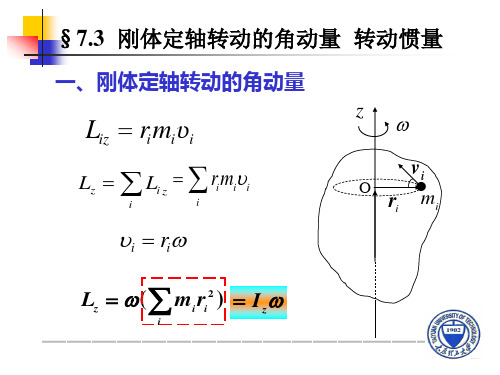
2 a 2 h / t 自由落体公式：
r
I+I0
T m
T
mg
联系方程： a / r 2h / (rt 2 )
解得：
2 gt I mr 2 ( 1) I 0 2h
例3 已知：弧形闸门 例3 ， R，m， rc 2 3 R o(z) 2 Io 7 9 mR ，a 0.1g，
I x 2 dm x 2 dx
1 3 x 3
l 2 l 2
l 2 l 2
l/2 O
l/2 x dx
x
l3 12
m l3 m 1 将 代入, I ml 2 l 12 l 12
例2 均匀细棒绕垂直于通过左端点转轴的转动惯量。
解：任取一质元 dm dx
i i
I x mi yi2
i
I y mi xi2
i
因此， I
z
Ix Iy
特例：薄圆板 Ix =Iy=mR2/4
6、性质
转动惯量具有可加性 刚体对某轴的转动惯量
各个部分对转轴转动惯量的和
=
例
o l r
Io I杆o I盘o
1 I 杆o m l l 2 3 1 I 盘o mr r 2 mr (r l ) 2 2
T1
x T2 m2 a2 N
[解]建立坐标系，令 x 轴坚直向上， m1 取逆时针方向为正的转动方向。 a1
m1 g T1 m1a1
T2 m2 g m2a2
1 T1 R T2 R mR 2 2
T1
T2
mg
例1
a1 a2 R 由于绳子不可伸长且不打滑 ，
物理-定轴转动刚体的角动量定理和角动量守恒定律
或 Lz = I = 恒量
当刚体相对惯性系中某给定转轴的合外力矩为 零时，该刚体对同一转轴的角动量保持不变。
——对转轴的角动量守恒定律
二、定轴转动中的角动量守恒
说明 1、 关于该守恒定律的条件：
Mz Miz 0
特别地，若每一个力的力矩均为零，即 则
二、定轴转动中的角动量守恒
M iz ri Fi sini 0 的几种情况
10
f
20
O1 R1 A
R2 O2 fB
随堂练习
当两圆柱接触处无相对滑动时，两者转速相反
10
20
O1 R1 A
R2 O2 B
且两者接触点的线速率相等！
二、定轴转动中的角动量守恒
由定轴转动的角动量定理
Mz
dLz dt
若刚体所受对转轴的合外力矩 M z 0，则有
dLz d ( I ) 0
dt
dt
二、定轴转动中的角动量守恒
(3) 对共轴非刚体系（其中各质元到转轴的距离可 变则）系：统的转动惯量可变，此时系统对转轴的角动量守恒，
即：I =恒量
• 特别地，若各质元的 保持一致，
Lz =I =恒量
当 I 增大时， 就减小； 当 I 减小时， 就增大 。
二、定轴转动中的角动量守恒
例如：花样滑冰运动员在冰面上旋转时 运动了角动量守恒定律
（1）
（2）
（3）
二、定轴转动中的角动量守恒
2、对转轴的角动量守恒定律的适用范围： • 不仅适用于刚体， • 也适用于绕同一转轴转动的任意质点系。
二、定轴转动中的角动量守恒
3、对转轴的角动量守恒的几种典型表现 (1) 对定轴刚体：I 不变， 大小和方向均不变；
角动量与刚体转动
这个例子表明，对于一个运动质点，在指定参考 系中，相对不同的固定参考点，有不同的角动量。质 点动量的方向不指向参考点时，它具有绕定点转动的 倾向，角动量不为零。如果质点作惯性运动 ( M 0) ， 质点角动量是守恒量。 [例题2] 质点 m 在 z 0平面内以速率 v 绕原点O逆时 针匀速转动。圆周轨道半径为 r ，求它相对于原点O 的角动量。 l 解：质点的动量矢量随时 变化，但它相对于原点O o r 的角动量却是个常矢量。 m v
立即得到
dl M dt
——称为质点的角动量定理
式中 M r F 是合外力相对惯性系中固定参考 点的力矩。
l r mv 是质点 m 相对于同一参考点的角
动量 。
表明相对于同一参考点，质点受到的合(外)力 矩等于质点角动量的时间变化率。
这个定理把质点所受的合外力矩和它角动量的瞬 时变化率联系起来了。 显然，若 M 0 则
r
m
F
在小球与 O点距离缩短的过程中，轨道是缓慢 收缩的螺旋线，径向拉力并不垂直于轨道切线， 正是拉力的切向分量使小球有切向加速度，速率 增加。
小球动能变化
Ek Ek 0 1 2 1 2 1 2 r02 mv mv0 mv0 ( 2 1) 2 2 2 r
小球轨道半径由 r0收缩到 r的过程中，拉力 F 所作的功
i
注意：外力矩与参考点的选择有关。
二、
系统内力性质的小结
⑴ 内力成对出现，所有内力的矢量和为零。 ⑵ 一对内力的功与参考系的选择无关，一对保守 内力的功还与路径无关且等于系统相关势能的减少， 非保守内力的功是系统机械能和其它形式能量转换 的量度。 ⑶ 在任一过程中，所有内力冲量的矢量和为零。 ⑷ 内力不影响系统质心的运动状态，不改变系统 的总动量。内力的冲量使总动量在系统内部重新分 配。 ⑸ 系统内力相对任一固定参考点的力矩矢量和 为零，内力矩不改变系统的总角动量。
3-3刚体定轴转动的角动量定理和角动量守恒定律
为零,角动量守恒
v0
v0
mv0l mv0l 0 mvl mvl J
v l
6 v0 7l
1 2 J ml 3
代入上式
L J const.
即转动过程中角动量(大小、方向)保持不变 角动量守恒定律比转动定律适用范围更广泛， 这里可以有
J 00 J11
但是
J 0 J1
讨论
1）角动量守恒条件
M 0
2）若 J 不变， 不变；若 J 变， 也变， 但
L J 不变.
3） 内力矩不改变系统的角动量. 4）在冲击等问题中 内力矩>>外力矩，角动量保持不变。 5）角动量守恒定律是自然界的一个基本定律.
力矩。合外力矩为 0 ，小球角动
量守恒 。 有：
N
mg
L = mvr = 恒量
即： m v1 r1 =m v2 r2
例2 光滑桌面上有一长2l，质量为m的细棒， 起初静止。两个质量m，速率v0的小球，如图 与细棒完全非弹性碰撞，碰撞后与细棒一起绕 中心轴转动，求系统碰撞后的角速度 解：系统的合外力矩
d( ) d( J ) dL M J J dt dt dt
刚体所受的(对轴的)外力矩等于刚体(对轴的) 角动量的时间变化率。 或写作
Mdt dL
t2 t1
对于一段时间过程有
t2
t1
Mdt dL L末 L初
三、定轴转动刚体的角动量守恒定律 如合外力矩等于零
6）转动系统由多个物体(刚体或质点)组成， 角动量守恒定律的形式为
i
J ii J i 0i 0
i
m
m
系统内各物体的角 动量必须是对同一 固定轴而言的。
刚体转动及角动量守恒ppt
匀直细杆对端垂轴旳
平行移轴定理
对质心轴旳转动惯量 对新轴旳转动惯量
质心
例如：
时
新轴对心轴旳平移量
新轴 质心轴
代入可得 端
匀质薄圆盘对圆心垂盘轴算旳 例
取半径为 微宽为 旳窄环带旳质量为质元
球体算例 匀质实心球对心轴旳 可看成是许多半径不同旳共轴 薄圆盘旳转动惯量 旳迭加 距 为 、半径为 、微厚为 旳薄圆盘旳转动惯量为
a = Rb
T2 – m2 g = m2a ( T1 – T2 ) R = Ib
及
I
=
1 2
mR2
得
b=
(m1-m2)g
R(m1+ m2+ m
2)
常量
故
由
m2
a
G2
m1
a
G1
(m1-m2)g
R(m1+ m2+ m 2)
t (m1-m2)g
g 2 (rad)
R(m1+ m2+ m 2)
两匀直细杆
q
转动定两律者瞬例时题角加五速度之比
与 时刻相应，何时
则何时
，
何时 恒定 则何时 恒定。
匀直 细杆一 端为轴 水平静 止释放
转动定律例转题动 二( T2 – T1 ) R = Ib
I=mR2 2
R
m
T2
T1
a
m2
m1
b
平动 m2 g – T2 = m2a
T2
T1
T1 – m1 g = m1a
线-角 a = Rb
T2
T1
联立解得
a
G2
力矩旳功算例 拨动圆盘转一周，摩擦阻力矩旳功旳大小
3-2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
第三章 刚体与流体
t2 t1
M
dt
J
J11
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
二、刚体定轴转动的角动量守恒定律
t2 t1
M
dt
J2
J1
若M 0 , 则J 常量
如果刚体所受合外力矩等于零，或者不受外力矩的 作用，则刚体的角动量守恒．此即角动量守恒定律．
茹科夫斯基转椅
第三章 刚体与流体
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
第三章 刚体与流体
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
例4 一根长度为L=0.60m的均匀棒，绕其端点O转
动时的转动惯量为J=0.12kgm2．当棒摆到竖直位置
时，其角速度为0=2.4rad/s．此时棒的下端和一质量
第三章 刚体与流体
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
M d L d(J) t2 M d t 2d(J)
dt
dt
t1
1
t2 t1
M
dt
J2
J1
——角动量定理
合外力矩的冲量矩（角冲量）
刚体所受合外力矩的冲量矩等于在这段时间内刚体 角动量的增量．
t1 t2时间内，J1 J2
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
3-2 刚体定轴转动的角动量 角动量定理 角动量守恒定律 一、刚体定轴转动的角动量 角动量定理
转动定律 M J J d d(J)
dt dt
令 L J，称为绕定轴转动刚体的角动量，则
M dL dt
刚体绕定轴转动时，作用于刚体的合外力矩 M 等于 刚体绕此轴的角动量 L 随时间的变化率.
t2 t1
M
dt
J
J11
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
二、刚体定轴转动的角动量守恒定律
t2 t1
M
dt
J2
J1
若M 0 , 则J 常量
如果刚体所受合外力矩等于零，或者不受外力矩的 作用，则刚体的角动量守恒．此即角动量守恒定律．
茹科夫斯基转椅
第三章 刚体与流体
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
第三章 刚体与流体
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
例4 一根长度为L=0.60m的均匀棒，绕其端点O转
动时的转动惯量为J=0.12kgm2．当棒摆到竖直位置
时，其角速度为0=2.4rad/s．此时棒的下端和一质量
第三章 刚体与流体
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
M d L d(J) t2 M d t 2d(J)
dt
dt
t1
1
t2 t1
M
dt
J2
J1
——角动量定理
合外力矩的冲量矩（角冲量）
刚体所受合外力矩的冲量矩等于在这段时间内刚体 角动量的增量．
t1 t2时间内，J1 J2
3 – 2 刚体定轴转动的角动量 角动量定理 角动量守恒定律
3-2 刚体定轴转动的角动量 角动量定理 角动量守恒定律 一、刚体定轴转动的角动量 角动量定理
转动定律 M J J d d(J)
dt dt
令 L J，称为绕定轴转动刚体的角动量，则
M dL dt
刚体绕定轴转动时，作用于刚体的合外力矩 M 等于 刚体绕此轴的角动量 L 随时间的变化率.
《大学物理》34刚体定轴转动的角动量定理角动量守恒定律.
矩为零故角动量守恒。
设子弹射入后杆起摆的角速度为ω，则有：
1 m v 0 a ( ML2 ma 2 ) 3
子弹射入后一起摆动的过程只有重力做功，故系统机 械能守恒。
1 1 L 2 2 2 ( ML ma ) mga (1 cos60 ) Mg (1 cos60 ) 2 3 2
1
2.刚体的角动量定理及守恒定律
刚体所受合外力矩与角加速度关系为
d M J J dt
利用角动量表示
dJ dL M dt dt
刚体绕定轴转动时，作用于刚体的合外力矩等于刚 体绕此轴的角动量对时间的变化率。这是刚体角动 量定理的一种形式。
当合外力矩为零时
d J dL M dt dt
如果质点所受合外力矩为零，则质点的角动量保持不变， 这就是质点的角动量守恒定律。
1. 质点角动量定理及守恒定律
例：我国第一颗人造地球卫星沿椭圆轨道绕地球运动，地心为该椭圆 的一个焦点。已知地球半径 R ，卫星的近地点到地面距离 l ，卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ，求它在远地点速率 v2 。
3.4刚体定轴转动的角动量定理 角动量守恒定律
一、冲量矩 角动量 1.冲量矩
定义：力矩与力矩作用时间的乘积称为冲量矩。
数学表达：
M dt
0
t
2.角动量
整个刚体的角动量就是刚体上每一个质元的角动 量——即每个质元的动量对转轴之矩的和。
2.1质点的角动量
o
r
v
o
L
m
L
r
m
J 恒量
如果物体所受合外力矩为零，或不受外力矩的作用， 物体的角动量保持不变，这就是角动量守恒定律。
设子弹射入后杆起摆的角速度为ω，则有：
1 m v 0 a ( ML2 ma 2 ) 3
子弹射入后一起摆动的过程只有重力做功，故系统机 械能守恒。
1 1 L 2 2 2 ( ML ma ) mga (1 cos60 ) Mg (1 cos60 ) 2 3 2
1
2.刚体的角动量定理及守恒定律
刚体所受合外力矩与角加速度关系为
d M J J dt
利用角动量表示
dJ dL M dt dt
刚体绕定轴转动时，作用于刚体的合外力矩等于刚 体绕此轴的角动量对时间的变化率。这是刚体角动 量定理的一种形式。
当合外力矩为零时
d J dL M dt dt
如果质点所受合外力矩为零，则质点的角动量保持不变， 这就是质点的角动量守恒定律。
1. 质点角动量定理及守恒定律
例：我国第一颗人造地球卫星沿椭圆轨道绕地球运动，地心为该椭圆 的一个焦点。已知地球半径 R ，卫星的近地点到地面距离 l ，卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ，求它在远地点速率 v2 。
3.4刚体定轴转动的角动量定理 角动量守恒定律
一、冲量矩 角动量 1.冲量矩
定义：力矩与力矩作用时间的乘积称为冲量矩。
数学表达：
M dt
0
t
2.角动量
整个刚体的角动量就是刚体上每一个质元的角动 量——即每个质元的动量对转轴之矩的和。
2.1质点的角动量
o
r
v
o
L
m
L
r
m
J 恒量
如果物体所受合外力矩为零，或不受外力矩的作用， 物体的角动量保持不变，这就是角动量守恒定律。
刚体绕定轴转动定律和角动量定理的表达式
刚体绕定轴转动定律和角动量定理的表达
式
刚体绕定轴转动定律和角动量定理是物理学中的一对重要定律，它们描述了刚体绕定轴转动的动力学过程。
首先，刚体绕定轴转动定律表明，当刚体绕定轴转动时，角加速度与作用于该刚体的合力成正比，且方向与合力方向一致，可用公式表示为：α=F/I，其中α为角加速度，F为合力，I为惯性矩。
其次，角动量定理表明，刚体绕定轴转动时，角动量的变化量等于作用于刚体的合力矩的积分，可以用公式表示为：ΔL=∫F·ds，其中ΔL为角动量的变化量，F为合力，ds为沿着转动轴的增量。
这两个定律对刚体绕定轴转动的过程有着重要的解释作用。
它们揭示了角加速度与合力之间的关系，以及角动量的变化量与合力矩之间的关系。
同时，它们也为刚体绕定轴转动的动力学研究提供了重要的参考依据，从而为我们更好地理解刚体绕定轴转动的动力学过程提供指导。
总之，刚体绕定轴转动定律和角动量定理是物理学中的重要定律，它们描述了刚体绕定轴转动的动力学过程，并为我们更好地理解刚体绕定轴转动的动力学过程提供指导。
刚体定轴转动的角动量定理和角动量守恒定律课件
转动惯量的特性
只与刚体的质量和各质点到转动轴 的距离有关，与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ，等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量，具有方向和大小；对 于定轴转动，角动量位于转轴上；角 动量是相对量，与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种，一种是基于牛顿第二定律和转动定理推导，另一种是通过分析系统的能 量变化来证明。通过这些证明方法，可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明，对于不受外力矩或所受外力矩的矢量和为零的系统，其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用，如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例，其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时，可以将其视为 刚体定轴转动，这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时，也是一个刚体定 轴转动的例子，其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时，可以通过改变身体的姿势来改变转动惯量，从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例
只与刚体的质量和各质点到转动轴 的距离有关，与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ，等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量，具有方向和大小；对 于定轴转动，角动量位于转轴上；角 动量是相对量，与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种，一种是基于牛顿第二定律和转动定理推导，另一种是通过分析系统的能 量变化来证明。通过这些证明方法，可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明，对于不受外力矩或所受外力矩的矢量和为零的系统，其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用，如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例，其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时，可以将其视为 刚体定轴转动，这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时，也是一个刚体定 轴转动的例子，其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时，可以通过改变身体的姿势来改变转动惯量，从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例
4.3刚体转动角动量 角动量守恒定律
Mdt I2 I1
L I 常量
四 刚体定轴转动的角动量守恒定律 若 M 0 ，则 讨论
守 恒条件
M 0
内力矩不改变系统的角动量.
在冲击等问题中
M in M ex L 常量
角动量守恒定律是自然界的一个基本定律.
有许多现象都可以 用角动量守恒来说明. 花样滑冰 跳水运动员跳水 自然界中存在多种守恒定律 动量守恒定律 能量守恒定律 角动量守恒定律 电荷守恒定律 质量守恒定律 宇称守恒定律等
1 3 J 2 r dr l 0 12 1 ml 2 12
l/2 2
如转轴过端点垂直于棒
1 2 J r dr ml 0 3
l 2
例3 一质量为 m 、半径为 R 的均匀圆盘，求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 ， 在盘上取半径为 ，宽为 dr 的圆环
注意
d
C
mO
I O I C md
2
1 圆盘对P 轴 J P mR 2 mR 2 的转动惯量 2
P
R O m
三 刚体定轴转动的角动量定理
由质点系角动量定理
dLz d ( I ) Mz dt dt
Hale Waihona Puke t2t1M z dt I2 I1
刚体定轴转动的角动量定理
t2
t1
克服直升飞机机身反转的措施：
装置尾浆推动大 气产生克服机身 反转的力矩 装置反向转动的双 旋翼产生反向角动 量而相互抵消
质量为M，长度为L的均匀杆可绕水平轴O在铅直面内 自由转动，一质量为m的小球以水平速度v与杆的下端 相碰,碰后以反向v’运动，求碰后杆的角速度？
力学刚体转动与角动量的计算
力学刚体转动与角动量的计算力学是研究物体在力的作用下的运动规律的学科，而刚体转动是力学中的一个重要概念。
在刚体转动中，角动量是描述刚体运动状态和性质的重要物理量。
本文将介绍刚体转动与角动量的计算方法。
一、刚体转动的基本概念刚体是具有固定形状和大小的物体，其内部各点相对位置保持不变。
刚体转动是指刚体绕固定点或固定轴进行的运动。
在刚体转动中，我们需要了解以下几个基本概念：1. 转动轴：刚体绕其进行旋转的轴线。
2. 转动中心：物体上的一点，它相对于其他点的位置保持不变。
3. 角度：物体绕转动轴旋转的角度大小。
4. 角速度：物体单位时间内绕转动轴旋转的角度。
二、刚体转动的角动量公式角动量是刚体转动过程中的关键物理量，用L表示。
角动量的计算公式为：L = Iω其中，L为角动量，I为刚体转动轴的转动惯量，ω为角速度。
三、刚体转动惯量的计算方法刚体转动惯量是描述刚体绕转动轴旋转惯性的物理量，用I表示。
不同形状和分布的刚体转动惯量的计算方法不同。
下面列举几种常见形状的刚体转动惯量计算方法：1. 绕平行轴的转动惯量计算公式：若刚体的转动轴与通过质心的平行轴重合，则转动惯量可通过以下公式计算：I = Σmiri²其中，Σmi为刚体各质点的质量之和，ri为质点到转动轴的距离。
2. 绕垂直轴的转动惯量计算公式：若刚体绕垂直于通过质心的轴旋转，转动惯量可通过以下公式计算：I = Σm(x²+y²)其中，m为质点的质量，x和y分别为质点在平面上与转动轴的坐标。
3. 特殊刚体的转动惯量计算公式：对于一些特殊形状的刚体，如球体、圆盘、圆环等，其转动惯量有相应的计算公式。
四、实例演算以计算绕垂直轴旋转的圆盘的转动惯量为例。
假设圆盘的质量为m，半径为r，转动轴垂直于圆盘面且通过圆心。
根据转动惯量计算公式：I = Σm(x²+y²)对于圆盘，可以将其看作由无数个质点组成。
每个质点的质量为dm=dm，坐标为(x,y)，则有：I = ∫(x²+y²)dm由于圆盘具有对称性，每个质点的x坐标和y坐标平方的期望值相等，即：I = 2∫x²dm= 2∫x²ρdV其中，ρ为单位体积的质量，dV为体积元素。
定轴转动的角动量定理 角动量守恒定律
O
C
零点， 表示棒这时的角速度, 零点，用ω表示棒这时的角速度,则
l 1 11 2 2 2 mg = J ω ＝ ml ω 2 2 23
（ 1）
第二阶段是碰撞过程 。 因碰撞时间极短， 第二阶段是 碰撞过程。 因碰撞时间极短 ， 自由的 碰撞过程 冲力极大，物体虽然受到地面的摩擦力， 冲力极大，物体虽然受到地面的摩擦力，但可以忽略 这样，棒与物体相撞时， 。这样，棒与物体相撞时，它们组成的系统所受的对 的外力矩为零，所以， 转轴O的外力矩为零，所以，这个系统的对O轴的角 动量守恒。 表示物体碰撞后的速度， 动量守恒。我们用v表示物体碰撞后的速度，则
讨论： 讨论：
a.对于绕固定转轴转动的刚体，因J保持不变， 对于绕固定转轴转动的刚体， 保持不变 保持不变， 对于绕固定转轴转动的刚体 当合外力矩为零时，其角速度恒定。 当合外力矩为零时，其角速度恒定。
当 M z = 0时， J =恒量
ω
=恒量
b.若系统由若干个刚体构成,当合外力矩为零时,系 若系统由若干个刚体构成,当合外力矩为零时, 若系统由若干个刚体构成 统的角动量依然守恒。 统的角动量依然守恒。J 大→ ω , J 小→ 大。 小 ω
(6)
l h = + 3 µ s − 6 µ sl 2
的匀质细杆， 例13：一长为 l 的匀质细杆，可绕通过中心的固定 13： 水平轴在铅垂面内自由转动， 水平轴在铅垂面内自由转动，开始时杆静止于水平位 置。一质量与杆相同的昆虫以速度 v0 垂直落到距点 O点 l/4 处的杆上，昆虫落下后立即向杆的端点爬行 处的杆上， ，如图所示。若要使杆以匀角速度转动 如图所示。 求: 昆虫沿杆爬行的速度。 昆虫沿杆爬行的速度。
r r vi ∆m i L r ri
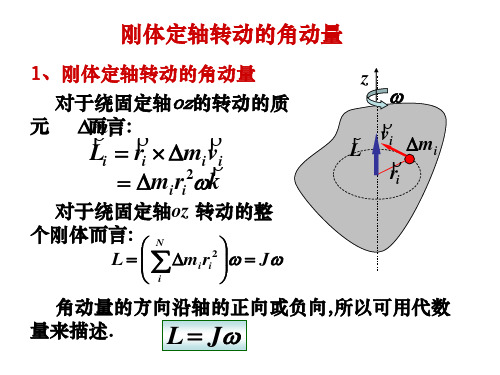
C
零点， 表示棒这时的角速度, 零点，用ω表示棒这时的角速度,则
l 1 11 2 2 2 mg = J ω ＝ ml ω 2 2 23
（ 1）
第二阶段是碰撞过程 。 因碰撞时间极短， 第二阶段是 碰撞过程。 因碰撞时间极短 ， 自由的 碰撞过程 冲力极大，物体虽然受到地面的摩擦力， 冲力极大，物体虽然受到地面的摩擦力，但可以忽略 这样，棒与物体相撞时， 。这样，棒与物体相撞时，它们组成的系统所受的对 的外力矩为零，所以， 转轴O的外力矩为零，所以，这个系统的对O轴的角 动量守恒。 表示物体碰撞后的速度， 动量守恒。我们用v表示物体碰撞后的速度，则
讨论： 讨论：
a.对于绕固定转轴转动的刚体，因J保持不变， 对于绕固定转轴转动的刚体， 保持不变 保持不变， 对于绕固定转轴转动的刚体 当合外力矩为零时，其角速度恒定。 当合外力矩为零时，其角速度恒定。
当 M z = 0时， J =恒量
ω
=恒量
b.若系统由若干个刚体构成,当合外力矩为零时,系 若系统由若干个刚体构成,当合外力矩为零时, 若系统由若干个刚体构成 统的角动量依然守恒。 统的角动量依然守恒。J 大→ ω , J 小→ 大。 小 ω
(6)
l h = + 3 µ s − 6 µ sl 2
的匀质细杆， 例13：一长为 l 的匀质细杆，可绕通过中心的固定 13： 水平轴在铅垂面内自由转动， 水平轴在铅垂面内自由转动，开始时杆静止于水平位 置。一质量与杆相同的昆虫以速度 v0 垂直落到距点 O点 l/4 处的杆上，昆虫落下后立即向杆的端点爬行 处的杆上， ，如图所示。若要使杆以匀角速度转动 如图所示。 求: 昆虫沿杆爬行的速度。 昆虫沿杆爬行的速度。
r r vi ∆m i L r ri
刚体的转动 角动量守恒定律
L
r
mv
二.力矩
M
r
F
大小：M
方向： r
rF F
sin
单位： N m 量纲： ML2T 2
三.角动量定理
质点所受的合外力矩等于它的角动量对时
间的变化率
M
dL
dt
2.8 角动量 角动量守恒定律
一L.角动r量 mv二.力M矩 r三.角F动量定理
M
dL
dt
四.角动量守恒定律：如果对于某一固定点，质 点所受的合外力矩为零，则此质点对该固定
x dx
IB
1 3
m L2
1 mL2 12
m
L 2
2
B A h O质
IC
1 XmL2 12
IA
1 12
m L2
m h2
IB
1 mL2 12
m
L
2
2
平行轴定理：绕任意轴的转 动惯量等于绕过质心的平行 的转动惯量加上质量与两轴 间距的平方
I IC md2
d
A
C
例2）半径为R的质量均匀分布的细圆环及薄圆 盘，质量均为m，试分别求出对通过质心并与 环面或盘面垂直的转轴的转动惯量。
质心运动定理反映了物体的平动规律。
2.刚体的定轴转动 刚体的各质元在运动中都绕一固定轴作圆 周运动，称为刚体作定轴转动。
3.刚体的一般运动
蔡斯勒斯定理：刚体的任一位移总可以表示 为一个随质心的平动加上绕质心的转动。
三. 刚体定轴转动的特点
每一质点都作圆心在轴上，圆平面垂直轴，
且角位置.角速度.角加速度都相同的圆周运动
复习
冲量：
dI Fdt
I
动量定理：
刚体的角动量 转动动能 转动惯量
I 1 mr 2 2
6、圆筒（转轴沿几何轴）
I
1 2
m(r12
r22 )
7、圆柱体（转轴通过中心与圆柱体垂直）
I 1 mr 2 1 ml 2
4
12
8、圆柱体（转轴沿几何轴）
I 1 mr 2 2
9、薄球壳（转轴沿直径）
I 2 mr 2 3
10、球体（转轴沿直径）
I 2 mr 2 5
两轴间的距离平方的乘积： J J C md 2
如： JC
1 2
mR2
J
JC
J JC mR 2
m
1 mR2 mR2
R
2
刚体绕质心轴的转动惯量最小
三、垂直轴定理
定理表述：质量平面分布的刚体，绕垂直于
平面轴的转动惯量等于平面内两正交轴的转
动惯量之和：J z J x J y
ml 2 12
mh2
这个例题表明，同一刚体对不同位置的转
轴，转动惯量并不相同。
h
A
B
Ox
l
dx
转动惯量的计算
例题4-4 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R，质量为m，密度均匀。
R r dr
解 设圆盘的质量面密度为，在圆盘上取一半径为r、
宽度为dr的圆环（如图），环的面积为2rdr，环的
“平行轴定理”
圆盘对P 轴 的转动惯量
J P JC mh 2
PR Om
JP
1 2
mR2
mR2
JB
ml 2 12
mh2
h
A
B
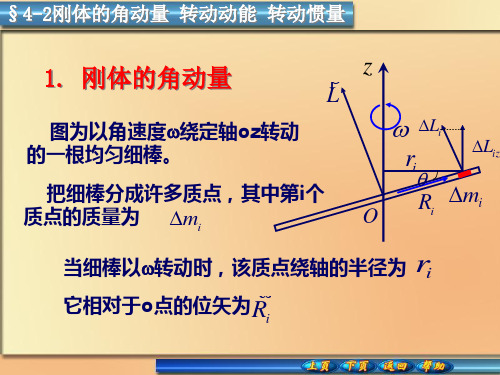
6、圆筒（转轴沿几何轴）
I
1 2
m(r12
r22 )
7、圆柱体（转轴通过中心与圆柱体垂直）
I 1 mr 2 1 ml 2
4
12
8、圆柱体（转轴沿几何轴）
I 1 mr 2 2
9、薄球壳（转轴沿直径）
I 2 mr 2 3
10、球体（转轴沿直径）
I 2 mr 2 5
两轴间的距离平方的乘积： J J C md 2
如： JC
1 2
mR2
J
JC
J JC mR 2
m
1 mR2 mR2
R
2
刚体绕质心轴的转动惯量最小
三、垂直轴定理
定理表述：质量平面分布的刚体，绕垂直于
平面轴的转动惯量等于平面内两正交轴的转
动惯量之和：J z J x J y
ml 2 12
mh2
这个例题表明，同一刚体对不同位置的转
轴，转动惯量并不相同。
h
A
B
Ox
l
dx
转动惯量的计算
例题4-4 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R，质量为m，密度均匀。
R r dr
解 设圆盘的质量面密度为，在圆盘上取一半径为r、
宽度为dr的圆环（如图），环的面积为2rdr，环的
“平行轴定理”
圆盘对P 轴 的转动惯量
J P JC mh 2
PR Om
JP
1 2
mR2
mR2
JB
ml 2 12
mh2
h
A
B
物理-刚体定轴转动的角动量与转动惯性
一、刚体对定轴的角动量
刚体相对转轴的角动量 量 值
(1) I 为刚体对转轴的转动惯量
(2)角动量 与角速度
L z
的方向沿转轴， 的方向相同。
z
Lz I
二、刚体对定轴的转动惯量
说明
1、对同一轴的转动惯量具有可加性； 2、刚体的转动惯性不仅与其质量有关，
还与其形状、大小、质量分布及转轴的位 置有关；
二、刚体对定轴的转动惯量
3、对于质量连续分布 的刚体
dm
V 表示刚体所占据的空间 区域。
二、刚体对定轴的转动惯量
质量为线分布
dl
质量为面分布
dS dS
质量线密度： 质量面密度：
质量为体分布
dV dV
质量体密度：
关键在于根据质量分布特点，选取恰当的质量微元！
二、刚体对定轴的转动惯量
例1：分别求匀直细杆对质心轴、端垂轴的转动惯量 设单位长度的质量（质量的线密度）为 dm dr
（轴与圆环平面垂直并通过圆心）
解： 在细圆环上任取一质元dm
OR dm
讨论：(1) 质量与半径均相等的匀质薄圆筒对同一轴 的I =？ 结果：同匀质细圆环！ 原因：对同一轴的质量分布没变！
二、刚体对定轴的转动惯量
例2 求质量为m、半径为R的匀质细圆环的转动惯量。
（轴与圆环平面垂直并通过圆心） 解： 在细圆环上任取一质元dm
第十六讲
刚体对定轴的角动量与转动惯量
一、刚体对定轴的角动量
刚体相对转轴的角动量
定 义
刚体相对转轴任一点的角 动量沿转轴的分量。
量 值
一、刚体对定轴的角动量
(1) 质元
量
Li
m对i 转轴上o点的角动
大学物理——第3章-角动量定理和刚体的转动
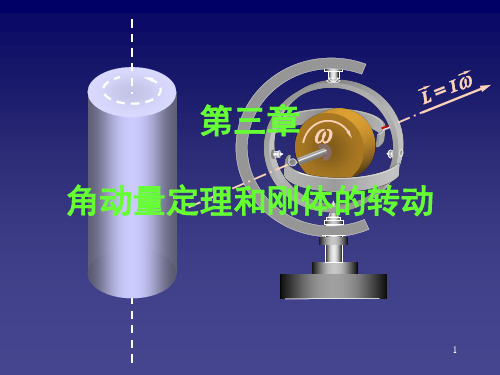
M
α
I
有何联系?
13
实验指出,定轴转动的刚体的角加速度 α与刚体所受的合外 力矩 M 成正比,与刚体的转动惯量 I 成反比.
v dω v M = Iα = I dt
v
定轴转动定理
v v F = ma
定轴转动定律在转动问题中的地 位相当于平动时的牛顿第二定律
应用转动定理解题步骤与牛顿第二定律时完全相同.
1 1 2 2 2 Eki = miυi = mi ri ω 2 2
质点质量 整个刚体的动能:
N
圆周运动的速率和半径
1 N 2 2 Ek = ∑Eki = (∑mi ri )ω 2 i=1 i=1
刚体对转轴的转动惯量:I
7
刚体定轴转动动能公式
物体的平动动能(质点动能)
1 2 Ek = Iω 2
角速度 ω 转动惯量 I 物体绕轴的转动惯性
λ :质量线密度 σ :质量面密度 ρ :质量体密度
10
I = ∫ r 2dm
单位: kg m2
转动惯量的大小取决于刚体的质量,质量分布及转轴的位置.
O
O l/2 O′
1 I= ml2 12
O
O O′
1 2 I = ml 3
r
O′
1 I = mr2 4
O′
1 I = mr2 2
11
平行轴
垂直轴
平行轴定理 质量为 m 的刚体,如果对其质心轴的转动惯量为 IC,则对任 一与该轴平行,相距为 d 的转轴的转动惯量:
2 θ 3Rω0 n= = 2π 16π g
26
讨论
用定轴转动的动能定理较之用转动定律求解, 省去了求角加速度,而直接求得,更为简捷.
第3章刚体转动动能和角动量
2 Mdθ = Jω 2 / 2 − J 0ω 0 / 2 ∫
17
牛顿力学的知识结构
外 力 牛 顿 第 二 定 律
F = dP dt M = dL dt
力 对时间累积
动 量 守 恒 作 功 机 械 能 守 恒 外 力 矩 为 零 角 动 量 守 恒
18
力对时间累积
为 牛 顿 第 三 定 律
12 21
df = µ gdm m σ= 2 dm = σ 2π rdr πR 2 R 2 M = − ∫ µσ 2π gr dr = − mg µ R 0 3 2π 4π A = ∫ Mdθ = − mg µ R 0 3 dM = −rdf
Байду номын сангаас
r
6
光滑， 例2：已知：均匀直杆质量为 ，长为 ，轴o光滑， ：已知：均匀直杆质量为m，长为l， 初始静止在水平位置。 AO = l / 4 初始静止在水平位置。
ω0 例1：在摩擦系数为µ桌面上有 细杆， 细杆，质量为 m、长度为 l， 、 ， m, l o 以初始角速度 ω0 绕垂直于杆 的质心轴转动， 的质心轴转动，问细杆经过多 µ 长时间停止转动。 长时间停止转动。 以细杆为研究对象，受力分析， 解：以细杆为研究对象，受力分析，重力及桌面的 支持力不产生力矩，只有摩擦力产生力矩。 支持力不产生力矩，只有摩擦力产生力矩。
刚体定轴转动动能 角动量
1
转动中的功和能
一、力矩的功
设刚体上P点受到外力 的作用， 设刚体上 点受到外力 F 的作用， 点受到 位移为 d r , 功为 d A ,
z
0′
F ∥
r
F
F⊥
0′
dθ
dr
P
r
P
17
牛顿力学的知识结构
外 力 牛 顿 第 二 定 律
F = dP dt M = dL dt
力 对时间累积
动 量 守 恒 作 功 机 械 能 守 恒 外 力 矩 为 零 角 动 量 守 恒
18
力对时间累积
为 牛 顿 第 三 定 律
12 21
df = µ gdm m σ= 2 dm = σ 2π rdr πR 2 R 2 M = − ∫ µσ 2π gr dr = − mg µ R 0 3 2π 4π A = ∫ Mdθ = − mg µ R 0 3 dM = −rdf
Байду номын сангаас
r
6
光滑， 例2：已知：均匀直杆质量为 ，长为 ，轴o光滑， ：已知：均匀直杆质量为m，长为l， 初始静止在水平位置。 AO = l / 4 初始静止在水平位置。
ω0 例1：在摩擦系数为µ桌面上有 细杆， 细杆，质量为 m、长度为 l， 、 ， m, l o 以初始角速度 ω0 绕垂直于杆 的质心轴转动， 的质心轴转动，问细杆经过多 µ 长时间停止转动。 长时间停止转动。 以细杆为研究对象，受力分析， 解：以细杆为研究对象，受力分析，重力及桌面的 支持力不产生力矩，只有摩擦力产生力矩。 支持力不产生力矩，只有摩擦力产生力矩。
刚体定轴转动动能 角动量
1
转动中的功和能
一、力矩的功
设刚体上P点受到外力 的作用， 设刚体上 点受到外力 F 的作用， 点受到 位移为 d r , 功为 d A ,
z
0′
F ∥
r
F
F⊥
0′
dθ
dr
P
r
P
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可能出现的情况是
（4）以上结果都不对。
（请点击你要选择的项目）
既忽略 滑轮质量
两人质量相等 小议链接1
（1）两人同时到达；
又忽略
轮绳摩擦
终点线
一 人 用 力 上 爬
终点线
一 人 握 绳 不 动
（2）用力上爬者先到； （3）握绳不动者先到；
可能出现的情况是
（4）以上结果都不对。
（请点击你要选择的项目）
可应用质点系角动量定理进行具体分析讨论。
第二节
刚体：形状固定的质点系（含无数质点、不形变、理想固体。）
平动
定轴转动
平面运动
4-2
定点运动 一般运动
两刚点体的r任连o意线tation刚o体f 每rig点id-限b刚o制d体在y质一w心i平th
保持方向不 绕同一轴线 面内，转轴
两称种为方向，可设顺时针为正向，用代数微和分代形替式矢量和。 量和时成对相消
质点系角动量守恒
由
外
若
则
或
恒矢量
当质点系所受的合外力矩为零时，其角动量守恒。
既忽略 滑轮质量
两人质量相等 随堂小议
（1）两人同时到达；
又忽略
轮绳摩擦
终点线
一 人 用 力 上 爬
终点线
一 人 握 绳 不 动
（2）用力上爬者先到； （3）握绳不动者先到；
为零时，质点对该点的角动量的时间变化率 为
零，即质点对该点的角动量 守恒。
称为
若质点所受的合外力的方向始终通过参考点，其角动量守恒。如行星绕 太阳运动，以及微观粒子中与此类似的运动模型，服从角动量守恒定律。
应用质点的开角动普量勒守恒第定律二可定以证律明
开普勒第二定律
行星与太阳的连线在相同时间内扫过相等的面积
归纳
质点的 角动归量定纳理
角动量的时间变化率
所受的合外力矩
冲量矩
角动量的增量
当
0 时， 有
0
即
物理意义：当质点不受外力矩或合外力矩为零 （如有心力作用）时，质点的角动量 前后不改变。
（后面再以定律的形式表述这一重要结论）
质点角动量守恒
根据质点的 角动量定理
若
则
即
常矢量
当质点 所受的合外力对某参
所决定
的平面，由右螺旋法 则定指向。
得
质点 对给定参考点 的
角动量的时间变化率
所受的合外力矩
称为质点的 角动量定理 的微分形式
如果各分力与O点共面，力矩只含正、反两种方向。可设顺时针为正 向，用代数法求合力矩。
积分形式 质点的角动量定理也可用积分形式表达
由
称为 冲量矩
角动量的增量
变
大小会变
太 阳 系 中 的 行 星
变变 变
大小未必会变。靠什么判断？
质点角动量定理
导致角动量 随时间变化的根本原因是什么？ 思路： 分析 与什么有关？
由
则
两平行矢量的叉乘积为零
得
质点 对参考点 的
角动量的时间变化率
等于
位置 矢量
叉乘
所受的 合外力
而微分形是式力矩的矢量表达：
即 力矩
本章题头
内容提要
Contents chapter 4
角动量与角动量守恒
angular momentum and law of conservation of angular momentum
刚体的定轴转动
rotation of rigid-body with a fixed axis
刚体作定轴转动时的功能关系
外
质点受外力
外
矩的矢量和
微分形式
内 内
外 外
内力矩在求矢 量和时成对相消
微、积分形式
将
的微分对形时式间求导
外
质点系的角动量 的时间变化率
质点受某外给力定 矩的矢参量考和点
的积分形式
内
外
内
得
质点系所内受的
外
质外点系的
内
质的点时若系间各的变质角化点动率冲的量速量度矩或所受外力外与参考点质 矩共角点 的面动受 矢，外 量量则力 和其增角量动量外内或力矩只在含求正矢反外
位矢 r
m
质量
定la义对w：Oof点c运的o动an角n质s动ge点ur量lvmaa为rtimonomofeanntugmulaaOrnmd omentum
L r p r mv
大小：L rm v sin L
v
方向： r ( m v ) r
问题的提出
问题的提出
质点 对
点的角动量
大小
地 球 上 的 单 摆
（2）用力上爬者先到； （3）握绳不动者先到；
可能出现的情况是
（4）以上结果都不对。
（请点击你要选择的项目）
小议分析
质点系
忽略轮、绳质量及轴摩擦
若
系 统受合外力矩为零，角动量守恒。
系统的末 态角动量
得
系统的初 态角动量
不论体力强弱，两人等速上升。
同高从静态开始 往上爬
若
系统受合外力矩不为零，角动量不守恒。
既忽略 滑轮质量
两人质量相等 小议链接2
（1）两人同时到达；
又忽略
轮绳摩擦
终点线
一 人 用 力 上 爬
终点线
一 人 握 绳 不 动
（2）用力上爬者先到； （3）握绳不动者先到；
可能出现的情况是
（4）以上结果都不对。
（请点击你要选择的项目）
既忽略 滑轮质量
两人质量相等 小议链接3
（1）两人同时到达；
这就是质点的 角动量定理 的积分形式
例如，
单摆的角动量大小为 L = mv r, v为变量。 在 t = 0 时从水 平位置静止释放，初角动量大小为 L0= m v0 r =0； 时刻 t 下 摆至铅垂位置， 角动量大小为 L⊥ = m v⊥ r 。则此过程单摆 所受的冲量矩大小等于 L-L0= m v⊥ r = m r 2gr 。
又忽略
轮绳摩擦
终点线
一 人 用 力 上 爬
终点线
一 人 握 绳 不 动
（2）用力上爬者先到； （3）握绳不动者先到；
可能出现的情况是
（4）以上结果都不对。
（请点击你要选择的项目）
既忽略 滑轮质量
两人质量相等 小议链接4
（1）两人同时到达；
又忽略
轮绳摩擦
终点线
一 人 用 力 上 爬
终点线
一 人 握 绳 不 动
时刻 m 对 O 的角动量大小为
定律证明
瞬间 位矢扫过的微面积
即
（称为掠面速率）
因行星受的合外力总指向是太阳，角动量 守恒。
则
常量 故，位矢在相同时间内扫过的面积相等
质点系角动量
惯性系中某给定参考点
质点系角动量定理
将
对时间求导
某给定 参考点
内
外
得
内
质点系的角动量 的时间变化率
称为
外
relation of work with energy in rotation of rigid-body
刚体的角动量守恒
law of conservation of angular momentum of rigid-body
第一节
大量天文观测表明 4 - 1 速度 v
v
rmv sin 常量