事件发生的可能性完结

合集下载

事故发生的可能性L判断准则

风险度
等级
应采取的行动/控制措施
实施期限
20-25
巨大风险
在米取措施降低危害前，不能继续作业，对改进措施进行评估
立刻
15-16
重大风险
采取紧急措施降低风险，建立运行控制程序，定期检查、测量及评估
立即或近期整改
9-12
中等
可考虑建立目标、建立操作规程，加强培训及沟通
2年内治理
4-8
可接受
可考虑建立操作规程、作业指导书但需定期检查
>25
2套装置停工、或设备停工
行业内、省内影响
3
不符合上级公司或行业的
截肢、骨折、听
>10
1套装置停工或
地区影响
安全方针、制度、规定等
力丧失、慢性病
设备
2
不符合公司的安全操作程序、规定
轻微受伤、间歇不舒服
<10
受影响不大，几乎
不停工
公司及周边范围
1
完全符合
无伤亡
无损失
没有停工
形象没有
受损
风险等级判定准则及控制措施R
3
没有保护措施（如没有保护装置、没有个人防护用品等），或未严格按操作程序执行，或危害的发生容易被发现（现场有监测系统），或曾经作过监测，或过去曾经发生类似事故或事件，或在异常情况下类似事故或事件。
2
危害一旦发生能及时发现，并定期进行监测，或现场有防范控制措施，并能有效执行，或过去偶尔发生事故或事件。
事故发生的可能性L判断准则
等级
标准
5
在现场没有米取防范、监测、保护、控制措施，或危害的发生不能被发现（没有监测系统），或在正常情况下经常发生此类事故或事件。

概率论-事件发生的可能性

A与B的共同元素 A的补集在A中而不在B中的元素
A与B无公共元素
事件含义样本空间，必然事件不可能事件样本点基本事件一个事件 A发生导致B发生事件A与B相等 A与B至少有一个发生
A与B同时发生 A的对立事件 A发生而B不发生
A与B互斥
§2 概率
概率是事件发生可能性的数量指标。
即在多次重复后，某结果出现的比率。
D与B,D与E互不相容
C与E为对应事件。
B与C，B与A，E与A相容
A与C,A与D,C与D,B与E也是相容的。
符号 Ω Φ ω∈Ω {ω} A Ω A B A=B A∪B
A∩B Ā A-B
A∩B=φ
集合含义全集空集集合的元素单点集一个集合 A的元素在B中集合A与B相等 A与B的所有元素
3) ABC D 4) ABC D 5) ABCD BACD CBAD DBC A ABCD
例子P55 --11:
P( A)

2 P42 P53

2/5
例子P55 --12:
例子P55 --13:
例子P55 --14:
例子P55 16--18
例子P56 19--22
例子P56 23--26
用图形表示，即
A
B
也可定义多个事件的交。交与并运算还满足分配律： (A∪B)∩C=(A∩C)∪(B∩C) (A∩B)∪C=(A∪C)∩(B∪C) 用不同的记号，可写为 (A+B)C=AC+BC (AB)+C=(A+C)(B+C)
5、事件的差事件A发生而事件B不发生，是一个事件，称为事件A与B的差。它由属于A但不属于B的所有样本点组成。记作A-B 如：A={1,2,3},B={1,3,5}

事件发生的可能性

O 事缔谚+g ；A 甬羞，有的强白面然性．若谪直毛苛矗一口山东刘玉东忤．囱的F {有不叫能竹褂究事件发生的cD 能性实!际就足研究随肌耻软的统t I 规律【f J j 随机『见象只钆牡蝻忖．因此该部分内容有r 1泛的应用忤、、一一、掌握事件的分类啊什的分类是针对’#件的发生与行进行的，可分为炳炎：1确定m 件：事先能够确定是了蹦￡乍的事件也就是说确定‘缸什冉定发生和定j 二发叶三两种．其巾把一定能发，卜的舢件叫做必然书什．把一定小发／I ：的班件叫做不可能水什【解读】：(1)确定市仆址仟似人郜叶i 能政变的串’站．如“抛}I ；』：的物体一定会湛剑地面L ”这一事件足；芒发生的，这足山’r 地球的t 』l 力所决定的(2)埘J 小I |T 能事件，它腻丁确定。

J 【件．不哥误队为“一定币发生的事仆”胜不确定事仆21；确定市什：事先尤法确定足pr 发乍的事件叫4：确定事什．义叫随机m 件【解读】：小确定蕾仲发小。

J p r 俯仃似然4陀，不能…r ，它发生．J ’．就认为E 址必然椎¨．也小能洲7,J 已小发生，就以为它足1、可能中。

什f c ¨”报告川f 、川¨r 能列我校”，n 的同。

学观：“蛐I 果报秆川下周豇的刮我校．邶幺’E 就足确譬占端孛斤①严㈣o餐定事件巾的必然萝件”迁有的I川’’产c兑：“如果报告Ⅲ下川小到我校．那么岜就足确定书件巾的不uf能事件”这阳种说法都是锵涅的．J卜确的c兑泌灶：不论报告p“l、周足甫到我校，“报告团F周可能刊我校”仍属于不确定班仆=、理解事件发生的可能性l确定事件发，t的^r能性．确定事件发生的叫f能性足确定的妊然事件柱一定条件卜．j￡发生的可能性足】00％，m不_J能郴件魁水远斗：会发生的事件．其发生柏nr能性足0．2．不确定书件发，1．的可能悱不确定1|I=件发生的可能性是有人小的，)￡大小ur以埘过火馈的。

蛙验束探索依据不确定事件发，E的可能性的人小．订州种情形需引起我们的注意：一是通过寅验发生的，T能巾I：很大的茸件，即很可能发生市件；一是通过宴蝓发生的--r能性很小的事件．即小太可能发生T|1=件注意：(1)根‘-r能发1：事件足指发生的可能性非常大．似小属于必然耵件；(2)小太川能发生班什灶指发生的可能中l：扑常小．f口4i属于不可能*件．三、学会认定确定事件和不确定事件例行r列市件：，J从～剐}I-兜牌巾任抽一帐足照桃；(2设朽水分．种子会发芽：o枚均匀的娅币抛f U后，小魁J卜面胡上，i【_c魁反断帕1．儿-f-属于必然事件的是．小r能事件的足，4：确定事件的是．匮益I●I{挺据事件发生的可能性大小进行分析，对丁二①，有五种情形．ⅡⅡ红桃、黑桃、梅花、矗块、王，因此从一削扑克牌叶]征舢一张是黑桃具有可能性，但不确定，所以①这个书件属r不确定事件．刑于②．根据植物学知识．种子发芽需饕{个条件．即水分、空气和适宜的温度．j。

事件发生的可能性L判断准则

立即或近期整改
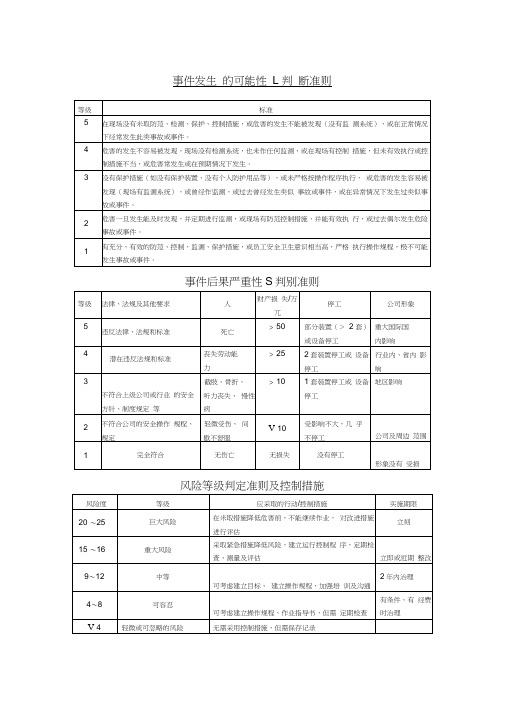
9〜12
中等
可考虑建立目标、建立操作规程，加强培训及沟通
2年内治理
4〜8
可容忍
可考虑建立操作规程、作业指导书，但需定期检查
有条件、有经费时治理
V4
轻微或可忽略的风险
无需采用控制措施，但需保存记录
工作危害分析（
序号
工作
步骤
危害或潜在事件（人、机、
环、管）
危害形式/事
故类型
死亡
>50
部分装置（＞2套）或设备停工
重大国际国
内影响
4
潜在违反法规和标准
丧失劳动能
力
>25
2套装置停工或设备停工
行业内、省内影响
3
不符合上级公司或行业的安全方针、制度规定等
截肢、骨折、听力丧失、慢性病
>10
1套装置停工或设备停工
地区影响
2
不符合公司的安全操作规程、规定
轻微受伤、间歇不舒服
V10
受影响不大，几乎不停工
公司及周边范围
1
完全符合
无伤亡
无损失
没有停工
形象没有受损
风险等级判定准则及控制措施
风险度
等级
应采取的行动/控制措施
实施期限
20〜25
巨大风险
在米取措施降低危害前，不能继险
采取紧急措施降低风险，建立运行控制程序，定期检查、测量及评估
主要
后果
以往发生频率及现有安全控制措施
可能性L
^严重性
S
风险度
R
建议改
进措施
发生频率
管理
措施

人教版五年级数学上册第四单元可能性-事件发生的可能性PPT课件

课堂练习
4. 按要求涂一涂。【教材P47 练习十一第4题】
（1）摸出的一定是蓝方块。
（2）摸出的不可能是黄球
答案不唯一
课堂练习
（3）摸出的可能是粉色三角形。
答案不唯一
课堂小结
回去收集生活中存在可能性的实例，并与同学相互交流。
巩固练习
下列情况中，一定发生的在括号里画“√”，不可能的画“×”，可能的画“○”。【选自《创优作业100分》 P31 第二题】
第4单元可能性
课程结束
人教版部编版五年级数学上册授课老师：XX
1 红色
号盒
蓝色
子黄色
绿色
2 红色
号盒
蓝色
子黄色
绿色
探究新知
记录
次数
记录
次数
1号盒子。
探究新知
哪个盒子里肯定能摸出红棋子?
1号盒子。
1号 2号
哪个盒子里不可能摸出绿棋子?
探究新知
2号盒子。
在2号盒子里哪可个能盒摸子出里什可么能颜摸色出的绿棋棋子子？？
1号 2号
绿、红、黄、蓝四种颜色的棋子都有可能被摸出。
课堂练习
1.说一说指针可能停在哪种颜色上。【教材P47 练习十一第1题】
答：可能停在蓝色、红色、黄色、绿色上。
课堂练习
2. 一个正方体，六个面上分别写着数字1~6。掷一次，可能掷出哪些数字？【教材P47 练习十一第2题】
答：可能掷出1、2、3、4、5、6。
课堂练习
3. 从盒子里摸出一个球，结果会是什么？连一连。【教材P47 练习十一第3题】
1.从装有红球和黑球的盒子里摸出红球。（ ○ ） 2.太阳从西方升起。（ × ） 3.明天会下雨。（ ○ ）

第1课时事件发生的可能性

不可预知用“可能”描述
哪个盒子里肯定能摸出红棋子?
1号
2号
1号盒子。
哪个盒子里不可能摸出绿棋子?
1号盒子。
状元成才路
哪个盒子我里们可先能来摸出一绿摸棋吧子！?
1号
2号
2号盒子。
在2号盒子里可能摸出什么颜色的棋子?
绿、红、黄、蓝四种颜色的棋子都有可能被摸出。
1.选一选，填一填。
一定可能不可能
（1）三天后（可能）不会下雨。（2）鱼儿（一定）生活在水里。（3）我一生下来（不可能）会跑。（4）太阳（一定）从东方升起。
事件发生的可能性
这个状元箱成才路子里有写着唱歌，跳舞，朗诵等今节天目是的元卡旦片，，我每们人开抽个取班一级张联。欢会。
每人表演一个节目。
状元成才路
三张卡片分别写着唱歌、跳舞、朗诵，小明可能会抽到什么节目？
可以和小伙伴一起抽一抽试试看。
也可能是朗诵。
可能是唱歌。三种情况都有可能。
状元成才路
状元成才路
2.选一选，填一填。一定可能不可能 A.摸出的（一定）是红球 B.（不可能）摸出红球 C.摸出的（可能）是红球
状元成才路
3.涂一涂。（1）摸出的一定是红方块。
状元成才路
（2）摸出的不可能是蓝球
答案不唯一
状元成才路
（3）摸出的可能是黄球
答案不唯一
状元成才路
事件发生的可能性
可预知用“一定”“不可能”描述
小明抽完还剩两张，
接下来小丽可能会
我抽到了跳舞。
抽到什么？
唱歌和朗诵都有可能。不可能是跳舞。
状元成才路
我抽到了朗诵。最后说只说有你一是张怎了样，想小的？雪会抽到什么？

事件发生的可能性

可能性教学内容：P104～105教学目标：1、初步体验有些事件的发生是确定的，有些事件的发生是不确定的。

2、结合自己的经验对生活中的一些事件用“一定”、“不可能”、“可能”表达3、培养学生的判断能力、语文表达能力和运用所学知识解决实际问题的能力。

教学重点：初步体验有些事件发生的确定与不确定，能对一些简单事件发生的可能性做出描述与判断，感受数学与生活的联系。

教学难点：用“一定”、“不可能”、“可能”去正确判断事情发的的确定与不确定。

教具准备：课件；长方体盒子；红色球、蓝色球若干个；教学过程：一、游戏导入，激发兴趣教师出示一元硬币问：“这是什么？用它可以干什么？”生：一元钱，可以用来买东西。

生：还可以用来玩正反面游戏！师：你会玩吗？能介绍一下是怎么玩的吗？现在想不想玩？师：（抛出硬币后盖住）谁来猜？能确定吗？师：硬币抛下来可能是正面，也可能是反面。

有没有可能既是正面又是反面呢？生：不可能师：这节课我们就一起学习“可能性”。

（板书课题）二、摸球游戏，体验可能性同学们，我知道你们最喜欢做游戏了，现在我们就一起来玩一个摸球的游戏，好不好。

宣布游戏规则：1、注意纪律，不能乱叫，要举手回答问题。

(能不能做到？)2、摸球的时候要这样，先搅几下，然后摸出来，自己看一下是什么颜色的，再向大家展示一下，最后放回去。

你们会了吗？⑴、体验一（一定）：师：同学们看，老师把球装到盒子里，一个，二个……（装进6个红色的），好了，现在我再把它摇一摇，谁来摸？（生摸球）师：告诉大家你摸到了一个什么颜色的球。

师：放回去，我再摇一摇，谁再来摸。

（生摸球）师：告诉大家你摸到的是什么颜色的球。

师：哦，也是红色的，我把它放回去，我再摇一摇，谁再来摸。

（指一名同学上来）师：好，摸到了吗？先不拿出来，让他们猜一猜你摸到的是什么颜色的球。

（生一口同声红色的球）师：一定吗？（生大声说：一定）师：真的一定吗，请你拿出来让同学们看看。

师：果真是红色的，同学们真厉害。

事件发生的可能性

事件发生的可能性教学目标：1.学生初步体验生活中有些事件的发生是确定的，有些则是不确定的。

2.学生理解“一定”“不可能”“可能”的意义，能够用“一定”“不可能”“可能”描绘生活中的现象。

3.学生感受“一定”“不可能”“可能”在一定条件下能够互相转化。

教学重点：会用“一定”“可能”“不可能”等词语来描绘事件发生的情况。

教学难点：事件发生的确定性和不确定性。

教学准备：PPT课件教学过程：一、引入新课1.师生游戏。

（1）师：同学们，我们一起来玩一个游戏，好吗？老师手里有一个漂亮的玻璃球，请你们猜猜看，藏在老师的哪只手里？学生自由猜测。

（2）学生：在左手，在右手。

师：看来大家的意见不一样，那老师来帮帮你们吧。

（教师慢慢松开右手，再重新握紧拳头）老师的右手里面没有，那玻璃球应该在哪里呢？学生：在左手。

（3）师：你们为什么肯定玻璃球一定在左手呢？2.揭题，板书课题。

师：同学们，在日常生活中，有些事件不能确定它发生的结果，有些事件能确定它发生的结果，类似的例子还有很多。

这节课我们一起来研究事件发生的可能性。

板书课题：可能性二、自主探索，体验新知。

1.教学情景图。

（1）课件出示情景图，问：下面请同学们认真观察情景图，同桌之间交流一下，你们获得了哪些信息呢。

（2）组织学生汇报：元旦联欢会上，抽卡片决定每人表演哪种节目，卡片上分别写有唱歌、跳舞和朗诵。

（3）师：假如让你抽一次，可能有什么结果？下面再请同学们交流一下可能有什么结果。

（点名学生回答）学生自由交流：抽到唱歌、跳舞和朗诵三种情况都有可能。

（4）师：那每个同学抽到的情况是不是确定的呢？生：不确定。

师：因为每个同学抽到的卡片情况是不确定的，所以有些事件的发生具有不确定性。

生活中还有很多类似这样的事情，同学们能举例说一下吗？（点名学生回答）（比方我们能够想一下这个周末的天气，有可能是阳光明媚，有可能是多云，还有可能是小雨）2.教学例1。

（出示课件图片）（1）师：盒子里有三张卡片分别写着唱歌、跳舞、朗诵。

23.1事件发生的可能性

在同一个条件下，事件发生可能性的大小，一般通过它们所占的时间的多少，数量的多少，以及联系实际来考虑事件发生的可能性大小.
例如上述试验中，（1）摸出1个黄球；（2）摸出1个白球；（3）摸出1个绿球；（4）摸出一个红球；（5）摸出一个球颜色是红色或者黄色或者白色.
如果我们用P1，P2，P3，P4，P5来分别表示它们事情发生可能性的大小，那么如何把它们从大到小排列呢？
【课题】23．1事件发生的可能性
学习目标：
1、初步感受有些事件的发生是不确定的，有些事件发生是确定的；
2、会区分生活中的必然事件，不可能事件和随机事件；
3、能正确判断随机事件中事情发生的可能性大小。
知
识
链
接
与
概
念
生
成
【自我探究】
说一说：（1）生活中哪些事情是肯定发生的？哪些事情是肯定不会发生的？
（2）生活中哪些事情是可能发生也可能不发生的？
①“从地面往上抛的硬币会落下”是随机事件；（）
②“软木塞沉到水底”是不可能事件；（）
③“买一张彩票中大奖”是必然事件；（）
④“明天会下雨”是随机事件.（）
2、指出下列事件中，哪些是必然事件，哪些是不可能事件，哪些是随机事件？
①在十进制中1+1=2；（）
②1+2>3；（）
③在一副扑克牌中任意抽10张牌，其中有4张A；（）
分析：事件5是必然事件，所以可能性最大，而事件3是不可能事件，所以可能性为0，而事件1，2，4都是随机事件通过它们个数的多少来判断发生可能性的大小，即事件2“不太可能”发生，事件4“很有可能”发生，事件1“有可能”发生.
所以他们从大到小的顺序是：P5，P4，P1，P2，P3
巩

【同步备课】第四单元第1课时事件发生的可能性(教案)五年级数学上册最新人教版

第1课时大事发生的可能性教学内容教科书P44例1和P45上面的“做一做”，完成教科书P47“练习十一”第1~4题。

教学目标1.在生疏的生活情境中初步体验大事发生的确定性和不确定性。

2.初步能用“肯定”“可能”“不行能”等词语来描述生活中大事发生的可能性，感受数学与生活的联系。

3.培育思维的严谨性、口头表达力量和小组合作力量。

教学重点通过活动让同学充分体验大事发生的确定性和不确定性。

教学难点利用大事发生的可能性的相关学问解决实际问题。

教学预备课件、海宝、卡片、（同学4人为一组）预备的纸盒和棋子。

教学过程一、故事导入，揭示课题同学们，你们宠爱听故事吗？老师给大家讲一个有关可能性的故事吧。

古罗马帝国有一个忠臣受奸人陷害，被判处死刑。

但依据当时法律的规定，他有一个打算生死的机会，就是抽生死签。

（出示：生签死签）抽到“生签”就能免一死，抽到“死签”就马上处死。

同学们，这位忠臣是生是死能确定吗？为什么？生：有可能生，也有可能他会死，这就是一种可能性。

国王想置他于死地，在“生死签”上做起了手脚，偷偷地将“生”的签都换成了“死”的签。

同学们，这位大臣的命运将会如何？为什么？生：他不行能活下来，肯定会死。

由于现在两张都是“死签”，他必死无疑！师：幸运的是，奸臣的小动作被一位富有正义感的士兵观察了，他赶忙把这件事静静地告知了这位被害的忠臣。

同学们，快帮帮这位忠臣想想方法吧，他要怎样才能脱身呢？同学各抒己见。

师：想不想知道这位忠臣是怎么做的？这位忠臣特殊聪慧，当大法官要他抽取生死牌的时候，他严峻其事地抽取了其中的一张，然后快速将它塞进嘴里一口吞下。

大法官急了：“你…你…你怎么…这…这…这可怎么办？”这时旁边的一位师爷说：“大人，别急！看看盒子里剩下的另外一张签是什么，不就可以知道犯人抽到的是什么了吗？”同学们，盒子里剩下的是什么？这位忠臣最终的命运会是怎样的？生：盒子里剩下的是死签，就说明他抽到的是生签，那他就不会死了，肯定能活下来。

五年级上事件发生的可能性

五年级上事件发生的可能性在我们的日常生活中，很多事情的发生都存在着一定的可能性。

而在五年级的数学学习中，我们开始接触到“事件发生的可能性”这个有趣又实用的知识。

当我们抛硬币时，正面朝上或者反面朝上，这两种结果都有可能出现。

同样，在抽奖活动中，我们有可能中奖，也有可能不中奖。

那么，如何来判断这些事件发生的可能性大小呢？首先，我们要明白什么是“确定事件”和“不确定事件”。

确定事件就是一定会发生或者一定不会发生的事情。

比如，太阳从东边升起，这是一定会发生的，就是确定事件。

而不确定事件呢，就是结果有多种可能，不能肯定会发生哪种结果。

比如说，明天可能会下雨，这就是不确定事件。

在判断事件发生的可能性大小时，我们通常会考虑不同结果出现的数量。

比如，一个盒子里放着 5 个红球和 3 个白球，从盒子里任意摸出一个球，摸到红球的可能性就比摸到白球的可能性大。

因为红球的数量多于白球的数量。

我们再来看一个例子。

在一个抽奖箱里，有 10 张奖券，其中 2 张是一等奖，3 张是二等奖，5 张是三等奖。

那么抽到一等奖的可能性就比较小，抽到三等奖的可能性就比较大。

在实际生活中，我们也经常会用到事件发生可能性的知识。

比如，在玩游戏的时候，我们会根据可能性的大小来制定游戏规则，让游戏更加公平有趣。

还有，在体育比赛中，预测比赛结果也是基于对各种可能性的分析。

比如，两支球队比赛，一支球队实力很强，过往战绩也很好，那么这支球队获胜的可能性就相对较大。

但这也不是绝对的，因为比赛中存在很多不确定因素，弱队也有可能爆冷获胜。

另外，在做决策的时候，我们也会考虑事件发生的可能性。

比如，在选择投资项目时，会分析不同项目成功的可能性和收益，从而做出更明智的选择。

对于五年级的我们来说，理解事件发生的可能性不仅能帮助我们更好地学习数学，还能让我们更加理性地看待生活中的各种现象和问题。

比如说，天气预报说明天有 80%的可能性会下雨，那么我们出门的时候就很可能会带上雨伞。

事件发生的可能性L判断准则

死亡
＞50
部分装置（＞2套）或设备停工
重大国际国内影响
4
潜在违反法规和标准
丧失劳动能力
＞25
2套装置停工或设备停工
行业内、省内影响
3
不符合上级公司或行业的安全方针、制度规定等
截肢、骨折、听力丧失、慢性病
＞10
1套装置停工或设备停工
地区影响
2
不符合公司的安全操作规程、规定
轻微受伤、间歇不舒服
＜10
受影响不大，几乎不停工
公司及周边范围
1
完全符合
无伤亡
无损失
没有停工
形象没有
受损
风险等级判定准则及控制措施
风险度
等级
应采取的行动/控制措施
实施期限
20～25
巨大风险
在采取措施降低危害前，不能继续作业，对改进措施进行评估
立刻
15～16
重大风险
采取紧急措施降低风险，建立运行控制程序，定期检查、测量及评估
立即或近期整改
9～12
2
危害一旦发生能及时发现，并定期进行监测，或现场有防范控制措施，并能有效执行，或过去偶尔发生危险事故或事件。
1
有充分、有效的防范、控制、监测、保护措施，或员工安全卫生意识相当高，严格执行操作规程，极不可能发生事故或事件。
事件后果严重性S判别准则
等级
法律、法规及其他要求
人
财产损失/万元
停工
公司形象
5
违反法律、法规和标准
事件发生的可能性L判断准则
等级
标准
5
在现场没有采取防范、检测、保护、控制措施，或危害的发生不能被发现（没有监测系统），或在正常情况下经常发生此类事故或事件。

概率论-事件发生的可能性

概率论
概率论－事件发生的可能性
教师介绍
阚海斌（博士、教授、博士导师）办公室：袁成英计算机楼217室 Email: hbkan@
第一章随机事件与概率
§1 随机事件
一、必然现象与随机现象 1、必然现象
在一定条件下肯定会发生的现象
如水100ºC沸腾，苹果从树上掉落
这是因为由图
A
B
A+B=A+(B-A)
由于A与B-A互斥故P(A+B)=P(A)+P(B-A) 再由(3)得证。可见，只需P(AB)=0加法法则就成立。若是多个事件之和，公式会变复杂。
P(A+B+C) =P(A+B)+P(C)-P((A+B)C) =P(A)+P(B)-P(AB)+P(C)-P(AC+BC)
(2)每次试验中，各基本事件发生的可能性相同。
这种试验称为古典概型试验。
定义1 若试验结果一共有n个基本事件组成，且这些事件的出现具有相同的可能性，且事件A由其中某m个基本事件组成，则事件A的概率为
P(A)

有利于A的基本事件数试验的基本事件总数
＝
m n
例1 掷一枚硬币，出现正面的概率解：设硬币是均匀的
用图形表示，即
AB
n个事件A1,…,An中至少有一个发生，是一个事件。称为事件A1,…,An的和。记作A1+…+An或A1∪…∪An
可列个事件A1,A2,…,An,…中至少有一个发生
称为事件A1,A2,…,An,…的和

记作 Ai 或UAi
i＝1
i＝1
若A={1,2,3},B={1,3,5},C={1,3,4}

概率论-事件发生的可能性

1、事件的包含
若事件A发生必然导致事件B发生，即属于A的每个样本点也属等价的说法是：B不发生，则A也不发生。
用图形表示，即
AB
例如A={4},B={2,4,6},则A B
对任何事件A,有φ A Ω
2、事件的相等若AB且BA，称事件A与B相等。即A与B中的样本点完全相同。记作A=B 掷一颗骰子 A表示点数小于3，B表示点数为1或2 则A=B
=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC) 其中要注意(AC)(BC)=ABC 类似地，可以证明
P(A1+A2+A3+A4)=P(A1)+P(A2)+P(A3)+P(A4) -P(A1A2)-P(A1A3)-P(A1A4)-P(A2A3)-P(A2A4)-P(A3A4) +P(A1A2A3)+P(A1A2A4)+P(A1A3A4)+P(A2A3A4) -P(A1A2A3A4)
特别地，对立事件的概率之和为1。
P(A)+P(Ā)=1
常用形式为 P(A)=1-P(Ā)
(3)若B A，则 P(B A) P(B) P(A) 一般有 P(B-A)=P(B)-P(AB)
这是因为 B=(B-A)+AB 见右图
B
A
(4)P(A+B)=P(A)+P(B)-P(AB) 称为广义加法法则
这是因为由图
A
B
A+B=A+(B-A)
由于A与B-A互斥故P(A+B)=P(A)+P(B-A) 再由(3)得证。可见，只需P(AB)=0加法法则就成立。若是多个事件之和，公式会变复杂。

事件发生的可能性完结

事故发生的可能性L判断准则

概率论-事件发生的可能性

事件发生的可能性

事件发生的可能性L判断准则

人教版五年级数学上册第四单元可能性-事件发生的可能性PPT课件

第1课时 事件发生的可能性

事件发生的可能性

事件发生的可能性

23.1事件发生的可能性

【同步备课】第四单元 第1课时 事件发生的可能性(教案)五年级数学上册 最新人教版

五年级上事件发生的可能性

事件发生的可能性L判断准则

概率论-事件发生的可能性

概率论-事件发生的可能性

第1课时事件发生的可能性

【同步备课】第四单元第1课时事件发生的可能性(教案)五年级数学上册最新人教版