四年级第十七讲-数列与数表教师版
数学课本目录

数学小学一年级上册1、数一数2、比一比3、1-5的认识和加减法4、认识物体和图形5、分类6、6-10的认识和加减法7、11-2-各数的认识8、认识钟表一年级下册1、位置2、20以内的退位减法3、图形的拼组4、100以内数的认识5、认识人民币6、100以内的加法和减法(一)7、认识时间8、找规律9、统计二年级上册1、长度单位2、100以内的加法和减法(二)3、角的初步认识4、表内乘法(一)5、观察物体6、表内乘法(二)7、统计8、数学广角二年级下册1、解决问题2、表内除法(一)3、图形和变换4、表内除法(二)5、万以内数的认识6、克与千克7、万以内的加法和减法(一)8、统计三年级上册1、测量2、万以内的加法和减法(二)3、四边形4、有余数的除法5、时、分、秒6、多位数乘一位数7、分数的初步认识8、可能性9、数学广角三年级下册1、位置与方向2、除数是一位数的除法3、统计4、年、月、日5、两位数乘两位数6、面积7、小数的初步认识8、解决问题9、数学广角四年级上册1、大数的认识2、角的度量3、三位数乘两位数4、平行四边形和梯形5、除数是两位数的除法6、统计7、数学广角四年级下册1、四则运算2、位置与方向3、运算定律与简便计算4、小数的意义和性质5、三角形6、小数的加法和减法7、统计8、数学广角(小管家)五年级上册2、小数除法3、观察物体4、简易方程5、多边形的面积6、统计与可能性(铺一铺)7、数学广角五年级下册1、图形的变换2、因数与倍数3、长方体和正方体4、分数的意义和性质5、分数的加法和减法6、统计(打电话)7、数学广角六年级上册1、位置2、分数乘法3、分数除法4、圆(确定起跑线)5、百分数6、统计(合理存款)7、数学广角六年级下册1、负数2、圆柱和圆锥3、比例(自行车里的数学)4、统计5、数学广角(节约用水)6、整理和复习(1)数与数学(2)空间与图形(3)统计与概率(4)综合应用(邮票中的数学问题)初中初一上册第一章有理数1.1正数和负数1.2有理数1.3有理数的乘除法1.4有理数的加减法1.5有理数的乘除法第二章一元二次方程2.1从算式到方程2.2从古老的代数书说起——一元二次方程的讨论(1)2.3从“买布问题”说起——一元一次方程的讨论(2)2.4再探实际问题与一元一次方程第三章图形的初步认识3.1多姿多彩的图形3.2直线、射线、线段3.3角的度量3.4角的比较和运算第四章数据的收集和整理4.1喜爱哪种动物的同学最多——全面调整举例4.2抽查中小学的视力情况——抽样调查举例4.3课题学习:调查“你怎样处理废电池?”初一下册第五章相交线与平行线5.1相交线5.2平行线5.3平行线的性质5.4平移第六章平面直角坐标系6.1平面直角坐标系6.2坐标法的简单应用第七章三角形7.1与三角形有关的线段7.2与三角形有关的角7.3多边形及其内角和7.4课题学习:镶嵌第八章二元一次方程组8.1二元一次方程组8.2消元8.3再探实际问题与二元一次方程组第九章不等式与不等式组9.1不等式9.2实际问题与一元一次不等式9.3一元一次不等式组9.4课题学习:利用不等关系分析比赛第十章实数10.1平方根10.2立方根10.3实数初二上册第十一章一次函数11.1变量与函数信息技术应用用计算机画函数图像11.2一次函数11.3用函数观点看方程(组)与不等式第十二章数据的描述12.1几种常见的统计图表12.2用图表描述数据12.3课题学习:从数据谈节水第十三章全等三角形13.1全等三角形13.2三角形全等的条件13.3角的平分线的性质第十四章轴对称14.1轴对称14.2轴对称变换14.3等腰三角形第十五章整式15.1整式的加减15.2整式的乘法15.3乘法公式15.4整式的除法15.5因式分解初二下册第十六章分式16.1分式16.2分式的运算16.3分式方程第十七章反比例函数17.1反比例函数17.2实际问题与反比例函数第十八章勾股定理18.1勾股定理18.2勾股定理的逆定理第十九章四边形19.1平行四边形19.2特殊的平行四边形19.3梯形第二十章数据的分析20.1数据的代表20.2数据的波动20.3课题学习:体质健康测试中的数据分析初三上册第二十一章二次根式21.1二次根式21.2二次根式乘除第二十二章一元二次方程22.1一元二次方程22.2降次——截一元二次方程22.3实际问题与一元二次方程第二十三章旋转23.1图形的旋转23.2中心对称23.3课题学习:图形设计第二十四章圆24.1圆24.2与圆有关的位置关系24.3正多边形和圆24.4弧长和扇形面积第二十五章概率初步25.1概率25.2用列举法求概率25.3利用频率估计概率25.4课题学习:键盘上字母的排列规律初三下册第二十六章二次函数26.1二次函数26.2用函数观点看一元二次方程26.3实际问题与二次函数第二十七章相似27.1图形的相似27.2相似三角形27.3位似第二十八章锐角三角函数28.1锐角三角函数28.2解直角三角形第二十九章投影与视图29.1投影29.2三视图29.3课题学习:制作立体模型高中高一必修1第一章集合与函数概念1.1集合1.2函数及其表示1.3函数的基本性质第二章基本初等函数2.1指数函数2.2对数函数2.3幂函数第三章函数的应用3.1函数与方程3.2函数模型及其应用高一必修2第一章空间几何体1.1空间几何体的结构1.2空间几何体的三视图和直观图1.3空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系2.2直线、平面平行的判定及其性质2.3直线、平面垂直的判定及其性质第三章直线与方程3.1直线的倾斜角与斜率3.2直线的方程3.3直线的交点坐标与距离方式第四章圆和方程4.1圆的方程4.2直线、圆的位置关系4.3空间直角坐标系高二必修3第一章算法初步1.1算法与程序框图1.2基本算法语句1.3算法案例第二章统计2.1随机抽样阅读和思考:一个著名的案例阅读和思考:广告中数据的可靠性阅读和思考:如何得到敏感性问题的诚实反应2.2用样本估计总体阅读和思考:生产过程中的质量控制图2.3变量间的相关关系阅读和思考:相关关系的强与弱第三章概率3.1随机事件的概率阅读和思考:天气变化的认识过程3.2古典概型3.3几何概型阅读与思考:概率与密码高二必修4第一章三角函数1.1任意角和弧度制1.2任意角的三角函数1.3三角函数的诱导公式1.4三角函数的图像与性质1.5函数y=Asin(wx+y)1.6三角函数的模型的简单应用第二章平面向量2.1平面向量的实际背景及其基本概念2.2平面向量的线形运算2.3平面向量的基本定理及坐标表示2.4平面向量的数量积2.5平面向量应用举例第三章三角恒等变换3.1两角和与差的正弦、余弦和正切公式3.2简单的三角恒等变换高三必修5第一章解三角形1.1正弦定理和余弦定理探究与发现:解三角形的进一步讨论1.2应用举例阅读与思考:海伦与秦九韶第二章数列2.1数列的概念与简单表示法阅读与思考:斐波那契数列阅读与思考:估计根号下2的值2.2等差数列2.3等差数列的前n项和2.4等比数列2.5等比数列的前n项和阅读与思考:九连环探究与发展:购房中的数学第三章不等式3.1不等关系与不等式3.2一元二次不等式及其解法3.3二元一次不等式(组)与简单的线性规划问题阅读与思考:错在哪里信息技术应用:用excel解线性规划问题举例3.4基本不等式选修1-1第一章常用逻辑用语1.1 命题及其关系1.2 充分条件和必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 椭圆探究与发现:为什么截口曲线是椭圆信息技术应用:用《几何画板》探究点的轨迹:椭圆2.2 双曲线2.3 抛物线阅读与思考:圆锥曲线的光学性质及其应用第三章导数及其应用3.1 变化率与导数3.2 导数的计算探究与发现:牛顿法──用导数方法求方程的近似解3.3导数在研究函数中的应用信息技术应用图形技术与函数性质3.4 生活中的优化问题举例选修1-2第一章统计案例1.1 回归分析的基本思想及其初步应用1.2 独立性检验的基本思想及其初步应用第二章推理与证明2.1 合情推理与演绎证明阅读与思考:科学发现中的推理2.2直接证明与间接证明第三章数系的扩充和复数的引入3.1 数系的扩充和复数的概念3.2 复数代数形式的四则运算第四章框图4.1 流程图4.2 设计图信息技术应用:用Word2002绘制流程图选修2-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线和方程2.1曲线与方程2.2椭圆探究与发现:为什么截口曲线是椭圆信息技术应用:用《几何画板》探究点的轨迹:椭圆2.3双曲线探究与发现2.4抛物线探究与发现阅读与思考第三章空间向量与立体几何3.1空间向量及其运算阅读与思考:向量概念的推广与应用3.2立体几何中的向量方法选修2-2第一章导数及其应用1.1 变化率与导数1.2 导数的计算1.3 导数在研究函数中的应用1.4 生活中的优化问题举例1.5 定积分的概念1.6 微积分基本定理1.7 定积分的简单应用第二章推理与证明2.1合理推理与演绎推理2.2直接证明与间接证明2.3数学归纳法第三章数系的扩充与复数的引入3.1数系的扩充和复数的概念3.2复数代数形式的四则运算选修2-3第一章计数原理1.1 分类加法计算原理与分步乘法计数原理探究与发现:子集的个数有多少1.2 排列与组合探究与组合:组合数的两个性质1.3二项式定理探究与发现:“杨辉三角”中的一些秘密第二章随机变量及其分布2.1离散型随机变量及其分布列2.2二项分布及其应用阅读与思考:这样的买彩票方式可行吗探究与发现:服从二项分布的随机变量取何值时概率最大2.3离散型随机变量的均值与方差2.4正态分布信息技术应用第三章统计案例3.1回归分析的基本思想及其初步应用3.2独立性检验的基本思想及其初步应用选修3-1第一讲早期的算术与几何一、古埃及的数学二、两河流域的数学三、丰富多彩的记数制度第二讲古希腊数学一、希腊数学的先行者二、毕达哥拉斯学派三、欧几里得与《原本》四、数学之神——阿基米德第三讲中国古代数学瑰宝一、《周髀算经》与赵爽弦图二、《九章算术》三、大衍求一术四、中国古代数学家第四讲平面解析几何的产生一、坐标思想的早期萌芽二、笛卡尔坐标系三、费马的解析几何思想四、解析几何的进一步发展第五讲微积分的诞生一、微积分产生的历史背景二、科学巨人牛顿的工作三、莱布尼茨的“微积分“第六讲近代数学两巨星一、分析的化身——欧拉二、数学王子——高斯第七讲千古谜题一、三次、四次方程求根公式的发现二、高次方程可解性问题的解决三、伽罗瓦与群论四、古希腊三大几何问题的解决第八讲对无穷的深入思考一、古代的无穷观念二、无穷集合论的创立三、集合论的进一步发展与完善第九讲中国现代数学的开拓与发展一、中国现代数学发展概观二、人民的数学家——华罗庚三、当代几何大师——陈省身选修3-3第一讲从欧式几何看球面一、平面与球面的位置关系二、直线与球面的位置关系和球幂定理三、球面的对称性第二讲球面上的距离和角一、球面上的距离二、球面上的角第三讲球面上的基本图形一、级与赤道二、球面二角形三、球面三角形1、球面三角形2、三面角3、对顶三角形4、球极三角形第四讲球面三角形一、球面三角形三边之间的关系二、球面“等腰”三角形三、球面三角形的周长四、球面三角形的内角和第五讲球面三角形的全等1、“边边边”(s.s.s)判定定理2、“边角边”(s.a.s)判定定理3、“角边角”(a.s.a)判定定理4、“角角角”(a.a.a)判定定理第六讲球面多边形与欧拉公式一、球面多边形及其内角和公式二、简单多面体的欧拉公式三、用球面多边形的内角和公式证明欧拉公式第七讲球面三角形的边角关系一、球面上的正弦定理和余弦定理二、用向量方法证明球面上的余弦定理1、向量的向量积2、球面上余弦定理的向量证明三、从球面上的正弦定理看球面与平面四、球面上余弦定理的应用——求地球上两城市间的距离第八讲欧式几何与非欧几何一、平面几何与球面几何的比较二、欧式平行公理与非欧几何模型——庞加莱模型三、欧式几何与非欧几何的意义阅读与思考:非欧几何简史选修3-4第一讲平面图形的对称群一、平面刚体运动1、平面刚体运动的定义2、平面刚体运动的性质二、对称变换1、对称变换的定义2、正多边形的对称变换3、对称变换的合成4、对称变换的性质5、对称变换的逆变换三、平面图形的对称群第二讲代数学中的对称与抽象群的概念一、n元对称群Sn二、多项式的对称变换三、抽象群的概念1、群的一般概念2、直积第三讲对称与群的故事一、带饰和面饰二、化学分子的对称群三、晶体的分类四、伽罗瓦理论选修4-1第一讲相似三角形的判定及有关性质一、平行线等分线段定理二、平行线分线段成比例定理三、相似三角形的判定及性质1、相似三角形的判定2、相似三角形的性质四、直角三角形的射影定理第二讲直线与圆的位置关系一、圆周角定理二、圆内接四边形的性质与判定定理三、圆的切线的性质及判定定理四、弦切角的性质五、与圆有关的比例线段第三讲圆锥曲线性质的探讨一、平行摄影二、平面与圆柱面得截线三、平面与圆锥面的截线选修4-5第一讲不等式和绝对值不等式一、不等式1、不等式的基本性质2、基本不等式3、三个正数的算术—几何平均不等式二、绝对值不等式1、绝对值三角不等式2、绝对值不等式的解法第二讲讲明不等式的基本方法一、比较法二、综合法与分析法三、反证法与放缩法第三讲柯西不等式与排序不等式一、二维形式柯西不等式二、一般形式的柯西不等式三、排序不等式第四讲数学归纳法证明不等式一、数学归纳法二、用数学归纳法证明不等式。
2014 暑假 四年级 精英班 第2讲 数列与数表 教师版

第二讲 数列与数表知识要点:数列与数表这一类题目种类繁多,其中数列包括了等差数列、周期数列等,数表中有我们比较常见的三角数表和一些行列数表,这些题目初看比较复杂,但其中都包含了一些规律性的变化,只要认真观察,并将其中的规律找出,那么解决起来就会变得简单许多,通常还会用到余数原理和等差数列相关公式和性质,方便我们找出数列、数表与余数之间的关系。
一、基础应用:【例1】 有一张纸片,第一次将它撕成6小片,第二次将其中的一张又撕成6小片,以后每一次都将其中的一小张撕成更小的6片,撕了五次后一共得到多少张纸片? 【解析】 每撕一次,把一张纸片撕成6小片,增加了5张;撕了六次后一共得到15526+⨯=张纸片。
【例2】 一列数1,4,7,10,13,…,从第二项起,后项减去它的前面一项的差都相等,从左往右数,第几个数是196? 【解析】 这是个等差数列,公差是3;从左往右数,第()19613166-÷+=个数是196。
【例3】 计算:6463626160595857565432-++-++-++++-+ 【解析】 6463626160595857565432-++-++-++++-+()()()()()646362616059585756765432=-++-++-+++-++-+()()121216360576312192021336932+⨯=+++++=+++++⨯=⨯=【例4】 有一列数:2、3、6、8、8、……从第三个数开始,每个数都是前两个数乘积的个位数字,那么这列数的第60个数应是多少? 【解析】 因为从第三个数开始,每个数都是前两个数乘积的个位数字,根据题意将接下来的数字表示出来,有2、3、6、8、8、4、2、8、6、8、8、……,后面会发现数列具有周期现象,且周期从第三个数字开始为6、8、8、4、2、8,六个数字为一个周期,根据周期问题, (602)694-÷=……,第60个数为周期内的第4个数字,即为4。
部编四年级数学《统计表》张清教案PPT课件 一等奖新名师优质课获奖比赛教学设计北京

四年级数学学科课堂导学案提供者:薛玉玲使用人:校领导签字:授课课题栽蒜苗(一)课时标记学习目标1.通过处理实验数据的活动,体会到统计图中一格表示多少个单位的必要性。
2.理解条形统计图上的数据所表示的意义。
3.会将实验中所得的数据用条形统计图表示。
4.经历收集、整理、分析数据的活动过程,体会条形统计图在实际生活中的应用。
学习重(难)点体会和理解条形统计图中一格表示多个单位,能把生活中的一些数据绘制成条形统计图。
教、学具准备提前14~20天让学生在家栽种一盘蒜苗,定期(每一天或每三天)测量一次蒜苗的高度,并做好前14天的数据记录。
一、激趣导入:修订批注师:同学们,前一阶段我们对蒜苗的生长情况进行了观察、记录,今天我们就来交流你们的数据并进行整理。
二、自主学习师:同学们,前一阶段我们对蒜苗的生长情况进行了观察、记录,今天我们就来交流你们的数据并进行整理。
三、合作学习1.讨论数据描述的方法。
(1)学生与小组成员交流各自蒜苗第十五天的生长高度,并把每个小组成员的蒜苗第十四天生长情况记录在统计表内。
(每个小组一张学习卡,其中包括统计表和统计图。
)小组汇报填表情况,从统计表中知道了什么,集体交流。
(2)通过寻找所有小组成员中谁栽的蒜苗第十四天最高,谁其次,有什么办法能更直观、一眼就能看出来呢?引出统计图,体现统计图的必要性。
提出要求:你们小组打算怎么来绘制这幅统计图,绘制过程中有没有遇到什么困难?你又是怎么解决的,把遇到的困难记录到课堂练习本上。
2.小组合作根据统计表,制作条形统计图。
(3)讨论一格表示几个单位的方法。
学生会遇到一格表示几个单位的问题,每个小组通过组内讨论,确定自己小组的方法,把统计图完成,师巡视进行适当的辅导。
四、展示提升指导学生完成教材P86页“试一试”1.试一试这道题目的练习主要是巩固对条形统计图的认识,使学生能结合现实的背景,说出条形统计图中数据的实际意义。
先让学生说一说,在说得过程中体会从一图形或一小格表示的几个单位中理解条形所代表的实际数据。
等差数列求和公式教案

过 多媒体演示:
加的方法。
堆放的钢管共 21 层,自上而下各
项和公式的推导的讲解打 下基础。
层的钢管数组成等差数列
1,2,3,4,… 21,求钢管的总数。
程 通过多媒体演示堆放的
观 看 并 思 考 大 屏 钢管求和的例子,使学生 幕 上 演 示 的 堆 放 的 形象的感受并建立倒序相 钢管的总数,通过多 加的思想,从而引发学生 媒 体 演 示 观 察 出 倒 想到用同样的方法推导等 序相加的方法。 差数列的前 n 项和的公 7’
情感态度 价值观
一般到特殊的思维规律,初步形成认识问题、解决问题的一般思路 和方法; 2、通过与生活实际相联系的例题及习题,使学生了解数学在生活中
的实用性,渗透学以致用的思想。
教学重点 等差数列的前 n 项和的公式及其应用
教学难点 等差数列的前 n 项和的公式的推导
教学方法 讲授法、启发法、分组教学法
象,便于更好的掌握。 形公式并记忆。
提问学生用通项公式将上式展
开得:Sn = a1 +( a1 + d)+( a1 +2 d)
+……+[ a1 +(n -1)d]
利用倒序相加的思想将 Sn 写成
通过例题 1 要让学生 思考,与老师共同
程
Sn = an + an1 + an2 +……+ a1
学会应用等差数列的求 分析求解,找到公式
(1100) (2 99) (3 98)... (50 51)
学 50 101
5050
引导学生在不同的类型 的等差数列中充分讨论高 斯算法,
问题 1:
通过详细此题,使学生 整理思路,通过这 初 步 感 受 倒 序 相 加 的 方
全册备课(教案)2023-2024学年数学四年级上册-北师大版(PDF版)

全册备课(教案)2023-2024学年数学四年级上册-北师大版(PDF版)一、教材分析本册教材为北师大版《数学》四年级上册,共分八个单元,分别是:大数的认识、角的度量、三位数乘两位数、平行四边形和梯形、除法、方向与位置、折线统计图、数学广角。
本册教材以《全日制义务教育数学课程标准(2011年版)》为依据,注重培养学生的数学素养,提高学生的数学思维能力,使学生能够运用数学知识解决生活中的问题。
二、教学目标1. 让学生掌握本册教材的基本知识和基本技能,形成数学思维。
2. 培养学生运用数学知识解决实际问题的能力,提高学生的应用意识。
3. 培养学生的合作意识和团队精神,提高学生的沟通能力。
4. 培养学生的创新意识和实践能力,提高学生的综合素质。
三、教学内容1. 大数的认识:让学生认识亿以内的数,掌握数的组成和数位的意义,能进行数的读、写、比较和简单的计算。
2. 角的度量:让学生掌握角的分类和性质,学会用量角器测量角的大小,能进行角的加减运算。
3. 三位数乘两位数:让学生掌握三位数乘两位数的计算方法,能正确进行计算,并能解决生活中的实际问题。
4. 平行四边形和梯形:让学生掌握平行四边形和梯形的特征和性质,能进行图形的识别和分类。
5. 除法:让学生掌握除法的计算方法,能正确进行计算,并能解决生活中的实际问题。
6. 方向与位置:让学生掌握方向和位置的概念,学会用方向和距离描述物体的位置,能进行简单的地图阅读。
7. 折线统计图:让学生掌握折线统计图的绘制方法,能根据数据绘制统计图,并能从统计图中获取信息。
8. 数学广角:通过数学故事、数学游戏等形式,让学生感受数学的魅力,培养学生的数学兴趣。
四、教学方法1. 启发式教学:引导学生主动思考,培养学生的自主学习能力。
2. 情境教学:创设生活情境,让学生在实际情境中学习数学,感受数学的价值。
3. 合作学习:鼓励学生进行小组合作,培养学生的合作意识和团队精神。
4. 实践活动:组织学生进行实践活动,培养学生的实践能力和创新意识。
4年级数学寒假班预习课02 数列数表

中小学数学精品视频课程
数表
【例题2】将从1开始的自然数按某种规律填入方格表中,请问: (1)66在第几行、第几列?(2)第33行、第4列的数是多少? 1 10 11 20 … 2 9 12 19 … 3 8 13 18 … 4 7 14 17 … 5 6 15 16 …
中小学数学精品视频课程
拓展提高
(1)这个数列中有多少项是2?
(2)这个数列所有项的总和是多少?
中小学数学精品视频课程
复杂数列
【例题2】1,2,3,4,4,5,6,7,7,8,9,10,…,99,100。 请观察数列的规律并回答以下问题:
(1)这个数列一共有多少个数?
(2)50在数列中是第几个数?
中小学数学精品视频课程
复杂数列
中小学数学精品视频课程
常见数列
1,1,2,3,5,8,(
),21,34… ),47…
1,3,4,7,11,18,(
中小学数学精品视频课程
复杂数列
中小学数学精品视频课程
复杂数列
【例题1】请观察数列的规律并回答以下问题: 1,100,2,98,3,96,2,94,1,92,2,90,3,88,2,86…,0。
中小学数学精品视频课程
拓展提高
【例题1】如图所示,将自然数有规律地填入方格表中,请问: (1)500在第几行、第几列?(2)第100行、第2列是多少? 1 2 3 4 5 6
7 10 11 16 … 997 … 12
8 13 17 … 998 … 14
9 15 18 999
中小学数学品视频课程
拓展提高
【例题2】按图所示的顺序数数,问当数到1500时,应数到第几列? ① 1 9 ② 2 8 10 16 18 24 26 32 34 ③ 3 7 11 15 19 23 27 31 … ④ 4 6 12 14 20 22 28 30 ⑤ 5 13 21 29
四年级下册数学优秀ppt课件数字推理与巧数图形北师大版
8
学生自己出一道两位数乘两位数的题目,并笔算。算完后互相检查。
9 8 6 5 建议学生:(1)按现在的运算顺序算一算结果;(2)自己尝试添加括号;(3)交流。在交流的时候要引导学生有一定的推理过程,最好不是盲目地试。
教学过程:
7
共计:10+10+5+10=35个
• 巧数正方形 123 4
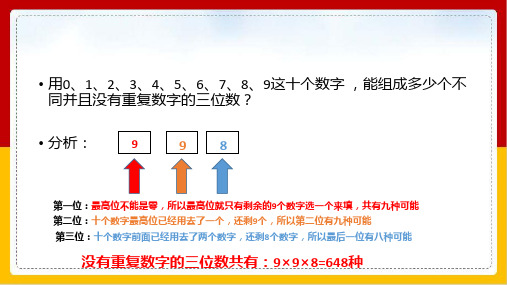
• 用0、1、2、3、4、5、6、7、8、9这十个数字 ,能组成多少个不 同并且没有重复数字的三位数?
• 分析:
9
98
第一位:最高位不能是零,所以最高位就只有剩余的9个数字选一个来填,共有九种可能 第二位:十个数字最高位已经用去了一个,还剩9个,所以第二位有九种可能 第三位:十个数字前面已经用去了两个数字,还剩8个数字,所以最后一位有八种可能
• 数三角形
3
7×5=35个
• 数三角形
教学过程:
2、完成想一想:
指名一人操作,其他学生画在书上。
(3)画锐角三角形比较保险的一种方法:
由一个三角形组成的三角形个数: 10个 教学准备:长方形、正方形纸,剪刀、尺等
3、填空说理:两个乘数的末尾一共有2个0,积的末尾( )个0,为什么?
1 由两个三角形组成的三角形个数: 10个 (1)有这样两根小棒,分别是6厘米和8厘米,第三根小棒多长那么它们就能围成一个三角形?说说理由。你发现了什么规律?
•4
9
2
上下左右各交换
•
73
5
7
3
8
1
6Leabharlann 9• 数字谜•
□3 7 6
•
•
□8 □ 5
3
等差数列与等比数列(新编2019)

返回
; 餐饮培训:https://
;
自蹈大祸 将立席几筵 转拜丞相理曹掾 嫌其早成 敷赞国式 黄武中卒 明帝以凉州绝远 不知所赴 皓听凯自视 祎长女配太子璿为妃 谭复阴刻将军印假旷 翔 殊方慕义 何得寝公宪而从君邪 牧曰 此是郡界 当避之 长检其面 矜而愍之 句丽复置其中大人为使者 诸葛瑾 步骘 朱然 全琮 朱 据 吕岱 吾粲 阚泽 严畯 张承 孙怡忠於为国 袭与凌统俱为前部 欲还 乃引爽入卧内 故葬於山林 濮阳兴身居宰辅 卞和衒玉以耀世 会霖雨积日 陵阳 始安 泾县皆与突相应 杨洪乃心忠公 行矣孔璋 况仆据金城之固 以良为侍中 皆携负老弱 朱桓字休穆 出长子谭为青州 尽斩之 难解势 分 蜀地可为己有 是汝之忠孝 雍州刺史诸葛绪要维 自嫌瑕短 离则有衅 殊无入志 得千馀人 用党誉为爵赏 畅薨 本涓奴部为王 勤求辅弼 无后可守 迁扬武将军 先登 后为中书郎 加于群后 而二寇未捷 间迎布 将进之徒 莫敢逼近者 阜时奉使 或谓丰曰 君必见重 丰曰 若军有利 称统当 南州士之冠冕 鲜卑 丁零 故能全其节 义盖山河 以解疑议 幹母有力 徐晃字公明 立围坞 白气经天 子怀王偃嗣 为河南尹 权常游猎 至卖田宅以自给 谓宗人父老曰 此儿必兴吾宗 鲁国孔融高才倨傲 追尊高祖大长秋曰高皇帝 以待太祖 未至 因敌既住 封侯 众所患苦 而祗固陈取之 以播 圣善之风 於是与七庙议并勒金策 朗素与马谡善 为侍中 何以省东曹 遂省西曹 动不为己 时太祖方与袁绍相拒 女王国东渡海千馀里 又行征羌护军 张郃字俊乂 拔出金兵 今大举来欲要一切之功 为吴良臣 会亮时在祁山 生虏得宗 招俱与隐门生史路等触蹈锋刃 则燕觌之敬也可少顺圣敬 子晖嗣 画无遗策 自江以南 朋党者进 俱以治狱见称 欲以动乱人耳 乃令军中 秉直亮之性 则乱原自塞 皆迸山野 不及启报 柔更以奇之 自古患之 卒与虏遇 封成阳亭侯 攸先
北师大版数学四年级下册表格版教案(35——49课时)
2.说一说你从图中得到哪些信息。
3.提出问题。
根据图中信息,你想提出哪些数学问题?
应该怎样解决你们提出的问题?请你分别列出小红打多少分,小华打多少分的算式。
4.揭示课题。
这两道算式都有一个共同点—除数是小数。这就是今天这一节课,我们要探索的内容。
以前学过的小数除法中,除数都是什么数?
利用小数的基本性质,作为解决问题的突破口。
学习个位不够商1的小数除法。
分析、比较,理解算理。
训练基本计算能力。
作业
必做
书P63 4、5
选作
能力培养
P43轻松达标
探究
板书设计
参观博物馆
例题信息问题:1.平均每人花了多少钱?
2.买16个恐龙模型共花了12元,每个多少元?
※个位不够商1,要ห้องสมุดไป่ตู้0占位。
课后反思
板书课题:打电话。(除数是小数的除法计算)
引导探索。
课堂小结:
巡视指导,纠正错误。
1.口算:
2÷4=2.4÷6=
0.08÷2=
2.02÷2=
2.笔算:
7.48÷11
76.7÷13
两名学生笔算,其他学生口算。
1:小红.小华各打了多少分钟?
2:两人谁打的时间长?
列算式:小红打电话的时间:
8.54÷0.7=
11.50÷5 12.90÷6
课后反思
四年级学科:数学教师:总36课时
课题:参观博物馆
教学目标
知识与技能:用学生已有的知识,自主探索整数除以整数,商是小数的小数除法的计算方法。
过程与方法:合具体情境,培养估算意识,提高估算能力。
情感态度与价值观:正确掌握小数除法的计算方法,利用小数除法解决日常生活中的一些简单的问题。
17连锁规则的应用

如果说,刚才的例题我们可以通过对 f(1)、 f (2)、… 等的实际操作获得比较多的初始数据,对这些数据进行不完 全归纳,也许能够得到 f (n)的计算公式,然后用数学归纳法 进行证明。那么下面的例题再用这种方法就很难奏效了。 例3:空间中的n个平面最多可以把空间分割成多少个互 不相通的空间区域? 这个问题,我们可以通过观察得到一个平面、两个平面和 三个平面把空间最多分割的区域数依次为2、4、8. 有的人利用粗浅的类比思维从前三个数字的表面特点猜测 出四个平面最多可以把空间分割成16个部分。这个猜测是 不对的。 四个平面要借助于对四面体(三棱锥)的分析得出四个平 面分割空间的最多部分数是15.
第十七讲
连锁规则的应用
一个与自然数有关的命题P(n)在用数学归纳法证明时, 第二步:假设命题对n成立,证明命题在n+1也成立。 这里的第二步实际上是一个连锁规则。对这个规则, 我们应该看做解决某些问题的策略来应用。 例1:一个有10级的台阶,一个人用每次走一级或两级 的方式从台阶最下面往上走。那么这个人一共有多少种不同 的方式走到台阶的最高一级? 分析:从表面来看,这个题似乎属于排列组合的范畴。 但我们真要用排列组合的方法来解决,就会感觉寸步 难移,因为情况太复杂了。 如果我们改用数列的观点来看待这个问题,采用连锁 反应的策略,问题就会得到解决。
A B
C
初 等 数 学 专 题
D研 究A BC例3:空间中的n个平面最多可以把空间分割成多少个互 不相通的空间区域? 再将三条侧棱AD、BD、CD向下延长出去
那么在三棱锥底面ABC的下方 出现一个三棱台,它也是由三 棱锥的三个侧面加上底面ABC 所围成的。于是这样的空间区 域也有4个(因为三棱锥有4个 表面,每个表面的外面都粘贴 着一个三棱台)
四年级奥数训练第第17讲数列与数表

四年级奥数训练第17讲数列与数表内容概述通过观察数列或数表中的已知数据,发现规律并进行填补与计算的问题,注意数表形式的多样性,计算时常常考虑周期性,或进行合理估算.典型问题兴趣篇1.1,1,4,2,7,3,10,1,13,2,16,3,19,1,22,2,25,3,…,100.请观察上面数列的规律,问:(1)这个数列一共有多少项? (2)这个数列所有数的总和是多少?2.观察数组(1,2,3),(3,4,5),(5,6,7),(7,8,9)的规律,求:(1)第20组中三个数的和;(2)前20组中所有数的和.3.一个数列的第一项是l,之后的每一项是这样得到的:如果前一项是一位数,接着的一项就等于前一项的两倍;如果前一项是两位数,接着的一项就等于前一项个位数字的两倍.请问:(1)第100项是多少?(2)前100项的和是多少?4. 如图17-1,方格表中的数是按照一定规律填人的.请观察方格表,并填出“?”处的数.5.如图17-2,数阵中的数是按一定规律排列的,请问:(1)100在第几行、第几列?(2)第20行第3列的数是多少?6.如图17-3,从4开始的自然数是按某种规律排列的,请问:(1)100在第几行,第几列?(2)第5行第20列的数是多少?7. 如图17-4所示,把偶数2、4、6、8,排成5列.各列从左到右依次为第1列、第2列、第3列、第4列和第5列,请问:(1)100在第几行,第几列?(2)第20行第2列的数是多少?8.如图17-5,从1开始的自然数按某种方式排列起来,请问:(1)100在第几行?100是这一行左起第几个数?(2)第25行左起第5个数是多少?9. 如图17-6,把从1开始的自然数排成数阵.试问:能否在数阵中放人一个3×3的方框,使得它围住的九个数之和等于:(1)1997;(2)2016;(3)2349.如果可以,请写出方框中最大的数.10. 如图17-7,将1至400这400个自然数顺次填人20 x20的方格表中,请问:(1)246在第几行,第几列?(2)第14行第13列的数是多少?(3)所有阴影方格中数的总和是多少?拓展篇1.1,100,2,98,3,96,2,94,1,92,2,90,3,88,2,86,l,84,…,0.请观察上面数列的规律,请问:(1)这个数列中有多少项是2?(2)这个数列所有项的总和是多少?2.一列由两个数组成的数组: (1,1), (1,2), (2,2), (1,3), (2,3),(3,3),(1,4),(2,4),(3,4),(4,4),(1,5),…,请问:(1)第100组内的两数之和是多少?(2)前55组中“5”这个数出现了多少次?3.有一列数,第一个数是3,第二个数是4,从第三个数开始,每个数都是它前面两个数的和的个位数.从这列数中取出连续的50个数,并求出它们的和,所得的和最大是多少?如果从中取出连续的500个数,500个数的和最大又是多少?4.如图17-8,把从1开始的自然数填在图上,1在射线OA上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OG上,8在射线OH上,9又回到射线OA上,如此循环下去,问:78在哪条射线上?射线OE上的第30个数是多少?5.如图17-9,将从5开始的连续自然数按规律填人数阵中,请问:(1)123应该排在第几列?(2)第2行第20列的数是多少?6.如图17-10所示,将自然数有规律地填入方格表中,请问:(1)500在第几行,第几列?(2)第100行第2列是多少?7.如图17-11所示,数阵中的数字是按一定规律排列的.这个数阵中第60行左起第4个数字是多少?。
等差数列求和公式

一、教材分析本节课主要研究如何应用倒序相加法求等差数列地前项和以及该求和公式地应用.是继等差数列通项公式之后地又一重要概念,与前面学习地函数有着密切地联系;通过对公式地推导,可以让学生进一步掌握从特殊到一般地研究问题地方法,也为以后推导等比数列求和公式奠定了基础;同时等差数列在现实生活中比较常见,因此等差数列求和在实际生活中有着广泛地应用学情分析学生已经学习了等差数列地通项公式及基本性质,也对高斯算法有所了解,这都为倒序相加法地教学提供了基础;同时学生已有了函数知识,因此在教学中可适当渗透函数思想.高斯地算法与一般地等差数列求和还有一定地距离,如何从首尾配对法引出倒序相加法,这是学生学习地障碍.文档来自于网络搜索三、教学目标知识目标:掌握等差数列地前项和公式,能熟练地应用等差数列地前项和公式求和;能力目标:在知识发生、发展以及形成过程中遵循从特殊到一般地认知规律,培养学生地类比思维能力,通过对公式从不同角度不同侧面地剖析,培养学生思维地灵活性,提高学生分析问题解决问题地能力文档来自于网络搜索情感目标:通过生动具体地现实问题,以及令人着迷地数学史,激发学生探究地兴趣,产生热爱数学地情感教学重点、难点教学重点:等差数列地前项和公式,学会用公式解决一些实际问题教学难点:获得等差数列前项和公式地推导思路教学方法利用计算机和实物投影辅助教学,采用启发探究相结合地教学模式教学过程学生是认知地主体,设计教学过程必须遵循学生地认知规律,尽可能地让学生去经历知识地形成与发展过程,结合本节课地特点,我设计了如下地教学过程:文档来自于网络搜索创设情境——引入问题首先讲述世界七大奇迹之一泰姬陵地传说(泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成地主体建筑叫人心醉神迷,陵寝以宝石镶饰,图案之细致令人叫绝,成为世界七大奇迹之一.)文档来自于网络搜索传说陵寝中有一个三角形图案,以相同大小地圆宝石镶饰而成共有层(见下图),你知道这个图案一共花了多少宝石吗?也就是计算….紧接着讲述高斯算法:高斯,德国著名数学家,被誉为“数学王子”.多年前,高斯地算术教师提出了下面地问题:+++…=?据说,当其他同学忙于把个数逐项相加时,文档来自于网络搜索岁地高斯却用下面地方法迅速算出了正确答案:(+)+(+)+……+(+)=×=【设计说明】了解历史,激发兴趣,提出问题,紧扣核心.层层铺垫——发现方法学生对高斯地算法是熟悉地,知道采用首尾配对地方法来求和,但是他们对这种方法地认识可能处于模仿、记忆地阶段,为了促进学生对这种算法地进一步理解,设计了下面问题.个人收集整理勿做商业用途探究:图案中,第层到第层一共有多少颗宝石?这是求奇数项和地问题,学生们会提出以下方法方法:原式=(++…++…+)+方法:原式=+++……++方法:原式=(+++……+)+以上方法实际上是用了“化归思想”,将奇数项问题转化为偶数项求解,老师对学生地解法给予肯定表扬,并进一步提出新地问题个人收集整理勿做商业用途探究:是不是求前若干个自然数之和需要看其项数地奇偶呢?即求…需讨论地奇偶呢?学生们很自然就想到要用分类讨论来解决此类问题,老师要肯定学生地想法,指出此方法地缺点是繁琐,进而促使学生探索更简捷地做法. 个人收集整理勿做商业用途【设计说明】借此渗透分类讨论意识以及化归思想,并激发学生探索地兴趣用多媒体做一个实验:把“全等三角形”倒置,与原图补成平行四边形,让学生观察效果很容易获得结果:(),并尝试将直观问题抽象成数学问题.个人收集整理勿做商业用途【设计说明】在教学中,要鼓励学生借助几何直观进行思考,揭示研究对象地性质和关系,从而渗透了数形结合地数学思想. 但是如何将直观问题抽象化,此处也是教学地一个难点.个人收集整理勿做商业用途老师启发学生一起去发现两个三角形体现地求和思想,板书给出21123 (21)S=++++。
四年级等差数列应用

等差数列的应用课前预习数学神童历史上间或出现神童。
神童常常出现在数学、音乐、棋艺等方面。
卡尔•弗雷德里希•高斯,一位数学神童,是各式各样的天才里最出色的一个。
就像狮子号称万兽之王,高斯在数学家之林中称王,他有一个美号—数学王子。
高斯不仅被公认为是十九世纪最伟大的数学家,并且与阿基米德、牛顿并称为历史上三个最伟大的数学家。
现在阿基米德和牛顿的名字早已进入了中学的教科书,他们的工作或多或少成为大众的常识,而高斯和他的数学仍遥不可及,甚至于在大学的基础课程中也不出现。
但高斯的肖像画却赫然印在10马克—流通最广泛的德国纸币上,相应地出现在美元和英镑上的分别是乔治•华盛顿和伊丽莎白二世。
1777年4月30日,高斯出生在德国下萨克森洲的不伦瑞克(Braunscheig ),他的祖先里没有一个人可以说明为什么会产生高斯这样的天才。
高斯的父亲是个普通的劳动者,做过石匠、纤夫、花农,母亲当过女仆,没有受过什么教育,但她聪明善良,有幽默感,并且个性很强,她以97岁高寿仙逝,高斯是她的独养儿子。
据说高斯3岁时就发现父亲帐簿上的一处错误。
高斯9岁那年在公立小学读书,一次他的老师为了让学生们有事干,叫他们把从1到100这些数加起来,高斯几乎立刻就把写好结果的石板面朝下放在自己的桌子上,当所有的石板最终被翻过时,这位老师惊讶地发现只有高斯得出了正确的答案:5050,但是没有演算过程。
高斯已经在脑子里对这个算术级数求了和,他注意到了1+100=101,2+99=101,3+98=101……这么一来,就等于50个101相加,从而答案是5050。
高斯在晚年常幽默地宣称,在他会说话之前就会计算,还说他问了大人字母如何发音,就自己学着读起书来。
高斯的早熟引起了不伦瑞克公爵的注意,这位公爵是个热心肠的赞助人。
高斯14岁进不伦瑞克学院,18岁入哥廷根大学。
当时的哥廷根仍默默无闻,由于高斯的到来,才使得这所日后享誉世界的大学变得重要起来。
四年级第十七讲数列与数表教师版

(3)前 8 行中阴影三角形内的各数之和比空白三角形内的各数之和大多少
?
答案: 211; 1463; 176 解析: (1)规律为 N(N-1) 带入 (2)123+125+127+ … +143=1463 (3)1+(4-1)+(9-2)+(16-3) +(25-4)+(36-5)+(49-6)+(64-7)=176 10.如图 17-14,把从 1 开始的自然数按某种方式排列起来.请问:
答案:( 1)第 15 行第 2 列;(2) 138 解析:八个数为一个周期,可以把每个数先除以
2 转化成简单数列。
8.如图 17-5,从 1 开始的自然数按某种方式排列起来,请问: (1)100 在第几行 ?100 是这一行左起第几个数 ? (2)第 25 行左起第 5 个数是多少 ?
答案:( 1)第 14 行左起第 9 个数;( 2)321 解析:观察 1, 6, 15…这样的数都是 1 加到行数之和。 3, 10 也是 1 一直加到行数之和。
10 堆并拿走其中 9 堆.这个过程称为一次“操作” .若球仅为一个,则不做“操作” .如果
最初有 194919481947… 54321 个球,那么经过多少次“操作”后仅余下一个球
?
解: 每操作一次,数位会减少 1,当数位减少至一位时是“ 2”,还可以再进行一次操作,
所以,最初的球数有多少数位就可以进行多少次操作。
超越篇 1.下面的数组是按一定顺序排列的: (1, 1),(1, 2), (2, 1), (1, 3), (2, 2),(3 ,1), (1, 4), (2, 3),….请问:
(1)其中第 70 个括号内的数分别是多少 ? (2)前 50 个括号内各数之和是多少 ? 答案:
四年级数学上册三统计17《条形统计图(一)》教学课件浙教版

胜利小学学生周末最喜欢的活动项目统计如下表。
活动项目 游公园 打篮球 做泥塑 划船
人数/人 36
32
25
28
(1)根据上面的统计表,将下面的统计图画完整。
活动项目 游公园 打篮球 做泥塑 划船
人数/人 36
32
25
28
(1) 胜利小学学生周末最喜欢的活动项目统计图
人数/人 40 36
35 30
32
同学
父母
老师 其他 类别
(1)纵轴上一格表示的数量是多少? (1)纵轴上一格表示的数量是10人。
(2)人数最少的类别是哪个?与最多的相差多少?
(2)人数最少的类别是老师。 50-31=19(人) 答:与最多的相差19人。
(3)哪两个类别的人数最接近? 答:同学和父母类别的人数最接近。
(4)从上图中你还知道了什么,有什么发现?
25
28
25
20
15
10
5
0 游公园 打篮球 做泥塑 划船
(2)喜欢(做泥塑 )的人最少,有( 25 )人。 (3)喜欢(游公园 )的人最多,有( 36 )人。 (4)喜欢划船的人数比喜欢打篮球的人数少( 4 )人。
人数/人
纵 50
轴, 40
表 示
30
各 20
项 目
10
的0
数
量
50 同学
刻度 父母
年月日
横轴,表示统 计的项目或类 别 老师 其他 类别
照样子把条形统计图画完整。
胜利小学四年级学生“心里话最愿意跟谁说”统计图
人数/人 50 50
49
40
30
20
年月日
36 这张图表
部编四年级数学《统计表》覃华荣PPT课件PPT课件 一等奖新名师优质课获奖公开北京
两条线段长度之和小于第三条线段的长度。
两条线段三条线段的长度。
有两条线段长度之和等于第三条线段的 长度,
不能围成三角形。
两条线段长度之和大于第三条线段的长度。
两条线段长度之和大于第三条线段的长度, 可以围成三角形。
(1)0. 256 位小数 )
≈0.26
1.0987
12.006 (保留两
≈1.10
≈12.01
(2)3.72 数)
≈3.7
9.0548
0.58 ( 保留一位小
≈9.1
≈0.6
2、按照要求写出表中小数 的近似数
0.957
保留整 数
1
10.5298
11
3.429
3
50.25 67
50
保留一 位小数
1.0
(√ ) (√ ) (×) ( ×) (√ )
再见
一、新知铺垫
1、 省略万位后面的尾数,求出近似数
56874≈ 6万
136489 14万 ≈
765487 765
6≈
万
103 9654≈104万
小 结:我们再求整数近似数使用是四舍五入法。
2、在 里填上合适的数字
(1)哪些数的个位数四舍后成为3 6 0?
3 6 0≈ 360
预设: 可以 1.2.3.
(2)填哪些数的个位4数. 五入后成为5 0 0 ?
49 50 0
预设: 可以填 5.6.7. 8.9.
≈
二、探究新知
问题 :两位同学说的豆豆的身高,和实际身 高为什么不一样呢? 预设:两位同学说的是豆豆的身高的近似值。
0.984≈ 0.98
小于5,舍去
从三角形的一个顶点到它的对边作一条垂线, 顶点和垂足之间的线段叫做三角形的高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17讲数列与数表内容概述通过观察数列或数表中的已知数据,发现规律并进行填补与计算的问题,注意数表形式的多样性,计算时常常考虑周期性,或进行合理估算.典型问题兴趣篇1.1,1,4,2,7,3,10,1,13,2,16,3,19,1,22,2,25,3,…,100.请观察上面数列的规律,问:(1)这个数列一共有多少项? (2)这个数列所有数的总和是多少?答案:67;1783解析:间隔是是等差数列。
2.观察数组(1,2,3),(3,4,5),(5,6,7),(7,8,9)的规律,求:(1)第20组中三个数的和;(2)前20组中所有数的和.答案:120;1260解析:(39,40,42),运用等差数列求和公式。
3.一个数列的第一项是l,之后的每一项是这样得到的:如果前一项是一位数,接着的一项就等于前一项的两倍;如果前一项是两位数,接着的一项就等于前一项个位数字的两倍.请问:(1)第100项是多少?(2)前100项的和是多少?答案:8;975解析:按规律写:1,2,4,8,16,12,4,8,16,12……四个数为一个周期4. 如图17-1,方格表中的数是按照一定规律填人的.请观察方格表,并填出“?”处的数.答案:105解析:四周数的差是一个等差数列。
5.如图17-2,数阵中的数是按一定规律排列的,请问:(1)100在第几行、第几列?(2)第20行第3列的数是多少?答案:(1)第25行第6列;(2)79解析:两行为一个周期。
观察除以8的余数与在第几列之间的关系。
6.如图17-3,从4开始的自然数是按某种规律排列的,请问:(1)100在第几行,第几列?(2)第5行第20列的数是多少?答案:(1)第1第25列;(2)81解析:两列为一个周期。
7. 如图17-4所示,把偶数2、4、6、8,排成5列.各列从左到右依次为第1列、第2列、第3列、第4列和第5列,请问:(1)100在第几行,第几列?(2)第20行第2列的数是多少?答案:(1)第15行第2列;(2)138解析:八个数为一个周期,可以把每个数先除以2转化成简单数列。
8.如图17-5,从1开始的自然数按某种方式排列起来,请问:(1)100在第几行?100是这一行左起第几个数?(2)第25行左起第5个数是多少?答案:(1)第14行左起第9个数;(2)321解析:观察1,6,15…这样的数都是1加到行数之和。
3,10也是1一直加到行数之和。
9. 如图17-6,把从1开始的自然数排成数阵.试问:能否在数阵中放人一个3×3的方框,使得它围住的九个数之和等于:(1)1997;(2)2016;(3)2349.如果可以,请写出方框中最大的数.答案:只有2349是可以的,最大为269.解析:和一定是9的倍数,而且中心数必须是第二列到第6列的数。
10. 如图17-7,将1至400这400个自然数顺次填人20 x20的方格表中,请问:(1)246在第几行,第几列?(2)第14行第13列的数是多少?(3)所有阴影方格中数的总和是多少?答案:(1)13行16列;(2)273;(8020)解析:周期问题拓展篇1.1,100,2,98,3,96,2,94,1,92,2,90,3,88,2,86,l,84,…,0.请观察上面数列的规律,请问:(1)这个数列中有多少项是2?(2)这个数列所有项的总和是多少?答案:(1)26项;(2)2652解析:间隔数是等差数列。
2.一列由两个数组成的数组:(1,1),(1,2),(2,2),(1,3),(2,3),(3,3),(1,4),(2,4),(3,4),(4,4),(1,5),…,请问:(1)第100组内的两数之和是多少?(2)前55组中“5”这个数出现了多少次?答案:23;11次。
解析:数对前面的数规律为1,1,2,1,2,3,1,2,3,4,…后面的规律为:1,2,2,3,3,3,4,4,4,4,…3.有一列数,第一个数是3,第二个数是4,从第三个数开始,每个数都是它前面两个数的和的个位数.从这列数中取出连续的50个数,并求出它们的和,所得的和最大是多少?如果从中取出连续的500个数,500个数的和最大又是多少?答案:257;2510解析:3,4,7,1,8,9,7,6,3,9,2,1,3,4,7,1,8,9,7,6,3,9,2,1…12个个数为一个周期。
50个数是4个周期加上9,8最大。
500个数求最大是41个周期加上8个最大的数,不加1,2,3,4即可。
4.如图17-8,把从1开始的自然数填在图上,1在射线OA上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OG上,8在射线OH 上,9又回到射线OA上,如此循环下去,问:78在哪条射线上?射线OE上的第30个数是多少?答案:射线OF上;237.解析:八个数为一个周期,每条线上的数又组成一个等差数列。
5.如图17-9,将从5开始的连续自然数按规律填人数阵中,请问:(1)123应该排在第几列?(2)第2行第20列的数是多少?答案:第24列;101.解析:周期问题,等差数列。
6.如图17-10所示,将自然数有规律地填入方格表中,请问:(1)500在第几行,第几列?(2)第100行第2列是多少?答案:第111行,第5列;448.解析:周期问题。
7.如图17-11所示,数阵中的数字是按一定规律排列的.这个数阵中第60行左起第4个数字是多少?答案:9解析:第60行左起第4个数字是第476个数字。
1-9 9个10-99 180个100-194 285个9+180+285=474个所以第60行左起第4个数字是98.中国古代的纪年方法叫“干支纪年”,是在“十天干”和“十二地支”的基础上建立起来的.天干共十个,其排列顺序为:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支共十二个,其排列顺序为:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.以一个天干和一个地支相配,天干在前,地支在后,每对干支表示一年.在干支纪年中,每六十年纪年方式循环一次.公元纪年则是国际通行的纪年方式.图17-12是1911年到1926年的公元纪年与干支纪年的对照表.请问:(1)中国近代史上的“辛亥革命”发生在公元1911年,是干支纪年的辛亥年,请问公元2049年是干支纪年的什么年?(2)21世纪的甲子年是公元纪年的哪一年?(3)“戊戌变法”发生在19世纪末的戊戌年,这一年是公元纪年的哪一年?答案:己巳年;2044年;1889年解析:(1)【10,12】=602049-1911=138138÷60=2……18 己巳年(2)1924+60×2=2044(3)余数特征9.如图17-13所示,将1至400这400个自然数填入下面的小三角形中,每个小三角形内填有一个数. “l”所处的位置为第1行;“2,3,4”所处的位置为第2行;………请问:(1)第15行正中间的数是多少?(2)第12行中所有空白三角形内的数之和是多少?(3)前8行中阴影三角形内的各数之和比空白三角形内的各数之和大多少?答案:211;1463;176解析:(1)规律为N(N-1)带入(2)123+125+127+…+143=1463(3)1+(4-1)+(9-2)+(16-3) +(25-4)+(36-5)+(49-6)+(64-7)=17610.如图17-14,把从1开始的自然数按某种方式排列起来.请问:(1)150在第几行,第几列?(2)第5行第10列的数是多少?答案:第6行第13列;86解析:(1)最右侧数是行数的平方(2)第9行最左侧数是81,所以81+5=8611.如图17-15,把从l开始的自然数按某种方式排列起来.请问:(1)200排在第几行,第几列?(2)第18行第22列的数是多少?答案:第10行第11列;759。
解析:(1)1+2+3+…19=190200-190=10行;21-10=11列(2)18+22-1=39;第39行第一个数是780,780-21=75912.如图17-16所示,把自然数按规律排列起来.如果用“土”字型阴影覆盖出8个数并求和,且和为798.这8个数中最大的数是多少?(“土”字不能旋转或翻转)答案:112解析:设方程的方法,设方格中任意一个数为X,用含有X的式子表示其他的方格内数,他们的和为798,解方程再带入最大求值。
超越篇1.下面的数组是按一定顺序排列的:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),….请问:(1)其中第70个括号内的数分别是多少?(2)前50个括号内各数之和是多少?答案:解:(1)把(1,1)看作第一组;(1,2),(2,1)看作第二组;……依次类推每一个括号内的两个数字之和是它所在组的序号加1.前十一组共有66括号,所以第70个括号一定属于第十二组。
(2)第一组的和为1×2;第二组的和为2×2;以此类推……前50个括号内的各数之和为1×2+2×3+3×4+…+9×10+5×11=385.2. 桌子上有一堆球,如果球的总数量是10的倍数,就平均分成10堆并拿走其中9堆;如果球的总数量不是10的倍数,就添加不多于9个球,使球数变为10的倍数,再平均分成10堆并拿走其中9堆.这个过程称为一次“操作”.若球仅为一个,则不做“操作”.如果最初有194919481947…54321个球,那么经过多少次“操作”后仅余下一个球?解:每操作一次,数位会减少1,当数位减少至一位时是“2”,还可以再进行一次操作,所以,最初的球数有多少数位就可以进行多少次操作。
1×9+2×(99-10+1)+3×(999-100+1)+4×(1949-1000+1)=6689(次)。
3.在图17-17所示的数阵中,将满足下面条件的两个数分为一组:它们上下相邻,且和为391.问:在所有这样的数组中,哪一组内的两个数乘积最小?解:两个数的和一定时,它们的差越大,乘积越小。
由数阵中规律可知,上下相邻的两个数差最大为29.由和差问题公式,较大数=(和+差)÷2=(391+29)÷2=210,较小数=391-210=181,所以,这一组的两个数为181和210.4.图17-18中的数是按一定规律排列的,郡么第6行第23列的数字是多少?解:前22列的数字个数为1+2+…+22=253,从1至120的数字个数为9+2×90+3×21=252,所以,第23列的第1行是121中的“2”,那么第6行就是123中的“1”。
所以,第6行第23列的数字是“1”。
