哈工大集合论习题课-第六章树及割集习题课(学生)
哈工大集合论习题课第六章树及割集习题课(学生)

第六章树及割集习题课 1讲堂例题例1 设 T 是一棵树, T 有 3 个度为 3 极点, 1 个 2 度极点,其余均是 1 度极点。
则( 1)求 T 有几个 1 度极点?( 2)画出知足上述要求的不一样构的两棵树。
剖析:关于任一棵树 T ,其极点数 p 和边数 q 的关系是:q p 1且pdeg(v i )2q ,依据这些性质简单求解。
i 1解:(1)设该树T的极点数为p,边数为q,并设树T中有x个 1 度极点。
于是pdeg(v i ) 3 3 1 2 x 2q 且 p 3 1 x, q p 1,得x 5 。
i 1( 2)知足上述要求的两棵不一样构的无向树,如图 1 所示。
图1例 2 设 G 是一棵树且(G ) k ,证明G中起码有k个度为1极点。
证:设T 中有 p 个极点,s个树叶,则 T 中其余 p s 个极点的度数均大于等于 2,且起码有一个极点的度大于等于k 。
由握手定理可得:ps ,有s k 。
2q 2 p 2deg( v i ) 2( p s 1) ki 1所以 T 中起码有 k 个树叶。
习题例1 若无向图G中有p个极点,p 1条边,则G为树。
这个命题正确吗?为何?解:不正确。
K 3与平庸图构成的非连通图中有四个极点三条边,明显它不是树。
例2 设树T中有2n个度为 1 的极点,有3n个度为 2 的极点,有n个度为 3 的极点,则这棵树有多少个极点和多少条边?解:设 T 有 p 个极点, q 条边,则q p 12n 3n n 1 6n 1。
由deg(v) 2q 有: 1 2n 2 3n 3 n 2q 2(6n 1)12n 2 ,解得: n =2。
v V故 q 11, p12 。
例 3 证明恰有两个极点度数为 1 的树必为一条通路。
证:设 T 是一棵拥有两个极点度数为 1 的( p,q)树,则q p 1且p2( p 1) 。
deg(v i ) 2qi 1又 T 除两个极点度数为 1 外,其余极点度均大于等于 2,故p p 22( p 1) ,即deg(v i )2deg(v i )i 1i 1p22) 。
哈工大集合与图论习题

集合与图论习题第一章习题.画出具有个顶点地所有无向图(同构地只算一个)..画出具有个顶点地所有有向图(同构地只算一个)..画出具有个、个、个顶点地三次图..某次宴会上,许多人互相握手.证明:握过奇数次手地人数为偶数(注意,是偶数)..证明:哥尼斯堡七桥问题无解..设与是图地两个不同顶点.若与间有两条不同地通道(迹),则中是否有回路?.证明:一个连通地(,)图中≥..设是一个(,)图,δ()≥[],试证是连通地..证明:在一个连通图中,两条最长地路有一个公共地顶点..在一个有个人地宴会上,每个人至少有个朋友(≤≤).试证:有不少于个人,使得他们按某种方法坐在一张圆桌旁,每人地左、右均是他地朋友.b5E2R。
.一个图是连通地,当且仅当将划分成两个非空子集和时,总有一条联结地一个顶点与地一个顶点地边..设是图.证明:若δ()≥ ,则包含长至少是δ()地回路..设是一个(,)图,证明:()≥,则中有回路;()若≥,则包含两个边不重地回路..证明:若图不是连通图,则是连通图..设是个(,)图,试证:()δ()·δ()≤[()]([()]),若≡,,( )() δ()·δ()≤[()]·[()],若≡( ).证明:每一个自补图有或个顶点..构造一个有个顶点而没有三角形地三次图,其中≥..给出一个个顶点地非哈密顿图地例子,使得每一对不邻接地顶点和,均有≥.试求中不同地哈密顿回路地个数..试证:图四中地图不是哈密顿图..完全偶图,为哈密顿图地充分必要条件是什么?.菱形面体地表面上有无哈密顿回路?.设是一个(≥)个顶点地图.和是地两个不邻接地顶点,并且≥.证明:是哈密顿图当且仅当是哈密顿图..设是一个有个顶点地图.证明:若>δ(),则有长至少为δ()地路..证明具有奇数顶点地偶图不是哈密顿图..证明:若为奇数,则中有()个两两无公共边地哈密顿回路..中国邮路问题:一个邮递员从邮局出发投递信件,然后返回邮局.若他必须至少一次走过他所管辖范围内地每条街道,那么如何选择投递路线,以便走尽可能少地路程.这个问题是我国数学家管梅谷于年首先提出地,国外称之为中国邮路问题.p1Ean。
哈工大集合论习题

第一章 习题1.写出方程2210x x ++=的根所构成的集合。
2.下列命题中哪些是真的,哪些为假 3设有n 个集合12,,,n A A A 且121n A A A A ⊆⊆⊆⊆,试证:12n A A A ===4.设{,{}}S φφ=,试求2S?5.设S 恰有n 个元素,证明2S有2n个元素。
6.设A 、B 是集合,证明:(\)()\A B B A B B B φ=⇔=7.设A 、B 是集合,试证A B A B φ=⇔=∆8. 设A 、B 、C 是集合,证明:()()A B C A B C ∆∆=∆∆9.设A 、B 、C 为集合,证明\()(\)\A B C A B C =10.设A ,B ,C 为集合,证明: ()\(\)(\)A B C A C B C =11.设A,B,C 为集合,证明:()\(\)(\)A B C A C B C =12.设A,B,C 都是集合,若A B A C =且A B B C =,试证B=C 。
13.设A,B,C 为集合,试证:(\)\(\)\(\)A B C A B C B =14.设X Y Z ⊆⊆,证明\(\)(\)Z Y X X Z Y =15.下列命题是否成立? (1)(\)\(\)A B C A B C =(2)(\)()\AB C A B C =(3)\()()\A B C A B B = 16.下列命题哪个为真? a)对任何集合A,B,C ,若AB BC =,则A=C 。
b)设A,B,C 为任何集合,若A B A C =,则B=C 。
c)对任何集合A,B ,222A BAB =。
d)对任何集合A,B ,222A B AB =。
e)对任何集合A,B ,\22\2A BA B =。
f)对任何集合A,B ,222A BAB∆=∆。
17.设R,S,T 是任何三个集合,试证:(1)()()S T S T S T ∆=∆;(2)()()()R S T R S R T ∆⊇∆∆;(3)()()()()()R S R T R ST R S R T ∆∆⊆∆⊆∆∆;(4)()()()RS T RS R T ∆⊇∆ 18.设A 为任一集,{}IB ξξ∈为任一集族(I φ≠),证明:()()IIA B A B ξξξξ∈∈=19.填空:设A,B 是两个集合。
哈工大电路习题答案
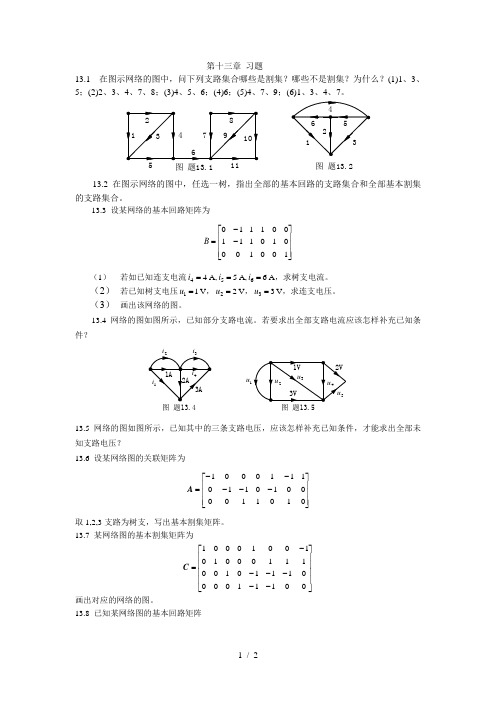
第十三章 习题13.1 在图示网络的图中,问下列支路集合哪些是割集?哪些不是割集?为什么?(1)1、3、5;(2)2、3、4、7、8;(3)4、5、6;(4)6;(5)4、7、9;(6)1、3、4、7。
图 题13.1图 题13.213.2 在图示网络的图中,任选一树,指出全部的基本回路的支路集合和全部基本割集的支路集合。
13.3 设某网络的基本回路矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100100010111001110B(1) 若如已知连支电流44=i A,55=i A,66=i A ,求树支电流。
(2) 若已知树支电压11=u V ,22=u V ,33=u V ,求连支电压。
(3) 画出该网络的图。
13.4 网络的图如图所示,已知部分支路电流。
若要求出全部支路电流应该怎样补充已知条件?图 题13.41u 图 题13.513.5 网络的图如图所示,已知其中的三条支路电压,应该怎样补充已知条件,才能求出全部未知支路电压?13.6 设某网络图的关联矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=010110000101101110001A取1,2,3支路为树支,写出基本割集矩阵。
13.7 某网络图的基本割集矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=00111000011101001110001010010001C 画出对应的网络的图。
13.8 已知某网络图的基本回路矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=10111000011101001100001001100001B 试写出此网络的基本割集矩阵C 。
13.9 某网络有6条支路,已知3条支路的电阻分别是Ω=21R ,Ω=52R ,Ω=103R ;其余3条支路的电压分别是44=u V ,65=u V ,126-=u V 。
又知该网络的基本回路矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=110100*********001B试求全部支路电流。
13.10 图示网络的图,根据所选的树,列出独立的KCL 方程和独立的KVL 方程,并写成矩阵形式。
哈工大概率论练习题

哈工大概率论练习题第一章随机事件与概率4.已知P(A)=P(B)=P(C)=0.25, P(AB)=0, P(AC)=P(BC)=1/16,则A,B,C 都不发生的概率为_____5. 设两个相互独立的事件A 和B 都不发生的概率为1/9,A 发生B 不发生的概率与B 发生而A 不发生的概率要等,则P(A)=____6. 设A,B,C 两两独立,则A,B,C 相互独立充分必要条件是()A. A 与BC 独立B.AB 与A ∪C 独立C. AB 与AC 独立D. A ∪B 与A ∪C 相独立7. 设事件A,B 满足P(A)=0.5, P(B)=0.6, P(B|A )=0.6, 则P (A ∪B )=_____8. 事件 A,B 满足P(A)=P(B)=0.5,P(A| B )=P(B),则下列正确的是()A. P(AB)=0.25B. P(A-B)=0.75C. P(A B -)=0.5D. P(A ∪B ) =19. 设事件A,B 仅发生一个的概率为0.3, 且P(A)+P(B)=0.5,则A,B 至少有一个不发生的概率为_____10. 设事件A,B 相互独立,事件B,C 互不相容,事件A 与C 不能同时发生,且P(A)=P(B)=0.5, P(C)=0.2,则事件A,B 和C 中仅C 发生或仅C 不发生的概率为_____11. 设A,B,C 为三个事件且A,B 相互独立,则以下结论中不正确的是()A. 若P(C)=1,则AC 与BC 也独立B. 若P(C)=1, 则A ∪C 与B 也独立C. 若P(C)=1,则A-C 与A 也独立D. 若C 属于B,则A 与C 也独立12. 若事件A,B,C 相互独立,且P(A)=0.25,P(B)=0.5,P(C)=0.4,则A,B,C 至少有一个不发生的概率是_______13. 设事件A 和B 满足P(B|A)=1,则()A. A 是必然事件B. P (A|B ) =0C. B ?AD. A ?B14. 在投掷一枚均匀硬币的4次独立试验中,若已知至少1次已经反面朝上,则这时得到至少 3次正面朝上的概率为______15. 已知P (B )>0,A 1A 2=¢,则下列各式中不正确的是()A. P(A 1A 2|B)=0B. P(A 1∪ A 2|B)=P(A 1|B)+P(A 2|B)C. P (1A 2A |B)=1D. P(1A ∪2A |B)=116.设A,B 为两事件,且P(A)=P,P(AB)=P(AB ),则P(B)=_____17.设A,B 为两个事件,P(A)≠P(B)>0,且B 属于A,则()一定成立 A. P(A|B)=1 B.P(B|A)=1 C. P(B|A ) =1 D. P(A|B )=018. 已知P(A)=0.5,P(B)=0.6,P(B|A)=0.8则P(A ∪B)=_____19. 设事件A 与BA 互不相容,且P(A)=P, P(B)=q, 求下列事件的概率,则P(A B )=______20. 5人以上以摸彩的方式决定谁能得一张电影票,今设Ai 表示第 i 个人摸到(i=0,1,2,3,4,5),则下列结果中有一个是对的,它是()A. P(A 3|1A 2A )=1/3B. P(1A A 2)=1/5C. P(1A A 2)=1/4D. P(A 5)=1/521.若P(A|C )≥P(B|C),P(A|C )≥P(B|C ) 则下列()成立A. P(A) ≥P(B)B. P(A)=P(B)C. P(A)≤P(B)D.P(A)=P(B)+P(C)22. 设相互独立的三个事件A,B,C 满足条件:P(A)=0.4 ,P(B)=0.5 ,P(C)=0.5,则P(A-C|AB ∪C)=______23.设AB ?C,则()成立 A. C ?AB B. A ?C 且B ?C C.B A ? C ? D.A C ?或B ?C24. 已知P(A)=P(B)=P(C)=0.25,P(AB)=P(AC)=P(BC)=1/8,P(ABC)=1/16,则A,B,C 恰有一个发生的概率为_______25. 设A,B 为任意两个事件,则下列关系成式立的是()A. (A ∪B )-B=AB. (A ∪B )-B ?AC. (A ∪B )-B ?AD. (A-B) ∪B=A26. 设事件A,B 满足P(B|A)=P(B |A )=0.2,P(A)=1/3,则P(B)=____27. 对于任意两事件A,B ,与A ∪B=B 不等价的是()A. A ?BB. B ?AC. A B =¢D. A B=¢28. 设事件A,B 满足:P(B|A)=P(B |A )=1/3,则P(B)=______29. 设0<p(a)<1,0<p(b)<="">A. A 与B 独立B. P(B|A)=P(B|A )C. A 与B 互不相容D.P(A|B )=P(A|B)30. 在区间(0,1)中随意地取两个数则“两数之和小于6/5”的概率为_______31. 在一张打上方格的纸上随机地投一枚硬币,若方格的长度为a,硬币的直径为2b(2b<a)且硬币落在每一处的是等可能的则硬币与方格线不相交的概率为_____< p="">32. 在有三个小孩的家庭中,已知至少有一个女孩子,求该家庭中至少有一个男孩子的概率_______33. 两人约定上午9点到10点在公园见面,试求一人要等另一个人半小时以上的概率_____34. 随机事件A ?B,0<p(a)<="">A. P(A ∪B)=P(A)B. P(AB)=P(A)C. P(B-A)=P(B)-P(A)D. P(B|A)=P(B)第二章条件概率与独立性1. 某炮台上有三门炮,假定第一门炮的命中率为0.4,第二门炮的命中率为0.3,第三门炮的命中率为0.5,今三门炮向同一目标各发射一发炮弹,结果有两弹中靶,求第一门炮中靶的概率?2.甲袋中有2个白球,3个黑球,乙袋中有3个白球2个黑球,从甲袋中取出一个放入乙袋,再从乙袋中任取一个,若放入乙袋的球和从乙袋中取出的球是同色的,求放入乙袋的是黑球的概率?3.袋中有8个正品,2个次品,任取3个,取后不入回,若第3次取到的次品,求前2次取到的是正品概率。
第六章部分习题答案

第六章部分习题答案第七题原题:在这道习题中,我们探讨CRC的某些性质。
对于在6.2.3节中给出的⽣成多项式G(=1001),回答下列问题: a.为什么它能够检测数据D中的任何单⽐特差错? b.上述G能够检测任何奇数⽐特差错吗?为什么?解题思路:本题思路很简单,将题⽬转换⼀下,就是⼀个能被G模2整除的数,如果突然增⼤某个值,那么它还能被G模2整除吗?注意:根据第六章内容,模2运算加不进位、减不借位,因此可以认为都是增⼤某个值。
a问题解答:如果第i位⽐特被翻转,则被校验的数⼤⼩变为:K = (D * 2r)XOR R + 2i,其中(D * 2r)XOR R这部分能被G模2整除,剩下的2i是否能被G模2整除呢?答案是不能,因为G中有2位是1,明显是除不尽的。
b问题解答:可以注意到,G=1001这个数能被11模2整除,但是任何包含奇数个1的数(这些1不必要连续)不能被11模2整除。
因此能够检测出来。
第⼋题原题:在6.3节中,我们提供了时隙ALOHA效率推导的概要。
在本习题中,我们将完成这个推导。
a.前⾯讲过,当有N个活跃节点时,时隙ALOHA的效率是Np(1-p)N-1。
求出使这个表达式最⼤化的p值p*。
b.使⽤在(a)中求出的p值,令N接近于⽆穷,求出时隙ALOHA的效率。
(提⽰:当N接近于⽆穷时,(1 - 1/N)N接近于1/e。
)解题思路:涉及到⼀些⾼等数学求导和极限的知识。
a问题解答:对于⼀个连续函数的最⼤值,我们可以通过求导的⽅式来计算,原式 f(p) = Np(1-p)N-1则其导数 f`(p) = (Np)`(1-p)N-1 - Np((1-p)N-1)`= N(1-p)N-1 - Np(N - 1)(1-p)N-2= N(1-p)N-2((1 - p) - p(N - 1))= N(1-p)N-2(1 - pN)当导数为0时,能取到最⼤值,则此时p=1/N,即p*=1/N。
b问题解答:将a问题求出的p*带⼊原式,变形为N*1/N(1 - 1/N)N-1=(1 - 1/N)N-1。
哈工大集合论与图论第六章作业题答案

第六章图的基本概念P习题2061.画出具有4个顶点的所有无向图(同构的只算一个)。
11个2.画出具有3个顶点的所有有向图(同构的只算一个)。
16个3.画出具有4个、6个、8个顶点的三次图。
略4.某次宴会上,许多人互相握手。
证明:握过奇数次手的人数为偶数(注意,0是偶数)。
把实际问题转化为图论问题,然后用握手定理的推论。
P习题2091.设u与v是图G的两个不同顶点。
若u与v间有两条不同的通道(迹),则G 中是否有圈?若u与v间有两条不同的通道,G中无圈若u与v间有两条不同的迹,G中有圈2.证明:一个连通的(p,q)图中q≥p-1。
数学归纳法3.设G是一个(p,q)图,且2/)2>p-q,则G是连通的。
p)(1(-6.在一个有n个人的宴会上,每个人至少有m个朋友(2≤m≤n)。
试证:有不少于m+1个人,使得他们按某种方法坐在一张圆桌旁,每人的左、右均是他的朋友。
证明:把实际问题转化为图论问题,就和下面的题一样了。
8.设G是图。
证明:若δ(G)≥2,则G包含长至少是δ(G)+1的圈。
这两个题和这个题一样的证明方法。
P习题2161.证明:若图G不是连通图,则G c 是连通图。
2.证明:每一个自补图有4n或4n+1个顶点。
P习题2281.给出一个10个顶点的非哈密顿图的例子,使得每一对不邻接的顶点u和v,均有:degu+degv≥9。
下图中任意一对不邻接的顶点u和v,均有:degu+degv≥9。
2.试求Kp中不同的哈密顿圈的个数。
(p-1)!/24.完全偶图Km,n为哈密顿图的充分必要条件是什么?10.证明具有奇数顶点的偶图不是哈密顿图。
哈工大2006年秋季学期《集合论与图论》试题

哈工大2006年秋季学期《集合论与图论》试题哈工大 2006年秋季学期《集合论与图论》试题本试题满分90,平时作业分满分10分。
一、(10分,每小题1分)判断下列各命题真伪(真命题打“√”号,假命题打“×”号):1.从{1,2,3}到{4,5}共有9个不同的映射。
()2.从{1,2,3}到{4,5}共有5个不同的满射。
()3.从{4,5}到{1,2,3}共3个不同的单射。
()4.集合{1,2,…,10}上共有2100个不同的二元关系。
()5.如果A为可数集,则2A也是可数集合。
()6.欧拉图中没有割点。
()7.有向图的每一条弧必在某个强支中。
()8.P为正整数,Kp的顶点连通度为P-1。
()9.(P,P)连通图至少有2个生成树。
()10.每个有2个支的不连通图,若每个顶点的度均大于或等于2,则该图至少有2个圈。
()二、(20分,每小题2分)计算题。
对每一小题给出计算结果:1.{1,2,…,n}上有多少个反自反且对称的二元关系?()2.把置换123456789579413826分解成循环置换的乘积。
()3.计算下面两个图G1和G2的色数。
()G1:G2:(答:G1的色数为,G2的色数为)4.设X为集合,R为X上的偏序关系,计算1iiR ∞=等于什么。
()5.求下面的有向图D的邻接矩阵和可达矩阵。
D=-------------------:()6.一个有向图D=(V,A)满足什么条件是V到V的一个映射的图?()7.P个顶点的无向连通图G的邻接矩阵中至少有多少个1?()8.设X为n 个元素的集合,X上有多少个二元运算?()9.9个学生,每个学生向其他学生中的3个学生各送一张贺年卡。
确定能否使每个学生收到的卡均来自其送过卡的相同人?为什么?()10.某次会议有100人参加,每人可以是诚实的,也可能是虚伪的。
已经知道下面两项事实:(1)这100人中至少有一人是诚实的;(2)任两人中至少有一人是虚伪的。
哈工大集合论习题课-第三章 关系习题课(学生)

习 题 课例1设{,,}A a b c =,给出A 上的一个二元关系,使其同时不满足自反性、反自反性、对称性、反对称和传递性的二元关系,并画出R 的关系图。
解:{(,),(,),(,),(,)}R a a b c c b a c =,关系图如图所示。
例2 设X 是一个集合,X =n ,求:1.X 上的二元关系有多少?()22n 2. X 上的自反的二元关系有多少? 3. X 上的反自反的二元关系有多少?解:因为把所有的反自反的二元关系的每个都加上对角线上的序对,就变成了自反的关系,因此,自反的与反自反的个数一样多。
即22nn-4. X 上的对称的二元关系有多少?2222n n n nn -++=,故共有222n n+个对称的关系。
5. X 上的反对称的二元关系有多少?22(32)n n n -∙6. X 上既是自反的也是反自反的二元关系的个数;(0)个7.X 上既不是自反的也不是反自反的二元关系有多少?2(2(22))n nn --解:解:可用容斥原理来计算设B 表示所有自反关系构成的集合,C 表示所有反自反关系构成的集合,则22nnB C -==。
而B C φ=,故B C B C =+,从而CC B C S B C S B C =-=--2222222222222(22)n n n n n n n n n n n ----=--=-=-于是,既不是自反的,也不是反自反关系共有22(22)n nn --个。
8.自反的且对称的关系有多少?[此结果与“反自反的且对称的关系有多少?”是一样多]即有222n n -(对角线上全去掉)9.自反的或对称的关系有多少?解:设B 表示自反关系的集合,C 表示对称关系的集合,则自反或对称关系的集合为:22222222n n n n nnB C B C B C +--=+-=+-。
10.X 上既是反自反的也是反对称的二元关系的个数为:223n n -;11.X 上既是对称的也是反对称的关系个数;解:X 上既是对称的也是反对称的关系X R I ⊆,故有2n 。
离散数学-第六章集合代数课后练习习题及答案

离散数学-第六章集合代数课后练习习题及答案第六章作业评分要求:1.合计57分2.给出每小题得分(注意:写出扣分理由).3.总得分在采分点1处正确设置.一有限集合计数问题(合计20分:每小题10分,正确定义集合得4分,方法与过程4分,结果2分)要求:掌握集合的定义方法以及处理有限集合计数问题的基本方法1对60个人的调查表明,有25人阅读《每周新闻》杂志,26人阅读《时代》杂志,26人阅读《财富》杂志,9人阅读《每周新闻》和《财富》杂志,11人阅读《每周新闻》和《时代》杂志,8人阅读《时代》和《财富》杂志,还有8人什么杂志也不读.(1)求阅读全部3种杂志的人数;(2)分别求只阅读《每周新闻》、《时代》和《财富》杂志的人数.解定义集合:设E={某|某是调查对象},A={某|某阅读《每周新闻》},B={某|某阅读《时代》},C={某|某阅读《财富》}由条件得|E|=60,|A|=25,|B|=26,|C|=26,|A∩C|=9,|A∩B|=11,|B∩C|=8,|E-A∪B∪C|=8(1)阅读全部3种杂志的人数=|A∩B∩C|=|A∪B∪C|-(|A|+|B|+|C|)+(|A∩B|+|A∩C|+|B∩C|)=(60-8)-(25+26+26)+(11+9+8)=3(2)只阅读《每周新闻》的人数=|A-B∪C|=|A-A∩(B∪C)|=|A-(A∩B)∪(A∩C)|=|A|-(|A∩B|+|A∩C|-|A∩B∩C|)=25-(11+9-3)=8同理可得只阅读《时代》的人数为10,只阅读《财富》的人数为12.2使用容斥原理求不超过120的素数个数.分析:本题有一定难度,难在如何定义集合.考虑到素数只有1和其自身两个素因子,而不超过120的合数的最小素因子一定是2,3,5或7(比120开方小的素数),也就是说,不超过120的合数一定是2,3,5或7的倍数.因此,可定义4条性质分别为2,3,5或7的倍数,先求出不超过120的所有的合数,再得出素数的个数.解定义集合:设全集E={某|某∈Z∧1≤某∧某≤120}A={2k|k∈Z∧k≥1∧2k≤120},B={3k|k∈Z∧k≥1∧3k≤120},C={5 k|k∈Z∧k≥1∧5k≤120},D={7k|k∈Z∧k≥1∧7k≤120}.则不超过120的合数的个数=|A∪B∪C∪D|-4(因为2,3,5,7不是合数)=(|A|+|B|+|C|+|D|)-(|A∩B|+|A∩C|+|A∩D|+|B∩C|+|B∩D|+|C∩D|)+(|A∩B∩C|+|A∩B∩D| +|A∩C∩D|+|B∩C∩D|)-|A∩B∩C∩D|-4=(60+40+24+17)-(20+12+8+8+5+3)+(4+2+1+1)-0-4(理由见说明部分)=89因此不超过120的素数个数=120-1-89=30(因为1不是素数)说明:|A|=int(120/2);|AB|=int(120/lcd(2,3));|ABC|=int(120/lcd(2,3,5));|ABCD|=int(120/lcd(2,3,5,7)).二集合关系证明1设A,B,C是任意集合,证明(1)(A-B)-C=A-(B∪C)(2)A∩CB∩C∧A-CB-CAB(合计12分:每小题6分;格式3分,过程每错一步扣1分)证明(1)逻辑演算法:某,某∈(A-B)-C某∈(A-B)∧某∈C(-定义)(某∈A∧某∈B)∧某∈C(-定义)某∈A∧(某∈B∧某∈C)(∧的结合律)某∈A∧(某∈B∨某∈C)(德摩根律)某∈A∧某∈B∪C(∪定义)某∈A-B∪C(-定义)所以(A-B)-C=A-(B∪C).集合演算法(A-B)-C=(A∩~B)∩~C(补交转换律)=A∩(~B∩~C)(∩的结合律)=A∩~(B∪C)(德摩根律)=A-(B∪C)(补交转换律)得证.(2)逻辑演算法:某,某∈A某∈A∩(C∪~C)(排中律,同一律)某∈(A∩C)∪(A∩~C)(∪对∩的分配率)某∈A∩C∨某∈A-C(∪的定义,补交转换律)某∈B∩C∨某∈B-C(已知条件A∩CB∩C与A-CB-C)某∈(B∩C)∪(B-C)(∪的定义)某∈(B∩C)∪(B∩~C)(补交转换律)某∈B∩(C∪~C)(∩对∪的分配率)某∈B(排中律,同一律)所以AB.集合演算法A=A∩(C∪~C)(同一律,排中律)=(A∩C)∪(A∩~C)(∩对∪的分配率)=(A∩C)∪(A-C)(补交转换律)(B∩C)∪(B-C)(已知条件A∩CB∩C与A-CB-C)=(B∩C)∪(B∩~C)(补交转换律)=B∩(C∪~C)(∩对∪的分配率)=B(排中律,同一律)得证.方法三因为A∩CB∩C,A-CB-C,所以(A∩C)∪(A-C)(B∩C)∪(B-C)|,整理即得AB,得证.2求下列等式成立的充分必要条件(1)A-B=B-A(2)(A-B)∩(A-C)=(合计10分:每小题5分;正确给出充分必要条件2分,理由3分)解(1)A-B=B-A方法一两边同时∪A得:A=(B-A)∪A=B∪ABA;同理可得AB,综合可得A=B.另一方面,当A=B时显然有A-B=B-A.因此所求充要条件为A=B.方法二某,某∈A-B∧某∈B-A某∈(A-B)∩(B-A)某∈所以A-B=B-AA-B=∧B-A=AB∧BAA=B因此A=B即为所求.(2)(A-B)∩(A-C)=(A∩~B)∩(A∩~C)=A∩(~B∩~C)=A∩~(B∪C)=A -(B∪C)=AB∪C所以AB∪C即为所求充要条件.说明:这类题型一般先求出必要条件,再验证其充分性.三设全集为n元集,按照某种给定顺序排列为E={某1,某2,…,某n}.在计算机中可以用长为n的0,1串表示E的子集.令m元子集A={某i1,某i2,…,某im},则A所对应的0,1串为j1j2…jn,其中当k=i1,i2,…,im时jk=1,其它情况下jk=0.例如,E={1,2,…,8},则A={1,2,5,6}和B={3,7}对应的0,1串分别为11001100和00100010.(1)设A对应的0,1串为10110010,则~A对应的0,1串是什么(2)设A与B对应的0,1串分别为i1i2…in和j1j2…jn,且A∪B,A∩B,A-B,A⊕B对应的0,1串分别为a1a2…an,b1b2…bn,c1c2…cn,d1d2…dn,求ak,bk,ck,dk,k=1,2,…,n.(合计15分:(1)3分;(2)12分,每个结果正确2分,求解过程4分)解下述运算是二进制数的位运算(1)01001101(2)ak=ik∨jk,bk=ik∧jk,ck=ik∧jk,dk=(ik∧jk)∨(ik∧jk).说明:这里ck和dk的求解可以使用主范式求解.ck,dk的真值表如下ik001jk010ck0010dk011011因此可用主析取范式表示ck和dk如下:ckm2=ik∧jkdkm1∨m2=(ik∧jk)∨(ik∧jk).。
哈工大集合论习题课-第六章 树及割集 习题课(学生)
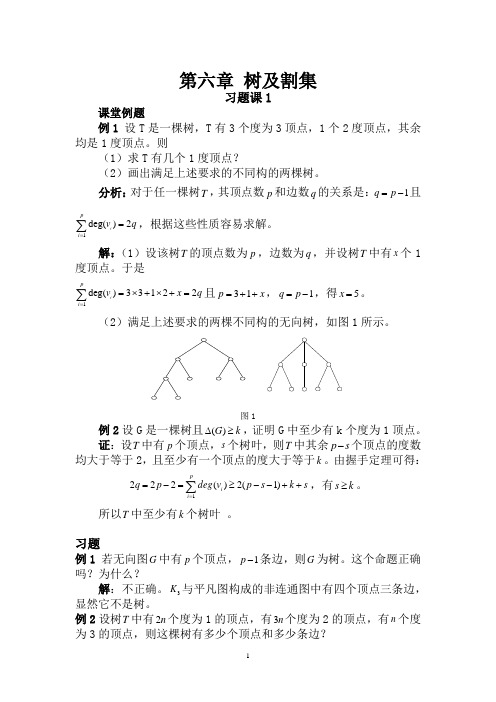
第六章 树及割集习题课1课堂例题例1 设T 是一棵树,T 有3个度为3顶点,1个2度顶点,其余均是1度顶点。
则(1)求T 有几个1度顶点?(2)画出满足上述要求的不同构的两棵树。
分析:对于任一棵树T ,其顶点数p 和边数q 的关系是:1q p =-且1deg()2ipi v q ==∑,根据这些性质容易求解。
解:(1)设该树T 的顶点数为p ,边数为q ,并设树T 中有x 个1度顶点。
于是1deg()33122ipi v x q ==⨯+⨯+=∑且31p x =++,1q p =-,得5x =。
(2)满足上述要求的两棵不同构的无向树,如图1所示。
图1例2设G 是一棵树且()G k ∆≥,证明G 中至少有k 个度为1顶点。
证:设T 中有p 个顶点,s 个树叶,则T 中其余p s -个顶点的度数均大于等于2,且至少有一个顶点的度大于等于k 。
由握手定理可得:1222()2(1)pi i q p deg v p s k s ==-=≥--++∑,有s k ≥。
所以T 中至少有k 个树叶 。
习题例1 若无向图G 中有p 个顶点,1p -条边,则G 为树。
这个命题正确吗?为什么?解:不正确。
3K 与平凡图构成的非连通图中有四个顶点三条边,显然它不是树。
例2设树T 中有2n 个度为1的顶点,有3n 个度为2的顶点,有n 个度为3的顶点,则这棵树有多少个顶点和多少条边?解:设T 有p 个顶点,q 条边,则123161q p n n n n =-=++-=-。
由deg()2v Vv q ∈=∑有:1223322(61)122n n n q n n ⨯+⨯+⨯==-=-,解得:n =2。
故11,12q p ==。
例3证明恰有两个顶点度数为1的树必为一条通路。
证:设T 是一棵具有两个顶点度数为1的(,)p q 树,则1q p =-且1deg()2pii v q ==∑2(1)p =-。
又T 除两个顶点度数为1外,其他顶点度均大于等于2,故211deg()2deg()2(1)p p iii i v v p -===+=-∑∑,即21deg()2(2)p ii v p -==-∑。
离散数学集合论哈工大答案

反之, x X ( Z \ Y ) ,则 x X 或 x Z \ Y 。 若 x X ,则由 X Y Z 有 x Y , x Z ,故 x Y \ X ,因此 x Z \ (Y \ X ) 。 若 x Z \ Y ,则 x Z 但 x Y ,故 x Y \ X ,因此 x Z \ (Y \ X ) 。从而
1
解: 2S { ,{ },{{ }},{ ,{ }}} 7.设 S 恰有 n 个元素,证明 2S 有 2n 个元素。 证明: (1)当 n=0 时, S , 2 S { }, 2S 1 20 ,命题成立。 (2)假设当 n k ( k 0, k N ) 时命题成立,即 2 S 2k ( S k 时) 。那么对 于 S1 ( S1 k 1 ) , 2S1 中的元素可分为两类,一类为不包含 S1 中某一元素 x 的 集合,另一类为包含 x 的集合。显然,这两类元素个数均为 2k 。因而 2 S1 2k 1 , 亦即命题在 n k 1 时也成立。 由(1) 、 (2) ,可证得命题在 n N 时均成立。
S T ( S T ) ( S T ) 。
反之,因为 ( S T ) ( S T ) ,故
教材习题解答
第一章 集合及其运算
P8 习题 3. 写出方程 x 2 2 x 1 0 的根所构成的集合。 解: x 2 2 x 1 0 的根为 x 1 ,故所求集合为 {1} 4.下列命题中哪些是真的,哪些为假 a)对每个集 A, A ;b)对每个集 A, A ; c)对每个集 A, A { A} ;d)对每个集 A, A A ; e)对每个集 A, A A ;f)对每个集 A, A { A} ; g)对每个集 A, A 2 A ;h)对每个集 A, A 2 A ; i)对每个集 A, { A} 2 A ;j)对每个集 A, { A} 2 A ; k)对每个集 A, 2 A ;l)对每个集 A, 2 A ; m)对每个集 A, A { A} ;n) { } ; o) {} 中没有任何元素;p)若 A B ,则 2 A 2 B q)对任何集 A, A {x | x A} ;r)对任何集 A, {x | x A} { y | y A} ; s)对任何集 A,y A y {x | x A} ; t)对任何集 A, {x | x A} { A | A A} ; 答案:假真真假真假真假真假真真假假假真真真真真 5.设有 n 个集合 A1 , A2 , , An 且 A1 A2 An A1 ,试证: A1 A2 An 证明:由 A1 A2 A4 An A1 ,可得 A1 A2 且 A2 A1 ,故 A1 A2 。 同理可得: A1 A3 A4 An 因此 A1 A2 A3 An 6.设 S { ,{ }} ,试求 2S ?
哈工大编译原理习题及答案

1.1何谓源程序、目标程序、翻译程序、编译程序和解释程序?它们之间可能有何种关系?1.2一个典型的编译系统通常由哪些部分组成?各部分的主要功能是什么?1.3选择一种你所熟悉的程序设计语言,试列出此语言中的全部关键字,并通过上机使用该语言以判明这些关键字是否为保留字。
1.4选取一种你所熟悉的语言,试对它进行分析,以找出此语言中的括号、关键字END以及逗号有多少种不同的用途。
1.5试用你常用的一种高级语言编写一短小的程序,上机进行编译和运行,记录下操作步骤和输出信息,如果可能,请卸出中间代码和目标代码。
第一章习题解答1.解:源程序是指以某种程序设计语言所编写的程序。
目标程序是指编译程序(或解释程序)将源程序处理加工而得的另一种语言(目标语言)的程序。
翻译程序是将某种语言翻译成另一种语言的程序的统称。
编译程序与解释程序均为翻译程序,但二者工作方法不同。
解释程序的特点是并不先将高级语言程序全部翻译成机器代码,而是每读入一条高级语言程序语句,就用解释程序将其翻译成一段机器指令并执行之,然后再读入下一条语句继续进行解释、执行,如此反复。
即边解释边执行,翻译所得的指令序列并不保存。
编译程序的特点是先将高级语言程序翻译成机器语言程序,将其保存到指定的空间中,在用户需要时再执行之。
即先翻译、后执行。
2.解:一般说来,编译程序主要由词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、代码优化程序、目标代码生成程序、信息表管理程序、错误检查处理程序组成。
3.解:C语言的关键字有:auto break case char const continue default do double else enum externfloat for goto if int long register return short signed sizeof static struct switch typedef union unsigned void volatile while。
黑龙江省哈尔滨工大学附中高考数学一轮复习 集合与逻辑单元精品练习

哈尔滨工程大学附中2014三维设计高考数学一轮单元复习精品练习:集合与逻辑本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有关命题的说法正确的是( )A .命题“若1,12==x x 则”的否命题为:“若1,12≠=x x 则”;B .“1-=x ”是“0652=--x x ”的必要不充分条件;C .命题“01,2<-+∈∃x x R x 使得”的否定是:“01,2>-+∈∀x x R x 均有”;D .命题“若y x y x sin sin ,==则”的逆否命题为真命题;【答案】D2.下列命题中的假命题是( )A .x ∀∈R 120x -,>B .x ∀∈N 2(1)0x *,->C .0x ∃∈R,lg 01x <D .0x ∃∈R,tan 02x =【答案】B3.设集合{1,2,3,4,5}U =,{1,3,5},{2,3,5}A B ==,则图中阴影部分表示的集合是( )A .{1,2,4}B .{4}C .{3,5}D .∅【答案】A4.如果命题“非p 为真”,命题“p 且q 为假”,那么下列选项一定正确的是( )A .q 为真B .q 为假C .p 或q 为真D .p 或q 不一定为真【答案】D5.“220a b +=”是“0a =或0b =”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件【答案】A6. 2>x ”是“0)2)(1(>-+x x ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A7.命题“若x=1,则x 2-3x+2=0”以及它的逆命题,否命题和逆否命题中,真命题的个数是( )A .0B .2C .3D .4【答案】B8.集合}20{,M =,}|{M x x P ∈=,则下列关系中,正确的是( ) A .MP B .P M C . M P = D . M P ⊆ 【答案】D9.已知集合{1,0,1},{|cos ,}M N y y x x M =-==∈,则集合N 的真子集个数为( )A .3B .4C .7D .8【答案】B10.已知命题p ::若x +y ≠3,则x ≠1或y ≠2;命题q :若b 2=ac ,则a,b,c 成等比数列,下列选项中为真命题的是( )A . pB . qC . p ∧qD .(⌝p )∨q【答案】A11.设集合A={x|y=x 2-1},B={y|y=x 2-1},C={(x,y )|y=x 2-1},则下列关系错误..的是( ) A .B ∩C=Ф B .A ∩C=ФC .A ∩B=BD .A ∪B=C 【答案】D12.下列说法正确的是( )A . *N ϕ∈B . Z ∈-2C . Φ∈0D .Q ⊆2【答案】B第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.下列说法及计算不正确的是 。
哈工大集合与图论习题

集合与图论习题第一章习题1.画出具有4个顶点的所有无向图(同构的只算一个)。
2.画出具有3个顶点的所有有向图(同构的只算一个)。
3.画出具有4个、6个、8个顶点的三次图。
4.某次宴会上,许多人互相握手。
证明:握过奇数次手的人数为偶数(注意,0是偶数)。
5.证明:哥尼斯堡七桥问题无解。
6.设u与v是图G的两个不同顶点。
若u与v间有两条不同的通道(迹),则G中是否有回路?7.证明:一个连通的(p,q)图中q ≥p-1。
8.设G是一个(p,q)图,δ(G)≥[p/2],试证G是连通的。
9.证明:在一个连通图中,两条最长的路有一个公共的顶点。
10.在一个有n个人的宴会上,每个人至少有m个朋友(2≤m≤n)。
试证:有不少于m+1个人,使得他们按某种方法坐在一张圆桌旁,每人的左、右均是他的朋友。
11.一个图G是连通的,当且仅当将V划分成两个非空子集V1和V2时,G总有一条联结V1的一个顶点与V2的一个顶点的边。
12.设G是图。
证明:若δ(G)≥ 2,则G包含长至少是δ(G)+1的回路。
13.设G是一个(p,q)图,证明:(a)q≥p,则G中有回路;(b)若q≥p+4,则G包含两个边不重的回路。
14.证明:若图G不是连通图,则G c 是连通图。
15.设G是个(p,q)图,试证:(a)δ(G)·δ(G C)≤[(p-1)/2]([(p+1)/2]+1),若p≡0,1,2(mod 4)(b) δ(G)·δ(G C)≤[(p-3)/2]·[(p+1)/2],若p≡3(mod 4)16.证明:每一个自补图有4n或4n+1个顶点。
17.构造一个有2n个顶点而没有三角形的三次图,其中n≥3。
18.给出一个10个顶点的非哈密顿图的例子,使得每一对不邻接的顶点u和v,均有degu+degv≥919.试求Kp中不同的哈密顿回路的个数。
20.试证:图四中的图不是哈密顿图。
21.完全偶图Km,n为哈密顿图的充分必要条件是什么?22.菱形12面体的表面上有无哈密顿回路?23.设G 是一个p(p ≥3)个顶点的图。
数据结构与算法课件:DS06_第5章二叉树、第6章树 习题

1.以二叉链表作为存储结构,设计算法求出 二叉树T中度为0、度为1和度为2的结点数。
【题目分析】结点计数可以在遍历中解决。 根据“访问根结点”在“递归遍历左子树” 和“递归遍历右子树”中位置的不同,而有 前序、后序和中序遍历。
∥设置三个全局变量,分别记度为2,1和叶子结点的个数 int n2,n1,n0; void Count(BinaryTreeNode<T>* t) { if(t)
【题目分析】按完全二叉树形式顺序存储二叉树时,无元素
的位置要当作“虚结点”。设虚结点取二叉树结点以外的值 (这里设为0)。设结点序号为i,则当i<=(2h-1)/2时,若其2i 和2i+1位置为虚结点,则i为叶子结点;当i>(2h-1)/2时,若i 位置不是虚结点,则必为叶子结点。
n=pow(2,h)-1; //高度为h的树的最多结点数
while(top!=0 && s[top].tag==1) //tag为1表示右子树访问过,栈顶可弹出
{ if(s[top].t->data ==x)
while(bt[n]==0) //BT足够大,且初始化为全0后再存储元素
n--;
//求出树的实际结点数
2020/9/Βιβλιοθήκη 815int Leaves(int BT[],int n)
∥计算深度为h以一维数组BT作为存储结构的二叉树的叶子结点 数,n为数组长度
{ int num=0; ∥记叶子结点数
for(i=1;i<=n;i++)
【题目分析】后序遍历最后访问根结点,当 访问到值为x的结点时,栈中所有元素均为 该结点的祖先。
void Search(BinaryTreeNode<T>* bt,T x) ∥在二叉树bt中,查找值为x的结点,并打印其所有祖先 { typedef struct
第6章习题及解答

本章解答只给出算法描述,1~10题略。
算法中二叉树的二叉存储结构描述如下:typedef struct BTNode{datatype data;struct BTNode *lchild,*rchild;}BTNode ,*BiTree;⒈对于下图所示二叉树,试给出:⑴它的顺序存储结构示意图;⑵它的二叉链表存储结构示意图;⑶它的三叉链表存储结构示意。
⒉证明:在结点数多于1的哈夫曼树中不存在度为1的结点。
⒊证明:若哈夫曼树中有n 个叶结点,则树中共有2n -1个结点。
⒋证明:由二叉树的前序序列和中序序列可以唯一地确定一棵二叉树。
⒌已知一棵度为m 的树中有n1个度为1的结点,n2个度为2的结点,……,nm 个度为m 的结点,问该树中共有多少个叶子结点?有多少个非终端结点?⒍设高度为h 的二叉树上只有度为0和度为2的结点,问该二叉树的结点数可能达到的最大值和最小值。
⒎求表达式(a +b*(c -d ))-e/f 的波兰式(前缀式)和逆波兰式(后缀式)。
⒏画出和下列已知序列对应的二叉树:二叉树的先序次序访问序列为:GFKDAIEBCHJ ;二叉树的中序访问次序为:DIAEKFCJHBG 。
⒐画出和下列已知序列对应的二叉树:二叉树的后序次序访问序列为:CFEGDBJLKIHA ;二叉树的中序访问次序为:CBEFDGAJIKLH 。
⒑画出和下列已知序列对应的二叉树:二叉树的层次序列为:ABCDEFGHIJ ;二叉树的中序次序为:DBGEHJACIF 。
⒒给定一棵用二叉表示的二叉树,其根指针为root 。
试写出求二叉树结点的数目的算法(递归算法或非递归算法)。
int count (BiTree t){if (t= =NULL)return (0);elsereturn (count(t->lchild)+count(t->rchild)+1);( 1题图)}⒓请设计一个算法,要求该算法把二叉树的叶结点按从左至右的顺序链成一个单链表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 树及割集习题课1课堂例题例1 设T 是一棵树,T 有3个度为3顶点,1个2度顶点,其余均是1度顶点。
则(1)求T 有几个1度顶点(2)画出满足上述要求的不同构的两棵树。
分析:对于任一棵树T ,其顶点数p 和边数q 的关系是:1q p =-且1deg()2ipi v q ==∑,根据这些性质容易求解。
解:(1)设该树T 的顶点数为p ,边数为q ,并设树T 中有x 个1度顶点。
于是1deg()33122ipi v x q ==⨯+⨯+=∑且31p x =++,1q p =-,得5x =。
(2)满足上述要求的两棵不同构的无向树,如图1所示。
图1例2设G 是一棵树且()G k ∆≥,证明G 中至少有k 个度为1顶点。
证:设T 中有p 个顶点,s 个树叶,则T 中其余p s -个顶点的度数均大于等于2,且至少有一个顶点的度大于等于k 。
由握手定理可得:1222()2(1)pi i q p deg v p s k s ==-=≥--++∑,有s k ≥。
所以T 中至少有k 个树叶 。
习题例1 若无向图G 中有p 个顶点,1p -条边,则G 为树。
这个命题正确吗为什么解:不正确。
3K 与平凡图构成的非连通图中有四个顶点三条边,显然它不是树。
例2设树T 中有2n 个度为1的顶点,有3n 个度为2的顶点,有n 个度为3的顶点,则这棵树有多少个顶点和多少条边解:设T 有p 个顶点,q 条边,则123161q p n n n n =-=++-=-。
由deg()2v Vv q ∈=∑有:1223322(61)122n n n q n n ⨯+⨯+⨯==-=-,解得:n =2。
故11,12q p ==。
例3证明恰有两个顶点度数为1的树必为一条通路。
证:设T 是一棵具有两个顶点度数为1的(,)p q 树,则1q p =-且1deg()2pii v q ==∑2(1)p =-。
又T 除两个顶点度数为1外,其他顶点度均大于等于2,故211deg()2deg()2(1)p p iii i v v p -===+=-∑∑,即21deg()2(2)p ii v p -==-∑。
因此2p -个分支点的度数都恰为2,即T 为一条通路。
例4 画出具有4、5、6、7个顶点的所有非同构的无向树。
解:4个顶点的非同构的无向树有两棵,如图21(),()a b 所示; 5个顶点的非同构的无向树有3棵,如图21(),(),()c d e 所示。
(a ) (b) (c) (d) (e)图26个顶点的非同构的无向树有6棵,如图3所示。
图37个顶点的非同构的无向树有11棵,如图4所示。
所画出的树具有6条边,因而七个顶点的度数之和应为12。
由于每个顶点的度数均大于等于1,因而可产生以下七种度数序列127(,,,)d d d L :(1)1111116;(2)1111125;(3)1111134;(4)1111224;(5)1111233;(6)1112223;(7)1122222。
在(1)中只有一个星形图,因而只能产生1棵树1T 。
在(2),(3)中有两个星形图,因而也只能各产生1棵非同构的树,分别设为 23,T T 。
在(4),(5)中有三个星形图,但三个星形图是各有两个是同构的,因而各可产生两棵非同构的树,分别设为45,T T 和67,T T 。
在(6)中,有四个星形图,有三个是同构的,考虑到不同的排 列情况,共可产生三棵非同构的树,设为8910,,T T T 。
在(7)中,有五个星形图,都是同构的,因而可产生1棵树, 设为11T 。
七个顶点的所有非同构的树111T T :如图2所示。
T 1 T 2 T 3 T 4 T 5 T 6T 7 T 8 T 9 T 10 T 11图4例5设无向图G 是由(2)k k ≥棵树构成的森林,至少在G 中添加多少条边才能使G 成为一棵树解:设G 中的k 个连通分支为:12,,,k T T T L ,i v ∈i T ,1,2,,i k =L 。
在G 中添加边1{,}i i v v +,1,2,,1i k =-L ,设所得新图为T ,则T 连通且无回路,因而T 为树。
故所加边的条数1k -是使得G 为树的最小数目。
例6 证明:任意一棵非平凡树都是偶图。
分析:若考虑一下数据结构中树(即有向树)的定义,则可以很简单地将树中的顶点按层次分类,偶数层顶点归于顶点集0V ,奇数层顶点归于顶点集1V ,图G 中每条边的端点一个属于0V ,另一个属于1V ,而不可能存在关联同一个顶点集的边。
同理,对于无向树,可以从任何一个顶点V 出发,给该树的顶点标记奇偶性,例如,v 标记0,与v 相邻的顶点标记1,再给与标记为1的所有相邻的顶点标记0,依次类推,直到把所有的顶点标记完为止。
最后,根据树的性质证明,任何边只可能关联1V (标记为 1的顶点集)和0V (标记为0的顶点集)之间的顶点。
证1从任何一个顶点v 出发,给该树的顶点做标记,v 标记0,与v 相邻的顶点标记1,然后再给与标记为1的所有顶点相邻的顶点标记0,……,依次类推,直到把所有的顶点标记完为止。
下面证明:对于任何边只能关联1V (标记为1的顶点集)和0V (标记为0的顶点集)之间的顶点。
不妨假设,若某条边e 关联1V 中的两个顶点,设为1v 和2v ,又因为根据上述的标记法则,有1v 到v 的路1P 和2v 到v 的路2P 。
设1P 与2P 离1v 和2v 最近的顶点为u ,所以,树中存在回路:11221v PuP v ev ,与树中无回路的性质矛盾。
所以,任意边只能关联1V (标记为1的顶点集)和0V (标记为0的顶点集)之间的顶点。
所以,任意一棵非平凡树都是偶图。
证2 设T 是任一棵非平凡树,则T 无回路,即T 中所有回路长都是零。
而零是偶数,故由偶图的判定定理可知T 是偶图。
例7(1)一棵无向树有i n 个度数为i 的顶点,1,2,,i k =L 。
23,,,k n n n L 均为已知数,问1n 应为多少(2)在(1)中,若(3)r n r k ≤≤未知,()j n j r ≠均为已知数,问rn 应为多少解:(1)设T 为有p 个顶点,q 条边无向树,则1q p =-,1ki i p n ==∑。
由握手定理:1deg 2pii vq ==∑,有11deg 222p ki i i i v in q p =====-∑∑,即112222kki i i i in p n ===-=-∑∑。
①由式①可知:122222(2)2kkki i i i i i n in n i n ====-+=-+∑∑∑。
(2)对于3r ≥,由①可知:11(2)22k r i i i r n i n r =≠=---⎡⎤⎢⎥⎢⎥⎣⎦∑。
例8证明:任一非平凡树最长路的两个端点都是树叶。
证:设T 为一棵非平凡的无向树,12k L v v v =L 为T 中最长的路,若端点1v 和k v 中至少有一个不是树叶,不妨设k v 不是树叶,即有deg()2k v ≥,则k v 除与L 上的顶点1k v -相邻外,必存在1k v +与k v 相邻,而1k v +不在L 上,否则将产生回路。
于是11k k v v v +L 仍为T 的一条比L 更长的路,这与L 为最长的路矛盾。
故k v 必为树叶。
同理,1v 也是树叶。
例9设无向图G 中有p 个顶点,1q -条边,则G 为连通图当且仅当G 中无回路。
证:必要性:因为G 中有p 个顶点,边数1q p =-,又因为G 是连通的,由定理可知G 为树,因而G 中无回路。
充分性:因为G 中无回路,又边数1q p =-,由定理可知G 为树,所以G 是连通的。
例10设G 是一个(,)p g 图,证明:若g p ≥,则G 中必有回路。
证:(1)设G 是连通的,则若G 中无回路,则G 是树,故1q p =-与q p ≥矛盾。
故G 中必有回路。
(2)设G 不连通,则G 中有(2)k k ≥个分支,12,,,k G G G L 。
若G 中无回路,则G 的各个分支(1,2,,)i G i k =L 中也无回路,于是各个分支都是树,所以有:1i i q p =-,1,2,,i k =L 。
相加得:(2)q p k k =-≥与q p ≥矛盾,故G 中必有回路。
综上所述,图G 中必有回路。
例11设12,,,p d d d L 是p 个正整数,2p ≥,且122pi i d p ==-∑。
证明存在一棵顶点度数为12,,,p d d d L 的树。
证:对顶点p 进行归纳证明。
当2p =时,122222d d +=⋅-=,则121d d ==,故以12,d d 为度数的树存在,即为一条边。
设对任意1p -个正整数121,,,p d d d -L ,只要112(1)2p i i d p -==--∑,则存在一棵顶点度数为121,,,p d d d -L 的树。
对p 个正整数'''12,,,pd d d L ,若有'122pi i d p ==-∑,则'''12,,,p d d d L 中必有一个数为1,必有一个数大于等于2;不妨设''11,2p d d =≥,因此对1p -个正整数''''231,,,,1p pd d d d --L ,有1''2(1)2(1)2p i p i d d p -=+-=--∑,故存在一棵顶点度数为''''231,,,,1p p d d d d --L 的树'T 。
设'T 中u 的度数为'1p d -,在'T 中增加一个顶点v 及边{,}u v ,得到一个图T ,则T 为树。
又T 的顶点度数为'''12,,,pd d d L ,故由归纳法知原命题成立。
例题例1 G 的一条边e 不包含在G 的任一回路中当且仅当e 是G 的桥。
分析:这个题给出了判断桥的充要条件,应该记住。
证:必要性:设e 是连通图G 的桥,e 关联的两个顶点是u 和v 。
若e 包含在G 的一个回路中,那么除边e uv =外还有一条分别以u 和v 为端点的路,所以删去边e 后,G 仍是连通的,这与e 是桥相矛盾。
充分性:若边e 不包含在G 的任意回路中,则连接顶点u 和v 只有边e ,而不会有其它连接u 和v 的路。
因为若连接u 和v 还有不同于边e 的路,此路与边e 就组成了一条包含边e 的回路,从而导致矛盾。
所以,删去边e 后,u 和v 就不连通了,故边e 是桥。
例2设G 是连通图,满足下面条件之一的边应具有什么性质(1)在G 的任何生成树中; (2)不在G 的任何生成树中。
