第七章抽样推断案例
第七章 抽样设计与推断(改)

第七章抽样设计与推断第一节抽样设计一、抽样推断与抽样设计的概念(一)抽样推断抽样推断(Sampling inference)是在抽样调查的基础上,利用样本的实际资料计算样本指标(统计量),并据以推算总体相应特征值(总体参数)的一种统计分析方法。
抽样推断具有如下特点:第一,抽样推断是建立在随机取样的基础上。
按随机原则抽取样本单位,是抽样推断的前提。
所谓随机原则就是在抽选调查单位的过程中,完全排除人为的主观因素的干扰,以保证使现象总体中的每一个个体都有一定的可能性被选中。
换句话讲,哪些单元能够被选作调查单位纯属偶然因素的影响所致。
这里需说明几点:①随机并非“随意”。
随机是有严格的科学含义的,可用概率来描述,而“随便”仍带有人为的或主观的因素,它不是一个科学的概念;②随机原则不等于等概率原则;③随机原则一般要求总体中每个单元均有一个非零的概率被抽中;④抽样概率对总体参数的估计有影响。
只有坚持抽取的随机原则,才能使被抽中单位的频数分布类型与调查对象相同,从而增强被抽中单位对总体的代表性,达到推断总体的目的。
第二,抽样推断是由部分推算整体的—种认识方法。
即对抽取的调查单位进行调查研究,取得调查单位的实际资料,计算出调查单位的指标数值,并据以推断和估计总体的指标数值。
第三,抽样推断以概率论中的大数法则和中心极限定理为理论依据。
第四,抽样误差可以事先计算和控制。
抽样调查除具有十分明显的特色之外,还在实际应用过程中发挥着突出的作用。
其一,抽样调查能够解决全面调查所无法解决的现象的调查问题。
在实际工作中,对某些现象常常可能一方面需要了解其全面情况,另一方面又由于现象自身的特性决定了无法通过全面调查获取资料。
此时,只有使用抽样调查。
该类现象主要有:(1)产品质量的破坏性检验。
如轮胎的里程寿命试验,青砖的抗折耐压试验,炮弹的杀伤力试验,弹簧的抗拉强度试验等等。
(2)无限总体的调查。
无限总体所包含的总体单位数目无限多个,无法一一调查。
第7章抽样

随机抽样技术的优缺点
(1) 优点 ①随机抽样是从总体中按照随机原则抽取一部分单位进行的 调查。 ②随机抽样技术能够计算调查结果的可靠程度。 (2) 不足 ① 对所有调查样本都给予平等看待,难以体现重点。 ② 抽样范围比较广,所需时间长,参加调查的人员和费用多。 ③ 需要具有一定专业技术的专业人员进行抽样和资料分析。 一般调查人员难以胜任。 ④抽样框难以构建。 ⑤比其他概率抽样精确度低,标准差较大。 30
24
1.简单随机抽样 • 又称纯随机抽样,即对总体单位不进行任何分组 排列,仅按随机原则直接从总体中抽取样本,以 使总体中的每一个单位均有同等的被抽取的机会。
• 这是最基本,最简单的的机率抽样方法。它易于 理解,样本结果可以推断总体,大多数统计推论 方法都假定数据是由简单随机抽样法法获得的。
25
1.简单随机抽样 • 每个单位被选取的机会是相同的。就好像把各个 单位的名字写在大小相同的纸上,放到一个箱子 中,由我们抽取,每个个案都有被抽到的可能, 而且机会相同。如平日常见的摸彩或摇奖,在数 学上则会利用随机数表来抽取样本。
第七章
抽样
1
本章的学习目标 一、抽样的概念
二、抽样的基本过程
三、概率抽样
四、非概率抽样
五、样本量的确定
六、 PPS抽样简介
七、 KISH表的运用
2
一、抽样的概念
3
(一)什么是抽样?
• 抽样就在我们的日常生活中。抽血化验,尝试水 温,窥一斑而知全豹。
• 抽样,就是从研究总体中抽取一部分的过程。 • 抽样调查,就是从研究总体中抽取一部分代表加 以调查研究,然后用所得结果推论和说明总体的 特性。这也称为推论统计。
2.等距抽样
• 又称系统抽样或机械抽样。 • 具体做法: • 1)将总体的所有单位按一定顺序排列起来; • 2)计算抽样间隔R=N/n;
抽样 推断

实例导入
1.71: 1(以农业户为1)。另外,财产拥有的差距远大于收入差距, 全国城乡居民家庭人均财产(房产、金融资产和耐用消费品财产)分配 的基尼系数保守测算达到0.653,最高20%与最低20%的家庭的 人均财产均值比为72.4:1,
第二,“看病难、看病贵”,“就业失业问题”和“收入差距过 大、贫富分化”是最突出的三个社会问题。在调查的17个社会问题 中,“看病难、看病贵”被排在第一位,说明这个问题在当前反映比 较强烈。根据这次调查结果,城乡家庭人均年消费总支出中,医疗支 出占11.8%,教育支出占10.6%(排除无教育支出户占18.2%), 远高于交通通信支出(7.4%)和衣着支出(6.3%),这也从一个侧面
building cities),是指以单位和个人实际缴纳的增值税、 消费税、营业税(以下简称“三税”)的税额为计税依据而征 收的一种税。城市维护建设税的特征:一是具有附加税性质。 它以纳税人实际缴纳的“三税”税额为计税依据,附加于“ 三税”税额,本身并没有类似于其他税种的特定、独立的征 税对象。二是具有特定目的。城市维护建设税税款专门用于 城市的公用事业和公共设施的维护建设。
每个单位都进行观察,只能组织抽样调查,取得部分的实际资料,来
估计和判断总体的数量特征,以达到对现象总体的认识。
2.抽样推断的特点
抽样推断的特点归纳起来有以下几点:
下一页
第一节 抽样推断概述
第一,抽样推断是一种由部分推算整体的研究方法。虽然认识总体 的数量特征是目的,但在实际生活中人们通常只能掌握部分的实际资 料,这就会在认识上形成全局与局部的矛盾。这种矛盾在现实中是大 量存在的。例如,要了解某一品种棉花纤维的长度,一般不可能对每 根纤维都进行检测;又如要了解某种种子的发芽率,通常也不可能对 所有的种子都进行催芽试验;城市居民家庭收支、民意测验等,也难 以开展挨家挨户的调查。如果在方法上不能解决这个问题,那么统计 的认识活动就会受到限制,统计科学也很难得到发展。抽样推断原理 解决了这一矛盾,它科学地论证了样本指标和相应的总体参数之间存 在着内在联系,而且两者的误差分布也是有规律可循的,这就有效地
(抽样检验)第七章第一次课抽样原理与方法

(抽样检验)第七章第⼀次课抽样原理与⽅法第⼀节抽样⽅案的制定在科学研究中,除了进⾏控制试验外,有时也要进⾏调查研究。
调查研究是对已有的事实通过各种⽅式进⾏了解,然后⽤统计的⽅法对所得数据进⾏分析,从⽽找出其中的规律性。
例如,了解畜禽品种及⽔产资源状况;探索和分析对某种疾病有效的防治规律、措施以及新的检验⼿段和⽅法等。
由于现场调查⽴⾜于⽣产实际,所以它是研究和解决实际问题的⼀种重要研究⽅法。
同时,控制试验的研究课题,往往是在调查研究的基础上确定的;试验研究的成果,⼜必须在其推⼴应⽤后经调查得以验证。
为了使调查研究⼯作有⽬的、有计划、有步骤地顺利开展,必须事先拟定⼀个详细的调查计划。
调查计划应包括以下⼏个内容:(⼀) 调查研究的⽬的任何⼀项调查研究都要有明确的⽬的,即通过调查了解什么问题,解决什么问题。
例如,家畜健康状况的调查的⽬的是评定家畜健康⽔平;畜禽品种资源调查的⽬的是了解畜禽品种的数量、分布与品种特征特性等情况。
同时,调查研究的⽬的还应该突出重点,⼀次调查应针对主要问题收集必要的数据,深⼊分析,为主要问题的解决提出相应的措施和办法。
(⼆) 调查的对象与范围根据调查的⽬的,确定调查的对象、地区和范围,划清调查总体的同质范围、时间范围和地区范围。
例如,四川省家禽品种资源调查,调查地区为四川省,调查总体和对象为全省各市、县的家禽,调查时间从2000年1⽉到2000年12⽉。
(三) 调查的项⽬调查项⽬的确定要紧紧围绕调查⽬的。
调查项⽬确定的正确与否直接关系到调查的质量。
因此,项⽬应尽量齐全,重要的项⽬不能漏掉;项⽬内容要具体、明确,不能模棱两可。
应按不同的指标顺序以表格形式列⽰出来,以达到顺利完成搜集资料的⽬的。
例如,家禽品种资源调查项⽬有:种类(鸡、鸭、鹅等)、品种(柴鸡、来航、⽩洛克等),数量、体重、产蛋性能等项⽬。
调查项⽬有⼀般项⽬和重点项⽬之分。
⼀般项⽬主要是指调查对象的⼀般情况,⽤于区分和查找,如畜主姓名、住址及编号等。
学习情境七 抽样推断 课件- 《统计学》同步教学(财经出版社)

代替总体比例的标准差 P(1 P) ,因此公式可以 写成:
情境七 抽样推断
一、 抽样推 断概述
二、 总体的 参数估计
三、 必要样本 容量的确定
参数估计的概念 参数估计就是用样本统计量去估计总体的参数。
(一)参数估计的概念 用来估计一个总体参数的任何样本统计数称为
一个估计量,用符号 ˆ 表示。样本均值、样本比 例、样本方差等都可以是一个估计量。
常见的抽样误差有:抽样平均数与总体平均数 的差,抽样成数与总 体成数的差(p﹣P)
情境七 抽样推断
一、 抽样推 断概述
二、 总体的 参数估计
三、 必要样本 容量的确定
抽样误差的影响因素 1.抽样误差的大小与样本容量的多少有关 2.抽样误差的大小与总体标志变动程度有关 3.抽样误差的大小与抽样方法有关 4.抽样误差的大小与不同的抽样组织方式有关
情境七 抽样推断
一、 抽样推 断概述
二、 总体的 参数估计
三、 必要样本 容量的确定
当总体单位数(N)很大时,公式中的N-1可以 用N代替,所以,在实际计算时,不重复抽样的平 均数的平均误差可用下式计算:
情境七 抽样推断
一、 抽样推 断概述
二、 总体的 参数估计
三、 必要样本 容量的确定
在抽样推断的过程中,总体平均数的方差是未 知的,因此在实际统计工作中,有时采用样本标准 差s来代替,即
总体指标是根据总体中各单位的标志值或标志 属性计算的,反应总体数量特征的综合指标。
情境七 抽样推断
一、 抽样推 断概述
二、 总体的 参数估计
三、 必要样本 容量的确定
情境七 抽样推断
一、 抽样推 断概述
二、 总体的 参数估计
第七章 归纳推理案例

某市繁星商厦服装部在前一阵疲软的服装市场中打了一个反季节 销售的胜仗。据统计,其皮衣的销售额在6、7、8三个月连续成 倍数增长,6月527件,7月1269件,8月3218件。市有关主管部 门希望在今年冬天向全市各大商场推广这种反季节销售的策略, 力争在今年11、12月和明年1月使全市的夏衣销售能有大突破。 以下哪项如果为真,能够最好地说明该市有关主管部门的这 种希望可能会遇到麻烦? A. 皮衣的价格可以在夏天一降再降,是因为厂家可以在皮衣淡 季的时候购买原材料,其价格可以降低30%。 B. 皮衣的生产企业为了使生产销售可以正常循环,宁愿自己保 本或者微利,把利润压缩了55%。 C. 盛夏里搞皮衣反季节销售的不只是繁星商厦一家。但只有繁 星商厦同时推出了售后服务,由消协规定的三个月延长到七个月, 打消了很多消费者的顾虑,所以在诸商家中独领风骚。 D. 根据最近进行的消费者心理调查的结果,买夏衣重流行、买 冬衣重实惠是消费者的极为普遍的心理。
【案例】巧匠鲁班 鲁班是春秋时鲁国的巧匠。据传说,他有一次 承造一座大宫殿,需用很多木材,他叫徒弟上山去 砍伐大树。当时还没有锯子,用斧子砍,一天砍不 了多少棵树,木料供应不上,他很着急,就亲自上 山看看。山非常陡,他在爬山的时候,一只手拉着 丝茅草,一下子就把手指头拉破了,流出血来。鲁 班非常惊奇,一根小草为什么会这样厉害?在回家 的路上,他就摘下一棵丝茅草,带回家去研究。他 发现丝茅草的两边有许多小细齿,这些小细齿非常 锋利,用手指去扯,就划破了一个口子。这一下把 鲁班提醒了。他想,如果像丝茅草那样,打成有齿 的铁片,不就可以锯树了吗?于是,他就和铁匠一 起试制了一条带齿的铁片,拿去锯树,果然成功了。 有了锯子,木料供应问题就解决了。
【解题分析】 市有关主管部门的建议依据类比推理:夏季反季节 销售冬季服装获得成功,因此若在冬季反季节销售 夏季服装也将获得成功。 显然这个类比结论是可错的,题目所要求的就是找 出使这个类比不成立的理由。 选项A、B、C都只是部分地说明了繁星商厦反季节 销售冬装取得成功的原因,与“反季节销售夏装是 否会取得成功”毫不相干。而选项E则解释了原因: 买冬衣重实惠,在夏天买冬衣便宜,所以夏季反季 节销售容易取得成功;买夏衣重流行,而在冬天无 法知道来年夏天流行什么,因此冬季反季节销售夏 衣不大容易取得成功。
第七章 抽样推断 (《统计学》PPT课件)

接作为相应全及指标的估计值。
2.定义:设x_
表示总体平均数
__
X
的估计值,p^ 表示
总体成数P的估计值,则有:
__ _
X x
或
^
Pp
27
第四节 抽样估计
二、总体参数的点估计
3. 性质:
用抽样指标估计总体指标时,要求抽样指标
的平均数等于被估计的总体指标;E(
_
x)
__
X
_
E( p) P
用抽样指标估计总体指标时,要求当样本容 量n充分大时抽样指标充分靠近总体指标;
6
第一节 抽样推断概述
二、有关抽样的基本范畴
2.指标
:根据全及总体各个单位的标志值或标 志特征计算的,用来反映全及总体某种属性的综合 指标;
:由样本总体各单位标志值或标志特征 计算出的综合指标。
注:对于一个确定的问题,全及指标是唯一的, 样本指标不是唯一确定的,即样本指标的随机变量。
7
抽样推断
2.种类:
根据抽样资料计算样本指标,并以此直接作 为相应全及指标的估计值;
根据给定的概率保证程度的要求,利用实 际抽样资料,求出总体被估计值的上限和下限,即给 出总体参数可能存在的区间范围,而不是直接给出总 体参数的估计值。
26
第四节 抽样估计
二、总体参数的点估计
根据抽样资料计算样本指标,并以此直
n
N
22
第三节 抽样误差
三、抽样极限误差
在抽样推断中可允许的误差范围,等于样本指 标可允许变动的上限或下限与总体指标之差的绝对值。
2.计算公式:
_ __
_
__ _
抽样平均数极限误差: 或
_ x- X
抽样推断-37页PPT文档资料

x :抽样平均数的抽样误极差限 p : 抽 样 成 数 的 抽 样 极 限差误
x
xX
xXx
x
x
P pP ppPpp
26
(xx,xx)或( pp,pp)称为置. 信区
23.09.2019
第二节 抽样误差 五、抽样误差的概率度
用 除以 (或者 除 用以 ),得到 t, t数 就值 称
样本又称子样,是从全及总体中随机抽取出来,作为代表 这一总体的那部分单位组成的集合体,一般用n表示。
总 体N (唯一)
7
样 本n (非唯一)
23.09.2019
第一节 统计推断概述 四、抽样推断中的基本概念
(二)总体指标和样本指标
总体指标是根据总体各单位的标志值或标志 特征计算的,反映总体数量特征的综合指标, 称为全及指标,由总体各单位的标志值或标 志特征所决定,全及指标的指标值是确定的, 唯一的,所以又称为参数。
15
23.09.2019
不同抽样方法的样本个数
重复抽样
考虑顺序 BnN=Nn
抽样方法
不考虑顺序 D n N C n N n 1 ( N n 1 ) n N ! n ( 2 ) N
不重复抽样
考虑顺序 A n N N ( N 1 ) ( N n 1 )
n
d.可以通过调整样本单位数n来控制抽样平均误差。
23
23.09.2019
第二节 抽样误差
抽样平均误差的计算
重复抽样
不重复抽样
样本平均数 的平均误差
2
x
nn
2 (1n)
x
nN
样本成数 的平均误差
第七章 归纳推理案例

ቤተ መጻሕፍቲ ባይዱ
【案例分析】 财主要求每一根都划得着,只能一根根地试, 不然怎么知道每一根都划得着。从逻辑学上讲,这 是完全归纳推理。
贝蒂荣法则
1879年,在巴黎警察厅抄写卡片的贝蒂荣厌倦了自己的工作,他 放弃现有工作转而进行人体测量。他开始测量登记在案的一些囚 犯的身体的部分部位,并记录下来。资料积累到一定的程度后, 贝蒂荣进行了分析和归类,并运用到囚犯识别上。1883.2,贝蒂 荣运用人体测定法则成功识别出一名囚犯的前科身份。1884年, 他鉴别了300名有前科的罪犯,而且也没有遇到两个人人体测量 资料完全相同的情况。于是法国人认为以测量人体某些不变部位 的骨骼为基础的贝蒂荣法则是19世纪警务中最伟大的发明,这个 发明不仅使法国而且使全世界的辨真工作不再出错。由此贝蒂荣 法则在历史上风靡一时。岂料在后来一次鉴别中贝蒂荣却发现了 两名人体测量数据完全一样的囚犯,贝蒂荣法则失败了。 怎样看待贝蒂荣法则的失败?
利用人体测量数据识别囚犯的贝蒂荣法则是运用何种推理得出的?
贝蒂荣法则
贝蒂荣法则是运用不完全归纳推理获得的。 其推理形式是: 对第一个犯人的辨真贝蒂荣法则是有效的, 对第二个犯人的辨真贝蒂荣法则是有效的, …… 对N个犯人的辨真贝蒂荣法则是有效的, N个犯人是所有犯人中的一部分 目前没有发现贝蒂荣法则对犯人辨真无效, 所以,对所有犯人的辨真贝蒂荣法则是有效的。 这个推理前提和结论间不具有必然性关系,而是或然 性的,即前提不能保证结论必然真。
某大学30名学生参加一项旨在提高约会技巧的计划。在参加这项 计划前一个月,他们平均已经有过一次约会。30名学生被分成两 组:第一组与6名志愿者进行6次“实习性”约会,并从约会对象 得到对其外表和行为的看法的反馈;第二组仅为对照组。在进行 实习性约会前,每组都要分别填写社交忧惧调查表,并对其社交 技巧评定分数。进行实习性约会后,第一组需要再次填写调查表。 结果表明:第一组较之对照组表现出更少社交忧惧,在社交场合 更多自信,以及更易进行约会。显然,实际进行约会,能够提高 我们社会交际的水平。 以下哪项如果为真,最可能质疑上述推断? A. 这种训练计划能否普遍开展,专家们对此有不同的看法。 B. 参加这项训练计划的学生并非随机抽取的,但是所有报名的 学生并不知道实验计划将要包括的内容。 C. 对照组在事后一直抱怨他们并不知道计划已经开始,因此, 他们所填写的调查表因为对未来有期待而填得比较悲观。 D. 填写社交忧惧调查表时,学生需要对约会的情况进行一定的 回忆,男学生普遍对约会对象评价得较为客观,而女学生则显得 比较感性。
统计学-07抽样推断

6 368
4 2 5 3 4 3 3 4 5 4 2 1 54
3
4 6 11 14 18 21 24 28 33 37 39 40 45 49 52
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
370 371 388 402 410 446 453 470 477 490 499 502 503 51 520 6
可编辑ppt
12
第三步:抽取调查单位
半距起点、等距抽样
可编辑ppt
13
半距起点、等距抽样
➢ 以第一个抽样距离的一半处作为第一个调查单 位
➢ 以后毎隔一个抽样距离抽取一个调查单位 ➢ 直到最后一个调查单位抽出为止
可编辑ppt
14
以抽取6户为例,抽取的户数依次为:
第1户 n1=17.5÷2=8.75 为第3号户 第2户 n2=8.75+17.5=26.25 为第8号户 第3户 n3=26.25+17.5=43.75 为第13号户 第4户 n4=43.75+17.5=61.25 为第19号户 第5户 n5=61.25+17.5=78.75 为第24号户 第6户 n6=78.75+17.5=96.25 为第28号户
可编辑ppt
22
7.2 抽样分布及抽样推断理论依据 ——基础知识:概率
发生概率很小的事件称为小概率事件(small probability event);
小概率事件不那么可能发生,但它往往比 很可能发生的事件更值得研究。
在某种意义上,新闻媒体的主要注意力大
都集中在小概率事件上。
可编辑ppt
23
例如:对某镇农户进行家计调查,以自然村庄划分群,
任务七统计分析——抽样推断52页PPT

66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
任务七统计分析——抽样推断
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
统计7抽样推断
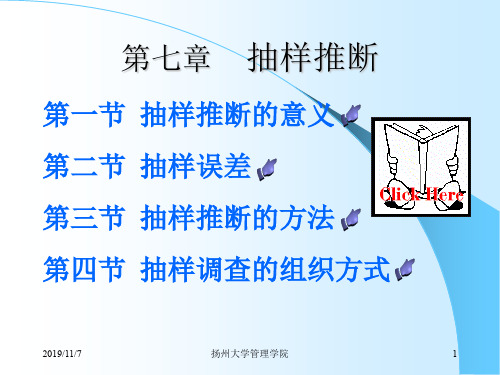
则: 300 15(小时)
x
n
400
x
2 1 n
n N
3002 1 400 13.42(小时) 400 2000
计算结果表明:根据部分产品推断全部产品的平均使用寿命 时,采用不重复抽样比重复抽样的平均误差要小。
2019/11/7
13
(三)样本容量和样本个数
样本容量:一个样本包含的单位数。用 “n”表示。 一般要求 n ≥30大样本
样本个数:从一个全及总体中可能抽取的样本数目。
(四)重复抽样和不重复抽样
重复抽样:又称回置抽样。
考虑顺序时,可能组成的样本数目: N n
不考虑顺序时,可能组成的样本数目:
Cn N n1
不重复抽样:又称不回置抽样。
Xi
E
n i1
Xi
x
lim
P
n i1
Xi
n
x
n
n
D Xi i1
n n
1
x t2
e 2 dt (x)
2
2019/11/7
扬州大学管理学院
20
本定理的证明在20世纪20年代由林德伯格和莱 维给出,因证明较复杂,在此从略。
由于随机抽样的偶然因素使样本各单位的结构 不足以代表总体各单位的结构,而引起抽样指标和 全及指标之间的绝对离差为抽样误差。
2019/11/7
扬州大学管理学院
23
(二)影响抽样误差大小的因素
1、总体各单位标志值的变异程度 2、样本的单位数 3、抽样方法 4、抽样推断的组织形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 设总体N个单位中,有N1个单位具有某 种属性,N0个不具有某种属性, N1 +N0=N, P为总体中具有某种属性的单位数所占的比 重,Q为布局有某种属性的单位所占的比重, 则总体成数为:
N1 P N
N 0 N N1 Q 1 P N N
iii. 总体标准差、总体方差
X X N
1、重复抽样(重置抽样、放回抽样) 基本的特点和做法 样本个数的计算:Nn(可重复排列数)
•
• • • •
2、不重复抽样(不重置抽样、不放回抽样)
基本的特点和做法 样本个数的计算: (不重复排列数) N(N-1)(N-2)......(N-n+1)=N!/(N-n)! 以上都是考虑顺序的抽样!
五、总体分布、样本分布和抽样分布
一个任意分 布的总体
x
n
当样本容量足够 大时(n 30) , 样本均值的抽样 分布逐渐趋于正 态分布
x
x
中心极限定理
(central limit theorem)
第七章 抽样推断
本章内容
第一节 抽样推断概述 第二节 抽样推断的几个基本概念 第三节 抽样误差 第四节 参数估计的一般问题 第五节 一个总体参数的区间估计 第六节 样本容量的确定——抽样方案设计
本章重点
第三、五、六节内容
本章难点
第三、五节内容
具体要求
理解-抽样推断的含义、作用及基本概念
2
2
2.样本指标(统计量)
i. 样本平均数
ii. 样本成数
x x n
n1 ˆ n
n0 n n1 ˆ q 1 p n n
iii. 样本标准差、样本方差
x x s n 1
2
2
• 四、重复抽样和不重复抽样
•
• • •
抽取样本有两种基本方法,不同的方法会影响抽样 的误差。
N ( N 1)( N 2)( N n 1) P
n N
三、总体指标和样本指标
• 1.总体指标(参数) i. 总体平均数 X N
ii. 总体成数 • 当研究的是总体个单位的属性特征时, 只能用一定的术语来描述,所以就应该计算 比重结构指标,称为总体成数。用大写 P 表示,它说明了总体中具有某种标志的单位 数在总体中所占的比重。
样 本
3.抽样分布(sampling distribution)
样本统计量的概率分布,是一种理论分布
在重复选取容量为n的样本时,由该统计量的所有 可能取值形成的相对频数分布
随机变量是 样本统计量
样本均值, 样本比例,样本方差等
结果来自容量相同的所有可能样本 提供了样本统计量长远而稳定的信息,是进行 推断的理论基础,也是抽样推断科学性的重要 依据
=10
n=4 x 5 n =16 x 2.5
= 50
X
x 50
x
总体分布
抽样分布
中心极限定理
(central limit theorem)
从均值为,方差为 2的一个任意总体中抽取容量为n的 样本,当n充分大时,样本均值的抽样分布近似服从均 值为μ,方差为σ2/n的正态分布
§7.2抽样推断的几个基本概念
一、全及总体和抽样(样本)总体
1、全及总体又称母体,简称总体,它是指所要认 识的,具有某种共同性质的许多单位的集合体。 组成全及总体的单位称为总体单位,全及总体的单 位数一般用N表示。
2、抽样总体又称子样,简称样本,是从全及总体 中随机抽取的那一部分单位所构成的集合体。 组成抽样总体的单位称为样本单位,样本单位数亦 称样本容量,一般用n表示。 样本单位数的范围:1<n<N
•
• •
n N 抽样比例:
大样本:n≥30;小样本:n<30 重点理解:如果说对于一次抽样调查, 全及总体是唯一确定的,那么抽样总体就不是 这样,样本是不确定的,一个全及总体可能抽 出很多个样本总体,样本的个数和样本的容量 有关,也和抽样的方法有关。
二、样本容量和样本个数
• 1.样本容量:是指一个样本所包含的单位数, 通常用n表示。(总体单位数用N表示) • 2.样本个数:样本可能数目,是从一个总体中 可能抽取的样本个数。 • 如:样本容量为n • 重复抽样:样本个数为 N n • 不重复抽样:样本个数为
抽样分布的形成过程
(sampling distribution)
总体
样 本
计算样本统计 量 如:样本均值 、比例、方差
样本均值的抽样分布 与中心极限定理
当总体服从正态分布N(μ,σ2)时,来自该总体的所有 容量为 n 的样本的均值 x 也服从正态分布, x 的数 学期望为μ,方差为σ2/n。即x~N(μ,σ2/n)
判断。
• 二、抽样推断的特点
•
• 1、抽样推断是非全面调查。可以节省人力 物力和财力,取得事半功倍的效果。 2、抽样推断是按随机原则抽选调查单位。
• •
•
3、抽样推断是用样本的指标数值去推算总
体的指标数值。
4、抽样推断运用的是概率原理。
5、抽样推断中产生的误差可以事先计算并加 以控制。
• 三、抽样推断的作用(适用范围)
掌握-抽样误差的计算、参数估计的方法等。
一、抽样推断的概念
§7.1抽样推断概述
“抽样推断、抽样调查和抽样估计”基本上
是相同的意思。『回顾第二节“抽样调查”的概
念』
抽样推断是按照随机原则从全部研究对象中
抽取一部分单位进行观察,并根据被抽取的那部
分单位的数量特征,运用一定的数理统计方法,
对总体的数量性作出具有一定可靠程度的估计和
•
• 1、对无限总体全面情况的了解,必须采用抽 样推断。 2、对破坏性或消耗性检查,必须采用抽样调 查。
•
3、对某些可以但事实上不必或不可能进行全 面调查的现象总体,可以采用抽样推断获取相关 资料。
4、抽样调查可以对全面调查得来的资料进行 验证,并据以进行补充和修改。
•
•
5、抽样推断可以用于生产过程的质量控制。
1.总体分布 (population distribution)
总体中各元素的观察值所形成的分布 分布通常是未知的 可以假定它服从某种分布
总体
2.样本分布 (sample distribution)
一个样本中各观察值的分布 也称经验分布 当样本容量n逐渐增大时,样本分布逐渐接近总 体的分布
