2018年-第16届希望杯考前训练100题-四年级
希望杯考前100题 (1)

1.计算:25278⨯⨯.2.计算:9876987989+++.3.计算:504812108642+-⋅⋅⋅+-+-+-.4.计算:20172015201620152014201620162017⨯-⨯-⨯+⨯.5.计算:1468715÷+÷.6.已知142857)2(99999=÷÷a ,求a .7.某数被27除,商是8,余数是5,求这个数.8.定义:)2()3(-⨯+=*B A B A ,求1715*.9.除法算式中,余数最大是多少?10.有5个连续偶数之和恰好等于4个连续奇数之和,如1311971210864+++=++++,请写出一个符合要求的式子.11.将36表示成三个大于1的自然数的乘积(不考虑三个自然数的相乘顺序),共有几种不同的表示方法?12.用数字2,0,1,7可以组成多少个不重复的三位数?13.用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是?14.如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数.15.2017和某个小于100的自然数的和等于两个连续自然数之积,求这个小于100的自然数.16.某两位数的十位数字与个位数字互换后,新数比原数大36,求原来的两位数.17.abc 是一个三为偶数,已知b 是c 的三倍,且c a b +=,求abc .18.在乘法算式2524232221201918171615⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯的计算结果中,最多有多少个连续的0?19.在2018后面加一个两位数,使它成为一个能被7整除的六位数,则这个两位数最大的是多少?20.求能同时被3,5,7整除的最小的五位数.21.用一个自然数分别去除25,38,43,三个余数之和为18,求这个自然数.22.一个数被3除余2,被5除余4,被7除余6,则这个数最小是几?23.自然数a 是3的倍数,2-a 是4的倍数,3-a 是5的倍数,则a 最小是多少?24.d b a 、、是一位数字,并且21=-cd ab ,611=-ab cd ,则ad 等于多少?25.求能被2,3,5整除的最小四位数.26.488是一个四位数,数学老师说:“我再这个□中先后填入3个数字,所得的3个四位数,依次可被9,11,7整除.”数学老师先后填入的3个数字和是多少?27.从1,2,3,4,5,6这6个数字中,任取2个组成两位数,这些两位数中,3的倍数有多少个?28.已知y x 、是大于0的自然数,且100=+y x ,若x 是3的倍数,y 是5的倍数,则)(y x ,的不同取值有几对?29.如图的算式中,F E D C B A 、、、、、表示不同的一位数,求F E D C B A 、、、、、表示的数.30.在1~500中,不能被2整除,也不能被3整除,又不能被5整除的数有多少?31.在1到200之间去掉所有完全平方数,剩下的自然数的和是多少?32.如图,共端点A 的射线a 与d 互相垂直,a 与c 的夹角是︒60,b 与d 的夹角是︒45,求b 与c 夹角的度数.33.如图,在正方形ABCD 中,BM CM 3=,若梯形AMCD 的周长比ABM ∆的周长大6,求正方形的边长.34.将同样的两张正方形透明塑料薄片部分重合地放于桌面上(如图:=+S S 正方形),已知ABCD 的周长是60厘米,求长方形ABCD 的面积.35.如图,一只小蚂蚁从点A 出发,沿折线爬行一周,问:小蚂蚁爬行了多少米?36.一个长方形的长和宽都增加3厘米后,长方形的面积增加了63平方厘米,求原长方形的周长.37.用长是22厘米的铁丝网围成一个长和宽都是整数厘米数的长方形,有几种方法?38.如图,︒=∠+∠+∠+∠+∠+∠180654321,图中比平角小的角有多少个?39.如图,用11个边长为1的正方形卡片拼成数字“2”,求图中长方形的个数(不包括正方形).40.数一数,图中共有多少个平行四边形?41.数一数,图中有多少个三角形?42.数一数,图中有多少个三角形?43.已知一数列:1,3,4,7,11,18,…,这个数列的第10个数是多少?44.有白棋子和黑棋子共2018枚,按如图规律从左到右排成一行,其中黑子多少枚?45.观察下面按一定规律排列的一列数:,,,,,,,,,,,545352514342413231211……求第2017个数.46.如图,用小正方形摆成下列图形,按摆放规律,第25个图形需要多少个小正方形?47.如图13所示的数字是电子表中经常可见的数字2和5的表示形式、把图中左边的数字2向右翻转一次可得到右边的数字5,再向右翻转一次又会得到原来的数字2、那么将图中所示的数字25翻转一次得到的数字是多少?48.有张、王、李三个工人、甲、乙、丙三个工厂、以及车工、钳工和电工三种工作、已知:①王不在甲厂;②张不在乙厂;③在甲厂的不是钳工;④在乙厂的是车工;⑤王不是车工这三个人分别在哪个工厂、干什么工作?49.一个两位数除以它的各位数字之和、余数最大是多少?50.5个人围成一圈做游戏、每人都有一袋小石子.游戏开始时、第一个人给第二个人1颗石子第二个人给第三个人2颗石子、第三个人给第四个人3颗石子、第四个人给第五个人4颗石子、第五个人给第一个人5颗石子,……、如此操作5圈后所有人袋中的石子都一样多若所有石子的总数为1990颗、问游戏前每个人袋中分别有多少颗石子?51.将2017个小球放到10个箱子中、要求每个箱子中的小球的数目中都带有数字7请给出一种摆放方法.52.箱子里有2018个小球、编号分别为1,2,3,……,2018,现从箱子中摸出1616个小球、将它们的编号相乘、求积的个位数字.53.自然数n的十位数字是4、个位数字是2、各个数位上的数字之和为42、且n是42的倍数、求满足上述条件的最小的自然数.54.一副扑克牌有52张、依惯例A、J,Q、K依次视为1点、11点、12点、13点、任意抽出若干张牌、不计花色、如果抽出的牌中必定有3张牌的点数相同、那么至少要取几张牌?如果抽出的牌中必定有2张牌的点数之和等于15、那么至少要取几张牌?55.小明、小强、小红三个人在一起玩提迷藏的游戏、小明对小强说:“我在你的正北方5米处”,小红对小强说:“我在你的正南方6米处”,若小强走1米需要6步、那么先抓小明再去抓小红一共需要走多少步?56.10个50g的砝码和5个100g的砝码同时放在天平的左右两侧才能使天平保持平衡、那么在天平左侧放2个1kg的砝码、右侧放6个300g的砝码、要使天平保持平衡还要在右侧放几个50g的砝码?57.在一个周长是200米的池塘周围植树、每隔5米植一棵、需要准备多少稞树苗?58.在120米长的跑道右侧插16面彩旗、求相邻两面彩旗之间的距离.59.今年、小军4岁、爸爸31岁、再过多少年爸爸的年龄是小军的4倍.60.亮亮比品晶小6岁、16年后亮亮的年龄是晶晶今年的年龄的2倍、问:晶晶今年几岁?61.父亲今年45岁、儿子今年15岁、多少年前父亲的年龄是儿子年龄的7倍?62.2011年、妈妈的年齡等于她的两个孩子的年龄和的5倍、2017年她的年龄等于两个孩子的年龄和的2倍、求2018年时妈妈的年龄.63.某学习小组数学成绩的统计图如图所示,求该小组的平均成绩.64.统计十位同学在一次数学考试中的成绩、已知前四名的平均分是95分、后六名的平均分比十人的总平均分少6分、求这十位同学的平均分.65.李家求包了100亩地种玉米、亩产量600斤、刘家比李家少承包了20亩、结果两家的总产量相同.问:(1)刘家玉米的总产量是多少斤?(2)李家玉米的宙产量比刘家的少多少斤?66.桔子、苹果、梨共有六箱、这六箱水果的重量(单位:千克)分别为:15,16,18,19,20,31,其中苹果的重量是梨的一半、桔子只有一箱这六个箱子中分别装的是什么水果?67.每本书的版权页上都印有:开本、印张、宇数、定价等等.如:“开本:720mm*米960mm1/16印张:12字数:240千字”求这本书平均每页有多少宇?(注:16开、即1个印张16页)68.某校规定语文、英语、数学三科考试成绩的平均分在95分以上才有可能被评为三好学生若在一次期末考试中、希希语文考了96分、英语考了92分、那么他数学至少得多少分才有可能被评为三好学生?69.1个西瓜可换5个苹果、2个苹果可换3根香蕉、5根香蕉可换8个桃予、那么60个桃子可换几个西瓜?70.7头牛可换16只羊、2只羊可换21只兔、则3头牛可换多少只兔?71.有两块地、平均亩产粮食650千克、其中第一块地5亩、亩产粮食670千克如果第二块地亩产粮食645千克、第二块地有多少亩?72.妈妈去市场买菜已知买肉和鸡蛋共用了77元、买鸡蛋和青菜共用了60元、买肉和青菜共用了103元、那么、买青菜用了多少钱?73.已知5个连续奇数的和是125、求其中最小的奇数.74.2018是4个连续自然数的和、其中最大的数是多少.75.两个数的和是900、其中较大数是较小数的19倍、则这两个数分别是多少?76.甲、乙、内三数之和为180、乙比两的3倍少2、甲比内的2倍多8、求甲、乙、丙三个数.77.8个连续的自然数从小到大排列、若后5个数的和比前3个数的和的2倍大12、求这8个数中最小的数.78.甲、乙两校共有学生432人、为了照顾学生就近入学、经协商由甲校调入乙校16人、这样甲校比乙校还多24人问甲、乙两校原来各有多少人?79.学校里有排球24个、足球的个数比排球的2倍少5个、学校有排球、足球共多少个?80.某商店从皮具厂以每个100元的价格购进了60个皮箱、这些皮箱共卖了8100元这个商店从这60个皮箱上共获得多少利润?每个皮箱盈利多少元?81.买5斤西红柿用了12元、比买6斤茄子少用了1元8角、求每斤茄子的价钱.82.小娟同学去文具店买笔、已知水彩笔1元7角一支、圆珠笔1元2角一支、她带了15元钱正好用完则小娟购买了多少支水彩笔和多少支圆珠笔?83.甲盒和乙盒内分别放有51个和78个乒乓球、要使甲盒内乒乓球的个数是乙盒内乒乓球个数的两倍、需要从乙盒中取出多少个乒乓球放人甲盒?84.有1元、5元*10元的人民币共46张、面值共计200元、已知1元的比5元的多4张、那么10元的人民币有几张?85.一名商人购进1000个万花筒、每销售一个可以获得2元的利润、每遇到一个残次品则会损失8元、全部售完后、商人共获得1900元利润问:这批万花筒中有多少个残次品?86.解放军某部野外拉练、晴天每天行50千米、雨天每天行40千米、12天内共行550千米、问这期间有多少天是雨天?87.秋天到了、姐姐和妹妹一起去捡地上的枫叶、姐姐捡五角枫(一片树叶有五个角}、妹妹捡三角枫(一片树叶有三个角}、若姐姐妹妹捡的枫叶共有102个角、且姐姐比妹妹捡的枫叶数量多6片、问:姐姐和妹妹分别捡了多少片枫叶?(所有叶的角都是完整的).88.袋子中有黑白两种颜色的棋子、黑子的个数是白子的个数的2倍、每次从袋中同时取出3个黑子和2个白子、某次取完后、白子剩下1个、黑子剩下27个、求袋中原有白子的个数.89.把40枚棋子分成27堆、其中每堆中的棋子数为1、2或3如果只有1枚棋子的堆数是其余堆数的2倍、那么恰含2枚棋子的有几堆?90.已知2017年的元旦是星期日、那么在2017年11月11是星期几?91.一个牧场上长满了牧草、牧草每天均速地生长、17头牛30天可将草吃完、19头牛20天可将草吃完现有若干头牛吃了5天后、卖掉了3头牛、余下的牛再吃2天便将草吃完问:原有多少头牛吃草(草均匀生长).92.一个牧场上长满了牧草、牧草每天匀速地生长、16只羊吃20天可将草吃完、20只羊15天可将草吃完现在牧场上有12只羊吃牧草、5天后、又增加了12只羊、还要多少天可以将牧场上的牧草吃完?93.甲、乙两个机器人分别从A、B两点同时出发、相向而行.甲到达B点时、乙距离点A 还差12米、乙到达A点时、甲超过B点20米、求A、B两点间的距离.94.甲、乙两人分别从A、B两地以65米/分和55米/分的速度同时出发相向而行、10分钟后相遇、求A、B两地的距离是多少米、并求出相遇点距离A、B两地的中点多少米.95.乌龟和兔子在全长为1000米的赛道上比赛、兔子的速度是乌龟速度的15倍但兔子在比赛的过程中休息了一会儿、醒来时发现乌龟刚好到达终点、而此时十兔子还差100米才到终点、则在免子休息期间乌龟爬行了多少米.96.一列火车全长通过长335米的桥需26秒、以同样的速度通过长1075米的桥要63秒、这列火车长多少米?97.甲、乙两地相距300千米、一辆汽车原计划用6小时从甲地到乙地、汽车行驶了一半路程、因故停留了30分钟、如果按原定时间到达乙地、汽车在后半段路程时速度应提高多少?98.一条小船往返于相距144千米的甲、乙两码头之间、从甲到乙顺流航行需要6小时、从乙到甲逆流航行需要8小时那么一个漂流瓶从甲码头顺流漂到乙码头需要多久?99.甲由A地出发去B地、同时乙由B地出发去A地、经过12分钟两人过了相遇点后相距100米、已知甲行全程要20分钟、乙每分钟行65米、A、B两地相距多少米?100.两个顽皮的孩子逆着自动扶梯行驶的方向行走、男孩每秒可走3级梯级、女孩每秒可走2个梯级、结果从扶梯的一端到达另一端男孩走了100秒、女孩走了200秒.问:该扶梯共有多少个台阶?。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

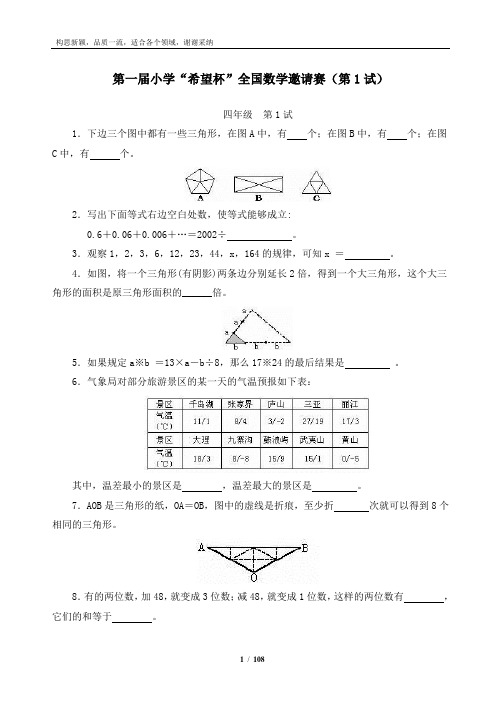
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
希望杯考前100题 (1)

37. 字母 W、M、T、C 分别代表 4 个不同的数字,并且WW × MM + WT + C = 2017 , 求W + M + T + C 的值.
38. 字母 a,b,c 表示 3 个不同的非零数字,若 abc + bc + c = 724 ,求 a + b + c .
常州学而思 双师课堂
受益一生的能力
64. 如图,矩形 ABCD 中,F 为 BC 的中点,CE=2DE,矩形 ABCD 的面积为 3,求阴影部 分的面积.
D
E
C
F
A
B
65. 在边长是 1 米的正六边形内任意丢放 7 颗小石子,则总有两颗小石子的距离不大 1 米, 请说明理由.
常州学而思 双师课堂
受益一生的能力
66. 某次考试共有 10 道判断题.小张划了 5 个钩和 5 个叉,结果对了 8 道;小李划了 2 个 钩和 8 个叉.结果对了 6 道;小王一道都不会,索性全部打叉,那么他至少可以蒙对多 少道题?
12. 桌上有一些纸片,每张纸片上都有编号(不是按顺序编的),马小虎同学错把 6 和 69 拿倒了,导致这些编号的平均数多出 1,问这些纸片共有多少张?
常州学而思 双师课堂
受益一生的能力
13. 有一串数,最前面的 4 个数是 2,0,1,8,从第 5 个数起,每一个数都是它前面相邻 4 个数之和的个位数字,问在这一串数中,会依次出现 2,0,1,7 这 4 个数吗?
14. 某工人每小时内需先生产 2 个 A 产品,再生产 3 个 B 产品,最后生产 1 个 C 产品,则 第 725 个产品是哪种产品?
15. 著名的哥德巴赫猜想可以陈述为:任意大于 2 的偶数,都可表示成两个质数之和.将偶 数 88 表示成两个质数的和,有几种表示方法?( a + b 和 b + a 视为同一种表示方法)
希望杯四年级培训100题(word格式)

希望杯四年级培训100题(word格式)2014年希望杯四年级培训题1、计算:67+135—5×7+264÷82、计算:13+29+32+46+57+68+71+85+943、计算:364×25÷(14÷4)4、计算:(1953+1956+1958+1962+1959+1947+1957)÷75、将运算符号“+、—、×、÷”填在下⾯的圆圈中,使得算式成⽴。
2○2○2○2○2 = 56、在四个数:10、10、4、4之间填⼊“+”、“—”、“×”、“÷”、“()”使写出的算式的计算结果是24。
7、连个⾃然数的和是94,积2013,求这两个数。
8、按顺序排列的7个数,它们的平均数是9,已知前4个数的平均数是5,后四个数的平均数是12,求第四个数。
9、若5个连续⾃然数的和是1256,求这5个连续⾃然数中最⼩的数。
10、20⾄24这5个连续⾃然数的和再加上2000等于另外4个连续⾃然数的和,求另外四个连续⾃然数中最⼩的数。
11、有三个数c b a ,,,要求计算)(c b a +-,李军算成了c b a +-,结果多100,求c。
12、⼀个两位数,在它的两个数字中间添⼀个0,就⽐原来的数多720,这样的两位数最⼤是多少?13、四位数6823的a倍是各位数字不同的最⼩的六位数,求a。
14、六位数aabccd满⾜:=aabccd?dddddd求d。
15、某⼿机的号码是habcbdeefcg,已知其中不同的字母表⽰1、2、3、…、9中不同的数字,d最⼤,h⽐d⼩2,⽽且h<<<<,<a<fcge请写出这个⼿机的号码。
16、将1、2、3、4、5、6分别写到⼀个正⽅体的六个⾯内,将相对两个⾯内的数作为⼀个长⽅形的长和宽,计算这样得到的长⽅形的⾯积和,求和的最⼤值、最⼩值。
17、⽤21根⼩棒摆成10个三⾓形,如图1.按照这种⽅式,⽤65根⼩棒能摆出多少个三⾓形?18、观察下⾯算式的规律,求第100个算式的得数。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
2019年“希望杯”四年培训题100题汇总(含答案)

小学“希望杯”全国数学邀请赛四年级培训题1.计算:2017×2071+2077×2017-2037×2017-2111×2017.2.计算:9999×2222+3333×3334.3.比较大小:A=2016×2018,B=2017×2017,C=2015×2019.4.定义新运算:a⊗⊗ b= a ⨯⋅⋅⋅⨯⨯b b b 个,求(1 ⊗ 4) ⊗ (2 ⊗ 3).5.一个自然数,各个数位上的数字之和是74,这个数最小是多少?6.一个三位数被3 除余1,被5 除余3,被7 除余5,这个数最大是多少?7.一个整除算式,被除数比商大126,除数是7,求被除数.8.一个三位数,它的各位数字之和是20,十位数字比个位数字大1,如果将百位数字与个位数字对调,得到的三位数比原三位数大198,求原数.9.在从1 开始的n 个连续的自然数中,去掉其中的一个数,余下各数的和是2017,求去掉的数.10.若干个数的平均数是17,加入一个新数2017 后,这组数的平均数变成21,原来共有多少个数?11.用2,0,1,7 这四个数字可以组成多少个没有重复数字的四位偶数?12.已知a,b,c 是三个质数,且a < b < c,a + b ×c = 93,求a,b,c.13.a,b,c 是彼此不同的非0 自然数,若a + b + c = 6,求四位奇数aabc 中最小的那个.14.a,b,c 是彼此不同的非0 自然数,若a + b + c = 6,求四位数aabc 中最大的那个.15.三位数abc 是质数,a,b,c 也是质数,cba 是偶数,ab 是5 的倍数,求三位数abc .16.求被7 除,余数是3 的最小的三位数.17.求被7 除,余数是4 的最大的四位数.18.将分别写有数字3,7,8 的三张卡片排成三位数abc,使它是43 的倍数,求abc .19.已知a,b,c 是不同的质数,且三位数abc 能同时被3,7 整除,求abc .20.用写有2,3,5,7 的四张纸片可以排成多少个小于1000 的质数?21.四位数abbc 可被两位数ac 整除,若a < c,a + c = 5,求b.22.在下面的算式里加上一对括号,使算式成立. 1×2×3+4×5+6+7+8+9=100.23.在等号左边添上适当的运算符号、括号,使等式成立.9 9 9 9 = 8.24.从1 至9 的自然数中选择8 个数填入下面的方框中,使得计算结果尽量大,那么这个结果最大是多少?25.在图1 的算式中,A,B,C,D 代表0~9 中四个各不相同的数字,且A 是最小的质数,求四位数ABCD。
第十六届小学“希望杯”全国数学邀请赛 四年级

第十六届小学“希望杯”全国数学邀请赛四年级1.计算:69×56+64×28=_________.2.琳琳早上6:41出发,7:20到校,她在路上用了________分钟。
3.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子贵324元,一张桌子______元。
4.有三箱苹果,每次称两箱,三次称得的质量分别是80千克、84千克、90千克,则最轻的一箱苹果重_________千克。
5.一个减法算式中,被减数、减数、差的和是2018,则被减数是________。
6.已知△,○,□是3个不同的数,并且△+△+△=○+○,□+□+□=○+○+○+○,△+○+○+□=60,那么△+○+□=__________。
7.图1中有_______个正方形。
8.把一块周长为156厘米的大长方形纸板剪成两块相同的小长方形纸板,若每块小长方形纸板的周长都是108厘米,则原来大长方形纸板较长的边长_______厘米。
9.如图2,面积都是30平方厘米的两个正方形错开2厘米摆放,图中阴影部分的面积是________平方厘米。
10.在同一张纸上任意画两个相同的正方形,组成一个新的图形,则新图形的对称轴最多有________条。
11.把320本书分给某班学生,无论如何分配,总有一个学生至少分到9本,那么这班最多有_________人。
12.甲、乙、丙是三个机器人,已知乙的速度是甲的9倍,丙的速度是乙的7倍,它们从相同的地点同时出发沿相同的路线行走,当乙领先甲36厘米时,丙领先乙_______厘米。
13.如图3,∠1=∠2=∠3=∠4=∠5,且图中所有的锐角的和是420°,则∠BOD=_______度。
14.四年级一班的全体学生按顺序站成一排,小松的前面有18个人,若保持排列的顺序不变,把队伍分成人数相等的3队,这时,小松的前面有6个人,则四年级一班共有________个人。
15.在打印从1到10000的自然数时,由于打印机有故障,所有3都被打印成X,如:3被打印成X,123被打印成12X,则这10000个数中有_____个数被打错。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
四年级希望杯数学竞赛历届全部试题

第一届小学“希望杯”全国数学邀请赛四年级第1试1.观察1,2,3,6,12,23,44,x,164的规律,可知x =______ 。
2.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
3.如果规定a※b =13×a-b÷8,那么17※24的最后结果是______。
4.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折______ 次就可以得到8个相同的三角形。
5.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有______ ,它们的和等于_____ 。
6.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书______ 本。
7.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有______ 个,小朋友共______ 组。
8.在 a=20032003×2002和 b=20022003×2003中,较大的数是______ ,它比较小的数大______ 。
9.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是______ 。
10.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了______ 元,每本书价______ 元。
11.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影部分的面积是______ 。
12.如图,水平桌面(桌面不反光)上放有两个同样大小的足球M、N,每个足球的正上方悬挂有相同的灯泡。
最新年 第16届希望杯考前训练100题 四年级资料

第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1.整数的四则运算,运算定律,简便运算。
2.基本图形,图形的拼组(分、合、移、补),图形的变换,折叠与展开。
3.角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4.整除概念,数的整除特征,带余数除法,平均数。
5.几何计数(数图形),找规律,归纳,统计,可能性。
6.数谜,分析推理能力,数位,十进制表示法。
7.生活数学(钟表,时间,人民币,位置与方向,长度,质量的单位)。
8.应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
考前100题选讲1.计算:8×27×25。
2.计算:9+98+987+9876。
3.计算:2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
5.计算:15÷7+68÷14。
6.已知999999÷(a÷2)=142857,求a7.某数被27除,商是8,余数是5,求这个数。
8.定义:A*B=(A+3)×(B-2),求15*17。
9.除法算式△÷7=12……□中,余数最大是多少?10.有5个连续偶数之和恰好等于4个连续奇数之和,如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积(不考虑三个自然数的相乘顺序)。
共有几种不同的表示方法?12.用数字2,0,1,7可以组成多少个不重复的三位数?13.用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是多少?14.如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数?15.2017和某个小于100的自然数的和正好等于两个连续自然数之积,求这个小于100的自然数。
2019年“希望杯”四年培训题100题汇总(含答案)

小学“希望杯”全国数学邀请赛四年级培训题1.计算:2017×2071+2077×2017-2037×2017-2111×2017.2.计算:9999×2222+3333×3334.3.比较大小:A=2016×2018,B=2017×2017,C=2015×2019.4.定义新运算:a⊗⊗ b= a ⨯⋅⋅⋅⨯⨯b b b 个,求(1 ⊗ 4) ⊗ (2 ⊗ 3).5.一个自然数,各个数位上的数字之和是74,这个数最小是多少?6.一个三位数被3 除余1,被5 除余3,被7 除余5,这个数最大是多少?7.一个整除算式,被除数比商大126,除数是7,求被除数.8.一个三位数,它的各位数字之和是20,十位数字比个位数字大1,如果将百位数字与个位数字对调,得到的三位数比原三位数大198,求原数.9.在从1 开始的n 个连续的自然数中,去掉其中的一个数,余下各数的和是2017,求去掉的数.10.若干个数的平均数是17,加入一个新数2017 后,这组数的平均数变成21,原来共有多少个数?11.用2,0,1,7 这四个数字可以组成多少个没有重复数字的四位偶数?12.已知a,b,c 是三个质数,且a < b < c,a + b ×c = 93,求a,b,c.13.a,b,c 是彼此不同的非0 自然数,若a + b + c = 6,求四位奇数aabc 中最小的那个.14.a,b,c 是彼此不同的非0 自然数,若a + b + c = 6,求四位数aabc 中最大的那个.15.三位数abc 是质数,a,b,c 也是质数,cba 是偶数,ab 是5 的倍数,求三位数abc .16.求被7 除,余数是3 的最小的三位数.17.求被7 除,余数是4 的最大的四位数.18.将分别写有数字3,7,8 的三张卡片排成三位数abc,使它是43 的倍数,求abc .19.已知a,b,c 是不同的质数,且三位数abc 能同时被3,7 整除,求abc .20.用写有2,3,5,7 的四张纸片可以排成多少个小于1000 的质数?21.四位数abbc 可被两位数ac 整除,若a < c,a + c = 5,求b.22.在下面的算式里加上一对括号,使算式成立. 1×2×3+4×5+6+7+8+9=100.23.在等号左边添上适当的运算符号、括号,使等式成立.9 9 9 9 = 8.24.从1 至9 的自然数中选择8 个数填入下面的方框中,使得计算结果尽量大,那么这个结果最大是多少?25.在图1 的算式中,A,B,C,D 代表0~9 中四个各不相同的数字,且A 是最小的质数,求四位数ABCD。
2018年-第16届希望杯考前训练100题-四年级

第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1.整数的四则运算,运算定律,简便运算。
2.基本图形,图形的拼组(分、合、移、补),图形的变换,折叠与展开。
3.角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4.整除概念,数的整除特征,带余数除法,平均数。
5.几何计数(数图形),找规律,归纳,统计,可能性。
6.数谜,分析推理能力,数位,十进制表示法。
7.生活数学(钟表,时间,人民币,位置与方向,长度,质量的单位)。
8.应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
考前100题选讲1.计算:8×27×25。
2.计算:9+98+987+9876。
3.计算:2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
5.计算:15÷7+68÷14。
6.已知999999÷(a÷2)=142857,求a7.某数被27除,商是8,余数是5,求这个数。
8.定义:A*B=(A+3)×(B-2),求15*17。
9.除法算式△÷7=12……□中,余数最大是多少?10.有5个连续偶数之和恰好等于4个连续奇数之和,如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积(不考虑三个自然数的相乘顺序)。
共有几种不同的表示方法?12.用数字2,0,1,7可以组成多少个不重复的三位数?13.用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是多少?14.如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数?15.2017和某个小于100的自然数的和正好等于两个连续自然数之积,求这个小于100的自然数。
2016年希望杯100题四年级组(含答案)

45.一根绳子,若截去 5 米,刚可绕花坛 6 圈,若增加 13 米,则可绕花坛 8 圈,求这 根绳子的长度. 46.如图 9,四个长方形和一个边长是 5 的正方形纸片围成一个风车型的图案,图案的 外轮廓的长是 52,求长方形的长.
47.求图 10 的周长. (单位:厘米)
48. 如图 11, 从长方形纸片上裁掉两个正方形 ABCD 和正方形 CEFG, 其中正方形 ABCD 的面积是 49 平方厘米,求余下的长方形纸片 DGFH 的周长.
6 99 9 的结果有多少个 3?
2015 个 2015 个
56.已知图 14 中任意一个“田”字格中的四个数的和相等,求 A、B、C、D 中最大数 和最小数的差.
57.已知图 15 中任意相邻的三个格子中的数字之和都相等,这六个数字之和是 30,求 A+E+F.
58.编号是 1,2,3,…,36 号的 36 名同学按编号顺序面向里站成一圈.第一次,编 号是 1 的同学向后转,第二次,编号是 2,3 的同学向后转,第三次,编号是 4,5,6 的同 学向后转,…,第 36 次,全体同学向后转,这时,面向里的同学有多少名? 59.a,b 是 1 至 200 中的两个不相等的自然数,求 a b a b 的最大值. 60.一把钥匙只能开一把锁,现在有 8 把钥匙,7 把锁,最多要试多少次能把 7 把锁和 相应的钥匙搭配起来? 61.甲、乙、丙、丁、戊五人参加 100 米比赛,比赛结束后,甲说: “我的名次排在丁 前面,丙后面. ”丙说: “戊在我前面冲过终点. ”丁说: “我比乙跑的快. ” 请根据他们的说法排出他们比赛的名次. 62.有编号为 1,2,3,…,100 的 100 个感应灯.开始时它们都处于关闭状态.第 1 次,将编号是的倍数的感应灯按一下;第 2 次,将编号是 2 的倍数的感应灯按一下;第 3 次 n 100 将编号是 3 的倍数的感应灯按一下;…;如此下去,最后一次,将编号能被 100 整除的感应灯按一下.问:此时,有几个感应灯还亮着? 63.小超从 1 至 9 的 9 个数中选出 5 个数求和,得 23;小明也从 1 至 9 的 9 个数中选 出 5 个数求和,得 24.如果两人选的数中只有一个是相同的,求这个相同的数. 64.某年 7 月恰有 4 个星期一和 4 个星期四,这月的 15 号是星期几? 65.在长是 156 米的小路的一侧等距离地种植 13 棵树,路的两端都要植,求相邻两棵 树之间的距离. 66. 某正方形操场四周等距离地种植了 108 棵杨柳, 小红从操场某角处的树下开始绕操 场跑步,当她跑过第 500 棵树时,这棵树是她所在操场边上跑过的树中的第几棵?(正方形 操场四个顶点处都种了树) 67.小林 3 岁的时候,爷爷 53 岁,那么小林 10 岁时,爷爷年龄是小林的多少倍? 68.晶晶比哥哥小 3 岁,且 2 年后哥哥的年龄是 4 年前晶晶的年龄的 2 倍,问晶晶今年 几岁? 69.今年,丹丹和父亲、母亲的年龄和是 100 岁,若 6 年前母亲的年龄是丹丹年龄的 4 倍,11 年前,父亲的年龄是丹丹年龄的 8 倍,问:丹丹今年几岁? 70.某课外兴趣小组共有 30 人,他们每个人都在暑假期间采集了一些生物标本,其中 21 人采集了植物标本,16 人采集了动物标本,既采集了植物标本又采集了动物标本的有多 少人? 71.光明小学四年级(1)班 35 人,他们的数学平均成绩为 90 分,其中男生的平均成 绩为 88 分,女生的平均成绩为 95 分,求女生的人数. 72.一堆模具中长方形模具的数量是圆形模具的 2 倍,现要将它们装箱出售,每 24 个 长方形模具和 9 个圆形模具合装一箱,如此装了若干箱后,长方形模具还剩 8 个,圆形模具 还剩 37 个,求长方形模具共有多少个? 73.小芳读本故事书,若每天读 16 页,22 天恰好读完,实际上读时,她前若干天每天 读 20 页,此后每天都比前一天少读 1 页,又经过 7 天,她恰好读完这本书,求小芳之前读 了几天?
2016 年希望杯 100 题四年级组

70.某课外兴趣小组共有 30 人,他们每个人都在暑假期间采集了一些生物标本,其中 21 人采集 了植物标本,16 人采集了动物标本,既采集了植物标本又采集了动物标本的有多少人? 71.光明小学四年级(1)班 35 人,他们的数学平均成绩为 90 分,其中男生的平均成绩为 88 分,女 生的平均成绩为 95 分,求女生的人数. 72.一堆模具中长方形模具的数量是圆形模具的 2 倍,现要将它们装箱出售,每 24 个长方形模 具和 9 个圆形模具合装一箱,如此装了若干箱后,长方形模具还剩 8 个,圆形模具还剩 37 个,求 长方形模具共有多少个? 73.小芳读本故事书,若每天读 16 页,22 天恰好读完,实际上读时,她前若干天每天读 20 页,此后 每天都比前一天少读 1 页,又经过 7 天,她恰好读完这本书,求小芳之前读了几天? 74.某班共有 45 人,在一次歌唱与朗诵的比赛中,参加唱歌比赛的同学有 30 人,参加朗诵比赛的 同学有 25 人,若每个同学至少参加一项比赛,问两项比赛都参加的同学有多少人? 75.某班举办回收旧书的活动,将收到的书放到几个箱子里.如果每个箱子放 160 本,恰好放完: 如果每个箱子多放 10 本书,则剩下 20 本书和两个空箱子.问:一共有多少个箱子,多少本书? 76.有三堆棋子,从第一堆拿出 15 个棋子放到第二堆,再从第二堆拿出 18 个放到第三堆,最后从 第三堆拿出 12 个放到第一堆,这时每堆都有 180 个棋子.求原来每堆棋子的个数. 77.一名商人购进 1000 个万花筒,每销售一个可以获得 2 元的利润,每遇到一个残次品则会损 失 6 元,全部售完后,商人共获得 1904 元利润,问:这批万花筒中有多少个残次品? 78.体育老师带来一些排球,同学们分成若干组使用,6 人一组则缺 1 个球,8 人一组则多 1 个球, 问:共有多少名同学? 79.四年级其中考试科目包括语文、数学、英语三门功课,四(1)班总成绩的平均分为 85 分,语 文成绩的平均分为 90 分,数学成绩的平均分比英语成绩的平均分少 25 分,求英语成绩的平均 分. 80.不透明的箱子里面有红白两色的小球共 120 个,且红球是白球的 5 倍,问:红球比白球多几 个? 81.一个书架有两层,若从第一层拿出 14 本书放到第二层,那么第二层上的书的数量是第一层 的 3 倍,若从第二层拿出 12 本书放到第一层,则两层所放的书数量相等,书架上有多少本书? 82.某天清晨,容器中有 380 个细菌,在白天有光时,容器中的细菌减少 70 个,夜间无光时,容器中 的细菌将增加 30 个,则经过 8 个白天 7 个夜间后,容器中还剩多少个细菌. 83.矩形的边长是自然数,它的面积是 3003,求矩形的最小周长. 84.幼儿园的老师给班里的小朋友领来 40 只桔子,200 块饼干,120 块奶糖,平均分发完毕,还剩 4 只桔子,20 块饼干,12 粒奶糖.问:班里共有多少位小朋友? 85. 如果一个自然数从右往左看和从左往右看都一样 , 则称这个数为“回文数” . 例如 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第16 届希望杯考前训练100 题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1. 整数的四则运算,运算定律,简便运算。
2. 基本图形,图形的拼组(分、合、移、补),图形的变换,折叠与展开。
3. 角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4. 整除概念,数的整除特征,带余数除法,平均数。
5. 几何计数(数图形),找规律,归纳,统计,可能性。
6. 数谜,分析推理能力,数位,十进制表示法。
7. 生活数学(钟表,时间,人民币,位置与方向,长度,质量的单位)。
8. 应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
考前100 题选讲1. 计算:8X 27X 25。
2. 计算:9+98+987+9876。
3. 计算:2-4+6-8+10-12+ …-48+50。
4. 计算:2017 X 2016+2016X 2014-2015 X 2016-2015X2017 。
5. 计算:15 - 7+68 - 14。
6. 已知999999 - (a- 2)=142857 ,求a7. 某数被27 除,商是8,余数是5,求这个数。
8. 定义:A*B=(A+3)X (B-2),求15*17。
9. 除法算式△十7=12……□中,余数最大是多少?10. 有5 个连续偶数之和恰好等于4 个连续奇数之和,如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11. 将36 表示成三个大于1 的自然数的乘积(不考虑三个自然数的相乘顺序)。
共有几种不同的表示方法?12. 用数字2, 0, 1, 7可以组成多少个不重复的三位数?13. 用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是多少?14. 如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数?15.2017和某个小于100的自然数的和正好等于两个连续自然数之积,求这个小于100的自然数。
16. 某两位数的十位数字与个位数字互换后,新数比原数大36,求原来的两位数。
17. abc是一个三位偶数,已知b是c的三倍,且b=a+c,求abc。
18. 在乘法运算15X 16 X 17X 18X 19 X 20X 21 X 22X 23X 24X 25的计算结果中,最后有多少个连续的0?19. 在2018后面加一个两位数,使它成为一个能被7整除的六位数,则这个两位数最大的是多少?20. 求能同时被3, 5, 7整除的最小的五位数。
21. 用一个自然数分别去除25, 38, 43,三个余数之和为18,求这个自然数。
22. 一个数被3除余2,被5除余4,被7除余6,则这个数最小是几?23. 自然数a是3的倍数,a-2是4的倍数,a-3是5的倍数,则a最小是多少?24. a , b, d是一位数字,并且ab-cd=21, cd1- 1ab=6,则ad等于多少。
25. 求能被2, 3, 5整除的最小四位数。
26.488 □是一个四位数,数学老师说:“我在这个口中先后填人3个数字,所得的3个四位数,依次可被9, 11, 7整除。
”数学老师先后填人的3个数字和是多少?27. 从1, 2, 3, 4, 5, 6这6个数字中,任取2个组成两位数,这些两位数中,3的倍数有多少个?28. 已知x, y是大于0的自然数,且x+y=100。
若x是3的倍数,y是5的倍数,则(x, y)的不同取值有几对?29. 如图1的算式中,A, B, C, D, E, F表示不同的一位数,求A, B, C, D, E, F表示的数。
A B C D ______ CD C 8 C £CA H C D30. 在1LI 500中,不能被2整除,也不能被3整除,又不能被5整除的数有多少个?31. 在1到200之间去掉所有完全平方数,剩下的自然数的和是多少 ?32. 如图2,共端点A 的射线a 与d 互相垂直,a 与c 的夹角是60°。
b 与d 的夹角是45° ,求b 与c 夹角的度数。
33. 如图3,在正方形 ABCD 中,CM=3BM 若梯形AMC 啲周长比厶ABM 勺周长大6,求正方形的边长。
34•将同样的两张正方形透明塑料薄片部分重合地放于桌面上 长是60厘米,求长方形 ABCD 勺面积。
S1 ----------------H|| ||S ! S |< … i II |i1圈d35. 如图5, 一只小蚂蚁从点 A 出发,沿折线爬行一周,问:小蚂蚁爬行了多少米?(如图4, s+s=rn 方形),已加ABCD 勺周36. 一个长方形的长和宽都增加 3厘米后,长方形的面积增加了 63平方厘米,求原长方形的周 长。
37. 用长是22厘米的铁丝围成一个长和宽都是整厘米数的长方形 ,有几种方法?38. 如图6,/ 1 + Z 2+Z 3+Z 4+/ 5+/6=180°,图中比平角小的角有多少个?42. 数一数,图中有多少个三角形?43. 已知一列数:1 , 3, 4, 7, 11, 18,…,这列数的第10个是多少?44. 有白棋子和黑棋子共 2018枚,按照图11的规律从左到右排成一行,其中黑棋子多少枚?39.如图7用11个边长为1的正方形卡片拼成数字 2”,求图中长方形的个数 (不包括正方形)。
40. 数一数,图中共有多少个平行四边形? 41. 数一数,图中有多少个三角形?1o« o“o・••oeoeeoe**—图n1 12 1 23 1 2 3 445. 观察下面按一定规律排列的一列数:1,丄,1,,,2,話,,,-……求第2017个数。
233444555546. 如图12,用小正方形摆成下列图形,按摆放规律,第25个图形需要多少个小正方形?占二二E E二二4 L E三二En1247. 如图13所示的数字是电子表中经常可见的数字2和5的表示形式,把图中左边的数字2向右翻转一次可得到右边的数字5,再向右翻转一次又会得到原来的数字2,那么将图2所示的数字25翻转一次得到的数字是多少?□ C匚□图13.,.;48. 有张,王,李三个工人,甲、乙、丙三个工厂,以及车工,钳工和电工三种工作,已知:①王不在甲厂;②张不在乙厂;③在甲厂的不是钳工;④在乙厂的是车工;⑤王不是车工。
这三个人分别在哪个工厂,干什么工作?49. 一个两位数除以它的各位数字之和,余数最大是多少?50.5个人围成一圈做游戏,每人都有一袋小石子。
游戏开始时,第一个人给第二个人1颗石子,第二个人给第三个人2颗石子,第三个人给第四个人3颗石子,第四个人给第五个人4颗石子,第五个人给第一个人5颗石子,……,如此操作5圈后所有人袋中的石千都一样多。
若所有石子的总数为1990颗,问游戏前每个人袋中分别有多少颗石子?51•将2017个小球放到10个箱子中,要求每个箱子中的小球的数目中都带有数字7.请给出一种摆放方法。
52. 箱子里有2018个小球,编号分别为1, 2, 3,…,2018。
现从箱子中摸出1616个小球,将它们的编号相乘,求积的个位数字。
53. 自然数n的十位数字是4,个位数字是2,各个数位上的数字之和为42,且是42的倍数,求满足上述条件的最小的自然数。
54. 一副扑克牌有52张,依惯例A J,Q K依次视为1点,11点,12点,13点,任意抽出若干张牌,不计花色,如果抽出的牌中必定有3张牌的点数相同,那么至少要取几张牌?如果抽出的牌中必定有 2 张牌的点数之和等于15, 那么至少要取几张牌?55. 小明、小强、小红三个人在一起玩捉速藏的游戏, 小明对小强说: “我在你的正北方5米处”, 小红对小强说:“我在你的正南方6米处”。
若小强走 1 米需要6步,那么先抓小明再去抓小红一共需要走多少步?56.10个50g的砝码和5个100g的砝码同时放在天平的左右两侧才能使天平保待平衡,那么在天平左侧放2个1kg的砝码,右侧放6个300g的砝码,要使天平保持平衡还要在右侧放几个50g的砝码。
57. 在一个周长是200 米的池塘周围植树 , 每隔5 米植一棵 , 需要准备多少棵树苗?58. 在120米长的跑道右侧插16面彩旗,求相邻两面彩旗之间的距离。
59. 今年, 小军4岁, 爸爸31 岁, 再过多少年爸爸的年龄是小军的4倍。
60. 亮亮比晶晶小6岁, 16 年后亮亮的年龄是晶晶今年的年齡的2倍,问:晶晶今年几岁?61 .父亲今年45岁,儿子今年15岁, 多少年前父亲的年龄是儿子年龄的7倍?62.2011 年, 妈妈的年齡等于她的两个孩子的年龄和的5倍, 2017年她的年龄等于两个孩子的年龄和的2倍。
求2018年时妈妈的年龄。
63. 某学习小组数学成绩的统计图如图14, 求该小组的平均成绩64.统计十位同学在一次数学考试中的成绩,已知前四名的平均分是93分,后六名的平均分比十人的总平均分少6分,求这十位同学的平均分65.李家承包了100亩地种玉米,亩产量600斤,刘家比李家少承包了20亩,结果两家的总产量相同,问:(1)刘家玉米的总产量是多少斤?(2)李家玉米的亩产量比刘家的少多少斤?66. 橘子、苹果、梨共有六箱,这六箱水果的重量(单位:千克)分别为:15,16,18,19,20,31,其中苹果的重量是梨的一半,橘子只有一箱。
这六个箱子中分别装的是什么水果?67. 每本书的版权贞上都印有:开本、印张,字数,定价等等。
如:“开本:720mm* 960mm 1/16 印张:12 字数:240千字”。
求这本书平均每页有多少字?(注:16开,即1个印张16页)68. 某校规定语文,英语,数学三料考试成绩的平均分在95分以上才有可能被评为三好学生,若在一次期末考试中,希希语文考了96分,英语考了92分,那么他数学至少得多少分才有可能被评为三好学生?69.1个西瓜可换5个苹果,2个苹果可换3根香蕉,5根香蕉可换8个桃子,那么60个桃子可换几个西瓜?70.7头牛可换16只羊,2只羊可换21只兔,则3头牛可换多少只兔?71. 有两块地,平均亩产粮食650千克,其中第一块地5亩,亩产粮食670千克。
如果第二块地亩产粮食645千克,第二块地有多少亩?72. 妈妈去市场买菜,已知买肉和鸡蛋共用了77元,买鸡蛋和青架共用了60元,买肉和青菜共用了103 元,那么,买青菜用了多少钱?73. 已知5个连续奇数的和是125,求其中最小的奇数。
74.2018 是4 个连续自然数的和,其中最大的数是多少。
75. 两个数的和是900,其中较大数是较小数的19倍,则这两个数分别是多少?76.甲、乙,丙三数之和为180,乙比丙的3倍少2,甲比丙的2倍多8,求甲、乙、丙三数。
