平面电磁波的波动方程共20页文档
合集下载
平面波的波动方程

§17-5 平面波的波动方程 -
各种平面波都满足下列方程
y y =u t x
2 2 2 2 2
称为平面波的波动方程 平面简谐波波动式是它的解
例2
弦上的横波,设线密度 张力T 不变) 弦上的横波,设线密度,张力T(不变)
T
αT
2
T
α
1
T sinα2 T sinα1 ≈ T(tgα2 tgα1 ) 2 y y y y = T dx = dx 2 =T x x x x 2 2 T y T y u= =
y1 = Acos(ωt kx) y2 = Acos(ωt + kx)
y = y1 + y2 = 2 Acos kx cosωt
y = y1 + y2 = 2 Acos kx cosωt
3. 振幅
kx = ±nπ
腹-腹
n = 012L 波腹 ,,
x =
λ
2
kx = ±( 2n +1)
节-节 腹-节
二、波的干涉 1.相干条件 相干条件 频率相同,振动方向相同, 频率相同,振动方向相同,相位差恒定 两相干波在空间相遇, 两相干波在空间相遇,某些点的振动始终加强另一 些点的振动始终减弱,即出现干涉现象。 些点的振动始终减弱,即出现干涉现象。
设 y1 = A cos(ωt +1 kr ) 1 1
3 λ 2
P
解:
Q
R
= 1 2 k(r1 r2 ) 3 = k λ = 3π 减弱 2
A= 0
三、驻波 当两列振幅相同,频率相同, 当两列振幅相同,频率相同,振动方向相同的 波以相反方向传波时,叠加形成驻波 驻波。 波以相反方向传波时,叠加形成驻波。 1. 演示: Zlcai 演示: 2.表达式 表达式 设
各种平面波都满足下列方程
y y =u t x
2 2 2 2 2
称为平面波的波动方程 平面简谐波波动式是它的解
例2
弦上的横波,设线密度 张力T 不变) 弦上的横波,设线密度,张力T(不变)
T
αT
2
T
α
1
T sinα2 T sinα1 ≈ T(tgα2 tgα1 ) 2 y y y y = T dx = dx 2 =T x x x x 2 2 T y T y u= =
y1 = Acos(ωt kx) y2 = Acos(ωt + kx)
y = y1 + y2 = 2 Acos kx cosωt
y = y1 + y2 = 2 Acos kx cosωt
3. 振幅
kx = ±nπ
腹-腹
n = 012L 波腹 ,,
x =
λ
2
kx = ±( 2n +1)
节-节 腹-节
二、波的干涉 1.相干条件 相干条件 频率相同,振动方向相同, 频率相同,振动方向相同,相位差恒定 两相干波在空间相遇, 两相干波在空间相遇,某些点的振动始终加强另一 些点的振动始终减弱,即出现干涉现象。 些点的振动始终减弱,即出现干涉现象。
设 y1 = A cos(ωt +1 kr ) 1 1
3 λ 2
P
解:
Q
R
= 1 2 k(r1 r2 ) 3 = k λ = 3π 减弱 2
A= 0
三、驻波 当两列振幅相同,频率相同, 当两列振幅相同,频率相同,振动方向相同的 波以相反方向传波时,叠加形成驻波 驻波。 波以相反方向传波时,叠加形成驻波。 1. 演示: Zlcai 演示: 2.表达式 表达式 设
14-2平面简谐波的波动方程

波源(x=0) 的简谐运动 方法1
yO A cos t
x t u
O点的振动状态传到P所需时间
t时刻 P 点相位与 O 点 ( t t )时刻相位相同
yP (t) yO (t t)
P点的振动方程
x y P A cos t u
x
2 π)
(2)
2 π)
由于 uT u
所以(1)、(2)是一致的
x x0 波源在x0处: y A cos t u 2π y A cos t ( x x0 )
如果波沿x轴的负方向传播,则P点的相位要比O点的相 位超前 t x u x x0
P在 t=0 时刻过平衡位置向负向运动 ——波向左移
y(m)
0.2 O 1
t=0 P
2
yP(m) x(m)
0.2 O 0.1 0.2
t (s)
3 yO 0.2 cos(10πt π) 2 x 3 波向-x方向传播 y 0.2 cos[10 π(t ) π] 10 2 π π b) 以 P 为参考点 P yP 0 2cos( 10π t ) 2 2 波向-x方向传播 x 1 π 0 2 cos[10 π(t x ) π ] y 0 2 cos[10 π(t ) ] 10 2 10 2
(3) 波形图中 x1 和 x2 两质点的相位差
x1 y1 A cos t u 1 x2 y2 A cos t u
相位差:
y u O
x1 x2
平面电磁波

• 考虑到真空的介电常数为ε0. 磁导率为μ0. 得:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式(7 -30) 中 • 为真空中的光速. 由于一切媒质的相对介电常数εr >1. 而且一般媒
质的相对磁导率μr≈1. 因此. 理想电介质中均匀平面波的相速通常 小于真空中的光速. 但是要注意. 电磁波的相速有时可以超过光速. 可 见. 相速不一定代表能量传播速度. • 式(7 -30) 中 • 是频率为f 的平面波在真空中传播时的波长.
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式(7 -9) 是一个二阶常微分方程. 其通解为: • 式中第一项代表沿正z 方向传播的波. 第二项代表沿负z 方向传播的
波. 为了便于讨论平面波的波动特性. 仅考虑沿正z 方向传播的波. 令 上式第二项为零. 即 • 式中. Ex0为z =0 处电场强度的有效值. Ex (z) 对应的瞬时值为:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 媒质电场强度与磁场强度的振幅之比称为波阻抗. 也称为媒质的特征 阻抗. 或者本征阻抗. 以Zc表示. 即
• 由上述讨论可知. 平面波的波阻抗为复数. 电场强度与磁场强度的空间 相位不同. 复能流密度的实部及虚部均不会为零. 意味着平面波在传播 过程中. 既有能量的单向传播. 又有能量的双向或交换传播.
上一页 下一页 返回
7. 2 自由空间中的平面波
• 将ω =2πf 和式(7 -19) 代入式(7 -20). 得: • 式(7 -21) 描述了平面波的相速vp、频率f 与波长λ 之间的关系.
平面波的频率是由波源决定的. 它与源的频率始终相同. 但是平面波的 相速与媒质特性有关. 因此. 平面波的波长也与媒质特性有关. • 将式(7 -14a) 代入式(7 -18) 中. 得:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式(7 -30) 中 • 为真空中的光速. 由于一切媒质的相对介电常数εr >1. 而且一般媒
质的相对磁导率μr≈1. 因此. 理想电介质中均匀平面波的相速通常 小于真空中的光速. 但是要注意. 电磁波的相速有时可以超过光速. 可 见. 相速不一定代表能量传播速度. • 式(7 -30) 中 • 是频率为f 的平面波在真空中传播时的波长.
上一页 下一页 返回
7. 2 自由空间中的平面波
• 式(7 -9) 是一个二阶常微分方程. 其通解为: • 式中第一项代表沿正z 方向传播的波. 第二项代表沿负z 方向传播的
波. 为了便于讨论平面波的波动特性. 仅考虑沿正z 方向传播的波. 令 上式第二项为零. 即 • 式中. Ex0为z =0 处电场强度的有效值. Ex (z) 对应的瞬时值为:
上一页 下一页 返回
7. 2 自由空间中的平面波
• 媒质电场强度与磁场强度的振幅之比称为波阻抗. 也称为媒质的特征 阻抗. 或者本征阻抗. 以Zc表示. 即
• 由上述讨论可知. 平面波的波阻抗为复数. 电场强度与磁场强度的空间 相位不同. 复能流密度的实部及虚部均不会为零. 意味着平面波在传播 过程中. 既有能量的单向传播. 又有能量的双向或交换传播.
上一页 下一页 返回
7. 2 自由空间中的平面波
• 将ω =2πf 和式(7 -19) 代入式(7 -20). 得: • 式(7 -21) 描述了平面波的相速vp、频率f 与波长λ 之间的关系.
平面波的频率是由波源决定的. 它与源的频率始终相同. 但是平面波的 相速与媒质特性有关. 因此. 平面波的波长也与媒质特性有关. • 将式(7 -14a) 代入式(7 -18) 中. 得:
第二节平面简谐波的波动方程

上页 下页 返回 退出
解:由题意 波长 周期
T
u
1
0.40 m
8 105 s
(1)原点处质点的振动表达式
y0 A cos t 0.1103 cos(25 103 t )m
(2)波函数
x y A cos (t ) u
3
x 3 0.110 cos 25 10 (t ) m 3 5 10
(6)3T/4时的波形如下图中实线所示,波峰M1和M2已 分别右移 3 4 而到达 M 1 '和 M 2 '处。
y /cm
M1
0.5 0.4 0.2 0 0.2 0.4 0.5
M1'
M2
M2'
a
10 20
b
30 40 50 60 70
x /cm t=3T/4
上页 下页 返回 退出
例3 :如图是一平面余弦横波在时刻t=0的波形。此波形以 v=0.08m/s 的速度沿ox轴正向传播。 求:(1) a、b两点振动方向; (2) O点振动方程; (3) 波动表式 解:⑴ 由于波沿x正向传播,因 此任意时刻任意点都将重复其前 的点(图中左侧点)的振动,由 此可知: a点将向下振动; b点将向上振动。
上页 下页 返回 退出
P处质点在时刻t 的位移为:
yP (t ) = Acos ω x t - + 0 u
波 函 数
因此,波线上任一点在任一时刻的位移都能 由上式给出。此即所求的沿x 轴正方向前进 的平面简谐波的波函数。 沿x轴负方向传播的平面简谐波的波函数:
T
上页 下页 返回 退出
电磁波波动方程

u
1
0 0
1
3 10 m
8
s
——光速 c
推测:光也是电磁波! 在介质中 u
c
r r
c n
n r r — 折射率 在光波段 r 1 , E 与物质作用的主要是 E 矢量
——通常被称为光矢量!
章 静电场 第17第 章11 电磁波
11-2 库仑定律 17-1 电磁波波动方程
在自由空间
D 0
B 0
B E t D H t
章 静电场 第17第 章11 电磁波
结合 可以得到:
和
E 2 E 2 t 2 H 2 H 2 t
2 Ey 2E y 2 2 x t
2 Hz 2 Hz 2 2 x t
电磁波波速为:
即:若设电场方向沿y方向, 磁场必为z方向!
y
Ey
Hz
u
x
u
1
z
章 2 库仑定律 17-1 电磁波波动方程
*电磁波波速与光矢量* 真空中
2
2 2 2 2 2 2 2 x y z
章 静电场 第17第 章11 电磁波
D E BH
11-2 库仑定律 17-1 电磁波波动方程
其中
11-2 库仑定律 17-1 电磁波波动方程
当电磁波沿 x 方向传播时
比较波动方程
2 2x x 1 2 2 2 x u t
平面电磁波及其性质

E=f1(
z v
t)
B=f1(
z v
t)
这是行波的表示式,表 示源点的振动经过一定 的时间推迟才传播到场 点。
(二)波动方程的平面简谐波解 (Simple Harmonic Wave)
A:电场振幅矢量
E=Acos( z t) A':磁场振幅矢量
v
:角频率
B=A'cos( z t)
v
(
z v
t
)称为位相
E=Acoskx cos y cos z cos t
平面波的复数形式:
E=Aexp[i(k • r t)]
x
P(x,y,z)
k
复振幅:
r
E=Aexp(ik • r) o
z
y
s=r k
复振幅:只关心光波在 空间的分布。
(三)平面电磁波的性质
1、横波特性:电矢量和磁矢量的方向均垂直波的传播
平面电磁波及其性质
(一)波动方程的平面波解
1、方程求解:
设光波沿z轴正向传播
y
=x 0
x
y0
y
z0Leabharlann zz0zx
v
z
结果:2 E 1 2 E 0 v2 t 2
2E 1 2E 0 z 2 v2 t 2
令 = z t, z t,代入上式则有
v
v
E=f1
(
z v
t)
f
2
(
z v
t)
T E=Acos(kz t)
(10-25) (10-26)
上式是一个具有单一频率、在时间和空间上 无限延伸的波。
说明2点:
在空间域中(时间轴为某
在时间域中(空间某点)
电磁场波动方程

定态波动方程
vv
2E k 2E 0
2
v B
k
2
v B
0
其中:
Helmhotz方程
▪ 定态情况下的电磁场方程可以写成:
vv 2E k2E 0
v
E 0
v B
i
v E
Helmhotz 方程
或者
vv 2B k2B 0
v B 0
v E
i
k2
v B
其中:
是定态下介质电磁特性参数
此处的 Ev、Bv 是电磁场的振幅,时间变化部分不包含在内
v B
0
v 2E
0 0
v 2E t 2
0
v
v 2B
0 0
2B t 2
0
在真空中电磁场满足 “波动方程”
▪ 真空中电、磁场形式上可以分离:
v 2E
1
v 2E
0
c2 t 2
v 2B
1
v 2B 0
c2 t 2
v E 0
v B 0
电波动方程+横波条件 磁波动方程+横波条件
其中
称为真空中光速
但不能替代麦克斯韦方程,还需要考虑电场与磁场的联系
二、时谐波(又称定态波)及其方程
▪
任一时域函数
v
Et
,可以视为由频域函数
v
E
叠加而成,反之亦
然。这就是富里叶(Fourier)变换:
v
E t
v E
eit
d
Ev
1
v E
t
eit
dt
2
正变换 逆变换
▪ 对电磁场作富里叶变换:
v
E
v X,t
第四章 电磁波的传播 §1. 平面电磁波§2. 电磁波在介质界面上的反射和折射§3. 有导体存在时电磁波的

知 H
E
较大,非铁磁
B
可取 = 0
(2) E k 在与 k 垂直平面上可将 E 分解成两个分量
(3) H k, 且 H E
(4)
nn ((EH22EH1)1
0 )0
即 Et E't E"t Ht H 't H"t
(5) ' ,
sin 2 sin " 1
(1 2 0 )
电磁波:迅变电磁场, 导体内 = ?
电流:J
E
电荷:
E
/
,
J
E
J
0
t
t
J
,
d dt,
t
0e
t = 0 时,导体内 = 0 , 然后 随 t 按指数衰减 t = 时,( = / 特征时间) = 0 / e
导体内的自由电荷分布
t = 0 时,导体内 = 0 , 然后 随 t 按指数衰减
o
y
x
平面电磁波的特性: (证明 see next page)
(1) 电磁波是横波, E k , B k
(2) E B , E B 沿 k 方向
(3) E 和 B同相,振幅比 E / B = v
平面电磁波
证明平面电磁波的特性
E 0
E
E0
ei
(
k
xt
)
E0
ei
( k xt
)i(k
E"
2 1 cos
2sin "cos
E 1 cos 2 cos" sin( ")
振幅关系 Fresnel 公式
(2) E || 入射面: (Ht H )
第7章平面波

3 无源
电场的波动方程:
同 理
2E
2E t 2
0
磁场的波动方程:
2H
2H t 2
0
——都是2阶偏微分矢量方程。
注意条件:在各向同性, 均匀, 无源, 无损耗的介质中
4
第四第四页页,,共共5599页页。。
如何求解?
❖ 分解矢量方程为标量方 程……
2E
2E t 2
0
2 Ex
2Ex t 2
w2H y
0
Scalar Helmholtz equations 11
第第十十一一页页,共共5599页页。。
均匀平面波的标量解
2Ex z 2
k2Ex 0
k 2 2
Ex E0e jkz E0e jkz
+z方向,入射波
-z方向,反射波
为了给出完整的时间空间表示式,往往又恢复ejωt因子
Ex
2E
2E t 2
0
2Ex z 2
2Ex t 2
0
2H
2H t 2
0
2H y z 2
2H y t 2
0
复数形式:
For time harmonic field, E E0e jwt
Therefore,
j, 2 2
t
t 2
B B0e jwt
2Ex z 2
w2Ex
0
2H y z 2
v c 3108
2 f 314
k 2 v
2 v 2 3.14 3108 6106 m 6000km
314
所以当传输距离达到1500km,线路首端和末端电压差可达一个幅值,不能视为集中参数电路。
19
第十九页,共59页。
电磁场波动方程
§4.1
平面电磁波
电磁场波动方程 时谐电磁波 平面电磁波 电磁波的能量和能流
一、自由空间的电磁场波动方程
麦克斯韦方程组
B E 无源情况下 t D H J f 0, t Jf 0 D B 0 真空中: D 0 E, B 0 H
2 E 2 E 0 0 2 0 t 2 B 2 B 0 0 2 0 t
在真空中电磁场满足 “波动方程”
真空中电、磁场形式上可以分离:
2 1 E 2 E 2 2 0 c t 2 1 B 2 B 2 2 0 c t
的变化频率有关:
D E D t E t
B H B t H t
对一般的介质中的电磁场,不满足波动方程
0
0
介质中的微观粒子(如电子)由于其惯性,来不及响应外场
第四章
电磁波的传播
引
存在:
言
当 t 0 时,电场和磁场相耦合,相互为源,可以脱离电荷、电流而
E
B 0 t E 0 t
电磁波
B
E E E E
B
B
B
B
传播问题是指:研究电磁场在空间存在一定介
质和导体的情况下的波动。在真空与介质、介质与
2 E E B 0 0 2 t t 2 2 E E E E
B E t D H t D 0 B 0
电动力学课件 4.1 平面电磁波
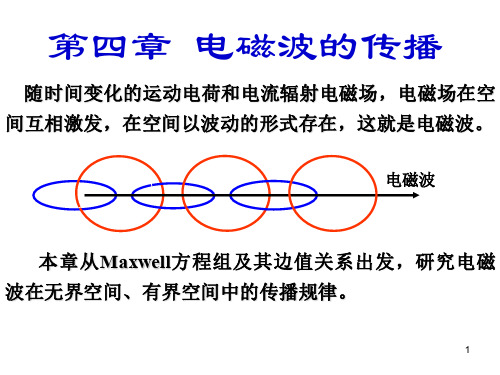
ε 和 μ随频率而变的现象称为介质的色散.
对色散介质,一般情况下
D E
, B H
B H D E ,
对角频率 ω一定的单色电磁波,有
对线性均匀各向同性的介质,当介质无色散或电磁波为单色波 时,电磁场的波动方程为
E x , t E 0e B x , t B0 e
i t E
ΦE、 ΦB 为与空间 位置有关的相位
利用欧拉公式 e i cos i sin ,时谐场的复数形式为
E x e it B x e i t E x , B x 为复数矢量
讨论一种最基本的解,它是存在于全空间中的平面波
设电磁波沿X轴方向传播,其场强在与x轴正交的平面上各点具有 相同的值,即E和B仅与x,t有关,而与y,z无关.这种电磁波称为 平面电磁波,其波阵面(等相位点组成的面)为与 x轴正交的平面
x
平面波
12
在这情形下亥姆霍兹方程化为一维的常微分方程
2E k 2E 0
k x t C
14
单色平面电磁波的基本物理量
E x , t E0e
k
i k x t
1) 波矢 k 的方向表示波的传播方向,大小表示2π长度上完整波的 数目 2
2) 相位为 k x t,等相面方程为 k x t C 3) 在同一时刻,在垂直于k 的平面上任一点,平面波的相位均相等 ,因此垂直于 k 的平面是等相面, k 是等相面的法向,即k 为等相面 的传播方向。 4) 在同一时刻,相位差为2π的两个等相面的距离λ称为波长
第七章 平面电磁波

与波动方程
d2 dx
f
2
1 v2
d2 f dt 2
0 对比可知,方
程的解同样具有波的形式,是为电磁波。
f f (t x) f (t x)
v
v
4
f f t z
f
v f
t1 > t2 > t3
z固定
z
t
z vt2 t1 vt
5
波的形式取决于边界条件和初始条件
x
驻波
x
行波
等相面在沿波矢 k 方向上距离与时间的关系为
t kr C v dr 1 dt k
是为相速,即等相面沿其法线方向的传播速度, 也即平面波的传播速度。如果媒质的特性与频率 无关,即、与频率无关,则不同频率的平面电 磁波的相速与频率无关,媒质称为无色散媒质。 一般情况下,媒质总是存在色散。
18 109
(J
/
m3)
ez
108
18 109
(J
/
m3)
1.5
108 ( m
/
s)
ez
108
120
(W
/
m2)
25
二、均匀平面波的特征参量
1、平面波的一般表达式
直角坐标系内平面方程为:
ax by cz C
其中矢量 n aex bey cez 为平面的法向矢量
因此平面n方程r可表a达x为:by cz C
9
Re
Er,
t
t
Re
iEre it
ReReexeixiExEmexmictosx t x i sint x
exExm sint x
Em t
Re
E t
电磁场导论之平面电磁波

y
得
H z 1 E y 1 t x x
2 E y cos(t x E )
2 E y sin(t x E )
上式对时间积分,略去表示恒定分量的积分常数, 并将 代入,得
H ( x ,t ) 2E y cos(t x E )
4 10 7 120 377 9 10 / 36
50 50 8 H cos(6 10 x) cos(6 108 x) e z Z0 377
3)坡因亭矢量
穿过园环的功率
~ H * ] 50 50 e 1250 e S av Re[ E x x 377 2 377 2
波动方程复数形式改写为
2Ey x 2 k 2Ey
2H z k 2H z x 2
在无限大导电媒质中,没有反射波的情况下, 其通解为 kx x jx
E y ( x) E y e
Ey e
e
( x) H e kx H e x e jx Hz z z
1250 ~ P S av dA (2.5) 2 65.1W A 377
2013-8-19 第七章均匀平面波 15
例7-2 已知某移动电话基站发射电磁波的磁场强度 (有效值相量) j(17.3 y ) 3 H 50e e x (A/m) 求:1)频率和波长; 2)电场强度(有效值相量); 3)坡印亭矢量的平均值。
解:1)因为相位系数=17.3,空气中v=3108m/s, 得 v 17.3 3 108 f 826 106 Hz 2 2 2
2 0.363 m 17.3
得
H z 1 E y 1 t x x
2 E y cos(t x E )
2 E y sin(t x E )
上式对时间积分,略去表示恒定分量的积分常数, 并将 代入,得
H ( x ,t ) 2E y cos(t x E )
4 10 7 120 377 9 10 / 36
50 50 8 H cos(6 10 x) cos(6 108 x) e z Z0 377
3)坡因亭矢量
穿过园环的功率
~ H * ] 50 50 e 1250 e S av Re[ E x x 377 2 377 2
波动方程复数形式改写为
2Ey x 2 k 2Ey
2H z k 2H z x 2
在无限大导电媒质中,没有反射波的情况下, 其通解为 kx x jx
E y ( x) E y e
Ey e
e
( x) H e kx H e x e jx Hz z z
1250 ~ P S av dA (2.5) 2 65.1W A 377
2013-8-19 第七章均匀平面波 15
例7-2 已知某移动电话基站发射电磁波的磁场强度 (有效值相量) j(17.3 y ) 3 H 50e e x (A/m) 求:1)频率和波长; 2)电场强度(有效值相量); 3)坡印亭矢量的平均值。
解:1)因为相位系数=17.3,空气中v=3108m/s, 得 v 17.3 3 108 f 826 106 Hz 2 2 2
2 0.363 m 17.3
电磁波的波动方程

电磁波的波动方程
电磁波的方程:
设在真空中无电荷与电流,电磁场方程为:
对第三式取旋度: ,
因为:,即:
,
而且:
令:
所以:。
同样地求出磁场的方程:
这就是电磁场的场量所满足的波动方程,c 是真空中电磁波的波速。
这样,麦克斯韦电磁场理论预言了电磁波的存在,真空中电磁波的波速精确地与真空中的光速一致,由此麦克斯韦进一步断定光是一种电磁波,从而揭示了光的电磁本质。
1888年赫兹用实验证实了这个预言。
赫兹的发现导致了无线电的诞生,开辟了电子技术的新纪元。
