离散傅里叶变换及其快速算法.
第2章 离散傅里叶变换和快速算法.ppt

杨毅明 第2章 离散傅里叶变换和快速算法
2.1.1 离散傅里叶级数
离散傅里叶级数的定义:
X~ (k )
N 1 ~x (n)e
j 2 N
kn
n0
~x (n)
杨毅明 第2章 离散傅里叶变换和快速算法
2.2 利用DFT做连续信号的频谱分析
离散傅里叶变换可以用来分析连续时间信号的频谱,其 原理如下:
这种方法存在如下问题: 混叠,泄漏,栅栏效应,分辨率,周期效应。 根据例6(书上63页)说明上面5个问题。
杨毅明 第2章 离散傅里叶变换和快速算法
clear;close all; f=10;a=4;T=1/(a*f);t=0:T:3; x=sin(2*pi*f*t); subplot(211);plot(t,x);xlabel('t/s');ylabel('x(t)'); N=length(t);n=0:N-1;k=n; W=exp(-j*2*pi/N*k'*n); X=W*conj(x'); subplot(212);stem(k,abs(X),'.');xlabel('k');ylabel('X(k)');
N 1 ~x1 (m) ~x2 (n rL m) RN (n)
m0
r
yL (n rL) RN (n) r
杨毅明 第2章 离散傅里叶变换和快速算法
yL(n)和yC(n) 的关系
yC (n) yL (n rL) RN (n) r
第三章 离散傅里叶变换(DFT)及其快速算法-庄

频域
离散
周期
时域的离散造成频域的延拓(周期性)。根据 对偶性,频域的离散也会造成时域的延拓(周 期散化,
令 d 0 从而 k 0
k 2F0 , N
j 0 kT N 1 n 0
s 0
n 0
N 1
j
2 kn N
0 k N 1
N称为DFT变换区间长度, N M
令
WN e
j
2 N
,记作旋转因子
傅里叶变换与逆变换对为:
kn X (k ) DFT [ x(n)] x(n)WN n 0 N 1 N 1
0 k N 1 0 n N 1
N
示周期序列的频谱特性,即DFT能够描述FT的特征
24
2.DFT与FT、ZT之间的关系
有限长序列
x(n) n 0,1, 2, M 1
N M
DFT与ZT、FT、DFS
X ( z ) ZT [ x(n)] X (e ) FT [ x(n)]
j j
n
x(n) z
7
2 时域:以Ts 采样,频域延拓周期 s Ts 2 频域:以0 采样,时域延拓周期T0 0
x(n)
T0 1 F0
Ts
1 fs
t n
| X (e
jk0T
)|
s
2 Ts
0
2 T0
k
8
四种形式归纳
类型
傅里叶变换 傅里叶级数
时间函数
连续 非周期
频率函数
N
(1)
1-z -8 X(z)= , -1 1-z
第2章 离散傅里叶变换(DFT)及其快速算法(FFT)

电信系信息技术教研室
2.1.1 离散傅里叶级数DFS
信号特性的时频域对应关系 连续 离散 周期
非周期 周期 离散
电信系信息技术教研室
2.1.1 离散傅里叶级数DFS
?如何对周期为N的周期序列进行频域分析……
如: ~(n) ~(n kN ) x x 周期序列不能进行Z变换,因为其在 n=-到+ 都 周而复始永不衰减,即 z 平面上没有收敛域,所以 其DTFT亦不存在。但是,如同连续时间周期信号可用 傅氏级数表达,周期序列也可用离散的傅氏级数来表 示。
2 1 2 1
X (2) 0 X (6) 0
X (3) 1 j X (7 ) 1 j
2 1 2 1
电信系信息技术教研室
解法二:公式解
N 1 j 2 N 7 j 2 8 kn
X
k
DFS x n
mk
ki mk ~ ~ x (i ) wN wN X ( k ) i 0
N 1
电信系信息技术教研室
3)共轭对称性
x 对于复序列 ~n ,其共轭序列为
~* ~* DFS x n X k
* *
~* x n
,则:
~ ~ DFSx n X k
解:上述序列的基本周期为 N=4,因而
W4 = e-j2π /4 = -j,
~ X (k )
~ X (0) ~ X (1 ) ~ X (2) ~ X (3)
n0
3
nk ~ x ( n )W 4
3
n0
3
~ ( n )W x 4
离散傅里叶变换及其快速算法

N
1
~x (i)wNki
wmk N
X~
(k
)
i0
由于 ~x (n) 与 X~(k ) 对称的特点,同样可证明
IDFS X~(k l) wNnl ~x(n)
3)共轭对称性
对于复序列~x n 其共轭序列~x *n 满足
DFS ~x * n X~ * k
•时域上周期序列的离散傅里叶级数在频域上仍是一个 周期序列。
X~(k) ~x (n) 是一个周期序列的离散傅里叶级数(DFS) 变换对,这种对称关系可表为:
~x (n) IDFS [ X~ (k )] 1 N 1 X~ (k )e j2 / N nk
N n0
X~ (k ) DFS [~x (n)] N 1 ~x (n)e j2 / N kn n0
证:
DFS ~x * n N1 ~x * (n)WNnk
n0
N
(
1
~x (n)WNnk
)*
X~ *
k
n0
同理:
DFS ~x * n X~*k
进一步可得
DFSRe{~x n} 1 DFS[~x n ~x * n]
§2.1 离散傅里叶变换(DFT)
为了便于更好地理解DFT的概念,先讨论周期序列及其 离散傅里叶级数(DFS)表示。
§2.1.1 离散傅里叶级数(DFS) 一个周期为N的周期序列,即
~x(n) ~x(n kN)
, k为任意整数,N为周期
周期序列不能进行Z变换,因为其在 n=-到+ 都周而 复始永不衰减,即 z 平面上没有收敛域。但是,正象连 续时间周期信号可用傅氏级数表达,周期序列也可用离散 的傅氏级数来表示,也即用周期为N的正弦序列来表示。
离散傅里叶变换及其快速算法

离散傅里叶变换及其快速算法离散傅里叶变换(Discrete Fourier Transform,DFT)是一种将离散信号转换为频域表示的数学工具。
它在信号处理、图像处理、通信等领域有广泛的应用。
而快速傅里叶变换(Fast Fourier Transform,FFT)是一种能够高效计算DFT的算法,大大减少了计算量。
首先,我们来看一下DFT的原理。
给定一个有限长度的离散信号序列x(n),DFT将其转换为频谱X(k),其中k为频率索引,取值范围为0到N-1,N为序列的长度。
DFT的定义公式如下:X(k) = Σ x(n) * exp(-j * 2π * nk / N)其中,exp为自然指数函数,j为虚数单位。
DFT将信号分解为了N个复数的和,这些复数代表了不同频率分量在信号中的贡献。
然而,直接计算DFT的时间复杂度非常高,为O(N^2)。
为了提高计算效率,Cooley和Tukey于1965年提出了FFT算法。
FFT算法基于以下性质:若N为2的整数次幂,则DFT可以被分解为两个较小长度的DFT的线性组合。
具体来说,将N个点的DFT拆分为长度为N/2的两个DFT,然后再对这两个子序列进行DFT,最后将两个子序列的结果组合起来。
这个过程可以递归地进行,直到序列长度为1,即可得到最终的DFT结果。
FFT算法的时间复杂度为O(NlogN),远远小于直接计算DFT的复杂度。
这使得FFT成为了处理大规模数据的首选方法之一、此外,FFT还有其他一些优点,如可并行化计算、对称性质等。
FFT算法可以采用不同的实现方式,最著名的是基于蝶形运算的Cooley-Tukey算法。
这种实现方式将FFT过程分为了两个阶段:置换阶段和蝶形运算阶段。
置换阶段通过将信号重新排序,将原始序列分为奇偶两个子序列,并计算每个子序列的DFT。
这个过程可以递归地应用于子序列,直到长度为1蝶形运算阶段是FFT算法的核心部分。
蝶形运算是指将两个频域上的复数进行运算,得到新的复数。
离散傅里叶变换及快速算法

(5-5)
W e N
j
2 N
的性质:
正交性,周期性,
共轭对称性(偶序列),可约性。
§5.离散傅里叶变换及快速算法
1.离散傅里叶级数
1.2离散傅里叶级的计算
例5-1 求出下面周期序列的DFS
x(n) 0 ,1,2,3, 0 ,1,2,3, 0,1,2,3
n0
为改进嵌套循环计算的效率,将循环结构改为矩阵形式计算
§5.离散傅里叶变换及快速算法
0.概述
离散时间傅里叶变换(DTFT)是通过周期频谱 来描述一个离散信号序列,即DTFT是连续变 量w的连续函数。离散傅里叶变换(DFT)则是 针对有限长序列,是对DTFT采样后得到的离 散序列。 此种表示方法非常有利于数值计算以及数字信 号处理算法的DSP硬件实现。 本章将研究离散傅里叶级数,离散傅里叶变换 (DFT),及离散傅里叶变换的快速算法FFT。
(5-3)
n0
称之为离散傅里叶级数DFS的系数。是一个基波周期为N的 周期序列。
X (k) X (k N)
§5.离散傅里叶变换及快速算法
W e 在DFS变换中引入复数 N
j
2 N
将DFS正反变换描述为
N 1
X (k) x(n)WNnk
n0
x (n)
1 N
N 1
X (k )WNnk
k 0
n0
x(n)
1 N
N 1
X (k )WNnk
k 0
x
1 N
WN* X
WN WNkn 0
k,n
N
1
1 1
1
WN1
1
W ( N 1) N
1
W ( N 1) N
《数字信号处理》C3离散傅里叶变换及快速算法

j
n
x(n) z n
M 1 n 0
n x ( n ) z jn
X ( e ) DTFT [ x ( n )]
n
x ( n )e
M 1 n 0
jn ( ) x n e
2 j X ( e ) FT [ x N ( n )] N ( k ) DFS [ x N ( n )] X X ( k ) DFT [ x ( n )]N
n 0
N 1
n
1 n0 N
N 1
X (k )W
k 0
N 1
nk N
n z
1 N 1 N 1 nk n X (k ) WN z N k 0 n 0
N 1 1 N 1 k 1 n X (k ) WN z N k 0 n 0
(n) ak e x
k 0 N 1 j 2 kn N
2 2 T 0 0T NT N
为什么是有限项之和? 如何求系数?
( n )e x
n 0
N 1
j
2 mn N
2 2 j kn j mn ak e N e N n 0 k 0 N 1 N 1
N 1
ak ak lN
周期
3.1 周期序列的傅里叶级数
第3章 离散傅里叶变换(DFT)及其快速算法(FFT)

1 x(n) IDFT [ X (k )]N N
k 0
N 1
X (k )WN k n , n 0, 1, , N 1
也可以表示为矩阵形式: x DN1 X
DN1
称为N点IDFT矩阵,定义为:
1 1 1 1 W 1 WN 2 N 1 1 WN 2 WN 4 N ( N 1) WN 2( N 1) 1 WN 1 WN ( N 1) 2( N 1) WN WN ( N 1)( N 1)
3.1.3 DFT的矩阵表示
X (k ) DFT [ x(n)]N
n 0
N 1
k x(n)WN n , k 0, 1, , N 1
也可以表示成矩阵形式: X DN x 式中,X是N点DFT频域序列向量:
X [ X (0) X (1) X ( N 2) X ( N 1)]T
2
N 1
k
DFT与DTFT变换
DFT所表示的不是序列的频谱,而是对序列频谱的一个采样! 采样间隔为2/N;N越大,X(k)越能反映X()的形状。
(2)序列的N点DFT是序列的Z变换在单位圆上的N点等间隔采样, 频率采样间隔为2/N。
X (k ) X ( z )
z e
j 2 k N
M 1
n 0
比较前面三式,得到:X (k ) X (e j )
结论:
2 k N
, k 0, 1, 2,, N 1
(1)序列的N点DFT是序列的傅里叶变换(DTFT)在频率区间 [0,2]上的N点等间隔采样,采样间隔为2/N。
X (e j )
X (k )
离散傅里叶变换及其快速算法

ak 也是以 N周期的周期序列,满足 ak
~ X (k ) Nak
ak 。令 ln
(3.5)
将式(3.4)代入,得
N 1 j kn ~ ~ N X ( k ) x ( n )e n 0 2
k
(3.6)
~ X (k ) 式中, 是以N为周期的周期序列,称为
~ x (n) 的离散傅里叶级数,用DFS表示。
~(k ), N 相位为 幅度为 X
~ arg[ X (k )]
。
基波分量的频率为 2 N ,幅度为
~ 为arg[ X (1)]
~ X (1) N
,相位
。
x ( n ) 以 N 8 为周期 n) 【例3-1】设 x(n) R4 (,将
进行周期延拓,得到周期序列 幅频特性。
~ x ( n)
2016-12-8
解:根据定义求解
14 12 e 8e
j
j
2 k 6
10e
j
j
2 2k 6 j 2 5k 6
2 3k 6
6e
2 4k 6
10e
X (0) 60 X (3) 0
X (1) 9 j 3 3 X (4) 3 j 3
X (2) 3 j 3 X (5) 9 j 3 3
x 3(n )
当k取奇数( k=2m+1 ,m=0,1,…, N/4-1 )时
N n(2 m 1) X 1(2m 1) x 1(n ) x 1 n 4 W N 2 n 0 N 4 1 N n mn x 1(n ) x 1 n W W N N 4 4 n 0 2
离散傅里叶变换及其快速计算方法

X N (k ) X '( z )
z WN k
n
x '(n)WNkn
24
X '( z ) Z [ x '(n)]
X N (k ) X '( z )
xN ( n)
z WN k
x '(n rN )
r
频域抽样序列 的得到的
是原来非周期序列 ′ 基于
j
2
mk
N
~
X (k )
2
j
mk ~
~
mk ~
N
DFS [ x ( n m)] WN X (k ) e
X (k )
Note:时域延迟,频域有线性相移
3、调制性质
~
DFS [WNln x(n)] X (k l )
13
4、周期卷积和(时域)
~
~
~
若 Y (k ) X 1 (k ) X 2 (k )
N 1
1
nk
x ( n) x ( n) R ( n)
X ( k )W N RN ( n)
N
N k 0
x(n),X(k)
代替
( , (
DFT变换对(标准形式):
2
N 1
N 1
j nk
nk
N
X
(
k
)
DFT
[
x
(
n
)]
x
(
n
)
W
=
x
(
周期为点的周期延拓
第四章 离散傅里叶变换及其快速算法

离散 连续
周期延拓 非周期
4.1 离散傅里叶变换的定义
kn X (k ) DFT [ x(n)] x(n)WN , n 0 N 1 N 1 n 0 2 kn N
= x ( n )e
j
k=0, 1, , N-1
X ( k )WN kn k 0 N 1
1 x(n) IDFT [ X (k )] N 1 N
4 N
x D1X N
W N ( N 1 ) 2 ( N 1 ) WN W N ( N 1 )( N 1 ) 1
1
D
1 N
W N 2 ( N 1 )
1 DN N
dftmtx(N) 函数产生N×N的DFT矩阵DN conj(dftmtx(N))/N 函数产生N×N的IDFT矩阵DN-1
二、 圆周移位性质
1. 序列的圆周移位 x(n)的圆周移位定义为
y(n)=x((n+m))N RN(n) 其过程为: 1)、将x(n)以N为周期进行周期延拓得x((n))N 2)、将x((n))N左移m位,得x((n+m))N 3)、取其主值序列x((n+m))N RN(n) 循环移位过程如图所示
WNN 1
2 WN ( N 1)
WNN 1 2 WN ( N 1) ( WN N 1) ( N 1)
DFT
IDFT矩阵形式为
1 1 1 W 1 N 1 D 1 1 W N 2 N N 1 W N ( N 1 ) 1 W N 2 W
0 n N `1 0 k N `1
DFT 则: x1 (n) x2 (n) X1 ( K ) X 2 ( K )
第3章 离散傅里叶变换及其快速算法

N 1
X (k) DFT [x(n)] x(n)WNkn n0
0 k N 1
x(n)
IDFT [X (k)]
1 N
N 1
X (k )WNkn
k 0
0 n N 1
x(n) 与 X(k) 是一个有限长序列离散傅里叶变换 对,已知 x(n) 就能唯一地确定 X(k) ,同样已知 X(k) 也就唯一地确定 x(n) ,实际上 x(n) 与 X(k) 都是长度 为 N 的序列(复序列)都有N个独立值,因而具有等 量的信息。
X k 2, 1 j , 0, 1 j
DFT特性:
以下讨论DFT的一些主要特性,这些特性 都与周期序列的DFS有关。
假定x(n)与y(n)是长度为N的有限长序列, 其各自的离散傅里叶变换分别为:
X(k)=DFT[x(n)] Y(k)=DFT[y(n)]
(1) 线性 DFT[ax(n)+by(n)]=aX(k)+bY(k), a,b 为 任 意
X 1 X 2
1 1
j 1
1 1
j 2 j2
2
1 j 2
X
3
1
j
1
j
1
j
2j
直接利用定义求
解:
N 1
X k xnWNnk
3
j 2 nk
xne 4 ,
0 k N 1
n0
n0
3
X 0 xne0 4 j6
n0
X 1
3
xne
j 2
n
x0
x1e
j 2
有限长序列隐含着周期性。
DFT的矩阵方程表示
x(0)
x
x(1)
实验四 离散傅里叶变换及其快速算法

实验四 离散傅里叶变换及其快速算法一、 实验目的掌握快速傅立叶变换的应用方法;二、 实验仪器:电脑一台,MATLAB6.5或更高级版本软件一套。
三、 实验原理和实例分析 (一)离散傅里叶变换离散傅立叶级数变换是周期序列,仍不便于计算机计算。
但离散傅立叶级数虽是周期序列,却只有N 个独立的数值,所以它的许多特性可以通过有限长序列延拓来得到。
对于一个长度为N 的有限长序列)(n x ,也即)(n x 只在)1(~0-=N n 个点上有非零值,其余皆为零,即⎩⎨⎧-≤≤=其他,010),()(N n n x n x把序列)(n x 以N 为周期进行周期延拓得到周期序列)(~n x ,则有:⎪⎩⎪⎨⎧-≤≤=其他,010),()(~N n n x n x所以,有限长序列)(n x 的离散傅立叶变换(DFT)为:10,)()]([)(10-≤≤==∑-=-N n W n x n x DFT k X N n knN逆变换为:10,)(1)]([)(10-≤≤==∑-=-N n W k X N k X IDFT n x N n kn N若将DFT 变换的定义写成矩阵形式,则得到: X=A ﹒x ,其中DFT 变换矩阵A 为⎪⎪⎩⎪⎪⎨⎧=---2)1(111...1...............11...11N NN N N N N W W W W ADftmtx 函数:用来计算DFT 变换矩阵A 的函数A =dftmta (n ):返回n ×n 的DFT 变换矩阵A 。
若x 为给定长度的行向量,则y =x*A ,返回x 的DFT 变换y 。
Ai =conj (dftmtx (n ))/n ;返回n ×n 的IDFT 变换矩阵Ai 。
【实例4-1】 >> A=dftmtx(4) >> Ai=conj(dftmtx(4))/4 运行结果A =1.0000 1.0000 1.0000 1.0000 1.0000 0 - 1.0000i -1.0000 0 + 1.0000i1.0000 -1.0000 1.0000 -1.0000 1.0000 0 + 1.0000i -1.0000 0 - 1.0000i Ai =0.2500 0.2500 0.2500 0.2500 0.2500 0 + 0.2500i -0.2500 0 - 0.2500i0.2500 -0.2500 0.2500 -0.2500 0.2500 0 - 0.2500i -0.2500 0 + 0.2500i【实例4-2】如果)4/sin()8/sin()(ππn n n x +=是一个N =16的有限序列,用MATLAB 求其DFT 的结果,并画出其结果图,如图4-1所示。
离散傅里叶变换及其快速算法
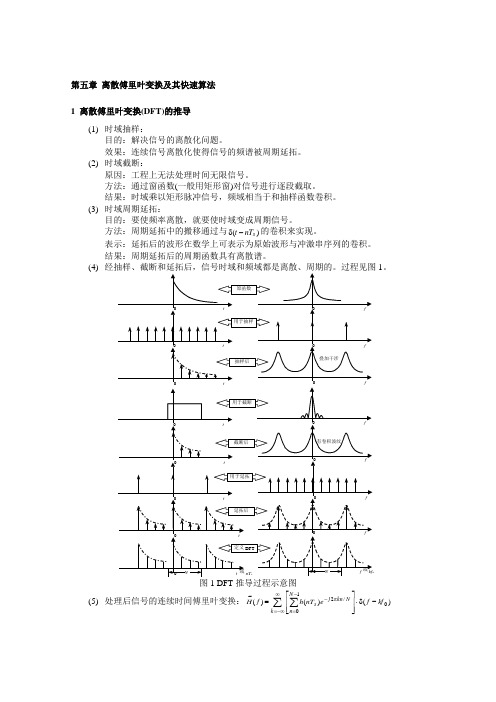
第五章 离散傅里叶变换及其快速算法 1 离散傅里叶变换(DFT)的推导(1) 时域抽样:目的:解决信号的离散化问题。
效果:连续信号离散化使得信号的频谱被周期延拓。
(2) 时域截断:原因:工程上无法处理时间无限信号。
方法:通过窗函数(一般用矩形窗)对信号进行逐段截取。
结果:时域乘以矩形脉冲信号,频域相当于和抽样函数卷积。
(3) 时域周期延拓:目的:要使频率离散,就要使时域变成周期信号。
方法:周期延拓中的搬移通过与)(s nT t -δ的卷积来实现。
表示:延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。
结果:周期延拓后的周期函数具有离散谱。
(4)1。
图1 DFT 推导过程示意图(5) 处理后信号的连续时间傅里叶变换:∑∑∞-∞=-=π--δ⋅⎥⎥⎦⎤⎢⎢⎣⎡=k N n N kn j s kf f e nT h f H )()()(~010/2(i))(~f H 是离散函数,仅在离散频率点SNT kT k kf f ===00处存在冲激,强度为k a ,其余各点为0。
(ii) )(~f H 是周期函数,周期为ss T NT N T N Nf 100===,每个周期内有N 个不同的幅值。
(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。
2 DFT 及IDFT 的定义(1) DFT 定义:设()s nT h 是连续函数)(t h 的N 个抽样值1,,1,0-=N n ,这N 个点的宽度为N 的DFT 为:[])1,...,1,0(,)()(10/2-=⎪⎪⎭⎫⎝⎛==∆-=π-∑N k NTk H enT h nT h DFT s N n Nnk j s s N (2) IDFT 定义:设⎪⎪⎭⎫⎝⎛s NT kH 是连续频率函数)(f H 的N 个抽样值1,,1,0-=N k , 这N 个点的宽度为N 的IDFT 为:())1,...,1,0(,110/21-==⎪⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛∆-=π--∑N k nT h e NTkH NNT kH DFT s N k N nk j s sN (3) N nk j e /2π-称为N 点DFT 的变换核函数,N nk j e /2π称为N 点IDFT 的变换核函数。
[理学]离散傅里叶变换及其快速算法
![[理学]离散傅里叶变换及其快速算法](https://img.taocdn.com/s3/m/a4bbbd1b0912a21615792901.png)
FFT原理
• FFT算法主要利用了 WNnk 的两个性质:
1. 对称性
W
( nk N ) 2
W nk
nk ) N
2. 周期性
W nk W
mod( nk ) N
mod(
表示用N除nk之后的余数
• FFT算法利用
WNnk
的对称性和周期性,将一个大的
DFT分解成一些逐次变小的DFT来计算。 • 分解过程遵循两条规则: ①对时间进行偶奇分解——按时间抽取的FFT算法 ②对频率进行前后分解——按频率抽取的FFT算法
X (e j )e jn d
傅里叶变换对小结
• 傅里叶级数(FS)(时域:连续周期;频域:非周期离散)
1 Xk T
T 2
T 2
x(t )e jk1t dt
x(t )
k
X k e jk1t
k 0, 1, 2,
• 傅里叶变换(FT)(时域:连续非周期;频域:非周期连续)
1
有时会造成能量分散现象,称之为频谱泄漏。
• 余弦信号被矩形窗截断形成的泄漏 余弦信号被矩形窗截断形成的泄漏
• 对于连续周期函数,在符合采样定理的条件下, 保证窗函数b(t)的时段τ等于被截函数的周期T的 整倍数,可以保证逆变换后准确地恢复原波形, 不产生泄漏。 • 对于随机振动信号(非周期函数),控制泄漏的 方法是采用特定的窗函数,以达到控制旁瓣的效 果。
1 fs t
N T N t fs
fN= fs/2称为 Nyquist频率, 或称混叠频率
N T 2 f max
• 若提高采样频率fs将使采样时间减少,从而造成频率分辨 率Δf变粗。可先使信号通过一个低通滤波器,使滤波后的 信号中的最高频率成为fmax ,然后根据采样定理来确定采 样频率fs 。通常fs是fmax的3~4倍
第三章 离散傅里叶变换(DFT)及其快速算法(FFT)2

由8点DIT-FFT运算流图可以发现,第L级共有2L-1个 不同的旋转因子。 N=23=8时的各级旋转因子表示如下: 0 L=1时 WNp WN
L=2时 L=3时
0 2 WNp WN , WNp WN
0 1 2 3 WNp WN ,WNp WN ,WNp WN ,WNp WN
倒 二进制数 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1
序 十进制数 J 0 4 2 6 1 5 3 7
X (0), X (1), X (2), X (7)
12
由8点DIT-FFT运算流图可见,N=2M时,其DIT-FFT运算流图 由M级蝶形构成,每级有N/2个蝶形。因此,每级需要N/2 次复数乘法运算和N次复数加法运算,M级蝶形所需复数乘 法次数CM(2)和复数加法次数CA(2)分别为
CM (2) N N M log2 N 2 2
CA (2) NM N log 2 N
N=2M点的FFT共进行M级运算,每级由N/2个蝶形运算组成。同一级中,每个 蝶形的两个输入数据只对计算本蝶形有用,而且每个蝶形的输入、输出数 据节点又同在一条水平线上,这就意味着计算完一个蝶形后,所得输出数 据可立即存入原输入数据所占用的存储单元。这样,经过M级运算后,原 来存放输入序列数据的N个存储单元(A(0),A(1),…,A(N-1))中便依次存放 X(k)的N个值。这种利用同一存储单元存储蝶形计算输入、输出数据的方 法称为原位(址)计算。 • 节约内存单元,降低设备成本
0 WN 0 WN 0 WN
2 WN
X (0) X (1) X (2) X (3) X (4) X (5) X (6) X (7)
20
W N0
0 WN 0 WN 0 WN
第三章离散傅里叶变换及其快速算法

= W nl x ( n) IDFT [Y ( k )]
N
数字信号处理 第3章 © 2004
三.共轭复序列的DFT 设 x (n) x(n) 的共轭复序列,则 为
D [ x (n) ] X ( ( N k ) ) N RN ( k ) FT
证明: [ x (n)] DFT
nk
y * ( n)
N
k 0
1
N 1
X ( k ) W N
n 0
N 1
N 1
nk
y * ( n)
N
k 0
1
N 1
X ( k )
n 0
W N y ( n)
nk
*
N
k 0
1
N 1
X ( k )Y * (k )
数字信号处理 第3章 © 2004
当x(n)=y(n)时,则有:
x((9))16 x(9)
x((5)) 8 x(5)
N=16
x(( 4))16 x(12)
数字信号处理 第3章 © 2004
x 2.有限长序列x(n)和周期序列 ~ ( n ) 的关系 x 有限长序列x(n)是周期序列~ ( n )的主值序 列,而 ~ ( n ) 是x(n)的周期延拓。 x
x r ( n) 1 [ x(n) x (n)]
*
2 1 * jxi (n) [ x(n) x (n)] 2
用 X e (k ) 和 X o (k ) 分别表示实部与虚部序列的DFT: 1 * X e (k ) DFT [ x r (n)] DFT { [ x(n) x (n)]} 2
二.循环移位性质
离散傅里叶变换及其快速算法

w nk N
又如
w
N N
/
2
1,
因此
w(kN / 2) N
wNk
利用这些周期性和对称性,使DFT运算中有些项可合并;
2)利用
w
nk N
的周期性和对称性,把长度为N点的大点数的DFT
运算依次分解为若干个小点数的DFT。因为DFT的计算量正比于N2,
N小,计算量也就小。
FFT算法正是基于这样的基本思想发展起来的。它有多种形式,
n0
N / 21
X (2r 1) [x(n) x(n N / 2)]WNn(2r1)
n0
N / 21
[x(n) (n)=x(n)+x(n+N/2) b(n)=[x(n)-x(n+N/2]wnN
这两个序列都是N/2点的序列,将其代入上两式,得
结果仍然储存在同一组存储器中,直到最后 输出,中间无需其它存储器,这叫原位计算 。 每一级运算均可在原位进行,这种原位运算 结构可节省存储单元,降低设备成本,还可 节省寻址的时间。
21
(3)序数重排
对按时间抽取FFT的原位运算结构,当运算完毕
时,正好顺序存放着 X(0),X(1),X(2),
…,X(7),因此可直接按顺序输出,但这种原
但基本上可分为两类:时间抽取法和频率抽取法。
6
2、按时间抽取的FFT(N点DFT运算的分解) 先从一个特殊情况开始,假定N是2的整数次方,
N=2M,M:正整数
首先将序列x(n)分解为两组,一组为偶数项,一组为奇数 项,
x(2r) x1(r) x(2r 1) x2 (r
)
r 0,1,, N/2-1
位运算的输入 x(n)却不能按这种自然顺序存入
离散傅里叶变换及其快速计算方法(DFT、FFT)

0
2 (弧度,数字频率)
0
fs /2
fs f (Hz,模拟频率)
0
s /2
s (弧度/秒,模拟角频率)
25
DFS 定义:几点说明
频率成份
•
直流分量:
当 k=0 时, 号的直流分量(DC
N 1
X%(0) x%(n)WN 0n n0
Component),
N 1
x%(n)
,n此0是时信X%(得号0)到/的N的平傅均里值叶;级数的系数称为信
1
X%(k
)e
j
(
2 N
)km
N k0
变量m替换为n,得
x%(n)
1 N
N
1
X%(
k
)e
j
(
2
N
) kn
k0
1 N
N 1
X%(k )WN kn
k0
21
DFS 定义:反变换
DFS 变换对:时域周期序列与频域周期序列间的关系
N 1
X%(k ) x%(n)WN kn
n0
x%(n)
1 N
N 1
5
3.1 问题的提出:傅里叶变换的四种形式 (2)
1. 连续信号(非周期)的付氏变换
x(t)
X ()
t
x(t) X (),
t
x(t) 1 X ()e jt d
2
X () x(t)e jt dt
时域连续函数造成频域是非周期的谱 时域的非周期造成频域是连续的谱
6
3.1 问题的提出:傅里叶变换的四种形式 (3)
(1)必须是时间限x制(n() 有 限 时宽0),
其它
0
知识2 离散傅里叶变换及其快速算法

用Fourier 变换来表示序列和线性时不变系统的频域特征,但是频谱()ωj e X 是ω的连续函书,用计算机处理和分析频谱是不方便的。
那么就需要像时序信号那样,通过采集把连续信号变为离散信号,也对连续频谱采样而得到离散频谱,然后用数字电路或计算机进行处理和分析。
有限长序列在应用中有重要的作用,通过它可以导出另一种Fourier 变换表达式,即离散傅里叶变换(DFT),此为解决频谱离散化的有效方法,同时DFT 的高效算法——快速傅里叶变换FFT 。
周期序列一个周期为N 的周期序列~x ,对于所有的n ,应该满足:()()为整数k kN n x x +=~~周期序列的周期N ,一般使用最小周期作为周期。
与连续时间周期函数相比,周期序列由于n 及N 均为整数,周期序列中应用最广泛的序列是:kn Njkn NeWπ2-=(2-1)ImRe1上图就是周期序列nN W (N=8),从n=0开始到8取完周期内的所有值。
令k = 1时,nN W 就是一个周期序列。
当n 从0依次加1到N-1时,序列nN W 取完周期内的所有值,这些值可以看成是Z 平面上以原点为圆心的单位圆被N 等分的交点的的坐标值。
k 为其他数值时,knN W 的最小周期也许不是N ,但是N 一定是knN W 的周期。
knN W 的性质很明显:周期性:knN W =nN k NW )(-=)(N n k NW -对称性:kn N W -=()*kn N W =nk N NW )(-=)(n N k NW -正交性:()()∑-=⎩⎨⎧==10n 0,N k knNr rN n N W其他为整数 或者 ()()∑-=⎩⎨⎧==1n 0,N n kn Nr rN k N W其他为整数 一个周期为N 的周期序列()n x ~,在n=∞-到n=+∞的范围内仅有N 个序列值是独立的其中一个周期内的N 个序列值足以表征整个序列的特征。
而对于长度为N 的有限长序列,只讨论n=0到N-1之间的N 个序列值,其余皆为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DFS的几个主要特性:
假设~x(n)、~y(n) 都是周期为 N 的两个周期序列,各自的 离散傅里叶级数为:
1)线性
X~(k ) DFS~x(n) Y~(k ) DFS~y(n)
a , b为任意常数DFS a~x (n) b~y(n) aX~(k ) bY~(k )
2)序列移位
DFS~x(n
3) X~ (k ) 为周期序列,周期为N。
X~ (k mN ) N 1 ~x (n)e j2 / N (kmN)n n0 N 1 ~x (n)e j2 / N kn X~ (k ) n0
•时域上周期序列的离散傅里叶级数在频域上仍是一个周期序列
X~ (k ) ~x (n) 是一个周期序列的离散傅里叶级数(DFS)变换
§2.1 离散傅里叶变换(DFT)
为了便于更好地理解DFT的概念,先讨论周期序列及其离散傅里 叶级数(DFS)表示。
§2.1.1 离散傅里叶级数(DFS)
一个周期为N的周期序列,即
~x (n) ~x (n kN) , k为任意整数,N为周期
周期序列不能进行Z变换,因为其在 n=-到+ 都周而复始永不 衰减,即 z 平面上没有收敛域。但是,正象连续时间周期信号可 用傅氏级数表达,周期序列也可用离散的傅氏级数来表示,也即用
DFS ~x * n X~ * k
证: 同理:
DFS ~x * n N1 ~x * (n)WNnk n0
N
(
1
~x (n)WNnk
)*
X~ *
k
n0
DFS ~x * n X~*k
进一步可得
DFSRe{~x n} 1 DFS[~x n ~x * n]
2 1 [ X~(k) X~ * (N k)]
对,这种对称关系可表为:
~x (n) IDFS [ X~ (k )] 1 N 1 X~ (k )e j2 / N nk
N n0
X~ (k ) DFS [~x (n)] N 1 ~x (n)e j2 / N kn n0
习惯上:记
WN e j 2, / N
则DFS变换对可写为
X~(k) N 1 ~x (n)WNkn DFS~x (n) n0
第二章 离散傅里叶变换及其快速算法
离散傅里叶变换不仅具有明确的物理意义,相对于DTFT
他更便于用计算机处理。但是,直至上个世纪六十年代,由 于数字计算机的处理速度较低以及离散傅里叶变换的计算量 较大,离散傅里叶变换长期得不到真正的应用,快速离散傅 里叶变换算法的提出,才得以显现出离散傅里叶变换的强大 功能,并被广泛地应用于各种数字信号处理系统中。近年来, 计算机的处理速率有了惊人的发展,同时在数字信号处理领 域出现了许多新的方法,但在许多应用中始终无法替代离散 傅里叶变换及其快速算法。
~x(n)
1 N
N
1
X~
(k
)W
N
kn
k 0
IDFS
X~ (k )
DFS[·] ——离散傅里叶级数变换
IDFS[·]——离散傅里叶级数反变换。
DFS变换对公式表明,一个周期序列虽然是无穷长序列, 但是只要知道它一个周期的内容(一个周期内信号的变化情 况),其它的内容也就都知道了,所以这种无穷长序列实际 上只有N个序列值的信息是有用的,因此周期序列与有限长序 列有着本质的联系。
2
共轭偶对称分量
DFSRe~x n
X~e
k
1 2
[
X~
(k)
X~ *
(N
k
)]
共轭奇对称分量
DFS
j
Im~x n
X~o
k
1 2
[
X~
(k
)
X~ * ( N
k
)]
4)周期卷积
若 F~(k ) X~(k )Y~(k ) 频域乘积,时域卷积
则 ~f (n) IDFS F~(k) N1 ~x (m)~y(n m) m0
将周期序列展成离散傅里叶级数时,只需取 k=0 到(N-1) 这 N个独立的谐波分量,所以一个周期序列的离散傅里叶级数只 需包含这N个复指数,
~x (n) 1 N 1 X~ (k )e j2 / N kn
N K 0
利用正弦序列的周期性可求解系数 X~ (k ) 。
e 将上式两边乘以
j(2 / N )rn
eN
n0
1 0
k r sN kr
上式中[ ]部分显然在0~N-1中只有当k=r时才有值为1,其他任意
k值时均为零,所以有
N
1
~x (
n)e
j
2
N
rn
X~(r)
n0
或写为
X~ (k )
N 1
~x (n)e
j
2
N
k n
n0
0 k N 1
1) 可求 N 次谐波的系数
X~ (k )
2) X~ (k ) 也是一个由 N 个独立谐波分量组成的傅立叶级数
wmk N
N
1
~x (i)wNki
wmk N
X~
(k
)
i0
由于 ~x (n) 与 X~(k ) 对称的特点,同样可证明
IDFS X~(k l) wNnl ~x(n)
时域的移位等于频域乘一个旋转因子,即一个系数; 频移也一样,只是相差一个符号
3)共轭对称性
对于复序列 ~x n 其共轭序列~x *n 满足
IDFS X~
m) wNmk X~(k
(k l) wNnl ~x (n)
)
证因为~x (n) 及 wNkn 都是以N为周期的函数,所以有
DFS
~x (n m)
N 1 ~x (n
m)wNkn
N
1
m~x (i)
wNki
wkm N
n0
im
wmk N
N 1m~x (i)wNki
imLeabharlann 或N 1 ~y (m)~x (n m)
m0
两者 N必须相同
周期卷积
证:~f (n) IDFS
周期为N的正弦序列来表示。
周期为N的正弦序列其基频成分为:
e1 (n) e j2 / N n e K次谐波序列为:k (n) e j 2 / N kn
但离散级数所有谐波成分中只有N个是独立的,这是与连 续傅氏级数的不同之处,
即
e j2 / N (kN )n e j2 / N kn
因此 ekN (n) ek (n)
,并对一个周期求和
N
1
~x (n)e
j
2 N
rn
1
N
1
N
1
X~
(k
)e
j
2 N
(
k
r
)n
1
N
1
X~
(k
N
)
1
e
j
2 N
(k
r
)
n
n0
N n0 k0
N k0
n0
N 1 k 0
X~ (k )[
1 N
1 e j 2 (k r ) 1 e j 2 (k r ) / N
]
1
N
N 1 j( 2 )(k r )n
