2016年浙江省丽水市中考数学试卷(解析版)

合集下载

2016丽水中考数学答案

浙江省2016年初中毕业升学考试(丽水卷)数学试卷参考答案及评分标准一、选择题(本题有10小题,每小题3分,共30分)二、填空题(本题有6小题,每小题4分,共24分)11. a (m －3) 12.70° 13.23 14.1 16.(1)4m m+；三、解答题(本题有8小题,第17～19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分) 17.(本题6分)解:原式 ……6分 18.(本题6分)解:去括号,得3 x －5＜4＋6x ,移项,得3x －6x ＜4＋5,合并同类项,得－3x ＜9,两边都除以－3,得x ＞－3. ……6分 19.(本题6分)解:在Rt △ABC 中,BC =2,∠A =30°,∴2tan tan30BC AC A ︒=== 由题意,得EF =AC =23.在Rt △EFC 中,∠E =45°,∴CF =EF ·cos45°=23×22=6.∴AF =AC －CF =23－6. ……6分 20.(本题8分)解:(1) “跳绳”项目的女生人数=4006002602402+-=(人). ……2分 (2)观察男、女生各项目平均成绩统计图可知：立定跳远、游泳、跳绳三项目的男、女生总平均成绩均小于9分,投篮项目的男、女生总平均成绩一定大于9分.掷实心球项目的男、女生总平均成绩=4008.76009.29400600⨯+⨯=+.∴属于“优秀”项目的有投篮、掷实心球两个项目. ……3分(3)A类(识图能力):能用两统计图中的一个图提出合理化建议.如:“游泳”项目考试的人最多,可选考“游泳”.B类(数据分析能力):能结合两统计图的数据提出合理化建议.如:“投篮”项目人数虽然不是最多,但平均成绩较高,建议选“投篮”.C类(综合运用能力):能利用两统计图中的数据并结合学生实际提出合理化建议.如:“跳绳”项目的报名人数少,男、女生的平均成绩都很低,若不是跳绳水平很高，建议不选择该项目.)注：符合A类给1分；符合B类给2分；符合C类给3分. ……3分21.(本题8分)解:(1)∵从起点到紫金大桥用了35分钟,且平均速度是0.3千米/分,∴a=0.3×35=10.5(千米). ……2分(2)①∵线段OA经过点O(0,0),A(35,10.5),∴OA的函数解析式是S=0.3t (0≤t≤35).∴当S=2.1时,0.3t=2.1,解得t=7.∵该运动员从第一次过C点到第二次过C点所用的时间为68分钟,∴该运动员从起点到第二次过C点共用的时间是7+68=75(分钟).∴AB经过(35,10.5),(75,2.1)两点.设AB所在直线的函数解析式是S=kt+b,∴3510.575 2.1k bk b+=⎧⎨+=⎩，解得0.2117.85kb=-⎧⎨=⎩.∴AB 所在直线的函数解析式是S =－0.21t +17.85. ……4分②∵该运动员跑完赛程所用的时间即为直线AB 与x 轴交点横坐标的值. ∴当S =0时,－0.21t +17.85=0 ,解得, t =85.∴该运动员跑完赛程用时85分钟. ……2分 22.(本题10分)解:(1)连结OD ,BD ,∵AB 是半圆O 的切线,∴AB ⊥BC ,即∠ABO=90°. ∵AB=AD ,∴∠ABD =∠ADB ,∵OB=OD ,∴∠DBO =∠BDO ,∴∠ABD ＋∠DBO =∠ADB ＋∠BDO ,∴∠ADO =∠ABO=90°,∴AD 是半圆O 的切线. ……3分(2)由(1),∠ADO =∠ABO=90°,∴∠A=360°－∠ADO －∠ABO －∠BOD=180°－∠BOD .而∠DOC =180°－∠BOD ,∴∠A=∠DOC .∵AD 是半圆O 的切线,∴∠ODE=90°.∴∠ODC ＋∠CDE =90°.∵BC 是直径,∴∠ODC ＋∠BDO =90°.∴∠BDO=∠CDE , ∵∠BDO=∠OBD ,∴∠DOC =2∠BDO .∴∠DOC =2∠CDE ,∴∠A=2∠CDE . ……4分 (3)∵∠CDE=27°,∴由(2),得∠DOC=2∠CDE=54°, ∴∠BOD=180°－54°=126°.EA D C··∵OB=2,∴BD l =πππ571802126180=⨯⨯=R n . ……3分 23.(本题10分) 解:(1)∵110a =＞0,∴抛物线顶点为最低点.∵y =110x 2－45x ＋3=110( x －4)2＋75. ∴绳子最低点离地面的距离为75米. ……3分 (2)由(1)可知,BD =8.令x =0得y =3,∴A (0,3),C (8,3)由题意得:抛物线F 1的顶点坐标为(2,1.8),∴设F 1的解析式为:y =a (x －2)2＋1.8. 将(0,3)代入,得:4a ＋1.8=3,解得: a=0.3,∴抛物线F 1为: y =0.3(x －2)2＋1.8.当x =3时,y =0.3×1＋1.8=2.1,∴MN 的长度为2.1米. ……3分 (3)∵MN =CD =3,∴根据抛物线的对称性可知抛物线F 2的顶点在ND 的垂直平分线上, ∴抛物线F 2的顶点坐标为(12m ＋4,k ),∴抛物线F 2的解析式为:y =14(x －12m －4)2＋k . 把C (8,3)代入,得:14(4－12m )2＋k =3,∴k =－14(4－12m )2＋3,∴k =－116(m －8)2＋3. ∴k 是关于m 的二次函数.又∵由已知m<8,在对称轴的左侧,∴k 随m 的增大而增大. ∴当k =2时,－116(m －8)2＋3=2,解得: m 1=4, m 2=12 (不符合题意,舍去) . 当k =2.5时,－116(m －8)2＋3=2.5,解得: m 1=8－ m 2= 8＋(不符合题意,舍去). ∴m 的取值范围是4≤m ≤8－ ……4分 24.(本题12分)解:(1)∵在矩形ABCD 中,∠DCE=90°，∵F 是斜边DE 的中点,∴CF =EF ,∴∠FEC =∠FCE . 又∵∠BFC =90°,且E 为BC 的中点,∴EF =EC ,∴CF =CE . 在△BFC 与△DCE 中,∵∠BFC =∠DCE , CF =CE ,∠FCB =∠DEC , ∴△BFC ≌△DCE . ……4分 (2)设CE =a ,由BE =2CE ,得BE =2a ,BC =3a .ABCDEF∵∠FEC =∠FCE ,∠BFC =∠DCE =90°,∴△BFC ∽△DCE . ∴CF BC EC ED=,即132EDa a ED =,∴22132ED a =,∴226ED a =.∴DC .∴CD BC ==. ……4分（3）过C ′作C ′H ⊥AF 于点H ,连结CC ′交EF 于M ,由(2)得:FC =FE =FD ,∠FEC =∠FCE .∵AD ∥BC ,∴∠ADF =∠CEF ,∴∠ADF =∠BCF . ∵AD =BC ,∴△ADF ≌△BCF ,∴∠AFD =∠BFC =90°. ∵C ′H ⊥AF ,C ′C ⊥EF ,∴∠HFE =∠C ′HF =∠C ′MF =90°.∴四边形C ′MFH 是矩形,∴FM= C ′H =5102.设EM =x ,则FC =FE =x +5102. 在Rt △EMC 和Rt △FMC 中,由勾股定理得:CE 2－EM 2=CF 2－FM 2.∴2222)5102()5102(1-+=-x x ,解得:10101=x ,2102-=x (舍去) . 由(2)得,CF BCEC ED=,将CE=1,BE=n 代入计算,得CF =222+n . ∴51021010222+=+n ,解得:4=n . ……4分E。

2016浙江(杭州、金华、丽水、绍兴、台州、温州市)中考试题集合

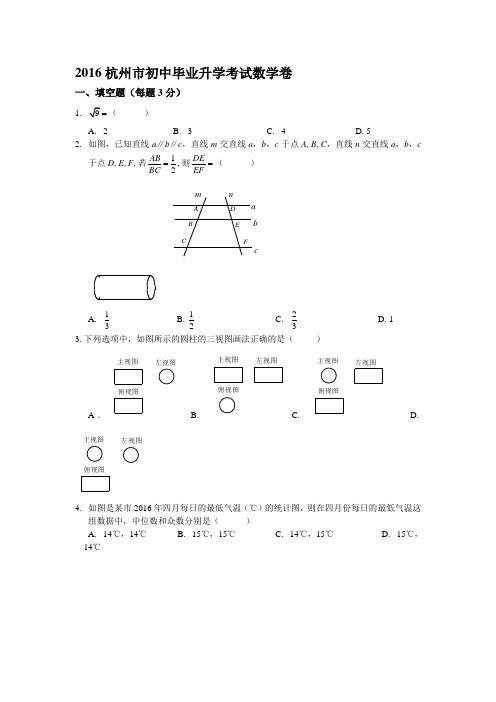
2016杭州市初中毕业升学考试数学卷一、填空题（每题3分）1（）A. 2B. 3C. 4D.52. 如图，已知直线a∥b∥c，直线m交直线a，b，c于点A,B,C，直线n交直线a，b，c于点D,E,F,若12ABBC=,则DEEF=（）FEDCBAcbanmA. 13B.12C.23D.13.下列选项中，如图所示的圆柱的三视图画法正确的是（）A．俯视图左视图主视图B.俯视图左视图主视图C.主视图左视图俯视图D.主视图左视图俯视图4. 如图是某市2016年四月每日的最低气温（℃）的统计图，则在四月份每日的最低气温这组数据中，中位数和众数分别是（）A. 14℃，14℃B. 15℃，15℃C. 14℃，15℃D. 15℃，14℃5. 下列各式变形中，正确的是（） A . 236x x x = B . x = C .211x x x x⎛⎫-÷=- ⎪⎝⎭D .2211124x x x ⎛⎫-+=-+ ⎪⎝⎭6. 已知甲煤场有煤518吨，乙煤场有煤106吨，为了使甲煤场存煤是乙煤场的2倍，需要从甲煤场运煤到乙煤场，设从甲煤场运煤x 吨到乙煤场，则可列方程为（）A . ()5182106x =+B .5182106x -=⨯C . ()5182106x x -=+D .()5182106x x +=-7. 设函数(0,0)ky k x x=≠>的图像如图所示，若1z y =，则z 关于x 的函数图像可能为（）A. B. C. D.8. 如图，已知AC 是O 的直径，点B 在圆周上（不与A 、C 重合），点D 在AC 的延长线上，连接BD 交O 于点E ,若∠AOB =3∠ADB ,则（）DA(第7题图) （第8题图）（第12题图）A . DE EB =B .EB =C .DO =D .DE OB =9. 已知直角三角形纸片的两条直角边分别为m 和n （m n <），过锐角三角形顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形，则（） A .2220m mn n ++= B .2220m mn n -+= C .2220m mn n +-= D .2220m mn n --= 10. 设a ，b 是实数，定义@的一种运算如下：()()22@a b a b a b =+--则下列结论： ①若@0a b =，则0a =或0b = ②()@@@a b c a b a c +=+ ③不存在实数a ，b ，满足 ④设a ，b 是矩形的长和宽，若矩形的周长固定，则当a =b 时, @a b 最大.其中正确的是 .A .②③④B .①③④C . ①②④D . ①②③二、填空题（每题4分）11. tan 60︒= .12. 已知一包糖果共有5种颜色（糖果只有颜色差别），如图是这包糖果分布百分比的统计图，在这包糖果中任意取一粒，则取出糖果的颜色为绿色或棕色的概率是 .13. 若整式22x ky +（k 为不等于零的常数）能在有理数范围内因式分解，则K 的值可以是（写出一个即可）.14. 在菱形ABCD 中，∠A =30°，在同一平面内，以对角线BD 为底边作顶角为120°的等腰三角形BDE ,则∠EBC 的度数为 15. 在平面直角坐标系中，已知A (2，3),B （0,1），C （3,1），若线段AC 与BD 互相平分，则点D 关于坐标原点的对称点的坐标为 .16. 已知关于x 的方程2m x =的解满足()30325x y n n x y n -=-⎧<<⎨+=⎩，若1y >，则m 的取值范围是 .三、解答题17.（6分）计算11623⎛⎫÷-+ ⎪⎝⎭，方方同学的计算过程如下，原式=1166121823⎛⎫÷-+÷=-+ ⎪⎝⎭=6.请你判断方方的计算过程是否正确，若不正确，请你写出正确的计算过程.18.(8分)某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量（辆）百分比的统计图如图所示.根据统计图回答下列问题：（1）若第一季度的汽车销售量为2120辆，求该季的汽车产量; (2)圆圆同学说：“因为第二，第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%，所以第二季度的汽车产量一定高于第三季度的汽车产量”，你觉得圆圆说的对吗？为什么？19.（8分）如图，在△ABC 中，点D ，E 分别在边AB ，AC 上，∠AED =∠B ，射线AG 分别交线段DE ，BC 于点F ，G ，且AD DFAC CG=. （1）求证：△ADF ∽△ACG ；（2）若12AD AC =,求AFFG的值. GFE DCBA20.(10分)把一个足球垂直水平地面向上踢，时间为t （秒）是该足球距离地面的高度h （米）适用公式()22004h t t t =-≤≤.(1)当t =3时,求足球距离地面的高度；（2）当足球距离地面的高度为10米时，求t .(3)若存在实数1212,()t t t t ≠当t =1t 或2t 时，足球距离地面的高度都为m （米），求m 的取值范围.21.(10分)如图，已知四边形ABCD 和四边形DEFG 为正方形，点E 在线段DE 上，点A ,D ,G在同一直线上，且AD =3，DE =1，连接AC ，CG ,AE ，并延长AE 交CG 于点H . (1) 求sin EAC ∠的值. (2)求线段AH 的长.H G FEDCBA22.(12分)已知函数()212,0y ax bx y ax b ab =+=+≠.在同一平面直角坐标系中. （1）若函数1y 的图像过点（-1,0），函数2y 的图像过点（1,2），求a ，b 的值. (2)若函数2y 的图像经过1y 的顶点.①求证：20a b +=；②当312x <<时，比较1y ,2y 的大小.23.(12分)在线段AB 的同侧作射线AM 和BN ，若∠MAB 与∠NBA 的平分线分别交射线BN ，AM 于点E ，F ,AE 和BF 交于点P .如图，点点同学发现当射线AM ,BN 交于点C ；且∠ACB =60°时，有一下两个结论：①∠APB =120°；②AF +BE =AB .那么，当AM 平行BN 时：（1）点点发现的结论还成立吗？若成立，请给与证明，若不成立，请求出∠APB 的度数，写出AF ，BE ，AB 长度之间的等量关系，并给与证明；（2）设点Q 为线段AE 上一点，QB =5，若AF +BE =16，四边形ABEF 的面积为，求AQ 的长.PFE MNCB A2016年浙江省丽水市中考数学试卷一、选择题：每小题3分，共30分 1．（3分）（2016•丽水）下列四个数中，与﹣2的和为0的数是（） A ．﹣2 B ．2 C ．0 D ．﹣ 2．（3分）（2016•丽水）计算32×3﹣1的结果是（） A ．3 B ．﹣3 C ．2 D ．﹣2 3．（3分）（2016•丽水）下列图形中，属于立体图形的是（）A ．B ．C ．D ．4．（3分）（2016•丽水）+的运算结果正确的是（） A ．B ．C ．D ．a+b5．（3分）（2016•丽水）某校对全体学生开展心理健康知识测试，七、八、九三个年级共有A ．七年级的合格率最高B ．八年级的学生人数为262名C ．八年级的合格率高于全校的合格率D ．九年级的合格人数最少 6．（3分）（2016•丽水）下列一元二次方程没有实数根的是（）A ．x 2+2x+1=0 B ．x 2+x+2=0 C ．x 2﹣1=0 D ．x 2﹣2x ﹣1=0 7．（3分）（2016•丽水）如图，▱ABCD 的对角线AC ，BD 交于点O ，已知AD=8，BD=12，AC=6，则△OBC 的周长为（）A．13 B．17 C．20 D．268．（3分）（2016•丽水）在直角坐标系中，点M，N在同一个正比例函数图象上的是（）A．M（2，﹣3），N（﹣4，6）B．M（﹣2，3），N（4，6）C．M（﹣2，﹣3），N（4，﹣6）D．M（2，3），N（﹣4，6）9．（3分）（2016•丽水）用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（）A．B．C．D．10．（3分）（2016•丽水）如图，已知⊙O是等腰Rt△ABC的外接圆，点D是上一点，BD交AC于点E，若BC=4，AD=，则AE的长是（）A．3 B．2 C．1 D．1.2二、填空题：每小题4分，共24分11．（4分）（2016•丽水）分解因式：am﹣3a=．12．（4分）（2016•丽水）如图，在△ABC中，∠A=63°，直线MN∥BC，且分别与AB，AC相交于点D，E，若∠AEN=133°，则∠B的度数为．13．（4分）（2016•丽水）箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是．14．（4分）（2016•丽水）已知x2+2x﹣1=0，则3x2+6x﹣2=．15．（4分）（2016•丽水）如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为点E，F，延长BD至G，使得DG=BD，连结EG，FG，若AE=DE，则=．16．（4分）（2016•丽水）如图，一次函数y=﹣x+b与反比例函数y=（x＞0）的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连结OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m．（1）b=（用含m的代数式表示）；（2）若S△OAF+S四边形EFBC=4，则m的值是．三、解答题17．（6分）（2016•丽水）计算：（﹣3）0﹣|﹣|+．18．（6分）（2016•丽水）解不等式：3x﹣5＜2（2+3x）19．（6分）（2016•丽水）数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含45°的三角板的斜边与含30°的三角板的长直角边相等，于是，小陆同学提出一个问题：如图，将一副三角板直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC=2，求AF的长．请你运用所学的数学知识解决这个问题．20．（8分）（2016•丽水）为了帮助九年级学生做好体育考试项目的选考工作，某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩，并绘制成如图两个统计图，请结合统计图信息解决问题．（1）“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍，求“跳绳”项目的女生人数；（2）若一个考试项目的男、女生总平均成绩不小于9分为“优秀”，试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目，并说明理由；（3）请结合统计图信息和实际情况，给该校九年级学生体育考试项目的选择提出合理化建议．21．（8分）（2016•丽水）2016年3月27日“丽水半程马拉松竞赛”在莲都举行，某运动员从起点万地广场西门出发，途经紫金大桥，沿比赛路线跑回中点万地广场西门．设该运动员离开起点的路程S（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，根据图象提供的信息，解答下列问题：（1）求图中a的值；（2）组委会在距离起点2.1千米处设立一个拍摄点C，该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟．①求AB所在直线的函数解析式；②该运动员跑完赛程用时多少分钟？22．（10分）（2016•丽水）如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD，BC的延长线相交于点E．（1）求证：AD是半圆O的切线；（2）连结CD，求证：∠A=2∠CDE；（3）若∠CDE=27°，OB=2，求的长．23．（10分）（2016•丽水）如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y=x2﹣x+3的绳子．（1）求绳子最低点离地面的距离；（2）因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F1的最低点距MN为1米，离地面1.8米，求MN的长；（3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为，设MN离AB的距离为m，抛物线F2的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．24．（12分）（2016•丽水）如图，矩形ABCD中，点E为BC上一点，F为DE的中点，且∠BFC=90°．（1）当E为BC中点时，求证：△BCF≌△DEC；（2）当BE=2EC时，求的值；（3）设CE=1，BE=n，作点C关于DE的对称点C′，连结FC′，AF，若点C′到AF的距离是，求n的值．2016年浙江省金华市中考数学试卷一、选择题（本题有10小题，每小题3分，共30分）1．（3分）（2016•金华）实数﹣的绝对值是（）A．2 B．C．﹣D．﹣2．（3分）（2016•金华）若实数a，b在数轴上的位置如图所示，则下列判断错误的是（）A．a＜0 B．ab＜0 C．a＜b D．a，b互为倒数3．（3分）（2016•金华）如图是加工零件的尺寸要求，现有下列直径尺寸的产品（单位：mm），其中不合格的是（）A．Φ45.02B．Φ44.9C．Φ44.98D．Φ45.014．（3分）（2016•金华）从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体，得到的几何体如图所示，则该几何体的左视图正确的是（）A．B．C．D．5．（3分）（2016•金华）一元二次方程x2﹣3x﹣2=0的两根为x1，x2，则下列结论正确的是（）A．x1=﹣1，x2=2 B．x1=1，x2=﹣2 C．x1+x2=3 D．x1x2=26．（3分）（2016•金华）如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD 的是（）A．AC=BD B．∠CAB=∠DBA C．∠C=∠D D．BC=AD7．（3分）（2016•金华）小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为（）A．B．C．D．8．（3分）（2016•金华）一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，BA与CA的夹角为θ．现要在楼梯上铺一条地毯，已知CA=4米，楼梯宽度1米，则地毯的面积至少需要（）A．米2B．米2C．（4+）米2D．（4+4tanθ）米29．（3分）（2016•金华）足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在（）A．点C B．点D或点EC．线段DE（异于端点）上一点D．线段CD（异于端点）上一点10．（3分）（2016•金华）在四边形ABCD中，∠B=90°，AC=4，AB∥CD，DH垂直平分AC，点H为垂足．设AB=x，AD=y，则y关于x的函数关系用图象大致可以表示为（）A．B．C．D．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）（2016•金华）不等式3x+1＜﹣2的解集是．12．（4分）（2016•金华）能够说明“=x不成立”的x的值是（写出一个即可）．13．（4分）（2016•金华）为监测某河道水质，进行了6次水质检测，绘制了如图的氨氮含量的折线统计图．若这6次水质检测氨氮含量平均数为1.5mg/L，则第3次检测得到的氨氮含量是mg/L．14．（4分）（2016•金华）如图，已知AB∥CD，BC∥DE．若∠A=20°，∠C=120°，则∠AED 的度数是．15．（4分）（2016•金华）如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是．16．（4分）（2016•金华）由6根钢管首尾顺次铰接而成六边形钢架ABCDEF，相邻两钢管可以转动．已知各钢管的长度为AB=DE=1米，BC=CD=EF=FA=2米．（铰接点长度忽略不计）（1）转动钢管得到三角形钢架，如图1，则点A，E之间的距离是米．（2）转动钢管得到如图2所示的六边形钢架，有∠A=∠B=∠C=∠D=120°，现用三根钢条连接顶点使该钢架不能活动，则所用三根钢条总长度的最小值是米．三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）17．（6分）（2016•金华）计算：﹣（﹣1）2016﹣3tan60°+（﹣2016）0．18．（6分）（2016•金华）解方程组．19．（6分）（2016•金华）某校组织学生排球垫球训练，训练前后，对每个学生进行考核．现随机抽取部分学生，统计了训练前后两次考核成绩，并按“A，B，C”三个等次绘制了如图不完整的统计图．试根据统计图信息，解答下列问题：（1）抽取的学生中，训练后“A”等次的人数是多少？并补全统计图．（2）若学校有600名学生，请估计该校训练后成绩为“A”等次的人数．20．（8分）（2016•金华）如图1表示同一时刻的韩国首尔时间和北京时间，两地时差为整数．（1）设北京时间为x（时），首尔时间为y（时），就0≤x≤12，求y关于x的函数表达式，（2）如图2表示同一时刻的英国伦敦时间（夏时制）和北京时间，两地时差为整数．如果现在伦敦（夏时制）时间为7：30，那么此时韩国首尔时间是多少？21．（8分）（2016•金华）如图，直线y=x﹣与x，y轴分别交于点A，B，与反比例函数y=（k＞0）图象交于点C，D，过点A作x轴的垂线交该反比例函数图象于点E．（1）求点A的坐标．（2）若AE=AC．①求k的值．②试判断点E与点D是否关于原点O成中心对称？并说明理由．22．（10分）（2016•金华）四边形ABCD的对角线交于点E，有AE=EC，BE=ED，以AB 为直径的半圆过点E，圆心为O．（1）利用图1，求证：四边形ABCD是菱形．（2）如图2，若CD的延长线与半圆相切于点F，已知直径AB=8．①连结OE，求△OBE的面积．②求弧AE的长．23．（10分）（2016•金华）在平面直角坐标系中，点O为原点，平行于x轴的直线与抛物线L：y=ax2相交于A，B两点（点B在第一象限），点D在AB的延长线上．（1）已知a=1，点B的纵坐标为2．①如图1，向右平移抛物线L使该抛物线过点B，与AB的延长线交于点C，求AC的长．②如图2，若BD=AB，过点B，D的抛物线L2，其顶点M在x轴上，求该抛物线的函数表达式．（2）如图3，若BD=AB，过O，B，D三点的抛物线L3，顶点为P，对应函数的二次项系数为a3，过点P作PE∥x轴，交抛物线L于E，F两点，求的值，并直接写出的值．24．（12分）（2016•金华）在平面直角坐标系中，点O为原点，点A的坐标为（﹣6，0）．如图1，正方形OBCD的顶点B在x轴的负半轴上，点C在第二象限．现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG．（1）如图2，若α=60°，OE=OA，求直线EF的函数表达式．（2）若α为锐角，tanα=，当AE取得最小值时，求正方形OEFG的面积．（3）当正方形OEFG的顶点F落在y轴上时，直线AE与直线FG相交于点P，△OEP的其中两边之比能否为：1？若能，求点P的坐标；若不能，试说明理由。

浙江省丽水市中考数学真题试题(带解析)

丽水市中考数学试题解析卷一、选择题(共10小题，每小题3分，满分30分)1．(•丽水)如果零上2℃记作＋2℃，那么零下3℃记作( )A．－3℃B．－2℃C．＋3℃D．＋2℃考点：正数和负数。

专题：计算题。

分析：一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．解答：解：“正”和“负”相对，∴如果零上2℃记作＋2℃，那么零下3℃记作－3℃，故选A．点评：此题考查了正数和负数，解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．2．(•丽水)计算3a•(2b)的结果是( )A．3ab B．6a C．6ab D．5ab考点：单项式乘单项式。

分析：根据单项式与单项式相乘，把他们的系数分别相乘，相同字母的幂分别相加，其余字母连同他的指数不变，作为积的因式，计算即可．解答：解：3a•(2b)＝3×2a•b＝6ab．故选C．点评：本题考查了单项式与单项式相乘，熟练掌握运算法则是解题的关键．3．(•丽水)如图，数轴的单位长度为1，如果点A，B表示的数的绝对值相等，那么点A表示的数是( ) A．－4 B．－2 C．0 D．4考点：绝对值；数轴。

专题：计算题。

分析：如果点A，B表示的数的绝对值相等，那么AB的中点即为坐标原点．解答：解：如图，AC的中点即数轴的原点O．根据数轴可以得到点A表示的数是－2．故选B．点评：此题考查了数轴有关内容，用几何方法借助数轴来求解，非常直观，体现了数形结合的优点．确定数轴的原点是解决本题的关键．4．(•丽水)把分式方程转化为一元一次方程时，方程两边需同乘以( )A．x B．2x C．x＋4 D．x(x＋4)考点：解分式方程。

分析：根据各分母寻找公分母x(x＋4)，方程两边乘最简公分母，可以把分式方程转化为整式方程．解答：解：由两个分母(x＋4)和x可得最简公分母为x(x＋4)，所以方程两边应同时乘以x(x＋4)．故选D．点评：本题考查解分式方程去分母的能力，确定最简公分母应根据所给分式的分母来决定．5．(•丽水)在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是( )A．①B．②C．③D．④考点：利用旋转设计图案。

浙江省丽水市中考数学真题及答案

浙江省丽水市中考数学真题及答案（满分为120分,考试时间为120分钟）卷 Ⅰ一、选择题（本题有10小题,每小题3分,共30分） 1．实数3的相反数是( )A ．3-B ．3C ．13-D ．132．分式52x x +-的值是零,则x 的值为( ) A ．2 B ．5 C ．2- D ．5-3．下列多项式中,能运用平方差公式分解因式的是( ) A ．22a b + B ．22a b - C ．22a b - D ．22a b -- 4．下列四个图形中,是中心对称图形的是( )A ．B ．C ．D ．5．如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )A ．12 B ．13 C ．23 D ．166．如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b ,得到//a b ．理由是( )A ．连结直线外一点与直线上各点的所有线段中,垂线段最短B ．在同一平面内,垂直于同一条直线的两条直线互相平行C ．在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D ．经过直线外一点,有且只有一条直线与这条直线平行7．已知点(2-,)(2a ,)(3b ,)c 在函数(0)ky k x=>的图象上,则下列判断正确的是( )A ．a b c <<B ．b a c <<C ．a c b <<D ．c b a <<8．如图,O 是等边ABC ∆的内切圆,分别切AB ,BC ,AC 于点E ,F ,D ,P 是DF 上一点,则EPF ∠的度数是( )A ．65︒B ．60︒C ．58︒D ．50︒9．如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x ．则列出方程正确的是( )A ．3252x x ⨯+=B ．3205102x x ⨯+=⨯C ．320520x x ⨯++=D ．3(20)5102x x ⨯++=+10．如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH ．连结EG ,BD 相交于点O 、BD 与HC 相交于点P ．若GO GP =,则ABCD EFGHS S 正方形正方形的值是( )A．1+．2．5- D ．154卷 Ⅱ二、填空题（本题有6小题,每小题4分,共24分）11．点(,2)P m 在第二象限内,则m 的值可以是（写出一个即可）．12．数据1,2,4,5,3的中位数是．13．如图为一个长方体,则该几何体主视图的面积为2cm．14．如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是︒．15．如图是小明画的卡通图形,每个正六边形的边长都相等,相邻两正六边形的边重合,点A, B,C均为正六边形的顶点,AB与地面BC所成的锐角为β．则tanβ的值是．16．图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD（点A与点B重合）,点O是夹子转轴位置,OE ACOE OF cm==,⊥于点F,1⊥于点E,OF BD=,:2:3==,CE DFCE AE=．按图示方式用手指按夹子,夹子两边绕点O转AC BD cm6动．（1）当E,F两点的距离最大时,以点A,B,C,D为顶点的四边形的周长是cm．（2）当夹子的开口最大（即点C与点D重合）时,A,B两点的距离为cm．三、解答题（本题有8小题,共66分,各小题都必须写出解答过程）17．（6分）计算：0(2020)4tan 45|3|-+-︒+-． 18．（6分）解不等式：552(2)x x -<+．19．（6分）某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查（每人必须且只选其中一项）,得到如图两幅不完整的统计图表．请根据图表信息回答下列问题：抽取的学生最喜爱体育锻炼项目的统计表（1）求参与问卷调查的学生总人数．（2）在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人？（3）该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数． 20．（8分）如图,AB 的半径2OA =,OC AB ⊥于点C ,60AOC ∠=︒．（1）求弦AB 的长．（2）求AB 的长．21．（8分）某地区山峰的高度每增加1百米,气温大约降低0.6C ︒,气温(C)T ︒和高度h （百米）的函数关系如图所示．类别项目人数（人)A 跳绳 59B 健身操 ▲C 俯卧撑 31D 开合跳 ▲E 其它22请根据图象解决下列问题：（1）求高度为5百米时的气温；（2）求T 关于h 的函数表达式；（3）测得山顶的气温为6C ︒,求该山峰的高度．22．（10分）如图,在ABC ∆中,AB =45B ∠=︒,60C ∠=︒．（1）求BC 边上的高线长．（2）点E 为线段AB 的中点,点F 在边AC 上,连结EF ,沿EF 将AEF ∆折叠得到PEF ∆． ①如图2,当点P 落在BC 上时,求AEP ∠的度数． ②如图3,连结AP ,当PF AC ⊥时,求AP 的长．23．（10分）如图,在平面直角坐标系中,已知二次函数21()42y x m =--+图象的顶点为A ,与y 轴交于点B ,异于顶点A 的点(1,)C n 在该函数图象上．（1）当5m =时,求n 的值．（2）当2n =时,若点A 在第一象限内,结合图象,求当2y 时,自变量x 的取值范围．（3）作直线AC 与y 轴相交于点D ．当点B 在x 轴上方,且在线段OD 上时,求m 的取值范围．24．（12分）如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F,已知8OB=．（1）求证：四边形AEFD为菱形．（2）求四边形AEFD的面积．（3）若点P在x轴正半轴上（异于点)D,点Q在y轴上,平面内是否存在点G,使得以点A, P,Q,G为顶点的四边形与四边形AEFD相似？若存在,求点P的坐标；若不存在,试说明理由．答案与解析卷Ⅰ一、选择题（本题有10小题,每小题3分,共30分）1．实数3的相反数是()A．3- B．3 C．13- D．13【知识考点】相反数；实数的性质【思路分析】直接利用相反数的定义分析得出答案．【解题过程】解：实数3的相反数是：3-．故选：A．【总结归纳】此题主要考查了实数的性质,正确掌握相反数的定义是解题关键．2．分式52xx+-的值是零,则x的值为()A．2 B．5 C．2- D．5-【知识考点】分式的值为零的条件【思路分析】利用分式值为零的条件可得50x+=,且20x-≠,再解即可．【解题过程】解：由题意得：50x+=,且20x-≠,解得：5x=-,故选：D．【总结归纳】此题主要考查了分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零．注意：“分母不为零”这个条件不能少． 3．下列多项式中,能运用平方差公式分解因式的是( ) A ．22a b + B ．22a b - C ．22a b - D ．22a b -- 【知识考点】因式分解-运用公式法【思路分析】根据能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反进行分析即可．【解题过程】解：A 、22a b +不能运用平方差公式分解,故此选项错误；B 、22a b -不能运用平方差公式分解,故此选项错误；C 、22a b -能运用平方差公式分解,故此选项正确；D 、22a b --不能运用平方差公式分解,故此选项错误；故选：C ．【总结归纳】此题考查了平方差公式,熟练掌握平方差公式是解本题的关键． 4．下列四个图形中,是中心对称图形的是( )A ．B ．C ．D ．【知识考点】中心对称图形【思路分析】根据中心对称图形的概念对各图形分析判断即可得解．【解题过程】解：A 、该图形不是中心对称图形,故本选项不合题意；B 、该图形不是中心对称图形,故本选项不合题意；C 、该图形是中心对称图形,故本选项符合题意；D 、该图形不是中心对称图形,故本选项不合题意；故选：C ．【总结归纳】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合．5．如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )A ．12 B ．13 C ．23 D ．16【知识考点】概率公式【思路分析】根据概率公式直接求解即可．【解题过程】解：共有6张卡片,其中写有1号的有3张,∴从中任意摸出一张,摸到1号卡片的概率是3162=；故选：A ．【总结归纳】此题考查了概率的求法,用到的知识点为：可能性等于所求情况数与总情况数之比．6．如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b ,得到//a b ．理由是( )A ．连结直线外一点与直线上各点的所有线段中,垂线段最短B ．在同一平面内,垂直于同一条直线的两条直线互相平行C ．在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D ．经过直线外一点,有且只有一条直线与这条直线平行【知识考点】平行公理及推论；平行线的判定与性质【思路分析】根据垂直于同一条直线的两条直线平行判断即可．【解题过程】解：由题意a AB ⊥,b AB ⊥, //a b ∴（垂直于同一条直线的两条直线平行）,故选：B ．【总结归纳】本题考查平行线的判定,平行公理等知识,解题的关键是理解题意,灵活运用所学知识解决问题．7．已知点(2-,)(2a ,)(3b ,)c 在函数(0)ky k x=>的图象上,则下列判断正确的是( )A ．a b c <<B ．b a c <<C ．a c b <<D ．c b a << 【知识考点】反比例函数图象上点的坐标特征【思路分析】根据反比例函数的性质得到函数(0)ky k x=>的图象分布在第一、三象限,在每一象限,y 随x 的增大而减小,则0b c >>,0a <．【解题过程】解：0k >,∴函数(0)ky k x=>的图象分布在第一、三象限,在每一象限,y 随x 的增大而减小, 2023-<<<, 0b c ∴>>,0a <,a cb ∴<<．故选：C ．【总结归纳】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数的性质是解题的关键．8．如图,O 是等边ABC ∆的内切圆,分别切AB ,BC ,AC 于点E ,F ,D ,P 是DF 上一点,则EPF ∠的度数是( )A ．65︒B ．60︒C ．58︒D ．50︒【知识考点】三角形的内切圆与内心；圆周角定理；等边三角形的性质；切线的性质【思路分析】如图,连接OE ,OF ．求出EOF ∠的度数即可解决问题．【解题过程】解：如图,连接OE ,OF ．O 是ABC ∆的内切圆,E ,F 是切点, OE AB ∴⊥,OF BC ⊥,90OEB OFB ∴∠=∠=︒, ABC ∆是等边三角形,60B ∴∠=︒, 120EOF ∴∠=︒,1602EPF EOF ∴∠=∠=︒,故选：B ．【总结归纳】本题考查三角形的内切圆与内心,切线的性质,圆周角定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型．9．如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x ．则列出方程正确的是( )A ．3252x x ⨯+=B ．3205102x x ⨯+=⨯C ．320520x x ⨯++=D ．3(20)5102x x ⨯++=+【知识考点】由实际问题抽象出一元一次方程【思路分析】直接利用表示十位数的方法进而得出等式即可．【解题过程】解：设“□”内数字为x ,根据题意可得： 3(20)5102x x ⨯++=+．故选：D ．【总结归纳】此题主要考查了由实际问题抽象出一元一次方程,正确表示十位数是解题关键． 10．如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH ．连结EG ,BD 相交于点O 、BD 与HC 相交于点P ．若GO GP =,则ABCD EFGHS S 正方形正方形的值是( )A．1+．2．5- D ．154【知识考点】勾股定理的证明【思路分析】证明()BPG BCG ASA ∆≅∆,得出PG CG =．设OG PG CG x ===,则2EG x =,FG =,由勾股定理得出22(4BC x =+,则可得出答案．【解题过程】解：四边形EFGH 为正方形, 45EGH ∴∠=︒,90FGH ∠=︒, OG GP =,67.5GOP OPG ∴∠=∠=︒, 22.5PBG ∴∠=︒,又45DBC ∠=︒, 22.5GBC ∴∠=︒, PBG GBC ∴∠=∠,90BGP BG ∠=∠=︒,BG BG =,()BPG BCG ASA ∴∆≅∆,PG CG ∴=．设OG PG CG x ===, O 为EG ,BD 的交点,2EG x ∴=,FG =,四个全等的直角三角形拼成“赵爽弦图”, BF CG x ∴==, BG x ∴=,22222221)(4BC BG CG x x x ∴=+=+=+,∴(22422ABCD EFGHx S S x+==+正方形正方形．故选：B ．【总结归纳】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,直角三角形的性质等知识,熟练掌握勾股定理的应用是解题的关键．卷 Ⅱ说明：本卷共有2大题,14小题,共90分。

中考丽水数学试题及答案

中考丽水数学试题及答案一、选择题（每题3分，共30分）1. 若a、b、c是三角形的三边长，且a^2 + b^2 = c^2，则该三角形是直角三角形。

A. 正确B. 错误答案：A2. 函数y = 2x + 3的图象经过第一、二、三象限。

A. 正确B. 错误答案：A3. 已知x = 2是方程x^2 - 5x + 6 = 0的解，则另一个解是x = 3。

A. 正确B. 错误答案：B4. 一个数的相反数是它本身，则这个数是0。

A. 正确B. 错误答案：A5. 圆的周长与它的半径成正比例。

A. 正确B. 错误答案：A6. 一个正数的算术平方根一定大于这个数。

A. 正确B. 错误答案：B7. 一个数的立方根与它本身相等的数是±1和0。

A. 正确B. 错误答案：A8. 一组数据的平均数是5，中位数是4，众数是6，则这组数据可能的中位数是4。

A. 正确B. 错误答案：A9. 一个等腰三角形的两边长分别是3和5，则它的周长是13。

A. 正确B. 错误答案：B10. 一个多边形的内角和是外角和的3倍，则这个多边形是八边形。

A. 正确B. 错误答案：A二、填空题（每题3分，共30分）11. 已知一个等腰三角形的底边长为6，腰长为5，则其周长为16。

12. 一个数的绝对值是5，则这个数是±5。

13. 一个数的平方是25，则这个数是±5。

14. 一个数的立方是-8，则这个数是-2。

15. 一个数的倒数是2，则这个数是1/2。

16. 一个数的相反数是-3，则这个数是3。

17. 一个数的算术平方根是3，则这个数是9。

18. 一个数的立方根是2，则这个数是8。

19. 一个数的平方根是±2，则这个数是4。

20. 一个数的平方是16，则这个数是±4。

三、解答题（共40分）21. 计算：(2x^2 - 3x + 1) - (x^2 - 4x + 5) = x^2 + x - 4。

22. 解方程：2x^2 - 5x - 3 = 0，解得x1 = -1/2，x2 = 3。

浙江省丽水市 2016年中考数学真题试卷附解析

2016年浙江省丽水市中考数学试卷参考答案与试题解析一、选择题：每小题3分，共30分1．(2016·浙江丽水)下列四个数中，与﹣2的和为0的数是（）A．﹣2 B．2 C．0 D．﹣【考点】相反数．【分析】找出﹣2的相反数即为所求．【解答】解：下列四个数中，与﹣2的和为0的数是2，故选B2．(2016·浙江丽水)计算32×3﹣1的结果是（）A．3 B．﹣3 C．2 D．﹣2【考点】负整数指数幂．【分析】根据同底数幂的乘法底数不变指数相加，可得答案．【解答】解：32×3﹣1=32﹣1=3．故选：A．3．(2016·浙江丽水)下列图形中，属于立体图形的是（）A．B．C．D．【考点】认识立体图形．【分析】根据平面图形所表示的各个部分都在同一平面内，立体图形是各部分不在同一平面内的几何，由一个或多个面围成的可以存在于现实生活中的三维图形，可得答案．【解答】解：A、角是平面图形，故A错误；B、圆是平面图形，故B错误；C、圆锥是立体图形，故C正确；D、三角形是平面图形，故D错误．故选：C．4．(2016·浙江丽水)+的运算结果正确的是（）A．B．C．D．a+b【考点】分式的加减法．【分析】首先通分，把、都化成以ab为分母的分式，然后根据同分母分式加减法法则，求出+的运算结果正确的是哪个即可．【解答】解：+=+=故+的运算结果正确的是．故选：C．5．(2016·浙江丽水)某校对全体学生开展心理健康知识测试，七、八、九三个年级共有800B．八年级的学生人数为262名C．八年级的合格率高于全校的合格率D．九年级的合格人数最少【考点】统计表．【分析】分析统计表，可得出各年级合格的人数，然后结合选项进行回答即可．【解答】解：∵七、八、九年级的人数不确定，∴无法求得七、八、九年级的合格率．∴A错误、C错误．由统计表可知八年级合格人数是262人，故B错误．∵270＞262＞254，∴九年级合格人数最少．故D正确．故选；D．6．(2016·浙江丽水)下列一元二次方程没有实数根的是（）A．x2+2x+1=0 B．x2+x+2=0 C．x2﹣1=0 D．x2﹣2x﹣1=0【考点】根的判别式．【分析】求出每个方程的根的判别式，然后根据判别式的正负情况即可作出判断．【解答】解：A、△=22﹣4×1×1=0，方程有两个相等实数根，此选项错误；B、△=12﹣4×1×2=﹣7＜0，方程没有实数根，此选项正确；C、△=0﹣4×1×（﹣1）=4＞0，方程有两个不等的实数根，此选项错误；D、△=（﹣2）2﹣4×1×（﹣1）=8＞0，方程有两个不等的实数根，此选项错误；故选：B．7．(2016·浙江丽水)如图，▱ABCD的对角线AC，BD交于点O，已知AD=8，BD=12，AC=6，则△OBC的周长为（）A．13 B．17 C．20 D．26【考点】平行四边形的性质．【分析】由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．【解答】解：∵四边形ABCD是平行四边形，∴OA=OC=3，OB=OD=6，BC=AD=8，∴△OBC的周长=OB+OC+AD=3+6+8=17．故选：B．8．(2016·浙江丽水)在直角坐标系中，点M，N在同一个正比例函数图象上的是（）A．M（2，﹣3），N（﹣4，6） B．M（﹣2，3），N（4，6）C．M（﹣2，﹣3），N（4，﹣6）D．M（2，3），N（﹣4，6）【考点】一次函数图象上点的坐标特征．【分析】设正比例函数的解析式为y=kx，根据4个选项中得点M的坐标求出k的值，再代入N点的坐标去验证点N是否在正比例函数图象上，由此即可得出结论．【解答】解：设正比例函数的解析式为y=kx，A、﹣3=2k，解得：k=﹣，﹣4×（﹣）=6，6=6，∴点N在正比例函数y=﹣x的图象上；B、3=﹣2k，解得：k=﹣，4×（﹣）=﹣6，﹣6≠6，∴点N不在正比例函数y=﹣x的图象上；C、﹣3=﹣2k，解得：k=，4×=6，6≠﹣6，∴点N不在正比例函数y=x的图象上；D、3=2k，解得：k=，﹣4×=﹣6，﹣6≠6，∴点N不在正比例函数y=x的图象上．故选A．9．(2016·浙江丽水)用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（）A．B．C．D．【考点】作图—复杂作图．【分析】根据过直线外一点作已知直线的垂线作图即可求解．【解答】解：A、根据垂径定理作图的方法可知，CD是Rt△ABC斜边AB上的高线，不符合题意；B、根据直径所对的圆周角是直角的方法可知，CD是Rt△ABC斜边AB上的高线，不符合题意；C、根据相交两圆的公共弦的性质可知，CD是Rt△ABC斜边AB上的高线，不符合题意；D、无法证明CD是Rt△ABC斜边AB上的高线，符合题意．故选：D．10．(2016·浙江丽水)如图，已知⊙O是等腰Rt△ABC的外接圆，点D是上一点，BD交AC于点E，若BC=4，AD=，则AE的长是（）A．3 B．2 C．1 D．1.2【考点】三角形的外接圆与外心．【分析】利用圆周角性质和等腰三角形性质，确定AB为圆的直径，利用相似三角形的判定及性质，确定△ADE和△BCE边长之间的关系，利用相似比求出线段AE的长度即可．【解答】解：∵等腰Rt△ABC，BC=4，∴AB为⊙O的直径，AC=4，AB=4，∴∠D=90°，在Rt△ABD中，AD=，AB=4，∴BD=，∵∠D=∠C，∠DAC=∠CBE，∴△ADE∽△BCE，∵AD：BC=：4=1：5，∴相似比为1：5，设AE=x，∴BE=5x，∴DE=﹣5x，∴CE=28﹣25x，∵AC=4，∴x+28﹣25x=4，解得：x=1．故选：C．二、填空题：每小题4分，共24分11．(2016·浙江丽水)分解因式：am﹣3a=a（m﹣3）．【考点】因式分解-提公因式法．【分析】根据提公因式法的一般步骤进行因式分解即可．【解答】解：am﹣3a=a（m﹣3）．故答案为：a（m﹣3）．12．(2016·浙江丽水)如图，在△ABC中，∠A=63°，直线MN∥BC，且分别与AB，AC相交于点D，E，若∠AEN=133°，则∠B的度数为70°．【考点】相似三角形的判定与性质；平行线的性质．【分析】根据平行线的性质只要求出∠ADE，由∠AEN=∠A+∠ADE计算即可．【解答】解：∵∠AEN=∠A+∠ADE，∠AEN=133°，∠A=63°，∴∠ADE=70°，∵MN∥BC，∴∠B=∠ADE=70°，故答案为70°．13．(2016·浙江丽水)箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是．【考点】列表法与树状图法．【分析】根据题意可以列出相应的树状图，从而可以得到恰好为1个黑球和1个红球的概率．【解答】解：由题意可得，故恰好为1个黑球和1个红球的概率是：，故答案为；．14．(2016·浙江丽水)已知x2+2x﹣1=0，则3x2+6x﹣2=1．【考点】代数式求值．【分析】直接利用已知得出x2+2x=1，再代入原式求出答案．【解答】解：∵x2+2x﹣1=0，∴x2+2x=1，∴3x2+6x﹣2=3（x2﹣2x）﹣2=3×1﹣2=1．故答案为：1．15．(2016·浙江丽水)如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为点E，F，延长BD至G，使得DG=BD，连结EG，FG，若AE=DE，则=．【考点】菱形的性质．【分析】连接AC、EF，根据菱形的对角线互相垂直平分可得AC⊥BD，根据线段垂直平分线上的点到线段两端点的距离相等可得AB=BD，然后判断出△ABD是等边三角形，再根据等边三角形的三个角都是60°求出∠ADB=60°，设EF与BD相交于点H，AB=4x，然后根据三角形的中位线平行于第三边并且等于第三边的一半求出EH，再求出DH，从而得到GH，利用勾股定理列式求出EG，最后求出比值即可．【解答】解：如图，连接AC、EF，在菱形ABCD中，AC⊥BD，∵BE⊥AD，AE=DE，∴AB=BD，又∵菱形的边AB=AD，∴△ABD是等边三角形，∴∠ADB=60°，设EF与BD相交于点H，AB=4x，∵AE=DE，∴由菱形的对称性，CF=DF，∴EF是△ACD的中位线，∴DH=DO=BD=x，在Rt△EDH中，EH=DH=x，∵DG=BD，∴GH=BD+DH=4x+x=5x，在Rt△EGH中，由勾股定理得，EG===2x，所以，==．故答案为：．16．(2016·浙江丽水)如图，一次函数y=﹣x+b与反比例函数y=（x＞0）的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连结OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m．（1）b=m+（用含m的代数式表示）；=4，则m的值是．（2）若S△OAF+S四边形EFBC【考点】反比例函数与一次函数的交点问题．【分析】（1）根据待定系数法点A的纵坐标相等列出等式即可解决问题．（2）作AM⊥OD于M，BN⊥OC于N．记△AOF面积为S，则△OEF面积为2﹣S，四边形EFBN面积为4﹣S，△OBC和△OAD面积都是6﹣2S，△ADM面积为4﹣2S=2（2﹣s），所以S△ADM=2S△OEF，推出EF=AM=NB，得B（2m，）代入直线解析式即可解决问题．【解答】解：（1）∵点A在反比例函数y=（x＞0）的图象上，且点A的横坐标为m，∴点A的纵坐标为，即点A的坐标为（m，）．令一次函数y=﹣x+b中x=m，则y=﹣m+b，∴﹣m+b=即b=m+．故答案为：m+．（2）作AM⊥OD于M，BN⊥OC于N．∵反比例函数y=，一次函数y=﹣x+b都是关于直线y=x对称，∴AD=BC，OD=OC，DM=AM=BN=CN，记△AOF面积为S，则△OEF面积为2﹣S，四边形EFBN面积为4﹣S，△OBC和△OAD面积都是6﹣2S，△ADM 面积为4﹣2S=2（2﹣s），∴S△ADM=2S△OEF，∴EF=AM=NB，∴点B坐标（2m，）代入直线y=﹣x+m+，∴=﹣2m=m+，整理得到m2=2，∵m＞0，∴m=．故答案为．三、解答题17．(2016·浙江丽水)计算：（﹣3）0﹣|﹣|+．【考点】实数的运算；零指数幂．【分析】原式利用零指数幂法则，绝对值的代数意义，以及二次根式性质计算即可得到结果．【解答】解：原式=1﹣+2=1+．18．(2016·浙江丽水)解不等式：3x﹣5＜2（2+3x）【考点】解一元一次不等式．【分析】先去括号，然后移项及合并同类项，系数化为1，即可解答本题．【解答】解：3x﹣5＜2（2+3x），去括号，得3x﹣5＜4+6x，移项及合并同类项，得﹣3x＜9，系数化为1，得x＞﹣3．故原不等式组的解集是：x＞﹣3．19．(2016·浙江丽水)数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含45°的三角板的斜边与含30°的三角板的长直角边相等，于是，小陆同学提出一个问题：如图，将一副三角板直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC=2，求AF的长．请你运用所学的数学知识解决这个问题．【考点】特殊角的三角函数值．【分析】根据正切的定义求出AC，根据正弦的定义求出CF，计算即可．【解答】解：在Rt△ABC中，BC=2，∠A=30°，AC==2，则EF=AC=2，∵∠E=45°，∴FC=EF•sinE=，∴AF=AC﹣FC=2﹣．20．(2016·浙江丽水)为了帮助九年级学生做好体育考试项目的选考工作，某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩，并绘制成如图两个统计图，请结合统计图信息解决问题．（1）“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍，求“跳绳”项目的女生人数；（2）若一个考试项目的男、女生总平均成绩不小于9分为“优秀”，试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目，并说明理由；（3）请结合统计图信息和实际情况，给该校九年级学生体育考试项目的选择提出合理化建议．【考点】条形统计图；频数（率）分布折线图．【分析】（1）先根据统计图得到“掷实心球”项目男、女生总人数，除以2可求“跳绳”项目男、女生总人数，再减去“跳绳”项目男生人数，即可得到“跳绳”项目的女生人数；（2）根据平均数公式得到该县上届毕业生的考试项目中达到“优秀”的有哪些项目即可求解；（3）根据统计图提出合理化建议，合理即可．【解答】解：（1）÷2﹣260=1000÷2﹣260=500﹣260=240（人）答：“跳绳”项目的女生人数是240人；（2）“掷实心球”项目平均分：÷=÷1000=9000÷1000=9（分），投篮项目平均分大于9分，其余项目平均分小于9分．故该县上届毕业生的考试项目中达到“优秀”的有投篮，掷实心球两个项目．（3）如：游泳项目考试的人数最多，可以选考游泳．21．(2016·浙江丽水)2016年3月27日“丽水半程马拉松竞赛”在莲都举行，某运动员从起点万地广场西门出发，途经紫金大桥，沿比赛路线跑回中点万地广场西门．设该运动员离开起点的路程S（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，根据图象提供的信息，解答下列问题：（1）求图中a的值；（2）组委会在距离起点2.1千米处设立一个拍摄点C，该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟．①求AB所在直线的函数解析式；②该运动员跑完赛程用时多少分钟？【考点】一次函数综合题．【分析】（1）根据路程=速度×时间，即可解决问题．（2）①先求出A、B两点坐标即可解决问题．②令s=0，求出x的值即可解决问题．【解答】解：（1）∵从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，∴a=0.3×35=10.5千米．（2）①∵线段OA经过点O（0，0），A（35，10.5），∴直线OA解析式为y=0.3t（0≤t≤35），∴当s=2.1时，0.3t=2.1，解得t=7，∵该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟，∴该运动员从起点点到第二次经过C点所用的时间是7+68=75分钟，∴直线AB经过（35，10.5），（75，2.1），设直线AB解析式s=kt+b，∴解得，∴直线AB 解析式为s=﹣0.21t+17.85．②该运动员跑完赛程用的时间即为直线AB与x轴交点的横坐标，∴当s=0，时，﹣0.21t+17.85=0，解得t=85∴该运动员跑完赛程用时85分钟．22．(2016·浙江丽水)如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD，BC的延长线相交于点E．（1）求证：AD是半圆O的切线；（2）连结CD，求证：∠A=2∠CDE；（3）若∠CDE=27°，OB=2，求的长．【考点】切线的判定与性质；弧长的计算．【分析】（1）连接OD，BD，根据圆周角定理得到∠ABO=90°，根据等腰三角形的性质得到∠ABD=∠ADB，∠DBO=∠BDO，根据等式的性质得到∠ADO=∠ABO=90°，根据切线的判定定理即可得到即可；（2）由AD是半圆O的切线得到∠ODE=90°，于是得到∠ODC+∠CDE=90°，根据圆周角定理得到∠ODC+∠BDO=90°，等量代换得到∠DOC=2∠BDO，∠DOC=2∠CDE即可得到结论；（3）根据已知条件得到∠DOC=2∠CDE=54°，根据平角的定义得到∠BOD=180°﹣54°=126°，然后由弧长的公式即可计算出结果．【解答】（1）证明：连接OD，BD，∵AB是⊙O的直径，∴AB⊥BC，即∠ABO=90°，∵AB=AD，∴∠ABD=∠ADB，∵OB=OD，∴∠DBO=∠BDO，∴∠ABD+∠DBO=∠ADB+∠BDO，∴∠ADO=∠ABO=90°，∴AD是半圆O的切线；（2）证明：由（1）知，∠ADO=∠ABO=90°，∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD，∵AD是半圆O的切线，∴∠ODE=90°，∴∠ODC+∠CDE=90°，∵BC是⊙O的直径，∴∠ODC+∠BDO=90°，∴∠BDO=∠CDE，∵∠BDO=∠OBD，∴∠DOC=2∠BDO，∴∠DOC=2∠CDE，∴∠A=∠CDE；（3）解：∵∠CDE=27°，∴∠DOC=2∠CDE=54°，∴∠BOD=180°﹣54°=126°，∵OB=2，∴的长==π．23．(2016·浙江丽水)如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y=x2﹣x+3的绳子．（1）求绳子最低点离地面的距离；（2）因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F1的最低点距MN为1米，离地面1.8米，求MN的长；（3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为，设MN离AB的距离为m，抛物线F2的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．【考点】二次函数的应用．【分析】（1）直接利用配方法求出二次函数最值得出答案；（2）利用顶点式求出抛物线F1的解析式，进而得出x=3时，y的值，进而得出MN的长；（3）根据题意得出抛物线F2的解析式，得出k的值，进而得出m的取值范围．【解答】解：（1）∵a=＞0，∴抛物线顶点为最低点，∵y=x2﹣x+3=（x﹣4）2+，∴绳子最低点离地面的距离为：m；（2）由（1）可知，BD=8，令x=0得y=3，∴A（0，3），C（8，3），由题意可得：抛物线F1的顶点坐标为：（2，1.8），设F1的解析式为：y=a（x﹣2）2+1.8，将（0，3）代入得：4a+1.8=3，解得：a=0.3，∴抛物线F1为：y=0.3（x﹣2）2+1.8，当x=3时，y=0.3×1+1.8=2.1，∴MN的长度为：2.1m；（3）∵MN=DC=3，∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上，∴抛物线F2的顶点坐标为：（m+4，k），∴抛物线F2的解析式为：y=（x﹣m﹣4）2+k，把C（8，3）代入得：（4﹣m﹣4）2+k=3，解得：k=﹣（4﹣m）2+3，∴k=﹣（m﹣8）2+3，∴k是关于m的二次函数，又∵由已知m＜8，在对称轴的左侧，∴k随m的增大而增大，∴当k=2时，﹣（m﹣8）2+3=2，解得：m1=4，m2=12（不符合题意，舍去），当k=2.5时，﹣（m﹣8）2+3=2.5，解得：m18﹣24，m2=8+2（不符合题意，舍去），∴m的取值范围是：4≤m≤8﹣2．24．(2016·浙江丽水)如图，矩形ABCD中，点E为BC上一点，F为DE的中点，且∠BFC=90°．（1）当E为BC中点时，求证：△BCF≌△DEC；（2）当BE=2EC时，求的值；（3）设CE=1，BE=n，作点C关于DE的对称点C′，连结FC′，AF，若点C′到AF的距离是，求n的值．【考点】四边形综合题．【分析】（1）由矩形和直角三角形斜边上的中线性质得出CF=DE=EF，由等腰三角形的性质得出∠FEC=∠FCE，证出CF=CE，由ASA证明△BCF≌△DEC即可；（2）设CE=a，则BE=2a，BC=3a，证明△BCF∽△DEC，得出对应边成比例=，得出ED2=6a2，由勾股定理得出DC=a，即可得出结果；（3）过C′作C′H⊥AF于点H，连接CC′交EF于M，由直角三角形斜边上的中线性质得出∠FEC=∠FCE，证出∠ADF=∠BCF，由SAS证明△ADF≌△BCF，得出∠AFD=∠BFC=90°，证出四边形C′MFH是矩形，得出FM=C′H=，设EM=x，则FC=FE=x+，由勾股定理得出方程，解方程求出EM=，FC=FE=+；由（2）得：，把CE=1，BE=n代入计算即可得出n的值．【解答】（1）证明；∵在矩形ABCD中，∠DCE=90°，F是斜边DE的中点，∴CF=DE=EF，∴∠FEC=∠FCE，∵∠BFC=90°，E为BC中点，∴EF=EC，∴CF=CE，在△BCF和△DEC中，，∴△BCF≌△DEC（ASA）；（2）解：设CE=a，由BE=2CE，得：BE=2a，BC=3a，∵CF是Rt△DCE斜边上的中线，∴CF=DE，∵∠FEC=∠FCE，∠BFC=∠DCE=90°，∴△BCF∽△DEC，∴=，即：=，解得：ED2=6a2，由勾股定理得：DC===a，∴==；（3）解：过C′作C′H⊥AF于点H，连接CC′交EF于M，如图所示：∵CF是Rt△DCE斜边上的中线，∴FC=FE=FD，∴∠FEC=∠FCE，∵四边形ABCD是矩形，∴AD∥BC，AD=BC，∴∠ADF=∠CEF，∴∠ADF=∠BCF，在△ADF和△BCF中，，∴△ADF≌△BCF（SAS），∴∠AFD=∠BFC=90°，∵CH⊥AF，C′C⊥EF，∠HFE=∠C′HF=∠C′MF=90°，∴四边形C′MFH是矩形，∴FM=C′H=，设EM=x，则FC=FE=x+，在Rt△EMC和Rt△FMC中，由勾股定理得：CE2﹣EM2=CF2﹣FM2，∴12﹣x2=（x+）2﹣（）2，解得：x=，或x=﹣（舍去），∴EM=，FC=FE=+；由（2）得：，把CE=1，BE=n代入计算得：CF=，∴，解得：n=42016年广西南宁市中考数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题3分，共36分）1．(2016·广西南宁)﹣2的相反数是（）A．﹣2 B．0 C．2 D．4【考点】相反数．【分析】根据只有符号不同的两个数叫做互为相反数解答．【解答】解：﹣2的相反数是2．故选C．【点评】本题考查了相反数的定义，是基础题，熟记概念是解题的关键．2．(2016·广西南宁)把一个正六棱柱如图1摆放，光线由上向下照射此正六棱柱时的正投影是（）A．B．C．D．【考点】平行投影．【分析】根据平行投影特点以及图中正六棱柱的摆放位置即可求解．【解答】解：把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是正六边形．故选A．【点评】本题考查了平行投影特点，不同位置，不同时间，影子的大小、形状可能不同，具体形状应按照物体的外形即光线情况而定．3．(2016·广西南宁)据《南国早报》报道：2016年广西高考报名人数约为332000人，创历史新高，其中数据332000用科学记数法表示为（）A．0.332×106B．3.32×105C．3.32×104D．33.2×104【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将332000用科学记数法表示为：3.32×105．故选：B．【点评】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．4．(2016·广西南宁)已知正比例函数y=3x的图象经过点（1，m），则m的值为（）A．B．3 C．﹣D．﹣3【考点】一次函数图象上点的坐标特征．【分析】本题较为简单，把坐标代入解析式即可求出m的值．【解答】解：把点（1，m）代入y=3x，可得：m=3，故选B【点评】此题考查一次函数的问题，利用待定系数法直接代入求出未知系数m，比较简单．5．(2016·广西南宁)某校规定学生的学期数学成绩满分为100分，其中研究性学习成绩占40%，期末卷面成绩占60%，小明的两项成绩（百分制）依次是80分，90分，则小明这学期的数学成绩是（）A．80分B．82分C．84分D．86分【考点】加权平均数．【分析】利用加权平均数的公式直接计算即可得出答案．【解答】解：由加权平均数的公式可知===86，故选D．【点评】本题主要考查加权平均数的计算，掌握加权平均数的公式=是解题的关键．6．(2016·广西南宁)如图，厂房屋顶人字形（等腰三角形）钢架的跨度BC=10米，∠B=36°，则中柱AD（D为底边中点）的长是（）A．5sin36°米B．5cos36°米C．5tan36°米D．10tan36°米【考点】解直角三角形的应用．【分析】根据等腰三角形的性质得到DC=BD=5米，在Rt△ABD中，利用∠B的正切进行计算即可得到AD的长度．【解答】解：∵AB=AC，AD⊥BC，BC=10米，∴DC=BD=5米，在Rt△ADC中，∠B=36°，∴tan36°=，即AD=BD•tan36°=5tan36°（米）．故选：C．【点评】本题考查了解直角三角形的应用．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．7．(2016·广西南宁)下列运算正确的是（）A．a2﹣a=a B．ax+ay=axy C．m2•m4=m6D．（y3）2=y5【考点】幂的乘方与积的乘方；合并同类项；同底数幂的乘法．【分析】结合选项分别进行幂的乘方与积的乘方、合并同类项、同底数幂的乘法等运算，然后选择正确答案．【解答】解：A、a2和a不是同类项，不能合并，故本选项错误；B、ax和ay不是同类项，不能合并，故本选项错误；C、m2•m4=m6，计算正确，故本选项正确；D、（y3）2=y6≠y5，故本选项错误．故选C．【点评】本题考查了幂的乘方与积的乘方、合并同类项、同底数幂的乘法的知识，解答本题的关键在于掌握各知识点的运算法则．8．(2016·广西南宁)下列各曲线中表示y是x的函数的是（）A．B．C．D．【考点】函数的概念．【分析】根据函数的意义求解即可求出答案．【解答】解：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，故D正确．故选D．【点评】主要考查了函数的定义．注意函数的意义反映在图象上简单的判断方法是：做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．9．(2016·广西南宁)如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，则∠P的度数为（）A．140° B．70° C．60° D．40°【考点】圆周角定理．【分析】先根据四边形内角和定理求出∠DOE的度数，再由圆周角定理即可得出结论．【解答】解：∵CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，∴∠DOE=180°﹣40°=140°，∴∠P=∠DOE=70°．故选B．【点评】本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．10．(2016·广西南宁)超市店庆促销，某种书包原价每个x元，第一次降价打“八折”，第二次降价每个又减10元，经两次降价后售价为90元，则得到方程（）A．0.8x﹣10=90 B．0.08x﹣10=90 C．90﹣0.8x=10 D．x﹣0.8x﹣10=90【考点】由实际问题抽象出一元一次方程．【分析】设某种书包原价每个x元，根据题意列出方程解答即可．【解答】解：设某种书包原价每个x元，可得：0.8x﹣10=90，故选A【点评】本题考查一元一次方程，解题的关键是明确题意，能列出每次降价后的售价．11．(2016·广西南宁)有3个正方形如图所示放置，阴影部分的面积依次记为S1，S2，则S1：S2等于（）A．1：B．1：2 C．2：3 D．4：9【考点】正方形的性质．【分析】设小正方形的边长为x，再根据相似的性质求出S1、S2与正方形面积的关系，然后进行计算即可得出答案．【解答】解：设小正方形的边长为x，根据图形可得：∵=，∴=，∴=，∴S1=S，正方形ABCD∴S1=x2，∵=，∴=，∴S2=S，正方形ABCD∴S2=x2，∴S1：S2=x2：x2=4：9；故选D．【点评】此题考查了正方形的性质，用到的知识点是正方形的性质、相似三角形的性质、正方形的面积公式，关键是根据题意求出S1、S2与正方形面积的关系．12．(2016·广西南宁)二次函数y=ax2+bx+c（a≠0）和正比例函数y=x的图象如图所示，则方程ax2+（b﹣）x+c=0（a≠0）的两根之和（）A．大于0 B．等于0 C．小于0 D．不能确定【考点】抛物线与x轴的交点．【分析】设ax2+bx+c=0（a≠0）的两根为x1，x2，由二次函数的图象可知x1+x2＞0，a＞0，设方程ax2+（b﹣）x+c=0（a≠0）的两根为a，b再根据根与系数的关系即可得出结论．【解答】解：设ax2+bx+c=0（a≠0）的两根为x1，x2，∵由二次函数的图象可知x1+x2＞0，a＞0，∴﹣＞0．设方程ax2+（b﹣）x+c=0（a≠0）的两根为a，b，则a+b=﹣=﹣+，∵a＞0，∴＞0，∴a+b＞0．故选C．【点评】本题考查的是抛物线与x轴的交点，熟知抛物线与x轴的交点与一元二次方程根的关系是解答此题的关键．二、填空题（本大题共6小题，每小题3分，共18分）13．(2016·广西南宁)若二次根式有意义，则x的取值范围是x≥1．【考点】二次根式有意义的条件．【分析】根据二次根式的性质可知，被开方数大于等于0，列出不等式即可求出x的取值范围．【解答】解：根据二次根式有意义的条件，x﹣1≥0，∴x≥1．故答案为：x≥1．【点评】此题考查了二次根式有意义的条件，只要保证被开方数为非负数即可．14．(2016·广西南宁)如图，平行线AB，CD被直线AE所截，∠1=50°，则∠A=50°．【考点】平行线的性质．【分析】根据两直线平行，同位角相等可得∠1=∠A．【解答】解：∵AB∥CD，∴∠A=∠1，∵∠1=50°，∴∠A=50°，故答案为50°．【点评】本题主要考查了平行线的性质，解题的关键是掌握两直线平行，同位角相等．15．(2016·广西南宁)分解因式：a2﹣9=（a+3）（a﹣3）．【考点】因式分解-运用公式法．【分析】直接利用平方差公式分解因式进而得出答案．【解答】解：a2﹣9=（a+3）（a﹣3）．故答案为：（a+3）（a﹣3）．【点评】此题主要考查了公式法分解因式，熟练应用平方差公式是解题关键．16．(2016·广西南宁)如图，在4×4正方形网格中，有3个小正方形已经涂黑，若再涂黑任意一个白色的小正方形如图所示，反比例函数y=（k≠0，x＞0）的图象经过矩形OABC的对角线AC的中点D．若矩形OABC的面积为8，则k的值为2．【考点】反比例函数系数k的几何意义．【分析】过D作DE⊥OA于E，设D（m，），于是得到OA=2m，OC=，根据矩形的面积列方程即可得到结论．【解答】解：过D作DE⊥OA于E，设D（m，），∴OE=m．DE=，∵点D是矩形OABC的对角线AC的中点，∴OA=2m，OC=，∵矩形OABC的面积为8，∴OA•OC=2m•=8，∴k=2，故答案为：2．【点评】本题考查了反比例函数系数k的几何意义，矩形的性质，根据矩形的面积列出方程是解题的关键．18．(2016·广西南宁)观察下列等式：在上述数字宝塔中，从上往下数，2016在第44层．【考点】规律型：数字的变化类．【分析】先按图示规律计算出每一层的第一个数和最后一个数；发现第一个数分别是每一层层数的平方，那么只要知道2016介于哪两个数的平方即可，通过计算可知：442＜2016＜452，则2016在第44层．【解答】解：第一层：第一个数为12=1，最后一个数为22﹣1=3，第二层：第一个数为22=4，最后一个数为23﹣1=8，第三层：第一个数为32=9，最后一个数为24﹣1=15，∵442=1936，452=2025，又∵1936＜2016＜2025，∴在上述数字宝塔中，从上往下数，2016在第44层，故答案为：44【点评】本题考查了数学变化类的规律题，这类题的解题思路是：①从第一个数起，认真观察、仔细思考，能不能用平方或奇偶或加、减、乘、除等规律来表示；②利用方程来解决问题，先设一个未知数，找到符合条件的方程即可；本题以每一行的第一个数为突破口，找出其规律，得出结论．三、解答题（本大题共8小题，共66分）19．(2016·广西南宁)计算：|﹣2|+4cos30°﹣（）﹣3+．【考点】实数的运算；负整数指数幂；特殊角的三角函数值．【分析】直接利用绝对值的性质以及特殊角的三角函数值、负整数指数幂的性质、二次根式的性质化简，进而求出答案．【解答】解：原式=2+4×﹣8+2=4﹣6．【点评】此题主要考查了实数运算，正确利用负整数指数幂的性质化简是解题关键．20．(2016·广西南宁)解不等式组，并把解集在数轴上表示出来．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．【解答】解：，解①得x≤1，解②得x＞﹣3，，不等式组的解集是：﹣3＜x≤1．【点评】本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．21．(2016·广西南宁)如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A （2，2），B（4，0），C（4，﹣4）（1）请画出△ABC向左平移6个单位长度后得到的△A1B1C1；。

丽水市中考数学试卷及答案解析

浙江省丽水市中考数学试卷解析（本试卷满分120分，考试时间120分钟）参考公式：抛物线2y ax bx c =++的顶点坐标为24,24b b ac a a ⎛⎫-- ⎪⎝⎭.一、选择题（本题有10小题，每小题3分，共30分）1. （浙江丽水3分）在数-3，-2，0，3中，大小在-1和2之间的数是【】A. -3B. -2C. 0D. 3 【答案】C.【考点】有理数大小比较.【分析】在－1和2之间的数必然大于－1，小于2，四个答案中只有0符合条件. 故选C. 2. （浙江丽水3分）计算32)(a 结果正确的是【】A. 23a B. 6a C. 5a D. a 6 【答案】B. 【考点】幂的乘方.【分析】根据幂的乘方运算法则计算作出判断：23236()a a a ⨯==.故选B.3. （浙江丽水3分）由4个相同小立方体搭成的几何体如图所示，则它的主视图是【】A.B. C. D.【答案】A.【考点】简单组合体的三视图．【分析】找到从正面看所得到的图形即可，从正面看易得有两层，下层有2个正方形，上层左边有一个正方形．故选A ． 4. （浙江丽水3分）分式x--11可变形为【】 A. 11--x B. x +11 C. x +-11 D. 11-x【答案】D.【考点】分式的基本性质．【分析】根据分式的性质，分子分母都乘以﹣1，分式的值不变，可得答案：分式11x--的分子分母都乘以﹣1，得11x-.故选D．5. （浙江丽水3分）一个多边形的每个内角均为120°，则这个多边形是【】A. 四边形B. 五边形C. 六边形D. 七边形【答案】C.【考点】多边形的外角性质．【分析】∵多边形的每个内角均为120°，∴外角的度数是：180°﹣120°=60°．∵多边形的外角和是360°，∴这个多边形的边数是：360÷60=6．故选C．6. （浙江丽水3分）如图，数轴上所表示关于x的不等式组的解集是【】A. x≥2B. x>2C. x>-1D. -1<x≤2【答案】A.【考点】在数轴上表示不等式的解。

2016年浙江省丽水市中考数学模拟试卷(二)及答案

2016年浙江省丽水市中考数学模拟试卷（二）一、选择题（共10小题，每小题4分，满分40分）1．下列的运算中，其结果正确的是（）A．x+2=5 B． 16x2﹣7x2=9x2 C． x8÷x2=x4 D． x（﹣xy）2=x2y22．下列各图中，沿着虚线将正方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是（）A． B． C． D．3．下列计算错误的是（）A． x3•x4=x7 B．（x2）3=x6 C． x3÷x3=x D． x4+x4=2x44．关于x的不等式组只有4个整数解，则a的取值范围是（）A．﹣5≤a≤﹣ B．﹣5≤a＜﹣ C．﹣5＜a≤﹣ D．﹣5＜a＜﹣5．甲、乙、丙、丁四名运动员参加4×100米接力赛，甲必须为第一接力棒或第四接力棒的运动员，那么这四名运动员在比赛过程的接棒顺序有（）A． 3种 B． 4种 C． 6种 D． 12种6．若a＞0，则点P（﹣a，2）应在（）A．第﹣象限内 B．第二象限内 C．第三象限内 D．第四象限内7．设a=﹣，b=2﹣，c=﹣2，则a，b，c的大小关系是（）A． a＞b＞c B． a＞c＞b C． c＞b＞a D． b＞c＞a8．如图，一圆内切四边形ABCD，且AB=16，CD=10，则四边形的周长为（）A． 50 B． 52 C． 54 D． 569．给出下列4个结论：①边长相等的多边形内角都相等；②等腰梯形既是轴对称图形又是中心对称图形；③三角形的内切圆和外接圆是同心圆；④圆心到直线上一点的距离恰好等于圆的半径，则该直线是圆的切线．其中正确结论的个数有（）A． 0个 B． 1个 C． 2个 D． 3个10．如图，在△ABC中，已知∠C=90°，AC=60cm，AB=100cm，a，b，c…是在△ABC内部的矩形，它们的一个顶点在AB上，一组对边分别在AC上或与AC平行，另一组对边分别在BC 上或与BC平行．若各矩形在AC上的边长相等，矩形a的一边长是72cm，则这样的矩形a、b、c…的个数是（）A． 6 B． 7 C． 8 D． 9一．填空题，每小题5分，满分25分11．计算= ．12．已知摄氏温度（℃）与华氏温度（℉）之间的转换关系是：摄氏温度=×（华氏温度﹣32）．若华氏温度是68℉，则摄氏温度是℃．13．在直角坐标系中，O是坐标原点．点P（m，n）在反比例函数y=的图象上．若m=k，n=k﹣2，则k= ；若m+n=k，OP=2，且此反比例函数y=满足：当x＞0时，y随x的增大而减小，则k= ．14．诗云：“远望巍巍塔七层，灯光点点倍加增，共灯三百八十一，试问尖头几盏灯？”请回答：．15．如图，将一块斜边长为12cm，∠B=60°的直角三角板ABC，绕点C沿逆时针方向旋转90°至△A′B′C′的位置，再沿CB向右平移，使点B′刚好落在斜边AB上，那么此三角板向右平移的距离是cm．三、解答题16．解方程：x2+2x+3﹣=0．17．已知：如图，AM是△ABC的中线，∠DAM=∠BAM，CD∥AB．求证：AB=AD+CD．18．某酒厂生产A，B两种品牌的酒，每天两种酒共生产700瓶，每种酒每瓶的成本和利润如下表所示，设每天共获利y元，每天生产A种品牌的酒x瓶．A B成本（元）5035利润（元）2015（1）请写出y关于x的关系式；（2）如果该厂每天至少投入成本30 000元，那么每天至少获利多少元？（3）要使每天的利润率最大，应生产A，B两种酒各多少瓶？19．已知直线l及l外一点A，分别按下列要求写出画法，并保留两图痕迹．（1）在图1中，只用圆规在直线l上画出两点B，C，使得点A，B，C是一个等腰三角形的三个顶点；（2）在图2中，只用圆规在直线l外画出一点P，使得点A，P所在直线与直线l平行．20．如图，已知Rt△ADC中，∠D=90°，以AD为直径的⊙O交斜边AC于F，OE∥AC，交DC 于E．（1）求证：EF为⊙O的切线；（2）求证：2EF2=CF•OE．21．如图，直角坐标系中，已知点A（2，4），B（5，0），动点P从B点出发沿BO向终点O 运动，动点Q从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了xs．（1）Q点的坐标为（用含x的代数式表示）；（2）当x为何值时，△APQ是一个以AP为腰的等腰三角形？（3）记PQ的中点为G．请你探求点G随点P，Q运动所形成的图形，并说明理由．2016年浙江省丽水市中考数学模拟试卷（二）参考答案与试题解析一、选择题（共10小题，每小题4分，满分40分）1．下列的运算中，其结果正确的是（）A．x+2=5 B． 16x2﹣7x2=9x2 C． x8÷x2=x4 D． x（﹣xy）2=x2y2考点：整式的混合运算．分析：利用整式运算的方法逐一计算，进一步比较得出答案即可．解答：解：A、3x+2不能合并，此选项错误；B、16x2﹣7x2=9x2，此选项正确；C、x8÷x2=x6，此选项错误；D、x（﹣xy）2=x3y2，此选项错误．故选：B．点评：此题考查整式的混合运算，掌握符号的判定与运算的方法是解决问题的关键．2．下列各图中，沿着虚线将正方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是（）A． B． C． D．考点：剪纸问题；正方形的性质．专题：压轴题；操作型．分析：第一个正方形沿虚线剪成两部分，这两部分可拼成平行四边形；第二个既可以拼成平行四边形，也可以拼成下三角和梯形；第三个拼成的图形为特殊的平行四边形正方形；第四个可拼成平行四边形．解答：解：故选B．点评：本题主要考查剪纸问题，充分考查了学生的空间想象能力．3．下列计算错误的是（）A． x3•x4=x7 B．（x2）3=x6 C． x3÷x3=x D． x4+x4=2x4考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．分析：根据同底数幂相乘，底数不变指数相加；幂的乘方，底数不变指数相乘；同底数幂相除，底数不变指数相减；合并同类项，只把系数相加减，字母与字母的次数不变，对各选项分析判断后利用排除法求解．解答：解：A、x3•x4=x7，正确；B、（x2）3=x6，正确；C、应为x3÷x3=1，故本选项错误；D、x4+x4=2x4，正确．故选C．点评：本题主要考查同底数幂的乘法，幂的乘方，同底数幂的除法，合并同类项的法则，熟练掌握运算性质是解题的关键．4．关于x的不等式组只有4个整数解，则a的取值范围是（）A．﹣5≤a≤﹣ B．﹣5≤a＜﹣ C．﹣5＜a≤﹣ D．﹣5＜a＜﹣考点：一元一次不等式组的整数解．专题：计算题；压轴题．分析：首先确定不等式组的解集，先利用含a的式子表示，根据整数解的个数就可以确定有哪些整数解，根据解的情况可以得到关于a的不等式，从而求出a的范围．解答：解：不等式组的解集是2﹣3a＜x＜21，因为不等式组只有4个整数解，则这4个解是20，19，18，17．所以可以得到16≤2﹣3a＜17，解得﹣5＜a≤﹣．故选：C．点评：正确解出不等式组的解集，正确确定2﹣3a的范围，是解决本题的关键．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．5．甲、乙、丙、丁四名运动员参加4×100米接力赛，甲必须为第一接力棒或第四接力棒的运动员，那么这四名运动员在比赛过程的接棒顺序有（）A． 3种 B． 4种 C． 6种 D． 12种考点：推理与论证．专题：压轴题．分析：若甲作第一棒时，乙、丙、丁有6种排列方法；若甲作第四棒时，也有6种排列方法．所以共有12种接棒顺序．解答：解：当甲作第一棒时，接棒顺序有：①甲、乙、丙、丁；②甲、乙、丁、丙；③甲、丙、乙、丁；③甲、丙、丁、乙；⑤甲、丁、乙、丙；⑥甲、丁、丙、乙．因此共有6种接棒顺序．同理当甲做第四棒时，也有6种接棒顺序．因此共有6+6=12种接棒顺序．故选D．点评：此题主要是考虑乙、丙、丁的排列方法．解决此类题时，最好按序排列，以免造成头绪混乱，漏解错解的状况．6．若a＞0，则点P（﹣a，2）应在（）A．第﹣象限内 B．第二象限内 C．第三象限内 D．第四象限内考点：点的坐标．分析：应先判断出所求的点的横纵坐标的符号，进而判断点P所在的象限．解答：解：∵a＞0，∴﹣a＜0，∵点P的横坐标是负数，纵坐标是正数，∴点P在平面直角坐标系的第二象限．故选B．点评：解决本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．7．设a=﹣，b=2﹣，c=﹣2，则a，b，c的大小关系是（）A． a＞b＞c B．a＞c＞b C． c＞b＞a D． b＞c＞a考点：实数大小比较．分析：先把各无理数进行估算，再比较大小即可．也可以通过比较它们倒数的大小解决问题．解答：解：∵≈1.73，≈1.4，≈2.23，∴a=﹣≈1.73﹣1.41=0.32；b=2﹣≈2﹣1.73=0.27；c=﹣2≈2.23﹣2=0.23．∵0.32＞0.27＞0.23，∴a＞b＞c．故选A．点评：本题考查了同学们对无理数大小的估算能力，比较简单．8．如图，一圆内切四边形ABCD，且AB=16，CD=10，则四边形的周长为（）A． 50 B． 52 C． 54 D． 56考点：切线长定理．分析：根据切线长定理，可以证明圆外切四边形的性质：圆外切四边形的两组对边和相等，从而可求得四边形的周长．解答：解：由题意可得圆外切四边形的两组对边和相等，所以四边形的周长=2（16+10）=52．故选B．点评：熟悉圆外切四边形的性质：圆外切四边形的两组对边和相等．9．给出下列4个结论：①边长相等的多边形内角都相等；②等腰梯形既是轴对称图形又是中心对称图形；③三角形的内切圆和外接圆是同心圆；④圆心到直线上一点的距离恰好等于圆的半径，则该直线是圆的切线．其中正确结论的个数有（）A． 0个 B． 1个 C． 2个 D． 3个考点：等腰梯形的性质；多边形；三角形的外接圆与外心；三角形的内切圆与内心．分析：对各个结论进行分析从而确定正确的答案．解答：解：①：比如一般的菱形的各边相等，但各角不相等，所以命题错误；②：等腰梯形不是中心对称图形，所以命题错误；③：三角形的内切圆的圆心是三条角平分线的交点，外接圆的圆心是三条垂直平分线的交点，只有等边三角形才能重合，所以命题错误；④：圆心到直线的距离等于半径的直线，是圆的切线，不能说圆心到直线上一点的距离，错误．故选A．点评：理解各个概念，说明一个命题的错误，只需举出反例即可．10．如图，在△ABC中，已知∠C=90°，AC=60cm，AB=100cm，a，b，c…是在△ABC内部的矩形，它们的一个顶点在AB上，一组对边分别在AC上或与AC平行，另一组对边分别在BC 上或与BC平行．若各矩形在AC上的边长相等，矩形a的一边长是72cm，则这样的矩形a、b、c…的个数是（）A． 6 B． 7 C． 8 D． 9考点：勾股定理的应用．专题：压轴题；规律型．分析：根据勾股定理可以求出每阶台阶的宽，依据BC的长，即可解答．解答：解：如图，易证△BDE≌△EFG≌△GKH≌△HLM，可得BD=EF=GK=HL=BC﹣DC=﹣72=8cm．根据此规律，共有80÷8﹣1=9个这样的矩形．故选D．点评：本题将勾股定理和规律的探索与实际问题相结合，有一定的难度，善于观察题目的信息是解题以及学好数学的关键．一．填空题，每小题5分，满分25分11．计算= ．考点：分母有理化．专题：计算题．分析：运用二次根式的乘法法则，将分子的二次根式化为积的形式，约分，比较简便．解答：解：原式==．故答案为：．点评：主要考查了二次根式的化简和二次根式的运算法则．注意最简二次根式的条件是：①被开方数的因数是整数，因式是整式；②被开方数中不含能开得尽方的因数因式．上述两个条件同时具备（缺一不可）的二次根式叫最简二次根式．12．已知摄氏温度（℃）与华氏温度（℉）之间的转换关系是：摄氏温度=×（华氏温度﹣32）．若华氏温度是68℉，则摄氏温度是20 ℃．考点：有理数的混合运算．专题：应用题．分析：把华式温度68℉，直接代入摄式温度=×（华式温度﹣32），求值即可．解答：解：当华式温度=68℉，摄式温度=×（华式温度﹣32）=×（68﹣32）=×36=20℃．点评：注意按照两者的转换公式进行计算，熟练有理数的混合运算法则．13．在直角坐标系中，O是坐标原点．点P（m，n）在反比例函数y=的图象上．若m=k，n=k﹣2，则k= 3 ；若m+n=k，OP=2，且此反比例函数y=满足：当x＞0时，y随x 的增大而减小，则k= 2 ．考点：反比例函数图象上点的坐标特征；反比例函数的性质．分析：把点P的坐标代入反比例函数关系式来求k的值；当k＞0时，反比例函数y=的图象：当x＞0时，y随x的增大而减小．解答：解：∵点P（m，n）在反比例函数y=的图象上．且m=k，n=k﹣2，∴k﹣2=，解得 k=3；∵m+n=k，OP=2，∴，解得 k=2或k=﹣1．又∵当x＞0时，y随x的增大而减小，∴k＞0，∴k=2符合题意．故答案是：3；2．点评：本题考查了反比例函数的性质，反比例函数图象上点的坐标特征．所有在反比例函数上的点的横纵坐标的积应等于比例系数．14．诗云：“远望巍巍塔七层，灯光点点倍加增，共灯三百八十一，试问尖头几盏灯？”请回答：3盏灯．考点：一元一次方程的应用．分析：要求尖头几盏灯，就要先设出求知数，再根据倍加增求出各层的灯数，然后根据共灯三百八十一的等量关系列出方程求解．解答：解：设顶层有x盏灯．根据题意得：x+2x+4x+8x+16x+32x+64x=381，解得：x=3．因此尖头（最顶层）有3盏灯．故答案为：3盏灯．点评：本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．15．如图，将一块斜边长为12cm，∠B=60°的直角三角板ABC，绕点C沿逆时针方向旋转90°至△A′B′C′的位置，再沿CB向右平移，使点B′刚好落在斜边AB上，那么此三角板向右平移的距离是（）cm．考点：解直角三角形；平移的性质；旋转的性质．专题：压轴题．分析：综合利用直角三角形的性质和锐角三角函数的概念及旋转，平移的性质解题．解答：解：如图，BC=AB•cos60°=6．由平移的性质知：∠WQS=∠ACB=90°，WQ=BC=6，∴BQ=WQ•cot60°=2．∴QC=BC﹣BQ=6﹣2．点评：本题考查了学生综合运用数学知识的能力，注意旋转和平移后的图形与原图形全等．三、解答题16．解方程：x2+2x+3﹣=0．考点：无理方程．分析：设=y，则原方程即可转化为关于y的方程，解方程求得y的值，然后转化为关于x的方程，从而求解．解答：解：设=y，则x2+2x=y2﹣5，则原式即：y2﹣y﹣2=0，解得：y1=2，y2=﹣1（舍去），则x2+2x=4﹣5，即（x+1）2=0，解得x1=x2=﹣1．点评：本题考查了无理方程的解法，在解无理方程是最常用的方法是两边平方法及换元法，本题用了换元法．17．已知：如图，AM是△ABC的中线，∠DAM=∠BAM，CD∥AB．求证：AB=AD+CD．考点：全等三角形的判定与性质．分析：首先画出辅助线：延长AM，与CD的延长线相交于点N．再证明△ABM≌△NCM，可得AB=CN，再证明AD=ND，即可得到AB=CN=AD+CD．解答：证明：延长AM，与CD的延长线相交于点N．∵CD∥AB，∴∠BAM=∠N．又∵∠BMA=∠CMN，BM=CM，∴△ABM≌△NCM．∴AB=CN．∵∠BAM=∠N，∠DAM=∠BAM，∴∠DAM=∠N．∴AD=ND．∴AB=CN=AD+CD．点评：此题主要考查了全等三角形的判定与性质，解题的关键是证明AD=ND，AB=CN．18．某酒厂生产A，B两种品牌的酒，每天两种酒共生产700瓶，每种酒每瓶的成本和利润如下表所示，设每天共获利y元，每天生产A种品牌的酒x瓶．A B成本（元）5035利润（元）2015（1）请写出y关于x的关系式；（2）如果该厂每天至少投入成本30 000元，那么每天至少获利多少元？（3）要使每天的利润率最大，应生产A，B两种酒各多少瓶？考点：一元一次不等式的应用；一次函数的应用．专题：图表型．分析：（1）获利y元=A种品牌的酒的获利+B种品牌的酒的获利．（2）关系式为：A种品牌的酒的成本+B种品牌的酒的成本≥30 000，算出x的最小整数值代入（1）即可（3）关键描述语是：利润率最大，应选取利润率最大的生产最大数量．解答：解：（1）根据题意，得y=20x+15（700﹣x），即y=5x+10500．（2）根据题意，得50x+35（700﹣x）≥30000，解得x≥=366．因为x是整数，所以取x=367，代入y=5x+10500，得y=12335．答：每天至少获利12335元．（3）生产A种酒的利润率为=；生产B种酒的利润率为=，因为＜，所以要使每天的利润率最大，应生产A种酒0瓶，B种酒700瓶．答：应生产A种酒0瓶，B种酒700瓶．点评：解决本题的关键是读懂题意，根据关键描述语找到符合题意的等量关系和不等关系式组．19．已知直线l及l外一点A，分别按下列要求写出画法，并保留两图痕迹．（1）在图1中，只用圆规在直线l上画出两点B，C，使得点A，B，C是一个等腰三角形的三个顶点；（2）在图2中，只用圆规在直线l外画出一点P，使得点A，P所在直线与直线l平行．考点：作图—复杂作图．专题：压轴题．分析：（1）以点A为圆心，大于点A到直线l的距离长为半径画弧，与直线l交于B，C 两点，则点B，C即为所求．或在直线l上任取一点B，以点B为圆心，AB长为半径画弧，与直线l交于点C，则点B，C即为所求；（2）在直线l上任取B，C两点，以点A为圆心，BC长为半径画弧，以点C为圆心，AB长为半径画弧，两弧交于点P．则点P即为所求．解答：解：（1）画法一：以点A为圆心，大于点A到直线l的距离长为半径画弧，与直线l交于B，C两点，则点B，C即为所求．画法二：在直线l上任取一点B，以点B为圆心，AB长为半径画弧，与直线l交于点C，则点B，C 即为所求．（2）画法：在直线l上任取B，C两点，以点A为圆心，BC长为半径画弧，以点C为圆心，AB长为半径画弧，两弧交于点P．则点P即为所求．点评：此题通过作图考查了等腰三角形的性质和平行四边形的性质．20．如图，已知Rt△ADC中，∠D=90°，以AD为直径的⊙O交斜边AC于F，OE∥AC，交DC 于E．（1）求证：EF为⊙O的切线；（2）求证：2EF2=CF•OE．考点：切线的判定；相似三角形的判定与性质．专题：证明题．分析：（1）连接OF、DF交OE于点G，在△ODF和△EFD中，利用等边对等角证明∠ODF=∠OFD，∠EDF=∠EFD，则∠OFE=∠ODC=90°，从而证得；（2）利用切割线定理，以及直角三角形斜边上的中线等于斜边的一半，利用CD分别表示出2EF2和CF•OE，即可证得．解答：证明：（1）连接OF、DF交OE于点G．∵AD是圆的直径，∴∠AFD=90°，即∠DF⊥AC，又∵OE∥AC，∴OE⊥DF，又∵OD=OF，∴DG=GF，∠ODF=∠OFD，∴DE=EF，∴∠EDF=∠EFD，∴∠OFE=∠ODC=90°，∴OF⊥EF，则EF是圆的切线；（2）证明：∵O是AB的中点，OE∥AC，∴OE是△ABC的中位线，∴OE=AC，即AC=2OE，又∵CD是圆的切线，∴CD2=CF•AC=2CF•OE，即CF•OE=CD2．∵在直角△DFC中，E是CD的中点，∴EF=C D，即CD=2EF，∴2EF2=CD2，∴2EF2=CF•OE．点评：本题考查了切线的判定定理、切割线定理和直角三角形的性质定理，利用CD分别表示出2EF2和CF•OE是关键．21．如图，直角坐标系中，已知点A（2，4），B（5，0），动点P从B点出发沿BO向终点O 运动，动点Q从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了xs．（1）Q点的坐标为（2+，4﹣）（用含x的代数式表示）；（2）当x为何值时，△APQ是一个以AP为腰的等腰三角形？（3）记PQ的中点为G．请你探求点G随点P，Q运动所形成的图形，并说明理由．考点：等腰三角形的判定；一元二次方程的应用；坐标与图形性质；待定系数法求一次函数解析式；勾股定理．专题：压轴题．分析：（1）如果过点A作OB的垂线，不难求出cos∠ABO=，sin∠ABO=，因此，Q移动时，横向移动的速度是1•cos∠ABO=单位/秒，纵向移动的速度是1•sin∠ABO=单位/秒，因此Q得坐标就可表示为（2+，4﹣）．（2）有了A、Q的坐标，如果分别过A、Q做x轴的垂线，通过构成的直角三角形，不难用x表示出AQ、AP和PQ的值，然后分AP=AQ，PQ=AP两种情况进行讨论，得出x的值．（3）通过观察G点似乎应该在三角形ABO的中位线上，因此它的轨迹应该是个线段．可设AB、BO的中点分别为点M、N，设M N、PQ相交于点G′，只要证明G′与G重合，也就是G′是QP的中点即可．过点P作PK∥AO交AB于点K．只要证明KM=QM就行了，根据三角形AOB为等腰三角形，AQ、PK、MN都平行，不难得出AQ=BK，AM=BM，因此便可得出KM=QM 了．由此便可得出G′是PQ中点，与G重合．解答：解：（1）（2+，4﹣）．（2）由题意，得P（5﹣x，0），0＜x≤5由勾股定理求得PQ2=（﹣3）2+（4﹣）2AP2=（3﹣x）2+42若AQ=AP，则x2=（3﹣x）2+42，解得x=若PQ=AP则（﹣3）2+（4﹣）2=（3﹣x）2+42即x2﹣10x=0，解得x1=0（舍去），x2=经检验，当x=或x=时，△APQ是一个以AP为腰的等腰三角形．（3）设AB、BO的中点分别为点M、N，则点G随点P、Q运动所形成的图形是线段MN设MN，PQ相交于点G′，过点P作PK∥AO交AB于点K∴PK∥AO∥MN∴△A0B∽△KPB∽△MNB．∵AB=OB∴BK=BP=AQ，BM=BN∴BK﹣BM=AQ﹣BM，BK﹣BM=AQ﹣AM即KM=QM∴PG′=QG′∴G′是PQ的中点即点G′与点G重合．∴点G随点P、Q运动所形成的图形是△OBA的中位线MN．点评：本题考查综合应用点的坐标，等腰三角形的判定等知识进行推理论证、运算及探究证明的能力．。

浙江省丽水市中考数学试卷

浙江省丽水市中考数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共6题；共12分)1. （2分）①4的算术平方根是±2；②与-是同类二次根式；③点P（2，3）关于原点对称的点的坐标是（-2，-3）；④抛物线y=-（x-3）2+1的顶点坐标是（3，1）．其中正确的是（）A . ①②④B . ①③C . ②④D . ②③④2. （2分）下列各组式子中，属于同类项的是（）A . 与B . ab与acC . 与-2yxD . a与b3. （2分）中国是严重缺水的国家之一，人均淡水资源为世界人均量的四分之一，所以我们应该为中国节水，也为世界节水。

若每人每天浪费水0.32L，那么100万人每天浪费的水，用科学记数法表示为（）A . 3.2×107LB . 3.2×106LC . 3.2×105LD . 3.2×104L4. （2分）下列调查适合作普查的是（）A . 了解在校大学生的主要娱乐方式B . 了解重庆市居民对废电池的处理情况C . 日光灯管厂要检测一批灯管的使用寿命D . 对甲型H7N9流感患者的同一车厢的乘客进行医学检查5. （2分）如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A 等于（）A . 25°；B . 30°；C . 45°；D . 60°.6. （2分） (2016九上·仙游期中) 已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（）A . 不能确定B . 相离C . 相切D . 相交二、填空题 (共10题；共10分)7. （1分）已知|x|=|﹣3|，则x的值为________8. （1分）一个三角形的三个外角中，最多有________个角是锐角？9. （1分）(2016七上·萧山月考) 对于两个不同的有理数a，b定义一种新的运算如下：，如，那么 =________.10. （1分）如图所示，直角梯形ABCD的中位线EF的长为a，垂直于底的腰AB的长为b，则图中阴影部分的面积等于________．11. （1分）(2017·集宁模拟) 计算：﹣2tan60°+（﹣1）0﹣（）﹣1=________．12. （1分） (2016九下·大庆期末) 如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=________．13. （1分） (2016九上·乌拉特前旗期中) 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为________14. （1分）(2017·延边模拟) 如图，线段OA=4，点C是OA的中点，以线段CA为对角线作正方形ABCD．将线段OA绕点O向逆时针方向旋转60°，得到线段OA′和正方形A′B′C′D′．在旋转过程中，正方形ABCD扫过的面积是________．（结果保留π）15. （1分）(2017·黔东南模拟) 如图所示，一次函数y=kx+b（k≠0）与反比例函数y= （m≠0）的图象交于A、B两点，则关于x的不等式kx+b＜的解集为________．16. （1分）(2017·邹平模拟) 观察下列各式：22﹣1=1×3，32﹣1=2×4，42﹣1=3×5，52﹣1=4×6，…，根据上述规律，第n个等式应表示为________．三、解答题 (共12题；共116分)17. （5分）解不等式组，并求它的整数解．18. （10分） (2018八上·梁子湖期末)（1）解方程：；（2）化简： .19. （10分） (2018九上·萧山开学考) 解下列一元二次方程（1） 5x﹣2=（2﹣5x）（3x+4）（2） 4（x+3）2=25（x﹣2）220. （11分）(2017·独山模拟) 某校八年级共有800名学生，准备调查他们对“低碳”知识的了解程度．（1）在确定调查方式时，团委设计了以下三种方案：方案一：调查八年级部分女生；方案二：调查八年级部分男生；方案三：到八年级每个班去随机调查一定数量的学生．请问其中最具有代表性的一个方案是________；（2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将两个统计图补充完整；（3）请你估计该校八年级约有多少名学生比较了解“低碳”知识．21. （10分）(2019·丹阳模拟) 已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD.（1）求证：四边形AODE是矩形；（2）若AB＝2，∠BCD＝120°，求四边形AODE的面积.22. （15分）(2014·湖州) 已知某市2013年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系如图所示．（1）当x≥50时，求y关于x的函数关系式；（2）若某企业2013年10月份的水费为620元，求该企业2013年10月份的用水量；（3）为贯彻省委“五水共治”发展战略，鼓励企业节约用水，该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费，规定：若企业月用水量x超过80吨，则除按2013年收费标准收取水费外，超过80吨部分每吨另加收元，若某企业2014年3月份的水费和污水处理费共600元，求这个企业该月的用水量．23. （10分）在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只能选两人打第一场．（1）如果确定小亮打第一场，再从其余三人中随机选取一人打第一场，求恰好选中大刚的概率.（2）如果确定小亮做裁判，用“手心、手背”的方法决定其余三人哪两人打第一场．游戏规则是：三人同时伸“手心、手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始，这三人伸出“手心”或“手背”都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率．24. （10分） (2017九上·台江期中) 二次函数中y=ax2+bx﹣3的x、y满足表：x…﹣10123…y…0﹣3﹣4﹣3m…（1）求该二次函数的解析式；（2）求m的值并直接写出对称轴及顶点坐标．25. （5分）如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为30°，看这栋大楼底部C的俯角为60°，热气球A的高度为240米，求这栋大楼的高度．26. （10分）如图，是一个照相机成像的示意图，像高MN，景物高度AB、CD为水平视线，根据物体成像原理知：AB∥MN，C D⊥MN．（1）如果像高MN是35mm，焦距CL是50mm，拍摄的景物高度AB是4.9m，拍摄点离景物的距离LD是多少？（2）如果要完整的拍摄高度是2m的景物，拍摄点离景物有4m，像高不变，则相机的焦距应调整为多少毫米？27. （10分）(2019·锦州) 已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF.（1）如图1，当BC＝AC，CE＝CD，DF＝AD时，求证：①∠CAD＝∠CDF，②BD＝EF；（2）如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由.28. （10分） (2017七下·兴化期末) 已知A=2a -7，B=a2- 4a+3，C= a2 +6a-28，其中．（1）求证：B-A＞0，并指出A与B的大小关系；（2）阅读对B因式分解的方法：解：B=a2- 4a+3=a2- 4a+4-1=（a-2）2-1=（a-2+1）（a-2-1）=（a-1）（a-3）.请完成下面的两个问题：①仿照上述方法分解因式：x2- 4x-96；②指出A与C哪个大？并说明你的理由．参考答案一、选择题 (共6题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共10题；共10分)7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共12题；共116分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、22-3、23-1、23-2、24-1、24-2、25-1、26-1、26-2、27-1、27-2、28-1、28-2、。

浙江省2016年初中毕业升学考试(丽水卷)

浙江省2016年初中毕业升学考试（丽水卷）科学试题卷考生须知：1．全卷共四大题，36小题，满分为180分。

考试时间为120分钟，本次考试采用闭卷形式。

2．全卷分为卷Ⅰ（选择题）和卷Ⅱ（非选择题）两部分，全部在“答题纸”上作答。

卷Ⅰ的答案必须用2B 铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在“答题纸”的相应位置上。

3．请用黑色字迹钢笔或签字笔在“答题纸”上先填写姓名和准考证号。

4．本卷可能用到的相对原子质量：H —1 C —12 N —14 O —16 Na —23 Cl —35.5 5．本卷计算中g 取10牛/千克。

卷Ⅰ一、选择题（本大题共有15小题，1-5小题每题4分，6-15小题每题3分，共50分。

请选出一个符合题意的正确选项，不选、多选、错选均不得分）1．能给人类带来光和热，离地球最近且属于恒星是 A ．太阳 B ．火星 C ．水星 D ．金星 2．下列做法不符合．．．实验室安全守则的是 A ．打翻燃着的酒精灯，用湿抹布盖灭 B ．为避免中毒，不得品偿化学药品C ．为避免触电事故，不能用湿手接触电源D ．实验结束后，将有毒溶剂直接倒入水槽 3．如图现象中，由于光的折射形成的像是4．解剖一朵花，观察其结构，在子房内看到的白色小颗粒是A ．柱头B ．胚珠C ．花药D ．花粉5．缙云烧饼名扬海内外。

如图是烧饼制作从揉团到压扁过程，则面团变成面饼后对桌面的 A ．压力变小 B ．压力变大 C ．压强变小D ．压强变大 6．北京时间2016年2月12日，美国科学家宣布探测到来自遥远天体的引力波信号，这个发现可以帮助科学家探索宇宙的诞生和发展。

下列说法正确的是A ．宇宙是有起源的、膨胀的、演化的B ．太阳是宇宙的中心C ．宇宙中星系间的距离是恒定不变的D ．地球是宇宙的中心7．如图是“用双氧水制取收集一瓶氧气”实验的主要步骤，其中操作错误的是地图经放大镜成的像 C蜡烛通过小孔成的像 A 花瓶在镜中成的像 B 亭子在水中成的像D面团面饼A ．加入药品B ．收集气体C ．检查装置气密性D ．验满8．下列物质的性质与用途不对应．．．的一项是9．如图四个实验中，用来探究电磁感应现象的是10．2015年浙江籍女科学家屠呦呦获得诺贝尔医学或生理学奖，她提取的青蒿素化学式为C 15H 22O 5。

2016年丽水市中考数学试题解析版

2016年浙江省丽水市中考数学试卷A .七年级的合格率最高B. 八年级的学生人数为 262名 C. 八年级的合格率高于全校的合格率 D .九年级的合格人数最少 6. 下列一元二次方程没有实数根的是(2A. x +2x+仁0 7. 如图，？ABCD 周长为()年级七年级八年级九年级合格人数270262254800名学生，各年级七、八、九三个年级共有 ( )B. ------- C . D . a+ba+h a+h ab某校对全体学生开展心理健康知识测试, 的合格人数如表所示，则下列说法正确的是 1. 2. A . 3. 、选择题：每小题 3分，共30分下列四个数中，与-2的和为0的数是()B . 2C . 0D .-32 >3-1的结果是( ) B . - 3 C . 2D . - 2计算 3下列图形中，属于立体图形的是( 4. -+的运算结果正确的是(5. ) 2 2 2B . x +x+2=0C . x -仁0D . x - 2x -仁0的对角线 AC , BD 交于点O ,已知AD=8 , BD=12 , AC=6，则△ OBC 的A .B .C .A . 13B . 17C . 20D . 26&在直角坐标系中，点M, N在同一个正比例函数图象上的是( )A. M (2,- 3), N (- 4, 6)B. M (- 2, 3), N (4, 6)C. M (- 2,- 3) , N (4, -6)D. M (2,3), N (- 4, 6)9.用直尺和圆规作Rt△ ABC斜边AB上的高线CD，以下四个作图中，作法错误的是()BC=4 ,AD=，贝U AE 的长是(二、填空题：每小题 4分，共24分 11 .分解因式： am - 3a= ____________ .12•如图，在△ ABC 中，/ A=63 °直线MN // BC ,且分别与AB , AC 相交于点D , E ，若 / AEN=133 °则/ B 的度数为 _________________ .13•箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是 _______________ .2 214.已知 x +2x - 1=0，贝U 3x +6x - 2= ___________ .15•如图，在菱形 ABCD 中，过点B 作BE 丄AD , BF 丄CD ，垂足分别为点 E , F ,延长BD 至 G ,使得 DG=BD ，连结 EG , FG ,若 AE=DE 「:= ___________________ .©16.如图，一次函数 y= - x+b 与反比例函数 y= . (x >0)的图象交于 A , B 两点，与x 轴、 y 轴分别交于C , D 两点，连结OA , OB ，过A 作AE 丄x 轴于点E ，交OB 于点F ,设点A 的横坐标为m . (1) b= ___________ (用含m 的代数式表示)；D . 1.210.如图，已知O O 是等腰Rt △ ABC 的外接圆，点 D 是■，上一点，BD 交AC 于点E ,若(2) 、△ OAF +S 四边形EFBC =4，贝V m 的值是三、解答题 17•计算：(—3)I — 一1+18.解不等式：3x - 5V 2 (2+3x )19•数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含 45。

2016浙江丽水中考数学解析

2016年浙江省丽水市中考数学试卷（满分150分，考试时间120分钟）一、选择题（本题有10小题，每小题3分，共30分）1. (2016淅江丽水，1，3分)下列四个数中，与-2的和为0的数是（）A.-2B.2C.0D.-12【答案】B .【逐步提示】本题考查相反数的概念，解题关键在于掌握互为相反数据两个数的和为0的性质.①利用相反数的定义；②找出-2的相反数即可.【详细解答】解：因为-2的相反数是2，所以与-2的和为0的数是2，故选择B.【解后反思】互为相反数的两个数的和为0.【关键词】相反数.2. (2016淅江丽水，2，3分)计算32×3-1的结果是( )A.3B.-3C.2D.-2【答案】A .【逐步提示】本题考查实数的计算，解题关键在于理解负指数的意义. ①先算乘方；②再算乘法.【详细解答】解：32×3-1=9×13=3,故选择A.【解后反思】实数的运算按照顺序顺序及运算法则进行计算，先算乘方开方，再算乘除，最后算加减.【关键词】有理数的乘方；负指数幂. 3. (2016淅江丽水，3，3分)下列图形中，属于立体图形的是( )【答案】C .【逐步提示】本题考查立体图形与平面图形的判断，解题关键在于理解立体图形与平面图形的区别. ①观察图形是否有用虚线表示着的部分；②用虚线表示着图形的为立体图形.【详细解答】解：C 选项中的图形有部分用虚线表示着，代表看不到的部分，表明为立体图形，故选择C.【解后反思】平面图形的各部分都能看到，表现在平面上都为实线；立体图形有看得到的部分用实线表示，而看不到的部分用虚线表示着，故有虚线表示着的图形为立体图形.【关键词】平面图形；立体图形.4. (2016淅江丽水，4，3分)1a +1b 的运算结果正确的是( ) A.1a b + B.2a b + C.a b ab+ D.ab 【答案】C .【逐步提示】本题考查异分母分式的加法，解题关键在于通分. ①通分；②合并.ABCD【详细解答】解：1a +1b =a ab +b ab =a b ab，故选择C. 【解后反思】异分母分式相加减，先通分转化为同分母分式再进行加减.【关键词】分式加减；通分.5. (2016淅江丽水，5，3分)某校对全体学生开展心理健康知识测试，七、八、九三个年级共有800名学生，各年级的合格人数如右表所示，则下列说法正确的是( )A.七年级的合格率最高B. 八年级的学生人数为262名C. 八年级的合格率高于全校的合格率D.九年级的合格人数最少【答案】D .【逐步提示】本题考查统计表的意义的理解及相关计算，解题关键在于正确理解统计表中数据的意义. ①分析题意学生共有800人，三个年级的及格人数在表中，每个年级中不及格的人数则不能推算出来；②三个年级的及格率不能判断高低.【详细解答】解：由题意学生共有800人及三个年级的及格人数，并未出现不及格人数，所以无法对三个年级的及格率高低进行判断，所以A 、C 错误；八年级及格学生数为262名，是否有不及格的不能做出判断，故B 错误；三个年级及格人数九年级最少可以判断是正确的，故选D.【解后反思】学生分为及格与不及格两种，哪个年级都可能有不及格的学生.全面、合理、充分理解图形中的信息，为解题打基础.【关键词】统计；统计表.6. (2016淅江丽水，6，3分)下列一元二次方程没有实数根的是( )A. x 2+2x+1=0B. x 2+x+2=0C. x 2-1=0D. x 2-2x-1=0【答案】B .【逐步提示】本题考查一元二次方程根的判别式的应用，解题关键在于理解判别式的意义. ①计算各方程△=b 2-4ac 的值；②根据△=b 2-4ac 的符号进行判断.【详细解答】解：A 选项Δ＝0,方程有两个相等的实数根；B 选项Δ＝-7<0,方程没有实数根；C 选项Δ＝4>0,方程有两个不相等的实数根；D 选项Δ＝8>0,方程有两个不相等的实数根，故选择B.【解后反思】一元二次方程ax 2+bx+c=0,当Δ＝b 2-4ac=0时,方程有两个相等的实数根；当Δ＝b 2-4ac<0时,方程没有实数根；Δ＝b 2-4ac>0时,方程有两个不相等的实数根.【关键词】一元二次方程；一元二次方程根的判别式.7. (2016淅江丽水，7，3分)如图，□ABCD 的对角线AC ，BD 交于点O ，已知AD=8,BD=12,AC=6,则△OBC 的周长为( ) A.13 B.17 C.20 D.26【答案】B . 【逐步提示】本题考查平行四边形的性质，解题关键在于将三角形周长转化为平行四边形的对角线长与边长. ①根据平行四边形的性质得到BC 及OB+OC 的长；②求得△OBC 的周长.【详细解答】解：由题意得BC=AD=8, OB+OC=12(AC+BD)=9,所以△OBC 的周长=8+9=17，故选择B.【解后反思】平行四边形的对角线互相平分,平行四边形的对边相等,对角相等.求三角形ODCB A周长可以分别三条线段的长，也可以将一条或两条线段加起来整体求和.【关键词】平行四边形的性质.8. (2016淅江丽水，8，3分)在直角坐标系中，点M，N在同一个正比例函数图象上的是( )A.M(2,-3), N(-4,6)B. M(-2, 3), N(4,6)C. M(-2,-3), N(4, -6)D. M(2,3), N(-4,6)【答案】A.【逐步提示】本题考查正比例函数的图象和性质，解题关键在于理解正比例函数图象上点的横、纵坐标比值间的关系.①若每个点的横、纵坐标的比值相等，则两点位于同一正比例函数的图象上；②否则两点不在同一正比例函数的图象上.【详细解答】解：A选项中横、纵坐标的比值均为-23，B、C、D选项的横纵坐标之比不相等，有的是23，有的是-23，故选择A.【解后反思】同一正比例函数图象上点的横、纵坐标的比值相等.此题也可以根据一点坐标写出正比例函数的解析式，然后将另一点的坐标代入解析式进行验证.【关键词】正比例函数的图象和性质.9. (2016淅江丽水，9，3分)用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是( )A. B. C. D.【答案】D.【逐步提示】本题考查三角形的高的尺规作图，解题关键在于根据作图痕迹确定作图方法.①根据痕迹确定作图方法；②根据作图方法确定CD是否为斜边上的高线.【详细解答】解：A根据过直线外一点作已知直线的垂线的方法得到斜边AB上的高线CD，故正确；B选项通过作直径所对的圆周角构造斜边AB上的高线CD，故正确；C选项根据两圆连心线垂直平分公共弦得到斜边AB上的高线CD，故正确；D选项中的CD不一定是斜边AB上的高线，故错误，故选择D.【解后反思】作垂线的尺规作图的方法：连一点作已知直线的垂线；构造直径所对的圆周角；两圆连心线垂直平分公共弦；线段的垂直平分线.【关键词】三角形的高；尺规作图.10. (2016淅江丽水，10，3分)如图，已知⊙O是等腰Rt△ABC的外接圆，点D是AC上一点，BD交AC于点E，若BC=4,AD=45，则AE的长是( )A.3B.2C.1D.1.2【答案】C.【逐步提示】本题考查弧、弦、圆周角间关系，相似三角形的判定及性质等知识，解题关键在于根据DE的长度验证选项.①根据题意确定BD的长；②根据△CBE∽△DAE的相似比采用验证法确定正确答案.【详细解答】解：因为AC=BC=4,由勾股定理得所以285，△CBE∽△DAE，所以AE：BE=DE：CE=AD：CB=45：4=15，所以BE˙DE=AE˙CE.若AE=3,则BE=15>285,故错误；若AE=2,则BE=10>285,故错误；若AE=1,则BE=5,DE=35,CE=4-1=3,此时满足BE˙DE=AE˙CE，故AE=1时正确；若AE=1.2,则BE=6>285,故错误,故选择C.【解后反思】直接计算AE的长比较困难，可以采用比较法，验证法确定线段的长，如本题据题意确定图形中各线段间的关系，然后根据已知条件对所给选项进行验证从而得出正确的结论，验证法是解选择题的一种基本方法.【关键词】圆；相似三角形的性质；验证法.二、填空题（本题有6小题，每小题4分，共24分.）11.(2016淅江丽水，11，4分)分解因式：am-3a= .【答案】a(m-3) .【逐步提示】本题考查分解因式，解题的关键在于掌握因式分解的基本方法.利用提公因式法分解因式.【详细解答】解：am-3a =a(m-3).【解后反思】因式分解的步骤为：一提公因式；二看公式.公式包括平方差公式与完全平方公式，要能用公式法分解必须有平方项，如果是平方差就用平方差公式来分解，如果是平方和需要看还有没有两数乘积的2倍，如果没有两数乘积的2倍就不能分解，因式分解必须进行到不能再分解为止.【关键词】分解因式——提公因式法.12. (2016淅江丽水，12，4分)如图，在△ABC中，∠A=63°，直线MN∥BC，且分别与AB，AC相交于点D，E，若∠AEN=133°,则∠B的度数为( )【答案】70°.【逐步提示】本题考查三角形外角及平行线的性质，解题的关键在于三角形内角与外角关系的应用.①由三角形内角和求得∠ADE；②根据平行线的性质求得∠B.【详细解答】解：因为∠AEN=133°，∠A=63°，所以∠ADE=∠AEN-∠A= =133°-63°=70°，因为MN∥BC，所以∠B=∠ADE=70°.【解后反思】三角形一个外角等于不相邻两个内角的和；两直线平行，同位角相等，内错角相等，同旁内角互补.求角度有两条途径：一是直接求解；二是间接求解，①将此角转化为与了相等的其他角；②先求此线段的和、差、倍、分，再转化为线段的长.【关键词】三角形的外角；平行线的性质.13. (2016淅江丽水，13，4分)箱子里放有2个黑球和2个红球，它们除颜色外其余都相同，现从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是＿＿＿.【答案】2 3 .【逐步提示】本题考查概率的计算，解题的关键在于确定所有可能情况数与满足条件的情况数.①根据树状图或列表法确定所有可能情况；②从中确定出一红一黑的情况数，最后计算概率.【详细解答】解：画树状图如下：通过树状图分析，从箱子里摸球共有12种情况，其中摸到1红1黑的共有8种情况，故从箱子里随机摸出两个球，恰好为1个黑球和1个红球的概率是812=23，故答案为23.【解后反思】概率的计算先根据树状图或列表法确定所有可能情况，再从中确定满足条件的情况数，最后计算概率.【关键词】概率计算.14. (2016淅江丽水，14，4分) 已知x2+2x-1=0，则3x2+6x-2= .【答案】1.【逐步提示】本题考查整体代入法求代数式的值，解题的关键在于将待求式转化为已知式.采用整体代入法求值.【详细解答】解：3x2+6x-2=3（x2+2x-1）+1=0+1=1，故答案为1.【解后反思】整体代入法求值的关键在于对所求代数式的变形，将所求代数式变换为包含已知代数式的形式，再整体代入求值，变形方法包括拆项、添项、乘除某个因数或因式等.【关键词】整体思想；一元二次方程的值.15. (2016淅江丽水，15，4分)如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为E，F，延长BD至G，使得DG=BD，连接EG，FG，若AE=DE，则EGAB= .【答案】2.【逐步提示】本题考查菱形的性质，等边三角形的性质，特殊角的三角函数，解题的关键在于作出辅助线.①设出菱形的边长，用菱形的边长表示菱形中相关线段的长度；②连接EF，通过勾股定理确定EG的长，最后求得比值.【详细解答】解：因为AE=DE，BE⊥AD于E，所以AB=BD，又DG=BD，所以AB=AD=CB=CD=BD，所以△ABD与△CBD均为等边三角形，所以∠ABD=60°，所以∠EBD=30°，连接EF，交DB于H，设AB=AD=2,则ED=AE=1，DH=12,EH=2，HG=52，由勾股定理得EGAB=2.【解后反思】题目当中没有数据时，设出线段的长度可利于题目的计算，线段的长度的确定以利用以利于计算为标准. 求线段比值有两条途径：一是直接求解，即分别求得两线段的值，再计算比值；二是间接求解，通过相似、平行线等方法将线段的比转化为其他线段的比来计算.【关键词】菱形；勾股定理.16. (2016淅江丽水，16，4分如图，一次函数y=-x+b与反比例函数y=4x(x>0)的图象交于A，B两点，与x轴，y轴分别交于C，D两点，连接OA，OB，过A作AE⊥x轴于点E，交OB于点F.设点A的横坐标为m.(1)b= (用含m的代数式表示)（2）若S△OAF+S四边形EFBC=4,则m的值是.【答案】(1) m+4m.（2【逐步提示】本题考查一次函数与反比例函数的综合应用，不规则图形面积的计算，解决问题的关键在于作出辅助线确定△OEF与△BMC高的关系.①将点A横坐标代入反比例函数求得纵坐标，再将点A坐标代入一次函数即得b的值；②根据两函数的解析式求得A，B两点坐标，根据阴影部分面积间的关系推导出A，B，C三点横坐标间关系，通过方程求得m的值.【详细解答】解：由于点A在反比例函数y=4x上，所以设A点坐标（m,4m）,将点A 坐标代入一次函数得b= m+4m,所以点D（0, m+4m），点C（m+4m,0）.两函数解析式联立得44y x mmyx⎧=-++⎪⎪⎨⎪=⎪⎩，解得B点坐标为（4m，m），作BM⊥OC于M，则MC=OE=m,因为S 矩形AGOE =S △OAF + S △OAG + S △OEF = S △OAF +S 四边形EFBC =4，所以S △OAG + S △OEF = S 四边形EFBC = S 梯形EFBM + S △BMC = S △OBM -S △OEF + S △BMC ，因为S △OAG = S △OBM ，所以S △OEF = -S △OEF + S △BMC ，所以2S △OEF =S △BMC ,由于两个三角形底相等，所以MB=2EF ，所以EF 为△OBM 中位线，所以OE=EM=MC ，所以4m=2 m,解得【解后反思】将不规则图形转化为规则图形，通过图形间的转换得到各点坐标间的关系从而解决问题.【关键词】一次函数；反比例函数；阴影部分面积.三．解答题（本题有8小时，第17～19题第题6分，共66分）17. (2016淅江丽水，17，6分)计算：（-3）0【逐步提示】本题考查实数的计算，解决问题的关键在于理解实数的计算法则.根据运算法则进行计算.【详细解答】解：原式【解后反思】非零数的零次幂等于1；正数的绝对值是它本身，负数的绝对值是它的相反数，零的绝对值是零.【关键词】二次根式；零指数.18.(2016淅江丽水，18，6分)解不等式：3x-5<2(2+3x)【逐步提示】本题考查不等式的解，解决问题的关键在于运用法则进行计算.根据解不等式的步骤解不等式.【详细解答】解：去括号得：3x-5<4+6x ，移项得：3x-6x <4+5，合并同类项得：-3x <9，化系数为1得x>-3.【解后反思】不等式两边同时乘以或除以一个负数时不等号的方向要改变.【关键词】不等式的解法.19. (2016淅江丽水，19，6分)数据拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含45°的三角板的斜边与含30°的三角板的长直角边相等.于是，小陆同学提出一个问题：如图，将一副三角板直角顶点重合拼放在一起，点B ，C ，E 在同一相线上.若BC=2,求AF 的长.请你运用所学的数学知识解决这个问题.【逐步提示】本题考查特殊角的三角函数的应用，特殊角的三角函数值是解决问题的关键.①根据特殊角的三角函数由一条边长求得其他直角边长；②再通过分解法求得AF 的长.【详细解答】解：在RtA △ABC 中,BC=2, ∠A=30°, ∴由AC=tan A BC =2tan 30°由题意,得在RtA △EFC 中, ∠E=45°, ∴CF=EF×cos45°∴AF=AC-FC=2【解后反思】根据三角函数求得相关线段的长度是解题的关键.关键词】三角函数；三角板.20. (2016淅江丽水，20，8分)为了帮助九年级学生做好体育考试项目的选考工作，某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩，并制成如下两个统计图.请结合统计图信息解决问题：（1）“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍，求“跳绳”项目的女生人数；（2）若一个考试项目的男、女生总平均成绩不小于9分为“优秀”，试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目，并说明理由；（3）请结合统计图信息和实际情况，给该校九年级学生体育考试项目的选择提出合理化建议.【逐步提示】本题考查利用条形图及折线图解决实际问题，解决问题的关键在于理解统计图所表示的实际意义.（1）根据条形统计图中的数据作答；（2）根据折线统计图中的数据作答；（3）可从识图能力,数据分析能力,综合运用能力三方面对问题进行解答.【详细解答】解：（1）“跳绳”项目的女生人数=4006002+-260=240(人)；（2）观察男、女各项目平均成绩统计图可知：立定跳远、游泳、跳绳三项目的男、女生总平均成绩均小于9分，投篮项目的男、女生总平均成绩一定大于9分.投实心球项目的的男、女生总平均成绩=4008.76009.2400600⨯+⨯+=9，所以属于“优秀”项目的有投篮、掷实心球两个项目；（3）A 类（识图能力）：能用两统计图中的一个图提出合理化建议.如：游泳项目考试的人最多，可选考游泳.B 类（数据分析能力）：结合两统计图的数据提出合理化建议.如：“投篮”项目人数虽然不是最多，但平均成绩较高，建议选“投篮”.C类（综合运用能力）：能利用两统计图的数据并结合学生实际提出合理化建议.如：“跳绳”项目的报名人数少，男、女生的平均成绩都很低，若不是跳绳水平很高，建议不选择该项目.【解后反思】统计类问题的许多条件隐含在图表中，需要认真读图表，从图形中分析出有用的信息，然后作答.【关键词】条形统计图；折线统计图；统计思想方法.三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）21.(2016淅江丽水，21，8分)2016年3月27日“丽水半程马拉松竞赛”在莲都举行，某运动员从起点万地广场西门出发，途经紫金大桥，沿比赛路线回终点万地广场西门.设该运动员离开起点的路程S（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，根据图象提供的信息，解答下列问题：（1）求图中a的值；（2）组委会在距离起点2.1千米处设立一个拍摄点C，该运动员从第一次过C点到第二次过C点所用的时间为68分钟.①求AB所在直线的函数解析式；②该运动员跑完赛程用时多少分钟？【逐步提示】本题考查一次函数的实际应用，解决问题的关键在于理解一次函数图象中各关键点所表示的意义.（1）根据速度和时间计算路程；（2）①根据运动时间求出第二次经过C点时所用的时间，根据两点法求得AB的解析式；②根据直线AB的解析式求出运动员跑完赛程所用时间.【详细解答】解：（1）∵从起点到紫金大桥的平均速度是0.3千米/分，用时35分钟，∴a=0.3×35=10.5(千米).（2）①∵线段OA经过点O（0，0），A（35，10.5），，∴OA的函数解析式是S=0.3t(0≤t≤35).∴当S=2.1时，0.3t=2.1，解得t=7.∵该运动员从第一次过C点到第二次过C点所用的时间为68分钟，∴该运动员从起点到第二次过C共用的时间是7+68=75（分钟）.∴AB经过（35，10.5），（75，2.1）两设AB所在直线的函数解析式是S=kt+b,∴3510.5,75 2.1.k bk b+=⎧⎨+=⎩，解得0.21,17.85.kb=-⎧⎨=⎩∴AB所在直线的函数解析式是S=-0.21t+17.85②∵该运动员跑完赛程所用的时间即为直线AB与x轴交点横坐标的值∴当S=0时，-0.21t+17.85=0，解得t=85.∴该运动员跑完赛程用时85分钟.【解后反思】正比例函数及反比例函数的解析式需要一个点的坐标即可求出；一次函数的解析式需要两个点的坐标才能求出；二次函数的解析式需要三个点的坐标才能求出.【关键词】一次函数应用；待定系数法求函数的解析式.22. (2016淅江丽水，22，10分)如图，AB 是以BC 为直径的半圆O 的切线，D 为半圆上一点，AD=AB ，AD ，BC 的延长线相交于点E.⑴求证：AD 是半圆O 的切线；⑵连接CD ，求证：∠A=2∠CDE ；⑶若∠CDE =27°，OB=2,求BD 的长.【逐步提示】本题考查圆的相关性质，切线的判定，弧长的计算等，解决问题的关键在于辅助线的添加.⑴连接OD ，BD ，根据经过半径的外端，垂直于半径的直线为圆的切线进行证明； ⑵由各角间的关系进行推导得出结论；⑶由同角的余角相等推出∠DOC 的度数，再求出BD 的长.【详细解答】解：⑴连接OD ，BD ，∵AB 是半圆O 的切线，∴AB ⊥BC ，即∠ABO=90°. ∵AB=AD ，∴∠ABD=∠ADB ，∵OB=OD ，∴∠DBO=∠BDO ，∴∠ABD+∠DBO=∠ADB+∠BDO ，∴∠ADO=∠ABO=90°，∴AD 是半圆O 的切线. ⑵由⑴，∠ADO=∠ABO=90°，∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD. 而∠DOC=180°-∠BOD ∴∠A=∠DOC ，∵AD 是半圆O 的切线，∴∠ODE=90°，∴∠ODC+∠CDE =90°.∵BC 是直径，∴∠ODC+∠BDO =90°.∴∠BDO=∠CDE ，∵∠BDO=∠OBD ，∴∠ DOC =2∠BDO∴∠DOC =2∠CDE ，∴∠A =2∠CDE.⑶∵∠CDE=27°，∴由⑵得，∠ DOC =2∠CDE=54°，∴∠BOD =180°-54°=126°， ∵OB=2，∴BD l =1262180p 创=75π. 【解后反思】从同一点引两圆的两条切线，切线长相等；直径所对的圆周角相等；同角或等角的余角相等.【关键词】圆的切线的判定和性质；圆周角. 23. (2016淅江丽水，23，10分)如图，地面BD 上两根等长立柱AB ，CD 之间悬挂一根近似成抛物线y=110x 2-45x+3的绳子.（1）求绳子最低点离地面的距离；（2）因实际需要要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2）,使左边抛物线F1的最低点距MN为1米，离地面1.8米，求MN的长；（3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为14，设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时，求m的取值范围.【逐步提示】本题考查二次函数的实际应用，解决问题的关键在于根据题意表示顶点的坐标.（1）将二次函数的一般式化为顶点式求得；（2）借助顶点式设出二次函数的解析式，代入A点坐标求得解析式，再根据N点横坐标求得MN的长；（3）抛物线的二次项系数始终为14，说明二次函数的形状不变，要过同一点C时，只能是顶点的位置发生变化，顶点位置满足坐标(12m+4,k),从而得到二次函数的解析式，然后根据k的取值范围确定出m的取值范围.【详细解答】解:(1)∵a=110>0,∴抛物线顶点为最低点.∵y=110x2-45x+3=110(x-4)2+75，∴绳子最低点离地面的距离为75米.(2)由(1)可知,BD=8,令x=0得y=3, ∴A(0,3),C(8,3)，由题意得:抛物线F1的解析式为y=a(x-2)2+1.8.将(0,3)代入,得:4a+1.8=3,解得:a=0.3, ∴抛物线F1的解析式为y=0.3(x-2)2+1.8.当x=3时,y=0.3×1+1.8=2.1,所以MN的长度为2.1米.(3)∵MN=CD=3,∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,∴抛物线F2的顶点坐标为(12m+4,k), ∴抛物线F2的解析式为:y=14(x-12m-4)2+k把C(8,3)代入,得：14(4-12m)2+k=3, ∴k=-14(4-12m)2+3∴k=-116(m-8)2+3,∴k是关于m的二次函数.又∵由已知m<8，在对称轴的左侧，∴k随m的增大而增大.∴k=2时，-116(m-8)2+3=2,解得：m1=4,m2=12(不符合题意，舍去).k=2.5时，-116(m-8)2+3=2.5,解得：m12(不符合题意，舍去).∴m的取值范围是4≤m≤8【解后反思】在已知顶点的情况下利用顶点式列二次函数的解析式，抛物线平移前后二次项系数不变.【关键词】二次函数的应用.24. (2016淅江丽水，24，12分)如图，矩形ABCD 中，点E 为BC 上一点，F 为DE 的中点，且∠BFC=90°；（1）当E 为BC 中点时，求证：△BCF ≌△DEC ；（2）当BE=2EC 时，求CD BC的值；（3）设CE=1,BE=n,作点C 关于DE 的对称点C′，连接FC′，AF ，若点C′到AF的距离是5，求n 的值.【逐步提示】本题考查矩形的性质，三角形全等的判定方法及性质，相似三角形的判定及性质，勾股定理等知识，解决问题的关键在于通过辅助线将未知条件转化到同一图形当中.（1）由矩形的性质及直角三角形斜边中线的性质根据ASA 判定△BFC ≌△DCE ；（2）通过相似三角形用同一量表示出CD 、BC 间的关系，通过比例式求得CD BC的值；（3）过C′作C′H ⊥AF 于点H ，连接CC′交EF 于M ，通过Rt △EMC 和Rt △FMC 建立方程经计算求得CF 的长，再由△BFC ∽△DCE 计算出CF 的长，两者建立方程计算出n 的值.【详细解答】解：（1）∵在矩形ABCD 中，∠DCE=90°,F 是斜边DE 的中点，∴CF=EF ，∴∠FEC=∠FCE.又∵∠DCE=90°,且E 为BC 的中点，∴EF=EC ，∴CF=CE在△BFC 与△DCE 中，∵∠BFC=∠DCE ，CF=CE ，∠FCB=∠DEC ，∴△BFC ≌△DCE.（2）设CE=a ，由BE=2CE ，得BE=2a,BC=3a.∵∠FEC=∠FCE, ∠BFC=∠DCE=90°, ∴△BFC ∽△DCE ∴CF BC EC ED =,即132ED a a ED=，∴12ED 2=3a 2, ∴ED 2=62, ∴∴CD BC=3a=3（3）过C′作C′H ⊥AF 于点H ，连接CC′交EF 于M ，由（2）得：FC=EF=FD ，∠FEC=∠FCE.∵AD ∥BC ，∴∠ADF=∠CEF ，∴∠ADF=∠BCF.∵AD=BC ，∴△ADF ≌△BCF ，∴∠AFD=∠BFC=90°∵C′H ⊥AF ，C′C ⊥EF ，∴∠HFE=∠C′HF=∠C′MF=90°.∴四边形C′MFH 是矩形，∴FM=C′H=5.设EM=x ，则. 在Rt △EMC 和Rt △FMC 中，由勾股定理得：22CE EM -= CF 2-FM 2∴1 2-x 2) 2)2，解得：x 1,x 2-由（2）得，CF BC EC ED =，将CE=1,BE=n 代入计算，得CF=2.∴2=10+5，解得：n=4. 【解后反思】借助于相似三角形边长之比求相关线段的比值；利用双直角三角形公共边长建立方程求解相关线段的长度.【关键词】矩形的判定及性质；全等三角形；相似三角形的判定及性质；勾股定理.。