数列中的整数问题
给出一个包含n个整数的数列,问整数a在数列中的第一次出现是第几个。

给出一个包含n个整数的数列,问整数a在数列中的第一次出现是第几个。
在解决此类问题时,我们可以先给出一个计算题的背景;
我们给出的是一个包含n个整数的数列,数列中的每个数字都有一个编号,比如说1号,
2号,3号,......,n号。
那么我们要求的是,数列中整数a在数列中的第一次出现是第几
个数字?
为了解决这个问题,我们需要首先仔细分析问题,对题目中给出的条件及要求是否有足够
的准确性,以便我们清晰地了解题目type和条件,以便明确问题的解决方法。
从上面的分析,我们可以得出结论:此题是一个查找的问题,我们要在给定的n个整数中,找出我们要求的a项,即要求整数a在数列中的第一次出现是第几个数字。
对于此问题,解决的最常见的方法就是采用循环遍历的方法,即我们从数列中的第一个元
素开始遍历,一一比较,直到找到我们要求的a项,这时就可以知道其第一次出现是第几
个元素。
从上述方法可知,解决此类问题,不仅要清晰地分析问题,而且还要采用正确的方法,才
能得到准确的答案。
因此,通过仔细分析问题,使用正确的方法,我们就可以找到数列中
整数a在数列中的第一次出现是第几个数字。
fibonacci数列递归算法的实现,集合全排列问题递归算法的实现,整数划分问题递归算

Fibonacci数列、集合全排列和整数划分问题Fibonacci数列Fibonacci数列是一个由0和1开始,每个后续数字等于前两个数字之和的数列。
以下是Fibonacci数列的递归算法实现:// 递归实现Fibonacci数列function fibonacci(n) { if (n <= 1){ return n; } return fibonacci(n - 1) + fibonacci(n - 2);}集合全排列集合全排列问题是指给定一个集合,求该集合中元素的全排列。
以下是集合全排列的递归算法实现:// 递归实现集合全排列function permute(arr, start = 0) { if (start === arr.length) { console.log(arr); // 输出当前排列 } for (let i = start; i < arr.length; i++) { // 交换当前元素与起始位置元素 [arr[start], arr[i]] = [arr[i], arr[start]]; permute(arr, start + 1); // 递归调用下一次排列 [arr[start],arr[i]] = [arr[i], arr[start]]; // 恢复当前元素与起始位置元素的交换 }}整数划分整数划分问题是指将一个整数拆分成多个正整数的和,求所有的划分方式。
以下是整数划分的递归算法实现:// 递归实现整数划分function partition(n, max, prefix = []) { if (n === 0) { console.log(prefix); // 输出当前划分 } for (let i = Math.min(max, n); i >= 1; i--) { partition(n - i, i, [...prefix, i]); // 递归调用下一次划分 }}。
与数列有关的不定方程的整数解问题初探

与数列有关的不定方程的整数解问题初探一、引言数列是我们在数学学科中常见的概念,而不定方程则是我们在初等数论和高等代数中学习的一个重要概念。
在实际应用中,数列和不定方程经常出现在一起,这篇文章将重点探讨与数列有关的不定方程的整数解问题。
二、数列与不定方程数列是按一定规律排列的数,也可称为序列。
数列在数学中的基本概念是不同的,它们可能是线性、比例、等差、等比数列等各种类型,但无论哪种类型,数列都可以用递推公式进行表达。
而不定方程则是一种带有未知数的方程,它通常的形式是$f(x,y)=0$,其中 $x$ 和 $y$ 都是未知数,每个 $x$ 和 $y$ 的取值都可以使该方程成立。
不定方程的解通常被称为整数解(或非负整数解、正整数解等)。
三、与数列有关的不定方程的整数解问题在实际应用中,我们有时需要求解与数列有关的不定方程的整数解问题,例如下面这个经典问题:【问题】求解正整数 $a$ 和 $b$,使得 $a^2-b^2=100$。
我们可以通过枚举发现 $a=11$,$b=9$ 或者 $a=50$,$b=48$ 都是方程的解。
但这种方法并不是很高效,特别是当方程的解特别多时,我们很难通过枚举的方式来找到所有的解。
对于这种问题,我们可以采用分析的方法。
对于上面的问题,我们不妨设$a+b=p$,$a-b=q$,其中$p$ 和$q$ 都是正整数。
不难发现,由于 $a$ 和 $b$ 都是正整数,所以 $p$ 和 $q$ 都大于 $1$。
将上面的式子代入原方程得:$$(\frac{p+q}{2})^2-(\frac{p-q}{2})^2=100$$这是一个关于 $p$ 和 $q$ 的不定方程,我们可以将它化简为:$$pq=50$$这时,我们可以列举 $50$ 的各个因数来确定 $p$ 和 $q$ 的值,从而得到 $a$ 和 $b$ 的值。
例如,当 $p=25$,$q=2$ 时,我们有:$$a=\frac{p+q}{2}=13,b=\frac{p-q}{2}=12$$当 $p=10$,$q=5$ 时,我们有:$$a=\frac{p+q}{2}=7,b=\frac{p-q}{2}=3$$通过这种方法,我们可以找到所有的解,而不必进行枚举。
数列极限定义中的任意正数的理解

数列极限定义中的任意正数的理解在数学中,数列极限是一个重要的概念,它描述了数列中的数随着项数的增加逐渐趋近于某个确定的值。
在数列极限定义中,我们要求这个确定的值为任意正数。
那么,数列极限到底是如何定义的呢?数列极限的定义是这样的:对于任意正数ε(读作epsilon),存在一个正整数N,使得当n大于N时,数列的第n项与极限之间的差的绝对值小于ε。
换句话说,无论我们选择多小的正数ε,总存在一个项数N,使得从第N项开始,数列的每一项都与极限之间的差的绝对值都小于ε。
这个定义可能有些抽象,我们可以通过一些具体的数列来理解。
例如,考虑数列an = 1/n,其中n是正整数。
我们可以发现,随着n 的增大,an的值逐渐趋近于0。
根据数列极限的定义,我们可以选择任意小的正数ε,然后找到一个项数N,使得当n大于N时,an 与0的差的绝对值小于ε。
这个例子中,我们可以选择ε=0.001,然后找到N=1000,当n大于1000时,an与0的差的绝对值小于0.001。
也就是说,从第1001项开始,an的值都在0.001的范围内。
数列极限的定义可以用来判断数列是否收敛,即数列是否存在极限。
如果一个数列存在极限,我们称其为收敛数列;如果一个数列不存在极限,我们称其为发散数列。
根据数列极限的定义,如果对于任意正数ε,存在一个项数N,使得从第N项开始,数列的每一项都与极限之间的差的绝对值小于ε,那么这个数列就是收敛数列;如果存在一个正数ε,无论我们选择多小的项数N,总存在一个项数n 大于N,使得数列的第n项与极限之间的差的绝对值大于ε,那么这个数列就是发散数列。
例如,数列bn = (-1)^n,其中n是正整数。
这个数列的项交替取正负值,没有固定的趋势。
我们可以发现,无论我们选择多小的正数ε,总能找到一个项数N,使得从第N项开始,数列的每一项与极限之间的差的绝对值大于ε。
因此,这个数列是一个发散数列。
数列极限的定义也可以用来证明数列的极限。
学而思讲义四年级数学第一讲:整数与数列.pdf

第一讲 整数与数列一、复习等差数列1、通项公式:什么时候用?——知道首项和公差,求某一项 第n 项=首项+公差×(n-1)2、项数公式:什么时候用?——知道首项、末项及公差,求项数 项数=(末项-首项)÷公差+13、求和公式(高斯公式):什么时候用?——任何一个等差数列求和和=(首项+末项)×项数÷2辅助记忆:装皮鞋4、中项公式:什么时候用?——对于容易找到中项的等差数列求和 和=中项×项数 注意:高斯公式与中项公式的联系高斯公式:和=(首项+末项)×项数÷2二、常用公式 1、从1开始连续奇数求和=项数2即:1 + 3 + 5 + 7 + … +(2n-1)= n 2图示:2、金字塔数列=中项2 即:1 + 2 + 3 + … +(n-1)+ n +(n-1)+ … + 3 + 2 + 1 = n 2图示:1 3 5 7 9四年级秋季班(七级下) 1.2 三、平方差公式:a 2 - b 2=(a+b)×(a-b)……两数平方差=两数和×两数差几何证明:a 2 -b 2表示的是图中大正方形减去黑色小正方形后的空白部分的面积,沿虚线将空白部分减成两部分再拼接起来,即为一个长方形的面积。
该长方形长为a+b,宽为a-b,面积为(a+b)×(a-b),得证。
特例: 两数相差为1,其平方差就是两数和372-362=(37+36)×(37-36)=37+36四、平方差公式拓展:(逆向思维)既然平方差=和×差,那么两个数相乘能否转化为平方差的形式呢?1、若两数的奇偶性相同,则这两数的乘积可化为平方差的形式。
如:41×3941=a+b,39=a-b ,利用和差公式即可算出a=40,b=1(a 即是41与39的平均数)所以 41×39=(40+1)×(40-1)=402-122、进而,若两数相差不大,且两数和为整十整百时,乘积改写为平方差可简化计算如:68×72=(70-2)×(70+2)=702-22=4900-4=4896五、自然数列的平方和公式12+22+32+…+n 2=n(n+1)(2n+1)÷6图示证明:a b 12 23 3 3 ……n n n …左边的正三角形即为自然数列的平方和,将其翻转两次得到右边的两个三角形数表。
数列极限证明中的_N语言问题

使
1 n
<
ln( 1 + ln2
E)
成立的
N,
并不能保证
1 n
<
ln( 1+ E) lnn
成立. 这里, 误将探求使 nn - 1 < E成立的充分条
件当必要条件来探求, 逻辑关系上出错. 正确证法 记n n = 1+ hn , hn > 0( n > 1) , 则
n=
(1+
hn ) n >
n( n2
CAO H ui Zhen
( Science Depa rtment of Oujiang College, Wenzhou U niversit y, Wenzhou, Zhejiang 325035, P RC)
Abstr act: F or a proof about a nubmer sequence, a quest ion is called in, and t hen answered wit h a corr ect E2N descript ion. Fr om which, t he logic in t he E2N descript ion is analyzed in det ail, and examples ar e given t o show t he t rickiest par t in limit proving.
ny ]
n) =
1 2
.
错误证法 对任意 E> 0, 为使
n( n + 1 -
n) -
1 2
<
1 2
1+
1 n
< E,
只要
数列中的不定方程整数解问题

无理数≠有理数
处理方法:找矛盾 (有理数与无理数)
若p+r-2q=0,则 q2 pr 0 数学思想:分类讨论
……
热身训练
an 7 bm n2 7 4m2
2m n2m n 7 2m n 2m n 15 ?
存在 有(正整数)解 处理方法:解方程(因式分解、分解质因数、范围) 数学思想:分类讨论
2aq
ap
ar
2 2q
2p
2r
2q1 pห้องสมุดไป่ตู้ 1 2r p
偶数 ≠ 奇数
……
不存在 无(正整数)解
处理方法:找矛盾 (奇数与偶数) 数学思想:化归(消元) 分类讨论
热身训练
aq2 ap ar q
2
2
p
2 r
2
q2 pr 2 p r 2q
若p+r-2q≠0,则 2 q2 pr
典例剖析
典例剖析
总结反思
解题之道
转化策略 数列中的一类存在性问题 → 不定方程的整数解问题
常用 处理方法
存在 有(正整数)解 不存在 无(正整数)解
因式分解 分解质因数
奇数与偶数
解方程 范围
找矛盾 有理数与无理数
分离常数 整除
利用单调性(有界)
数学思想 分类讨论 特殊与一般 转化与化归
核心素养
心中有数
存在性问题在数列解答题中的考查
在历年江苏高考卷中
2008年 第19题
2009年 第17题
2014年 第20题
2015年 第20题
2018年 2019年
第20题
?
江苏省13大市高三期末考试中
无锡
第20题
整数与数列

整数与数列【知识导学】一、枚举法将所有可能情况全部列举出来,再从中找到最大或最小的情况。
二、极端分析法从最极端的情况出发考虑。
三、最值原理1.和一定,差小积大;2.积一定,差小和小。
四、1.拆若干个不可以重复的数,乘积最大:从2开始的连续自然数;2.拆若干个可以重复的数,乘积最大:多3,少2,无1。
【例1】在五位数12345的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到122345),这样得到的六位数最大可能是多少?【即学即练1】在五位数1234的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到12234),这样得到的五位数最大可能是多少?【例2】电视台要播放一部30集的电视连续剧。
如果要求每天安排播出的集数互不相等,不能不播,该电视连续剧最多可以播几天?【即学即练2】19个苹果要分给一群小朋友,每一个小朋友所分得的苹果数都要不一样,且每位小朋友至少要有一个苹果。
问:这群小朋友最多有几位?【例3】(1)周长为100米的长方形中,面积最大是平方米。
(2)面积为100平方米的长方形中,周长最小是米。
【即学即练3】用24根长1厘米的小棍围成一个长方形,这个长方形的面积最大是多少?如果用22根呢?【例4】用1,2,3,4,5,6这6个数字各一次,分别组成两个三位数,求积最大时算式是是什么?【即学即练4】请将2,3,4,5,6,8”的方格中,要使得算式结果最大,应该怎么填?【例5】(1)3个互不相同的自然数之和是17,它们的乘积最大可能是多少?(2)若干个互不相同的自然数之和是17,它们的乘积最大可能是多少?【即学即练5】3个自然数之和是17,它们的乘积最大可能是多少?【例6】把16拆成若干个可重复自然数的和,使这些自然数的乘积最大,最大乘积是多少?【即学即练6】把12拆成若干个可重复自然数的和,使这些自然数的乘积最大,最大乘积是多少?【巩固练习】1、在三位数234的某一位数字后面再插入一个同样的数字,这样得到的四位数最大可能是多少?2、有4袋糖块,其中任意3袋糖块的数量总和都超过60块。
取整函数与数列的变化规律分析

取整函数与数列的变化规律分析在数学领域中,取整函数是一种常见的数学函数,用于将实数映射为最接近且小于或等于该实数的整数。
它一般表示为符号“[x]”,其中x 是待取整的实数。
在本文中,我们将分析取整函数与数列的变化规律,并探讨它们之间的关系。
一、取整函数取整函数,也被称为向下取整函数或地板函数,它的定义如下:对于任意实数x,取整函数[ ]将x映射为最大的整数n,使得n ≤ x。
例如,[3.6] = 3,[-2.3] = -3。
取整函数的主要特点是将实数映射为整数,且保持不等式关系。
即对于任意实数a和b,如果a ≤ b,则[ a ] ≤ [ b ]。
取整函数在实际应用中具有广泛的用途。
例如,在计算机科学中,取整函数常用于对浮点数进行取整运算,以满足特定需求。
在统计学中,取整函数可用于对实验数据进行近似处理,以简化计算。
二、数列的变化规律数列是按照一定规则排列的一系列数字的集合。
在数列中,每个数字被称为数列的项,而产生数列的方法被称为数列的变化规律。
数列的变化规律可以是以等差或等比的方式变化,也可以是按照其他规则进行变化。
数列的变化规律有时可以通过观察前几项来确定,并使用数学方法进行验证和推导。
在分析数列的变化规律时,我们可以借助取整函数来观察数列中的整数项。
通过分析数列中的整数项的特点,我们可以推测数列的变化规律。
三、取整函数与数列的关系在某些数列中,取整函数与数列的项之间存在着一定的关系。
这种关系可以帮助我们进一步理解数列的变化规律。
例如,考虑以下数列:2.1, 3.2, 4.5, 6.8, 9.1, ...我们可以观察到该数列中的每个数都经过了取整函数的处理。
具体而言,[2.1] = 2,[3.2] = 3,[4.5] = 4,[6.8] = 6,[9.1] = 9,...通过分析这些取整后的整数项,我们可以发现数列的变化规律是每一项都是前一项加1。
即2, 3, 4, 6, 9, ...这个例子说明了取整函数与数列之间的关系。
简单整数数列的计算
=30×4+15
=135
例【3】计算:101+102+103+104+105+106+107+108+109+110
分析此题中每个数里都包含了一个100,可以把这10个100分离出来,转化为例【1】
解101+102+103+104+105+106+107+108+109+110
配对求和
(简单整数数列的计算)
知识要点:配对技巧项数的确定
小朋友们,你听过德国著名数学家、物理学家和天文学家高斯的故事吗?他从小就聪颖过人,还在他8岁的时候,老师给班上同学出了一道题:1+2+3+4+……+99+100=?8岁的高斯很快报出了得数:5050。这个答案完全正确!最让老师吃惊的是,小高斯计算的速度如此快捷!那么,小高斯是用什么办法算得这么快的呢?原来,根据所给算式的特点,他用了一种巧妙的方法——配对求和。采用这种方法,很多整数数列求和的问题都能迎刃而解了。
=100×10+(1+2+3+4+5+6+7+8+9+10)
=1000+11×5
=1055
例【4】计算500-(11+13+15+17+19+21+23+25+27+29)
分析先用配对的方法计算11+13+15+17+19+21+23+25+27+29
11+13+15+17+19+21+23+25+27+29
典型例题
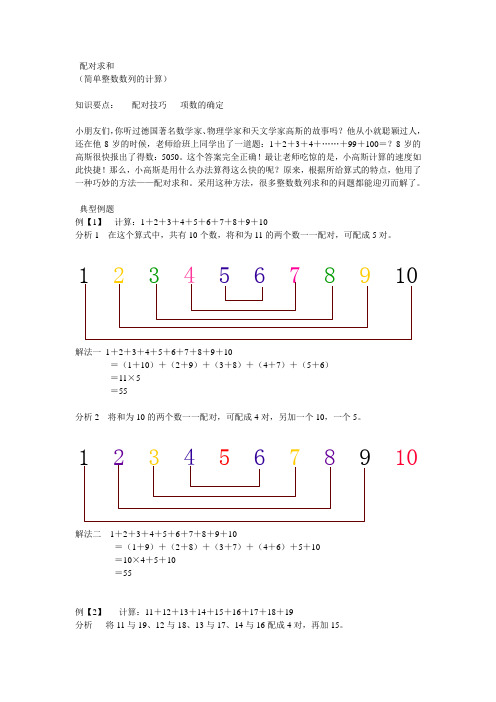
例【1】计算:1+2+3+4+5+6+7+8+9+10
分析1在这个算式中,共有10个数,将和为11的两个数一一配对,可配成5对。
解法一1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11×5
=55
新高考数学数列经典题型专题提升-第19讲 数列的取整问题(原卷版)

第19讲 数列的取整问题一、单选题1.(2021·全国·高三专题练习)设正项数列的前n 项和满足,记表示不超过x 的最大整数,.若数列的前n 项和为,则使得成立的n 的最小值为()A .1179B .1178C .2019D .20202.(2021·全国·高三专题练习)设[x ]表示不超过x 的最大整数,如[-3.14]=-4,[3.14]=3.已知数列{a n }满足:a 1=1,a n +1=a n +n +1(n ∈N *),则=()A .1B .2C .3D .43.(2021·江西省吉水县第二中学高一期中)高斯函数,也称为取整函数,即表示不超过x 的最大整数. 如: 已知正项数列的前项和为,且满足,则( )A .3B .14C .15D .164.(2021·江西·南昌市八一中学高一月考)对于实数,表示不超过的最大整数.已知数列的通项公式项和为,则( ).A .155B .167C .173D .1795.(2021·河南·高二月考(理))定义函数,其中表示不超过的最大整数,例如,,,,当时,的值域为,记集合中元素的个数为,数列的前项和为,则( )A .B .2C .D .6.(2021·四川射洪·模拟预测(文))定义函数,其中表示不超过的最大整数,例如:,,.当时,的值域为.记集合中元素的个数为,则{}n a n S ()2114n n S a =+[]x 212020n n a b ⎡⎤=+⎢⎥⎣⎦{}n b n T 2020n T ≥12320201111a a a a ⎡⎤++++⎢⎥⎣⎦ []x []x []2.32=,[]1.5 2.-=-{}n a n n S 112n n n S a a ⎛⎫=+ ⎪⎝⎭1264111S S S ⎡⎤++⋅⋅⋅+=⎢⎥⎣⎦1x []x x {}n a n a =n n S [][][]1250S S S +++=L ()[]f x x x ⎡⎤=⎣⎦[]x x []21.1-=-[]1.11=[]33=[)()0,x n n *∈∈N ()f x n A n A n a 111n a +⎧⎫⎨⎬-⎩⎭n n S 2021S =202110104040202120211011()[[]]f x x x =[]x x [1.3]1=[ 1.5]2-=-[2]2=*[))0,(x n n N ∈∈()f x n A n A n a的值为( )A .B .C .D .7.(2021·全国·高三月考(理))高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的美誉,用其名字命名的“高斯函数”:设用表示不超过的最大整数,则称为高斯函数,也称取整函数.在数列中,记为不超过的最大整数,则称数列为的取整数列,设数列满足,,记数列的前项和为,则数列的前项和为( )A .B .C .D .8.(2021·浙江省杭州第二中学模拟预测)定义表示不超过的最大整数,若数列的通项公式为,则满足等式( )A .30B .29C .28D .279.(2021·全国·高三专题练习(理))已知各项均为正数的数列的前n 项和为,且,.若表示不超过x 的最大整数,,则数列的前2021项和()A .1010B .1011C .2021D .202210.(2021·全国·高三专题练习(文))已知数列满足,,其中表示不超过实数的最大整数,则下列说法正确的是()A .存在,使得B .是等差数列C .的个位数是4D .的个位数是311.(2021·青海西宁·一模(理))若是函数的极值点,数列2020211i ia =-∑40402021201920212019202020191010x =R []x x []y x={}n a []n a n a []{}n a {}n a {}n a 11a =1213n n a a +⎡⎤⎡⎤+⎢⎥⎢⎥⎣⎦⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦{}n a n n S 21211n n S S -+⎧⎫⎨⎬⎩⎭101050420215052021101020215042022[]x x {}n a 31n a n =-310125555a a a a ⎡⎤⎡⎤⎡⎤⎡⎤++++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ {}n a n S 11a =()()1111n n n n a a a a ++-=+[]x 2(1)2n n n b S ⎡⎤+=⎢⎥⎣⎦{}n b 2021T ={}n a 11a =()1*N n a n +=∈⎢⎥⎣⎦[]x x *N n ∈132n n a -≤12n a ⎧⎫-⎨⎬⎩⎭2020a 2021a 1x =()()4312 1n n n f x a x a x a x n N *++=--+∈{}n a满足,,设,记表示不超过的最大整数.设,若不等式,对恒成立,则实数的最大值为( )A .B .C .D .12.(2021·全国·高三专题练习(理))已知函数(,),其中表示不超过的最大整数,如,,.定义是函数的值域中的元素个数,数列的前项和为,数列对均成立,则最小正整数的值为( )A .B .C .D .13.(2021·浙江·高三专题练习)如果,,,就称表示的整数部分,表示的小数部分.已知数列满足,,则等于( )A .B .C .D .二、多选题14.(2021·重庆南开中学高三月考)已知数列满足,,其中表示不超过实数的最大整数,则下列说法正确的是()A .存在,使得B .是等比数列C .的个位数是5D .的个位数是1三、填空题15.(2021·上海·华师大二附中高三月考)设数列满足,,,数列前n 项和为,且(且),若表示不超过x 的最大整数,数列的前n 项和为,则_____________.16.(2021·重庆·西南大学附中高三开学考试)设数列满足,,,数列前n11a =23a =31log n n b a+=[]x x 12231202020202020n n n S b b b b b b +⎡⎤=++⋅⋅⋅+⎢⎥⎣⎦n S t ≥n N *∀∈t 2020201910101009()[[]]f x x x =1n x n <<+n ∈+N []x x [ 2.1]3-=-[3]3-=-[2.5]2=n a ()f x {}n a n n S 1110ni i mS =<∑n ∈+N m 17181920{}[]x x x =+[]x Z ∈{}01x ≤<[]x x {}x x {}n a 1a ={}12[]n n n a a a +=+20192018a a-2019201866{}n a 11a =()1n a n *+=∈⎢⎥⎣⎦N []x []x n *∈N 132n n a -≤12n a ⎧⎫-⎨⎬⎩⎭2020a 2021a {}n a 12a =26a =312a =n S 211131n n n n S S S S +-+-+=-+*n N ∈2n ≥[]x ()21n n n b a ⎡⎤+=⎢⎢⎥⎣⎦{}n b n T 2020T ={}n a 12a =26a =312a ={}n a项和为,且(且).若表示不超过x 的最大整数,,数列的前n 项和为,则的值为___________.17.(2021·江西省石城中学高一月考(文))已知正项数列的前项和为,且满足,则_______.(其中表少不超过的最大整数).18.(2021·江西省铜鼓中学高一月考(理))已知正项数列的前n 项和为,且,则不超过的最大整数是_____________.19.(2021·全国·高三专题练习(文))已知表示不超过的最大整数,例如:,在数列中,,记为数列的前项和,则 ___________.20.(2021·四川·石室中学一模(文))已知数列的前项和为,点在上,表示不超过的最大整数,则_______________________.21.(2021·全国全国·模拟预测)黎曼猜想由数学家波恩哈德·黎曼于1859年提出,是至今仍未解决的世界难题.黎曼猜想研究的是无穷级数,我们经常从无穷级数的部分和入手.已知正项数列的前项和为,且满足,则______(其中表示不超过的最大整数).22.(2021·上海·位育中学三模)已知正项等比数列中,,,用表示实数的小数部分,如,,记,则数列的前15项的和为______.四、双空题23.(2021·北京师大附中高一月考)定义函数,其中表示不超过x 的最大整数,例如:,, 当时,的值域为(1)____________.n S 211131n n n n S S S S +-+-+=-+n N ∈g 2n ≥[]x 2(1)n n n b a ⎡⎤+=⎢⎥⎣⎦{}n b n T 2022T {}n a n n S 112n n n S a a ⎛⎫=+ ⎪⎝⎭2132109111S S S S S S ⎡⎤+=⎢⎥+++⎣⎦[]x x {}n a n S 11()2n n na S a +=122025111S S S +++ []x x [2.3]2=[]1.52-=-{}n a []lg ,n a n n N +=∈n T {}n a n 2021T ={}n a n n S (),n n a y x =[]x x 122021202120212021222S S S ⎡⎤++⋯+=⎢⎥⎣⎦()1111123ss s sn s n ξ∞-===+++⋅⋅⋅∑1111123s s s s n +++⋅⋅⋅+{}n a n n S 112nn n S a a ⎛⎫=+ ⎪⎝⎭12100111S S S ⎡⎤++⋅⋅⋅+=⎢⎥⎣⎦[]x x {}n a 3123a a a =42563a ={}x x {}1.50.5={}2.40.4={}n n b a ={}n b 15S ()[[]]f x x x =[]x [1.3]1=[ 1.5]2-=-[2] 2.=*[))0,(x n n N ∈∈()f x .n A 7(2f =(2)集合中元素的个数为__________.24.(2021·福建·三明一中模拟预测)黎曼猜想由数学家波恩哈德∙黎曼于1859年提出,是至今仍未解决的世界难题.黎曼猜想研究的是无穷级数,我们经常从无穷级数的部分和入手.已知正项数列的前n 项和为﹐且满足,则__________,__________.(其中表示不超过x 的最大整数)25.(2021·广东珠海·高三月考)定义函数,其中表示不超过x 的最大整数,例如,,当时,的值域为,记集合中元素的个数为,则(1)_________;(2)_________.五、解答题26.(2021·河南·高三月考(文))已知公比大于的等比数列满足,,定义为不超过的最大整数,例如,,,,记在区间()上值域包含的元素个数为.(1)求数列和的通项公式;(2)求数列的前项和.27.(2021·福建·高三月考)等差数列中,,.(1)求的通项公式;(2) 设,求数列的前10项和,其中表示不超过的最大整数,如,.28.(2021·福建·泉州五中高二期中)已知函数的最小值为0,其中.(1)求的值(2)若对任意的,有恒成立,求实数的最小值;(3)记,为不超过的最大整数,求的值.29.(2021·广东南海·高三开学考试)已知数列的前项和,令,其中10A 1111()123ss s sn n nξ∞-===+++∑ 1111123s s s sn ++++ {}n a nS 11()2n n n a S a +=n S =12100111S S S ⎡⎤++=⎢⎥⎣⎦ []x ()][][f x x x =[]x [][][]1.31, 1.52,22=-=-=[)0,,N x n n *∈∈()f x n A n A n a 2a =211nk ka ==-∑1{}n a 5115a a -=2416a a ⋅=[]x x []1.31=[]1.52-=-[]22=()[]f x x =[)1,n n -*n ∈N n b {}n a {}n b {}n n a nb +n n S {}n a 344a a +=576a a +={}n a []n n b a ={}n b []x x []0.90=[]2.62=()()ln f x x x a =-+0a >a [)0,x ∈+∞2()f x kx ≤k 12ln(21)21nn i S n i ==-+-∑[]x x []n S {}n a n (1)2n n n S +=3log na nb ⎡⎤=⎣⎦[]x表示不超过的最大整数,,.(1)求;(2)求;(3)求数列的前项之和.30.(2021·全国·高二课时练习)已知各项均为正数的无穷数列的前项和为,且,.(1)求数列的通项公式;(2)记表示不超过的最大整数,如,. 令,求数列的前项和.31.(2021·浙江·模拟预测)已知数列满足,,数列满足,.(1)数列,的通项公式;(2)若,求使成立(表示不超过的最大整数)的最大整数的值.32.(2021·全国·高三专题练习(理))高斯函数中用表示不超过的最大整数,对应的为的小数部分,已知数列的前项和为,数列满足.已知函数在上单调递减.(1)若数列,其前项为,求.(2)若数列(即为的小数部分),求的最大值.33.(2021·广东汕头·三模)已知数列的前n 项和为,数列是首项为,公差为的等差数列,若表示不超过x 的最大整数,如,.(1)求数列的通项公式;(2)若,求数列的前2020项的和.34.(2021·全国·高三专题练习)已知各项均为正数的数列的前n 项和为,,x []0.90=83log 1⎡⎤=⎣⎦n a 100b {}n b ()*31m m N -∈{}n a n n S 11a =1(1)(1)n n nS n S n n +=+++*()N n ∈{}n a []x x [0.99]0=[3.01]3=n b ={}n b 5151T {}n a 112a =123n n a a ++={}nb 11b =()211n n nb n b n n +-+=+{}n a {}n b ()1n n n nc b b a +=-[][][][]1222021n c c c c +++⋅⋅⋅+≤[]n c n c n []x x {}[]x x x =-x n a n 112n-n b 2n n b n a =()22x x f x =[)4,+∞[]n n c b =n n S 10S {}n n d b =n d n b n d {}n a n S n S n ⎧⎫⎨⎬⎩⎭1214[]x []0.50=[]lg 4992={}n a []lg n n b a ={}n b {}n a n S 11a =.(1)求证;数列是等差数列,并求的通项公式;(2)若表示不超过的最大整数,如,,求证:.35.(2021·浙江·温岭中学高三月考)正项等差数列和等比数列{b n }满足.(1)求数列,的通项公式;(2)若数列,,求最大整数,使得.36.(2021·全国·高三专题练习)在①;②;③是与的等比中项,三个条件中任选一个,补充在下面问题中,并给出解答.问题:已知为公差不为零的等差数列,其前项和为为等比数列,其前项和为常数,,(1)求数列的通项公式;(2)令其中表示不超过的最大整数,求的值.注:如果选择多个条件分别解答,按第一个解答计分.37.(2021·全国·高三专题练习)已知等比数列的公比为,且,数列满足,.(1)求数列的通项公式.(2)规定:表示不超过的最大整数,如,.若,,记求的值,并指出相应的取值范围.)*,2n a n n =∈≥N {}n a []x x []122-=-,[]2,12=222121111n a a a ⎡⎤+++=⎢⎥⎣⎦ {}n a 1211221,22n n n a a a n a b b b +=+++=- {}n a {}n b ()()111n n n n n n b c b a b a ++-=--12n n S c c c =+++ 0n 020202021n S <3514a a +=428S =8a 5a 13a {}n a n {},n n S b n 2,nn T λλ=+11a b ={}{}n n a b ,[]lg n n c a =,[]x x 123100c c c c +++⋯+{}n a ()1λλ>11a ={}n b 11n n n b b a λ++-=-111b λ=-{}n b []x x []1.22-=-[]2.12=2λ=122n n c b n =+-()1232n n T c c c c n =+++⋅⋅⋅+≥2221n n n T T T ⎡⎤-+⎢⎥-⎣⎦n。
数列中的整数问题典例精讲

数列中的整数问题典例精讲1.已知数列a n 的通项公式为a n =2n -7,若a m a m +1a m +2为数列a n 中的项,则m =思路:a m a m +1a m +2=2m -7 2m -5 2m -3,a n 中的项为大于等于-5(a 1=-5)的奇数,所以考虑将a m a m +1a m +2向奇数形式变形:2m -7 2m -5 2m -3=2m -3 -4 ⋅2m -3 -2 2m -3=2m -3 -6+82m -3=2m -9+82m -3,可得82m -3应该为大于等于4的偶数,所以82m -3=4或82m -3=8,解得m =52(舍)或m =2答案:m =22.已知等差数列a n 的公差d >0,设a n 的前n 项和为S n ,a 1=1,S 2⋅S 3=36(1)求a n 的通项公式(2)求m ,k m ,k ∈N ∗ 的值,使得a m +a m +1+⋯+a m +k =653.已知数列a n 的前n 项和为S n ,且S n =12n 2+112n n ∈N ∗ (1)求数列a n 的通项公式(2)设f n =a n (n =2k -1,k ∈N ∗)3a n -13(n =2k ,k ∈N ∗) ,是否存在m ∈N ∗,使得f m +15 =5f m 成立?若存在,求出m 的值;若不存在,请说明理由解:(1)S n =12n 2+112n ,S n -1=12n -1 2+112n -1 n ≥2 ∴a n =S n -S n -1=n +5n ≥2 ①∵a 1=S 1=12+112=6符合①∴a n =n +5(2)思路:f n 按照奇偶分段,所以要确定m +15,m 的奇偶。
观察可发现无论m 为何值,m +15,m 均为一奇一偶,所以只需要对m 的奇偶进行分类讨论,解出符合条件的m 即可解:f n =a n =n +5,n =2k -13a n -13=3n +2,n =2k 当m 为奇数时,m +15为偶数∴f m +15 =5f m ⇒3m +15 +2=5m +5解得:m =11当m 为偶数时,m +15为奇数∴f m +15 =5f m ⇒m +15 +5=53m +2解得:m =57(舍)综上所述:m =114.已知各项均为整数的数列a n 满足a 3=-1,a 7=4,前6项依次成等差数列,从第五项起依次成等比数列(1)求数列a n 的通项公式(2)求出所有的正整数m ,使得a m +a m +1+a m +2=a m a m +1a m +2解:(1)设前6项的公差为d ,则a 5=a 3+2d =-1+2d ,a 6=a 3+4d =-1+4d∵a 5,a 6,a 7成等比数列,∴a 26=a 5⋅a 7⇒4d -1 2=42d -1解得:d =1∴n ≤6时,a n =a 3+n -3 d =n -4∴a 5=1,a 6=2,则q =2∴n >7时,a n =a 6⋅q n -6=2n -5∴a n =n -4,n ≤62n -5,n >7 (2)思路:由于数列a n 分为两部分,当n ≥5时,即为公比是2的等比数列,所以考虑对于数列的前几项可进行验证,n ≥5后成等比数列,从而可进行抽象的计算,看是否能够找到符合条件的m 。
奥数四年级—数列问题

练 例3、计算11+15+19+......+99。 习
解:首项=11, 末项=99
总项数=(末项-首项)÷公差 + 1
总项数=(99-11)÷4+1 =23 公差=15-11=4
直接列公式: =(首项+末项)×(项数÷2) =(11+99)× (23÷2) =110×11.5 =1265
练 习
练 例2、求首项是3,公差是5的等差数列的前 习 1999项的和。
首项=3, 末项=?? 不知道,要先求! 总项数=1999, 公差=5 3,8,13,18,23,28,..... 解:第1项=3 第2项=3+(5×1)=8 第3项=3+(5×2)=13 第4项=3+(5×3)=18 第5项=3+(5×4)=23 第6项=3+(5×5)=28 ...... 第1999项=3+(5×1998)=9993
公式:(首项+末项)×(项数÷2) =(1+2006)× (2006÷2) =2007×1003 =2013021
练 例1、计算 习 1+2+3+…+2006
首项=1, 总项数=2006, 末项=2006 公差=1
直接列公式: =(首项+末项)×(项数÷2) =(1+2006)× (2006÷2) =2007×1003 =2013021
数列问题
(一)数列的基本知识
(1)1、2、3、4、5、6…… (2)2、4、6、8、10、12…… (3)5、10、15、20、25、30
像这样按照一定规律排列成的一列数我们称它为数列 数列中的每一个数称为一项; 第1项称为首项;最后1项称为末项; 在第几个位置上的数就叫第几项; 有多少项称为项数;
高考数学中的常见数论问题

高考数学中的常见数论问题数论作为数学的一个重要分支,是研究整数性质的学科。
在高考数学中,数论经常出现,也是考生需要关注和掌握的重点内容之一。
本文将介绍高考数学中的常见数论问题,包括整数性质、除法算法、同余模运算、最大公因数和最小公倍数以及相关的应用。
一、整数性质1.整数的奇偶性质奇数是不能被2整除的整数,偶数是能被2整除的整数。
一个整数能否被另一个整数整除,取决于它们的奇偶性质。
2.约数和倍数一个整数a除以b(b≠0)所得的商q和余数r,使得a=b×q+r(0≤r <|b|),则a是b的倍数,b是a的约数。
求解约数和倍数问题时,可以运用约数的性质进行推导和判断。
3.质数和合数质数是只能被1和本身整除的大于1的整数,合数是除了1和本身外还有其他约数的整数。
求解质数和合数问题时,可以使用试除法,将待判断的数除以小于它一半的整数,若都没有余数为0的情况,则该数为质数。
二、除法算法1.带余除法当两个整数相除时,可以得到一个商和一个余数。
用带余除法可以得到被除数和除数的关系,即a=b×q+r(0≤r<|b|)。
2.长除法长除法是一种将一个多位数除以一个一位数的方法。
通过长除法的计算过程,可以确定除数、被除数和商的关系,并求解除法问题。
三、同余模运算1.同余关系对于整数a、b和正整数m,若m|(a-b),即a和b除以m所得的余数相同,那么称a与b对模m同余。
同余关系有以下性质:如果a≡b(mod m),则a+c≡b+c(mod m);如果a≡b(mod m),则a×c≡b×c(mod m)。
2.模运算的应用同余模运算在数论问题的解决中有广泛的应用。
例如,在年份、时间和距离的计算中,利用同余模运算可以得到简洁的计算结果。
四、最大公因数和最小公倍数1.最大公因数两个或多个整数公有的约数中,最大的一个称为最大公因数。
求最大公因数时,可以使用辗转相除法,将两个整数的较大数除以较小数,余数为0时,较小数即为最大公因数。
数学整数知识点归纳总结

数学整数知识点归纳总结整数是数学中的一种基本概念,它包括正整数、负整数和零。
在数学的学习过程中,了解和掌握整数的知识点对于解决各种数学问题起到至关重要的作用。
本文将对整数的一些重要知识点进行归纳总结,帮助读者更好地理解和运用整数的概念。
一、整数的概念和性质1. 整数的定义:整数是由正整数、负整数和零组成的数集,用符号“Z”表示。
2. 整数的绝对值:整数a的绝对值记作|a|,表示a与0的距离。
对于正整数a,其绝对值就是a本身;对于负整数a,其绝对值是-a。
3. 整数的大小比较:正整数大于负整数,正整数之间大小比较按照位数和位数内各位数字大小进行。
例如,3比-4大,12比7大,-34比-56大。
4. 整数的相反数:对于整数a,其相反数记作-a,满足a和-a的和为0。
例如,3和-3互为相反数。
5. 整数的加法和减法:整数的加法运算遵循正数加正数、负数加负数的法则,减法可以转化为加上相反数的操作。
6. 整数的乘法和除法:正整数和负整数相乘得到负数,两个负整数相乘得到正数;正整数除以正整数得到正数,负整数除以负整数得到正数。
二、整数的运算规则1. 加法规则:整数的加法满足交换律和结合律,即a+b=b+a,(a+b)+c=a+(b+c)。
2. 减法规则:减法可以转化为加法,即a-b=a+(-b)。
3. 乘法规则:整数的乘法满足交换律和结合律,即a*b=b*a,(a*b)*c=a*(b*c)。
4. 除法规则:整数的除法没有交换律和结合律,除法的结果可以是有限的小数也可以是无限循环小数。
5. 分配律:对于整数a、b和c,乘法满足分配律,即a*(b+c)=a*b+a*c。
三、整除与余数的概念和应用1. 整数的整除性:对于两个整数a和b,如果a能被b整除(余数为0),则称a为b的倍数,b为a的因数。
2. 整数的整除性质:如果a能被b整除,b能被c整除,则a能被c 整除。
3. 奇数和偶数:整数中,能被2整除的数为偶数,不能被2整除的数为奇数。
完整版)初中数学找规律解题方法及技巧

完整版)初中数学找规律解题方法及技巧初中数学找规律解题方法及技巧通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
因此,将变量和序列号放在一起进行比较,就更容易发现其中的奥秘。
初中数学考试中,数列的找规律题经常出现,本文就此类题的解题方法进行探索。
一、基本方法——看增幅一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a1+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅。
然后再简化代数式a+(n-1)b。
例如,4、10、16、22、28……,求第n位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,因此,第n位数是:4+(n-1)6=6n-2.二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求出,方法就简单的多了。
三)增幅不相等,但是增幅同比增加,即增幅为等比数列,如:2、3、5、9、17增幅为1、2、4、8.四)增幅不相等,且增幅也不以同等幅度增加(即增幅的增幅也不相等)。
此类题大概没有通用解法,只能用分析观察的方法,但是,此类题包括第二类的题,如用分析观察法,也有一些技巧。
二、基本技巧一)标出序列号:找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
找出的规律,通常包含序列号。
因此,将变量和序列号放在一起进行比较,就更容易发现其中的奥秘。
数列中不定方程问题的几种解题策略

数列中不定方程问题的几种解题策略王海东(江苏省丹阳市第五中学,212300)数列是高中数学的重要内容,又是学习高等数学的基础,在高考中占有极其重要的地位.数列中不定方程的整数解问题逐渐成为一个新的热点,在近年来的高考模拟卷中,这类问题屡见不鲜,本文中的例题也都是近年来大市模考题的改编.本文试图对与数列有关的不定方程的整数解问题的解法作初步的探讨,以期给同学们的学习带来帮助。
题型一:二元不定方程 双变量的不定方程,在高中阶段主要是求出此类不定方程的整数解,方法较灵活,下面介绍3种常用的方法。
方法 1.因式分解法:先将不定方程两边的数分解为质因数的乘积,多项式分解为若干个因式的乘积,再由题意分类讨论求解。
题1(2014·浙江卷)已知等差数列{}n a 的公差d >0。
设{}n a 的前n 项和为n S ,11=a ,3632=⋅S S 。
(1)求d 及S n ; (2)求m ,k (m ,k ∈N *)的值,使得65...21=+++++++k m m m m a a a a .解析(1)略(2)由(1)得2,12n S n a n n =-=(n ∈N *)=+++++++k m m m m a a a a ...21()2122121-++-+k m m k )()1)(12(+-+=k k m 所以65)1)(12(=+-+k k m ,由m ,k ∈N *知1112>+≥-+k k m65151365⨯=⨯=,故⎩⎨⎧=+=-+511312k k m 所以⎩⎨⎧==45k m 点评 本题中将不定方程变形为()()135112⨯=+⋅-+k k m ,因为分解方式是唯一的,所以可以得到关于k m ,的二元一次方程组求解。
方法 2.利用整除性质 在二元不定方程中,当其中一个变量很好分离时,可分离变量后利用整除性质解决.题2。
设数列{}n b 的通项公式为2121n n b n t-=-+,问:是否存在正整数t ,使得12m b b b ,,(3)m m ≥∈N ,成等差数列?若存在,求出t 和m 的值;若不存在,请说明理由.解析:要使得12,,m b b b 成等差数列,则212m b b b =+即:312123121m t t m t -=+++-+ 即:431m t =+- ∵,m t N *∈,∴t 只能取2,3,5 当2t =时,7m =;当3t =时,5m =;当5t =时,4m =.点评 本题利用t 表示 m 从而由431m t =+-得到14-t 是整数,于是1-t 是4的约数,从而估计出可能的所有取值,再逐一检验即可,当然,本题也可以利用m 表示t 来处理。
给出一个包含n个整数的数列,问整数a在数列中的第一次出现是第几个

给出一个包含n个整数的数列,问整数a在数列中的第一次出现是第几个
给定一个包含n个整数的数列,要查询整数a第一次出现的位置。
算法思路:遍历数列,找到第一个出现a的元素位置,输出该位置并结束程序。
具体实现方法:使用循环从数列的第一个元素开始遍历,遇到第一个等于a的元素时,输出该元素的下标并结束程序;若遍历完整个数列仍未找到等于a的元素,则输出“a不存在于数列中”。
代码实现(Python):
```python
n = int(input('请输入整数的个数:'))
a_list = list(map(int, input('请输入n个整数,以空格分隔:').split()))
a = int(input('请输入要查询的整数:'))
for i in range(n):
if a_list[i] == a:
print('整数a在数列中第一次出现的位置是', i + 1)
break
else:
print('a不存在于数列中')
```
以上代码中,`break`语句用于跳出循环,`else`语句用于在循环正常结束时执行。
如果在循环过程中已经找到了等于a的元素,那么程序会先执行`break`语句跳出循环,然后不会执行`else`语句;如果循环正常结束了,即遍历完数列后仍未找到等于a的元素,那么程序会执行`else`语句输出提示信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列中的整数问题一、基础知识:1、整数的基本性质:(1)整数的和,差,积仍为整数(2)整数的奇偶性:若()21n k k Z =+∈,则称n 为奇数;若()2n k k Z =∈,则称n 为偶数,在加,减,乘法运算中,其结果有以下规律:①奇数±奇数=偶数②奇数±偶数=奇数③偶数±偶数=偶数④奇数⨯偶数=偶数⑤偶数⨯偶数=偶数⑥奇数⨯奇数=奇数(3)若,a b Z ∈,且a b <,则1a b ≤-(4)已知,,a b R a b ∈<,若n Z ∈,且(),n a b ∈,则n 只能取到有限多个整数(也有可能无解)(5)若aZ ∈,称a 能被b 整除,则有:①b a≤②b 为a 的一个因数(6)最小数原理:自然数集的任何非空子集,均有一个最小的自然数2、整数性质的应用:(1)若变量属于整数,则利用方程与不等式均可求出变量的值:在实数范围内,若要求得变量的值,通常要依赖方程,而不等式只能解得变量的范围。
但是在整数范围内,除了方程,在不等式中也可以利用整数的离散性求出变量的值(即性质(4)),例如:若(),2,5n N n ∈∈,则n 的取值只能是3,4。
所以在涉及求整数的值时,思路不要局限于寻找等量关系,构造不等关系依然可以求解。
(2)整除问题:若表达式形式较为简单,可通过对常数进行因数分解,进而确定变量的取值;若表达式次数较高,则可以先利用二项式定理去掉高次的项,再进行处理。
(3)多元整数不定方程:当变量的值为整数时,不定方程的解可能有有限多组解。
通常的处理方式有两个:①通过对表达式进行因式分解,对另一侧的常数进行因数分解,进而将不定方程拆成多个方程的方程组,进而解出变量②将一个字母视为变量(其余视为参数)并进行参变分离,求出含变量函数的值域,进而将参数置于一个范围内,再利用整数离散性求得参数的值(4)反证法:运用反证法处理整数问题时,常见的矛盾有以下几点:①所解得变量非整数,或不符合已知范围②等式两侧为一奇一偶3、整数问题通常会与数列联系起来,其特征就是数列中项的序数,以及前n 项和的项数,均为正整数。
二、典型例题:例1:已知数列{}n a 的通项公式为27n a n =-,若12m m m a a a ++为数列{}n a 中的项,则m =____例2:若数列12-=n a n ,求,m k (*,m k N ∈)的值,使得1265m m m m k a a a a +++++++= .引申探究:若将(1)中1265m m m m k a a a a +++++++= 改成1265m m m m k a a a a +++++++= 300,试求,m k (*,m k N ∈)的值.思路:由题意知65)1)(12(1=+-+=+++++k k m a a a k n n n ,由*,m k N ∈知,2112≥+>-+k k m ,所以⎩⎨⎧=+=-+511312k k m ,故⎩⎨⎧==45k m .引申探究:由题意知300)1)(12(1=+-+=+++++k k m a a a k n n n ,由*,m k N ∈知,2112≥+>-+k k m ,且112+-+k k m 与同为奇数或同为偶数,又300)1)(12(=+-+k k m ,故112+-+k k m 与同为偶数,所以⎩⎨⎧⨯=+⨯⨯=-+⎩⎨⎧⨯=+⨯⨯=-+3215521252153212k k m or k k m 解得⎩⎨⎧==⎩⎨⎧==524911k m or k m .例3:已知数列{}n a 的前n 项和为n S ,且()211122n S n n n N *=+∈(1)求数列{}n a 的通项公式(2)设()(21,)313(2,)n n a n k k N f n a n k k N **⎧=-∈⎪=⎨-=∈⎪⎩,是否存在m N *∈,使得()()155f m f m +=成立?若存在,求出m 的值;若不存在,请说明理由例4:已知各项均为整数的数列{}n a 满足371,4a a =-=,前6项依次成等差数列,从第五项起依次成等比数列(1)求数列{}n a 的通项公式(2)求出所有的正整数m ,使得1212m m m m m m a a a a a a ++++++=解:(1)设前6项的公差为d ,则5363212,414a a d d a a d d=+=-+=+=-+567,,a a a 成等比数列,()()2265741421a a a d d ∴=⋅⇒-=-解得:1d =6n ∴≤时,()334n a a n d n =+-=-561,2a a ∴==,则2q =7n ∴>时,6562n n n a a q --=⋅=54,62,7n n n n a n --≤⎧∴=⎨>⎩(2)思路:由于数列{}n a 分为两部分,当5n ≥时,即为公比是2的等比数列,所以考虑对于数列的前几项可进行验证,5n ≥后成等比数列,从而可进行抽象的计算,看是否能够找到符合条件的m 。
解:由(1)可得:{}:3,2,1,0,1,2,4,8,n a --- 则当1m =时,1231236a a a a a a ++=-=当2m =时,2342342342342,0,a a a a a a a a a a a a ++=-=++≠当3m =时,3453450a a a a a a ++==当4m =时,4564564564563,0,a a a a a a a a a a a a ++==++≠当5m ≥时,假设存在m ,使得1212m m m m m m a a a a a a ++++++=则有()531221242m m --++=即:5312277227=2m m m ---⋅=⇒5m ≥ 273m ∴-≥2732287m -∴≥=>,从而277=2m -无解5m ∴≥时,不存在这样的m ,使得1212m m m m m m a a a a a a ++++++=综上所述:1m =或3m =例5:已知数列{}n a 的前n 项和为n S ,且满足12a =-,1320n n a S +++=(*n ∈N ).(1)求2a ,3a 的值;(2)求数列{}n a 的通项公式;(3)是否存在整数对(,)m n ,使得等式248n n a m a m -⋅=+成立?若存在,请求出所有满m n;若不存在,请说明理由.足条件的(,)例6:已知数列{}n a 是各项均不为0的等差数列,n S 是其前n 项和,且满足221n n a S -=,令11n n n b a a +=,数列{}n b 的前n 项和为nT (1)求数列{}n a 的通项公式及nT (2)是否存在正整数(),1m n m n <<,使得1,,m n T T T 成等比数列?若存在,求出所有的,m n 的值;若不存在,请说明理由。
例7:已知各项均为正数的数列{}n a 满足:13a =,且()2211210,n n n n n a a a a a n N *++---=∈(1)设1n n nb a a =-,求数列{}n b 的通项公式(2)设2221222212111,n n n nS a a a T a a a =+++=+++ ,求n n S T +,并确定最小正整数n ,使得n n S T +为整数例8:已知{}n a 为等差数列,前n 项和为n S ,若4224,21n n S S a a ==+(1)求na (2)对m N *∀∈,将{}n a 中落入区间()22,2mm内项的个数记为{}mb ①求m b ②记2122m m mc b -=-,{}mc 的前m 项和记为m T ,是否存在,m t N *∈,使得111m m t T t T t c +-=-+成立?若存在,求出,m t 的值;若不存在,请说明理由例9:已知数列{}n a 是等差数列,数列{}n b 是等比数列,且对任意的n N *∈,都有:311222n n n a b a b a b n ++++=⋅ ,若18a =,则:(1)求数列{}{},n n a b 的通项公式(2)试探究:数列{}n b 中是否存在某一项,它可以表示为该数列中其它(),2r r N r ∈≥项的和?若存在,请求出该项,若不存在,请说明理由解:(1)311222n n n a b a b a b n ++++=⋅ ①()211221112n n n a b a b a b n +--+++=-⋅ ②①-②可得:()()()322212122n n n n n a b n n n n +++=⋅--=+≥令1n =,则4111122a b b =⋅⇒=令2n =,则()422113248a b a d b q =⋅⇒+=令3n =,则()523311422128a b a d b q =⋅⇒+=所以有:()()2848282128d q d q +=⎧⎪⎨+=⎪⎩,解得:42d q =⎧⎨=⎩44,2nn n a n b ∴=+=(2)思路:首先要把命题翻译为等式,将其他r 项可设为12,,,r t t t b b b ,设存在某项m b ,则12122222r r tttm m t t t b b b b =+++⇒=+++ ,设12r t t t <<< ,则同除以12t,就例10:已知等差数列{}n a 的首项为a ,公差为b ,等比数列{}n b 的首项为b ,公比为a ,其中,a b 均为大于1的正整数,且1123,a b b a <<,对于任意的n N *∈,均存在m N *∈,使得3m n a b +=成立,则n a =____________思路:本题的关键是求出,a b ,已知,a b 均为大于1的正整数,所以考虑从两个不等关系入手尝试求,a b 的值或范围:1123,2a b a b b a ba a b <⇒<<⇒<+,所以2a bba a b<⎧⎨<+⎩,从而根据不等号方向可得:223ba a b b b b <+<+=解得:3a <,所以132a a <<⇒=,从而()1313n m n a b a m b ba -+=⇒+-+=,代入2a =可得:()()11152521n n m b b b m ---+=⋅⇒=-+,因为1,21n b Z m Z -∈-+∈,所以11215n b m -=⎧⎨-+=⎩(舍)或12115n m b -⎧-+=⎨=⎩。
