山东省滕州一中高一10月月考试卷答案

合集下载

山东省滕州市第一中学2024-2025学年高三上学期10月月考化学试题 (含答案)

2024-2025学年度第一学期10月份阶段检测高三化学可能用到的相对原子质量：Ca-20 Cl-35.5 O-16 C-12 Ag-108 S-32 N-14一、单选题(共10题，每个小题只有一个正确选项，每题2分共20分)。

1. 科技是第一生产力，而化学与科技息息相关，下列说法不正确的是A. 杭州亚运主火炬燃料为零碳甲醇，甲醇具有还原性B. 国产大型邮轮“爱达・魔都号”采用的薄形钢板属于合金C. 清华大学研制的“天机芯”是全球首款异构融合类芯片，其主要成分和光导纤维不相同D. 冬奥场馆建筑应用了新材料碲化镉发电玻璃，碲和镉均属于过渡元素2. 下列有关化学实验安全规范的说法错误的是A. 眼睛溅进酸液，立即用大量水冲洗B. 废弃药品中含有的少量金属钠可用乙醇处理C. 开启盛装易挥发液体的试剂瓶前，应反复摇动D. 加热制备并用排水法收集，出现倒吸现象，应立即松开导管上的橡皮管3. 化学兴趣小组采用次氯酸钙与稀盐酸反应制取氯气，并探究了氯气的性质。

实验装置如图所示，下列说法正确的是A. 湿润的pH 试纸先变红后褪色，说明有酸性和漂白性B. f 处出现红色沉淀是因为被氧化为，遇生成弱电解质C. g 处变为橙色，h 处变为黄色，说明元素非金属性：D. 等量分别单独缓慢通过g 、h 、i 试管时，生成的氧化产物的物质的量之比为1：1：13KClO 2O 2Cl 2Fe +3Fe +3Fe +KSCN 3Fe(SCN)Cl Br I>>2Cl4. 过二硫酸钾(，其中S 为价)是工业上一种重要的消毒剂和织物漂白剂，可通过电解溶液制备。

它在100℃下能发生分解反应：(未配平)，设为阿伏加德罗常数的值，下列说法正确的是A. 中含有非极性共价键的数目为B. 分解，生成的分子数为C. 标准状况下，含有的原子数为D. 溶液中的离子总数为5. 草酸亚铁晶体()呈黄色，难溶于水，具有强还原性。

用下列装置制备草酸亚铁晶体。

山东省滕州市第一中学2022届高三上学期10月月考化学试题 Word版含答案

山东省滕州市第一中学2021—2022学年度高三上学期10月月考化学第I卷选择题（共60分）一、选择题（本题共20小题，每小题只有一个答案符合题意，每小题3分，共60分。

）1．化学与生活亲密相关，下列有关说法正确的是A“辽宁舰”上用于舰载机降落拦阻索的特种钢缆，属于新型无机非金属材料B氧氧化铁溶胶、含塑化剂的白酒、含有细菌的矿泉水均具有丁达尔效应C对“地沟油”蒸馏可以获得汽油D用K2FeO4代替Cl2处理饮用水，既有杀菌消毒作用，又有净水作用2. 下列有关NaHC03和Na2 C03性质的比较中，正确的是A．热稳定性：Na2C03 <NaHC03B．常温时在水中的溶解度：Na2C03 <NaHC03C．等质量的NaH C03和Na2C03与足量稀盐酸反应产生C02的量：Na2C03<NaHC03D．等物质的量的NaHC03和Na2 CO3与足量稀盐酸反应，NaHCO3放出的C02多3.下列说法中正确的是A.干冰、浓硫酸都是电解质B. Na2O2晶体中既含有离子键又含有共价键C. CaO, Fe2O3、Al2O3既属于碱性氧化物，又属于离子化合物D．含同一元素的不同化合物，该元素的化合价越高，其氧化性越强4.原子序数依次增大的a、b、c、d，它们的最外层电子数分别为1、6、7、1。

a－的电子层结构与氦相同，b和c的次外层有8个电子，c－和d+的电子层结构相同。

下列叙述错误的是（）A．元素的非金属性强弱次序为：c＞b＞aB．a和其他3种元素均能形成共价化合物C．d和其他3种元素均能形成离子化合物D．元素a 、b、c各自最高和最低化合价的代数和分别为0、4、65.某羧酸酯的分子式为C10H18O3，1mol该酯完全水解可得到1mol羧酸和1mol乙醇，该羧酸的分子式为A．C8H16O2B．C8H16O3C．C8H14O2D．C8H14O36.已知阿伏加德罗常数的值为N A。

下列说法正确的是A．28gN2与足量氢气反应，转移电子的数目为6N AB. 标准状况下，11.2LHF含有的分子数为0.5N AC. 标准状况下，22.4L14CO2与44g14CO2所含分子数均为N AD. 2L0.2mol·L-1的稀硝酸与适量铁恰好反应（还原产物只有NO），生成NO的分子数为0.1N A7.下列试验中，所选装置或试验设计合理的是①②③④⑤A. 图⑤所示装置中盛有饱和Na2SO3溶液除去SO2中含有的少量HClB. 用乙醇提取碘水中的碘选择图③所示装置C. 用图①和②所示装置进行粗盐提纯D. 用图④所示装置进行石油分馏试验制取汽油8. 下列离子或分子组在溶液中能大量共存,且满足相应要求的是选项离子要求A K+、NO3-、Cl-、HS-c(K+)<c(Cl-)B Fe3+、NO3-、S2-、Cl-逐滴滴加盐酸马上有气体产生C Na+、HCO3-、Mg2+、SO42-逐滴滴加氨水马上有沉淀产生D NO3-、Al3+、NH4+、CH3COOH 滴加NaOH浓溶液马上有气体产生9.下列各组离子在相应的条件下肯定能大量共存的是A．在碱性溶液中：CO32－、K+、S2-、Na+B．与铝粉反应放出氢气的无色溶液中：NO3－、Mg2+、Na+、SO42－C．在c(H+)／c(OH－)=1×1012的溶液中：NH4+、AlO2－、C1－、K+D．在中性溶液中：Fe3+、C1－、NO3－、A13+10.下列离子方程式与所述事实相符且正确的是A．Ca(HCO3)2溶液中加入少量NaOH溶液：Ca2＋＋2HCO3－＋2OH－＝CaCO3↓＋CO32－＋2H2OB．向含有0.4molFeBr2的溶液中通入0.3molCl2充分反应：4Fe2＋＋2Br－＋3Cl2＝4Fe3＋＋6Cl－＋Br2C．向明矾溶液中加入Ba(OH)2溶液至生成的沉淀物质的量最多：Al3＋＋2SO42－＋2Ba2＋＋4OH－＝AlO2－＋2BaSO4↓＋2H2OD．磁性氧化铁溶于稀硝酸：Fe3O4＋8H＋＋NO3－＝3Fe3＋＋NO↑＋4H2O11.下表中试验操作、现象和所得出的结论正确的是选项试验操作试验现象结论A 用激光笔照射鸡蛋白水溶液有丁达尔效应鸡蛋白分子直径介于1nm～100nm B向某氯化亚铁溶液中加入Na2O2粉末消灭红褐色沉淀说明原氯化亚铁已氧化变质C 碳酸盐X加热分解，产生的气体通入酸化的BaCl2溶液产生白色沉淀X可能是NaHCO3D 潮湿的KI淀粉试纸靠近气体Y 试纸变蓝Y肯定是Cl212.某同学鉴定甲盐溶液的流程如图所示，下列说法正确的是A. 假如甲中含有S2－，则乙是硫磺沉淀B．假如乙是AgCl沉淀，那么甲是FeCl3C．丙中确定含有Fe3＋，所以甲是FeBr2D．甲中含有铁元素，可能显示+2或者+3价13.铬是人体必需的微量元素，它与脂类代谢有亲密联系，能增加人体内胆固醇的分解和排泄，但铬过量会引起污染，危害人类健康。

山东省滕州市第一中学高一化学10月月考试题

2014-2015学年度山东省滕州市第一中学高一第一学期10月月考化学试题时量：90分钟分值：100分可能用到的相对原子质量：C：12、 H：1、 S：32、 O：16、N：14、 Mg：24、 Na：23 Ba：137一、选择题（每小题只有一个答案符合题意，每小题2分，共10小题，共计20分）。

1．下列关于“摩尔”的说法正确的是（）A．摩尔是一个物理量 B．摩尔是表示物质的量C．摩尔是物质的量的单位D．摩尔是表示物质数量的单位2．下列仪器加热时不需垫石棉网的是（）A．烧杯B．蒸馏烧瓶C．锥形瓶D．蒸发皿3．先将甲物质放于托盘天平右盘进行称量，再将乙物质放在左盘进行称量，若两次都使用了游码，且砝码和游码的读数均相等，甲、乙两物质的质量（）A．小于B．等于C．大于D．不能确定4．下列物质中含氢原子数最多的是（）A．2mol CH4B．3mol NH3C．4mol H3PO4D．5mol H25．下列说法错误的是（）A．6．02×1023是阿伏加德罗常数的近似值B．阿伏加德常数个微粒的物质的量是1molC．1mol 12C原子的质量为12gD．硫酸的摩尔质量是98克6．下列说法正确的是（）A．在标准状况下，1mol水的体积是22．4LB．1molH2所占的体积一定是22．4LC．在标准状况下，N A个任何分子所占的体积约为22．4LD．在标准状况下，总质量为28g N2和CO的混合气体，其体积约为22．4L7．Na2CO3俗名纯碱，下面是对纯碱采用不同的分类，不正确的是（）A．Na2CO3是碱B．Na2CO3是盐C．Na2CO3是钠盐D．Na2CO3是碳酸盐8．世界卫生组织将ClO2列为A级高效安全灭菌消毒剂，它在食品保鲜、饮用水消毒等方面有广泛应用。

ClO2属于（）A．氧化物B．酸C．碱D．盐9．下列物质的水溶液能导电，但属于非电解质的是（）A．HCl B．Cl2C．NaHCO3D．CO210．下列各组离子在水溶液中能大量共存的是（）A．Na+、Ba2+、Cl、SO42-B．Ca2+、HCO3、Cl、K+C．Mg2+、Ag+、NO3、Cl D．H+、Cl、Na+、CO32二、选择题（每小题只有一个答案符合题意，每小题3分，共10小题，共计30分）11．设N A为阿伏加德罗常数，下列说法中，正确的是（）A．2．4 g金属镁所含电子数目为0．2 N AB．16 g CH4所含原子数目为N AC．17 g NH3 所含氢原子数目为4 N AD．18 g水所含分子数目为N A12．胶体区别于其他分散系的本质特征是（）A．胶体的分散质能通过滤纸空隙，而浊液的分散质不能B．产生丁达尔现象C．分散质粒子直径在1nm～100nm之间D．胶体在一定条件下能稳定存在13．某溶液中含有较大量的Cl－、 2CO、OH－3种阴离子，如果只取一次该溶液就能够分别将33种阴离子依次检验出来，下列实验操作顺序中，正确的是（）①滴加Mg（NO3）2溶液；②过滤；③滴加AgNO3溶液；④滴加Ba（NO3）2溶液A．①②④②③B．④②①②③C．①②③②④D．④②③②①14．关于容量瓶的叙述：①是配制准确物质的量浓度溶液的仪器；②不宜长时间贮存溶液；③能用来加热；④使用之前要检查是否漏水。

山东省滕州一中23届高三10月月考数学含答案

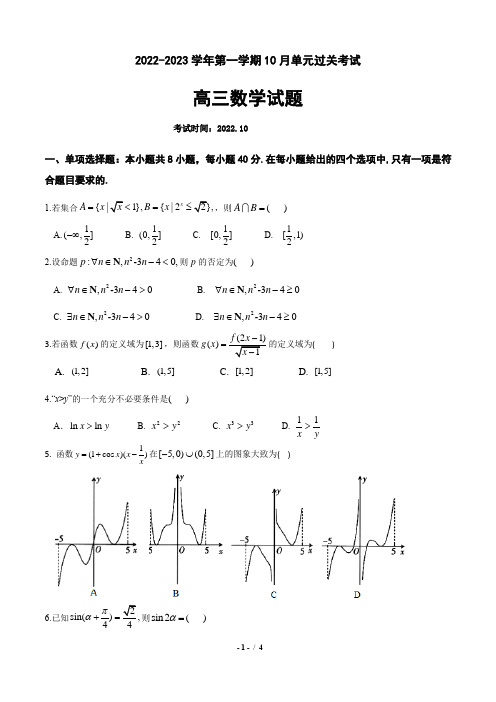
2022-2023学年第一学期10月单元过关考试高三数学试题考试时间：2022.10一、单项选择题：本小题共8小题，每小题40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{|1},{|22},x A x x B x =<=≤，则A B =( )A.1(,]2−∞B. 1(0,]2C. 1[0,]2D. 1[,1)22.设命题2:,340,N -p n n n ∀∈−<则p 的否定为( )A. 2,340N -n n n ∀∈−> B. 2,340N -n n n ∀∈−≥ C. 2,340N -n n n ∃∈−> D. 2,340N -n n n ∃∈−≥ 3.若函数()f x 的定义域为[1,3]，则函数(21)()1f xg x x −=−的定义域为( )A . (1,2]B . (1,5]C . [1,2] D. [1,5]4.“x >y ”的一个充分不必要条件是( )A ．ln ln x y > B. 22x y > C. 33x y > D.11x y> 5. 函数1(1cos )()y x x x=+−在[5,0)(0,5]−⋃上的图象大致为( )6.已知2sin(),44πα+=则sin 2α=( )A ．34−B.34C. 34± D. 74−7.若函数(2)f x +为偶函数，对任意12,[2,)x x ∈+∞，且12x x ≠，都有1212()[()()]0x x f x f x −−>，则( ) A ．233(log 6)()(log 12)2f f f << B. 323(log 12)()(log 6)2f f f << C. 323(log 12)(log 6)()2f f f << D. 233()(log 6)(log 12)2f f f <<8．过点(1,)P m 有n 条直线与函数()xf x xe =的图象相切，当n 取最大值时，实数m 的取值范围是( ) A ．25(,)e e −B. 25(,0)e −C. 1(,0)e− D. (,)e −∞ 二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对得5分，选对但不全的得2分，有选错的得0分．9.若110,a b<<则下列不等式中正确的是( ) A ．a b ab +< B . a b < C. a b < D .2b aa b+> 10.已知0a >，0b >，21a b +=，下列结论不．正确．．的是( ) A.12a b +的最小值为9 B. 22a b +的最小值为55C. 22log log a b +的最小值为3−D. 24a b +的最小值为22 11.已知函数()sin()(0,||)2f x x πωϕωϕ=+><的部分图象如图所示，则下列结论正确的是（）A.函数()f x 的图象可由sin 2y x =的图象向左平移3π个单位得到 B ．直线1112x π=−是()f x 图象的一条对称轴 C. 若12()()2f x f x −=，则12,2N*k x x k π−=∈ D.方程1()02f x −=在区间10[0,]3有七个实根12.已知函数(),()f x g x 的定义域为R ，()g x '为()g x 的导函数，且()()5,f x g x '+=()(4)5,f x g x '−−=若()g x 为偶函数，则下列结论一定正确的是（）A. (4)5f =B. (2)0g '=C. (1)(3)f f −=−D. (1)(3)10f f +=三、填空题：本大题共4小题，每小题5分，共20分.13.已知1{,1,2}2α∈±±±，若幂函数()f x x α=在区间上(,0)−∞单调递增，且其图象不过坐标原点，则α= .14.已知函数()3321xxf x x −=−−+，则不等式(21)(2)2f x f x −+−<的解集为 .15.若0θπ<<,且点(cos ,sin )P θθ与点(cos(),sin())66Q ππθθ++关于x 轴对称,则cos θ= . 16.已知1x x =和2x x =分别是函数2()2(0,xf x a ex a =−>且1)a ≠的极大值点与极小值点.若12x x <,则a 的取值范围是 .四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.17. (10分）已知命题p :函数f (x )=ax 2+2ax +1有零点,命题2:(40,2.,2]x x a q x −−+∈∞>∀−(1)若p 为真命题，求实数a 的取值范围；(2)若p,q 中恰有一个真命题，求实数a 的取值范围.18. (12分）已知2sin 4sin2.2αα=−(1)求cos -(1+sin +2)23sin -)sin()2παπαπαπα++（）（）（的值；(2)若(0,)απ∈，(0,)2πβ∈，2tan 6tan 10ββ+−=，求2αβ+的值．19.(12分）求值：cos10(1)(tan10;sin50︒︒︒1cos201(2)sin10(tan5).2sin20tan5+︒−︒⋅−︒︒︒20. (12分）已知定义在R上的函数()f x满足：对任意x，Ry∈都有()()()f x y f x f y+=+，且当0x>时，()0.f x>(1)判断并证明()f x的奇偶性；(2)判断函数()f x的单调性，并证明；(3)若1(2)(482)0x x x xf k f+⋅+−−>对任意[1,2]x∈−恒成立，求实数k的取值范围．21.(12分）已知函数2()ln1f x x x x=+−−(1)求函数的极值点；(2)若2()()xeg x f x mx=−在上单调递减，求实数m的取值范围．22.（12分）已知函数()2cos sinf x ax ax x x=−−(1)当1a=时，求()f x在[,]ππ−上的值域;(2)当0x>时，()0f x≥,求实数a的取值范围.()f x[1,)+∞2022-2023学年第一学期10月单元过关考试高三数学试题参考答案一、单项选择题CDAA DABB二、多项选择题9. ABD 10. BC 11. BD 12. ABD三、填空题13.-2 14.(,1)−∞15.4− 16.(1,)e 四、解答题17.解:(1)若 0a = , f (x )=1无零点,舍去;……………………………………..…..2分若 0a ≠ , 则若 2440a a ∆=−≥ ,故0,a <或1;a ≥综上, 0,a <或1;a ≥……………………………………………………………….4分(2)若q 为真命题,z 则2(,2],(1)3x x a ∀∈−+∞−>，所以3,a <…….…….6分因为p,q 中恰有一个真命题，所以a 的取值范围为[0,1)[3,)+∞……..10分18.解：2(1)sin 4sin 22αα=−，1cos sin 4()22cos 2ααα−∴=−=−，tan 2α∴=−，…………..……………....….2分cos -(1+sin +2)sin (1sin 2)23sin cos sin -)sin()2παπαααααπαπα−∴=−++（）（）（…………………....……………….4分2sin (sin cos )sin cos ααααα−=−sin (sin cos )ααα=−222sin sin cos sin cos ααααα−=+22tan tan 6.tan 15ααα−==+……………………………………………………….……….6分2(2)tan 6tan 10ββ+−=，22tan 1tan 21tan 3βββ∴==−，……………………………………………….……….8分 152tan tan 233tan(2)1151tan tan 21(2)33αβαβαβ−+−+∴+====−−−−⨯，…….……....…10分又(0,)απ∈，1(0,),tan 2023πββ∈=>，2(0,)2πβ∴∈，32(0,)2παβ+∈，32.4παβ∴+= ……………………………………………………....…….…….12分19.解：(1)原式cos10(tan10tan 60)sin 50︒=︒−︒︒sin10sin 60cos10()cos10cos 60sin 50︒︒︒=−︒︒︒sin (50)cos10 2.cos 10cos 60sin 50︒︒−︒=⨯=−︒︒………………………………………...……….6分 (2)因为1cos5sin 5tan 5tan 5sin 5cos5︒︒−︒=−︒︒︒22cos 5sin 52cos10sin 5cos5sin10︒−︒︒==︒︒︒，所以原式22cos 102cos10sin104sin10cos10sin10︒︒=−︒⋅︒︒︒cos10sin 20cos10sin(3010)2sin10sin102sin10sin10︒︒︒︒−︒=−=−︒︒︒︒cos10cos102sin102sin10︒︒−︒=−︒︒2sin102︒==︒………………………………………………............………12分20.解：(1)令0x y ==，得 (00)(0)(0)f f f +=+，所以 (0)0.f =...……………………1分令y x =−，得()()()(0)0f x x f x f x f −=+−==，即()()f x f x −=−，所以()f x 为R 上的奇函数．………………………………………..……....……………………3分(2)设21,x x >则210x x −>0x >时，()0f x >，2121()()()0f x f x f x x −=−>即当21x x >时21()(),f x f x >()f x ∴是R 上的增函数. …………..……....……………..…6分(3)由题知：1(2)(482)0(0)x x x x f k f f +⋅+−−>=，即1(2482)(0)xx x x f k f +⋅+−−>，又()y f x =是定义在R 上的增函数，所以124820x x x x k +⋅+−−>即22122x x k +>+−对任意[1,2]x ∈−恒成立，……………...…9分令2xt =，1[,4]2t ∈，设2()41g t t t =−+，所以max ()k g t >，当4t = 时，max ()(4)161611g t g ==−+=，所以 1.k >………………………………………………....………………………………….……12分. 21. .解：(1)由题意，()f x 定义域(0,)+∞，1(21)(1)()21x x f x x x x−+'=+−=，…………1分令()0f x '=得1.x =列表如下，所以，()f x 的极小值点是12，无极大值点. ………………..………………………………….......………4分 22(2)()ln 1x me g x x x x x =+−−−，222(21)()()x x x x me g x x −+−'=，()g x 在[1,)+∞上单调递减，()0g x ∴'在[1,)+∞上恒成立，220xx x me ∴+−即2max 2()x x xm e+，[1,).x ∈+∞在[1,)+∞上恒成立. …............………8分令22()xx x h x e +=，[1,),x ∈+∞2212()0x x h x e −'=<在[1,)+∞上恒成立，…………….…………...………10分 ()h x ∴在[1,)+∞上单调递减，max 22()(1)h x h e==，故实数m 的取值范围是22.m e………………………………………....……………………………..……….….………….……12分22.(1)由题意知()2cos sin ,f x x x x x =−− ()2(1cos sin f x x x x '=−+）……………...……1分 [,]x ππ∈−时，()0f x '≥恒成立，()f x 单调递增，……..……....…………..…...……3分()()()f f x f ππ∴−≤≤即()f x 的值域为[3,3]ππ−………….….………............………4分(2)注意到(0)0,()2cos sin cos f f x a a x ax x x '==−+−，若1a ≥，()(2cos )sin 2cos sin ,f x ax x x x x x x =−−≥−−由（1）知，当[0,]x π∈时，()(0)0f x f ≥=；当(,)x π∈+∞时，2cos sin 2110,x x x x x x x −−>−−=−>所以()0f x ≥恒成立，符合题意; ………...................................………7分若0,a ≤()(2cos )sin ,f x ax x x =−−当[0,]x π∈时，()0f x ≤，不合题意，舍去；……….9分若01,a <<因为当[0,]2x π∈时，()(21)sin cos 0f x a x ax x ''=++≥，所以()f x '单调递增，而(0)1,()2)022+f a f a ππ''=−=>（，故存在0(0,)2x π∈满足0()0f x '=，且(0,)2x π∈时，()0,()f x f x '<单调递减，()(0)0f x f ≤=，不合题意，舍去；综上可知，1a ≥.…………………………....………………………………………………………….………..…..………..……12分。

2019-2020学年山东省枣庄市滕州市第一中学高一上学期10月阶段性检测数学试题(解析版)

2019-2020学年山东省枣庄市滕州市第一中学高一上学期10月阶段性检测数学试题一、单选题1．下列说法正确的是（） A ．{1,2},{2,1}是两个集合 B ．{(0,2)}中有两个元素C ．6|x Q N x ⎧⎫∈∈⎨⎬⎩⎭是有限集 D ．{}2|20x Q x x ∈++=且是空集【答案】D【解析】根据集合的定义判断．【详解】由集合元素的无序性A 错；(0,2)作为一个有序数对，是集合中的一个元素，B 错；当1,*x n N n =∈时，6N x∈，因此x 有无数个C 错；222(1)10x x x ++=++=无实数解，更加无有理数解，集合{}2|20x Q x x ∈++=且是空集，D 正确，故选：D ．【点睛】本题考查集合的定义，考查集合元素的性质，属于基础题．2．设集合{|91}A x Z x =∈-<<，{|32}B x x =-<<，则A B =I （） A ．{|92}x x -<< B ．{0} C ．{|31}x x -<<D ．{2,1,0}--【答案】D【解析】确定集合A 中的元素，然后根据交集定义求解．【详解】由题意{8,7,6,5,4,3,2,1,0}A =--------，所以{2,1,0}A B =--I ．故选：D ．【点睛】本题考查集合的交集运算，解题关键是确定集合中的元素． 3．命题“所有能被2整除的数都是偶数”的否定是 A ．所有不能被2整除的数都是偶数B ．所有能被2整除的数都不是偶数C ．存在一个不能被2整除的数是偶数D ．存在一个能被2整除的数不是偶数【答案】D【解析】试题分析：命题“所有能被2整除的整数都是偶数”的否定是“存在一个能被2整除的数不是偶数”．故选D ．【考点】命题的否定．4．不等式2320x x -+->的解集是（） A ．(,1)-∞ B ．(2,)+∞C ．(1,2)D ．(,1)(2,)-∞⋃+∞【答案】C【解析】先化不等式的二次项系数为正，因式分解确定对应方程的根，然后结合二次函数性质写出解集．【详解】原不等式可化为：2320x x -+<，即(1)(2)0x x --<，12x <<，所以原不等式解集为(1,2)．故选：C ．【点睛】本题考查解一元二次不等式，解题关键是化二次项系数为正．5．若函数2()48f x x kx =--在[5,8]上是单调函数，则k 的取值范围是（） A ．(],40-∞B ．[40,64]C ．(][),4064,-∞⋃+∞D ．[)64,+∞【答案】C【解析】试题分析：二次函数对称轴为8k x =，函数在区间[5,8]上单调，所以88k≥或58k≤64k ∴≥或40k ≤ 【考点】二次函数单调性6．集合{1,4,}A x =，{}2,1B x =，且A B B =I ，则满足条件的实数x 的值为（）A ．1或0B ．1，0或2C ．0，2或-2D ．0，-1，2或-2【答案】C【解析】由A B B =I 得B A ⊆，再由集合包含关系求解．【详解】由A B B =I 得B A ⊆，所以2x A ∈，若24x =，2x =±，均符合题意，若2x x =，则0x =或1x =（舍去）．所以0,2,2x =-．故选：C ．【点睛】本题考查集合的包含关系，掌握子集的定义是解题关键． 7．对于函数(),y f x x R =∈,“()y f x =的图象关于轴对称”是“=()f x 是奇函数”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要【答案】B 【解析】【详解】由奇函数，偶函数的定义,容易得选项B 正确.8．若正数x 、y 满足x y xy +=，则4x y +的最小值等于（） A ．4 B ．5 C ．9 D ．13【答案】C【解析】由x y xy +=得1xy x =-（1x >），代入4x y +后变形，换元后用对勾函数的单调性求解．【详解】因为正数x 、y 满足x y xy +=，所以1xy x =-（1x >），所以441x x y x x +=+-441x x =++-，令1t x =-，0t >， 44455x y t t t t+=++=++，由对勾函数4()f t t t=+在(0,2]上单调递减，在[2,)+∞上单调递增，所以min ()(2)4f t f ==，所以4x y +的最小值为9，此时33,2x y ==．故选：C ．【点睛】本题考查用对勾函数的单调性求最值，解题关键是用代入法化二元函数为一元函数，构造对勾函数．变形时一定注意新元取值范围．9．已知函数()f x =若()()222544f a a f a a -+<++，则实数a 的取值范围是（）A ．1,(2,)2⎛⎫-∞+∞ ⎪⎝⎭UB ．[2,6)C ．10,[2,6)2⎛⎤⋃ ⎥⎝⎦D ．(0,6)【答案】C【解析】确定函数()f x 的定义域和单调性，利用单调性解不等式．【详解】易知函数()f x =的定义域是[2,)+∞，在定义域内单调递增，所以由()()222544f a a f a a -+<++得2222544a a a a ≤-+<++，解得102a <≤或26a ≤<．故选：C ．【点睛】本题考查函数的单调性，利用单调性解函数不等式是常用方法．10．定义在[]1,1-的函数()f x 满足下列两个条件：①任意的[]1,1x ∈-都有()()f x f x -=-；②任意的[],0,1m n ∈，当m n ≠，都有()()0f m f n m n-<-，则不等式(13)(1)f x f x -<-的解集是（） A ．10,2⎡⎫⎪⎢⎣⎭B ．12,23⎛⎤⎥⎝⎦C ．11,2⎡⎫-⎪⎢⎣⎭D ．2,13⎡⎤⎢⎥⎣⎦【答案】A【解析】满足①()f x 为奇函数，满足②()f x 在[]0,1是减函数，根据对称性和函数的连续性，可得()f x 在[]1,1-是减函数，将不等式等价转化为自变量关系，即可求解. 【详解】任意的[]1,1x ∈-都有()()f x f x -=-,()f x 为奇函数，任意的[],0,1m n ∈，设m n >，()()()()()()(),0,0f m f n f m f n f m f n m n m n m n m n---=--><--，()(),()f m f n f x ∴<∴在[]0,1是减函数，()f x 为奇函数，所以()f x 在[]1,0-是减函数，()f x 在0x =处连续， ()f x 在[]1,1-是减函数，(13)(1)f x f x -<-等价于，13111131x x x x -≤⎧⎪-≥-⎨⎪->-⎩，解得102x ≤<，所以不等式的解集为10,2⎡⎫⎪⎢⎣⎭.故选:A. 【点睛】本题考查抽象函数的不等式，注意函数性质的应用，属于中档题. 11．下列函数中，对任意x ，不满足()()22f x f x =的是（） A ．()f x x = B ．()2f x x =- C ．()f x x x =- D ．()1f x x =-【答案】D【解析】对于每个选项中的函数()y f x =，验证是否满足等式()()22f x f x =，即可得出正确选项. 【详解】对于A 选项，()22f x x =，()222f x x x ==，等式()()22f x f x =成立；对于B 选项，()()2224f x x x =⨯-=-，()2224f x x x =-⨯=-，等式()()22f x f x =成立；对于C 选项，()()2222f x x x x x =-=-，()22222f x x x x x =-=-，等式()()22f x f x =成立；对于D 选项，()()22122f x x x =-=-，()221f x x =-，等式()()22f x f x =不成立. 故选：D. 【点睛】本题考查函数解析式，考查函数解析式是否满足等式，一般利用验证法，考查计算能力，属于基础题.二、多选题12．当一个非空数集F 满足条件“若,a b F ∈，则+a b ，-a b ，ab F ∈，且当0b ≠时，aF b∈”时，称F 为一个数域，以下四个关于数域的命题：其中，真命题为（） A ．0是任何数域的元素B ．若数域F 有非零元素，则2019F ∈C ．集合{|3,}P x x k k ==∈Z 为数域D ．有理数集为数域【答案】ABD【解析】根据新概念数域的定义判断．【详解】若a F ∈，则0a a F -=∈，A 正确；若a F ∈且0a ≠，则1aF a=∈，由此211F =+∈，312F =+∈，依次类推2019F ∈，B 正确；{|33,}P x k k Z ==∈，3,6P P ∈∈，但36P ∉，P 不是数域，C 错误；,a b 是两个有理数，则,,,aa b a b ab b+-（0b ≠）都是有理数，所以有理数集是数域，D 正确．故选：ABD ．【点睛】本题考查新定义，解题关键是正确理解新定义数域，即数域中任意两个元素的和、差、积、商（分母不为0）仍然属于数域．13．下列四个命题：其中不正确．．．命题的是（） A ．函数()f x 在(0,)+∞上单调递增，在(,0]-∞上单调递增，则()f x 在R 上是增函数 B ．若函数2()2f x ax bx =++与x 轴没有交点，则280b a -<且0a > C ．当a b c >>时，则有ab ac >成立D ．1y x =+和2(1)y x =+表示同一个函数【答案】ABCD【解析】根据函数的性质，不等式的性质，函数的定义对各个选项进行判断，错误命题也可通过举反例说明．【详解】,0()ln ,0x x f x x x ≤⎧=⎨>⎩，满足在(0,)+∞上单调递增，在(,0]-∞上单调递增，但()f x 在R上不是增函数，A 错；0a b ==时，()2f x =，它的图象与x 轴无交点，不满足280b a -<且0a >，B 错；当a b c >>，但0c =时，ac bc =，不等式ab ac >不成立，C 错；2(1)y x =+1x =+，与1y x =+的对应法则不相同，值域也不相同，不是同一函数，D 错．故选：ABCD ．【点睛】本题考查判断命题的真假，考查函数的性质，不等式的性质，函数的定义等，对一个假命题可以通过举反例说明其为假．三、填空题14．已知()y f x =是定义在R 上的奇函数，当0x ≥时，2()2f x x x =-，则()f x 在R 上的表达式是________．【答案】222,0()2,0x x x f x x x x ⎧-≥=⎨--<⎩【解析】根据奇函数定义求出0x <时的解析式，再写出R 上的解析式即可．【详解】0x <时，0x ->，22()()[()2()]2f x f x x x x x =--=---⨯-=--，所以222,0()2,0x x x f x x x x ⎧-≥=⎨--<⎩．故答案为：222,0()2,0x x x f x x x x ⎧-≥=⎨--<⎩．【点睛】本题考查函数的奇偶性，掌握奇函数的定义是解题关键．15．若关于x 的不等式210mx mx +->的解集为∅，则实数m 的取值范围为．【答案】[4,0]-【解析】试题分析：当0m =时，不等式变形为10->，解集为∅，符合题意；当0m ≠时，依题意可得2{4040m m m m <⇒-≤<∆=+≤，综上可得40m -≤≤．【考点】一元二次不等式．【易错点睛】本题主要考查不等式中的一元二次不等式问题，难度一般．有很多同学做此题时直接考虑为一元二次不等式，其二次函数应开口向下且与x 轴至多有一个交点，而忽略二次项系数为0时的情况导致出现错误．当二次项系数含参数时一定要讨论是否为0，否则极易出错．16．设函数1,02()21,0,2x x f x x x x ⎧-<<⎪=⎨--≤≥⎪⎩或，则函数()y f x =与12y =的图象的交点个数是________．【答案】4【解析】直接解方程1()2f x =即可得．【详解】解方程1()2f x =，当02x <<时，112x -=，112x -=±，12x =或32x =，当0x <或2x >时，1212x --=，312x -=，312x -=±，12x =-或52x =，所以方程1()2f x =有4个解，即函数()y f x =与12y =的图象有4个交点．故答案为：4 【点睛】本题考查函数图象交点个数问题，解题方法是最基本的方法：解方程，方程()()f x g x =的解就是函数()y f x =和()y g x =的图象交点的横坐标．17．已知函数()f x 是定义在R 上的奇函数，且当0x ≥时2()f x x =，若对任意的[1,1]x a a ∈-+，恒有()22()f x a a f x +>，则实数a 的取值范围为________．【答案】(,1)(0,)2-∞--+∞U 【解析】先求出()f x 的解析式，判断单调性，确定函数性质：0a >时，2()()a f x f ax =，0a <时，2()()a f x f ax =-，然后利用单调性化简不等式，由不等式恒成立求参数范围．【详解】由于()f x 是奇函数，所以当0x <时，22()()()f x f x x x =--=--=-，即22,0(),0x x f x x x ⎧≥=⎨-<⎩，易知函数()f x 在R 上是增函数，（1）若0a =，则命题为[1,1]x ∈-时，2()0f x >恒成立，但此时(0)0f =，不合题意；（2）若0a >，则2()()a f x f ax =，不等式()22()f x a a f x +>为2()()f x a f ax +>，所以2x a ax +>，即20x ax a -+>对[1,1]x a a ∈-+恒成立，令2224()()24a a a g x x ax a x -=-+=-+，22211(1)(1)(1)2212()022g a a a a a a a a -=-+-+=-+=-+>，22(1)2412(1)10g a a a a +=++=+->，当112a a a -<<+，即02a <<时，2min 4(4)()044a a a a g x --==>，满足题意，显然2a ≥时，12aa ≤-，min ()(1)0g x g a =->，满足题意，因此0a >满足题意．（3）若0a <，2()()a f x f ax =-，不等式()22()f x a a f x +>为2()()f x a f ax +>-，所以2x a ax +>-，即20x ax a ++>对[1,1]x a a ∈-+恒成立，2224()()24a a a h x x ax a x -=++=++，当112a a a -<-<+，即203a -<<时，2min 4(4)()044a a a a g x --==<，不满足题意，当23a ≤-时，12a a -≥+，22min ()(1)2412(1)10g x g a a a a =+=++=+->，解得21a <--，综上a 的取值范围是2(,1)(0,)2-∞--+∞U ．故答案为：2(,1)(0,)2-∞--+∞U ．【点睛】本题考查函数的奇偶性与单调性，考查不等式恒成立问题．解题关键是用分类讨论思想，转化2(),0()(),0f ax a a f x f ax a ≥⎧=⎨-<⎩，然后根据函数单调性转化问题为二次不等式恒成立，再利用二次函数知识求出相应的二次函数最小值，由最小值大于0得届结论．四、解答题18．已知集合A ＝{x |2≤x ≤8}，B ＝{x |1＜x ＜6}，C ＝{x |x ＞a }，U ＝R. (1)求A ∪B ，(∁U A )∩B ； (2)若A ∩C ≠∅，求a 的取值范围．【答案】(1)；；（2）.【解析】【详解】试题分析：(1)根据数轴表示集合的交集，并集，和补集；交集就是两个集合的公共元素组成的集合，并集就是两个集合的所有元素组成的集合，补集就是属于全集，但不属于此集合的元素组成的集合；（2）同样是利用数轴，表示集合A 和C,若有公共元素，表示端点值. 试题解析：解 (1)A ∪B ＝{x|2≤x≤8}∪{x|1<x<6}＝{x|1<x≤8}． ∵C U A ＝{x|x<2或x>8}， ∴(C U A)∩B ＝{x|1<x<2}． (2)∵A∩C≠∅，∴a<8．【考点】集合的运算19．已知a >0，b >0，a ＋b ＝1，求证： (1)1118a b ab++≥；(2)11(1)(1)9a b++≥.【答案】(1)详见解析；(2)详见解析.【解析】试题分析：（1）1的代换，将不等式左边化为齐次：()2a b a b a b a b ab+++++,再根据基本不等式求最小值为8，证得结论（2）左边展开得1111a b ab+++，再根据（1）得证试题解析：证明：(1)∵a ＋b ＝1，a >0，b >0， ∴＋＋＝＋＋＝2＝2＝2＋4≥4＋4＝8(当且仅当a ＝b ＝时，等号成立)， ∴＋＋≥8.(2)∵ ＝＋＋＋1，由(1)知＋＋≥8. ∴≥9.20．已知函数2()(2)2()f x x a x a a R =-++∈. （1）求不等式()0f x <的解集；（2）若当x ∈R 时，()4f x ≥-恒成立，求实数a 的取值范围. 【答案】(1)见解析；(2) []2,6a ∈-【解析】（1）不等式()0f x <可化为：(2)()0x x a --<，比较a 与2的大小，进而求出解集．（2）()4f x ≥-恒成立即2(2)240x a x a -+++≥恒成立，则2(2)4(24)0a a ∆=+-+≤，进而求得答案．【详解】解：（1）不等式()0f x <可化为：(2)()0x x a --<，①当2a =时，不等()0f x <无解；②当2a >时，不等式()0f x <的解集为{}2x x a <<； ③当2a <时，不等式()0f x <的解集为{}2x a x <<.（2）由()4f x ≥-可化为：2(2)240x a x a -+++≥，必有：2(2)4(24)0a a ∆=+-+≤，化为24120a a --≤，解得：[]2,6a ∈-. 【点睛】本题考查含参不等式的解法以及恒成立问题，属于一般题．21．某企业生产A ，B 两种产品，根据市场调查和预测，A 产品的利润与投资额成正比，设比例系数为1k ，其关系如图1；B 产品的利润与投资额的算术平方根成正比，设比例系数为2k ，其关系如图2．（注：利润与投资额单位是万元）（1）分别将A ，B 两种产品的利润表示为投资额的函数，并求出1,k 2k 的值，写出它们的函数关系式；（2）该企业已筹集到10万元资金，并全部投入A ，B 两种产品的生产，问：怎样分配这10万元投资额，才能使企业获得最大利润，其最大利润为多少万元．【答案】（1）114k =，254k =．1(),4f x x =(0)x ≥，5(),4g x x =(0)x ≥．（2）A产品投入3．75万元，B 产品投入6．25万元时，企业获得最大利润为65(4.0625)16万元．【解析】（1）由已知给出的函数模型设出解析式，代入已知数据可得；（2）设A 产品投入x 万元，则B 产品投入10x -万元，设企业的利润为y 万元．则有()(10)y f x g x =+-，(010)x ≤≤，用换元法转化为求二次函数在给定区间上最值问题．【详解】解析：（1）设投资额为x 万元，A 产品的利润为()f x 万元，B 产品的利润为()g x 万元，由题设1()f x k x =，()g x k =．由图知1(1)4f =，所以114k =，又5(4)2g =，所以254k =．所以1(),4f x x =(0)x ≥，()g x =(0)x ≥．（2）设A 产品投入x 万元，则B 产品投入10x -万元，设企业的利润为y 万元．1()(10)4y f x g x x =+-=+(010)x ≤≤，t =，则221051565,444216t y t t -⎛⎫=+=--+ ⎪⎝⎭(0t ≤≤．所以当52t =时，max 6516y =，此时251510 3.7544x =-==． ∴当A 产品投入3.75万元，B 产品投入6.25万元时，企业获得最大利润为6516即4.0625万元．【点睛】本题考查函数模型的应用．已知函数模型，直接设出解析式形式代入已知数据即可得函数解析式．换元法是求得最大值的关键．22．已知()f x 是二次函数，且满足(0)2,(1)()23f f x f x x =+-=+ （1）求函数()f x 的解析式（2）设()()2h x f x tx =-，当[1,)x ∈+∞时，求函数()h x 的最小值【答案】（1）2()22f x x x =++（2）()2min 52,(2)21,(2)t t h x t t t -≤⎧=⎨-++⎩＞【解析】（1）设2()(0)f x ax bx c a =++≠，利用()02f =可取c ，利用恒等式(1)()23f x f x x +-=+可求,a b ，从而得到()f x 的解析式.（2）由（1）可得2()2(1)2h x x t x =+-+，分2t ≤和2t >两种情况讨论即可. 【详解】（1）设2()(0)f x ax bx c a =++≠，∵(0)2,(1)()23f f x f x x =+-=+，∴()()2221123c a x b x c ax bx c x =⎧⎪⎨⎡⎤++++-++=+⎪⎣⎦⎩，即2223c ax a b x =⎧⎨++=+⎩，所以2223c a a b =⎧⎪=⎨⎪+=⎩，解得212c a b =⎧⎪=⎨⎪=⎩，∴2()22f x x x =++.（2）由题意得2()2(1)2h x x t x =+-+，对称轴为直线1x t =-，①当11t -≤即2t ≤时，函数在[1,)+∞单调递增()min (1)52h x h t ==-； ②当11t ->即2t >时，函数在[1,1]t -单调递减，在[1,)t -+∞单调递增，()2min (1)21h x h t t t =-=-++，综上：()2min 52,(2)21,(2)t t h x t t t -≤⎧=⎨-++>⎩【点睛】求二次函数的解析式，应根据题设条件设出合理的解析式的形式（如一般式、双根式、顶点式），二次函数在给定范围的最值问题，应该根据开口方向和最值的类型选择合理的分类方法.23．已知定义在R 上的函数()f x 对任意实数,x y 都满足()()()f x y f x f y +=+，且当0x >时，()0f x >．（1）判断函数()f x 的奇偶性，并证明；（2）判断函数()f x 的单调性，并证明；（3）解不等式()2(22)0f x ax f x a -+-<．【答案】（1）()f x 为奇函数．证明见解析（2）()f x 在R 上为增函数．证明见解析（3）当2a <-时不等式的解集是{|2}x a x <<-．当2a >-时不等式的解集是{|2}x x a -<<．当2a =-时不等式的解集是∅．【解析】（1）用赋值法求出(0)0f =，然后令y x =-可得奇偶性；（2）利用单调性的定义证明单调性；（3）由奇函数性质化不等式为2()(22)f x ax f a x -<-，由单调性转化为二次不等式，再分类得出解集．【详解】（1）解：()f x 为奇函数．证明：因为()()()f x y f x f y +=+，令0y =，得(0)()(0)f x f x f +=+对任意的x 都成立，所以(0)0f =．又令y x =-，则()()()0f x x f x f x -=+-=，所以()()f x f x -=-，所以()f x 是奇函数．（2）解：()f x 在R 上为增函数．证明：12,x x R ∀∈，且使12x x >由()f x 是奇函数，得()()()()()121212f x f x f x f x f x x -=+-=-．因为当0x >时，()0f x >，而120x x ->，所以()120f x x ->，所以()()12f x f x >，所以()f x 在R 上为增函数．（3）解：由()2(22)0f x ax f x a -+-<，得()2(22)f x ax f x a -<--．因为()f x 是奇函数，所以()2(22)f x ax f x a -<-+．又()f x 在R 上为增函数，所以222x ax x a -<-+．即2(2)20x a x a +--<，所以()(2)0x a x -+<．所以当2a <-时不等式的解集是{|2}x a x <<-．当2a >-时不等式的解集是{|2}x x a -<<．当2a =-时不等式的解集是∅．【点睛】本题考查抽象函数的奇偶性与单调性，考查利用奇偶性和单调性解函数不等式及分类讨论解二次不等式．掌握奇偶性与单调性的定义是解题关键．解抽象函数的基础是掌握赋值法．。

山东省滕州市第一中学2014-2015学年高一10月月考语文试题

山东省滕州市第一中学2014-2015学年高一10月月考语文试题时量120分钟分值100分一、语言知识及运用（共5题，每题3分）1、下列加点字的注音全都不相同的一项是A．忤．视/抵牾．瑕疵．/目眦．尽裂炮．烙/刨．根问底挟．持/汗流浃．背B．翘．首/憔．悴累．赘/危如累．卵创．伤/满目疮．痍即．使/既．往不咎C．箴．言/缄．默嗔．怪/嗔．目而视瞭．望/眼花缭．乱叱咤．/姹．紫嫣红D．刀俎．/狙．击裨．益/稗．官野史琴弦．/头晕目眩．吭．声/引吭．高歌2、把下列句子组成语意连贯的语段，排序最恰当的一项是①从窗内往外看时，那一朵白莲已经谢了，白瓣儿小船般散飘在水面。

②那一朵红莲，昨夜还是含苞的，今晨却开满了，亭亭地在绿叶中间立着。

③梗上只留个小小的莲蓬，和几根淡黄色的花须。

④半夜里听见繁杂的雨声，早起是浓阴的天，我觉得有些烦闷。

A．①②④③B．①③②④C．④①②③D．④①③②3．下列加点的成语，使用恰当的一组是A．这篇文章不仅结构混乱，而且文不加点．．．．，令人费解。

B．家用电器降价刺激了市民消费欲的增长，原本趋于滞销的彩电，现在一下子成了炙．手可热．．．的商品C．齐白石画展在美术馆开幕了，国画研究院的画家竟相观摩，艺术爱好者也趋之若鹜．．．．。

D．不涉及切身利益时，面纱尚存，一到关键时刻，或是一触及到底线，马上图穷匕见．．．．。

见了之后呢，再也回不到从前。

4、依次填入下面一段文字横线处的语句，衔接最恰当的一组是（）直到五四之前，中国诗坛还是旧诗一统天下。

①新诗的倡导者们主张废除陈旧的格律，其着眼点当然不仅仅在于形式。

②尽管旧诗曾有着灿烂的过去，但到了上个世纪初，已成强弩之末。

③它那固定的形式、格律已使它很难容纳新的思想、新的内容。

④这同时也是一场深刻的思想革命，向旧诗所代表的传统思想与美学观念发起挑战。

⑤很难适应急剧变化的现代社会读者的审美要求。

A．①④②③⑤B．②③⑤①④C．①④③②⑤D．②①④⑤③5、下列诗句都是描绘秋景的，与《沁园春·长沙》意境相似的一项是（）A．枯藤老树昏鸦，小桥流水人家，古道西风瘦马，夕阳西下，断肠人在天涯。

山东省滕州市第一中学2024-2025学年高一上学期10月月考数学试卷

山东省滕州市第一中学2024-2025学年高一上学期10月月考数学试卷一、单选题1．设集合{}0123,,,A =，{},,101,23,B =-，则R ()A B =I ð（） A ．∅B ． {}1,2C ．{}1-D ．{}1,2,32．设集合{}260M x x x =+-=，{}N 16N x x =∈<<，则M N =I （）A ．{}12x x <<B ．{}3C ．{}36x x -<<D ．{}23．“1a a<”是“1a <-”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．若正数x ，y 满足44x y +=，则11x y+的最小值为（）A ．2B ．94C ．3D ．835．下列四组函数中，不是同一个函数的一组是（）A ．()f x x =与()g x =B ．()21f x x =+与()21g t t =+C ．()xf x x =与()1,01,0x g x x >⎧=⎨-<⎩D ．()2f x =与()g x =6．已知函数()f x 的定义域为[)0,+∞，则函数()25f x y x -=-的定义域为（）A ．()()2,55,-+∞UB ．[)()2,55,-+∞UC ．()()2,55,⋃+∞D ．[)()2,55,+∞U7．下列命题中真命题的个数是（）①函数()1f x =和()0g x x =是同一个函数；②“()2210a b +-=”是“()10a b -=”的必要条件；③集合{|A y y ==，{|B x y ==表示同一集合.A ．0B ．1C ．2D ．38．若a b >，且2ab =，则22(1)(1)a b a b-++-的最小值为（）A ．2B ．4C ．4D ．2二、多选题9．下列四个结论中正确的是（） A ．22,,4250x y x y x y ∃∈+-++=RB ．命题“2,3210x x x ∀∈--<R ”的否定是“2000,3210x x x ∃∈-->R ” C ．21,4x x x ∀∈+>R D ．“a b >”是“1a b >+”的必要不充分条件10．已知非零实数,a b >，下列结论中错误的结论有（）A ．11a b< B ．22a b > C ．22ab a b > D ．2211ab a b> 11．已知关于x 一元二次不等式220ax ax b -+>的解集为{}A x m x n =<<（其中m n <），关于x 一元二次不等式222ax ax b -+>-的解集为{}B x p x q =<<，则（）A ．AB B =I B ．()A B B ⋃⊆C ．m n p q +=+D ．当2b <-时，2q p q+的最小值为3三、填空题12．已知集合{}221,,0A a a =-，{}1,5,9B a a =--，若满足{}9A B ⋂=，则实数a 的值为．13．已知关于x 的不等式210mx mx -+≤，若此不等式的解集为∅，则实数m 的取值范围是 14．已知关于x 的不等式组()224502525x x x x x k ⎧-++<⎪⎨+<-+⎪⎩的解集中存在整数解且只有一个整数解，则k 的取值范围为.四、解答题15．设集合{}{}|121,|25A x a x a B x x =+<<-=-<<. (1)若3a =，求()R A B ⋃ð；(2)是否存在实数a ，使得A B A =U ，若存在，求实数a 的取值范围，否则说明理由. 16．设m ∈R ，已知集合3211x A xx +⎧⎫=<⎨⎬-⎩⎭，(){}2220B x x m x m =+--<. (1)当1m =时，求A B U ；(2)若“x B ∈”是“x A ∈”的必要不充分条件，求m 的取值范围.17．中国建设新的芯片工厂的速度处于世界前列，这是朝着提高半导体自给率目标迈出的重要一步.根据国际半导体产业协会(SEMI)的数据，在截至2024年的4年里，中国计划建设31家大型半导体工厂.某公司打算在2023年度建设某型芯片的生产线，建设该生产线的成本为300万元，若该型芯片生产线在2024年产出x 万枚芯片，还需要投入物料及人工等成本()V x （单位：万元），已知当05x <≤时，()125V x =；当520x <≤时，()240100V x x x =+-；当20x >时，()160081600V x x x=+-，已知生产的该型芯片都能以每枚80元的价格售出. (1)已知2024年该型芯片生产线的利润为()P x （单位：万元），试求出()P x 的函数解析式. (2)请你为该型芯片的生产线的产量做一个计划，使得2024年该型芯片的生产线所获利润最大，并预测最大利润.18．已知函数()f x 对任意x 满足：()()324f x f x x --=，二次函数()g x 满足：()()24g x g x x +-=且()14g =-.(1)求()f x ，()g x 的解析式；(2)若R a ∈，解关于x 的不等式()()()()2143a x a x g x f x +-+->-.19．对于函数()f x ，若()f x x =，则称实数x 为()f x 的“不动点”，若()()f f x x =，则称实数x 为()f x 的“稳定点”，函数()f x 的“不动点”和“稳定点”组成的集合分别记为A 和B ，即(){}A x f x x ==，()(){}B x f f x x ==.(1)对于函数()21f x x =-，分别求出集合A 和B ； (2)对于所有的函数()f x ，证明：A B ⊆；(3)设()2f x x ax b =++，若{}1,3A =-，求集合B .。

高一物理月考试题及答案-山东滕州市第一中学-2015学年高一10月月考试题

2014-2015学年度山东省滕州市第一中学高一第一学期10月月考物理试题时量：90分钟分值：100分一、选择题（本大题共12个小题，每小题4分．共48分。

1、2、10、11是多项选择题，其余是单项选择题。

多项选择题全部选对的得4分，选对但不全的得2分，有选错的得0分）。

1、物体沿一直线运动，下列说法正确的是（）A ．物体在某一时刻的速度为3 m/s ，则物体在1 s 内一定走3 mB ．物体在某一秒内的平均速度为3 m/s ，则物体在这一秒内的位移是3 mC ．物体在某一段时间内的平均速度为3 m/s ，则物体在这一秒内位移一定是3 mD ．物体在某段位移内的平均速度是3 m/s ，则物体在这段位移的一半时的速度一定是3m/s 2、一列火车从上海开往北京，下列叙述中，表示时间的是：（） A ．早上6时10分从上海发车 B ．列车预计在18时11分到达北京 C ．列车在9时45分到达途中南京站 D ．列车在南京站停车10分钟3、下列各选项中，所有物理量都是矢量的是（） A ．力、速率、加速度 B ．力、加速度、位移 C ．速率、位移、加速度D ．力、路程、速度4、某人从离地高为5m 处以某一初速度竖直向下抛一小球，在与地面相碰后弹起，上升到高为2m 处被接住，在这段过程中（）． A ．小球的位移为3m ，方向竖直向下，路程为7m B ．小球的位移为7m ，方向竖直向上，路程为7m C ．小球的位移为3m ，方向竖直向下，路程为3m D ．小球的位移为7m ，方向竖直向上，路程为3m5、物体的初速度为v 0，以加速度a 做匀加速直线运动，如果要它的速度增加到初速度的n 倍，则物体的位移是（）．A ．a v n 21202-B ．a v n 2202C ．av n 2120- D ．a v n 21202-6、自由下落的物体第n 秒内通过的位移比第（n －1）秒内通过的位移多多少（g 取10 m/s 2）（）．A ．10 mB ．5（2n ＋1） mC ．3（n ＋1） mD ．n 2n 2－1m7、一物体从H 高处自由下落，经时间t 落地，则当它下落t2时，离地的高度为（）．A ．H 2B ．H 4C ．34HD ．32H8、一辆汽车从静止开始由甲地出发，沿平直公路开往乙地，汽车先做匀加速运动，接着做匀减速运动，开到乙地刚好停止，其速度图象如图所示，那么在0～t 0和t 0～3t 0两段时间内的（）．A ．加速度大小之比为1∶3B ．加速度大小之比为3∶1C ．位移大小之比为2∶1D ．位移大小之比为1∶29、一玩具汽车由静止开始以恒定的加速度a 向东运动t s 后，加速度变为向西，大小不变，再经过t s 时，物体的运动情况是（）． A ．小汽车位于出发点以东，速度为零 B ．小汽车位于出发点以东，继续向东运动 C ．小汽车回到出发点，速度为零 D ．小汽车回到出发点，运动方向向西10、（多选）一物体做匀变速直线运动的位移（x ）与时间（t ）关系是x ＝6t-3t 2（t 以s 为单位，x 以m 为单位），则物体（）．A ．2s 后速度开始反向B ．1s 后速度开始反向C ．第1s 内的平均速度是3m/sD ．前2s 内的平均速度是9m/s11、（多选）某火箭由地面竖直向上发射时，其v-t 图像如图所示，则下列表述不正确的是（）．A ．火箭在t 2~t 3时间内向下运动B ．火箭在t 1~t 2时间内加速度最大C ．0~t 3时间内，火箭一直向上运动D ．火箭运动过程中的最大加速度大小为32t v 12、一辆做直线运动的汽车，以速度v 行驶了全程的一半，然后匀减速行驶了后一半，到达终点时恰好停止，全程的平均速度为（）． A ．v/2 B ．2v/3 C ．3v/4 D ．v/3 二、实验填空题（共2小题，每空2分，共16分）。

山东滕州一中2022-2023学年高三上学期10月月考语文试题

2022—2023学年第一学期10月单元过关考试高三语文1．答卷前，考生务必将自己的姓名、考生号、座位号等填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将答题卡交回。

一、现代文阅读(35分)（一）现代文阅读I（本题共5小题，17分）阅读下面的文字，完成1～5题。

材料一：在讲为什么我们要保存过去时代里所创造的一些建筑物之前，先要明了：建筑是什么？最简单地说，建筑就是人类盖的房子，为解决他们生活上“住”的问题。

那就是：解决他们安全食宿的地方、生产工作的地方和娱乐休息的地方。

“衣、食、住”自古是相提并论的，因为它们都是人类生活最基本的需要。

为了这需要，人类才不断和自然作斗争。

建筑又是艺术创造。

人类对他们所使用的生产工具、衣服、器皿、武器等，从石器时代的遗物中我们就可看出，在这些实用器物的实用要求之外，总要有某种加工，以满足美的要求，也就是文化的要求，在住屋也是一样。

从古至今，人类在住屋上总是或多或少地下过工夫，以求造型上的美观。

例如：自有史以来无数的民族，在不同的地方，不同的时代，同时在建筑艺术上，是继续不断地各自努力，从没有停止过的。

建筑活动也反映当时的社会生活和当时的政治经济制度，如宫殿、庙宇、民居、仓库、城墙、堡垒、作坊、农舍，有的是直接为生产服务，有的是被统治阶级利用以巩固政权，有的被他们独占享受，在封建时代建筑的精华是集中在宫殿建筑和宗教建筑等等上，它是为统治阶级所利用以作为压迫人民的工具的。

不同的民族的衣食、工具、器物、家具，都有不同的民族性格或民族特征。

无论是哪一种工艺，包括建筑，不论属于什么时代，总是有它的一贯的民族精神的。

以上几点，不但说明建筑是什么，同时也说明它是各民族文化的一种重要的代表。

从考古角度考虑各个时代的建筑问题时，实物得到保存，就意味着各时代所产生过的文化证据之得到保存。

山东省滕州一中2020-2021学年高一第一学期10月月考数学试题【含解析】

山东省滕州一中2020-2021学年高一第一学期10月月考数学试题【含解析】一､单项选择题1. 已知集合{}{}{}1,2,3,4,5,6,7,8,92,3,4,51,2,3,6,7U A B ===，，，则()UB A ⋂=（） A. {}1,6 B. {}6,7 C. {}6,7,8 D. {}1,6,7【答案】D 【解析】【分析】先求出UA ，然后再求()UB A ⋂即可求解.【详解】由集合{}{}{}1,2,3,4,5,6,7,8,92,3,4,51,2,3,6,7U A B ===，，则{}1,6,7,8,9UA =.所以(){}1,6,7UB A ⋂=故选：D【点睛】本题主要考查集合补集、交集的概念和运算，属于基础题. 2. 设命题p ：k ∃∈N ，223k k >+，则p ⌝为（） A. ∀∈k N ，223k k >+ B. k ∃∈N ，223k k <+ C. ∀∈k N ，223k k ≤+ D. k ∃∈N ，223k k ≤+【答案】C 【解析】【分析】特称命题否定为全称命题，改量词，否结论即可【详解】解：因为命题p ：k ∃∈N ，223k k >+，所以p ⌝：∀∈k N ，223k k ≤+，故选：C【点睛】此题考查命题的否定，属于基础题 3. 下列各组函数中，表示同一函数的是（）A. ()2f x x =+与24()2x g x x -=-B. ()1f x x =+与1,1,()1, 1.x x g x x x --<⎧=⎨+≥⎩C. ()1f x =与0()g x x =D. ()32(R)f x x x =+∈与()32(R)g t t t =+∈【答案】D 【解析】【分析】根据相等函数的定义域和对应关系相同依次讨论各选项即可得答案.【详解】解：对于A 选项，()2f x x =+定义域为R ，24()2x g x x -=-的定义域为{}2x x ≠，故不满足条件；对于B 选项，1,1()11,1x x f x x x x +≥-⎧=+=⎨--<-⎩，显然与1,1,()1, 1.x x g x x x --<⎧=⎨+≥⎩的对应关系不同，故不满足条件；对于C 选项，()1f x =定义域为R ，0()g x x =的定义域为{}0x x ≠，故不满足条件；对于D 选项，()32(R)f x x x =+∈与()32(R)g t t t =+∈定义域相同，对应关系相同，故满足条件．故选：D ．【点睛】本题考查函数相等的概念，熟练掌握函数相等概念是解题的关键，是基础题． 4. 设,R a b ∈，则“4a b +≤”是“2a ≤且2b ≤”的（） A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】B 【解析】根据充分条件与必要条件的概念，直接判断，即可得出结果.【详解】若1a =-，3b =，满足4a b +≤，但不满足“2a ≤且2b ≤”；所以“4a b +≤”不是“2a ≤且2b ≤”的充分条件；若2a ≤且2b ≤，则4a b +≤显然成立；所以“4a b +≤”是“2a ≤且2b ≤”的必要条件；因此，“4a b +≤”是“2a ≤且2b ≤”的必要而不充分条件. 故选：B .【点睛】本题主要考查必要不充分条件的判定，属于基础题型. 5. 下列说法中，错误．．的是（） A. 若0b a >>，0m >，则a m ab m b +>+ B. 若22a b c c >，则a b > C. 若22a b >，0ab >，则11a b<D. 若a b >，c d <，则a c b d ->-【答案】C 【解析】【分析】根据作差法比较大小，即可判定A 正确；根据不等式的性质，可得BD 正确；根据特殊值，可判断C 错.【详解】A 选项，若0b a >>，0m >，则()()()0m b a a m a ab mb ab am b m b b b m b b m -++---==>+++，故A 正确；B 选项，若22a bc c>，根据不等式的可乘性，可得a b >，故B 正确； C 选项，若2a =-，1b =-，则满足22a b >，0ab >，但112->-，故C 错；D 选项，若a b >，c d <，则c d ->-，所以a c b d ->-，故D 正确. 故选：C.【点睛】本题主要考查根据不等式的性质判断所给不等式是否成立，属于基础题.6. 已知函数()()2,1,11,1x x f x f x x ⎧<⎪=⎨--≥⎪⎩，则()2020f =（）A. 1-B. 2020-C. 1D. 2020【答案】B【分析】先利用分段函数及周期性求得()()202002020f f =-，再代入计算即得结果.【详解】函数()()2,1,11,1x x f x f x x ⎧<⎪=⎨--≥⎪⎩，则()()()()20202019120182...02020020202020f f f f =-=-==-=-=-. 故选：B.【点睛】本题考查了分段函数求函数值，属于基础题. 7. 已知函数()xf x x m=-，若函数()f x 在区间2,上单调递减，则实数m 的取值范围为（） A. ()0,2 B. (]0,2C. [)2,+∞D.2,【答案】B 【解析】【分析】由于()1x mf x x m x m==+--在区间2,上单调递减，则有2m ≤且0m >，从而可求出m 的取值范围【详解】解：因为2x >时，0x m -≠，所以2m ≤，因为()1x mf x x m x m==+--在2,上单调递减，所以0m >，综上02m <≤，故选：B【点睛】此题考查由函数的单调性求参数的范围问题，考查分析问题的能力，属于基础题8. 已知函数2240()0x x x f x x x ⎧+<=⎨-≥⎩，，，若()()5f f m ≥，则实数m 的取值范围是（）A. )5,⎡+∞⎣B. 5⎡⎤⎣⎦C. (,5-∞-D.5,0⎡⎤-⎣⎦【答案】A【分析】根据题中条件，得到()()()2450f m f m f m ⎧⎡⎤+≥⎪⎣⎦⎨<⎪⎩，解得()5f m ≤-，分别讨论0m <，0m ≥两种情况，即可得出结果.【详解】因为2240()0x x x f x x x ⎧+<=⎨-≥⎩，，，20x -≤，为使()()5f f m ≥，只能()0f m <，即有()()()2450f m f m f m ⎧⎡⎤+≥⎪⎣⎦⎨<⎪⎩，解得()5f m ≤-，当0m <时，245m m +≤-，无解；当0m ≥时，25m -≤-，解得5m ≥5m ≤-5m ≥综上，5m ≥. 故选：A【点睛】本题主要考查解分段函数不等式，涉及一元二次不等式的解法，属于常考题型.二､多项选择题9. 已知集合{}{}2|60,|10,A x x x B x mx =--==-=AB B =，则实数m 取值为（）A.13B. 12-C. 13-D. 0【答案】ABD 【解析】【分析】先求集合A ，由AB B =得B A ⊆，然后分B =∅和B ≠∅两种情况求解即可【详解】解：由260x x --=，得2x =-或3x =，所以{}2,3A =-，因为AB B =，所以B A ⊆，当B =∅时，方程10mx -=无解，则0m =，当B ≠∅时，即0m ≠，方程10mx -=的解为1x m=，因为B A ⊆，所以12m =-或13m=，解得12m =-或13m =，综上0m =，或12m =-，或13m =，故选：ABD【点睛】此题考查集合的交集的性质，考查由集合间的包含关系求参数的值，属于基础题 10. 下列命题正确．．的是（） A. 若0x <，则4x x+的最小值为4 B. 若R x ∈，则22132x x +++的最小值为3 C. 若22,R,15a b a b ab ∈+=-，则ab 的最大值为5 D. 若0,0,24a b a b >>+=，则ab 的最大值为2 【答案】CD 【解析】【分析】对于A ，由于0x <，所以对4x x+变形后再利用基本不等式求最值判断即可；对于B ，不满足基本不等式的条件；对于C ，D 利用基本不等式判断即可【详解】解：对于A ，因为0x <，所以444[()]2()4x x x x x x+=--+≤--⋅---，当且仅当2x =-取等号，所以4x x+有最大值4-，所以A 错误；对于B ，22221132122x x x x ++=+++++，而22122x x +=+不成立，所以22132x x +++的最小值不等于3，而其最小值为72，对于C ，由22,R,15a b a b ab ∈+=-可知22152ab a b ab -=+≥，得5≤ab ，当且仅当a b =时取等号，ab 的最大值为5，所以C 正确；对于D ，由于0,0,24a b a b >>+=，所以4222a b ab =+≥即2ab ≤，当且仅当2a b =，即2,1a b ==时取等号，所以ab 的最大值为2，故选：CD【点睛】此题考查基本不等式的应用，利用基本不等式求最值时要注意“一正二定三相等”的条件，属于基础题11. 已知()f x 为定义在R 上的函数，对任意的,x y ∈R ，都有()()()f x y f x f y +=+，并且当0x <时，有()0f x <，则（） A. (0)0f =B. 若(2)2f =，则(2)2f -=C. ()f x 在(),-∞+∞上为增函数D. 若(2)2f =，且2()(25)4f a f a -->，则实数a 的取值范围为()(),11,-∞+∞【答案】ACD 【解析】【分析】取0x y ==即可求得(0)f 的值，令y x =-，易得()()0f x f x +-=，从而可判断其奇偶性；设1x ，2x R ∈且12x x <，作差21()()f x f x -后判断其符号即可证得()f x 为R 上的增函数；依题意可得(4)4f =，原不等式等价于()2()(25)4f a f a f >-+，再根据函数的单调性转化为自变量的不等式，解得即可；【详解】解：取0x y ==得，则(00)(0)(0)f f f +=+，即(0)0f =；故A 正确；取y x =-代入，得(0)()()f f x f x =+-，又(0)0f =，于是()()f x f x -=-，()f x ∴为奇函数；因为(2)2f =，所以()()222f f -=-=-，故B 错误；设1x ，2x R ∈且12x x <，则()11222121()()()()()f x f x f x f x f x x f x x -=+-=-=--，由120x x -<知，12()0f x x -<，所以21()()0f x f x ->21()()f x f x ∴>，∴函数()f x 为R 上的增函数．故C 正确；因为(2)2f =，所以(4)(2)(2)4f f f =+=，所以2()(25)4f a f a -->等价于()2()(25)4f a f a f -->，即()2()(25)4f a f a f >-+所以2()(254)f a f a >-+等价于2254a a >-+，即()210a ->，解得1a >或1a <，故D 正确；故选：ACD【点睛】本题主要考查抽象函数的应用，函数奇偶性的判断以及函数不等式的解法，利用函数奇偶性和单调性之间的关系是解决本题的关键，属于中档题．12. 若对任意满足22x y +=的正实数,,x y 223524x y x yxy+++2*2(N )m m >∈恒成立，则正整数．．．m 的取值为（）A. 1B. 2C. 3D. 4【答案】AB 【解析】【分析】由已知条件可得223524x y x y xy +++22494x y xy xy++=494x yy x =++，然后利用基本不等式求出其最小值为16，再由2162m >可求出m 的值，从而可求出正整数m 的取值【详解】解：因为22x y +=，且0,0x y >>，所以2222222352435435(2)x y x y x y x y x y xy xy xy ++++++++==22494x y xyxy ++=494x y y x=++ 492416x yy x≥⋅=，当且仅当49x y y x =，即64,77x y ==时取等号，所以223524x y x yxy+++的最小值为16，所以由2162m >，得2222m -<<，因为m N +∈，所以1m =或2m =，故选：AB【点睛】此题考查基本不等式的应用，考查数学转化思想和计算能力，属于中档题三､填空题13. 函数2()4f x x x =-+的值域为__________________. 【答案】[]0,2 【解析】【分析】先求出函数的定义域，再令24(04)t x x x =-+≤≤，则y t =，然后利用配方法结合二次函数的性质求出t 的取值范围，从而可求出函数的值域【详解】解：由240x x -+≥，得04x ≤≤，令24(04)t x x x =-+≤≤，则yt =因为224(2)4t x x x =-+=--+，04x ≤≤ 所以04t ≤≤，所以02t ≤≤，即02y ≤≤，所以函数2()4f x x x =-+的值域为[]0,2，故答案为：[]0,2【点睛】此题考查求复合函数的值域，利用了换元法，属于基础题14. 若{},,min ,,,a ab a b b a b ≤⎧=⎨>⎩则函数{}2()min ,23f x x x =---的最大值为________.【答案】1- 【解析】【分析】由223x x ---，解得13x -，再利用单调性，即可求出其最大值．【详解】解：由223x x ---，解得13x -．∴①当13x -时，函数{}2()min ,2323f x x x x =---=--，其最大值()11f -=-；②当1x ≤-或3x ≥时，函数{}22()min ,23f x x x x =---=-，其最大值为1-．综上可知：函数()f x 的最大值是1-．故答案为：1-．【点睛】充分理解定{},min a b 表示a ，b 中的较小者和掌握函数的单调性是解题的关键，属于基础题15. 若0,x y z >>>则2211269()x xz z x x y xy++-+-的最小值为_______.【答案】4 【解析】【分析】根据题意将原式变形为()()2222211112693()x xz z x xy xy x z x x y xy x xy xy ⎛⎫++-+=-++++- ⎪--⎝⎭，再结合基本不等式求解即可得答案.【详解】解：因为0x y z >>>，所以20x xy ->，0xy >，所以210x xy>-，10xy >，所以222222111126969()x xz z x xy xy x xz z x x y xy x xy xy++-+=-++++-+--()()222113x xy xy x z x xy xy ⎛⎫=-++++- ⎪-⎝⎭()()222112234x xy xy x z x xy xy≥-⋅⋅-=-，当且仅当2=1130x xy xy x z ⎧-⎪=⎨⎪-=⎩，即222,23x y z ===时等号成立，故答案为：4.【点睛】本题考查利用基本不等式求最值，解题的关键是将原式适当的变形，是中档题. 16. 函数()21f x x =++的单调递减区间为_______；函数21,,()3,,x x k g x kx x k ⎧++<=⎨-≥⎩若()g x 是定义在R 上的减函数，则实数k 的值为____________. 【答案】 (1). (),2-∞- (2). 2- 【解析】【分析】由于3,2()1,2x x f x x x +≥-⎧=⎨--<-⎩，从而可求出其减区间；由为21,,()3,,x x k g x kx x k ⎧++<=⎨-≥⎩在R 上为减函数，可得21y x =++在(,)k -∞上为减函数，3y kx =-在[,)k +∞上为减函数，从而得2213k k k ≤-⎧⎨--≥-⎩，进而可求出k 的值【详解】解：由()21f x x =++，得3,2()1,2x x f x x x +≥-⎧=⎨--<-⎩，所以()f x 的递减区间为(),2-∞-；因为21,,()3,,x x k g x kx x k ⎧++<=⎨-≥⎩在R 上为减函数，所以21y x =++在(,)k -∞上为减函数，3y kx =-在[,)k +∞上为减函数，所以2213k k k ≤-⎧⎨--≥-⎩，得221k k ≤-⎧⎨-≤≤⎩，解得2k =-，故答案为：(),2-∞-，2-【点睛】此题考查分段函数的单调性问题，考查由单调性求参数的范围，属于中档题四､解答题17. 已知全集U =R ，集合}{2A x x =>，}{44B x x =-<<. （1）求()UA B ；（2）定义{A B x x A -=∈且}x B ∉，求A B -，()A A B --.【答案】（1）}{4x x ≤-；（2）}{4A B x x -=≥，()}{24A A B x x --=<<. 【解析】【分析】（1）根据并集的概念，先求AB ，再由补集的概念，即可得出结果；（2）根据题中条件，可直接求出A B -，进而可求出()A A B --. 【详解】（1）因为}{2A x x =>，}{44B x x =-<<，所以}{4A B x x ⋃=>-，则()}{4UA B x x ⋃=≤-；（2）因为{A B x x A -=∈且}x B ∉，所以}{4A B x x -=≥，因此()}{24A A B x x --=<<.【点睛】本题主要考查集合的并集和补集运算，考查集合的新定义，属于基础题型. 18. 已知函数4()f x x x=+. （1）求()(2)ff ；（2）判断函数()f x 在区间[]2,4上的单调性，并证明；（3）关于x 的不等式4x m x+<在区间[]2,4上有解，求实数m 的取值范围. 【答案】（1）5；（2）()f x 在区间[]2,4上单调递增，证明见解析；（3）()4,+∞. 【解析】【分析】（1）由题意可得()24f =，故()()()24ff f =可得出答案.（2）利用函数的单调性的定义证明函数单调性的步骤证明即可. （3）不等式4x m x+<在区间[]2,4上有解, 所以min ()m f x >,由单调性求出函数()f x 的最小值即可.【详解】解：（1）()42242f =+=，()()()424454f f f ==+= （2）()f x 在区间[]2,4上单调递增.证明：∀1x ，2x ∈[]2,4，且12x x <，12121244()()f x f x x x x x ⎛⎫⎛⎫-=+-+ ⎪ ⎪⎝⎭⎝⎭()121244x x x x ⎛⎫=-+- ⎪⎝⎭()2112124()x x x x x x -=-+()()1212124x x x x x x --=1x ，2x ∈[]2,4，且12x x <，1212120,40,0.x x x x x x ∴>->-<，12()()0f x f x ∴-<，即12()()f x f x <. ∴函数()f x 在区间[]2,4上是增函数.（3）由（2）知min ()(2)4f x f == 因为关于x 的不等式4x m x+<在区间[]2,4上有解，所以min ()m f x >. 所以4m >.所以实数m 的取值范围是()4,+∞【点睛】本题考查利用单调性的定义证明函数的单调性，解决不等式有解问题，属于中档题. 19. （1）若,0,a b >且3ab a b =++，求ab 的最小值；（2）若,0,a b >且ab a b =+，求4a b +的最小值. 【答案】（1）9；（2）9. 【解析】【分析】（1）利用基本不等式可得230ab ab -≥，再解不等式即可得解；（2）依题意可得111a b+=，再利用基本不等式乘“1”法计算可得；【详解】解：（1）,0a b >，2a b ab ∴+≥323ab a b ab =++≥.230ab ab ∴-≥，()310ab ab ∴≥.10ab +>，30ab ≥.3ab ≥9.ab ∴≥当且仅当3a b ==，等号成立.故当3a b ==时，ab 的最小值为9. （2）,0,a b >且ab a b =+.1a b ab+∴=，111a b +=()114445a b a b a b a b b a ⎛⎫∴+=++=++ ⎪⎝⎭459a bb a≥+=.当且仅当2b a =，即3,32a b ==时，等号成立. 故当3,32a b ==时，4a b +的最小值为9 【得解】本题考查的是基本不等式，注意不等式使用的条件“一正、二定、三相等”，要配凑成和为定值的形式，并关注取等号的条件，属于中档题． 20. 已知不等式2320ax x -+>的解集为{1,x x <或}x b >，（1）求实数,a b 的值；（2）解关于x 的不等式2()0cx ac b x ab ++>-()c R ∈.【答案】（1）12a b =⎧⎨=⎩；（2）当0c <时，原不等式的解集为：2{|1}x x c <<；当0c 时，原不等式的解集为：{|1}<x x ；当02c <<时，原不等式的解集为：{|1,x x <或2}x c>；当2c =时，原不等式的解集为：{|1}x x ≠；当2>c 时，原不等式的解集为：2{|,x x c<或1}x > 【解析】【分析】（1）由题知1和b 是方程2320ax x -+>的根，利用韦达定理即可求出a , b 的值.（2）由（1）知不等式为2(2)20cx c x +-+>，讨论2c 和2的大小，写出对应的解集即可.【详解】解：（1）因为不等式2320ax x -+>的解集为{1,x x <或}x b <所以1和b 是方程2320ax x -+=的两个实数根.故：3121b a b a ⎧+=⎪⎪⎨⎪⨯=⎪⎩，解得12a b =⎧⎨=⎩. 经验证，符合条件.（2）由（1）知不等式2()0cx ac b x ab ++>-，即2(2)20cx c x +-+>，即(2)(1)0cx x -->.当0c时，2(1)0x -->，解得1x <.当0c <时，(2)(1)0cx x -->即2()(1)0x x c--<，解得21x c<<当0c >时，(2)(1)0cx x -->即2()(1)0x x c -->.比较2c与1的大小当21c =，即2c =时，解得1x ≠ 当21c >，即02c <<时，解得1,x <或2x c > 当21c <，即2>c 时，解得2,x c<或1x > 综上所述，当0c <时，原不等式的解集为：2{|1}x x c<< 当0c时，原不等式的解集为：{|1}<x x当02c <<时，原不等式的解集为：{|1,x x <或2}x c> 当2c =时，原不等式的解集为：{|1}x x ≠ 当2>c 时，原不等式的解集为：2{|,x x c<或1}x > 【点睛】考查一元二次不等式的解法，主要考查一元二次不等式与一元二次方程之间的关系的不等式的解法；考查含参不等式的解法，分类讨论为解题的关键，属于中档题.21. 2020年滕州某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元.每生产x (百辆)新能源汽车，需另投入成本()C x 万元，且210100,040()?36005014500,40x x x C x x x x ⎧+<<⎪=⎨+-≥⎪⎩由市场调研知，每辆车售价5万元，且生产的车辆当年能全部销售完.（1）求出2020年的利润()L x (万元)关于年产量x (百辆)的函数关系式；(利润=销售额-成本)（2）2020年产量为多少百辆时，企业所获利润最大？并求出最大利润.【答案】（1）2104002500,040()36002000(),40x x x L x x x x ⎧-+-<<⎪=⎨-+≥⎪⎩；（2）产60百辆时，该企业获得利润最大，且最大利润为1880万元. 【解析】【分析】（1）根据年利润=销售额-投入的总成本-固定成本，分040x <<和40x ≥两种情况得到()L x 与x 的分段函数关系式；（2）当040x <<时根据二次函数求最大值的方法来求()L x 的最大值，当40x ≥时，利用基本不等式求()L x 的最大值，最后综合即可【详解】解：（1）当040x <<时，2()5100101002500L x x x x =⨯---2104002500x x =-+-当40x ≥时，3600()5100501L x x x x =⨯--3600450025002000()x x+-=-+ 所以2104002500,040()36002000(),40x x x L x x x x ⎧-+-<<⎪=⎨-+≥⎪⎩（2）当040x <<时，2()10(20)1500L x x =--+，当20x时，max ()1500L x =；当40x ≥时，3600()2000()L x x x =-+360020002x x≤-⋅20001201880=-=， (当且仅当3600x x=，即60x =时，“=”成立) 因为18801500>，所以，当60x =时，即2020年生产60百辆时，该企业获得利润最大，且最大利润为1880万元.【点睛】此题考查函数的实际应用，基本不等式的应用，考查转化思想及计算能力，属于中档题22. 已知函数()23.f x x ax =++（1）当[]2,2x ∈-时，()f x a ≥恒成立，求实数a 的取值范围；（2）关于x 的不等式()0f x <的解集为{}|6x m x m <<+，求实数a 的值.【答案】（1）[]7,2-；（2）6a =±. 【解析】【分析】（1）设()23g x x ax a =++-，根据题意，对[]2,2x ∀∈-，()0g x ≥恒成立；分别讨论22a -≤-，22a -≥，222a-<-<三种情况，即可得出结果；（2）由不等式的解集，根据三个二次之间的关系，结合韦达定理，结合题中条件，即可得出结果.【详解】（1）当[]2,2x ∈-，设()23g x x ax a =++-，对称轴为2ax =-，由题意知对[]2,2x ∀∈-，()0g x ≥恒成立；（1）当22a-≤-，即4a ≥时，()g x 在[]22-,上单调递增，此时只需()42730a g a ≥⎧⎨-=-≥⎩，此时无解；（2）当22a-≥，即4a ≤-时，()g x []22-,上单调递减，此时只需()4270a g a ≤-⎧⎨=+≥⎩，解得74a -≤≤-；（3）当222a-<-<，即44a -<<时，此时只需2443024a a a g a -<<⎧⎪⎨⎛⎫-=--+≥ ⎪⎪⎝⎭⎩，解得42a -<≤；综上所述，a 的取值范围是[]7,2-.（2）因为()0f x <即230x ax ++<的解集为{}|26x m x m <<+，所以1x m =和226x m =+2x ax 30++=的两个实数根；由韦达定理可知12123x x ax x +=-⎧⎨=⎩，且1226x x -=； ()222121212412x x x x x x a ∴-=+-=-，所以有22412a =-，解得 6.a =±【点睛】本题主要考查一元二次不等式恒成立求参数的问题，考查由不等式的解集求参数的问题，属于常考题型.。

2019-2020学年山东省枣庄市滕州一中高三(上)10月月考数学试卷

2019-2020学年山东省枣庄市滕州一中高三（上）10月月考数学试卷试题数：23.满分：1501.（单选题.4分）已知集合A={x|x2＜1}.集合B={x|log2x＜0}.则A∩B等于（）A.（0.1）B.（-1.0）C.（-1.1）D.（-∞.1）2.（单选题.4分）已知向量a⃗ =（2.1）. b⃗⃗ =（1.k）. a⃗⊥（2 a⃗ - b⃗⃗）.则k=（）A.-8B.-6C.6D.83.（单选题.4分）已知椭圆x2a2+y2b2=1（a＞b＞0）与双曲线x2a2−y2b2=12（a＞0.b＞0）的焦点相同.则双曲线渐近线方程为（）A.y=± √33xB.y=± √3 xC.y=± √22xD.y=± √2 x4.（单选题.4分）已知正实数a.b.c满足log2a=log3b=log6c.则（）A.a=bcB.b2=acC.c=abD.c2=ab5.（单选题.4分）已知α.β是不重合的平面.m.n是不重合的直线.则m⊥α的一个充分条件是（）A.m⊥n.n⊂αB.m || β.α⊥βC.n⊥α.n⊥β.m⊥βD.α∩β=n.α⊥β.m⊥n6.（单选题.4分）如图Rt△ABC 中.∠ABC= π2 .AC=2AB.∠BAC 平分线交△ABC 的外接圆于点D.设 AB ⃗⃗⃗⃗⃗⃗=a ⃗，AC ⃗⃗⃗⃗⃗⃗=b ⃗⃗ .则向量 AD ⃗⃗⃗⃗⃗⃗ =（）A. a ⃗+b⃗⃗ B. 12a ⃗+b ⃗⃗ C. a ⃗+12b⃗⃗ D. a ⃗+23b⃗⃗ 7.（单选题.4分）设函数f （x ）= 1e x −1+a.若f （x ）为奇函数.则不等式f （x ）＞1的解集为（） A.（0.1） B.（-∞.ln3） C.（0.ln3） D.（0.2）8.（单选题.4分）已知函数f （x ）=Acos （ωx+φ）（A ＞0.ω＞0. |φ|＜π2) 的图象如图所示.令g （x ）=f （x ）+f'（x ）.则下列关于函数的说法中正确的是（）A.若函数h （x ）=g （x ）+2的两个不同零点分别为x 1.x 2.则|x 1-x 2|的最小值为 π2 B.函数g （x ）的最大值为2C.函数g （x ）的图象上存在点P.使得在P 点处的切线与直线y=-3x+1平行D.函数g （x ）图象的对称轴方程为 x =kπ+5π12(k ∈Z )9.（单选题.4分）已知双曲线C ： x 2a2 −y 2b 2=1（a ＞0.b ＞0）的左、右焦点分别为F 1、F 2.实轴长为4.渐近线方程为y= ±12x .|MF 1|-|MF 2|=4.点N 在圆x 2+y 2-4y=0上.则|MN|+|MF 1|的最小值为（）A.2 +√7B.5C.6D.710.（单选题.4分）已知函数 f (x )={2x −xlnx ，x ＞0−x 2−32x ，x ≤0 .若方程f （x ）=kx+1有四个不相等的实根.则实数k 的取值范围是（） A. (13，1) B. (13，2) C. (12，45) D. (12，1)11.（多选题.4分）关于函数f （x ）=cos （2x- π3 ）+cos （2x+ π6 ）.下列其中正确命题命题是（）A.y=f （x ）的最大值为 √2B.y=f （x ）是以π为最小正周期的周期函数C.y=f （x ）在区间（ π24 . 13π24 ）上单调递减D.将函数y= √2 cos2x 的图象向左平移 π24个单位后.将与已知函数的图象重合12.（多选题.4分）设等比数列{a n }的公比为q.其前n 项的和为s n .前n 项的积为T n .并满足条件a 1＞1.a 2019a 2020＞1. a 2019−1a 2020−1 ＜0.下列结论错误的是（）A.S 2019＞S 2020B.a 2019．a 2021-1＞0C.T 2020是数列{T n }中的最大值D.数列{T n }无最小值13.（多选题.4分）如图.在正方体ABCD-A 1B 1C 1D 1中.点F 是线段BC 1上的动点.则下列说法正确的是（）A.当点F 移动至BC 1中点时.直线A 1F 与平面BDC 1所成角最大且为60°B.无论点F 在BC 1上怎么移动.都有A 1F⊥B 1DC.当点F 移动至BC 1中点时.才有A 1F 与B 1D 相交于一点.记为点E.且 A 1EEF =2D.无论点F 在BC 1上怎么移动.异面直线A 1F 与CD 所成角都不可能是30° 14.（填空题.4分）抛物线y 2=4x 上的点到直线x-y+4=0的最小距离为___ ．15.（填空题.4分）过点M （ 12 .1）的直线与圆C ：（x-1）2+y 2=4交于A 、B 两点.C 为圆心.当∠ACB 最小时.直线的方程为___ ．16.（填空题.4分）已知a ＞-1.b ＞0.a+2b=1.则 1a+1 + 2b 的最小值为___ ．17.（填空题.4分）已知函数f （x ）= {x 2+4a ，x ＞01+log a |x −1|，x ≤0 （a ＞0且a≠1）在R 上单调递增.且关于x 的方程|f （x ）|=x+3恰有两个不相等的实数解.则a 的取值范围是___ ． 18.（问答题.10分）已知函数 f (x )=√3cos (2x −π3)−2sinxcosx ．（Ⅰ）f （x ）的最小正周期；（Ⅱ）当 x ∈[−π4，π4] 时.求f （x ）的最值．19.（问答题.14分）已知{a n }为等差数列.前n 项和为S n （n∈N *）.{b n }是首项为2的等比数列.且公比大于0.b 2+b 3=12.b 3=a 4-2a 1.S 11=11b 4．（Ⅰ）求{a n }和{b n }的通项公式；（Ⅱ）求数列{a 2n b n }的前n 项和（n∈N *）．20.（问答题.14分）在△ABC 中.设a.b.c 分别是角A.B.C 的对边.已知向量 m ⃗⃗⃗ =（a.sinC-sinB ）. n ⃗⃗ =（b+c.sinA+sinB ）.且 m ⃗⃗⃗ || n ⃗⃗ （1）求角C 的大小（2）若c=3.求△ABC 的周长的取值范围．21.（问答题.14分）如图.在正三棱柱ABC-A1B1C1中.AB=AA1=2.E.F分别为AB.B1C1的中点．（1）求证：B1E || 平面ACF；（2）求平面CEB1与平面ACF所成二面角（锐角）的余弦值．+y2=1.O为坐22.（问答题.15分）已知平行四边形OMAN的三个顶点M.A.N都在椭圆C：x22标原点．）时.求直线MN的方程；（1）当点A的坐标为（1. √22（2）证明：平行四边形OMAN的面积为定值．23.（问答题.15分）已知函数f（x）=alnx+x2+（a+2）x．（1）讨论函数f（x）的单调性；）＞0．（2）设a＜0.若不相等的两个正数x1.x2满足f（x1）=f（x2）.证明：f′（x1+x222019-2020学年山东省枣庄市滕州一中高三（上）10月月考数学试卷参考答案与试题解析试题数：23.满分：1501.（单选题.4分）已知集合A={x|x2＜1}.集合B={x|log2x＜0}.则A∩B等于（）A.（0.1）B.（-1.0）C.（-1.1）D.（-∞.1）【正确答案】：A【解析】：先化简集合.即解一元二次不等式x2＜1.和对数不等式log2x＜0.再求交集．【解答】：解：根据题意：集合A={x|-1＜x＜1}.集合B={x|0＜x＜1}∴A∩B=（0.1）故选：A．【点评】：本题通过集合运算来考查不等式的解法．2.（单选题.4分）已知向量a⃗ =（2.1）. b⃗⃗ =（1.k）. a⃗⊥（2 a⃗ - b⃗⃗）.则k=（）A.-8B.-6C.6D.8【正确答案】：D【解析】：可求出2a⃗−b⃗⃗=(3，2−k) .根据a⃗⊥(2a⃗−b⃗⃗)即可得出a⃗•(2a⃗−b⃗⃗)=0 .进行数量积的坐标运算即可求出k的值．【解答】：解：2a⃗−b⃗⃗=(3，2−k)；∵ a⃗⊥(2a⃗−b⃗⃗)；∴ a⃗•(2a⃗−b⃗⃗)=6+2−k=0；∴k=8．故选：D．【点评】：考查向量垂直的充要条件.向量坐标的减法、数乘和数量积的运算．3.（单选题.4分）已知椭圆x2a2+y2b2=1（a＞b＞0）与双曲线x2a2−y2b2=12（a＞0.b＞0）的焦点相同.则双曲线渐近线方程为（）A.y=± √33xB.y=± √3 xC.y=± √22xD.y=± √2 x【正确答案】：A【解析】：设双曲线的焦距为2c.由题意可得2a2-2b2=a2+b2.即有a.b的关系.结合双曲线的基本量关系和离心率公式.计算可得所求值．【解答】：解：依题意椭圆x 2a2+y2b2=1（a＞b＞0）与双曲线x2a2−y2b2=12（a＞0.b＞0）的焦点相同.可得：a2-b2= 12 a2+ 12b2.即a2=3b2.∴ ba =√33.可得√2a√2=√33∴双曲线的渐近线方程为：y=± √33x故选：A．【点评】：本题考查椭圆和双曲线的方程和性质.考查焦点坐标和渐近线方程的求法.考查方程思想和运算能力.属于基础题．4.（单选题.4分）已知正实数a.b.c满足log2a=log3b=log6c.则（）A.a=bcB.b2=acC.c=abD.c2=ab【正确答案】：C【解析】：设log2a=log3b=log6c=k.则a=2k.b=3k.c=6k.由此能推导出c=ab．【解答】：解：∵正实数a.b.c 满足log 2a=log 3b=log 6c. ∴设log 2a=log 3b=log 6c=k. 则a=2k .b=3k .c=6k . ∴c=ab ．故选：C ．【点评】：本题考查命题真假的判断.考查对数性质、运算法则等基础知识.考查运算求解能力.是基础题．5.（单选题.4分）已知α.β是不重合的平面.m.n 是不重合的直线.则m⊥α的一个充分条件是（） A.m⊥n .n⊂α B.m || β.α⊥β C.n⊥α.n⊥β.m⊥β D.α∩β=n .α⊥β.m⊥n 【正确答案】：C【解析】：根据空间直线和平面垂直的判定定理以及性质结合充分条件和必要条件的定义进行求解即可．【解答】：解：当n⊥β.m⊥β时.m || n. 当n⊥α时.m⊥α.即充分性成立. 即m⊥α的一个充分条件是C. 故选：C ．【点评】：本题主要考查充分条件和必要条件的判断.结合空间直线和平面垂直的位置关系是解决本题的关键．6.（单选题.4分）如图Rt△ABC 中.∠ABC= π2 .AC=2AB.∠BAC 平分线交△ABC 的外接圆于点D.设 AB ⃗⃗⃗⃗⃗⃗=a ⃗，AC ⃗⃗⃗⃗⃗⃗=b ⃗⃗ .则向量 AD ⃗⃗⃗⃗⃗⃗ =（）A. a ⃗+b⃗⃗ B. 12a ⃗+b⃗⃗C. a ⃗+12b ⃗⃗ D. a ⃗+23b ⃗⃗ 【正确答案】：C【解析】：根据Rt△ABC 中.的边角关系.结合圆的性质.得到四边形ABDO 为菱形.所以 AD ⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗⃗+AO ⃗⃗⃗⃗⃗⃗ = a ⃗+12b⃗⃗ ．【解答】：解：设圆的半径为r.在Rt△ABC 中.∠ABC= π2 .AC=2AB. 所以∠BAC= π3 .∠ACB= π6 .∠BAC 平分线交△ABC 的外接圆于点D. 所以∠ACB=∠BAD=∠CAD= π6 . 则根据圆的性质BD=CD=AB.又因为在Rt△ABC 中.AB= 12AC =r=OD.所以四边形ABDO 为菱形.所以 AD ⃗⃗⃗⃗⃗⃗ = AB ⃗⃗⃗⃗⃗⃗+AO ⃗⃗⃗⃗⃗⃗ = a ⃗+12b⃗⃗ ．故选：C ．【点评】：本题考查了向量的平行四边形法则.共线向量基本定理.圆的性质等知识.考查分析解决问题的能力和计算能力．属于中档题．7.（单选题.4分）设函数f （x ）= 1e x −1 +a.若f （x ）为奇函数.则不等式f （x ）＞1的解集为（） A.（0.1） B.（-∞.ln3） C.（0.ln3） D.（0.2）【正确答案】：C【解析】：根据题意.由奇函数的性质可得f （-x ）+f （x ）=0.即（1e (−x )−1+a ）+（1e x −1+a ）=-1+2a=0.解可得a= 12 .即可得f （x ）= 1e x −1 + 12 .据此分析函数f （x ）的单调性以及值域.结合解析式可得f （ln3）=1.据此分析可得答案．【解答】：解：根据题意.函数f （x ）= 1e x −1 +a.其定义域为{x|x≠0} 若f （x ）为奇函数.则f （-x ）+f （x ）=0.即（ 1e (−x )−1 +a ）+（ 1e x −1 +a ）=-1+2a=0.解可得a= 12 .则f （x ）= 1e x −1 + 12又由y=e x -1在（0.+∞）为增函数其y ＞0.则f （x ）= 1e x −1 + 12 在（0.1）上为减函数且f （x ）＞0.则f （x ）在（-∞.0）上减函数且f （x ）＜0. 又由f （ln3）= 1e ln3−1 + 12 =1. 则f （x ）＞1⇒f （x ）＞f （ln3）.则有0＜x ＜ln3.即不等式的解集为（0.ln3）；故选：C ．【点评】：本题考查函数的奇偶性与单调性的判定以及应用.关键是利用奇函数的性质求出a 的值.属于基础题．8.（单选题.4分）已知函数f （x ）=Acos （ωx+φ）（A ＞0.ω＞0. |φ|＜π2) 的图象如图所示.令g （x ）=f （x ）+f'（x ）.则下列关于函数的说法中正确的是（）A.若函数h （x ）=g （x ）+2的两个不同零点分别为x 1.x 2.则|x 1-x 2|的最小值为 π2 B.函数g （x ）的最大值为2C.函数g （x ）的图象上存在点P.使得在P 点处的切线与直线y=-3x+1平行D.函数g （x ）图象的对称轴方程为 x =kπ+5π12(k ∈Z ) 【正确答案】：A【解析】：由图象结合最值可求A.结合周期可求ω.然后代入f （ π6 ）=2.及|φ|＜ 12π .可求φ.从而可求f （x ）.进而可求g （x ）.结合正弦函数.余弦函数的性质分别进行判断【解答】：解：由图象可知.A=2. T4=2π3−π6 = 12π .∴T=2π.ω=1.∴f （x ）=2cos （x+φ）.∵f （ π6）=2cos （ π6+φ）=2.且|φ|＜ 12π . ∴φ=- π6 .f （x ）=2cos （x- π6 ）.∵g（x）=f（x）+f'（x）=2cos（x- π6）-2sin（x- π6）=2 √2 cos（x+ π12）.A：由h（x）=g（x）+2=0可得cos（x+ π12）=- √22.则|x1-x2|的最小值为5π4−3π4= π2.故A正确；B：结合余弦函数的性质可知.f（x）的最大值2 √2 .故B错误；C：根据导数的几何意义可知.过点P的切线斜率k=f′（x）=-2 √2 sin（x+ π12）∈[−2√2，2√2] .不存在斜率为-3的切线方程.故C错误；D：令x+ π12=kπ可得.x=k π−π12.k∈z.故D错误．故选：A．【点评】：本题主要考查了由y=Asin（ωx+φ）的部分图象求函数解析式及正弦与余弦函数性质的综合应用.属于中档试题．9.（单选题.4分）已知双曲线C：x2a2−y2b2=1（a＞0.b＞0）的左、右焦点分别为F1、F2.实轴长为4.渐近线方程为y= ±12x .|MF1|-|MF2|=4.点N在圆x2+y2-4y=0上.则|MN|+|MF1|的最小值为（）A.2 +√7B.5C.6D.7【正确答案】：B【解析】：求得双曲线的a.b.可得双曲线方程.求得焦点坐标.运用双曲线的定义和三点共线取得最小值.连接CF2.交双曲线于M.圆于N.计算可得所求最小值．【解答】：解：由题意可得2a=4.即a=2.渐近线方程为y=± 12 x.即有ba= 12.即b=1.可得双曲线方程为x 24-y2=1.焦点为F1（- √5 .0）.F2.（√5 .0）.由双曲线的定义可得|MF1|=2a+|MF2|=4+|MF2|.由圆x2+y2-4y=0可得圆心C（0.2）.半径r=2.|MN|+|MF1|=4+|MN|+|MF2|.连接CF2.交双曲线于M.圆于N.可得|MN|+|MF2|取得最小值.且为|CF2|= √4+5 =3.则则|MN|+|MF 1|的最小值为4+3-2=5．故选：B ．【点评】：本题考查双曲线的定义、方程和性质.考查圆的方程的运用.以及三点共线取得最值.考查数形结合思想和运算能力.属于中档题．10.（单选题.4分）已知函数 f (x )={2x −xlnx ，x ＞0−x 2−32x ，x ≤0 .若方程f （x ）=kx+1有四个不相等的实根.则实数k 的取值范围是（） A. (13，1) B. (13，2) C. (12，45) D. (12，1) 【正确答案】：D【解析】：由方程的根的个数与函数图象交点个数的关系得：方程f （x ）=kx+1有四个不相等的实根.等价于函数f （x ）的图象与直线y=kx+1有四个交点.结合导数求函数图象的切线方程可得： ① 当直线y=kx+1与函数f （x ）=-x 2- 32x 相切时.k= 12. ② 当直线y=kx+1与函数f （x ）=2x-xlnx 相切时.利用导数的几何意义可得：k=1.再结合像图知函数f （x ）的图象与直线y=kx+1有四个交点时.实数k 的取值范围是 12＜k ＜1 .得解．【解答】：解：方程f （x ）=kx+1有四个不相等的实根. 等价于函数f （x ）的图象与直线y=kx+1有四个交点. 易得： ① 当直线y=kx+1与函数f （x ）=-x 2- 32x 相切时.k= 12 .② 当直线y=kx+1与函数f （x ）=2x-xlnx 相切时.利用导数的几何意义可得：k=1.即由图知函数f （x ）的图象与直线y=kx+1有四个交点时. 实数k 的取值范围是 12＜k ＜1 . 故选：D ．【点评】：本题考查了方程的根的个数与函数图象交点个数的关系及利用导数求函数图象的切线方程.属中档题．11.（多选题.4分）关于函数f （x ）=cos （2x- π3 ）+cos （2x+ π6 ）.下列其中正确命题命题是（）A.y=f （x ）的最大值为 √2B.y=f （x ）是以π为最小正周期的周期函数C.y=f （x ）在区间（ π24 . 13π24 ）上单调递减D.将函数y= √2 cos2x 的图象向左平移 π24个单位后.将与已知函数的图象重合【正确答案】：AB【解析】：利用两角和差的正余弦公式可把f （x ）化为 √2 sin （2x+ 5π12 ）.进而利用正弦函数的性质即可判断出答案．【解答】：解：f （x ）=cos （2x- π3 ）+cos （2x+ π6 ）= 1+√32 cos2x+ √3−12 sin2x= √2 （ √6+√24cos2x+√6−√24 sin2x ）= √2 sin （2x+ 5π12）. 对于A.函数f （x ）的最大值为 √2 .故A 正确；对于B.函数f （x ）的最小正周期T= 2π2 =π.故B 正确；对于C.令- π2 +2kπ≤2x+ 5π12 ≤ π2 +2kπ（k∈Z ）.解得- 1124 π+kπ≤x≤ π24 +kπ（k∈Z ）.故C 错误；对于D.将函数y= √2 cos2x 的图象向左平移 π24 个单位后.得到y= √2 cos2（x+ π24 ）= √2 cos （2x+ π12 ）= √2 sin （ π2 -2x- π12 ）=- √2 sin （2x- 512π ）≠f （x ）.故D 错误．故选：AB．【点评】：熟练掌握两角和差的正余弦公式、正弦函数的性质是解题的关键．12.（多选题.4分）设等比数列{a n}的公比为q.其前n项的和为s n.前n项的积为T n.并满足条件＜0.下列结论错误的是（）a1＞1.a2019a2020＞1. a2019−1a2020−1A.S2019＞S2020B.a2019．a2021-1＞0C.T2020是数列{T n}中的最大值D.数列{T n}无最小值【正确答案】：ABC【解析】：推导出a2019＞1.0＜a2020＜1.0＜q＜1.由此能求出结果．【解答】：解：∵等比数列{a n}的公比为q.其前n项的和为s n.前n项的积为T n.＜0.并满足条件a1＞1.a2019a2020＞1. a2019−1a2020−1∴a2019＞1.0＜a2020＜1.∴0＜q＜1.在A中.∵a2020＞0.∴S2019＜S2020.故A错误；在B中.a2019＞1.a2021-1＜0.∴a2019．a2021-1= a20202 -1＜0.故B错误；∴T2019是数列{T n}中的最大项.故C错误；在D中.数列{T n}无最小值.故D正确．故选：ABC．【点评】：本题考查命题真假的判断.考查等比数列的性质等基础知识.考查运算求解能力.是基础题．13.（多选题.4分）如图.在正方体ABCD-A1B1C1D1中.点F是线段BC1上的动点.则下列说法正确的是（）A.当点F移动至BC1中点时.直线A1F与平面BDC1所成角最大且为60°B.无论点F在BC1上怎么移动.都有A1F⊥B1DC.当点F移动至BC1中点时.才有A1F与B1D相交于一点.记为点E.且A1EEF=2D.无论点F在BC1上怎么移动.异面直线A1F与CD所成角都不可能是30°【正确答案】：BCD【解析】：根据题意.分别对选项中的命题进行分析、判断正误即可．【解答】：解：对于A.当点F移动到BC1的中点时.直线A1F与平面BDC1所成角由小到大再到小.如图1所示；且F为B1C的中点时最大角的余弦值为OFA1F =√66√62= 13＜12.最大角大于60°.所以A错误；对于B.在正方形中.DB1⊥面A1BC1.又A1F⊂面A1BC1.所以A1F⊥B1D.因此B正确；对于C.F为BC1的中点时.也是B1C的中点.它们共面于平面A1B1CD.且必相交．为E.连A1D和B1F.如图2.根据△A1DE∽△FB1E.可得A1FEF = DA1B1F=2.所以C正确；对于D.当点F从B运动到C1时.异面直线A1F与CD所成角由大到小再到大.且F为B1C的中点时最小角的正切值为√221= √22＞√33.最小角大于30°.所以D正确．故选：BCD．【点评】：本题考查异面直线所成角的余弦值的求法.考查空间中线线、线面、面面间的位置关系等基础知识.考查空间想象能力、运算求解能力.考查化归与转化思想、数形结合思想.是中档题．14.（填空题.4分）抛物线y2=4x上的点到直线x-y+4=0的最小距离为___ ．【正确答案】：[1] 3√22【解析】：先设出与直线平行且与抛物线相切的直线.与抛物线联立消去x.根据判别式等于0求得k.则切线方程可得.进而与抛物线方程联立求得切点的坐标.进而根据点到直线的距离求得答案．【解答】：解：设与直线l ：x-y+4=0平行.且与抛物线y 2=4x 相切的直线为x-y+k=0．由 {x −y +k =0y 2=4x .消x 得y 2-4y+4k=0．∴△=42-16k=0.解得k=1.即切线为x-y+1=0．由 {x −y +1=0y 2=4x .解得点P （1.2）．∴最短距离d= √12+12= 3√22．故答案为： 3√22．【点评】：本题主要考查了抛物线的应用.考查了学生数形结合和转化与化归的思想． 15.（填空题.4分）过点M （ 12 .1）的直线与圆C ：（x-1）2+y 2=4交于A 、B 两点.C 为圆心.当∠ACB 最小时.直线的方程为___ ．【正确答案】：[1]2x-4y+3=0【解析】：根据题意.分析可得点M 在圆C 的内部.由直线和圆相交的性质可得当∠ACB 最小时.直线AB 与直线MC 垂直.根据两条直线垂直的性质.求得直线l 的斜率.再用点斜式求得直线l 的方程．【解答】：解：根据题意.圆C ：（x-1）2+y 2=4.其圆心C （1.0）.半径r=2. 又由点M （ 12 .1）.则有（ 12 -1）2+12＜4.即点M 在圆C 的内部.由直线AB 和圆相交的性质可得.当∠ACB 最小时.圆心C 到直线AB 的距离最大.此时直线AB 与直线MC 垂直；此时k MC = 1−012−1=-2.直线AB 的斜率k= 12 .此时直线AB 的方程为：y-1= 12 （x- 12）.即2x-4y+3=0. 故答案为：2x-4y+3=0．【点评】：本题考点是直线与圆的位置关系.注意分析∠ACB 最小的条件.属于基础题． 16.（填空题.4分）已知a ＞-1.b ＞0.a+2b=1.则 1a+1 + 2b 的最小值为___ ．【正确答案】：[1] 92【解析】：根据条件可得a+1+2b2=1 .然后由 1a+1 + 2b = (1a+1+2b )a+1+2b2利用基本不等式求出 1a+1 + 2b的最小值．【解答】：解：∵a ＞-1.b ＞0.a+2b=1.∴ a+1+2b2=1 .∴ 1a+1 + 2b = (1a+1+2b )a+1+2b2= 12[5+2ba+1+2(a+1)b ] ≥ 12[5+2√2ba+1•2(a+1)b ] = 92. 当且仅当a+1=b.即 a =−13 . b =23 时取等号. ∴1a+1 + 2b 的最小值为 92．故答案为： 92 ．【点评】：本题考查了利用基本不等式求最值.考查了转化思想和计算能力.属基础题． 17.（填空题.4分）已知函数f （x ）= {x 2+4a ，x ＞01+log a |x −1|，x ≤0 （a ＞0且a≠1）在R 上单调递增.且关于x 的方程|f （x ）|=x+3恰有两个不相等的实数解.则a 的取值范围是___ ．【正确答案】：[1] [14，34]∪{1316}【解析】：由题意可知f （x ）在两段上均为增函数.且f （x ）在（0.+∞）上的最小值大于或等于f （0）.作出|f （x ）|和y=x+3的图象.根据交点个数判断4a 与3的大小关系.以及直线和抛物线相切的条件.列出不等式组解出．【解答】：解：∵f （x ）是R 上的单调递增函数. ∴y=1+log a |x-1|在（-∞.0]上单调递增. 可得0＜a ＜1.且0+4a≥1+0.即 14 ≤a ＜1.作出y=|f （x ）|和y=x+3的函数示意图如图所示：由图象可知|f （x ）|=x+3在（0.+∞）上有且只有一解. 可得4a≤3.或x 2+4a=x+3.即有△=1-4（4a-3）=0. 即有 14 ≤a≤ 34 或a= 1316 ；由1+log a |x-1|=0.解得x=1- 1a ≤-3.即x≤0时.有且只有一解．则a 的范围是[ 14 . 34 ]∪{ 1316 }．故答案为：[ 14 . 34]∪{ 1316}．【点评】：本题考查分段函数的单调性.函数零点的个数判断.结合函数图象判断端点值的大小是关键.属于中档题．18.（问答题.10分）已知函数f(x)=√3cos(2x−π3)−2sinxcosx．（Ⅰ）f（x）的最小正周期；（Ⅱ）当x∈[−π4，π4]时.求f（x）的最值．【正确答案】：【解析】：（Ⅰ）首先利用和三角函数的恒等变换.把函数的关系式变形成正弦型函数.进一步求出函数的周期．（Ⅱ）利用函数的关系式.进一步利用函数的定义域求出函数的值域．【解答】：解：（Ⅰ）f(x)=√3cos(2x−π3)−2sinxcosx .= 12sin2x+√32cos2x .= sin(2x+π3) .所以f（x）的最小正周期T=2π2=π．（Ⅱ）因为−π4≤x≤π4.所以−π6≤2x+π3≤5π6．所以：1≥ sin(2x+π3)≥sin(−π6)=−12．所以当x∈[−π4，π4]时.1≥ f(x)≥−12．．则：函数f（x）的最大值为1.函数f（x）的最小值为- 12【点评】：本题考查的知识要点：三角函数关系式的恒等变换.正弦型函数的性质的应用．19.（问答题.14分）已知{a n}为等差数列.前n项和为S n（n∈N*）.{b n}是首项为2的等比数列.且公比大于0.b2+b3=12.b3=a4-2a1.S11=11b4．（Ⅰ）求{a n}和{b n}的通项公式；（Ⅱ）求数列{a2n b n}的前n项和（n∈N*）．【正确答案】：【解析】：（Ⅰ）设等差数列{a n}的公差为d.等比数列{b n}的公比为q．通过b2+b3=12.求出q.得到b n=2n．然后求出公差d.推出a n=3n-2．（Ⅱ）设数列{a2n b n}的前n项和为T n.利用错位相减法.转化求解数列{a2n b n}的前n项和即可．【解答】：（Ⅰ）解：设等差数列{a n}的公差为d.等比数列{b n}的公比为q．由已知b2+b3=12.得b1(q+q2)=12 .而b1=2.所以q2+q-6=0．又因为q＞0.解得q=2．所以. b n=2n．由b3=a4-2a1.可得3d-a1=8．由S11=11b4.可得a1+5d=16.联立① ② .解得a1=1.d=3.由此可得a n=3n-2．所以.{a n}的通项公式为a n=3n-2.{b n}的通项公式为b n=2n．（Ⅱ）解：设数列{a2n b n}的前n项和为T n.由a2n=6n-2.有T n=4×2+10×22+16×23+⋯+(6n−2)×2n . 2T n=4×22+10×23+16×24+⋯+(6n−8)×2n+(6n−2)×2n+1 .−上述两式相减.得−T n=4×2+6×22+6×23+⋯+6×2n−(6n−2)×2n+1 = 12×(1−2n)1−24−(6n−2)×2n+1=−(3n−4)2n+2−16．得T n=(3n−4)2n+2+16．所以.数列{a2n b n}的前n项和为（3n-4）2n+2+16．【点评】：本题考查等差数列以及等比数列通项公式的求法.数列求和.考查转化思想以及计算能力．20.（问答题.14分）在△ABC中.设a.b.c分别是角A.B.C的对边.已知向量m⃗⃗⃗ =（a.sinC-sinB）. n⃗⃗ =（b+c.sinA+sinB）.且m⃗⃗⃗ || n⃗⃗（1）求角C的大小（2）若c=3.求△ABC的周长的取值范围．【正确答案】：【解析】：（1）由向量平行的性质.正弦定理可得a2+b2-c2=-ab.由余弦定理得：cosC=- 12.即可得解C的值．（2）由正弦定理.三角函数恒等变换的应用可求周长为：a+b+c=2 √3 sin（A+ π3）+3.由0＜A＜π3.利用正弦函数的性质即可求解．【解答】：解：（1）由向量m⃗⃗⃗ =（a.sinC-sinB）. n⃗⃗ =（b+c.sinA+sinB）.且m⃗⃗⃗ || n⃗⃗ .得：a（sinA+sinB）=（b+c）（sinC-sinB）由正弦定理.得：a（a+b）=（b+c）（c-b）化为：a2+b2-c2=-ab.由余弦定理.得：cosC=- 12.所以.C= 2π3.（2）因为C= 2π3.所以.B= π3 -A.由B＞0.得：0＜A＜π3.由正弦定理.得：asinA =bsinB=csinC=2 √3 .△ABC 的周长为：a+b+c=2 √3（sinA+sinB）+3=2 √3 [sinA+sin（π3-A）]+3.=2 √3 sin（A+ π3）+3.由0＜A＜π3 .得：π3＜A+ π3＜2π3. √32＜sin（A+ π3）≤1.所以.周长C=2 √3 sin（A+ π3）+3∈（6.2 √3 +3]．【点评】：本题主要考查了向量平行的性质.正弦定理.余弦定理.三角函数恒等变换的应用在解三角形中的综合应用.考查了计算能力和转化思想.属于中档题．21.（问答题.14分）如图.在正三棱柱ABC-A1B1C1中.AB=AA1=2.E.F分别为AB.B1C1的中点．（1）求证：B1E || 平面ACF；（2）求平面CEB1与平面ACF所成二面角（锐角）的余弦值．【正确答案】：【解析】：（1）取AC的中点M.连结EM.FM.推导出EM || BC.且EM= 12BC.四边形EMFB1为平行四边形.B1E || FM.由此能证明B1E || 平面ACF．（2）取BC中点O.连结AO.OF.以O为原点.分别以OB.AO.OF为x.y.z轴.建立空间直角坐标系.利用向量法能求出平面CEB1与平面ACF所成二面角（锐角）的余弦值．【解答】：证明：（1）取AC的中点M.连结EM.FM.在△ABC中.∵E为AB的中点.∴EM || BC.且EM= 12BC.又F为B1C1的中点.B1C1 || BC.∴B1F || BC.且B1F= 12BC .∴EM || B1F.且EM=B1F.∴四边形EMFB1为平行四边形.∴B1E || FM.又MF⊂平面ACF.BE⊄平面ACF.∴B1E || 平面ACF．解：（2）取BC中点O.连结AO.OF.则AO⊥BC.OF⊥平面ABC.以O为原点.分别以OB.AO.OF为x.y.z轴.建立空间直角坐标系.则A（0.- √3 .0）.B（1.0.0）.C（-1.0.0）.E（12，−√32.0）.F（0.0.2）.B1（1.0.2）.CE ⃗⃗⃗⃗⃗⃗ =（ 32，−√32 .0）. CF ⃗⃗⃗⃗⃗⃗ =（1.0.2）. CA ⃗⃗⃗⃗⃗⃗ =（1.- √3 .0）. CB 1⃗⃗⃗⃗⃗⃗⃗⃗ =（2.0.2）. 设平面CEB 1的一个法向量 m ⃗⃗⃗ =（x.y.z ）.则 {m ⃗⃗⃗•CE ⃗⃗⃗⃗⃗⃗=√3x −y =0m ⃗⃗⃗•CB 1⃗⃗⃗⃗⃗⃗⃗⃗=x +z =0.令x=1．则 m ⃗⃗⃗ =（1. √3 .-1）. 同理得平面ACF 的一个法向量为 n ⃗⃗ =（1. √33 .- 12 ）.则cos ＜ m ⃗⃗⃗，n ⃗⃗ ＞= m ⃗⃗⃗⃗•n ⃗⃗|m ⃗⃗⃗⃗|•|n ⃗⃗| = √28519. ∴平面CEB 1与平面ACF 所成二面角（锐角）的余弦值为√28519 ．【点评】：本题考查线面垂直性质定理、线面垂直、线面平行判定与性质定理以及利用空间向量求线面角与二面角.考查基本分析求解能力.属中档题．22.（问答题.15分）已知平行四边形OMAN 的三个顶点M.A.N 都在椭圆C ： x 22 +y 2=1.O 为坐标原点．（1）当点A 的坐标为（1. √22 ）时.求直线MN 的方程；（2）证明：平行四边形OMAN 的面积为定值．【正确答案】：【解析】：（1）根据点差法即可求出直线MN 的方程.（2）将直线MN 的方程代入椭圆方程.由向量的坐标运算.即可求得A 点坐标.即可求出整理得4m 2=2k 2+1.利用韦达定理.弦长公式即可及点到直线的距离公式求得平行四边形OMAN 的面积【解答】：解：（1）∵点A 的坐标为（1. √22 ）.∴OA 的中点坐标为（ 12 . √24 ）.∵四边形OMAN 为平行四边形.∴MN 的中点坐标为（ 12 . √24 ）.设M （x 1.y 1）.N （x 2.y 2）.∴x 1+x 2=1.y 1+y 2= √22∴ {x 122+y 12=1x 222+y 22=1 .两式相减可得 12 （x 1+x 2）（x 1-x 2）+（y 1+y 2）（y 1-y 2）=0.即 12 （x 1-x 2）+ √22 （y 1-y 2）=0.∴k MN = y 1−y 2x 1−x 2 =- √22 . ∴直线MN 的方程为y- √24 =- √22 （x- 12 ）.即x+ √2 y-1=0.证明（2）：设直线MN 的方程为：y=kx+m 与椭圆C 相交于M 、N 两点.设M （x 1.y 1）.N （x 2.y 2）.将其代入 x 22 +y 2=1得（2k 2+1）x 2+4kmx+2（m 2-1）=0.△=16k 2m 2-8（2k 2+1）（m 2-1）＞0 即2k 2+1＞m 2.又x 1+x 2=- 4km 2k 2+1 .x 1•x 2= 2(m 2−1)2k 2+1 .∴y 1+y 2=k （x 1+x 2）+2m=- 4k 2m 2k 2+1 +2m= 2m 2k 2+1. ∵四边形OMPAN 为平行四边形．∴ OA ⃗⃗⃗⃗⃗⃗ = OM ⃗⃗⃗⃗⃗⃗⃗ + ON⃗⃗⃗⃗⃗⃗⃗ =（x 1+x 2.y 1+y 2）=（- 4km 2k 2+1 . 2m 2k 2+1） ∴点A 坐标为（- 4km 2k 2+1 . 2m 2k 2+1 ）∵点A 在椭圆C 上.∴ 8k2m2 (2k2+1)2 + 4m2(2k2+1)=1.整理得4m2=2k2+1∴|MN|= √1+k2• √(x1+x2)2−4x1x2 = √1+k2• 2√2•√2k2+1−m22k2+1= √1+k2• 2√2•√3m24m2 = √1+k2• √62|m|∵点O到直线MN的距离为d=√1+k2.∴S OMAN=2× 12|MN|•d= √1+k2• √62|m|•√1+k2= √62．【点评】：本题考查椭圆的标准方程.考查直线与椭圆的位置关系.考查点到直线的距离公式.韦达定理.弦长公式.向量的坐标运算.考查计算能力.属于难题．23.（问答题.15分）已知函数f（x）=alnx+x2+（a+2）x．（1）讨论函数f（x）的单调性；（2）设a＜0.若不相等的两个正数x1.x2满足f（x1）=f（x2）.证明：f′（x1+x22）＞0．【正确答案】：【解析】：（1）先求导.再分类讨论.根据导数和函数的单调性的关系即可判断.（2）根据不相等的两个正数x1.x2满足f（x1）=f（x2）.可得x2+x1+a+2= a(lnx1−lnx2)x2−x1.再得到f′（x1+x22）= ax2−x1（2(x2x1−1)x2x1+1-ln x2x1）.令x2x1=t＞1.构造函数g（t）= 2t−2t+1-lnt.利用导数求出函数的最值即可证明．【解答】：解：（1）f′（x）= ax +2x+（a+2）= 2x2+(a+2)x+ax= (2x+a)(x+1)x.x＞0.当a≥0时.f′（x）＞0.∴f（x）在（0.+∞）单调递增.当a＜0时.当0＜x＜- a2时.f′（x）＜0.当x＞- a2时.f′（x）＞0.∴f（x）在（0.- a2）上单调递减.在（- a2.+∞）上单调递增.证明（2）∵f（x1）=f（x2）.∴alnx1+x12+（a+2）x1=alnx2+x22+（a+2）x2.∴a（lnx1+lnx2）=x22-x12+（a+2）（x2-x1）=（x2-x1）（x2+x1+a+2）∴x 2+x 1+a+2=a (lnx 1−lnx 2)x 2−x 1 . ∵f′（x ）= a x +2x+（a+2）.∴f′（ x 1+x 22 ）= 2a x 1+x 2 +x 2+x 1+a+2= 2a x 1+x 2 + a (lnx 1−lnx 2)x 2−x 1=a （ 2x 1+x 2 - ln x 2x 1x 2−x 1 ）= a x 2−x 1 （ 2(x 2−x 1)x 2+x 1 -ln x 2x 1 ）= a x 2−x 1 （ 2(x 2x 1−1)x 2x 1+1 -ln x 2x 1 ）. 不妨设x 2＞x 1＞0.则 x2x 1 ＞1. 要证明：f （x 1+x 22 ）＞0.a ＜0. 只要证2(x 2x 1−1)x 2x 1+1 -ln x 2x 1 ＜0. 令 x 2x 1=t ＞1. ∴g （t ）= 2t−2t+1 -lnt=2- 4t+1 -lnt.∴g′（t ）= 4(t+1)2 - 1t = 4t−(t+1)2t (t+1)2 =- (t−1)2t (t+1)2 ＜0. ∴g （t ）在（1.+∞）上单调递减.∴g （t ）＜g （1）= 2−21+1 -ln1=0.∴ 2(x 2x 1−1)x 2x 1+1 -ln x2x 1 ＜0. ∴f′（x 1+x 22）＞0．【点评】：本题考查了导数和函数的单调性的关系.导数和函数的最值的关系.考查了运算求解能力.转化与化归能力.考查了函数与方程的思想.分类讨论的思想.属于难题．。

枣庄市滕州一中2021-2022学年高一化学上学期10月月考试卷(带答案)

2021级高一年级阶段性检测化学试卷2021.10.11全卷100分时间90分钟第Ⅰ卷(选择题共50分)可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Al 27 S 32 Cl 35.5 Fe 56一、选择题(本题包括10小题，每小题2分，共20分。

每题仅选1个选项。

)1. 1811年提出分子学说，系统地解决了在物质组成和原子量测定方面存在的混乱问题的科学家是( ) A.英国科学家波义耳 B.法国科学家拉瓦锡 C.俄国科学家门捷列夫 D.意大利科学家阿伏加德罗2．某化学教师为 “氯气与金属钠反应”设计了如图装置的实验。

实验操作：先给钠预热，到钠熔融成圆球时，撤火，通入氯气，即可见钠着火燃烧，生成大量白烟。

以下叙述中错误的是( )A ．反应生成的大量白烟是氯化钠晶体B ．玻璃管尾部塞一团浸有NaOH 溶液的棉球是用于吸收过量的氯气，以免其污染空气C ．钠着火燃烧产生苍白色火焰D ．发生的反应为2Na ＋Cl 2=====点燃2NaCl3．查阅资料发现，金属钠不仅跟氧气和水反应，还能跟多种物质反应，其中包括与酒精在常温的反应，要研究金属钠跟酒精反应的性质以及它与金属钠跟水反应的异同点，下列研究方法中用不到的是( ) A ．分类法 B ．观察法 C ．实验法 D ．比较法 4．下列关于金属钠的说法不正确的是( )A ．金属钠在空气中燃烧，生成淡黄色过氧化钠固体B ．用小刀切下一小块金属钠备用，剩余的金属钠不应放回原试剂瓶中C ．少量的金属钠保存在煤油中，多量的金属钠一般用石蜡油封存D ．钠和钾的合金可用作原子反应堆的导热剂5．下图是一种试验某气体化学性质的实验装置，图中B 为开关。

如先打开B ，在A 处通入干燥的氯气，C 中红色布条颜色无变化；当关闭B 时，C 处红色布条退色。

则D 瓶中盛有的溶液是( ) A ．浓硫酸 B ．饱和氯化钠溶液 C ．浓氢氧化钠溶液 D ．氢氧化钙悬浊液6．将一小块金属钠放入下列溶液中，既有气体，又有白色沉淀产生的是( ) ①MgSO 4溶液②饱和石灰水③CuSO 4溶液④稀Na 2SO 4溶液⑤饱和食盐水 A ．①②⑤ B ．①④⑤ C ．①②③ D ．②③④7．下列实验现象与新制氯水中的某些成分(括号内物质)没有关系的是( ) A ．将NaHCO 3固体加入新制氯水中，有无色无味气泡冒出(H +) B ．使蓝色石蕊试纸先变红后退色(H +、Cl 2) C ．新制氯水呈浅黄绿色(Cl 2)D ．滴加AgNO 3溶液生成白色沉淀(Cl −) 8．下列叙述正确的是( )A ．常温常压下1molN 2的体积约为22.4 LB ．SO 42−的摩尔质量96 gC ．4.4 g CO 2的物质的量为0.1 molD ．0.5 mol H 2O 的质量是9 g·mol −19．下列溶液中，酸根阴离子浓度大小顺序正确的是()①60 mL 0.7mol·L−1NaCl溶液②50 mL 0.6mol·L−1HNO3溶液③60 mL 0.5mol·L−1CuCl2溶液④50 mL 0.5mol·L−1Al2(SO4)3溶液A．④＞③＞①＞② B．①＞②＞③＝④C．①＞②＝③＞④ D．②＞①＞③＞④10．用N A表示阿伏加德罗常数的值，下列叙述不正确的是()A．常温常压下，2 mol CO2含有的氧原子数为4N AB．7.8 gNa2O2与足量水发生反应，生成O2的分子数为0.1N AC．标准状况下，22.4 L氖气所含原子数为N AD．N A个CH4分子在标准状况下的体积约为22.4 L二、选择题(本题包括10小题，每小题3分，共30分。

山东枣庄市滕州一中2022届高三上学期10月月考语文试题及答案(逐题解析) 人教版高三

山东枣庄市滕州一中2022届高三上学期10月月考语文试题及答案（逐题解析）人教版高三高三年级10月份月考语文试题注意事项：1．本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

答题前，考生务必将自己的姓名、考生号填写在答题卡上。

2．回答第I卷时，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在试卷上无效。

3．回答第II卷时，将答案写在答题卡上，写在试卷上无效。

4．考试结束，将答题卡交回。

第I卷(选择题)(共45分)本卷共35小题。

共45分。

在每个小题给出的四个选项中，只有一项是符合题目要求的。

一、现代文阅读（35分）（一）现代文阅读1（本题共5小题，19分）阅读下面的文字，完成下面小题。

材料一:生态文学在中国发展的时间不长，仍是一个新兴的文学形态。

生态文学作家们努力探索和尝试，让生态文学理念和实践在中国大地扎下根来。

总结当代生态文学创作面貌，主要有以下三方面特质。

报告文学表现突出，多种文学体裁并进。

早期生态文学多采取第一人称叙述视角，文学形式以报告文学和散文居多。

报告文学如徐刚写沙漠化防治的《穿越风沙线》，岳非丘写长江污染防治的《只有一条长江》等，可谓第一人称表达范例。

散文如苇岸写华北大平原上动物、植物及农事活动的《大地上的事情》等，影响深远。

近年来，小说和儿童文学领域也不乏生态文学佳作，带给我们惊喜。

长篇小说周建新写人与海的《老滩》，儿童文学如黑鹤写动物的《银狐》等，都可圈可点。

全面观照生态文明建设各领域进展。

近年来，大气、水、土壤污染防治以及植被保护成效明显，生态文学作家以自觉的使命感和担当精神，关注和思考生态环境问题，热情讴歌和礼赞生态环境保护者。

陈启文《穿越共和盆地》真实记录与反映新中国治沙成就，李云峰《汾河行思录》关注水土保持生态建设，等等。

这些作品涉及生态文明建设多个领域，呼吁人们提高生态环保意识，以更大力度、更多措施开创社会主义生态文明建设新局面。

山东省滕州一中2020-2021学年度第一学期10月月考高一数学试题(含答案)

即 (cx 2)(x 1) 0 ．当 c 0 时， 2(x 1) 0 ，解得 x 1.…………………4 分
当 c 0 时， (cx 2)(x 1) 0 即 (x 2)(x 1) 0 ，解得 2 x 1...........6 分
c
c
当 c 0 时， (cx 2)(x 1) 0 即 (x 2)(x 1) 0 .比较 2 与 1 的大小
解：(I) f 2 4 , f f 2 5 ………………………………………………………2 分
（II） f x 在区间2, 4 上单调递
增. …………………………………………………………3 分
证明： x1 ， x2 2, 4 ，且 x1 x2 ，
f
(x1)
f
(x2 )
x1
4 x1
解: （Ⅰ）因为不等式 ax2 3x 2 0 的解集为{x x 1, 或x b} ，
所以1和
b
是方程
ax2
3x
2
0
的两个实数根．故：
1 1
b b
3 a 2 a
，解得
a b
1 2
．........ 2
分
经验证，符合条件.
（Ⅱ）由（Ⅰ）知不等式 cx2 (ac b)x ab 0 ，即 cx2 (c 2)x 2 0 ，
c
c
当 2 1，即 c 2 时，解得 x 1 ………………………………………7 分 c
当 2 1，即 0 c 2 时，解得 x 1, 或 x 2 ………………………………………9 分
c
c
当 2 1，即 c 2 时，解得 x 2 , 或 x 1 ……………………………………………11 分
f
(x)min .

山东省滕州一中高一10月月考试卷答案

度第一学期10月单元检测2020.10高一数学试题参考答案及评分标准一、单项选择题（每小题5分,共40分）9．ABD 10．CD 11．ACD 12．AB 三、填空题(每小题5分,共20分第16题第一空2分，第二空3分）13．[]0,2 14．1- 15．4 16．(),2-∞- ；2-.(写(],2-∞-也得分.)三、解答题(共70分)(注意：答案仅提供一种解法，学生的其他正确解法应依据本评分标准，酌情赋分.) 17．（本小题满分10分）解：(I)}{}{|2,|44.A x x B x x =>=-<<}{|4A B x x ∴=>-, …3分()}{|4U C A B x x ∴=≤-. ……………………………5分(II)∵}{,,|B x A x x B A ∉∈=-且∴}{|4A B x x -=≥, ……………………8分()}{|24A A B x x --=<<. ……………………………10分18．（本小题满分12分）解：(I) ()24f =,()()25ff =………………………………………………………2分（II ）()f x 在区间[]2,4上单调递增. …………………………………………………………3分证明：∀1x ，2x ∈[]2,4，且12x x <，12121244()()f x f x x x x x ⎛⎫⎛⎫-=+-+ ⎪ ⎪⎝⎭⎝⎭ ()121244x x x x ⎛⎫=-+- ⎪⎝⎭()2112124()x x x x x x -=-+ ()()1212124x x x x x x --=…………………………………………………………6分1x ，2x ∈[]2,4，且12x x <，1212120,40,0.x x x x x x ∴>->-<， 12()()0f x f x ∴-<，即12()()f x f x <．∴函数()f x 在区间[]2,4上是增函数．……………………………………8分（III ）由（2）知min ()(2)4f x f ==…………………………………………10分因为关于x 的不等式4x m x+<在区间[]2,4上有解，所以min ()m f x >. 所以4m >.所以实数m 的取值范围是()4,+∞ ……………………………12分 19．（本小题满分12分）解：(I),0a b >，a b ∴+≥33ab a b =++≥.……………2分30ab ∴-≥,)310∴≥.10ab +>，30≥.3≥9.ab ∴≥………………………………………………………………5分当且仅当 3a b ==，等号成立.故当3a b ==时，ab 的最小值为9.………6分 (II),0,a b >且ab a b =+.1a b ab +∴=,111a b+=.……………………8分 ()114445a b a b a b a b b a ⎛⎫∴+=++=++ ⎪⎝⎭59a ≥+=.……………………11分当且仅当 2b a =，即3,32a b ==时，等号成立. 故当3,32a b ==时，4a b +的最小值为9.………………………………………12分 20．（本小题满分12分）解: （Ⅰ）因为不等式2320ax x -+>的解集为{1,}x x x b <<或，所以1和b 是方程2320ax x -+=的两个实数根．故：3121b a b a ⎧+=⎪⎪⎨⎪⨯=⎪⎩，解得12a b =⎧⎨=⎩． ... 2分经验证，符合条件.（Ⅱ）由（Ⅰ）知不等式2()0cx ac b x ab ++>-，即2(2)20cx c x +-+>，即(2)(1)0cx x -->．当0c =时，2(1)0x -->，解得1x <.…………………4分当0c <时，(2)(1)0cx x -->即2()(1)0x x c --<，解得21x c <<...........6分当0c >时，(2)(1)0cx x -->即2()(1)0x x c -->.比较2c与1的大小当21c =，即2c =时，解得1x ≠………………………………………7分当21c >，即02c <<时，解得1,x <或2x c >………………………………………9分当21c <，即2c >时，解得2,x c<或1x >……………………………………………11分综上所述，当0c <时，原不等式的解集为：2{|1}x x c<<当0c =时，原不等式的解集为：{|1}x x <当02c <<时，原不等式的解集为： {|1,x x <或2}x c> 当2c =时，原不等式的解集为：{|1}x x ≠当2c >时，原不等式的解集为：2{|,x x c<或1}x >…………………………12分 21．（本小题满分12分）解：（Ⅰ）当040x <<时，2()5100101002500L x x x x =⨯--- 2104002500x x =-+-………2分当40x ≥时，3600()5100501L x x x x =⨯--3600450025002000()x x +-=-+……4分所以2104002500, 040,()36002000(), 40. x x x L x x x x ⎧-+-<<⎪=⎨-+≥⎪⎩................................ 6分（Ⅱ）当040x <<时， 2()10(20)1500L x x =--+，当20x =时， max ()1500L x =； ............................................ 8分当40x ≥时， 3600()2000()L x x x=-+2000≤-20001201880=-=，（当且仅当3600x x=，即60x =时，“=”成立） .............................. 10分因为18801500>，所以，当60x =时，即2020年生产60百辆时，该企业获得利润最大，且最大利润为1880万元． ................................................... 12分22（本小题满分12分）解：(Ⅰ)当[]2,2-∈x ，设(),32a ax x x g -++=对称轴为2ax -=由题意知对[]2,2x ∀∈-，()0g x ≥恒成立. （1）当,22-≤-a即4≥a 时，()x g 在[]2,2-上单调递增，此时只需(),03724⎩⎨⎧≥-=-≥a g a 此时无解. …………………………2分（2）当,22≥-a即4-≤a 时，()x g 在[]2,2-上单调递减，此时只需(),0724⎩⎨⎧≥+=-≤a g a 解得47-≤≤-a …………………4分（3）当222<-<-a时，即44<<-a 时，此时只需,0342442⎪⎩⎪⎨⎧≥+--=⎪⎭⎫⎝⎛-<<-a a a g a 解得24≤<-a 综上所述,a 的取值范围是[]7,2-. ………………………………6分方法二： []2,2x ∀∈-，设230x ax a ++-≥()()213a x x -≥-+（1）当1x =时,R a ∈ （2）当[)2,1x ∈-时，()()22min 33.(),()211x x a g x g x x x -+-+≤==--令，2a ≤.（3）当(]1,2x ∈时，()()22max 33(),()7.11x x a g x g x x x -+-+≥==---.，7a ≥-.（Ⅱ）()0f x <即 230x ax ++<的解集为{|x m x m <<+，所以1x m =和2x m =+032=++ax x 的两个实数根．由韦达定理可知121212,3,x x a x x x x +=-=-= ………………………………………………8分 ()222121212412x x x x x x a ∴-=+-=-………………………………………………10分所以有22412a =- 解得 6.a =± ………………………………………………12分方法二：230x ax ++<的解集为{|x m x m <<+所以m和m +032=++ax x 的两个实数根．由韦达定理可知2,( 3.m a m m ⎧+=-⎪⎨+=⎪⎩①②……………………………8分由②得(2230,9.m m +-=+=所以33m m ==--…………………………………………10分代入①式可得 6.a =±…………………………………………………12分。

山东省滕州市第一中学高一语文10月月考试题

2014-2015学年度山东省滕州市第一中学高一第一学期10月月考语文试题时量: 120分钟分值: 100分一、语言知识及运用（共5题，每题3分）1、下列加点字的注音全都不相同的一项是A．忤．视/抵牾．瑕疵．/目眦．尽裂炮．烙/刨．根问底挟．持/汗流浃．背B．翘．首/憔．悴累．赘/危如累．卵创．伤/满目疮．痍即．使/既．往不咎C．箴．言/缄．默嗔．怪/嗔．目而视瞭．望/眼花缭．乱叱咤．/姹．紫嫣红D．刀俎．/狙．击裨．益/稗．官野史琴弦．/头晕目眩．吭．声/引吭．高歌2、把下列句子组成语意连贯的语段，排序最恰当的一项是①从窗内往外看时，那一朵白莲已经谢了，白瓣儿小船般散飘在水面。

②那一朵红莲，昨夜还是含苞的，今晨却开满了，亭亭地在绿叶中间立着。

③梗上只留个小小的莲蓬，和几根淡黄色的花须。

④半夜里听见繁杂的雨声，早起是浓阴的天，我觉得有些烦闷。

B．家用电器降价刺激了市民消费欲的增长，原本趋于滞销的彩电，现在一下子成了炙手．．可热．．的商品C．齐白石画展在美术馆开幕了，国画研究院的画家竟相观摩，艺术爱好者也趋之若鹜．．．．。

D．不涉及切身利益时，面纱尚存，一到关键时刻，或是一触及到底线，马上图穷匕见．．．．。

见了之后呢，再也回不到从前。

4、依次填入下面一段文字横线处的语句，衔接最恰当的一组是（）直到五四之前，中国诗坛还是旧诗一统天下。

①新诗的倡导者们主张废除陈旧的格律，其着眼点当然不仅仅在于形式。

②尽管旧诗曾有着灿烂的过去，但到了上个世纪初，已成强弩之末。

③它那固定的形式、格律已使它很难容纳新的思想、新的内容。

④这同时也是一场深刻的思想革命，向旧诗所代表的传统思想与美学观念发起挑战。

⑤很难适应急剧变化的现代社会读者的审美要求。

A．①④②③⑤ B．②③⑤①④C．①④③②⑤ D．②①④⑤③5、下列诗句都是描绘秋景的，与《沁园春·长沙》意境相似的一项是（）A．枯藤老树昏鸦，小桥流水人家，古道西风瘦马，夕阳西下，断肠人在天涯。

山东省滕州市第一中学2022高一英语10月阶段性检测试题(含解析)

A
In recent years，Myanmar has opened its doors to western tourism．This once-closed state in Southeast Asia is a gold mine for those who enjoy the ancient Buddhist culture of the region．Compared to its neighbors，the landscape of Myanmar has been left largely undamaged．There are so many reasons why Myanmar is amazing and has been rated one of the top Asian tourist destinations for 2022．Here are some of its scenic spots：
C. She hasn’t become a good waitress.
听第9段材料,回答第13至16题。
13. How does the woman think Mark feels?
A. Anxious. B. Unhappy. C. Frightened.
14. What was Catherine doing when the speakers got home?
1. What is Linda?
A. A writer. B. A student. C. A teacher.
2. What is the man afraid of?
A. Having an accident. B. Missing the interview. C. Saying something wrong.