振动力学作业
《振动力学》习题集(含答案)【精选】精心总结

令 引起的静变形为 ,则有:
,即
令 + 引起的静变形为 ,同理有:
得:
则系统的自由振动可表示为:
其中系统的固有频率为:
注意到 与 方向相反,得系统的自由振动为:
1.9质量为m、长为l的均质杆和弹簧k及阻尼器c构成振动系统,如图E1.9所示。以杆偏角 为广义坐标,建立系统的动力学方程,给出存在自由振动的条件。若在弹簧原长处立即释手,问杆的最大振幅是多少?发生在何时?最大角速度是多少?发生在何时?是否在过静平衡位置时?
解:
(1)保持水平位置:
(2)微幅转动:
故:
2.10求图T 2-10所示系统的固有频率,刚性杆的质量忽略不计。
图T 2-10答案图T 2-10
解:
m的位置:
, ,
,
,
2.11图T 2-11所示是一个倒置的摆。摆球质量为m,刚杆质量可忽略,每个弹簧的刚度为 。
(1)求倒摆作微幅振动时的固有频率;
(2)摆球质量m为0.9 kg时,测得频率 为1.5 Hz,m为1.8 kg时,测得频率为0.75 Hz,问摆球质量为多少千克时恰使系统处于不稳定平衡状态?
图E1.2
解:
如图,令 为柱体的转角,则系统的动能和势能分别为:
利用 和 可得:
1.3转动惯量为J的圆盘由三段抗扭刚度分别为 , 和 的轴约束,如图E1.3所示。求系统的固有频率。
图E1.3
解:
系统的动能为:
和 相当于串联,则有:
以上两式联立可得:
系统的势能为:
利用 和 可得:
1.4在图E1.4所示的系统中,已知 ,横杆质量不计。求固有频率。
图E1.4答案图E1.4
解:
对m进行受力分析可得:
振动力学》习题集(含答案)

《振动力学》习题集(含答案)质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。
求系统的固有频率。
图解: 系统的动能为:()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得: ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
图解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得: ()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。
求系统的固有频率。
图解: 系统的动能为:221θ&J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得: ()()3232132k k J k k k k k n +++=ω在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
振动作业

振动作业1.立方体木块质量为m 静止在平静的湖面上,水的密度为ρ,浸水深度为h ,表面积为s, 在竖直方向做小幅振动。
(1)证明若只考虑重力和水的浮力,则木块做简谐振动; (2)求振动周期。
解:(1)因木块平衡时mg gsh ρ=当有位移x 时木块所受合力()F mg gs h x gsx ρρ=-+=-由牛顿定律有22d x gsx m dt ρ-= 即220d x gsxdt mρ+= 令2gsm ρω= 则2220d x x dtω+= 所以木块做简谐振动(2)222T Tππωω=∴== 2.轻弹簧下端连接一质量为m 的物块,静止时弹簧在弹性限度内伸长0l 。
突然物块断裂,有一半脱落,余下的一半物块开始振动,证明物块做简谐振动并写出振动表达式。
解:设弹性系数为k 则0mg mg kl k l ==剩下一半物块的平衡位置为1x 则11222l mmg g kx x k === 以半个物块的平衡位置为坐标原点竖直向下为x 轴正方向,当物块有位移x 时所受合力1()2m F g k x x kx =-+=- 222m d x kx dt∴-= 2220d x k x dt m∴+= 所以物块做简谐振动 取开始时刻为计时起点,则t=0时位移0012l x x == 速度00v = 则00A x ϕ== 又因为22k mω=所以振动表达式为0cos()0)2l x A t ωϕ=+=+3.某质点的振动曲线如图,用旋转矢量法求初相位和圆频率,并写出质点的振动方程。
解:0.02002A t x v ===> 3ϕ∴=-t=5 x=0 56t πω=6πω∴= cos()0.02cos()63x A t t ππωϕ∴=+=- 4.质量为10克的小球与轻弹簧组成的系统,按0.5cos(8)3x t ππ=+的规律而振动,式中各量均为SI 制。
求:(1)振动的园频率、周期、振幅、初相位、速度及加速度的最大值;(2)t=1s t=2s 时刻的相位各为多少?解:将运动方程与标准式比较cos()x A t ωϕ=+得825.12/rad s ωπ== 0.252T s ωπ== 0.5A m = 3πϕ= sin()dx v A t dt ωωϕ==-+ 2cos()dva A t dtωωϕ==-+ 12.6/m v A m s ω∴== 2316/m a A m s ω==5.如图所示圆半径为10厘米,根据矢量图写出个图对应的振动的振动方程x(m)解:在旋转矢量图中振幅对应旋转半径,所以A=10cm=0.1m t=0时刻矢量与x 轴夹角为初相位ϕ 所以33444a b c πϕϕπϕπ===-t 时刻矢量与x 轴夹角为相位t ωϕ+ 所以ωπ=c o s ()0.1c o s ()4a x A t t πωϕπ=+=+ 3cos()0.1cos()4b x A t t πωϕπ=+=+3cos()0.1cos()4c x A t t πωϕπ=+=-6.如图所示根据振动位移曲线写出各条曲线的振动方程解:由图知各条曲线对应的初相位为12πϕ=-2ϕπ= 32πϕ=221/T r a d s Tππω=∴== 1cos()0.1cos()2x A t t πωϕ=+=-2cos()0.1cos()x A t t ωϕπ=+=+3cos()0.1cos()2x A t t πωϕ=+=+7.一原长0.6米的弹簧,上端固定,下端挂一质量为0.2kg 的小球。
《振动力学》习题集(含答案)
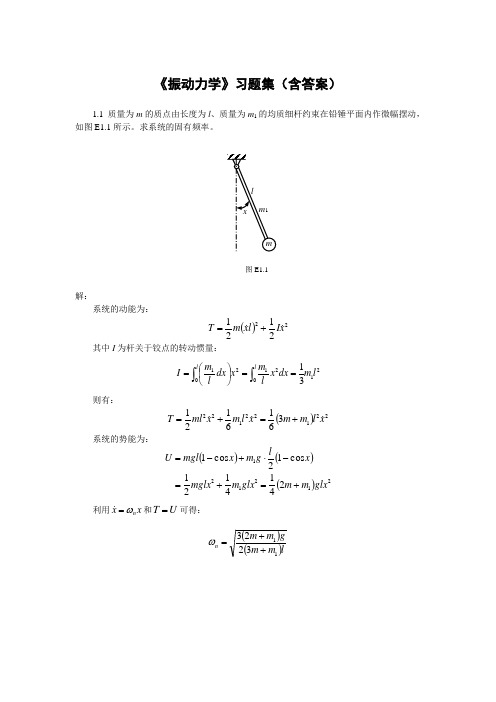
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》作业资料(含答案解析)

《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
振动力学习题集含答案

解:
,
动量守恒:
,
平衡位置:
,
,
故:
故:
2.4在图E2.4所示系统中,已知m, , , 和 ,初始时物块静止且两弹簧均为原长。求物块运动规律。
图E2.4答案图E2.4
解:
取坐标轴 和 ,对连接点A列平衡方程:
即:
(1)
对m列运动微分方程:
即:
(2)
由(1),(2)消去 得:
图E2.7
解:
,
s=1时共振,振幅为:
(1)
远离共振点时,振幅为:
(2)
由(2)
由(1)
, ,
故:
2.7求图T 2-7中系统的固有频率,悬臂梁端点的刚度分别是 及 ,悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解:
和 为串联,等效刚度为: 。(因为总变形为求和)
和 为并联(因为 的变形等于 的变形),则:
图E1.9答案图E1.9
解:
利用动量矩定理得:
,
,
,
,
1.12面积为S、质量为m的薄板连接于弹簧下端,在粘性流体中振动,如图E1.12所示。作用于薄板的阻尼力为 ,2S为薄板总面积,v为速度。若测得薄板无阻尼自由振动的周期为 ,在粘性流体中自由振动的周期为 。求系数 。
图E1.12
解:
平面在液体中上下振动时:
和 为串联(因为总变形为求和),故:
故:
2.9如图T 2-9所示,一质量m连接在一刚性杆上,杆的质量忽略不计,求下列情况系统作垂直振动的固有频率:
(1)振动过程中杆被约束保持水平位置;
(2)杆可以在铅锤平面内微幅转动;
(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
振动力学-习题

《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示,重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置,另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
图2-1 图2-2 2-2 一均质等直杆,长为l ,重量为w ,用两根长h 的相同的铅垂线悬挂成水平位置, 如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程,并求 出振动固有周期。
2-3 一半圆薄壁筒,平均半径为R , 置于粗糙平面上做微幅摆动,如图2-3所示。
试求 其摆动的固有频率。
图2-3 图2-4 2-4 如图2-4 所示,一质量m 连接在一刚性杆上,杆的质量忽略不计,试求下列情况 系统作垂直振动的固有频率:(1)振动过程中杆被约束保持水平位置;(2)杆可以在铅垂平面内微幅转动;(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
2-5 试求图2-5所示系统中均质刚性杆AB在A点的等效质量。
已知杆的质量为m,A 端弹簧的刚度为k。
并问铰链支座C放在何处时使系统的固有频率最高?图2-5 图2-62-6 在图2-6所示的系统中,四个弹簧均未受力。
已知m=50kg,19800N mk=,234900N mk k==,419600N mk=。
试问:(1)若将支撑缓慢撤去,质量块将下落多少距离?(2)若将支撑突然撤去,质量块又将下落多少距离?2-7 图2-7所示系统,质量为m2的均质圆盘在水平面上作无滑动的滚动,鼓轮绕轴的转动惯量为I,忽略绳子的弹性、质量及各轴承间的摩擦力。
试求此系统的固有频率。
图2-72-8 如图2-8所示的系统中,钢杆质量不计,建立系统的运动微分方程,并求临界阻尼系数及阻尼固有频率。
图2-82-9 图2-9所示的系统中,m =1kg ,k =224N/m ,c =48N.s/m ,l 1=l =0.49m ,l 2=l /2,l 3=l /4,不计钢杆质量。
振动力学习题集含答案

解:
利用动量矩定理得:
,
,
,
,
面积为S、质量为m的薄板连接于弹簧下端,在粘性流体中振动,如图所示。作用于薄板的阻尼力为 ,2S为薄板总面积,v为速度。若测得薄板无阻尼自由振动的周期为 ,在粘性流体中自由振动的周期为 。求系数 。
图
解:
平面在液体中上下振动时:
,
,
图所示系统中,已知m,c, , , 和 。求系统动力学方程和稳态响应。
(2)
若取下面为平衡位置,求解如下:
,
图T 2-17所示的系统中,四个弹簧均未受力,k1=k2=k3=k4=k,试问:
(1)若将支承缓慢撤去,质量块将下落多少距离?
(2)若将支承突然撤去,质量块又将下落多少距离?
图T 2-17
解:
(1) ,
(2) ,
如图T 2-19所示,质量为m2的均质圆盘在水平面上可作无滑动的滚动,鼓轮绕轴的转动惯量为I,忽略绳子的弹性、质量及各轴承间的摩擦力,求此系统的固有频率。
因此有:
图所示阶梯杆系统中已知m,ρ,S,E和k。求纵向振动的频率方程。
图
解:
模态函数的一般形式为:
题设边界条件为:
,
边界条件可化作:
,
导出C2= 0及频率方程:
,其中
长为l、密度为ρ、抗扭刚度为GIp的的等直圆轴一端有转动惯量为J的圆盘,另一端连接抗扭刚度为k的弹簧,如图所示。求系统扭振的频率方程。
《振动力学》习题集(含答案)
质量为m的质点由长度为l、质量为m1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。求系统的固有频率。
图
解:
系统的动能为:
其中I为杆关于铰点的转动惯量:
振动力学习题集含答案
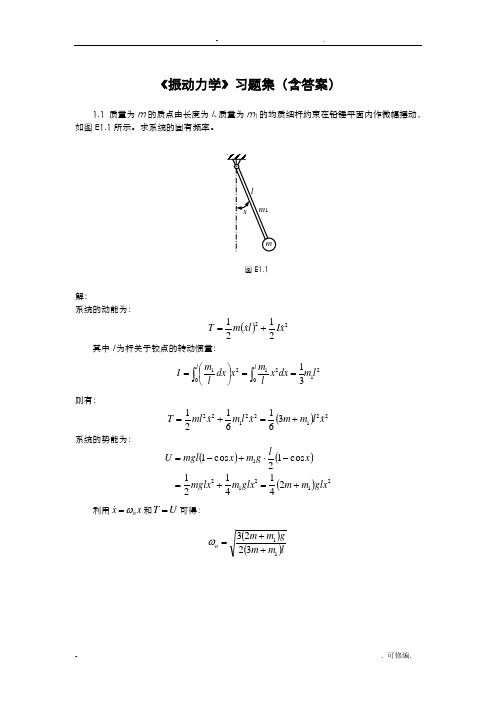
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+= 系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集[含答案]
![《振动力学》习题集[含答案]](https://img.taocdn.com/s3/m/bf1e364afad6195f302ba63b.png)
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)
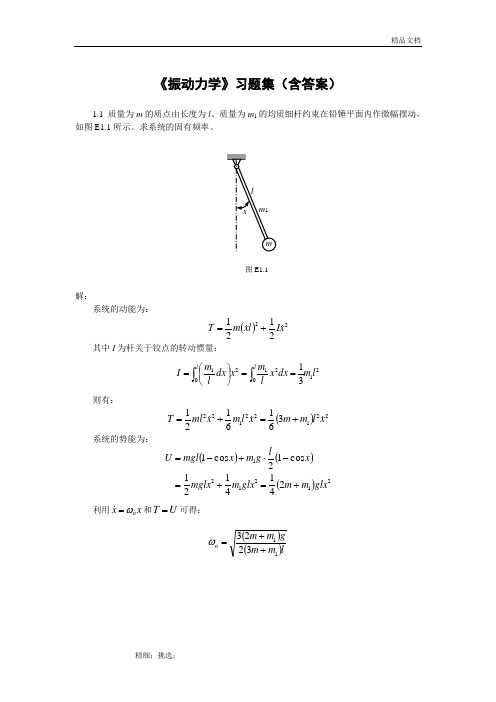
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)
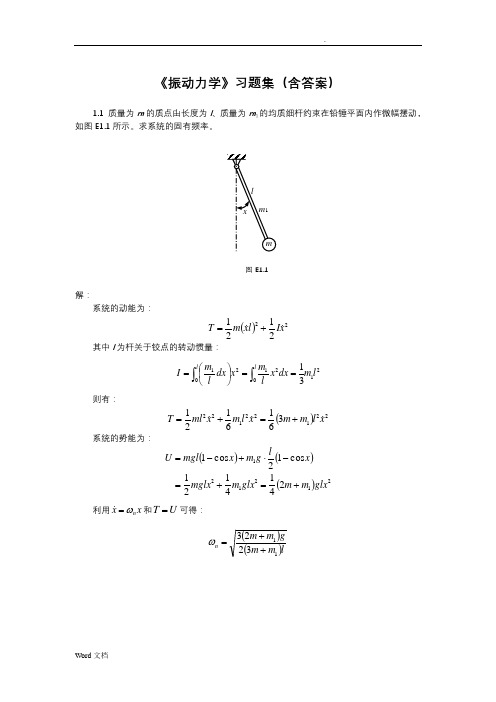
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案解析)
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含标准答案)

《振动力学》习题集(含答案)————————————————————————————————作者:————————————————————————————————日期:《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得: ()()lm m gm m n 113223++=ωml m 1 x1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得: ()mkR a R mR a R k n 343422+=+=ωkk A Ca R θ1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ&J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得: ()()3232132k k J k k k k k n +++=ωkk 2 kJ1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》课程作业
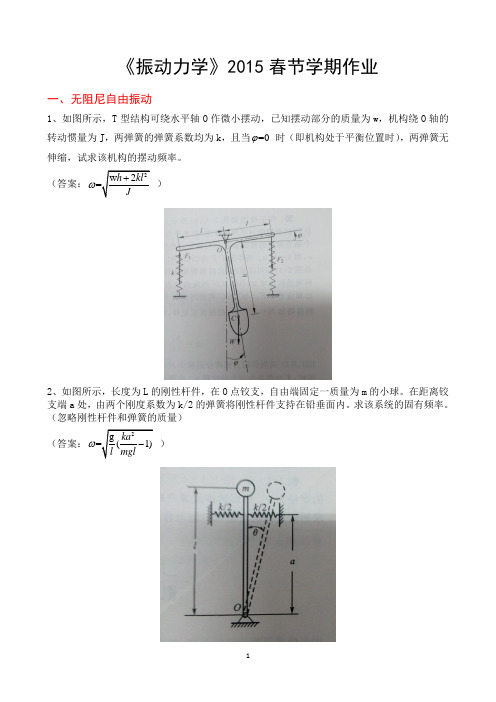
《振动力学》2015春节学期作业一、无阻尼自由振动1、如图所示,T型结构可绕水平轴O作微小摆动,已知摆动部分的质量为w,机构绕O轴的ϕ时(即机构处于平衡位置时),两弹簧无转动惯量为J,两弹簧的弹簧系数均为k,且当=0伸缩,试求该机构的摆动频率。
(答案:ω)2、如图所示,长度为L的刚性杆件,在O点铰支,自由端固定一质量为m的小球。
在距离铰支端a处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:ω)3、如图所示,悬臂梁长为L,截面抗弯刚度为EI,梁的自由端有质量为m的质量块,弹簧刚度为k,求系统的固有频率。
(答案:ω=)4、如图所示,半径为R的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有角频率。
(答案:ω=)5、如图所示,抗弯刚度为62EI=⨯⋅的梁AB,借弹簧支撑于A,B两点处,弹簧系3010(N m)数均为300(/)=的物W N k N m=。
忽略梁的质量,试求位于B点左边3m处,重量为1000()块自由振动的周期。
(答案:T=0.533s)6、一个重W的水箱,借助四根端点嵌固的竖置管柱支撑着。
每根柱子的长为L,抗弯刚度为EI。
试求该水箱顺水平方向自由振动的周期。
(管柱的质量忽略不计)T=)(答案:27、《结构动力学基础》,第2章课后习题,第1题、第2题、第8题二、有阻尼自由振动1、如图所示,库伦曾用下述方法测定液体的粘性系数'c :在弹簧上悬挂一薄板A ,先测出薄板在空气中的振动周期1T ,然后测出在待测粘性系数的液体中的振动周期2T 。
设液体对薄板的阻力等于2A 'c v ,其中2A 为薄板的表面面积,v 为薄板的速度。
如薄板重W ,试有测得的数据1T 和2T ,求出粘性系数'c 。
空气对薄板的阻力不计。
(答案:'c =)2、物体质量为2kg ,挂在弹簧下端。
弹簧常数k=48.02N/cm,求临界阻尼系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振动力学
——高转速振动
电机起动过程研究
姓名:史龙繁
班级:机制091班
学号:2009200116
院系:新科学院机电系
前言(发展背景)
高转速振动电机是一种新型的工程建设中使用的特殊电机。
这种电机采用频率为200Hz,电压为42V的电源供电,电机转速达11500r/mm,所以,这种电机是一种低压、中频、高转速的安全型电机。
同时,这种电机作为振动器的动力源全封闭于振动体内,其噪声影响得到较好的控制,是符合环保要求的低噪声振动器的关键部件。
高转速振动电机结构类似于笼型感应电机,电机由定转子组成,但其定子不是固定的。
定子上对称布置三相绕阻,绕阻多采用2A接法,转子采用铜条笼型转子,槽型为闭口槽。
受工况限制,该种电机长径比大于2:1,电机铁耗大、定转子漏抗系数大,电机在启动之初,定转子铁心中交变磁通频率分别为200Hz或接近200Hz,电机温升变化很快,而且相对于380V、50Hz同功率的普通笼型电机而言,这种电机的起动电流大很多。
在实际应用中,这种电机常常单电源供电多台并联运行,多台并联运行将加剧对电源的不利影响。
因此,该种电机起动过程应尽可能短,从而达到控制电机温升,延长电机寿命,并减小电机起动对电源影响的目的。
很明显,研究振动电机的起动过程有利于该种电机的优化设计和应用。
1.高转速振动电机起动过程的数学模型
为简化问题的研究,假设所建数学模型遵循下述原则:(1)高转速振动电机定转子侧均按电动机惯例分析;(2)定子三相绕阻对称;(3)气隙均匀;(4)基于上述假设,给出高转速振动电机的双轴系统(dq0系统)数学模型。
l-1 数学模型
高转速振动电机三相对称情况下运行时,可将定转子侧绕组用双轴系统下的定转子绕组代替,从而将三相坐标系统下的各相存在的自感、互感时变系数转换为常系数,使所建数学系模型得到简化。
在双轴系统下,定转子绕阻各参数矩阵形式如下:
在上述矩阵中,带下标s及r的参数分别表示定子和转子绕组系数,带下标d、q的参数表示为定子或转子的d、q轴绕组的参数。
在电机起动过程中,电机转速是变化的,电机起动电流参数因角速度的变化而变化。
因此,在起动过程中,高转速振动电机双轴数学模型包括两部分,即电压方程式和运动方程式,这两部分组成的数学模型如下:
式中:L表示磁链与电流之间的关系矩阵,即电感矩阵;H表示高转速振动电机的惯性常数;G表示定子d轴、q轴磁链旋转产生的电势系数矩阵;表示电机的负载转矩;表示高转速振动电机的机械阻尼系数。
1.2 数学模型输入参数及系数处理
高转速振动电机起动时三相坐标系下输入中频低压电源,即:
将三相坐标系下的输入参数转换成双轴系统输入参数,即:
数学模型中有关系数包括下述几个方面:
(1)惯性常数及机械阻尼系数
由机械运动动力学知,电机转轴只做旋转运动时,电机惯性常数为:
式中:为电源频率(Hz);为视在功率(KVA);n为同步转速(r/min);为电机飞轮矩。
高转速振动电机起动时,电机转轴所作运动由两种形式即旋转运动与复杂的高频振动方式复合而成。
在起动过程中,因为电机转速的变化,高频振动的速度、加速度不一致。
高频振动影响电机惯性常数大小,精确计算考虑高频振动影响时的惯性常数,必须按贮存能量一致的原则,将高频振动等效折算为旋转运动。
显然,这种办法非常复杂,考虑到高转速振动电机旋转部分的转动惯量往往数值较小,转速上升很快,而电机高频振动幅值能很快上升到1.5mm左右,电机大部分机械能转换成为了高频振动能量,高频振动贮能数值大约相当于旋转部分的85%左右(给定转速情况下)。
因此,在分析起动过程中,H数值按1.85倍的关系计算,即电机惯性常数公式修改为:
在电机惯性常数表达式中,与电机铁心长度成正比,计算电机起动性能时应注意考虑这种关系。
数值很小,但对高转速电机而言,机械阻尼转矩是明显的,必须计算机械阻尼转矩。
(2)电感矩阵L及旋转电势系数矩阵G:
式中:为定转子绕组问的互感;为定子绕组自感;为转子绕组自感;并且正比于
铁心长度和定子绕组每相串联匝数;包括两部分,其中一部分正比于铁芯长
度和定子绕组每相串联匝数的平方;另一部分为。
也包括两部分,其中一部分正比于铁芯长度;另一部分为。
假设铁芯长度、定子绕组串联匝数试算值对应的参数
值为,参数与铁芯长度及定子绕组每相串联匝数之间的数学关系模型如下:
表达式(8)一(12)说明通过调整电机铁心长度、绕组串联匝数可改变数学模型微分方程(1)、(2)、(3)的系数矩阵。
因此,调整铁
心长度大小及串联匝数多少,可获得不同的起动性能曲线,也可设计控制电机的起动过程所需时间。
2 起动过程的计算与分析
2.1 起动过程的的数值计算
由于所建数学模型由非线性微分方程组成,因此采用数值计算法计算电机的起动过程。
现要求高转速振动电机能在3秒钟表内完成起动过程。
电机额定功率为0.5kW,额定电压为42V,额定电流为1IA,额定转速为11500r/min,定子绕阻接法为2Δ。
假设:选定相电流、相电压额定值为电流、电压基值;选定视在功率为功率基值;转矩基值按公式
计算。
那么应用所建数学模型采用龙格——库塔法可计算得出不同线圈匝数及不同铁心长度的高转速振动电机的起动性能曲线(如图1~6)。
2.2 起动过程的分析
图1—6是在电机槽型、绕组连接方法确定后,优化绕组线圈匝数和铁心长度情况下,计算得到的电机空载起动性能曲线。
图1、图2、图3分别是相电流、电机转速、电磁转矩与起动时问之间的关系曲线;图4是电磁转矩随角速度变化的关系曲线;图5是电机起动刚开始时,电磁转矩的变化曲线;图6是电机起动过程中一个特定时间段内电机电流变化情况,图6表明了电机起动完毕前后一定时间段内电流的变化特征。
图2表明在t=3秒时电机转速达到11000r/min,电机起动完毕,在此过程中,电机转速
随时间变化近似地按线性关系变化。
电机起动完毕后,其最高转速接近同步转速,在整个起动过程中,电机转速未能越过同步转速;图4则表明电机从起动到稳定工作点时,不存在转矩和转速围绕平衡点摆动的现象。
上述两种现象有别于50Hz电源供电的异步电机的起动性能。
其原因是:在接近同步转速时,由于50Hz电源供电的异步电机在电磁过渡过程中,转子电流衰减变化慢,相当于电机存在一激磁电源,从而产生与同步电机类似的机电振荡现象;而200Hz电源供电的异步电机虽然存在电磁过渡过程,但转子电流衰减变化快,不再存在明显的激磁电源现象,所以高频振动电机起动过程中即没有“摆动现象”,也不会出现“超同步现象”。
图3表明起动过程中电机的最大转矩可达转矩基值的1.6倍,即额定转矩的2.4倍。
电机稳定运行时、最大转矩值与该值是相当的,这说明,最大转矩倍数值是合适的。
图5表明电机起动开始阶段,电磁转矩存在交变转矩,其频率为基频,该交变转矩在很短时间内(O.2秒)衰减至零。
电磁转矩的主要成分为单向转矩,交变分量影响很小,所以图2中转速变化具有线性特征。
图1和图6表明在电机的起动过程中,起动电流存在基频交变分量,还存在着非周期分量和低频交变分量。
其中:非周期分量很快衰减为零;低频交变分量频率与转速成正比,随转子非周期电流衰减而衰减,在电机转速接近同步转速时,该分量迅速降为零。
因为低频交变分量在整个起动过程中都存在,所以起动电流数值可达额定值的4倍左右。
3 结论
通过上述实例计算,我们可以得出如下结论:
(1)高转速振动起动电机起动过程中起动电流含有明显的低频分量,该分量导致了起动过程中起动电流有效值较大,无论从控制电机温升、延长电机寿命,还是从减小其对电源影响的角度来讲,应该优化设计电机的起动过程,控制电机的启动时间。
通过调整设计参数即铁心长度和线圈匝数可实现这一目的。
(2)高转速振动电机起动过程中,转速与时间之间存在近似的线性关系。
起动过程不存在“超同步现象”和“摆动现象”。
(3)高转速振动电机起动过程中存在基频交变转矩分量,该分量衰减速度很快,对电机起动性能影响很小。
参考文献
【1】R.Enrolls.Practical Guide to Vibrator Erolls【M】.Paris.1968
【2】高景德等.交流电机及其系统的分析【M】.北京:清华大学出版社,1993
【3】振动电机及其在粮食机械中的应用朱华里 1997年《郑州粮食学院学报》
【4】永磁式直线同步电机的特性分析王淑红 1998年《太原理工大学学报》
【5】动圈式永磁直线振动电机的静动态分析王淑红2006年《微特电机》
【6】单振动电机激振的直线振动机之动力学分析丁应生 1998年《粮食与饲料工业》【7】动磁式直线振动电机的特性研究卢琴芬叶云岳 2005年《中国电机工程学报》【8】三振动电机自动同步椭圆振动筛的同步立论侯勇俊 2007年《西南石油大学学报》【9】振动筛振动电机安装轴的断裂分析及对策李诗龙 2004年《轻工机械》
【10】移动电话用振动电机的发展趋势刘少波 2001年《微特电机》
【11】永磁直线振动电机的优化设计孙明施王群京 2000年《微特电机》。
