动量守恒定律在碰撞中的应用几种常见模型分析
多次碰撞模型(解析版)-动量守恒的十种模型

动量守恒的十种模型多次碰撞模型模型解读所谓多次碰撞模型是指,两个物体或多个物体发生多次碰撞,且这些碰撞满足某种规律。
【典例精析】1(2024湖南长沙高三适应性考试)如图,将火车停在足够长的平直铁轨上。
(1)若整列火车质量为M,所受阻力恒为F0,当整列火车速度为v时,发动机的功率为P0,求此时火车的加速度;(2)若整列火车所受阻力恒为F0,某次测试时整列火车的运动分为两个阶段。
第一阶段火车受到大小为kF0的恒定牵引力由静止启动,位移为x时,发动机的实际功率正好等于额定功率,然后进入第二阶段;第二阶段发动机保持额定功率继续前进,已知两个阶段用时相等,第二阶段的末速度为初速度2倍。
求第二阶段火车的位移;(3)若整列火车由1节动力车头和23节无动力车厢组成,动力车头质量为2m,每节无动力车厢质量均为m。
火车在启动前,车头会先向后退一段距离,使得各相邻车厢之间的连接挂钩松弛,车厢无间距紧挨着,然后车头从静止开始启动,逐节带动各节车厢直至最后一节车厢启动。
启动过程中车头牵引力恒为F,忽略一切阻力。
为了研究方便,将车头及相邻车厢之间的连接挂钩简化为不可伸长的长度为l的轻绳,绳子绷直的瞬间相连的物体间可看做发生完全非弹性碰撞,碰撞时间忽略不计。
整个启动过程中,带动第几节无动力车厢前,车头的速度达到最大?【参考答案】(1)P0-F0vMv;(2)(k+1)x;(3)3【名师解析】(1)根据P0=F1v 可知F1=P0 v根据牛顿第二定律F1-F0=Ma 解得a=P0-F0v Mv(2)设火车第一阶段运动时间为t,末速度为v2,第二阶段的位移为x2由动能定理得k-1F0x=12Mv22再由动量定理得(k-1)F0t=Mv2发动机的额定功率P m=kF0v2由上可知,第二阶段的初速度为v2,末速度为2v2,由动能定理得P m t-F0x2=12M2v22-v22解得x2=(k+1)x(3)设拖动第n节车厢前,车头的速度为u n,绳子绷直后车头的速度为u′n,拖动第一节车厢前,对车头由动能定理得12⋅2mu21=Fl绳子绷直,对车头和第一节车厢由动量守恒定律得2mu1=(2m+m)u′1同理,拖动第n节车厢前,对于车头和前(n-1)节车厢由动能定理得1 22m+n-1mu2n=122m+n-1mu 2n-1+Fl绳子绷直,对于车头和前n节车厢由动量守恒定律得[2m+(n-1)m]u n=(2m+nm)u′n 由上式得u n=n+1n+2u n可推出u n-1=nn+1u n-1联立有n+12u2n=n2u2n-1+2n+1Fl m令a n=(n+1)2u n2,得到a n=a n-1+n+12Fl ma n-1=a n-2+n2Flm a n-2=a n-3+n-12Fl m⋯⋯a2=a1+32Flm 其中a1=4Flm上几式相加得到a n=a1+n+4n-1Fl m则n +122u n =n 2+3nFl m解得u 2n=n 2+3nn +1 2⋅Fl m =n +1 2+n +1 -2n +1 2⋅Fl m =1+1n +1-2(n +1)2 ⋅Fl m 当1n +1=14,即n =3时有最大值。
微专题Ⅰ 动量守恒定律几种模型分析(学生版) 2024-2025学年高二物理同步(人教版选修第一册)

1、掌握动量守恒定律中的几种重要考试模型,清晰如何分析及进行运用。
[例题1](2024春•高新区期末)如图所示,一小车静止于光滑水平面,其上固定一光滑弯曲轨道,例题3]如甲图所示,水平光滑地面上用两颗钉子的小车,小车的四分之一圆弧轨道是光滑的,半径为切,视为质点的质量为m=1kg的物块从(1)两小球速度相同时,弹簧最短,弹性势能最大A.m B=4mB.第一次碰撞过程中,弹簧弹性势能的最大值为0.6m v20C.第一次碰撞过程中,弹簧压缩量的最大值为0.768v0t0D.第一次碰撞过程中,弹簧压缩量的最大值为1.128v0t0例题5](2024•黄陂区校级一模)质量为2kg的小球b静止在光滑的水平地面上,左端连接一水平A.π+2m,π―2mA.球A沿槽C下滑过程中,槽B.整个过程中球A、球B和槽C.球A第一次滑至槽C最低点过程中,球D.球A与弹簧作用后,能够追上槽[例题7](2024春•天河区校级期末)如图所示,水平桌面光滑,轻弹簧一端固定在墙上,另一端A.动量不守恒,机械能守恒[例题10](2022秋•历下区校级期中)向空中发射一枚炮弹,不计空气阻力,当此炮弹的速度恰好例题12]有人对鞭炮中炸药爆炸的威力产生了浓厚的兴趣,他设计如下实验,在一光滑水平面上放置两个大小相等(可视为质点)紧挨着的1.(多选)(2024•济南三模)质量为A.子弹击中物块后瞬间,物块水平方向的速度大小变为B.子弹击中物块后瞬间,物块竖直方向的速度大小变为C.物块下落的总时间为A.滑块从A到B时速度大小等于A.滑块C与弹簧脱离的瞬间获得的速度v c=1m/sB.轻弹簧长度最短时,所具有的弹性势能E p=12JC.滑块C在传送带上因摩擦产生的热量Q1=8J(2024春•温州期中)为了探究物体间碰撞特性,设计了如图所示的实验装置。
水平直轨道AB、CD和水平传送带平滑无缝连接,两半径均为管道DEF与轨道CD和足够长的水平直轨道2m的滑块c用劲度系数k=100N/m的轻质弹簧连接,静置于轨道的滑块a以初速度v0=17m/s从A处进入,经传送带和(1)物块a到达D点的速度;(2)物块a刚到达与O1等高的E点时对轨道的压力的大小;(3)若a、b两物块碰后粘在一起,则在接下来的运动中弹簧的最大压缩量。
高中物理第08章动量守恒 动量守恒定律应用(四种模型)

08、(2013·高考新课标全国卷Ⅱ,35 题)如图所示,光滑水平直轨道上有三个质量均为 m 的物 块 A、B、C.B 的左侧固定一轻弹簧(弹簧左侧的挡板质量不计).设 A 以速度 v0 朝 B 运动,压缩 弹簧;当 A、 B 速度相等时,B 与 C 恰好相碰并粘接在一起,然后继续运动.假设 B 和 C 碰撞过 程时间极短,求从 A 开始压缩弹簧直至与弹黄分离的过程中, (1)整个系统损失的机械能; (2)弹簧被压缩到最短时的1、如图所示,一排人站在沿 x 轴的水平轨道旁,原点 O 两侧的人的序号都记为 n(n=1,2, 3……) .每人只有一个沙袋,x>0 一侧的每个沙袋质量为 m=14 kg,x<0 一侧的每个沙袋质量为 m′=10 kg.一质量为 M=48 kg 的小车以某初速度从原点出发向正 x 方向滑行.不计轨道阻力, 当车每经过一人身旁时,此人就把沙袋以水平速度 v 朝与车速相反的方向沿车面扔到车上,v 的 大小等于扔此袋之前的瞬间车速大小的 2n 倍(n 是此人的序号数) . (1)空车出发后,车上堆积了几个沙袋时车就反向滑行? (2)车上最终有大小沙袋共多少个?
ECNU
LEX
高中物理第 08 章动量守恒 动量守恒定律应用(四种模型)
Lex Li
一、子弹木块模型 01、 如图所示, 一根质量不计、 长为 1 m, 能承受最大拉力为 14 N 的绳子, 一端固定在天花板上, 另一端系一质量为 1 kg 的小球,整个装置处于静止状态,一颗质量为 10 g、水平速度为 500 m/s 的子弹水平击穿小球后刚好将将绳子拉断, (g 取 10 m/s ) 。求: (1)小球此时的速度大小; (2)子弹此时的速度大小。
2
02、一颗质量为 m,速度为 v0 的子弹竖直向上射穿质量为 M 的木块后继续上升,子弹从射穿木块 到再回到原木块处所经过的时间为 T,那么当子弹射出木块后,求: (1)子弹身穿木块时的速度大小; (2)木块上升的最大高度为多少?
碰撞及类碰撞模型归类例析

碰撞及类碰撞模型归类例析“碰撞”是高中物理中的一个重要模型,它涉及动量定理、动量守恒定律、机械能守恒定律、能量守恒定律等诸多知识。
处理碰撞问题,需要先根据题意选取恰当的研究对象,合理选取研究过程,并把握该过程的核心要素,再判断研究对象的动量是否守恒、机械能是否守恒,然后根据相应物理规律列方程求解。
一、碰撞的特点:(1)作用时间极短,内力远大于外力,因为极短相互作用时间内可以忽略外力的影响,对系统而言动量保持不变,即总动量总是守恒的;(2)系统能量不能凭空增加,在碰撞过程中,因为没有其他形式的能量转化为动能,所以总动能一定不会增加,在完全弹性碰撞过程中动能守恒,然而在非弹性碰撞中,系统动能减小,总之碰撞不会导致系统动能增加;(3)在碰撞过程中,当两物体碰后速度相等,即发生完全非弹性碰撞时,系统动能损失最大; (4)在碰撞过程中,两物体产生的位移可以忽略不计。
二、常见的碰撞模型: 1.弹性碰撞弹性碰撞是高中物理碰撞问题中最常见的模型,对该碰撞问题的处理所依据的物理原理也相对容易理解。
所谓的弹性碰撞是指研究对象之间在碰撞的瞬间动能没有损失。
(1)动静碰撞模型如图所示,在光滑的水平面上质量为m 1的小球以速度v 1与质量为m 2的静止小球发生弹性碰撞.小球发生的是弹性碰撞,由动量守恒和能量守恒,得111122m v m v m v ''=+ ,222111122111222m v m v m v ''=+ 由上两式解得:121112m m v v m m -'=+ ,121122m v v m m '=+ 推论:① 若m 1 = m 2,可得v'1 = 0、v'2 = v 1,相当于两球交换速度。
② 若m 1 > m 2,则v'1>0 且v'2>0,即v'1和v'2均为正值,表示碰撞后两球的运动方向与v 1相同. ③ 若m 1>>m 2,则m 1-m 2≈m 1,m 1 + m 2≈m 1,可得v'1 = v1,v'2 = 2v 1。
专题强化八 碰撞类的四类模型

专题强化八碰撞类的四类模型【专题解读 1.本专题主要研究碰撞过程的特点和满足的物理规律,并对碰撞模型进行拓展分析。
2.会分析物体的正碰模型、“滑块—弹簧”、“滑块—斜面”、“滑块—木板”碰撞模型的特点,并会应用相应规律解决问题。
3.用到的知识、规律和方法有:牛顿运动定律和匀变速直线运动规律,动量守恒定律,动能定理和能量守恒定律。
模型一“物体与物体”正碰模型1.碰撞问题遵守的三条原则(1)动量守恒:p1+p2=p1′+p2′。
(2)动能不增加:E k1+E k2≥E k1′+E k2′。
(3)速度要符合实际情况①碰前两物体同向运动,若要发生碰撞,则应有v后>v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′≥v后′。
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
2.弹性碰撞的结论(1)m1v1+m2v2=m1v1′+m2v2′12m1v 21+12m2v22=12m1v1′2+12m2v2′2v1′=(m1-m2)v1+2m2v2m1+m2v2′=(m2-m1)v2+2m1v1m1+m2(2)若v2=0时,v1′=m1-m2m1+m2v1v2′=2m1m1+m2v1讨论:①若m1=m2,则v1′=0,v2′=v1(速度交换);②若m1>m2,则v1′>0,v2′>0(碰后,两物体沿同一方向运动);③若m1≫m2,则v1′≈v1,v2′≈2v1;④若m1<m2,则v1′<0,v2′>0(碰后,两物体沿相反方向运动);⑤若m1≪m2,则v1′≈-v1,v2′≈0。
3.非弹性碰撞碰撞结束后,动能有部分损失。
m1v1+m2v2=m1v1′+m2v2′12m1v 21+12m2v22=12m1v1′2+12m2v2′2+ΔE k损4.完全非弹性碰撞碰撞结束后,两物体合二为一,以同一速度运动,动能损失最大。
m1v1+m2v2=(m1+m2)v12m1v 21+12m2v22=12(m1+m2)v2+ΔE k损max【真题示例1(2020·全国Ⅲ卷,15)甲、乙两个物块在光滑水平桌面上沿同一直线运动,甲追上乙,并与乙发生碰撞,碰撞前后甲、乙的速度随时间的变化如图1中实线所示。
动量守恒定律应用:典型模型
P11
二.中子的发现
三.反冲现象与火箭的发射
一.碰撞问题的定量分析 P11
例1 例2
(1)解题步骤
(2)解题格式
教材作业:P17 评讲
预备问题:两球发生弹性碰撞,碰撞前、后小球m1是 否反向? 怎样判断?
①根据动量守恒得:?
m1v0 = m1v1+m2v2
①
②根据机械能守恒得:?
(2).人船模型
2.多次碰撞问题
3.多次碰撞问题
子弹(板块)模型
v0
光滑
v0
光滑
(1)隔离法: ①从动力学、运动学角度看
②从功能关系角度看
(2)整体法: 从系统动量守恒、能量守恒角度看
如图,光滑的曲面轨道的水平出口跟停在光滑 水平面上的平板小车的上表面相平。质量为m的小 滑块从光滑轨道上高度为H的位置,由静止开始滑 下并滑上平板小车,使得小车在光滑水平面上滑 ② ① 动。最终小滑块停到板面上的Q点。若平板小车的 ③ 质量为3m。求: (1)小滑块到达轨道底 端时的速度大小 (2)小滑块滑上小车后, 平板小车可达到的 最大速度 (3)该过程系统产生的总内能
光滑
如图,质量为m 的人站在质量为M 长为L小船的 右端,小船静止在水面上。当人向左走到船的左端 ① ② 时,求:船移动的方向和离岸的距离为多少?
分析: 抓“指向词”
任意时刻: mv1 = Mv2
①
v1 F v2 F
微元思想: 经极短时间∆t:
mv1∆t = Mv2∆t
m∆x1 = M∆x2
累积思想:
联立①②可解得:
1 2
(1)当m1 > m2时:
(2)当m1 = m2时:
(3)当m1 < m2时:
知识点48动量守恒定律在三类模型问题中的应用(拔尖)

学问点48:动量守恒定律在三类模型问题中的应用考点一:系统动量守恒的推断【学问思维方法技巧】〔1〕系统动量守恒适用条件①抱负守恒:不受外力或所受外力的合力为零.②近似守恒:系统内各物体间相互作用的内力远大于它所受到的外力.如碰撞、爆炸、反冲。
③某一方向守恒:假如系统在某一方向上所受外力的合力为零,那么系统在这一方向上动量守恒.如滑块-斜面(曲面)模型。
〔2〕推断系统动量是否守恒的“三留意〞:①留意所选取的系统——所选的系统组成不同,结论往往不同。
②留意所讨论的运动过程——系统的运动分为多个过程时,有的过程动量守恒,另一过程那么可能不守恒。
③留意守恒条件——整体不满意系统动量守恒条件时,在某一方向可能满意动量守恒条件。
题型一:系统动量抱负守恒【典例1拔尖题】(多项选择)如下图,一男孩站在小车上,并和木箱一起在光滑的水平冰面上向右匀速运动,木箱与小车挨得很近.现男孩用力向右快速推开木箱.在男孩推开木箱的过程中,以下说法正确的选项是( )A. 木箱的动量的增加量等于男孩动量的削减量B. 男孩对木箱推力的冲量大小等于木箱对男孩推力的冲量大小C. 男孩推开木箱后,男孩和小车的速度可能变为零D. 对于小车、男孩和木箱组成的系统,推开木箱前后的总动能不变【典例1拔尖题】【答案】BC【解析】由于水平冰面光滑,男孩、小车和木箱组成的系统所受合外力为零,系统动量守恒,站在小车上的男孩用力向右快速推出木箱的过程中,木箱的动量增加量等于男孩和小车动量的削减量,故A错误;男孩对木箱的推力和木箱对男孩的推力是作用力与反作用力,冲量等大反向,男孩对木箱推力的冲量大小等于木箱对男孩推力的冲量大小,故B正确;男孩、小车受到与初动量反向的冲量,推开木箱后,男孩和小车的速度可能变为零,故C 正确;男孩、小车与木箱三者组成的系统所受合力为零,系统动量守恒,推开木箱的过程不行能是弹性碰撞,推开前后的总动能变化,故D错误.题型二:系统动量近似守恒【典例2拔尖题】如下图,水平面上有一平板车,某人站在车上抡起锤子从与肩等高处挥下,打在车的左端,打后车与锤相对静止。
动量守恒定律的典型模型及其应用

1、“人船模型”是动量守恒定律的拓展应用, 它把速度和质量的关系推广到质量和位移 的关系。即: m1v1=m2v2 则:m1s1= m2s2 2、此结论与人在船上行走的速度大小无关。不论
是匀速行走还是变速行走,甚至往返行走,只要 人最终到达船的左端,那么结论都是相同的。
3、人船模型的适用条件是:两个物体组成的
M m h
作业
1.将质量为 m = 2 kg 的木块,以水平速度v0 = 5m/s 射到静止在光滑水平面上的平板车上 ,小车的质量为M = 8 kg ,物块与小车间的摩擦因数μ = 0.4 ,取 g = 10 m/s2.假设平板车足够长,求: (1)木块和小车最后的共同速度
碰撞中弹簧模型
• 图中,轻弹簧的一端固定,另一端与滑块B相连,B静 止在水平直导轨上,弹簧处在原长状态。另一质量与B 相同滑块A,从导轨上的P点以某一初速度向B滑行,当 A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B 紧贴在一起运动,但互不粘连。已知最后A恰好返回出 发点P并停止,滑块A和B与导轨的滑动摩擦因数都为 • 运动过程中弹簧最大形变量为l2,重力加速度为g,求A 从P出发时的初速度v0。
v0
s2
s1
L
1 2 1 2 对子弹用动能定理: f s1 mv 0 mv ……① 2 2 1 ……② 对木块用动能定理: f s2 Mv 2 2
①、②相减得: f L 故子弹打进 木块的深度:
1 1 Mm 2 2 mv 0 M mv 2 v 0 ……③ 2 2 2M m
6m/s 882J
v0
1.运动性质:子弹对地在滑动摩擦力作用下匀减 速直线运动;木块在滑动摩擦力作用下做匀加速 运动。
2.符合的规律:子弹和木块组成的系统动量守恒, 机械能不守恒。
在四种常见模型中应用动量守恒定律(解析版)

在四种常见模型中应用动量守恒定律导练目标导练内容目标1人船模型和类人船模型目标2反冲和爆炸模型目标3弹簧模型目标4板块模型【知识导学与典例导练】一、人船模型和类人船模型1.适用条件①系统由两个物体组成且相互作用前静止,系统总动量为零;②动量守恒或某方向动量守恒.2.常用结论设人走动时船的速度大小为v 船,人的速度大小为v 人,以船运动的方向为正方向,则m 船v 船-m 人v 人=0,可得m 船v 船=m 人v 人;因人和船组成的系统在水平方向动量始终守恒,故有m 船v 船t =m 人v 人t ,即:m 船x 船=m 人x 人,由图可看出x 船+x 人=L ,可解得:x 人=m 船m 人+m 船L ;x 船=m 人m 人+m 船L3.类人船模型类型一类型二类型三类型四类型五1有一条捕鱼小船停靠在湖边码头,小船又窄又长(估计一吨左右),一位同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行码头自由停泊,轻轻从船尾上船,走到船头后停下来,而后轻轻下船,用卷尺测出船后退的距离为d ,然后用卷尺测出船长L ,已知他自身的质量为m ,则渔船的质量()A.m (L +d )dB.md (L -d )C.mL dD.m (L -d )d【答案】D【详解】因水平方向动量守恒,可知人运动的位移为(L -d )由动量守恒定律可知m (L -d )=Md解得船的质量为M =m (L -d )d故选D 。
2如图所示,滑块和小球的质量分别为M 、m 。
滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O 由一不可伸长的轻绳相连,轻绳长为L ,重力加速度为g 。
开始时,轻绳处于水平拉直状态,小球和滑块均静止。
现将小球由静止释放,下列说法正确的是( )。
A.滑块和小球组成的系统动量守恒B.滑块和小球组成的系统水平方向动量守恒C.滑块的最大速率为2m 2gLM (M +m )D.滑块向右移动的最大位移为mM +mL【答案】BC【详解】A .小球下摆过程中竖直方向有分加速度,系统的合外力不为零,因此系统动量不守恒,A 错误;B .绳子上拉力属于内力,系统在水平方向不受外力作用,因此系统水平方向动量守恒,B 正确;C .当小球落到最低点时,只有水平方向速度,此时小球和滑块的速度均达到最大,取水平向右为正方向,系统水平方向动量守恒有Mv 1-mv 2=0由系统机械能守恒有mgL =12mv 22+Mv 21解得滑块的最大速率v 1=2m 2gLM (M +m ),C 正确;D .设滑块向右移动的最大位移为x ,根据水平动量守恒得M x t -m 2L -x t =0解得x =2mM +mL ,D 错误;故选BC 。
动量守恒定律中的典型模型

动量守恒定律中的典型模型1、子弹打木块模型包括木块在长木板上滑动的模型,其实是一类题型,解决方法基本相同。
一般要用到动量守恒、动量定理、动能定理及动力学等规律,综合性强、能力要求高,是高中物理中常见的题型之一,也是高考中经常出现的题型。
例1:质量为2m、长为L的木块置于光滑的水平面上,质量为m的子弹以初速度V0水平向右射穿木块后,速度为V0/2。
设木块对子弹的阻力F恒定。
求:(1)子弹穿过木块的过程中木块的位移(2)若木块固定在传送带上,使木块随传送带始终以恒定速度u<V0水平向右运动,则子弹的最终速度是多少例2、如图所示,在光滑水平面上放有质量为2m的木板,木板左端放一质量为m的可视为质点的木块。
两者间的动摩擦因数为μ,现让两者以V0的速度一起向竖直墙向右运动,木板和墙的碰撞不损失机械能,碰后两者最终一起运动。
求碰后:(1)木块相对木板运动的距离s(2)木块相对地面向右运动的最大距离L2、人船模型例3、一条质量为M,长为L的小船静止在平静的水面上,一个质量为m的人站立在船头.如果不计水对船运动的阻力,那么当人从船头走到船尾时,船的位移多大?例4、载人气球原静止于高h的高空,气球质量为M,人的质量为m,若人沿绳梯滑至地面,则绳梯至少为多长?3、弹簧木块模型例5、质量为m 的物块甲以3m/s 的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为m 的物体乙以4m/s 的速度与甲相向运动,如图所示。
则( )A .甲、乙两物块在弹簧压缩过程中,由于弹力作用,动量不守恒 B .当两物块相距最近时,甲物块的速率为零C .当甲物块的速率为1m/s 时,乙物块的速率可能为2m/s ,也可能为0D .甲物块的速率可能达到5m/s例6、如图所示,光滑的水平面上有m A =2kg ,m B = m C =1kg 的三个物体,用轻弹簧将A 与B 连接.在A 、C 两边用力使三个物体靠近,A 、B 间的弹簧被压缩,此过程外力做功72 J ,然后从静止开始释放,求:(1)当物体B 与C 分离时,B 对C 做的功有多少?(2)当弹簧再次恢复到原长时,A 、B 的速度各是多大?例7、如图所示,光滑水平地面上静止放置两由弹簧相连木块A 和B,一质量为m 子弹,以速度v 0,水平击中木块A,并留在其中,A 的质量为3m,B 的质量为4m.(1)求弹簧第一次最短时的弹性势能(2)何时B 的速度最大,最大速度是多少?4、碰撞、爆炸、反冲Ⅰ、碰撞分类(两物体相互作用,且均设系统合外力为零)(1)按碰撞前后系统的动能损失分类,碰撞可分为弹性碰撞、非弹性碰撞和完全非弹性碰撞. (2)弹性碰撞前后系统动能相等.其基本方程为① m 1v 1+m 2v 2=m 1 v 1'+m 2 v 2' ②222211222211'21'212121v m v m v m v m +=+ . (3)A 、B 两物体发生弹性碰撞,设碰前A 初速度为v 0,B 静止,则基本方程为 ① m A v 0=m A v A +m B v B ,②2220212121BB A A A v m v m v m += 可解出碰后速度0v m m m m v B A B A A +-=,C B Amv oBAv B =02v m m m BA A+.若m A =m B ,则v A = 0 ,v B = v 0 ,即质量相等的两物体发生弹性碰撞的前后,两物体速度互相交换(这一结论也适用于B 初速度不为零时).(4)完全非弹性碰撞有两个主要特征.①碰撞过程中系统的动能损失最大.②碰后两物体速度相等. Ⅱ、形变与恢复(1)在弹性形变增大的过程中,系统中两物体的总动能减小,弹性势能增大,在形变减小(恢复)的过程中,系统的弹性势能减小,总动能增大.在系统形变量最大时,两物体速度相等.(2)若形变不能完全恢复,则相互作用过程中产生的内能增量等于系统的机械能损失. Ⅲ、反冲(1)物体向同一方向抛出(冲出)一部分时(通常一小部分),剩余部分将获得相反方向的动量增量,这一过程称为反冲.(2)若所受合外力为零或合外力的冲量可以忽略,则反冲过程动量守恒.反冲运动中,物体的动能不断增大,这是因为有其他形式能转化为动能.例如火箭运动中,是气体燃烧释放的化学能转化为火箭和喷出气体的动能.例8、一个不稳定的原子核质量为M ,处于静止状态,放出一个质量为m 的粒子后反冲。
动量守恒定律的典型模型及其应用知识讲解

• (2)碰后B后退的最大距离是多少?
碰撞中弹簧模型 P215 第12 高考模拟2.
P215 新题快递. • 在一个足够大的光滑平面内,有两质量相同的木
块A、B,中间用一轻质弹簧相连.如图所示.用一 水平恒力F拉B,A、B一起经过一定时间的匀加速 直线运动后撤去力F.撤去力F后,A、B两物体的情 况足( ). • (A)在任意时刻,A、B两物体的加速度大小相等 • (B)弹簧伸长到最长时,A、B的动量相等 • (C)弹簧恢复原长时,A、B的动量相等 • (D)弹簧压缩到最短时,系统的总动能最小
ABD
• 图中,轻弹簧的一端固定,另一端与滑块B相连,B静 止在水平直导轨上,弹簧处在原长状态。另一质量与B 相同滑块A,从导轨上的P点以某一初速度向B滑行,当 A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B
紧贴在一起运动,但互不粘连。已知最后A恰好返回出
发点P并停止,滑块A和B与导轨的滑动摩擦因数都为
AC
(A)ΔpA=-3kg·m/s,
ΔpB=3 kg·m/s.
图2
(B)ΔpA=4kg·m/s,
ΔpB=-4 kg·m/s.
(C)ΔpA=-5 kg·m/s, ΔpB=5 kg·m/ s.
• 如图所示,半径和动能都相等的两个小球 相向而行,甲球质量m甲大于乙球质量
• m乙,水平面是光滑的,两球做对心碰撞 以后的运动情况可能是下述哪些情况?
2 特例:质量相等的两物体发生弹性正碰
v1
m1 m2 v10 2m2v20 m1 m2
v2
m2 m1 v20 2m1v10 m1 m2
碰后实现动量和动能的全部转移 (即交换了速度)
动量守恒中几种常见的模型

模型四:
带弹簧的木板与滑块模型
如图所示,坡道顶端距水平面高度为h,质量为m1的小物块 A从坡道顶端由静止滑下,进入水平面上的滑道时无机械能 损失,为使A制动,将轻弹簧的一端固定在水平滑道延长线 M处的墙上,另一端与质量为m2的档板B相连,弹簧处于原 长时,B恰位于滑道的末端O点.A与B碰撞时间极短,碰后 结合在一起共同压缩弹簧,已知在OM段A、B与水平面间的 动摩擦因数均为μ,其余各处的摩擦不计,重力加速度为g, 求: (1)物块A在与挡板B碰撞前瞬间速度v的大小; (2)弹簧最大压缩量为d时的弹性势能Ep(设弹簧处于原长 时弹性势能为零).
解:当人从船头走到船尾的过程中,人和船组成的系统都
在水平方向上不受力的作用,故系统水平方向动量守恒。
设某时刻人对地的速度为V2,船对地的速度为V1,则
mV2-MV1=0,即
V1 M V2 m
在人从船头走到船尾的过程中每一时刻系统的动量均守恒, 故mV2t-MV1t=0,即 m所s以2-Ms1 s1m=m0LM,而, ss21+msM2=LML。,
从AB碰撞到弹簧压缩最短过程:
1 2
m1
m2
v'2
Ep
W
代入数据得:Ep m12 gh μm1 m2gd
m1 m2
思考:如果题目让你求解整个系统所产生的热量和压缩 弹簧过程产生的热量,又该怎么求?
规律总结:带弹簧的木板与滑块的模型,可以分为三 个过程:A物体下滑过程,遵循的是机械能守恒定律或 动能定理; A物体碰撞B物体过程,由于内力远大于外力,遵循动 量守恒定律; A、B压缩弹簧的过程,又遵循能量守恒定律(摩擦力 做功,机械能不守恒),分清物理过程,应用物理规 律建立方程,是解决这类问题的关键。
动量守恒定律的典型模型及其应用+课件

动能损失为
E=12m1v12012m2v22012 m1m2v2
m1m1
2m1 m2
v10v20 2
解决碰撞问题须同时遵守的三个原则:
一. 系统动量守恒原则
二. 能量不增加的原则
三. 物理情景可行性原则
例如: 追赶碰撞:
碰撞前: V追赶 V被追
碰撞后:
在前面运动的物体的速度一定不 小于在后面运动的物体的速度
2 特例: 质量相等的两物体发生弹性正碰
v1
m1 m2 v10 2m2v20 m1 m2
v2
m2 m1 v20 2m1v10 m1 m2
碰后实现动量和动能的全部转移 (即交换了速度) 第219页2题
完全非弹性碰撞
碰撞后系统以相同的速度运动 v1=v2=v 动量守恒:
m 1 v 1 0 m 2 v 2 0 m 1 m 2 v
ABD
• 图中,轻弹簧的一端固定,另一端与滑块B相连,B静 止在水平直导轨上,弹簧处在原长状态。另一质量与B 相同滑块A,从导轨上的P点以某一初速度向B滑行,当 A滑过距离l1时,与B相碰,碰撞时间极短,碰后A.B紧
贴在一起运动,但互不粘连。已知最后A恰好返回出发
点P并停止,滑块A和B与导轨的滑动摩擦因数都为
高三物理重点专题
动量守恒定律的典型模型 及其应用
动量守恒定律的典型应用 几个模型:
(一)碰撞中动量守恒 (二)反冲运动、爆炸模型
(三)子弹打木块类的问题:
(四)人船模型: 平均动量守恒
• (1)在弹性形变增大的过程中,系统中两物 体的总动能减小,弹性势能增大,在系统形变 量最大时,两物体速度相等. 在形变减小(恢 复)的过程中,系统的弹性势能减小,总动能 增大.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
恒,ΔEK=Q = f 滑d相对
类似题型
如图所示,把质量m=20kg的物体以水平速度v0=5m/s抛上 静止在水平地面的平板小车的左端。小车质量M=80kg,已知 物体与平板间的动摩擦因数μ=0.8,小车与地面间的摩擦可忽略 不计,g取10m/s2,求:(1)要物块不从小车上掉下,小车至 少多长?(2)物体相对小车静止时,物体和小车相对地面的 加速度各是多大?
v0
分析:第一问即是在它们有共同速度时的,发生的相对位移d 必须得小于小车的长度 第二问:由动量守恒定律即可求得
模型3:人船模型
例:静止在水面上的小船长为L,质量为M,在 船的最右端站有一质量为m的人,不计水的阻力, 当人从最右端走到最左端的过程中,小船移动的 距离是多大?
S2
S1
m M
S2
S1
条件: 系统动量守衡且系统初动量为零.
处理方法: 利用系统动量守衡的瞬时性和物体间作用的
等时性,求解每个物体的对地位移.
m v1 = M v2
m v1 t = M v2 t
m s1 = M s2
---------------- ①
s1 + s2 = L
-----------②
结论: 人船对地位移为将二者相对位移按质量反比分配关系
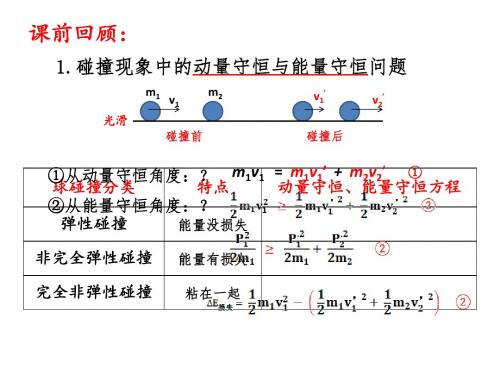
动量守恒定律在碰撞中的应用
——几种常见模型分析
一、几种常见的动量守恒模型:
1、碰撞类 2、子弹打木块类 3、人船模型类 4、弹簧类
模型2:子弹打击木块
子弹打木块实际上是一种完全非弹性碰撞。作为一个典型 ,它的特点是:子弹以水平速度射向原来静止的木块,并留在 木块中跟木块共同运动。
如图所示,质量为 m 的子弹以初速度 v0射向静止在光滑水 平面上的质量为 M 的木块,并留在木块中不再射出,子弹钻入 木块深度为 d.求木块与子弹相对静止时的速度,木块对子弹的
m1v1=m2v2 则:m1s1= m2s2 2、此结论与人在船上行走的速度大小无关。不论
是匀速行走还是变速行走,甚至往返行走,只要 人最终到达船的左端,那么结论都是相同的。
3、人船模型的适用条件是:两个物体组成的 系统动量守恒,系统的合动量为零。
类似题型
练习:载人气球原静止在高度为H的高空,气球的质 量为M,人的质量为m,现人要沿气球上的软绳梯滑 至地面,则绳梯至少要多长?
两边同乘时间t,ml1=Ml2,
而l 1+l 2=L,
∴
l2
mL Mm
l2 l1
应该注意到:此结论与人在船上行走的速度大小无关。不
论是匀速行走还是变速行走,甚至往返行走,只要人最终 到达船的左端,那么结论都是相同的。
总结:人船模型
1、“人船模型”是动量守恒定律的拓展应用, 它把速度和质量的关系推广到质量和位移 的关系。即:
练习:如图所示,质量为m的小物体B连着轻弹 簧静止于光滑水平面上,质量为2m的小物体A 以速度v0向右运动,则 当弹簧被压缩到最短时,弹性势能Ep为多大?
A V0
B
二、碰撞问题的典型应用总结
相互作用的两个物体在很多情况下,皆可 当作碰撞处理,那么对相互作用中两个物 体相距恰“最近”、相距恰“最远”或恰 上升到“最高点”等一类临界问题,求解 的关键都是“速度相等”。
平均阻力的大小和该过程中木块前进的距离.
解析:子弹和木块最后共同运动,相当于完全非弹性碰撞. 从动量的角度看,子弹射入木块过程中系统动量守恒: mv0=(M+m)v 从能量的角度看,该过程系统损失的动能全部转化为系统 的内能.设平均阻力大小为 f,设子弹、木块的位移大小分别为 s1、s2,如图 1-3-5 所示,显然有 s1-s2=d 对子弹用动能定理:fs1=12mv20-12mv2① 对木块用动能定理:fs2=12Mv2②
(2)物体A以速度V0滑到静止在光滑 水平面上的小车B上,当A在B上滑行的 距离最远时,A、B相对静止, A、B两 物体的速度必相等。
A V0 B
课堂练习
质量为M的木板静止在光滑的水平面上, 一质量为m的木块(可视为质点)以初速度 V0向右滑上木板,木板与木块间的动摩擦 因数为μ ,求:木板的最大速度?
s人
M mM
L
m s船 mM L
练习: 质量为m的人站在质量为M,长为L的静止小船 的右端,小船的左端靠在岸边。当他向左走到船的左端 时,船左端离岸多远?
解:先画出示意图。人、船系统动量守恒,总动
量始终为零,所以人、船动量大小始终相等。从
图中可以看出,人、船的位移大小之和等于L。
设人、船位移大小分别为l1、l2 ,则:mv1=Mv2,
m V0 M
(3)质量为M的滑块静止在光滑水平面
上,滑块的光滑弧面底部与桌面相切,一 质量为M的小球以速度V0向滑块滚来,设 小球不能越过滑块,则小球到达滑块上的
最高点时(即小球的竖直向上速度为零), 两物体的速度肯定相等。
课堂练习
如图所示,质量为M的滑块静止在光滑的水平 桌面上,滑块的光滑弧面底部与桌面相切,一个 质量为m的小球以速度v0向滑块滚来,设小球不 能越过滑块,则小球到达最高点时,小球与滑块 的速度各是多少?
①、②相减得:
fd=12mv20-12(M+m)v2=2MM+mmv20③
即 f=2dMMm+v20m s2=12Mv2/f=Mm+dm.
从能量角度分析:损失 的动能转化为内能
所以:Q=f阻力d相对
练习:子弹以一定的初速度射入放在光滑水平面上的 木块中,并共同运动下列说法中正确的是:(ACD) A、子弹克服阻力做的功等于木块动能的增加与摩
(1)光滑水平面上的A物体以速度V0去撞 击静止的B物体,A、B物体相距最近时,两 物体速度必相等(此时弹簧最短,其压缩量最 大)。
课堂练习
质量均为2kg的物体A、B,在B物体上 固定一轻弹簧,则A以速度6m/s碰上弹簧并 和速度为3m/s的B相碰,则碰撞中AB相距最 近时AB的速度为多少?弹簧获得的最大弹 性势能为多少?
擦生的热的总和 B、木块对子弹做功的绝对值等于子弹对木块做的功 C、木块对子弹的冲量大小等于子弹对木块的冲量 D、系统损失的机械能等于子弹损失的动能和子弹
对木块所做的功的差
总结:子弹打木块的模型
1.运动性质:子弹对地在滑动摩擦力作用下匀减
速直线运动;木块在滑动摩擦力作用下做匀加速 运动。
2.符合的规律:子弹和木块组成的系统动量守恒, 机械能不守恒。
S
H
H
模型4:弹簧模型 思考
水 (1)何时两物体相距最近,即弹簧最短
平
Nv
N
面 光
F弹
F弹
滑, 弹
G
G
簧
两物体速度相等时弹簧最短,且损失的动能
ቤተ መጻሕፍቲ ባይዱ
开
转化为弹性势能
始 (2)何时两物体相距最近,即弹簧最短
时
v
处
于
原
长
两物体速度相等时弹簧最长,且损失的动能
转化为弹性势能
弹簧弹力联系的“两体模型”
注意:状态的把握 由于弹簧的弹力随形变量变化,所以弹 簧弹力联系的“两体模型”一般都是作加速 度变化的复杂运动,所以通常需要用“动量 关系”和“能量关系”分析求解。复杂的运 动过程不容易明确,特殊的状态必须把握: 弹簧最长(短)时两体的速度相同;弹簧自 由时两体的速度最大(小)。
