2理论力学---第七章刚体的简单运动
理论力学刚体运动

Ek ( t ) Ek ( t0 ) A外
§6.2 作用在刚体上的力系 一、力系
1、定义:同时作用在一个刚体的一组力称为力系。
2、分类: ①共面力系:所有的力位于同一平面内。 a) 共点力系(汇交力系):所有力的作用线交 于一点的力系。 b) 平行力系:所有力互相平行或反平行。 ②异面力系:力的作用线不在一个平面内。
二、力系等效
1、等效力系的定义 如果在两个力系作用下,刚体的运动相同,则这 两个力系互为等效力系。
2、力系的等效条件:
F1i F2 j
r1i F1i r1 j F1 j
i j
i
j
3、零力系:力系力的矢量和为零,对固定参考点 的力矩和为零的力系。 说明:①所有的零力系都等效 ②任何力系加上零力系后与原力系等效 ③最简单的零力系是一对平衡力组成的力系
2
角动量定理: dL dt
M外
2、平衡条件: Fi 0,
i
且 Mi 0
i
(对任一定点成立)
例 质量为 m ,长为 a 的匀质杆 AB 由系于两端长是 a 的线悬于 O 点,在 B 端挂质量为 m 的重物。求平衡 时杆与水平方向的夹角θ及每根线中的张力 TA 和 TB 。
2、异面力系: 等效于一个单力与一个力偶
z -F3 A F1
F F3
O
x
B F2
y
§6.3 刚体的平衡
刚体运动 平动: 直线平动、曲线平动
转动: 定轴转动、一般转动 平动:运动过程中刚体任一直线的方向保持不变。
转动:刚体上一直线相对参考系的角度发生变化。
O
刚体的一般运动(n=6)
O
《理论力学》课程教学大纲72

《理论⼒学》课程教学⼤纲72《理论⼒学》课程教学⼤纲⼀、课程的基本情况课程中⽂名称:理论⼒学课程英⽂名称:Theoretical Mechanics课程代码:0701017课程类别:专业基础课课程性质:必修课总学时:72 讲课学时:72 实验学时:0课程学分:4授课对象:机械类及相近专业本科学⽣前导课程:⾼等数学⼆、教学⽬的理论⼒学为⼯程类学科的基础课程之⼀。
理论⼒学教育不仅可以培养学⽣的⼒学素质,⽽且可以加强学⽣的⼯程概念。
这对于他们向其他学科或其他⼯程领域扩展是很有利的。
是相关专业后续课程的理论和设计以及⼯程设计规范的基础。
通过理论⼒学的学习可以使学⽣了解刚体的特性及其研究⽅法;了解理论⼒学基本理论以及在⼯程实际中的应⽤;了解理论⼒学与其他相关课程的联系。
三、教学基本要求绪论0.1理论⼒学的研究对象0.2理论⼒学的发展简史0.3理论⼒学的内容和研究⽅法0.4理论⼒学的应⽤及和其他学科的关系基本要求:1.了解理论⼒学的研究对象和内容。
2.了解理论⼒学与其他课程的关系。
3.了解理论⼒学在各个不同领域的应⽤。
重点与难点:1.理论⼒学的内容和研究⽅法。
第⼀部分静⼒学第1章静⼒学公理和物体的受⼒分析1.1静⼒学公理1.2约束和约束⼒1.3物体的受⼒分析和受⼒图基本要求:1.深⼊地理解⼒、刚体、平衡和约束等重要概念,深⼊理解⼒的基本性质。
2.明确基本约束的特征,正确地对物体系统进⾏受⼒分析。
重点与难点:1.约束和物体系的受⼒分析。
2.物体系统的受⼒分析和受⼒图。
第2章平⾯汇交⼒系与平⾯⼒偶系2.1平⾯汇交⼒系合成与平衡⼏何法2.2平⾯汇交⼒系合成与平衡的解析法2.2平⾯⼒对点之矩概念及计算2.3平⾯⼒偶基本要求:1.清晰的理解汇交⼒系和⼒偶系的合成。
2.熟练解汇交⼒系的平衡问题。
3.清晰的理解⼒对点的矩,并能熟练的计算。
4.深⼊理解⼒偶和⼒偶矩的概念。
明确⼒偶的性质和⼒偶的等效条件。
重点与难点:1.汇交⼒系的平衡⽅程。
理论力学填空选择

第一章 静力学公理和物体的受力分析一、是非判断题1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ) 1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( ) 1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( ) 1.4 力的可传性只适用于刚体,不适用于变形体。
( ) 1.5 两点受力的构件都是二力杆。
( )1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( ) 1.7 力的平行四边形法则只适用于刚体。
( ) 1.8 凡矢量都可以应用平行四边形法则合成。
( ) 1.9 只要物体平衡,都能应用加减平衡力系公理。
( ) 1.10 凡是平衡力系,它的作用效果都等于零。
( ) 1.11 合力总是比分力大。
( ) 1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( ) 1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ) 1.14 当软绳受两个等值反向的压力时,可以平衡。
( ) 1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ) 1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
1.17 凡是两端用铰链连接的直杆都是二力杆。
( )1.18 如图所示三铰拱,受力F ,F 1作用, 其中F 作用于铰C 的销子上,则AC 、 BC 构件都不是二力构件。
( )二、填空题1.1 力对物体的作用效应一般分为 效应和 效应。
1.2 对非自由体的运动所预加的限制条件称为 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 ;约束力由 力引起,且随 力的改变而改变。
1.3 图示三铰拱架中,若将作用于构件AC 上的力偶M处的约束力 。
A. 都不变;B. 只有C 处的不改变;C. 都改变;D. 只有C 处的改变。
第二章 一、 是非判断题1.1当刚体受三个不平行的力作用时,只要这三个力的作用线汇交于同一点,则刚体一定处于平衡状态。
理论力学7—刚体的平面运动

A
[vB ]AB [v A ]AB
平面图形上任意两点的速度在其连线上的投影( 大小和方向)相等。这就是速度投影定理。
例7-3 用速度投影定理解例1。 解:由速度投影定理得 vB
[vB ]AB [v A ]AB
B
vA cos30 vB cos60
解得
30°
vA
A
vB 10 3 cm s
0
O
I
vCA与vA方向一致且相等, 点C的速度
vC vA vCA 2vA
7.2 平面图形上各点的速度
7.2.2 投影法
vB v A vBA
vBA
vB vA
B
将两边同时向AB方向投影:
[vB ]AAB,因 此[vBA]AB=0。于是
M
x
xO f1 (t ), yO f2 (t ), f3 (t )
这就是刚体的平面运动方程。
运动分解
y S O' O M
x
如果O'位置不动,则平面图形此时绕轴O'做定 轴转动; 如果O'M方位不变,则平面图形做平移。因此刚 体的平面运动包含了平移和定轴转动两种情况。 但能不能说平移和定轴转动是刚体平面运动的特 殊情况呢? 不能!
M
7.1 刚体平面运动的描述 而垂直于图形S的任 一 条 直 线 A1A2 必 然 作平移。 A1A2 的 运 动 可 用 其与图形S的交 点A的运动来代 替。无数的点A 构成了平面S。
A1 N A S
A2
M
因此,刚体的平面运动可以简化为平面图 形S在其自身平面内的运动。
刚体的平面运动方程 平面图形S在其平面上的位 y 置完全可由图形内任意线段 S O'M的位置来确定,而要确 定此线段的位置,只需确定 O' 线段上任一点O'的位置和线 段O'M与固定坐标轴Ox间的 O 夹角 即可。点O'的坐标和 角 都是时间t的函数,即
07-理论力学-第二部分运动学第七章点的合成运动

运动学/点的合成运动
动 点: AB杆上的A点 动 系: 凸轮 定 系: 地面 绝对运动: 直线 相对运动:曲线(圆弧) 牵连运动: 直线平移
1616
运动学/点的合成运动
动 点:A(在AB杆上) 动 系:偏心轮C 定 系: 地面 绝对运动:直线 相对运动:圆周(C) 牵连运动: 定轴转动
22
运动学/点的合成运动
另一方面,在实际问题中,不仅要在固联在地面上 的参考系上还要在相对于地面运动着的参考系上观察和 研究物体的运动。下面先看几个例子。
33
运动学/点的合成运动
44
55
本章将用点的合成运动的方法来研究这类问题。 66
第七章 点的合成运动
§7-1 §7-2 §7-3
§7-4
r 2
r 2
r2
l2
r2
l 2(
) 3030
运动学/点的合成运动
例4 圆盘凸轮机构
已知:OC=e ,R 3e ,(匀角速度),图示瞬时, OCCA,且O,A,B三点共线。求:从动杆AB的速度。
解:选取动点:AB 上的A点
动系:圆盘
绝对运动:直线 相对运动:圆周
由
定系:基座 va
牵连运动:定轴 ve vr
▼动点相对动系、定系必须 有运动,不能和动系在同一 物体上。
▼以上可归结为一点、两系 、三运动。
2020
运动学/点的合成运动
四、 运动方程及坐标变换 可以利用坐标变换来建立绝对、
相对和牵连运动之间的关系。
以二维问题为例。设定系 ,
动系
。动点M,如图所示。
(1)绝对运动方程: x x(t), y y(t)
大小 ? OA
刚体的简单运动—刚体绕定轴的转动(理论力学)

主轴转动两圈后停止 0
2 02 2
0 10π2 2 4π
负号表示 的转向与主轴转动方向相反,故为减速运动。
小结
1.刚体绕定轴转动 刚体运动时,有上或其扩展部分有两点保持不动,这种运动
为刚体的绕定轴转动。通过两点的直线称为转轴,不在转轴上 的各点都在垂直于转轴的平面内做圆周运动。
2.角速度
三、定轴转动的角速度和角加速度
1、角速度
lim
Δt 0
Δ Δt
d
dt
代数量 正负与转角相同
若已知转动方程 f (t)
f (t)
刚体转动的快慢和方向 单位为 rad/s
2、角加速度
设当t 时刻为 , t +△t 时刻为 +△
角加速度
lim
t 0
t
d
dt
d2
dt2
f (t)
表征角速度变化的快慢 单位:rad/s2 (代数量)
§6-2 刚体绕定轴的转动
一、刚体绕定轴转动
刚体运动时,其上或其扩展部分有两点保持不动, 这种运动为刚体的绕定轴转动。通过两点的直线称为 转轴,不在转轴上的各点都在垂直于转轴的平面内做 圆周运动。
二、转角和转动方程
____ 转角,单位弧度(rad)
=f(t)
转动方程
方向规定: 从Z轴正向看
逆时针为正
f (t) 刚体转动的快慢和方向 单位为 rad/s (代数量)
3.角加速度
f (t)
如果与同号,则转动是加速的;如果与异号,则转动是减
速的。
如果与同号,则转动是加速的; 如果与异号,则转动是减速的。
与同号,转动加速
与异号,转动减速
O
理论力学重难点及相应题解

运动学部分:一、点的运动学重点难点分析1.重点:点的运动的基本概念(速度与加速度,切向加速度和法向加速度的物理意义等);选择坐标系,建立运动方程,求速度、加速度。
求点的运动轨迹。
2.难点:运动方程的建立。
解题指导:1.第一类问题(求导):建立运动方程然后求导。
若已知点的运动轨迹,且方程易于写出时,一般用自然法,否则用直角坐标法。
根据点的运动性质选取相应的坐标系,对于自然法要确定坐标原点和正向。
不管用哪种方法,注意将点置于一般位置,而不能置于特殊位置。
根据运动条件和几何关系把点的坐标表示为与时间有关的几何参数的函数,即可得点的运动方程。
2.第二类问题(积分):由加速度和初始条件求运动方程,即积分并确定积分常数。
二、刚体的简单运动重点难点分析:1.重点:刚体平移、定轴转动基本概念;刚体运动方程,刚体上任一点的速度和加速度。
2.难点:曲线平移。
解题指导:首先正确判断刚体运动的性质。
其后的分析与点的运动分析一样分两类问题进行。
建立刚体运动方程时,应将刚体置于一般位置。
三、点的合成运动(重要)重点难点分析:1.重点:动点和动系的选择;三种运动的分析。
速度合成与加速度合成定理的运用。
2.难点:动点和动系的选择。
解题指导:1.动点的选择、动系的确定和三种运动的分析常常是同时进行的,不可能按顺序完全分开。
2.常见的运动学问题中动点和动系的选择大致可分以下五类:(1)两个(或多个)不坟大小的物体独立运动,(如飞机、海上的船舶等)对该类问题,可根据情况任选一个物体为动点,而将动系建立在另一个物体上。
由于不考虑物体的大小,因此动系(刚体)与物体(点)只在一个点上连接,可视为铰接,建立的是平移动坐标系。
(2)一个小物体(点)相对一个大物体(刚体)运动,此时选小物体为动点,动系建立在大物体上。
(3)两个物体通过接触而产生运动关系。
其中一个物体的接触只发生在一个点上,而另一个物体的接触只发生在一条线上。
选动点为前一物体的接触点,动系则建立在后一物体上。
理论力学第7章 刚体平面运动

基础部分——运动学第7 章刚体平面运动连杆作什么运动呢?行星齿轮机构行星轮作什么运动?第7章刚体平面运动运动过程中,刚体上任一点到某一固定平面的距离保持不变刚体上任一点都在与某一固定平面平行的平面内运动沿直线轨道滚动的车轮机械臂小臂的运动平面运动的刚体在自身平面内运动的平面图形SxyOxyOASIIxyOA SII平面图形上任一线段的位置位置x Ay AϕB )(1t f x A =)(2t f y A =)(3t f =ϕ平面运动平移+ 转动xyOASIIxAyAϕB基点⇒O ′O O ′O O ′O′三种运动?平面运动基点平移基点转动注意:平移动系不一定固结与某一实际刚不一定固结与某一实际刚体。
O ′xyO平移动系O'x'y'x ′y ′O ′基点推广结论:刚体的平面运动可以分解为随基点的平移和绕基点的转动问题一:x yOA SIIx Ay AϕB问题二:随基点的平移与基点的选择有无关系绕基点的转动与基点的选择有无关系结论:同一瞬时平面图形绕任一基点转动的ω、α都相同。
动点re a 点的速度合成定理SAv ωABB v A v ?=B v x ′y ′基点BA v 三种运动?大小? 方向?BAA B v v v +=AωA Av BAv Bv平面图形上任一点的速度等于基点的速度与该点随图形绕基点转动速度的矢量和。
SAv ωABAv BAv Bv BAA B v v v +=试一试:基点法作平面运动。
[例7-1] 曲柄—滑块机构解:转动。
r 3ABOωϕAv Bv BAv 基点大小方向?AvBA3ABOωϕAv B v BAv Av ABω转向?= v 滑块Bϕ大小方向A 32SAv ωAB Av BAv Bv 平面图形上任意两点的速度在该两点连线上的投影(大小和正负号)相等。
速度投影定理[][]ABA AB B v v =[]ABBA vr 3再分析例7-1ABOωϕAv Bv Bv解:请比较两种方法A 32如何解释这种现象?观察到了什么现象?[先看一照片]若选取速度为零的点作为基点,则求解速度问题•基点法•速度投影法优点:缺点:优点:缺点:SAv ωAv BAv Bv AA 为基点B有没有更好的方法呢?Aω0≠ω唯一存在AL ′证明:MAA M v v v +=SA v v MAv LMPωAv PA =∴0=⋅−=ωPA v v A P ∵该瞬时瞬时速度中心速度瞬心唯一性:瞬时性:不共线,故速度均不为零。
理论力学1-7章答案

习题7-1图Oυ(a)υυ(b)习题7-3图第7章 点的复合运动7-1 图示车A 沿半径R 的圆弧轨道运动,其速度为v A 。
车B 沿直线轨道行驶,其速度为v B 。
试问坐在车A 中的观察者所看到车B 的相对速度v B /A ,与坐在车B 中的观察者看到车A 的相对速度v A /B ,是否有B A A B //v v -=?(试用矢量三角形加以分析。
)答:B A A B //v v -≠1.以A 为动系,B 为动点,此时绝对运动:直线;相对运动:平面曲线;牵连运动:定轴转动。
为了定量举例,设R OB 3=,v v v B A ==,则v v 3e =∴ ⎩⎨⎧︒==6021/θv v A B2.以B 为动系,A 为动点。
牵连运动为:平移;绝对运动:圆周运动;相对运动:平面曲线。
此时⎪⎩⎪⎨⎧︒==4522/θv v B A ∴ B A A B //v v -≠7-3 图示记录装置中的鼓轮以等角速度0ω转动,鼓轮的半径为r 。
自动记录笔连接在沿铅垂方向并按)sin(1t a y ω=规律运动的构件上。
试求记录笔在纸带上所画曲线的方程。
解:t r x 0ω= (1) )sin(1t a y ω=(2)由(1)0ωr xt =代入(2),得)sin(01r xa y ωω=7-5 图示铰接四边形机构中,O 1A = O 2B = 100mm ,O 1O 2 = AB ,杆O 1A 以等角速度ω= 2rad/s 绕轴O 1转动。
AB 杆上有一套筒C ,此套筒与杆CD 相铰接,机构的各部件都在同一铅垂面内。
试求当ϕ= ︒60,CD 杆的速度和加速度。
解:1.动点:C (CD 上),动系:AB ,绝对:直线,相对:直线,牵连:平移。
2.r e a v v v +=(图a ) v e = v A01.02121.0cos e a =⨯⨯==ϕv v m/s (↑)3. r e a a a a +=(图b )4.021.022e =⨯==ωr a m/s 2 346.030cos e a =︒=a a m/s 2(↑)习题7-5图习题7-7图习题7-9图υ(a) (b)(a)7-7 图示瓦特离心调速器以角速度ω绕铅垂轴转动。
哈工大版理论力学复习题

理论力学复习题一、是非题1. 若一平面力系向A,B两点简化的结果相同,则其主矢为零主矩必定不为零。
2. 首尾相接构成一封闭力多边形的平面力系是平衡力系。
3. 力系的主矢和主矩都与简化中心的位置有关。
4. 当力系简化为合力偶时,主矩与简化中心的位置无关5.平面一般力系平衡的充要条件是力系的合力为零。
二、选择题1.将平面力系向平面内任意两点简化,所得的主矢相等,主矩也相等,且主矩不为零,则该力系简化的最后结果为------。
①一个力②一个力偶③平衡2.关于平面力系的主矢和主矩,以下表述中正确的是①主矢的大小、方向与简化中心无关②主矩的大小、转向一定与简化中心的选择有关③当平面力系对某点的主矩为零时,该力系向任何一点简化结果为一合力④当平面力系对某点的主矩不为零时,该力系向任一点简化的结果均不可能为一合力3.下列表述中正确的是①任何平面力系都具有三个独立的平衡方程式②任何平面力系只能列出三个平衡方程式③在平面力系的平衡方程式的基本形式中,两个投影轴必须相互垂直④平面力系如果平衡,该力系在任意选取的投影轴上投影的代数和必为零4. 图示的四个平面平衡结构中,属于静定结构的是三、填空1. 图示桁架。
已知力1p 、 和长度a 。
则杆1内力=_________; 杆2内力=_________; 杆3内力=_________。
2. 矩为M =10k N .m 的力偶作用在图示结构上。
若 a =1m ,不计各杆自重,则支座D 的约束力=_________,图示方向。
3. 一平面汇交力系的汇交点为A ,B为力系平面内的另一点,且满足方程。
若此力系不平衡,则力系简化为_________。
4.若一平面平行力系中的力与Y 轴不垂直,且满足方程0y F =∑。
若此力系不平衡,则力系简化为_________。
答案:一、1、×2、×3、×4、√5、×二、1、② 2、① 3、④ 4、③三、1、0、P 1、0 2、=10KN(--)(提示:先从CB 及绳处断开,以右部分为研究对象,以B 为矩心,列力矩方程,则D 处竖直方向力为零,再以整体为研究对象以A 为矩心,列力矩方程可求出D 处)3.过A 、B 两点的一个力4、一个力偶第三章 练习题一、是非题1.力对点之矩是定位矢量,力对轴之矩是代数量。
理论力学运动学知识点总结

理论力学运动学知识点总结第一篇:理论力学运动学知识点总结运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中,始终与它的最初位置平行,此种运动称为刚体平行移动,或平移。
·刚体作平移时,刚体内各点的轨迹形状完全相同,各点的轨迹可能是直线,也可能是曲线。
·刚体作平移时,在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
• 刚体运动时,其中有两点保持不动,此运动称为刚体绕定轴转动,或转动。
• 刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
• 角速度ω表示刚体转动快慢程度和转向,是代数量,以用矢量表示。
,当α与ω。
角速度也可• 角加速度表示角速度对时间的变化率,是代数量,同号时,刚体作匀加速转动;当α 与ω异号时,刚体作匀减速转动。
角加速度也可以用矢量表示。
• 绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系:。
速度、加速度的代数值为。
• 传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
• 绝对运动:动点相对于定参考系的运动;• 相对运动:动点相对于动参考系的运动;• 牵连运动:动参考系相对于定参考系的运动。
2.点的速度合成定理。
• 绝对速度:动点相对于定参考系运动的速度;• 相对速度:动点相对于动参考系运动的速度;• 牵连速度:动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
• 绝对加速度:动点相对于定参考系运动的加速度;• 相对加速度:动点相对于动参考系运动的加速度;• 牵连加速度:动参考系上与动点相重合的那一点相对于定参考系运动的加速度;• 科氏加速度:牵连运动为转动时,牵连运动和相对运动相互影响而出现的一项附加的加速度。
• 当动参考系作平移或 = 0,或与平行时,= 0。
刚体的简单运动—转动刚体内各点的速度和加速度(理论力学)
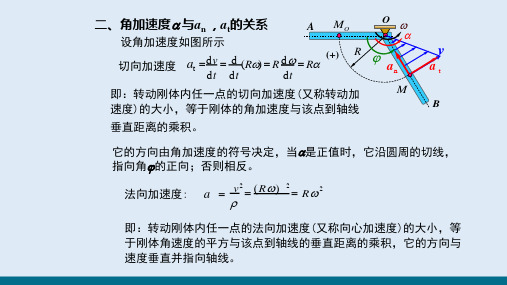
设角加速度如图所示
A MO
O
切向加速度 at dv d (R) R d R (+)
dt dt
dt
R
an
v
at
即:转动刚体内任一点的切向加速度(又称转动加 速度)的大小,等于刚体的角加速度与该点到轴线
M
B
垂直距离的乘积。
它的方向由角加速度的符号决定,当是正值时,它沿圆周的切线,
[例]半径R=0.2m的圆轮绕定轴O的转动方程 t 2 4t ,单位为弧度。 求t=1s时,轮缘上任一点M的速度和加速度。如在此轮缘上绕一柔软而不
可伸长的绳子并在绳端悬一物体A,求当t=1s时,物体A的速度和加速度。 解:圆轮在任一瞬时的角速度和角加速度为
d 2t 4
dt
d2 2
• ①滑轮3s内的转数; • ②重物B在3s内的行程;
• ③重物B在t=3s时的速度;
• ④滑轮边上C点在初瞬时的加速度;
• ⑤滑轮边上C点在t=3s时的加速度。
解:① 因为绳子不可以伸长,所以有
C aA 1m/s2
aCt 1 2 rad/s2
R 0.5
( )常数
vC
vA
1.5m /s, 0 vC
4.5m /s2
a (at )2 (an )2 12 4.52 4.61 m/s2
C
C
C
tan aCt 1 0.222, 12.5
aCn 4.5
⑤ t=3s 时,
at a
1m/s2,a n
R 2
2
0.5 9
40.5m/s2
a 12 40.52 40.51m/s2,tan 1 0.0247, 1.41 C
理论力学第7章(点的合成运动)

点的速度合成定理是瞬时矢量式,共包括大小‚方向
六个元素,已知任意四个元素,就能求出其他两个。 二、应用举例
[例] 桥式吊车 已知:小
车水平运行,速度为v平, 物块A相对小车垂直上升 的速度为v。求物块A的 运行速度。
解:选取动点: 物块A 动系: 小车 静系: 地面 相对运动: 直线; 相对速度vr =v 方向 牵连运动: 平动; 牵连速度ve=v平 方向 绝对运动: 曲线; 绝对速度va 的大小, 方向待求。
由速度合成定理 va= vr+ ve , 作出速度平行四边形 如图示。
v a v e tg 30 0 2 3 e 3 v AB 2 3 e ( ) 3
动点:AB杆上的A点 动系:偏心轮
绝对运动:直线 相对运动:圆周(曲线) 牵连运动:定轴转动
铰接四边形O1A=O2B=100mm, O1O2=AB,杆 O1A以等角速度 ω =2rad/s绕轴O1转动。 AB杆上有一套筒C,此套筒与杆CD相铰接 ,机构的各部件都在同一铅垂平面内。
)
[例3] 圆盘凸轮机构 已知:OC=e , R 3e , (匀角速度) 图示瞬时, OCCA 且 O、A、B三点共线。 求:从动杆AB的速度。
解:动点取直杆上A点,动系固结于圆盘, 静系固结于基座。 绝对速度 va = ? 待求,方向//AB 相对速度 vr = ? 未知,方向CA 牵连速度 ve =OA=2e , 方向 OA
y
O C
x
x
合成运动:相对某一参考体的运动可由相对于其它参考 体的几个运动组合而成,称这种运动为合成运动
动点:要研究的点
两个参考系: 一般把固定在地球上的坐标系称为静参考系; 用 Oxyz表示; 固定在相对地球运动的参考体上的坐标系称为动参考系; 用 Oxyz 表示。
理论力学07刚体的平面运动

\AB vBA / AB l /l ( )
22
速度投影法 研究AB, vA l ,
方向OA, vB方向沿BO直线
根据速度投影定理 vB AB vA AB
vA vB sin \vB vA / sin
l / sin 45o 2l()不能求出 AB
即若平面图形在运动过程中某瞬时的角速度等于零,则该瞬时
图形上任意两点的加速度在这两点连线上的投影相等.
26
加速度瞬心的确定.
将任一点加速度
和 aA,由方程
aA
分解为两个正交分量 aτA+anA
aAn
aB
aA
aBA
a
n BA
要使 aB 0 ,必须 aAn aBAn
a
A
a
BA
点A的加速度 aA 等值反向,其绝对加速度 aQ 0
Q点就称为图形在该瞬时的加速度瞬心.
[注] 一般情况下,加速度瞬心与速度瞬心不是同一个点. 一般情况下,对于加速度没有类似于速度投影定理的关
系式. 即一般情况下,图形上任意两点A, B的加速度
aA AB aB AB
若某瞬时图形 =0, 即瞬时平动, 则有 aAAB aB AB
指向与 转向一致.
根据速度合成定理 va ve vr , 则B点速度为:
vB vA vBA
13
即平面图形上任一点的速度等于基点的速度与该点随图形绕 基点转动的速度的矢量和.这种求解速度的方法称为基点法,
也称为合成法.它是求解平面图形内一点速度的基本方法.
二.速度投影法
由于A, B点是任意的,因此 vB vA vBA 表示了图形上任 意两点速度间的关系.由于恒有 vBAAB ,因此将上式在AB
07 刚体的简单运动Hxj

角位移
Δ d lim * lim Δt 0 Δt 0 Δt dt
说明: 角速度单位是rad/s,工程单位n rpm(r/min或转/分) 换算关系为:
2n n 0.105n rad/s 60 30
3、 角加速度 设当t 时刻为 , t +△t 时刻为+△ (1) 平均角加速度
R
0.4m/s
a
M t t 1
R
t 1
d 2 R 2 dt
t 1
d 2 t 2 4t R dt 2
t 1
v
0.4m / s 2
a
M n t 1
R
2 t 1
0.2 2 0.8m / s
2
2
A
aA
全加速度大小及方向
a a 2 a 2 0.4 2 0.82 0.894m/s2 t n t 1 t 1 2 t 1 arctan 2 arctan t 1 4
§7-1 刚体的平行移动
一、概念 刚体运动时,如果在刚体内任取一直线段,在运动过程中 该直线段始终与其最初位置平行,这种运动称为平行移动 (translation),简称平移或平动。
河南理工大学力学系
理论力学
第七章 刚体的简单运动
二、刚体平行移动的性质 设刚体作平行移动,如图。在刚 体内任取两点A和B,设其矢径分别为 rA和rB,则两条矢端曲线就是两点的轨 迹。由图中几何关系可知
1、 转动方程 Ⅰ和Ⅱ夹角 ---转角(位 置角),单位为弧度(rad)
• 定轴转动方程 对着z轴正向看
t
7 2
• 的正、负规定 逆为正 顺为负
理论力学7—刚体的平面运动2
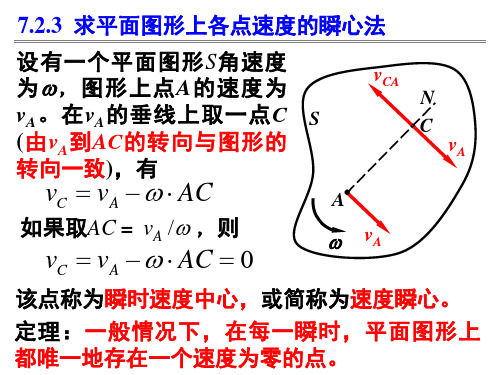
vC
vC C C 2 w BC
3 rw 3
习题7-12 图示小型精压机的传动机构,OA= O1B=r=0.1m,EB=BD=AD=l=0.4 m,在 图示瞬时OA⊥AD,O1B⊥ED,O1D在水平位 置,OD和EF在铅直位置。已知曲柄OA的转速 n=120 rpm,求此时压头F 的速度。
a C O r r
t
w
O
vO
n aCO
aO aO
aO r
vO r
aO
2
t aCO
C
aCO rw
n 2
r(
)
2
vO r
w
vO r
,
aO r
a C O a O , a C O vO / r
t n 2
取如图的投影轴, 将各矢量 投影到投影轴上得
y
aCx aO aCO 0
A2 A4
vA2
A1
v A 3 2 rw 2 v
2 rw 2v
例7-7 曲柄肘杆式压床如图。已知曲柄OA长r, 以匀角速度w 转动,AB = BC = BD = l,当曲柄 与水平线成30º 角时,连杆AB处于水平位置,而 肘杆DB与铅垂线也成30º 角。试求图示位置时, 杆AB、BC的角速度以及冲头C 的速度。 解:连杆AB作平面运动,瞬 D 30º 心在点C1,则
7.2.3 求平面图形上各点速度的瞬心法
设有一个平面图形S角速度 vCA 为 w ,图形上点A的速度为 N vA 。在vA 的垂线上取一点C S C (由vA 到AC的转向与图形的 vA 转向一致),有 vC v A w A C A 如果取AC= vA /w ,则 w vA vC v A w A C 0
理论力学习题册答案

第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)精选)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WA DBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame )a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体精选)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

解
设轮缘上任 1 点 M 的全加速度为 a,切向加速度 a t = rα ,法向加速度 a n = ω r ,如图
2
7-11b 所示。
tan θ =
把
α=
dω , θ = 60° 代入上式,得 dt
at α = 2 an ω
dω tan 60° = dt2
ω
分离变量后,两边积分:
∫ω
得
ω
0
dω
ω
2
=∫
⎤ ⎡ ⎥ ⎢ sin ω t 0 θ = tan −1 ⎢ ⎥ ⎢ h − cos ω 0 t ⎥ ⎥ ⎢ ⎦ ⎣r
故
50 π ⋅ 600 100π r ω1 = rad/s ⋅ = 100 − 5t 30 10 − 0.5t d dω 5 000 π d ⎛ 1 000π ⎞ α2 = 2 = ⎜ ⎟= dt dt ⎝ 100 − 5t ⎠ (100 − 5π )2
故得
h1 =
h4 = 2 mm 6
图 7-7
7-8 如图 7-8 所示,纸盘由厚度为 a 的纸条卷成,令纸盘的中心不动,而以等速 v 拉纸条。求 纸盘的角加速度(以半径 r 的函数表示) 。 解 纸盘作定轴转动,当纸盘转过 2π rad 时半径减小 a。设纸盘转过 dθ 角时半径增加 dr ,则
dθ =
y
B
t aB
α j
O
vA x
ω
(a) 图 7-12
aC
(b)
i 45° A n
C
t aC
解
由图 7-12b 得出
84
理论力学(第七版)课后题答案 哈工大.高等教育出版社
v A = 0.2 j m/s , v A = ω × Ri , ω × 0.1i = 0.200 j , ω = 2k ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.齿轮传动 1.外啮合
vC vD
C rC D rD
C D
rD rC
20
设C主动轮,D从动轮,
定义齿轮传动比
iCD
C D
rD rC
zD zC
iCD
C D
其中:
齿数Z 2r
t
21
2.内啮合 因为是做纯滚动(即没有相对滑动)
vF vE vF vE
F rF E rE
齿轮传动比
iEF
传动比:
i12
1 2
R2 R1
z2 z1
外:“-”, 内: “+”。
25
2、多级
V
n1
itota=l i1 i2 in
1 k 从动轮齿数(半径)乘积
主动轮齿数(半径)乘积
26
§7-5 角速度和角加速度的矢量表示
点的速度和加速度的矢量表示
一. 角速度和角加速度的矢量表示
按右手定则规定
α
a r
an v
v r
a r an v
29
三、v,a的矢积表示小结
引入 ω ωk,α k
而 v Rω r sin θ rωsin ω,r
v ωr
R
而 α r rsin θ R aτ
r
ωv ωRωsin90 Rω2 an
2
A
B
定义: 刚体上任一直线始终与初始位置平行。
1.水平曲线轨迹上行驶的火车箱是否平移? 否。
2.平移时,刚体上各点轨迹是平行直线,对吗? 不一定。可是平行曲线。
3
二.刚体平动时内部各点的轨迹、速度和加速度
rB
rA
rAB
vB
drB dt
d dt (rA
rAB)
drA dt
drAB dt
第七章 刚体的简单运动
§7–1 刚体的平行移动 §7–2 刚体的定轴转动 §7–3 转动刚体内各点的速度与加速度 §7–4 轮系的传动比 §7–5 以矢量表示角速度和角加速度
以矢积表示点的速度和加速度
1
§7-1刚体的平行移动(平动) 一.刚体平动的定义:
如果在物体内任取一条直线,在运动过程中这条直线 始终与它的最初位置平行,这种运动称为平行移动,简称 平动。
持不动-----称为刚体绕定轴的转动,简称刚体的转动。
不动的直线称为转轴。
7
定义: 定轴转动-----刚体运动时其上或其延展部分有一根不动直线。
1.指出下列物体是否作定轴转动?
轮 否。
是
R
车厢是
8
二.转角和转动方程
---转角,单位弧度(rad)
=f(t)---为转动方程 方向规定: 从z 轴正向看去,
r dt
r
又 d A av, A π r2 dt
d A d r av dr dt
即 2 πr d r av, d r av
dt
d t 2 πr
故
av2 2π r3
av
r
18
〔例7-3〕已知 O1A O2B 2 r, AB O1O2 ,ω0 常数 ,求两
轮边缘上点的加速度。
s R v Rω
aτ Rα
an
v2 R
Rω2
14
〔例7-1〕试画出图中刚体上M¸N两点在图示位置时的速度和
加速度。 (O1 AO2B,O1O2 AB)
α
15
α
16
〔例7-2〕 卷带盘。已知v=常数,带厚a,求α。
av
r
17
rω v
对该式求导
d r ω rα 0 dt
α 1ωdr , ω v
vA
(drAB 0) dt
同理:aB
d 2rB dt 2
d2 dt 2
(rA
rAB )
d 2rA dt 2
aA
∴ vA vB
aA aB
4
定理: 刚体平移时,其上各点轨迹形状相同且相互平行,
任一瞬时各点速度相同、各点加速度也相同。
因此,研究刚体的平动,可以归结为研究刚体内 任一点的运动。
5
1.已知 l, ,求vM ,aM ?
3.匀速转动和匀变速转动 当 =常数,为匀速转动;当α =常数,为匀变速转动。
常用公式
0 t
0
t
1t 2
2
与点的运动相类似。
11
§7-3 转动刚体内各点的速度和加速度
一、速度
S R
v dS R d
z
dt dt
v R
ω M0
sφ 各点速度分v布图M
v R
ω
二、加速度
a
dv dt
vA
A
0 aA
O1
a
vM 1
rM 1
2
B
O2
轮1平移
a1 aA
a1 2 rω02
又 vM vA vM 2 rω0
ω2 2ω0 2 ω2 0
a2 0,a2 a2n ,a2 r 2 ω0 2 4 rω02
19
§7-4 轮系的传动比
我们常见到在工程中,用一系列互相啮合的齿轮来实现变速, 它们变速的基本原理是什么呢?
, 的方向。
大小:| ||ddt |
方向如图 k
d
dt
d
dt
k
k
α α
27
二 刚体内任一点的线速度和线加速度的矢积表示
α v r
| r |rsin R
α
v R
28
a
dv dt
d
( r
dt
)
d
dt
r
ddrt
α a r v
a | r | r sin R
| an || v |vsin90o 2R
E F
rF rE
ZF ZE
22
二.皮带轮系传动
vA vB (而不是vA vB 方向不同 )
ArA BrB 皮带传动
i
AB
A B
rB rA
23
三.轮系的传动分级 1. 单级 (无滑动)
v
1
R1
R2 2
1 R1 2 R2 大小: 1 R2
2 R1 方向: 相反
24
v
1
2
R2
R1
方向: 相同
d dt
(R)
d
dt
R
R,
an
v2
(R)2
R
R
2
α
a R ∴ an R 2
αa
| a全 || an a | an2 a 2 R 2 4
ω
tg a R an 2R 2
各点加速度的分1布3 图
三. 公式小结: 转动方程 、角速度、角加速度
t
t t
点的运动
点在 转轴的平面内圆周运动
逆时针为正 顺时针为负
9
三、定轴转动的角速度和角加速度
1.角速度: 2.角加速度:
d
dt
d d 2
dt dt2
ω的单位: rad/s α 的单位:rad/s2
10
工程中常用单位:n = 转/分(r / min)
则n与的关系为:
2n n n (rad/s)
60 30 10
α与方向一致为加速转动, α与 方向相反为减速转动
l
A
M
vM vA l ,aM aA l 2。
2.图示瞬时AB杆中点M切向加速度为0,求 aM方向?
AB瞬时平移,vM vA , 铅直向上。
故 aM 向上,且为0, 故 aM 水平。
aM vM
B
vA
M
A
6
§7-2 刚体的定轴转动
一.刚体绕定轴转动的特征及其简化 当刚体运动时,刚体内某一直线上的所有各点始终保
