第1章静止电荷的电场(之二)
大学物理 第一章静止电荷的电场(必看)

q2d (A) 2 S 0
Байду номын сангаас
)。
q2d (B) S 0 q2d (D) S 0
q2 F Eq 2S 0
q2d (C) 2 S 0
d
d
q E 2 0 2S 0
q 2d A Fd 2S 0
量等于该闭合面内所包围的电荷代数和除以真空的
介电常数,数学表达式为
1 E ds
s
0 ( s面内)
q
典型电荷的电场
(1)点电荷
E
q 4 0 r
2
er
(2)半径为R 、带电量为Q均匀带电球面
E0
E Q 4 0 r
2
rR
er
rR
(3)均匀带电无限长直线
E 2 0 r
2 ES 2 xS
底面
E
x
0
0
d x 时: 2 q DS
2 ES DS
0
D E 2 0
例 题 15 15、如图所示,一无限长的均匀带电圆柱体,
体电荷密度为 ,截面半径为 R 。
求:
(1)柱内( r R )电场强度分布?
(2)柱外(r R)的电场强度分布?
直线中垂线的P点到带电直线中心o的距离
OP L
时,P点的电场强度大小。 解(1)
dE
E
L 2 L 2
y
L r ax 2
o
x
1 1 ( ) L 4 0 ( a x) 2 4 0 a a L 2
dq 4 0 r 2 dx
大学物理第一章 静电场

静止电荷的电场
本章是静电部分重点,主要讨 论如何描述电场,即从电荷在电场 中受力的角度建立电场强度的概念。 重点讨论用两种方法求场强分布。
1
一、基本概念
1. 电荷
(1) 种类 只有两种 (2) 电荷是量子化的(charge quantization ) 自然界物体所带电荷:q = ne (3) 电荷遵从守恒定律 (law of conservation of charge) (4) 电量是相对论不变量
dE
dq 4 o r
e 2 r
13
例2 均匀带电直线,带电量为q,长为L,
求空中任意一点P的场强。
解:
(1)取电荷元
q dq dl dl L
y
dq
(2)电荷元产生 元场强大小 1 dq dE 4 0 r 2
L
dl
r
o
x
P
14
dE
x
方向:与dq到场点的矢径 r
q 1 1 Ey 4 0 L x 2 ( L d )2 x2 d 2
式中:
x是场点到带电线的垂直距离
d 是垂足到直线下端点的距离(取绝对值)
17
(5)长直带电线周围任一点电场强度
大小:
E E E E E E
2 x 2 y 2 z 2 x
2. 数学表达式:
q1q2 F k 2 er r
er :
单位矢径
大小:等于1 方向:从施力电荷(场源) 指向受力电荷(场点) 3
1 k 8.988 1012 Nm 2 / c 2 4 o
o 8.8510 12 C 2 / Nm 2
高中选修3-1,2电与磁物理知识点

第一章、电 场一、电荷 :1、自然界中有且只有两种电荷:丝绸摩擦过的玻璃棒带正电,毛皮摩擦过的橡胶棒带负电。
电荷间的相互作用:同种电荷相互排斥,异种电荷相互吸引。
2、电荷守恒定律:电荷既不会创造,也不会消灭,只能从一个物体转移到另一个物体,或从物体的一个部分转移到另一个部分。
“起电”的三种方法:摩擦起电,接触起电,感应起电。
实质都是电子的转移引起:失去电子带正电,得到电子带等量负电。
3、电荷量Q :电荷的多少元电荷:带最小电荷量的电荷。
自然界中所有带电体带的电荷量都是元电荷的整数倍。
密立根油滴实验测出:e=1.6×10—19C 。
点电荷:与所研究的空间相比,不计大小与形状的带电体。
库仑定律:真空中两个点电荷之间相互作用的静电力,跟它们的电荷量的乘积成正比,跟它们的距离的平方成反比。
公式: k = 9×109 N ·m 2/C 2二、电场:1、电荷间的作用通过电场产生。
电场是一种客观存在的一种物质。
电场的基本性质是对放入其中的电荷有力的作用。
2、电场强度E :放入电场中的电荷所受电场力与它的电荷量q 的比。
E=F/q 单位:N/C 或V/mE 是电场的一种特性,只取决于电场本身,与F 、q 等无关。
普通电场场强点电荷周围电场场强匀强电场场强公式 E=F/qE=U/d 方向 与正电荷受电场力方向相同 与负电荷受电场力方向相反沿半径方向背离+Q 沿半径方向指向—Q由“+Q ”指向 “—Q ” 大小电场线越密,场强越大各处场强一样大3、电场线:形象描述场强大小与方向的线,实际上不存在。
疏密表示场强大小,切线方向表示场强方向。
一率从“+Q ”指向“—Q ”。
正试探电荷在电场中受电场力顺电场线,负电荷在电场中受电场力逆电场线。
电场线的轨迹不一定是带电粒子在电场中运动的轨迹。
只有电场线为直线,带电粒子初速度为零时,两条轨迹才重合。
任意两根电场线都不相交。
4、静电平衡时的导体净电荷只分布在外表面上,内部合场强处处为零。
第1章 真空中的静电场1 静电的基本现象和基本规律

(3)上面给出的库仑定律只适用于惯性体系中静止的 点电荷,存在相对运动时库仑定律要作小小的修改。 (4) 库仑定律是电学中的基本定律是整个电学的基础。 关于库仑定律的发现,请同学们参考有关书籍,阅后必然 受益不浅,很有启发。 (5) 平方反比律与光子静止质量是否为零有着密切关 系。
提问
通过回顾库仑定律的发现,你有什么体会?
k=
1 4πε 0
= 8.99 × 10 9 Nm 2 C − 2 ≈ 9.0 × 10 9 Nm 2 / C 2
在计算过程中,一般都将k当作一个常数处理,不是 这种形式也应凑成这种形式。 1 9 2 2
k= 4πε 0 ≈ 9.0 × 10 Nm / C
在CGSE制中, k=1。CGSE制仍然有人用,因为其公 式非常简洁。
下面看一个核反应的例子,β衰变的一般反应式:
A z
XN= Y
A z +1 N −1
+ e +ν e
−
其中 A:质量; Z:原子序数即电荷数; N:中子数; ν e : 为反电子中微子。
根据物质的电结构,我们可以更好地理解和掌握电 荷守恒定律。众所周知:
⎧ ⎧电子 ⎪ ⎪ ⎪原子⎨ 物质⎨ ⎪原子核 ⎪ ⎩ ⎪分子 ⎩ (带负电) ⎧质子 (带正电) ⎨ ⎩中子 (不带电)
(2) 库仑定律与万有引力定律
GM 1 M 2 0 F引 = − r12 2 r12
G:万有引力常数,数值 为6.67 ×10-11牛顿米2/千克2 或6.67×10-8达因厘米2/克2 “-”表示吸引力,在 F引 的 作用下,趋向于使r12减小 (因为M1和M2恒大于零)。
两者的相同之处在于:都是长程力,具有平方反比 的特征,且都满足牛顿第三定律; 不同之处: (a) 电荷有正有负,所以存在引力和斥力, 而质量恒 为正,只有引力而没有斥力。 (b) 静电力可以屏蔽,而万有引力却无法屏蔽。 (c) 静电力远大于引力。以电子和质子间的库仑力和 万有引力为例,可以得到F电/F引~2.3×1039,因此通常在 讨论原子、固体、液体的结构及化学作用时,只需考虑库 仑力,而忽略引力。
大学物理电磁学典型习题

部分习题解答第一章 静止电荷的电场1、10 解:(一定要有必要的文字说明)在圆环上与角度θ相应的点的附近取一长度dl ,其上电量 dq =λdl =0λsinθdl ,该电荷在O 点产生的场强的大小为==204RdqdE πε2004sin R dl πεθλθπελsin 400R =θd dE 的方向与θ有关,图中与电荷 dq 对O 点的径矢方向相反。
其沿两坐标轴方向的分量分别为 θθθπελθd RdE dE x cos sin 4cos 00-=-=θθπελθd RdE dE y 200sin 4sin -=-=整个圆环上电荷在圆心处产生的场强的两个分量分别为==⎰x x dE E R004πελ-⎰=πθθθ200cos sin d==⎰Y y dE E R004πελ-⎰-=πελθθ200024sin Rd 所以圆心处场强为 E = E y j = R004ελ-j 1、11 解:先将带电系统看成一个完整的均匀带电圆环计算场强,然后扣除空隙处电荷产生的场强;空隙的宽度与圆半径相比很小,可以把空隙处的电荷看成点电荷。
空隙宽度m d 2102-⨯=,圆半径m r 5.0=,塑料杆长m d r l 12.32=-=π 杆上线电荷密度m C lq/1019-⨯==λ 一个均匀带电圆环,由于电荷分布关于圆心对称,环上对称的二电荷元在圆心处产生的场强互相抵消,因而整个圆环在圆心处的场强E 1= 0 空隙处点电荷设为q /,则q / =d λ,他在圆心处产生的场强m V rdr q E /72.0442020/2===πελπε 方向由空隙指向圆心。
空隙处的电荷实际上不存在,因此圆心处场强等于均匀带电圆环在该点产生的场强与空隙处电荷在该点产生的场强之差,故m V E E E /72.021-=-= 负号表示场强方向从圆心指向空隙。
1、12 解:设想半圆形线CAD 与半圆形线ABC 构成一个圆形如图,且圆上线电荷密度均为λ。
《中学物理》第3册 电磁学 第1章 静电场—知识重点

《中学物理》第3册电磁学第1章静电场知识重点在“第1章静电场”是电学的基础,也是学生学习《中学物理》的难点内容。
本章的基础知识多、而且概念抽象,如:电场强度、电势、点电荷电场、匀强电场、电荷守恒定律、库仑定律、电力线、等势面、静电感应、电容器等。
一、库仑定律库仑定律:①大小:在真空中,2点电荷之间的作用力(F),与它们所带的电量(Q1)和(Q2)乘积成正比,与它们之间的距离平方(r2)成反比。
②方向:作用力的方向,在2点电荷之间的连线上。
③性质:同种电荷相斥,异种电荷相吸。
④公式:其中:F:电场力(库仑力)。
单位:牛顿(N)。
k:静电常数。
k = 9.0×109。
单位:牛顿·米2/库仑2 (N·m2 / C2)。
静电常数:在真空中2个相距为1米(m)、电荷量都为1库仑(C)的点电荷(Q1Q2)之间的相互作用力(F)为9.0×109牛顿(N)。
Q1Q2:2点电荷分别所带的电量。
单位:库仑(C)。
r:2点电荷之间的距离。
单位:米(m)。
注意:①库仑定律公式适用的条件:一是在真空中,或空气中。
二是静止的点电荷。
是指2个距离(r)足够大的体电荷。
②不能认为当r无限小时,F就无限大。
因为当r无限小时,2电荷已经失去了作为点电荷的前提。
③不用把表示正、负电荷的“+、-”符号,代入公式中进行计算。
可以用绝对值来计算。
计算的结果:可以根据电荷的正、负,来确定作用力为“引力/斥力”?以及作用力的方向。
④库仑力遵守牛顿第三定律。
2电荷之间是:作用力和反作用力。
(不要错误地认为:电荷量大的,对电荷量小的,作用力就大。
)附录:电量的单位:库仑(C)。
库仑(C):当流过某曲面的电流1安培时,每秒钟所通过的电量定义为1 库仑。
即:1 库仑(C)= 1 安培·秒(A·S)二、电场强度⒈电场强度①电场强度(E)为放入电场某一点的电荷,受到的电场的作用力(F),与它的电量(q)的比值。
【高中物理】高中物理(人教版)选修1-1同步教师用书:第1章-第2节-电场

二、电场学习目标知识脉络1.知道电场是客观存在的物质,认识电场.2.理解电场强度的概念,会用电场强度描述电场.(重点)3.知道电场线,了解电场线的特点.(重点)4.学会用电场线描述常见电场的分布.(难点、重点)电场和电场强度[先填空]1.电场(1)只要有电荷存在,电荷的周围就有电场.电荷间相互作用是通过电场实现的.(2)电场的基本性质是对放入其中的电荷有力的作用.(3)电场虽然看不见、摸不着,但它是客观存在的物质.2.试探电荷在电场中放入的电荷,它的电荷量要非常小,体积也要充分小.3.电场强度(1)定义:放入电场中某点的电荷,所受静电力F跟它的电荷量的比值,叫做该点的电场强度,简称场强.(2)公式:E=F q.(3)单位:牛每库(N/C).(4)方向:电场强度是矢量,不仅有大小,还有方向.物理学上规定:正电荷在电场中某点所受电场力的方向为该点场强的方向,负电荷受电场力的方向与该点场强的方向相反.(5)物理意义:电场强度是描述电场强弱和方向的物理量. [再判断]1.在电荷周围有电场,其是客观存在的.(√)2.如果把放入电场中某点的试探电荷取走,则那点的电场强度变为0.(×)3.电荷在电场中的受力方向就是该点的场强方向.(×)[后思考]1.两个相隔一定距离的电荷可以产生相互作用,电荷之间是通过什么来传递相互作用呢?【提示】 电荷之间是通过电场产生相互作用的.2.电场强度的方向就是电荷受力的方向,对吗?【提示】 不对.正电荷在电场中某点受电场力的方向为该点场强方向.负电荷受电场力的方向与该点场强方向相反.1.对电场强度的理解(1)电场强度是描述电场性质的物理量,与放入电场中的电荷无关,它的大小是由电场本身来决定的.(2)公式E =F q 是电场强度的定义式,适用于一切电场,但E 不随F 和q 的变化而变化,不能说E 与F 成正比,也不能说E 与q 成反比.定义式仅告诉我们一种测量场强大小的方法.(3)在电场中的同一点,F q 是不变的;在电场中的不同点,F q 往往不同,即F q 完全由电场本身性质决定,与放不放试探电荷,放入试探电荷的电性、电荷量多少均无关系.(4)电场强度是矢量.空间某一点有几个电场叠加,该点的合场强可用平行四边形定则计算.即几个点电荷的电场中某点的场强等于各个点电荷在该点单独产生的场强的矢量和.2.点电荷的电场根据电场强度的定义式可得点电荷Q 在空间中形成电场的电场强度的表达式:E =k Q r 2(r 为空间某点到点电荷的距离).1.(多选)由电场强度的定义式E =F q 可知,在电场中的同一点( )【导学号:46852003】A .电场强度E 跟F 成正比,跟q 成反比B .无论试探电荷q 值(不为零)如何变化,F 与q 的比值始终不变C .电场中某点的场强为零,则处在该点的电荷受到的静电力一定为零D .一个不带电的小球在P 点受到的静电力为零,则P 点的场强一定为零【解析】 由E =F q 知,电场中某点场强E 只由电场本身决定,与是否引入试探电荷q 及q 的大小、正负无关,故A 项错,B 项对;由F =qE 知,E =0时,F 一定为零,F =0,E 不一定为零,故C 项对,D 项错.【答案】 BC2.场源电荷Q =2×10-4 C ,是正点电荷;试探电荷q =-2×10-5 C ,是负点电荷.它们相距r =2 m 而静止,且都在真空中,如图1-2-1所示.求:图1-2-1(1)q 受的电场力;(2)q 所在的B 点的场强E B ;(3)只将q 换为q ′=4×10-5 C 的正点电荷,再求q ′受力及B 点的场强.【解析】 (1)由库仑定律得F =k Q ·q r 2=9×109×2×10-4×2×10-522N =9 N. 方向在A 与B 的连线上,且由B 指向A .(2)因电场强度的定义式:E =F q ,所以E B =92×10-5 N/C =4.5×105 N/C. 方向沿A 、B 连线向右.(3)由库仑定律F ′=k Q ·q ′r 2=9×109×2×10-4×4×10-522N =18 N. 方向沿A 、B 连线向右,E B =F ′q ′=184×10-5 N/C =4.5×105 N/C. 方向沿A 、B 连线向右. 【答案】 (1)9 N ,方向在A 与B 连线上,且由B 指向A(2)4.5×105 N/C ,方向沿A 、B 连线向右(3)18 N ,方向沿A 、B 连线向右;4.5×105 N/C ,方向沿A 、B 连线向右1.电场强度的大小和方向都取决于电场本身.2.电场强度的大小虽然可由F q 来量度,但与试探电荷的存在与否无关.3.电场力F =qE 取决于电荷量q 及电场中这一点的电场强度E 的大小.电 场 线[先填空]1.概念为了直观形象地描述电场中各点电场强度的分布,在电场中画出一系列曲线,曲线上每一点的切线方向表示该点的电场强度方向.2.电场线的特点(1)始于正电荷(或无穷远),终止于无穷远(或负电荷).(2)任意两条电场线都不相交.(3)在同一幅电场分布图中,电场越强的地方,电场线越密.3.匀强电场(1)定义:场强大小和方向处处相同的电场.(2)电场线:匀强电场中的电场线是距离相等的平行线.(3)获取方法:平行正对的两金属板分别带有等量的正负电荷后,在两板之间除边缘外就是匀强电场.[再判断]1.电场线是客观存在的物质.(×)2.电场线只能表示电场强度的方向.(×)3.电场中未画电场线的地方电场强度为0.(×)[后思考]1.电场中的电场线是真实存在的吗?【提示】不是.电场线是人们为形象地描述电场而假想的,是一种物理模型.2.为什么任意两条电场线都不相交?【提示】电场线上每一点的切线方向表示该点的电场强度方向.若相交则该点会有两个电场强度的方向,与实际不符合.1.电场线的特点(1)不相交(空间任何一点,只能有一个确定的场强方向);(2)不闭合(起于正电荷或来自无穷远处,止于负电荷或伸向无穷远处);(3)电场线上各处的切线方向(或在电场中电场线的方向)表示场强的方向;(4)电场线的疏密程度表示场强的大小.电场线越密场强越大,越疏场强越小.2.几种常见带电体周围的电场线分布电场电场线图样简要描述电场特点正点电荷发散状直线离点电荷近处电场强度大,方向背离正电荷负点电荷会聚状直线离点电荷近处电场强度大,方向指向负电荷等量同种相斥状曲线连线上:中点场强最小(为零),靠近电荷变大电荷中垂线:中点场强最小(为零),向外移动先变大后变小等量异种电荷相吸状曲线连线上:中点场强最小,靠近电荷变大中垂线:中点场强最大,向外移动逐渐变小匀强电场(两平行板正对,中间部分为匀强电场)平行的、等间距的、同向的直线大小相等,方向相同3.(多选)如图1-2-2中带箭头的直线是某一电场中的一条电场线,在这条直线上有A、B两点,用E A、E B表示A、B两处的场强大小,则()图1-2-2【导学号:46852004】A.A、B两点的场强方向相同B.电场线从A指向B,所以E A>E BC.A、B同在一条电场线上,且电场线是直线,所以E A=E BD.不知A、B附近的电场线分布状况,E A、E B的大小不能确定【解析】根据电场线的物理意义,线上各点的切线方向表示该点的场强方向.因题中的电场线是直线,所以A、B两点的场强方向相同,都沿着电场线向右;因为电场线的疏密程度反映了场强的大小,但由于题中仅画出一条电场线,不知道A、B附近电场线的分布状况,所以无法确定E A、E B的大小,故A、D 项正确.【答案】AD4.如图1-2-3是静电场中一部分电场线的分布,下列说法中正确的是()图1-2-3A.这个电场可能是负点电荷的电场B.点电荷q在A点处受到的电场力比在B点处受到的电场力大C.点电荷q在A点处的瞬时加速度比在B点处的瞬时加速度小(不计重力) D.负电荷在B点处受到的电场力的方向沿B点切线方向【解析】负点电荷的电场是会聚状直线,A项错误;电场线的疏密程度表示电场的强弱,所以有E A>E B,又有F=qE,故电场力F A>F B,B项正确;由牛顿第二定律知,加速度a=Fm,所以a A>a B,C项错误;因为“B点切线方向”即B点场强方向,而负电荷所受电场力的方向与场强方向相反,D项错误.【答案】 B5.在如图所示的各电场中,A、B两点场强相同的是()【导学号:46852005】A.B.C. D.【解析】A选项中A、B两点电场强度大小相等,但方向不同;B选项中E A>E B;C选项中是匀强电场;D选项中E B>E A,且方向也不同.故只有C正确.【答案】 C电场线不是客观存在的,它只是用来描述电场的方向和定性地描述电场的强弱,并不是带电粒子在电场中的运动轨迹,带电粒子在电场中的运动轨迹是由带电粒子受的合外力与初速度共同决定的.但电场线能反映带电粒子在电场线上各点受电场力的方向.高中物理考试答题技巧及注意事项在考场上,时间就是我们致胜的法宝,与其犹犹豫豫不知如何落笔,倒不如多学习答题技巧。
第1章静电场 第2节库仑定律

物体做变加速运动 当速度方向a 0时 , 速度到达最大.
思 路 提 示 1.物 体 做 变 加 速 直 线 运动,当a 0时 , v到 达 最 大
2.物 体 做 变 加 速 曲 线 运 动 , 当 物 体 所 受 合力 外 与 v垂 直 时 , 即 在 v方 向 分 力 平 衡 时 , v到 达 最 大 .
学习目标:1.明确点电荷是个理想模型,知道带电体 简化为点电荷的条件,感悟理想模型. 2.理解库仑定律的内容及公式,知道库仑定律的适 用条件. 3.运用库仑定律并结合力学规律求解有关问题. 4.通过静电力与万有引力的对比,体会自然规律的 多样性和统一性. 重点难点: 库仑定律的内容及公式的理解和灵活应
所示,分别在A、B两点放置点电荷Q1=+2×10-14C和Q2=-2×10-14C, 在AB的垂直平分线上有一点C,且AB=AC=BC=6×10-2m,如果有一 高能电子在C点处,它所受的库仑力的大小和方向如何?(静电 力常量k=9.0×109N· m2/C2 ) F2
解 析 : 高 能 电 子 C受 力 如图 Q1e Q 2e 由库仑定律得: k 2 ,F2 k 2 1F r r θ 则 F 2F1cos 2F1cos600 8.0 102 1N 2 方 向 : 平 行 AB向 左
5.两个正点电荷Q1=Q和Q2=4Q分别置于固定在光滑绝缘水平面上 的A、B两点,A、B两点相距L,且A、B两点正好位于水平光滑绝 缘半圆细管的两个端点出口处,如图所示. (1)现将另一正点电荷置于A、B连线上靠近A处静止释放,它 在AB连线上运动过程中能达到最大速度的位置离A点的距离. (2)若把该点电荷放于绝缘管内靠近A点处由静止释放,试确 定它在管内运动过程中速度为最大值时的位置P.即求出图中PA 和AB连线的夹角θ .
1静电场

i n 或 E
4 0 ri
qi
ri
习题:在点电荷系的电场中,任一点电 场强度等于点电荷系中每一电荷在该点产生的 电强强度矢量和。
若带电体可看作是电荷连续分布的,如图示
把带电体看作是由许多个电荷元组成,然后利 用场强叠加原理。
dq
Q
dV
r
dE
P
三种带电形式:
电荷元: d q 线电荷 面电荷
0 0 0
若 r >> l ql 1 E= 4 ( r 2+ l 2 4 ) 3 2 ε π
0
~ 4ε r3 = 4ε r3 π π
0 0
ql
pe
pe E=4 ε π r3
0
电偶极子 E
1 4
0
r
3
p 3 r pr
电偶极子在电场中所受的力
M = f l sin θ l = q E l sinθ = pe E sinθ
0
2ε a 4ε a π π 无限长均匀带电 λ E = 2 直线的场强: πε a
0 0 0
Ex =0 Ey = E = 2 ×
8
λ
=
λ
习题: 一根很长的绝缘棒,均匀带电(如图), 单位长度上的电荷量为l 。试求距棒的一端垂直 距离为d 的P点处的电场强度。 + + + + + + + + + +
F
F
pe
答案:(B)
例: 一电偶极子原来与一均匀电场平行,将它转到与 电场反平行时,外力作功0.1 J。问当此电偶极子与场 强成45°时,作用于它的力偶矩有多大? 解:
大学物理电磁学

大学物理电磁学
第一章:静止电荷的电场
讲授内容:电荷、库仑定律、电场和电场强度以及场强叠加原理、电场线和电通量、高斯定律、利用高斯定律求静电场的分布基本要求:掌握静电场场强的概念及其叠加原理、能求解连续带电体的场强分布;理解用高斯定理律计算电场的条件和方法本章重点:电场强度的矢量叠加性、高斯定律
本章难点:微积分的应用
1.库仑定律
注意:矢量符号的印刷体以黑体加粗表示,手写书写体时必须带上标箭头。
2. 叠加原理:两个以上的点电荷对一个点电荷的作用力等于各个点电荷。
单独存在时对该点电荷的作用的矢量和。
3.电场:是电荷周围空间里存在的一种特殊物质。
4.电场强度:是用来表示电场的强弱和方向的物理量,下面是定义式。
5.电场线:是为了直观形象地描述电场分布而在电场中引入的一些假想的曲线。
电场线的特性:
a.始于由正电荷,止于负电荷;
b.电场线不相交;
c.静电场线不闭合;
(曲线上每一点的切线方向为电场方向;电场线的疏密程度代表场强大小)
6.电通量:通过电场中某一个面的电场线数叫做通过这个面的电场强度通量。
注:一般规定由内向外的方向为各处面元法向的正方向。
7.高斯定律:
8.电偶极子:电偶极子由等量异号电荷构成,电偶极矩方向由负电荷指向正电荷。
第一章静电场的基本规律

l
ql 3 2 2 4 0 (r l ) 2 4
方向沿X轴的反方向。
4
3)偶极子 等量异号电荷±q,当 l >>电荷自身线度 l << 系统到场点的距离,称为偶极子系统
偶极矩:p ql
偶极子的场:
方向由- q指向+q
4 0 1 P': E 4 0
P:E
1
2p r3 p r3
电
磁
学
主讲:郑鹉 王海
参考教材:《电磁学》梁灿彬等 高教社 《电磁学》赵凯华等有两种:
静电场的基本规律
电荷
一、两种电荷:
正电荷(+),负电荷( ) 同种电荷间相互排斥;异种电荷间相互吸引。
2、电量
物体所带电荷数量的多少
3、电荷的量子化
物体所带电量的最小单元
e 1.6 10
E
1 4 0
1
2p r3
E
4 0
p r3
q 1 1 P点 E E E 2 2 4 0 (r l ) (r l ) 2 2 l 2 l 2 (r ) (r ) q 2rl 2 2 q E 4 0 (r l ) 2 (r l ) 2 4 0 (r l ) 2 (r l ) 2 2 2 2 2 q 2l l2 2 4 0 3 r (1 2 ) 4r
略l/r的平方项,且利用 偶极矩:p ql
P:E
1 4 0
2p r3
E
1 4 0
2p 3 r
P’点
略l/r的平方项,且利用 偶极矩:p ql
P': E 1 4 0 p r3
05静电场——习题课
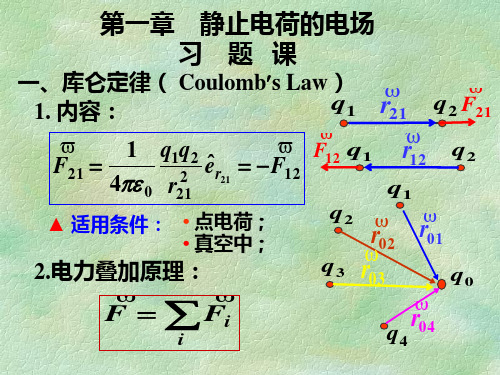
1.14(1)点电荷 位于边长为 的正立方体的中心, ( )点电荷q位于边长为 的正立方体的中心, 位于边长为a 通过此立方体的每一面的电通量各是多少? 通过此立方体的每一面的电通量各是多少? (2)若电荷移至正方体的一个顶点上,那么通过每 )若电荷移至正方体的一个顶点上, 个面的电通量又各是多少? 个面的电通量又各是多少? q 解: 1)由于立方体的 6 个侧面对于其 ( ) ● 中心对称, 则由Gauss定理知,通过各 定理知, 中心对称, 则由 定理知 个面的电通量都相等。 个面的电通量都相等。且等于整个闭合 q ● 高斯面电能量的六分之一, 高斯面电能量的六分之一,所以每个面 通过的电通量应为 q / (6ε0)。 。 填空题1039 (本题 分)在边长为 的正 本题3分 在边长为a的正 填空题 a 方形平面的中垂线上,距中心o点 方形平面的中垂线上,距中心 点a/2 处 q 有一电量q的正电荷,则通过该平面的电 有一电量 的正电荷, 的正电荷 ● a a/2 场强度通量为 q / (6ε0) 。 为边长作一个正六面体。 解:以a 为边长作一个正六面体。
ε0
E = 0 (r < a ) r > a , q int = 2π al σ , E 在筒外, 在筒外, δa (r ≥ a ) E = ε 0r o E-r 曲线如图。 曲线如图。
E∝1 r
a
r
1.18 两个无限长同轴圆筒半径分别为R1和R2,单位长 两个无限长同轴圆筒半径分别为 度带电量分别为+λ和 。求内筒内、 度带电量分别为 和-λ。求内筒内、两筒间及外筒外的 电场分布。 电场分布。 根据电场分布的轴对称性, 解:根据电场分布的轴对称性,可以选与圆筒同轴的圆 柱面(上下封顶 作高斯面。再根据高斯定律即可得出: 上下封顶)作高斯面 柱面 上下封顶 作高斯面。再根据高斯定律即可得出: 在筒内, 在筒内,r < R1 : E = 0 在筒间, 在筒间, R1 < r < R2 :
第一章静电场

第一章静电场1、1电荷及其守恒定律一、电荷1.物体磁铁:物理具备迎合不磁铁轻小物体的性质,我们就说道它具有电荷。
2.两种电荷(美国科学家富兰克林命名):(1)正电荷:用丝绸摩擦过的玻璃棒所带的电荷称为正电荷(用正数表示)。
(2)负电荷:用毛皮摩擦过的橡胶棒所带的电荷称为负电荷(用负电荷表示)。
二、物质的组成物质→分子→原子→原子核(质子与中子)电子自由电子:在金属中离原子核最远的电子往往脱离原子核的束缚而在金属中自由移动,这样的电子叫作自由电子。
三、起电方式1.摩擦起电(1)原因:相同物质的原子核束缚电子的本领相同。
(2)本质:电子从一个物体转移到另一个物体上,得到电子的物体带负电,失回去电子的物体拎正电。
(3)规律:两个相互摩擦的物体带上了等量异种电荷。
(4)对象:绝缘体之间。
2.感应起电(1)静电感应现象:把电荷紧邻不磁铁的导体时,可以并使导体磁铁的现象,表示为静电感应现象。
(2)感应器起至电:利用静电感应并使物体磁铁叫作感应器起至电。
(3)原因:带电体对导体中的自由电子迎合或排挤导致。
(4)本质:电荷从物体的一部分转移到另一部分,电荷的总量不变。
(5)规律:近端带异种电荷,远端带同种电荷(近异远同)。
(6)对象:导体与带电体之间。
3.接触起电(1)碰触起至电:带电体和不磁铁导体碰触,总会存有一部分电荷从带电体跑到不带电导体上去,使它变成带电体,这种方法叫接触起电。
(2)本质:电荷从一个物体迁移至另一个物体上,电荷总量维持不变。
(3)电荷分配原则(完全相同的金属体):a、一带一不带或都带同种平均分配;3.电荷间的相互作用(力):同种电荷互相排斥,异种电荷互相迎合。
b、一带正另一带负先正负电荷中和再平均分配。
(4)对象:导体与带电体之间。
四、电荷守恒定律:内容:电荷既不能radioactive,也不能消失,它就可以从一个物体迁移至另一个物体或者物体的一部分转移到另一部分,在转移过程中,电荷的总量保持不变。
大学物理电磁学公式总结汇总

大学物理电磁学公式总结汇总普通物理学教程大学物理电磁学公式总结,下面给大家整理了关于大学物理电磁学公式总结,方便大家学习大学物理电磁学公式总结1定律和定理1. 矢量叠加原理:任意一矢量可看成其独立的分量的和。
即:=∑ (把式中换成、、、、、就分别成了位置、速度、加速度、力、电场强度和磁感应强度的叠加原理)。
2. 牛顿定律:=m (或= );牛顿第三定律:′= ;万有引力定律:3. 动量定理:→动量守恒:条件4. 角动量定理:→角动量守恒:条件5. 动能原理:(比较势能定义式:)6. 功能原理:A外+A非保内=ΔE→机械能守恒:ΔE=0条件A 外+A非保内=07. 理想气体状态方程:或P=nkT(n=N/V,k=R/N0)8. 能量均分原理:在平衡态下,物质分子的每个自由度都具有相同的平均动能,其大小都为kT/2。
克劳修斯表述:不可能把热量从低温物体传到高温物体而不产生其它影响。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用的功而不产生其它影响。
实质:在孤立系统内部发生的过程,总是由热力学概率小的宏观状态向热力学概率大的状态进行。
亦即在孤立系统内部所发生的过程总是沿着无序性增大的方向进行。
9. 热力学第一定律:ΔE=Q+A10.热力学第二定律:孤立系统:ΔS0(熵增加原理)11. 库仑定律:(k=1/4πε0)12. 高斯定理:(静电场是有源场)→无穷大平板:E=σ/2ε013. 环路定理:(静电场无旋,因此是保守场)θ2Ir P o Rθ1I14. 毕奥—沙伐尔定律:直长载流导线:无限长载流导线:载流圆圈:,圆弧:电磁学1. 定义:= /q0 单位:N/C =V/mB=Fmax/qv;方向,小磁针指向(S→N);单位:特斯拉(T)=104高斯(G)① 和:=q( + × )洛仑兹公式②电势:电势差:电动势:( )③电通量:磁通量:磁通链:ΦB=NφB单位:韦伯(Wb)Θ ⊕-q +qS④电偶极矩:=q 磁矩:=I =IS⑤电容:C=q/U 单位:法拉(F)乘自感:L=Ψ/I 单位:亨利(H)乘互感:M=Ψ21/I1=Ψ12/I2 单位:亨利(H)⑥电流:I = ; 乘位移电流:ID =ε0 单位:安培(A)⑦乘能流密度:2. 实验定律① 库仑定律:②毕奥—沙伐尔定律:③安培定律:d =I ×④电磁感应定律:ε感= –动生电动势:感生电动势:( i为感生电场)乘⑤欧姆定律:U=IR( =ρ )其中ρ为电导率3. 乘定理(麦克斯韦方程组)电场的高斯定理:( 静是有源场)( 感是无源场)磁场的高斯定理:( 稳是无源场)( 感是无源场)电场的环路定理:(静电场无旋)(感生电场有旋;变化的磁场产生感生电场)安培环路定理:(稳恒磁场有旋)(变化的电场产生感生磁场)4. 常用公式①无限长载流导线:螺线管:B=nμ0I② 带电粒子在匀强磁场中:半径周期磁矩在匀强磁场中:受力F=0;受力矩③电容器储能:Wc= CU2 乘电场能量密度:ωe= ε0E2 电磁场能量密度:ω= ε0E2+ B2乘电感储能:WL= LI2 乘磁场能量密度:ωB= B2 电磁场能流密度:S=ωV④ 乘电磁波:C= =3.0×108m/s 在介质中V=C/n,频率f=ν=波动学大学物理电磁学公式总结2概念(2113定义和相关公式)1. 位置矢量:,其5261在直角坐标系中:; 角位置:4102θ16532. 速度:平均速度:速率:( )角速度:角速度与速度的关系:V=rω3. 加速度:或平均加速度:角加速度:在自然坐标系中其中(=rβ),(=r2 ω)4. 力:=m (或= ) 力矩:(大小:M=rFcosθ方向:右手螺旋法则)5. 动量:,角动量:(大小:L=rmvcosθ方向:右手螺旋法则)6. 冲量:(= Δt);功:(气体对外做功:A=∫PdV)mg(重力) → mgh-kx(弹性力) → kx2/2F= (万有引力) → =Ep(静电力) →7. 动能:mV2/28. 势能:A保= –ΔEp不同相互作用力势能形式不同且零点选择不同其形式不同,在默认势能零点的情况下:机械能:E=EK+EP9. 热量:其中:摩尔热容量C与过程有关,等容热容量Cv 与等压热容量Cp之间的关系为:Cp= Cv+R10. 压强:11. 分子平均平动能:;理想气体内能:12. 麦克斯韦速率分布函数:(意义:在V附近单位速度间隔内的分子数所占比率)13. 平均速率:方均根速率:;最可几速率:14. 熵:S=KlnΩ(Ω为热力学几率,即:一种宏观态包含的微观态数)15. 电场强度:= /q0 (对点电荷:)16. 电势:(对点电荷);电势能:Wa=qUa(A= –ΔW)17. 电容:C=Q/U ;电容器储能:W=CU2/2;电场能量密度ωe=ε0E2/218. 磁感应强度:大小,B=Fmax/qv(T);方向,小磁针指向(S→N)。
第1章 真空中的静电场2 电场,电场强度,场强叠加原理

3.电荷连续分布时的电场强度 E 一个带电体,从微观结构上看,电荷集中在一个个 带电的微观粒子(比如电子、原子核等)上边。但从宏观 上看,人们往往把电荷看成是连续分布的。根据不同的情 况,有时把电荷看成在一定体积内连续分布(体分布); 有时把电荷看成在一定曲面上连续分布(面分布);有时 把电荷看成在一定曲线上连续分布(线分布)等等。这样 从数学上说,求和变成了积分运算。
1 4πε 0
(
ql
2 2
r +l
) 4
3
2
方向沿 - x方向。
讨论
A. 电偶极子-----一对等量异号的点电荷组成的带电体 系,它们之间的 距离 l远比场点到它们的距离 r小得多时, 这样的带电体系叫做电偶极子。在这种情况下,可作近 似:r >> l ,于是有: i
l⎞ ⎛ l⎞ ⎛ ⎜r + ⎟ − ⎜r − ⎟ 1 1 2lr 2⎠ ⎝ 2⎠ ⎝ = = − 2 2 2 2 l⎞ ⎛ l⎞ l⎞ l⎞ ⎛ 2 l2 ⎛ ⎛ ⎛ ⎜r − ⎜r − ⎟ ⎜r + ⎟ ⎜r − ⎟ ⎜r + ⎟ ⎜ 2⎠ 2⎠ 2⎠ ⎝ 2⎠ ⎝ ⎝ ⎝ 4 ⎝
ii
(
l
2 2
r +l
4
)
3
2
l ≈ 3 r
1 P ql = E≈ 3 所以在中垂面上E的大小为: 4πε 0 r 4πε 0 r 3 1
B. 由上述结果可以看出,电偶极子的场强与距离r 的三次方成正比,它比点电荷的场强随距离r递减的速度 快得多。 1 ( 点电荷: E ∝ r 2 ) C. 实际中电偶极子的例子很多,比如下一章我们 将看到,在外电场的作用下,电介质(即绝缘体)的原子 或分子里正、负电荷产生微小的相对位移,形成电偶极子 。在无线电发射天线中,经常要用到振荡偶极子(在第十 章中会介绍)。
电磁学(地物)课件 第一章-1

e 1.60218921019库仑
• 二、库仑定律(coulomb’s law) • 法国物理学家(1736-1806)
• 点电荷之间的相互作用规律 • 点电荷:
• 库仑定律:真空中两个静止点电荷之间的作用力:
F10
k
q0q1 | r10 |3
r10
F01
三 、 叠加原理:
3、任意带电体
(将连续分布带电体无限分割为一个个电荷元)
连续带电体的电场
对电荷连续分布的带电体,可划分为无限多个电荷
元dq(点电荷), 用点电荷的场强公式积分:
Q E
dE
Q
dq
Q 4 0r 2 er
dq dV
r 体电荷分布 dq dq dV
P
dV
dE
面电荷分布 dq dq ds
Ey
4 0 a
(cos1
cos2 )
当直线长度
Ex Ey
0
4
L 0a
2
{
1 2
第一章 真空中的静电场
• 1.1 电荷守恒 • 1.2 库仑定律 • 1.3 叠加原理 • 1.4 电场强度 • 1.5 高斯定理 • 1.6 环路定理 • 1.7 电势
一、电荷 电为物质的一种基本特性,电不能离开物质而
存在,不存在不依附物质的“单独电荷”。 1、电荷的种类:两种 2、最小电量、电荷的量子性 3、电荷的对称性 4、电荷守恒
q0 40r3
电场强度E是 坐标函数E(x,y,z)
单位: N c
or
伏特 米
电场是带电体周围的一个具有特定性质的空 间,该空间的任一点,外来电荷都会受到一定 大小、方向的作用力。
第一章 静电场 电场力的性质

第一章 静电场考点一 电场力的性质笔记整理:一、电荷及其守恒定律 1.电荷及其相互作用(1)自然界的电荷分为正电荷、负电荷两种。
(2)同种电荷相互排斥,异种电荷相互吸引。
2.起电的三种方式3.元电荷电荷的多少叫做电荷量,把电子所带的电荷量的大小叫元电荷,用e 表示。
所有带电体的电荷量等于e 的整数倍,电荷量是不能连续变化的物理量,e =1.60×10-19C 。
比荷(荷质比):粒子的带电量与质量的比值。
电子的比荷:111076.1/⨯=e m e C/kg二、库仑定律 1.库仑定律真空中两个静止点电荷之间的相互作用力,作用力的方向在它们的连线上。
221rq q kF = 静电力常量:9100.9⨯=k N·m 2/C 2 (1)库仑定律适用于真空中,也可近似地用于空气中。
(2)点电荷:当带电体本身大小、形状及电荷分布对它们之间的作用力的影响可以忽略时,带电体就可以看做是点电荷。
它是一个理想模型,实际上是不存在的。
(3)任何一个带电体都可以看成是由许多点电荷组成的。
任意两点电荷之间的作用力都遵守库仑定律,可用矢量求和法求合力。
(4)库仑扭秤实验(法国)2.万有引力与库仑力的关系(1)形式相似 221r m m GF =,221r q q k F =。
摩擦起电接触起电感应起电电荷(电子)发生转移本质−−→−(2)计算可知,电子和质子间的万有引力要比静电引力小的多(39101.2⨯=引库F F ),因此在研究微观带电粒子间的相互作用时,主要考虑静电力,万有引力虽然存在,但相比之下非常小,可忽略不计。
三、电场 电场强度 1.电场电荷之间的相互作用通过电场来实现,电荷的周围都存在电场,电场是物质的一种存在形式。
电场不同于生活中常见的物质,其不由分子原子组成,看不见摸不着,无法称量,但可以叠加,是客观存在的,具有物质的基本属性——能量.基本性质:①引入电场中的任何带电体都将受到电场力的作用,且同一点电荷在电场中不同点处受到的电场力的大小或方向都可能不一样.②电场能使引入其中的导体产生静电感应现象.③当带电体在电场中移动时,电场力将对带电体做功,这表示电场具有能量.2.电场强度(E )(1)试探电荷和场源电荷:检验电荷是一种理想化模型,它是电量很小的点电荷,将其放入电场后对原电场强度无影响(2)电场强度:电场中某一点的电荷受到的电场力F 跟它的电荷量q 的比值,叫做该点的电场强度,简称场强.用E 表示。
物理选修31粤教全程导学笔记课件:第一章 电场 第二节

例3 (多选)两个质量分别是m1、m2的小球(可视为质点),各用丝线悬挂 在同一点,当两球分别带同种电荷,且电荷量分别为q1、q2时,两丝线 张开一定的角度θ1、θ2,如图5所示,此时两个小球处于同一水平面上, 则下列说法正确的是
A.若m1>m2,则θ1>θ2
√B.若m1=m2,则θ1=θ2
√C.若m1<m2,则θ1>θ2
电荷.( √ )
(5)若点电荷q1的电荷量大于q2的电荷量,则q1对q2的静电力大于q2对q1的静电
力.( × )
(6)根据库仑定律表达式F=kqr1q2 2 ,当两电荷之间的距离r→0时,两电荷之间的
库仑力F→∞.( × )
答案
2.真空中两个点电荷,它们之间的静电力为F,如果将两个点电荷的距离 增大为原来的4倍,电荷量都增大为原来的2倍.它们之间静电力的大小变
知识探究
一、点电荷 电荷间的相互作用力
[导学探究] 什么是点电荷?实际带电体看成点电荷的条件是什么? 答案 点电荷是用来代替带电体的点,当带电体的形状、大小及电荷分 布对它们之间的作用力的影响可以忽略时,带电体可以看做点电荷.
答案
[知识梳理] 1.点电荷:当带电体间的距离比它们自身的大小 大得多 ,以致带电体上 的电荷分布状况 对它们之间的作用力的影响可以忽略时,这样的带电体 就可以看做带电的点,叫做点电荷 . 2.说明 (1)点电荷是只有电荷量,没有大小、形状的理想化模型,是一种科学抽 象,类似于力学中的质点,实际中并不存在. (2)带电体能否看做点电荷,不取决于带电体的大小,而取决于它们的形 状、大小与距离相比能否忽略.即将带电体看做点电荷的前提条件是带电 体间的距离远大于带电体本身的尺寸.
图7
1234
解析 答案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Gauss’ Law :? —— In cases of high symmetry, this will be MUCH EASIER than the brute force method. Furthermore, Gauss’ law serves as a guide for understanding more complicated problems.
a
a
Fundamental Law of Electrostatics
Coulomb’s Law Force between two point charges Gauss’ Law Relationship between electric flux and charges The two laws are fundamental laws of electrostatics. Coulomb’s law Gauss’ law Gauss’ law Coulomb’s law
Chapter 1, ACT 1
Examine the electric field lines produced by the charges in this figure.
Which statement is true? q1 q2
(a) q1 and q2 have the same sign (b) q1 and q2 have the opposite signs and (c) q1 and q2 have the opposite signs and
Consider three imaginary spheres centered on:
a) +q (blue) b) -q (red) c) midpoint (yellow)
All lines leave a),
flux through a) is positive All lines enter b),
Electric Flux…
In more general situations, the electric field may vary over the surface. Therefore, the electric flux Fe through the surface is given by:
The electric flux Fe through the surface is defined as the product of electric field strength E and surface area S.
Electric Flux…
If the surface is not perpendicular to the field. The normal to the surface of area S is at an angle to the uniform electric field. The electric flux Fe through the surface is given by:
Electric Flux…
Let’s look at the formula (1.16) on page 23.
Electric Flux…
First consider an electric field that is uniform in both magnitude and direction. The rectangular surface is perpendicular to the field. The normal to the surface of area S is parallel to the uniform electric field.
dS 4 r
closed surface
q r
P
E
Derivation of Gauss’ Law…
Electric Flux
Electric flux : Define: Number of field lines passing through an area of interest. Units: N·m2/C. The number of lines per unit area is proportional to the magnitude of . What’s the relationship between electric flux and ?
The Story Thus Far
We want to be able to calculate the electric fields from various charge arrangements. Two ways:
Brute Force: Add up / integrate contribution from each charge —— Often this is pretty difficult. Ex: infinite line of charge
left
right
The Sign Problem...
For a closed surface, we choose the direction of dS pointing out.
A differential surface element, with its vector
dS
Electric Dipole: Flux
Electric Flux…
Electric flux Fe through the closed surface S is given by:
Ex: Flux through a cube or a sphere
The Sign Problem
For an open surface we can choose the direction of dS two different ways. to the left or to the right flux would be different these two ways different by a minus sign
c
a
flux through b) is negative
Equal amounts of leaving
b
and entering lines for c),
flux through c) is zero
Chapter 1, Act 2
Imagine a cube of side a positioned in a region of constant electric field as shown Which of the following statements about the net electric flux Fe through the surface of this cube is true?
Chapter 1(continued)
c
a
r a a
b
a
r
Today’s Agenda
Electric Flux(电通量) Gauss’ Law(高斯定理) Application of Gauss’ Law Uniformly Charged Sphere Infinite Line of Charge Infinite Sheet of Charge Two Infinite Sheets of Charge
There is an easier way. Gauss’ Law states the net flux Φe is proportional to the NET enclosed charge qin . The NET charge is zero in the cube. But, what is Gauss’ Law ???
( Coulomb’s law Gauss’ law ) From Coulomb’s law, we know that the magnitude of q the electric field of a positive point charge is E 2 4 r 0 and the direction of E is radial outward. The net electric flux through the closed surface of radius r is:
(a) Fe = 0
(b) Fe 2a2
(c) Fe 6a2
Chapter 1, Act 2 Solution
Therefore, the total flux through the cu Fe = 0
(b) Fe 2a2
(c) Fe 6a2
Chapter 1, Act 2 Solution
the electric field.
E dS on the bottom face is negative. ( dS is down; E is up)
E dS on the top face is positive. ( dS is up; E is up)
(c) q1 and q2 have the opposite signs and Gauss’ law will make it easier!
