最新球体积公式(数学史)讲课稿
高中数学《球的表面积和体积》课件

课前自主学习
课堂互动探究
随堂巩固训练
课后课时精练
[变式训练2] 如图,半球内有一个内接正方体,正方体的一个面在半球 的底面圆内,若正方体棱长为 6,求球的表面积和体积.
课前自主学习
课堂互动探究
随堂巩固训练
课后课时精练
解 作轴截面如图所示,
CC′= 6,AC= 2· 6=2 3, 设球的半径为 R, 则 R2=OC2+CC′2=( 3)2+( 6)2=9, ∴R=3,∴S 球=4πR2=36π,V 球=43πR3=36π.
4.设三棱柱的侧棱垂直于底面,所有棱的长都为 a,顶点都在一个球面 上,则该球的表面积为( )
课前自主学习
课堂互动探究
随堂巩固训练
课后课时精练
答案
例 3 过球的半径的中点,作一垂直于这条半径的截面,截面面积是 48π cm2,求球的表面积.
[解] 如图所示,设 O′为截面圆圆心,则 OO′⊥O′A,O′A 为截 面圆的半径,OA 为球的半径 R.
课前自主学习
课堂互动探究
随堂巩固训练
课后课时精练
课堂互动探究
随堂巩固训练
课后课时精练
随堂巩固训练
课前自主学习
课堂合作研究
随堂基础巩固
课后课时精练
1.若一个球的体积为 4 3π,则它的表面积为( ) A.12π B.3π C.43π D. 3π
答案 A 解析 设球的半径为 R,则有43πR3=4 3π,解得 R= 3,则球的表面积 S=4π×( 3)2=12π.
课前自主学习
课堂互动探究
随堂巩固训练
课后课时精练
答案
解析
3.一个正方体与一个球的表面积相等,那么它们的体积的比值是( )
人教版六年级数学上册-球体的体积说课稿

人教版六年级数学上册-球体的体积说课稿简介本节课是人教版六年级数学上册的第X单元第X课,主要内容是介绍球体的体积计算方法。
通过本节课的研究,学生将能够理解球体的概念、掌握计算球体体积的方法,并能运用所学知识解决实际问题。
研究目标1. 了解球体的定义和特点;2. 掌握计算球体体积的公式;3. 运用所学知识计算球体的体积。
教学重点1. 球体的定义和特点;2. 如何计算球体的体积。
教学难点1. 运用所学知识解决实际问题。
教学准备1. 教师准备一个球体模型;2. 黑板、彩笔、擦子。
教学过程导入新课1. 教师出示一个球体模型,引导学生观察并提问:“大家知道这是什么几何体吗?”2. 学生回答:“是球体。
”3. 教师继续问:“球体有什么特点?”等待学生回答。
探究球体的体积1. 教师引导学生思考如何计算球体的体积。
2. 教师与学生共同探讨,引导学生找出计算球体体积的方法。
3. 教师板书并解释计算球体体积的公式:$V = \frac{4}{3}\pi r^3$,其中$V$表示体积,$r$表示球体半径。
4. 教师通过几个例子演示如何使用公式计算球体的体积,引导学生进行思考和讨论。
运用所学知识解决实际问题1. 教师设计一些实际问题,要求学生运用所学知识计算球体的体积。
2. 学生独立或小组完成练题,并互相核对答案。
3. 教师给予学生积极的肯定和评价。
总结1. 教师和学生共同总结本节课的研究内容和重点;2. 教师强调掌握计算球体体积的方法,能够运用所学知识解决实际问题。
作业练册上的相关题。
扩展1. 学生可以自行查找更多关于球体的实际应用;2. 学生可以探索其他几何体的体积计算方式。
通过本节课的学习,学生将能够熟练计算球体的体积,并将所学知识应用到实际生活中。
同时,通过探索和扩展,学生能够培养出更好的数学思维能力和解决问题的能力。
希望本节课能够顺利进行,让学生对球体的体积有更深入的理解和掌握。
【高中数学课件】球的体积ppt课件

复习
一、体积和体积单位。 二、公理5和两个推论。 三、公理6。
公理6的应用:求几何体的体积。
未知体积的 几何体M
参照体Q
公理6
VM = VQ
主要的思想方法:
1.化未知为已知; 2.把空间问题转化为平面问题; 3.割补法。
V长方体=Sh
公理6
天马行空官方博客:
V球 =
4 3
R3
例题
例 有一种空心钢球,重142g,测 得外径等于5.0cm。求它的内径(钢的 密度是7. 9g/cm 3 )。
解:设空心钢球的内径为2xcm,那么 钢球的质量是
7.9•[
4 3
•(
5 2
)
3-
4 3
x
3
]=142,
解得 x 2.24, 2x 4.5(cm)。
答:空心钢球的内径约为4. 5厘米。
R3
V半球 =
2 3
R3
r2 =R2-l 2 S截面 =R2 -l2
r R
l
lR
l
r2 =R2-l 2 S圆 =r2 = (R2 - l 2) =R2 -l2
S圆环=R2 -l2 S圆 =S圆环
1 2
V球
=R2•R
1 3
R2•R =
2 3
R3
所以
V球 =
4 3
R3
定理 如果球的半径是R,那么它 的体积是
课堂练习
填空题 1.球的半径扩大为原来 的2倍,它的球面 面积变为原来 ( 4)倍,它的体积变为原 来的( 8)倍。
2.球面面积膨胀为原来的二倍,体积变为
原来的( 2 2 )倍。
3.球的大圆面积扩大为原来的二倍,球的
球的体积和表面积PPT课件

h
实验:排液法测小球的体积
h
实验:排液法测小球的体积
h
实验:排液法测小球的体积
h
实验:排液法测小球的体积
H
h
小 球 它 的 排 体 等 开 积 于 液 体 的 体 曹冲称象 积
回顾圆面积公式的推导
n=6 A1 O A2 假设将圆n等分,则
n=12 An
O p A1 A2 A3
割
圆
术
早在公元三世纪,我国数学家刘徽为推 导圆的面积公式而发明了“倍边法割圆术”。 他用加倍的方式不断增加圆内接正多边形的 边数,使其面积与圆的面积之差更小,即所 谓“割之弥细,所失弥小”。这样重复下去, 就达到了“割之又割,以至于不可再割,则 与圆合体而无所失矣”。这是世界上最早的 “极限”思想。
R
●
● ●
O
·
M
●
D
C
1、一个四面体的所有的棱都为 ,四个顶点在同 一球面上,则此球的表面积( )
圆锥
旋转体
圆柱
圆台
球体
• 圆柱、圆锥和圆台的侧面积公式: S侧=π(r+R)l 当r=R时,S侧=2πRl,即圆柱的侧面积公式. 当r=0时,S侧=rRl,即圆锥的侧面积公式. 其中r表示上底面半径,R表示上底面半径,l表示 母线长
• 直棱柱、直棱锥和直棱台的侧面积公式: S侧=(c+c’)h’/2 当c=c’时,S侧=ch’,即棱柱的侧面积公式. 当c’=0时,S侧=ch’/2,即棱锥的侧面积公式.
D A D1 A1 B1 O B
C A C1
D B D1 O
C
略解:
C1 B1
A1
变题1.如果球O切于这个正方体的六个面,则有R=————。 。
球的表面积与体积PPT课件

5,15,求它的外接球表面积 .
四面体与球的“接切”问题
典型:正四面体ABCD的棱长为a,求 其内切球半径r与外接球半径R.
思考:若正四面体变成正三棱锥,方法 是否有变化?
1、内切球球心到多面体各面的距离均相等,外接球 球心到多面体各顶点的距离均相等 2、正多面体的内切球和外接球的球心重合 3、正棱锥的内切球和外接球球心都在高线上,但不 重合 4、基本方法:构造三角形利用相似比和勾股定理 5、体积分割是求内切球半径的通用做法
R
2R
R
2
延伸阅读:割圆术
早在公元三世纪,我国数学家刘徽 为推导圆的面积公式而发明了“倍 边法割圆术”。
他用加倍的方式不断增加圆内接正
多边形的边数,使其面积与圆的面
积之差更小,即所谓“割之弥细,
所失弥小”。这样重复下去,就达
到了“割之又割,以至于不可再割, 思考:能否也
则与圆合体而无所失矣”。
采取“分割”与
球与正方体的“接切”问题
典型:有三个球,一球切于正方体的各面,一球切 于正方体的各侧棱,一球过正方体的各顶点,求 这三个球的体积之比.
a
r1
a 2
a
r2
2a 2
a
r3
3a 2
a
2a
2a
•画出正确的截面:(1)中截面;(2)对角面 •找准数量关系
球与正方体的“接切”问题
1.一个正方体的顶点都在 球面上,它的棱长 是4cm,求这个球队体积. 2.钢球直径5cm,把钢球放入一个正方 体的 有盖纸盒中,至少要用 多少纸? 3.半球内有一内接正方体 ,正方体的一个面 在半球的底面圆上,若 正方体的一边长为
球体积公式(数学史)

格证明。
阿基米德(Archimedes. 约公元前287—212年)
研究中算史的日本专家三上义夫指出,从刘徽到祖 冲之父子通过“合盖”(即牟合方盖)得出球体积“可 谓中算史上几何处理方法之最高发达,荀与希腊阿基米 德之积分方法及其所言与外接圆柱之关系,一比较研究 之,亦一趣事也”
思考问题:刘徽、祖冲之父子、阿基米德都是蜚声中外的数 学家,他们如何解决球体的计算问题呢?
(1)
牟合方盖内切半球图
(2)
正方形内切圆
牟合方盖“内棋” 图
合盖“外棋”分解图
合盖“外棋”截面图
倒立阳马图
(1)
等轴圆柱及内切球
(2)
球体切割图
力学原理与球体积计算
1. 数学研究中的算法倾向与演绎倾向 2. “以棋验术”的直觉方法与“数学物理”方
法 3. “截面原理”与“有限迭加” 4. 问题求解与因果论证 5. 几何代数化与微积分的应用
中国数学史
祖冲之(公元429-500)
刘徽(生于公元250左右)
西方数学史
阿阿基基米米德德突这破一希成腊果古, 被典古时代期传几记何作定家性普研鲁究塔的 克传说统:,“重几视何定学量中研不究可,
能发找现到了更球难、做球的缺问、题椭,球
也体不体可积能公找式到及更抛简物练线、弓
更形清面楚积的公陈式述,和并证给明予。严”
球体积公式的发现与证明
怎样计算球的体积 发现球体积公式的过程和方法 证明球体积公式的思路和方法
图1 用祖暅原理证明球体积公式
图2 用切割法证明球体积公式
图3 用定积分计算球体积
数学是人类文化的重要组成部分。运用数学史材 料进行数学教育是国际数学教育界共同关注的问题。
球体积公式的发现和证明,是度量几何发展进程 中具有标志意义的成果。
球体积公式(数学史)

中国数学史
祖冲之(公元429-500)
刘徽(生于公元250左右)
西方数学史
阿基米德突破希腊古 阿基米德这一成果, 典时期几何定性研究的 被古代传记作家普鲁塔 传统,重视定量研究, 克说:“几何学中不可 发现了球、球缺、椭球 能找到更难做的问题, 体体积公式及抛物线弓 也不可能找到更简练、 更清楚的陈述和证明。” 形面积公式,并给予严 格证明。
学家,他们如何解决球体的计算问题呢?
一、刘徽的“牟合方盖”与祖暅的“幂势既同,则积不容 异” ——中算家对球体积的探求 二、阿基米德的“力学原理”与“穷竭法” ——古希腊学者对球体积公式的发现与证明 三、异曲同工、弹奏千古名篇
——球体积公式与古代数学研究传统
牟合方盖
开立圆术的分解
(1)
(2 )
阿基米德(Archimedes. 约公元前287—212年)
研究中算史的日本专家三上义夫指出,从刘徽到祖
冲之父子通过“合盖”(即牟合方盖)得出球体积“可
谓中算史上几何处理方法之最高发达,荀与希腊阿基米 德之积分方法及其所言与外接圆柱之关系,一比较研究
之,亦一趣事也”
思考问题:刘徽、祖冲之父子、阿基米德都是蜚声中外的数
4. 问题求解与因果论证
5. 几何代数化与微积分的应用
球体积公式的发现与证明
怎样计算球的体积 发现球体积公式的过程和方法 证明球体积公式的思路和方法
图1 用祖暅原理证明球式
图3 用定积分计算球体积
数学是人类文化的重要组成部分。运用数学史材 料进行数学教育是国际数学教育界共同关注的问题。
球体积公式的发现和证明,是度量几何发展进程 中具有标志意义的成果。
(3)
正方体内切正交圆柱图
牟合方盖图
高中数学球的体积和表面积课件课件

V柱体 = S h
S `= S
V台体 =
h S + SS ` + S `
S `=
(
)
V锥体 =
Sh
运用类似的方法我们还能证实这样一个有趣的结论 : 一个底面半径和高都等于 R 的圆柱 , 挖去一个以上底 面为底面, 下底面圆心为顶点的圆锥后, 所得几何体的 体积与一个半径为R的半球的体积相等 (图 − − ). 由此得到 V球 = π R ⋅ R − π R R = π R , 所以
棱柱 (圆柱 )可由多边形 (圆)沿某一方向平移得到 ,因此 , 两个底面积相等、 两个底面积相等、高也 相等的棱柱 (圆柱 )应该具有相 等的体积 (图 − − ).
恒 恒 这一点可用祖日 原理来说明.有关祖日 原理的介绍见阅读材料 .
h
h
S
S
S
图 − −
柱体 (棱柱、圆柱 )的体积等于它的底面积S和高h的 积, 即 V柱体 = S h .
V= .
≈ .
(mm ) =
(个).
.
(cm ).
约有毛坯
. ×
÷( . × .
个.
)≈
答 这堆毛坯约有
例 图 − − 是一个奖杯的三视图 (单位 : cm ), 试画 出它的直观图 , 并计算这个奖杯的体积 ( 精确到 . cm ).
解 采用斜二测画法 .先画底座, 这是一个正四棱台; 再画杯身,是长方体; 最后画出球体.如图 − − .
R
O
图 − −
这时, 这些 "准锥体" 的 高趋向于球半径 R, 底 面积 S , S , S ,⋅ ⋅ ⋅的和趋 向于球面积 , 所有这些" 准锥体"的体积和趋向 于球体积,因此
沪教版数学高三上册球的体积公式解读课件

那么最大的球的体积是其余两个球体 练习:已知椭圆的标准方程为
高等于底面半径的旋转体体积对比 即先把半球分割成n部分,再求出每一部分的近似体积,并将这些近似值相加,得出半球的近似体积,最后考虑n变为无穷大的情形,
下面我们就运用上述方法导出球的体积公式
即先把半球分割成n部分,再求出每一部分的近似体积,并将这些近似值相加,得出半球的近似体积,最后考虑n变为无穷大的情形,
第i层“小圆片”下底面的半径: 由半球的近似体积推出准确体积.
高等于底面半径的旋转体体积对比
如果网格分的越细,则: “小锥体”就越接近小棱锥
问题:已知球的半径为R,用R表示球的体积.
球的公式
球的表面积 S 4 R2
球的体积
V 4 R3
3
解读一:极限求解
学习球的知识要注意和圆的有关指示结合起来.所以 我们先来回忆圆面积计算公式的导出方法.
我们把一个半径为R的圆分成若干等分,然后如上图重新
拼接起来,把一个圆近似的看成是边长分别是 R和R的矩形.
那么圆的面积就近似等于R2 .
积和的________倍 由半球的近似体积推出准确体积.
球面被分割成n个网格,表面积分别为: 练习:已知椭圆的标准方程为 当所分份数不断增加时,精确程度就越来越高; 我们把一个半径为R的圆分成若干等分,然后如上图重新拼接起来,把一个圆近似的看成是边长分别是 练习:已知椭圆的标准方程为 如果网格分的越细,则: “小锥体”就越接近小棱锥 练习:已知椭圆的标准方程为
则球的体积为: 即先把半球分割成n部分,再求出每一部分的近似体积,并将这些近似值相加,得出半球的近似体积,最后考虑n变为无穷大的情形,
高一数学文化赏析:祖暅原理和球的体积 课件
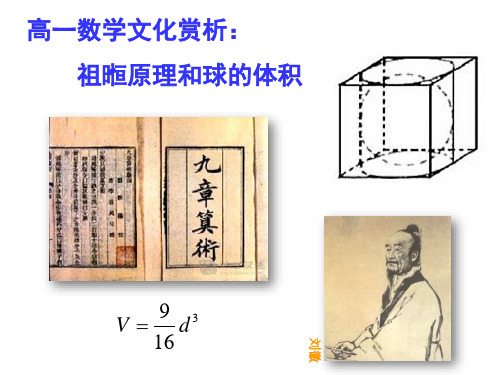
V球
2V半球
(2 V圆柱
V圆锥)
4 R3
球等简单的旋转体的
体积,其主要方法是构造转化,关键在截面特性。
(2)在研究数学问题时,要遵循一种规律:未知问题转 化为已知问题来解决。
求八分之一牟合方盖体积
缘幂势既同,则积不容异
祖暅
V牟合方盖
8(V小立方
V剩余 )
2 3 V立方体
V剩余 V倒立锥
祖暅原理:体积可以看成是由面积叠加而成,用一组平行平面截两个 空间图形,若在任意等高处的截面面积都对应相等,则两空间图形的体 积必然相等。
思考球的体积公式的推导还有其他方法吗?
R
高一数学文化赏析: 祖暅原理和球的体积
V 9 d3 16
刘徽
刘徽:若把圆柱与其内切球体积之比认为是方圆率之比, 则算得的球积失之过多,但若取3为圆周率之值,又失之过少。 多寡相互抵消,误差虽然减小,但终究不能相掩,球积仍嫌过大。
牟合方盖
S圆 r2
S正方形 4r 2 4
V球
V牟 4
祖暅原理求球体积公式

祖暅原理求球体积公式在咱们的数学世界里,有一个特别厉害的原理叫做祖暅原理。
这祖暅原理啊,可是解决球体积公式的一把神奇钥匙。
咱先来说说祖暅原理到底是啥。
简单来讲,就是两个高度相等的立体,如果在任意等高处的截面面积都相等,那这两个立体的体积就相等。
听起来有点绕是不?咱举个例子。
比如说有两根粗细不一样的柱子,但是从同样的高度去横着切一刀,得到的两个面大小都一样,那这两根柱子的体积就是一样的。
那这祖暅原理和球体积公式有啥关系呢?这就得好好说道说道啦。
咱们可以把球想象成一个特别圆滑的大皮球。
要算出这个大皮球的体积,可不容易。
但是聪明的古人就想到了办法。
假设咱们有一个半球,半径是r 。
然后在半球的旁边放一个圆柱体,圆柱体的底面半径也是 r ,高也是 r 。
接着再在圆柱体上扣掉一个圆锥。
这时候神奇的事情就发生了。
咱们来看看这几个图形在不同高度的截面。
先看半球,在距离球顶高度为 h 的地方,截面是一个圆,这个圆的面积可以通过一些数学知识算出来,是π(r² - h²)。
再看那个组合体,在同样高度 h 的地方,圆柱体的截面是一个半径为 r 的圆,面积是πr²。
圆锥在这个高度的截面也是一个圆,面积是πh²。
所以组合体在这个高度的截面面积就是πr² - πh²,也就是π(r² - h²)。
瞧见没,在任意等高处,半球和这个组合体的截面面积都相等。
根据祖暅原理,它们的体积就相等。
那这个组合体的体积就好算了。
圆柱体的体积是πr²×r = πr³,圆锥的体积是1/3×πr²×r = 1/3πr³。
所以组合体的体积就是πr³ - 1/3πr³ = 2/3πr³。
因为半球的体积和这个组合体的体积相等,所以半球的体积就是2/3πr³,那整个球的体积就是4/3πr³。
高中数学球体的体积和表面积课件

空间集合体
球体的体积和表面积
高中数学
新知探究
祖暅原理: 两等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
h
h
新知探究
球的体积公式的推导 先来研究半球(半径为R)的体积计算。为了应用祖暅原理,我们需要找到一个能够求体积的, 使它和半球高度一样,并且用任何一个水平面去截它们时,得到的截面面积都相等的几何体。
V
V
B1 B
O1 A1
O
A
B1 B
O1 h
Ox
研究旋转体问题时注意使用轴截面
A1
A R
随堂练习
4、圆柱形容器内壁底面半径为5cm,两个直径为5cm的玻璃小球浸没于容器的水中。若同时取
5
出这两个小球,则容器中的水面将下降 3
cm.
5、半径为R的三个小球两两外切放在桌面上,与这三个小球都外切的第四个小球与桌面也相切, 求这个小球的半径。
解:设球的内径是2xcm,那么球的质量为:
[ 4 (50)3 4 x3] 7.9 145000.
3 23
x3 11239.42,解得 x 22.4.
答:钢球是空心的.其内径约为45cm.
新知探究
例2、 如图表示一个用鲜花作成的花柱,它的下面是一个直径为1m、高为3m的圆柱形物体,上
10.9150 1635(朵)
答:装饰这个花柱大约需要1635朵鲜花.
新知探究
例3、如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的体积等于圆柱体积的 2 ; 3
(2)球的表面积等于圆柱的侧面积.
RO
随堂练习
(1)若球的表面积变为原来的2倍,则半径变为原来的 2 倍.
球的体积和表面积公开课一等奖优质课大赛微课获奖课件

O•
VABCD
D
1 3
3 2 4
2
6 1 2
3
B
1
3 r S全 3 2 2 3 r
V多面体
1 3
S
C 全
r
r内切球
6 2 S球 8 5 2
6
第26页
练习、三棱锥A – BCD两条棱 AB = CD = 6, 其余各棱长均为5,求三棱锥内切球体积。
取 CD 中点 E,连 AE、BE A
43
192π
r R
30o
第13页
球与多面体内切、外接
球半径r和正方体 棱长a有什么关系?
.r
a
第14页
一、 球体体积与表面积
①
V球
4
3
R3
二、球与多面体接、切
② S球面 4 R2
定义1:若一个多面体各顶点都在一个球球面上, 则称这个多面体是这个球内接多面体, 这个球是这个 多面体外接球 。
定义2:若一个多面体各面都与一个球球面相切, 则称这个多面体是这个球外切多面体, 这个球是这个多面体内切球 。
第11页
【点击双基】
1.下列四个命题中错误个数是
①通过球面上任意两点,能够作且只能够作一个球大
圆 ②球面积是它大圆面积四倍 ③球面上两点球面距
离,是这两点所在截面圆上以这两点为端点劣弧长
A.0 B.1 C.2 D.3
C
2.(江苏,4)一平面截一球得到直径为6 cm圆面,球心到这个平面距离是4 cm, 则该球体积是
球体积比本来增长了 _____2__2___1_ 倍;
2、两个半径为 1 铁球,熔化后成铸成一
个球,这个大球半径为 ______3_2__。
体积及体积公式解说稿

体积与体积公式
同学们,我们已经学习了长方体和正方体,也知道了长方体中相交与一点的三条棱的长度分别叫做长方体的长,宽,高。
而正方体是特殊的长方体,正方体中相交与一点的三条棱的长度叫做棱长。
长方体有6个面,相对的两个面向等。
表面积:(长×宽+长×高+宽×高)×2.正方体有6个面,6个面全相等。
表面积:6×边长×边长。
那什么是体积呢?体积又怎么计算呢?下面老师来重点讲一下体积及体积公式。
体积就是物体所占空间的大小。
物体所占空间不同,其体积也不同。
而体积就等于底面积乘以高,用字母表示为v=s h,而长方体和正方体底面的面积就是它们的底面积。
所以它们的体积公式为:
长方体体积=长×宽×高,用字母表示为:v=a·b·h
正方体体积=棱长×棱长×棱长,用字母表示为:v=a·a·a
其中要注意计量体积要用体积单位。
常用的体积单位有立方厘米,立方分米和立方米。
这就是长方体和正方体的体积及体积公式,谢谢大家!。
天眼体积公式范文

天眼体积公式范文
首先,我们需要明确球体的定义。
球体是由所有距离一个固定点相等
于半径的点所组成的几何体。
球体具有很多重要的性质和公式,其中包括
体积公式。
球体的体积公式是:V=(4/3)πr³,其中V表示体积,π表示圆周率,r表示球体的半径。
这个公式非常简洁明了,也是很容易理解的。
我们可
以看到,球体的体积与半径的三次方成正比,而与π的比例也是一个常数。
天眼的直径为500米,即半径r=250米(因为r是半径)。
将半径代入球体体积公式中,我们可以得到天眼的体积公式:
V=(4/3)π(250)³
经过计算,我们得到天眼的体积约为523亿立方米。
这是一个非常庞
大的数字,显示出了天眼的巨大规模和令人惊叹的设计。
天眼作为世界上最大的球面射电望远镜,它的体积对应着它的存储和
接收能力,足以收集大量的射电信号,帮助研究人员观测和研究宇宙的奥秘。
由于天眼具有较大的体积,它所能观测的范围也更广阔,能够接收到
更远的射电信号,探测更遥远的宇宙。
通过天眼体积公式,我们可以更好地理解和欣赏天眼的规模和功能。
它的建设和运作无疑是中国在天文学研究方面的一项伟大成就,也是世界
科学技术发展的重要里程碑。
总之,天眼的体积公式是计算球体体积的一种数学公式。
通过该公式,我们可以计算出天眼的巨大体积,进一步认识和理解天眼的规模和功能,
体会到科学研究的伟大力量。
星球体积公式

星球体积公式
星球体积公式是一个用来计算星球体积的数学公式。
它被广泛应用于各种领域,如天文学、地质学和物理学等。
这个公式可以帮助我们了解星球的大小和结构,以及它们对我们的生活有何影响。
星球体积公式的基本形式是:
V = (4/3) × π × r³
其中,V表示星球的体积,π是圆周率,r是星球半径。
这个公式的推导是基于几何学原理。
我们知道,球体是一个完全由曲面组成的几何体,其体积可以通过将球体分割成无限小的体积元来计算。
每个体积元的体积可以表示为dV = πr²dh,其中dh是体积元的高度。
通过对所有体积元进行积分,我们可以得到球体的体积公式。
星球体积公式的应用非常广泛。
在天文学中,它通常用于计算行星、卫星和恒星等天体的大小。
例如,我们可以使用这个公式来计算地球的体积,从而了解地球的大小和质量。
在地质学中,这个公式也经常用于计算火山、陨石坑和陨石等天然物体的体积。
此外,在物理学中,星球体积公式也可以应用于计算物体的密度和质量等参数。
当然,这个公式并不完美。
它假设星球是一个完美的球体,而实际
上很少有天体是完全圆形的。
此外,它也没有考虑星球的自转和形变等因素。
因此,在应用这个公式时,我们需要根据实际情况进行适当的修正和调整。
星球体积公式是一个非常有用的数学工具,可以帮助我们了解天体的大小和结构。
虽然它并不完美,但在许多领域仍然被广泛应用。
我们相信,在未来的研究中,这个公式还将发挥更大的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好! 谢谢!
格证明。
阿基米德(Archimedes. 约公元前287—212年)
研究中算史的日本专家三上义夫指出,从刘徽到祖 冲之父子通过“合盖”(即牟合方盖)得出球体积“可 谓中算史上几何处理方法之最高发达,荀与希腊阿基米 德之积分方法及其所言与外接圆柱之关系,一比较研究 之,亦一趣事也”
思考问题:刘徽、祖冲之父子、阿基米德都是蜚声中外的数 学家,他们如何解决球体的计算问题呢?
(1)
牟合方盖内切半球图
(2)
正方形内切圆
牟合方盖“内棋” 图
合盖“外棋”分解图Biblioteka 盖“外棋”截面图倒立阳马图
(1)
等轴圆柱及内切球
(2)
球体切割图
力学原理与球体积计算
1. 数学研究中的算法倾向与演绎倾向 2. “以棋验术”的直觉方法与“数学物理”方
法 3. “截面原理”与“有限迭加” 4. 问题求解与因果论证 5. 几何代数化与微积分的应用
一、刘徽的“牟合方盖”与祖暅的“幂势既同,则积不容 异”
——中算家对球体积的探求 二、阿基米德的“力学原理”与“穷竭法”
——古希腊学者对球体积公式的发现与证明 三、异曲同工、弹奏千古名篇
——球体积公式与古代数学研究传统
牟合方盖
开立圆术的分解
(1)
正方体内切正交圆柱图
(2)
牟合方盖图
(3)
1/8牟合方盖
中国数学史
祖冲之(公元429-500)
刘徽(生于公元250左右)
西方数学史
阿阿基基米米德德突这破一希成腊果古, 被典古时代期传几记何作定家性普研鲁究塔的 克传说统:,“重几视何定学量中研不究可,
能发找现到了更球难、做球的缺问、题椭,球
也体不体可积能公找式到及更抛简物练线、弓
更形清面楚积的公陈式述,和并证给明予。严”
球体积公式(数学史)
怎样计算球的体积 发现球体积公式的过程和方法 证明球体积公式的思路和方法
图1 用祖暅原理证明球体积公式
图2 用切割法证明球体积公式
图3 用定积分计算球体积
数学是人类文化的重要组成部分。运用数学史材 料进行数学教育是国际数学教育界共同关注的问题。
球体积公式的发现和证明,是度量几何发展进程 中具有标志意义的成果。
