最优化线性规划 (1)(1)

合集下载

最优化方法第二章(1)

2.1 线性规划的各种形式 1. 标准形式和典范形式如下形式的线称为线性规划的标准形式。 bi 称为右端项。采用向量－矩阵表示法，标准形式可以简写为。 T min c x; s.t. Ax b （2.2） x 0.
min c j x j j 1 n s.t. aij x j bi , i 1, 2, , m j 1 x j 0, j 1, 2, , n.
无关。
定理2.3 设 x D ,则
x R 引理2.2 设 A a1 , a2 , , an mn ， ( A) m ， D。则
D {x Ax b , x 0}
x 是（2.2）的基本容许解 x
是 D 的极点。从几何角度讲，例2.3中的约束条件 x1 x2 x3 6 x1 2 x2 4 x3 18 x1 , x2 , x3 0 表示空间一条直线在第一象限中的直线段部分。如图所示：
不失一般性，假定单位矩阵位于前 m 列，即典范形式呈现为
min c1 x1 c2 x2 cn xn s.t. x1 x2
其中 bi 0(i 1, 2,, m) 。用向量－矩阵表示法，那么（2.3）可简写成
x j 0,
a1, m 1 xm 1 a1, n xn b1 a2, m 1 xm 1 a2, n xn b2 （2.3） xm am , m 1 xm 1 am , n xn bm j 1, 2, , n
x1 x2 1 x1 x2 3 x1 , x2 0. 化为标准形式，并用图解法求解原问题，给出标准形式的解。
解对第1个约束引入松弛变量 x3 ，对第2个约束引入剩余变量 x4 。于是，该线性规划的标准形式为

线性规划的基本定理-最优化方法

j 1
j 1
现构造两个点X（1），X（2），使满足
X（1）=（x1+αλ1,…, xk+αλk ,0,…,0）T X（2）=（x1-αλ1,…, xk-αλk ,0,…,0）T
线性规划解的基本定理
定理2：设X是可行域D的极点，那么，X最多有m个正分量。
证明：设X=(x1，···xk，0，···，0)T，若k>m，由
z=λx+(1-λ)y
这说明当0 ≤ λ ≤1 时，λx+(1λ)y 表示以x.y为端点的直线段上的所有点，因而它代表以 x.y为端点的直线段。
一般地，如果x.y是n维欧氏空间Rn中的两点，则有如下定义：
如果 x=(x1…xn)T,y=(y1…yn)T是Rn中任意两点，定义z=λx+(1-λ)y(0≤λ≤1),z=(z1…zn)T 的点所构成的集合为以x,y为端点的线段，对应λ=0， λ=1的点 x, y叫做这线段的端点，而对应 0<λ<1的点叫做这线段的内点。
表明X不是D的极点，与已知条件矛盾，故k≤m。
线性规划解的基本定理
定理1.4：对标准形式的线性规划，基可行解与可行域的极点一一对应。
证明：首先证明极点必是基可行解。设X是极点，由定理1.3,可设X=(x1,…xk,0,…,0)T xj>0,k≤m 若X不是基可行解，由定理1.2，向P1,P2,…,Pk应线性相关。仿照定理1.3的证明过程，可推导出X 不是极点，与已知条件矛盾。故可知X是基可行解。
其次证明充分性。设X的正分量为x1，x2,…,xk，其对应的列向量P1,P2,…,Pk线性无关。显然k≤m。
若k=m，则P1,P2,…,Pk可用来构成一个基，所以X是基本解。而已知X是可行解，故X又是基可行解。

重庆大学最优化方法习题答案

ax z = x1 + x2 3x1 + x2 ≥ 2
s.t.x1 + 2x2 ≤ 5 x1, x2 ≥ 0
解：根据条件，可行域为下面图形中的阴影部分，，有图形可知，原问题在 A 点取得最优值，最优值 z=5
（2） min z = x1 − 6x2 2x1 + x2 ≤ 1
s.t.− x1 + x2 ≤ 7 x1, x2 ≥ 0
解：图中阴影部分表示可行域，由图可知原问题在点 A 处取得最优值，最优值 z=-6.
（3） max z = 3x1 + 2x2
− x1 + x2 ≤ 1 s.t.x1 − 2x2 ≥ −4
x1, x2 ≥ 0
解：如图所示，可行域为图中阴影部分，易得原线性规划问题为无界解。
所以 x(2) , x(4) , x(6) 是原问题的基可行解， x(6) 是最优解，最优值是 z = −3 。
（2） max z = x1 + x2 − 2x3 + x 4 − x5
x1 + x2 + x3 + x4 = 1 s.t.− x1 + 2x2 + x5 = 4
xi ≥ 0,i = 1,2,3,4,5
解：易知
x1
的系数列向
量
p1
= 1− 1
，
x2
的系数列向
量
p2
=
1
2
，
x3
的系
数列向量
1
1
0
p3
=
0
，
x4
的系数列向量
p4
=
0
，
x5
的系数列向量

最优化方法-线性规划的基本定理

其次证明充分性。设X的正分量为x1，x2,…,xk，其对应的列向量P1,P2,…,Pk线性无关。显然k≤m。
若k=m，则P1,P2,…,Pk可用来构成一个基，所以X是基本解。而已知X是可行解，故X又是基可行解。
若k<m，由于A的秩为m，比可从A中再挑出m-k个列向量，与P1,P2,…,Pk ，一起构成一个线性无关极大组，即为一个基，由此可知X是基可行解。
定义1.7：设集合S是n维欧式空间En中的闭凸集，d是En中的非零向量。如果对于S的每个点X，以及一切非负的数λ，都有
X+λd∈S，λ≥0
则称向量d是凸集S的一个方向。如果d1， d2是S的方向，且d1≠αd2， ∀ α>0，则d1， d2是两个不同的方向。
进一步，如果d是凸集S的一个方向，且不能表示为S的另外两个不同的方向的正组合，则称d是S的一个极方向。
约定A是行满秩的m行n列矩阵。
2、基、基向量、基变量、基本解、基本可行解、可行基、最优解、最优基
基：矩阵A中一个m阶非奇异子矩阵基向量：基的列向量基变量：基向量对应的变量基本解：非基变量全为零的解
基本可行解：非基变量为零，基变量都大于等于零的解
可行基：基可行解对应的基最优解：基本解中使目标函数最大的解最优基：最优解对应的基
X=λX（1）+（1-λ）X（2）
上式的分量表达形式为显然，当j>m时，有
x
j
xj
xj1 xj1x j2
1 0

xj2
,
j

1,
2,
,n
m
再由于X（1），X（2）均是可行点，故可推知 xjiPj b,i 1, 2
两式相减，得

线性规划解决最优化问题的数学方法

线性规划解决最优化问题的数学方法线性规划是一种常见的数学方法，用来解决最优化问题。

它能够帮助我们在给定一组线性约束条件下，找到最优的目标函数值。

在实际应用中，线性规划方法被广泛用于制定优化决策、资源配置、生产计划等领域。

本文将介绍线性规划的基本概念、公式以及解决最优化问题的具体步骤。

一、线性规划的基本概念与公式线性规划的目标是在给定约束条件下，找到使目标函数（也称为优化函数）取得最大或最小值的解。

它包含三个基本要素：决策变量、约束条件和目标函数。

1. 决策变量：决策变量是问题中需要确定的变量，它们可以是实数、整数或布尔变量。

决策变量的取值范围和类型由问题的实际情况决定。

2. 约束条件：约束条件是对决策变量的限制条件，它们可以是线性等式或不等式。

约束条件用于描述问题的限制条件，例如资源约束、技术限制等。

3. 目标函数：目标函数是求解问题的目标，它可以是最小化或最大化一个线性函数。

目标函数的形式通常是关于决策变量的线性组合。

线性规划问题可以用如下的标准形式表示：最小化 Z = c₁x₁ + c₂x₂ + ... + cₙxₙ约束条件：a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ ≤ b₁a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ ≤ b₂...aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ ≤ bₙ非负约束：x₁ ≥ 0, x₂ ≥ 0, ... , xₙ ≥ 0其中，Z为目标函数值，c₁, c₂, ... , cₙ为目标函数的系数，aᵢₙ为约束条件的系数，b₁, b₂, ... , bₙ为约束条件的常数项，x₁, x₂, ... , xₙ为决策变量。

二、线性规划的解决步骤解决线性规划问题一般可以遵循以下步骤：1. 定义问题：明确问题的目标函数、约束条件和决策变量，并将其转化为标准形式。

2. 建立数学模型：根据问题的实际情况，根据标准形式建立数学模型，将问题转化为求解目标函数最大或最小值的数学问题。

最优化方法：第2章线性规划

Z=CBB-1b+(σm+1,
σm+k ,
xm+1
σn
)
CB B-1b+σ m+k
xn
因为 m+k 0，故当λ→+∞时，Z→+∞。
用初等变换求改进了的基本可行解
假设Ｂ是线性规划 maxZ=CX,AX=b,X 0的可行基，则
AX=b
(BN)
XB XN
b
(I,B-1 N)
➢ 若在化标准形式前，m个约束方程都是“≤”的形式，那么在化标准形时只需在一个约束不等式左端都加上一个松弛变量xn+i (i=12…m)。
➢ 若在化标准形式前，约束方程中有“≥”不等式，那么在化标准形时除了在方程式左端减去剩余变量使不等式变成等式以外，还必须在左端再加上一个非负新变量，称为人工变量．
单纯形法简介
考虑到如下线性规划问题 maxZ=CX AX=b X 0
其中Ａ一个m×n矩阵，且秩为m，ｂ总可以被调整为一个m维非负列向量，Ｃ为n维行向量，Ｘ为n维列向量。
根据线性规划基本定理：如果可行域Ｄ={ Ｘ∈Ｒn / ＡＸ=ｂ，Ｘ≥0}非空有界，则Ｄ上的最优目标函数值Ｚ=ＣＸ一定可以在Ｄ的一个顶点上达到。这个重要的定理启发了Dantzig的单纯形法，即将寻优的目标集中在D的各个顶点上。
非基变量所对应的价值系数子向量。
要判定 Z=CBB-1b 是否已经达到最大值，只需将
XB =B-1b-B-1NX N 代入目标函数，使目标函数用非基变量
表示，即：
Z=CX=(CBCN
)
XB XN
=CBXB +CNXN =CB (B-1b-B-1NXN )+CNXN

最优化方法-线性规划

引言
对线性规划贡献最大的是美国数学家G.B.Dantig(丹捷格)，他在1947年提出了求解线性规划的单纯形法（Simple Method），并同时给出了许多很有价值的理论，为线性规划奠定了理论基础。在1953年，丹捷格又提出了改进单纯形法， 1954年Lemke(兰母凯)提出了对偶单纯形法（dual simplex method）。在1976年， R. G. Bland 提出避免出现循环的方法后，使线性规划的理论更加完善。但在1972年，V. Klee和G .Minmty 构造了一个例子，发现单纯形法的迭代次数是指数次运算，不是好方法——并不是多项式算法（多项式算法被认为是好算法），这对单纯形法提出了挑战。
min Ζ ’=-Ζ =-(c1x1+c2x2+…+cnxn)
（三）若xj<0，令xj=xj’-xj”,xj’≥0,xj”≥0 利用矩阵和向量的符号，线性规划问题可以写为
minΖ =CX s.t. AX=b X≥0 minΖ =CX s.t. Σ xjPj=b C=(c1,c2, …,cn)
a11 a12 …a1n A= ┆ ┆ ┆ am1 am2 …amn b1 b2 ┆ bm x1 x2 X= ┆ xn
化一般问题为标准形式： (一)若ak1x1+ak2x2+…aknxn≤bk 加一变量xn+k≥0（松驰变量），改写为 ak1x1+ak2x2+…aknxn+xn+k=bk 若ak1x1+ak2x2+…aknxn≥bk 减一变量xn+k≥0(剩余变量），改写为 ak1x1+ak2x2+…aknxn-xn+k=bk (二) 若目标函数为maxΖ =c1x1+c2x2+…+cnxn

【最优化】线性规划基本概述

【最优化】线性规划基本概述什么是线性规划：线性规划就是特殊的有约束优化问题，⽬的是通过⼀组线性等式或者不等式下得可⾏集合点，来寻找⼀个⽬标函数的极值；通常来说，极值可以是极⼤极⼩，但是⼀般采⽤极⼩，看到相关的案例，求极⼤值直接前⾯加负号变为极⼩值即可；线性规划的基本问题形式：线性规划问题可以采⽤最基本的数学符号进⾏描述：minimize c T xsubject to Ax=bx>=0;对于上述可以这样理解，对于某个参数向量x，所满⾜的可⾏域条件为Ax=b，也成为约束⽅程，可⾏域内点集由该⽅程组确定，其中值得注意的是可⾏域条件不⼀定为等式，只需要线性即可；c T x为⽬标等式，两个都为向量，所以值为⼀个单值，旨在找到⼀个极⼩值，使得满⾜minimize的要求；因此，对于任何的问题，都可以转为标准的问题形式进⾏求解；其中，⽐较有意思的是约束条件实际定义了求解的维数，也就是如何直观的通过对x的选择，使得c T x最⼤；如果从空间思想来考虑，就可以分为简单⼆维和三位情况下的最优化；如果是简单的⼆维情况：c T x相当于ax1+bx2，相当于⼆维平⾯上的⼀条直线，其中要求的是如何选定x1,x2的值，使得k=ax1+bx2存在最⼤最⼩值（因为向量c相当于已经确定了斜率）；⽽约束条件也为围成的⼀系列可⾏域，在⼆维平⾯内选择点，使得k=ax1+bx2最⼤，也就是和x2轴交点值最⼤；如下图所⽰，书上也给了⼀个很好的例⼦：⽽对于多维情况，则需要涉及凸多⾯体问题：c T x中的c的个数已经限定了多维空间下n的⽬标函数；约束条件Ax=b，其中A为m*n维数向量，定义了m个超平⾯所围成的⼀个凸多⾯体，并且假设该多⾯体⾮空有界；书上讨论了很多种情况，例如多⾯体超平⾯的维数问题；但是这⾥还是说⼀下常规的转换求法；根据c T x得到⼀个超平⾯c T x=0；找到⼀个⽀撑超平⾯c T x=β，使得整个胞体M在半平⾯，且M和超平⾯交集为M'；所以⽆论任何属于负半区的点y，都会有c T y<β；⽽任何属于M’的点y，都有c T y=β；所以可得到⽀撑超平⾯的点是极值点，同样如果⽀撑超平⾯为单点情况下，仍然适⽤；线性规划问题的标准型：对于标准型，和之前谈到的基本形式类似，实对所有⾼维线性规划下的问题做⼀个基本的形式定义；minimize c T xsubject to Ax=bx>=0值得注意的是Ax=b的条件，所有⼤于等于的线性条件都应该转为等于进⾏讨论，个⼈认为是使得所构成的解集范围是多胞体⽽⾮多个超平⾯围成的范围；⽽对于⾮标准形式，往往有Ax>=b或者Ax<=b，所以通过变换来变成⼀般的标准形式；其中注意下不同的说辞，Ax>=b,Ax<=b，⽆⾮就是加减y⽽已，保持y>=0即可，两种情况称之为剩余变量y和松弛变量y，名字记不记住感觉⽆伤⼤雅；基本解：当给出线性规划的基本形式之后，就可以对基本解进⾏构造；总的来说，解和传统的线性齐次、⾮齐次⽅程组不同，主要关注两个类型：1.基本解；2.可⾏解；两者其实有交集，交集的形式为基本可⾏解；基本解求法：可⾏解求法：可⾏解本质就是满⾜标准形式的解，也就是满⾜Ax=b,且x>=0的解，两个条件缺⼀不可；⽽基本可⾏解就是既为基本解满⾜x>=0的解；对于书上，有给出的相关例题，说明怎么求解可⾏解和基本解：基本解的性质：最优可⾏解：能够使得⽬标函数c T x取最⼩值的解；最优基本可⾏解：该最有可⾏解为基本解；其中对于线性规划来说，有挺重要的⼀条性质：1.如果存在可⾏解，则⼀定存在基本可⾏解；2.如果存在最优可⾏解，则必定存在最优基本可⾏解；基本可⾏解的实际意义：如果对于⼀个凸集，求⽬标函数极值，则必定取值点必定是凸集上的极点，对应的就是可⾏基本解；所以最后只需要寻找可⾏基本解中哪⼀个可以使得⽬标函数c T x最⼤(最⼩)，就可以得到最优基本可⾏解；【注意】关于为什么要找极点：根据前⾯⼆维推⼴⾄多维的推导，都是根据⽀撑超平⾯来进⾏极值寻找，所以找极值点也就相当于找使得距离原点超平⾯最远的⽀撑超平⾯；所以有定理：如若存在⼀个可⾏解组成的凸集，集合中的所有n维向量x满⾜Ax=b，x>=0，其中A维m*n维向量，则x是凸集中的极值点当且仅当x是Ax=b，x>=0的基本可⾏解；证明过程如下所⽰：。

数值最优化(李董辉)第九章线性规划

1 ' 2 ' 3 ' 1 17
1 x 3 2 x1 x5 2 x 4 16 4 x1 1 x2 3 x5 4
1 ' 2 ' 3 ' 1 17
令非基变量
x1 x 5 0
得到另一基可行解
例9.2.3
试以下例来讨论如何用单纯形法求
（生产计划安排问题）某工厂在计划期内要安排生产Ⅰ、 Ⅱ两种产品，已知生产单位产品所需的设备台时及A、B 两种原材料的消耗，如表1-1所示。
资源产品
设
备
原材料 A 原材料 B
Ⅰ 1 4 0
Ⅱ 2 0 4
拥有量
8台时 16 kg 12 kg
该工厂
• 每生产一件产品Ⅰ可获利2元， • 每生产一件产品Ⅱ可获利3元， • 问应如何安排计划使该工厂获利最多?
x1 x2 a 1 , m 1 x m 1 a 1 n x n b1 a 2 , m 1 x m 1 a 2 n x n b 2
1 22
x m a m , m 1 x m 1 a m x n b m x
x
(1)
(0,3,2,16,
0) , 且 z 9
T
z 9 2 x1
3 4
x5
• 从目标函数的表达式可以看到，非基变量x1的系数是正的，说明目标函数值还可以增大，X(1) 还不是最优解。 • 于是再用上述方法，确定换入、换出变量，继续迭代，再得到另一个基可行解X(2) X(2)=(2,3,0,8,0)T • 再经过一次迭代，再得到一个基可行解X(3) X(3)=(4,2,0,0,4)T • 而这时得到目标函数的表达式是： z=14-1.5x3-0.125x4 (1-19)

最优化计算方法-第5章(线性规划)

第五章线性规划线性规划（Linear Programming，简记为LP）是数学规划的一个重要的分支，其应用极其广泛．1939年，前苏联数学家康托洛维奇（Л.B.Kah ）在《生产组织与计划中的数学方法》一书中，最早提出和研究了线性规划问题．1947年美国数学家丹泽格（G. B. Dantzig）提出了一般线性规划的数学模型及求解线性规划的通用方法─单纯形方法，为这门科学奠定了基础．此后30年，线性规划的理论和算法逐步丰富和发展．1979年前苏联数学家哈奇扬提出了利用求解线性不等式组的椭球法求解线性规划问题，这一工作有重要的理论意义，但实用价值不高．1984年在美国工作的印度数学家卡玛卡(N. Karmarkar)提出了求解线性规划的一个新的内点法，这是一个有实用价值的多项式时间算法．这些为线性规划更好地应用于实际提供了完善的理论基础和算法．第一节线性规划问题及其数学模型一、问题的提出例1 某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品，已知条件如表所示。

问应如何安排计划使该工厂获利最多？ⅠⅡ现有资源设备原材料A 原材料B 14248台时16kg12kg每件利润23ⅠⅡ现有资源设备原材料A 原材料B 1402048台时16kg12kg每件利润23解: 设x 1、x 2 分别表示在计划期内产品Ⅰ、Ⅱ的产量。

12max 23z x x =+..s t 1228x x +≤1416x ≤2412x ≤12,0x x ≥二、线性规划问题的标准型112211112211211222221122123max ..,,0n nn n n n m m m mn n mn z c x c x c x s t a x a x a x b a x a x a x b a x a x a x b x x x x =+++⎧⎪+++=⎪⎪+++=⎨⎪⎪+++=⎪≥⎩，，其中1,,0m b b ≥11max ..,1,2,,0,1,2,,nj jj nij j i j j z c x s t a x b i mx j n=====≥=∑∑ 12(,,,)T n c c c =c 12(,,,)Tn x x x =x 12(,,,)Tm b b b =b 111212122212n nm m mn a a a a a a a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A 12[,,,]n = p p pmax ..()Tz s t ⎧=⎪=≥⎨⎪≥⎩c x Ax b b x 001max ..()Tnj j j z s tx =⎧=⎪⎪=≥⎨⎪⎪≥⎩∑c xp bb x 00对于不是标准形式的线性规划问题，可以通过下列方法将线性规划的数学模型化为标准形式：（1）目标函数的转换对min z 可以化max()z -（2）右端项的转换对0i b <，给方程两边同时乘以1-（3）约束条件的转换约束条件为≤方程左边加上一个变量,称为松弛变量约束条件为≥方程左边减上一个变量,称为剩余变量（4）变量的非负约束变量j x 无限制时，令,,0j j j j j x x x x x ''''''=-≥变量0j x ≤时，令j jx x '=-例将下列线性规划模型转化为标准形式12312312312312min 23..7232500x x x s t x x x x x x x x x x x -+-⎧⎪++≤⎪⎪-+≥⎨⎪--=-⎪≥≥⎪⎩，解（1）变量的非负约束令345x x x =-1245max 233x x x x -+-..s t 612457x x x x x ++-+=712452x x x x x -+--=12453225x x x x -++-=§2 两变量线性规划问题的图解法例1 求下列线性规划的解12121212max ..284300z x x s t x x x x x x =+⎧⎪+≤⎪⎪≤⎨⎪≤⎪≥≥⎪⎩，解（1）画可行域c A B D C 2x 1x O （2）画出目标函数的梯度向量：（3）作目标函数的一条等值线,120x x z +=将等值线沿梯度方向移动当等值线即将离开可行例2 求下列线性规划的解12121212max 2..284300z x x s t x x x x x x =+⎧⎪+≤⎪⎪≤⎨⎪≤⎪≥≥⎪⎩，解（1）画可行域c A B D C 2x 1x O （2）画出目标函数的梯度向量：（3）作目标函数的一条等值线,1202x x z +=将等值线沿梯度方向移动当等值线即将离开可行域时与可行域“最后的交点点为问题的最优解例3 求下列线性规划的解12121212max ..2200z x x s t x x x x x x =+⎧⎪-≤⎪⎨-≥-⎪⎪≥≥⎩，c2x 1x O无解例4 求下列线性规划的解12121212min 3..123600z x x s t x x x x x x =-⎧⎪≤⎪⎨≥⎪⎪≥≥⎩++，2x 1x O线性规划问题的性质：（1）线性规划的可行域为凸集，顶点个数有限．若可行域非空有界，则可行域为凸多边形．（2）线性规划可能有唯一最优解，可能有无数多个最优解，也可能无解最优解．无最优解可能是目标函数在可行域上无界，也可能可行域为空集．（３）若线性规划有最优解，则最优解必可在可行域的某个顶点达到．若两个顶点都为最优解，那么这两点连线上的所有点都是线性规划的最优解．§3 线性规划解的概念及其性质1 线性规划解的概念考虑线性规划问题max ..()Tz s t ⎧=⎪=≥⎨⎪≥⎩c x Ax b b x 00定义.1 矩阵A 中任何一组m 个线性无关的列向量构成的可逆矩阵B 称为线性规划的一个基矩阵与这些列向量对应的变量称为基变量(basis variable ）其余变量称为基对应的非基变量(nonbasis variable ）B 若设一个基为12(,,)m B p p p = ，12,,,m x x x ——为基B 对应的基变量1,,m n x x + ——为基B 对应的非基变量1B m x x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1m N n x x x +⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦12(,,,)m m n ++= N p p p (,)=A B N 从而令=Ax b 则(,)N x ⎡⎤=⎢⎥⎣⎦B x B N b11B Nx B b B Nx --=-B N Bx Nx b+=令0N x =则1B x B b-=10B b -⎡⎤⎢⎥⎣⎦——基本解（basis solution ）满足10B b -⎡⎤≥⎢⎥⎣⎦,=≥0Ax b x 的基本解——基本可行解（basis feasible solution ）对应的基称为可行基（feasible basis ）．B 可以写成即:定义4 若基本可行解中所有基变量都为正，这样的基本可行解称为非退化解（non-degenerate solution）．若基本可行解中某基变量为零，这样的基本可行解称为退化解（degenerate solution）．例1212112max ..28400z x x s t x x x x x =-⎧⎪+≤⎪⎨≤⎪⎪≥≥⎩，标准化得：12123141234max ..28400,00z x x s t x x x x x x x x x =-⎧⎪++=⎪⎨+=⎪⎪≥≥≥≥⎩，，12341210(,,,)1001⎡⎤==⎢⎥⎣⎦A p p p p 子阵是否为基基变量非基变量基本解目标函数值134(,)=B p p 34,x x 12,x x (0,0,8,4)是231(,)=B p p 31,x x 24,x x (4,0,4,0)312(,)=B p p 12,x x 34,x x (4,2,0,0)424(,)=B p p 24,x x 13,x x (0,4,0,4)-4514(,)=B p p 14,x x 23,x x (8,0,0,4)-是是是是042基本可行解1x O(4,0)(4,2)(0,4)(8,0)2x 顶点2 解的判别定理定理1 最优解的判别准则设B 为线性规划LP 的一个基，1(1)0-≥B b 1(2)T T--≥0Bc B A c 则基对应的基本可行解1-⎡⎤⎢⎥⎣⎦0B b 是LP 的最优解．1(1,2,,)σ--== TBj j j c B p c j n 为变量对应的检验数j x 112[0,,0,,,]σσσ-++-= ，T TBm m n c B A c 显然基变量对应得检验数为零．定理2 无穷多个最优解的判别定理在线性规划的最优解中，某个非基变量对应的检验数为零，则线性规划有无数多最优解．定理3 无界解的判别定理设B 为线性规划的一个可行基，若基本可行解中s x 对应的检验数0σ<s ，且1-≤0s B p 则线性规划具有无界解（或称无解）．某非基变量§3.4 单纯形表设B 为线性规划的一个基，x 为对应的可行解，则=Ax b两边同乘得1-B 11--=B Ax B b两边同乘得T Bc 11T T --=BBc B Ax c B b T z =c xTz -=c x 11T T --+-=TBBz c B Ax c x c B b 11(T T --+-=)TBBz c B A c x c B b1111()T TT z ----⎧+-=⎨=⎩BBc B A c x c B b B Ax B b 11111T T Tz ----⎡⎤⎡⎤-⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦0BBc B b c B A c x B A B b 定义矩阵1111TT----⎡⎤-⎢⎥⎣⎦T BBc B b c B A c B bB A 为基B 对应的单纯形表（table of simplex ）,记为()T B1111()T T----⎡⎤-=⎢⎥⎣⎦T BBc B b c B A c T B B bB A 检验数函数值基变量的值各变量的系数100T b -=Bc B b 101020(,,,)--= T TBn c B A c b b b 10201-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥ b b B b则单纯形表可写成000101011102()⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦B n n m m mn b b b b b b T b b b 1112121222111112(,,)---⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦n n n m m mn b b b b b b B A B p B p bb b上例中1212112max ..28400z x x s t x x x x x =-⎧⎪+≤⎪⎨≤⎪⎪≥≥⎩，标准化得：121231412max ..28400z x x s t x x x x x x x =-⎧⎪++=⎪⎨+=⎪⎪≥≥⎩，12341210(,,,)1001⎡⎤==⎢⎥⎣⎦A p p p p 子阵是否为基基变量非基变量基本解目标函数值134(,)=B p p 34,x x 12,x x (0,0,8,4)是231(,)=B p p 31,x x 24,x x (4,0,4,0)312(,)=B p p 12,x x 34,x x (4,2,0,0)424(,)=B p p 24,x x 13,x x (0,4,0,4)-4514(,)=B p p 14,x x 23,x x (8,0,0,4)-是是是是042基本可行解1x O(4,0)(4,2)(0,4)(8,0)2x 顶点13410(,)01⎡⎤==⎢⎥⎣⎦B p p 231(,)=B p p 12341210(,,,)1001⎡⎤==⎢⎥⎣⎦A p p p p T(0,0)=B C 10()T⎡⎤-=⎢⎥⎣⎦c T B b A 34011008121041001z x x -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦23140101()4021141001x x ⎡⎤⎢⎥=-⎢⎥⎢⎥z T B 121101--⎡⎤=⎢⎥⎣⎦B 31401014021141001z x x ⎡⎤⎢⎥−−→-⎢⎥⎢⎥⎣⎦T(0,1)=B C单纯形表的特点：1、基变量对应的检验数为零2、基变量的系数构成单位阵§5旋转变换（基变换）设已知12(,,,,,)= r m j j j j B p p p p T()=B 1 r m j j j z x x x 1sn x x x 0001001011110102⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦sn s n r r rs rn m m ms mn b b b b b b b b b b b b b b b b为了将s x 变为基变量，而将r j x 变为非基变量，必须使表中的第s 列向量变为单位向量，变换按下列步骤进行：（1）将()T B 中第r 行，第s 列的元素化为1．01(,,,,,1,,) rj r rnr rs rs rs rsb b b b b b b b （2）将()T B 中第s 列的的其余元素化为0．0101(,,,,,0,,)---- is rn is rj is r is r i i ij in rs rs rs rsb b b b b b b b b b b b b b b b由此得出变换后矩阵中各元素的变换关系式如下，其中,01== ，，，rjrj rsb b j nb ,,01,01=-≠== ，，，，，，is rjij ij rsb b b b i r i m j nb 变换式称为旋转变换rs b 称为旋转元，r称为旋转行称为旋转列，s s x 称为入基变量，称为出基变量，r j x {,}r s定理3.5.1,01== ，，，rj rj rsb b j n b ,,0,01=-≠== ，，，，，is rj ij ij rsb b b b i r i m j n b 在变换之下，将基12(,,,,,)= r m j j j j B p p p p 的单纯形表变为基12(,,,,,)= m j s j j B p p p p 的单纯形表第6节单纯形法基本思路是：线性规划(通常是求最小值的形式)若有最优解，其必定在可行域(在相应几何空间中是一个凸多面体)的顶点达到，故从某一个顶点出发，沿着凸多面体的棱向另一顶点迭代，使得目标函数的值增加,经过有限次迭代，将达到最优解点.1.入基变量及出基变量的确定入基变量的确定由上面可知，目标函数用非基变量表示的形式为01n j jj m z z x σ=+=-∑若某检验数0j σ<则j x 的系数大于零，将j x 由零变为非零，目标函数值增大．所以，为了使的取值目标函数值增加，可以将某检验数0j σ<对应的非基变量j x 中的某个变为基变量．{}min 0j s j σ=<则s x 可选作为入基变量．即：在负检验数中，列标最小的检验数对应的非基变量入基．２．出基变量的确定在确定出基变量时应满足两个原则：（1）目标函数值不减；（2）保证新的基本解为基本可行解．0min 0,0i is is b b i m b θ⎧⎫=>≤≤⎨⎬⎩⎭min ,00i is is b r i b i m b θ⎧⎫==>≤≤⎨⎬⎩⎭，2 单纯形法设已知一个初始可行基及B T()B 基变量指标集合为{}1,,B m J j j = 非基变量的指标集合为{}1,2,,\N BJ n J =单纯形法若所有()00j N b j J ≥∈，则停止，最优解为0,1,,0,ij i j N x b i m x j J **⎧==⎪⎨=∈⎪⎩否则转（2）．（1）最优性检验（2）选入基变量{}0min 0,j N s j b j J =<∈若()01~is b i m ≤=,则停止,(LP)无最优解，否则转(3)（3）选出基变量0min 0,0i is is b b i m b θ⎧⎫=>≤≤⎨⎬⎩⎭0min ,00i is is b r i b i m b θ⎧⎫==>≤≤⎨⎬⎩⎭，（4）作{},r s 旋转运算,01rj rj rsb b j n b == ，，，,,01,01is rj ij ij rsb b b b i r i m j n b =-≠== ，，，，，，得B 的单纯形表()()ijT B b =，以ij b 代替ij b ，转(1)例1 求线性规划问题的解解标准型为:121231425max 2328416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥12121212max 2328416.412,0z x x x x x s t x x x =++≤⎧⎪≤⎪⎨≤⎪⎪≥⎩12123142512345max 2328416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥⎩-20-381612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢0T()B =0345[,,]B p p p =00T()T c B bA ⎡⎤-=⎢⎥⎣⎦-20-381612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣0T()B =8/116/408-3441202101001/400400135z x x 12345x x x x x 01/20⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢1/4-41x08-3441202101001/400400135z x x 12345x x x x x 01/20⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/4-1x 4/212/40140244011/201001/40002-15z x 12345x x x x x 3/21/80⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/8-1x 32x 1/2例2求线性规划问题的解解标准型为:121231425max 228416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥12121212max 228416.412,0z x x x x x s t x x x =++≤⎧⎪≤⎪⎨≤⎪⎪≥⎩12123142512345max 228416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥⎩-10-281612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢0T()B =0345[,,]B p p p =00T()T c B bA ⎡⎤-=⎢⎥⎣⎦-10-281612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣0T()B =8/116/404-2441202101001/400400135z x x 12345x x x x x 01/40⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢1/4-41x0-2441202101001/400400135z x x 12345x x x x x 00⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/4-1x 4/212/4080244011/201001/400015z x 12345x x x x x 100⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/8-1x 32x 41/42-1/2080244011/201001/400015z x 12345x x x x x 100⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/8-1x 2x 2T 0803280101/410101/2-004-12z 12345x x x x x 00⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣01x 2x 42-1/25x 11212x k x k x =+12120,1,1k k k k ≤≤+=全部最优解为§7 两阶段法第二阶段从初始可行基开始，用单纯形法求解原问题．（LP ）max ..(0)0T z c x s t Ax b b x ⎧=⎪=≥⎨⎪≥⎩（ALP ）max ..0()T w s t z ⎧=-⎪-=⎪⎨+≥⎪⎪≥⎩00T e y c x A =b b x y x 第一阶段引入人工变量，构造辅助问题，求辅助问题的最优解，得出原问题的初始可行基及对应的基本可行解．（ALP）12112211112211121122222211212312max..0 ,,,,0mn nn nn nm m mn n m mn mw y y ys t z c x c x c xa x a x a x y ba x a x a x y ba x a x a x y bx x x x y y y=----⎧⎪----=⎪⎪++++=⎪++++=⎨⎪⎪++++=⎪⎪≥⎩，，，，，121111211112122122212000000100()010001m m m m i i i in i=1i i i n n n m m m mn b a a a c c c b a a a T B b a a a b a a a ===⎡⎤----⎢⎥⎢⎥---⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦∑∑∑∑。

最优化方法习题答案

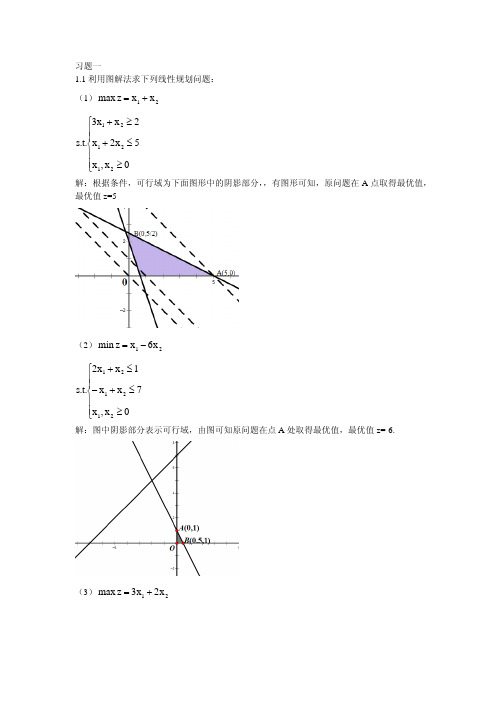
习题一1.1利用图解法求下列线性规划问题：（1）21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解：根据条件，可行域为下面图形中的阴影部分，，有图形可知，原问题在A 点取得最优值，最优值z=5（2）21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解：图中阴影部分表示可行域，由图可知原问题在点A 处取得最优值，最优值z=-6.（3）21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解：如图所示，可行域为图中阴影部分，易得原线性规划问题为无界解。

（4）21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解：由图可知该线性规划可行域为空，则原问题无可行解。

1.2 对下列线性规划问题，找出所有的基解，基可行解，并求出最优解和最优值。

（1）4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解：易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1，2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2，3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3，4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。

①因为21p ,p 线性无关，故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ，令非基变量为0x x 43==，得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21，所以得到一个基解)0,0,311,31(x )1(-=是非基可行解； ②因为31p ,p 线性无关，可得基解)0,511,0,52(x)2(=，543z 2=；③因为41p ,p 线性无关，可得基解611,0,0,31(x )3(-=，是非基可行解；④因为32p ,p 线性无关，可得基解)0,1,2,0(x )4(=，1z 4-=；⑤因为42p ,p 线性相关，42x ,x 不能构成基变量； ⑥因为43p ,p 线性无关，可得基解)1,1,0,0(x )6(=，3z 6-=；所以)6()4()2(x ,x ,x是原问题的基可行解，)6(x 是最优解，最优值是3z -=。

最优化方法以往填空题

（1）线性规划1212121max 23..43510x x s t x x x x x -+≤-+≥-≥的对偶规划为。

（2）用乘子法求解问题12min ()..0f x s t x x -=，其增广Lagrange 函数为。

（3）在三维空间3R 中，集合22{(,,)|1,0,0,0}x y z x y x y z +≤≥≥≥的极点构成的集合为。

（4）用黄金分割法求解某个函数在区间[-5,1]上的极小点，若要求缩短后的区间的长度小于1，则需要计算函数值的次数为。

（5）对二次函数22121()2f x x x =+，取初始点(0)(2,1)T x =，用最速下降法一步得到的下一迭代点(1)x= 。

（6）函数2212112212(,)221f x x x x x ax x x =+++++为严格凸函数，则常数a 的取值范围是。

（7）对于二次规划22121212121212min 22246..2055000x x x x x x s t x x x x x x +-----≥--≥≥≥，点(0,1)T的有效集为，写出在(0,1)T的一个可行下降方向：。

1）线性规划1212122min 2..243510x x s t x x x x x --≥-+≤≤的对偶规划为。

（2）用外罚函数法求解问题12min ()..0f x s t x x -=，其增广目标函数为。

（3）用黄金分割法求函数在[0,1]上的极小点，第一步所取的两个点为。

（4）若221212()3f x x x ax x =++为严格凸函数，则a 的取值范围是，用Newton 法求该函数的极小点，取(0)(2,3)T x=，迭代一步得到的点为。

（5）在最速下降法，Newton 法，FR 方法，DFP 方法，BFGS 方法中不具备二次终止性的算法为。

（6）已知两个向量12(1,),(1,1)T T p a p ==-关于矩阵2113⎡⎤⎢⎥⎣⎦共轭，则a = 。

最优化方法习题答案

x3
-M
0
0
0
5
-1
1
2
x4
x5
1+ 2 M
0
3
ห้องสมุดไป่ตู้
x2
1 3
1
x5
2 3
0
以 x1 为换入基， x5 作为换出基有
-1- M 3
1 3 1
3
-M
0
0
0
5
3
-1
1
1
3
x1
x2
x3
x4
x5
0
x2
0
x1
1
0
1
2
1
1
2
0
1
2
3
3 M
-5.5
2
2
1
1
1.5
2
2
3 3
0.5
22
以 x 4 换入， x 2 换出有
⑤因为 p2 , p4 线性相关， x 2 , x 4 不能构成基变量；
⑥因为 p3, p4 线性无关，可得基解 x(6) (0,0,1,1) ， z6 3 ；
所以 x(2) , x(4) , x(6) 是原问题的基可行解， x(6) 是最优解，最优值是 z 3 。
（2） max z x1 x2 2x3 x4 x5
x1 2x2 3x3 4x4 7 s.t.2x1 x2 x3 2x4 3
x1, x2 , x3, x4 0
解：易知
x1 的系数列向量
p1

1

2
，x 2
的系数列向量
p2

2
1

第二章最优化线性规划

D1+D2=R2是凸集
第七页，共一百七十一页。
7
凸集的线性组合是凸集.
定义2.1.2 k
设xi∈
Rn,i=1,…,k,实数i≥0,
则 x i xi 称为x1,x2, …,xk的凸组合.
i 1
k
i 1,
i1
两点的凸组合
(zǔhé)
三点的凸组合多点的凸组合
容易(róngyì)证明:凸集中任意有限个点的凸组合仍然在该凸集中.
(ii)若约束条件是小于等于型，则在该约束条件不等式左边加上一个新变量——称为松弛变量，将不等式改为(ɡǎi wéi)等式。如
x 1 2 x 2 3 x 3 8 x 1 2 x 2 3 x 3 x 4 8
(iii)若约束条件是大于等于型，则在该约束条件不等式左边减去一个新变量——称为剩余变量，将不等式改为等式。如
第十七页，共一百七十一页。
17
凸函数的判断(pànduàn)
第十八页，共一百七十一页。
18
一阶条件(tiáojiàn)
设在凸集D Rn上f(x)可微,则f(x)在D上为凸函数的充要条件是对任意的x,y ∈ D,都有
f(y)≥f(x)+ f(x)T(y-x)
设在凸集D Rn上f(x)可微,则f(x)在D上为严格凸函数
x 1 2 x 2 3 x 3 8 x 1 2 x 2 3 x 3 x 4 8
第二十九页，共一百七十一页。
29
一般(yībān)形式转化为标准型
(iv)若某个约束方程右端项 bi 0 ，则在约束方程两端乘以（-1），不等号改变方向，然后 (ránhòu)再将不等式化为等式。
(v) 若变量(biànliàng)xj无非负约束，则引入非负变量

最优化方法-线性规划

可行解
基本可行解
基本解
m 基本解数量 C n
是否在基本可行解中一定存在最优解？
退化：非零分量个数小于的基本解为退化的基解；称 m 本
否则称非退化的基本。如果 LP)的所有基本解都是解 ( 非退化的，称LP)是非退化的。 (
(1) 一组决策变量； (2) 一个线性目标函数； (3) 一组线性的约束条件。
线性规划模型 )的一般形式： (LP
min (max)
c x
i i 1
n
i
a11 x1 a12 x 2 a1n x n ( , )b1 a x a x a x ( , )b 22 2 2n n 2 21 1 s.t . a x a x a x ( , )b m2 2 mn n m m1 1 x i ( , )0 , i 1 , 2 ,, n
二. 标准型
1. 标准型
m in
c x
i 1 i
பைடு நூலகம்
n
i
a11 x1 a12 x 2 a1n x n b1 a x a x a x b 22 2 2n n 2 21 1 s.t . a x a x a x b m2 2 mn n m m1 1 x i 0 , i 1 , 2 , , n
A
B
x1 x1 2 x2 4
极大值点为顶点B。
o
C
2 x1 x2 5
例 3 将例2中的目标函数改为 x1 2 x2 。 z x2 解：分析同例2。等值线：1 2 x2 z。 x

最优化理论和方法-第二章线性规划基本理论和算法

其中向量表示：
给定，变量是
定义标准形有必要吗?
其中
给定，变量是
标准形的特征：极小化、等式约束、变量非负
第 2 章线性规划: 基本理论与方法
数学规划基础
LHY-SMSS-BUAA
例4. 化成标准形
等价于
最优化问题的等价表述指两个问题的最优值相等、差一个常数、或者互为相反数，由其中一个问题的最优解可以得到另一个的最优解。
cT
( x* )T
( 1, 1)
( 0, 0)
( 0, 1) (x1, 0), x1 ≥ 0 ( 1, 0) (0, x2), x2∈[0,1] (-1, -1) 没有有限解
解的几何特征
惟一的顶点一条边一条边无(下)界
第 2 章线性规划: 基本理论与方法
数学规划基础
LHY-SMSS-BUAA
只要有 m 个单位列 e1 , e2 , … , em 即可，次序可以打乱！
◎ 规范形的系数的一种解释
yj B1aj aj y1ja1 y2 ja2 ymjam
规范形第 j 列的系数是用当前基表示 aj 时的系数！
第 2 章线性规划: 基本理论与方法
数学规划基础
LHY-SMSS-BUAA
第 2 章线性规划: 基本理论与方法
数学规划基础
LHY-SMSS-BUAA
线性规划问题解的几种情况
提示: 学习单纯形法之前,请务必学习并理解书上 p.19, 例2.2.1.
第 2 章线性规划: 基本理论与方法
数学规划基础
LHY-SMSS-BUAA
2.2 单纯形法
• 适用形式：标准形(基本可行解等价于极点) • 理论基础：线性规划的基本定理！ • 基本思想：从约束集的某个极点/BFS开始，依次

o最优化1-线性规划

��
Min ෍ ��
��=��
��
��. ��.
෍ �� = ��
��=��
∀�� ∈ {1,2,…,m}
−�� we have �� = . �� = is called a basic solution. �� is called basic variables, �� is called nonbasic variables. • If the basic solution is also feasible, this is , ��−�� ≥ ��, then X is called a basic feasible solution.
�� ≥ ��
Where �� ∈ �� , A is an �� × �� matrix with full row rank, �� ∈ �� ▫ Polyhedron set: {�� ∈ �� |�� ≥ ��} ▫ Let �� ∈ �� be a given polyhedron. A vector �� ∈ �� is an extreme point of P if there does not exist ��, �� ∈ �� ,and�� ∈ (��, ��) such that �� = �� + �� − ��

最优化线性规划 (1)(1)

最优化方法第二章(1)

线性规划的基本定理-最优化方法

重庆大学最优化方法习题答案

最优化方法-线性规划的基本定理

线性规划解决最优化问题的数学方法

最优化方法：第2章 线性规划

最优化方法-线性规划

【最优化】线性规划基本概述

数值最优化(李董辉)第九章 线性规划

最优化计算方法-第5章(线性规划)

最优化方法习题答案

最优化方法以往填空题

最优化方法习题答案

第二章 最优化 线性规划

最优化方法-线性规划

最优化理论和方法-第二章 线性规划基本理论和算法

o最优化1-线性规划

最优化方法：第2章线性规划

数值最优化(李董辉)第九章线性规划

第二章最优化线性规划

最优化理论和方法-第二章线性规划基本理论和算法