医学统计学课件--主成分分析与因子分析(第20章)解析
医学统计学--主成分分析及因子分析(第20章)

2019/1/25
医学统计学
3
一、基本思想
数据的降维、数据的解释 将原来众多具有一定相关性的指标,组 合成一组新的相互无关的综合指标。 从中选取几个较少的综合指标尽可能多 的反映原来众多指标的信息。 这种既减少了指标的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。
2019/1/25 医学统计学 4
例
1 2 140.0 141.6 76.0 76.2 36.3 31.4 32.0 29.0 23.0 22..0 16.1 15.6 61.1 60.6 38.7 38.8 32.4 32.5 23.1 21.8 71.3 65.7 41.8 41.7 31.6 29.0 22.3 19.8 20.5医学统计学 17.5
第20章
主成分分析 与因子分析
Principal Components Analysis & Factor Analysis
第二军医大学卫生统计学教研室 张罗漫
2019/1/25 医学统计学 1
讲课内容:
第一节 主成分分析
第二节 因子分析
2019/1/25
医学统计学
2
第一节
主成分分析
Principal Components Analysis
某地 208 名 14 岁男中学生 15 项形态指标测试结果
指标、单位
身高 (X1) cm 坐高 (X2) cm 体重 (X3) kg 肩宽 (X4) cm 骨盆宽 (X5) cm 手长 (X6) cm 上肢长 (X7) cm 小腿加足高 (X8) cm 小腿长 (X9) cm 足长 (X10) cm 胸围 (X11) cm 大腿围 (X12) cm 小腿围 (X13) cm 上臂紧张围 (X14) cm 2019/1/25(X15) cm 上臂放松围
因子分析、主成分分析92页PPT

1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
因子分析、主成分分析
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
Байду номын сангаас
医学统计学课件--主成分分析及因子分析(第20章)

指标、单位
身高 (X1) cm 坐高 (X2) cm 体重 (X3) kg 肩宽 (X4) cm 骨盆宽 (X5) cm 手长 (X6) cm 上肢长 (X7) cm 小腿加足高 (X8) cm 小腿长 (X9) cm 足长 (X10) cm 胸围 (X11) cm 大腿围 (X12) cm 小腿围 (X13) cm 上臂紧张围 (X14) cm 上臂0放1.0松8.2围020(X15) cm
208
176.6
89.7
57.7
37.0
26.5
19.0
75.8
48.8
42.0
26.6
79.0
49.0
35.5
24.0
22.0
5
如何利用这些指标对每一儿童的生长发育 作出正确评价?
➢ 仅用单一指标: 结论片面; 没有充分利用原有数据信息。
➢ 利用所有指标:
各指标评价的结论可能不一致,使综合
评价困难;
➢数据的降维、数据的解释 将原来众多具有一定相关性的指标,组 合成一组新的相互无关的综合指标。 从中选取几个较少的综合指标尽可能多 的反映原来众多指标的信息。
➢这种既减少了指标的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。
01.08.2020
医学统计学
4
某地 208 名 14 岁男中学生 15 项形态指标测试结果
r21 ai1+ (r22- i) ai2+ + r2m aim=0
rm1 ai1+ rm2 ai2+ + (rmm- i) aim =0
i为矩阵R的第i个特征值, 共有m个非 负特征值,由大到小的顺序排列为:
1≥ 2≥ ≥ m≥0
理学主成份分析和因子分析PPT课件

数学、物理、化学、语文、历史、英语)见 STUDENT.SAV 。 • 根据数据进行主成分分析。
第27页/共61页
SPSS结果分析
• 有比较高的相关系数,可以使用主成分分析方法。
第28页/共61页
特征值和贡献率
• 前2个主成分的贡献率为81.42%。
主成分分析
第1页/共61页
主成分分析的原理
• 多元统计分析处理的是多变量(多指标)问题。 由于变量较多,增加了分析问题的复杂性。但 在实际问题中,变量之间可能存在一定的相关 性,因此,多变量中可能存在信息的重叠。人 们自然希望通过克服相关性、重叠性,用较少 的变量来代替原来较多的变量,而这种代替可 以反映原来多个变量的大部分信息,这实际上
• •••
•
••
x1
是“降维”的 有效办法。
• •• •
第6页/共61页
主成分分析的几何意义
F2
•对坐标轴进行旋转,
n个点在F1轴上的方
差达到最大,即在
此方向上包含了有
关n个样品的最大量
信息。
•因此,欲将二维空
间的点投影到某个
多元统计主成分分析与因子分析20
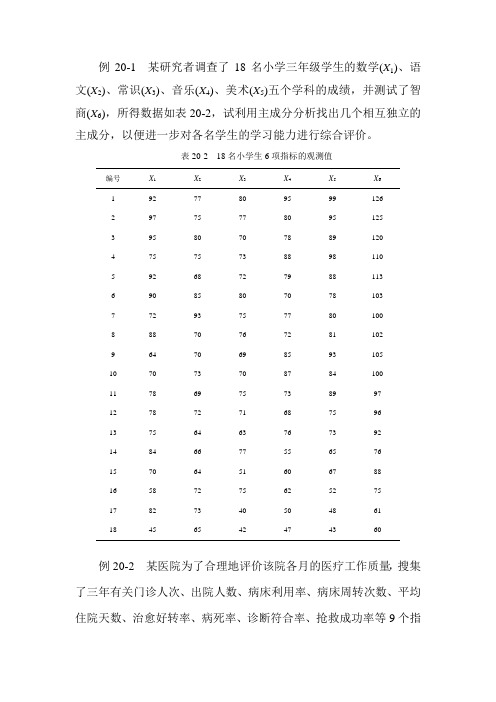
例20-1 某研究者调查了18名小学三年级学生的数学(X1)、语文(X2)、常识(X3)、音乐(X4)、美术(X5)五个学科的成绩,并测试了智商(X6),所得数据如表20-2,试利用主成分分析找出几个相互独立的主成分,以便进一步对各名学生的学习能力进行综合评价。
表20-2 18名小学生6项指标的观测值编号XX2X3X4X5X611 92 77 80 95 99 1262 97 75 77 80 95 1253 95 80 70 78 89 1204 75 75 73 88 98 1105 92 68 72 79 88 1136 90 85 80 70 78 1037 72 93 75 77 80 1008 88 70 76 72 81 1029 64 70 69 85 93 10510 70 73 70 87 84 10011 78 69 75 73 89 9712 78 72 71 68 75 9613 75 64 63 76 73 9214 84 66 77 55 65 7615 70 64 51 60 67 8816 58 72 75 62 52 7517 82 73 40 50 48 6118 45 65 42 47 43 60例20-2 某医院为了合理地评价该院各月的医疗工作质量,搜集了三年有关门诊人次、出院人数、病床利用率、病床周转次数、平均住院天数、治愈好转率、病死率、诊断符合率、抢救成功率等9个指标数据,如表20-8。
现采用因子分析方法,探讨其综合评价指标体系。
表20-8 某医院三年的医疗工作质量有关指标实测值年月X0门诊人次X1出院人数X2病床利用率X3病床周转次数X4平均住院天数X5治愈好转率X6(%)病死率X7(%)诊断符合率X8(%)抢救成功率X9(%)91.01 4.34 389 99.06 1.23 25.46 93.15 3.56 97.51 61.66 91.02 3.45 271 88.28 0.85 23.55 94.31 2.44 97.94 73.33 91.03 4.38 385 103.97 1.21 26.54 92.53 4.02 98.48 76.79 91.04 4.18 377 99.48 1.19 26.89 93.86 2.92 99.41 63.16 91.05 4.32 378 102.01 1.19 27.63 93.18 1.99 99.71 80.00 91.06 4.13 349 97.55 1.10 27.34 90.63 4.38 99.03 63.16 91.07 4.57 361 91.66 1.14 24.89 90.60 2.73 99.69 73.53 91.08 4.31 209 62.18 0.52 31.74 91.67 3.65 99.48 61.11 91.09 4.06 425 83.27 0.93 26.56 93.81 3.09 99.48 70.73 91.10 4.43 458 92.39 0.95 24.26 91.12 4.21 99.76 79.07 91.11 4.13 496 95.43 1.03 28.75 93.43 3.50 99.10 80.4991.12 4.10 514 92.99 1.07 26.31 93.24 4.22 100.00 78.9592.01 4.11 490 80.90 0.97 26.90 93.68 4.97 99.77 80.53 92.02 3.53 344 79.66 0.68 31.87 94.77 3.59 100.00 81.97 92.03 4.16 508 90.98 1.01 29.43 95.75 2.77 98.72 62.86 92.04 4.17 545 92.98 1.08 26.92 94.89 3.14 99.41 82.35 92.05 4.16 507 95.10 1.01 25.82 94.41 2.80 99.35 60.61 92.06 4.86 540 93.17 1.07 27.59 93.47 2.77 99.80 70.21 92.07 5.06 552 84.38 1.10 27.56 95.15 3.10 98.63 69.23 92.08 4.03 453 72.69 0.90 26.03 91.94 4.50 99.05 60.42 例题20-1(EX20-1.dta):. factor x1-x6,pc means(obs=18)Variable | Mean Std. Dev. Min Max-------------+----------------------------------------------------x1 | 78.05556 13.73048 45 97x2 | 72.83333 7.48528 64 93x3 | 68.66667 12.09278 40 80x4 | 72.33333 13.35048 47 95x5 | 77.61111 16.92245 43 99x6 | 97.16667 19.43087 60 126(principal components; 6 components retained)Component Eigenvalue Difference Proportion Cumulative------------------------------------------------------------------1 3.98290 3.15150 0.6638 0.66382 0.83141 0.16837 0.1386 0.80243 0.66304 0.25100 0.1105 0.91294 0.41204 0.34801 0.0687 0.98165 0.06403 0.01746 0.0107 0.99226 0.04658 . 0.0078 1.0000EigenvectorsVariable | 1 2 3 4 5 6-------------+----------------------------------------------------------------- x1 | 0.34279 0.07105 0.88272 0.11837 0.28759 0.03902 x2 | 0.25355 0.91405 -0.20001 0.23378 -0.02013 0.07183 x3 | 0.40390 0.11256 -0.04505 -0.90612 0.00644 -0.03269 x4 | 0.44669 -0.23400 -0.40532 0.20194 0.71151 -0.18548 x5 | 0.47278 -0.26333 -0.12004 0.15439 -0.29697 0.76203 x6 | 0.48167 -0.15064 0.00855 0.21369 -0.56781 -0.61413. factor x1-x6,mine(0.01) pcf(obs=18)(principal component factors; 6 factors retained)Factor Eigenvalue Difference Proportion Cumulative------------------------------------------------------------------1 3.98290 3.15150 0.6638 0.66382 0.83141 0.16837 0.1386 0.80243 0.66304 0.25100 0.1105 0.91294 0.41204 0.34801 0.0687 0.98165 0.06403 0.01746 0.0107 0.99226 0.04658 . 0.0078 1.0000Factor LoadingsVariable | 1 2 3 4 5 6-------------+----------------------------------------------------------------- x1 | 0.68412 0.06479 0.71878 0.07598 0.07277 0.00842 x2 | 0.50602 0.83345 -0.16286 0.15006 -0.00509 0.01550 x3 | 0.80608 0.10264 -0.03668 -0.58164 0.00163 -0.00706 x4 | 0.89147 -0.21337 -0.33004 0.12963 0.18005 -0.04003 x5 | 0.94355 -0.24011 -0.09774 0.09911 -0.07515 0.16446 x6 | 0.96128 -0.13735 0.00697 0.13717 -0.14368 -0.13254Factor LoadingsVariable |Uniqueness-------------+----------x1 | 0.00000x2 | -0.00000x3 | 0.00000x4 | 0.00000x5 | 0.00000x6 | 0.00000. score z1-z3(based on unrotated factors)(3 scorings not used)Scoring CoefficientsVariable | 1 2 3-------------+--------------------------------x1 | 0.17176 0.07793 1.08407x2 | 0.12705 1.00245 -0.24563x3 | 0.20238 0.12345 -0.05533x4 | 0.22383 -0.25663 -0.49777x5 | 0.23690 -0.28880 -0.14742x6 | 0.24135 -0.16521 0.01051. quietly factor x1-x6,mine(0.01) pcf. gen f=(z1*r(lambda1)+z2*r(lambda2)+z3*r(lambda3))/6. egen totalscore=rsum(x1-x6). gsort - f. l totalscore id z1-z3 ftotalsc~e id z1 z2 z3 f1. 569 1 1.472416 -.2930345 -.103475 .92537492. 549 2 1.130913 -.1980218 .9642215 .82983243. 532 3 .8939767 .5721344 .7984022 .76094524. 506 6 .584383 1.801504 .5787218 .70150685. 497 7 .5194059 2.576505 -1.362115 .55128936. 512 5 .602061 -.9741927 .9138077 .36564827. 519 4 .7785597 -.4411606 -1.086971 .33557338. 489 8 .3009298 -.3406681 .8300895 .24428699. 481 11 .2087767 -.6547917 -.0317313 .044349910. 484 10 .2948939 -.4248423 -1.248548 -.001086411. 460 12 -.0994829 .0496813 .1959662 -.037498712. 486 9 .3067468 -1.02853 -1.620377 -.117959513. 423 14 -.6322086 -.0679534 1.400122 -.274364714. 443 13 -.3502443 -1.206041 -.0247946 -.402356815. 394 16 -.9661463 .6634074 -.9886871 -.658673816. 400 15 -1.015548 -.9129516 .2820022 -.769481317. 354 17 -1.665773 .9942052 1.5082 -.801338318. 302 18 -2.363658 -.1152501 -1.004835 -1.696048Stata命令与结果例题20-2(EX20-2.dta):. factor x1-x9,mine(0.7) pcf(obs=36)(principal component factors; 4 factors retained)Factor Eigenvalue Difference Proportion Cumulative ------------------------------------------------------------------1 2.80742 0.81629 0.3119 0.31192 1.99113 0.54281 0.2212 0.53323 1.44832 0.66325 0.1609 0.69414 0.78507 0.10437 0.0872 0.78135 0.68070 0.13944 0.0756 0.85706 0.54126 0.08823 0.0601 0.91717 0.45303 0.27852 0.0503 0.96748 0.17451 0.05596 0.0194 0.98689 0.11855 . 0.0132 1.0000Factor LoadingsVariable | 1 2 3 4 Uniqueness -------------+------------------------------------------------------ x1 | -0.25458 0.77000 0.00776 0.47017 0.12117 x2 | 0.76587 0.12768 0.09055 0.50844 0.13043 x3 | 0.24434 0.77639 -0.08574 -0.44304 0.13387 x4 | 0.68927 0.66058 -0.07059 -0.01973 0.08316 x5 | -0.72423 0.12457 0.44013 0.18939 0.23038 x6 | 0.03930 -0.07076 0.88821 -0.00886 0.20445 x7 | -0.40462 -0.16381 -0.66326 0.24270 0.31063 x8 | -0.62276 0.40190 0.04132 -0.11635 0.43540 x9 | 0.73732 -0.36590 0.05894 0.02089 0.31856. factor x1-x9,factors(4) pf(obs=36)(principal factors; 4 factors retained)Factor Eigenvalue Difference Proportion Cumulative ------------------------------------------------------------------1 2.40201 0.79050 0.4839 0.48392 1.61150 0.71022 0.3246 0.80853 0.90129 0.51338 0.1816 0.99004 0.38791 0.27032 0.0781 1.06825 0.11759 0.08361 0.0237 1.09196 0.03398 0.05967 0.0068 1.09877 -0.02569 0.13818 -0.0052 1.09358 -0.16386 0.13655 -0.0330 1.06059 -0.30041 . -0.0605 1.0000Factor LoadingsVariable | 1 2 3 4 Uniqueness -------------+------------------------------------------------------ x1 | -0.17845 0.68836 0.03313 0.33591 0.38038 x2 | 0.72998 0.02943 0.12835 0.36037 0.31992 x3 | 0.28705 0.68771 -0.06434 -0.34304 0.32284 x4 | 0.73937 0.57953 -0.03613 -0.02279 0.11565 x5 | -0.65592 0.17695 0.38109 0.08571 0.38587 x6 | 0.02066 -0.07004 0.70535 -0.08488 0.48995 x7 | -0.34171 -0.07658 -0.48097 0.11116 0.63368 x8 | -0.49809 0.36120 0.02159 -0.00544 0.62095 x9 | 0.64242 -0.39427 0.06102 0.00849 0.42805。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1≥ 2≥ ≥ m≥0
i=Var(Zi)
2020/11/8
观测指
X1
X2
X11
X12
X21
X22
标 Xm X1m X2m
n
2020/11/8
Xn1
Xn2
医学统计学
Xnm
15
(一)主成分的求法 1. 对各原始指标值进行标准化
X'ij
Xij Xj Sj
j 1, 2 ,, m
为了方便,仍用Xij表示Xij’。
2020/11/8
医学统计学
16
标准化后的数据矩阵
量越多。
2020/11/8
医学统计学
7
二、数学模型及几何意义
Z1 a11X1 a12X2 a1mXm Z2 a21X1 a22X2 a2mXm
Zm am1X1 am2X2 amm Xm
2020/11/8
医学统计学
8
Z=AX
Z1
a11 a12 … a1m
X1
Z2 =
a21 a22 … a2m
208
176.6
89.7
57.7
37.0
26.5
19.0
75.8
48.8
42.0
26.6
79.0
49.0
35.5
24.0
22.0
5
如何利用这些指标对每一儿童的生长发育 作出正确评价?
➢ 仅用单一指标: 结论片面; 没有充分利用原有数据信息。
➢ 利用所有指标:
各指标评价的结论可能不一致,使综合
评价困难;
例
1
2
140.0
141.6
76.0
76.2
36.3
31.4
32.0
29.0
23.0
22..0
16.1
15.6
61.1
60.6
38.7
38.8
32.4
32.5
23.1
21.8
71.3
65.7
41.8
41.7
31.6
29.0
22.3
19.8
20.5医学统计学 17.5
号
…… …… …… …… …… …… …… …… …… …… …… …… …… …… …… ……
X2
┇
┇
┇
…┇
┇
Zm
am1 am2 … amm
Xm
2020/11/8
医学统计学
9
第一主成分
Z1 a11X1 a12X2 a1mXm a121 a122 a12m 1
Var (Z1 ) 在所有Zi中最大
2020/11/8
医学统计学
10
第二主成分
Z2 a21X1 a22X2 a2m Xm
2020/11/8
医学统计学
20
(r11- i) ai1+ r12 ai2+ + r1m aim =0
r21 ai1+ (r22- i) ai2+ + r2m aim=0
rm1 ai1+ rm2 ai2+ + (rmm- i) aim =0
i为矩阵R的第i个特征值, 共有m个非 负特征值,由大到小的顺序排列为:
X=
X11
X21
X n1
X12 X22
Xn2
X1m
X2m
Xnm
2020, X2 , … , Xm 的相关矩阵R
r11
R=Cov(X)
=
r21
rm1
r12 r1m
r22 r2m
rm2
rmm
2020/11/8
医学统计学
2020/11/8
医学统计学
3
一、基本思想
➢数据的降维、数据的解释 将原来众多具有一定相关性的指标,组 合成一组新的相互无关的综合指标。 从中选取几个较少的综合指标尽可能多 的反映原来众多指标的信息。
➢这种既减少了指标的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。
2020/11/8
医学统计学
a
2 21
a
2 22
a
2 2m
1
Z1与Z
无关,互相垂直:
2
a a 21 11 a a 22 12 a a 2m 1m 0
Var (Z2 )在所有Zi中为第2大。
……
理论上主成分个数最多为m个(指标个数)
实际工作中确定的主成分个数总是小于m个
2020/11/8
医学统计学
11
相关 变异
-2
2020/11/8
X2 2
1
-1
0
1
-1
-2
医学统计学
2
X1
12
Z2 2
X2 2
1
1
1
2
Z1
-2
-1
1
2
0
X1
-1
-1
-1
-2
-2
-2
2020/11/8
医学统计学
13
相关
变异
Z2 2
1
2
Z1
1
0
-1
-1
-2
-2
2020/11/8
医学统计学
14
三、主成分的求法及性质
表 20-1 主成分分析的原始数据表
样品号
1 2
第20章
主成分分析 与因子分析
Principal Components Analysis & Factor Analysis
第二军医大学卫生统计学教研室 张罗漫
2020/11/8
医学统计学
1
讲课内容:
第一节 主成分分析 第二节 因子分析
2020/11/8
医学统计学
2
第一节 主成分分析
Principal Components Analysis
18
(X X)(X X) n1
(X X)(Y Y) n1
协方差
r (X X)(Y Y) lXY Pearson 相关系数 (X X)2 (Y Y)2 lXXlYY
r (X X) (Y Y) (X X)2 (Y Y)2
r 1 n1
2020/11/8
XX SX
YS医Y学Y统计 学
4
某地 208 名 14 岁男中学生 15 项形态指标测试结果
指标、单位
身高 (X1) cm 坐高 (X2) cm 体重 (X3) kg 肩宽 (X4) cm 骨盆宽 (X5) cm 手长 (X6) cm 上肢长 (X7) cm 小腿加足高 (X8) cm 小腿长 (X9) cm 足长 (X10) cm 胸围 (X11) cm 大腿围 (X12) cm 小腿围 (X13) cm 上臂紧张围 (X14) cm 上臂2放02松0/1围1/8(X15) cm
标准化后的协方差
19
3. 求出矩阵R的全部特征值(eigenvalue) i, 第i个主成分的组合系数ai1, ai2, , aim满
足方程组:
(r11- i) ai1+ r12 ai2+ + r1m aim =0 r21 ai1+ (r22- i) ai2+ + r2m aim=0
rm1 ai1+ rm2 ai2+ + (rmm- i) aim =0
工作量大。
2020/11/8
医学统计学
6
➢ 找出几个综合指标(长度、围度、特体),这 些综合指标是原始指标的线性组合,既保留 了原始指标的信息,且互不相关。
➢ 各综合指标提供的“信息”量大小用其方差 来衡量。
➢ 衡量一个指标的好坏除了正确性与精确性外,
还必须能充分反映个体间的变异,一
项指标在个体间的变异越大,提供的信息
