2-3线性方程组有解的判定定理
线性代数第三章线性方程组第4节线性方程组解的结构

c1
1 0
c2
0 1
k1
1 1
k2
2 2
1
0
0
1
得 c1 k2
cc12
k1 k1
2k2 2k2
c1 k2
即 c1 k2 0
cc12
k1 k1
2k2 2k2
0 0
c1 k2 0
解得 c1 k2,c2 k2,k1 k2.
取
k2 k 0,
则方程组(Ⅰ)、(Ⅱ)的公共解为
(kk21
(k1 k2 )
k2 k2
)0 0
解之得到
k1 k2.
当k1 k2 0时,向量
k1(0,1,1, 0)T k2 (1, 2, 2,1)T k2[(0,1,1, 0)T (1, 2, 2,1)T
满足方程组(Ⅰ).
k2 (1,1,1,1)T
并且它也是方程组(Ⅱ)的解,故它是方程组(Ⅰ)与(Ⅱ)的 公共解.
定理3.17 若0是非齐次线性方程组AX=b的一个解,则方程组 AX=b的任意一个解 都可以表示为 0 其中 是其导出组AX=0的某个解,0称为方程组
AX=b的一个特解.
例7 求线性方程组
x1 2x2 3x3 x4 3x5 5
3x1
2x1 4x2
x2 2x4 6x5 1 5x3 6x4 3x5
0 0
x1 5x2 6x3 8x4 6x5 0
的一个基础解系.并求方程组的通解.
解 方程组中方程个数小于未知量的个数,所以方程组有 无穷多解.
对方程组的系数矩阵施以初等行变换,化为简化的阶 梯形矩阵:
3 1 6 4 2
A 2
2
3 5
3
1 5 6 8 6
2.6线性方程组解的一般理论

x4
0
,
1
,
0
x5 0 0 1
2 2 6
1
1
5
1
1
,2
0
,3
0
0
1
0
0
0
1
一般解 c11 c22 c33
(c1, c2, c3为任意常数.)
8
三、非齐次线性方程组解的结构
x11 x22 xnn (I) 0 (II)
第二章 线性方程组 §2.6 线性方程组解的一般理论
一、线性方程组有解的判定定理 二、齐次线性方程组解的结构 三、非齐次线性方程组解的结构
1
一、线性方程组有解的判定定理
定理1 线性方程组 x11 x22 xnn (I) 有解
r( A) r( A) 推论1 线性方程组(I)无解 r(A) r( A) 推论2 线性方程组(I)有唯一解 r(A) r(A) n 推论3 线性方程组(I)有无穷多解 r(A) r(A) n
方程组的三个解向量 1,2 ,3满足
1
0
1
1 2 2, 2 3 1, 3 1 0
3
1
1
求 非 齐 次 线 性 方 程 组 一 的 般 解.
19
解 A是m 3矩阵, r(A) 1,
导出组的基础解系中有 含3 1 2个线性无关的解向量.
令1 2 a, 2 3 b, 3 1 c,则
其中k1 , k 2为任意实数.
21
A
2 1
3 0
1 2
1 2
3 6
0 0
0 0
1 0
1 0
1 0
5 0
0
0
4
5
3
线性方程组的解的判定

1 2 0
5 7 0
2 5
,
0
得同解方程组:
x1
x2
x3 5x4 2, 2x3 7 x4 5,
即
:
x1 x2
2
x3 x3
5 7
x4 x4
2, 5,
令 x3=c1, x4=c2, 则方程组的通解为:
x1 c1 5c2 2,
x2 c1 7c2 5,
x3
c1 ,
x4 x4
,
令 x3=c1, x4=c2, 方程组的通解为:
x1
1 3
c1
7 3
c2
x2
5 3
c1
1 3
c2
,
(c1 , c2
R).
x3 c1
x4 c2
求解齐次线性方程组步骤:
将系数矩阵用初等行变换化成行最简形矩阵, 写 出同解方程组(用自由未知量表示) , 即可写出其通解.
对于齐次线性方程组 Amn x 0 有如下推论: 推论1 若 m<n , 方程组 Amn x 0必有非零解. 推论2 若 m=n , 方程组 Amn x 0有非零解的充要 条件是 | A | 0.
三、矩阵方程有解的判定
定理3.3 矩阵方程AX=B有解的充要条件 是 R(A)=R(A|B).
利用此定理可以证明如下的矩阵秩的不等式: 定理3.4 设 AB=C, 则 R(C) min{ R(A), R(B)}.
2个定理的证明均见课本Page90.
x1
b1
记: 系数矩阵为A=(aij),
x
x2
,
b
b2
,
则线性方程组可记为: Ax=b. xn
bm
问题:如何利用系数矩阵 A 和增广矩阵 B=(A|b) 来 讨论线性方程组 Ax=b 的解?
4.1 线性方程组有解的条件

(1) 0, 3, R( A) R(B) 3, 方程组有唯一解; 故: (2) 0, R( A) 1, R(B) 2, 方程组无解;
(3) 3, R( A) R(B) 2, 方程组有无限多个解。
1 1 2 3 1 0 1 1
此时
B
r
0
3
3
6
r
0
1
1
2
,
0 0 0 0 0 0 0 0
x1 1 1 1 2
x2 x3
c1
1
0
c2
0
2
0
1 2
, c1
, c2
R.
x4 0 1 0
例4
对于线性方程组
(1 x1
)
(1
x1
)
x2 x2
x3 x3
0, 3,
书本P112,T6
x1 x2 (1 )x3 ,
问取何值时,有解?有无穷多个解? 并求无穷多解的通解。
c1n d1
c2n
d2
M M
crn
dr
0 0
d
r 1
0
M M
0 0
初等变换不改变矩阵的秩,故有:R( A) R( A) r,
增广矩阵B 通过初等行 变换化为阶
梯型矩阵B
R(B)
R(B)
r, r
1,
当dr1 0, 当dr1 0.
故:
方程组(1)有解的充分必要条件为 dr1 0 ,此时R(A)=R(B)。
令 x3 c1, x4 c2,把它写成通常的参数形式
x1
21
4 3
c2
,
x3 c1,
x4
c2 ,
5
4.2线性方程组有无解的判定

1
Q r ( A) = r ( A ) = 3, ∴ 原方程组有惟一解:x1 = −
λ
, x2 =
2
λ
, x3 =
λ −1 . λ
当λ
1 1 − 2 − 3 1 0 − 1 − 1 = −3 时, A → 0 − 3 3 6 → 0 1 − 1 − 2(行简化阶梯形矩阵) 0 0 0 0) 0 0 0 0
是否有解线性方程组的线性组合不是且表出方式不惟一的线性组合为何值时且表出方式惟一的线性组合为何值时的线性组合不能表为为何值时的线性组合不能表为方程组有惟一解故惟一线性表出为可由行简化阶梯形矩阵阶梯形矩阵方程组有无穷多解其一般解为且表出方式不惟一
§4.2 线性方程组有无解的判定 线性方程组的一般形式:
同解方程组为
5 5 x1 − x3 + x4 = 0 3 3 x + 7 x − 1 x = 1, 2 3 3 3 4
故一般解为
5 5 x1 = x3 − x4 3 3 ( x3 , x 4为自由未知量 ). x = 1− 7 x + 1 x , 3 4 2 3 3
1 −1 1 3 1 −1 2 −1 M 3 1 −1 2 −1 MM 3 →0 0 −5 2 −6 解(1) A = 4 −4 3 −2 M 6 → 0 0 −5 2 MM −6 = 4 1 −1 −3 1 M 1 0 0 −5 0 MM −2 0 0 0 2 (阶梯形矩阵)
⇔ r ( A) = r ( A ) = n,
有无穷多解 ⇔ r ( A) = r ( A ) < n.
解线性方程组的步骤: (1)利用矩阵的初等行变换将方程组的增广矩阵化 为阶梯形矩阵,判断是否有解. (2)有解时,继续利用矩阵的初等行变换将阶梯形 矩阵化为行简化阶梯形矩阵. (3)根据行简化阶梯形矩阵,写出方程组的解.
3.向量组的线性相关性与线性方程组的解

§3.1 线性方程组解的判定1.定理3.1:n 元线性方程组AX=b ,其中A=(a 12a 12•••a 1n a 21a 22•••a 2n••••a m1a m2•••a mn),x=( x 1x 2••x n ) ,b=( b 1b 2••b m )(1)无解的充要条件是R(A)<R(A,b);(2)有惟一解的充要条件是R(A)=R(A,b)=n , (3)有无穷多解的充要条件是R(A)=R(A,b)<n.注:(1)R(A,b)先化为行阶梯形,判别。
有解时再化为行最简形求解。
(2)R(A)=m 时,AX=b 有解。
(3)R(A)=r 时,有n-r 个自由未知量,未必是后面n-r 个。
2.定理3.2:n 元线性方程组AX=0(1)有惟一解(只有零解)的充要条件是R(A)=n ; (2)有无穷多解(有非零解)充要条件是R(A)<n .注:(1)m <n,AX=0必有非零解。
3.定理3.3:矩阵方程AX=B 有解的充要条件是R(A)=R(A,B) 求解线性方程组例1. {4x 1+2x 2−x 3=23x 1−x 2+2x 3 =1011x 1+3x 2 =8例2. {2x 1+x 2−x 3+x 4 =14x 1+2x 2−2x 3+x 4=22x 1+x 2 −x 3−x 4 =1例3. 求解齐次线性方程组{3x 1+ 4x 2−5x 3+ 7x 4 =02x 1−3x 2+3x 3− 2x 4 =04x 1+11x 2−13x 3+16x 4=07x 1−2x 2+ x 3+ 3x 4 =0例4.写出一个以X=C 1(2−310)+C 2(−2401)为通解的齐次线性方程组。
例5(每年).(1)λ取何值时,非齐次线性方程组{ λx 1+x 2+x 3=1x 1+λx 2+x 3=λx 1+x 2+λx 3=λ2(1)有惟一解;(2)无解;(3)有无穷多组解?并在有无穷多组解时求出通解.(2)非齐次线性方程组{x 1+x 2+2x 3=02x 1+x 2+ax 3=13x 1+2x 2+4x 3=b当a,b 取何值时,(1)有惟一解;(2)无解;(3)有无穷多组解?并求出通解.例5(12/13学年).设A=(λ110λ−1011λ), b=(a11),已知Ax=b 存在两个不同的解:(1)求λ,a;(2)求Ax=b 的通解。
2-3工程数学非齐次线性方程组

x1 = x2 + x4 在对应的齐次线性方程 组 中,取 x3 = 2x4 x2 1 0 = 及 x4 0 1
x1 1 1 则 = 及 x 0 2 3 得对应的齐次线性方程 组的基础解系 1 1 1 0 ξ1 = , ξ 2 = 0 2 0 1
9
例1 求解方程组
x1 − 2 x2 + 3 x3 − x4 = 1, 3 x1 − x2 + 5 x3 − 3 x4 = 2, 2 x + x + 2 x − 2 x = 3. 1 2 3 4
解 对增广矩阵 B施行初等行变换
1 − 2 3 − 1 1 B = 3 − 1 5 − 3 2 2 1 2 − 2 3
系,∗是方程组A X = b的一个特解,则 η X = K1ξ1 + K 2 ξ 2 + L + K n − r ξ n − r + η ,
∗
K1 , K 2 , L, K n为任意实数. 的通解.
是方程组 A X = b
6
根据以上定理可知,当方程组( 根据以上定理可知,当方程组(2.3.1)有解时,它 )有解时, 有唯一解的充要条件是其导出组只有零解; 有唯一解的充要条件是其导出组只有零解;它有无 穷多组解的充要条件是其导出组( 穷多组解的充要条件是其导出组(2.2.1)有无穷多 ) 组解。 组解。
第三节
非齐次线性方程组
一、解的判定和解的结构 二、用初等行变换求线性方程组的通解
1
一、非齐次线性方程组有解的判定条件
对非齐次线性方程组
线性方程组的解的判定

1 4
1
r1
- 2r2
0
0 1
-2 2
-5 3 4
r2
(-3)
0
0
0
3 0
3
0 0 0 0
即得与原方程组同解的方程组
x1 x2
2 2
x3 x3
5
3 4
3
x4 x4
0, 0,
由此即得
x1 x2
2
x3
5 3
x4
,
-2
x3
-
4 3
x4
,
( x3 , x4 可任意取值).
令 x3 c1, x4 c2,把它写成通常的参数形式
x4 0 - 2x4
0
.
x1 - x2 - 4 x3 - 3 x4 0
解 对系数矩阵 A 施行初等行变换:
1 A 2
1
2 1 -1
2 -2 -4
1 - 2 - 3
r2 r3
-
2r1 r1
1 0 0
2 -3 -3
2 -6 -6
1 - 4 - 4
r3 - r2
1 0
2 1
2 2
即( AX1, AX2 ,L AXn ) (b1,b2 ,L bn ) 所以等价于AXi bi ,i 1,2,L n. () : 若R( A) R( AMB), ( AMB) ( A,b1,b2,L bn ), 又R( A) R( AMbi ) R( AMB), R( A) R( AMbi ) 由定理2知,存在X i ,使得AX i bi 故存在X ,使得AX B
求出它的一切解.
解证 对增广矩阵B进行初等变换, 方程组的增广矩阵为
1 - 1 0 0 0 a1
线性方程组解的判定与解的结构

***学院数学分析课程论文线性方程组解的判定与解的结构院系数学与统计学院专业数学与应用数学(师范)姓名*******年级 2009级学号200906034***指导教师 ** 2011年6月线性方程组解的判定与解的结构姓名******(重庆三峡学院数学与计算机科学学院09级数本?班)摘 要:线性方程组是否有解,用系数矩阵和增广矩阵的秩来刻画.在方程组有解且有 多个解的情况下,解的结构就是了解解与解之间的关系. 关键词:矩阵; 秩; 线性方程组; 解引言通过系数矩阵和增广矩阵的秩是否相同来给出判定线性方程组的解的判别条件.在了解了线性方程组的判别条件之后,我们进一步讨论解的结构.对于齐次线性方程组,解的线性组合还是方程组的解.在线性方程组有无穷个解时可用有限多个解表示出来.另外以下还涉及到线性方程组通解的表达方式.1 基本性质下面我们分析一个线性方程组的问题,导出线性方程组有解的判别条件. 对于线性方程组11112211211222221122n n n n s s sn n sa x a x a xb a x a x a x b a x a x a x b ++⋅⋅⋅+=⎧⎪++⋅⋅⋅+=⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=⎩ (1)引入向量112111s αααα⎡⎤⎢⎥⎢⎥=⎢⎥⋅⋅⋅⎢⎥⎣⎦,122222s αααα⎡⎤⎢⎥⎢⎥=⎢⎥⋅⋅⋅⎢⎥⎣⎦,…12n n nsn αααα⎡⎤⎢⎥⎢⎥=⎢⎥⋅⋅⋅⎢⎥⎣⎦,12s b b b β⎡⎤⎢⎥⎢⎥=⎢⎥⋅⋅⋅⎢⎥⎣⎦ 方程(1)可以表示为1122n n x x x αααβ++⋅⋅⋅+=性质 线性方程组⑴有解的充分必要条件为向量β可以表成向量组α1,α2,…,αn 的线性组合.定理1 线性方程组⑴有解的充分必要条件为它的系数矩阵111212122212n n s s sn a a a a a a A a a a ⋅⋅⋅⎛⎫⎪⋅⋅⋅⎪= ⎪⋅⋅⋅ ⎪⋅⋅⋅⎝⎭与增广矩阵A =⎛⎝111212122212n ns s sna a a a a a a a a ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 12s b b b ⎫⎪⎪⎪⎪⎭有相同的秩.证明 先证必要性,设线性方程组(1)有解,就说说,β可以经过向量组1α,2α,⋅⋅⋅nα线性表出.由此立即推出,向量组1α,2α,⋅⋅⋅n α与向量组1α,2α,⋅⋅⋅n α,β等价,因而有相同的秩,这两个向量组分别是矩阵A 与A 的列向量组.因此矩阵A 与A 有相同的秩. 再证充分性,设矩阵A 与A 有相同的秩,就是说,它们的列向量1α,2α,⋅⋅⋅n α与1α,2α,⋅⋅⋅n α,β有相同的秩,令它们的秩为r. 1α,2α,⋅⋅⋅n α中的极大线性无关组是由r个向量组成,无妨设1α,2α,⋅⋅⋅r α是它的一个极大线性无关组.显然1α,2α,⋅⋅⋅r α也是向量组1α,2α,⋅⋅⋅n α,β的一个极大线性无关组,因此向量β可以经1α,2α,⋅⋅⋅r α线性表出,既然β可以经1α,2α,⋅⋅⋅r α线性表出,当然它可以经1α,2α,⋅⋅⋅n α线性表出.因此,方程组(1)有解.证毕定理2 对于线性方程组⑴,若()()R A R A r ==,则当r= n 时,有唯一解;当r< n 时,有无穷多解.证明 设D 是矩阵A 的一个不为零的r 级子式(当然它也是A 的一个不为零的子式),为了方便起见,不妨设D 位于A 的左上角.显然, A 的前r 行就是一个极大线性无关组,第r +1,…,s 行都可以经它们线性表出.因此,方程组⑴与11112211211222221122n n n n r r rn n ra x a x a xb a x a x a x b a x a x a x b ++⋅⋅⋅+=⎧⎪++⋅⋅⋅+=⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=⎩ (2)同解.当r =n 时,由克兰姆法则,方程组(2)有唯一解,即方程组⑴有唯一解.当r ﹤n 时,将方程组(2)改写为111122111,111211222222,1121122,11r r r r n n r r r r n nr r rr r r r r r rn n a x a x a x b a x a x a x a x a x b a x a x a x a x a x b a x a x ++++++++⋅⋅⋅+=--⋅⋅⋅-⎧⎪++⋅⋅⋅+=--⋅⋅⋅-⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=--⋅⋅⋅-⎩(3)(3)作为12,r x x x ⋅⋅⋅的一个方程组,它的系数行列式D≠0.由克兰姆法则,对于12,r x x x ⋅⋅⋅的任意一组值,方程组(3),也就是方程组⑴,都有唯一的解.由于自由未知量12,r x x x ⋅⋅⋅可任意取值,所以方程组(1)有无穷多个解. 证毕在解决了线性方程组有解的判别条件之后,我们进一步探讨线性方程组解的结构.所谓解的结构问题就是解与解之间的关系问题.上面我们提到,n 元线性方程组的解是n 维向量,在解不是唯一的情况下,作为方程组的解的这些问题之间有什么关系呢?我们先看齐次方程组的情形.设111122121122221122000n n n ns s sn n a x a x a x a x a x a x a x a x a x ++⋅⋅⋅+=⎧⎪++⋅⋅⋅+=⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=⎩ (4)是一齐次线性方程组,它的解所成的集合具有下面两个重要性质:性质1 两个解的和还是方程组的解.设()12,,,n k k k ⋅⋅⋅与()12,,,n l l l ⋅⋅⋅是方程组(4)的两个解.这就是说,把它们代入方程组,每个方程成恒等式,即10nij jj a k==∑ (i=1,2,...,s ), 10nij jj a l==∑ (i=1,2,...,s ), 把两个就解的和()1122,,,n n k l k l k l ++⋅⋅⋅+(5)代入方程组,得11()00n nijjijjj j a ck c a kc ====⋅=∑∑ (i=1,2,...,s )这说明(5)也是方程组的解. 证毕性质2 一个解的倍数还是方程组的解.设()12,,,n k k k ⋅⋅⋅是(4)的一个解,不难看出()12,,,n ck ck ck ⋅⋅⋅还是方程组的解,因为11()00n nijjijjj j a ck c a kc ====⋅=∑∑ (i=1,2,...,s )由性质1和性质2得:性质3 方程组(4)的解的任一线性组合还是(4)的解.2 基础解系定义 齐次线性方程组(4)的一组解,若满足 1) 12,,,r ηηη⋅⋅⋅线性无关;2)(4)的任一解可由12,,,r ηηη⋅⋅⋅线性表出. 则称12,,,r ηηη⋅⋅⋅为(4)的一个基础解系.3 基础解系的存在性定理1 在齐次线性方程组有非零解的情况下,它有基础解系,并且基础解系所含解向量的个数等于n r -,其中)(A R r =()r R A =.证:若()R A r n =<,不防设1112121222120r r r r rra a a a a a a a a ⋅⋅⋅⋅⋅⋅≠⋅⋅⋅⋅⋅⋅2,则方程组(4)与方程组11112211,11121122222,1121122,11r r r r n n r r r r n nr r rr r r r r rn n a x a x a x a x a x a x a x a x a x a x a x a x a x a x a x ++++++++⋅⋅⋅+=--⋅⋅⋅-⎧⎪++⋅⋅⋅+=--⋅⋅⋅-⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=--⋅⋅⋅-⎩(6) 同解,用n r -组数 (1,0,…,0), (0,1,…,0), …, (0,0,…,1)代入自由未知量11(,,,)r r n x x x ++⋯⋯,就得到(6)的解,也就是(4)的n r -个解()()()111121221222,1,2,,,,,1,0,,0,,,,0,1,,0,,,,0,0,,1r r n rn r n r n r r c c c c c c c cc ηηη----=⋅⋅⋅⋅⋅⋅⎧⎪=⋅⋅⋅⋅⋅⋅⎪⎨⋅⋅⋅⎪⎪=⋅⋅⋅⋅⋅⋅⎩则12,,,n r ηηη-⋅⋅⋅为方程组(4)的一个基础解系. ⅰ) 12,,,n r ηηη-⋅⋅⋅线性无关事实上,若11220n r n r k k k ηηη--+⋅⋅⋅+=,即1122n r n r k k k ηηη--+⋅⋅⋅+=()()12*,,*,,,,0,,0,0,0,,0n r k k k -⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅比较最后n r -个分量,得 120n r k k k -==⋅⋅⋅==. 因此, 12,,,n r ηηη-⋅⋅⋅线性无关.ⅱ) 任取方程组(4)的一个解()12,,,n c c c η=⋅⋅⋅,η可由12,,,n r ηηη-⋅⋅⋅线性表出. 事实上,由12,,,n r ηηη-⋅⋅⋅是方程组(4)的解知:1122r r n n r c c c ηηη++-+⋅⋅⋅+也为(4)的解,又1122r r n n r c c c ηηη++-+⋅⋅⋅+=(n r c c ,,,*,*,1 +)它与η的最后n r -个分量相同,即自由未知量的值相同,所以它们为 同一个解,即11r n n r c c ηηη+-=++…….由ⅰ) ⅱ)知,12,,,n r ηηη-⋅⋅⋅为(4)的一个基础解系. 证毕推论 任一与方程组(4)的某一基础解系等价的线性无关的向量组都是方程组(4)的基础解系.证明:12,,,t ηηη⋅⋅⋅为(4)的一个基础解系,12,,,s ααα⋅⋅⋅线性无关,且与12,,,t ηηη⋅⋅⋅等价,则s t =,且i α可由12,,,t ηηη⋅⋅⋅线性表出,即i α也为(4)的解向量.任取方程组(4)的一个解向量η,则η可由12,,,t ηηη⋅⋅⋅线性表出,从而η可由12,,,t ααα⋅⋅⋅线性表出.又12,,,t ααα⋅⋅⋅线性无关,所以12,,,t ααα⋅⋅⋅也是基础解系. 证毕4 基础解系的求法我们只要找到齐次线性方程组的n r -个自由未知量,就可以获得它的基础解系.具体地说,我们先通过初等行变换把系数矩阵化为阶梯形,那么阶梯形的非零行数就是系数矩阵的秩.把每一个非零行最左端的未知量保留在方程组的左端,其余n r -个未知量移到等式右端,再令右端n r -个未知量其中的一个为1,其余为零,这样可以得到n r -个解向量12,,,n r ηηη-⋅⋅⋅,这n r -个解向量12,,,n r ηηη-⋅⋅⋅构成了方程组的基础解系. 方程组(4)的任一解即通解可表为 1112,,,,t k k k k k P ηηη=+⋅⋅⋅+⋅⋅⋅∈例1 求齐次线性方程组1245123412345123453020426340242470x x x x x x x x x x x x x x x x x x +--=⎧⎪-+-=⎪⎨-++-=⎪⎪+-+-=⎩ 的一个基础解系.解 用初等行变换把系数矩阵化为阶梯形:1103111031112100222142634000312424700000----⎡⎤⎡⎤⎢⎥⎢⎥-----⎢⎥⎢⎥→⎢⎥⎢⎥---⎢⎥⎢⎥--⎣⎦⎣⎦, 于是r 3)(=A ,基础解系中有-n r=5-3=2个向量. "于是()3r A =,基础解系中有532n r -=-=个向量." 阶梯形矩阵所对应的方程组为124523454530222030x x x x x x x x x x +--=⎧⎪---=⎨⎪-=⎩ 移项,得1245245534532223x x x x x x x x x x x+-=⎧⎪-=+⎨⎪=⎩ 取351,0x x ==,得一个解向量 1(1,1,1,0,0)η=-; 取350,1x x ==,得另一解向量2751(,,0,,1)663η=.取351,0x x ==得一个解向量1(1,1,1,0,0)η=-; 取350,1x x ==得一个解向量1751(,,0,,1)663η=.12,ηη即为方程组的一个基础解系,方程组的全部解可表示为)(212221P k k k k ∈+ηη对于非齐次线性方程组解11112211211222221122n n n n r r rn n ra x a x a xb a x a x a x b a x a x a x b ++⋅⋅⋅+=⎧⎪++⋅⋅⋅+=⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=⎩ (7)令0,1,,i i s ==⋅⋅⋅,得111122121122221122000n n n ns s sn n a x a x a x a x a x a x a x a x a x ++⋅⋅⋅+=⎧⎪++⋅⋅⋅+=⎪⎨⋅⋅⋅⎪⎪++⋅⋅⋅+=⎩ (8) 称(8)为(7)的导出组.5 解的性质性质1 设12,ξξ为方程组(7)的两个解,则12ξξ-为其导出组(8) 的解.证明 ()112,,,n k k k ξ=⋅⋅⋅,()212,,,n l l l ξ=⋅⋅⋅是方程组(7)的两个 解,即11,, 1,2,...,nnij ji ij j i j j a kb a l b i s =====∑∑它们的差是12ξξ- =()1122,,,n n k l k l k l --⋅⋅⋅-, 显然有111()0, 1,2,...,nn nij jj ij j ij j i i j j j a kl a k a l b b i s ===-=-=-==∑∑∑即12ξξ-=()1122,,,n n k l k l k l --⋅⋅⋅-是导出组(8)的一个解. 证毕性质2 设ξ为方程组(7)的一个解,η为其导出组(8)的解,则ξη+仍为方程组(7)的解.证明 设ξ=()12,,,n k k k ⋅⋅⋅是方程组(7)的一个解,即1(1,2,)nij ji j a kb i s ===⋅⋅⋅∑又设η=()12,,,n l l l ⋅⋅⋅是导出组(8)的一个解, 即10(1,2,)nij jj a li s ===⋅⋅⋅∑显然111()0(1,2,)nnnij jj ij j ij j i i j j j a kl a k a l b b i s ===+=+=+==⋅⋅⋅∑∑∑.证毕6 解的结构定理 若0γ为(7)的一个特解,则方程组(7)的任一解γ皆可表成0γγη=+,其中η为其导出组(8)的一个解.从而有:方程组(7)的一般解为011n r n r k k γγηη--=++⋅⋅⋅+其中0γ为(7)的一个特解,12,,,n r ηηη-⋅⋅⋅为导出组(8)的一个基础解系.证明 显然00()γγγγ=+-,有性质1知,0γγ-是导出组(4)的一个解,令0γγη-=,则 0γγη=+.证毕推论 方程组(7)在有解的条件下,有唯一解⇔(7)的导出组(8)只有零解.7 求非齐次线性方程组(7)的一般解的步骤1)求出其导出组的基础解系12,,,t ηηη⋅⋅⋅ 2)求出其一个特解0γ3)方程组(7)的一般解为011t t k k γγηη=++⋅⋅⋅+. 例2 求解方程组1234123412340311232x x x x x x x x x x x x ⎧⎪--+=⎪-+-=⎨⎪⎪--+=-⎩ 解:221323112.0.5111101111011011/2111310024100021/211231/200121/200000r r r r r r r r r A -+-+------⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=--−−−→-−−−→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭⎝⎭可见()()R A R A =,方程组有解,并有1243412212x x x x x =++⎧⎨=+⎩取240x x ==,则131/2x x == ,即得原方程组的一个特解0(1/2,0,1/2,0)γ=0(12,0,12,0)γ=.下面求导出组的基础解系: 导出组与 124342x x x x x =+⎧⎨=⎩同解.取241,0x x ==,得1(1,1,0,0)η=; 取240,1x x ==,得2(1,0,2,1)η=. 于是原方程组的通解为0112212,(,)k k k k R γγηη=++∈.参考文献1 北京大学数学系几何与代数小组教研室.高等代数(第三版)[M]. 北京:高等教育出版社,19642 同济大学数学教研室编.线性代数[M].第三版,北京:高等教育出版社,19993 谢帮杰.线性代数[M].北京:人民教育出版社,1978.4 北京大学力学系.高等代数[M].北京:人民教育出版社,19795 邓建中,刘之行.计算方法[M].西安:西安交通大学出版社,20016 赵德修, 孙清华.线性代数题解精选[M].武汉:华中科技大学出版社,2001The Determinant and Structure of Solution ofLinear equationsXingming ****(Class one of Grand 2009, Mathematics and Application Mathematics, College of Maths and Computering Science, Chongqing Three Goreges University )Abstract:Making use of the rank of coefficient matrix and augmented matrix to judge the solution of linear equations. The equations have to solve and a number of cases, the solution of the structure is to understand the relationship between work and solutions.Keywords:matrix; rank ; linear equations; solvement10。
《线性代数》 线性方程组

A 2
5
3
③+①(-3) 0
1
1
3 8
0 1 6
③+②(-1)
1
0
3 1
2
1
0 0 5
对于齐次线性方程组,要使其有非零解,
则要求: 秩r(A)n 3
故 5 = , 0 , = 5 时 当 即 r A 2 , 3
此时方程组有非零解。 这时系数矩阵变为:
1 3 2
如果常数项 b1,b2,,bm不全为0,则 称为:非齐次线性方程组。
5、方程组的解:
方程组的解是满足方程组的未知量的
一组取值: x 1 c 1 ,x 2 c 2 , ,x n c n .
也可记c1为 ,c2,: ,cn) (
例如:
显然,
5x1 x2 2x3 0 2x1 x2 x3 0 9x1 2x2 5x3 0
经济数学基础
《线性代数》
第三章 线性方程组
本章重点:
•线性方程组的解的判定和求法
本章难点:
•解的判定定理
一、线性方程组的有关概念
1、n元线性方程组为:
a11x1 a12x2 a1nxn b1,
a21x1 a12x2 a1nxn b2,
am1x1 am2x2 amnxn bm.
ai: j 第 i个方,第 程 j个未知 xj的量 系数;
1 1 0 x1 1
1
0
2x2
2
0 3 4 x3 3
由线性方程组可惟一确定增广矩阵;反之 由增广矩阵,也可以惟一确定线性方程组。
【例2】已知方程组的增广矩阵如下,试写出
它的线性方程组
1 1 0 1
A 1 0 2 2
【解】:x1x2 1
线性组合与线性相关2
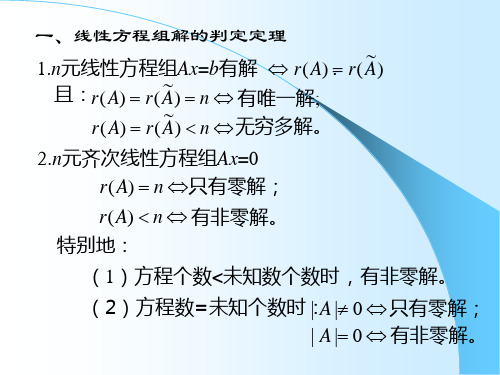
⇔ x1α1+x2α2+···+xsαs=β 有解 ⇔ r(α1,α2,···,αs)=r(α1,α2,···,αs,β)
在此前提下,表示法唯一
⇔ x1α1+x2α2+···+xsαs=β 有唯一解 ⇔ r(α1,α2,···,αs)=r(α1,α2,···,αs ,β)=s ⇔ α1,α2,···,αs线性无关。
7. 向量个数大于维向量维数时,向量组线性相关。 8. n个n维向量组线性相关的条件是它们所构成矩阵 的行列式等于零。 小结:判断n维向量组α1,α2,···,αs是否线性相关 ,可先 比较向量个数s与向量维数n的大小: 1.若s>n ,则向量组线性相关,无需计算。 2.若s=n ,则可计算向量组构成矩阵A的行列式, A 当|A|=0时 ,向量组线性相关; = 此法也适用于 ,向量组线性无关。 当|A|≠0时 前两种情形。 3.若s<n ,则计算r(α1,α2,···,αs) 当r(α1,α2,···,αs) < s时,向量组线性相关; 当r(α1,α2,···,αs) = s时,向量组线性无关。
1 −1 2 0 −1 3 0 0 0 0 0 0
r (α1 , α 2 , α 3 ) = 2 < 3
所以α1,α2,α3线性相关;
r (α1 , α 2 ) = 2 所以α1,α2线性无关。
例:如果β可由α1,α2,···,αs 线性表示,则表示法唯一的 充要条件是α1,α2,···,αs线性无关。 分析:β可由α1,α2,···,αs线性表示
例:设有向量组α1=(1,0,-1,2)T,α2=(-1,-1,2,-4)T,
α3=(2,3,-5,10)T, 试讨论向量组α1,α2,α3及向量组 α1,α2的线性相关性。 1 −1 2 1 −1 2 解:α1 , α 2 , α 3 ) = 0 − 1 3 0 − 1 3 ( − 1 2 − 5 0 1 −3 2 − 4 10 0 − 2 6
第三章-线性方程组的解

线性代数——第 3章
所以方程组的通解为
x1 1 0 1 2 x2 = c 1 + c 0 + 0 . x3 2 0 4 2 1 2 其中c2 ,c4 任意. 0 1 0 x4
可写成矩阵方程:
Ax b
B ( A, b)
线性代数——第 3章
例
1 2 2 1 1 0 2 4 8 2 设A , b 3 2 4 2 3 3 6 0 6 4
求矩阵A及矩阵B ( A b)的秩.
线性代数——第 3章
定理1 (1) (2) (3)
n元线性方程组Ax=b
无解的充分必要条件是R(A)<R(A,b); 有唯一解的充分必要条件是R(A)=R(A,b)=n; 有无穷多个解的充分必要条件是R(A)=R(A,b)<n;
线性代数——第 3章
1 0 0 ~ B0 0 0 x1
5 x1 2c2 3 c2 , x 2c 4 c , 2 2 3 2 x c , 3 1 x4 c 2 ,
线性代数——第 3章
2、非齐次线性方程组 增广矩阵化成行阶梯形矩阵,便可判断其是否有 解.若有解,化成行最简形矩阵,便可写出其通解. 例2 求解非齐次线性方程组
线性代数——第 3章
解
对系数矩阵 A 施行初等行变换:
1 2 2 1 1 2 2 1 r2 2r1 A 2 1 2 2 0 3 6 4 1 1 4 3 r3 r1 0 3 6 4
d d
线性方程组的解

x1 x 2 xn
故方程组有唯一解, 故方程组有唯一解
= d1 , = d2 , M = dn ,
~ 3. 若R(A) =R(B)= r <n,则B中的 r+1= 0 中的d 则 中的 ~ 不出现),于是B对应的方程组 ),于是 对应的方程组B (或dr+1不出现),于是 对应的方程组
d1 d2 M dr d r +1 0 M 0
1. 若R(A)<R(B), 则r+1行对应矛盾方程 行对应矛盾方程0=1, < 行对应矛盾方程 故方程组无解. 故方程组无解 2. 若R(A) =R(B)= r = n,则B中的 r+1=0(或dr+1 中的d 则 ~中的 ( ~ 不出现), ),且 都不出现,于是B对应方程组 不出现),且bij都不出现,于是 对应方程组
由于参数c 可取任意值, 由于参数 1,···, cn-r可取任意值, 故方程组有 无限多个解.证毕. 无限多个解.证毕. 称为线性方程组的通解. 解(6)称为线性方程组的通解 称为线性方程组的通解
(6)
由定理4容易得出线性方程组理论中两个最 由定理 容易得出线性方程组理论中两个最 基本的定理: 基本的定理 定理5 定理5 n 元非齐次线性方程组 Am×n x = b 有解
的充分必要条件是系数 矩阵 A 的秩等于增广矩 阵 B = ( A, b ) 的秩.
定理6 定理 n 元齐次线性方程组 Am×n x = 0 有非零解
的充分必要条件是系数 矩阵的秩 R( A) < n.
下面把定理5推广到矩阵方程 下面把定理 推广到矩阵方程 定理7 矩阵方程AX=B有解的充分必要条件是 定理 矩阵方程 有解的充分必要条件是 R(A) =R(A, B) . 矩阵, 矩阵, 证 设A为m×n矩阵 X为n×l矩阵 则B为m×l 为 × 矩阵 为 × 矩阵 为 × 矩阵. 按列分块, 矩阵 把X和B按列分块 记为 和 按列分块
线性组合与线性相关
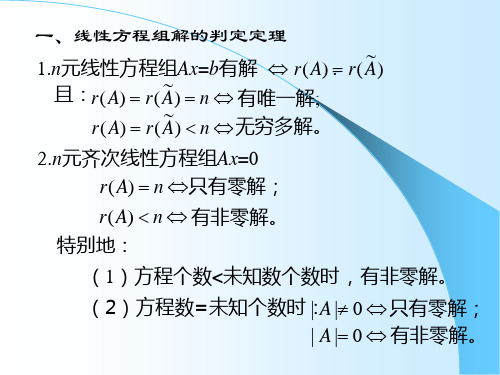
一、线性方程组解的判定定理 1.n元线性方程组Ax=b有解 r( A) . r( A~)
且:r( A) r( A~) n 有唯一解; r( A) r( A~) n 无穷多解。
五、关于向量组线性相关性的主要结论
1.零向量是线性相关的,一个非零向量是线性无关的。 2.两个向量线性相关的充分条件是对应分量成比例。 3.含有零向量的向量组线性相关。 4.部分组线性相关,则整个向量组组线性相关;
向量组线性无关,则其部分组线性无关。 5. 线性无关向量组的“加长”向量组线性无关;
向量组线性无关,则其部分组线性无关。
1 0 0 单位向量组
思考:1 0,2 1,3 0
0 0 1
线性无关
1
0
0
0 1 0
判断1
0
,2
0
,3
1
的线性相关性。
1 3 5
2
4
6
讨论方程组x11+x22+x33=O的解, 前三个方程是 x11+x2 2+x3 3=O ,从而x1=x2=x3=0
1 1 1
1 1 1
答案:1. A 1 2 3,| A | t 5 或 A 0 1 2
1 3 t
0 0 t 5
所以,t=5时线性相关,t≠5时线性无关。
2.t取任何值,向量组都线性相关。(4个3维向量)
条件是其中每个向量都不能可由其余向量线性表示。
例:两个向量α1,α2线性相关的充要条件是它们对应 的分量成比例。
线性方程组有解的判别定理

非齐次线性方程组同解的讨论摘要 本文主要讨论两个非齐次线性方程组有相同解的条件,即如何判定这两个非齐次线性方程组有相同的解.关键词 非齐次线性方程组 同解 陪集 零空间引言 无论是解齐次线性方程组,还是解非齐次线性方程组.所用的方法都是消元法,即对其系数矩阵或增广矩阵施以行的初等变换,而得到比较简单的同解方程组.用矩阵理论来说,就是系数矩阵或增广矩阵左乘以可逆矩阵后所得线性方程组与原线性方程组据有相同的解.这仅为问题的一面,而问题的反面是,如果两个非齐次线性方程组同解,则它们的系数矩阵或增广矩阵之间是否存在一个可逆矩阵?答案是肯定的,此即是本文主要解决的问题。
下面是一个非齐次线性方程组,我们用矩阵的形式写出11121121222212n n m m mn ma x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ 令 A= 111212122212n n m m mn a a a a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ ,b= 12m b b b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦。
即非齐次线性方程组可写成Ax b =。
一 、线性方程组同解的性质引理 1 如果非齐次线性方程组Ax b =与Bx d =同解,则矩阵[]A b 与[]B d 的秩相等.证明 设非齐次线性方程组Ax b =的导出组的基础解系为111,,,r ξξξ ,其中1r 为矩阵[]A b 的秩,再设非齐次线性方程组Bx=d 的导出组的基础解系为212,,,r ηηη ,其中2r 为矩阵[]B d 的秩,如果*η是非齐次线性方程组Ax=b 与Bx=d 特解,由于这两个方程组同解,所以向量组1*11,,,,r ξξξη 与向量组2*12,,,,r ηηηη 等价。
从而这两个线性无关的向量组所含的向量个数相等,于是有12,r r =则矩阵[]A b 与[]B d 的秩相等.引理[1]2 设A 、B 为m n ⨯矩阵,则齐次线性方程组0Ax =与0Bx =同解的充要条件是存在可逆矩阵P 使得PA B =.证明 充分性显然成立。
线性方程组有解的判定定理

设 RA RB rr n,
则 B 的行阶梯形矩阵中含 r 个非零行,
把这 r 行的第一个非零元所对应的未知量作为 非自由未知量,
其余n - r个作为自由未知量,
并令 n - r个自由未知量全取0,
即可得方程组的一个解.
证毕
小结 RA RB n Ax b有唯一解
RA RB n Ax b有无穷多解.
-5 3 4
3
0 0 0 0
即得与原方程组同解的方程组
x1 x2
2 2
x3 x3
5
3 4
3
x4 x4
0, 0,
由此即得
x1 x2
2
x3
5 3
x4
,
-2
x3
-
4 3
x4
,
( x3 , x4 可任意取值).
令 x3 c1, x4 c2,把它写成通常的参数形式
x1
2c1
5 3
解 对增广矩阵B进行初等变换,
1 - 2 3 - 1 1 B 3 -1 5 - 3 2
2 1 2 - 2 3
1 - 2 3 - 1 1
0 5 - 4 0 -1
0 50 -04 0 12
显然,R( A) 2, R(B) 3, 故方程组无解.
例3 求解非齐次方程组的通解
x1 x1
c2 ,
x2
-2c1
-
4 3
c2 ,
x3 c1,
x4
c2
,
5
x1 x2 x3 x4
c1
2 -2 1 0
c2
3 -4
3 0
1
.
例2 求解非齐次线性方程组
x1 3 x1
线性方程组的解

对比
齐次线性方程组
Ax 0
R( A) n Ax 0只有零解; R( A) < n Ax 0有非零解.
AX B , 称为非齐次方程组 ;
AX 0 , 称为对应于 AX B 的齐次方程组。
利用方程组系数矩阵A和增广矩阵B的秩,
可以很容易的看出线性方程组AX=b是否有解
1 齐次方程组
定理 设A是mn矩阵,则齐次线性方程组Ax=0 有非零解的充要条件是R(A)<n. 证明 必要性 用反证法 设方程组Am×nx=0有非零解。假设R(A)=n, 则在A中存在一个n阶非零子式D,使得D所对应 的方程组只有零解(克莱默法则),这与条件矛 盾,因此R(A)<n
总之, 线性方程组(1)有解 R( A) R( A).
R(A) R(B ) n R(A) R(B ) < n 附 若 R( A) R( A) r , 且 r 级子式
Ax b有唯一解;
Ax b有无穷多解.
a11 ar 1
a1r arr
0,
则方程组(1)与下面的方程组是同解的.
几个重要的推论
• 推论1 齐次线性方程组有非零解的充分必 要条件是其系数矩阵的秩r小于未知量的个 数n.
• 推论2 含有n个未知量n个方程的齐次线性 方程组有非零解的充分必要条件是其系数 行列式等于零.
• 推论3 如果在一个齐次线性方程组中,方 程的个数m小于未知量的个数n,那么这个方程 组必有非零解.
第4节 n元线性方程组解的判定定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组 Ax = 0 只有零解 ( 有非零解 )的充分必要 条件是系数行列式
定理 2 n 元非齐次线性方程组 Am×n x = b 有解 的充分必要条件是系数 矩阵 A 的秩等于增广矩 阵 B = ( A, b ) 的秩 .
证 设 A = (α 1 , α 2 , L , α n ), 这里 α 1 , α 2 , L , α n 是 A 的列向量组, 的列向量组,则 Ax = b 可写成 (4) x 1α 1 + x 2α 2 + L + x nα n = b .
5 1 0 − 2 − 1 2 2 1 3 r3 − r2 4 r1 − 2r2 4 0 1 2 0 1 2 3 r2 ÷ ( −3) 3 0 0 0 0 0 0 0 0 即得与原方程组同解的方程组
5 x1 − 2x3 − 3 x4 = 0, 4 x2 + 2x3 + x4 = 0, 3
L 从而方程组( 从而方程组( 2)有解 ⇔ b 可由 α 1 , α 2, , α n L 线性表示 ⇔ R ( A ) = rank (α 1 , α 2, , α n ) = 证毕 rank (α 1 , α 2, , α n, b ) = R ( B ). L
推论
Ax = b有唯一解 ⇔ R(A) = R(B ) = n Ax = b有无穷多解. ⇔ R(A) = R(B ) < n 有无穷多解.
三、线性方程组的求解
例1 求解齐次线性方程组 x1 + 2 x2 + x3 + x4 = 0 2 x1 + x2 − 2 x3 − 2 x4 = 0 . x − x − 4x − 3x = 0 1 2 3 4 解
施行初等行变换: 对系数矩阵 A 施行初等行变换: 1 2 2 1 1 2 2 1 r2 − 2r1 A = 2 1 − 2 − 2 0 − 3 − 6 − 4 1 − 1 − 4 − 3 r3 − r1 0 − 3 − 6 − 4
第三节 线性方程组的解
•
一、线性方程组的基本概念 二、线性方程组解的判定定理 三、线性方程组的求解
• •
一、线性方程组的基本概念
设线性方程组 a11 x1 + a12 x2 + L + a1n xn = b1 a x + a x + L+ a x = b 21 1 22 2 2n n 2 (1) LLLLLLLLLLLL an1 x1 + an 2 x2 + L + ann xn = bn 令 b1 x1 a11 a12 L a1n b a21 a22 L a2 n x = x2 , b = 2 A= M M , L L L L b x a n n m 1 am 2 L amn
显然, 显然, R( A) = 2, R( B ) = 3,
故方程组无解. 故方程组无解.
例3 求解非齐次方程组的通解
x1 − x2 − x3 + x4 = 0 . x1 − x2 + x3 − 3 x4 = 1 x − x − 2x + 3x = −1 2 1 2 3 4
解 对增广矩阵 进行初等变换 对增广矩阵B进行初等变换
λ
1− λ (1 − λ )(2 + λ )
λ (1 − λ ) 2 (1 − λ )(1 + λ )
λ2
(1) 当λ = 1时,
1 1 1 1 B ~ 0 0 0 0 0 0 0 0
R ( A ) = R ( B ) < 3, 方程组有无穷多解 .
所以方程组的通解为
x1 1 0 1 2 x2 1 0 0 x = x 2 0 + x4 2 + 1 2 . 3 0 1 0 x 4
其中 x 2 , x 4 任意 .
x1 − x 2 x − x 3 2 例4 证明方程组 x 3 − x4 x − x 5 4 x5 − x1 求出它的一切解. 求出它的一切解.
= a1 = a2 = a3 = a4 = a5
有解的充要条件
在有解的情况下, 是 a1 + a 2 + a 3 + a4 + a5 = 0.在有解的情况下,
例2 求解非齐次线性方程组 x1 − 2 x2 + 3 x3 − x4 = 1, 3 x1 − x2 + 5 x3 − 3 x4 = 2, 2 x + x + 2 x − 2 x = 3. 1 2 3 4 对增广矩阵B进行初等变换, 对增广矩阵 进行初等变换, 进行初等变换 1 − 2 3 − 1 1 r2 − 2r1 1 − 2 3 − 1 1 r −r B = 3 − 1 5 − 3 2 3 1 0 5 − 4 0 − 1 2 1 2 − 2 3 r3 − r2 0 0 − 4 0 1 2 5 0 解
定义: 的任一解, 定义:含有 n − r 个参数的方程组 (1 )的任一解, 称为线性方程组的通解 , 这里 r = R ( A ).
齐次线性方程组:系数矩阵化成行最简形矩阵, 齐次线性方程组:系数矩阵化成行最简形矩阵, 便可写出其通解. 便可写出其通解 非齐次线性方程组:增广矩阵化成行阶梯形矩 非齐次线性方程组: 便可判断其是否有解.若有解, 阵,便可判断其是否有解.若有解,化成行最 简形矩阵,便可写出其通解. 简形矩阵,便可写出其通解
λ
1
λ
1 1 λ ~1 λ2 λ
λ λ2 λ 1 λ
1 1 1 1
1 1 λ ~ 0 λ −1 1− λ 0 1 − λ 1 − λ2
λ2 2 λ −λ 1 − λ2
1 1 λ λ2 2 ~ 0 λ −1 1− λ λ −λ 0 0 2 − λ − λ2 1 + λ − λ 2 − λ3 1 1 = 0 λ −1 0 0
5 x1 = 2x3 + 3 x4 , 由此即得 4 x2 = −2x3 − x4 , ( x3 , x4 可任意取值 ). 3
令 x 3 = c1 , x4 = c2,把它写成通常的参数 形式 5 5 x1 = 2c2 + c2 , x1 2 3 3 x = −2c − 4 c , x2 − 2 c − 4 . 2 2 2 ∴ = c1 + 2 3 3 x3 1 x = c , 0 3 1 0 x 4 x4 = c2 , 1
x1 = 1 − x2 − x3 其通解为 x2 = x2 x = x 3 3
( x 2 , x 3为任意实数 ).
(2) 当λ ≠ 1时,
1 1 λ B ~ 0 1 −1 0 0 2 + λ
这时又分两种情形: 这时又分两种情形:
λ2 −λ 2 (1 + λ )
解证 对增广矩阵 进行初等变换, 对增广矩阵B进行初等变换, 进行初等变换 方程组的增广矩阵为
0 0 1 −1 0 1 −1 0 0 0 0 1 −1 0 B= 0 0 0 1 −1 0 −1 0 0 0 1
1 0 0 ~ 0 0 0 0 −1 0 1 −1 0 0 0 1 −1 0 0 0 1 −1 0 0 0 0
则上述方程组( ) 则上述方程组(1)可写成向量方程 Ax = b
(2)
为方程组(1)的系数矩阵, 称A为方程组 的系数矩阵 B=(A,b)为(1)的增广 为方程组 为 的 有解 则称它是相容 如果 矩阵. 如果 有解,则称它是相容的 如果(1)没有 矩阵 如果(1)有解 则称它是相容的;如果 没有 则称它不相容 解,则称它不相容 则称它不相容. 则称(1)为 若常数项 b1 , b2 ,L , bn不全为零 , 则称 为非 齐次线性方程组; 齐次线性方程组 若常数项 b1 , b2 ,L, bn 全为零 , 此时称(1)为齐次线性方程组 此时称 为齐次线性方程组.
0 0 1 −1 −1 1 1 − 1 − 1 1 B = 1 − 1 1 − 3 1 ~ 0 0 2 − 4 1 1 − 1 − 2 3 − 1 2 0 0 − 1 2 − 1 2
1 − 1 0 − 1 1 2 ~ 0 0 1 − 2 1 2 . 0 0 0 0 0
1) λ ≠ −2时, R( A) = R( B ) = 3, 方程组有唯一解 :
由于R( A) = R( B ) = 2, 故方程组有解,且有 故方程组有解,
x1 = x2 + x4 + 1 2 x = x + 0x x1 = x2 + x4 + 1 2 2 2 4 ⇔ x 3 = 2 x4 + 1 2 x 3 = 0 x 2 + 2 x4 + 1 2 x 4 = 0 x 2 + x4
例5 设有线性方程组
λx1 + x2 + x3 = 1 x1 + λx2 + x3 = λ x + x + λ x = λ2 1 2 3
问λ取何值时 , 有解 ? 有无穷多个解 ?
作初等行变换, 解 对增广矩阵 B = ( A, b ) 作初等行变换,
B =1 1 λ 1 1 1
R ( A ) = rank (α 1 , α 2, , α n ) < n . L
解的充分必要条件是系 数矩阵的秩 R( A) = n. 推论1 n 元齐次线性方程组 Am×n x = 0 只有零
