高等数学曲线积分和曲面积分PPT课件
合集下载
高等数学曲线积分和曲面积分课件

投影区域为Dxy , R(x, y, z)在S上连续,则
R(x, y, z)dxdy R(x, y,( z x, y))dxdy.
S
D xy
其中,当S取上侧时,取“+”号。
其余的类似积分。
11-6 高斯公式
注意公式使用条件 (2) 利用高斯公式
添加辅助面的技巧
(辅助面一般取平行坐标面的平面)
(3) 两类曲面积分的转化
11-1 对弧长的曲线积分
11-2 对坐标的曲线积分
习题11-3 格林公式及其应用
设闭区间D由分段光滑的曲线L围成,函数P x, y及 Qx, y在D上具有一阶连续的偏导数,则有
D
Q x
P y
dxdx
L
Pdx
Qdy成立,其中L取正向。
需要说明以下几点:
(1)格林公式说明了平面闭区域D上的二重积分可通过
沿闭区域D的边界曲线上的曲线积分来表达,即面积分
可以转化为线积分。
(2)格林公式的简单应用:设闭区域D由分段光滑的
曲线L围成,则D的面积A=
1 2
L
xdy
ydx.
(3)在应用格林公式时,首先检验格林公式的条件
是否满足,即P x, y,Q x, y在由分段光滑的闭曲线
所围成的闭区域额D上具有一阶连续偏导数,当条件
不满足时,公式不能用。例如考虑积分
xdy ydx L x2 y2 ,
其中L是区域D的边界曲线,如果D包含原点,那么
P 与 Q 在原点就不存在,就不可能连续,这时就不 y x
能运用格林公式将其转化为二重积分。
解:
解:
第十一章 曲线积分与曲面积分(正式)

f ( 0
( k , k , k )
记作
lim
n
k 1
k
, k , k ) s k
f ( x, y, z ) d s
Mk sk M k 1
都存在, 则称此极限为函数f(x,y,z)在曲线 上对弧长的曲线积分, 或第一类曲线积分。 f(x,y,z)称为被积函数, 称为积分弧段。
o
1x
例2 计算 I
L
x d s , 其中L为双纽线
(x2 y2 ) 2 a2(x2 y2 ) (a 0)
解:在极坐标系下 L : r a cos 2 ,
2 2
y
它在第一象限部分为
L1 : r a cos 2
利用对称性,得
(0
4
)
o
x
I 4 x d s 4 4 r cos L
L
L
( 2) f ( x , y ) d s
L
f ( x , y ) ds f ( x , y ) ds
L1 L2
( L 由L1, L2组成) (3)设在L上f(x,y) ≤g(x,y),则
L
f ( x , y ) d s g( x , y ) d s
L
特别地,有
| f ( x, y) d s | | f ( x, y) |d s
第十一章 曲线积分与曲面积分
教学内容
第一节 对弧长的曲线积分
第二节 对坐标的曲线积分
第三节 格林公式及其应用
第四节 对面积的曲面积分
第五节 对坐标的曲面积分 第六节 高斯公式 *通量与散度 *环流量与旋度
第七节 斯托克斯公式
( k , k , k )
记作
lim
n
k 1
k
, k , k ) s k
f ( x, y, z ) d s
Mk sk M k 1
都存在, 则称此极限为函数f(x,y,z)在曲线 上对弧长的曲线积分, 或第一类曲线积分。 f(x,y,z)称为被积函数, 称为积分弧段。
o
1x
例2 计算 I
L
x d s , 其中L为双纽线
(x2 y2 ) 2 a2(x2 y2 ) (a 0)
解:在极坐标系下 L : r a cos 2 ,
2 2
y
它在第一象限部分为
L1 : r a cos 2
利用对称性,得
(0
4
)
o
x
I 4 x d s 4 4 r cos L
L
L
( 2) f ( x , y ) d s
L
f ( x , y ) ds f ( x , y ) ds
L1 L2
( L 由L1, L2组成) (3)设在L上f(x,y) ≤g(x,y),则
L
f ( x , y ) d s g( x , y ) d s
L
特别地,有
| f ( x, y) d s | | f ( x, y) |d s
第十一章 曲线积分与曲面积分
教学内容
第一节 对弧长的曲线积分
第二节 对坐标的曲线积分
第三节 格林公式及其应用
第四节 对面积的曲面积分
第五节 对坐标的曲面积分 第六节 高斯公式 *通量与散度 *环流量与旋度
第七节 斯托克斯公式
高数课件11曲线积分曲面积分
L L1 L2
f (x, y ) ds.
(2) 若积分曲线 L 关于 y 轴对称, y 轴两侧的区域分别记为 L1 , L2 . i. 若 f (x, y ) 关于 x 为奇函数, 则 ˆ f (x, y ) ds = 0.
L
ii. 若 f (x, y ) 关于 x 为偶函数, 则 ˆ ˆ ˆ f (x, y ) ds = 2 f (x, y ) ds = 2
È
如果曲线方程为 x = φ(y ), y ∈ [a, b], 则曲线的参数方程为
8 > > < > > :
x = φ(y ),
a ≤ y ≤ b,
y = y, ˆ
b a
因此,
ˆ f (x, y ) ds =
L
8 > > > > > < > > > > &+ φ′2 (y ) dy.
ˆ 例 4 计算 分.
L
(x2 + y 2 ) ds, 其中 L 是以原点为圆心, 半径为 R 的圆周的左半部
y R
R
O
x
−R
6
解: 显然, 曲线的参数方程为
8 > > < > > :
x = R cos θ, y = R sin θ, ˆ
π 3π ≤θ≤ . 2 2
因此,
ˆ (x + y ) ds =
y
1
B
Mn−1
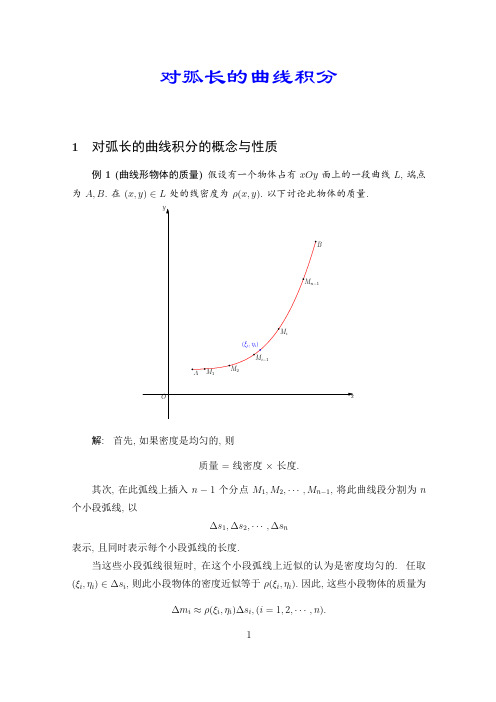
F (ξi , ηi ) Mi (ξi , ηi ) Mi−1 A M1 M2
O
x
#» 解: 首先, 如果力 F 是恒力, 且移动路线是从 A 沿直线到 B, 则所作的功为 #» # » W = F · AB. 其次, 在曲线 L 上依次插入 n−1 个分点 M1 (x1 , y1 ), M2 (x2 , y2 ), · · · , Mn−1 (xn−1 , yn−1 ), 将此曲线段分割为 n 个小段曲线, 以 AM1 , M1 M2 , · · · , Mn−1 B 9
f (x, y ) ds.
(2) 若积分曲线 L 关于 y 轴对称, y 轴两侧的区域分别记为 L1 , L2 . i. 若 f (x, y ) 关于 x 为奇函数, 则 ˆ f (x, y ) ds = 0.
L
ii. 若 f (x, y ) 关于 x 为偶函数, 则 ˆ ˆ ˆ f (x, y ) ds = 2 f (x, y ) ds = 2
È
如果曲线方程为 x = φ(y ), y ∈ [a, b], 则曲线的参数方程为
8 > > < > > :
x = φ(y ),
a ≤ y ≤ b,
y = y, ˆ
b a
因此,
ˆ f (x, y ) ds =
L
8 > > > > > < > > > > &+ φ′2 (y ) dy.
ˆ 例 4 计算 分.
L
(x2 + y 2 ) ds, 其中 L 是以原点为圆心, 半径为 R 的圆周的左半部
y R
R
O
x
−R
6
解: 显然, 曲线的参数方程为
8 > > < > > :
x = R cos θ, y = R sin θ, ˆ
π 3π ≤θ≤ . 2 2
因此,
ˆ (x + y ) ds =
y
1
B
Mn−1
F (ξi , ηi ) Mi (ξi , ηi ) Mi−1 A M1 M2
O
x
#» 解: 首先, 如果力 F 是恒力, 且移动路线是从 A 沿直线到 B, 则所作的功为 #» # » W = F · AB. 其次, 在曲线 L 上依次插入 n−1 个分点 M1 (x1 , y1 ), M2 (x2 , y2 ), · · · , Mn−1 (xn−1 , yn−1 ), 将此曲线段分割为 n 个小段曲线, 以 AM1 , M1 M2 , · · · , Mn−1 B 9
第10章-曲线积分与曲面积分 高等数学教学课件

f (x, y) d s
f (x, y) d s.
L( A,B)
L( B, A)
性质2 设, 为常数,则
L[ f (x, y) g(x, y)]d s L f (x, y)d s L g(x, y)d s.
性质3 若积分路径L可分成两段光滑曲线弧L1,L2, 则
f (x, y) d s f (x, y) d s f (x, y) d s.
把 L分成n个有向小弧段
¼ A0 A1, ¼ A1A2,L , ¼ Ai1Ai ,L , ¼ An1An, (A0(x0, y0) A, An (xn, yn) B).
令xi xi xi1, yi yi yi1,在¼ Ai1Ai上任取点Mi (i ,i ), i 1, 2,L , n,若当小弧段的长度的最大值 0时,和
若L是闭曲线,即L的两个端点重合,那么f (x, y)
在闭曲线L上对弧长的曲线积分记为
ÑL f (x, y) d s.
函数f (x, y, z)在曲线弧上对弧长的曲线积分为
n
f (x, y, z) d s lim 0
i 1
f (xi , yi , zi )si.
性质1 对弧长的曲线积分与曲线L的方向无关,即
方程为x =a cos t, y =a sin t, z = kt, 0 t 2p, k>0.
解 Q x' t asint, y' t a cost, z' t k,
[x '(t)]2 [( y '(t)]2 [z '(t)]2 a2 k2 ,
(x2 y2 z2 ds 2p (a2 k 2t2 ) a2 k 2 dt
d r d xi d yj d zk,即有
数学分析第二十一章课件曲线积分与曲面积分

k f(x ,y ,z )d s k f(x ,y ,z )d s
» A B
» A B
(4) f( x ,y ,z ) d s f( x ,y ,z ) d s f( x ,y ,z ) d s
» A B
» A C
C » B
2020/6/1
例1
设L 是椭圆
x2 a2
y b
2
在2 第1 一象限部分,
f( x ,y ,z ) d s f( x ,y ,z x ,y )1 z x 2 x ,y z 2 y x ,y d x d y
S
D x y
2020/6/1
当 S : x x ( u , v ) ,y y ( u , v ) , z z ( u , v ) , ( u , v ) D 时
第二十一章 曲线积分与曲面积分
2020/6/1
i §1. 第一型曲线积分与曲面积分
背景:前面,求几何体的质量 1.第一型曲线曲、面积分
我们的问题是,设有空间的曲线段L,其上每点有线性密度, 如何
求其质量为简单起见,设空间曲线段L是可以求长的,其端点为A,B又设
密度函数f (x, y, z) 在曲线L上连续,我们来求这曲线段L的质量.
说明 1)公式的记忆:“代进去”
2)S的方程为xxy,z,y,zDyz或 y yz,x, z,xDzx 时公式如何
3)当 f(x,y,z)1时,为曲面S的面积公式
4)当光滑曲面S由参数方程:x x u ,v ,y y (u ,v ),z (u ,v ),u,vD
时面积元素 ds EGF2dudv 这时
f( x ,y ,z ) d s f( x ( u ,v ) ,y u ,v ,z u ,v )E G F 2 d u d v
曲线积分与曲面积分复习课件

关于变量 x 和 y 均为偶函数,因此只要计算 | xyz | dS在第一
卦限部分,再4倍即可,即本题利用对称性计算比较简便。 解:设 在第一卦限的部分为 1 ,则 1在 xoy 面上的投影
区域为: Dxy : x 2 y 2 1, x 0, y 0
于是
| xyz | dS 4 xyzdS
2 0
1
2 (令 u 1 4r )
2 sin2
2 0
5 1
u2 1 2 1 ( ) u udu 4 4
5 1 2 2 2 ( u 1 ) u du 1 32
125 5 1 420
2 【例4】 计算曲面积分 (ax by cz d ) dS ,其中为球面
称性计算比较简单。
2 2 2 2 2 2 2 2 ( ax by cz d ) a x b y c z d , 解:因
由奇偶对称性可知,上述未写出项的积分值均为0,而由
2 2 2 轮换对称性易知 x dS y dS z dS ,故
2. 可加性: f ( x ,
1 2
y , z )dS f ( x , y , z )dS f ( x , y , z )dS
1 2
3. 的体积: S dS
ቤተ መጻሕፍቲ ባይዱ
f ( x, y, z ) g( x, y, z ) ,则 4. 单调性: 若 在上,
0 i 1 i i
n
i
)S i
2.物理意义:
M ( x , y , z )dS
高数下第十一章曲线积分与曲面积分ppt课件

2、 x 2 yzds,其中 L为折线 ABCD,这里 A , B , C , D 依次为点(0,0,0),(0,0,2),(1,0,2),(1,3,2);
3、 ( x 2 y 2 )ds,其中 L为曲线 L
x a(cos t t sin t)
y
a(sin
t
t
cos
2
2
例3 求I xyzds, 其中 : x a cos , y a sin ,
z k的一段. (0 2)
解
I
2
a2 cos sin k
a2 k 2d
0
1 ka2 a2 k2 . 2
8
例3 求I x2ds, 其中为圆周 x2 y2 z2 a2 , x y z 0.
t
)
(0 t 2 );
10
练习题答案 1、ea (2 a) 2;
4
2、9;
3. 22a3 (1 22 );
11
二、对坐标的曲线积分的概念
1. 定义:
函数 P(x,y)在有向曲线弧L上对坐标 x 的曲线积分
n
L
P( x,
y)dx
lim
0
i 1
P(i ,i
6
例1
求I
L xyds,L来自:椭圆 x y
a cos t, bsin t,
(第象限).
解 I 2 a cos t b sin t (a sin t)2 (b cos t)2dt 0
ab 2 sin t cos t a2 sin2 t b2 cos2 tdt 0
高等数学专题讲座曲线积分与曲面积分课件

Dxy (上侧取“+”, 下侧取“”)
• 若 : x x( y, z) , ( y, z) Dyz ,则有
P(x,
y,
z)
d
ydz
Dyz
P(x(
y,
z)
,
y, z) d y d z
(前正后负)
• 若 : y y(z, x), (z, x) Dzx , 则有
Q(x, y, z) d z d x Dzx Q (x, y(z, x), z ) d z d x (右正左负)
2 a2 d s 4 π a3
3
3
例5. 求 I (z y) d x (x z) dy (x y) dz, 其中
:
x2 x
y
y
2
z
1 2
,
从 z 轴正向看为顺时针方向.
解: 取 的参数方程 x cos t, y sin t, z 2 cost sin t
y x
四、对面积的曲面积分
n
1. 定义: f (x, y, z) dS lim
0
f (i ,i , i ) Si
i 1
2. 计算:
基本思路: 求曲线积分 转 化 计算二重积分
设 :z z(x, y),(x, y) Dxy , 则
f (x, y, z) dS
f (x, y, z(x, y) )
n
1. 定义
L
f
(x,
y) ds
lim
0 k 1
f (k ,k )sk
n
2. 性质
f (x, y, z) ds lim f
0 k 1
(k ,k , k )sk
(1) f (x, y, z) g(x, y, z) ds
高数课件第十章 曲线积分与曲面积分

Σ: x−y+z = 在第四卦限部分的上侧 1 在第四卦限部分的上侧.
解: (c sα,c sβ,c sγ) = 1 ( ,− ,1 o o o 1 1) 3 1 I =∫∫ [f (x y z)+x−2f (x y z)−y+f (x y z)+z]dS , , , , , , ∑ 3 1 =∫∫ [x−y+z]dS ∑ 3 1 1 3 1 =∫∫ dS= . = ∑ 3 3 2 2
+∫ ( x y−3 y2 +y2) d 32 x y u(x y =∫ 5x d , ) x 0
4 0
x
y
32 2 3 1 3 =x + x y −xy + y 3 2 因此方程的通解为 5 3 2 2 3 1 3 x + x y −xy + y =C 2 3
5
y
(x y , )
o (x0 x ,)
2π R 2 2 2
π
+ ∫ dθ ∫π dϕ ∫
2 0 3
2π
π
2 R cos ϕ
0
r cos ϕ ⋅ r sin ϕ dr
2 2 2
第十章 曲线积分与曲面积分
1. 第一类曲线积分 物质曲线质量) (物质曲线质量) 2. 第二类曲线积分 变力作功) (变力作功) 3. 第一类曲面积分 曲面薄板质量) (曲面薄板质量) 4. 第二类曲面积分 通量) (通量)
曲线积分
曲面积分
1. 第一类曲线积分的计算
(1)利用参数方程化为定积分 利用参数方程化为定积分 • 对光滑曲线弧
f (x y d =∫ f[ ( )ψ( ) φ 2( )+ ′2( )dt ∫ , ) s α φt , t ] ′ t ψ t L
第八讲曲线积分与曲面积分(1)

L
P(y, z, x)dy Q(y, z, x)dz R(y, z, x)dx
L
P(z, x, y)dz Q(z, x, y)dx R(z, x, y)dy
L
例1 计算
(1) (x x2 y4)ds ,其中x2 y2 a2 (a 0)
;L
[2xy 3x2 4y2 sin ( x2 y2 )]ds,
所以它的参数方程为
x y
acost ,t a asint
[0,2
]
将其代入 z x2 y2 得
z (acost)2 (a asint)2 2a2(1 sint),t [0,2 ]
所以 Γ 的参数方程为
x acost
Γ: y a asint ,t [0,2 ]
cz z
c
[
cz cost]2 [ cz sin t]2 cz
cz sin t tan t tan z
cz cost
c
令
tz c
即得以z为参数的L2的参数方程.
(3)以y为参数,得 x y2 , z y2 y4 , y y
a
a2
二、曲线积分的计算
1. 注的意,到因曲此线它积的分自的变被量积应函满数足积分f (曲x,线是y)方定程义,在所积以分计曲算线曲上
e ds y-x
AB
1
e2 1-2 x
0
2dx
2 (e 1) 2
BE
:
y
x 1
x
,x x
[-
1 2
,0],
e
BE
P(y, z, x)dy Q(y, z, x)dz R(y, z, x)dx
L
P(z, x, y)dz Q(z, x, y)dx R(z, x, y)dy
L
例1 计算
(1) (x x2 y4)ds ,其中x2 y2 a2 (a 0)
;L
[2xy 3x2 4y2 sin ( x2 y2 )]ds,
所以它的参数方程为
x y
acost ,t a asint
[0,2
]
将其代入 z x2 y2 得
z (acost)2 (a asint)2 2a2(1 sint),t [0,2 ]
所以 Γ 的参数方程为
x acost
Γ: y a asint ,t [0,2 ]
cz z
c
[
cz cost]2 [ cz sin t]2 cz
cz sin t tan t tan z
cz cost
c
令
tz c
即得以z为参数的L2的参数方程.
(3)以y为参数,得 x y2 , z y2 y4 , y y
a
a2
二、曲线积分的计算
1. 注的意,到因曲此线它积的分自的变被量积应函满数足积分f (曲x,线是y)方定程义,在所积以分计曲算线曲上
e ds y-x
AB
1
e2 1-2 x
0
2dx
2 (e 1) 2
BE
:
y
x 1
x
,x x
[-
1 2
,0],
e
BE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)在应用格林公式时,首先检验格林公式的条件
是否满足,即P x, y,Q x, y在由分段光滑的闭曲线
所围成的闭区域额D上具有一阶连续偏导数,当条件
Ñ 不满足时,公式不能用。例如考虑积分
xdy ydx L x2 y2 ,
其中L是区域D的边界曲线,如果D包含原点,那么
P 与 Q 在原点就不存在,就不可能连续,这时就不 y x
能运用格林公式将其转化为二重积分。
解:
解:
解:
11-4 对面积的曲面积分
解:
11-5 对坐标的曲面积分
对坐标的曲面积分的计算是本节的重要知识点,
其计算方法如下:
(1)若光滑曲面S表示为z=z(x,y),S在xOy面上的
投影区域为Dxy , R(x, y, z)在S上连续,则
注意公式使用条件 (2) 利用高斯公式
添加辅助面的技巧
(辅助面一般取平行坐标面的平面)
(3) 两类曲面积分的转化
11-1 对弧长的曲线积分
11-2 对坐标的曲线积分
习题11-3 格林公式及其应用
设闭区间D由分段光滑的曲线L围成,函数P x, y及 Qx, y在D上具有一阶连续的偏导数,则有
二、曲面积分的计算法
1. 基本方法
曲面积分
第一类( 第二类(
对面积 对坐标
) )
转化
二重积分
(1) 选择积分变量 — 代入曲面方程
(2)
积分元素投影
第一类: 第二类:
始终非负 有向投影
(3) 确定二重积分域
— 把曲面积分域投影到相关坐标面
2. 基本技巧 (1) 利用对称性及重心公式简化计算
高等数学曲线积分和曲面积分
一、曲线积分的计算法
1. 基本方法 曲线积分
第一类 ( 对弧长 ) 第二类 ( 对坐标 )
转化
定积分
用参数方程
(1) 选择积分变量 用直角坐标方程
用极坐标方程
第一类: 下小上大 (2) 确定积分上下限
第二类: 下始上终
2. 基本技巧 (1) 利用对称性及重心公式简化计算 ; (2) 利用积分与路径无关的等价条件; (3) 利用格林公式 (注意加辅助线的技巧) ; (4) 利用斯托克斯公式 ; (5) 利用两类曲线积分的联系公式 .
R(x, y, z)dxdy R(x, y,( z x, y))dxdy.
S
D xy
其中,当S取上侧时,取“+”号。
其余的类似。
计算对坐标的曲面积D
Q x
P y
dxdx
ÑL Pdx
Qdy成立,其中L取正向。
需要说明以下几点:
(1)格林公式说明了平面闭区域D上的二重积分可通过
沿闭区域D的边界曲线上的曲线积分来表达,即面积分
可以转化为线积分。
(2)格林公式的简单应用:设闭区域D由分段光滑的
曲线L围成,则D的面积A=
1 2
ÑL xdy
ydx.
