运筹学习题答案(第七章)
运筹学第七章答案

[课后习题全解]7.2 解(1)建立数学模型(2)计算原理1)梯度法(最速下降法)a. 给定初始近似点不妨为(0,0,0),精度,不妨为,若则即为近似极小点.b. 若,求步长.并计算步长求法用近似最佳步长.c. 一般地,若,则即为所求的近似解;若则求步长,并确定下一个近似点如此继续,直至达到要求的精度为止.2)近似最佳步长求法由,求出步长.7.3 解(1)的海塞矩阵为知为严格凸函数,为凸函数,为凹函数,所以不是一个凸规划问题.(2)的海塞矩阵为则为严格凸函数,为凹函数,为凸函数,所以上述非线性规划不是凸规划.7.6 解计算结果如表7-2所示.表7-2迭代次数123由可知相邻两步的搜索方向正交.7.10 解 因为现从,开始于是故故得到极小值点7.12 解取由于,所以由得故由于故为近似极小点.7.13 解(1)用最速下降法(2)牛顿法得极小点(3)变尺度法得极小点7.15 解原非线性规划等同于(1)其作用约束的是所以得则有存在可行下降方向.(2)其作用约束的是所以即即(无可行解)不存在可行下降方向.(3)其作用约束的是所以所以存在可行下降方向.7.17 解(1)原式等同于写出目标函数和约束函数的梯度对第一个和第二个约束条件分别引入广义拉格朗日乘子,得点为,则有1)令,无解;2)令,解之得是点,目标函数值;3)令,解之得是点,目标函数值;4)令,则是点,,但不是最优. 此问题不是凸规划,故极小点1和5是最优点.(2)原式等同于写出目标函数和约束函数的梯度引入广义拉格朗日乘子,得点为,则有1)令,无解;2)令,则不是点;3)令,则不是点;4)令,则是点,目标函数值由于该非线性规划问题为凸规划,故是全局极小点.] 7.18 解这个非线性规划的条件为极大点是,但它不是约束条件的正则点.7.21 解构造惩罚函数由则的解为当时,;当时,.当时,趋于原问题的极小值. .7.22 解构造惩罚函数解得最优解为7.24 解构造障碍函数得最优解。
(完整版)运筹学》习题答案运筹学答案

《运筹学》习题答案一、单选题1.用动态规划求解工程线路问题时,什么样的网络问题可以转化为定步数问题求解()BA.任意网络B.无回路有向网络C.混合网络D.容量网络2.通过什么方法或者技巧可以把工程线路问题转化为动态规划问题?()BA.非线性问题的线性化技巧B.静态问题的动态处理C.引入虚拟产地或者销地D.引入人工变量3.静态问题的动态处理最常用的方法是?BA.非线性问题的线性化技巧B.人为的引入时段C.引入虚拟产地或者销地D.网络建模4.串联系统可靠性问题动态规划模型的特点是()DA.状态变量的选取B.决策变量的选取C.有虚拟产地或者销地D.目标函数取乘积形式5.在网络计划技术中,进行时间与成本优化时,一般地说,随着施工周期的缩短,直接费用是( )。
CA.降低的B.不增不减的C.增加的D.难以估计的6.最小枝权树算法是从已接接点出发,把( )的接点连接上CA.最远B.较远C.最近D.较近7.在箭线式网络固中,( )的说法是错误的。
DA.结点不占用时间也不消耗资源B.结点表示前接活动的完成和后续活动的开始C.箭线代表活动D.结点的最早出现时间和最迟出现时间是同一个时间8.如图所示,在锅炉房与各车间之间铺设暖气管最小的管道总长度是( )。
CA.1200B.1400C.1300D.17009.在求最短路线问题中,已知起点到A,B,C三相邻结点的距离分别为15km,20km,25km,则()。
DA.最短路线—定通过A点B.最短路线一定通过B点C.最短路线一定通过C点D.不能判断最短路线通过哪一点10.在一棵树中,如果在某两点间加上条边,则图一定( )AA.存在一个圈B.存在两个圈C.存在三个圈D.不含圈11.网络图关键线路的长度( )工程完工期。
CA.大于B.小于C.等于D.不一定等于12.在计算最大流量时,我们选中的每一条路线( )。
CA.一定是一条最短的路线B.一定不是一条最短的路线C.是使某一条支线流量饱和的路线D.是任一条支路流量都不饱和的路线13.从甲市到乙市之间有—公路网络,为了尽快从甲市驱车赶到乙市,应借用()CA.树的逐步生成法B.求最小技校树法C.求最短路线法D.求最大流量法14.为了在各住宅之间安装一个供水管道.若要求用材料最省,则应使用( )。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
《运筹学》 第七章决策分析习题及 答案

《运筹学》第七章决策分析习题及答案摸索题(1)简述决策的分类及决策的程序;(2)试述构成一个决策咨询题的几个因素;(3)简述确定型决策、风险型决策和不确定型决策之间的区不。
不确定型决策能否转化成风险型决策?(4)什么是决策矩阵?收益矩阵,缺失矩阵,风险矩阵,后悔值矩阵在含义方面有什么区不;(5)试述不确定型决策在决策中常用的四种准则,即等可能性准则、最大最小准则、折衷准则及后悔值准则。
指出它们之间的区不与联系;(6)试述效用的概念及其在决策中的意义和作用;(7)如何确定效用曲线;效用曲线分为几类,它们分不表达了决策者对待决策风险的什么态度;(8)什么是转折概率?如何确定转折概率?(9)什么是乐观系数,它反映了决策人的什么心理状态?判定下列讲法是否正确(1)不管决策咨询题如何变化,一个人的效用曲线总是不变的;(2)具有中间型效用曲线的决策者,对收入的增长和对金钞票的缺失都不敏锐;(3)考虑下面的利润矩阵(表中数字矩阵为利润)S 3 1 15 14 10 -3 S 417221012分不用以下四种决策准则求最优策略:(1)等可能性准则(2)最大最小准则(3)折衷准则(取=0.5)(4)后悔值准则。
某种子商店期望订购一批种子。
据已往体会,种子的销售量可能为500,1000,1500或2000公斤。
假定每公斤种子的订购价为6元,销售价为9元,剩余种子的处理价为每公斤3元。
要求:(1)建立损益矩阵;(2)分不用悲观法、乐观法(最大最大)及等可能法决定该商店应订购的种子数;(3)建立后悔矩阵,并用后悔值法决定商店应订购的种子数。
按照已往的资料,一家超级商场每天所需面包数(当天市场需求量)可能是下列当中的某一个:100,150,200,250,300,但其概率分布不明白。
如果一个面包当天卖不掉,则可在当天终止时每个0.5元处理掉。
新奇面包每个售价1.2元,进价0.9元,假设进货量限制在需求量中的某一个,要求(1)建立面包进货咨询题的损益矩阵;(2)分不用处理不确定型决策咨询题的各种方法确定进货量。
运筹学部分课后习题解答

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a)12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA上的点都为最优解,即该问题有无穷多最优解,这时的最优值为min 3z=23032⨯+⨯= P47 1.3 用图解法和单纯形法求解线性规划问题a)12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集OABCO,且可知B点为最优值点,即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩,即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法: 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →10 5B CB X b 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题:1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题;(2)已知原问题最优解为)0,4,2,2(*=X ,试根据对偶理论,直接求出对偶问题的最优解。
运筹学习题答案(第七章)

page 19 9 July 2013
School of Management
运筹学教程
第七章习题解答
7.10 用顺序解法计算7.1题,7.4题。 解:略。
page 20 9 July 2013
School of Management
运筹学教程
第七章习题解答
7.11 某工厂生产三种产品,各种产品重量与利润 关系如表7-22所示,现将此三种产品运往市场出售, 运输能力总重量不超过6t,问应运输每种产品各多少 件可使总利润最大。 解:只运产品2两件,最大总利润260(千元)。
运筹学教程
同样适合第三版黄皮版
page 1 9 July 2013
School of Management
运筹学教程(第二版) 习题解答
安徽大学管理学院
洪 文
电话:5108157(H),5107443(O) E-mail: Hongwen9509_cn@
运筹学教程
第七章习题解答
7.1 现有天然气站A,需铺设管道到用气单位E, 可以选择的设计路线如下图所示,Bl,…,D2各点是 中间加压站,各线路的费用已标在线段旁(单位:万 元),试设计费用低的路线。
max F x 1 2 x 2 x 3 x 3 4 x 2 2 x 3
2 2
(2)
x1 x 2 x 3 3 x i 0 , ( i 1, 2 , 3 )
解: x 1 1, x 2 1, x 3 1, F 4
page 18 9 July 2013
page 23 9 July 2013
概率 0.4 0.3 0.3
School of Management
运筹学教程
运筹学习题答案第七章共29页PPT资料

安徽大学管理学院
电话:5108157(H),5107443(O) E-mail: Hongwen9509_cnsina
洪文
运筹学教程
第七章习题解答
7.1 现有天然气站A,需铺设管道到用气单位E,
可中以间选加择压的站设 ,计各路线线路如的下费图用所已示标,在线Bl,段…旁,(单D位2各:点万是 元),试设计费用低的路线。
-
-
1
64
2
0 64 68 -
-
2
68
3
0 64 68 78 -
3
78
4
0 64 68 78 76 3
78
page 9 5/5/2020
School of Management
运筹学教程
第七章习题解答
状态(可能的 投资数)
0 1 2 3 4
工厂2 决策(分配资金)
01234
0
-
-
-
-
64 42 -
7.5 为保证某设备正常运转,需对串联工作的三
种不同零件Al,A2,A3,分别确定备件数量。若增加 备用零件的数量,可提高设备正常运转的可靠性,但
费用要增加,而总投资额为8千元。已知备用零件数与
它的可靠性和费用关系如表7-2l所示,求Al,A2,A3的 备用零件数量各为多少时,可使设备运转的可靠性最
运行模型后,1月生产5,2月生产6,最小费用为67。
page 7 5/5/2020
School of Management
运筹学教程
第七章习题解答
7.4 某公司有资金4万元,可向A,B,C三个项目 投资,已知各项目不同投资额的相应效益值如表7-20 所示,问如何分配资金可使总效益最大。
运筹学教材习题答案详解

B1:2.0
3
需要量(套)
200
150
问怎样下料使得(1)用料最少;(2)余料最少.
【解】第一步:求下料方案,见下表。
方案
一
二
三
四
五
六
七
八
九
十
十一
十二
十三
十四
需要量
B1:2.7m
2
1
1
1
0
0
0
0
0
0
0
0
0
0
300
B2:2m
0
1
0
0
3
2
2
1
1
1
0
0
0
0
450
A1:1.7m
0
0
1
0
0
1
0
2
1
0
3
2
1
0
(2)
【解】最优解X=(3/4,7/2);最优值Z=-45/4
(3)
【解】最优解X=(4,1);最优值Z=-10
(4)
【解】最优解X=(3/2,1/4);最优值Z=7/4
(5) 【解】最优解X=(3,0);最优值Z=3
(6)
【解】无界解。
(7)
【解】无可行解。
(8)
【解】最优解X=(2,4);最优值Z=13
【解】设x1、x2、x3分别为产品A、B、C的产量,则数学模型为
1.3建筑公司需要用6m长的塑钢材料制作A、B两种型号的窗架.两种窗架所需材料规格及数量如表1-23所示:
表1-23窗架所需材料规格及数量
型号A
型号B
每套窗架需要材料
长度(m)
运筹学部分课后习题解答

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a)12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA上的点都为最优解,即该问题有无穷多最优解,这时的最优值为min 3z=23032⨯+⨯= P47 1.3 用图解法和单纯形法求解线性规划问题a)12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集OABCO,且可知B点为最优值点,即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩,即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法: 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →10 5B CB Xb 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题:1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题;(2)已知原问题最优解为)0,4,2,2(*=X ,试根据对偶理论,直接求出对偶问题的最优解。
《管理运筹学》第四版课后习题答案
(4)3 车间 ,因为增加的利 润最大。
(5)在400 到正无 穷的范 围内 变化,最优产 品的 组合不 变。
(6)不变,因为在 0,500 的范 围内。
(7)所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时,约束条件 1 的右 边值 在 200,440 变化,对 偶价格仍 为 50(同理解释 其他 约 束条件)。
当 c1 不变时 ,c2 在 负无穷 到 6.4 的范 围内变 化,最优 解不 变。 (5)约 束条件 1 的右 边值 在 780 000,1500 000 变化,对偶价格仍 为 0.057(其他同理) 。 (6)不能,因为允 许减少的百分比与允 许 增加的百分比之和 4 2 100% ,理由
4.25 3.6
11.解: 设圆 桌和衣柜的生 产件数分 别为 x、y,所获 利润为 z,则 z=6x+10y.
0.18x 0.08x
x0 y0
0.09 y 0.28 y
72 2x y 800
56 2x 7 y 即 x0
1400 作出可行域.平移 6x+ 10y=0 ,如图
y0
2x y 800
x 350
得
即 C(350,100) .当直线 6x+ 10y=0 即 3x+ 5y=0 平移
x1
0.2
,函数值为 3.6。
x2 0.6
图 2-2
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
运筹学习题答案(第七章)

64
68 78 78
42
108 110 120
50 114 118
60 124
66
0
1 2 3
64
108 114 124
School of Management
运筹学教程
第七章习题解答
工厂1 状态(可 能的投资 数) 4 决策(分配资金) 0 124 1 155 2 154 3 124 4 66 最优 决策 1 最优决 策的效 益值 155
page 13 11 July 2013
School of Management
运筹学教程
第七章习题解答
7.6 某工厂有l 000台机器,可以在高、低两种不 同负荷下进行生产,假没在高负荷下生产时,产品的 年产量s1和投入的机器数量y1的关系为s1=8y1,机器的 完好率为0.7;在低负荷下生产时,产品的年产量s2 和 投入的机器数量y2 的关系为s2=5y2 ,机器的完好率为 0.9。现在要求制定一个5年生产计划,问应如何安排 使在5年内的产品总产量最高。 解:y=0表示低负荷,y=1表示高负荷 Y(1)=0 Y(2)=0 Y(3)=1 Y(4)=1 Y(5)=1 各月的产量如下: X(1)=5000,X(2)=4500,X(3)=64800, X(4)=4536,X(5)=3175.2
page 6 11 July 2013
表7-19 1 5
2 3
3 2
4 1
School of Management
运筹学教程
第七章习题解答
解:xi表示生产量,Ii表示存储量,yi表示控制变 量, yi=1表示该月进行生产。 该问题的模型如下: min=5*(x1+x2+x3+x4) +(I0+I1+I2+I3+I4) +4*(Y1+Y2+Y3+Y4); I0=0;I4=0; I0+x1-I1=5; I1+x2-I2=3; I2+x3-I3=2; I3+x4-I4=1; x1<6*Y1;x2<6*Y2;x3<6*Y3;x4<6*Y4; @bin(Y1);@bin(Y2);@bin(Y3);@bin(Y4); 运行模型后,1月生产5,2月生产6,最小费用为67。
运筹学第7章答案
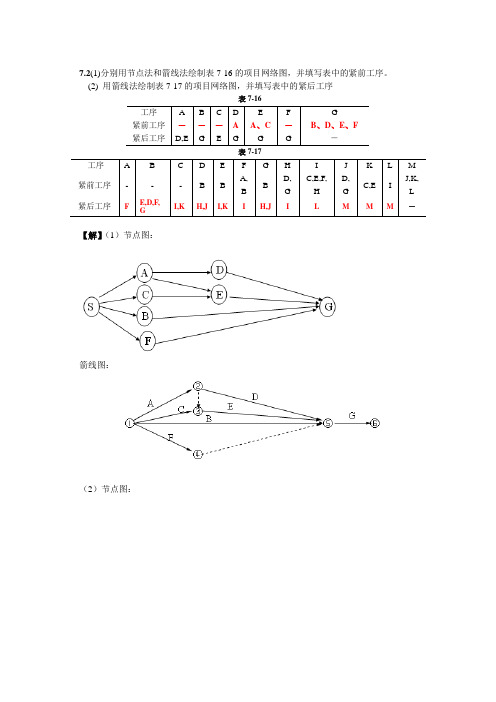
7.2(1)分别用节点法和箭线法绘制表7-16的项目网络图,并填写表中的紧前工序。
(2) 用箭线法绘制表7-17的项目网络图,并填写表中的紧后工序表7-16表7-17【解】(1)节点图:箭线图:(2)节点图:箭线图:7.3根据项目工序明细表7-18:(1)画出网络图。
(2)计算工序的最早开始、最迟开始时间和总时差。
(3)找出关键路线和关键工序。
表7-18【解】(1)网络图(2)网络参数(3)关键路线:①→②→③→④→⑤→⑥→⑦;关键工序:A、C、D、G;完工期:48周。
7.4 表7-19给出了项目的工序明细表。
表7-19(2)在网络图上求工序的最早开始、最迟开始时间。
(3)用表格表示工序的最早最迟开始和完成时间、总时差和自由时差。
(4)找出所有关键路线及对应的关键工序。
(5)求项目的完工期。
【解】(1)网络图(2)工序最早开始、最迟开始时间(3)用表格表示工序的最早最迟开始和完成时间、总时差和自由时差(4)关键路线及对应的关键工序关键路线有两条,第一条:①→②→⑤→⑥→⑦→○11→○12;关键工序:B,E,G,H,K,M 第二条:①→④→⑧→⑨→○11→○12;关键工序:C,F,L,M (5)项目的完工期为62天。
7.5已知项目各工序的三种估计时间如表7-20所示。
求: 表7-20 (1)绘制网络图并计算各工序的期望时间和方差。
(2)关键工序和关键路线。
(3)项目完工时间的期望值。
(4)假设完工期服从正态分布,项目在56小时内完工的概率是多少。
(5)使完工的概率为0.98,最少需要多长时间。
【解】(1)网络图(2)关键工序:A,C,E,F ;关键路线:①→②→④→⑤→⑥(3) 项目完工时间的期望值:10.17+14.83+17.17+11.83=54(小时)完工期的方差为0.25+0.25+0.6944+0.6944=1.88891.37437σ(4)X 0=56,05654(1.45520.9271.37437n n X μσ⎛⎫--⎛⎫Φ=Φ⎪ ⎪⎝⎭⎝⎭Φ=)=56天内完工的概率为0.927(5) p=0.98,0{)()0.98, 2.05p X X Z Z ≤=Φ==0 2.05 1.37445456.82X Z σμ+=⨯+==要使完工期的概率达到0.98,则至少需要56.82小时。
运筹学第五、六、七、八章答案

运筹学第五、六、七、八章答案5.2 用元素差额法直接给出表5-53及表5-54下列两个运输问题的近似最优解.表5-53 B1 B2 B3 B4 B5 Ai A1 19 16 10 21 9 18 A2 14 13 5 24 7 30 A3 25 30 20 11 23 10 A4 7 8 6 10 4 42 Bj 15 25 35 20 5 表5-54 B1 B2 B3 B4 Ai A1 5 3 8 6 16 A2 10 7 12 15 24 A3 17 4 8 9 30 Bj 20 25 10 15 【解】表5-53。
Z=824 表5-54 Z=495 5.3 求表5-55及表5-56所示运输问题的最优方案.(1)用闭回路法求检验数(表5-55)表5-55 B1 B2 B3 B4 Ai A1 10 5 2 3 70 A2 4 3 1 2 80 A3 5 6 4 4 30 bj 60 60 40 20(2)用位势法求检验数(表5-56)表5-56 B1 B2 B3 B4 Ai A1 9 15 4 8 10 A2 3 1 7 6 30 A3 2 10 13 4 20 A4 4 5 8 3 43 bj 20 15 50 15 【解】(1)(2)5.4 求下列运输问题的最优解(1)C1目标函数求最小值;(2)C2目标函数求最大值 15 45 20 40 60 30 50 40(3)目标函数最小值,B1的需求为30≤b1≤50, B2的需求为40,B3的需求为20≤b3≤60,A1不可达A4,B4的需求为30.【解】(1)(2)(3)先化为平衡表 B11 B12 B2 B31 B32 B4 ai A1 4 4 9 7 7 M 70 A2 6 6 5 3 3 2 20 A3 8 8 5 9 9 10 50 A4 M 0 M M 0 M 40 bj 30 20 40 20 40 30 180 最优解:5.5(1)建立数学模型设xij(I=1,2,3;j=1,2)为甲、乙、丙三种型号的客车每天发往B1,B2两城市的台班数,则(2)写平衡运价表将第一、二等式两边同除以40,加入松驰变量x13,x23和x33将不等式化为等式,则平衡表为:B1 B2 B3 ai 甲乙丙 80 60 50 65 50 40 0 0 0 5 10 15 bj 10 15 5 为了平衡表简单,故表中运价没有乘以40,最优解不变(3)最优调度方案:即甲第天发5辆车到B1城市,乙每天发5辆车到B1城市,5辆车到B2城市,丙每天发10辆车到B2城市,多余5辆,最大收入为Z=40(5×80+5×60+5×50+10×40)=54000(元)5.6(1)设xij为第i月生产的产品第j月交货的台数,则此生产计划问题的数学模型为(2)化为运输问题后运价表(即生产费用加上存储费用)如下,其中第5列是虚设销地费用为零,需求量为30。
运筹学 第七章 第八章习题解答

7-8 解:(a) 如图所示,c = 20 kPaS h e a r s t r e n g t h , τf (k P a )Normal stress, σn (kPa)tan φ = (83-52)/(200-100) = 0.31,所以,φ = arctan0.31 = 17.2︒(b) 该平面上的抗剪强度τf = c+σn tan φ = 20+260*tan17.2︒ = 20+80.6=100.6 (kPa) ∵ 该平面上的剪切应力τ = 92 kPa < τf∴ 不发生破坏7-10 解答:(a) 作图:分别做有效应力莫尔圆、总应力莫尔圆(图略)在总应力莫尔圆上做试样I 和II 的强度包线,有图可知c = 0, 113400700400700)/2σ(σ)/2σ(σsin φ3131cu =+-=+-=,∴ φcu = 16︒在有效应力莫尔圆上做试样I 和II 的强度包线,有图可知c ’=0, 0.556620300280)-(400280)-(700400700)/2'σ(σ)/2σ(σsin 3131==+-=+-='φ' ∴ φ’=37︒(b) 试样II 破坏时的有效大小主应力σ1’= σ1-u=700-280= 420 kPaσ3’= σ3-u=400-280= 120 kPa∴ (σ1’- σ3’)/2 = (420-120)/2 = 150 kPa(σ1’+ σ3’)/2 = (420+120)/2 = 270 kPa当采用有效应力及有效应力抗剪强度指标时,2αf = 2(45+φ’/2) = 2(45︒+34︒/2)= 124︒破坏面上的法向有效应力()()αcos2'σ'σ21'σ'σ21σ3131-++== 270+150*cos124︒ = 186 kPa︒ = 124 kPa(c ) 对于试样I 而言:破坏时主应力差(或偏主应力)∆σ1= σ1 - σ3 = 350-200 = 150 kPa 常规三轴试验中,试样在剪切过程中围压σ3保持不变 ∴∆σ3 = 0 孔压增量∆u 1 =量测的孔压u f =140 kPa (隐含:三轴试验中初始孔压 = 0) ∴ A = ∆u 3/(∆σ1-∆σ3) = ∆u 3/∆σ1 =140/150 = 0.937-11解答假设在σ3 = 150 kP 下试样发生剪切破坏,则此时试样必定处于极限平衡状态, 试样的有效围压σ3f ’= σ3f –u f = 150-100 = 50 kP此时破坏面与大主应力作用面的夹角αf = 45+φ’/2 = 45+28/2 = 59︒ 试样的大主应力σ1f ’然而,试样真正的大主应力σ1’=200-100 = 100 (kPa) > 假定计算所得σ1f’(183kPa)∴假定不合理,不发生破坏7-14 解答1)所得抗剪强度指标c d/φd分别与c’/φ’相等,c d =c’,φd=φ’,σ3’=σ3 = 200 kPa2)CD试验试样剪切破坏时, σ1f’必定满足下述极限平衡条件=439+71=510 (kPa)第八章本章习题较简单,习题类型和计算步骤雷同PPT中的例题。
上交大《物流运筹学》教学资料包 课后习题答案 第七章

第七章项目计划技术一、思考与练习(1)请指出图7-14(a)(b)(c)(d)所示网络图的错误,若能改正,试给予改正。
(a)(b)(c)(d)图7-14 网络图示例解(a)工序d、e具有完全相同的箭尾结点与箭头结点。
应在结点②和④之间增加一个结点和一个虚工序。
(b)图中有⑤和⑦两个终端结点,应去掉一个,将工序f,g归结到一个结点。
此外,虚工序④→⑥可省略。
(c)图中有两个始点和两个终点,均可合并。
(d)工序a,d,e形成循环,不允许。
(2)已知表7-10所列资料:表7-10 工序时间表要求:①绘制项目计划图;②计算各结点的最早时间和最迟时间;③计算各工序的最早开工、最早完工、最迟开工及最迟完工时间;④计算各工序的时差;⑤确定关键路线。
解①项目计划图如下:②结点1的最早时间是0,最晚时间是0;结点2的最早时间是3,最晚时间是3;结点3的最早时间是7,最晚时间是8;结点4的最早时间是8,最晚时间是8;结点5的最早时间是12,最晚时间是14;结点6的最早时间是15,最晚时间是17;结点7的最早时间是15,最晚时间是15;结点8的最早时间是15,最晚时间是15;结点9的最早时间是16,最晚时间是19;结点10的最早时间是17,最晚时间是17;结点11的最早时间是19,最晚时间是19。
③、④各工序的最早开工、最早完工、最迟开工、最迟完工时间以及各工序的时差见下表。
工序最早 开工(,)ES t i j最早 完工(,)EF t i j 最迟 开工(,)LS t i j 最迟 完工(,)LF t i j总时差(,)R i j单时差(,)r i j关键 工作A 0 3 0 3 0 0 1→2B 3 7 4 8 1 1C 3 8 3 8 0 0 2→4D 8 15 8 15 0 0 4→7E 8 15 8 15 0 0 4→8F 8 16 11 19 3 3G 8 12 10 14 2 0H 15 17 15 17 0 0 7→10I 12 15 14 17 2 2 J1719171910→11⑤由上表可知关键路线为1→2→4→7→10→11或1→2→4→8→10→11(3)某工程各工序关系及各工序所需时间如表7-11所示,试绘制项目计划图,计算事项及工序的6个时间参数的表格,并指出关键路径。
运筹学课后习题答案
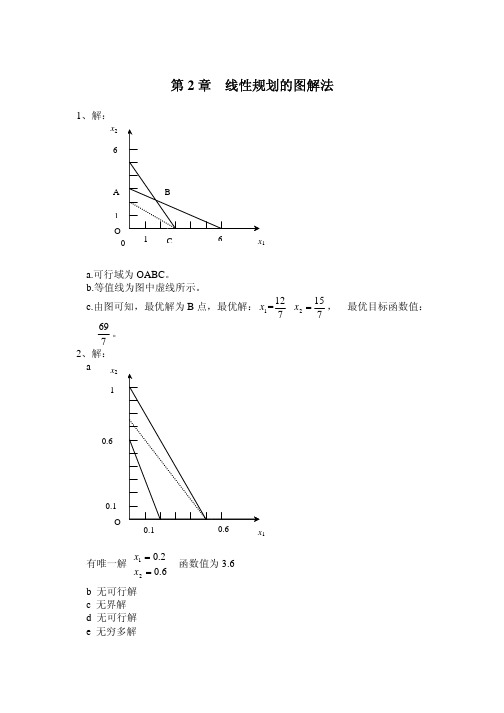
s1 = 2, s2 = 0
5 、解: 标准形式: min f = 11x1 + 8x2 + 0s1 + 0s2 + 0s3
10x1 + 2x2 − s1 = 20 3x1 + 3x2 − s2 = 18 4x1 + 9x2 − s3 = 36 x1, x2 , s1, s2 , s3 ≥ 0
s1 = 0, s2 = 0, s3 = 13 6 、解:
3 车间每增加 1 工时,总利润增加 200 元 2、4 车间每增加 1 工时,总利润不增加。 d 3 车间,因为增加的利润最大 e 在 400 到正无穷的范围内变化,最优产品的组合不变
f 不变 因为在 [0,500]的范围内
g 所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条
件 1 的右边值在 [200,440]变化,对偶价格仍为 50(同理解释其他约束条件)
2、解:从上午 11 时到下午 10 时分成 11 个班次,设 xi 表示第 i 班次安排的临时 工的人数,则可列出下面的数学模型: min f=16(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11) s.t. x1+1 ≥ 9 x1+x2+1 ≥ 9 x1+x2+x3+2 ≥ 9 x1+x2+x3+x4+2 ≥ 3
x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0, x10=0,x11=0 最优值为 320。
a、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
运筹学习题答案
第一章习题1.思考题(1)微分学求极值的方法为什么不适用于线性规划的求解(2)线性规划的标准形有哪些限制如何把一般的线性规划化为标准形式(3)图解法主要步骤是什么从中可以看出线性规划最优解有那些特点(4)什么是线性规划的可行解,基本解,基可行解引入基本解和基可行解有什么作用(5)对于任意基可行解,为什么必须把目标函数用非基变量表示出来什么是检验数它有什么作用如何计算检验数(6)确定换出变量的法则是什么违背这一法则,会发生什么问题(7)如何进行换基迭代运算(8)大M法与两阶段法的要点是什么两者有什么共同点有什么区别(9)松弛变量与人工变量有什么区别试从定义和处理方式两方面分析。
(10)如何判定线性规划有唯一最优解,无穷多最优解和无最优解为什么2.建立下列问题的线性规划模型:(1)某厂生产A,B,C三种产品,每件产品消耗的原料和设备台时如表1-18所示:润最大的模型。
(2)某公司打算利用具有下列成分(见表1-19)的合金配制一种新型合金100公斤,新合金含铅,锌,锡的比例为3:2:5。
如何安排配方,使成本最低(3)某医院每天各时间段至少需要配备护理人员数量见表1-20。
表1-20假定每人上班后连续工作8小时,试建立使总人数最少的计划安排模型。
能否利用初等数学的视察法,求出它的最优解(4)某工地需要30套三角架,其结构尺寸如图1-6所示。
仓库现有长6.5米的钢材。
如何下料,使消耗的钢材最少图1-63. 用图解法求下列线性规划的最优解:⎪⎪⎩⎪⎪⎨⎧≥≤+-≥+≥++=0,425.134 12 64 min )1(2121212121x x x x x x x x x x z⎪⎪⎩⎪⎪⎨⎧≥≤+≥+-≤++=0,82 5 1032 44 max )2(2121212121x x x x x x x x x x z⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤-≤+-≤++=0,6054 4 22232 96 max )3(21221212121x x x x x xx x x x xz⎪⎩⎪⎨⎧≥≤+-≥++=0,1 1234 3 max )4(21212121x x x x x x x x z4. 把下列线性规划化为标准形式:⎪⎪⎩⎪⎪⎨⎧≥≤=-++-≥-+≤-+-+-=无约束432143213214313210,,01 32 212 min )1(x x x x x x x x x x x x x x x x x z⎪⎪⎩⎪⎪⎨⎧≤≤≥+-≤++=无约束211212121,02182 32 max )2(x x x x x x x x x z5. 判定下列集合是否凸集:(1)R 1={(x 1,x 2)|x 12+2x 22≤2}(2)R 2={(x 1,x 2)|x 12-2x 2+3≥0,x 2≥0,|x 1|≤1} (3)R 3={(x 1,x 2)|x 1x 2≥1,x 1≥1,x 2≥0}6. 求出下列线性规划的所有基本解,并指出其中的基可行解和最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
School of Management
运筹学教程
第七章习题解答
7.8 将数 分成3个正数之和,使其乘积为最大。 将数48分成 个正数之和 使其乘积为最大。 分成 个正数之和, 解: x(1)+x(2)+x(3) =48 x(1)=x(2)=x(3)=16 x(1)*x(2)*x(3)=4096
2 2 max F = x1 + 2 x 2 + x 3 ⋅ x3 − 4 x 2 − 2 x3 ( 2 ) x1 + x 2 + x3 = 3 xi ≥ 0, (i = 1, 2,3) 解: x1 = 1, x 2 = 1, x3 = 1, F = − 4
page 18 5 April 2012
page 19 5 April 2012
School of Management
运筹学教程
第七章习题解答
7.10 用顺序解法计算 题,7.4题。 用顺序解法计算7.1题 题 解:略。
page 20 5 April 2012
School of Management
运筹学教程
第七章习题解答
7.11 某工厂生产三种产品,各种产品重量与利润 某工厂生产三种产品, 关系如表7-22所示,现将此三种产品运往市场出售, 所示, 关系如表 所示 现将此三种产品运往市场出售, 运输能力总重量不超过6t, 运输能力总重量不超过 ,问应运输每种产品各多少 件可使总利润最大。 件可使总利润最大。 只运产品2两件 最大总利润260(千元)。 两件, 解:只运产品 两件,最大总利润 (千元)。 表7-22 重量(t/件) 利润(千元/件) 重量(t/件 利润(千元/ (t/ 2 80 3 130 4 180
page 5 5 April 2012
School of Management
运筹学教程
第七章习题解答
page 6 5 April 2012
School of Management
运筹学教程
第七章习题解答
7.3 某厂每月生产某种产品最多 某厂每月生产某种产品最多600件,当月生产 件 的产品若未销出,就需存贮(刚入库的产品 刚入库的产品, 的产品若未销出,就需存贮 刚入库的产品,该月不付 存贮费)。月初就已存的产品需支付存储费, 存贮费 。月初就已存的产品需支付存储费,每100件 件 每月1千元 已知每100件产品的生产费为 千元。在进 千元。 件产品的生产费为5千元 每月 千元。已知每 件产品的生产费为 千元。 行生产的月份工厂要支出经营费4千元.市场需求如表 行生产的月份工厂要支出经营费 千元. 千元 7-19所示,假定 月初及 月底库存量为零,试问每月 所示, 月初及4月底库存量为零 所示 假定1月初及 月底库存量为零, 应生产多少产品,才能在满足需求条件下, 应生产多少产品,才能在满足需求条件下,使总生产 及存贮费用之和最小。 及存贮费用之和最小。 表7-19 1 5
月份 产品(100件 产品(100件)
page 7 5 April 2012
2 3
3 2
4 1
School of Management
运筹学教程
第七章习题解答
表示生产量, 表示存储量, 解:xi表示生产量,Ii表示存储量,yi表示控制变 表示该月进行生产。 量, yi=1表示该月进行生产。 表示该月进行生产 该问题的模型如下: 该问题的模型如下: min=5*(x1+x2+x3+x4) +(I0+I1+I2+I3+I4) +4*(Y1+Y2+Y3+Y4); I0=0;I4=0; I0+x1-I1=5; I1+x2-I2=3; I2+x3-I3=2; I3+x4-I4=1; x1<6*Y1;x2<6*Y2;x3<6*Y3;x4<6*Y4; @bin(Y1);@bin(Y2);@bin(Y3);@bin(Y4); 运行模型后, 月生产 月生产5, 月生产 月生产6,最小费用为67。 运行模型后,1月生产 ,2月生产 ,最小费用为 。
运筹学教程
第七章习题解答
7.1 现有天然气站 ,需铺设管道到用气单位 , 现有天然气站A,需铺设管道到用气单位E, 可以选择的设计路线如下图所示, 可以选择的设计路线如下图所示,Bl,…,D2各点是 中间加压站,各线路的费用已标在线段旁(单位:万 中间加压站,各线路的费用已标在线段旁 单位: 单位 元),试设计费用低的路线。 ,试设计费用低的路线。
page 3 5 April 2012
School of Management
运筹学教程
第七章习题解答
page 4 5 April 2012
School of Management
运筹学教程
第七章习题解答
7.2 一艘货轮在 港装货后驶往 港,中途需靠港 一艘货轮在A港装货后驶往 港装货后驶往F港 加油、淡水三次,从A港到 港部可能的航运路线及两 加油、淡水三次, 港到F港部可能的航运路线及两 港到 港之间距离如下图所示, 港有 个码头F 港有3个码头 港之间距离如下图所示,F港有 个码头 1,F2, F3 ,试 求最合理靠的码头及航线,使总路程最短。 求最合理靠的码头及航线,使总路程最短。
表7-20 投资额 项目 0 A B C 0 0 0 1 41 42 64 2 48 50 68 3 60 60 78 4 66 66 76 单位:万元 单位:
page 9 5 April 2012
School of Management
运筹学教程
第七章习题解答
工厂3 工厂 决策(分配资金) 决策(分配资金) 状态( 状态(可能的 投资数) 投资数) 0 1 2 3 4
page 12 5 April 2012
School of Management
运筹学教程
第七章习题解答
7.5 为保证某设备正常运转,需对串联工作的三 为保证某设备正常运转, 种不同零件A 分别确定备件数量。 种不同零件 l , A2 , A3 , 分别确定备件数量 。 若增加 备用零件的数量,可提高设备正常运转的可靠性, 备用零件的数量 , 可提高设备正常运转的可靠性 , 但 费用要增加,而总投资额为8千元。已知备用零件数与 费用要增加,而总投资额为 千元。 千元 它的可靠性和费用关系如表7-2l所示,求Al,A2,A3的 所示, 它的可靠性和费用关系如表 所示 备用零件数量各为多少时, 备用零件数量各为多少时 , 可使设备运转的可靠性最 高。
page 17 5 April 2012
School of Management
运筹Байду номын сангаас教程
第七章习题解答
7.9 用动态规划方法求解: 用动态规划方法求解:
2 max F = x1 ⋅ x 2 ⋅ x3 (1) x1 + x 2 + x3 = 4 xi ≥ 0, (i = 1, 2,3) 解 : x1 = 1, x 2 = 2, x3 = 1, F = 4
表7-21 可靠性 备件数 Al 1 2 3
page 13 5 April 2012
备用零件费用(千元 备用零件费用 千元) 千元 A3 0.1 0.2 0.7 Al 1 2 3 A2 3 5 6 A3 2 3 4
A2 0.2 0.5 0.9
0.3 0.4 0.5
School of Management
page 11 5 April 2012
0 0 64 68 78 78
1 42 108 110 120
2 50 114 118
3 60 124
4 66
最优 决策 0 0 1 2 3
最优决策 的效益值 0 64 108 114 124
School of Management
运筹学教程
第七章习题解答
工厂1 工厂 状态( 状态(可 能的投资 数) 4 决策(分配资金) 决策(分配资金) 0 124 1 155 2 154 3 124 4 66 最优 决策 1 最优决 策的效 益值 155
运筹学教程
第七章习题解答
最优解: 购买1, 购买1, 购买3。 最优解: Al购买 , A2购买 , A3购买 。可靠性 为0.042。 。
page 14 5 April 2012
School of Management
运筹学教程
第七章习题解答
7.6 某工厂有 000台机器,可以在高、低两种不 某工厂有l 台机器, 台机器 可以在高、 同负荷下进行生产,假没在高负荷下生产时, 同负荷下进行生产 , 假没在高负荷下生产时 , 产品的 年产量s1和投入的机器数量y1的关系为s1=8y1, 机器的 年产量 和投入的机器数量 的关系为 完好率为0.7;在低负荷下生产时,产品的年产量s 完好率为 ; 在低负荷下生产时 , 产品的年产量 2 和 投入的机器数量y 的关系为s 投入的机器数量 2 的关系为 2=5y2 , 机器的完好率为 0.9。 现在要求制定一个 年生产计划 , 问应如何安排 年生产计划, 。 现在要求制定一个5年生产计划 使在5年内的产品总产量最高 年内的产品总产量最高。 使在 年内的产品总产量最高。 表示低负荷, 解:y=0表示低负荷,y=1表示高负荷 表示低负荷 表示高负荷 Y(1)=0 Y(2)=0 Y(3)=1 Y(4)=1 Y(5)=1 各月的产量如下: 各月的产量如下: X(1)=5000,X(2)=4500,X(3)=64800, , , , X(4)=4536,X(5)=3175.2 ,
page 15 5 April 2012
School of Management
运筹学教程
第七章习题解答
某工厂接受一项特殊产品订货,要在3 7.7 某工厂接受一项特殊产品订货,要在3个月 后提供某种产品1 000kg,一次交货。 后提供某种产品1 000kg,一次交货。由于该产品用 途特殊,该厂原无存货,交货后也不留库存。 途特殊,该厂原无存货,交货后也不留库存。已知生 产费用与月产量关系为: 产费用与月产量关系为: C=1000+3d+0.005d2, = 其中(d为月产量 为月产量(kg),(C为该月费用 元)。每月库存成 为该月费用(元 。 其中 为月产量 , 为该月费用 本为2元 库存量按月初与月未存贮量的平均数计算, 本为 元/kg,库存量按月初与月未存贮量的平均数计算, 库存量按月初与月未存贮量的平均数计算 问如何决定3个月的产量使总费用最小 个月的产量使总费用最小。 问如何决定 个月的产量使总费用最小。 各月的产量如下: 解:各月的产量如下: D(1)=433.33, D(2)=333.33, , , D(3)=233.33。 最小费用为 。 最小费用为13566.67(元) (
