数列求和方法总结PPT课件
合集下载
数列求和的几种方法PPT课件

第2页/共11页
练习:(2003s)设f x 1 ,利用课本中
2x 2 推导等差数列前n项和的公式的方法,可求得
f 5 f 4 f 0 f 5 f 6
的值为 3 2 。
第3页/共11页
2、错位相减法
例2:求: 1 2
2 22
3 23
n 2n
1 an n 2n
问题:什么时候用错位相减的方法求数列和?
通过拆项,能将数列转化成两个或若干个等差或等比数 列的和或差的形式来求和。
第6页/共11页
4、拆项抵消
例4:求: 1 1
2
1 2
3
1
nn
1
1 11
an nn 1 n n 1
问题:什么时候用拆项抵消的方法求数列和?
将数列的每一项(实际就是通项)拆分成两项, 在求和时除前、后若干项外,中间各项能够相互抵消。
n
1 2
5 4
9 8
......
4n 2n
3.
5 求:S
n
1
3 2
5 4
7 8
......
(1)n1
2n 1 2n1
.
第10页/共11页
感谢观看!
第11页/共11页
1 2
1
1 3
1 ...... 2 2 3
1 n 1
. n
第9页/共11页
练习:
(1)求数列 :1 1,2 1,3 1 3 9 27
,, n
1 3n
的
和S
.
n
(2)求数列 :1 ,11,111,,111(n个1) 的和Sn.
(3)求:S
n
1 1
3
1
练习:(2003s)设f x 1 ,利用课本中
2x 2 推导等差数列前n项和的公式的方法,可求得
f 5 f 4 f 0 f 5 f 6
的值为 3 2 。
第3页/共11页
2、错位相减法
例2:求: 1 2
2 22
3 23
n 2n
1 an n 2n
问题:什么时候用错位相减的方法求数列和?
通过拆项,能将数列转化成两个或若干个等差或等比数 列的和或差的形式来求和。
第6页/共11页
4、拆项抵消
例4:求: 1 1
2
1 2
3
1
nn
1
1 11
an nn 1 n n 1
问题:什么时候用拆项抵消的方法求数列和?
将数列的每一项(实际就是通项)拆分成两项, 在求和时除前、后若干项外,中间各项能够相互抵消。
n
1 2
5 4
9 8
......
4n 2n
3.
5 求:S
n
1
3 2
5 4
7 8
......
(1)n1
2n 1 2n1
.
第10页/共11页
感谢观看!
第11页/共11页
1 2
1
1 3
1 ...... 2 2 3
1 n 1
. n
第9页/共11页
练习:
(1)求数列 :1 1,2 1,3 1 3 9 27
,, n
1 3n
的
和S
.
n
(2)求数列 :1 ,11,111,,111(n个1) 的和Sn.
(3)求:S
n
1 1
3
1
数列的求和方法(ppt)

分组求和法:有一等比或者其他常见数列(即可用倒序相加,错位相减或 裂项相消求和的数列),然后分别求和,之后再进行合并即可算出原数列的前n项 和。
错位相减法:形如An=BnCn,其中{Bn}为等差数列,首项为b1,公差为d;{Cn}为等 比数列,首项为c1,公比为q。对数列{An}进行求和,首先列出Sn,记为①式;再把① 式中所有项同乘等比数列{Cn}的公比q,即得qSn,记为②式;然后①②两式错开一位 做差,从而得到{An}的前n项和。这种数列求和方式叫作错位相减。
数列的求和方法(ppt)
演讲人
目录
01
数列概念
02
等差数列思维导图
数列求和的七种方法:倒序相加法、分组求和法、错位相减法、裂项相消法、乘 公比错项相减(等差×等比)、公式法、迭加法。
倒序相加法:如果一个数列{an},与首末两端等“距离”的两项和相等或者等于 同一个常数,则求该数列的前n项和即可用倒序相加法。例如等差数列的求和公 式,就可以用该方法进行证明。
等差数列思维导图
一般地来说如果一个数列从第2项起,每一项与它的前一项的差等于同一个常 数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字 母d表示,前n项和用Sn表示。
谢谢
裂项相消法:裂项相消法把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和。
乘公比错项相减(等差×等比):这种方法是在推导等比数列的前 n 项和公式时所用的 方法,这种方法主要用于求数列(anxbn)的前n项和,其中(an),(bn)分别是 等差数列和等比数列。
公式法:对等差数列、等比数列,求前n项和Sn可直接用等差、等 比数列的前n项和公式进行求解。运用公式求解的注意事项:首先 要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
错位相减法:形如An=BnCn,其中{Bn}为等差数列,首项为b1,公差为d;{Cn}为等 比数列,首项为c1,公比为q。对数列{An}进行求和,首先列出Sn,记为①式;再把① 式中所有项同乘等比数列{Cn}的公比q,即得qSn,记为②式;然后①②两式错开一位 做差,从而得到{An}的前n项和。这种数列求和方式叫作错位相减。
数列的求和方法(ppt)
演讲人
目录
01
数列概念
02
等差数列思维导图
数列求和的七种方法:倒序相加法、分组求和法、错位相减法、裂项相消法、乘 公比错项相减(等差×等比)、公式法、迭加法。
倒序相加法:如果一个数列{an},与首末两端等“距离”的两项和相等或者等于 同一个常数,则求该数列的前n项和即可用倒序相加法。例如等差数列的求和公 式,就可以用该方法进行证明。
等差数列思维导图
一般地来说如果一个数列从第2项起,每一项与它的前一项的差等于同一个常 数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字 母d表示,前n项和用Sn表示。
谢谢
裂项相消法:裂项相消法把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和。
乘公比错项相减(等差×等比):这种方法是在推导等比数列的前 n 项和公式时所用的 方法,这种方法主要用于求数列(anxbn)的前n项和,其中(an),(bn)分别是 等差数列和等比数列。
公式法:对等差数列、等比数列,求前n项和Sn可直接用等差、等 比数列的前n项和公式进行求解。运用公式求解的注意事项:首先 要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
专题数列求和的几种方法.ppt

求: bn 的前n项和
1 1(1 1 ) an an1 d an an1
}
满足
Sn b1 b2 b3 bn
1 ( 1 1 ) 1 ( 1 1 ) 1 ( 1 1 )
d a1 a2 d a2 a3
d an an1
1(1 1 1 1 d a1 a2 a2 a3
1 1 ) an an1
数 列 求和
1运用公式法
等差或等比数列直 接应用求和公式
2 分组求和法 3 错位相减法 4 裂项相消法 5 倒序相加法
化归思想转化 成等差、等比 数列求
1 2 2 3 3 4 n(n 1)
分析:设数列的通项为bn,则
bn
n(n 1)
6( 1 n
1) n 1
Sn
b1
b2
bn
6[(1
1) 2
(1 2
1) 3
(1 n
1 )] n 1
6(1 1 ) 6n n1 n1
例4、设{1an bn anan1
解: bn
}是公差d 不为零的等差数列 ,{bn
1(1 1 ) n .
d a1 an1
a1an 1
若
an
( An
1 B)(
An
C)
,则求Sn用 裂项相消法
.
常见的拆项公式有:
1. 1 1 1 n(n 1) n n 1
2. 1 1 ( 1 1 ) n(n k) k n n k
3.
1
1( 1 1 )
(2n 1)(2n 1) 2 2n 1 2n 1
1.公式法:
即直接用求和公式,求数列的前n和Sn
①等差数列的前n项和公式:
Sn
n(a1 2
1 1(1 1 ) an an1 d an an1
}
满足
Sn b1 b2 b3 bn
1 ( 1 1 ) 1 ( 1 1 ) 1 ( 1 1 )
d a1 a2 d a2 a3
d an an1
1(1 1 1 1 d a1 a2 a2 a3
1 1 ) an an1
数 列 求和
1运用公式法
等差或等比数列直 接应用求和公式
2 分组求和法 3 错位相减法 4 裂项相消法 5 倒序相加法
化归思想转化 成等差、等比 数列求
1 2 2 3 3 4 n(n 1)
分析:设数列的通项为bn,则
bn
n(n 1)
6( 1 n
1) n 1
Sn
b1
b2
bn
6[(1
1) 2
(1 2
1) 3
(1 n
1 )] n 1
6(1 1 ) 6n n1 n1
例4、设{1an bn anan1
解: bn
}是公差d 不为零的等差数列 ,{bn
1(1 1 ) n .
d a1 an1
a1an 1
若
an
( An
1 B)(
An
C)
,则求Sn用 裂项相消法
.
常见的拆项公式有:
1. 1 1 1 n(n 1) n n 1
2. 1 1 ( 1 1 ) n(n k) k n n k
3.
1
1( 1 1 )
(2n 1)(2n 1) 2 2n 1 2n 1
1.公式法:
即直接用求和公式,求数列的前n和Sn
①等差数列的前n项和公式:
Sn
n(a1 2
数列求和各种方法总结归纳课件PPT

[冲关锦囊]
用错位相减法求和时,应注意 (1)要善于识别题目类型,特别是等比数列公比为负数
的情形; (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“
错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
[精析考题] [例3] (2011·全国新课标卷)等比数列{an}的各项均为正数,且2a1+ 3a2=1,a32=9a2a6. (1)求数列{an}的通项公式; (2)设bn=log3a1+log3a2+…+log3an,求数列{b1n}的前n项和.
(1)an=kn+b,利用等差数列前n项和公式直接求解;
所以,当n>1时,①-②得 用错位相减法求和时,应注意
①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.
①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.
数列求和各种方法总结归纳
二、非等差、等比数列求和的常用方法 1.倒序相加法
如果一个数列{an},首末两端等“距离”的两项的和相等 或等于同一常数,那么求这个数列的前n项和即可用倒 序相加法,如等差数列的前n项和即是用此法推导的.
2.分组求和法 若一个数列的通项公式是由若干个等差数列或等比数列 或可求和的数列组成,则求和时可用分组转化法,分别 求和而后相加减.
∴bn+1+1=2bn+2=2(bn+1).
∴((11b))要a1n=善=0于k,n识b+1别b+,题1利=目用1类≠等0型.差n1,数-特列别n前是+n1等项比1和数公列=式公直-比接为求n负解2+数n;1.
所以数列{b1n}的前n项和为-n2+n1.
[巧练模拟]—————(课堂突破保分题,分分必保!)
数列求和方法总结PPT课件

有一类数列,既不是等差数列,也不是等比 数列,若将这类数列适当拆开,可分为几个等差、 等比或常见的数列,然后分别求和,再将其合并 即可.
-
6
例2:求数列的前n项和:1 1, 1 4, 1 7, , 1 3n 2,…
a a2
a n1
-
7
练习 : 求数列1 1 2
,3 1 4
,5
1 8
-
1
本节概要 数列求和的常用方法
-
2
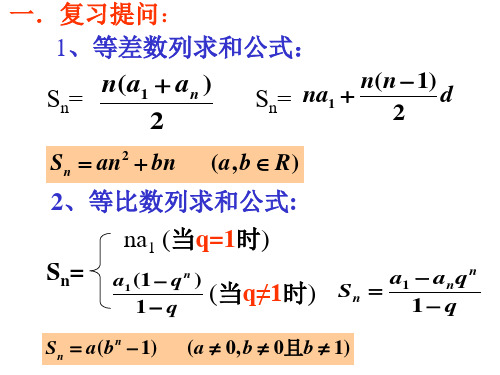
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
(q
1)
.
自然数方幂和公式:1 2 3 n 1 n(n 1) 2
12 22 32 n2 1 n(n 1)(2n 1) 6
2n 2n
…………………………………①
1 2
Sn
2 22
4 23
6 24
2n 2 n1
………………………………②
(设制错位)
①-②得(1
1 2
)S
n
2 2
2 22
2 23
2 24
2 2n
2n 2 n 1
2 1 2n 2n1 2n1
∴
Sn
4
n2 2 n 1
-
17
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
-
18
例
5.设
f
(x)
4 x , 则f 4x 2
2024年高考数学一轮复习(新高考版)《数列求和》课件ppt

跟踪训练2 (2023·重庆模拟)在①a1=1,nan+1=(n+1)·an,② 2a1 + 2a2 +…+2an =2n+1-2这两个条件中任选一个,补充在下面的问题中并作答. 问题:在数列{an}中,已知________. 注:如果选择多个条件分别解答,按第一个解答计分. (1)求{an}的通项公式;
(2)若bn=
2an 1 3an
,求数列{bn}的前n项和Sn.
由(1)可知 bn=2n3-n 1,
则 Sn=311+332+…+2n3-n 1,
①
13Sn=312+333+…+2n3-n 3+23nn-+11.
②
两式相减得23Sn=13+322+323+…+32n-23nn-+11=13+2911--313n1-1-23nn-+11
教材改编题
2.数列{an}的前 n 项和为 Sn.若 an=nn1+1,则 S5 等于
A.1
√B.56
C.16
D.310
因为 an=nn1+1=1n-n+1 1, 所以 S5=a1+a2+…+a5=1-12+12-13+…-16=56.
教材改编题
3.Sn=12+12+38+…+2nn等于
2n-n-1 A. 2n
第六章 数 列
§6.5 数列求和
考试要求
1.熟练掌握等差、等比数列的前n项和公式. 2.掌握非等差数列、非等比数列求和的几种常用方法.
内容索引
第一部分
落实主干知识
第二部分
探究核心题型
第三部分
课时精练
第
一 部 分
落实主干知识
知识梳理
数列求和的几种常用方法
1.公式法
直接利用等差数列、等比数列的前n项和公式求和.
数列求和(23张PPT)

n 1 n 1 n 1 n 1 (1 6n 5) (a1 an ) 2 2 4 ( 1 4 ) a ( 1 4 ) 2 2 2 2 1 4 2 1 4
2
n2
9n 3n 14 6
2
例2. (天津卷)已知数列
问题解决
a n 的通项公式如下:
0 n 1 n 2 n
n n ,
则 Sn
(n 1)C nC
n n 0 n
n1 n 1 n
3C 2C C
2 n 1 n n 2 n
0 n n n
(n 1)C nC 3C
Sn (n 2) 2
0 n n1 1 n 3 n
2C
n n
n1 n
n b a x n (2)令 n
( x R) ,求知数列
a n 的通项公式如下:
,
6n 5 an n 2
n为奇数 n为偶数
。
s 求数列的前 n 项的和 n
例
a n 1. (北京 卷) 已 知数列 是等差 数列, 且
1 Sn 3 2 k 3 k 2k 1 思考题.已知 k 1
n
,
1 Sn 4 求证:
问题解决
C 2 C 3 C ( n 1 ) C 例3.求和
0 n 1 n 2 n n n
C 2 C 3 C ( n 1 ) C S 【解析】设 n
,
6n 5 an n 2
n为奇数 n为偶数
n n (a1 an 1 ) n 3 2 2 2 9 n 15n 8 a ( 1 4 ) 2 2 Sn 6 2 1 4 n2 2 2 9n 3n 14 n为奇数 6
2
n2
9n 3n 14 6
2
例2. (天津卷)已知数列
问题解决
a n 的通项公式如下:
0 n 1 n 2 n
n n ,
则 Sn
(n 1)C nC
n n 0 n
n1 n 1 n
3C 2C C
2 n 1 n n 2 n
0 n n n
(n 1)C nC 3C
Sn (n 2) 2
0 n n1 1 n 3 n
2C
n n
n1 n
n b a x n (2)令 n
( x R) ,求知数列
a n 的通项公式如下:
,
6n 5 an n 2
n为奇数 n为偶数
。
s 求数列的前 n 项的和 n
例
a n 1. (北京 卷) 已 知数列 是等差 数列, 且
1 Sn 3 2 k 3 k 2k 1 思考题.已知 k 1
n
,
1 Sn 4 求证:
问题解决
C 2 C 3 C ( n 1 ) C 例3.求和
0 n 1 n 2 n n n
C 2 C 3 C ( n 1 ) C S 【解析】设 n
,
6n 5 an n 2
n为奇数 n为偶数
n n (a1 an 1 ) n 3 2 2 2 9 n 15n 8 a ( 1 4 ) 2 2 Sn 6 2 1 4 n2 2 2 9n 3n 14 n为奇数 6
数列求和的常用方法总结归纳PPT

等比数列)的数列,可采用错位相减的方法进行求和.
例6:(1)已知数列{an}的首项a1 2,an 3an1 (2 n 2),
bn log3(an 1),cn anbn n. ①证明:{an 1}是等比数列; ②求数列{cn }的前n项和S n .
Sn
3 4
(1 2
n
1 )3n1 4
(2)已知{an}是递增的等差数列,a2,a4是方程x2 5x 6 0的根.
(2)求和Sn
1
(1
1) 2
(1
1 2
1) 4
(1
1 2
1 4
1 2n1 ).
Sn
1 2n1
2n 2
三、并项求和法: 若数列的通项公式中含有形如(1)n,或通项公式
需分奇偶讨论的数列,可采用并项的方法进行求和.
例3:(1)设Sn是数列{an}的前n项和,已知 a1 1,S n 2 2an1. ①求数列{an}的通项公式;
4x 4x
2
, 令bn
g
(
an ), 2021
求数列{bn
}的前2020项和T2020
.
T2020 1010
五 、 裂 项 相 消 法 : 若通项项公式为分式,可 待定系数法 对定系数法
对分式进行裂项 .
例5:(1)设数列{an}满足a1 3a2 (2n 1)an 2n.
2
①求数列{an}的通项公式;
D.10200
四 、 倒 序 相 加 法 :若数列首末两端等“距离”的两项和相等(通项公式常与
函数有关),可采用倒序相加的方法进行求和.
例4:(1)已知函数 y f (x)满足f (x) f (1 x) 1,若数列{an}满足
例6:(1)已知数列{an}的首项a1 2,an 3an1 (2 n 2),
bn log3(an 1),cn anbn n. ①证明:{an 1}是等比数列; ②求数列{cn }的前n项和S n .
Sn
3 4
(1 2
n
1 )3n1 4
(2)已知{an}是递增的等差数列,a2,a4是方程x2 5x 6 0的根.
(2)求和Sn
1
(1
1) 2
(1
1 2
1) 4
(1
1 2
1 4
1 2n1 ).
Sn
1 2n1
2n 2
三、并项求和法: 若数列的通项公式中含有形如(1)n,或通项公式
需分奇偶讨论的数列,可采用并项的方法进行求和.
例3:(1)设Sn是数列{an}的前n项和,已知 a1 1,S n 2 2an1. ①求数列{an}的通项公式;
4x 4x
2
, 令bn
g
(
an ), 2021
求数列{bn
}的前2020项和T2020
.
T2020 1010
五 、 裂 项 相 消 法 : 若通项项公式为分式,可 待定系数法 对定系数法
对分式进行裂项 .
例5:(1)设数列{an}满足a1 3a2 (2n 1)an 2n.
2
①求数列{an}的通项公式;
D.10200
四 、 倒 序 相 加 法 :若数列首末两端等“距离”的两项和相等(通项公式常与
函数有关),可采用倒序相加的方法进行求和.
例4:(1)已知函数 y f (x)满足f (x) f (1 x) 1,若数列{an}满足
数列求和ppt课件

1
20
(2)设bn=
,数列{bn}的前n项和为Sn,若Sm= ,求m的值.
·+1
41
1
1
1
1
1
【解析】(2)由(1)知,bn=
=
= ·(
),
·+1 (2−1)(2+1) 2 2−1 2+1
1
1
1 1
1
1
1
1
所以Sn= [(1- )+( - )+…+(
)]= (1)=
.
2
3
3
D.
2
【解析】选C.S2 023=a1+(a2+a3+a4)+(a5+a6+a7)+…+(a2 021+a2 022+a2 023)=
1+cos
2π
5π
2 018π
2 021π
2π
5π
+cos +…+cos
+cos
=1+337×(cos +cos )=1.
3
3
3
3
3
3
)
2 , 当为奇数时,
和.形如an=(-1)nf(n)类型,可采用两项合并求解.
考点二裂项相消法求和
模型一
1
b n=
({an}为等差数列)型
+1
1
[例1](1)数列{an}中,an=
,则数列{an}的前2
(+1)
024项和S2 024=
1
1 1
【解析】由题意得,an=
= - ,
20
(2)设bn=
,数列{bn}的前n项和为Sn,若Sm= ,求m的值.
·+1
41
1
1
1
1
1
【解析】(2)由(1)知,bn=
=
= ·(
),
·+1 (2−1)(2+1) 2 2−1 2+1
1
1
1 1
1
1
1
1
所以Sn= [(1- )+( - )+…+(
)]= (1)=
.
2
3
3
D.
2
【解析】选C.S2 023=a1+(a2+a3+a4)+(a5+a6+a7)+…+(a2 021+a2 022+a2 023)=
1+cos
2π
5π
2 018π
2 021π
2π
5π
+cos +…+cos
+cos
=1+337×(cos +cos )=1.
3
3
3
3
3
3
)
2 , 当为奇数时,
和.形如an=(-1)nf(n)类型,可采用两项合并求解.
考点二裂项相消法求和
模型一
1
b n=
({an}为等差数列)型
+1
1
[例1](1)数列{an}中,an=
,则数列{an}的前2
(+1)
024项和S2 024=
1
1 1
【解析】由题意得,an=
= - ,
数列求和方法总结(课堂PPT)

数列求和方法总结
主讲人:陈鑫城 1
本节概要 数列求和的常用方法 公式法 分组求和法 裂项相消法 错位相减法 倒序相加法
2
一、公式法
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
①-②得( 1 1 2 )S n 2 2 2 2 2 2 2 3 2 2 4 2 2 n 2 2 n n 1221n1
2n
2n1
∴
Sn
4n2 2n1
16
17
五、倒序相加法
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
18
例
5.设
f
(x)
a a2
an 1
7
练:习 求数 11 2列 ,31 4,51 8,,2n121n,
的n 前 项.和
8
三、裂项相消法
“裂项相消法”,此法常用于形如{1/f(n)g(n)} 的数列求和,其中f(n),g(n)是关于n(n∈N)的 一次函数。把数列中的每一项都拆成两项或几项 的差,从而产生一些可以相消的项,最后剩下有 限的几项
9
例 3 : Sn求 1 1221 3 n(1 n 1 )
10
练习:
11
12
13
四、错位相减法
这种方法是在推导等比数列的前n项和公式时 所用的方法,这种方法主要用于求数列{an· bn} 的前n项和,其中{ an }、{ bn }分别是等差数列和 等比数列.
主讲人:陈鑫城 1
本节概要 数列求和的常用方法 公式法 分组求和法 裂项相消法 错位相减法 倒序相加法
2
一、公式法
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
①-②得( 1 1 2 )S n 2 2 2 2 2 2 2 3 2 2 4 2 2 n 2 2 n n 1221n1
2n
2n1
∴
Sn
4n2 2n1
16
17
五、倒序相加法
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
18
例
5.设
f
(x)
a a2
an 1
7
练:习 求数 11 2列 ,31 4,51 8,,2n121n,
的n 前 项.和
8
三、裂项相消法
“裂项相消法”,此法常用于形如{1/f(n)g(n)} 的数列求和,其中f(n),g(n)是关于n(n∈N)的 一次函数。把数列中的每一项都拆成两项或几项 的差,从而产生一些可以相消的项,最后剩下有 限的几项
9
例 3 : Sn求 1 1221 3 n(1 n 1 )
10
练习:
11
12
13
四、错位相减法
这种方法是在推导等比数列的前n项和公式时 所用的方法,这种方法主要用于求数列{an· bn} 的前n项和,其中{ an }、{ bn }分别是等差数列和 等比数列.
第四节 数列求和 课件(共48张PPT)

-
1 n+3
)=
1 2
56-n+1 2-n+1 3. 答案:1256-n+1 2-n+1 3
考点1 分组转化法求和 [例1] (2020·焦作模拟)已知{an}为等差数列,且 a2=3,{an}前4项的和为16,数列{bn}满足b1=4,b4= 88,且数列{bn-an}为等比数列. (1)求数列{an}和{bn-an}的通项公式; (2
an=n(n1+k)型
[例2] (2020·中山七校联考)已知数列{an}为公差 不为0的等差数列,满足a1=5,且a2,a9,a30成等比数列.
(1)求{an}的通项公式; (2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=
3,求数列b1n的前n项和Tn.
1.裂项时常用的三种变形.
(1)n(n1+1)=n1-n+1 1.
(2)n(n1+2)=12n1-n+1 2.
(3)(2n-1)1(2n+1)=122n1-1-2n1+1.
(4)
1 n+
n+1=
n+1-
n.
2.应用裂项相消法时,应注意消项的规律具有对称 性,即前面剩第几项则后面剩倒数第几项.
3.在应用错位相减法求和时,若等比数列的公比为 参数,应分公比等于1和不等于1两种情况求解.
) B. 2 020-1
C. 2 021-1 D. 2 021+1
解析:由f(4)=2,可得4α=2,解得α=12,
则f(x)= x.
所以an=
1 f(n+1)+f(n)
=
1 n+1+
= n
n+1 -
n,
所以S2 020=a1+a2+a3+…+a2 020=( 2 - 1 )+ ( 3- 2)+( 4- 3)+…+( 2 021- 2 020)=
数列求和的几种方法课件ppt
2、设法消去中间项:
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
数列求和常用方法ppt课件

1求数列a思路点拨利用a成等比数列可求公差d从而得出a成等比数列得12d18d12d由等比数列前n项和公式分组法有一类数列既不是等差数列也不是等比数列若将这类数列适当拆开可分为几个等差等比或常见的数列然后分别求和再将其合并即例例22思路点拨数列a可看作是由等差数列n与等比数列对应项求和得到的因此可拆分成两个数列
ppt课件
错位相减法 对于形如{anbn}的数列的前n项和Sn的求法(其中 {an}是等差数列,{bn}是等比数列),可采用错位 相减法.具体解法是:Sn乘以某一个合适的常 数(一般情况下乘以数列{bn}的公比q)后,与Sn错 位相减,使其转化为等比数列问题来解.
ppt课件
例5 (2010年高考课标全国卷改编)设等比 数列{an}满足a1=2,a4=128. (1)求数列{an}的通项公式; (2)令bn=nan,求数列{bn}的前n项和Sn. 【思路点拨】 利用公式求得an,再利用错位相 减法求Sn.
2
当n是奇数时, Sn=1+(32-22)+(52-42)+…+[n2-(n-1)2] =1+5+9+…+(2n-1)= n ( n 1 ) .
2
故Sn=(-1)n-1n ( n 1 ) (n∈N*).
2
ppt课件
方法感悟 1.注意对以下求和方式的理解 (1)倒序相加法用的时候有局限性,只有与首、末 两项等距离的两项之和是个常数时才可以用. (2)裂项相消法用得较多,一般是把通项公式分解 为两个式子的差,再相加抵消.在抵消时,有的 是依次抵消,有的是间隔抵消,特别是间隔抵消 时要注意规律性. (3)错位相减法是构造了一个新的等比数列,再用 公式法求和.
ppt课件
6.并项法
ppt课件
错位相减法 对于形如{anbn}的数列的前n项和Sn的求法(其中 {an}是等差数列,{bn}是等比数列),可采用错位 相减法.具体解法是:Sn乘以某一个合适的常 数(一般情况下乘以数列{bn}的公比q)后,与Sn错 位相减,使其转化为等比数列问题来解.
ppt课件
例5 (2010年高考课标全国卷改编)设等比 数列{an}满足a1=2,a4=128. (1)求数列{an}的通项公式; (2)令bn=nan,求数列{bn}的前n项和Sn. 【思路点拨】 利用公式求得an,再利用错位相 减法求Sn.
2
当n是奇数时, Sn=1+(32-22)+(52-42)+…+[n2-(n-1)2] =1+5+9+…+(2n-1)= n ( n 1 ) .
2
故Sn=(-1)n-1n ( n 1 ) (n∈N*).
2
ppt课件
方法感悟 1.注意对以下求和方式的理解 (1)倒序相加法用的时候有局限性,只有与首、末 两项等距离的两项之和是个常数时才可以用. (2)裂项相消法用得较多,一般是把通项公式分解 为两个式子的差,再相加抵消.在抵消时,有的 是依次抵消,有的是间隔抵消,特别是间隔抵消 时要注意规律性. (3)错位相减法是构造了一个新的等比数列,再用 公式法求和.
ppt课件
6.并项法
数列求和ppt课件

法,分别求和后相加减.
把数列的通项拆成两项之差,在求和时中间的
一些项可以相互抵消,从而求得前n项和.
如果一个数列的各项是由一个等差数列和一个等
比数列的对应项之积构成的,那么求这个数列的前n项
和即可用错位相减法求解.
如果一个数列{an}与首末两端等“距离”的
(4)倒序相加法:
两项的和相等或等于同一个常数,那么求这个数
an,n 为奇数,
2.若数列{cn}的通项公式为 cn=
其中数列{an},{bn}
bn,n 为偶数,
是等比数列或等差数列,可采用分组求和法求{cn}的前 n 项和.
聚焦必备知识
11
突破核心命题
限时规范训练
1.(2023·全国乙卷)记Sn为等差数列{an}的前n项和,已知a2=11,S10
=40.
(1)求{an}的通项公式;
列的前n项和即可用倒序相加法求解.
(3)错位相减法:
聚焦必备知识
4
常用结论
1.一些常见的数列的前 n 项和
n(n+1)
(1)1+2+3+…+n=
;
2
(2)2+4+6+…+2n=n(n+1);
(3)1+3+5+…+2n-1=n2.
突破核心命题
限时规范训练
聚焦必备知识
5
突破核心命题
限时规范训练
裂项相消法:适用的通项公式如下
( + ) +
聚焦必备知识
16
突破核心命题
考 点 二 裂项相消法求和
1
(1)数列{an}的前 n 项和为 Sn.若 an=
,则 Sn=____
n(n+1)
训练2
已知Sn是数列{an}的前n项和,Sn=n2.
把数列的通项拆成两项之差,在求和时中间的
一些项可以相互抵消,从而求得前n项和.
如果一个数列的各项是由一个等差数列和一个等
比数列的对应项之积构成的,那么求这个数列的前n项
和即可用错位相减法求解.
如果一个数列{an}与首末两端等“距离”的
(4)倒序相加法:
两项的和相等或等于同一个常数,那么求这个数
an,n 为奇数,
2.若数列{cn}的通项公式为 cn=
其中数列{an},{bn}
bn,n 为偶数,
是等比数列或等差数列,可采用分组求和法求{cn}的前 n 项和.
聚焦必备知识
11
突破核心命题
限时规范训练
1.(2023·全国乙卷)记Sn为等差数列{an}的前n项和,已知a2=11,S10
=40.
(1)求{an}的通项公式;
列的前n项和即可用倒序相加法求解.
(3)错位相减法:
聚焦必备知识
4
常用结论
1.一些常见的数列的前 n 项和
n(n+1)
(1)1+2+3+…+n=
;
2
(2)2+4+6+…+2n=n(n+1);
(3)1+3+5+…+2n-1=n2.
突破核心命题
限时规范训练
聚焦必备知识
5
突破核心命题
限时规范训练
裂项相消法:适用的通项公式如下
( + ) +
聚焦必备知识
16
突破核心命题
考 点 二 裂项相消法求和
1
(1)数列{an}的前 n 项和为 Sn.若 an=
,则 Sn=____
n(n+1)
训练2
已知Sn是数列{an}的前n项和,Sn=n2.
第七章 第四节 数列求和 课件(共42张PPT)

1.一些常见数列的前 n 项和公式 (1)1+2+3+4+…+n=n(n+ 2 1) ; (2)1+3+5+7+…+2n-1=n2; (3)2+4+6+8+…+2n=n2+n.
2.三种常见的拆项公式
1 (1)n(n+1)
=1n
-n+1 1
;
1 (2)(2n-1)(2n+1)
=12
2n1-1-2n1+1
答案: (1)× (2)√ (3)√
2.(必修 5P47T4 改编)数列{an}的前 n 项和为 Sn,若 an=n(n1+1) ,
则 S5 等于( )
A.1
B.56
C.16
D.310
B [∵an=n(n1+1) =1n -n+1 1 ,∴S5=a1+a2+…+a5=1-12 +12 -13 +…+15 -16 =56 .]
所以 an=-2n1+1 (n 为正奇数), 若 n 为奇数,则 an-1=-2an+21n =(-2)-2n1+1 +21n , 所以 an=21n (n 为正偶数), 所以 a3=-214 =-116 , 因为 an=-2n1+1 (n 为正奇数),所以-a1=--212 =212 ,
因为 an=21n (n 为正偶数),所以 a2=212 , 所以-a1+a2=2×212 , 因为-a3=--214 =214 ,a4=214 , 所以-a3+a4=2×214 , …… -a99+a100=2×21100 .
(2)因为 an=2n,所以 bn=(n+1)log2an=(n+1)log22n=n(n+1), 所以,2n2b+n2 2n =n(n2+1) =21n-n+1 1 , 所以 Tn=21-12+12-13+…+1n-n+1 1 =21-n+1 1 =n2+n1 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
14
例4:求和 :Sn 1 3x 5x 2 7x3 (2n 1)x n1
-
15
-
16
练习:求数列
24 2 , 2,
前n项的和
解:由题可知,{
2n 2n
}的通项是等差数列{2n}的通项与等比数列{
1 2n }的通项之积
设 Sn
2 4 2 22
6 23
2n 2n
…………………………………①
1 2
Sn
2 22
4 23
6 24
2n 2 n1
………………………………②
(设制错位)
①-②得(1
1 2
)S
n
2 2
2 22
2 23
2 24
2 2n
2n 2 n 1
2 1 2n 2n1 2n1
∴
Sn
4
n2 2 n 1
-
17
这是推导等差数列的前n项和公式时所用的 方法,就是将一个数列倒过来排列,再把它与原 数列相加。
-
18
例
5.设
f
(x)
4 x , 则f 4x 2
1 11
f
2 11
f
3 11
f
10 11
(
)
A.4
B. 5
C. 6
D. 10
-
19
优化方案《数列求和》大本小本完成!!
-
20
13 23 33 n3 [1 n(n 1)]2
2
-
3
例
1.设{an}为等差数列, Sn 为数列{an}的前
n
项和,已知
S7
7,
S15
75
, Tn
为数列{ Sn n
} 的前
n
项
和,求Tn .
-
4
练习:求 1 + a + a 2 + a 3 + …… + a n (a为非零实数)的值
-
5
, ,2n 1
1 2n
,
的前n项和.
-
8
“裂项相消法”,此法常用于形如{1/f(n)g(n)} 的数列求和,其中f(n),g(n)是关于n(n∈N)的 一次函数。把数列中的每一项都拆成两项或几项 的差,从而产生一些可以相消的项,最后剩下有 限的几项
-
9
例3:求Sn
1 1 2
1 23
1 n (n
有一类数列,既不是等差数列,也不是等比 数列,若将这类数列适当拆开,可分为几个等差、 等比或常见的数列,然后分别求和,再将其合并 即可.
-
6
例2:求数列的前n项和:1 1, 1 4, 1 7, , 1 3n 2,…
a a2
a n1
-
7
练习 : 求数列1 1 2
,3 1 4
,5
1 8
-
1
本节概要 数列求和的常用方法
-
2
等差数列前 n 项和公式:
Sn
n(a1 2
an )
na1
n(n 1) 2
d
.
等比数列前 n
项和公式:
Sn
na1(q a1(1
1) qn)
1 q
a1 anq 1 q
(q
1)
.
自然数方幂和公式:1 2 3 n 1 n(n 1) 2
12 22 32 n2 1 n(n 1)(2n 1) 6
1)
-
10
-
11
1
练习:已知数列{anan+1}的前
n
项和
Sn, 1 =
1
。求
anan+1 2n-12n+1
Sn。
-
12
-
13
这种方法是在推导等比数列的前n项和公式时 所用的方法,这种方法主要用于求数列{an· bn} 的前n项和,其中{ an }、{ bn }分别是等差数列和 等比数列.
