数学物理方法第一章解析函数1.4初等函数
数学物理方法第一章

(或微商),以 f '(z) 或 df/dz 表示
讨论:
1、从形式上看,复变函数导数的定义与实变函数的定义相同,
因而实变函数论中关于导数的规则和公式往往可以适用于实变 函数。
则
x cos y sin
z (cos i sin )
z e
i
指数式
讨论:i)复数的辐角不能唯一地确定。如果 0 是其中一个辐角, 则
0 2k (k 0,1,2,) 也是其辐角,把属于 [0,2 ) 的辐角称为主值辐角,记为arg z .
存在,且连续,并
且满足柯西-黎曼条件。 证明:由于这些偏导数连续,二元函数 u 和 v 的增量可分别写为
各 个
,于是有
根据柯西-黎曼条件,上式即
这一极限是与 z 0 无关的有限值。证毕。
讨论:复变函数与实变函数的导数有本质上的差别,复变函数 可微,不但要求复变函数的实部与虚部可微,而且还要求其实 部与虚部满足柯西-黎曼条件。
单连通区域:在区域 B 做任何简单的闭曲线,曲线包围 的点全属于 B。否则为多连通区域。
三、复变函数例
多项式
a0 a1 z a2 z an z
2
n
n 为正整数
有理分式
a0 a1 z a2 z 2 an z n b0 b1 z b2 z 2 bm z m
ii)当 1时,z cos i sin ei 称为单位复数。
iii)复数 z 的共轭复数
z x iy (cos isin ) e
大学物理与数学方法总结

n z不同,Sin z=1 =ïïîïïí춶-=¶¶¶¶=¶¶x v yu y v x u这是复变函数可导的必要条件。
函数可导的充要条件是:函数f(z)的偏导数yvx v yux u ¶¶¶¶¶¶¶¶,,,存在且连续,并且满足柯西—黎曼方程。
在极坐标系下的柯西—黎曼方程:ïïîïïí춶-=¶¶¶¶=¶¶r jr jr r v u v u11四 解析函数若函数f(z)在点0z 及其领域上处处可导,则称f(z)在0z 点解析。
又若f(z)在区域B 上每一点都解析,则称f(z)是区域B 上的解析函数。
上的解析函数。
解析函数是一类特殊的复变函数,具有以下主要性质: 1. 若函数f(z) = u +iv 在区域在区域B 上解析,则上解析,则 u(x,y)=1C ,v(x,y)=2C(1C ,2C 为常数)是B 上的两组正交曲线族。
2. 若函数f(z) = u +iv 在区域在区域B 上解析,则u,v 均为B 上的调和函数。
由性质2可以知道,若给定一个二元调和函数,若给定一个二元调和函数,我们可以将它看做某个解析函数我们可以将它看做某个解析函数的实部的实部(或虚部)(或虚部),利用柯西—黎曼方程求出相应的虚部黎曼方程求出相应的虚部(或实部)(或实部),也就是确定这个解析函数。
这个解析函数。
dy y v dx x v dv ¶¶+¶¶=根据柯西—黎曼方程,上式可变为,上式可变为 dy x u dx y u dv ¶¶+¶¶-=于是利用曲线积分法、凑全微分显示法或不定积分法可确定这个解析函数。
数学物理方法习题解答_Tex

(3) cos 5ϕ. 解:由乘幂的公式
(cos ϕ + i sin ϕ)n = cos nϕ + i sin nϕ).
及二项式定理
(a + b)n = an + nan−1 b + n(n − 1) n−2 2 n! a b + ··· + an−k bk + · · · . 2! (n − k )!k !
4
√ √ 3
a2
a2
2 2
a2 + b2 + a + i
a2 + b2 − a
(2)
i. i = 1 cos π π + 2nπ + i sin + 2nπ 2 2 π 2 + nπ + i sin 6 3 √ 3 i = ei( 6 + 3 nπ) .
π 2
解:因
,
所以
√ 3 i= √ 3 1 cos π 2 + nπ 6 3 ,
z = cos 3π 3π + i sin . 2 2
指数式:
z = ei 2 .
3π
3. 计算下列数值(a、b和ϕ为实常数). √ (1) a + ib. √ (2) 3 i. (3) cos 5ϕ. (1)
√ a + ib.
解:先化a + ib为三角式
a + ib = cos ϕ = √ xiangap@ a2 + b2 (cos ϕ + i sin ϕ), sin ϕ = √ b . a2 + b2 供教学参考
指数式:
z = i = ei 2 .
π
(1) −i. 解:−i本身即为代数式. 三角式:
大学高数第一章函数和极限

x1
x1
x1
x1
3lim x2 2 lim x 1
x1
x1
312 2 11 2
可见,上例求极限,可以直接用定理 1.1 中的(1).
只须将 x x0 之 x0 代入函数中的 x 处运算即可。
例 求 limx(x 2) x2 x2 1
解:lx im 2 x(xx2 12)
limx(x2) xl i2m (x2 1)
必经过点(0,1)
f(x)log2 x
f (x)log0.5 x
正弦、余弦函数基本性质
解析式: ysinx/cosx
基本特征:定义域为实数集R,值域为[-1,1],最小正
周期T为 2
正切、余切函数基本性质
解析式: ytanx/cotx
基本性质:正切函数定义域为 {x|x2k,,余kZ}
医用高等数学
第1章 函数和极限
1.1 函数 1.1.1函数的概念
定义 1.1 设 X ,Y 是非空数集,对于集合 X 中的任意一个数 x , 在集合 Y 中均有确定值 y 与其对应,则称 y 是 x 的函数,记为:
y f (x) ,其中 x 称为自变量, y 称为因变量,
其中,集合 X 称为定义域,集合 Y 称为值域。
无界的。
如:函数 y sin x ,在 ,内有界,且:| y | 1
1.1.3复合函数
定义 1.2 如变量 y 是变量 u 的函数,变量 u 又是 变量 x 的函数,即: y f (u), u (x) , 且 u (x) 的值域与 y f (u) 的定义域有公共部分, 则称 y 是 x 的复合函数,记作: y f [(x)]
例 讨论函数 f (x) | x | 当 x 0 时的极限. x
初等解析函数和多值函数.ppt

(vi) lim ez不存在。
z
证明:(iv) w' lim ezz ez
ez lim
ez 1
z0 z
z0 z
lim ez ex cos y i sin y 1
z0
z
lim ez 1 x1 iy 1 ez
z 0
z
(3) 三角函数 sin z 1 eiz eiz , cos z 1 eiz eiz
点,则连续Байду номын сангаас变的幅角回到原来
的值,而w的值也回到w1。但如
果曲线包含原点,则旋转一周后,w的值不再回到w1,而
是回到w2:
w re 3
i
0 3
2 3
2
我们称z=0为w 3 z 的支点。
定义(支点):若z绕某点旋转一周回到初始点,多值函数 w=f(z)由一个分支变到另外一个分支,我们称这样的点 为多值函数的支点。
bn zn
(2) 指数函数 w ez exeiy ex (cos y i sin y)
指数函数的性质:
(i) ez 0
(ii) 对于实数z=x来说,复数域中的指数定义与实数域中
的定义一致。
(iii) ez1ez2 ez1z2
(iv) 指数函数处处解析,且:w' ez
(v) ezi2k ez
所以:w l n z ln r iarg(z)
显然:w Lnz l n z i2n , n 0, 1,
如在w平面上用平行于实轴 的直线画出一个宽为2的条 带,例如图中的I,则z与w 为一一对应的关系。I为z=ew 的单叶性区域。
同样,对数函数也存在两个 支点:z=0和z=。两个支点间的任意连线就构成了支割线。 支割线映射为w平面上的单值分支之间的端线:
解析函数的充要条件初等函数

一. 解析函数的充要条件
设函数 w f( z ) u ( x ,y ) iv ( x ,y ) 在点 z x iy 可导 , 则
f(z z) f(z) z
[ u ( x x , y y ) iv ( x x , y y ) [ ] u ( x , y ) iv ( x , y )] x i y
v v v x y x y 3 4 x y
x 0 y 0
其 lim 中 0 , ( k 1 , 2 , 3 , 4 ) k
f ( z z ) f ( z ) u i v u v u v ( i ) x ( i ) y ( i ) x ( i ) y 1 3 2 4 x x y y
所以u(x, y),v(x, y)在点(x, y)处可微.
" "(由函数u(x,y) ,v (x,y)在点(x,y)处可微及满足
C-R方程 f (z)在点z=x+iy处可导)
∵u(x,y),v(x,y)在(x,y)点可微,即: u u u x y x y 1 2 x y
lim ( z )0
令:f (z+Δz) f (z)=Δu+iΔv,f (z)= a+ib, (Δz)=1+i2 故(1)式可写为 Δu+iΔv = (a+ib)(Δx+iΔy)+(1+i2)(Δx+iΔy) =(aΔx-bΔy+1Δx2Δy)
+i(bΔx+aΔy+2Δx+1Δy) 因此 Δu=aΔxbΔy+1Δx2Δy , Δv=bΔx+aΔy+2Δx1Δy
初等函数
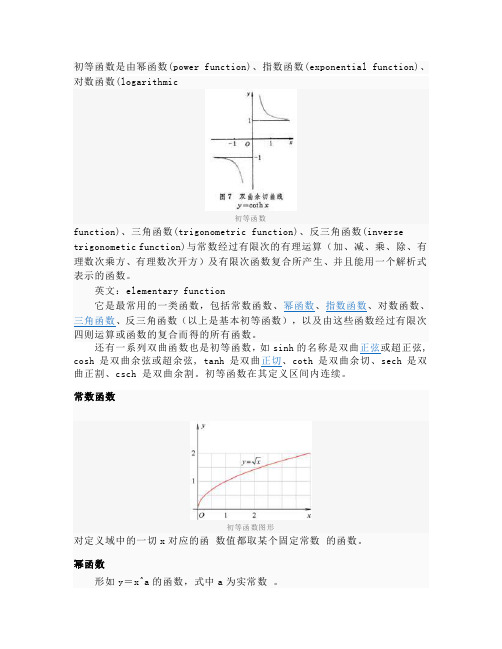
初等函数是由幂函数(power function)、指数函数(exponential function)、对数函数(logarithmic初等函数function)、三角函数(trigonometric function)、反三角函数(inverse trigonometic function)与常数经过有限次的有理运算(加、减、乘、除、有理数次乘方、有理数次开方)及有限次函数复合所产生、并且能用一个解析式表示的函数。
英文:elementary function它是最常用的一类函数,包括常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数(以上是基本初等函数),以及由这些函数经过有限次四则运算或函数的复合而得的所有函数。
还有一系列双曲函数也是初等函数,如sinh 的名称是双曲正弦或超正弦, cosh 是双曲余弦或超余弦, tanh 是双曲正切、coth 是双曲余切、sech 是双曲正割、csch 是双曲余割。
初等函数在其定义区间内连续。
常数函数初等函数图形对定义域中的一切x对应的函数值都取某个固定常数的函数。
幂函数形如y=x^a的函数,式中a为实常数。
指数函数形如y=a^x的函数,式中a为不等于1的正常数。
对数函数指数函数的反函数,记作y=loga a x,式中a为不等于1的正常数。
指数函数与对数函数之间成立关系式,loga ax=x。
三角函数即正弦函数y=sinx ,余弦函数y=cosx ,正切函数y=tanx,余切函数y=cotx ,正割函数y=secx,余割函数y=cscx(见三角学)。
反三角函数三角函数的反函数——反正弦函数y = arc sinx ,反余弦函数 y =arc cosx (-1≤x≤1,初等函数0≤y≤π),反正切函数 y=arc tanx ,反余切函数 y = arc cotx(-∞<x<+∞,θ<y<π)等。
以上这些函数常统称为基本初等函数。
双曲正弦或超正弦sinh x =(e^x- e^(-x))/2双曲余弦或超余弦cosh x =(e^x + e^(-x))/2双曲正切tanh x =sinh x / cosh x双曲余切coth x = 1 / tanh x双曲正割sech x = 1 / cosh x双曲余割csch x = 1 / sinh x一个初等函数,除了可以用初等解析式表示以外,往往还有其他表示形式,例如,三角函数 y=sinx 可以用无穷级数表为初等函数可以按照解析表达式分类为:初等函数是最先被研究的一类函数,它与人类的生产和生活密切相关,并且应用广泛。
《初等解析函数》课件

初等解析函数是数学中重要的基础概念,对理解和应用许多数学和物理学原理具有重要意义等函数 (包括幂函数、指数函数、对数函数、三角 函数和反三角函数)经过有限次的代数运算 得到的函数。
2 常见的初等函数有哪些?
常见的初等函数包括多项式函数、有理函数、 指数函数、对数函数、三角函数和反三角函 数等。
双曲函数的性质
双曲函数具有一系列有趣的性质,如双曲函数的导 数、反函数和幂函数等,这些性质在数学和物理中 具有广泛的应用。
初等解析函数的运算
1 求和、差、积、商、复合等运算
初等解析函数可以进行基本的运算,如求和、求差、求积、求商和进行复合等运算,这些运算有助于 分析和求解复杂函数。
应用
1
初等解析函数在实际问题中的应
参考资料
• 高等数学教材 • 《初等解析函数》教材 • 数学网站
三角函数的性质与图像
三角函数具有周期性、对称性和单调性等特点,它 们的图像能够帮助我们分析函数的行为。
指数函数
指数函数的定义与图像
指数函数是以常数e(自然对数的底数)为底的幂函 数,它的图像呈现出指数增长或指数衰减的趋势。
指数函数的性质
指数函数具有指数运算的性质,如乘方法则、对数 关系和指数法则等,这些性质对于求解方程和研究 增长和衰减过程非常重要。
《初等解析函数》PPT课 件
欢迎大家来到《初等解析函数》PPT课件。本课程将深入介绍初等解析函数的 概念、分类和运算,并探讨其在实际问题中的应用。
引言
什么是初等解析函数?
初等解析函数是指可用初等函数(包括常函数、幂函数、指数函数、对数函数、三角函数、 反三角函数等)以及有限次四则运算所得到的函数。
复合函数
解析函数理论中的初等函数概念

解析函数理论中的初等函数概念函数理论是数学中的一个分支,它研究的是函数的性质、特征,以及与其他对象的关系。
作为函数理论中的一个基本概念,初等函数一直是数学研究的重要课题之一。
本文将从初等函数的定义、性质、分类、以及一些常见的初等函数类型进行深入的解析。
一、初等函数的定义初等函数是一种我们日常生活中常见的一类函数。
所谓初等函数,指的是可以用四则运算和函数的有限次复合得到的函数。
其中,四则运算包括加、减、乘、除,而函数的有限次复合指的是对一个函数进行有限次嵌套。
通俗点说,初等函数就是可以通过基本数学操作和有限次函数嵌套来描述的函数。
一般来说,初等函数可以分为代数函数和三角函数两大类。
所谓代数函数,指的是关于变量的多项式函数,如幂函数、指数函数、对数函数以及各种三角函数。
而三角函数则是由正弦、余弦、正切等组成的一类函数。
二、初等函数的性质初等函数具有一些重要的性质,这些性质往往被广泛地应用在对初等函数的研究和分析中。
其中,一个最为基本的性质就是初等函数是可微函数。
这意味着,初等函数的导函数仍然是一个初等函数。
此外,初等函数还具有递归性质。
也就是说,初等函数可以通过有限次基本操作以及有限次函数嵌套,描述出一类新的初等函数。
这样,不断地递归下去,我们就可以描述出各种更加复杂的函数。
最后,初等函数还满足以下性质:初等函数的函数值可以用代数数、指数函数、三角函数以及它们的有限次嵌套,表示成有理数、无理数和常数的有限个代数运算。
三、初等函数的分类初等函数包括多种类型,常用的有以下几类:1. 幂函数幂函数是最简单的初等函数。
其表达式为 y=x^n,其中n是一个正整数。
幂函数分为偶次幂和奇次幂两种类型。
当n为偶数时,幂函数的图形具有对称性;而当n为奇数时,幂函数则呈现出一种非对称的形态。
2. 指数函数指数函数是初等函数中的另一种重要类型。
它的表达式为y=a^x,其中a为正实数且不等于1。
指数函数的图形具有一些特殊的性质,比如在x轴上方的函数值不断增加,而在x轴下方则不断减小。
数学物理方法第一章解析函数1.3微商及解析函数

一、微商及微分:
x 0 lim x 0 x i y y 0 x 1 lim x 0 x i y y 0
1.3 微商及解析函数
z z
f lim z 0 z
∴ f ( z) Re z, 在复平面处处不可导。
2 2
二、解析函数:
1.3 微商及解析函数
例 已知 v( x, y ) x y, 求解析函数 f ( z ) u iv
(1)用全微分法
u u v v du dx dy dx dy dx dy x y y x u d ( x y) c x y c
解析函数图例
1.3 微商及解析函数
1.3 微商及解析函数
1.3 微商及解析函数
小结 一、微商及微分:
1、微商: 2、微分:
1.3 微商及解析函数
Δf f ( z ) lim Δz 0 Δz dw f ( z )dz
3、 求导、微分法则: 4. 可导的必要条件 5.可导的充分条件:
问:(1)可否用这四个公式来判断函数是否可导?N (2)可否用求导公式判断函数是否可导?Y
二、解析函数:
1. 定义:
1.3 微商及解析函数
若w f(z) 在z 0 点及 N(z 0 , ε) 可导,则称 w f(z) 在z 0点解析。 若w f(z) 在区域内处处可导,则称 w f(z) 在区域内解析。
u v
1 v
1 u
一、微商及微分:
5.可导的充分条件:
1.3 微商及解析函数
(1) u x ,u y ;v x ,v y 均连续 (2) u,v 满足C R条件
数学物理方法第一章

1.1 复数与复数运算
(一)复数的基本概念
复数定义:复数——形如 z=x+iy 的数 (x,y 为实数,i2 =−1,i:虚数单位,一种记号约定)
将有争议的虚数合法化: 一维实数 二维实数
复数的本质:有序实数对 (大x家, 好y)
11
复数 :i2 = −1,为什么?
简单概念的引入可 解决世界性的难题 高斯:正十七边形作图
定义了虚数单位 i=(0, 1)
i 2=-1
复数 z 可记为 zxiy xRe z
特殊的复数:0
y I mz
(x, y) +(0, 0) = (x, y) 大家(好x, y) (0, 0) = (0, 0)
13
复数的共轭: z* x iy 与 z x iy 互为共轭 (xiy)(xiy)x2y2
f (x)
n0
f (n)(0) xn n!
例
f
(x)
e1/
x2
0
(满足泰勒展开条件)
x 0 在x0各阶导数均存在, x 0 在x=0各阶导数均存在,其值为0
f(x)
f(n)(0)xn 0
n0 n!
大家好
f (x)
4
复变函数论(theory of complex functions): 研究自变量是复数的函数的基本理论及应用的数学分支,
生了一些信心。在18世纪,尽管一些数学家已较为广泛地使用复
数,但无论欧拉还是别的数学家大对家这好 些数都还不甚清楚。
8
Euler 认为复数仅在想象中存在, 1777年,Euler采用 i 代表 1
4 复数真正被接受主要归功于德国数学家高斯 (C.F.Gauss,1777-1855), 1799年,他把复数的 思想融入到对代数学基本定理的证明中。
第一章复变函数和解析函数

7
2020/4/7
• 莱昂哈德·保罗·欧拉(Leonhard Paul Euler,1707年4月15日- 1783年9月18日)是一位瑞士数 学家和物理学家,近代数学先驱 之一,他一生大部分时间在俄罗 斯帝国和普鲁士度过。
• 欧拉在数学的多个领域,包括 微积分和图论都做出过重大发现。 他引进的许多数学术语和书写格 式,例如函数的记法"f(x)",一直 沿用至今。此外,他还在力学、 光学和天文学等学科有突出的贡 献。
ln x
ln xei 2k
2020/4/7
ln x ln ei i2k ln x i 2ik
16
(4)复数的运算规则 (注:运用到实数特例时,能够与实数的运算规则相符)
设z1=x1+iy1和 z2=x2+iy2是两个复数
加减 z1 ± z2 =(x1+iy1) ± (x2 +i y2 )
所以可以用平面上的一个点(x,y)或一个矢量
表示,通常把横轴叫实轴,纵轴叫虚轴,而把这种
用来表示复数的平面叫复平面。 复数的矢量表示法
由图:
y
x cos
y
sin
x2 y2
arctan
y x
y
z
P(x,y)
那么复数(复矢量)可以表示为 o
xx
z = x iy = cos isin .
2020/4/7
5
2020/4/7
6
学习要求与内容提要
目的与要求:掌握复变函数的基本概念和复函数可导 必要条件、掌握解析函数的概念、函数 解析的充要条件、复势的概念。
教学重点: 柯西-黎曼条件、复变函数解析的充要条件;
教学难点: 柯西-黎曼条件与复变函数可导充要条件、 复变函数解析的充要条件
《数学物理方法》第1章复变函数与解析函数

平时考勤:5%; 平时作业:10%; 期中考试:15% (第一篇的教学考核成绩) 期终考试:70% (期末考试成绩)
本课程的考试均以闭卷方式进行 。
2021/1/14
4
教材与参考书
教材:汪德新,《数学物理方法》,第三版,科学出
版社,2006年8月
参考书:
[1]吴崇试,数学物理方法,北京大学出版社 2003-12-26出版
zz1 (x1iy1) (x1iy1)(x2iy2) z2 (x2iy2) (x2iy2)(x2iy2)
x1xx222
y1y2 y22
i
x2y1x1y2 x22 y22
同样,利用复数的指数表示式将更方便.
z
z1 z2
1ei1 2ei2
e 1 i(12)
2
35
(6)开方 复数的开方是乘方的逆运算。
为共轭复数。 常用z* 表示z的共扼复数。 (z* )* =z 例: z1=2+3i与z2=2-3i 称z1与z2互为共轭复数。
17
复数能不能比较大小?!
18
§1.1.2 复数的几何表示
复数可以用平面上的点来表示,称为复 数的平面表示法;
球面上的点来表示,称为球面表示法。
19
1. 复数平面表示法
利用复数的指数表示式计算复数的乘积,往往更为
方便 z z 1 z 2 1 e i 12 e i 2 12 e i( 1 2 )
两复数乘积的几何意义是将两复数的模相乘而辐角
相加.
30
(4)乘方 乘方可由乘法规则得到,用n个z相乘
zn nein
31
【例1.1.1-A】试证明棣莫弗(De Moivre)公式
9
初等解析函数及其基本性质

§2 初等解析函数及其基本性质一、基本初等函数1.指数函数()y i y e z x sin cos exp +=加法定理 ()2121exp exp exp z z z z +=⋅。
z e z =exp ,即()y i y e e e e e x yi x yi x z sin cos +=⋅==+。
周期性 ze 是周期为()Z ∈k i k π2的周期函数。
2.对数函数定义2 满足()0≠=z z e w 的函数()z f w =称为复变量z 的对数函数,记为Lnz w =。
关于Lnz w =的表达式:令θi re z iv u w =+=,,则πθθk v r e re e e eu i iv u ivu 2,+==⇒==+,即Argz v z r u ===,ln ln 。
从而注:Lnz 是多值函数,Argz 是多值函数。
当Argz 取主值z arg 时,Lnz 为单值函数,称其为Lnz 的主值,记为z ln ,即z i z z arg ln ln +=⇒i k z Lnz π2ln +=注:当0>=x z 时,x x i x z ln arg ln ln =+=——实对数函数。
例2 证明对数运算性质:⑴2121Lnz Lnz z Lnz +=⋅;⑵2121Lnz Lnz z z Ln -=。
证明⑴ 由对数定义表达式,212121ln z iArgz z z z Lnz +=⋅()2121ln Argz Argz i z z ++⋅=2211ln ln iArgz z iArgz z +++=21Lnz Lnz +=;同理可证⑵式。
例3 求()⎪⎪⎭⎫⎝⎛+--i Ln 2321,3ln 及主值。
解 ()()i i π+=-+-=-3ln 213arg 3ln 3ln ; i k i i i i Ln π22321arg 2321ln 2321+⎪⎪⎭⎫ ⎝⎛+-++-=⎪⎪⎭⎫ ⎝⎛+- i k i k i πππ⎪⎭⎫ ⎝⎛+=++=3122321ln ;主值:i i i ππ32321ln 2321ln =+=⎪⎪⎭⎫ ⎝⎛+-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4 初等解析函数
二、初等多值函数
例1 讨论
w ( z a)( z b) 的支点
y
za
1
1.4 初等解析函数
答:支点为a,b
a oΒιβλιοθήκη z z b2b
x
思考: 函数 w 3 z 2 4 z 2 1 是几值函数? 有何支点?
答:6值,支点
1,2,
二、初等多值函数
2.对数函数
(1)定义
若z
1.4 初等解析函数
主值支: ln z ln z i arg z , 0 arg z 2
ew
则
w Lnz
(2)多值性的体现 z的幅角和w的虚部的对应关系 (3)支点 0 , (4)单值分枝 Lnz ln z i(arg z 2k ) , k 0,1,2,
Q( z) 0
1.4 初等解析函数
一、初等单值函数
1. 幂函数(图)
w z
3
一、初等单值函数
2.指数函数 (1)定义
1.4 初等解析函数
w e z e x iy e x (cos y i sin y)
复平面
z1 z2 z1 z 2
(2)解析区域
z
(3)与实函数相同的性质
(5)支割线 (6)黎曼面 (7)解析性 (8)性质 连接 0 , 割开z平面的线 无穷多叶 每一单值支均解析
Ln( z1 z2 ) Lnz1 Lnz2 Ln( z1 z2 ) Lnz1 Lnz2
二、初等多值函数
2.对数函数(图) 问:
1.4 初等解析函数
Lnz Lnz ? 2Lnz N Ln( z z )? Lnz Lnz ? 0 N
多值函数的支点一定是函数的奇点。
z
r
c1
二、初等多值函数
1.4 初等解析函数
z(二) 3
z(一)
W2
W1
二、初等多值函数
1.4 初等解析函数
z(二)
4
z(一) 2 0
W1 W2 W1
2
二、初等多值函数
根式函数(图)
1.4 初等解析函数
w3 z :
二、初等多值函数
黎曼面
1.4 初等解析函数
w z : 支点为 z 0, ;一阶。
则记 w n z 称根式函数
#
(n 2,3,) (2)多值性的体现 体现在z 的 幅角与w 的幅角的对应关系上
z
(3)支点
当变量绕其一周时函数值会改变的点
绕其 n 周后函数值还原的支点为n-1阶支点
(4)单值分支 限制z的变化范围得到的若干单值函数 c2 (5)支割线 连接支点割开z平面的线 (6)黎曼面 互相交叠的若干叶z平面 (7)解析性 每一单值支均解析
(2)解析区域 复平面 (除分母为0外) (3)与实函数相同性质
(4)新性质
(sin z )' cos z, (cos z )' sin z sin( z1 z2 ) sin z1 cos z2 cos z1 sin z2
sin z 和 cos z 可大于任何正数
#
一、初等单值函数
3. 三角函数(图)
1.4 初等解析函数
w sin z
w cos z
一、初等单值函数
4. 双曲函数
(1)定义
1.4 初等解析函数
e z e z e z e z sinh z , cosh z 2 2 sinh z cosh z tanh z , coth z , cosh z sinh z 1 1 sec hz , csc h z cosh z sinh z
§1.4 初等解析函数
一、初等单值函数
1. 幂函数
(1)定义
w z (n 0, 1, 2,)
n
(2)解析区域
除了z=0的复平面。
(3)与实函数相同的性质
z z z
m n
m n
;
(4)新性质 P( z ) a0 a1 z a2 z 2 an z n w (an , bm 0) 2 m Q( z ) b0 b1 z b2 z bm z
小结
一、初等单值函数
n
1.4 初等解析函数
w z (n 0, 1, 2,) z x iy x w e e e (cos y i sin y)
e z e z e z e z sinh z , cosh z 2 2 sinh z coth z tanh z , coth z , cosh z sinh z 1 1 sec hz , csc h z cosh z sinh z
eiz e iz eiz e iz sin z , cos z 2i 2 sin z cos z 1 1 tan z , cot z , sec , csc cos z sin z cos z sin z
二、初等多值函数
1.根式函数 若 w
n
小结
1.4 初等解析函数
z
则记 w n z 称根式函数
则
2.对数函数 若 z e w 概念:
(1)支点 (2)单值分枝 (3)支割线 (4)里曼面 (5)解析性
w Lnz
主值支: ln z ln z i arg z , 0 arg z 2
当变量绕其一周时函数值会改变的点
绕其 n 周后函数值还原的支点为n-1阶支点
e 0; e e e
(4)新性质
;
e
z i 2 kπ
e (k 0, 1, 2, )
z
e
z
的实部不一定大于0
#
一、初等单值函数
2.指数函数(图)
1.4 初等解析函数
we
z
一、初等单值函数
3. 三角函数
1.4 初等解析函数
eiz e iz eiz e iz , cos z (1)定义 sin z 2i 2 sin z cos z 1 1 tan z , cot z , sec , csc cos z sin z cos z sin z
限制z的变化范围得到的若干单值函数
连接支点割开z平面的线 互相交叠的若干叶z平面 每一单值支均解析
z=cplxgrid(30); cplxmap(z,z.^2); colorbar('vert'); title('z^2')
本节作业
1.4 初等解析函数
习题1.4
6(2);7(3)
(2)解析区域
复平面
(3)与实函数相同的性质 cosh 2 z sinh 2 z 1;
一、初等单值函数
1.4 初等解析函数
初等单值函数与相应实函数的定义 在形式上相同;
在其定义域内均解析; 除具有某些新性质外具有与相应实 函数所具有的性质。
二、初等多值函数
1.根式函数 n 若 (1)定义 w
