第十二章格林函数法

合集下载

格林函数

格林函数法求解稳定场问题1 格林函数法求解稳定场问题(Green ’s Function) Green ’s Function, 又名源函数，或影响函数，是数学物理中的一个重要概念。

从物理上看，一个数学物理方程表示一种特定的场和产生这种场的源之间关系：Heat Eq.：()2222 ,u a u f r t t∂-∇=∂v 表示温度场u 与热源(),f r t v之间关系 Poission ’s Eq.：()20u f r ρε∇=-=-v表示静电场u 与电荷分布()f r v之间的关系场可以由一个连续的体分布源、面分布源或线分布源产生，也可以由一个点源产生。

但是，最重要的是连续分布源所产生的场，可以由无限多个电源在同样空间所产生的场线性叠加得到。

例如，在有限体内连续分布电荷在无界区域中产生的电势：()''04r dV r r ρφπεΩ=-⎰r r r这就是把连续分布电荷体产生的电势用点电荷产生的电势叠加表示。

或者说，知道了一个点源的场，就可以通过叠加的方法算出任意源的场。

所以，研究点源及其所产生场之间的关系十分重要。

这里就引入Green ’s Functions 的概念。

Green ’s Functions ：代表一个点源所产生的场。

普遍而准确地说，格林函数是一个点源在一定的边界条件和初始条件下所产生的场。

所以，我们需要在特定的边值问题中来讨论 Green ’s Functions.下面，我们先给出Green ’s Functions 的意义，再介绍如何在几个典型区域求出格林函数，并证明格林函数的对称性，最后用格林函数法求解泊松方程的边值问题。

实际上，只限于讨论泊松方程的第一类边值问题所对应的 Green ’s Functions 。

2 泊松方程的格林函数静电场中常遇到的泊松方程的边值问题：()()()()()201 f s u r r u r u r r n ρεαβϕ⎧∇=-⎪⎪⎨∂⎡⎤⎪+=⎢⎥⎪∂⎣⎦⎩vv v v v 这里讨论的是静电场()u r v， ()f r ρv 代表自由电荷密度。

格林函数（ＰＤＦ）

T=0K 的费米子体系的格林函数虽然真实的系统从来也没有达到过零温, 但有很多量对温度并不特别敏感, 特别是低温下. 比如费米子体系, 在远低于费米温度时, 把系统处理为T=0K 是很好的近似.我们常常把系统描述为它的基态加上它的元激发. T=0K 的格林函数就是计算体系的基态和元激发的. 这样的计算适合电子气体和氦3液体.从T=0K 的格林函数中可以得到准粒子的有效质量, 寿命, 以及准粒子之间的散射解面(朗道费米液体理论中相互作用函数).量子统计中的格林函数方法是从粒子物理中处理量子电动力学中费曼—戴逊图形展开方法移植到凝聚态的多体问题中来的. 这个方法是研究有相互作用的多粒子体系的一个基本的强大的工具.;ˆˆˆ0i H H H+=我们知道, 系统的哈密顿量统常可写为如果相互作用部分比较小, 我们可以对它进行微扰展开. 费曼—戴逊图形展开方法就是一种微扰展开的方法. 它在很多问题上取得了很大的成功. 但并非所有问题都能解决. 比如在低能时, 量子色动力学用费曼—戴逊图形展开方法就不行. 再比如, 高温超导中的低掺杂情况, 也不能用微扰论来解决. 不过它是一个理解多体问题的基本框架.t t t a t a >>ΨΨ<+↑↑',|)()'(|00k k T=0K 的格林函数要研究的是形如下式的量这里是系统的基态. 基态动量为零. 上式中表示在时刻在基态上加上一个动量为粒子. 这个态的动量为. 一般地, 它不是系统的本征态.上式是表示时刻, 系统仍然处于这个态的几率. 这个式子是在海森堡绘景中的.0Ψt >Ψ+↑0|)(t a k k k 't 由于并不是系统的本征态, 原则上它可以用系统的总动量为的本征态来展开, 这些本征态的数量是非常巨大的, 而且能量是不同的. 这一点可以用经典粒子系统的类比来理解, 总动量为的组合方式有无限多种, 不同的组合方式动能和势能是不同的. 那么, 这个态可以展开为>Ψ+↑0|)(t a k k k ∑>Ψ>=Ψ+↑ii i c t a k k ||)(0>Ψi k |这里是总动量为的系统的本征态. 到时刻, 这个态演化为k 't )'(0||)'(t t iE ii i i ec t a −−+↑∑>Ψ>=Ψk k ∑−+↑↑>=ΨΨ<it t iE i i i ec c t a t a )'(*00|)()'(|k k 't 时刻, 系统仍然处于这个态的几率准粒子及其寿命>Ψ+↑0|)(t a k);(E c c i →由于这些本征态的数量巨大, 能量可以处理为连续化的, 也就是有∫∑∞∞−−−→dEeE D E c ec c t t iE it t iE i i i )'(2)'(*)(|)(|如果展开系数分布很宽, 比如constE D E c =)(|)(|2我们马上得到)'(2)'(t t dE et t iE −=∫∞∞−−πδ这是说马上系统就不处于开始的态上了.>Ψ+↑0|)(t a k 如果展开系数分布很窄, 比如)'()(|)(|2E E E D E c −=δ我们马上得到)'(')'()'(t t iE t t iE edE eE E −∞∞−−=−∫δ这是说系统以后永远呆在开始的态上了.>Ψ+↑0|)(t a k 如果展开系数分布为1222])'([)(|)(|−−+Δ=E E E D E c 则有)')('()'(1222])'([t t i E i t t iE ei dE eE E −Δ+∞∞−−−=−+Δ∫π也就是说, 这个几率随时间衰减, 寿命为. Δ=/1τ以上讨论其实是把海森堡的不确定性关系具体化了.洛仑兹分布这里的讨论其实很具一般性,适用于所有寿命有限的粒子.能量分布有宽度,寿命就有限.在时, 粒子之间无相互作用, ,以后随着时间的消逝相互作用缓慢地增长, 在时, 增加到实际大小, 这时系统达到真正的基态−∞→t >Φ>=−∞→Ψ0|)(|t I 0=t >Φ−∞>=−∞Ψ−∞>=Ψ00|),0(ˆ)(|),0(ˆ|U UI H此后, 当时, 再让相互作用缓慢地趋于零,,∞→t>Φ>≡Φ−∞∞>=Ψ∞000|ˆ|),(ˆ|)0,(ˆS UU H 这样就有iL H e U−>Φ∞>=Ψ00|)0,(ˆ|>Φ>=Φ−00||ˆiL e S系统又回到无相互作用的基态, 至多差一个相位因子绝热假设。

格林函数方法

格林函数方法
1、格林函数
格林函数（Green's function）是指由著名数学家.格林（Green）提出的数学方法，它是一种可以求解各种微分方程的技术。

格林函数的定义是对于任意给定的初值问题，在区间上的解的和等于给定的数值13。

其用法主要有两种：一种是用于求解某些有定型的初值问题；另一种是求解某些微分方程的积分解。

格林函数的结果可以用来解决复杂的初值问题和理解复杂的微分方程以及系统的时间变化。

2、格林函数的原理
格林函数可以用来解决一类有特定初值条件的常微分方程组。

它的原理是基于一种叫做拉普拉斯变换（Laplacetransform）的数学变换理论，它是一种将微分方程组变换成求积分方程组的方法，从而可以使原本困难的初值问题变得容易解决，其在解决物理学中不变解中特别有用。

3、格林函数的计算
对于特定的初值条件，可以使用格林函数计算出拉普拉斯变换得到的积分方程的结果，从而计算得到解析解。

计算过程比较复杂，需要用到积分变换和methods。

总之，格林函数是一种可以求解复杂常微分方程的有效数学方法，它基于拉普拉斯变换的原理，对于特定的初值问题，运用格林函数，可以计算出相应的解析解。

数学物理方法第十二章格林函数解的积分公式

数学工具
证明过程中可能需要使用到实变函数、复变函数、偏微分方程等数学工具。
证明难度
格林函数的积分公式证明比较复杂，需要深入理解数学物理方法和偏微分方程的基本原理。
04
格林函数在物理问题中的应用
在波动方程中的应用
波动方程是描述波动现象的基本方程，如声波、光波和水波等。格林函数在求解波动方程中发挥了重要作用，能够给出波函数的精确解或近似解。
要点三
应用实例
为了更好地理解格林函数解的积分公式，我们通过几个具体的物理问题进行了应用。这些例子包括波动方程、热传导方程等，通过这些例子，我们可以看到格林函数解的积分公式的实用性和广泛性。
对未来研究的展望
进一步探索格林函数的性质和应用
尽管我们已经对格林函数的性质和应用有了一定的了解，但仍有许多未知领域值得我们去探索。例如，我们可以研究格林函数在不同物理问题中的应用，或者探索格林函数在其他数学领域中的性质和应用。
积分公式的推广和应用
在本章中，我们得到了格林函数解的积分公式，但这个公式可能还有其他的推广和应用方式。例如，我们可以尝试将这个公式应用到其他类型的偏微分方程中，或者尝试将这个公式应用到其他领域的问题中。
与其他数学物理方法的结合
数学物理方法中的其他方法，如分离变量法、变分法等，也可以与格林函数解的积分公式相结合，以解决更复杂的物理问题。未来研究可以探索如何将这些方法有效地结合起来，以更好地解决实际问题。
03
不同类型的格林函数在求解偏微分方程时具有不同的应用范围和特点。
03
格林函数的积分公式
公式推导
公式推导
01
通过求解偏微分方程，将格林函数表示为积分形式，利用边界

微分方程格林函数法的研究

微分方程格林函数法的研究
微分方程格林函数法是一个非常具有挑战性的方法，用于求解非
线性、复杂的微分方程组。

它是由英国数学家格林在19世纪60年代
发明的，也被誉为“积分方程化解法”。

格林函数法利用“积分”的
思想去求解一组微分方程，把求解的复杂的微分方程组变成求解一组
数值的问题，最终把这一组数值解合成一个“格林函数”，并以此函
数为基础解微分方程组。

格林函数法的优势在于可以快速精确的求解复杂的微分方程组，
而且它可以在非常复杂的情况下求解微分方程组，如非线性的、多变
量的、不稳定的情况等。

此外，格林函数法还可以求解符号和数值混
合方程组，这在微分方程中是很少见的。

格林函数法的研究已经源远流长。

它一直是微积分学习者深入探
索的重要内容，更是理论物理学、数学物理学和动力系统分析的重要
工具。

在过去的几十年中，格林函数法已经被用于求解非线性的微分
方程，如传播方程、拟制数据的稳定性等。

随着信息技术的飞速发展，格林函数法也受到了广泛的应用，并在一些具有实际意义的复杂问题
上发挥重要作用，如气流扩散等。

总之，微分方程格林函数法已经成为解决复杂微分方程的一个重
要工具，它对微积分学习者和理论物理学家都有着重要的意义。

研究
者不仅可以借助格林函数法，来解决一些具有实际意义的微分方程，
而且应用在其他领域也有很好的效果，例如精确科学计算。

格林函数法

为第三边值问题的积分表示式
物理意义：右边第一个积分表示区域T中分布的源在r 点产生的场的总和；第二个积分代表边界上的状况对 r点场的影响的总和；两项积分中的格林函数相同。说明泊松方程的格林函数是点源在一定的边界条件下所产生的场。
对于拉普拉斯方程，f(r0)=0，因此可得拉普拉斯方程第一边值问题的解
因此，我们可设想一个等效的点电荷，它位于球外M1处，且在球面产生的电势与球内点电荷在球面产生的电势相反。由物理学知识可知，该设想的点电荷必位于OM0处的延长线上，如图所示，并记：
OM r, OM0 r0
在∑ε 上的解，该解表示位于球心r=r0处的电量为ε0的点电荷在半径为ε的球面上产生的电势，根据电磁学知识，该电势为：
1
G(r, r0 ) 4
因此我们可得∑ε面上的积分
Ò
u(r)
G n
G
u(r) n
dS
Ò
u(r
)
n
(1
4
)
1
4
u(r) n
dS
Ò
u(
r
)
n
(1
4
)
1
4
u(r n
)
2d
(r r0 ) (x x0) ( y y0) (z z0)
格林函数的物理意义：在物体内部（T内）处放置一个单位点电荷（或热源），而该物体的界面保持电位为零（或温度为零）, 那么该点电荷（或该点热源）在物体内产生的电势分布（或稳定温度分布），就是上述定解问题的解――格林函数。
格林函数互易定理：格林函数代表r0处的点源在r处所产生的影响，系统不变，则该影响等同于将移至r 处的该点源在r0处产生影响。故格林函数遵守如下的互易定理：

数学物理方法--格林函数法

G(r , r0)r(r )dV T

1
4

f
G(r , r0 ) dS. n
第二边值问题(诺依曼问题)
u(r , r ')
u n

f
第二边值问题格林函数
G(r , r ')ห้องสมุดไป่ตู้n

0
u(r0 )

1
4
G(r , r0)(r )dV T

(u
v n

v
u )dS n

T
(uv

vu)dV
法向导数
5
3. 边值问题边界条件
泊松方程
u
[
u n

u]

()
() 定义在
0, 0 0, 0
第一类边界条件第二类边界条件
0, 0 第三类边界条件
3
感应电荷是边界问题
2. 格林公式
第一格林公式：
区域 T，边界
定解＝通解＋边界条件求通解＝积分

定解＝积分＋边界条件（格林函数法）
T

设 u(r ) 和 v(r ) 在 T 中具有连续二阶导数，
在上有连续一阶导数。由高斯定理

uv dS (uv)dV
p
M (r)
o
M0 (r0 )
如右图，当导体外 M1 处有电荷 40q 时，镜像电荷
将在球内M0 处。
M1(r1)
像电荷的大小以及位置：

4 0 q
a r1

格林函数法数学物理方程

格林函数法
若L 一个带平滑系数的线性微分算子，当求解形如()L u f =的微分方程时，若对于任意的向量y 都存在广义函数()G x,y ，使得
[]()()L G δ=x x,y x-y
（此处下标x 表示L 作用于()G x,y 时将其当做以x 为自变量的广义函数，而y 为参数）若再令
()()()d u G f =⎰x x,y y y
将上式代入()L u f =则有
[]()()d ()()d ()()d ()L G f L G f f f δ⎡⎤===⎣⎦
⎰⎰⎰x x,y y y x,y y y x -y y y x 故此时()u x 是微分方程()L u f =的解。

采用上述方法求解微分方程的方法称为格林函数法，广义函数()G x,y 也称为格林函数。

数学物理方法知识体系
数学物理方法所要解决的问题：求解（偏）微分方程
本学期学过的求解方法：变量分离法、积分变换法、格林函数法
变量分离法涉及知识点：傅里叶级数、函数的正交系、贝塞尔函数（Chap.2~Chap.5）积分变换法涉及知识点：傅里叶变换、拉普拉斯变换、广义函数（Chap.7~Chap.9）格林函数法涉及知识点：格林函数（Chap.10）
例题数量统计。

第十二章格林函数法

13
故得到
( x ) G ( x x ) ( x )d G ( x x ) ( x ) 0 G ( x x ) ( x ) ds n n S
V
这就是用Green函数求解静电问题的一种形式解。讨论几点：
12
该式左边第二项为 1 1 ( x) ( x x )d ( x )
0
V
0
得到
1 1 G ( x x ) ( x )d ( x ) 0 0 V G ( x x ) ( x ) G ( x x ) ( x ) ds n n S
2 0
2
2、镜像法能解的情况：在求解区域内没有自由电荷，或者只有有限几个点电荷，并且区域边界或介质界面规则(电场能用等效电荷代替)+边界条件。
3
二、 Green函数法能解的情况
能用Green定理求解静电边值问题的情况: 给定区域V内电荷分布 (x ) 和区域V的边界面S 上各点的电势 φs 或电势法向导数
1 2 G ( x , x ) ( x x) 0 G ( x , x) 1 G ( x , x) 0, 或 S n 0S S
所在的位置， x 代表观察点，在（3）式和（4）式中，
(5)
7
五、Green公式和边值问题的解
G 0 在一个单位电荷在空间所激发的电势。因此 n S 即代表单位电荷在边界上所激发的电场，由Gauss定理知道
1 G( x x )ds n 0 S n G( x x )ds 0 S G( x x ) 0 n S

数学物理方法12格林函数

泊第一类边界条件：第一边值问题(狄里希利问题)
松方
第二类边界条件：第二边值问题(诺依曼问题)
程
第三类边界条件：第三边值问题
2、格林函数的引入及其物理意义
引入：为了求解泊松方程的定解问题，我们必须定义一个与此定解问题相应的格林函数 G(r, r0)
它满足如下定解问题，边值条件可以是第一、二、三类条件：
这就是第三边值问题解的积分表示式．
右边第一个积分表示区域 T 中分布的源 f (r0 ) 在 r
点产生的场的总和. 第二个积分则代表边界上的状况对 r
点场的影响的总和．两项积分中的格林函数相同．这说明泊松方程的格林函数是点源在一定的边界条件下所产生的场．
对于拉普拉斯方程
f (r0 ) 0
第一边值问题的解为
构建格林函数为
G(x,
y
|
x0 ,
y0 )
1 4π
(x ln[
(x
x0 )2 x0 )2
(y (y
y0 )2 y0 )2
]
边界外法线方向为负 y 轴，故有
G n
|
G y
|y0
=
1 2π
(x
y0 x0 )2
y02
1 π
y0 (x x0 )2
y02
1 π
(x
y0 x0 )2
y02
代入到拉普拉斯第一边值问题解的公式（14.2. 13），拉普拉斯方程的自由项 f 0 ,则由
G(r,
r0
)
1 2π
ln
|
r
1
r0
|
1 2π
ln
|
r
1
r1
|

《格林函数方法》课件

04
格林函数在工程问题中的应用
流体动力学问题
流体力学中的波动和散射问题
格林函数方法可以用于求解流体力学中的波动和散射问题，例如声波在流体中的传播、波动在管道中的传播等。
流体动力学中的边界层问题
格林函数方法可以用于求解流体力学中的边界层问题，例如流体在固体表面流动时的速度分布、温度分布等问题。
格林函数方法的优点
精确度高
格林函数方法基于严格的数学推导，能够精确地描述物理系统的响应。
适用范围广
该方法不仅适用于线性系统，也适用于非线性系统，具有较强的通用性。
易于实现
格林函数具有明确的物理意义，计算过程相对简单，易于编程实现。
可扩展性强
通过引入更多的格林函数，可以处理更复杂的物理问题。
弹性力学问题
总结词
格林函数在弹性力学问题中也有着重要的应用，它可以帮助我们求解弹性波的传播和散射问题。
详细描述
在弹性力学问题中，格林函数可以用于描述弹性波的传播和散射过程。通过求解格林函数，我们可以得到弹性波在各种不同介质中的传播规律和散射特性，这对于地震探测、声波传播、振动控制等领域有着重要的应用价值。
格林函数方法的缺点
计算量大
对于大规模系统，需要计算的格林函数数量较多，计算量较大。
对初值敏感
某些情况下，初值的选择对计算结果影响较大，需要仔细选择。
对噪声敏感
在数据中存在噪声时，格林函数方法可能会受到影响，导致结果失真。
对边界条件敏感
边界条件的设定对格林函数的计算结果有较大影响，需要谨慎处理。
格林函数方法的未来发展前景
03
格林函数在物理问题中的应用
电磁场问题
总结词
格林函数在电磁场问题中有着广泛的应用，它可以帮助我们求解电磁场中的散射和辐射问题。

格林函数方法

设假想点电荷在
2 0 2
P ，它的坐标为
4 0 2
（它在 OP 连线上，题中b对应这里的
2 0 2
2 R0 x 2 R R 2
0
R R R R 2 P P r x x R 2R cos R R R R0 Q R0 R02 R02 ∵ Q 1 Q (b R ) R R a R
（3）球外空间的格林函数
P’
P
设点电荷Q = 1 坐标为 P ( x, y , z )
观察点为 P( x, y, z )
R x
R x
x2 y2 z 2
x 2 y 2 z 2
R 相当于题中的 a ） R0 R（
PP r x x R 2 R 2 2RR cos

(x)
S
解法: (1)先求第一类边值问题的格林函数

1 G ( x , x ) ( x x )
2
G s 0
0
(2)
(2). 把(2)的解(格林函数)代入下式即可:
( x ) G ( x , x ) ( x )dV 0 ( x ) G ( x , x )dS V S n
§2.5
内容提要
格林函数方法
一、格林函数
二、用格林函数求解一般的边值问题
机动
目录
上页
下页
返回
结束
1. 处于 x 点上的单位点电荷的电荷分布密度: ( x ) ( x x )
回忆:点电荷密度的

函数表示

V
( x )dx ( x x )dV 1

第12章_格林函数法

电磁场的源场关系
源量： (r , t ) 或 q(r , t )
场量： E (r , t ) D(r , t )
电场
J (r , t ) 或 I (r , t )
B(r , t ) H (r , t )
磁场
比如：静电场
源量： (r )
场量： E (r ) D(r )
全电流定律：传导电流和时变的电场都能产生磁场电磁感应定律：电荷和时变的磁场都能产生电场（库仑电场(有源无旋场)和感应电场(无旋有源场)）磁通连续性原理：磁场是无散度场，磁力线总是闭合曲线高斯定理：电荷是产生电场的源
WangChengyou © Shandong University, Weihai
全电流定律：磁场强度沿任意闭合曲线的环量，等于穿过以该闭合曲线为周界的任意曲面的传导电流与位移电流之和。电磁感应定律：电场强度沿任意闭合曲线的环量，等于穿过以该闭合曲线为周界的任意曲面的磁通量变化率的负值。磁通连续性原理：穿过任意闭合曲面的磁感应强度的通量恒为0。高斯定理：穿过任意闭合曲面的电位移的通量等于该闭合曲面所包围的自由电荷的代数和。
T T
同理 vu dS vudV u vdV T T 两式相减有 uv dS vu dS (uv vu )dV

T
WangChengyou © Shandong University, Weihai
WangChengyou © Shandong University, Weihai
WangChengyou © Shandong University, Weihai
数学物理方法
第12章格林函数法

格林函数法

由格林函数的对称性可得
Ò u ( r ) T G ( r ,r 0 ) f( r 0 ) d V 0 [ u ( r 0 ) G ( n r 0 ,r 0 ) G ( r ,r 0 ) u ( n r 0 0 ) ] d S 0
解的基本思想：通过上面解的形式，我们容易观察出引
例1 试求球内的泊松方程的狄利克雷问题的格林函数。
解：该定解问题为三维，其基本解为
G0

4
1 rr r r0
G1 0 r R
G
1
则满足
G1
rR
G 0
rR

4
1 rr R r0
设产生 G 1 的等效点电荷电量q
、位置
rr
（在
1
rr
0
的延长线上
且在球形区域以外，这样方程自然满足）
r R
rr O
r r0
M0
M
q

R ቤተ መጻሕፍቲ ባይዱ0
0
r r1

R2
r
2 0
r r0
G=G0+G1

4
1 rr r r0
40qrr
r r1
M1
球形区域格林函数表达式；区域形状不同其格林函数也
会有所不同

4
1 rr r r0
4Rr00 rr0rr1

4
1 rr r r0
二维时 u r r l r r 0 G n r r 0 ;r r 0 d l0 S G r r ;r r 0 fr r 0 d S 0
上式为第一边值问题解的积分表示式
§5.2 用电像法求格林函数法

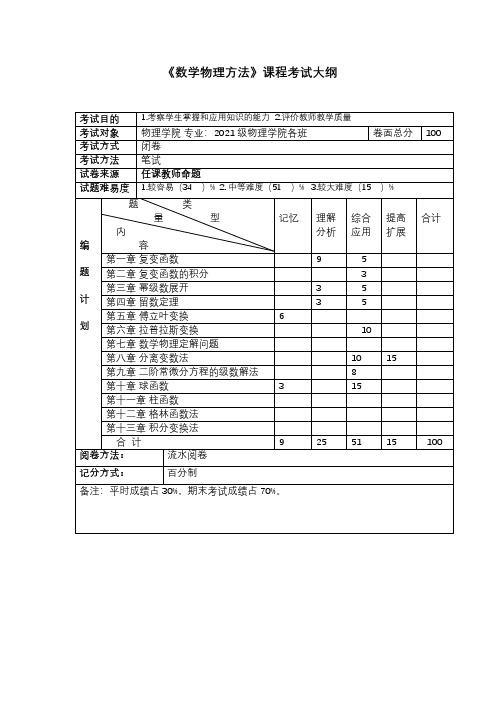
山东大学物理学院数学物理方法 2022-2023期末试题及解析

《数学物理方法》课程考试大纲2022-2023山东大学物理学院数学物理方法期末试题一、填空题(每题3分，共27分)1. 已知zz =cos (aa +iibb )，z 的代数表达式为________________2. 指出多值函数�(zz −aa )(zz −bb )的支点和阶数___________3. 已知级数∑aa nn xx nn ∞nn=0的收敛半径为A ，试问级数∑aa nn √1+bb nn nnxx nn ∞nn=0（|bb |<1）的收敛半径为_____________4.ssss nn 2zz zz 3的极点为_____，且为______ 阶极点5. 利用柯西公式计算∮zz 2−zz+1zz 2(zz−1)ddzz |zz |=2_______________6. 连带勒让德多项式的正交代数表达式为_______________7. 计算留数1(zz 2+1)2_________________________8. 从t=a 持续作用到t=b 的作用力ff (tt )，可以看作许多前后相继的瞬时力的总和，其数学表达形式为__________9. ∫3δδ(xx −ππ)[ee 2xx +cccccc xx ]ddxx 10−10=_________________ 二、简算题(每题5分，共15分)1. 将函数ff (zz )=1zz 2−3zz+2，在区域0<|zz −1|<1上展开为洛朗级数 2. �cos mmxx(xx 2+aa 2)2d xx ∞−∞，m>03. 已知解析函数ff =uu +iiνν，而uu =xx 3−3xxyy 2，试求ff三、 (8分)用级数法解微分方程yy ′′+xxyy ′+yy =0四、 (10分)在圆域ρρ<ρρ0上求解泊松方程的边值问题�ΔΔuu =aa +bb (xx 2−yy 2)uu ρρ=pp 0=cc五、 (15分)设有一均匀球体，在球面上的温度为cos 2θθ，试在稳定状态下求球内的温度分布（已知，PP 0(xx )=1，PP 1(xx )=xx , PP 2(xx )=12(3xx 2−1)）六、 (10分)利用拉普拉斯变换解RC 电路方程：�RRRR +1CC �RR dd tt tt=EE 0sin ωωttRR (0)=0七、 (15分)计算：⎩⎨⎧ðð2uu ððtt 2−aa 2ðð2uuððxx2=AA cos ππxx ll sin ωωttuu |xx=0=0, uu |xx=ll =0uu |tt=0=φφ(xx ), uu tt |tt=0=ψψ(xx )2022-2023 数学物理方法期末试题参考答案一、填空题(每题3分，共27分)1.【正解】 12(ee bb +ee −bb )cos aa +i2(ee −bb −ee bb )sin aa 【解析】cos (aa +i bb )=ee ss (aa+ss bb )+ee −ss (aa+ss bb )2=12(ee −bb ee ss aa+ee bb ee −ss aa )=12[e −bb(cos aa +isin aa )+e bb (cos aa −isin aa )]=12[(e bb+e −bb )cos aa +i(e −bb −e bb )sin aa ]=12(ee bb +ee −bb)cos aa +i 2(ee −bb−ee bb )sin aa 2.【正解】支点：z=a 、b 、∞；皆为一阶支点【解析】注意到函数为12次，且当z=a 、b 时函数置零，z=∞为熟知的支点，阶数皆为2−1=1 3.【正解】A【解析】由根值判别法，幂级数的收敛区间为ll ii ll nn→∞�aa nn ⋅(1+bb nn )nn⋅xxxx (−1,1)而|bb |<1⇒ll ii ll nn→∞√1+bb nn nn=1故收敛半径保持不变，仍为A 4.【正解】zz =0；一阶【解析】ll ii llzz→0ssss nn 2zz zz 3→∞，且ll ii ll zz→0zz ⋅ssss nn 2zz zz 3=1故zz =0为一阶极点5.【正解】2πi注意到原函数的极点为zz =0和zz =1，且分别为2阶与一阶极点，故上述积分即为II =2ππii �Re cc�ff (zz ),0]+Re cc [ff (zz ),1]��而Re cc [ff (zz ),0]=ll ii ll zz→0dd �zz 2−zz +1zz −1�ddzz=0Re cc [ff (zz ),1]=ll ii ll zz→1zz 2−zz +1zz 2=1因此II =2ππii6.【正解】�PP ll mm (xx )⋅PP kk mm (xx )ddxx =01−1(ll ≠kk ) 7. 【正解】Re cc [ff (zz ),ii ]=ll ii ll zz→ss dd �1(zz +ii )2�ddzz=−2[2ii ]−3Re cc [ff (zz ),−ii ]=ll ii ll zz→−ss dd �1(zz −ii )2�ddzz=−2[−2ii ]−38.【正解】∫ff (ττ)1−1δδ(tt −ττ)ddττ 9.【正解】ee 2ππ−1【解析】由δδ函数的挑选性，上述积分即为 (ee 2xx +cccccc xx )|xx=ππ=ee 2ππ−1 二、简算题(每题5分，共15分)1.【解析】在区域0<|zz −1|<1内ff (zz )=1zz 2−3zz +2=−12⋅11−zz 2−1zz −1=−12⋅11−zz 2−1zz ⋅11−1zzff (zz )=−�12kk+1zz kk ∞kk=0−�zz −(kk+1)∞kk=0 =−�zz kk−1kk=−∞−�12kk+1zz kk∞kk=02.【解析】由约旦引理，从上半平面的半圆弧补全围道，上半平面有一个二阶极点zz 0=iiaa ，该点的留数为RReeccff (zz 0) =limzz→zz 0d d zz e immzz(zz +aa i)2=lim zz→zz 0[i ll e immzz (zz +aa i)2−2e ss nn zz (zz +aa i)3] =−llaa +14aa 3ie −mmaaII =ππi ⋅(−llaa +14aa 3ie −mmaa )=llaa +14aa3ππe −mmaa 3.【解析】根据C-R 条件,有∂uu ∂xx =3xx 2−3yy 2=∂νν∂yy−∂uu ∂yy =6xxyy =∂νν∂xxddνν=−(−6xxyy )d xx +3(xx 2−yy 2)d yy =d(3xx 2yy −yy 3) 有νν=3xx 2yy −yy 3+CC ,代入得ff (zz )=xx 3−3xxyy 2+i(3xx 2yy −yy 3+CC ) =(xx +i yy )3+i CC =zz 3+i CC 0三、(8分)【解析】设 yy =�aa nn xx nn ∞nn=0 是方程的解,其中 aa 0,aa 1 是任意常数,则yy ′=�nnaa nn xx nn−1∞nn=1yy ′′=�nn (nn −1)aa nn xx nn−2∞nn=2=�(nn +2)(nn +1)aa nn+2xx nn ∞nn=0方程 yy ′′+xxyy ′+yy =0,得�[(nn +2)(nn +1)aa nn+2+nnaa nn +aa nn ]xx nn ∞nn=0=0故必有(nn +2)(nn +1)aa nn+2+(nn +1)aa nn =0即aa nn+2=−aa nnnn +2(nn =0,1,2,⋯ ) 可见,当 nn =2(kk −1) 时aa 2kk=(−12kk )aa 2kk−2=(−12kk )(−12kk −2)⋯(−12)aa 0=aa 0(−1)kkkk !2kk当nn =2kk −1时aa 2kk+1=(−12kk +1)aa 2kk−1=(−12kk +1)(−12kk −1)⋯(−13)aa 1=aa 1(−1)kk (2kk +1)!�aa 2nn xx 2nn ∞nn=0与�aa 2nn+1xx 2nn+1∞nn=0的收敛域均为(−∞,+∞) 故yy =�aa κκxx κκ∞κκ=0=�aa 2κκxx 2κκ∞κκ=0+�aa 2κκ+1xx 2κκ+1∞κκ=0=�aa 0(−1)nn nn !2nn xx 2nn∞nn=0+�aa 1(−1)nn (2nn +1)!xx 2nn+1∞ss=0即yy =aa 0e −xx 22+aa 1�(−1)nn (2nn +1)!xx 2nn+1∞nn=0,xx ∈(−∞,+∞)四、 (10分)【解析】首先找到满足方程的特解vv =aa 4(xx 2+yy 2)+bb 12(xx 4−yy 4)=aa 4ρρ2+bb 12(xx 2+yy 2)(xx 2−yy 2) =aa 4ρρ2+bb 12ρρ4cos 2φφ 令uu =vv +ww =aa 4ρρ2+bb 12ρρ4cos 2φφ+ww对于齐次方程，且满足球心为有限值的泊松方程通解为ww (ρρ,φφ)=�ρρnn (AA mm cos ll φφ+BB nn sin llφφ)∞mm=0代入边界条件，有 �ρρ0nn (AA mmcos ll φφ+BB nn sin llφφ)∞mm=0=cc −aa 4ρρ02−bb 12ρρ04cos 2φφ比较系数解得uu =vv +ww =cc +aa 4(ρρ2−ρρ02)+bb 12ρρ2(ρρ2−ρρ02)cos 2φφ 五、(15分)【解析】对于满足球心处为有限值的拉普拉斯方程通解为uu (rr ,θθ)=�AA ll rr l P ll (cos θθ)∞ll=0代入边界条件有�AA ll rr 0l P ll (cos θθ)∞ll=0=cos 2θθ=xx 2由于P 2(xx ) =12(3xx 2−1) ,有xx 2=13[1+2P 2(xx )]=13P 0(xx )+23P 2(xx )即�AA ll rr 0lP ll (cos θθ)∞ll=0=cos 2θθ=xx 2=13P 0(xx )+23P 2(xx )对比系数可得uu (rr ,θθ)=13+23⋅1rr 02⋅rr 2P 2(cos θθ)六、(10分)【解析】对方程进行拉普拉斯变换，有jj ‾RR +jj ‾ppCC =EE 0ωωpp 2+ωω2 解得jj ‾=ωωEE 0(RR +1ppCC )(pp 2+ωω2)再进行反演RR (tt )=EE 0ωωRR (−RRCC e llRRRRωω2RR 2CC 2+1+RRCC cos ωωtt +ωωRR 2CC 2sin ωωtt ωω2RR 2CC 2+1) =EE 0RR 2+1/CC 2ωω2(RR sin ωωtt +1CCωωcos ωωtt )−EE 0/CCωωRR 2+1/CC 2ωω2e −tt /RRRR七、(15分)【解析】应用冲量定理法，先求解vv uu −aa 2vv xxxx =0ννxx ∣x=0=0,vv x ∣x=l =0vv ∣tt=ττ+0=0,vv t ∣t=ττ+0=AA cos ππxxllsin ωωττ根据通解的一般形式并代入边界条件，可得vv (xx ,tt ;ττ)=AAllππaasin ωωττsin ππaa (tt −ττ)ll cos ππxx ll uu (xx ,tt )=�vv (xx ,tt ;ττ)tt=AAll ππaa cos ππxx ll �sin ωωττsin ππaa (tt −ττ)ll d ττtt 0=AAll ππaa 1ωω2−ππ2aa 2/ll 2(ωωsin ππaa ll tt −ππaa ll sin ωωtt )cos ππxx ll。

格林函数法(2)

1 rMM 0
相同。相同。
性质2 恒等于0. 性质2 在边界 Γ 上格林函数 G ( M , M 0 ) 恒等于0. 性质3 性质3 在区域 Ω 内，下面不等式成立
1 0 < G(M , M 0 ) < . 4πrMM 0
性质4 (对称性) 性质4 对称性) 格林函数 G ( M , M 0 )关于自变量 M 和参变量M 0 之间具有对称性质，之间具有对称性质，即若 M 1 , M 2 ∈ Ω, 则
G(M , M 0 ) = 1 − v, 4πrMM 0
来表示，此函数在导电面上恒等于0，导电面上恒等于0 来表示，此函数在导电面上恒等于其中函数 − v 正好表示导电面上感应电荷所产生的电位。正好表示导电面上感应电荷所产生的电位。
§4.4 两种特殊区域的格林函数及狄利克雷问题的解
由公式
1 G(M, M0 ) = − v, 4π rM0M
奇性部分则
∂G u ( M 0 ) = − ∫∫ u dS . ∂n Γ
(3)
正则部分
为拉普拉斯方程格林函数格林函数。称 G( M, M0 ) 为拉普拉斯方程格林函数。
如果能找到格林函数中的 v，则狄利克雷问题，
∇ 2u = 0, 在Ω内， u Γ = f .
1 G(M , M 0 ) = − v, 4πrMM 0
(3)
格林函数的几个重要性质：格林函数的几个重要性质：的几个重要性质性质1 性质1 格林函数 G ( M , M 0 )在除去 M = M 0 一点外 G 处处满足拉普拉斯方程，当处处满足拉普拉斯方程， M → M 0时， ( M , M 0 ) 趋于无穷大，其阶数和趋于无穷大，
所谓镜像法，点放置单位正电荷，所谓镜像法，就是在 M 0 ∈ Ω点放置单位正电荷，镜像法在区域 Ω 外找出 M 0关于边界 Γ 的像点 M 1 , 然点放置适当单位的负电荷，后在 M 1 点放置适当单位的负电荷，它产生的负电位与 M 0处正电荷产生的正电位在 Γ 上互相抵消。的内部，抵消。由于 M 0在边界 Γ 的内部，M 1 在边界 Γ 的外部，的外部， M 1 处的点电荷形成电场的电位在 Γ 内部是调和函数 v，且有， 1 vΓ = 4π rM0M 故 M 0和 M 1 处的电荷形成的电场在 Γ 上的电位就是所要求的格林函数。就是所要求的格林函数。

数学物理方程格林函数法优秀课件

由格林第三公式，得
u (,,) ( u n u n )d s u d V(7 )
由定解问题（5）（6）的自由项和边值条件，可得
而在 u dV un d s 中，f( xun,y在,z边)d界V 和上的值u 未 n知ds，因此(须x,进y,一z)步 n处d理s.。
( 1 1 )
将（10）和（11）带入到（9），
G u d V ( u n u n ) d s B ( u n u n ) d s ( 9 )
得到
G u d V ( u n u n )d s u (x ,y ,z ) u n (x ,y ,z )
5.3 半空间及圆域上的Dirichlet问题
由前面的分析，我们可以看出，只要求出了给定区域
上的格林函数，就可以得到该区域泊松方程狄利克雷问题的解。对一般区域，求格林函数并非易事。但对于某些特殊区域，可有一些方法。
5.3.1 半空间上的狄利克雷问题
设 { ( x ,y ,z ) |z 0 } , { ( x ,y ,z ) |z 0 } 考虑定解问题
基本解做研究偏微分方程时起着重要的作用。这里首先介绍拉普拉斯方程的基本解，并做一些特殊区域上由基本解生产格林函数，由此给出相应区域上的拉普拉斯方程或泊松方程边值问题的解的表达式。
5.2.1 基本解
设 P0(,,)R3 ，若做点 P0(,, ) 放置一单位正电荷，
则该电荷在空间产生的点位分布为（舍去介电常数 0 ）
uf(x,y,z),(x,y,z) (1)
u(x,y,0)(x,y),(x,y) R2 (2)
设 P0(,,)，则 P1(,,) 为 P 0 关于的对称点。
G (P G , P 0)( P 0 ,,P (0 x ),,(yx ,,zy ), z )

数学物理方法第12章-格林函数

T
∫∫ ϕ (r )G (r , r )dS . α
0 0 0 Σ
1
12.2
电像法求格林函数第一边值问题格林函数
∆v(r , r0 ) = δ (r − r0 )
v(r , r0 ) Σ = 0
⇒
v(r , r0 ) = G (r , r0 )
r r0
导体球内有一个点电荷，导体接地。求球内电势。电荷的存在，在导体上感应了电荷。球内的电势为自由电荷和感应电荷电势之和。将感应电荷的电势由一 “电像电荷”的电势表示
∂G ( r , r0 ) dS . ∂n
第一边值问题格林函数
u ( r0 ) = ∫∫∫ G ( r , r0 ) f ( r ) dV + ∫∫ ϕ ( r )
T Σ
第三边值问题
[α
∂u + β u ] Σ = ϕ (Σ ) ∂n
∆v(r , r0 ) = δ (r − r0 )
[α ∂v + βv] Σ = 0 ∂n
1 a + 4π r − r0 r0
1 a 4π r − 2 r0 r0
2
1 1 = r − r0 r 2 − 2rr0 cos θ + r02
在球面上
∂ ∂n
Σ
=
∂ ∂r
r =a
[
∂ 1 1 2r − 2r cos θ ]Σ =− ∂n r − r0 2 (r 2 − 2rr0 cos θ + r02 )3 / 2
[
∂ ∂ G (r , r0 )] Σ = [− G (r , r0 )] z =0 ∂n ∂z
Σ
∂u ( r ) ∂v ( r , r0 ) − u (r ) ]dS . ∂n ∂n

(整理)格林函数(免费)

§2.4 格林函数法解的积分公式在第七章至第十一章中主要介绍用分离变数法求解各类定解问题，本章将介绍另一种常用的方法——格林函数方法。

格林函数，又称点源影响函数，是数学物理中的一个重要概念。

格林函数代表一个点源在一定的边界条件和（或）初始条件下所产生的场。

知道了点源的场，就可以用迭加的方法计算出任意源所产生的场。

一、泊松方程的格林函数法为了得到以格林函数表示的泊松方程解的积分表示式，需要用到格林公式，为此，我们首先介绍格林公式。

设u （r ）和v （r ）在区域 T 及其边界 ∑ 上具有连续一阶导数，而在 T 中具有连续二阶导数，应用矢量分析的高斯定理将曲面积分⎰⎰∑⋅∇Sd v u化成体积积分.)(⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∇⋅∇+∆=∇⋅∇=⋅∇∑TTTvdV u vdV u dV v u S d v u（12-1-1）这叫作第一格林公式。

同理，又有.⎰⎰⎰⎰⎰⎰⎰⎰∇⋅∇+∆=⋅∇∑TTvdV u udV v S d u v（12-1-2）（12-1-1）与（12-1-2）两式相减，得,)()(⎰⎰⎰⎰⎰∆-∆=⋅∇-∇∑TdV u v v u S d u v v u亦即.)(⎰⎰⎰⎰⎰∆-∆=⎪⎭⎫ ⎝⎛∂∂-∂∂∑T dV u v v u dS n u v n vu（12-1-3）n ∂∂表示沿边界 ∑ 的外法向求导数。

（12-1-3）叫作第二格林公式。

现在讨论带有一定边界条件的泊松方程的求解问题。

泊松方程是)( ),(T r r f u ∈=∆（12-1-4）第一、第二、第三类边界条件可统一地表为),( M u n u ϕβα=⎥⎦⎤⎢⎣⎡+∂∂∑（12-1-5）其中 ϕ（M ）是区域边界 ∑ 上的给定函数。

α＝0，β ≠0为第一类边界条件，α ≠0，β＝0是第二类边界条件，α、β 都不等于零是第三类边界条件。

泊松方程与第一类边界条件构成的定解问题叫作第一边值问题或狄里希利问题，与第二类边界条件构成的定解问题叫作第二边值问题或诺依曼问题，与第三类边界条件构成的定解问题叫作第三边值问题。

格林函数

稳定问题的格林函数也可以利用静电场类比法得到。点源问题可以看成接地的导体边界内在 r’ 处有一个电量为 - ε 0 的点电荷。边界内部的电场由点电荷与导体中的感应电荷共同产生。在一些情况下，导体中所有感应电荷的作用可以用一个设想的等效电荷来代替，该等效电荷称为点电荷的电像。这种方法称为电像法发展和应用分类格林函数在地震工程学中的应用格林函数在地震工程学中是计算震源机制的函数。根据其发展和应用可以分为以下几类。
经验格林函数法
经验格林函数法是运用包含断层上一个点源动力学破裂的复杂效应、震源主场地速度结构的不均匀性影响的小震记录来叠加合成较大地震的地震动时程。其优点是信度较高、较为可靠；可是其缺点同样突出，即对小震记录的要求相当苛刻，必须具有与大震相同的震源机制，小震记录的信噪比要高等等。如果在震源区找不到良好的小震记录，就不能用经验格林函数法。
理论格林函数法
理论格林函数的计算是一个相当复杂的过程，目前只有对水平成层介质推导的解析公式。计算要借助计算机实现，且介质层数受到很大的限制，很少有多于两覆盖层的结果发表。
数值格林函数法
与实际地震动观测记录的比较表明，这种在时域合成的地震动模拟，对持时、峰值加速度、短周期（ 1 秒以下）反应谱幅值的预测精度都可以在大约 -50% 范围内，与经验模型的精度大体相当；对峰值速度和周期大于 1 秒的反应谱幅值，预测的误差要比经验模型的小。
格林函数
姓名：折再兴
学号：201241802027
专业：物理学
电话：15764212022
格林函数
摘要：从物理上看,一个数学物理方程是表示一种特定的"场"和产生这种场的"源"之间的关系.例如,热传导方程表示温度场和热源之间的关系,泊松方程表示静电场和电荷分布的关系,等等.这样,当源被分解成很多点源的叠加时,如果能设法知道点源产生的场,利用叠加原理,我们可以求出同样边界条件下任意源的场, 这种求解数学物理方程的方法就叫格林函数法.而点源产生的场就叫做格林函数。关键字：点电荷，函数表示，微分算符。正文：格林函数法是数学物理方程中一种常用的方法。格林函数是又称为源函数或影响函数，是英国人 G. 格林于 1828 年引入的。一个处于 X ’点上的单位点电荷所激发的电势 Ψ （ x ）满足泊松方程：

第十二章 格林函数法

格林函数

格林函数（ＰＤＦ）

格林函数方法

数学物理方法第十二章格林函数解的积分公式

微分方程格林函数法的研究

格林函数法

数学物理方法--格林函数法

格林函数法 数学物理方程

第十二章 格林函数法

数学物理方法12格林函数

《格林函数方法》课件

格林函数方法

第12章_格林函数法

格林函数法

山东大学物理学院 数学物理方法 2022-2023期末试题及解析

格林函数法(2)

数学物理方程 格林函数法优秀课件

数学物理方法第12章-格林函数

(整理)格林函数(免费)

格林函数

第十二章格林函数法

格林函数法数学物理方程

第十二章格林函数法

山东大学物理学院数学物理方法 2022-2023期末试题及解析

数学物理方程格林函数法优秀课件