线面平行、面面平行的判定及其性质习题课ppt课件
合集下载
线面平行面面平行的判定ppt课件

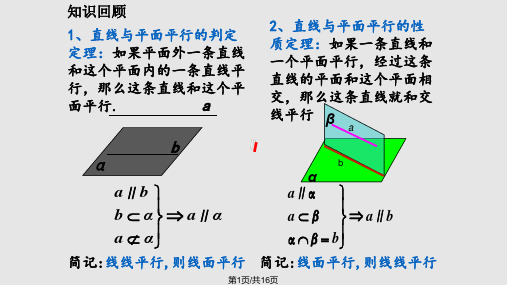
思考:1.平面 内有一条直线与平面 平行, , 平行吗?
2.平面 内有两条直线与平面 平行, , 平行吗?
面面平行的判定定理:如果一个平面内有两条相交直
线都平行于另一个平面,那么这两个平面平行.
用符号表示为: aa⊂ ∥βα,,bb⊂∥βα,a∩b=P⇒β∥α.
定理的本质:
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
1.如图 3,P 是平行四边形 ABCD 所在平面外一点,Q 是 PA 的中点.求证:PC接QO. ∵ABCD为平行四边形,
解:(1)在图 2 中,线段 BB1、BC、CC1、
C1B1、BC1 所在的直线与平面 ADD1A1 平行.
(2)在图 2 中,平面 A1B1C1D1、CC1D1D
与 AB 所在的直线平行.
图1
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
④若两条平行直线中的一条与一个平面平行, 则另一条也 与这个平面平行.
其中正确命题的个数是( B )
A.0 个
B.1 个
C.2 个
D.3 个
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
4.若 a、b 是异面直线,则下列命题中是假命题的是( D ) A.过 b 有一个平面与 a 平行 B.过 b 只有一个平面与 a 平行 C.过 b 有且只有一个平面与 a 平行 D.过 b 不存在与 a 平行的平面
2.平面 内有两条直线与平面 平行, , 平行吗?
面面平行的判定定理:如果一个平面内有两条相交直
线都平行于另一个平面,那么这两个平面平行.
用符号表示为: aa⊂ ∥βα,,bb⊂∥βα,a∩b=P⇒β∥α.
定理的本质:
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
1.如图 3,P 是平行四边形 ABCD 所在平面外一点,Q 是 PA 的中点.求证:PC接QO. ∵ABCD为平行四边形,
解:(1)在图 2 中,线段 BB1、BC、CC1、
C1B1、BC1 所在的直线与平面 ADD1A1 平行.
(2)在图 2 中,平面 A1B1C1D1、CC1D1D
与 AB 所在的直线平行.
图1
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
④若两条平行直线中的一条与一个平面平行, 则另一条也 与这个平面平行.
其中正确命题的个数是( B )
A.0 个
B.1 个
C.2 个
D.3 个
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
4.若 a、b 是异面直线,则下列命题中是假命题的是( D ) A.过 b 有一个平面与 a 平行 B.过 b 只有一个平面与 a 平行 C.过 b 有且只有一个平面与 a 平行 D.过 b 不存在与 a 平行的平面
线面及面面平行的性质课件

解: 由⑴,得 EF//BC, ⑵ EF//BC
EF//面AC BE、CF都与面相交. 线面平行 线线平行 A
D' A' D E
F P
B'
C'
C B
线面平行
例2.已知平面外的两条平行直线中的一条平行于这
个平面,求证:另一条也平行于这个平面. 且a//b,// , a,b , 已知:直线a、b,平面, a 求证: b//
平面与平面平行的性质定理
如果两个平行平面同时和第三个平面相交, 那么它们的交线平行 符号表示:
α//β α γ a a//b β γ b
面面平行→线线平行
由两个平面平行可以得到哪些结论呢?
1. 若两个平面互相平行,则其中一个平面 中的直线必平行于另一个平面; 2. 平行于同一平面的两平面平行;
l // l m
β
l
l // m
m
简记为: α “线面平行,则线线平行” 作用:判定直线与直线平行的重要依据。 关键: 寻找平面与平面的交线。
练习:
如果一条直线和一个平面平行,则这条直线( D )
A 只和这个平面内一条直线平行;
B 只和这个平面内两条相交直线不相交; C 和这个平面内的任意直线都平行; D 和这个平面内的任意直线都不相交。
a
过a作辅助平面, 提示: 且
b
c
例2.已知平面外的两条平行直线中的一条平行于这
个平面,求证:另一条也平行于这个平面. 求证: b// 且 证明:过a作平面, 性质定理 a // 且a//b,// , a,b , 已知:直线a、b,平面, a
c
A
线面、面面平行的判定与性质习题课课件

[例 3] (文)如下图,平面 α∥平面 β,线段 GH 与 α、
β 分别交于 A、B,线段 HF 与 α、β 分别交于 F、E,线 段 GD 与 α、β 分别交于 C、D,且 GA=9,AB=12,BH =16,S△ACF=72.求△BDE 的面积.
解析:因为 α∥β,所以 AC∥BD,AF∥BE.所以∠ FAC 与∠EBD 相等或互补.因为 AC∥BD,故△GAC∽
应用二面平行的判定定理时,两条相交直线的“相 交”二字决不可忽视.
4.要注意符合某条件的图形是否惟一,有无其它情 形.
一、转化的思想 解决空间线面、面面平行关系的问题关键是作好下 列转化
二、解题技巧 要能够灵活作出辅助线、面来解题,作辅助线、面 一定要以某一定理为理论依据.
线面平行的判定 [例 1] (文)如下图所示,矩形 ABCD 和梯形 BEFC 所在平面互相垂直,BE∥CF,求证:AE∥平面 DCF.
(文)(2011·济南调研)已知 m,n 是两条不同的直线, α,β,γ 是三个不同的平面,则下列命题正确的是( )
A.若 α⊥γ,α⊥β,则 γ∥β B.若 m∥n,m⊂α,n⊂β,则 α∥β C.若 α⊥β,m⊥β,则 m∥α D.若 m∥n,m⊥α,n⊥β,则 α∥β
解析:
由正方体交于同一顶点的三个面知 A 错;如上图
重点难点 重点:线面、面面平行的判定定理与性质定理及应 用 难点:定理的灵活运用
知识归纳
一、直线与平面平行
1.判定方法 (1)用定义:直线与平面无公共点.
(2)判定定理:
a⊄α
b⊂α⇒a∥α
a∥b
(3)其它方法: αa⊂∥ββ⇒a∥α
2.性质定理:
a∥α
a⊂β ⇒a∥b
β 分别交于 A、B,线段 HF 与 α、β 分别交于 F、E,线 段 GD 与 α、β 分别交于 C、D,且 GA=9,AB=12,BH =16,S△ACF=72.求△BDE 的面积.
解析:因为 α∥β,所以 AC∥BD,AF∥BE.所以∠ FAC 与∠EBD 相等或互补.因为 AC∥BD,故△GAC∽
应用二面平行的判定定理时,两条相交直线的“相 交”二字决不可忽视.
4.要注意符合某条件的图形是否惟一,有无其它情 形.
一、转化的思想 解决空间线面、面面平行关系的问题关键是作好下 列转化
二、解题技巧 要能够灵活作出辅助线、面来解题,作辅助线、面 一定要以某一定理为理论依据.
线面平行的判定 [例 1] (文)如下图所示,矩形 ABCD 和梯形 BEFC 所在平面互相垂直,BE∥CF,求证:AE∥平面 DCF.
(文)(2011·济南调研)已知 m,n 是两条不同的直线, α,β,γ 是三个不同的平面,则下列命题正确的是( )
A.若 α⊥γ,α⊥β,则 γ∥β B.若 m∥n,m⊂α,n⊂β,则 α∥β C.若 α⊥β,m⊥β,则 m∥α D.若 m∥n,m⊥α,n⊥β,则 α∥β
解析:
由正方体交于同一顶点的三个面知 A 错;如上图
重点难点 重点:线面、面面平行的判定定理与性质定理及应 用 难点:定理的灵活运用
知识归纳
一、直线与平面平行
1.判定方法 (1)用定义:直线与平面无公共点.
(2)判定定理:
a⊄α
b⊂α⇒a∥α
a∥b
(3)其它方法: αa⊂∥ββ⇒a∥α
2.性质定理:
a∥α
a⊂β ⇒a∥b
线面面面平行的判定与性质习题课更新PPT课件
A1
N B1
F C1
3.如图,正方ABCD—A1B1C1D1中,E为C1C的中点. 在棱AD上是否存在一点F,使得CF∥平面AD1E?
M F
M
F ●
第15页/共16页
谢谢您的观看!
第16页/共16页
思路一:由“面面平行”得到“线面平行.”
取 A1C1中点 E,连接 AE, B1E, 证面AB1E // 面BC1D
证明:
E
C1E // AD
C1E AD
ADC1E为平行四边形.
●
AE//C1D
AE 面BC1D C1D 同面B理C可1D证
AE // 面BC1D
B1E // 面BC1D
FA GC
D A
C1
B1 G
E C
B
第12页/共16页
课堂小结
知识: 线面平行、面面平行的判定与性质。
方法: 中位线
平行四边形 公理4
线线平行
性质 不成立 判定 性质
思想:
面面平行
判定 性质
线面平行
转化思想、“降维”与“升维”思想
第13页/共16页
课后作业
1、已知直线 a,b,c,平面 α,β,则下列正确的是( D)
ab A
∥
a ,b
∥
a
a∥b
b
简记:线面平行,则面面平行 简记:面面平行,则线线平行
第2页/共16页
5、如果两个平面平行,那么一个平面内的 直线与另一个平面有什么位置关系?
a //
a //
a
简记:面面平行,则线面平行.
第3页/共16页
基础练习
1、下面说法正确的有___(_4__)_(_5__)_.
课件1:线面、面面平行的判定与性质

又 DG⊄平面 AMC,FM⊂平面 AMC, ∴DG∥平面 AMC. 连结 GN,则 GN∥MC,GN⊄平面 AMC, MC⊂平面 AMC. ∴GN∥平面 AMC, 又 GN∩DG=G, ∴平面 DNG∥平面 AMC, 又 DN⊂平面 DNG, ∴DN∥平面 AMC.
[典例] (2013·陕西高考)如图,四棱柱 ABCD -A1B1C1D1 的底面 ABCD 是正方形,O 是底面中心, A1O⊥底面 ABCD, AB=AA1= 2.
(1)平面 AD1E∥平面 BGF; (2)D1E⊥AC.
证明:(1)∵E,F 分别是 B1B 和 D1D 的中点,
∴D1F 綊 BE.
∴四边形 BED1F 是平行四边形,∴D1E∥BF; 又∵D1E⊄平面 BGF,BF⊂平面 BGF, ∴D1E∥平面 BGF. ∵FG 是△DAD1 的中位线,∴FG∥AD1; 又 AD1⊄平面 BGF,FG⊂平面 BGF,
[类题通法] 判断面面平行的常用方法
(1)利用面面平行的判定定理; (2)面面平行的传递性(α∥β,β∥γ⇒α∥γ); (3)利用线面垂直的性质(l⊥α,l⊥β⇒α∥β).
[针对训练] 如图,在直四棱柱 ABCD -A1B1C1D1 中,底面是正方形,E,F, G 分别是棱 B1B,D1D,DA 的中点.求证:
2.(2014·济宁模拟)过三棱柱 ABC -A1B1C1 的任意两条棱的中 点作直线,其中与平面 ABB1A1 平行的直线共有________条. 解析:过三棱柱 ABC -A1B1C1 的任意两条棱的中点作直线, 记 AC,BC,A1C1,B1C1 的中点分别为 E,F,E1,F1,则 直线 EF,E1F1,EE1,FF1,E1F,EF1 均与平面 ABB1A1 平 行,故符合题意的直线共 6 条. 答案:6
《直线与平面平行》课件

的稳定性和美观性。
02
建筑测量
在建筑测量中,直线与平面平行的概念对于确定建筑物是否垂直和水平
非常重要。测量师使用铅锤和水平仪等工具来确保建筑物的基础、柱子
和横梁等结构与地面平行。
03
建筑结构分析
在建筑结构分析中,直线与平面平行的概念对于评估结构的稳定性和安
全性至关重要。工程师使用这些概念来分析建筑物的支撑结构和受力情
电子设备制造
在电子设备制造中,直线与平面平行的概念对于确保电子设备的精确度和质量非常重要。制造商使用这些概念来控制 装配和焊接过程,以确保电子元件的放置和连接正确。
电子设备维修
在电子设备维修中,直线与平面平行的概念对于检查和调整电子元件的位置非常重要。维修人员使用这 些概念来检查设备的平行度和垂直度,以确保设备的正常运行和性能。
文字描述
如果一条直线与一个平面平行, 那么这条直线与此平面内的任何 直线都平行。
解释
这个定理说明了直线与平面平行 的条件,即直线必须与平面内的 所有直线都平行,才能判定该直 线与该平面平行。
直线与平面平行判定定理的数学公式
数学公式
若直线$l$与平面$alpha$平行,则对于任意直线$m$在平面$alpha$上,都有 $l parallel m$。
02
若直线$l$与平面$alpha$平行, 则对于任意点$P$在平面$alpha$ 上,有$l cap P = emptyset$。
直线与平面平行性质定理的图形解释
当直线与平面平行时,该直线与平面 内的所有直线都保持平行关系,没有 交点。
在图形中,可以标出一些具体的点来 解释该性质定理,例如选择平面上的 一些点并观察它们是否与直线有交点 。
可以通过作一条与已知直线平行的直 线来验证该性质定理,观察新作的直 线是否与平面内的其他直线平行且无 交点。
线面平行(一)ppt课件

H
E
D
B
G
F
C
31
习题课
6.P为平行四边形ABCD所在平面外一点,M、N 分 别为AB、PC 的中点,平面PAD 平PBC =L
求证:(1)BC // L
P
(2)MN //平面PAD
L
E
N
D C
A
M
B
32
习题课
7. 如图,ABCD与ABEF是两个全等正方形,
AM=NF,
D
C
求证:MN // 平面BCE
B E
18
小结:
∪∪
1、直线和平面平行的判定定理
aα
bα a∥ b
a∥ α
2、解题技巧和规律 ①由线线平行得出线面平行;②解题时要注意
关注复杂图形中定理的基本图形;③解题时要充分 注意三角形的中位线,成比例线段(辅助线),过 直线的平面(辅助面),以促进问题的解决。
19
例3.已知P是平行四边形ABCD所在平面外一点,
(√ )
11
三、直线和平面平行的性质
直线和平面平行的性质定理:如果一条直线 和一个平面平行,经过这条直线的平面和这 个平面相交,那么这条直线和交线平行.
已知:a//,a,=b
求证:a//b
a
线面平行线线平行
b
12
性质定理证明
性质定理: 如果一条直线和一个平面平行,经过这条 直线的平面和这个平面相交,那么这条直 线和交线平行.
求证:a∥b
证明:过a做平面 c
d
∵a∥α∴a//c 同理可证a//d
c
∴c∥d
α
∵c ,d ∴c//β
b
a
δ
d
第八章 第三节 直线、平面平行的判定与性质 课件(共58张PPT)

第八章 立体几何初步
第三节 直线、平面平行的判定与性质
栏目一 知识·分步落实 栏目二 考点·分类突破 栏目三 微专题系列
栏目导引
课程标准
考向预测
1.以立体几何的定义、公理和定理为
出发,借助长方体,通过直观感知, 考情分析: 直线与平面以及平面与
了解空间中线面平行的有关性质与 平面平行的判定和性质仍会是高考
所以 A1G 綊 EB,所以四边形 A1EBG 是平行四边形,
所以 A1E∥GB. 因为 A1E⊄平面 BCHG,GB⊂平面 BCHG, 所以 A1E∥平面 BCHG. 又因为 A1E∩EF=E,所以平面 EFA1∥平面 BCHG.
1.如图,平面 α∥平面 β,△PAB 所在的平面与 α,β分别交于 CD,AB,
平行命题的判断 (1)解决与平行相关命题的判断问题,以与平行相关的判定定理和性质定 理为依据,注意定理中相关条件的检验,必须进行严密的逻辑推理. (2)如果判断某个命题错误,则往往利用正方体或其他几何体作为模型构 造反例说明.
直线与平面平行的判定与性质 角度一 直线与平面平行的判定
如图所示,斜三棱柱 ABC-A1B1C1 中,点 D,D1 分别为 AC,A1C1 的中点.求证:
BC∥平面ADF
BC⊂平面BCPQ
⇒BC∥PQ.
平面BCPQ∩平面ADF=PQ
PQ∥BC
PQ⊄平面ABCD PQ∥平面 ABCD.
BC⊂平面ABCD
应用线面平行的性质定理的关键是确定交线的位置,有时 需要经过已知直线作辅助平面来确定交线.该定理的作用是由线面平行转化 为线线平行.
1.(2020·深圳市统一测试)如图,在直四棱柱 ABCD-A1B1C1D1 中,底面 ABCD 是平行四边形,点 M,
第三节 直线、平面平行的判定与性质
栏目一 知识·分步落实 栏目二 考点·分类突破 栏目三 微专题系列
栏目导引
课程标准
考向预测
1.以立体几何的定义、公理和定理为
出发,借助长方体,通过直观感知, 考情分析: 直线与平面以及平面与
了解空间中线面平行的有关性质与 平面平行的判定和性质仍会是高考
所以 A1G 綊 EB,所以四边形 A1EBG 是平行四边形,
所以 A1E∥GB. 因为 A1E⊄平面 BCHG,GB⊂平面 BCHG, 所以 A1E∥平面 BCHG. 又因为 A1E∩EF=E,所以平面 EFA1∥平面 BCHG.
1.如图,平面 α∥平面 β,△PAB 所在的平面与 α,β分别交于 CD,AB,
平行命题的判断 (1)解决与平行相关命题的判断问题,以与平行相关的判定定理和性质定 理为依据,注意定理中相关条件的检验,必须进行严密的逻辑推理. (2)如果判断某个命题错误,则往往利用正方体或其他几何体作为模型构 造反例说明.
直线与平面平行的判定与性质 角度一 直线与平面平行的判定
如图所示,斜三棱柱 ABC-A1B1C1 中,点 D,D1 分别为 AC,A1C1 的中点.求证:
BC∥平面ADF
BC⊂平面BCPQ
⇒BC∥PQ.
平面BCPQ∩平面ADF=PQ
PQ∥BC
PQ⊄平面ABCD PQ∥平面 ABCD.
BC⊂平面ABCD
应用线面平行的性质定理的关键是确定交线的位置,有时 需要经过已知直线作辅助平面来确定交线.该定理的作用是由线面平行转化 为线线平行.
1.(2020·深圳市统一测试)如图,在直四棱柱 ABCD-A1B1C1D1 中,底面 ABCD 是平行四边形,点 M,
直线与平面平行的判定定理(公开课)ppt课件

若两向量的点积为零,则 它们垂直。
应用
通过计算直线方向向量与 平面法向量的点积,可以 判断直线与平面是否平行 。
判定定理三:法向量垂直
定义
若一直线与一平面平行, 则该直线的法向量与该平 面的法向量平行。
推论
若两向量平行,则它们的 分量成比例。
应用
通过比较直线法向量与平 面法向量的分量比例,可 以判断直线与平面是否平 行。
直线与平面平行的定义
阐述直线与平面平行的基本概念,为后续判定定理 的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和 作用,以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理 及其证明方法,理解相关概念, 能够运用所学知识解决相关问题 。
100%
过程与方法
应用举例二:判断两平面是否平行
方法一
利用平行平面的性质,通过证明一个 平面内有两条相交直线分别与另一个 平面平行,从而判定两个平面平行。
方法二
利用向量法,通过计算两个平面的法 向量是否共线,从而判定两个平面是 否平行。
应用举例三:解决实际问题中的平行问题
1 2
实例一
在建筑设计中,利用直线与平面平行的性质,确 保建筑物的立面、地面等各部分保持平行,以达 到美观和稳定的效果。
定义
应用
若一直线与一平面平行,则该直线与 该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜 率,可以判断直线与平面是否平行。
推论
若两直线的斜率相等,则它们或者平 行或者重合。
判定定理二:方向向量平行
01
02
03
定义
若一直线与一平面平行, 则该直线的方向向量与该 平面的法向量垂直。
应用
通过计算直线方向向量与 平面法向量的点积,可以 判断直线与平面是否平行 。
判定定理三:法向量垂直
定义
若一直线与一平面平行, 则该直线的法向量与该平 面的法向量平行。
推论
若两向量平行,则它们的 分量成比例。
应用
通过比较直线法向量与平 面法向量的分量比例,可 以判断直线与平面是否平 行。
直线与平面平行的定义
阐述直线与平面平行的基本概念,为后续判定定理 的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和 作用,以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理 及其证明方法,理解相关概念, 能够运用所学知识解决相关问题 。
100%
过程与方法
应用举例二:判断两平面是否平行
方法一
利用平行平面的性质,通过证明一个 平面内有两条相交直线分别与另一个 平面平行,从而判定两个平面平行。
方法二
利用向量法,通过计算两个平面的法 向量是否共线,从而判定两个平面是 否平行。
应用举例三:解决实际问题中的平行问题
1 2
实例一
在建筑设计中,利用直线与平面平行的性质,确 保建筑物的立面、地面等各部分保持平行,以达 到美观和稳定的效果。
定义
应用
若一直线与一平面平行,则该直线与 该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜 率,可以判断直线与平面是否平行。
推论
若两直线的斜率相等,则它们或者平 行或者重合。
判定定理二:方向向量平行
01
02
03
定义
若一直线与一平面平行, 则该直线的方向向量与该 平面的法向量垂直。
线线平行线面平行面面平行习题课ppt课件

A F
D1
B
M E
C1
A1
B1
•
2、空间四边形ABCD被一平面所截,E、F、G、H 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
分别
• 在AC、CB、BD、DA上,截面EFGH是矩形.
• (1) 求证: CD // 平面EFGH;
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其Байду номын сангаас 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1. 如图 , 正方体 AC1 中,点N在 BD上,点M在B1 C上 且CM = DN, 求证: MN // 平面AA1B1B .
D
C
N
=L
P
• 求证: (1)BC // L
•
(2)MN //平面PAD E
N
L
D C
A
M
B
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
4、如图,ABCD与ABEF是两个全等正方形,AM=NF,
• (2) 求异面直线AB、ACD 所成的角.
H
E
D
B
G
F
C
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
• 3、如图所示, P为平行四边形ABCD所在平面外一点,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)平面EFA1∥平面BCHG.
.
课堂小结
1、证明线面平行的方法: (1)定义法;(2)判定定理;(3)面面平行得线面平行 其中判定定理的运用关键是在平面内找一条线与已知直线平 行,可构造中位线或平行四边线。 2、线面平行怎么用?
找已知直线所在平面与已知平面的交线。
3、证明面面平行的方法: (1)定义法;(2)判定定理; (3)垂直于同一直线的两个平面平行; (4)两个平面同时与第三个平面平行,则这两个平面平行。 4、面面平行怎么用? (1)线面平行;(2)线线平行;(关键找交线) 5、区分判定定理与性质定理。 .
(2)判定定理:a⊂α,b⊂α, a∩b=A,a∥β,b∥β⇒
; //
(3)推论:a∩b=A,a,b⊂α,a′∩b′=A′,
a′,b′⊂β,a∥a′,b∥b′⇒____/_/ _.
.
复习回顾
6.两个平面平行的性质定理
(1)α∥β,a⊂α⇒_____a_/_/ ; (2)α∥β,γ∩α=a,γ∩β=b⇒_______. a // b
解:当F是棱PC的中点时,BF∥. 平面AEC.
课堂练习
1.下列条件能证明两平面平行的有___③__④_____。
①若一个平面内有两条直线与另一个平面平行; ②若一个平面内有无数条直线与另一个平面平行; ③若一个平面内任一条直线都平行于另一个平面; ④若一个平面内的两条相交直线都平行另一个平面
.
课堂练习
(2)判定定理:a⊄α,b⊂α,且a∥b⇒_____a_/;/
(3)其他判定方法:α∥β,a⊂α⇒_____a__/ /_.
.
复习回顾
3.直线和平面平行的性质定理:a∥α,a⊂β,α∩β=m⇒a_____m.
4.两个平∥面的位置关系有_平__行__、_相__交__.
5.两个平面平行的判定
(1)定义:__两__个__平__面__没__有__公__共__点___,称这两个平面平行;
2.2 线面平行、面面平行 的判定及其性质 习题课
➢线面平行、面面平行的判定 ➢线面平1】正方形ABCD与正方形ABEF所在平面相交于 AB,在AE, BD上各有一点P, Q,且AP=DQ. 求证: PQ∥平面BCE.
证明:方法一如图, 作PM∥AB交BE 于M, 作QN∥AB交BC于N,连接MN.
2.空间中,下列命题正确的是( D ).
A.若a∥α,b∥a,则b∥α B.若a∥α,b∥α,a⊂β,b⊂β,则β∥α C.若α∥β,b∥α,则b∥β D.若α∥β,a⊂α,则a∥β
.
课堂练习
3、如图,在三棱柱ABC—A1B1C1中,E,F,G, H
分别是AB,AC,A1B1,A1C1的中点, 求证:(1)B,C,H,G四点共面;
7.与垂直相关的平行的判定 (1)a⊥α,b⊥α⇒____a_/_/ _b _;
(2)a⊥α,a⊥β⇒_____/_/ ___.
.
思考题
如图所示,四边形ABCD是平行四边形,点P是平面ABCD外 一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平 面BDM于GH.求证:AP∥GH.
证明:如图所示,连接AC交BD于点O,连. 接MO.
复习回顾
1. 直线与平面的位置关系 直线 a 和平面α的位置关系有_平__行__、_相__交__、 _在__平__面___内,其中平__行__ 与_相__交__统称直线在平面外. 2. 直线和平面平行的判定 (1)定义:_直__线__和__平__面__没__有__公__共__点____, 则称直线 平行于平面;
.
例题剖析
方法二:如图,连接 AQ,并延长交 BC 延长线于 K, 连接 EK.
.
例题剖析
方法三:在平面 ABEF 内,过点 P 作 PM∥BE .
.
例题剖析
【例2】 如图,在底面是平行四边形的四棱锥P-ABCD 中,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一 点F,使BF∥平面AEC?证明你的结论.
.
课堂小结
1、证明线面平行的方法: (1)定义法;(2)判定定理;(3)面面平行得线面平行 其中判定定理的运用关键是在平面内找一条线与已知直线平 行,可构造中位线或平行四边线。 2、线面平行怎么用?
找已知直线所在平面与已知平面的交线。
3、证明面面平行的方法: (1)定义法;(2)判定定理; (3)垂直于同一直线的两个平面平行; (4)两个平面同时与第三个平面平行,则这两个平面平行。 4、面面平行怎么用? (1)线面平行;(2)线线平行;(关键找交线) 5、区分判定定理与性质定理。 .
(2)判定定理:a⊂α,b⊂α, a∩b=A,a∥β,b∥β⇒
; //
(3)推论:a∩b=A,a,b⊂α,a′∩b′=A′,
a′,b′⊂β,a∥a′,b∥b′⇒____/_/ _.
.
复习回顾
6.两个平面平行的性质定理
(1)α∥β,a⊂α⇒_____a_/_/ ; (2)α∥β,γ∩α=a,γ∩β=b⇒_______. a // b
解:当F是棱PC的中点时,BF∥. 平面AEC.
课堂练习
1.下列条件能证明两平面平行的有___③__④_____。
①若一个平面内有两条直线与另一个平面平行; ②若一个平面内有无数条直线与另一个平面平行; ③若一个平面内任一条直线都平行于另一个平面; ④若一个平面内的两条相交直线都平行另一个平面
.
课堂练习
(2)判定定理:a⊄α,b⊂α,且a∥b⇒_____a_/;/
(3)其他判定方法:α∥β,a⊂α⇒_____a__/ /_.
.
复习回顾
3.直线和平面平行的性质定理:a∥α,a⊂β,α∩β=m⇒a_____m.
4.两个平∥面的位置关系有_平__行__、_相__交__.
5.两个平面平行的判定
(1)定义:__两__个__平__面__没__有__公__共__点___,称这两个平面平行;
2.2 线面平行、面面平行 的判定及其性质 习题课
➢线面平行、面面平行的判定 ➢线面平1】正方形ABCD与正方形ABEF所在平面相交于 AB,在AE, BD上各有一点P, Q,且AP=DQ. 求证: PQ∥平面BCE.
证明:方法一如图, 作PM∥AB交BE 于M, 作QN∥AB交BC于N,连接MN.
2.空间中,下列命题正确的是( D ).
A.若a∥α,b∥a,则b∥α B.若a∥α,b∥α,a⊂β,b⊂β,则β∥α C.若α∥β,b∥α,则b∥β D.若α∥β,a⊂α,则a∥β
.
课堂练习
3、如图,在三棱柱ABC—A1B1C1中,E,F,G, H
分别是AB,AC,A1B1,A1C1的中点, 求证:(1)B,C,H,G四点共面;
7.与垂直相关的平行的判定 (1)a⊥α,b⊥α⇒____a_/_/ _b _;
(2)a⊥α,a⊥β⇒_____/_/ ___.
.
思考题
如图所示,四边形ABCD是平行四边形,点P是平面ABCD外 一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平 面BDM于GH.求证:AP∥GH.
证明:如图所示,连接AC交BD于点O,连. 接MO.
复习回顾
1. 直线与平面的位置关系 直线 a 和平面α的位置关系有_平__行__、_相__交__、 _在__平__面___内,其中平__行__ 与_相__交__统称直线在平面外. 2. 直线和平面平行的判定 (1)定义:_直__线__和__平__面__没__有__公__共__点____, 则称直线 平行于平面;
.
例题剖析
方法二:如图,连接 AQ,并延长交 BC 延长线于 K, 连接 EK.
.
例题剖析
方法三:在平面 ABEF 内,过点 P 作 PM∥BE .
.
例题剖析
【例2】 如图,在底面是平行四边形的四棱锥P-ABCD 中,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一 点F,使BF∥平面AEC?证明你的结论.
