半导体材料能带测试及计算
半导体导电类型

图 2 四探针法测量半导体电阻率示意图
数载流子寿命的方法有多种,广泛应用的是交流光电导衰退法,简便迅速,测量范围为 10~103μ s。,适
合于锗、硅材料。半导体材料电学参数测量方法列于表 3 中。
表 3 半导体材料电学参数测量方法
测试项目 导电
测量方法 (1)冷热探笔法
对象和特点
适用于电阻率不太高的材料,硅<100Ω cm;锗<20Ω cm 不适于低阻材料,硅,l~100Ω cm;锗,不适用。
半导体材料电学参数测量(electric parameter measurement for semiconductor material)
电学参数是半导体材料钡 0 量的重要内容。它主要包括导电类型、电阻率、寿命和迁 移率测量。
导电类型测量 半导体的导电过程存在电子和空穴两种载流子。多数载流子是电子 的称 n 型半导体;多数载流子是空穴的称 p 型半导体。测量导电类型就是确定半导体材料中 多数载流子的类别。常用的方法有冷热探针法、整流法等。冷热探针法是利用温差电效应的 原理,将两根温度不同的探针与半导体材料表面接触,两探针间外接检流计(或数字电压表) 形成一闭合回路,根据两个接触点处存在温差所引起的温差电流(或温差电压)的方向可以确 定导电类型。整流法是利用金属探针与半导体材料表面容易构成整流接触的特点,可根据检 流计的偏转方向或示波器的波形测定导电类型。常用三探针或四探针实现整流接触。霍耳效 应亦可测定半导体材料的导电类型。
半导体能带结构调控方法创新与电子器件性能提升测试

半导体能带结构调控方法创新与电子器件性能提升测试半导体材料作为现代电子器件的基础,其能带结构的调控对于电子器件的性能提升至关重要。
随着科学技术的不断发展,研究者们不断探索新的方法和技术来创新半导体能带结构调控方法,并进一步提升电子器件的性能。
半导体能带结构是指半导体材料内部价带和导带之间的能量差,也就是带隙。
通过调控半导体材料的能带结构,可以实现对电子束缚能级和载流子的控制,从而改变电子器件的性能。
近年来,研究者们提出了许多创新的半导体能带结构调控方法。
其中一种方法是通过掺杂调控来改变半导体的能带结构。
掺杂是将外界原子或离子引入到半导体材料中,通过改变原子的种类和掺杂浓度,可以有效地改变半导体的能带结构。
例如,通过掺杂氮原子可以减小半导体的带隙,使得半导体在可见光范围内具有吸收和发射光的能力,从而应用于光电器件领域。
另一种创新的方法是通过量子结构调控半导体的能带结构。
量子结构是指具有特定尺寸和形状的低维结构,如量子点、量子线和量子阱。
由于量子结构的尺寸效应和限制效应,其能带结构与体块材料存在差异。
通过调控量子结构的尺寸和形态,可以实现对半导体的能带结构调控。
例如,在量子点结构中,由于量子限制效应的作用,载流子的能级被束缚在量子点中,从而实现了光电器件的高效率转换。
此外,研究者还通过使用外加电场和外加应力等方法,来实现对半导体能带结构的调控。
外加电场可以改变半导体材料中电子和空穴的分布情况,从而改变半导体的能带结构。
外加应力可以改变半导体材料的晶格结构,从而调控能带结构。
通过这些方法,不仅可以改变半导体的能带结构,还可以调控其光电特性和电子输运性能。
针对半导体能带结构调控方法的创新,研究者们也开展了大量的电子器件性能提升测试。
其中,性能提升主要包括以下方面:首先是电子器件的速度提升。
通过调控半导体的能带结构,可以实现载流子的高速移动,从而提高电子器件的工作速度。
例如,在场效应晶体管中,通过调控材料的能带结构,可以增加载流子的迁移率,从而提高晶体管的开关速度。
半导体材料能带测试及计算
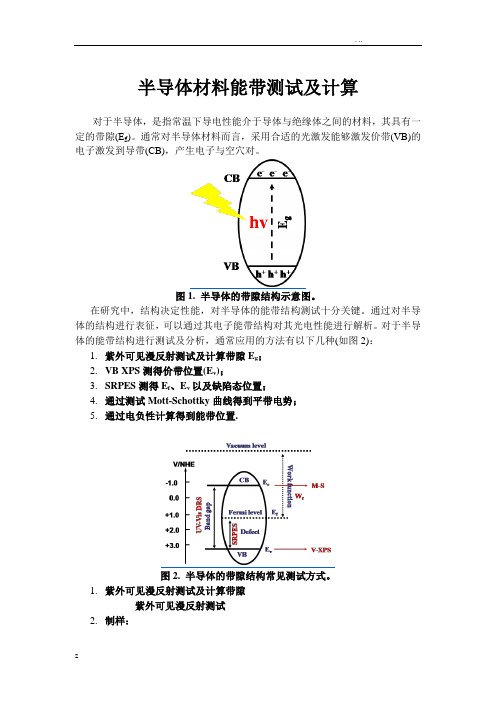
半导体材料能带测试及计算对于半导体,是指常温下导电性能介于导体与绝缘体之间的材料,其具有一定的带隙(E g)。
通常对半导体材料而言,采用合适的光激发能够激发价带(VB)的电子激发到导带(CB),产生电子与空穴对。
图1. 半导体的带隙结构示意图。
在研究中,结构决定性能,对半导体的能带结构测试十分关键。
通过对半导体的结构进行表征,可以通过其电子能带结构对其光电性能进行解析。
对于半导体的能带结构进行测试及分析,通常应用的方法有以下几种(如图2):1.紫外可见漫反射测试及计算带隙E g;2.VB XPS测得价带位置(E v);3.SRPES测得E f、E v以及缺陷态位置;4.通过测试Mott-Schottky曲线得到平带电势;5.通过电负性计算得到能带位置.图2. 半导体的带隙结构常见测试方式。
1.紫外可见漫反射测试及计算带隙紫外可见漫反射测试2.制样:背景测试制样:往图3左图所示的样品槽中加入适量的BaSO4粉末(由于BaSO4粉末几乎对光没有吸收,可做背景测试),然后用盖玻片将BaSO4粉末压实,使得BaSO4粉末填充整个样品槽,并压成一个平面,不能有凸出和凹陷,否者会影响测试结果。
样品测试制样:若样品较多足以填充样品槽,可以直接将样品填充样品槽并用盖玻片压平;若样品测试不够填充样品槽,可与BaSO4粉末混合,制成一系列等质量分数的样品,填充样品槽并用盖玻片压平。
图3. 紫外可见漫反射测试中的制样过程图。
1.测试:用积分球进行测试紫外可见漫反射(UV-Vis DRS),采用背景测试样(BaSO4粉末)测试背景基线(选择R%模式),以其为background测试基线,然后将样品放入到样品卡槽中进行测试,得到紫外可见漫反射光谱。
测试完一个样品后,重新制样,继续进行测试。
•测试数据处理数据的处理主要有两种方法:截线法和Tauc plot法。
截线法的基本原理是认为半导体的带边波长(λg)决定于禁带宽度E g。
(完整版)半导体材料光学带隙的计算

半导体材料光学带隙的计算禁带宽度是半导体的一个重要特征参量,其大小主要决定于半导体的能带结构,即与晶体结构和原子的结合性质等有关。
禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量,也就是产生本征激发所需要的最小能量。
禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值,用光谱测试法测得的禁带宽度值又叫作光学带隙。
下面以光谱测试法为例介绍半导体材料光学带隙的计算方法:对于半导体材料,其光学带隙和吸收系数之间的关系式为[1]:αhν=B(hν-Eg)m (1)其中α为摩尔吸收系数,h为普朗克常数,ν为入射光子频率, B 为比例常数,Eg为半导体材料的光学带隙,m的值与半导体材料以及跃迁类型相关:(1)当m=1/2 时,对应直接带隙半导体允许的偶极跃迁;(2)当m=3/2 时,对应直接带隙半导体禁戒的偶极跃迁;(3)当m=2 时,对应间接带隙半导体允许的跃迁;(4)当m=3 时,对应间接带隙半导体禁戒的跃迁。
下面介绍两种禁带宽度计算公式的推导方法:推导1:根据朗伯比尔定律可知:A=αb c (2)其中 A 为样品吸光度,b 为样品厚度,c 为浓度,其中bc 为一常数,若B1=(B/bc)1/m,则公式(1)可为:(Ahν)1/m=B1(hν-Eg) (3)根据公式(3),若以hν 值为x 轴,以(Ahν)1/m 值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
推导2:根据K-M 公式可知:F(R∞)=(1- R∞)2/2 R∞=K/S (4)其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2]),K 为吸收系数,S 为散射系数。
若假设半导体材料分散完全或者将样品置于600入射光持续光照下可认为K=2α[3]。
因在一定温度下样品散射系数为一常数,假设比例常数为B2,,我们可通过公式(4)和公式(1)可得:(F(R∞) hν)1/m=B2(hν-Eg) (5)根据公式(5),若以hν 值为x 轴,以(F(R∞) hν)1/m值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
半导体基础实验报告

竭诚为您提供优质文档/双击可除半导体基础实验报告篇一:半导体物理实验报告电子科技大学半导体物理实验报告姓名:艾合麦提江学号:20XX033040008班级:固电四班实验一半导体电学特性测试测量半导体霍尔系数具有十分重要的意义。
根据霍尔系数的符号可以判断材料的导电类型;根据霍尔系数及其与温度的关系,可以计算载流子的浓度,以及载流子浓度同温度的关系,由此可确定材料的禁带宽度和杂质电离能;通过霍尔系数和电阻率的联合测量.能够确定我流子的迁移约用微分霍尔效应法可测纵向载流子浓度分布;测量低温霍尔效应可以确定杂质补偿度。
霍尔效应是半导体磁敏器件的物理基础。
1980年发现的量子霍尔效应对科技进步具有重大意义。
早期测量霍尔系数采用矩形薄片样品.以及“桥式”样品。
1958年范德堡提出对任意形状样品电阻率和霍尔系数的测量方法,这是一种有实际意义的重要方法,目前已被广泛采用。
本实验的目的使学生更深入地理解霍尔效应的原理,掌握霍尔系数、电导率和迁移率的测试方法,确定样品的导电类型。
一、实验原理如图,一矩形半导体薄片,当沿其x方向通有均匀电流I,沿Z方向加有均匀磁感应强度的磁场时,则在y方向上产生电势差。
这种想象叫霍尔效应。
所生电势差用Vh表示,成为霍尔电压,其相应的电场称为霍尔电场ey。
实验表明,在弱磁场下,ey同J(电流密度)和b成正比ey=RhJb(1)式中Rh为比例系数,称为霍尔系数。
在不同的温度范围,Rh有不同的表达式。
在本征电离完全可以忽略的杂质电离区,且主要只有一种载流子的情况,当不考虑载流子速度的统计分布时,对空穴浓度为p的p型样品Rh?1?0(2)pq式中q为电子电量。
对电子浓度为n的n型样品Rh??1?0nq(3)当考虑载流子速度的统计分布时,式(2)、(3)应分别修改为??h?1??h?1Rh??Rh???pqnq??p??n(4)式中μh为霍尔迁移率。
μ为电导迁移率。
对于简单能带结构??h?(5)h??h?p??nγh称为霍尔因子,其值与半导体内的散射机制有关,对晶格散射γh=3π/8=1.18;对电离杂质散射γh=315π/512=1.93,在一般粗略计算中,γh可近似取为1.在半导体中主要由一种载流子导电的情况下,电导率为?n?nq?n和?p?pq?p(6)由(4)式得到Rh?ph?p和Rh?nh?n(7)测得Rh和σ后,μh为已知,再由μ(n,T)实验曲线用逐步逼近法查得μ,即可由式(4)算得n或p。
半导体材料中的能带结构和载流子输运机制

半导体材料中的能带结构和载流子输运机制半导体材料在现代科技中扮演着至关重要的角色,广泛应用于电子器件、光电子器件等领域。
要理解半导体材料的性质和性能,我们需要研究半导体材料中的能带结构和载流子输运机制。
一、能带结构能带结构是描述物质中电子能级分布的一种模型。
对于半导体材料来说,能带结构由价带和导带组成。
1. 价带:价带是能量较低的带,其中填满了电子。
在固体中,原子间的电子交互作用使得原子能级分裂成离散的能带,在固体中表现为连续的能量带。
价带中的电子处于较稳定的状态,不易被激发到导带。
2. 导带:导带是能量较高的带,其中没有电子。
当外界能量作用于原子或者晶格时,电子可获得足够的能量从价带跃迁到导带。
导带中的电子具有较高的能量,容易参与导电过程。
半导体的能带结构与金属和绝缘体有所不同。
金属中,价带与导带重叠,使得电子能够自由移动,导电性能好;而绝缘体中,价带与导带之间存在较大的能隙,电子能量不足以跃迁到导带,因此其导电性能很差。
半导体的能带结构介于金属和绝缘体之间,存在较小的能隙,能够通过适当的能量激发将电子从价带跃迁到导带,从而实现电子的导电。
二、载流子输运机制载流子是指电子和空穴,它们是半导体材料中的导电粒子。
载流子的输运过程影响着半导体材料的导电性能。
1. 电子输运:电子由外界电场驱动,从一个位置向另一个位置移动。
在半导体中,电子的输运通常分为漂移和扩散两种情况。
漂移是指电场作用下,电子沿着电场方向移动,与杂质或晶格碰撞,导致速度减小;扩散是指电子在浓度梯度作用下,从高浓度区域向低浓度区域扩散。
电子输运的基本原理可以用经典电动力学和半导体物理学中的牛顿第二定律和欧姆定律描述。
2. 空穴输运:空穴是电子跃迁到导带中留下的一个“空位”,在半导体材料中的移动过程也被称为空穴的输运。
空穴的运动类似于正电荷的运动。
当外界电场作用于半导体材料时,空穴会受到电场力的驱动,从一个位置移动到另一个位置。
空穴的输运过程中,同样存在漂移和扩散两种情况。
半导体材料光学带隙的计算

半导体材料光学带隙的计算禁带宽度是半导体的一个重要特征参量,其大小主要决定于半导体的能带结构,即与晶体结构和原子的结合性质等有关。
禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量,也就是产生本征激发所需要的最小能量。
禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值,用光谱测试法测得的禁带宽度值又叫作光学带隙。
下面以光谱测试法为例介绍半导体材料光学带隙的计算方法:对于半导体材料,其光学带隙和吸收系数之间的关系式为[1]:αhν=B(hν-Eg)m (1)其中α为摩尔吸收系数,h为普朗克常数,ν为入射光子频率, B 为比例常数,Eg为半导体材料的光学带隙,m的值与半导体材料以及跃迁类型相关:(1)当m=1/2 时,对应直接带隙半导体允许的偶极跃迁;(2)当m=3/2 时,对应直接带隙半导体禁戒的偶极跃迁;(3)当m=2 时,对应间接带隙半导体允许的跃迁;(4)当m=3 时,对应间接带隙半导体禁戒的跃迁。
下面介绍两种禁带宽度计算公式的推导方法:推导1:根据朗伯比尔定律可知:A=αb c (2)其中 A 为样品吸光度,b 为样品厚度,c 为浓度,其中bc 为一常数,若B1=(B/bc)1/m,则公式(1)可为:(Ahν)1/m=B1(hν-Eg) (3)根据公式(3),若以hν 值为x 轴,以(Ahν)1/m 值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
推导2:根据K-M 公式可知:F(R∞)=(1- R∞)2/2 R∞=K/S (4)其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2]),K 为吸收系数,S 为散射系数。
若假设半导体材料分散完全或者将样品置于600入射光持续光照下可认为K=2α[3]。
因在一定温度下样品散射系数为一常数,假设比例常数为B2,,我们可通过公式(4)和公式(1)可得:(F(R∞) hν)1/m=B2(hν-Eg) (5)根据公式(5),若以hν 值为x 轴,以(F(R∞) hν)1/m值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
实验5-1 半导体激光器的特性测试实验

光信息专业实验指导材料(试用)实验5-1 半导体激光器的特性测试[实验目的]1、通过测量半导体激光器工作时的功率、电压、电流,画出P-V、P-I、I-V曲线,让学生了解半导体的工作特性曲线;2、学会通过曲线计算半导体激光器的阈值,以及功率效率,外量子效率和外微分效率,并对三者进行比较;3、内置四套方波信号或者外加信号直接调制激光器,通过调整不同的静态工作点,和输入信号强度大小不同,观察到截至区,线性区,限流区的信号不同响应(信号畸变,线性无畸变),了解调制工作原理。
[实验仪器]实验室提供:半导体激光器实验箱(内置三个半导体激光器),示波器,两根电缆线。
[实验原理]半导体激光器是用半导体材料作为工作物质的一类激光器,由于物质结构上的差异,产生激光的具体过程比较特殊。
常用材料有砷化镓(GaAs)、硫化镉(CdS)、磷化铟(InP)、硫化锌(ZnS)等。
激励方式有电注入、电子束激励和光泵浦三种形式。
半导体激光器件,可分为同质结、单异质结、双异质结等几种。
同质结激光器和单异质结激光器室温时多为脉冲器件,而双异质结激光器室温时可实现连续工作。
半导体激光器具有体积小、效率高等优点,广泛应用于激光通信、印刷制版、光信息处理等方面。
一、半导体激光器的结构与工作原理1.半导体激光器的工作原理。
半导体材料多是晶体结构。
当大量原子规则而紧密地结合成晶体时,晶体中那些价电子都处在晶体能带上。
价电子所处的能带称价带(对应较低能量)。
与价带对应的高能带称导带,价带与导带之间的空域称为禁带。
当加外电场时,价带中电子跃迁到导带中去,在导带中可以自由运动而起导电作用。
同时,价带中失掉一个电子,相当于出现一个带正电的空穴,这种空穴在外电场的作用下,也能起导电作用。
因此,价带中空穴和导带中的电子都有导电作用,统称为载流子。
没有杂质的纯净半导体,称为本征半导体。
如果在本征半导体中掺入杂质原子,则在导带之下和价带之上形成了杂质能级,分别称为施主能级和受主能级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半导体材料能带测试及计算对于半导体,是指常温下导电性能介于导体与绝缘体之间的材料,其具有一定的带隙(E g)。
通常对半导体材料而言,采用合适的光激发能够激发价带(VB)的电子激发到导带(CB),产生电子与空穴对。
图1. 半导体的带隙结构示意图。
在研究中,结构决定性能,对半导体的能带结构测试十分关键。
通过对半导体的结构进行表征,可以通过其电子能带结构对其光电性能进行解析。
对于半导体的能带结构进行测试及分析,通常应用的方法有以下几种(如图2):1.紫外可见漫反射测试及计算带隙E g;2.VB XPS测得价带位置(E v);3.SRPES测得E f、E v以及缺陷态位置;4.通过测试Mott-Schottky曲线得到平带电势;5.通过电负性计算得到能带位置.图2. 半导体的带隙结构常见测试方式。
1.紫外可见漫反射测试及计算带隙紫外可见漫反射测试2.制样:背景测试制样:往图3左图所示的样品槽中加入适量的BaSO4粉末(由于BaSO4粉末几乎对光没有吸收,可做背景测试),然后用盖玻片将BaSO4粉末压实,使得BaSO4粉末填充整个样品槽,并压成一个平面,不能有凸出和凹陷,否者会影响测试结果。
样品测试制样:若样品较多足以填充样品槽,可以直接将样品填充样品槽并用盖玻片压平;若样品测试不够填充样品槽,可与BaSO4粉末混合,制成一系列等质量分数的样品,填充样品槽并用盖玻片压平。
图3. 紫外可见漫反射测试中的制样过程图。
1.测试:用积分球进行测试紫外可见漫反射(UV-Vis DRS),采用背景测试样(BaSO4粉末)测试背景基线(选择R%模式),以其为background测试基线,然后将样品放入到样品卡槽中进行测试,得到紫外可见漫反射光谱。
测试完一个样品后,重新制样,继续进行测试。
•测试数据处理数据的处理主要有两种方法:截线法和Tauc plot法。
截线法的基本原理是认为半导体的带边波长(λg)决定于禁带宽度E g。
两者之间存在E g(eV)=hc/λg=1240/λg(nm)的数量关系,可以通过求取λg来得到E g。
由于目前很少用到这种方法,故不做详细介绍,以下主要来介绍Tauc plot法。
具体操作:1、一般通过UV-Vis DRS测试可以得到样品在不同波长下的吸收,如图4所示;图4. 紫外可见漫反射图。
2. 根据(αhv)1/n = A(hv – Eg),其中α为吸光指数,h为普朗克常数,v为频率,Eg为半导体禁带宽度,A为常数。
其中,n与半导体类型相关,直接带隙半导体的n取1/2,间接带隙半导体的n为2。
3. 利用UV-Vis DRS数据分别求(αhv)1/n和hv=hc/λ, c为光速,λ为光的波长,所作图如图5所示。
所得谱图的纵坐标一般为吸收值Abs,α为吸光系数,两者成正比。
通过Tauc plot来求Eg时,不论采用Abs还是α,对Eg值无影响,可以直接用A替代α,但在论文中应说明。
4. 在origin中以(αhv)1/n对hv作图,所作图如图5所示ZnIn2S4为直接带隙半导体,n取1/2),将所得到图形中的直线部分外推至横坐标轴,交点即为禁带宽度值。
图5. Tauc plot图。
图6与图7所示是文献中通过测试UV-Vis DRS计算相应半导体的带隙Eg的图。
图6. W18O19以及Mo掺杂W18O19 (MWO-1)的紫外可见漫反射图和Tauc plot图。
图7. ZnIn2S4(ZIS)以及O掺杂ZIS的紫外可见漫反射图和Tauc plot图。
2.VB XPS测得价带位置(Ev)根据价带X射线光电子能谱(VB XPS)的测试数据作图,将所得到图形在0 eV附近的直线部分外推至与水平的延长线相交,交点即为Ev。
如图8,根据ZnIn2S4以及O掺杂ZnIn2S4的VB XPS图谱,在0 eV附近(2 eV 和1 eV)发现有直线部分进行延长,并将小于0 eV的水平部分延长得到的交点即分别为ZnIn2S4以及O掺杂ZnIn2S4的价带位置对应的能量(1.69 eV和0.73 eV)。
如图9为TiO2/C的VB XPS图谱,同理可得到其价带位置能量(3.09 eV)。
图8. ZnIn2S4(ZIS)以及O掺杂ZIS的VB XPS图。
图9. TiO2/C HNTs的VB XPS图。
3.SRPES 测得E f、E v以及缺陷态位置图2.3所示是文献中通过测同步辐射光电子发射光谱(SRPES)计算相应半导体的E f、E v以及缺陷态位置。
图2.3a是通过SRPES测得的价带结构谱图,通过做直线部分外推至与水平的延长线相交,得到价带顶与费米能级的能量差值(E VBM-E f);该谱图在靠近0 eV处(费米能级E f)为缺陷态的结构,如图2.3b所示,取将积分面积一分为二的能量位置定义为缺陷态的位置。
图2.3c是测得的二次电子的截止能量谱图,加速能量为39 eV,根据计算加速能量与截止能量的差值,即可得到该材料的功函数,进一步得到该材料的费米能级(E f)。
图10. W18O19以及Mo掺杂W18O19 (MWO-1)的SRPES图以及其带隙结构示意图。
4.通过测试Mott-Schottky曲线得到平带电势测试方法在一定浓度的Na2SO4溶液中测试Mott-Schottky曲线,具体的测试方法如下:1.配置一定浓度的Na2SO4溶液;2.将一定量待测样品分散于一定比例的乙醇与水混合液中,超声分散后,将导电玻璃片浸入(注意控制浸入面积)或将一定量样品滴在一定面积的导电玻璃上,待其干燥后可进行测试(此步骤制样一定要均匀,尽可能薄。
样品超声前可先进行研磨,超声时可在乙醇溶液中加入微量乙基纤维素或Nafion溶液);3.三电极体系测试,电解液为Na2SO4溶液,参比电极为Ag/AgCl电极,对电极为铂网电极,工作电极为具有待测样品的导电玻璃;4.在一定电压范围(一般为-1 ~ 1 V vs Ag/AgCl)进行测试,改变测试的频率(一般为500、1000以及2000 Hz),得到相应的测试曲线。
具体的设置界面如图11和图12所示。
图11. 测试设置界面1。
图12. 测试设置界面2。
•测试数据处理测试的数据转换为txt格式,根据测得的数据可计算半导体材料的平带电势。
对于半导体在溶液中形成的空间电荷层(耗尽层),可用以下公式计算其平带电势:斜率为负时对应p型半导体,斜率为正时对应n型半导体。
由于电极的电容由双电层电容(C dl)以及空间电荷电容(C sc)两部分组成,且但是一般C sc << C dl,故有C= C sc= C̋ ̋,根据txt数据(图13)的第一列(E)和第三列(Z ̋),分别转换为NHE电位以及C sc = C = C̋ ̋= -1/wZ ̋= -1/2πfZ ̋,做出1/C2-E图即可得到Mott-Schottky曲线,将直线部分外推至横坐标轴,交点即为平带电势。
一般对于n型半导体,导带底位置与平带电势一致,可认为平带电势为导带底位置。
图13. 保存的txt数据。
图14. Mott-Schottky曲线。
图15与图16所示是文献中通过测试Mott-Schottky曲线得到半导体的平带电位(导带位置E v)。
如图15,根据Co9S8和ZnIn2S4的Mott-Schottky曲线图,可以得到Co9S8和ZnIn2S4的平带电位分别为-0.75 eV和-0.95 eV,由于斜率为正时对应n型半导体,Co9S8和ZnIn2S4均为n型半导体,可以认为其导带位置为-0.75 eV和-0.95 eV。
如图16为P-In2O3和C-In2O3的Mott-Schottky曲线图,同理可得到其平带位置。
图15. Co9S8和ZnIn2S4的Mott-Schottky曲线图。
图16. P-In2O3和C-In2O3的Mott-Schottky曲线图。
5.通过计算得到能带位置对于纯的单一半导体,可根据测得的禁带宽度(0.5Eg)来计算其导带和价带位置:价带:E VB= X− Ee + 0.5Eg导带:E CB= X− Ee − 0.5Eg其中,X为半导体各元素的电负性的几何平均值计算的半导体的电负性,Ee 为自由电子在氢标电位下的能量。
值得注意的是,在半导体存在缺陷或者与其它材料复合时,实际的带隙结构计算可能存在偏差,一般通过前面提到的测试方法与该计算结合使用,得到比较合理的测试结果。
6.附录(常用半导体能带结构)附件下载地址:https:///s/1GRenMLRQxUXmOPOiPXDikA 提取码: pvs9参考文献:[1] S. Wang, B.Y. Guan, X. Wang, X.W.D. Lou, Formation of Hierarchical Co9S8@ZnIn2S4Heterostructured Cages as an Efficient Photocatalyst for Hydrogen Evolution, Journal of the American Chemical Society, 140 (2018) 15145-15148.[2] N. Zhang, A. Jalil, D. Wu, S. Chen, Y. Liu, C. Gao, W. Ye, Z. Qi, H. Ju, C. Wang, X. Wu, L. Song, J. Zhu, Y. Xiong, Refining Defect States in W18O49by Mo Doping: A Strategy for Tuning N2 Activation towards Solar-Driven Nitrogen Fixation, J Am Chem Soc, 140 (2018) 9434-9443.[3] W. Yang, L. Zhang, J. Xie, X. Zhang, Q. Liu, T. Yao, S. Wei, Q. Zhang, Y. Xie, Enhanced Photoexcited Carrier Separation in Oxygen-Doped ZnIn2S4Nanosheets for Hydrogen Evolution, Angew Chem Int Ed, 55 (2016) 6716-6720.[4] Z. Liang, X. Bai, P. Hao, Y. Guo, Y. Xue, J. Tian, H. Cui, Full solar spectrum photocatalytic oxygen evolution by carbon-coated TiO2 hierarchical nanotubes, Applied Catalysis B: Environmental, 243 (2018) 711-720.[5] Y.X. Pan, Y. You, S. Xin, Y. Li, G. Fu, Z. Cui, Y.L. Men, F.F. Cao, S.H. Yu, J.B. Goodenough, Photocatalytic CO2Reduction by Carbon-Coated Indium-Oxide Nanobelts, J Am Chem Soc, 139 (2017) 4123-4129.[6] American Mineralogist, Volume 85, pages 543–556, 2000.。
