气体物理化学
本章基本要求
掌握理想气体状态方程； 掌握理想气体的宏观定义及微观模型； 掌握分压力、分体积的概念及计算； 理解真实气体与理想气体的偏差、临界现象； 掌握饱和蒸气压概念； 理解范德华状态方程、对应状态原理和压缩因子图； 了解对比状态方程及其它真实气体方程。
3
1.1 理想气体与状态方程
1. 低压定律 波义尔定律： pV=常数 （n,T一定） 盖―吕萨克定律： V/T=常数（n,p一定） 阿伏加德罗定律： V/n=常数（T,p一定） 且
T=273.15K p=101.325kPa 时 1mol气体的体积 Vm=22.4×10-3 m3 由三个低压定律可导出理想气体状态方程
4
第一章 气体的 pVT 关系
1
教学内容及目的
教学内容 1. 理想气体
状态方程，分压定律，分体积定律。 2. 真实气体
真实气体与理想气体的偏差，范德华方程； 真实气体的液化(CO2的p-V图)，临界现象，临界参数。 3. 对应状态原理及压缩因子图 对比参数、对应状态原理； 用压缩因子图进行普遍化计算。 教学目的 学习或复习与物理化学相关的气体问题，为物理化学的学 习做好知识准备。
M = RT( / p) p→0 ， 以(r/ p)- p 作图，外推可得( / p) p→0。
5
3．（摩尔）气体常数 R
根据状态方程式R = pVm / T计算得到。 对于实际气体，R与压力、温度、气体种类有关。但温度
较高、压力较低时，R近于常数。当T 较高，p→0时，无 论何种气体，均有：
p=pB， 此规律即为道尔顿定律。
8
2. 分体积和阿马格定律
类似于分压的定义，对于任意混合气体中任一组分B的分压 VB等于总压V 乘以它的摩尔分数yB 即 VB=VyB 而 yB = nB / n
利用理想气体的性质，可得混合后气体的总体积： V = nRT/p=(n1+n2)RT/p = n1RT/p +n2RT/p =V1+V2
p=748 mmHg=99.73 kPa V(N2)=223.6 dm3 T=298K
m(NaN3)=？
V(N2)=75.0dm3
m(NaN3)=390.6 g ×75÷223.6=131.0 g
11
1.3 气体的液化及临界参数
1. 饱和蒸汽压的概念
恒定温度下：当水与水蒸汽达成动态平衡时，p*为温度T 时的饱和蒸汽压。且饱和蒸汽压随温度的变化而变化
g
p*(l)
液体的饱和蒸气压P* 沸点: 蒸气压等于外压时的温度;
T 一定
正常沸点: 101.325 kPa下的沸点; 标准沸点: 100 kPa下的沸点。
l
(相平衡) 如: 水的正常沸点为 100 ℃，标
准沸点为99.67℃
图1-1 液体的饱和蒸气压
12
2. 真实气体的p ～Vm图及气体的液化
对气体采取降温加压措 施使气体体积缩小，有 可能最终转化为液体。 但这种转化过程的p— V —T 关系遵循着一定 规律。
9
气体体积的计算实例
例：为了行车的安全，可在汽车中装备上空气袋，防止碰 撞时司机受到伤害。这种空气袋是用氮气充胀起来的，所 用的氮气是由叠氮化钠与三氧化二铁在火花的引发下反应 生成。总反应是： 6NaN3+Fe2O3(s) 3Na2O(s)+2Fe(s)+9N2(g) 在25℃、748mmHg下，要产生75.0dm3的N2，计算需要叠 氮化钠的质量。
R = (pVm) p→0/T = 8.3145 J·mol-1·K-1 ——摩尔气体常 数 注意 (1) 实际气体只有在温度较高，压力较低时的行为符合 理想气体。 (2) 摩尔气体常数R用8.3145 J·mol-1·K-1 (3) 气体的标准体积是指1mol理想气体在273.15K、 101.325kPa下的体积， 数值为 22.414 dm3。
解：根据化学反应方程式所显示出的n（NaN3）与 n（N2）的数量关系，可以进一步确定在给定条件 下，m（NaN3）与V（N2）的关系。
10
气体体积的计算实例
6NaN3+Fe2O3(s) 3Na2O(s)+2Fe(s)+9N2(g)
6mol
9mol
Mr(NaN3)=65.01 m(NaN3)=390.06 g
2. 理想气体的定义
任何温度、任何压力下均符合状态方程 pV = nRT 的 气体。
理想气体的状态方程：pV = nRT 其它形式：已知气体的质量m、摩尔质量M、密度，
利用关系式 摩尔体积Vm = V / n，n = m / M， = m / V 则改写为： pVm = RT
pV =（m/M）RT p = RT /M 最后一式可用来计算气体的摩尔质量
即恒温恒压混合，混合后的体积等于混合前各气体的体积之和 注意： （1）道尔顿定律和阿马格定律为理想气体状态方程的必然推论，
不用死记。 （2）对于理想气体的混合，恒温恒容混合前的压力等同于分压，
恒温恒压混合前的体积等同于分体积。对于实际气体，并不 相等。 （3）混合气体的（平均）摩尔质量 （见书11页）
7
1.2 理想气体的混合性质
1. 分压力和道尔顿定律 由于热力学计算的需要，定义任意混合气体（不管是理想
气体还是实际气体）中任一组分B的分压 pB等于总压 p 乘 以它的摩尔分数yB 即 pB = p yB 而 yB = nB / n 利用理想气体的性质，可得混合后气体的总压力： p=nRT/V=(n1+n2)RT/V = y1 nRT/V +y2 nRT/V =n1 RT/V +n2RT/V =p1+p2 即恒温恒容混合，混合后的压力等于混合前各气体的压力之和
6
4. 理想气体的微观模型
理想气体是指任意压力和任意温度下其状态均符合 pV = nRT 的气体。
若要具有这种性质，理想气体必须有如下特征： （1）分子本身没有体积
若有体积，在T恒定、压力p→∞ 时（pVm）不能保证为 常数。 （2）分子间无相互作用力
若有相互作用，在T恒定时，压力p = (n/V) RT ∝ n无法 满足，因为分子间的相互作用会影响压力。 实际气体性质：压力小，温度高时分子间相互作用小，体 积较大，所以行为接近理想气体。难液化的气体如H2、N2、 O2等通常可认为是理想气体 。
理想气体(物理化学)
即对于实际气体
lim pV nRT
p0
lim
p0
pVm
RT
看P10的图, 恒定温度下对几种气体pVm随压力的变化进行精确
测量，显然只有压力趋于零时，各种气体的pVm才具有相同的
数值 (pVm)p→0=RT
5000
4500 4000
N2 CH4
3500 3000
pVm / J mol 1 2500
2000 1500 1000
0
He
20 40 60 80 100 120 p/Mpa
而理想气体: pVm=RT(常数)， 水平线
注意：根据现在处理数据的统一标准要求，要用纯数作图、 列表。因此坐标轴上的标注应该为纯数，所以坐标轴上物理量的
表示应该为
物理量 单位
,如上图及下表:
列表时: p/MPa
…………
pVm/J . mol-1
…………
↑
↑
表头中物理量的表示: 物理量 表中均为纯数
单位
⑶ 低压气体可近似视作为理想气体。
即低压气体可近似使用理想气体状态方程计算p、T、V 关系。
二 理想气体的微观模型（p9）
按照分子运动论，理想气体微观模型应该是：
1. 分子间无作用力； 2. 分子本身没有体积 3. 分子不停顿地作无规则的热运动。
物质的量n确定时 f (p、V、T) =0 或四变量函数式 f (p、V、T、n) =0
固体、液体物质的体积V受压力p与温度T的影响很小,即它 们的可压缩性(p→ V)及热膨胀性(T→ V) 与气体物质相比小都
很小，在通常的物理化学讨论中常常忽略它们的体积随压力及
温度的变化。而气体物质p、V、T之间相互影响很大，所以这 一章我们先来讨论气体的p、V、T关系，并且气体体系是物理
理科物理化学章气体
对理想气体 VB= nB R T /P 对真实气体不适用。
§1.2 摩尔气体常数（R）
pVm / T J mol1 K1 R 8.3145
8
6
4
图1.4(a)
理想气体
T3 (531K) T2 (410K) T1(333K)
2
10
20
a Vm2
)(Vm
RT bp
b) RT
a ab Vm Vm2
高温时，忽略分子间的引力（忽略含a的项）
pVm RT bp
pVm > RT
低温时，压力又比较低，忽略分子的体积(含b项)
pVm
RT
a Vm
pVm < RT
当压力增加到一定限度后，b的效应越来越显著， 又将出现 pVm > RT 的情况。这就是在Boyle温度以下 时， pVm 的值会随压力先降低，然后升高。
p
3 pcVm2,c Vm2
Vm
Vm,c 3
8 3
pcVm,c Tc
T
p pc
3Vm2,c Vm2
Vm Vm,c
1 3
8T 3 Tc
对比状态和对比状态定律
p pc
3Vm2,c Vm2
Vm Vm,c
1 3
8 3
T Tc
定义： p
pc
Vm
Vm,c
T
Tc
代入上式，得van der Waals 对比状态方程
（2）当温度升到30.98℃时，等温线的水平部分缩 成一点，出现拐点，称为临界点。在这温度以上无 论加多大压力，气体均不能液化。
（3）在临界点以上，是气态的等温线，在高温或 低压下，气体接近于理想气体。
物理化学 第一章 绪论气体
物理化学讲课的内容
第一章 气体的pVT关系 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分热力学 第五章 相平衡
3-10周 讲课 40 h
第六章 化学平衡 第七章 电化学 第八章 化学动力学 第九章 界面现象与
描述真实气体的 pVT 关系的方法： 1）引入压缩因子Z，修正理想气体状态方程 2）引入 p、V 修正项，修正理想气体状态方程 3）使用经验公式，如维里方程，描述压缩因子Z 它们的共同特点是在低压下均可还原为理想气体状态方程
1. 真实气体的 pVm - p 图及波义尔温度
T > TB
pVm - p曲线都有左图所示三种
c
T4
说明Vm(g) 与Vm(l)之差减小。
l2 l1
l
g2 g1
T3
Tc
TT12gg´´12 g
T = Tc时， l – g 线变为拐点c c：临界点 ；Tc 临界温度； pc 临界压力； Vm,c 临界体积
Vm
临界点处气、液两相摩尔体积及其它性质完全相同，界
面消失气态、液态无法区分，此时：
V p m Tc 0 ,
类型。
pVm
T = TB T < TB
(1) pVm 随 p增加而上升； (2) pVm 随 p增加，开始不变， 然后增加
p 图1.4.1 气体在不同温度下的 pVm－p 图
(3) pVm 随 p增加，先降后升。
T > TB T = TB
对任何气体都有一个特殊温度 -
波义尔温度 TB ，在该温度下，压
（密闭容器）
水
乙醇
苯
t / ºC 20 40 60 80 100 120
物理化学第五版_01章_气体
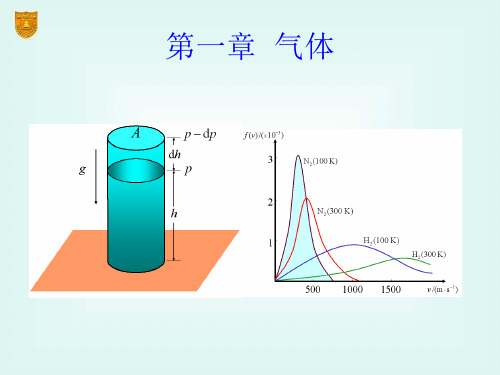
学平均速率与根均方速率
Maxwell 速率分布定律 设容器内有N个分子，速率在 v v dv 范围内的分子数为 d N v
则
d Nv Ndv
或
d Nv Nf (v)dv
f (v) 称为分子分布函数，
力却是一个定值，并且是一个宏观可测的物理量。
对于一定量的气体，当温度和体积一定时， 压力具有稳定的数值。 压力p是大量分子集合所产生的总效应，是 统计平均的结果。
压力和温度的统计概念
aa' , bb' 是两个半透膜
aa ' 只允许A分子出入
bb ' 只允许B分子出入
在中间交换能量，直至
双方分子的平均平动能相等
是摩尔气体常数，等于
是热力学温度，单位为 K
T (t /℃ 273.15)K
气体分子动理论的基本公式 气体分子的微观模型 (1)气体是大量分子的集合体 (2)气体分子不停地运动，呈均匀分布状态 (3)气体分子的碰撞是完全弹性的 设在体积为V的容器内，分子总数为N，单位体 积内的分子数为n（n = N/V），每个分子的质量为m。 令：在单位体积中各群的分子数分别是 n1 ，n2 ， … 等。则
n1 n2 ni ni n
i
气体分子动理论的基本公式 设其中第
i
群分子的速度为
u i ，它在 x, y, z
轴方向上的分速度为
2 ui 2 ui , x
ui, x , ui, y , ui, z ，则
2 ui , z
2 ui , y
在单位时间内，
在
物理化学 第一章 气 体
pV nRT
或
（1-1） (1-2)
pV
m RT M
其中的R称为摩尔气体常数，其值等于8.314J.K-1.mol-1，与气体种类无关。 理想气体状态方程只有理想气体完全遵守。 理想气体也可以定义为在任何温度、压强下都严格遵守理想气体状态方程的 气体。
实际气体处在温度较高、压力较低即气体十分稀薄时，能较好地符合这个关 系式。
图1.2 混合气体的分体积与总体积示意图
在压力很低的条件下，可得V=VA+VB，即混合气体的总体积等于所
有组分的分体积之和，称为阿马格分体积定律。通式为
V V i
式中 VB——组分B的分体积。 根据理想气体状态方程有
nB VB RT p
（1-5）
n总 V总 RT p
（1-
pV ZnRT
（1-16）
在压力较高或温度较低时，真实气体与理想气体的偏差较 大。定义“压缩因子（Z）”来衡量偏差的大小。
pV Z nRT
Z →
V V nRT / p V理想
等于同温、同压下，相同物质量的真实气体与理想气体的体
积之比。
理想气体的 pV=nRT ， Z =1。
对于真实气体，若Z＞1，则V＞ V(理想)，即真实气体的体积 大于理想气体的体积，说明真实气体比理想气体难于压缩；
（1-13）
称为截项维里方程，有较大的实用价值。 当压力达到几MPa时（5MPa左右），第三维里系数渐显重要，其近 似截断式为：
Z
pV B C 1 2 RT V V
（1-14）
第四节 对应态原理及普遍化压缩因子图 一.对应态原理 二.压缩因子法 三.普遍化压缩因子图
物理化学第一章气体
17
18
第一章 气体的pVT关系
1.了解理想气体的微观模型，能熟练使用理 想气体的状态方程 2.理解气体的液化和临界参数 3.了解真实气体的状态方程及对应状态原理 与压缩因子图 重点： 理想气体的状态方程、微观模型、 临界参数。 难点：对应状态原理与压缩因子图。
1
问题：1.理想气体的状态方程式主要有哪些 应用？ 2.何为理想气体混合物？在理想气体混合物中 某组分的分压是如何定义的？其物理意义如何，如 何计算？ 3.何为纯液体的饱和蒸气压？它与哪些因素
有关？
2
3
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体 液化及临界现象 实际气体 对应状态原理及压缩因子图 状态方程
如何变成理 想气体？
4
1.1 理想气体的状态方程
pV nRT
导出公式：
M mRT / pV
pM / RT
例：六氟化铀UF6是密度很大的一种气体，求在
适合条件:理想气体或低压下的真实气体
6
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体
液化及临界现象
实际气体 状态方程 对应状态原理及压缩因子图
7
1.3 气体的液化及临界参数
饱和蒸气压：指定温度下，密闭系统中某物质处 于气液平衡共存时其蒸气的压力。
临界参数：
9
b.求真实气体的压缩因子Z
真实气体的pVT关系： 对比参数： 对比压力: pr =p/pc
pVm ZRT
对比温度: Tr =T/Tc
对比体积: Vr =Vm/ Vm，c
《物理化学1气体》课件
04 气体反应动力学 与速率方程
气体反应速率的概念
反应速率
单位时间内反应物浓度减 少或产物浓度增加的量。
反应速率常数
反应速率与反应物浓度的 乘积，表示反应速率与浓 度的关系。
活化能
反应速率与温度的关系， 表示反应所需的最低能量 。
速率方程的建立与求解
质量作用定律
反应速率与反应物浓度的幂次方 成正比。
《物理化学1气体》ppt课 件
目 录
• 气体的基本性质 • 气体定律与热力学基础 • 气体混合物与分压定律 • 气体反应动力学与速率方程 • 气体化学反应平衡常数与计算
01 气体的基本性质
气体的定义与分类
总结词
气体的定义、分类及特性
详细描述
气体是物质的一种聚集状态，具有无固定形状和体积、流动性强等特性。根据气 体分子间相互作用力的不同，气体可分为理想气体和实际气体。理想气体忽略了 气体分子间的相互作用力，而实际气体则考虑了这种相互作用力。
理想气体定律
理想气体假设
理想气体状态方程，即PV=nRT，其 中P表示压强，V表示体积，n表示摩 尔数，R表示气体常数，T表示温度。
理想气体是一种假设的气体模型，其 分子之间没有相互作用力，分子本身 的体积可以忽略不计。
理想气体状态方程的应用
用于计算气体的压力、体积、温度等 物理量之间的关系，以及气体的热力 学性质。
热力学第一定律
热力学第一定律
01不
能消失，只能从一种形式转化为另一种形式。
内能和热量
02
内能是系统内部能量的总和，热量是系统与外界交换能量的量
度。
热力学第一定律的应用
03
用于计算系统的内能、热量、功等物理量之间的关系，以及系
物理化学气体性质习题答案
物理化学气体性质习题答案物理化学气体性质习题答案气体是物理化学中一个重要的研究对象，其性质和行为对于我们理解自然界和应用科学原理具有重要意义。
在学习物理化学的过程中，我们经常会遇到一些关于气体性质的习题。
下面，我将为大家提供一些常见气体性质习题的答案，希望能对大家的学习有所帮助。
1. 问题：一定体积的气体在恒定温度下，压强与摩尔数成正比。
如果将气体的摩尔数增加一倍，压强会发生什么变化？答案：根据查理定律，一定体积的气体在恒定温度下，压强与摩尔数成正比。
因此，当气体的摩尔数增加一倍时，压强也会增加一倍。
2. 问题：一定质量的气体在恒定温度下，体积与压强成反比。
如果将气体的压强减小一半，体积会发生什么变化？答案：根据波义耳定律，一定质量的气体在恒定温度下，体积与压强成反比。
因此，当气体的压强减小一半时，体积会增加两倍。
3. 问题：一定质量的气体在恒定温度下，体积与摩尔数成正比。
如果将气体的摩尔数减少一半，体积会发生什么变化？答案：一定质量的气体在恒定温度下，体积与摩尔数成正比。
因此，当气体的摩尔数减少一半时，体积也会减少一半。
4. 问题：一定质量的气体在恒定温度下，压强与体积成正比。
如果将气体的体积增加一倍，压强会发生什么变化？答案：根据阿伏伽德罗定律，一定质量的气体在恒定温度下，压强与体积成正比。
因此，当气体的体积增加一倍时，压强也会减少一倍。
5. 问题：一定质量的气体在恒定温度下，压强与摩尔数成正比。
如果将气体的摩尔数减少一半，压强会发生什么变化？答案：一定质量的气体在恒定温度下，压强与摩尔数成正比。
因此，当气体的摩尔数减少一半时，压强也会减少一半。
以上是一些常见的物理化学气体性质习题的答案。
通过解答这些习题，我们可以更好地理解气体的性质和行为。
当然，除了这些基本的性质关系，气体还有很多其他的性质和行为，例如气体的扩散性、气体的溶解度等等。
希望大家在学习和应用物理化学的过程中，能够深入理解气体的性质，掌握相关的理论知识，并能够灵活运用于实际问题的解决中。
常用气体的物理化学特性
kmol气体常数密度相对密度容积Rρs（m3/kmol ）（J/（kg·K ））（kg/Nm3）（空气=1）1氢H 2 2.016022.427041250.08990.06952一氧化碳CO28.010422.3984297 1.25060.96713甲烷CH 416.043022.36215180.71740.55484乙炔 C 2H 226.0380319 1.17090.90575乙烯C 2H 428.054022.2567296 1.26050.97486乙烷C 2H 630.070022.1872276 1.3553 1.0487丙烯C 3H 642.081021.9900197 1.9136 1.4798丙烷C 3H 844.097021.9362188 2.0102 1.5549丁烯C 4H 856.018021.6067148 2.5968 2.00810正丁烯n-C 4H 1058.124021.5036143 2.7030 2.09011异丁烯i-C 4H 1058.124021.5977143 2.6912 2.08112戊烯C 5H 1070.135021.2177118 3.3055 2.55613正戊烯C 5H 1272.151020.8910115 3.4537 2.67114苯C 6H 678.114020.3609106 3.8365 2.96715硫化氢H 2S34.07622.1802244 1.5363 1.18816二氧化碳CO 244.009822.2601188 1.9711 1.528917二氧化硫SO 264.05921.8821129 2.9275 2.26418氧O 231.998822.3923259 1.4291 1.105219氮N 228.013422.4035296 1.25040.967020空气28.96622.4003287 1.2931 1.000021水蒸气H 2O18.015421.6294610.8330.644一些常用气体的物理化学特性（0℃、0.101325MPa ）序号气体分子式分子量定压比热绝热指数临界压力临界温度临界导热系数向空气的扩散系数c k Pc Tc压缩因子λD×104（kJ/(Nm3·K)）（Mpa）（K）Z（W/(m·K)）(m2/s)1.2980 1.4070 1.29733.30.3040.21630.6111.302 1.403 3.4961330.2940.023000.1751.545 1.309 4.641190.70.2900.030240.1961.909 1.2690.018721.888 1.258 5.117283.10.2700.01642.244 1.198 4.884305.40.2850.018610.1082.675 1.170 4.600365.10.2742.96 1.161 4.256369.90.2770.015120.0881.1463.71 1.144 3.800425.20.2740.013490.0751.144 3.648408.10.2831.121 3.374469.50.2693.266 1.1200.0077921.557 1.3200.013141.62 1.3047.387304.20.2740.013720.1381.779 1.2721.315 1.400 5.076154.80.2920.0250.1781.302 1.402 3.394126.20.2970.024891.306 1.401 3.3766132.50.024891.491 1.33522.126470.2300.016170.220运动粘度动力粘度常数最低着火温度ν×106μ×106C(m 2/s)（kg·s/m 2)（℃）高93.000.85290400H 2+0.5O 2=H 2O 28601313.30 1.690104605CO+0.5O 2=CO 228320814.50 1.060190540CH 4+2O 2=CO 2+2H 2O 8909438.0500.960198335C 2H 2+2.5O 2=2CO 2+H 2O 7.460.950257425C 2H 4+3O 2=2CO 2+2H 2O 14119316.410.877287515C 2H 6+3.5O 2=2CO 2+3H 2O 15608983.990.780322460C 3H 6+4.5O 2=3CO 2+3H 2O 20598303.810.765324450C 3H 8+5O 2=3CO 2+4H 2022214872.810.747385C 4H 8+6O 2=4CO 2+4H 2O 27191342.530.697349365C 4H 10+6.5O 2=4CO 2+5H 2O 2879057460C 4H 10+6.5O 2=4CO 2+5H 2O 28735351.990.669290C 5H 10+7.5O 2=5CO 2+5H 2O 33780991.850.648260C 5H 12+8O 2=5CO 2+6H 2O35384531.820.712380560C 6H 6+7.5O 2=6CO 2+3H 2O 33037507.63 1.190331270H 2S+1.5O 2=SO 2+H 2O5625727.09 1.4302664.14 1.23041613.60 1.98013113.30 1.70011213.40 1.75011610.120.860673（kj/kmol ）热效应燃烧反应式CO 2低高低空气氧2420641275310794 2.380.5 1.02832081264412644 2.380.5 1.080293239842359069.52 2.0 2.0585025648811.90 2.5 2.013213545634385948214.28 3.0 2.01428792703516439716.66 3.5 3.01927808936718766721.42 4.5 3.020454241012709324423.80 5.0 4.0254300412584711769528.56 6.0 4.0265889413388512364930.94 6.5 4.0265343911304812285730.94 6.5 5.0315796915921114883735.707.5 5.0327430816937715673338.088.0 6.0317161416225915577035.707.5 1.051864425364233837.141.5理论烟Nm 3/Nm 3干kj/kmol ）热效应理论空气需要量，耗氧量（Nm 3/Nm 3干燃气）热值（kj/Nm 3）燃烧热量温度（℃）H 2ON 2V f 0下上1.0 1.882.88 4.075.922101.88 2.8812.574.223702.07.5210.52 5.015.020431.09.4012.40 2.580.026202.011.2815.28 2.734.023433.013.1618.16 2.913.021153.016.9222.92 2.011.722244.018.8025.80 2.19.521554.022.5630.56 1.610.05.024.4434.44 1.58.521305.024.4434.44 1.88.521185.028.2038.20 1.48.76.030.0841.08 1.48.33.028.2037.20 1.28.022581.05.647.644.345.51900爆炸极限（%）常压，20℃理论烟气量（Nm 3/Nm 3干燃气）。
物理化学 -气体
正确的表述应为：“物质的量为n”， “ 热力学温度为T ”
。2.对于复杂运算，一般不列出每一个物理量的 单位，而直接给出最后单位。
Vm
RT p
8.315 (273 .15 25) 100 10 3
m3 mol 1 24.79dm3 mol 1
1.2074 0.03575
－ 0.03564
2021/1/24
§0.4 物理量的表示及运算
1. 物理量的表示
y [y]
y
2021/1/24
x /[ x]
•示意图 x
§0.4 物理量的表示及运算
2.对数中的物理量
• ln x、ex中的 x 为无量纲的纯数
•因为 x 原为有量纲的物理量 → dx/x 无量纲 →dx/x = dlnx 无量纲→d(x /[x] d ln( x /[x]
2021/1/24
§0.4 物理量的表示及运算
注意
3.在图中表示函数关系均是数值关系，运算时即 使用数值方程。
[例如]
应用
ln
p
vap H m R
1 T
C
作 ln
P [P]
T
1 /[T ]
图，
由直线求 vapH m 时，即应用数值方程：
ln p vapH m / J mol 1 1 C
欢 迎 走 进《 物 理 化 学 》
2021/1/24
绪论
何谓物理化学(Physical chemistry)？
物理化学 是从物质的物理现象与化学现象的联系入手，
探求化学变化基本规律的一门学科。 “用物理的理论、物理的实验手段”，探求化 学变化基本规律的一门学科。