常用正交表
常用的正交表

常用的正交表什么是正交表?在实验设计中,我们经常需要测试多个因素对结果的影响。
为了提高实验效率和减少资源的浪费,我们可以使用正交表来设计实验。
正交表是一种特殊的试验方案,能够同时考察多个因素对结果的影响而不会产生混淆效应。
正交表是通过合理选择试验条件和参数组合,使得各种因素之间相互独立、互不干扰,从而能够准确地评估各个因素对结果的影响。
使用正交表进行实验设计可以节省时间和资源,并且能够得到可靠的实验结果。
常用的正交表类型1. 对称正交表对称正交表是最常见且最简单的一类正交表。
它具有以下特点:•因子水平数相同:每个因子都有相同数量的水平。
•每个水平出现次数相同:每个水平在整个试验中出现次数相等。
•每两个因子之间都有一样多次重复:所有因子之间都进行了完全重复。
对称正交表适用于因子较少、水平较少的情况。
2. 不完全对称正交表不完全对称正交表是对称正交表的一种扩展形式,它具有以下特点:•因子水平数不同:每个因子可以有不同数量的水平。
•每个水平出现次数相同:每个水平在整个试验中出现次数相等。
•不完全重复:因子之间可能存在一些不完全重复的情况。
不完全对称正交表适用于因子较多、水平较多的情况。
3. 完全对称正交表完全对称正交表是一种特殊的正交表,它具有以下特点:•因子水平数相同:每个因子都有相同数量的水平。
•每个水平出现次数相同:每个水平在整个试验中出现次数相等。
•完全重复:所有因子之间都进行了完全重复。
完全对称正交表适用于因子较少、水平较少,并且要求各种因素之间不产生混淆效应的情况。
正交表的应用领域正交表广泛应用于各个领域,包括但不限于:1.科学研究:在实验设计中使用正交表可以减少实验误差和浪费资源,提高实验效率和可靠性。
例如,在药物研发中,可以使用正交表来评估不同因素对药物效果的影响。
2.工程设计:在产品设计和工艺优化中,正交表可以帮助工程师确定最佳参数组合,提高产品质量和生产效率。
例如,在汽车制造中,可以使用正交表来评估不同因素对汽车性能的影响。
常用的正交表

正交表(Orthogonal Array)是一种设计实验的工具,特别适用于研究多因素对试验结果的影响。
正交表可以帮助科学家在有限的实验次数内获得较为全面的信息。
以下是一些常用的正交表:
1.L型正交表:
•L9:包含9个试验点,用于三因素的初步研究。
•L16:包含16个试验点,用于四因素的初步研究。
2.Taguchi正交表:
•L8:包含8个试验点,用于三因素的优化实验。
•L27:包含27个试验点,用于三因素的详细研究。
3.Plackett-Burman正交表:
•PB12:包含12个试验点,用于初步筛选12个因素中的重要因素。
•PB20:包含20个试验点,用于更多因素的初步筛选。
4.Box-Behnken正交表:
•3因素3水平的Box-Behnken正交表:用于优化实验,适用于三因素的研究。
5.中心合成法正交表:
•CCC-2:用于三因素的优化实验。
•CCC-3:用于四因素的优化实验。
6.格兰杰正交表:
•4水平格兰杰正交表:用于四因素的研究。
•5水平格兰杰正交表:用于五因素的研究。
7.斯坦纳正交表:
•S5:用于五因素的研究。
•S6:用于六因素的研究。
这些是一些常见的正交表,具体选择应根据实验设计的需要以及研究的因素数量来确定。
在设计实验时,科学家可以根据实际情况选择最适合的正交表,以达到经济高效地获取试验信息的目的。
常用正交表

附录一: 正交表正交表因子:有可能影响实验指标的条件;因子的水平/状态:影响实验因子的因素,在正交表中用“0-水平数-1”或“1-水平数”表示;正交表:记为L次数(水平数因子数),一般用Ln(mk)表示,L代表是正交表,n代表试验次数或正交表的行数,k代表最多可安排影响指标因素的个数或正交表的列数,m表示每个因素水平数,且有n=k*(m-1)+1。
例如:L4(23)表示实验次数为4,3个水平为2的因子。
1.单一水平正交表各列水平数相同的正交表称为等水平正交表。
如L4(23)、L8(27)、L12(211)等各列中的水平为2,称为2水平正交表;L9(34 )、L27(313 )等各列水平为3,称为3水平正交表。
表示为:Ln(mk),用n=k*(m-1)+1公式计算。
2. 混合水平正交表各列水平数不完全相同的正交表称为混合水平正交表。
如L8(4124)表中有一列的水平为4,有4列水平数为2。
也就是说该表可以安排一个4水平因素和4个2水平因素。
再如L16(4423),L16(41212)等都是混合水平正交表。
表示为:Ln(m1k1m2k2),用n=k1*(m1-1)+k2*(m2-1)+…kx*(mx-1)+1公式计算。
L4(23)列号1 2 3试验号1 1 1 12 1 2 23 2 1 24 2 2 1L8(27)列号1234567试验号11111111 21112222 31221122 41222211 52121 2 12L12(211)L16(215)L20(219)L9(34)L27(313)L8(4×24) L16(4×212)L16(42×29)L16(45)L16(42×29)L18(2×37)L16(44×23)L16(43×26)L25(56)人生有几件绝对不能失去的东西:自制的力量,冷静的头脑,希望和信心11L8(27)的交互作用列表1234567⑴325476⑵16745⑶7654⑷123⑸32⑹1⑺L16(215)二列间交互作用列表人生有几件绝对不能失去的东西:自制的力量,冷静的头脑,希望和信心12L27(313)二列间的交互作用列表人生有几件绝对不能失去的东西:自制的力量,冷静的头脑,希望和信心13。
常用正交表IQ

各种正交实验表说实在的,我对正交表也是一知半解,弄得不很清楚。
其数理统计原理更是摸不着火门。
好在本人收集了一系列的常用正交表,对付一般的正交试验应该没问题。
开始对正交表接触是在上《化工过程开发》那门课的时候,因为是考察科目,当时也没在意听。
现在觉得很后悔。
我搜集了很久,找了了这些常用的正交表,目的是想忠告那些与我一样上课没听的同学,好好把握来之不易上课时光。
现在大四了,成天在实验室做实验,写毕业论文,那还有闲心来看书。
我想以后工作了更是时间紧迫。
希望我搜集的这些常用正交表对你有所帮助。
至少给你一些启发。
废话不多说,转如正体。
由于博客系统自身的问题,上标和下标不能正常显示,采用字体颜色区分上标和下标。
红色为下标,蓝色为上标,请注意区分。
1、L4(23)序号 1 2 31 1 1 12 1 2 23 2 1 24 2 2 12、L8(27)序号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 23、L12(211)序号 1 2 3 4 5 6 7 8 9 10 111 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 14、L9(34)序号 1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 15、L16(45)序号 1 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 310 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 26、L25(56)序号 1 2 3 4 5 61 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1混合水平正交表7、L8(41×24)序号 1 2 3 4 51 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 28、L12(31×24)序号 1 2 3 4 51 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 29、L16(44×23)序号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2附录1:常用正交表(1)L4(23)列号 1 2 3试验号1 1 1 12 1 2 23 2 1 24 2 2 1(2)L8(27)列号 1 2 3 4 5 6 7试验号1 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 2(3)L12(211)列号 1 2 3 4 5 6 7 8 9 10 11 试验号1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 1列号 1 2 3 4试验号1 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 1 (5)L16(45)列号 1 2 3 4 5试验号1 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2 (6)L25(56)列号 1 2 3 4 5 6 试验号1 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1 (7)L8(4×24)1 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 2 (8)L12(3×24)列号 1 2 3 4 5试验号1 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 210 3 1 1 2 111 3 2 1 1 212 3 2 2 2 1 (9)L16(44×23)列号 1 2 3 4 5 6 7 试验号1 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2Excel表格在L9(34)正交试验数据处理中的应用L9(34)正交试验是医药工作中常用的实验方法之一。
常用正交试验计算表_显著性判断及表头安排等

8 14.5 15.3
0 0 210.25 234.09 0 0 54.15
60.15
0
0 29.8 111.005 114.3
8 12.4 17.4
0 0 153.76 302.76 0 0 38.52
75.78
0
0
8 14.9 14.9
0 0 222.01 222.01 0 0 57.67
56.63
SSj=Qj CT
Vj
SSj dfj
1、在因素 使用方法: 水平表填入
各水平 2、在正交 表中填入选 择的正交表 形式,常用 正交表在《 常用正交表 、交互作用 表、表头设 计》中选取 粘贴 3、填入试 验结果 4、在K值计 算区域输入 希望统计的 结果列名称 5、手工更 改MSE**的 计算与F判 据的两个自 由度选项 6、获得显 著与否的结 论 7、正交表 的使用及数 据处理参考 资料见上 图例说明: 不建议更改 的部分 需要判断, 更改的部分 根据需要更 改的部分
225
0
0
0
0
210.25 225
222.01 219.04
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
60.15 56.2
56.63
58.02
0
0
0
0
54.15 58.1
57.67
56.28
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
常用正交表对照图
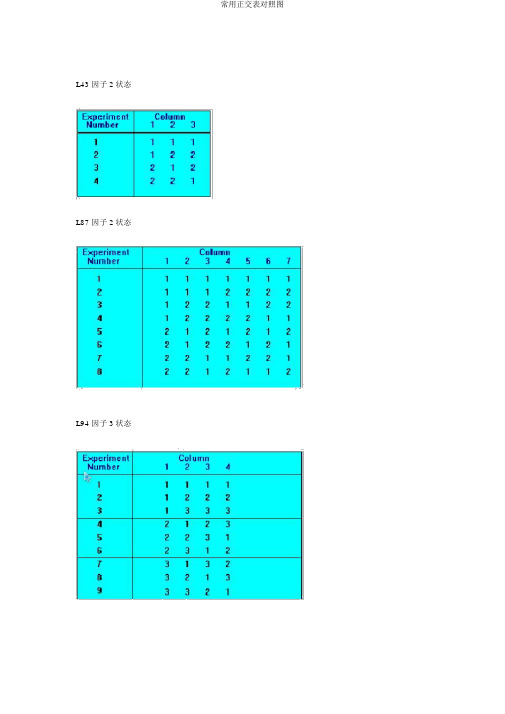
L43 因子 2状态L87 因子 2状态L94 因子 3状态15因子 2状态1因子 2状态和 7因子 3状态L187 因子 3状态187L (3)试验号列号1234567111111112122222231333333421122335222331162331122731213238323213193313212 101133221111211332121322113132123132142231213152312321163132312173213123183321231 13因子 3状态32因子两状态1因子 2状态和 11因子 5状态1因子 2状态和 25 因子 3状态31因子 2状态21因子 4状态L186因子 3状态和 1因子 6状态因子 1因子 2因子 3因子 4因子 5因子 6因子 7实验 10000000实验 20122011实验 30212102实验 40110223实验 50201214实验 60021125实验 71111110实验 81200121实验 91020212实验 101221003实验 111012024实验 121102205实验 132222220实验 142011201实验 152101022实验 162002113实验 172120104实验 182210015L84 因子 2状态和1因子4状态0因子 1因子 2因子 3因子 4因子 5实验 111111实验 212222实验 321122实验 422211实验 531212实验 632121实验 741221实验 842112L124 因子 2状态和1因子3状态L 12(3×24)试验号列号12345111111211122312212412221521211621222722122822122931212103112111321121232221L122 因子 2状态和1因子6状态L 12(6×22)试验号列号123121125123521422254116112712184229311106121162112322L498 因子 7状态498L (7)试验号列号12345678111111111212222222313333333414444444515555555 616666666 717777777 821234567 922345671 1023456712 1124567123 1225671234 1326712345 1427123456 1531357246 1632461357 1733572461 1834613572 1935724613 2036135724 2137246135 2241473625 2342514736 2443625147 2544736251 2645147362 2746251473 2847362514 2951526374 3052637415 3153741526 3254152637 3355263741 3456374152 3557415263 3661642753 3762753164 3863164275 3964275316 4065316427 4166427531 4267531642 4371765432 4472176543 4573217654 4674321765 4775432176 48765432174977654321 L164 因子 4状态和3因子2状态列号1234567试验号111111112122212231333212414442215212322162214212723411228243211193134122103243111113312221123421212134142212144231221154324111164413122。
常用正交表

L4_2_3所在列123因素ys1ys2ys3实验1z11z21z31实验2z11z22z32实验3z12z21z32实验4z12z22z31L8_2_7所在列1234567因素ys1ys2ys3ys4ys5ys6ys7实验1z11z21z31z41z51z61z71实验2z11z21z31z42z52z62z72实验3z11z22z32z41z51z62z72实验4z11z22z32z42z52z61z71实验5z12z21z32z41z52z61z72实验6z12z21z32z42z51z62z71实验7z12z22z31z41z52z62z71实验8z12z22z31z42z51z61z72L12_2_11所在列12345678因素ys1ys2ys3ys4ys5ys6ys7ys8实验1z11z21z31z41z51z61z71z81实验2z11z21z31z41z51z62z72z82实验3z11z21z32z42z52z61z71z81实验4z11z22z31z42z52z61z72z82实验5z11z22z32z41z52z62z71z82实验6z11z22z32z42z51z62z72z81实验7z12z21z32z42z51z61z72z82实验8z12z21z32z41z52z62z72z81实验9z12z21z31z42z52z62z71z82实验10z12z22z32z41z51z61z71z82实验11z12z22z31z42z51z62z71z81实验12z12z22z31z41z52z61z72z81L16_2_15所在列12345678因素ys1ys2ys3ys4ys5ys6ys7ys8实验1z11z21z31z41z51z61z71z81实验2z11z21z31z41z51z61z71z82实验3z11z21z31z42z52z62z72z81实验4z11z21z31z42z52z62z72z82实验5z11z22z32z41z51z62z72z81实验6z11z22z32z41z51z62z72z82实验7z11z22z32z42z52z61z71z81实验8z11z22z32z42z52z61z71z82实验9z12z21z32z41z52z61z72z81实验10z12z21z32z41z52z61z72z82实验11z12z21z32z42z51z62z71z81实验12z12z21z32z42z51z62z71z82实验13z12z22z31z41z52z62z71z81实验14z12z22z31z41z52z62z71z82L9_3_4所在列1234因素ys1ys2ys3ys4实验1z11z21z31z41实验2z11z22z32z42实验3z11z23z33z43实验4z12z21z32z43实验5z12z22z33z41实验6z12z23z31z42实验7z13z21z33z42实验8z13z22z31z43实验9z13z23z32z41L18_3_7所在列1234567因素ys1ys2ys3ys4ys5ys6ys7实验1z11z21z31z41z51z61z71实验2z11z22z32z42z52z62z72实验3z11z23z33z43z53z63z73实验4z12z21z31z42z52z63z73实验5z12z22z32z43z53z61z71实验6z12z23z33z41z51z62z72实验7z13z21z32z41z53z62z73实验8z13z22z33z42z51z63z71实验9z13z23z31z43z52z61z72实验10z11z21z33z43z52z62z71实验11z11z22z31z41z53z63z72实验12z11z23z32z42z51z61z73实验13z12z21z32z43z51z63z72实验14z12z22z33z41z52z61z73实验15z12z23z31z42z53z62z71实验16z13z21z33z42z53z61z72实验17z13z22z31z43z51z62z73实验18z13z23z32z41z52z63z71L27_3_13所在列12345678因素ys1ys2ys3ys4ys5ys6ys7ys8实验1z11z21z31z41z51z61z71z81实验2z11z21z31z41z52z62z72z82实验3z11z21z31z41z53z63z73z83实验4z11z22z32z42z51z61z71z82实验5z11z22z32z42z52z62z72z83实验6z11z22z32z42z53z63z73z81实验7z11z23z33z43z51z61z71z83实验8z11z23z33z43z52z62z72z81实验9z11z23z33z43z53z63z73z82实验10z12z21z32z43z51z62z73z81实验11z12z21z32z43z52z63z71z82实验12z12z21z32z43z53z61z72z83实验13z12z22z33z41z51z62z73z82实验18z12z23z31z42z53z61z72z82实验19z13z21z33z42z51z63z72z81实验20z13z21z33z42z52z61z73z82实验21z13z21z33z42z53z62z71z83实验22z13z22z31z43z51z63z72z82实验23z13z22z31z43z52z61z73z83实验24z13z22z31z43z53z62z71z81实验25z13z23z32z41z51z63z72z83实验26z13z23z32z41z52z61z73z81实验27z13z23z32z41z53z62z71z82L16_4_5所在列12345因素ys1ys2ys3ys4ys5实验1z11z21z31z41z51实验2z11z22z32z42z52实验3z11z23z33z43z53实验4z11z24z34z44z54实验5z12z21z32z43z54实验6z12z22z31z44z53实验7z12z23z34z41z52实验8z12z24z33z42z51实验9z13z21z33z44z52实验10z13z22z34z43z51实验11z13z23z31z42z54实验12z13z24z32z41z53实验13z14z21z34z42z53实验14z14z22z33z41z54实验15z14z23z32z44z51实验16z14z24z31z43z52L32_4_9所在列12345678因素ys1ys2ys3ys4ys5ys6ys7ys8实验1z11z21z31z41z51z61z71z81实验2z11z22z32z42z52z62z72z82实验3z11z23z33z43z53z63z73z83实验4z11z24z34z44z54z64z74z84实验5z12z21z31z42z52z63z73z84实验6z12z22z32z41z51z64z74z83实验7z12z23z33z44z54z61z71z82实验8z12z24z34z43z53z62z72z81实验9z13z21z32z43z54z61z72z83实验10z13z22z31z44z53z62z71z84实验11z13z23z34z41z52z63z74z81实验12z13z24z33z42z51z64z73z82实验13z14z21z32z44z53z63z74z82实验14z14z22z31z43z54z64z73z81实验15z14z23z34z42z51z61z72z84实验16z14z24z33z41z52z62z71z83实验21z12z21z34z42z53z64z71z83实验22z12z22z33z41z54z63z72z84实验23z12z23z32z44z51z62z73z81实验24z12z24z31z43z52z61z74z82实验25z13z21z33z43z51z62z74z84实验26z13z22z34z44z52z61z73z83实验27z13z23z31z41z53z64z72z82实验28z13z24z32z42z54z63z71z81实验29z14z21z33z44z52z64z72z81实验30z14z22z34z43z51z63z71z82实验31z14z23z31z42z54z62z74z83实验32z14z24z32z41z53z61z73z84L25_5_6所在列123456因素ys1ys2ys3ys4ys5ys6实验1z11z21z31z41z51z61实验2z11z22z32z42z52z62实验3z11z23z33z43z53z63实验4z11z24z34z44z54z64实验5z11z25z35z45z55z65实验6z12z21z32z43z54z65实验7z12z22z33z44z55z61实验8z12z23z34z45z51z62实验9z12z24z35z41z52z63实验10z12z25z31z42z53z64实验11z13z21z33z45z52z64实验12z13z22z34z41z53z65实验13z13z23z35z42z54z61实验14z13z24z31z43z55z62实验15z13z25z32z44z51z63实验16z14z21z34z42z55z63实验17z14z22z35z43z51z64实验18z14z23z31z44z52z65实验19z14z24z32z45z53z61实验20z14z25z33z41z54z63实验21z15z21z35z44z53z62实验22z15z22z31z45z54z63实验23z15z23z32z41z55z64实验24z15z24z33z42z51z65实验25z15z25z34z43z52z61L50_5_11所在列12345678因素ys1ys2ys3ys4ys5ys6ys7ys8实验1z11z21z31z41z51z61z71z81实验2z11z22z32z42z52z62z72z82实验3z11z23z33z43z53z63z73z83实验4z11z24z34z44z54z64z74z84实验5z11z25z35z45z55z65z75z85实验10z12z25z31z42z53z64z75z81实验11z13z21z33z45z52z64z74z81实验12z13z22z34z41z53z65z75z82实验13z13z23z35z42z54z61z71z83实验14z13z24z31z43z55z62z72z84实验15z13z25z32z44z51z63z73z85实验16z14z21z34z42z55z63z75z83实验17z14z22z35z43z51z64z71z84实验18z14z23z31z44z52z65z72z85实验19z14z24z32z45z53z61z73z81实验20z14z25z33z41z54z62z74z82实验21z15z21z35z44z53z62z74z83实验22z15z22z31z45z54z63z75z84实验23z15z23z32z41z55z64z71z85实验24z15z24z33z42z51z65z72z81实验25z15z25z34z43z52z61z73z82实验26z11z21z31z44z55z64z73z82实验27z11z22z32z45z51z65z74z83实验28z11z23z33z41z52z61z75z84实验29z11z24z34z42z53z62z71z85实验30z11z25z35z43z54z63z72z81实验31z12z21z32z41z53z63z72z84实验32z12z22z33z42z54z64z73z85实验33z12z23z34z43z55z65z74z81实验34z12z24z35z44z51z61z75z82实验35z12z25z31z45z52z62z71z83实验36z13z21z33z43z51z62z75z85实验37z13z22z34z44z52z63z71z81实验38z13z23z35z45z53z64z72z82实验39z13z24z31z41z54z65z73z83实验40z13z25z32z42z55z61z74z84实验41z14z21z34z45z54z61z72z85实验42z14z22z35z41z55z62z73z81实验43z14z23z31z42z51z63z74z82实验44z14z24z32z43z52z64z75z83实验45z14z25z33z44z53z65z71z84实验46z15z21z35z42z52z65z73z84实验47z15z22z31z43z53z61z74z85实验48z15z23z32z44z54z62z75z81实验49z15z24z33z45z55z63z71z82实验50z15z25z34z41z51z64z72z83使用帮助:1.选择适用的正交表。
常用的正交表

常用的正交表摘要:一、正交表的定义和作用二、常用的正交表类型1.均匀正交表2.平衡正交表3.中心对称正交表4.反对称正交表三、正交表在工程中的应用1.试验设计2.信号处理3.图像处理四、正交表的优缺点分析五、总结与展望正文:一、正交表的定义和作用正交表是一种特殊的矩阵,它的行和列都具有特殊的性质,如行向量之间相互正交,列向量之间相互正交。
正交表广泛应用于信号处理、图像处理、试验设计等领域,它能够有效地降低问题的复杂度,提高计算效率。
二、常用的正交表类型1.均匀正交表均匀正交表是一种具有相同行数的正交表,它的行向量在各个方向上具有相同的权重。
均匀正交表在信号处理和图像处理中具有较好的性能,但构造过程较为复杂。
2.平衡正交表平衡正交表是一种具有相同列数的正交表,它的列向量在各个方向上具有相同的权重。
平衡正交表在试验设计中具有较好的性能,能够有效地提高试验效率。
3.中心对称正交表中心对称正交表是一种具有特殊结构的正交表,它的行向量和列向量关于中心点对称。
中心对称正交表在信号处理和图像处理中具有较好的性能,且构造过程较为简单。
4.反对称正交表反对称正交表是一种具有特殊性质的正交表,它的行向量和列向量关于原点对称。
反对称正交表在工程中具有较好的性能,尤其在矩阵对角化、信号处理等方面具有较高的应用价值。
三、正交表在工程中的应用1.试验设计正交表在试验设计中能够有效地降低试验次数,提高试验效率。
通过选择合适的正交表,可以将试验次数从全排列减少到较小的值,从而降低试验成本。
2.信号处理正交表在信号处理中具有较好的性能,能够有效地降低信号的维度,提高信号处理的效率。
通过选择合适的正交表,可以将信号的维度从原始的高维空间降低到较低的维数,从而降低计算复杂度。
3.图像处理正交表在图像处理中具有较好的性能,能够有效地降低图像的维度,提高图像处理的效率。
通过选择合适的正交表,可以将图像的维度从原始的高维空间降低到较低的维数,从而降低计算复杂度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用正交表
注意:1、No.表示实验序号,列号表示正交表中列的序号。
2、交互作用表用来求两列间的两因素交互作用。
3、在表格设计的型式中用下列记号表示正交表各列的组别。
3
7
(三) 两列间的交互作用表
11
(五) L16(215)
(六) 两列间的交互作用表
(七) L32(231)
(八) 两列间的交互作用
(九) L(34)
1×37
(交互作用不牺牲列而出现,从1列和2列的二元表求得)。
注:3水平间的交互作用在剩下的3水平列中都各占有一部分
(十一) L27(313)
(十二) 二列间的交互作用表(L27(313))
(十三) L36(211×312)
注:a. 用1′,2′,3′,4′取代1,2,…11例,就成为L36(2×3)。
b. L36(211×312)中,因为交互作用与其它列不正交,所以最好应避免求这种交互作用的安排。
c. 这里表示的只是L36(23×313)型式的表格设计。
