四年级行程问题之一(相遇问题)
四年级奥数:行程问题(一)

所以小明比平时早出门 900÷60=15(分).
3、甲、乙两人环绕周长是 400 米的跑道跑步,如果两人从同一地点出发背向而行,那么经过 2 分钟相遇;如果两人从同一地点出发同向而行,那么经过 20 分钟两人相遇,已知甲的速度比乙快, 求甲、乙两人跑步的速度各是多少? 【解析】 由两人同一地点出发背向而行,经过 2 分钟相遇知两人每分钟共行 400÷2=200(米) 由两人从同一地点出发同向而行,经过 20 分钟相遇知甲每分钟比乙多走 400÷20=20(米) 根据和差问题的解法可知甲的速度是每分钟(200+20)÷2=110(米) 乙的速度为每分钟 110-20=90(米).
解:(1)从家到学校的距离的 2 倍:1400×2=2800(米) (2)从出发到相遇所需的时间:2800÷(200+80)=10(分) (3)相遇处到学校的距离:1400-80×10=600(米)
答:从出发到相遇,妹妹走了 10 分钟,相遇处离学校有 600 米.
【巩固拓展】 1、甲车每小时行 40 千米,乙车每小时行 60 千米.两车分别从 A,B 两地同时出发,相向而行, 相遇后 3 小时,甲车到达 B 地.求 A,B 两地的距离. 【解析】先画示意图如下:
例1
如图,A、B是一条道路的两端点,亮亮在A点,明明在B点,两人同时出发,相向而行.他 们在离A点100米的C点第一次相遇.亮亮到达B点后返回A点,明明到达A点后返回B点,两人在 离B点80米的D点第二次相遇.整个过程中,两人各自的速度都保持不变.求A、B间的距离.
【解析】 第一次相遇,两人共走了 1 个全程,其中亮亮走了 100 米; 从开始到第二次相遇,两人共走了 3 个全程,则亮亮走了 100×3=300(米),亮亮共走 的路程是一个全程多 80 米,所以 A、B 间的距离是:300-80=220(米)
四年级数学应用题专题相遇问题

四年级数学应用题专题相遇问题Revised by BETTY on December 25,2020四年级一、知识要点:相遇问题是行程问题的一种典型应用题,也是相向运动的问题.无论是走路、行车还是物体的移动,总是要涉及到三个量:路程、速度、时间.路程、速度、时间三者之间的数量关系路程=速度×时间,速度=路程÷时间,时间=路程÷速度.二、学法引导:相遇问题的计算关系式为:总路程=速度和×相遇时间“总路程”指两人从出发到相遇共同的路程;“速度和”指两人在单位时间内共同走的路程;“相遇时间”指从出发到相遇所经的时间.通常情况下对于相遇问题的求解还要借助线段图来进行直观地分析和理解题意,以突破难点.三、解题技巧:一般的相遇问题:甲从A地到B地,乙从B地到A地,然后两人在A地到B地之间的某处相遇,实质上是甲、乙两人一起走了A←→B这段路程,如果两人同时出发,那么有:(1)甲走的路程+乙走的路程=全程(2)甲(乙)走的路程=甲(乙)的速度×相遇时间(3)全程=(甲的速度+乙的速度)×相遇时间=速度和×相遇时间四、例题精讲:例1. 两列火车从两个车站同时相向出发,甲车每小时行48千米,乙车每小时行78千米,经过小时两车相遇.两个车站之间的铁路长多少千米?解法一、(48+78)×=126×=441(千米)答:两个车站之间的铁路长441千米.解法二、48×+78×=168+273=441(千米)答:两个车站之间的铁路长441千米.例2. A、D两地相距520千米,甲骑摩托车每小时行30千米,乙骑电动车每小时行驶20千米,几小时以后还相距70千米没有相遇?(520-70)÷(30+20)=450÷50=9(时)答:9小时以后还相距70千米没有相遇.例3. A、D两地相距520千米,甲骑摩托车每小时行30千米,乙骑电动车每小时行驶20千米,几小时相遇以后相距70千米?(520+70)÷(30+20)=590÷50=(时)答:小时相遇以后相距70千米例4. 甲、乙两站相距840千米,两列火车同时从两站相对开出,8小时后相遇,第一列火车的速度是每小时56千米,问第二列火车的速度是多少?解法一、(840-56×8)÷8=(840-448)÷8=392÷8=49(千米)答:第二列火车的速度是每小时49千米.解法二、840÷8-56=105-56=49(千米)答:第二列火车的速度是每小时49千米.例5. 甲、乙两城相距680千米,从甲城开往乙城的普通客车每小时行驶60千米,2小时后,快车从乙城开往甲城,每小时行80千米,快车开出几小时后两车相遇?(680-60×2)÷(60+80)=(680-120)÷140=560÷140=4(时)答:快车开出4小时后两车相遇.小结:解答一般的相遇问题,我们常规的思路是,抓住相遇问题的基本数量关系:(甲速+乙速)×相遇时间=路程来解答.但有一些相遇问题的已知和所求比较特殊,如果仍采用常规的解题思路就难以解决问题,针对各种不同的情况,下面介绍几种特殊的解题方法.一、抓住两个数量差并采用对应的思维方法例1. 甲车从A城到B城,速度是50千米/小时.乙车从B城到A城,速度是40千米/小时.两车同时出发,结果在离A、B两城的中点C 30千米的地方相遇,求A、B两城间的路程?分析与解:这道题的条件与问题如图所示.要求A、B两城的距离,关键是求出相遇时间.因路程是未知的,所以用路程÷(甲速+乙速)求相遇时间有一定的困难.抓住题设中隐含的两个数量差,即甲车与乙车的速度差:50千米/小时-40千米/小时=10千米/小时;相遇时两车的路差:30千米×2=60千米.再将其对应起来思维:正因为甲车每小时比乙车多走10千米,所以甲车多走60千米所花去的时间6小时正是两车相遇的时间.因此,求A、B两地距离的综合算式是:(50+40)×[30×2÷(50-40)]=90×[60÷10]=90×6=540(千米).答:A、B两地的路程是540千米.二、突出不变量并采用整体的思维方法例2. A、B两地间的公路长96千米,张华骑自行车自A往B,王涛骑摩托车自B 往A,他们同时出发,经过80分两人相遇,王涛到A地后马上折回,在第一次相遇后40分追上张华,王涛到B地后马上折回,问再过多少时间两个人再相遇?分析与解:根据题意张华、王涛三次相遇情况可画示意图.这道题如果从常规思路入手,运用相遇问题的基本数量关系来求解是非常不易的.但可根据题中小张、小王三次相遇各自的车速不变和在相距96千米的两地其同时相向而行相遇时间不变,进行整体思维.从图中可以看到:第三次相遇时,王涛走的路程是2AB+BE张华走的路程是AE,两人走的总路程是3个AB,所花的时间是80×3=240(分).可见,从第二次相遇到第三次相遇所经过的时间的综合算式是:80×3-80-40=120(分).答:再经过120分钟两人再次相遇.【模拟试题】(答题时间:30分钟)1、甲、乙两列火车同时从相距735千米的两地相向而行,甲列车每小时行85千米,乙列车每小时行90千米,几小时两列火车相遇?2、两列火车从两个车站同时相向出发,甲车每小时行85千米,乙车每小时行78千米,经过小时两车相遇.两个车站之间的铁路长多少千米?3、两人骑马同时从相距165千米的两地相对跑来,5小时相遇.第一匹马每小时跑15千米,第二匹马每小时跑多少千米第二匹马比第一匹马多跑多少千米4、小明和张楠分别从相距4320米的甲乙两地同时相对而行,小明骑车每分钟走160米,是张楠步行速度的2倍,多少分钟后两人相遇?5、甲、乙两艘轮船从相距654千米的两地相对开出而行,8小时两船还相距22千米.已知乙船每小时行42千米,甲船平均每小时行多少千米?6、一辆汽车和一辆自行车从相距千米的甲、乙两地同时出发,相向而行,3小时后两车相遇.已知汽车每小时比自行车多行千米,求汽车、自行车的速度各是多少?7、甲、乙两车同时从相距480千米的两地相对而行,甲车每小时行45千米,途中因汽车故障甲车停了1小时,5小时后两车相遇.乙车每小时行多少千米?【试题答案】1、甲、乙两列火车同时从相距735千米的两地相向而行,甲列车每小时行85千米,乙列车每小时行90千米,几小时两列火车相遇?735÷(85+90)=735÷175=(时)答:小时两列火车相遇.2、两列火车从两个车站同时相向出发,甲车每小时行85千米,乙车每小时行78千米,经过小时两车相遇.两个车站之间的铁路长多少千米?(85+78)×=163×=(千米)答:两个车站之间的铁路长千米.3、两人骑马同时从相距165千米的两地相对跑来,5小时相遇.第一匹马每小时跑15千米,第二匹马每小时跑多少千米第二匹马比第一匹马多跑多少千米165÷5-15 (18-15)× 5=33-15 =3×5=18(千米)=15(千米)答:第二匹马每小时跑18千米.第二匹马比第一匹马多跑15千米.4、小明和张楠分别从相距4320米的甲乙两地同时相对而行,小明骑车每分钟走160米,是张楠步行速度的2倍,多少分钟后两人相遇?4320÷(160÷2+160)=4320÷(80+160)=4320÷240=18(分钟)答:18分钟后两人相遇.5、甲、乙两艘轮船从相距654千米的两地相对开出而行,8小时两船还相距22千米.已知乙船每小时行42千米,甲船每小时行多少千米?(654-22)÷8-42=632÷8-42=79-42=37(千米)答:甲船平均每小时行驶37千米.6、一辆汽车和一辆自行车从相距千米的甲、乙两地同时出发,相向而行,3小时后两车相遇.已知汽车每小时比自行车多行千米,求汽车、自行车的速度各是多少?÷3=(千米)(-)÷2=26÷2=13(千米)13+=(千米)答:汽车每小时行驶千米,自行车每小时行驶13千米.7、甲、乙两车同时从相距480千米的两地相对而行,甲车每小时行45千米,途中因汽车故障甲车停了1小时,5小时后两车相遇.乙车每小时行多少千米?480-45×(5-1)=480-180=300(千米)300÷5=60(千米)答:乙车每小时行驶60千米.。
行程问题(一)相遇问题

行程问题(一)基本概念:行程问题是研究物体运动的,它研究的是物体速度、时间、路程三者之间的关系.基本公式:路程=速度×时间;路程÷时间=速度;路程÷速度=时间平均速度=总路程÷总时间相遇问题:速度和×相遇时间=相遇路程追及问题:追及时间=路程差÷速度差流水问题:顺水行程=(船速+水速)×顺水时间逆水行程=(船速-水速)×逆水时间顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2例1 两地相距360千米,一艘汽艇顺水行全程需要10小时,已知这条河的水流速度为每小时6千米。
往返两地的平均速度是每小时多少千米?1.有一条山路,一辆汽车上山时每小时行30千米,从原路返回下山时每小时行50千米,求汽车上、下山的平均速度。
2.甲、乙两个码头相距144千米,汽船从乙码头逆水行驶8小时到达甲码头,已知汽船在静水中每小时行驶21千米。
求汽船从甲码头顺流行驶几小时到达乙码头?3,甲船逆水航行300千米,需要15小时,返回原地需要10小时;乙船逆水航行同样的一段水路需要20小时,返回原地需要多少小时?例2 甲、乙两车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。
两车在距中点32千米处相遇,东、西两地相距多少千米?1,小玲每分钟行100米,小平每分钟行80米,两人同时从学校和少年宫出发,相向而行,并在离中点120米处相遇。
学校到少年宫有多少米?2,甲、乙二人同时从东村到西村,甲每分钟行120米,乙每分钟行100米,结果甲比乙早5分钟到达西村。
东村到西村的路程是多少米?例3 快车和慢车同时从甲、乙两地相向开出,乙车每小时行40千米,经过3小时,快车已驶过中点25千米,这时快车与慢车还相距7千米。
慢车每小时行多少千米?1,兄弟二人同时从学校和家中出发,相向而行。
四年级行程问题之一(相遇问题)

四年级行程问题之相遇问题研究路程、时间和速度这三者关系的问题称为行程问题。
行程问题主要包括相遇问题和追及问题。
相遇问题的特点是:总路程是由两人共同行完。
基本的计算公式如下:一、基本例题例1、甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米,两人几小时后相遇?例2、甲、乙两车分别从相距480千米的A、B两城同时出发相向而行,已知甲车从A城到B城需6小时,乙车从B城到A城需12小时,两车出发后几小时相遇?例3、东、西两村相距60千米,甲、乙两人骑车分别从东、西两村同时出发相向而行,5小时后两人相遇,已知甲每小时行5千米,求乙的速度是多少?例4、东、西两村相距55千米,甲、乙两人分别从东、西两村同时出发相向而行,5小时后两人相遇,已知甲每小时比乙多行1千米,求甲、乙两人的速度?例5、A、B两地相距200千米,甲开车从A地出发到B地,同时乙骑车从B地出发到A地,4小时后相遇,已知甲的速度是乙的4倍,求甲、乙两人的速度?例6、甲、乙两人分别从相距40千米的两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米,相遇时甲比乙多行多少千米?例7、小李和小王在环形的操场上跑步,操场的周长是400米,两人从同一起点同时出发相背而行,小李每秒跑3米,小王每秒跑5米。
(1)多少秒以后他们第一次相遇?(2)第一次相遇时两人各跑了多少米?(3)多少秒以后他们第二次相遇?第二次相遇时两人各跑了多少米?(4)多少秒以后他们5次相遇?(5)他们第6次相遇时一共跑了多少米?二、课内练习1、李明和张玫两人的家相距2公里,上午8时两人同时从家里出发,李明每分钟行120米,张玫每分钟行80米,两人几点几分相遇?相遇时李明比张玫多行多少米?2、甲、乙两车分别从相距240千米的A、B两城同时出发相向而行,已知甲车从A城到B城需3小时,乙车从B城到A城需5小时,两车出发后几小时相遇?3、东、西两村相距80千米,甲、乙两人骑车分别从东、西两村同时出发相向而行,4小时后两人相遇,已知甲每小时行8千米,求乙的速度是多少?4、东、西两村相距40千米,甲、乙两人分别从东、西两村同时出发相向而行,8小时后两人相遇,已知甲每小时比乙多行1千米,求甲、乙两人的速度?5、A、B两地相距320千米,甲车从A地出发到B地,同时乙车从B地出发到A地,4小时后相遇,已知甲车的速度是乙车的3倍,求甲、乙两车的速度?6、陈老师和刘老师在环形的操场上跑步,操场的周长是400米,两人从同一起点同时出发相背而行,陈老师每秒跑4米,刘老师每秒跑6米。
行程问题(一)相遇问题

行程问题(一)(相遇问题)例1:甲乙两辆列车同时从两地相对开出。
快车每小时行60千米,乙车每小时行55千米。
相遇时,甲车比乙车多行45千米,求两地相距多少千米?快慢两车同时从甲乙两地相对开出,快车每小时行80千米,慢车每小时行45千米,相遇时快车比慢车多行70千米。
求甲乙两地之间的路程。
例2:甲乙两队学生从相距18千米的两地同时出发,相向而行,一个同学骑自行车以每小时14千米的速度,在两队之间不停的往返联络,甲队每小时行5千米,乙队每小时行4千米。
两队相遇时,骑自行车的同学共行多少千米?两队同学同时从相距30千米的甲乙两地相向出发,一只鸽子以每小时二20千米的速度在两队之间不断往返送信,如果鸽子从同学们出发到相遇共飞行了30千米。
而甲队同学比乙队同学每小时多走0.4千米。
求两队同学的行走速度。
例3:甲乙两辆汽车从相距600千米的两地相对开出,甲车每小时行45千米,乙车每小时行40千米,甲车先开出2小时后,乙车才开出,问乙车行几小时后与甲车相遇?相遇时两车各行多少千米?甲乙两地相距1050千米,一辆快车以每小时150千米的速度从甲地开出,3小时后一辆慢车每小时90千米的速度从乙地开出,问慢车几小时后与快车相遇?相遇吋两车各行多少千米?例4:甲乙两车同时从ab两地相向出发,3小时后两车还相距120千米。
又行3小时两车又相距120千米,问ab两地相距多少千米?快慢车早上6时同时从甲乙两地相向开出。
中午12时两车相距50千米,继续行驶到14时,两车又相距170天。
甲乙两地相距多少千米?例5:甲乙两辆汽车从东西两地相向而行,甲车每小时行48千米,乙车每小时行42千米。
两车离中点21千米处相遇,求东西两地相距多少千米?甲乙两辆汽车同时从东西两城市相向而行,甲车每小时行60千米,乙车每小时行56千米。
两车在距中点16千米处相遇,求东西两城市相距多少千米?例6:甲乙两列火车同时从ab两站相向开出,在离a站60千米的地方相遇后,两车仍以原速继续前进,各车分别到达对方出发点后立即返回。
4年级-9-行程之相遇问题

行程之相遇问题甲从A地到B地,乙从B地到A地,然后两人在途中相遇,实质上是甲和乙一起走了A,B之间这段路程,如果两人同时出发,那么相遇路程=甲走的路程+乙走的路程=甲的速度×相遇时间+乙的速度×相遇时间=(甲的速度+乙的速度)×相遇时间=速度和×相遇时间.一般地,相遇问题的关系式为:速度和×相遇时间=路程和。
解决行程问题,常常要借助于线段图。
【例1】★一辆客车与一辆货车同时从甲、乙两个城市相对开出,客车每小时行46千米,货车每小时行48千米。
3.5小时两车相遇。
甲、乙两个城市的路程是多少千米?【小试牛刀】两地间的路程有255千米,两辆汽车同时从两地相对开出,甲车每小时行45千米,乙车每小时行40千米。
甲、乙两车相遇时,各行了多少千米?典型例题知识梳理【例2】大头儿子的家距离学校3000米,小头爸爸从家去学校接大头儿子放学,大头儿子从学校回家,他们同时出发,小头爸爸每分钟比大头儿子多走24米,50分钟后两人相遇,那么大头儿子的速度是每分钟走多少米?【小试牛刀】聪聪和明明同时从各自的家相对出发,明明每分钟走20米,聪聪骑着脚踏车每分钟比明明快42米,经过20分钟后两人相遇,你知道聪聪家和明明家的距离吗?【例3】A、B两地相距90米,包子从A地到B地需要30秒,菠萝从B地到A地需要15秒,现在包子和菠萝从A、B两地同时相对而行,相遇时包子与B地的距离是多少米?【例4】甲、乙两车分别从相距360千米的A、B两城同时出发,相对而行,已知甲车到达B城需4小时,乙车到达A城需12小时,问:两车出发后多长时间相遇?【例5】甲、乙两辆汽车分别从A、B两地出发相对而行,甲车先行1小时,甲车每小时行48千米,乙车每小时行50千米,5小时相遇,求A、B两地间的距离.【小试牛刀】甲、乙两列火车从相距770千米的两地相向而行,甲车每小时行45千米,乙车每小时行41千米,乙车先出发2小时后,甲车才出发.甲车行几小时后与乙车相遇?【例6】甲、乙两辆汽车分别从A、B两地出发相向而行,甲车先行3小时后乙车从B地出发,乙车出发5小时后两车还相距15千米.甲车每小时行48千米,乙车每小时行50千米.求A、B两地间相距多少千米?【小试牛刀】甲、乙两辆汽车从A、B两地同时相向开出,出发后2小时,两车相距141千米;出发后5小时,两车相遇.A、B两地相距多少千米?【例7】两列城铁从两城同时相对开出,一列城铁每小时走40千米,另一列城铁每小时走45千米,在途中每列车先后各停车4次,每次停车15分钟,经过7小时两车相遇,求两城的距离?【小试牛刀】两列城铁从两城同时相对开出,一列城铁每小时走40千米,另一列城铁每小时走45千米,在途中每列车先后各停车5次,每次停车12分钟,经过7小时两车相遇,求两城的距离?【例8】夏夏和冬冬同时从两地相向而行,夏夏每分钟行50米,冬冬每分钟行60米,两人在距两地中点50米处相遇,求两地的距离是多少米?【小试牛刀】甲乙两人同时从两地相向而行.甲每小时行5千米,乙每小时行4千米.两人相遇时乙比甲少行3千米.两地相距多少千米?【例9】甲乙二人同时分别自A、B两地出发相向而行,相遇之地距A、B中点300米,已知甲每分钟行100米,乙每分钟行70米,求A地至B地的距离.【小试牛刀】李明和王亮同时分别从两地骑车相向而行,李明每小时行18千米,王亮每小时行16千米,两人相遇时距全程中点3千米.问全程长多少千米?【例10】甲、乙两车分别同时从、B 两地相对开出,第一次在离A 地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B 地25千米处相遇.求、两地间的距离.【小试牛刀】甲、乙两车分别同时从A 、B 两地相对开出,第一次在离A 地90千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B 地30千米处相遇.求A 、B 两地间的距离?1.甲、乙两列火车从相距144千米的两地相向而行,甲车每小时行28千米,乙车每小时行22千米,乙车先出发2小时后,甲车才出发.甲车行几小时后与乙车相遇?2.妈妈从家出发到学校去接小红,妈妈每分钟走75米.妈妈走了3分钟后,小红从学校出发,小红每分钟走60米.再经过20分钟妈妈和小红相遇.从小红家到学校有多少米?3.甲乙两座城市相距530千米,货车和客车从两城同时出发,相向而行.货车每小时行50千米,客车每小时行70千米.客车在行驶中因故耽误1小时,然后继续向前行驶与货车相遇.问相遇时客车、货车各行驶多少千米?A AB 课后作业4.甲、乙两列火车从相距366千米的两个城市对面开来,甲列火车每小时行37千米,乙列火车每小时行36千米,甲列火车先开出2小时后,乙列火车才开出,问乙列火车行几小时后与甲列火车相遇?5.夏夏和冬冬同时从两地相向而行,两地相距1100米,夏夏每分钟行50米,冬冬每分钟行60米,问两人在距两地中点多远处相遇?6.王老师从甲地到乙地,每小时步行5千米,张老师从乙地到甲地,每小时步行4千米.两人同时出发,然后在离甲、乙两地的中点1千米的地方相遇,求甲、乙两地间的距离.7.树叶和月亮同时分别从两地骑车相向而行,树叶每小时行18千米,月亮每小时行16千米,两人相遇时距全程中点5千米.问全程长多少千米?8.甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
行程相遇

行程问题(1)---相遇问题相遇问题是指两个人或车辆(物体等)各按一定的速度从两地同时出发,沿着同一条道路相向而行,并由各种条件的变化而产生的一类应用题。
基本数量关系:速度和 X 相遇时间 = 相遇路程相遇路程÷速度和 = 相遇时间相遇路程÷相遇时间 = 速度和遇到行程问题,我们应该养成在草稿上根据题意画线段图的习惯,从而分析数量关系,确定各人行走时到达的位置,使问题得到解决。
例1:张华和李强同时从两地相对出发,张华步行每分钟走80米,李强骑自行车的速度是张华步行速度的3倍,经过5分钟后两人相遇。
求这两地相距多少米?例2:客车和货车同时从A,B两地相向开出,客车每小时行驶80千米,货车每小时行60千米,两车距中点30千米处相遇。
求A,B两地相距多少千米?例3:两个城市相距164千米,甲、乙两人骑自行车同时从两个城市出发,相向而行。
甲每小时行14千米,乙每小时行11千米,乙在中途修车耽误1小时,然后继续行驶,与甲相遇,求从出发到相遇经过几小时?例4:甲、乙两车同时从A,B两地出发,相向而行,经过4小时相遇,相遇后甲车继续行驶3小时到达B地,已知乙车每小时行驶54千米,求A, B两地相距多少千米?例5:甲、乙两地相距360千米,客车和货车同时从甲地出发驶向乙地。
客车每小时行驶60千米,货车每小时行驶40千米,客车到达乙地后停留0.5小时,又以原速返回甲地,求两车相遇的地点离乙地多少千米?例6:小青与小夏同时从甲、乙两地相对出发,第一次在距甲地60米处相遇,相遇后两人继续按原速前进,分别到达乙、甲两地后立即返回,两人第二次相遇在距离乙地15米处,则甲、乙两地的距离是多少米?练一练1.甲、乙两人从相距101千米的两地相向而行,甲先行2小时,乙再出发,甲每小时行13千米,乙每小时行12千米。
求乙出发后几小时两人相遇?2.一列快车和一列慢车,分别从甲、乙两地相对开出,快车每小时行驶105千米,慢车每小时行驶65千米,两车在距中点20千米处相遇。
小学四年级行程问题(相遇问题)例题加练习

例1、艾迪和薇儿同时从甲、乙两地出发,相向而行。
艾迪每分钟走60米,薇儿每分钟走45米,8分钟后两人相遇。
(1)1分钟后艾迪和薇儿一共走了多少米?
(2)相遇时艾迪和薇儿各走了多少米?
(3)甲、乙两地相距多少米?
练一练
甲、乙两车分别从A、B两地同时出发,相向而行,8小时相遇,若甲车每小时行40千米,乙车每小时行60千米,那么
(1)两车相遇时,甲车行了多少千米?乙车行了多少千米?
(2)求A、B两地的距离。
相遇时间=路程和÷速度和
例2、玩具车的速度是5m/s, 遥控车的速度是 6m/s, 两车从相距110米的跑道两端同时出发相向而行,经过几秒两车相遇。
练一练2
大王和小任从相距1000米的两地同时出发相向而行,大王的速度是7米/秒,小任的速度3米/秒,经过几秒后,两人相遇。
速度和=路程和÷相遇时间。
甲的速度=速度和-乙的速度。
例3、甲车与乙车从相距360千米的两地同时出发,相向而行,经过6小时相遇,已知甲车每小时行36千米,则乙车的速度是多少?
练一练3
小云和小白分别从相距14千米的甲、乙两地同时出发,相向而行,2小时后相遇。
已知小云每小时行3千米,那么小白每小时行多少千米?。
行程问题之相遇问题例题解析

行程问题之相遇问题例题解析一)相遇问题两个运动物体作相向运动或在环形跑道上作背向运动,随着时间的发展,必然面对面地相遇,这类问题叫做相遇问题。
它的特点是两个运动物体共同走完整个路程。
小学数学教材中的行程问题,一般是指相遇问题。
相遇问题根据数量关系可分成三种类型:求路程,求相遇时间,求速度。
它们的基本关系式如下:总路程=(甲速+乙速)×相遇时间相遇时间=总路程÷(甲速+乙速)另一个速度=甲乙速度和-已知的一个速度1.求路程(1)求两地间的距离例1 两辆汽车同时从甲、乙两地相对开出,一辆汽车每小时行56千米,另一辆汽车每小时行63千米,经过4小时后相遇。
甲乙两地相距多少千米?(适于五年级程度)解:两辆汽车从同时相对开出到相遇各行4小时。
一辆汽车的速度乘以它行驶的时间,就是它行驶的路程;另一辆汽车的速度乘以它行驶的时间,就是这辆汽车行驶的路程。
两车行驶路程之和,就是两地距离。
56×4=224(千米)63×4=252(千米)224+252=476(千米)综合算式:56×4+63×4=224+252=476(千米)答略。
例2 两列火车同时从相距480千米的两个城市出发,相向而行,甲车每小时行驶40千米,乙车每小时行驶42千米。
5小时后,两列火车相距多少千米?(适于五年级程度)解:此题的答案不能直接求出,先求出两车5小时共行多远后,从两地的距离480千米中,减去两车5小时共行的路程,所得就是两车的距离。
480-(40+42)×5=480-82×5=480-410=70(千米)答:5小时后两列火车相距70千米。
例4 两列火车从甲、乙两地同时出发对面开来,第一列火车每小时行驶60千米,第二列火车每小时行驶55千米。
两车相遇时,第一列火车比第二列火车多行了20千米。
求甲、乙两地间的距离。
(适于五年级程度)解:两车相遇时,两车的路程差是20千米。
四年级 奥数行程问题(相遇问题)

A
客车每小时走120千米
(540-120×1)÷(120+90) =420÷210 =2(小时) 答:货车出发2小时后两车相遇。
B
货车每小时走90千米
客车和货车共 同走的路程是 540千米吗?
2、甲、乙两地相距102千米。赵、李二人骑自行车分别 从两地同时、相向出发,赵每小时行15千米,李每小时 行14千米。李在途中因修车敢误了1小时,然后继续前 进。他们经过多少小时相遇?
乙每小时走4千米
甲、乙1小时共走多 少千米?走完这段路程 甲、乙一共需要几小时?
思维发散
1、A、B两地相距540千米。一列客车与一列货车分别从 A、B两地相向而行。客车每小时行120千米,货车每小 时行90千米,已知客车出发1小时后,货车才出发求货车 出发几小时后,两车相遇?
120千米
(540-120)千米
330÷(60+50) =330÷110 =3(小时)
80×3=240(千米)
骑摩托车的人与甲 乙两人是同时出发、同 时停止吗?那么骑摩托 车的人行驶的时间和甲、 乙两人的相遇时间有什 么关系?
答:摩托车行驶了240千米。
“中间往返”这类题目的核心就是往返行驶的时间与相遇时间相等。
思维发散
1、甲、乙两队同时从相隔50千米的两地出发,相向而行。 甲队每小时行15千米,乙队每小时行10千米,同时,一个 通讯员每小时行20千米,在两车队中间往返联络,问两队 相遇时,通讯员行了多少千米?
50÷(15+10)×20 =50÷25×20 =2×20 =40(千米)
答:通讯员行了多少千米。
通讯员行驶的时
间与两车队的相遇 时间有什么关系?
2、A、B两地相距648千米。甲、乙两列火车从A、B两地相 对开出,甲列火车每小时行驶60千米,乙列火车每小时行驶 48千米。乙出发时,从车厢里飞出一只鸽子,这只鸽子以每 小时80千米的速度在两列火车之间往返飞行(遇到一列车后 马上返回,向另一列车飞去)。当两列车相遇时,鸽子飞行 了多少千米?
四年级 奥数行程问题(相遇问题)

2×2÷(12-10)×(12+10) =4÷2×22 =2×22 =44(千米)
答:两地相距44千米。
甲一共比乙多 走了多少千米?
2、两列火车同时从A、B两地同时开出。客车每小时行 60千米,货车每小时行驶54千米,几小时后客车在超过 中点18千米处与货车相遇?求A、B两地相距多少千米。
18×2÷(60-54) =36÷6 =6(小时)
行程问题
——
甲车
乙车
相遇问题是行程问题中的重要一部分,相遇问题的特 征是:两个物体从两地出发,相向而行,共同行一段路程, 直至相遇。这类问题的基本数量关系是:总路程=速度和 ×相遇时间,这里的“速度和”是指两个物体在单位时间 内共同行的路程,还可以推导出以下的数量关系:
1.速度和=总路程÷相遇时间 2.相遇时间=总路程÷速度和
本讲我们主要解决以下几种类型:
1、一般相遇问题:如果两个物体是同时出发,那 么相遇路程就是两个物体原来相距的路程;如果两 个物体不是同时出发,那么它们的相遇路程等于两 个物体原来相距的路程减去其中一个物体先走的路 程;
2、中点相遇问题:相遇路程等于相遇地点与中 点距离的两倍;
3、往返相遇问题:同时出发,同时停止,则中间往 返的时间就相遇时间;
A
客车每小时走120千米
(540-120×1)÷(120+90) =420÷210 =2(小时) 答:货车出发2小时后两车相遇。
B
货车每小时走90千米
客车和货车共 同走的路程是 540千米吗?
2、甲、乙两地相距102千米。赵、李二人骑自行车分别 从两地同时、相向出发,赵每小时行15千米,李每小时 行14千米。李在途中因修车敢误了1小时,然后继续前 进。他们经过多少小时相遇?
四年级行程问题之一相遇问题完整版

四年级行程问题之一相遇问题HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】四年级行程问题之相遇问题研究路程、时间和速度这三者关系的问题称为行程问题。
行程问题主要包括相遇问题和追及问题。
相遇问题的特点是:总路程是由两人共同行完。
基本的计算公式如下:一、基本例题例1、甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米,两人几小时后相遇?例2、甲、乙两车分别从相距480千米的A、B两城同时出发相向而行,已知甲车从A城到B城需6小时,乙车从B城到A城需12小时,两车出发后几小时相遇?例3、东、西两村相距60千米,甲、乙两人骑车分别从东、西两村同时出发相向而行,5小时后两人相遇,已知甲每小时行5千米,求乙的速度是多少?例4、东、西两村相距55千米,甲、乙两人分别从东、西两村同时出发相向而行,5小时后两人相遇,已知甲每小时比乙多行1千米,求甲、乙两人的速度?例5、A、B两地相距200千米,甲开车从A地出发到B地,同时乙骑车从B地出发到A地,4小时后相遇,已知甲的速度是乙的4倍,求甲、乙两人的速度?例6、甲、乙两人分别从相距40千米的两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米,相遇时甲比乙多行多少千米?例7、小李和小王在环形的操场上跑步,操场的周长是400米,两人从同一起点同时出发相背而行,小李每秒跑3米,小王每秒跑5米。
(1)多少秒以后他们第一次相遇?(2)第一次相遇时两人各跑了多少米?(3)多少秒以后他们第二次相遇?第二次相遇时两人各跑了多少米?(4)多少秒以后他们5次相遇?(5)他们第6次相遇时一共跑了多少米?二、课内练习1、李明和张玫两人的家相距2公里,上午8时两人同时从家里出发,李明每分钟行120米,张玫每分钟行80米,两人几点几分相遇?相遇时李明比张玫多行多少米?2、甲、乙两车分别从相距240千米的A、B两城同时出发相向而行,已知甲车从A 城到B城需3小时,乙车从B城到A城需5小时,两车出发后几小时相遇?3、东、西两村相距80千米,甲、乙两人骑车分别从东、西两村同时出发相向而行,4小时后两人相遇,已知甲每小时行8千米,求乙的速度是多少?4、东、西两村相距40千米,甲、乙两人分别从东、西两村同时出发相向而行,8小时后两人相遇,已知甲每小时比乙多行1千米,求甲、乙两人的速度?5、A、B两地相距320千米,甲车从A地出发到B地,同时乙车从B地出发到A 地,4小时后相遇,已知甲车的速度是乙车的3倍,求甲、乙两车的速度?6、陈老师和刘老师在环形的操场上跑步,操场的周长是400米,两人从同一起点同时出发相背而行,陈老师每秒跑4米,刘老师每秒跑6米。
4年级行程问题入门-相遇问题1-例题+训练

相遇问题1知识导航相遇问题是行程问题应用题中的一种,它要求我们掌握以下三个关系式:路程和=速度和×相遇时间速度和=路程和÷相遇时间相遇时间=路程和÷速度和解答相遇问题,要特别注意两个物体出发地点是“两地”还是“同地”,出发时间是“同时”还是“先后”,运动方向是“同向”还是“相向”或“背向”,运动结果是“相遇”还是“相距”。
审题时找出这些关键词,对理清题意尤为重要。
同时还需注意单位是否统一。
解答相遇问题,一般采用直观画图的方法,帮助理解题意,分析数量关系,找到解题思路。
知识传递:掌握相遇问题基本结构、解题原理。
能力强化:理解题意的能力、分析能力、综合能力、空间想象能力。
思想方法:图形思想、公式思想、转化思想。
例题精讲一、基本关系应用(只列出综合算式,不计算、不作答)例1.小明跟丹丹两人分别从两地同时出发相向而行,小明每小时走6千米,丹丹每小时走5千米,两人经过2小时相遇,求两地相距多少千米?例2.甲、乙两人分别从相距22千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走5千米。
问两人几小时后相遇?例3.小红跟彤彤同时从相距1080米的两地相对而行,8分钟相遇。
已知小红每分钟走65米,彤彤每分钟走多少米?二、知识能力强化例1.甲、乙两辆客车从相距690千米的两地同时相向开出,甲车每小时行50千米,乙车每小时行42千米。
几小时后两车第一次相距138千米?几小时后两车第二次相距138千米?列式:列式:列式:例2.甲乙两人从相距280米的A、B两地同时出发,背向而行。
出发20分钟后两人相距2680米。
已知甲的速度与乙的速度相同,请问他们的速度是多少?思维训练1大头儿子家离学校1800米。
大头儿子放学以50米/分的速度走路回家,与此同时小头爸爸骑车以160米/分的速度去接大头儿子。
8分钟后两人还相距多远?例3.甲、乙两人从东西两地同时相向出发,两地相距10千米。
甲每小时走3千米,乙每小时走2千米。
行程问题第1讲——相遇问题

一、思维建模例1. (1)牛牛和丁丁两人分别每小时6千米和每小时4千米的速度行走,若他们从A、B两地同时出发,相向而行,5小时后相遇,则A、B两地相距多少千米?(2)甲车和乙车分别以每小时70千米,每小时50千米的速度从相距480千米的两地向对方的出发地前进。
多久后两车会相遇?思维巩固甲、乙两人分别以每小时8千米和每小时4千米的速度行走,若他们从A、B两地同时出发,相向而行,6小时后相遇,则A、B两地相距多少千米?例2.田田和阿普两家相距255千米,两人同时骑车,从家出发相对而行,3小时后相遇。
已知阿普每小时行60千米,则田田每小时行多少千米?思维巩固苹果和梨两家相距250千米,两人同时从家出发相对而行,5小时后相遇。
已知苹果每小时行30千米,则梨每小时行多少千米?例3.甲、乙两城相距780千米,货车和客车从两城同时出发,相向而行。
货车每小时行60千米,客车每小时行70千米,问:从出发开始经过多久两车第一次相距130千米?从出发开始经过多久两车第二次相距130千米?思维巩固甲车和乙车分别以每小时70千米,每小时50千米的速度从相距300千米的两地同时出发向对方前进。
当两车之间的距离是60千米时,是两车出发后多少小时?例4.甲、乙两辆汽车分别从A、B两地出发相对而行,甲车每小时行48千米,乙车每小时行50千米,若甲先出发1小时,再经过5小时相遇,求A、B两地间的距离。
思维巩固甲、乙两座城市相距530千米,货车和客车从两城同时出发,相向而行。
货车每小时行50千米,客车每小时行70千米。
客车在行驶中因故耽误1小时,然后继续向前行驶与货车相遇。
问相遇时客车、货车各行驶多少千米?例5.甲、乙两辆汽车分别从A、B两地出发相向而行,甲车先行3小时后乙车从B地出发,乙车出发5小时后两车还相距15千米。
甲车每小时行48千米,乙车每小时行50千米。
求A、B两地间相距多少千米?思维巩固甲、乙两列火车从相距942千米的两地相向而行,甲车每小时行45千米,乙车每小时行41千米,乙车先出发2小时后,甲车才出发。
四年级奥数:行程问题之相遇问题、追及问题

四年级奥数:行程问题之相遇问题、追及问题两个运动的物体,以不同的速度从不同地点出发沿同一线路相向而行,两个物体之间的距离不断缩短,直到相遇。
我们把这样的问题叫做相遇问题,相遇问题的关系式为:相遇路程=速度和×相遇时间。
解相遇问题一定要紧盯速度与相遇路程。
本篇我主要会讲到以下几种类型的题目:(1)一般相遇问题:如果两个物体是同时出发,那么相遇路程就是两个物体原来相距的路程;如果两个物体不是同时出发,那么它们的相遇路程等于两个物体原来相距的路程减去其中一个物体先走的路程;(2)中点相遇问题:相遇路程等于相遇地点与中点距离的两倍;(3)往返相遇问题:同时出发,同时停止,则中间往返的时间就是相遇时间;(4)环形相遇问题:同时、同地背向出发,相遇路程就是一周的长度。
一般相遇问题一般行程问题中,路程=速度×时间,速度=路程÷时间,时间=路程÷速度。
例题1,此类相遇问题中:相遇时间=相遇路程÷速度和。
中点相遇问题相遇问题中,路程差=速度差×时间差;速度差=路程差÷时间;时间=路程差÷速度差。
中点相遇问题中,快的多走的路程就是距离中点路程的两倍。
相遇时间=路程差÷速度差。
往返相遇问题往返相遇问题的关键是,往返行驶的时间与相遇时间相等。
环形相遇问题环形跑道上同时背向行驶,相遇几次,则相遇路程就是几个全程,再根据相遇时间=路程÷速度和求解。
在追及问题中,必定有一个物体的速度较快,而另一个物体速度较慢,解题的关键是找到追及路程。
追及问题的关系式为:追及时间×速度差=追及路程。
两种追及路线的追及路程分别是:(1)直线追及:如果两人同时同向不同地出发,那么追及路程就是两人相距的路程;如果两人同地同向不同时出发,那么追及路程就是先走的路程;(2)环形追及:如果两人同时、同地、同向出发,那么追及问题就是一周的长;如果是不同时或不同向或不同地出发,需要结合具体情景,借助示意图和列表进行分析。
行程问题之相遇问题

一、行程问题之相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和1、一般相遇问题:如果两个物体同时出发,那么相遇路程就是两个物体;如果两个物体不是同时出发,那么他们相遇路程等于两个物体减去。
2、中点相遇问题:相遇路程等于相遇地点与中点距离的倍。
3、往返相遇问题:同时出发,同时停止,则就是相遇时间。
4、环形相遇问题:同时、同地背向出发,相遇路程就是。
环形跑道上同时背向行驶,相遇几次,则相遇路程就是个全程。
题:客车和货车同时从甲、乙两地相对开出。
已知客车每小时行60千米,经过5小时后,客车已驶过中点25千米,这时与货车还相距20千米。
货车每小时行多少千米?甲、乙两地相距多少千米?二、行程问题之追及问题追及路程=追及时间×速度差追及时间=追及路程÷速度差速度差=追及路程÷追及时间1、直线追及:如果两人同时同向不同地出发,那么追及路程就是;如果两人同地同向不同时出发,那么追及路程就是。
2、环形追及:如果两人同时、同地、同向出发,那么追及路程就是;如果是不同时或不同向或不同地出发,需要结合具体背景,借助示意图和列表进行分析。
题:甲、乙两人由A到C,甲每分钟走80米,乙每分钟走50米。
乙比甲先走6分钟,两人同时到达C地。
求A、C两地的距离。
三、行程问题之过桥问题1、过一座桥:火车通过人所走的路程就是;火车通过桥所走的路程等于加上。
2、过两座桥:火车以相同的速度通过两座桥时,通过比较他们的与,可以求出火车行驶的速度。
(火车的速度=路程差÷速度差;火车的长度=×-)。
如果速度不同,先根据速度与时间的关系将速度变成相同。
路程不变时,速度增加一倍,时间减少一倍;速度减少一倍,时间增加一倍。
3、错车与超车:错车的过程就是相遇,从车头相对,到车尾离开,错车路程即相遇路程等于之和。
超车的过程就是追及,若车头对齐,则追及路程就是;若车尾对齐,则追及路程就是。
小学数学行程问题相遇问题最全版

行程问题---相遇问题1、甲乙两人分别从相距27.3千米的两地同时出发相向而行,甲每小时走6.2千米,乙每小时走4.3千米。
两人几小时后相遇?2、甲乙两艘轮船分别从A、B两港同时出发相向而行,甲船每小时行驶18.5千米,乙船每小时行驶15.6千米,经过6小时两船在途中相遇。
两地间的水路长多少千米?3、甲乙两车分别从相距480千米的A、B两城同时出发,相向而行,已知甲车从A城到B城需6小时,乙车从B城到A城需12小时。
两车出发后多少小时相遇?4、一列快车和一列慢车分别从甲乙两地同时相向而行。
快车10小时可以到达乙地,慢车15小时可以到达甲地。
已知快车每小时比慢车多行20千米,两车出发后几小时相遇?5、甲、乙两车同时从东、西两地相向开出,甲车每小时行56.4千米,乙车每小时行48.6千米。
两车在距中点42.9千米处相遇,东、西两地相距多少千米?6、.甲、乙两汽车同时从两地出发,相向而行。
甲汽车每小时行52.6千米,乙汽车每小时行55.4千米,两车在距中点16.8千米处相遇。
求两地之间的路程是多少千米?7、一辆汽车和一辆摩托车同时从A、B两城相对开出,汽车每小时行62.5千米,摩托车每小时行70千米,当摩托车行到两地中点处时,与汽车还相距30千米。
求A、B两城之间的距离?8、甲乙两地相距60千米,甲乙两人都骑自行车从A城同时出发,甲比乙每小时慢4千米,乙到B城当即折返,于距B城12千米处与甲相遇,那么甲的速度是多少?9、快车和慢车同时从甲、乙两地相向开出,快车每小时行40千米,经过3小时,快车已驶过中点25千米,这时快车与慢车还相距7千米。
慢车每小时行多少千米?10、兄弟二人同时从学校和家中出发,相向而行。
哥哥每分钟行120米,5分钟后哥哥已超过中点50米,这时兄弟二人还相距30米。
弟弟每分钟行多少米?11.汽车从甲地开往乙地,每小时行32千米。
4小时后,剩下的路比全程的一半少8千米,如果改用每小时56千米的速度行驶,再行几小时到达乙地?12、甲乙两车同时从A、B两地相对开出,4小时后相遇,甲车再开3小时到达B地。
行程问题(一)——相遇问题

行程问题(一)——相遇问题公式:路程=速度×时间速度=路程÷时间时间=路程÷速度例1、客车和货车同时从A、B两地相向开出,客车每小时行60千米,货车每小时行80千米。
两车在距中点30千米处相遇。
求A、B两地相距多少千米?练习1 甲、乙两车同时从东西两地相向而行,甲车速度56千米/小时,乙车速度48千米/小时,两车在离中点32千米处相遇。
求东西两地相距多少千米?练习2 甲乙两人同时从A、B两地相向而行,甲骑车每小时行16千米,乙骑摩托车每小时行65千米。
甲离出发点62.4千米处与乙相遇。
A、B两地相距多少千米?练习3 两艘宇宙飞船径直相向飞行,一艘飞船的速度为每分钟8千米,另一艘为每分钟12千米。
假设它们正好相距5000千米,那么在相遇前1分钟相距多少千米?例2 两地相距3千米,甲乙两人同时从两地出发相向而行。
甲每分钟行80米,乙每分钟行70米。
如果有一只狗与甲同行,狗每分钟跑150米,当狗遇到乙时立即返回,遇到甲后又迎乙跑去。
这样,狗不停地在甲乙之间往返跑,直到两人相遇为止。
那么狗在两人中间跑的路程是多少?练习1 两辆汽车从相距500千米的两城同时出发,相向而行。
一辆摩托车以每小时80千米的速度在两汽车之间不断往返联络。
已知两汽车的速度分别为40千米和60千米。
求两汽车相遇时,摩托车共行了多少千米?练习2 两队同学从相距30千米的甲乙两地相向出发,一只鸽子以每小时20千米的速度在两队同学之间不断往返送信。
如果鸽子从同学们出发到相遇共飞行了30千米,而甲队同学比乙队同学每小时多走0.4千米。
求两队同学的行走速度。
例3 甲乙两辆旅游车同时从A、B两地出发,相向而行,4小时相遇。
相遇后甲车继续行使了3小时到达B 地,乙车每小时行24千米。
问AB两地相距多少千米?练习1 甲乙两人从AB两地相向而行,6分钟相遇,相遇后甲继续走4分钟到达B地,乙每分钟行40米。
问:AB两地相距多少米?例4 甲乙两人同时从东西两镇出发相向而行,经过2小时40分钟,在途中相遇,相遇后各自继续前进。
四年级思维训练 行程问题

四年级思维训练行程问题(一)姓名相遇问题的特点及计算方法:(1)两者从两地同时出发相向而行;(2)两者从同一地点沿相反方向同时运动(即相背而行)。
总路程=相遇时间×速度和相遇时间=总路程÷速度和一个速度=总路程÷相遇时间—另一个速度【例1】甲、乙两人分别从相距30千米的两地,同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
两人几小时后相遇?【试一试】1.甲每小时19千米,乙每小时13千米,两人相背而行,8小时后两人相隔多远?2.甲从A地出发,每小时15千米,乙从B地出发,每小时9千米,6小时后,两人共行了多少千米?【例2】南北两村相距90千米,甲、乙两人分别从两村同时出发相向而行,甲每小时行10千米,5小时后两人相遇,乙的速度是多少?【试一试】1.晶晶、亮亮两人同时从相隔264千米的两地相向而行,晶晶每小时行20千米,6小时后两人相遇,亮亮的速度是多少?2、东西两镇相距45千米,甲、乙两人分别从两镇同时出发相向而行,甲每小时行的路程是乙的2倍,5小时后两人相遇。
两人的速度各是多少?【例3】货车和客车同时从东西两地相向而行,货车每小时行48千米,客车每小时行42千米,两车在中点18千米处相遇,求东西两地相距多少千米?【试一试】1.甲、乙两人同时分别从两地骑车相向而行,甲每小时行20千米,乙每小时行18千米。
两人相遇时距全程中点3千米,求全程长多少千米?2.甲、乙两辆汽车同时分别从东西两城相向开出,甲车每小时行60千米,乙每小时行56千米。
两车距中点16千米处相遇,求东西两城相距多少千米?【例4】王欣和陆亮两人同时从相距2000米的两地相向而行。
王欣每分钟行110米,陆亮每分钟行90米,如果一只狗与王欣同时同向而行,每分钟行500米,遇到陆亮后立即回头向王欣跑去,遇到王欣再向陆亮跑去。
这样不断来回,直到王欣和陆亮相遇为止,狗共行了多少米?【试一试】1.甲乙两队学生从相隔18千米的两地同时出发,相向而行。
应用题板块-行程问题之相遇追及(小学四年级奥数题)
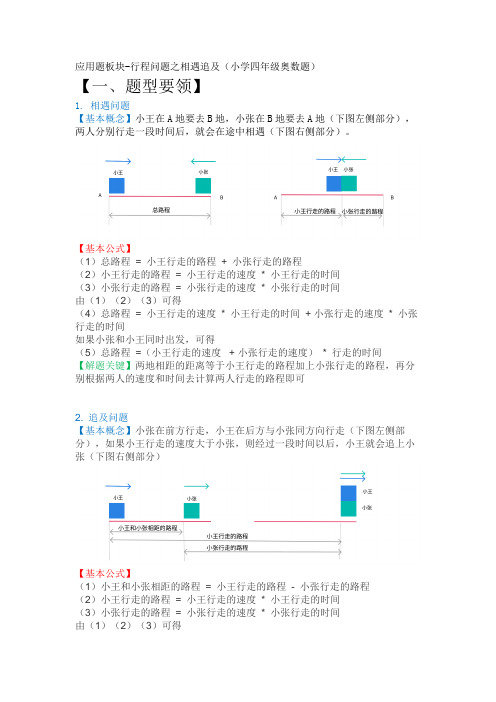
应用题板块-行程问题之相遇追及(小学四年级奥数题)【一、题型要领】1. 相遇问题【基本概念】小王在A地要去B地,小张在B地要去A地(下图左侧部分),两人分别行走一段时间后,就会在途中相遇(下图右侧部分)。
【基本公式】(1)总路程= 小王行走的路程+ 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)总路程= 小王行走的速度* 小王行走的时间+ 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)总路程=(小王行走的速度 + 小张行走的速度)* 行走的时间【解题关键】两地相距的距离等于小王行走的路程加上小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可2. 追及问题【基本概念】小张在前方行走,小王在后方与小张同方向行走(下图左侧部分),如果小王行走的速度大于小张,则经过一段时间以后,小王就会追上小张(下图右侧部分)【基本公式】(1)小王和小张相距的路程= 小王行走的路程- 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)小王和小张相距的路程 = 小王行走的速度* 小王行走的时间- 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)小王和小张相距的路程 =(小王行走的速度 - 小张行走的速度)* 行走的时间【解题关键】小王和小张相距的距离等于小王行走的路程减去小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可【举一反三】有一类题目是为赶时间,题目描述“为了节省XX时间从原本的速度x变成了之后的速度y”,解题时可以假象成另一个人以原速度提前走了XX 时间,而自身以修改后的速度从原地出发,最终两人同时到达终点,即可用“追及”问题解答【二、重点例题】例题1【题目】小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟,他们同时出发,几分钟后两人相遇?【分析】走同样长的距离,小张花费的时间是小王花费时间的36 ÷ 12 = 3(倍),因此自行车的速度是步行速度的3倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级行程问题之相遇问题
研究路程、时间和速度这三者关系的问题称为行程问题。
行程问题主要包括相遇问题和追及问题。
相遇问题的特点是:总路程是由两人共同行完。
基本的计算公式如下:
一、基本例题
例1、甲、乙两人分别从相距20千米的两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米,两人几小时后相遇?
例2、甲、乙两车分别从相距480千米的A、B两城同时出发相向而行,已知甲车从A城到B城需6小时,乙车从B城到A城需12小时,两车出发后几小时相遇?
例3、东、西两村相距60千米,甲、乙两人骑车分别从东、西两村同时出发相向而行,5小时后两人相遇,已知甲每小时行5千米,求乙的速度是多少?
例4、东、西两村相距55千米,甲、乙两人分别从东、西两村同时出发相向而行,5小时后两人相遇,已知甲每小时比乙多行1千米,求甲、乙两人的速度?
例5、A、B两地相距200千米,甲开车从A地出发到B地,同时乙骑车从B地出发到A地,4小时后相遇,已知甲的速度是乙的4倍,求甲、乙两人的速度?
例6、甲、乙两人分别从相距40千米的两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米,相遇时甲比乙多行多少千米?
例7、小李和小王在环形的操场上跑步,操场的周长是400米,两人从同一起点同时出发相背而行,小李每秒跑3米,小王每秒跑5米。
(1)多少秒以后他们第一次相遇?
(2)第一次相遇时两人各跑了多少米?
(3)多少秒以后他们第二次相遇?第二次相遇时两人各跑了多少米?
(4)多少秒以后他们5次相遇?
(5)他们第6次相遇时一共跑了多少米?
二、课内练习
1、李明和张玫两人的家相距2公里,上午8时两人同时从家里出发,李明每分钟行120米,张玫每分钟行80米,两人几点几分相遇?相遇时李明比张玫多行多少米?
2、甲、乙两车分别从相距240千米的A、B两城同时出发相向而行,已知甲车从A城到B城需3小时,乙车从B城到A城需5小时,两车出发后几小时相遇?
3、东、西两村相距80千米,甲、乙两人骑车分别从东、西两村同时出发相向而行,4小时后两人相遇,已知甲每小时行8千米,求乙的速度是多少?
4、东、西两村相距40千米,甲、乙两人分别从东、西两村同时出发相向而行,8小时后两人相遇,已知甲每小时比乙多行1千米,求甲、乙两人的速度?
5、A、B两地相距320千米,甲车从A地出发到B地,同时乙车从B地出发到A地,4小时后相遇,已知甲车的速度是乙车的3倍,求甲、乙两车的速度?
6、陈老师和刘老师在环形的操场上跑步,操场的周长是400米,两人从同一起点同时出发相背而行,陈老师每秒跑4米,刘老师每秒跑6米。
(1)多少秒后他们第3次相遇?
(2)第3次相遇时刘老师比陈老师多跑多少米?
(3)他们第7次相遇时,一共跑了多少米?
7、甲、乙两人分别从AB两地同时出发相向而行,出发后2小时后相距55千米,出发后5小时相距22千米,从出发到相遇共需要几小时?
三、作业
1、甲、乙两车分别从相距180千米的两地同时出发相向而行,甲车每小时行35千米,乙车每小时行25千米,两车几小时后相遇?
2、甲、乙两车分别从相距240千米的A、B两城同时出发相向而行,已知甲车从A城到B城需3小时,乙车从B城到A城需5小时,两车出发后几小时相遇?
4、学校到少年宫有3千米,陈林从学校到少年宫去,同时吴欣从少年宫回学校,20分钟后两人相遇,已知陈林每分钟比吴欣多行20米,求两人每分钟各行多少米?
5、A、B两地相距240千米,甲车从A地出发到B地,同时乙车从B地出发到A地,5小时后相遇,已知甲车的速度是乙车的2倍,求甲、乙两车的速度?
6、王欣欣和陆萌萌两人同时从相距2000米的两地相向而行,王欣欣每分钟行110米,陆萌萌每分钟行90米,如果一只狗与王欣欣同时同向而行,每分钟行500米,遇到陆萌萌后立即返回跑向王欣欣,遇到王欣欣后再立即跑向陆萌萌,这样不断来回,直到两人相遇为止。
狗共跑了多少米?
*7、甲、乙两人从相距100千米的两地出发相向而行,甲先出发1小时,两人在乙出发4小时后相遇。
已知甲比乙每小时多行2千米,求甲、乙各自的速度。
