离散数学第2次作业参考答案
离散数学习题答案及解析_2

离散数学习题答案习题一1、利用逻辑联结词把下列命题翻译成符号逻辑形式(1)他既是本片的编剧,又是导演--- P∧ Q(2)银行利率一降低,股价随之上扬--- P→ Q(3)尽管银行利率降低,股价却没有上扬--- P∧ Q(4)占据空间的、有质量而且不断变化的对象称为物质--- M ←→<S∧P∧T> (5)他今天不是乘火车去北京,就是随旅行团去了九寨沟 --- P▽ Q(6)小张身体单薄,但是极少生病,并且头脑好使--- P∧ Q ∧ R(7)不识庐山真面目,只缘身在此山中--- P→ Q〔解释:因为身在此山中,所以不识庐山真面目(8)两个三角形相似,当且仅当他们的对应角相等或者对应边成比例--- S ←→<E∨T>(9)如果一个整数能被6整除,那么它就能被2和3整除。
如果一个整数能被3整除,那么它的各位数字之和也能被3整除解:设 P –一个整数能被6整除Q –一个整数能被2整除 R –一个整数能被3整除S –一个整数各位数字之和能被3整除翻译为:〔P→〔Q ∧ R∧〔R→ S2、判别下面各语句是否命题,如果是命题,说出它的真值〔1BASIC语言是最完美的程序设计语言--- Y,T/F〔2这件事大概是小王干的--- N〔3x2 = 64 --- N〔4可导的实函数都是连续函数--- Y,T/F〔5我们要发扬连续作战的作风,再接再厉,争取更大的胜利--- N〔6客观规律是不以人们意志为转移的--- Y,T〔7到2020年,中国的国民生产总值将赶上和超过美国--- Y,N/A〔8凡事都有例外--- Y,F3、构造下列公式的真值表,并由此判别哪些公式是永真式、矛盾式或可满足式〔1〔P∨〔~P∧ Q→ Q〔2~〔4表略:〔2可满足式、〔3永真式、〔4可满足式4、利用真值表方法验证下列各式为永真式〔1~〔8略5、证明下列各等价式〔3P→〔Q∨ R⇔〔P→ Q∨〔P→ R证明:左式⇔~P∨Q∨ R⇔~P∨Q∨~P∨ R⇔〔~P∨Q∨〔~P∨ R⇔〔P→ Q∨〔P→ R⇔右式〔4〔P∧ Q∨〔R∧ Q∨〔R∧ P⇔〔P∨ Q∧〔R∨ Q∧〔R∨ P证明:左式⇔<〔P∨R∧ Q∨〔R∧ P⇔<〔P∨R∨R>>∧<〔P∨R∨P>>∧〔Q∨R∧〔Q∨P⇔〔P∨ Q∧〔R∨ Q∧〔R∨ P⇔右式6、如果P∨ Q ⇔ Q∨R,能否断定 P ⇔ R ?如果P∧ Q ⇔ Q∧R,能否断定 P ⇔ R?如果~P ⇔~R,能否断定 P ⇔ R?解:〔1如果P∨ Q ⇔ Q∨R,不能判断P ⇔ R,因为如果 Q = P∨ R, 那么P∨ Q⇔P ∨P∨ R ⇔ Q∨R,但P可以不等价于R.〔2如果P∧ Q ⇔ Q∧R,不能判断P ⇔ R,因为如果 Q = P∧ R, 那么P∧ Q⇔P ∧P∧ R ⇔ Q∧R,但P可以不等价于R.〔3如果~P ⇔~R,那么有P ⇔ R,因为~P ⇔~R,则~P <-> ~R为永真式,及有P <-> R为永真式,所以P ⇔ R.8、把下列各式用↑等价表示出来〔1<P∧Q>∨~P解:原式⇔ <<P↑Q>↑<P↑Q>>∨<P↑P>⇔ <<<P↑Q>↑<P↑Q>>↑<<P↑Q>↑<P↑Q>>>↑<<P↑P>↑<P↑P>>9、证明:{ ~→}是最小功能完备集合证明: 因为{~,∨}是最小功能完备集合,所以,如果{ ~→}能表示出∨,则其是功能完备集合。
离散数学第二次作业题及答案.doc

第2次作业一、单项选择题(本大题共40分,共20小题,每小题2分)1.假设A={a, b, c, d},考虑子集S= {{a, b}, {b, c}, {d}},则下列选项正确的是()oA.S是A的覆盖B.S是A的划分C.s既不是划分也不是覆盖D.以上选项都不正确2.设h是群G上的一个同态,|G|二12,山(G)|二3,则|K| (K是h的核)二_________________ ()A.1B.2C.D.3.L23 ), 设G是连通(n,m)的平面图,有r个面,且每个面的次数至少为L( 则A.m>3n-6B.Hl <c.m+n-r=2D.m+r-n二24.如果小王和小张都不去,则小李去。
设P:小王去。
Q:小张去。
R:小李去。
则命题符号化为_________ oA.-I QA-i PVRB.(Q->P)ARC.(n PAn QLRD.(PAQ)-R5.没有不犯错误的人。
M(x): x为人。
F (x) : x犯错误。
则命题可表示为()OA.(Vx) (M(x) F (x)B.(3x) (M(x) AF(x)C.(Vx) (M(x)AF(x))D.(3x) (M(x)-F(x)6.(1)燕子北冋,春天来了。
设P:燕了北回。
Q:春天來了。
则(1)可以表示为___________ oP->QQ-PC.UQD.P VQ7.命题公式(P->QA-i P)的类型是___________ 。
A.重言式B.矛盾式C.可满足式D.永真式6.一阶逻辑公式Vx(F(x, y)AG(y, z) )—VzF(z, y)是()前束范式封闭公式C.永真式D.永假式7.谓词公式(3x)P(x, y) A (Vx) (Q(x, z)-> Gx) (Vy)R(x, y, z)中的量词Vx 的辖域是()。
A.(Vx)(Q(x,z)->(3 x)( Vy)R(x,y ,z)B.Q(x, z)-> (Vy)R(x, y, z)C.Q (x, z) —(3x) (Vy) R (x, y, z)D.Q(x, z)8.关于半群的性质,下面说法不正确的是()A.若〈S,*>S且*在8上是封闭的,那么匸是一个半群,B<B, *>也是一个半群。
离散数学课后习题答案二

习题3.71. 列出关系}6|{=⋅⋅⋅∈><+d c b a d c b a d c b a 且,,,,,,Z 中所有有序4元组。
解 }6|{=⋅⋅⋅∈><+d c b a d c b a d c b a 且,,,,,,Z,2,1,3,1,3,1,2,1,2,3,1,1,3,2,1,1,1,1,1,6,1,1,6,1,1,6,1,1,6,1,1,1{><><><><><><><><=><><><><><><><><2,1,1,3,3,1,1,2,1,2,1,3,1,3,1,2,1,1,2,3,1,1,3,2,1,2,3,1,1,3,2,12. 列出二维表3.18所表示的多元关系中所有5元组。
假设不增加新的5元组,找出二维表3.18所有的主键码。
表3.18 航班信息航空公司 航班 登机口 目的地 起飞时间 Nadir 112 34 底特律 08:10 Acme 221 22 丹佛 08:17 Acme 122 33 安克雷奇 08:22 Acme 323 34 檀香山 08:30 Nadir 199 13 底特律 08:47 Acme 222 22 丹佛 09:10 Nadir 32234底特律09:44解 略3. 当施用投影运算5,3,2π到有序5元组><d c b a ,,,时你能得到什么?解 略4. 哪个投影运算用于除去一个6元组的第一、第二和第四个分量? 解 略5. 给出分别施用投影运算4,2,1π和选择运算Nadir 航空公司=σ到二维表3.18以后得到的表。
解对航班信息二维表进行投影运算5,3,2π后得到的二维表航班 登机口 起飞时间 112 34 08:10 221 22 08:17 122 33 08:22 323 34 08:30 199 13 08:47 222 22 09:10 3223409:44对航班信息二维表进行选择运算Nadir 航空公司= 后得到的二维表航空公司 航班 登机口 目的地 起飞时间 Nadir 112 34 底特律 08:10 Nadir 199 13 底特律 08:47 Nadir 32234底特律09:446. 把连接运算3J 用到5元组二维表和8元组二维表后所得二维表中有序多元组有多少个分量?解 略7. 构造把连接运算2J 用到二维表3.19和二维表3.20所得到的二维表。
离散数学答案第二章习题解答

第二章 谓词逻辑习题与解答1. 将下列命题符号化:(1) 所有的火车都比某些汽车快。
(2) 任何金属都可以溶解在某种液体中。
(3) 至少有一种金属可以溶解在所有液体中。
(4) 每个人都有自己喜欢的职业。
(5) 有些职业是所有的人都喜欢的。
解 (1) 取论域为所有交通工具的集合。
令x x T :)(是火车, x x C :)(是汽车, x y x F :),(比y 跑得快。
“所有的火车都比某些汽车快”可以符号化为))),()(()((y x F y C y x T x ∧∃→∀。
(2) 取论域为所有物质的集合。
令x x M :)(是金属, x x L :)(是液体, x y x D :),(可以溶解在y 中。
“任何金属都可以溶解在某种液体中” 可以符号化为))),()(()((y x D y L y x M x ∧∃→∀。
(3) 论域和谓词与(2)同。
“至少有一种金属可以溶解在所有液体中” 可以符号化为))),()(()((y x D y L y x M x →∀∧∃。
(4) 取论域为所有事物的集合。
令x x M :)(是人, x x J :)(是职业, x y x L :),(喜欢y 。
“每个人都有自己喜欢的职业” 可以符号化为))),()(()((y x L y J y x M x ∧∃→∀(5)论域和谓词与(4)同。
“有些职业是所有的人都喜欢的”可以符号化为))),()(()((x y L y M y x J x →∀∧∃。
2. 取论域为正整数集,用函数+(加法),•(乘法)和谓词<,=将下列命题符号化:(1) 没有既是奇数,又是偶数的正整数。
(2) 任何两个正整数都有最小公倍数。
(3) 没有最大的素数。
(4) 并非所有的素数都不是偶数。
解 先引进一些谓词如下:x y x D :),(能被y 整除,),(y x D 可表示为)(x y v v =•∃。
x x J :)(是奇数,)(x J 可表示为)2(x v v =•⌝∃。
离散数学课后习题答案(第二章)

b) 他是田径或球类运动员。 解:设 S(x) :x 是田径运动员。B(x) :x 是球类运动员。h:他 则有 S(h)∨B(h) c) 小莉是非常聪明和美丽的。 解:设 C(x) :x 是聪明的。B(x) :x 是美丽的。l:小莉。 则有 C(l)∧ B(l) d)若 m 是奇数,则 2m 不是奇数。 解:设 O(x) :x 是奇数。 则有 O(m)→¬ O(2m) 。 e)每一个有理数是实数。 解:设 R(x) :x 是实数。Q(x) :x 是有理数。 则有 (∀x) (Q(x)→R(x) ) f) 某些实数是有理数。 解:设 R(x) :x 是实数。Q(x) :x 是有理数。 则有 (∃x) (R(x)∧Q(x) ) g) 并非每个实数都是有理数。 解:设 R(x) :x 是实数。Q(x) :x 是有理数。 则有 ¬(∀x) (R(x)→Q(x) ) h)直线 A 平行于直线 B,当且仅当直线 A 不相交于直线 B。 解:设 P(x,y) :直线 x 平行于直线 y,G(x,y) :直线 x 相交于直线 y。 则有 P(A,B)�¬G(A,B) (2) 找出以下十二个句子所对应的谓词表达式。 a) 所有的教练员是运动员。 (J(x),L(x)) 解:设 J(x):x 是教练员。L(x):x 是运动员。 则有 (∀x) (J(x)→L(x) ) b) 某些运动员是大学生。 (S(x)) 解:设 S(x):x 是大学生。L(x):x 是运动员。 则有 (∃x) (L(x)∧S(x) ) c) 某些教练是年老的,但是健壮的。 (O(x),V(x) ) 解:设 J(x):x 是教练员。O(x):x 是年老的。V(x) :x 是健壮的。 则有 (∃x) (J(x)∧O(x)∧V(x) ) d) 金教练既不老但也不健壮的。 (j) 解:设 O(x):x 是年老的。V(x) :x 是健壮的。j:金教练 则有 ¬ O(j)∧¬V(j) e) 不是所有的运动员都是教练。 解:设 L(x):x 是运动员。J(x):x 是教练员。 则 ¬(∀x) (L(x)→J(x) ) f) 某些大学生运动员是国家选手。 (C(x) )
离散数学课后习题答案(第二章)

b) 他是田径或球类运动员。 解:设 S(x) :x 是田径运动员。B(x) :x 是球类运动员。h:他 则有 S(h)∨B(h) c) 小莉是非常聪明和美丽的。 解:设 C(x) :x 是聪明的。B(x) :x 是美丽的。l:小莉。 则有 C(l)∧ B(l) d)若 m 是奇数,则 2m 不是奇数。 解:设 O(x) :x 是奇数。 则有 O(m)→¬ O(2m) 。 e)每一个有理数是实数。 解:设 R(x) :x 是实数。Q(x) :x 是有理数。 则有 (∀x) (Q(x)→R(x) ) f) 某些实数是有理数。 解:设 R(x) :x 是实数。Q(x) :x 是有理数。 则有 (∃x) (R(x)∧Q(x) ) g) 并非每个实数都是有理数。 解:设 R(x) :x 是实数。Q(x) :x 是有理数。 则有 ¬(∀x) (R(x)→Q(x) ) h)直线 A 平行于直线 B,当且仅当直线 A 不相交于直线 B。 解:设 P(x,y) :直线 x 平行于直线 y,G(x,y) :直线 x 相交于直线 y。 则有 P(A,B)�¬G(A,B) (2) 找出以下十二个句子所对应的谓词表达式。 a) 所有的教练员是运动员。 (J(x),L(x)) 解:设 J(x):x 是教练员。L(x):x 是运动员。 则有 (∀x) (J(x)→L(x) ) b) 某些运动员是大学生。 (S(x)) 解:设 S(x):x 是大学生。L(x):x 是运动员。 则有 (∃x) (L(x)∧S(x) ) c) 某些教练是年老的,但是健壮的。 (O(x),V(x) ) 解:设 J(x):x 是教练员。O(x):x 是年老的。V(x) :x 是健壮的。 则有 (∃x) (J(x)∧O(x)∧V(x) ) d) 金教练既不老但也不健壮的。 (j) 解:设 O(x):x 是年老的。V(x) :x 是健壮的。j:金教练 则有 ¬ O(j)∧¬V(j) e) 不是所有的运动员都是教练。 解:设 L(x):x 是运动员。J(x):x 是教练员。 则 ¬(∀x) (L(x)→J(x) ) f) 某些大学生运动员是国家选手。 (C(x) )
离散数学练习题2 答案
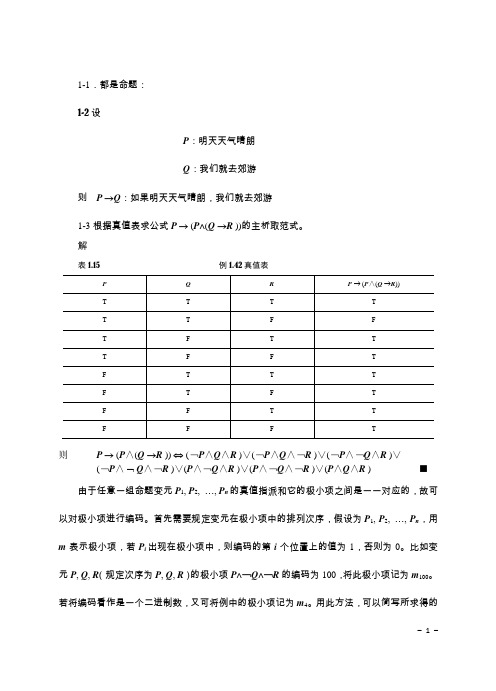
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
国家开放大学电大本科《离散数学》网络课形考任务2作业及答案

国家开放大学电大本科《离散数学》网络课形考任务2作业及答案此任务2 g选择题题目1 无向完全图K4是()、选择一项:A、树 B、欧拉图 C、汉密尔顿图 D、非平面图题目2 已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T 的树叶数为()、选择一项: A、4 B、8 C、3 D、5 题目3 设无向图G的邻接矩阵为 011111 0 0111 0 0 0 011 0 011 01 0 则G 的边数为( 选择一项: A、7 B、14 C、6 D、1 题目4 如图一所示,以下说法正确的是()、选择一项: A、 ((a, e), (b, c)}是边割集 B、{(a, e)}是边割集 C、{(d, e)}是边割集 D、((a, e)}是割边题目5 以下结论正确的是()、选择一项: A、有n个结点n-l条边的无向图都是树B、无向完全图都是平面图 C、树的每条边都是割边 D、无向完全图都是欧拉图题目6 若G是一个欧拉图,则G一定是()、选择一项: A、汉密尔顿图 B、连通图 C、平面图 D、对偶图题目7 设图G=, vGV,则下列结论成立的是()、选择一项:A、云 d做、)=2|% B、2>“ = |司 w C、 deg(v)=2|S| D、deg(v)=|E| 题目8 图G如图三所示,以下说法正确的是()、选择一项: A、(b, d}是点割集 B、{c}是点割集 C、{b, c}是点割集 D、 a是割点题目9 设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是()、选择一项: (a)是费连通的 B、 (d)是强连通的 C、 (c)是强连通的D、 (b)是强连通的题目10 设有向图(a)、(b)、(c)与(d)如图六所示,则下列结论成立的是()、选择一项: A、 (b)只是弱连通的 B、 (c)只是弱连通的 C、 (a)只是弱连通的 D、 (d)只是弱连通的判断逝题目11 设图G是有6个结点的连通图,结点的总度数为18,则可从G中删去4条边后使之变成树、()选择一项:对错题目12 汉密尔顿图一定是欧拉图、()选择一项:对错题目13 设连通平面图G的结点数为5,边数为6,则面数为4、()选择一项:对错题目14 设G是一个有7个结点16条边的连通图,则G为平面图、()选择一项:对错题目15 如图八所示的图G存在一条欧拉回路、()选择一项:对错题目16 设图G如图七所示,则图G的点割集是{f}、()选择一项:对错题目172>瞒)=2圜设G是一个图,结点集合为V,边集合为E,则代衫()选择一项:对错题目18 设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树、()选择一项:对错题目19 如图九所示的图G不是欧拉图而是汉密尔顿图、()选择一项:对错题目20 若图 G=,其中 V=( a, b, c, d }, E={ (a, b), (a, d), (b, c), (b, d)},则该图中的割边为(b, c)、()选择一项:对。
国家开放大学电大本科《离散数学》网络课形考任务2作业及答案

A. 有n个结点n-1条边的无向图都是树
B. 无向完全图都是平面图
C. 树的每条边都是割边
D. 无向完全图都是欧拉图
题目6
若G是一个欧拉图,则G一定是( ).
选择一项:
A. 汉密尔顿图
B. 连通图
C. 平面图
D. 对偶图
题目7
设图G=<V, E>,v∈V,则下列结论成立的是 ( ) .
选择一项:
选择一项:
对
错
题目17
设G是一个图,结点集合为V,边集合为E,则 ( )
选择一项:
对
错
题目18
设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.( )
选择一项:
对
错
题目19
如图九所示的图G不是欧拉图而是汉密尔顿图.( )
选择一项:
对
错
题目20
若图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, d),(b, c), (b, d)},则该图中的割边为(b, c).( )
题目8
图G如图三所示,以下说法正确的是 ( ).
选择一项:
A. {b, d}是点割集
B. {c}是点割集
C. {b, c}是点割集
D. a是割点
题目9
设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).
选择一项:
A. (a)是强连通的
B. (d)是强连通的
C. (c)是强连通的
选择一项:
对
错
题目12
汉密尔顿图一定是欧拉图.( )
选择一项:
对
离散数学课后习题答案 (2)

离散数学课后习题答案1. 第一章习题答案1.1 习题一答案1.1.1 习题一.1 答案根据题意,设集合A和B如下:Set A and BSet A and B在此情况下,我们可以得出以下结论:•A的幂集为{ {}, {a}, {b}, {a, b} };•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} };•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }。
因此,习题一.1的答案为:•A的幂集为{ {}, {a}, {b}, {a, b} };•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} };•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b,2), (b, 3) }。
1.1.2 习题一.2 答案根据题意,集合A和B如下所示:Set A and BSet A and B根据集合的定义,习题一.2要求我们判断以下命题的真假性:a)$A \\cap B = \\{ 2, 3 \\}$b)$\\emptyset \\in B$c)$A \\times B = \\{ (a, 2), (b, 1), (b, 3) \\}$d)$B \\subseteq A$接下来,我们来逐个判断这些命题的真假性。
a)首先计算集合A和B的交集:$A \\cap B = \\{ x\\,|\\, x \\in A \\, \\text{且} \\, x \\in B \\} = \\{ 2, 3 \\}$。
因此,命题a)为真。
b)大家都知道,空集合是任意集合的子集,因此空集合一定属于任意集合的幂集。
根据题意,$\\emptyset \\in B$,因此命题b)为真。
c)计算集合A和B的笛卡尔积:$A \\times B = \\{ (x, y) \\,|\\, x \\in A \\, \\text{且} \\, y \\in B \\} = \\{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) \\}$。
离散数学第2次作业参考答案

离散数学第二次作业参考答案学号: 姓名: 班级: 总分:1、 (每空5分,共30分)(1) 已知公式A 含有3个命题变项p , q , r ,并且它的成真赋值为000,011,110,那么命题公式A 的成假赋值为 001,010,100,101,111 ,主析取范式为 , 主合取范式为 M 1∧M 2∧M 4∧M 5∧M 7 。
(2) 已知公式A 含有3个命题变项,并且公式A 的主合取范式为134M M M ∧∧,那么公式A 的成真赋值为 000, 010,101,110,111 ,成假赋值为 001, 011, 100 ,公式A 的主析取范式为 。
2、(12分)用真值表法计算公式()p q r ⌝∨∧的主析取范式和主合取范式解:真值表为p q r p q ⌝∨ ()p q r ⌝∨∧0 0 0 1 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 0 0 1 0 1 0 0 1 1 0 1 0 1 1 111主析取范式:137m m m ∨∨主合取范式:02456M M M M M ∧∧∧∧3、(14分)甲、乙、丙、丁4人中有且仅有2个人参加围棋比赛。
关于谁参加了比赛,下列判断都是正确的:(1) 甲和乙只有一人参加。
(2) 若丙参加,则丁必参加。
(3) 乙或者丁至多参加一人。
(4) 丁不参加,则甲也不会参加。
问:哪两个人参加了比赛。
解:其它解题方法,只要解释清楚,答案正确就给分① 设p : 甲参加,q :乙参加,r :丙参加,s :丁参加。
② 4个条件分别符号化为()()p q p q ⌝∧∨∧⌝,()r s →,()q s ⌝∨⌝,()s p ⌝→⌝ 根据题意可得公式[()()]()()()p q p q r s q s s p ⌝∧∨∧⌝∧→∧⌝∨⌝∧⌝→⌝ 该公式的成真赋值为可能可行的方案。
③经过演算可得[()()]()()()()()()()()p q p q r s q s s p p q p q r s q s p s ⌝∧∨∧⌝∧→∧⌝∨⌝∧⌝→⌝⇔⌝∨⌝∧∨∧⌝∨∧⌝∨⌝∧⌝∨④由于p 和q 有且仅有一个为1,因此公式的成真赋值只能是10XX 或者01XX 。
离散数学(屈婉玲版)第二章习题答案

2.13 设解释I为:个体域D I ={-2,3,6},一元谓词F(X):X≤3,G(X):X>5,R(X):X≤7。
在I下求下列各式的真值。
(1)∀x(F(x)∧G(x))解:∀x(F(x)∧G(x))⇔(F(-2) ∧G(-2)) ∧(F(3) ∧G(3)) ∧(F(6) ∧G(6))⇔((-2≤3) ∧(-2>5)) ∧((3≤3) ∧(3>5)) ∧((6≤3) ∧(6<5))⇔((1 ∧0))∧((1 ∧0)) ∧((0 ∧0))⇔0∧0∧0⇔0(2) ∀x(R(x)→F(x))∨G(5)解:∀x(R(x)→F(x))∨G(5)⇔(R(-2)→F(-2))∧ (R(3)→F(3))∧ (R(6)→F(6))∨ G(5)⇔((-2≤7) →(-2≤3))∧ (( 3≤7) →(3≤3))∧ (( 6≤7) →(6≤3)) ∨ (5>5)⇔(1 →1)∧ (1 →1)∧ (1→0) ∨ 0⇔1∧ 1∧ 0 ∨ 0⇔0(3)∃x(F(x)∨G(x))解:∃x(F(x)∨G(x))⇔(F(-2) ∨ G(-2)) ∨ (F(3) ∨G(3)) ∨ (F(6) ∨G(6))⇔((-2≤3) ∨ (-2>5)) ∨ ((3≤3) ∨ (3>5)) ∨ ((6≤3) ∨ (6>5))⇔(1 ∨ 0) ∨ (1 ∨ 0) ∨ (0 ∨ 1)⇔1 ∨ 1 ∨ 1⇔12.14 求下列各式的前束范式,要求使用约束变项换名规则。
(1)⌝∃xF(x)→∀yG(x,y)(2) ⌝(∀xF(x,y) ∨∃yG(x,y) )解:(1)⌝∃xF(x)→∀yG(x,y)⇔⌝∃xF(x)→∀yG(z,y) 代替规则⇔∀x⌝F(x)→∀yG(z,y) 定理2.1(2 )⇔∃x(⌝F(x)→∀yG(z,y) 定理2.2(2)③⇔∃x∀y(⌝F(x)→G(z,y)) 定理2.2(1)④(2)⌝(∀xF(x,y) ∨∃yG(x,y) )⇔⌝(∀zF(z,y) ∨∃tG(x,t)) 换名规则⇔⌝(∀zF(z,y) )∧⌝(∃tG(x,t) )⇔∃z⌝F(z,y) ∧∀t⌝G(x,z)⇔∃z (⌝F(z,y) ∧∀t⌝G(x,z))⇔∃z ∀t(⌝F(z,y) ∧⌝G(x,t))2.15 求下列各式的前束范式,要求使用自由变项换名规则。
离散数学2及答案

离散数学2一、填空题(每小题2分,共30分)1 设():M x x 偶数, ():F x x 素数。
将命题“存在偶素数”符号化为: ))()((x F x M x ∧∃ 。
2 集合A={2,2,2,3}的幂集合P(A)={}3,2{},3{},2{,φ }。
3 设A={1,2,3},B={a,b},则=⨯B A 6 。
4 已知命题公式A 含有2个命题变项,其成真赋值为00、10、11,则其主合取范式为 1M 。
5 设p :北京比大连人口多,q :2+2=4,r :乌鸦是白色的。
则命题公式)()(r p r p ⌝∧↔∨⌝的真值为 0 。
6 无向图G 具有欧拉通路,当且仅当G 是 连通 图且无奇度顶点或有两个奇度顶点。
7 6阶无向树的总度数为 10 。
8设A={1,2,3},B={a, b},A 1={2},f={<1,a>,<2,a>,<3,b>},则=-))((11A f f { 1,2 }。
9 设B A f →:,若ran B f )(=,则称B A f →:是满射的。
10 设群>⊕=<}),.({b a P G ,其中⊕为对称差。
群方程φ=⊕}{b Y 的解=Y {b} 。
11 设p:我去自习,q:我去看电影,r:我有课。
则命题“如果我去自习或看电影,我就没有课”的符号化形式为r qp⌝→∨)(。
12 画出3阶有向完全图的2条边的2个非同构的生成子图。
13 下面运算表中的=-1a c 。
14 写出模4乘法<Z4,⊗ >的运算表⊗0 1 2 31230 0 0 00 1 2 30 2 0 20 3 2 115 设A(x)是任意的含自由出现个体变项x的公式,则⇔⌝∀)(xxA )(xAx⌝∃。
二、试解下列各题(每小题5分,共25分)1. 设A = {a , b , c , d }, R = {<a ,b >,<b ,a >,<b ,c >,<c ,d >}, 求3R 的的矩阵表示和关系图表示。
国家开发大学(电大)离散数学形考任务二部分答案

无向树T有8个结点,则T的边数为( ).选择一项:A. 7B. 9C. 8D. 6反馈你的回答不正确正确答案是:7题目2不正确获得5.00分中的0.00分标记题目题干设图G=<V, E>,v V,则下列结论成立的是( ) .选择一项:A.B. deg(v)=2| E |C. deg(v)=| E |D.反馈你的回答不正确正确答案是:题目3不正确获得5.00分中的0.00分标记题目题干设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).图五选择一项:A. (b)是强连通的B. (c)是强连通的C. (d)是强连通的D. (a)是强连通的反馈你的回答不正确正确答案是:(a)是强连通的题目4不正确获得5.00分中的0.00分标记题目题干设G是有n个结点,m条边的连通图,必须删去G的( )条边,才能确定G的一棵生成树.选择一项:A.B.C.D.反馈你的回答不正确正确答案是:题目5不正确获得5.00分中的0.00分标记题目题干无向完全图K4是().选择一项:A. 树B. 非平面图C. 欧拉图D. 汉密尔顿图反馈你的回答不正确正确答案是:汉密尔顿图题目6不正确获得5.00分中的0.00分标记题目题干已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T的树叶数为( ).选择一项:A. 8B. 3C. 4D. 5反馈你的回答不正确正确答案是:5题目7未回答满分5.00标记题目题干图G如图四所示,以下说法正确的是( ) .选择一项:A. {(a, d)}是边割集B. {(b, d)}是边割集C. {(a, d)}是割边D. {(a, d) ,(b, d)}是边割集反馈你的回答不正确正确答案是:{(a, d) ,(b, d)}是边割集题目8不正确获得5.00分中的0.00分标记题目题干以下结论正确的是( ).选择一项:A. 无向完全图都是平面图B. 无向完全图都是欧拉图C. 树的每条边都是割边D. 有n个结点n-1条边的无向图都是树反馈你的回答不正确正确答案是:树的每条边都是割边题目9不正确获得5.00分中的0.00分标记题目题干如图二所示,以下说法正确的是( ).图二选择一项:A. {d}是点割集B. e是割点C. {b, e}是点割集D. {a,e}是点割集反馈你的回答不正确正确答案是:e是割点题目10不正确获得5.00分中的0.00分标记题目题干若G是一个汉密尔顿图,则G一定是( ).选择一项:A. 欧拉图B. 连通图C. 平面图D. 对偶图你的回答不正确正确答案是:连通图标记题目信息文本判断题题目11正确获得5.00分中的5.00分标记题目题干设G是一个连通平面图,且有6个结点11条边,则G有7个面.( ) 选择一项:对错反馈正确的答案是“对”。
西南大学《离散数学》网上作业题及答案

[0004]《离散数学》网上作业题答案第1次作业[论述题]第1次作业一、填空题1. 设|A | = 5, |B | = 2, 则可定义A 到B 的函数( )个,其中有( )单射,( )个满射.2. 令G (x ): x 是金子,F (x ): x 是闪光的,则命题“金子都是闪光的,但闪光的未必是金子”符号化为( ).3. 设X 是非空集合,则X 的幂集P (X )关于集合的⋃运算的单位元是( ),零元是( ),P (X )关于集合的⋂运算的单位元是( ).4. 6阶非Abel 群的2阶子群共有( )个,3阶子群共有( )个,4阶子群共有( )个.5. 对于n 阶完全无向图K n , 当n 为( )时是Euler 图,当n ≥ ( )时是Hamilton 图,当n ( )时是平面图.二、单选题1. 幂集P (P (P (∅))) 为( )(A){{∅}, {∅, {∅}}}. (B){∅, {∅, {∅}}, {∅}}. (C){ ∅, {∅, {∅}}, {{∅}}, {∅}} (D){ ∅, {∅, {∅}}}. 2. 设R 是集合A 上的偏序关系,则1-⋃R R 是( ).(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上答案都不对 3. 下列( )组命题公式是不等值的.(A))(B A →⌝与B A ⌝∧. (B) )(B A ↔⌝与)()(B A B A ∧⌝∨⌝∧. (C))(C B A ∨→与C B A →⌝∧)(. (D))(C B A ∨→与)(C B A ∨∧⌝. 4.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法. 5.4阶完全无向图4K 中含3条边的不同构的生成子图有 (A)3 (B)4 (C)5 (D)2三、设A 和B 是集合,使B B A =-成立的充要条件是什么,并给出理由. 四、设R 和S 是集合A 上的对称关系,证明S R 对称的充要条件是R S S R =. 五、分别利用(1)等值演算法和(2)真值表求命题公式))(())((r q p p q r A ∨→→→∨⌝=的主析取范式和主合取范式.六、设G 是(n , m )无向图,若n m ≥,证明G 中必存在圈.参考答案:第1次作业答案一、1. 32,0,30.2.))()(())()((x G x F x x F x G x ⌝∧∃∧→∀.3.∅,X ,X .4. 3,1,0.5.n 为奇数,3,4≤n .二、1(C); 2(B); 3(D); 4(D); 5(A). 三、证 ==⇔=-B A B B A ∅. (⇐)显然.(⇒)因为B A B A ⋂=-,根据B B A =-得B B B B A ⋂=⋂⋂)(,于是B = ∅,进而A = ∅.四、解 由于R 和S 是对称的,所以S S R R==--11,.(⇐)因为R S S R =,两边取逆得11)()(--=R S S R ,而S R S R R S ==---111)(.所以S R S R =-1)(,因此S R 是对称关系.(⇒)由于S R 对称,所以S R S R =-1)(. 而R S R S S R ==---111)(,因而R S S R =.五、解 (1)等值演算法 A 的主合取范式:))(())((r q p p q r A ∨→→→∨⌝== ))(())((r q p p q r ∨∨⌝→∨⌝∨⌝ = )())((r q p p q r ∨∨⌝∨∨⌝∨⌝⌝= )()(r q p p q r ∨∨⌝∨⌝∧∧ = r q p ∨∨⌝(由吸收律得到). 于是,A 的主析取范式为))(())((r q p p q r A ∨→→→∨⌝== ∨⌝∧⌝∧∨⌝∧∧⌝∨∧⌝∧⌝∨⌝∧⌝∧⌝)()()()(r q p r q p r q p r q p)()()(r q p r q p r q p ∧∧∨⌝∧∧∨∧⌝∧.(2)真值表法命题公式))(())((r q p p q r A ∨→→→∨⌝=的真值表如下:由表可知,))(())((r q p p q r A ∨→→→∨⌝=的主合取范式为r q p A ∨∨⌝=.A 的主析取范式为A = ∨⌝∧⌝∧∨⌝∧∧⌝∨∧⌝∧⌝∨⌝∧⌝∧⌝)()()()(r q p r q p r q p r q p)()()(r q p r q p r q p ∧∧∨⌝∧∧∨∧⌝∧.七、证(反证)假设G 中不含圈. 设G 有k (k ≥ 1)个连通分支k G G G ,...,,21,其节点个数分别为k n n n ,...,,21,其边数分别为k m m m ,...,,21. 这时,i G 为树,根据树的基本性质有1-=i i n m )1(k i i ≤≤. 进而n k n n m m ki i k i i <-=-==∑∑==)1(11,与已知n m ≥矛盾. 证毕.第2次作业[论述题]第2次作业一、填空题1.设A = {2, {3}, 4, a }, B = {1, 3, 4, {a }}, 则{3}( )A ,{a }( )B ,{{a }}( )B .2. 设A = {1, 2, 3, 4, 5}上的关系R = {(1, 2), (3, 4), (2, 2)}, S = {(4, 2), (2, 5), (3, 1), (1, 3)}, 则=S R { }, =R S { },=R R { }.3. 在同构意义下,3阶群有( )个,4阶群有( )个,5阶群有( )个.4.任意有限布尔代数)1,0,,,,(⋅+B 均与集合代数( )同构,其元素个数为( ), 其中( )是B 的所有原子组成的集合.5. 不同构的5阶无向树有( )棵,不同构的5阶根树有( )棵.二、单选题1. 在有理数集合Q 上定义运算“*”如下:对于任意x , y ∈ Q ,y x * = x + y – xy ,则Q 关于*的单位元是( ).(A)x . (B)y . (C)1. (D)0.2. 设A = {1, 2, 3}, 下图分别给出了A 上的两个关系R 和S ,则S R 是( )关系.(A)自反. (B)对称. (C)传递. (D)等价.3.令T (x ): x 是火车,B (x ): x 是汽车,F (x , y ): x 比y 快,则“某些汽车比所有的火车慢”符号化为( ).(A)()()),()()(y x H x T x y B y →∀∧∃. (B)()()),()()(y x H x T x y B y ∧∀→∃. (C)()()),()()(y x H x T y B y x ∧→∃∀.G SG R(D)()()),()()(y x H x T x y B y →∀→∃.4. 整数集合Z 关于数的加法“+”和数的乘法“⋅”构成的代数结构(Z, +, ⋅)是( ). (A)域 (B)域和整环 (C)整环 (D) 有零因子环5.设G 是简单图,G 是G 的补图,若G G ≅,则称G 为自补图. 5阶不同构的自补图个数为( ).(A)0. (B)1. (C)2. (D)3.三、设C B g B A f →→:,:, 若g f 是单射,证明f 是单射,并举例说明g 不一定是单射.四、设A = {a , b , c , d }上的关系R = {(a , b ), (b , d ), (c , c ), (a , c )}, 画出R 的关系图,并求出R的自反闭包r (R )、对称闭包s (R )和传递闭包t (R ).五、设G 是(6,12) 的简单连通平面图,则G 的面由多少条边围成,为什么? 六、任意6个人中,一定有3个人彼此认识或有3个人彼此不认识.参考答案:第2次作业答案一、1. ∈,∈,⊆.2.{(1,5), (3, 2), (2, 5)}, {(4, 2), (3, 2), (1, 4)}, {(1, 2), (2, 2)}.3. 1, 2, 1.4. ,,,),((⋂⋃X P ∅, X ), 2n , n .5. 3, 9.二、1(D); 2(B); 3(A); 4(C); 5(C).三、证 对于任意A x x ∈21,,若)()(21x f x f =,则))(())((21x f g x f g =,于是))(())((21x f g x g f =. 由于g f 是单射,所以21x x =,因此f 是单射.例如,A = {a , b }, B = {1, 2, 3}, C = {α, β, γ}, f = {(a , 1), (b , 2)}, g = {(a , α), (b , β), (c , β)}, 这时)},2(),,1{(βα=g f ,它是A 到C 的单射,但g 不是单射. 四、解 R 的关系图如下:}),(),,(),,(),,(),,(),,(),,{()(d d b b a a c a c c d b b a R r =, }),(),,(),,(),,(),,(),,(),,{()(a c b d a b c a c c d b b a R s =. }),(),,(),,(),,(),,{()(d a c a c c d b b a R t =.五、证 根据Euler 公式,G 的面数为r = 12 – 6 +2 = 8. 由握手定理知,∑=⋅=vv 24122)deg(,而简单连通平面图的每个面至少由3条边围成,所以G 的每个面恰由3条边围成.六、证 用6个节点分别表示这6个人,可得6阶完全无向图6K . 若两个人认识,则在相应的两个节点所在的边上涂上红色,若两个人不认识,则在相应的两个节点所在的边上涂上蓝色.对于任意的6K 的节点v ,因为5)deg(=v ,与v 邻接的边有5条,当用红、蓝颜色去涂时,至少3条边涂的是同一种颜色,不妨设321,,vv vv vv 是红色. 若3条边21v v ,32v v ,31v v 是红色,则存在红色3K ,这意味着有3个人相互认识; 若21v v ,32v v ,31v v 都是蓝色,则存在蓝色3K ,这意味着有3个人相互不认识. 结论成立.第3次作业[论述题]第3次作业 参考答案:第3次作业一、1.{1, 3, {1, 2}, {3}};{{2, 3}, {1}};{1, 3, {1, 2}, {3}, {2, 3}, {1}}.2.0,1,0.3. ))()((x O x Z x →⌝∀.4. p n , p 为素数,n 为正整数.abd5. 是,3,10.二、1(B); 2(C); 3(D); 4(C); 5(A).三、证 对于任意C z ∈,由于g f 是满射,必存在A x ∈,使得z x f g x g f ==))(())(( . 令B x f y ∈=)(,有z y g =)(,因此,g 是满射.设},,{c b a A =,}3,2,1{=B ,},{βα=C ,令B A f →:,,:C B g →3)(,3)(,2)(===c f b f a f ,βαβ===)3(,)2(,)1(g g g .这时,α==))(())((a f g a g f ,β==))(())((b f g b g f ,显然有},{)(ran βα=g f ,g f 是满射. 而ran f = {2, 3},f 不是满射.四、证 (1)对于任意x ∈ Z , 由于x x x x +=+22, 所以(x , x ) ∈ R , 即R 是自反的. (2)因为(0, 0) ∈ R , 因此R 不是反自反的.(3)对于任意x , y ∈ Z , 若(x , y ) ∈ R , 则y y x x +=+22, 于是x x y y +=+22, 进而(y , x ) ∈ R , 即R 是对称的.(4)因为(2, -3) ∈ R 且(-3, 2) ∈ R ,因此R 不是反对称的.(5)对于任意x , y , z ∈ Z , 若(x , y ) ∈ R 且(y , z ) ∈ R , 则y y x x +=+22且z z y y +=+22,于是z z x x +=+22,所以(x , z ) ∈ R , 即R 是传递的. 综上所述,知R 是自反的、对称的和传递的.五、解 命题公式)())(q p q p A ⌝→↔→⌝=的真值表如下:A 的主析取范式为:)()(q p q p A ⌝∧∨∧=.A 的主合取范式为:)()(q p q p A ∨∧⌝∨=.六、证 对于任意的6K 的节点v ,因为5)deg(=v ,与v 邻接的边有5条,当用红、蓝颜色去涂时,至少3条边涂的是同一种颜色,不妨设321,,vv vv vv 是红色. 若3条边21v v ,32v v ,31v v 是红色,则存在红色3K ; 若21v v ,32v v ,31v v 都是蓝色,则存在蓝色.第4次作业[论述题]第4次作业 参考答案:第4次作业答案一、1.自反性、对称性和传递性.2. Abel.3. 6.4. 封闭性和结合性.5. 不含圈的连通.二、1(A); 2(C); 3(B); 4(D); 5(C).三、证 对于任意A b a ∈,,假定)()(b f a f =. 由于≤是偏序,于是a a ≤,所以)(a f a ∈,进而)(b f a ∈,根据定义知b a ≤. 同理可证,a b ≤. 根据偏序的反对称性有b a =,因此f 是单射.当b a ≤时,对于任意)(a f x ∈,于是a x ≤. 根据偏序的传递性有b x ≤,即)(b f x ∈,故)()(b f a f ⊆.四、证 (1) 与非联结词“↑”的运算表如下:(2)p p p p p ↑=∧⌝=⌝)(.)()()())((q p q p q p q p q p ↑↑↑=↑⌝=∧⌝⌝=∧. )()()()()(q q p p q p q p q p ↑↑↑=⌝↑⌝=⌝∧⌝⌝=∨.五、解 ))),(),((),,((v y vQ u x uQ z y x zP y x ∃→∃∧∃∀∀=))),(),((),,((v y vQ u x uQ z y x zP y x ∃∨⌝∃∧∃∀∀ =))),(),((),,((v y vQ u x Q u z y x zP y x ∃∨⌝∀∧∃∀∀=))),(),((),,((v y Q u x Q v u z y x zP y x ∨⌝∃∀∧∃∀∀ =))),(),((),,((v y Q u x Q z y x P v u z y x ∨⌝∧∃∀∃∀∀ 六、证 (1)根据Euler 公式,有2+-=n m r . (2)31052)2(5-≤⇒≤+-n m m n m . (3) 若Petersen 图是平面图,由于其每个面至少5条边围成,于是由(2)知3105-≤n m . 因为在Petersen 图中,m = 15, n = 10, 于是31010515-⋅≤,矛盾.第5次作业[论述题]第5次作业 参考答案:第5次作业答案一、1. 2n .2. 反自反、反对称、传递.3. 是.4. 独异点.5. 上确界和下确界. 二、1(C); 2(A); 3(B); 4 (D); 5(B).三、(1)证 对于任意∈),(),,(2211y x y x R ⨯ R ,若)),(()),((2211y x f y x f =,于是),(),(22221111y x y x y x y x -+=-+,进而2211y x y x +=+且2211y x y x -=-. 由此可得,2121,y y x x ==,因而),(),(2211y x y x =,故f 是单射.对于任意∈),(q p R ⨯ R ,取2,2qp y q p x -=+=,容易得知),(),()),((q p y x y x y x f =-+=.由上可知,f 是双射. (2)解 由上的证明过程知,⎪⎭⎫⎝⎛-+=-2,2)),((1y x y x y x f.(3)解 很显然If f =- 1R ⨯R ,即),()),)(((1y x y x f f=- .)2,2())()(),()(()),(()),)(((y x y x y x y x y x y x y x f y x f f =--+-++=-+= .四、解 }),(),,(),,(),,(),,{()(c c b b c b b a a a I R R r A =⋃=. }),(),,(),,(),,(),,{()(1b c a b c b b a a a RR R s =⋃=-.}),(),,(),,(),,{()(c a c b b a a a R t =. 五、证(1))(x xP ∀ P (2)P (c ) US(1) (3))))()(()((x R y Q x P x ∧→∀ P (4)))()(()(c R y Q c P ∧→ US(3) (5))()(c R y Q ∧ T(2)(4)I (6)Q (y ) T(5)I (7)R (c ) T(5)I (8))()(c R c P ∧ T(2)(7)I (9)))()((x R x P x ∧∀ UG(8) (10)))()(()(x R x P x y Q ∧∀∧ T(6)(9)I六、证 设G 是一棵阶数2≥的无向树,k k v v v v L 121...:-是G 中的最长路径. `若1v 和k v 至少有一个不是树叶,不妨设k v 不是树叶,即2)deg(≥k v ,则k v 除与1-k v 邻接外,还存在1+k v 与k v 邻接.若1+k v 在L 上,则G 中存在圈,不可能. 若1+k v 不在L 上,则G 中存在一条比L 长1的路径1121...+-k k k v v v v v ,与L 是G 中最长路径矛盾.第6次作业[论述题]第6次作业 参考答案:第6次作业答案一、1. 1,3,5,7,11,13,17,19.2. 平行.3. 010, 100, 101, 110, 111.4. 2.5. 3.二、1(B); 2(A); 3(D); 4(C); 5(A).三、(1)证 任意∈),(),,(2211y x y x R ×R , 若),(),(2211y x f y x f =,则),(),(22221111y x y x y x y x -+=-+,进而2211y x y x +=+且2211y x y x -=-,于是21x x =且21y y =,从而f 是单射.任意∈),(q p R ×R , 取⎪⎩⎪⎨⎧-=+=22q p y q p x , 通过计算易知),(),(q p y x f =,因此f 是满射. 故f 是双射.(2) 解 由上面的证明知,f 存在逆函数且⎪⎭⎫⎝⎛-+=-2,2),(1y x y x y x f.又()()),(2,2,1y x y x y x f y x f f=⎪⎭⎫⎝⎛-+=- ,即I f f=- 1R ×R ,而()()())2,2())()(),()((,,y x y x y x y x y x y x y x f y x f f =--+-++=++= .四、解 R 的传递闭包t (R )的关系图如下:于是,有t (R ) = {(1, 3), (3, 1), (2, 3), (4, 3), (4, 5), (6, 5), (1, 1), (3, 3),(2,1),(4,1)}. 五、解 首先写出命题公式()())()(p q r r q p A →→↔→→=的真值表如下:从真值表可得命题公式A 的主析取范式为:∨⌝∧⌝∧∨∧⌝∧∨∧∧=)()()(r q p r q p r q p A)()()(r q p r q p r q p ⌝∧⌝∧⌝∨∧⌝∧⌝∨⌝∧∧⌝.命题公式A 的主合取范式为:)()(r q p r q p A ∨⌝∨⌝∧⌝∨⌝∨=.七、解 对于2, 3, 5, 7, 8,先组合两个最小的权2+3 = 5, 得5, 5, 7, 8;在所得到的序列中再组合5+5 = 10, 重新排列后为7, 8, 10;再组合7+8 =15, 得10, 15;最后组合10+15 = 25.2515108710875587532 所求的最优2叉树树如下:。
2020离散数学 形考二

离散数学形考二标记题目信息文本单项选择题题目1正确获得5.00分中的5.00分标记题目题干已知无向图G的邻接矩阵为,则G有().选择一项:A. 5点,8边B. 6点,7边C. 5点,7边D. 6点,8边反馈你的回答正确正确答案是:5点,7边题目2正确获得5.00分中的5.00分标记题目题干设图G=<V, E>,v V,则下列结论成立的是( ) .选择一项:A. deg(v)=| E |B.C. deg(v)=2| E |D.反馈你的回答正确正确答案是:题目3正确获得5.00分中的5.00分标记题目题干图G如图三所示,以下说法正确的是( ).选择一项:A. a是割点B. {b, d}是点割集C. {b,c}是点割集D. {c}是点割集反馈你的回答正确正确答案是:{b,c}是点割集题目4正确获得5.00分中的5.00分标记题目题干如图一所示,以下说法正确的是( ) .选择一项:A. {(a, e)}是边割集B. {(a, e) ,(b, c)}是边割集C. {(d, e)}是边割集D. {(a, e)}是割边反馈你的回答正确正确答案是:{(d, e)}是边割集题目5不正确获得5.00分中的0.00分标记题目题干无向图G存在欧拉回路,当且仅当().选择一项:A. G连通且所有结点的度数全为偶数B. G连通且至多有两个奇数度结点C. G中所有结点的度数全为偶数D. G中至多有两个奇数度结点反馈你的回答不正确正确答案是:G连通且所有结点的度数全为偶数题目6正确获得5.00分中的5.00分标记题目题干无向完全图K4是().选择一项:A. 树B. 汉密尔顿图C. 欧拉图D. 非平面图反馈你的回答正确正确答案是:汉密尔顿图题目7正确获得5.00分中的5.00分标记题目题干设无向图G的邻接矩阵为,则G的边数为( ).选择一项:A. 1B. 6C. 7D. 14反馈你的回答正确正确答案是:7题目8正确获得5.00分中的5.00分标记题目题干若G是一个汉密尔顿图,则G一定是( ).选择一项:A. 平面图B. 对偶图C. 欧拉图D. 连通图反馈你的回答正确正确答案是:连通图题目9正确获得5.00分中的5.00分标记题目题干设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).图五选择一项:A. (b)是强连通的B. (d)是强连通的C. (c)是强连通的D. (a)是强连通的反馈你的回答正确正确答案是:(a)是强连通的题目10正确获得5.00分中的5.00分标记题目题干设G是连通平面图,有v个结点,e条边,r个面,则r= ( ).选择一项:A. e-v+2B. e+v+2C. e-v-2D. v+e-2反馈你的回答正确正确答案是:e-v+2标记题目信息文本判断题题目11正确获得5.00分中的5.00分标记题目题干设图G如图七所示,则图G的点割集是{f}.( )选择一项:对错反馈正确的答案是“错”。
吉林大学离散数学II试题A及答案

吉林大学离散数学II试题A及答案2004级《离散数学II 》期末考试试题(A 卷)满分80分,考试时间:2个小时一、[20分] 判断题(正确的在括号内打√号,错误的打?号)1、设(G ,?)是有限半群,而且有壹,如果关于运算?满足消去律,则(G ,?)是群。
()2、任意置换σ恰有一法写成轮换的乘积。
()3、设H 是G 的子群,则H 中的壹与G 的壹一致。
()4、设环R 是一个含壹环,则R 的子环R ’也一定是含壹环。
()5、设(R ,+, ?)是一个环,则 ? 运算一定满足交换律。
()6、按照剩余类的加法与乘法,环R 对于其理想N 的所有剩余类的集合R/N 是一个剩余环,则从R 到R/N 有一个同态映射存在。
()7、设F 是 q 元有限域,则 F 的q-1个非零元素在乘法下一定作成一个循环群。
() 8、下列部分序集都是格。
( )A B C D9、格的同态映射是保序的,反之,保序映射也是同态映射。
()10、下列4个格所对应的哈斯图不都是分配格。
( )A B C D二、[20分] (20分)(G,*)为群,其中运算*定义如表所示。
1. 写出子群(a);2. 设H=(a),证明(a)*c=c*(a);3. 找出所有2个元素的子群;4. 求出G 的元数除以(f)的元数的商;5. 求(f)的所有右陪集。
三、[10分] 设(R,+,?) 为一代数系统,其中R 为实数集合,+为实数加法,任取a,b ∈R ,a ?b=|a |b ,试判断(R,+,?)是否为环。
如果是,请证明你的结论;如果不是请说明理由。
四[10分] 下面给出的多项式是R 0上的质式吗?请给出证明。
(1)x 3-5x+5;(2)x 5+7x 2-3。
五、[14分] (1) 计算Φ24(x);(2) 构造元数为9的有限域(不要求写出加法与乘法运算表)。
六、[6分]设(G ,*)为循环群,生成元素为a 。
设(A,*)和(B,*)均为(G ,*)的子群,而a i 和a j 分别为(A,*)和(B,*)的生成元。
离散数学 第二章练习题答案

一、 选择题1.下列四个公式正确的是①)()())()((x xB x xA x B x A x ∀∧∀⇒∧∀ ②)()())()((x xB x xA x B x A x ∀∨∀⇒∨∀③)()())()((x xB x xA x B x A x ∃∨∃⇒∨∃ ④))()(()()(x B x A x x xB x xA ∧∃⇒∃∧∃A.①③B.①④C.③④D.②④2. 谓词公式)())()((x Q y yR x P x →∃∨∀中量词∀x 的辖域是( )(A) ))()((y yR x P x ∃∨∀ (B) P (x ) (C ) )()(y yR x P ∃∨ (D) )(x Q3. 谓词公式))()(()(x xQ x Q x x xP ⌝∃→⌝∀→∀的类型是( )(A ) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 蕴涵式4. 设个体域为整数集,下列公式中其真值为1的是( )(A ) )0(=+∃∀y x y x (B) )0(=+∀∃y x x y(C))0(=+∀∀y x y x (D) )0(=+∃⌝∃y x y x5. 设个体域{,}A a b =,公式()()xP x xS x ∀∧∃在中消去量词后应为 ( )(A) ()()P x S x ∧ (B ) ()()(()())P a P b S a S b ∧∧∨(C) ()()P a S b ∧ (D) ()()()()P a P b S a S b ∧∧∨6. 在谓词演算中,下列各式正确的是( )(A) (,)(,)x yA x y y xA x y ∃∀⇔∀∃ (B ) (,)(,)x yA x y y xA x y ∃∃⇔∃∃(C) (,)(,)x yA x y x yA x y ∃∀⇔∀∃ (D) (,)(,)x yA x y y xA x y ∀∀⇔∀∀7.下列各式不正确的是( )(A ) (()())()()x P x Q x xP x xQ x ∀∨⇔∀∨∀(B) (()())()()x P x Q x xP x xQ x ∀∧⇔∀∧∀(C) (()())()()x P x Q x xP x xQ x ∃∨⇔∃∨∃(D) (())()x P x Q xP x Q ∀∧⇔∀∧8. 设I 是如下一个解释:D ={a,b}, 01 0 1b) P(b,a) P(b,b) P(a,),(a a P 则在解释I 下取真值为1的公式是( ).(A) ∃x ∀yP(x,y) (B)∀x ∀yP(x,y) (C)∀xP(x,x) (D )∀x ∃yP(x,y).9. 设个体变元z y x ,,的论域都为自然数集合,(,,):,P x y z x y z +=(,,),(,):Q x y z x y z R x y x y ⋅=<:,则以下命题中( )是假命题.A .),0,(x x xP ∀B .),,(y y x yP x ∀∃C .),,(x x y yQ x ∃∀D .)0,(x xR ∀10. 下面不是命题的是( )A .()xP x ∀B .()()x P x ∃C .()()()x P x P y ∀∨D .()()(()())x y P x R y ∃∃→11公式()()()()x P x x Q x ∀→∀的前束范式为( )A .()()(()())x y P x Q y ∀∀→B .()()(()())x y P x Q y ∀∃→C .()()(()())x y P x Q y ∃∀→D .()()(()())x y P x Q y ∃∃→12. 公式()(())x P x Q ∀↔⇔( )A .(()())(()())x P x Q Q x P x ∀→∧→∀B .(()())(()())x P x Q Q x P x ∀→∧→∃C (()())(()())x P x Q Q x P x ∃→∧→∀D .(()())(()())x P x Q Q x P x ∃→∧→∃13. ()()(,)x y P x y ∀∃的否定是( )A .()()(,)x y P x y ∀∀⌝B .()()(,)x y P x y ∃∀⌝C .()()(,)x y P x y ∀∃⌝D .()()(,)x y P x y ∃∃⌝14.下列谓词公式与()(()())x A x B x ∀↓等价的是( )A .()()()()x A x xB x ∀↓∀ B .()()()()x A x x B x ∀↑∀C .()()()()x A x x B x ∃↓∃D .()()()()x A x x B x ∃↑∃15.在谓词演算中,()P a 是()xP x ∀的有效结论,其理论依据是( )A .USB .UGC .ESD .EG16. 设个体域是整数集合,P 代表∀x ∀y ((x <y )→(x -y <x )),下面4个命题中为真的是( )(A) P 是真命题 (B ) P 是假命题(C) P 是一阶逻辑公式,但不是命题 (D) P 不是一阶逻辑公式二、填空题1. 设全体域D 是正整数集合,确定下列命题的真值:(1) ()x y xy y ∀∃= ( 0 ) (2) ()+x y x y y ∃∀= ( 0 )(3) ()+x y x y x ∃∀= ( 0 ) (4) (2)x y y x ∀∃= ( 1 )2. 谓词公式()((,)())()((,)()())x P x y Q z y R x y z Q z ∀∨∧∃→∀中量词∀x 的辖域是3. 公式()(()(,)()(,))()x P x Q x y z R y z S x ∀→∨∃→中量的自由变量为 x,y 约束变量为 x,z4. 设个体域D ={1,2},那么谓词公式)()(y yB x xA ∀∨∃消去量词后的等值式为 .A (1)∨A (2)∨(B (1)∧B (2)) .5. 设个体域D ={a ,b },公式)),()((y x yH x G x ∃→∀消去量词化为. (G (a )→(H (a ,a )∨H (a ,b )))∧ (G (b )→(H (b ,a )∨H (b ,b )))6. 设N (x ):x 是自然数,Z (y );y 是整数,则命题“每个自然数都是整数,而有些整数不是自然数”符号化为 (()())(()())x N x Z x x Z x N x ∀→∧∃∧⌝7. 谓词公式∀x (F (x )→G (x ))∧⌝∀y (F (y )→G (y ))的类型是 永假式 .8. 设个体域{1,2},谓词P (1)=1,P(2)=0,Q(1)=0,Q (2)=1,则∀x (P (x )∨Q (x ))的真值是 19.只用联结词,,⌝∀→表示以下公式()(()())x P x Q x ∃∧= ()(()())x P x Q x ⌝∀→⌝()(()()())x P x y Q y ∃↔∀= ()((()()())(()()()))x P x y Q y y Q y P x ⌝∀→∀→⌝∀→ ()(()()())y x P x Q y ∀∀∨⌝= ()(()()())y Q y x P x ∀→∀三、计算及证明1. 求谓词公式))(())((a f R x Q P x ∧→∀的真值.其中P :4>3,Q (x ):x >1,R (x ):x ≤2.f (-3)=1,f (1)=5,f (5)= -3.a :5.个体域D =(-3,1,5).解:))(())((a f R x Q P x ∧→∀=))5(())5(())1(())3((f R Q P Q P Q P ∧→∧→∧-→=)3()11()01()01(-∧→∧→∧→R01100=∧∧∧=2.说明公式))(),(()(x xP y x yG x xP ∀→∃→∀是逻辑有效式(永真式).解:因为))(),(()(x xP y x yG x xP ∀→∃→∀是)(P Q P →→的代换实例,可知 ))(),(()(x xP y x yG x xP ∀→∃→∀是逻辑有效式.或 ))(),(()(x xP y x yG x xP ∀∨⌝∃∨⌝∀1)(),()(⇔∨⌝∃∨⌝∀⇔x P y x yG x xP3. 通过等值演算说明下列等值式成立: )()())()((x xQ x xP x Q x P x ∃→∀⇔→∃证:⇔→∃))()((x Q x P x )()((x Q x P x ∨⌝∃))()(x xQ x P x ∃∨⌝∃⇔)()(x xQ x xP ∃∨⌝∀⇔)()(x xQ x xP ∃→∀⇔4. 求谓词公式),,()),(),((z y x zH y x yG y x xF ∃∧∀→∀的前束范式解:),,()),(),((z y x zH y x yG y x xF ∃∧∀→∀),,()),(),((z y x zH y x yG y x xF ∃∧∀∨⌝∀⇔((,)(,))(,,)u F u y vG x v zH x y z ⇔∃⌝∨∀∧∃((,)(,))(,,))u F u y vG x v zH x y z ⇔∃⌝∨∀∧∃(((,)(,))(,,))u v z F u y G x v H x y z ⇔∃∀∃⌝∨∧(或(((,)(,))(,,))u v z F u y G x v H x y z ⇔∃∀∃→∧)5. 前提:∃xF (x ), ∀x (F (x )→G (x )∧H (x ))结论:∃x (F (x )∧H (x ))6. 构造推理证明))()(()()(x Q x P x x xQ x xP →∀⇒∀→∃. (提示:))()(()()(x B x A x x xB x xA ∨∀⇒∀∨∀.) 证 ① )()(x xQ x xP ∀→∃ 前提引入② )()(x xQ x xP ∀∨⌝∃ T ①,蕴含等值式③ )()(x xQ x P x ∀∨⌝∀ T ②,量词否定 ④ ))()((x Q x P x ∨⌝∀⑤ ))()((x Q x P x →∀ T ④,蕴含等值式 法2:(反证法)① (()())x P x Q x ⌝∀→ 前提引入② (()())x P x Q x ∃∧⌝ T E ①,③ ()()P c Q c ∧⌝ ES ②, ④ ()Q c ⌝ T ③ , ⑤ ()P c T ③,⑥()xP x ∃ EG ⑤ ⑦)()(x xQ x xP ∀→∃ P⑧()xQ x ∀ T ⑦⑨()Q c UG ⑧ ⑩()()Q c Q c ⌝∧ T ④。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
0
0
1
1
1
0
0
1
1
1
1
1
1
0
1
0
1
(3-2)主析取范式:
(4)由真值表和主析取范式分别可以验证该推理正确。
6、(每题12分,共24分)
(1)如果今天是星期六,我们就要到颐和园或圆明园去玩。如果颐和园游人太多,我们就不去颐和园。今天是星期六。颐和园游人太多。所以我们去圆明园玩。
解:
(1)令p:今天是星期六; q:我们要到颐和园玩; r:我们要到圆明园玩; s:颐和园游人太多.
5、(20分)用2种方法(真值表法、主析取范式法)判断下面推理是否正确。
若 是奇数,则 不能被2整除。若 是偶数,则 能被2整除。因此,如果 是偶数,则 不是奇数。
解:(1)简单命题符号化:
p: 是奇数,q: 能被2整除,r: 是偶数。
(2)前提和结论分别符号化为:
若 是奇数,则 不能被2整除: p→ q。
2018级离散数学第二次作业参考答案
学号:姓名:班级:总分:
1、(每空5分,共30分)
(1)已知公式A含有3个命题变项p,q,r,并且它的成真赋值为000,011,110,那么命题公式A的成假赋值为001,010,100,101,111,主析取范式为 ,主合取范式为M1∧M2∧M4∧M5∧M7。
(2)已知公式A含有3个命题变项,并且公式A的主合取范式为 ,那么公式A的成真赋值为000, 010,101,110,111,成假赋值为001, 011, 100,公式A的主析取范式为 。
解:
令p:小王是理科生, q:小王是文科生, r:小王的数学成绩很好.
前提: p→r, ¬q→p, ¬r
结论: q
证明
1p→r前提引入
2¬r前提引入
3¬p①②拒取式
4¬q→p前提引入
⑤q③④拒取式
2、(12分)用真值表法计算公式 的主析取范式和主合取范式
解:真值表为
p qr
0 0 0
1
0
0 0 1
1
1
0 1 0
1
0
0 1 1
1
1
1 0 0
0
0
1 0 1
0
0
1 1 0
1
0
1 1 1
1
1
主析取范式:
主Hale Waihona Puke 取范式:3、(14分)甲、乙、丙、丁4人中有且仅有2个人参加围棋比赛。关于谁参加了比赛,下列判断都是正确的:
③经过演算可得
2分
④由于p和q有且仅有一个为1,因此公式的成真赋值只能是10XX或者01XX。又由于有两个人参加,成真赋值就只能是1010或者1001或者0110或者0101。由于丙参加,丁必参加,因此,1010,0110被排除。再由于乙,丁至多只能参加一人,因此,0101被排除。
所以,公式的成真赋值只能是1001,即甲和丁参加围棋比赛。4分
若 是偶数,则 能被2整除: r→q。
因此,如果 是偶数,则 不是奇数:r→ p。
推理的形式结构:
((p→ q)∧(r→q))→(r→ p)
(3-1)
真值表
p
q
r
p→ q
r→q
r→ p
((p→ q)∧(r→q))→(r→ p)
0
0
0
1
1
1
1
0
0
1
1
0
1
1
0
1
0
1
1
1
1
0
1
1
1
1
1
1
1
0
0
1
1
1
1
1
0
(1)甲和乙只有一人参加。(2)若丙参加,则丁必参加。
(3)乙或者丁至多参加一人。(4)丁不参加,则甲也不会参加。
问:哪两个人参加了比赛。
解:其它解题方法,只要解释清楚,答案正确就给分
①设p:甲参加,q:乙参加,r:丙参加,s:丁参加。2分
②4个条件分别符号化为
, , , 4分
根据题意可得公式
2分
该公式的成真赋值为可能可行的方案。
前提: p→ (q∨r), s → ¬q, p, s.
结论: r.
证明
①p前提引入
②p→q∨r前提引入
③q∨r①②假言推理
④s前提引入
⑤s → ¬q前提引入
⑥¬q④⑤假言推理
⑦r③⑥析取三段论
(2)如果小王是理科生,则他的数学成绩一定很好。如果小王不是文科生,则他一定是理科生。小王的数学成绩不好。所以小王是文科生。
