高中数学 导数的概念课件
合集下载
高中数学课件导数的概念课件导数的概念第一课时
在时间段( t0+Dt)－ t0 = Dt 内，物体的平均速度为:
2021/4/27
vs(t0 t0DDtt) ts0(t0)D Dst
3.1 导数的概念
要精确地描述非匀速直线运动，就要知道物体在每一时 刻运动的快慢程度．如果物体的运动规律是 s =s(t )，那么物 体在时刻t 的瞬时速度v，就是物体在t 到 t+Dt 这段时间内， 当 Dt0 时平均速度．
率为
k limf(x0 Dx) f(x0)
Dx0
Dx
lim(1Dx)2 1(11)
Dx0
Dx
lim2Dx(Dx)2
Dx0
Dx
Dy
P
M
Dx
1
x
-1 O 1
2021/4/27
2
3.1 导数的概念
切线方程为: y22 (x1 )，
即
y2x
练习： P113 课后练习：1，2
2021/4/27
2． 瞬时速度 平均速度的概念
v 的极限．即
vD Ds tD lt i0m s(tD D tt)s(t)
2021/4/27
3.1 导数的概念
例1 物体作自由落体运动， 运动方程为： s 1 gt 2 ，其中位移
2 单位是m ，时间单位是s ， g=9.8m/s2．
求：(1) 物体在时间区间 [2，2.1]上的平均速度；
(2) 物体在时间区间[2，2.01] 上的平均速度；
( 3) 当Dt0,2Dt 2
平均速度 v 的极限为:
D D 即v 物 体D lt 在i0 v 时m 刻D lt t0i0 =2m s t(s )的2 g 瞬 时1 速.6 度( 9 m 等/s 于)19.6(m/s).
2021/4/27
vs(t0 t0DDtt) ts0(t0)D Dst
3.1 导数的概念
要精确地描述非匀速直线运动，就要知道物体在每一时 刻运动的快慢程度．如果物体的运动规律是 s =s(t )，那么物 体在时刻t 的瞬时速度v，就是物体在t 到 t+Dt 这段时间内， 当 Dt0 时平均速度．
率为
k limf(x0 Dx) f(x0)
Dx0
Dx
lim(1Dx)2 1(11)
Dx0
Dx
lim2Dx(Dx)2
Dx0
Dx
Dy
P
M
Dx
1
x
-1 O 1
2021/4/27
2
3.1 导数的概念
切线方程为: y22 (x1 )，
即
y2x
练习： P113 课后练习：1，2
2021/4/27
2． 瞬时速度 平均速度的概念
v 的极限．即
vD Ds tD lt i0m s(tD D tt)s(t)
2021/4/27
3.1 导数的概念
例1 物体作自由落体运动， 运动方程为： s 1 gt 2 ，其中位移
2 单位是m ，时间单位是s ， g=9.8m/s2．
求：(1) 物体在时间区间 [2，2.1]上的平均速度；
(2) 物体在时间区间[2，2.01] 上的平均速度；
( 3) 当Dt0,2Dt 2
平均速度 v 的极限为:
D D 即v 物 体D lt 在i0 v 时m 刻D lt t0i0 =2m s t(s )的2 g 瞬 时1 速.6 度( 9 m 等/s 于)19.6(m/s).
高中数学新教材选择性必修第二册《5.1导数的概念及其意义》课件
又f′(x0)＝6，∴6x0＝6，即x0＝1.
1.设函数y＝f(x)＝x2－1，当自变量x由1变为1.1时，函数的平均变化率为
√A.2.1
B.1.1
C.2
D.0
解析 ΔΔyx＝f11.1.1－－1f1＝00..211＝2.1.
12345
2.物体运动方程为 s(t)＝3t2(位移单位：m，时间单位：s)，若 v＝
思考1 割线PPn的斜率kn是多少？ 答案 割线 PPn 的斜率 kn＝fxxnn－－fx0x0.
思考2 当点Pn无限趋近于点P时，割线PPn的斜率kn与切线PT的斜率k有 什么关系？
答案 kn无限趋近于切线PT的斜率k.
梳理 (1)切线的定义：设PPn是曲线y＝f(x)的割线，当点Pn趋近于点P
解析 由平均变化率的定义可知，函数y＝f(x)在区间[x1，x2]，[x2，x3]， [x3，x4]上平均变化率分别为 fxx22－－fx1x1，fxx33－－fx2x2，fxx44－－fx3x3，结合图 象可以发现函数y＝f(x)的平均变化率最大的一个区间是[x3，x4].
12345
5.一物体的运动方程为s(t)＝7t2－13t＋8，则t0＝_1_时该物体的瞬时速度为1.
(3)函数的平均变化率可以表现出函数的变化趋势.自变量的改变量Δx取值 越小，越能准确体现函数的变化情况.
利用导数定义求导数：
(1)取极限前，要注意化简ΔΔyx，保证使 Δx→0 时分母不为 0. (2)函数在x0处的导数f′(x0)只与x0有关，与Δx无关. (3)导数可以描述事物的瞬时变化率，应用非常广泛.
2.若例3中的条件不变，试问物体在哪一时刻的瞬时速度为9 m/s. 解 设物体在t0时刻的瞬时速度为9 m/s. 又ΔΔst＝st0＋ΔΔtt－st0＝(2t0＋1)＋Δt. Δlit→m0ΔΔst＝Δlit→m0(2t0＋1＋Δt)＝2t0＋1.
1.设函数y＝f(x)＝x2－1，当自变量x由1变为1.1时，函数的平均变化率为
√A.2.1
B.1.1
C.2
D.0
解析 ΔΔyx＝f11.1.1－－1f1＝00..211＝2.1.
12345
2.物体运动方程为 s(t)＝3t2(位移单位：m，时间单位：s)，若 v＝
思考1 割线PPn的斜率kn是多少？ 答案 割线 PPn 的斜率 kn＝fxxnn－－fx0x0.
思考2 当点Pn无限趋近于点P时，割线PPn的斜率kn与切线PT的斜率k有 什么关系？
答案 kn无限趋近于切线PT的斜率k.
梳理 (1)切线的定义：设PPn是曲线y＝f(x)的割线，当点Pn趋近于点P
解析 由平均变化率的定义可知，函数y＝f(x)在区间[x1，x2]，[x2，x3]， [x3，x4]上平均变化率分别为 fxx22－－fx1x1，fxx33－－fx2x2，fxx44－－fx3x3，结合图 象可以发现函数y＝f(x)的平均变化率最大的一个区间是[x3，x4].
12345
5.一物体的运动方程为s(t)＝7t2－13t＋8，则t0＝_1_时该物体的瞬时速度为1.
(3)函数的平均变化率可以表现出函数的变化趋势.自变量的改变量Δx取值 越小，越能准确体现函数的变化情况.
利用导数定义求导数：
(1)取极限前，要注意化简ΔΔyx，保证使 Δx→0 时分母不为 0. (2)函数在x0处的导数f′(x0)只与x0有关，与Δx无关. (3)导数可以描述事物的瞬时变化率，应用非常广泛.
2.若例3中的条件不变，试问物体在哪一时刻的瞬时速度为9 m/s. 解 设物体在t0时刻的瞬时速度为9 m/s. 又ΔΔst＝st0＋ΔΔtt－st0＝(2t0＋1)＋Δt. Δlit→m0ΔΔst＝Δlit→m0(2t0＋1＋Δt)＝2t0＋1.
高中数学选择性必修二(人教版)《5.1.2 导数的概念及其几何意义》课件
－2＋1 Δx＝－12，
故曲线在点(－2，－1)处的切线方程为 y＋1＝－12(x＋2)，整理得 x
＋2y＋4＝0.
[方法技巧] 1．过曲线上一点求切线方程的 3 个步骤
2．过曲线外一点 P 求切线方程的 6 个步骤 (1)设切点(x0，f(x0))； (2)利用所设切点求斜率 k＝f′(x0)＝Δlitm→0 fx0＋ΔΔxx－fx0； (3)用(x0，f(x0))，P(x1，y1)表示斜率； (4)根据斜率相等求得 x0，然后求得斜率 k； (5)根据点斜式写出切线方程； (6)将切线方程化为一般式．
[学透用活]
[典例 3] 求曲线 f(x)＝2x在点(－2，－1)处的切线方程． [解] 由导数的几何意义，曲线在点(－2，－1)处的切线的斜率就等
于函数 f(x)＝2x在点(－2，－1)处的导数．
而 f′(－2)＝lim Δt→0
f－2＋Δx－f－2 Δx
＝lim Δt→0
－2＋2ΔΔxx＋1＝Δlitm→0
知识点二 导数的几何意义
(一)教材梳理填空
导数的几何意义 函数 y＝f(x)在 x＝x0 处的导数就是切线 PT 的斜率 k，即 k＝__Δlit_m→_0__—__ fx0＋Δx－fx0
————Δx———＝f′(x0)．
(二)基本知能小试
1．判断正误
(1)导函数 f′(x)的定义域与函数 f(x)的定义域相同．
解析：设直线 l 与曲线 C 的切点为(x0，y0)，
因为 y′＝lim Δt →0
x＋Δx3－x＋Δx2＋1－x3－x2＋1 Δx
＝3x2－2x，
则 y′| x＝x0＝3x20－2x0＝1，
解得 x0＝1 或 x0＝－13.
高中数学《导数的概念》公开课优秀课件
高中数学《导数的概念》公开课优秀课件标题：高中数学《导数的概念》公开课优秀课件尊敬的各位老师，大家好！今天我们将一起学习高中数学中一个非常重要的概念——导数的概念。
这个概念在微积分学中占据了重要的地位，对于我们理解函数的变化率，以及在科学、工程、经济和计算机科学等领域都有广泛的应用。
一、导数的定义首先，让我们来看看导数的定义。
假设有一个函数f(x)，在某一点x0的附近取一系列的点，这些点的横坐标是x0+Δx。
那么，函数f(x)在点x0的导数就是这一系列点的纵坐标f(x0+Δx)与横坐标之商的极限，记作f'(x0)。
二、导数的几何意义从几何意义上来看，导数表示函数在某一点处的切线的斜率。
当我们把函数在x0附近的点沿着横坐标逐渐移动时，该点的纵坐标会相应地变化，这个变化率就是导数。
三、导数的应用导数的应用非常广泛，它可以用来解决很多实际问题。
例如，在物理学中，导数被用来描述物体的运动学和动力学问题，如速度和加速度；在经济学中，导数被用来分析成本、收益和价格的变化；在计算机科学中，导数被用来研究图像处理和人工智能的问题。
四、导数的计算导数的计算有很多方法，其中最常见的方法是使用导数的定义。
我们可以根据定义来推导出一些基本的导数公式，如常数函数的导数为0，幂函数的导数与其指数有关，三角函数的导数与其角度有关等。
五、总结与复习今天我们学习了导数的概念和计算方法。
导数是微积分学的基础，它描述了函数在某一点处的变化率。
通过学习导数的定义和基本公式，我们可以解决很多实际问题。
六、作业与扩展阅读为了加深对导数概念的理解，请大家完成以下作业：1、复习并熟练掌握导数的基本定义和公式；2、自行寻找并解决一到两个与导数相关的问题（可以从物理、经济或计算机科学等领域寻找）。
同时，我推荐大家阅读《微积分的概念》这本书，作者是著名的数学家Richard Courant。
这本书对微积分的概念有深入且生动的解释，对于我们深入理解导数的概念非常有帮助。
高中数学导数的概念 PPT课件 图文
导数的定义:
从函数lyim=f(xf )(在x0x=x0x处) 的f瞬( x时0 )变化lim率是f: ,
x0
x
x0 x
我们称它为函数 y f ( x)在x x0
处的导数 , 记作 f ( x0 )或y xx0 ,即 :
f (x0 )
lim
x0
f
( x0
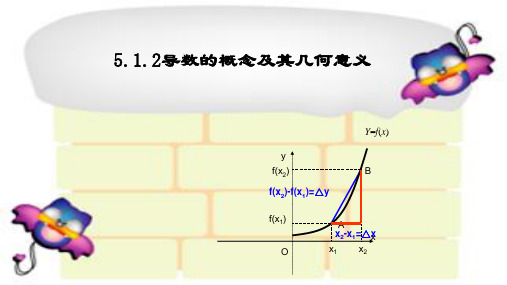
数值的改变量与自变的量改变量之比,即:
y f (x2) f (x1) .
x
x2 x1
我们用它来刻画函数在值区间[x1, x2]上变化的快慢.
对于一般函y数 f (x),在自变量 x从x0变到x1的
过程中,若设x x1 x0,则函数的平均变化:率是
y f (x1) f (x0) f (x0 x) f (x0).
x) x
f
(x0 )
例题讲解
例 1一条水管中流 y(单 过位 :m 的 3)时 水间 x(量 单位 :s) 的函y数 f(x)3x.求函y数 f(x)在x2处的导数 f(2)并 , 解释它的. 实际意义
解:当x从2变到2x时,函数值3从2变
到3(2x),函数值 y关于x的平均变化率 : 为
例2一名食品加工厂的上工班人后开始连续, 工作 生产的食品数 y(单 量位:kg)是其工作时x(间 单位:h) 的函数 y f (x).假设函y数 f (x)在x1和x3处 的导数分别: f为(1) 4和f (3) 3.5,试解释它们 的实际意. 义
如 其 解 4kg:果 生 的 f (保 产 1食) 持 速 品.4(表 这 度 即示 一 工该 生 作工 产 效,人 速 )那 率 为上 4度 么kg班 他/h后 .每 也1工 h时 就的作 可 是时以 说 ,候, 生一 其 产 f(3生 生 )3产 产 .5表 速 速 ,那 示 3.度 度 5么 k该 g为 /他 h工 .也每 人 就时 上 是可 ,如 班 说 33h.以 5的 果 k后g的 生 时 保 工食 产 ,候 持 作 .品 这
人教版高中数学选择性必修第二册5.1.2导数的概念及其几何意义【教学课件】
1 ． 曲 线 y ＝ x2 － 2x ＋ 3 在 点 A( － 1,6) 处 的 切 线 方 程 是
________________．
4x＋y－2＝0 解析：由导数的定义知 y′|x＝－1
＝ lim Δx→0
－1＋Δx2－2－1＋Δx＋3－－12＋2×－1－3 Δx
＝－4，
∴所求切线方程为 y－6＝－4(x＋1)，
(2)函数 y＝f(x)在 x＝x0 处的导数 f′(x0)就是切线 P0T 的斜率 k0，
即 k0＝lim Δx→0
fx0＋ΔΔxx－fx0＝f′(x0)．
3．导数的概念
当 x 变化时，y＝f′(x)就是 x 的函数，我们称它为 y＝f(x)的导函
数(简称导数)．y＝f(x)的导函数有时也记作 y′，即 f′(x)＝y′＝
得 f′(1)＝lim Δx→0
1＋ΔΔxx－1＝Δlixm→0
1＋1Δx＋1＝12，
∴f(x)在点(1,1)处的切线方程为 y－1＝21(x－1)．
即 x－2y＋1＝0.
探究题 2 抛物线 y＝x2在点 P 处的切线与直线 4x－y＋2＝0 平行，
求点 P 的坐标及切线方程．
解：设点 P 的坐标为(x0，y0)，
4．已知函数 f(x)＝lg(x＋1)，则 f′(2)的几何意义是
函数 f(x)＝lg(x＋1)的图象在点(2，lg 3)处切线的斜率． 5．曲线 y＝3x2－4x 在点(1，－1)处的切线方程为________．
y＝2x－3
解析：k＝f′(1)＝ lim Δx→0
31＋Δx2－41＋Δx－3×12－4×1 Δx
[(Δx)2－3Δx＋3]＝3，
所以切线的斜率为 3.
由点斜式可得切线方程为 y－1＝3(x＋1)，即 3x－y＋4＝0.
高中数学第五章导数的概念及其几何意义第2课时导数的几何意义pptx课件新人教A版选择性必修第二册
()
【答案】(1)A (2)D 【解析】(1)由导数的几何意义知，导函数递增，则说明函数切线斜 率随x增大而变大． (2) 从 导 函 数 的 图 象 可 知 两 个 函 数 在 x0 处 斜 率 相 同 ， 可 以 排 除 B ， C．再者导函数的函数值反映的是原函数的斜率大小，可明显看出y＝f(x) 的导函数的值在减小，所以原函数的斜率慢慢变小，排除A．
【预习自测】
判断正误(正确的画“√”，错误的画“×”)
(1)曲线y＝f(x)上的每一点都有切线．
()
(2)直线与曲线相切，则直线与已知曲线只有一个公共点． ( )
【答案】(1)× (2)×
导数的几何意义
(1)函数y＝f(x)在x＝x0处的导数f′(x0)就是切线P0T的斜率k0，即k0＝ __Δ_lxi_m→_0_f(_x_0＋__Δ_Δ_xx)_－__f_(x_0_)__＝f′(x0)．
易错警示 混淆曲线“在”或“过”某点的切线致误
求函数y＝x3－3x2＋x的图象上过原点的切线方程．
【错解】∵Δy＝f(Δx＋0)－f(0)＝(Δx)3－3(Δx)2＋Δx， ∴ΔΔyx＝1－3Δx＋(Δx)2， ∴f′(0)＝ lim [1－3Δx＋(Δx)2]＝1.
Δx→0
故所求切线方程为 y＝x.
(2)导数f′(x0)的几何意义是曲线 y＝f(x)在点(x0，f(x0))处的切线的 ___斜__率___，物理意义是运动物体在x0时刻的__瞬__时__速__度___．
【预习自测】
如果曲线y＝f(x)在点(x0，f(x0))处的切线方程为x＋2y－3＝0，那么 ()
A．f′(x0)>0
B．f′(x0)<0
【答案】3227 －31，2237 【解析】设直线 l 与曲线 C 的切点为(x0，y0)， 因为 y′＝Δlxi→m0(x＋Δx)3－(x＋ΔxΔ)2x＋1－(x3－x2＋1) ＝3x2－2x，则 y′|x＝x0＝3x20－2x0＝1，解得 x0＝1 或 x0＝－13，
【答案】(1)A (2)D 【解析】(1)由导数的几何意义知，导函数递增，则说明函数切线斜 率随x增大而变大． (2) 从 导 函 数 的 图 象 可 知 两 个 函 数 在 x0 处 斜 率 相 同 ， 可 以 排 除 B ， C．再者导函数的函数值反映的是原函数的斜率大小，可明显看出y＝f(x) 的导函数的值在减小，所以原函数的斜率慢慢变小，排除A．
【预习自测】
判断正误(正确的画“√”，错误的画“×”)
(1)曲线y＝f(x)上的每一点都有切线．
()
(2)直线与曲线相切，则直线与已知曲线只有一个公共点． ( )
【答案】(1)× (2)×
导数的几何意义
(1)函数y＝f(x)在x＝x0处的导数f′(x0)就是切线P0T的斜率k0，即k0＝ __Δ_lxi_m→_0_f(_x_0＋__Δ_Δ_xx)_－__f_(x_0_)__＝f′(x0)．
易错警示 混淆曲线“在”或“过”某点的切线致误
求函数y＝x3－3x2＋x的图象上过原点的切线方程．
【错解】∵Δy＝f(Δx＋0)－f(0)＝(Δx)3－3(Δx)2＋Δx， ∴ΔΔyx＝1－3Δx＋(Δx)2， ∴f′(0)＝ lim [1－3Δx＋(Δx)2]＝1.
Δx→0
故所求切线方程为 y＝x.
(2)导数f′(x0)的几何意义是曲线 y＝f(x)在点(x0，f(x0))处的切线的 ___斜__率___，物理意义是运动物体在x0时刻的__瞬__时__速__度___．
【预习自测】
如果曲线y＝f(x)在点(x0，f(x0))处的切线方程为x＋2y－3＝0，那么 ()
A．f′(x0)>0
B．f′(x0)<0
【答案】3227 －31，2237 【解析】设直线 l 与曲线 C 的切点为(x0，y0)， 因为 y′＝Δlxi→m0(x＋Δx)3－(x＋ΔxΔ)2x＋1－(x3－x2＋1) ＝3x2－2x，则 y′|x＝x0＝3x20－2x0＝1，解得 x0＝1 或 x0＝－13，
《高中数学导数讲解》课件
积分
导数是积分的基础，通过 求导可以推导出原函数的 表达式。
微分方程
导数在解决微分方程问题 中起到关键作用，如物理 中的动力学问题。
THANKS
感谢观看
பைடு நூலகம்
高中数学导数讲解
目录
• 导数的基本概念 • 导数的计算 • 导数的应用 • 导数的实际应用 • 导数的扩展知识
01
导数的基本概念
导数的定义
总结词
导数是函数在某一点的变化率，表示函数在该点的切线斜率。
详细描述
导数是微积分中的一个基本概念，用于描述函数在某一点附近的变化率。对于可导函数$f(x)$，其在点$x_0$处 的导数定义为$f'(x_0) = lim_{Delta x to 0} frac{Delta y}{Delta x}$，其中$Delta y = f(x_0 + Delta x) - f(x_0)$ 。导数表示函数在点$x_0$处的切线斜率。
01
02
03
起源
导数最初由牛顿和莱布尼 茨在17世纪分别独立发现 ，为微积分学奠定了基础 。
早期发展
18世纪，欧拉、拉格朗日 等数学家进一步发展了导 数理论，将其应用于函数 研究。
现代应用
随着数学的发展，导数在 物理、工程、经济等领域 得到广泛应用，成为解决 实际问题的重要工具。
导数的其他性质
导数的几何意义
详细描述
在物理中，导数具有实际意义。例如，物体运动的瞬时速度 可以由速度函数的导数表示，物质扩散的瞬时速度可以由扩 散函数的导数表示。导数可以描述物体或物质在极短时间内 速度或加速度的变化。
02
导数的计算
切线斜率与导数
切线斜率
导数描述了函数在某一点的切线斜率 ，即函数在该点的变化率。
新教材高中数学第5章导数的概念及其几何意义pptx课件新人教A版选择性必修第二册
根据导数的几何意义，可知函数y＝f (x)的切线斜率在[a，b]内单调
递增，观察图象，只有A选项符合．
发现规律 导数几何意义理解中的两个关键点
f ′(x0)＞0
关键点一：y＝f (x)在点x＝x0处的切线斜率为k，则k＞0⇔_________;
f ′(x0)＜0
f ′(x0)＝0
k＜0⇔__________；k＝0⇔_________．
[解]
Δ
+Δ 3 +1− 3 −1
＝
Δ
Δ
3 Δ 2 +3 2 Δ+ Δ 3
＝
Δ
＝3xΔx＋3x2＋(Δx)2，
Δ
则 lim ＝3x2，因此y′＝3x2．
Δ→0 Δ
设过点M(1，1)的直线与曲线y＝x3＋1相切于点(0 ，03 ＋1)，根据
导数的几何意义知曲线在点P处的切线的斜率为k＝302 ①，过点M和
如图，割线P0P的斜率k＝_____________．记Δx＝x－x
0，当点P沿着
曲线y＝f (x)无限趋近于点P0时，即当Δx→0时，k无限趋近于函数y＝
f (x)在x＝x0处的导数，因此，函数y＝f (x)在x＝x0
切线P0T
处的导数f ′(x0)就是_________的斜率k
0，即
0 +Δ − 0
1
2
3
4
5
2．函数y＝f (x)在x＝x0处的导数f ′(x0)的几何意义是(
)
A．在点(x0，f (x0))处与y＝f (x)的图象只有一个交点的直线的斜率
B．过点(x0，f (x0))的切线的斜率
C．点(x0，f (x0))与点(0，0)的连线的斜率
5.1.2导数的概念及其几何意义课件-高中数学人教A版选择性必修第二册
s
v ;
t
(2)求平均速度
（3）求极限 lim
x 0
s
s(t t ) s (t )
lim
.
t
t
x 0
2由导数的定义可得求导数的一般步骤：
（1）求函数的增量Δy=f(x0+Δt)－f(x0)
y
x
讲
课
人
：
邢
启
强
(2)求平均变化率
（3）求极限 f ' ( x0 ) lim
x 0
y
x
是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
10
解：我们用曲线h(t)在t=t0, t1,t2处的切线斜率，刻画曲线h(t)
在上述三个时刻附近的变化情况.
(1)当t=t0时，曲线h(t)在t=t0处的切线l0平行于t轴，h'(t0)=0.
x
1
lim [3 x 2 3 xx ( x ) 2 ] x 2 .
3 x 0
y
4
1
y x3
3
3
P
2
1
-2 -1
O
-1
x
1
2
-2
y | x 2 2 2 4.
即点P处的切线的斜率等于4.
讲
课
人
：
邢
启
强
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
根据导数的定义,
x
x
x
y
4 x x 2 7x
'
lim x 3 3,
v ;
t
(2)求平均速度
（3）求极限 lim
x 0
s
s(t t ) s (t )
lim
.
t
t
x 0
2由导数的定义可得求导数的一般步骤：
（1）求函数的增量Δy=f(x0+Δt)－f(x0)
y
x
讲
课
人
：
邢
启
强
(2)求平均变化率
（3）求极限 f ' ( x0 ) lim
x 0
y
x
是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
10
解：我们用曲线h(t)在t=t0, t1,t2处的切线斜率，刻画曲线h(t)
在上述三个时刻附近的变化情况.
(1)当t=t0时，曲线h(t)在t=t0处的切线l0平行于t轴，h'(t0)=0.
x
1
lim [3 x 2 3 xx ( x ) 2 ] x 2 .
3 x 0
y
4
1
y x3
3
3
P
2
1
-2 -1
O
-1
x
1
2
-2
y | x 2 2 2 4.
即点P处的切线的斜率等于4.
讲
课
人
：
邢
启
强
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
根据导数的定义,
x
x
x
y
4 x x 2 7x
'
lim x 3 3,
高中数学5-1-2导数的概念及其几何意义第1课时导数的概念课件新人教A版选择性必修第二册
【解题探究】利用导数的定义求解．
用导数定义求函数在某一点处的导数的步骤 (1)求函数的增量 Δy＝f(x0＋Δx)－f(x0)； (2)求平均变化率ΔΔyx＝f(x0＋ΔΔxx)－f(x0)； (3)求极限Δlxim→0ΔΔyx.
导数的定义的变形形式 Δlxi→m0f(x0－－ΔxΔ)－x f(x0)＝Δlxi→m0f(x0＋nnΔΔxx)－f(x0)＝Δlxi→m0f(x0＋Δx)2－Δxf(x0－Δx) ＝f′(x0)．
3．函数y＝x2＋x在x＝1到x＝1＋Δx之间的平均变化率为 ( )
A．Δx＋2
B．Δx＋3
C．2Δx＋(Δx)2
D．3Δx＋(Δx)2
【答案】B 【解析】Δy＝(1＋Δx)2＋(1＋Δx)－12－1＝(Δx)2＋3Δx，所以ΔΔyx＝
(Δx)2Δ＋x 3Δx＝Δx＋3.
导数的概念(瞬时变化率)
函数 f(x)在区间[x0，x0＋Δx]上的平均变化率为6x0Δx＋Δx3(Δx)2＝6x0＋ 3Δx.
【解题探究】直接利用概念求解．
求平均变化率的策略 (1)求 Δy 时，要把 f(Δx＋x)和 f(x)表示出来，再作差． (2)求平均变化率时，先计算自变量和函数值的改变量 Δx＝x1－x0，Δy ＝f(x1)－f(x0)，再利用公式ΔΔyx＝f(xx1)1－ －fx(0x0)求出平均变化率．
lim (6＋3Δx)＝6.
Δx→0
2．设f(x)＝ax3＋2，若f′(－1)＝3，则a＝________. 【答案】1 【解析】Δlxim→0a(－1＋Δx)3＋Δ2－x [a·(－1)3＋2]＝Δlxi→ m0(aΔx2－3aΔx＋3a) ＝3a＝3，∴a＝1.
课堂互动
题型1 求函数的平均变化率
人教版高中数学选择性必修2《导数的概念及其意义》PPT课件
高中数学
选择性必修第二册 RJ
RJA
第五章
1
5.1导数的概念及其意义
5.1.2 导数的概念
及其几何意义
学习目标
1.通过实例分析，经历由平均变化率过渡到瞬时变化率的过程.
2.理解函数平均变化率、瞬时变化率的概念以及它们之间的关系.
3.掌握函数平均变化率、瞬时变化率的求法.
4.掌握导数的概念及其几何意义，会用导数的概念求简单函数在某点处的导数及曲
4x (x) 2 7 x
x 3，
x
了原油温度在时刻x0附近的变化情况.
y
lim (x 3) 3.
x 0 x
x 0
所以f '(2) lim
同理可得 ′（6）＝5.
在第2 h与第6 h时，原油温度的瞬时变化率分别为−3 ℃/h与5 ℃/h.说明在第2 h附近，
y
所以v '(2) lim
lim t 2 2. 同理可得 ′（6）＝ − 6.
t 0 t
t 0
在第2 s与第6 s时，汽车的瞬时加速度分别是2 m/s2与−6 m/s2.说明在第2 s附近，汽车的速度
每秒大约增加2 m/s；在第6 s附近，汽车的速度每秒大约减少6 m/s.
我们知道，导数 ′（0）表示函数＝（）在＝0处的瞬时变化率，反映了函数
＝（）在＝0附近的变化情况.那么导数 ′（0）的几何意义是什么？
思考：观察函数＝（）的图象（如下图），平均变化率
原油温度大约以3 ℃/h的速率下降；在第6 h附近，原油温度大约以5 ℃/h的速率上升.
例3
一辆汽车在公路上沿直线变速行驶，假设 s时汽车的速度（单位：m/s）为
＝（）＝ − 2 + 6 + 60，求汽车在第2 s与第6 s时的瞬时加速度，并说明它们的意义.
选择性必修第二册 RJ
RJA
第五章
1
5.1导数的概念及其意义
5.1.2 导数的概念
及其几何意义
学习目标
1.通过实例分析，经历由平均变化率过渡到瞬时变化率的过程.
2.理解函数平均变化率、瞬时变化率的概念以及它们之间的关系.
3.掌握函数平均变化率、瞬时变化率的求法.
4.掌握导数的概念及其几何意义，会用导数的概念求简单函数在某点处的导数及曲
4x (x) 2 7 x
x 3，
x
了原油温度在时刻x0附近的变化情况.
y
lim (x 3) 3.
x 0 x
x 0
所以f '(2) lim
同理可得 ′（6）＝5.
在第2 h与第6 h时，原油温度的瞬时变化率分别为−3 ℃/h与5 ℃/h.说明在第2 h附近，
y
所以v '(2) lim
lim t 2 2. 同理可得 ′（6）＝ − 6.
t 0 t
t 0
在第2 s与第6 s时，汽车的瞬时加速度分别是2 m/s2与−6 m/s2.说明在第2 s附近，汽车的速度
每秒大约增加2 m/s；在第6 s附近，汽车的速度每秒大约减少6 m/s.
我们知道，导数 ′（0）表示函数＝（）在＝0处的瞬时变化率，反映了函数
＝（）在＝0附近的变化情况.那么导数 ′（0）的几何意义是什么？
思考：观察函数＝（）的图象（如下图），平均变化率
原油温度大约以3 ℃/h的速率下降；在第6 h附近，原油温度大约以5 ℃/h的速率上升.
例3
一辆汽车在公路上沿直线变速行驶，假设 s时汽车的速度（单位：m/s）为
＝（）＝ − 2 + 6 + 60，求汽车在第2 s与第6 s时的瞬时加速度，并说明它们的意义.
人教版高中数学 选择性必修二 A版5.1.2《导数的概念及其几何意义》课件PPT
作业设计
课本P70.
习题5.1： 1、2、3、4、5、6、7.
在PPT软件中双击图标ห้องสมุดไป่ตู้开配套教案
人教A版高中数学选择性必修二
5.1.2 导数的概念及其
几何意义
第五章 一元函数的导数及其应用
汇报人：XXX
人教A版高中数学选择性必修二
5.1.2 导数的概念及其
几何意义
第五章 一元函数的导数及其应用
汇报人：XXX
目 录
01
学习目标
02
新知讲解
03
课堂练习
04
课程小结
第一部分
学习目标
学习目标
1. 理解函数在0处的瞬时变化率即导数的概念并会求其值.
2.理解导数的几何意义，并会应用之求切线方程.
3.感受新概念的定义、运动变化的数学思想方法，从而
温馨提示：直接利用概念求平均变化率，先求出表达
式，再直接代入数据就可以得出相应的导
数的值.
跟踪练习
解析：当自变量从0变化到0＋Δ时，函数的平均变化
Δ+0 − 0
△
率为 ＝
△
Δ
＝
= 30 2 +30 △ + △
2
0 +△ 3 −0 3
Δ
当0＝1，Δ → 0时,
1
∆
2
1
∆)=1−2
2
1
2
× 22 )
课堂互动
∴物体在时刻t=2处的瞬时速度是1−2 .
课堂互动
3.已知 ＝2－3，则 在 = 0处的切线的方程
(
3 + = 0
解析： ′(0)＝
)
Δ
导数的概念及其几何意义课件-2023学年高二下学期数学北师大版(2019)选择性必修第二册
得k＝y′|x＝m＝4m.
由题意可知4m＝8，∴m＝2.
代入y＝2x2－7得n＝1.
故所求切点P为(2，1)．
＝ lim (4x＋2Δx)＝4x，
∆→0
高中数学
选择性必修第二册
北师大版
课堂小结
1.知识清单：
（1）导数的概念.
（2）导数的几何意义.
2. 方法技巧：
极限思想.
导数几何意义理解中的两个关键
观察函数 = 的图象，
平均变化率
∆ 0 +∆ −(0 )
=
∆
∆
表示什么?
瞬时变化率
′ 0 = ∆→0
∆
=
∆→0
∆
0 +∆ −(0 )
∆
表示什么？
二 导数的几何意义
函数 = ()在0 处的导数 ′ 0 ，是曲线 = ()在点
（1）当t=0 时，曲线h(t)在t=0 处的切线0 平行于t轴，ℎ′ 0 =0,
这时，在t=0 附近曲线比较平坦，几乎没有升降；
（2）当t=1 时，曲线h(t)在t=1 处的切线1 的斜率ℎ′ 1 <0,这时,
在t=1 附近曲线下降，即函数h(t)在t=1 附近单调递减；
（3）当t=2 时，曲线h(t)在t=2 处的切线2 的斜率ℎ′ 2 <0,
x0 处瞬时变化越慢.
高中数学
选择性必修第二册
北师大版
即时巩固
判断正误(正确的画“√”，错误的画“×”)
(1)函数y＝f (x)在x＝x0处的导数即为在该点处的斜率，也就是k＝f ′(x0)． ( √ )
(2)f ′(x1)＞f ′(x2)反映了曲线在x＝x1处比在x＝x2处瞬时变化率较大．
导数的概念(第1课时)(课件)高二数学(沪教版2020选择性必修第二册)
沪教版2020选修第一册
第 5章导数及其应用
5.1导数的概念（第1课时）
初等数学可以帮助我们对匀速运动进行描述分析 ， 也能够顺 利解决形状规则物体的测量问题 ． 然而 ， 人类在实际生活中 面临的问题往往更为复杂 ． 例如 ， 运动中速度在不断变化 ， 图形的边界不再是规则的 ， 等等 ． 要处理这一类问题 ， 本 质上要有处理变化和变化中的瞬时状态的数学工具 ． 这是初 等数学所缺乏的 ， 需要用到高等数学特别是微积分的知识 ．
在本节的学习中 ， 我们将利用运动中的平均速度趋近于瞬时 速度 ， 利用曲线的割线趋近于它的切线 ， 从而初步认识导数 这一刻画函数瞬时变化率的工具 ．
当我们乘坐高铁时 ， 常常会在车厢内看到如图 ５ -１- １ 所示的 列车信息显示屏 ． 如何理解图中 “ 速度 ３０７动过程 ． 一个自然的想法 是把整个运动时间分割成若干个时间段 ， 求每个时间段的平均 速度 ． 可以想象 ， 随着时间的分割越来越精细 ， 分段的平 均速度对整个运动的描述会越来越精确
但是 ， 系统学习高等数学的内容不是高中课程所能承担的任 务 ． 本章用比较直观和粗略的方式引入微积分中一个最基本 的概念 ——— 导数 ， 为我们研究函数性质提供了一个工具 ， 从而可以解决变速运动等现实问题
由于知识基础不足或者可能产生的理解困难 ， 本章某些公 式与定理没有给出证明 ． 我们仅仅要求同学们初步了解这 些公式 、 定理的用途 ，从而对导数的基本思想有所认识和 体会 ． 更深入的学习将在未来的大学课程中继续
宋老师数学精品工作室
“ THANKS ”
【答案】1；
宋老师数学精品工作室
2、已知函数f(x)＝3x2＋5，求：f(x)： （1）从0.1到0.2的平均变化率； （2）在区间[x0，x0＋Δx]上的平均变化率；
第 5章导数及其应用
5.1导数的概念（第1课时）
初等数学可以帮助我们对匀速运动进行描述分析 ， 也能够顺 利解决形状规则物体的测量问题 ． 然而 ， 人类在实际生活中 面临的问题往往更为复杂 ． 例如 ， 运动中速度在不断变化 ， 图形的边界不再是规则的 ， 等等 ． 要处理这一类问题 ， 本 质上要有处理变化和变化中的瞬时状态的数学工具 ． 这是初 等数学所缺乏的 ， 需要用到高等数学特别是微积分的知识 ．
在本节的学习中 ， 我们将利用运动中的平均速度趋近于瞬时 速度 ， 利用曲线的割线趋近于它的切线 ， 从而初步认识导数 这一刻画函数瞬时变化率的工具 ．
当我们乘坐高铁时 ， 常常会在车厢内看到如图 ５ -１- １ 所示的 列车信息显示屏 ． 如何理解图中 “ 速度 ３０７动过程 ． 一个自然的想法 是把整个运动时间分割成若干个时间段 ， 求每个时间段的平均 速度 ． 可以想象 ， 随着时间的分割越来越精细 ， 分段的平 均速度对整个运动的描述会越来越精确
但是 ， 系统学习高等数学的内容不是高中课程所能承担的任 务 ． 本章用比较直观和粗略的方式引入微积分中一个最基本 的概念 ——— 导数 ， 为我们研究函数性质提供了一个工具 ， 从而可以解决变速运动等现实问题
由于知识基础不足或者可能产生的理解困难 ， 本章某些公 式与定理没有给出证明 ． 我们仅仅要求同学们初步了解这 些公式 、 定理的用途 ，从而对导数的基本思想有所认识和 体会 ． 更深入的学习将在未来的大学课程中继续
宋老师数学精品工作室
“ THANKS ”
【答案】1；
宋老师数学精品工作室
2、已知函数f(x)＝3x2＋5，求：f(x)： （1）从0.1到0.2的平均变化率； （2）在区间[x0，x0＋Δx]上的平均变化率；
数学分析--导数 ppt课件
数，如果要讨论改函数在端点处的变化率时，就要对导数概念加以补充，引出单 侧导数的概念。
定义 2 设函数 y f (x) 在点 x0 的某右邻域 (x0 ,x 0 δ)上有定义，若右
极限 或
l i m Δ y l i m f ( x0 Δ x ) f ( x0 ) (0＜ x ＜ )
Δ x Δx 0
理 5.1， f(x) x 在 x x 0 0 处不可导。
当 x0 0 时，由于 D(x) 为有界函数, 因此得到
f(0)
lim
f(x)
f(0)
li
mxD(x)
0.
x0 x 0
x 0
ppt课件
下页 18
（二）函数在一点的单侧导数
类似于函数在一点有左、右极限, 对于定义在某个闭区间或半开区间上的函
dx
dx
运算，待到学过“微分”之后，将说明这个记号实际上是一个“商”，相应于上述各种
表示导数的形式，f |x x 0 或
dy dx
|xx0
。
ppt课件
下页 23
例 6 证明：
(i) ( xn ) nxn1, n 为正整数 ;
(ii) (sinx) cosx , (cosx) sinx
(iii)
y 1
－1/π
0
1/π
x
ppt课件
下页 22
（三）导函数 若函数在区间 I 上每一点都可导（对区间端点，仅考虑相应的单侧导数），则称 f
为 I 上的可导函数。此时对每一个χ∈I，都有 f 的一个导数 f '(x) （或单侧导数）与之
对应，这样就定义了一个在 I 上的函数，称为 f 在 I 上的导函数，也简称为导数，记作
5.1.2 导数的概念及其几何意义课件ppt
值
y
y
,即
x
x
=
f(x 0 +x)-f(x 0 )
x
叫做函数y=f(x)从x0到x0+Δx的平均变化率.
(x0+Δx)-x0
名师点析 (1)Δx是自变量的变化量,它可以为正,也可以为负,但不能等于零,
而Δy是相应函数值的变化量,它可以为正,可以为负,也可以等于零.
(2)函数平均变化率的物理意义:如果物体的运动规律是s=s(t),那么函数s(t)
Δ
所以 =-Δx-2x+3.故函数的导数
Δ
Δ
f'(x)= lim
Δ→0 Δ
= (-Δx-2x+3)=-2x+3.
Δ→0
反思感悟 (1)利用定义求函数 y=f(x)的导数的步骤
①求函数值的变化量 Δy=f(x+Δx)-f(x);
Δ
②求函数的平均变化率
Δ
③取极限,得
=
(+Δ)-()
(2)若函数y=f(x)在某区间[x0,x0+Δx]上的平均变化率为0,能不能说明函数值在区
间[x0,x0+Δx]上的函数值都相等?
提示 不能.因为函数在某区间[x0,x0+Δx]上的平均变化率为0只能说明
f(x0+Δx)=f(x0).
(3)函数y=f(x)在区间[x0,x0+Δx]上的平均变化率的几何意义是什么?
它是一个确定的值,与给定的函数及x(或x0)的位置有关,而与Δx无关;导函
数是对一个区间而言的,它是一个确定的函数,依赖于函数本身,也与Δx无
关.
微练习
求函数 y=f(x)= x的导数.
解 函数的导数为
y
y
,即
x
x
=
f(x 0 +x)-f(x 0 )
x
叫做函数y=f(x)从x0到x0+Δx的平均变化率.
(x0+Δx)-x0
名师点析 (1)Δx是自变量的变化量,它可以为正,也可以为负,但不能等于零,
而Δy是相应函数值的变化量,它可以为正,可以为负,也可以等于零.
(2)函数平均变化率的物理意义:如果物体的运动规律是s=s(t),那么函数s(t)
Δ
所以 =-Δx-2x+3.故函数的导数
Δ
Δ
f'(x)= lim
Δ→0 Δ
= (-Δx-2x+3)=-2x+3.
Δ→0
反思感悟 (1)利用定义求函数 y=f(x)的导数的步骤
①求函数值的变化量 Δy=f(x+Δx)-f(x);
Δ
②求函数的平均变化率
Δ
③取极限,得
=
(+Δ)-()
(2)若函数y=f(x)在某区间[x0,x0+Δx]上的平均变化率为0,能不能说明函数值在区
间[x0,x0+Δx]上的函数值都相等?
提示 不能.因为函数在某区间[x0,x0+Δx]上的平均变化率为0只能说明
f(x0+Δx)=f(x0).
(3)函数y=f(x)在区间[x0,x0+Δx]上的平均变化率的几何意义是什么?
它是一个确定的值,与给定的函数及x(或x0)的位置有关,而与Δx无关;导函
数是对一个区间而言的,它是一个确定的函数,依赖于函数本身,也与Δx无
关.
微练习
求函数 y=f(x)= x的导数.
解 函数的导数为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• [解析] (1)∵物体在t∈[3,5]内的时间变化 量为 • Δt＝5－3＝2， • 物体在t∈[3,5]内的位移变化量为 • Δs＝3×52＋2－(3×32＋2)＝3×(52－32)＝ Δ s 48 48 ， Δt ＝ 2 ＝24(m/s)． • ∴物体在t∈[3,5]上的平均速度为
• (2) 求物体的初速度 v0 即求物体在 t ＝ 0 时的瞬时速 度． • ∵物体在t＝0附近的平均变化率为
3 3 (4 ＋ Δ t ) ＋ 3 － (4 ＋3) Δs (3)∵ ＝ Δt Δt
＝48＋12Δt＋(Δt)2， Δs ∴当 Δt 无限趋近于 0 时， 无限趋近于 48. Δt ∴v(4)＝48.
一、选择题 f(1＋Δx)－f(1) 1． 设函数 f(x)可导， 则 liΔm 等于( x→0 3Δx A．f′(1) 1 C.3f′(1) B．3f′(1) D．f′(3) )
第三：函数 f(x)在 x0 处可导，是指 Δx→0 时， Δx 有极 Δy 限．如果 不存在极限，就说函数在点 x0 处不可导，或说 Δx 无导数；
第四：f′(x0)的不同表达方式： y′|x ＝ x0 ＝ f′(x0) ＝ li x→ mx0 f(x0＋Δx)－f(x0) . Δx f(x)－f(x0) ＝ li Δm x→0 x－x0
• [分析] 已知函数f(x)在x＝a处的导数为A， 要求所给的极限值，必须将已给极限式转 化为导数的意义．
[解析]
f(a＋Δx)－f(a) (1)∵liΔm ＝A， x→0 Δx
f(a－Δx)－f(a) 则 liΔm x→0 Δx f[a＋(－Δx)]－f(a) ＝－liΔm ＝－A x→0 －Δx f(a＋Δx)－f(a－Δx) ∴liΔm x→0 Δx f(a＋Δx)－f(a)＋f(a)－f(a－Δx) ＝liΔm x→0 Δx f(a＋Δx)－f(a) f(a)－f(a－Δx) ＝liΔm ＋liΔm x→0 x→0 Δx Δx
• 二、填空题 • 4 ． 自由 落体运 动在 t ＝ 4s 的 瞬 时速度 是 ________． • [答案] 39.2m/s
1 2 [解析] s＝ gt 2 1 1 2 2 g(t＋Δt) － gt 2 Δs 2 1 ＝ ＝gt＋ g·Δt Δt Δt 2 1 ＝4g＋2g·Δt. Δs 1 所以 v＝s′(t)＝liΔm t→0 Δt ＝liΔm t→0 (4g＋2gΔt) ＝4g≈4×9.8＝39.2(m/s)．
• • • • •
[例2] 求函数y＝x2在点x＝3处的导数． [分析] 利用导数定义求导． [解析] (1)求y在点x＝3处的增量． 取Δx≠0，Δy＝(3＋Δx)2－32＝6Δx＋(Δx)2. (2)算比值．
2 Δy 6Δx＋(Δx) ＝6＋Δx. Δx＝ Δx
Δy (3)Δx 趋近于 0 时，Δx趋近于 6. 因此 y 在点 x＝3 处的导数是 6.
(1)求函数 y＝ x在点 x＝1 处的导数； (2)求函数 y＝x2＋ax＋b 在点 x＝x0 处的导数．
[解析] (1)Δy＝ 1＋Δx－1，
1＋Δx－1 Δy 1 ＝ . Δx＝ Δx 1＋Δx＋1 liΔm x→0 1 1 1 ＝ ，所以 y′|x＝1＝ . 2 1＋Δx＋1 2
(2)y′|x＝x0 (x0＋Δx)2＋a(x0＋Δx)＋b－(x2 0＋ax0＋b) ＝liΔm x→0 Δx
＝liΔm x→0
2 2 x2 0＋2x0Δx＋(Δx) ＋ax0＋aΔx＋b－x0－ax0－b Δx
2x0Δx＋aΔx＋(Δx)2 ＝liΔm x→0 Δx ＝liΔm x→0 (2x0＋a＋Δx)＝2x0＋a.
[例 3]
若函数 f(x)在 x＝a 处的导数为 A，求：
f(a＋Δx)－f(a－Δx) (1)liΔm ； x→0 Δx f(a＋4t)－f(a＋5t) (2)litm . →0 t
1 ＝(v0－gt0)Δt－ g(Δt)2， 2 Δs 1 Δs ∴ ＝v0－gt0－ gΔt，当 Δt→0 时， →v0－gt0. Δt 2 Δt 故物体在 t0 时刻的瞬时速度为 v0－gt0.
• 以初速度v0(v0＞0)竖直上抛的物体，t秒时的高度为s(t)＝ v0t－ gt2，求物体在t0时刻的瞬时速度．
＝A＋A＝2A. f(a＋4t)－f(a＋5t) (2)litm →0 t f(a＋4t)－f(a)＋f(a)－f(a＋5t) ＝litm →0 t f(a＋4t)－f(a) f(a＋5t)－f(a) ＝4litm －5litm →0 →0 4t 5t ＝4A－5A＝－A.
• [点评] 概念是分析解决问题的重要依据， 只有熟练掌握概念的本质属性，把握其内 涵与外延，才能灵活地应用概念进行解题， 解决这类问题的关键是等价变形，使问题 转化．
Δs f(0＋Δt)－f(0) Δt ＝ Δt 29＋3[(0＋Δt)－3]2－29－3(0－3)2 ＝ ＝3Δt－18， Δt ∴物体在 t＝0 处的瞬时变化率为 Δs lim lim Δ t→初速度为－18m/s.
• (3)物体在t＝1时的瞬进速度即为函数在t＝1 处的瞬时变化率． • ∵物体在t＝1附近的平均变化率为
• • • • •
[例1] 已知自由落体的运动方程为s＝ gt2，求： (1)落体在t0到t0＋Δt这段时间内的平均速度； (2)落体在t0时的瞬时速度； (3)落体在t0＝2秒到t1＝2.1秒这段时间内的平均速度； (4)落体在t＝2秒时的瞬时速度．
[分析]
平均速度 v 即平均变化率， 而瞬时速度即是平
(2)落体在 t0 时的瞬时速度为 1 v＝liΔm t→0 v ＝liΔm t→0 2g(2t0＋Δt)＝gt0. (3)落体在 t0＝2 秒到 t1＝2.1 秒时，其时间增量 Δt＝t1 1 － t0 ＝ 0.1 秒，由 (1) 知平均速度为 v ＝ 2 g(2×2 ＋ 0.1) ＝ 2.05g≈2.05×9.8＝20.09(米/秒)． (4) 由 (2) 知 落 体 在 t0 ＝ 2 秒 的 瞬 时 速 度 为 v ＝ g×2≈9.8×2＝19.6(米/秒)．
• 如果一个质点从固定点 A 开始运动，在时 间t的位移函数y＝s(t)＝t3＋3. • 求：(1)t＝4时，物体的位移s(4)； • (2)t＝2到t＝4的平均速度； • (3)t＝4时，物体的速度v(4)．
[解析] (1)s(4)＝43＋3＝67. (2)t＝2 到 t＝4 的平均速度为
3 3 Δs s(4)－s(2) 4 ＋3－2 －3 64－8 ＝ ＝ ＝ ＝28. Δt 2 2 4－2
Δs f(1＋Δt)－f(1) Δt ＝ Δt 29＋3[(1＋Δt)－3]2－29－3(1－3)2 ＝ ＝3Δt－12. Δt ∴物体在 t＝1 处的瞬时变化率为 Δs lim lim Δ t→0 Δt ＝Δ t→0 (3Δt－12)＝－12. 即物体在 t＝1 时的速度为－12m/s.
• [点评]
• [点评] 应注意区分平均速度与瞬时速度的 概念、瞬时速度是运动物体在t0到t0＋Δt这 一段时间内的平均速度当Δt→0时的极限， 即运动方程s＝f(t)在t＝t0时对时间t的导数．
[ 解析 ]
1 1 2 2 ∵Δs ＝v0(t0＋Δt)－2g(t0＋Δt) －v0t0－2gt0
－1 1 ＝ ＝－2， 1＋0· (1＋ 1＋0) 1 ∴f′(1)＝－ . 2
均速度 v 在 Δt→0 时的极限值，为此，要求瞬时速度，应 先求出平均速度，再求 v 当 Δt→0 时的极限值．
[解析]
(1)落体在 t0 到 t0＋Δt 这段时间内路程的增量为
1 1 2 2 Δs＝2g(t0＋Δt) －2gt0 因此，落体在这段时间内的平均速度为： 1 1 2 2 g(t ＋Δt) － gt0 2 Δs 2 0 1 Δt(2t0＋Δt) v＝ ＝ ＝ g· Δt Δt 2 Δt 1 ＝2g(2t0＋Δt)．
• 5．对于函数y＝x2，其导数等于原来的函数 值的点是______________． • [答案] (0,0)和(2,4)
[ 解 析 ] 2x·Δx＋(Δx)2 Δx ＝liΔm x→0 (2x＋Δx)＝2x. 令 2x＝x2，得 x＝0 或 x＝2，此时 y＝0 或 y＝4，即所 求点为(0,0)和(2,4)． y′ ＝ li Δm x→0 (x＋Δx)2－x2 ＝ li Δm x→0 Δx
2 3t ＋2 s＝ 2 29 ＋ 3( t － 3)
(t≥3) ① . (0≤t<3) ②
• 求：(1)物体在t∈[3,5]内的平均速度； • (2)物体的初速度v0； • (3)物体在t＝1时的瞬时速度．
• [分析] 由题目可获取以下主要信息： • ①物体的运动方程已知； • ②求物体在某一时间段的平均速度和物体 在某一时刻的瞬时速度． • 解答本题可先根据要求的问题选好使用的 函数解析式，再根据求平均变化率和瞬时 变化率的方法求解平均速度和瞬时速度．
• [答案] C
[解析] f(1＋Δx)－f(1) 1 1 原式＝3liΔm ＝3f′(1)． x→0 Δx
• 2 ． 设 f(x) ＝ ax ＋ 4 ， 若 f′(1) ＝ 2 ， 则 a 等 于 ( ) • A．2 B．－2 • C．3 D．－3 • [答案] A
f(x)－f(1) [解析] f′(1)＝lixm ＝lixm →1 →1a＝a＝2. x－1
• [点评] 求函数y＝f(x)在点x0处的导数的方法． • 由导数的意义可知，求函数y＝f(x)在点x0处的导数 的方法是：
(1)求函数的增量 Δy＝f(x0＋Δx)－f(x0)； Δy f(x0＋Δx)－f(x0) (2)求平均变化率 ＝ ； Δx Δx Δy (3)Δx 趋近于 0 时，若Δx趋近于一个常数，则这个常 数就是函数在该点处的导数．
•
1．1.2 导数的概念