信息论 第二章定义公式总结
第二章 信息论基本概念

= P(xy)logP(y)/P(y|x)
XY
XY
XY
在这里同样利用自然对数性质:lnω ≤ ω -1 ,ω >0 当且仅当ω =1时,式取等 令ω =P(y)/P(y|x),引用 lnω ≤ ω -1 H(Y|X)-H(Y)≤ P(xy)[P(y)/P(y|x)-1]loge = [P(x)P(y)-P(xy)]loge XY =(1-1)loge=0
第二章 信息论基本概念
§2.1 信源的分类
(1) 发出单个符号的无记忆信源 1. 离散无记忆信源 (2) 发出符号序列的无记忆信源 离散信源 (1) 发出符号序列的有记忆信源 2. 离散有记忆信源 (2) 发出符号序列的马尔可夫信源
§2.2 自信息量和条件自信息量 一. 自信息量
XY
下面推导说明求条件熵用联合概率加权的理由 先取在一个条件y下,X集合的条件熵H(X|y)为: H(X|y)= P(x|y)I(x|y) X =- P(x|y)logP(x|y) X
进一步把H(X|y)在Y集合上取数学期望,就得条件熵H(X|Y)为:
H(X|Y)= P(y)H(X|y) Y =- P(y)P(x|y)logP(x|y) XY =- P(xy)logP(x|y) XY
由定义式可知,若一个以等概率出现的二进制码元(0,1), 即当P(0)=P(1)=1/2时 1 I(0)=I(1)=- log 2 2 = log 2 =1bit 2 在此引入不确定度概念 若 出现概率 → 1 (发生可能性大,包含的不确定度小) 出现概率 → 0 (发生可能性小,包含的不确定度大) 出现概率 = 1 (包含的不确定度为0) 注意:随机事件的不确定度在数量上等于它的自信息量,两 者单位相同,但含义却不相同。具有某种概率分布的随机事件 不管发生与否,都存在不确定度,不确定度表征了该事件的特 性,而自信息量是在该事件发生后给予观察者的信息量。
信息论与编码 第二章 信源与信息熵

信源
{ 连续信源: 话音、图像
2~3 1~2 0~1 2 1 0
电 压 5~6 4~5 范围 量化 5 4
3~4
3
电 压 -1~0 -2~-1 -3~-2 -4~-3 -5~-4 -6~-5 范围
散无记忆信源。可用一个离散型随机变量X来描述这
个信源输出的消息。
2.1.1 无记忆信源
发出单个符号的离散无记忆信源
可用一个离散型随机变量X来描述这个信源输出的消息。 随机变量X的样本空间就是符号集:
A {a1 , a2 ,, an }
X的概率分布为:
P { p(a1 ), p(a2 ),, p(an )}
2.2.2 离散信源熵
信源熵
——信源的平均不确定度。
H ( X ) E[ I ( X )] p( xi )log p( xi )
i
单位为bit/符号
信源熵是在平均意义上来表征信源的统计特性,它是信源X的函数。
当信源给定,各符号的概率空间就给定,信源熵就是一个确定的值。
不同的信源因概率空间不同而具有不同的信源熵。
无记忆信源
{ 发出符号序列的无记忆信源
发出单个符号的无记忆信源
{
离散 连续
2.1.1 无记忆信源
发出符号序列的信源
——每次发出1组含L个(L≥2)符号的符号序列来代表一 个消息的信源。
需要用随机序列(或随机矢量) X =(X1, X2,…, Xl, …, XL)来描 述信源输出的消息,用联合概率分布p(X1, X2,…, Xl, …, XL)来表 示信源特性。 当L=2时,此时信源为X =(X1, X2) ,其概率空间为:
信息论

自信息、互信息、信息熵、平均互信息,定义、公式(1)自信息:一个事件(消息)本身所包含的信息量,它是由事件的不确定性决定的。
比如抛掷一枚硬币的结果是正面这个消息所包含的信息量。
随机事件的自信息量定义为该事件发生概率的对数的负值。
设事件 的概率为 ,则它的自信息定义为 (2)互信息:一个事件所给出关于另一个事件的信息量,比如今天下雨所给出关于明天下雨的信息量。
一个事件 所给出关于另一个事件 的信息定义为互信息,用 表示。
(3)平均自信息(信息熵):事件集(用随机变量表示)所包含的平均信息量,它表示信源的平均不确定性。
比如抛掷一枚硬币的试验所包含的信息量。
随机变量X 的每一个可能取值的自信息 的统计平均值定义为随机变量X 的平均自信息量: (4)平均互信息:一个事件集所给出关于另一个事件集的平均信息量,比如今天的天气所给出关于明天的天气的信息量。
为了从整体上表示从一个随机变量Y 所给出关于另一个随机变量 X 的信息量,我们定义互信息 在的XY 联合概率空间中的统计平均值为随机变量X 和Y 间的平均互信息画出各种熵关系图。
并作简要说明I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(XY)当X,Y 统计独立时,I(X;Y)=0实际信源往往是有记忆信源。
对于相互间有依赖关系的N 维随机变量的联合熵存在以下关系(熵函数的链规则) :定理3.1 对于离散平稳信源,有以下几个结论: (1)条件熵 随N 的增加是递减的;(2)N 给定时平均符号熵大于等于条件熵 (3)平均符号熵 随N 的增加是递减的;(4)如果 ,则 存在,并且分组与非分组码,奇异与非奇异码,唯一可译码与非唯一可译码。
即时码与非即时码1. 分组码和非分组码将信源符号集中的每个信源符号固定地映射成一个码字 Si ,这样的码称为分组码W i 。
用分组码对信源符号进行编码时,为了使接收端能够迅速准确地将码译出,分组码必须具有一些直观属性。
信息论与编码公式总结

第一章绪论第二章信源与信息熵离散信源的信息量自信息量条件自信息量联合自信息量单符号离散信源熵熵的性质1.非负性2.对称性3.确定性4.扩展性5.连续性二元联合信源的共熵与条件熵二元联合信源的共熵二元联合信源的条件熵独立熵、联合熵与条件熵的关系独立熵、联合熵与条件熵的物理意义离散无记忆信源N次扩展信源离散信道的平均交互信息量离散信道三种描述方法1.概率空间描述2.转移矩阵描述3.图示法描述离散信道的互信息量互信息量性质1.互易性-对称性2.3.互信息量可正可负4.任何两个事件之间的互信息不可能大于其中任何一个事件的自信息量5.离散信道的平均互信息量平均互信息量与联合熵、独立熵的关系一般关系X 和Y 相互独立时X 和Y 一一对应时数据处理定理信息不增性连续信源的熵连续信源均匀分布:高斯分布:指数分布:连续信源的最大熵定理输出峰值受限时的最大熵(瞬时功率受限/幅度受限):当概率密度分布为均匀分布时,信源具有最大熵输出平均功率受限时的最大熵:当其概率密度函数为高斯分布时,具有最大熵均值受限时的最大熵:其输出信号幅度呈指数分布时连续信源X 具有最大熵值信源的剩余度/多余度/冗余度离散信源的剩余度/多余度/冗余度:连续信源的剩余度/多余度/:第三章信道容量离散无噪声信道的熵速率和信道容量熵速率:信道容量:几种离散无噪声信道举例:1、具有一一对应关系的无噪信道2、具有扩展性能的无噪信道3、具有归并性能的无噪信道离散有噪声信道的熵速率和信道容量接收熵速率:信道容量:连续信道中的熵速率与信道容量连续无噪声信道的熵速率和信道容量熵速率信道容量连续有噪声信道熵速率信道容量第四章信源编码编码的定义1、二元码/多元码2、同价码3、等长码4、变长码5、非奇异码/非奇异码6、单义码(单义码)7、非续长码(瞬时可译码/即时码)/续长码(非瞬时可译码/非即时码)单义码存在定理(克劳夫特Kraft 不等式)码树图平均码字长度编码定理定长编码定理:变长编码定理:离散无记忆平稳信道的编码定理(香农第二定理):最佳变长编码一、香农编码二、范诺(费诺)编码(1) 把原始信源的符号按概率从大到小重新排列。
信息论编码 第二章信息度量1

50个红球,50个黑球
Y
20个红球,其它4种 颜色各20个
Z
问题:能否度量、如何度量??
2.3.2信源熵数学描述
信源熵
• 定义:信源各个离散消息的自信息量的数学期望 (即概率加权的统计平均值)为信源的平均信息 量,一般称为信源的信息熵,也叫信源熵或香农 熵,有时也称为无条件熵或熵函数,简称熵。 • 公式: n 1 H ( X ) = E[ I ( xi )] = E[log2 ] = −∑ p( xi ) log2 p( xi ) p( xi ) i =1 • 熵函数的自变量是X,表示信源整体,实质上是无 记忆信源平均不确定度的度量。也是试验后平均 不确定性=携载的信息 信息量为熵 • 单位:以2为底,比特/符号 • 为什么要用熵这个词,与热熵的区别?
3
( 2)
∑ p ( x ) = 1, ∑ p ( y
i =1 m i j =1
n
m
j
) = 1,∑ p ( xi / y j ) = 1,
i =1 n
n
概 率 复 习
∑ p( y
j =1 n
j
/ xi ) = 1, ∑ ∑ p ( xi y j ) = 1
j =1 i =1 m
m
( 3) ( 4) (5)
1
对天气x1 ,Q p( x1 / y1 ) = 0,∴不必再考虑x1与y1之间 信息量
对天气 x 2 : I ( x 2 : y 1 ) = log
2
p ( x 2 / y1 ) = log p ( x2 )
2
1/ 2 = 1( bit ) 1/ 4
同理 I ( x 3 : y 1 ) = I ( x 4 : y 1 ) = 1( bit ), 这表明从 y 1 分别得到了
信息论理论基础(第二章)

§2.1 信息度量 §2.2 离散信源的熵 §2.3 二元联合信源的共熵与条件熵 §2.4 信源冗余度 §2.5 连续信源的熵 §2.6 熵速率和信道容量 §2.7 离散有噪信道的熵速率和信道容量 §2.8 连续有噪信道的熵速率和信道容量 §2.9 使信源与信道匹配的编码
2013-8-2 1
I ( xi ; y j ) I ( xi ) I ( xi | y j ) log p( xi | y j ) p( xi )
(2-5)
互信息量 I ( xi ; y j ) 实际上就是已知事件 y j 后,所消除的关于事件 x i 的不肯定性,它等于事件 x i 本身的不肯定性 I ( xi ) 减去已知事件 y j 后对 x i 仍然存在的不肯定性 I ( xi | y j ) 。 互信息量的引出使信息的传递得到了定量的表示,是信息论发展的一个重要的里程碑。这里还 应指出,互信息量的单位的取法与自信息量的相同,不再详述。
I ( xi | y j ) log p( xi | y j )
2013-8-2
(2-4)
9
自信息量的单位与所用对数的底有关,如下: ⑴ 通常取对数的底为 2,信息量的单位为比特(bit,binary unit)。比特是信息论中最常 用的信息量的单位,当取对数的底为 2 时,2 常省略。 注意:计算机术语中 bit 是位的单位(bit,binary digit),与信息量的单位不同。 ⑵ 若取自然对数(以 e 为底) ,自信息量的单位为奈特(nat,natural unit)。理论推导或 用于连续信源时用以 e 为底的对数比较方便。 1 nat= log2 e bit=1.443bit ⑶ 工程上用以 10 为底较方便。若以 10 为对数底,则信息量的单位为哈特莱(Hartley)。 这是用来纪念哈特莱首先提出用对数来度量信息的。 1 Hartley= log2 e bit=3.322bit
第二章-信息论基本概念

马尔可夫信源:以信源输出符号序列内各
符号间条件概率来反映记忆特性的一类信 源。 m阶马尔可夫信源:信源输出的当前符号 仅与前面m个符号有关的马尔可夫信源。
m 阶马尔可夫信源的数学 模型
X x1 x2 xn X x im1 m 1 P( ) p( ) X1 X m xi1 xim 此时,状态si ( xi1 , , xim )
1 a1 : 2
1 a2 : 4
E2
a1 : 3 4
E3
a3 :
1 4
E1
a3 :
1 4
E4
1 a2 : 4
a1 :1
E5
a1 :
1 4
a3 :
1 2
此信源满足马尔可夫信源的两个条件, 是马尔可夫信源,并且是齐次马尔可夫信源。
例: 设两位二进制码所代表的四个状态分别为 00,01,10,11,其 符号转移概率和状态转移概率由下列两表给出:
回顾: 单符号无记忆信源熵:H(X) bit/符号 bit/序列
符号序列无记忆信源熵:KH(X)
符号序列有记忆信源熵:联合熵 H(X1X2…XN) bit/序列
平均符号熵 极限熵
1 H ( X 1 X 2 X N ) bit/符号 N 1 H lim H N ( X ) lim H ( X 1 X 2 X N )bit/符号 N N N
5.在第k次发出的符号xik 与前面m个 符号有关。 (xik-m xik-m+1 xik-1 ) 称为状态 这种关联性用条件概率表示: p( xik | xik m xik 1 )
6.在第k次发出的符号xik ,状态改变 si =(xik-m xik-m+1 xik-1 ) sj =(xik-m+1 xik-m+1 xik ) 用状态转移概率表示: p ( S m 1 s j | S m si ) p ( xik | xik m xik 1 ) 7.齐次马尔可夫信源 p ( S m 1 s j | S m si ) =p ( S1 s j | S0 si ) =p ( s j | si )
《信息论》第二章课件

I(x|y) -logp(x|y)
p(x|y)要满足非负和归一化条件
★条件自信息的含义包含两方面:
y b j 给定,x 事件发生前 ai 事件发生的不确定性 y b j 给定,x 事件发生后 ai 事件包含的信息量
★自信息、条件自信息和联合自信息之间的关系
I(xy)= I(x)+ I(y|x)= I(y)+ I(x|y)
2.7
随机变量X和Y,符号集均为{0,1}
p( y 0 | x 0) p( y 1 | x 0) 1 2
p x (0)
2 3
p x (1)
1 3
p( y 1 | x 1) 1
求H(Y|X)
解:H (Y | X ) p( x) H (Y | x) p( x 0) H (Y | x 0) p( x 1) H (Y | x 1)
其中,q(ui)为节点ui的概率,H(ui)为节点ui的分支熵。
例
2.7
1/2 p 2/3
a1: p/3
b1: 2p/3
b2: 2/3
1/2
a2: p/3
r: 1
1-p
a3: 2(1-p)/3
1/3
a4: 1/3
条件熵
★
条件熵:联合集XY上,条件自信息I(y|x)的平均值
H (Y / X ) E [ I ( y / x)]
I ( x; y) I ( x) I ( x | y)
I(x;y)与 I(x|y)的区别?
互信息的性质
★ 互易性 ★ 当事件x,y统计独立时,互信息为0,即 I(x;y)=0 ★ 互信息可正可负 ★ 任何两事件之间的互信息不可能大于其中 任一事件的自信息
信息论第二章

2.2.2 离散信源熵
例2-2-2
一个布袋内放100个球,其中80个球是红色的, 20个球是白色的,若随机摸取一个球,猜测其颜 色,求平均摸取一次所能获得的自信息量。
解: 依据题意这一随机事件的概率空间为
X P
x1 0.8
x2 0.2
2021/7/30
其中:x1表示摸出的球为红球事件,x2表示摸出的球是白球事 件
2021/7/30
几个概念
1. 条件熵
定义: 在 给 定 yj 条 件 下 , xi 的 条 件 自 信 息 量 为 I(xi/yj)
,X 集合的条件熵H(X/yj)为
H(X/yj)=
p(xi/yj)I(xi/yj)
i
2021/7/30
在给定Y(即各个yj)条件下,X集合的条件 熵
H(X/Y)定义为
2021/7/30
3. 联合自信息量
定义:两个消息xi,yj同时出现的联合自信息量
I(xiyj)lop(g xiyj)
注意: a. 当xi,yj相互独立时,有P(xiyj)=P(xi)P(yj),那 么就有 I(xiyj)=I(xi)+I(yj)。 b. xiyj所包含的不确定度在数值上也等于它们的 自信息量。
1) 自信息量I(x1)和I(x2)只是表征信源中各个符号的不确 定度,一个信源总是包含着多个符号消息,各个符号消息
又按概率空间的先验概率分布,因而各个符号的自信息量
就不同。所以自信息量不能作为信源总体的信息量。
2021/7/30
2) 因为X中各符号xi的不确定度I(xi)为非负值,p(xi)也 是非负值,且0p(xi)1,故信源的平均不确定度H(X )也是非负量。
第二章-信息论基本概念(3-1)

3. I(X;Y) = H(X) + H(Y) – H(XY) H(X) +H(Y)——通信前,整个系统的先验平均不确定度 H(XY)—— 通信后,整个系统仍剩余的平均不确定度 I(X;Y)—— 通信前后,整个系统平均不确定度的减少量, 即传输的互信息。 [结论] I(X;Y)——平均每传送一个信源符号时, 流经信道的平均(有用)信息量 H(X/Y) H(X) I(X;Y) H(Y)
= P(yj)P(xi|yj)log2P(xi|yj)/P(xi) i j
= P(xiyj)log2P(xi|yj)/P(xi)
i j
二、物理意义 1. I(X;Y)= H(X) – H(X/Y) (1) H(X)——信源熵:X的不确定度 H(X/Y)——已知Y时,对X仍剩的不确定度(疑义度) [结论] I(X;Y) ——―Y已知”,X的平均不确定度的减少量, 即获得了I(X;Y) 的信息量
② 无记忆, 故p(ai)=p(xi1)p(xi2)…p(xiN)
二、熵 H(XN)=NH(X)
(1)当信源无记忆(序列中的符号之间无相关性)时
H ( X ) p(ai ) log2 p (ai ) { p( xil )[log 2 p( xil )]}
i
i l 1 l 1
(2) H(X)——信源含有的平均信息量(总,有用)
I(X;Y)——信宿收到的平均信息量(有用部分) [结论] H(X/Y)—因信道有扰而丢失的平均信息量,故称损失熵
2. I(Y;X)= H(Y) – H(Y/X)= I(X;Y) (1) H(Y)——信宿的平均信息量 I(X;Y)——信道传输的平均信息量 [结论] H(Y/X)——因信道有扰而产生的假平均信息量, 称噪声熵、散布度、扩散度 (2) H(Y)——Y的先验不定度 H(Y/X)——发出X后,关于Y的后验不定度 [结论] I(Y;X)——发X前后,Y平均不确定度的减少量
信息论第2章(信息量、熵及互信息量)PPT课件

信息论基础
The Basis of Information Theory
主题No2:信息量、熵和互信息量
在上一次课中我们提到香农对信息定性的 定义——事物运动状态或存在方式的不确定性 的描述。事实上,香农对信息不仅作了定性描 述,而且还进行了定量分析。
信源发出的消息常常是随机的,具有不确 定性。如果信源中某一消息的不确定性越大, 一旦发生,并为收信者收到,消除的不确定性 就越大,获得的信息也就越大。同时事件发生 的不确定性与事件发生的概率有关,概率越小, 不确定性就越大。
研究通信系统的目的就是要找到信息传输 过程的共同规律,以提高信息传输的可靠性、 有效性、保密性和认证性,以达到信息传输系 统最优化。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
I(X;Y)是一个用来衡量信道好坏的 非常好的工具。
计算条件熵的例子
例6 设一个二进制对称信道BSC:
其先验概率为p(0)=p(1)=1/2,试计算条 件熵. [解答]由已知条件得:
由条件熵的定义有:
结果表明,虽然每个字符的错误率只有 0.1,可导致整个信宿对信源的平均不确定 性达到了0.469,将近一半。可见通信系统 对信道的要求非常高。
信息论2-2

(2) H ( X ) H ( X )
例7:对例2中的马氏信源,计算其熵率。
例8:对例3中的二阶马氏信源,计算其熵率。
三、信源的冗余度
冗余度常用来描述信源输出符号携带信息的有效程度, 它表示给定信源在实际发出信息时所包含的多余信息。 冗余度来自两个方面:①信源符号间的相关性;②信 源符号分布的不均匀性。 定义:冗余度 log H ( X )
引理2.2.1 设 f (n)是满足 f (m n) f (m) f (n) 的半可 加数列,则: 1 1 lim f (n) inf f (n) n n n n
3. 平均符号熵
定义2.2.1:定义n长信源序列中平均每个信源符号所 携带的信息量为:
Hn (X ) 1 H ( X 1 , X 2 , , X n ) n
n
i 1 n
1. 熵的不等式
H ( X 1 , X 2 ,, X mn ) H ( X 1 , X 2 ,, X m ) H ( X m1 , X h(m) h(n),对任意整数 ,n成立 m
2. 半可加数列 若数列满足上述不等式,则称该数列为半可加数列.
存在,且:
H ( X ) inf
n
1 H ( X 1 , X 2 ,, X n ) n
Th2.2.3: 设 X {X 1 , X 2 ,, X n ,} 是平稳信源,则:
(1) H ( X ) l im H ( X n | X 1 , X 2 ,, X n1 ) 存在,且:
0.029 0.023
0.0225 0.021 0.0175
V K
X J,Q Z
0.008 0.003
0.002 0.001 0.001
信息论讲义-第二章

例
英文字母中“ 的出现概率为0.105, 的出现概率为0.105 的出现概率为0.023 英文字母中“e”的出现概率为0.105,“c”的出现概率为0.023, 的出现概率为0.023, “o”出现的概率为 0.001。分别计算它们的自信息量。 出现的概率为 0.001。分别计算它们的自信息量。 解:根据自信息量的定义 “e”的出现的信息量为 e 的出现的信息量为
n j
/ xi )
=
p( xi ) p( y j / xi ) p( y j )
m
, = p( y j ) p( xi / y j )
m j =1 j i j
p( y j / xi ) =
p( xi y j )
j =1 i j
∑ p( x y ) ∑ p( y ) p( x / y )
n
=
p( y j ) p( xi / y j )
释:
1 I ( x i ) = log = − log p( x i ) p( x i )
p(xi) ≤1, 表示事件 i出现的概率 , 表示事件x 出现的概率, 号的主要目的是: 取“-”号的主要目的是:使I(xi) ≥0 号的主要目的是
11
自信息量的单位 为底: 比特(bit) 以2为底: 比特(bit) (binary unit) 为底: 奈特(nat) 以e为底: 奈特(nat) (nature unit) 10为底 为底: 哈脱来(Hart) 以10为底: 哈脱来(Hart) (Hartley) 换算关系: 换算关系: 1 nat ≈ 1.443 bit 1 Hart ≈ 3.322 bit 一般取以2为底, bit的信息量就是二元概率 一般取以2为底,1 bit的信息量就是二元概率 空间在等概时的每个事件蕴含的自信息量。 空间在等概时的每个事件蕴含的自信息量。 计算机技术中的术语“比特” 注:计算机技术中的术语“比特”表示一个二 元数字, 元数字,每个二元数字所能提供的最大平均信息量 比特。 为1比特。
《信息论》第二章

29
I(X;Y)与信息熵的关系 与信息熵的关系
H ( XY )
H(X)
I(X;Y)=0 集合X与集合Y 相互独立的情况
H (Y )
30
I(X;Y)与信息熵的关系 与信息熵的关系
13
信息熵,条件熵,联合熵 信息熵,条件熵, 三者之间的关系
H ( XY ) = H ( X ) + H (Y | X ) H ( XY ) = H (Y ) + H ( X | Y )
当集合X 和集合Y 相互独立时有
H(X |Y ) = H(X ) H (Y | X ) = H (Y ) H ( XY ) = H ( X ) + H (Y )
14
离散二元信源的信息熵 H ( X ) = [ p log p + (1 p) log(1 p)]
1 X 0 p( x ) = p 1 p
15
例题
有两个二元随机变量X和 , 有两个二元随机变量 和Y,它们的联合概率为 p(xy) x = 0 x = 1 y = 0 1/8 3/8 y=1 3/8 1/8 并定义另一随机变量Z=XY(一般乘积),试计算: 并定义另一随机变量 (一般乘积 ,试计算: (1) H(X),H(Y),H(Z),H(XY),H(XZ),H(YZ) , , , , , , H(XYZ) (2) H(X|Y),H(X|Z),H(Z|X), H(Z|Y), H(Y|Z), , , , , , H(Y|XZ),H(Z|XY) ,
11
联合自信息量与联合熵
联合自信息量定义
信息论第二章ppt

特别,对于离散情形,记 xi 表示时刻t i 所取的值, { X (t )} 若 为平稳过程,则其各维联合概率分布均与 t i, t j,( i j) 时间起点无关,即当时 ,有 , P( x ) P( x ) ,
i j
P( xi xi1 ) P(x j x j 1 )
为描述随机过程在不同时刻的状态之间的统 计联系,一般可对任意个 n(n 2,3, ) 不同时 刻 t1, t2 , , tn T,引入 n 维随机变 量 ( X (t1 ), X (t2 ), , X (tn )) ,它的分布函数记为:
FX ( x1, x2 , , xn ; t1, t2 , , tn ) P{X (t1) x1, X (t2 ) x2 , , X (tn ) xn}, xi R, i 1,2, , n
当t1 t2 t
2
2 2 ( t ) C ( t , t ) R ( t , t ) X X X (t ) 时, X
。
如果对每一个 t T ,随机过程 {X (t ), t T }的二 阶矩 E[ X (t )] 都存在,则称它为二阶过程。二阶过 程的相关函数总存在。 例3. 求随机相位正弦波的均值函数、方差函 数和自过程
(1) 如果X (t ) E[ X (t )] X (t ) 以概率1成立,称随机过程{ X (t )} 的均值具有各态历经性; (2) 若对任意实数 ,RX ( ) E[ X (t) X (t )] X (t) X (t ) 以概率1成立,则称随机过程 {X (t )} 的自相关函数具有各 态历经性,特别当 0 时,称均方值具有各态历经 性; (3) 如果随机过程 { X (t )} 的均值和自相关函数都具有各 态历经性,则称 { X (t )}是各态历经过程,或称{ X (t )} 是各 态历经的。各态历经性有时也称作遍历性或埃尔谷德性。
信息论公式总结
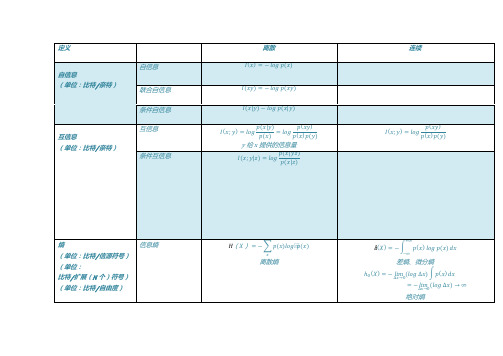
间的关系
I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)
I(X;Y)=H(X)+ H(Y)-H(XY)
对比:
平均互信息不熵的关系
; = −
; = + −
等式两边同时对 ()求和则为上式
I(X;Y|Z) =I(X;YZ)-I(X;Z)
0 = − ( ∆)
∆→0
= − ( ∆) → ∞
∆→0
绝对熵
= −
∆
∆ →0
=−
=−
=−
()
∆ ∆
∆ −
互信息的性质
2. ⊥ 时: I(x;y)=0
3.互信息可正可负(平均互信息非负)
4.任何两件事的互信息丌大于任一事件自信息:
(一
件事情的自信息是任何其他事件所能提供关于该事
件的最大信息量)
; ≤ , ; ; ≤ ,()
非负性 I(X;Y)≥0
1.非负性 I(X;Y)≥0
定义
自信息
(单位:比特/奈特)
互信息
(单位:比特/奈特)
熵
(单位:比特/信源符号)
(单位:
比特/扩展(N 个)符号)
(单位:比特/自由度)
离散
自信息
连续
= − ()
联合自信息
= − ()
条件自信息
(|) − (|)
互信息
; =
情况下丌满足)
6.确定性
任何一事件为 1,熵为 0
7.
(上凸性) = (1 ,2 , … , )是(1 ,2 , … , )
信息论

5. 连续性:
lim H
0
( p1,
p2 ,
, pq1 ,pq ) H ( p1, p2,
, pq )
即信源概率空间中概率分量的微小波动,不会引起 熵的变化。
BUPT Press
6.递推性
H ( p1, p2,
, pn1, q1, q2 ,
, qm ) H ( p1, p2,
,
pn )
pn H
定义2.6
nm
I ( X ;Y )
p( xi y j )I ( xi ; y j )
i1 j1
n i 1
m j 1
p( xi y j ) log
p( xi | y j ) p( xi )
n i 1
m j 1
p( xi y j ) log
1 p( xi )
n i 1
m j 1
p( xi y j ) log
互信息的引出,使信息得到了定量的表示,是信息论发展的一个重 要的里程碑。
BUPT Press
例2.2 某地二月份天气出现的概率分别为:晴1/2,阴 1/4,雨1/8,雪1/8。某天有人告诉你:”今天不是
晴天”,把这句话作为收到的消息y1 ,求收到y1 后, y1 与各种天气的互信息量。
BUPT Press
k 1
xq
p(
xq
)
BUPT Press
定义2.3 随机变量X的每一个可能取值的自信息 I (xi )的 统计平均值定义为随机变量X的平均自信息量:
q
H ( X ) E I (xi ) p(xi ) log p(xi ) i 1
这里q为的所有X可能取值的个数。
熵的单位也是与所取的对数底有关,根据所取的对数 底不同,可以是比特/符号、奈特/符号、哈特莱/符号或 者是r进制单位/符号。通常用比特/符号为单位。
信息论公式总结

离散
������ ������������ = ������ ������ + ������ ������ ������ = ������ ������ + ������ (������|������) ������ ������; ������ = ������ ������ − ������ ������ ������
������
=− ������ ������ =−
������
������ ������ ������������������ ������(������) ������������
������ ������������ ∆������ ������������������ ������ ������������ ∆������
证明:熵不增原理,所以取等条件一致 当且仅当各������������ 独立时,取“=” 熵函数的唯一性 尚不清楚 互易性:I(x;y)=I(y;x)
互信息的性质
2. ������ ⊥ ������时: I(x;y)=0 3.互信息可正可负(平均互信息非负) 4. 任何两件事的互信息不大于任一事件自信息: (一 件事情的自信息是任何其他事件所能提供关于该事 件的最大信息量)
含义:条件越多,熵越小
������ ������
������(������1 ������2 … ������������ ) ≤
������ =1
������(������������ )
������(������1 ������2 … ������������ ) ≤
������ =1
������(������������ )
=
������
������ ������ ������ ������������������ ������ ������ ������
第二章-信息论基本概念(3)(1)

K阶马尔可夫链每个状态由K个符号组成。若信源符号有D种, 阶马尔可夫链每个状态由K个符号组成。若信源符号有D 则状态数目M 则状态数目M为: M=DK
马尔可夫链可以用香农线图表示。(a),(b),(c)分别表示信源含两种字母(D=2)的一 马尔可夫链可以用香农线图表示。(a),(b),(c)分别表示信源含两种字母(D=2)的一 分别表示信源含两种字母(D 阶、二阶和三阶马尔可夫链的线图。(d),(e)分别表示D=3和D=4的一阶马尔可夫链的 二阶和三阶马尔可夫链的线图。(d),(e)分别表示D 分别表示 线图。 线图。
状态转移图(香农线图 状态转移图 香农线图) 香农线图
0:0.5 E1 0:0.6
E2
1:0.5 E3 1 1:0.4
是三种状态, 【注】E1、E2、E3是三种状态,箭头是指从一个状态转移到另 一个状态,旁边的数字代表发出的某符号和条件概率 一个状态,旁边的数字代表发出的某符号和条件概率p(ak/Ei) 。 这就是香农提出的马尔可夫状态转移图,也叫香农线图。 这就是香农提出的马尔可夫状态转移图,也叫香农线图。
3. 离散有记忆信源-马尔可夫信源 离散有记忆信源-
马尔可夫信源-非平稳离散信源中的一类特殊信源。 马尔可夫信源-非平稳离散信源中的一类特殊信源。 是由信源发出的各个符号之间的关连性构成一个整体消息。 是由信源发出的各个符号之间的关连性构成一个整体消息。 这种关连性用符号的转移概率 条件概率)表示: 转移概率( 这种关连性用符号的转移概率(条件概率)表示: 如:BOY P(B) P(O|B) P(Y|BO)
预备知识:-马尔可夫过程、 预备知识 -马尔可夫过程、马尔可夫链
马尔可夫过程: 马尔可夫过程: 对于任意的大于2的自然数n 在连续的时间T轴上有n 对于任意的大于2的自然数n,在连续的时间T轴上有n个不同时 刻,t1,t2,…,tn满足,在tn时刻的随机变量Xn与其前面(n-1) , 满足, 时刻的随机变量 与其前面( 个时刻的随机变量X 个时刻的随机变量 1,X2,…,Xn-1的关系可用它们之间的条件 , - 概率密度函数来表示,如果满足下式: 概率密度函数来表示,如果满足下式: p(Xn ,tn| Xn- 1 , tn-1 ,Xn-2, tn-2,…,X1,t1) ( , - - - - =p(Xn ,tn| Xn - 1,tn - 1) ( 则这种随机过程称为单纯马尔可夫过程(一阶马尔可夫过程) 则这种随机过程称为单纯马尔可夫过程(一阶马尔可夫过程) 单纯马尔可夫过程 K阶马尔可夫过程的特征为: 阶马尔可夫过程的特征为: 的特征为 p(Xn ,tn| Xn- 1 , tn-1 ,Xn-2, tn-2,…,X1,t1) ( , - - - - =p(Xn ,tn| Xn-1,tn-1 ,Xn-2, tn-2,…,Xn-k,tn-k) ( , - - - - - -
第二章-信息论基本概念(2)

p( xi | y j )
p( y j | xi )
如果X是观察输入,Y是观察输出
p( xi | y j ) 后验概率 I ( xi | y j ) lbp( xi | y j ) p( y j | xi )
转移概率
bit/符号
表示在观察到符号yj的条件下xi还剩下的不确定性
I ( y j | xi ) lbp( y j | xi )
[含义] 信源发xi前、后,信宿收到yj的不确定度的减少
(3) I(xi;yj) =I(xi) +I(yj) -I(xi,yj)
[注意] I(xi;yj) 与I(xi,yj) 不同!
2. 互信息的性质
(1) 对称性——I(xi ;yj) = I(yj ;xi)
(2) X与Y独立时——I(xi ;yj) = 0 (3) I(xi;yj) 可为正、负、0 当事件xi 和yj 统计独立时,互信息量为零;互信息量为正, 说明事件yj 的出现有助于肯定事件xi 的出现;反之,则是不 利的。造成不利的原因是由于信道存在干扰。 (4)任何两个事件之间的互信息量不可能大于其中任一事件的 自信息量 I(xi; yj) = I(yj; xi) ≤ I(xi) I(yj)
信源 X
信道
信宿 Y
1. 互信息量
互信息量为信源后验概率与先验概率比值的对数 : p ( xi / y j )
I(xi;yj)=log
p ( xi )
p(xi) ——先验概率:信源发xi的概率 p(xi/yj)——后验概率:信宿收到yj后,推测信源发xi的概率
(1) yj对xi的互信息 I(xi;yj) I(xi;yj)= I(xi)- I(xi/yj)
bit/符号
