组合图形的计数
四年级奥数第二讲图形的计数问题含答案

四年级奥数第⼆讲图形的计数问题含答案第⼆讲图形的计数问题⼀、知识点:⼏何图形计数问题往往没有显⽽易见的顺序,⽽且要数的对象通常是重叠交错的,要准确计数就需要⼀些智慧了.实际上,图形计数问题,通常采⽤⼀种简单原始的计数⽅法-⼀枚举法.具体⽽⾔,它是指把所要计数的对象⼀⼀列举出来,以保证枚举时⽆⼀重复、.⽆⼀遗漏,然后计算其总和.正确地解答较复杂的图形个数问题,有助于培养同学们思维的有序性和良好的学习习惯.⼆、典例剖析:例(1)数出右图中总共有多少个⾓分析:在∠AOB内有三条⾓分线OC1、OC2、OC3,∠AOB被这三条⾓分线分成4个基本⾓,那么∠AOB内总共有多少个⾓呢?⾸先有这4个基本⾓,其次是包含有2个基本⾓组成的⾓有3个(即∠AOC2、∠C1OC3、∠C2OB),然后是包含有3个基本⾓组成的⾓有2个(即∠AOC3、∠C1OB),最后是包含有4个基本⾓组成的⾓有1个(即∠AOB),所以∠AOB内总共有⾓:4+3+2+1=10(个)解:4+3+2+1=10(个)答:图中总共有10个⾓。
练⼀练:数⼀数右图中总共有多少个⾓?答案: 总共有⾓:10+9+8+…+4+3+2+1=55(个)例(2 )数⼀数共有多少条线段?共有多少个三⾓形?分析:①要数多少条线段:先看线段AB、AD、AE、AF、AC、上各有2个分点,各分成3条基本线段,再看BC、MN、GH这3条线段上各有3个分点,各分成4条基本线段.所以图中总共有线段是:(3+2+1)×5+(4+3+2+1)×3=30+30=60(条).②要数有多少个三⾓形,先看在△AGH中,在GH上有3个分点,分成基本⼩三⾓形有4个.所以在△AGH中共有三⾓形4+3+2+1=10(个).在△AMN与△ABC中,三⾓形有同样的个数,所以在△ABC中三⾓形个数总共:(4+3+2+1)×3=10×3=30(个)解::①在△ABC中共有线段是:(3+2+1)×5+(4+3+2+1)×3=30+30=60(条)②在△ABC中共有三⾓形是:(4+3+2+1)×3=10×3=30(个)答:在△ABC中共有线段60条,共有三⾓形30个。
数三角形数量的技巧

数三角形数量的技巧
数复杂图形中三角形的数量时,可以采用以下几种技巧:
1.顶点计数法:
选择一个顶点作为起始点,计算从该顶点出发能构成多少个不同的三角形。
例如,若一个顶点连接了n条线段,则以这个顶点为顶点的三角形数量为C(n,2)(组合数,即从n个不同元素中取两个元素的组合方式数)。
对于所有顶点重复此步骤,并确保不重复计算任何一个三角形。
2.层叠计数法:
当图形内有平行线或分层结构时,可以一层一层地数。
先计算没有横线分割的大三角形内部的小三角形数目,然后考虑每一层新增的三角形,利用累加或者乘积的方式得出总和。
3.边对角线法:
计算图中的线段数量,并注意线段如何形成三角形。
可以标记每条线段,对于每个顶点,统计由该顶点与其他点相连形成的三角形数量。
4.整体拆分法:
将复杂的图形分解成多个简单子图形,分别计算各个子图形中的三角形数量,再将它们相加。
5.递归或归纳法:
如果图形具有某种规律性或自相似性,可能可以通过递归算法来计算
各部分的三角形数量。
在实际操作中,根据图形的具体情况灵活运用这些方法,有时需要结合使用多种方法以确保准确无遗漏地计算出所有三角形的数量。
对于简单图形,直接观察即可快速得出结果;而对于较复杂的图形,则需更加细致地分析和分类计数。
小学五年级组合图形的计数(汇编)

()个
④
()个
3、数一数,下图各有多少个正方形
①
()个
②
firm n.公司()个
△immune adj.有免疫力的
纳尔逊?曼德拉(前南非共和国总统)
△catfish n.鲶鱼4、数一数,下面的图形中各有多少个三角形。
①
liquid n.液体
()个
②
severe adj.严重的;剧烈的;严厉的
△adventurer n.冒险家
△analytical adj.分析的
()个
加试题:数一数有()个梯形
leave out省去;遗漏;不考虑
lie n.谎话;谎言
数一数有()个长方形
组合图形的计数
例一、下图中共有()个平行四边形
例二、下图中共有()个长方形。
例三、下图共有( )个三角形.
例四、下图共有( )个三角形.
例五、下图有( )个长方形.
例六、下图中有()个正方形
组合图形的计数
1、数一数下面的图形中有几个平行四边形
()个
2数一数,下面图形中有多少个长方形①Fra bibliotek()个②
()个
第12章 图形的计数

第5讲 图形的计数赛点突破计数是组合数学的重要内容,计数的方法有分类法,分步法,递推法和与对应法等。
1.分类计数在计数时,为了做到不重复也不遗漏,可以先将图形按某个标准分类,然后将其每一类相的方法数加,便得到了总数。
这种方法叫做分类法。
2.分步计数在计数时,为了有序地思维,我们常将其分成若干步,然后将其每一步的方法数相乘,便得到了总数。
这种方法叫做分步法。
3.递推计数为了求出计数的总数,当所研究的对象数目较大时,我们常常对较小数量的对象进行观察,计算。
如果对研究对象的个数n 观察,计算后,发现由n=1的结果可以算出n=2的结果,由n=2的结果可以算出n=3的结果,等等,我们就找到了计数的规律。
这种方法叫做递推法。
4.对应计数在解决某些计数问题时,为了解决某个问题A ,我们将其中的研究对象和另一个问题B 中的研究对象配成对,通过解决B 问题来达到解决A 问题的目的。
这种方法叫做对应法范例解密例1.如图,直线上有6个点:A ,B ,C ,D ,E ,F ,以这些点为端点的线段有多少条?A C D E F解1 对于两条线段,只要有一个端点不同,就是不同的线段,我们以左端点为标准,将线段分5类分别计数:(1)以A 为左端点的线段有AB ,AC ,AD ,AE ,AF 共5条;(2)以B 为左端点的线段有BC ,BD ,BE ,BF 共4条;(3)以C 为左端点的线段有CD ,CE ,CF 共3条;(4)以D 为左端点的线段有DE ,DF 共2条;(5)以E 为左端点的线段只有EF 一条.所以,不同的线段一共有5+4+3+2+1=15(条).解2 因为每两点可以连一条线段,我们先取一点,有6种取法;再取第二点,有5种取法。
故一共有6×5=30种取法。
但因先取A 点再取B 点和先取B 点再取A 点得到的是同一条线段,在上述计数中被重复计算了,故实际上是30÷2=15种取法,即一共可以连45条线段。
组合计数的几个典型方法

组合计数的几个典型方法组合计数是数学中的一个分支,主要研究将多个事物进行组合的方法和技巧。
在现实生活和学术研究中,组合计数是非常重要的。
在此,我们将介绍几个典型的组合计数方法。
1. 直接计数法这个方法最简单和直接,也是最常见的方法。
直接计数法指的是通过简单的数学运算,如加减乘除等,来计算所需要的组合方案数。
举个例子,如果我们需要从1,2,3,4,5这五个数中选取3个数组成排列,那么我们可以用直接计数法得到:$5*4*3=60$。
2. 阶乘计数法阶乘计数法是指通过对组合元素进行阶乘计算来得到组合情况的方法。
因为阶乘的数值是很大的,所以这种方法一般用于较小规模的组合计数。
比如说,有10个人排队来参加比赛,如果要按照顺序进行比赛,那么第一名有10种选择,第二名有9种选择,第三名有8种选择,依次类推,那么总的组合情况就是$10!=3.628.800$种。
3. 组合计数法组合计数法是指通过对组合元素的选择进行计算得到组合情况数的方法。
组合计数法可以分为有放回组合和无放回组合。
有放回组合通常使用二项式定理进行计算,无放回组合通常使用错排公式进行计算。
比如说,如果我们要从5个人中选取3个人,得到的组合数可以根据二项式定理进行计算:$comb(5,3)=C_5^3=\frac{5!}{3!*(5-3)!}=10$。
4. 排列计数法排列计数法是指通过对元素的排列来计算组合情况数的方法。
排列计数法可以分为有放回排列和无放回排列。
比如说,如果我们将4个人任意排列,那么排列情况可以通过乘法原理进行计算:$4*3*2*1=24$。
总之,组合计数方法的选择要根据实际问题来判断,我们可以根据问题的特点合理选择计数方法,进而解决问题。
图形计数的多种方法和总结

数线段的5种方法和拓展例1数一数图中共有多少条线段?方法一:基本线段法(把图中单个的线段看作一个基本图形)由一个基本线段组成的线段有__4___条由二个基本线段组成的线段有__3___条由三个基本线段组成的线段有__2_由四个基本线段组成的线段有___1__条所以,图中一共有线段____4+3+2+1=10_______________条方法二:端点法加法(线段都是有两个端点组成,一个起点,一个终点)以A为起点的线段有__4___条以B为起点的线段有__3___条以C为起点的线段有__2___条以D为起点的线段有__1___条所以,图中一共有线段______4+3+2+1=10_____________条方法三:端点法乘法(线段都是有两个端点组成,一个起点,一个终点)端点数×间隔÷2=总条数5×4÷2=10方法四:标数法(基本线段法的简化版,可以快速得到结果)方法五:组合法(取两个点就可以组成一条线段)10124525=⨯⨯=C上面的五种方法都适应于所有的数线段的题,其中方法二和方法三可以延伸到握手问题,线段上端点数比较多可以用方法三,方法五可以解决不在一条直线上线段数握手问题1、有5个人,每两个人都需要握手一次,请问一共需要握手多少次?2、三年级有6个班,每两个班比赛拔河一次,这样一共要组织多少场比赛?3、有红、黄、蓝、白四只气球,如果每两只气球扎成一束,共有多少种不同的扎法?端点比较多不在一条直线上1. 平面上有12个点,任意三点都不在同一直线上,这些点可以连成多少条直线?1 2 4 3 A C 1 … C 2C 102 B …… 1 2 3 4 99 100。
2023-2024学年人教版数学二年级上册《期中考试卷》附答案解析

2023-2024学年二年级上学期期中数学试卷一、算一算。
1. 直接写出得数。
4×4=18-9=3×6=5×6-4=22-10=4×2=5+5=75-8+5=4×3=27-3=11+22=45+30-9=32-9=5×4=45+20=6×3+7=2. 用竖式计算。
46+15+27=64-38+25=78-24-17=二、填一填。
3. 根据“二六十二”这句乘法口诀写出两道乘法算式。
_____、_____4. 2个4相加,和是_____;2个4相乘,积是_____。
5. 5个6比3个6多(),比6个6少()。
6. 校门的左边摆了21盆花,右边摆了17盆花。
左边比右边多摆了_____盆,如果从左边搬走_____盆到右边,两边的盆数就同样多了。
7.15个气球,每()个一束,分成了()束;15个气球,平均分成()束,每束()个.8. 在横线上填上“>”“<”或“=”。
5×2_____3×3 4×4_____4+4 11_____6×2 3×2+2_____129. 4+4+4+4+4+4表示_____个_____相加,写成乘法算式_____。
10. 最大两位数与最大的一位数相差()。
11. 找规律填数。
(1)1,1,2,3,5,_____,_____。
(2)1,4,9,_____,25,_____。
12. 明明三天看完了一本86页的童话书,他第一天看了34页,第二天看了31页,明明前两天一共看了_____页,他第三天从_____页看起。
13. 小青蛙每次跳4格,连续跳了5次,一共跳了_____格。
14. 幼儿园有一些苹果,无论是分给5个小朋友还是分给6个小朋友,都会多出3个(每个小朋友分到的苹果个数相等),这些苹果最少有_____个。
15. 如图这样坐,4张桌子拼在一起排成一排,一共能坐_____人。
【小升初专项训练】01 组合图形的计数

第1讲组合图形的计数第一关【知识点】1.组合图形的概念:圆,三角形,正多边形,梯形,平行四边形为基本图形其余的为组合图形,可以用辅助线分解为基本图.2.组合图形的计数实质上就是分类数图形,解决方法是:(1)合理进行分类.(2)利用排列组合的有关公式进行每一个类的数量计算.(3)将所有的类的数量进行相加.(4)仔细检查,防止遗漏.【例1】图中有多少个三角形?【答案】3【例2】数一数,图中一共有多少个三角形?【答案】13【例3】数一数,图中一共有多少个三角形?【答案】27【例4】数一数,图中一共有多少个三角形?【答案】48【例5】数一数,图中一共有多少个三角形?【答案】9【例6】数一数,图中一共有多少个三角形?【答案】8【例7】数一数,图中一共有多少个三角形?【答案】8【例8】数一数,图中一共有多少个三角形?【答案】20;24;24【例9】数一数,图中一共有多少个三角形?【答案】35【例10】数一数,图中一共有多少个三角形?【答案】67【例11】数一数,图中一共有多少个三角形?【答案】11【例12】数一数,图中一共有多少个三角形?【答案】40【例13】图中,有多少个三角形?【答案】16【例14】数一数,图中一共有多少个三角形?【答案】8【例15】数一数,图中一共有多少个三角形?【答案】13【例16】数一数,图中一共有多少个三角形?【答案】12【例17】数一数,图中一共有多少个三角形?【答案】11【例18】数一数,图中一共有多少个三角形?【答案】20【例19】数一数,图中一共有多少个三角形?【答案】12【例20】如图中有多少个三角形?【答案】27【例21】如图中有多少个三角形?【答案】17【例22】如图中有多少个三角形?【答案】10【例23】数一数,图中有多少个三角形?【答案】27【例24】图中有多少个三角形?【答案】14【例25】图中有多少个三角形?【答案】11【例26】数一数,图中共有多少个三角形?【答案】15【例27】如图是一些等腰直角三角形组成的图形,图中一共有多少个三角形?【答案】23【例28】如图中,一共有多少个三角板?【答案】12【例29】如图中共能数出多少个三角形?【答案】24【例30】如图中共能数出多少个三角形?【答案】24【例31】在△ABC中,D1、D2、D3为AB边的内分点,E1、E2、E3为AC边的内分点,那么图中有 多少个三角形?【答案】64【例32】如图中共能数出多少个三角形?【答案】11【例33】如图中,共有多少个三角形?【答案】10【例34】数一数,图中共有多少个三角形?【答案】10【例35】数一数,图中共有多少个三角形?【答案】12【例36】数一数,图中共有多少个三角形?【答案】16【例37】数一数,图中共有多少个三角形?【答案】18【例38】数一数,图中共有多少个三角形?【答案】30【例39】数一数,图中共有多少个三角形?【答案】28【例40】如图中,一共有多少个三角形?【答案】32【例41】如图中,一共有多少个三角形?【答案】72【例42】如图中,一共有多少个三角形?【答案】22【例43】图中共有多少个三角形?【答案】60【例44】下图中共有多少个三角形?【答案】8【例45】下图中共有多少个三角形?【答案】24【例46】下图中共有多少个三角形?【答案】34【例47】下图中共有多少个三角形?【答案】35【例48】下图中共有多少个三角形?【答案】16【例49】下图中共有多少个三角形?【答案】30【例50】下图中共有多少个三角形?【答案】22【例51】下图中共有多少个三角形?【答案】62【例52】下图中共有多少个三角形?【答案】10【例53】下图中共有多少个三角形?【答案】35【例54】下图中共有多少个三角形?【答案】32【例55】下图“七角星”中共有多少个三角形?【答案】35【例56】下图中共有多少个三角形?【答案】20【例57】下图中共有多少个三角形?【答案】40【例58】如图,图中3个大三角形都是等边三角形,则图中共有多少个三角形?【答案】30【例59】如图中有多少个三角形?【答案】76【例60】如图中有多少个三角形?【答案】76【例61】如图中,包含“”的三角形有多少个?【答案】4【例62】如图,数一数其中共有多少个包含“☆”的三角形?【答案】8【例63】如图是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形若干个.那么,图中包含“*”号的大、小正三角形一共有多少个?【答案】6【例64】如图,图中包含“★”的大、小三角形共有多少个?【答案】12【例65】数一数如图中共有多少个包含“﹡”号的三角形?【答案】6【例66】图中,共有多少个直角三角形?【答案】16【例67】图中,共有多少个等边三角形?【答案】14【例68】数一数,图中一共有多少个正三角形?【答案】44【例69】如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G在一条直线上,则图中有多少个等腰直角三角形?【答案】22【例70】如图,连接一个正六边形的各顶点,问图中共有多少个等腰三角形(包括等边三角形)?【答案】38【例71】圆周上有8个点,把它们两两相连,若任意三条线都不交于一点,那么图中顶点全在圆内的三角形共有多少个?【答案】56【例72】如图,有这样的两条线,请问从这5个点中任选三个点可以构成多少个不同的三角形?【答案】8【例73】木板上钉有五颗钉子(如图所示,排成两行),用橡皮筋可以套出多少个三角形?【答案】9【例74】如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出多少个正三角形?【答案】13【例75】以平面上4个点为端点连接线段,形成的图形中最多可以有多少个三角形?【答案】8【例76】平面上有四个点,任意三个点都不在﹣条直线上.以这四个点为端点连接六条线段,在所组成的图形中用它们作顶点可以组成多少个三角形?【答案】4【例77】以平面上任意4个点为顶点的三角形中,钝角三角形最多有多少个?【答案】4【例78】从图中两个正方形的7个顶点中选出3个点作为顶点构成三角形,一共可以构成多少个不同的三角形?【答案】32【例79】如图由5个大小相同的正方形构成.以图中12个点为顶点的三角形共有多少个?【答案】200【例80】长方形内有2017个点,连同长方形的4个顶点在内,共有2021个点,任意3个点都不在同一条直线上,以这2021个点中的某三点为顶点,可作出多少个互不重叠的三角形?【答案】4036【例81】如图,是由9个点组成的点阵,那么以图中3个点为顶点的直角三角形有多少个?【答案】44【例82】如图有12个点,相邻两个点之间的距离是1厘米,这些点为顶点可以连成多少个面积为3平方厘米的三角形?【答案】26【例83】如图是由四个边长为1的小正方形组织的图形,图中共有9个格点(格点即为小正方形的顶点).如果以这些格点为顶点,那么一共可组成多少个等腰三角形?【答案】36【例84】如图是由32个面积为1的等边三角形组成的一个大的平行四边形,这个大的平行四边形内部及边上共有25个交叉点.以这些交叉点为顶点,可以连成多少个等边三角形?【答案】28【例85】在一个圆周上均匀分布10个点,以这些点为顶点,可以画出多少个不同的钝角三角形?(补充知识:由直径和圆周上的一点构成的三角形一定是直角三角形,其中直径的边所对的角是直角,所以如果圆周上三点在同一段半圆周上,则这三点构成钝角三角形)【答案】60【例86】用9个钉子钉成相互间隔为l厘米的正方阵(如图).如果用一根橡皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形有多少个?【答案】32【例87】如图由4个正六边形组成,每个面积是6,以这4个正六边形的顶点为顶点,可以连接面积为4的等边三角形有多少个?【答案】8【例88】如图,大三角形由9个形状、大小相同的等边三角形组成,共有10个顶点,以这些顶点为顶点构成的三角形中,面积与阴影部分面积相等的三角形共有多少个?【答案】36【例89】如图,一小正方形的边为边向小正方形外作四个正方形,再依次连接几个定点,若图中阴影三角形的面积是S,则面积为2S的三角形有_______个,面积为8S的正方形有_______个【答案】20;1【例90】如图由九个边长为1厘米的正方形组成,在如图中面积为0.5平方厘米的三角形有_______个.面积为1平方厘米的三角形有_______个,面积为1.5平方厘米的三角形有_______个,面积最大的三角形的面积是_______平方厘米.【答案】5;11;2;2.5【例91】在图中填上2条直线,最多能数出多少个三角形?【答案】10【例92】今有甲、乙两个大小相同的正三角形,各画出了一条两边中点的连线,如图,甲、乙位置左右对称,但甲、乙内部所画线段的位置不对称,从图中所示的位置开始,甲向右水平移动,直至两个三角形重叠后在离开.在移动过程中的每个位置,甲与乙所组成的图形中都有若干个三角形,那么三角形个数最多的位置,图形中有多少个三角形?【答案】11【例93】如图,在正方形的内部放入1个点,就可以把原来的正方形分成了4个小三角形;在正方形的内部放入2个点,就可以把原来的正方形分成了6个小三角形.那么如果在正方形的内部放入10个点,最多能把原来的正方形分成了多少个小三角形?【答案】22【例94】在一张三角形纸内任作2009个互不重合的点(所有的点都不在三角形的任意一条边上),以这2009个点和三角形纸的3个顶点为顶点的三角形,最多能剪出多少个?【答案】4019【例95】在三角形ABC中,D是BC的中点,图中面积相等的三角形共有多少对?【答案】6第二关【知识点】【例96】图中一共能数出多少正方形?【答案】26【例97】图中一共能数出多少正方形?【答案】55【例98】图中一共能数出多少正方形?【答案】26【例99】图中一共能数出多少正方形?【答案】23【例100】图中一共能数出多少正方形?【答案】14【例101】.将4×4的大正方形切割为16个1×1的小正方形,擦去其中的两条线段,得到如图所示图形.则图中一共有多少个正方形?【答案】22【例102】图中一共能数出多少正方形?【答案】20【例103】图中一共能数出多少正方形?【答案】13【例104】图中一共能数出多少正方形?【答案】17【例105】图中一共能数出多少正方形?【答案】35【例106】图中一共能数出多少正方形?【答案】46【例107】图中一共能数出多少正方形?【答案】10【例108】图中一共能数出多少正方形?【答案】14【例109】图中共有多少个正方形?【答案】17【例110】数一数,图中共有多少个正方形?【答案】23【例111】数一数,图中共有多少个正方形?【答案】18【例112】数一数,图中共有多少个正方形?【答案】11【例113】数一数,图中共有多少个正方形?【答案】20【例114】数一数,图中共有多少个正方形?【答案】15【例115】数一数,图中共有多少个正方形?【答案】28【例116】如图由相同的正方形和相同的等腰直角三角形构成,求正方形的个数。
小学四年级奥数分类专项思维练习(8)数线段与长方形(含答案)
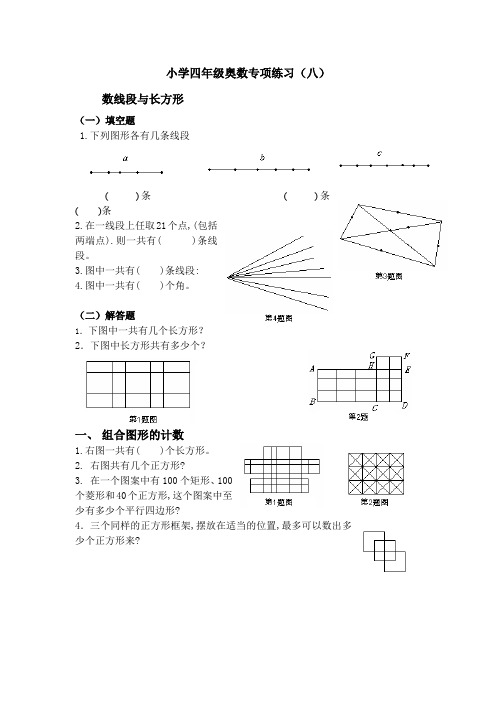
小学四年级奥数专项练习(八)数线段与长方形(一)填空题1.下列图形各有几条线段( )条( )条( )条2.在一线段上任取21个点,(包括两端点).则一共有( )条线段。
3.图中一共有( )条线段:4.图中一共有( )个角。
(二)解答题1.下图中一共有几个长方形?2.下图中长方形共有多少个?一、组合图形的计数1.右图一共有( )个长方形。
2. 右图共有几个正方形?3. 在一个图案中有100个矩形、100个菱形和40个正方形,这个图案中至少有多少个平行四边形?4.三个同样的正方形框架,摆放在适当的位置,最多可以数出多少个正方形来?数线段与长方形(一)填空题1.下列图形各有几条线段( )条( )条( )条答案:a有10条, b有15条, c有21条。
解析:a中以第一个端点为起点的线段有4条;以第二个端点为起点的线段有3条;以第三个端点为起点的线段有2条;以第四个端点为起点的线段有1条。
所以一共有:4+3+2+4=10条线段。
同理得出b中的线段有15条;c中的线段有21条。
2.在一线段上任取21个点,(包括两端点).则一共有( )条线段。
答案:(1+2+3+4+……+19+20)=(20+1)⨯20÷2=210(条)。
解析:点金术:如果线段上的基本线段有n条,则总的线段数为: 1+2+3+4+……+nn)1(2。
+n(=÷n+-)1⨯3.下图一共有( )条线段:答案:(1+2)⨯4+(3+2+1)⨯2=12+12=24(条)。
解析:如果图形比较复杂时,可以先找出线段条数相等的线段,再加起来。
4.下列图形中,一共有( )个角。
答案:6+5+4+3+2+1=21(个)。
解析:如果一个角内一共有几个基本角,则总的角(锐角)一共有:n)1(2。
+n⨯÷(二)解答题1.下图中一共有几个长方形?答案:(5+4+3+2+1)⨯(3+2+1)=(6⨯5÷2)⨯(4⨯3÷2)=15⨯6=90(个)。
小升初小学数学几何图形应用题专题练习《组合图形的计数》答案详解

几何图形—专题01《组合图形的计数》一.选择题1.(2019秋•丰台区期末)如图中,一共有线段()条.A.5B.7C.8D.9【解答】解:(321)(21)++++=+63=(条)9答:一共有线段9条.故选:D.2.(2019秋•皇姑区期末)数一数,图形中有()个三角形.A.3B.4C.5D.6【解答】解:根据题干分析可得:3216++=(个).答:图形中有6个三角形.故选:D.3.(2019秋•白云区期末)如图,以给出的点为端点,能画出()条线段.A.5B.6C.无数条++=(条)【解答】解:3216答:能画出6条线段.故选:B.4.(2019秋•迎江区期末)图中共有()条线段.A.8B.9C.10+++=(条).【解答】解:根据线段的定义可得:图中的线段有:432110答:图中共有10条线段.故选:C.5.(2019•郑州)如图所示,已知在正方形网格中,每个小方格都是边长为1的正方形,A和B两点在小方格的格点上,点C也在小方格的格点上,且以A,B,C为顶点的三角形的面积为1个平方单位,则满足条件的C点的个数为()A.3 个B.4 个C.5 个D.6 个∆的面积为1时,可分两种情况;当底边为2,高为1时,如图:【解答】解:由分析可知:ABC有6种情况;当底边为1,高为2时,没有符合的点使三角形的面积为1,所以符合条件的格点C共有6个.故选:D.6.(2018秋•长春期中)把6个完全相同的小正方体摆放在墙角,()摆法露在外面的面最多.A.B.C.D.++=(个)【解答】解:A、54312++=(个)B、54413C、54413++=(个)++=(个)D、55414<<121314故选:D.7.如图,每个小方格里最多放入一个“☆”,要想使得同一行、同一列或对角线上的三个小方格都不同时出现三个“☆”,那么这九个小方格里最多能放入()个.A.1B.5C.6D.7++=(个),【解答】解:如图2226答:九个小方格里最多能放入“☆”6个.故选:C.8.如图是用三个大小相等的圆制作出的图案,这个图案可以分割出10个同样的扇形.照这样用五个大小相等的圆制作出的图案,可以分割出()个同样的扇形.A.12B.14C.16+-⨯【解答】解:6(51)268=+=(个)14答:可以分割出14个同样的扇形.故选:B.二.填空题9.(2019秋•濉溪县期末)如图中有7个梯形,个平行四边形,个三角形.++=(个)【解答】解:梯形有:3227平行四边形有4个三角形有4个.答:有7个梯形,4个平行四边形,4个三角形.故答案为:7;4;4.10.(2019秋•薛城区期末)观察图中数角.3个直角,个锐角,个钝角.【解答】解:观察图可知:3个直角,7个锐角,2个钝角.故答案为:3,7,2.11.(2019春•端州区月考)是由4个小三角形拼成的.【解答】解:根据分析可得,+=(个)134答:是由4个小三角形拼成的.故答案为:4.12.(2019•深圳)如图中共有27个等边三角形.【解答】解:单个的小三角形有16个,由4个小三角形组成的三角形有7个,9个小三角形组成的大三角形有3个,16个小三角形组成的大三角形有1个,+++=(个)1673127答:如图中共有27个等边三角形.故答案为:27.13.(2019•北京模拟)用同样大小的木块堆成了如图所示的形状,这里共用了50个木块.【解答】解:第1层木块的个数为16,第2层木块的个数为15,第3层木块的个数为12,第4层木块的个数为7,+++=(个)161512750答:这里共用了50个木块.故答案为:50.14.(2019•湘潭模拟)平面中有15个红点,在这些红点间连一些线段,一个红点连出了几条线段,就在这个红点上标几.已知所有标有相同数的红点之间互不连线,那么这15个红点间最多连了85条线段.【解答】解:将15个点分为5组,每组分别有1,2,3,4,5个点,⨯+⨯+⨯+⨯+⨯÷(114213312411510)2=÷170285=(条)答:这15个红点间最多连了85条线段.故答案为:85.15.(2018秋•沧州期末)图中有10条线段.【解答】解:由图可知:以A、B、C、D、E为起点的线段各有4条;则图中线段的条数,剔除重复计算的线段后共有:⨯÷452202=÷=(条).10答:图中有10条线段.故答案为:10.16.(2018秋•长阳县期末)图中有10条线段,条射线,条直线.【解答】解:由分析可知:图中有10条线段,10条射线,1条直线;故答案为:10,10,1.17.(2018春•青龙县期末)如图中一共有55个三角形.++⋯++++【解答】解:底边上线段一共有:1094321=⨯+÷10(101)2=(个)55所以一共有55个三角形.故答案为:55.三.判断题18.(2019秋•文水县期末)淘气数出如图中有16条线段.⨯(判断对错)【解答】解:根据题干分析可得:(54321)26++++⨯+1526=⨯+306=+36=(条)所以图中一共有36条线段,淘气的说法是错误的.故答案为:⨯.19.(2019•亳州模拟)在一条线段上共有9个点,则这9个点可以构成38条线段.⨯(判断对错)【解答】解:8765432136+++++++=(条)即,在一条线段上共有9个点,则这9个点可以构成36条线段.原题说法错误.故答案为:⨯.20.(2018秋•惠州期末)如图,一共有15条线段.⨯(判断对错)【解答】解:762⨯÷422=÷21=(条)答:一共有21条线段.故题干的说法是错误的.故答案为:⨯.21.(2018•上海)在一条线段中间另有6个点,则这8个点可以构成27条线段.⨯(判断对错)【解答】解:这条线段上有628+=个点故这条线段上的线段共有:(1)8(81)2822n n-⨯-==(条).原题说法错误.故答案为:⨯.22.在一张纸上画3条直线,最多可以将纸分成7部分.√(判断对错)+++=(部分)【解答】解:11237答:最多可以将纸分成7部分.故题干的说法是正确的.故答案为:√.四.应用题23.如图中一共有几个角?⨯÷【解答】解:652=÷302=(个)15答:图中一共有15个角.24.观察下面的图,数一数,图中有多少个三角形?【解答】解:图中单个的三角形有16个;2个组合的三角形有16个;4个组合的三角形有8个;8个组合的三角形有4个.+++=(个).所以共有三角形:16168444答:图中有44个三角形.25.(2015•徐州)今有长度分别为1,2,⋯,9的线段各一条,现从中选出若干条线段组成“线段组”由这一组线段恰好可以拼成一个正方形,请通过分析说明这样的“线段组”的组数总共有多少?【解答】解:不同的选法有9种:选用8条的3种:+=+=+=+(边长为11),第1种(不用1):29384756+=+=+=+(边长为10),第2种(不用5):19283746+=+=+=+(边长为9),第3种(不用9):18273645选用7条的6种:+=+=+=(边长为9),第4种(不用1和8):2736459+=+=+=(边长为9),第5种(不用2和7):1836459+=+=+=(边长为9),第6种(不用3和6):1827459+=+=+=(边长为9),第7种(不用4和5):1827369+=+=+=(边长为8),第8种(不用4和9):1726358+=+=+=(边长为7),第9种(不用8和9):1625347=+=+,还剩3选用6条以下的除了最大的一条边,其余最多剩5条组成不了另三条相等的边如:61524没法组成6了.答:这样的“线段组”的组数总共有9种.26.一条线段上有21个点(包括两个端点),相邻两点的距离都是4厘米,所有线段长度的总和是多少?-=份,【解答】解:每相邻的两点之间的距离看作1个单位长度,最长的线段有21120(201)202+⨯÷=⨯2110=(个)210⨯÷+⨯÷+⨯÷+⋯+⨯÷+⨯÷2120220192191823222121=⨯⨯⨯÷(202122)321540=⨯=(厘米)415406160答:所有线段长度的总和是6160厘米.五.操作题27.(2017秋•瑞金市期中)数一数每个图形各有多少个小正方体.++=(个)【解答】解:(1)4318++=(个)(2)54110++=(个)(3)86317++=(个)(4)74213故答案为:8、10、17、13.28.(2017秋•瑞金市期中)数一数.图1一共10个角图2 一共有个三角形,个梯形,个平行四边形.-⨯÷【解答】解:(1)(51)52=÷202=(个)10答:一共10个角.+=(个)(2)三角形有112+++=(个)梯形有11114+=(个)平行四边形有213答:图中有2个三角形,4个梯形,3个平行四边形.故答案为:10;2,4,3.29.数一数、填一填.++=(个)【解答】解:(1)3216答:一共有6个角.++=(个)(2)94114答:一共有14个角.故答案为:.30.在“三子棋”中.棋盘为九宫格(如图),请问九宫格中可以三格相连的直线共有几条?并在图中画出来.【解答】解:如图答:九宫格中可以三格相连的直线共有8条.并在图中画出来如上图.31.(2016秋•七里河区校级期中)数一数15条线段.++++=(条)【解答】解:1234515答:有15条线段.故答案为:15.32.(2015秋•武汉期中)数数图中有多少条线段++++++【解答】解:(123)(1234)=+610=(条)16答:图中有16条线段.33.(2015春•江门校级期末)数一数,下面的图形有几个梯形?几个平行四边形?梯形有15个,平行四边形有个.【解答】解:由分析得出:++++++=(个)212133315平行四边形有3个答:梯形有15个,平行四边形有3个.故答案为:15,3.34.用四条直线分别画出交点数是1、3、5个的图形.(下图是交点数为4个的图形).4条直线最多能有几个交点?【解答】解:如图:答:4条直线最多能有6个交点.35.(1)请画一个60度的角(2)请画一个比平角小45度的角.(3)下图中各有几个角?【解答】解:(1)(2)(3)六.解答题36.(2019秋•綦江区期末)图中直角有5个,锐角有个,钝角有个.【解答】解:观察图形可知,图中直角有5个,锐角有2个,钝角有1个.故答案为:5,2,1.37.(2019秋•会宁县期末)下图一共有10条线段.【解答】解:由题意可得,图形中的线段有:AC,AD,AE,AB,CD,CE,CB,DE,DB,EB,共10条.故答案为:10.38.(2019春•黄冈期末)在原图中,分别添加1条、2条、3条竖线,每幅图中各包含多少个长方形?请将个数填入图形下方的括号里.【解答】解:由分析可得:故答案为:3;6;10.39.(2018秋•涿州市期末)数一数.【解答】解:角:4(41)62⨯-=(个)线段:5(51)102⨯-=(条)正方形:11⨯的正方形有6个,由22⨯个小方格构成的正方形有2个,628+=(个)如图所示:故答案为:6,10,8.40.(2018秋•高碑店市期末)观察如图所示的图形,第(1)个图形有3个三角形,第2个图形有8个三角形.(1)数一数,第(3)个图形中共有15个三角形;笫(4)个图形中共有个三角形.(2)根据你发现的规律判断:第(20)个图形共有个三角形.【解答】解:(1)(321)23++⨯+623=⨯+123=+15=(个)(4321)24+++⨯+1024=⨯+=+204=(个)24答:第(3)个图形中共有15个三角形;笫(4)个图形中共有24个三角形;(2)由(1)的计数方法可得:+⨯÷⨯+(120)202220=⨯÷⨯+21202220=+42020=(个)440答:第(20)个图形共有440个三角形.故答案为:15;24;440.41.(2016秋•七里河区校级期中)图中共有10个角.+++=(个)【解答】解:根据题干分析可得:432110答:一共有10个角.故答案为:10.。
组合数学中的排列与组合计数法

组合数学中的排列与组合计数法在我们的日常生活和各种学术领域中,组合数学的身影无处不在。
其中,排列与组合计数法作为组合数学的重要组成部分,为解决众多实际问题提供了强大的工具。
让我们一起来揭开它们神秘的面纱,了解其背后的原理和应用。
首先,我们来认识一下什么是排列。
简单来说,排列就是从给定的元素集合中选取若干个元素,按照一定的顺序进行排列。
比如说,从数字 1、2、3 中选取 2 个数字进行排列,就有 12、21、13、31、23、32 这六种情况。
排列的计算方法可以用公式表示。
如果从 n 个不同元素中取出 m 个元素进行排列,那么排列数记为 A(n, m),其计算公式为 A(n, m) = n!/(n m)!。
这里的“!”表示阶乘,例如 5! = 5 × 4 × 3 × 2 × 1 。
为了更好地理解排列,我们来看一个实际的例子。
假设有 5 个人参加跑步比赛,要确定前三名的名次,这就是一个排列问题。
第一名有 5 种可能,第二名有 4 种可能(因为第一名已经确定了一个人),第三名有 3 种可能。
所以总的排列数就是 A(5, 3) = 5! /(5 3)!= 60 种。
接下来,我们再聊聊组合。
组合与排列不同,它只关注选取的元素,而不考虑元素的顺序。
比如从 1、2、3 中选取 2 个数字的组合,就只有 12、13、23 这三种情况。
组合的计算方法也有相应的公式。
从 n 个不同元素中取出 m 个元素的组合数记为 C(n, m),其计算公式为 C(n, m) = n! / m! ×(n m)!。
同样通过一个例子来加深对组合的理解。
从 10 个不同的水果中选出 3 个水果,不考虑选择的顺序,这就是一个组合问题。
组合数 C(10, 3) = 10! / 3! ×(10 3)!= 120 。
排列和组合在实际生活中有广泛的应用。
比如在密码学中,密码的设置就涉及到排列组合的知识。
组合计数公式

组合计数公式组合计数公式,这可是数学里一个挺有意思的玩意儿!咱先来说说啥是组合计数公式。
简单来讲,它就是帮咱们数数,算算在一堆东西里挑出几个来,能有多少种不同的挑法。
比如说,从 5个苹果里选 2 个,有几种选法?这就得靠组合计数公式来帮忙啦。
组合计数公式里有个很重要的概念叫“组合数”,通常用 C(n, k) 来表示,意思是从 n 个不同元素中选取 k 个元素的组合数。
它的计算公式是:C(n, k) = n! / [k!(n - k)!] 。
这里面的“!”表示阶乘,比如说 5! = 5 × 4 × 3 × 2 × 1 。
我记得有一次,学校组织活动,要从班上的 20 个同学里选出 5 个参加比赛。
同学们都在那七嘴八舌地讨论到底有多少种选法。
这时候,我就跟他们说,咱们可以用组合计数公式来算算。
然后我就在黑板上写出了 C(20, 5) = 20! / [5!(20 - 5)!] ,算出来一共有 15504 种选法。
同学们都瞪大了眼睛,觉得太神奇了,原来数学能这么厉害,轻轻松松就算出了这么多种可能。
组合计数公式在生活中的应用可多啦。
比如说抽奖,从一堆号码里抽出几个中奖号码,这就是组合问题。
还有安排座位,一排有 10 个座位,选 3 个坐人,有多少种坐法,这也能用组合计数公式来解决。
再比如说,你去买水果,有 8 种水果,你只想买 3 种,那到底有多少种不同的买法?用组合计数公式一算就知道。
还有分东西,把 12 个玩具分给 4 个小朋友,每个小朋友至少一个,这也能通过组合计数公式来思考。
组合计数公式还能帮助咱们理解概率问题。
比如说扔骰子,扔两次,两次点数之和为 7 的概率是多少?这也得先通过组合计数公式算出总的可能性,再算出点数之和为 7 的可能性,最后就能算出概率啦。
在学习组合计数公式的时候,可别死记硬背,得理解它背后的道理。
多做几道题,多想想实际生活中的例子,这样才能真正掌握它。
三视图中的小正方体计数问题

三视图中的小正方体计数问题通过小正方体组合图形的三视图,确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。
解决这类问题如果没有掌握正确的方法,仅仅依赖空间想象去解决,不仅思维难度很大,还很容易出错。
通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层,理清了这些行、列、层的数量,小正方体的个数就迎刃而解了。
在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数。
以上方法可简要地概括为:“主俯看列,俯左看行,主左看层,分清行列层,计数不求人。
”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有()。
A.9箱B.10箱C.11箱D.12箱分析:由三视图可知,这堆货箱共有从前到后3行,从左到右3列。
由左视图:第一行均为1层,第二行最高2层,第三行最高3层;由主视图:第一列、第三列均为1层,第二列(中间列)最高为3层。
故第二行、第二列为2层,第三行第二列为3层,其余皆为1层。
各行、各列小正方体的个数如俯视图中所表示。
这堆货箱共有3+1+1+2+1+1=9(箱)。
练习题1.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来(如图),则这堆正方体货箱共有()A.4箱B.5箱C.6箱D.7箱2.在仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱从三个方向看到的图形画了出来,如图所示,则这堆正方体货箱共有()A.9箱B.10箱C.11箱D.12箱3.在某仓库里堆放着若干个相同的正方体货箱,管理员将这堆货箱的三视图画了出来(如图),则这堆正方体货箱共有()A.8箱B.9箱C.10箱D.11箱4.在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有()A.6个B.5个C.4个D.3个5.在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有()A.4个B.5个C.6个D.7个6.在学校教师办公室里堆放着若干个相同的正方体粉笔盒,某同学将这堆粉笔盒的三视图画了出来,如图,则这堆粉笔盒共有()A.2个B.3个C.4个D.5个7.在抗震救灾某仓库里放着若干个相同的正方体货箱,某摄影记者将这堆货箱的三视图照了出来(如图),则这堆正方体货箱共有()A.2箱B.3箱C.4箱D.5箱8.在一个仓库里堆积着若干个正方体的货箱,要搬运这些货箱很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个方法:将这堆货箱分别从正面、左面、上面所看到的平面图形画了出来,如图所示,你能根据这些平面图形帮他清点一下箱子的数量吗?这些正方体货箱的个数为()A.5 B.6 C.7 D.89.如图是抗争救灾某仓库里放着若干个正方体货箱,某摄影记者将这堆货箱的三视图照了出来,则这堆正方体货箱共有()A.5箱B.6箱C.7箱D.8箱10.在学校仓库里堆放着若干个盒相同的正方体小粉笔盒,仓库管理员将这堆粉笔盒的三视图画了出来,如图所示,则这堆正方体小粉笔盒共有()A.11盒B.10盒C.9盒D.8盒11.在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,如图,你能根据三视图,帮他清点一下箱子的数量吗?这些正方体箱的个数是()A.6 B.7 C.8 D.912.在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,如图,你能根据三视图,帮他清点一下箱子的数量吗?这些箱子的个数是()A.9 B.8 C.7 D.613.仓库里堆积着正方体的货箱若干,根据如图所示的三视图可得出箱子的个数是()A.6 B.7 C.8 D.914.一仓库管理员在清理仓库物品时,发现所有物品都是一些大小相同的正方体箱子.若摆放物品的三视图如图所示,则仓库最高摆放正方体的箱子的个数是()A.1个B.2个C.3个D.无法确定二、根据两种视图确定计数范围(结果不唯一的计数)(1)知道几何体的主视图和俯视图例2.如图2,是由若干个(大于8个)大小相同的正方体组成的一个几何体的主视图和俯视图,则这个几何体的左视图不可能是()。
排列组合第3阶07圆周上的排列组合问题

1. 将圆周上5个点按如下规则染色:先任选一点染成红色,然后依逆时针方向,第1步转过1个间隔将到达的那个点染红,第2步转过2个间隔将到达的那个点染红,第k 步转过k 个间隔将到达的那个点染红.一直进行下去,可得到_________个红点.解:将5个点依次编号0—4,且不妨设开始染红的是0号点,则第1步染红的是1号点,第2步染红的是3号点,第3步染红的又是1号点.故共可得3个红点.2. 在一圆周上有k 个数,k ≥3.若其中任意三个相邻之数,依顺时针方向分别设为,,a b c ,恒有b a c αβ=+,这里1αβαβ+=≥0,≥0,.证明这k 个数必互相相等.任取其中一数,记为0a ,其余各数依顺时针方向分别记为121,,,k a a a -….对任意的正整数,n k n p k i =⋅+≥, p 是正整数, i 是整数,且01i k -≤≤,令n i a a =,按题意,对任意正整数n,有11n n n a a a αβ-+=+.若0αβ⋅=,结论显然成立.否则,有11()()n n n n a a a a βα+--=-.令1n n n b a a +=-,则1n n b b αβ-=.设100a a b a -==,则()n n b a αβ= 当n k =,有110()k k k k a b a a a a a αβ+==-=-=.由此可得0a =或1αβ=.若0a =,即0,0,1,2n b n ==…,结论显然成立.若有1,αβ=即,0,1,2,n b a n ==…,知数列{}n a 是以0a 为首项,a 为公差的等差数列,则有,00k a a a ka ==+ 即0a =.结论得证. 3. 在一个圆周上均匀分布10个点,以这些点为顶点,可以画出多少个不同的钝角三角形?(补充知识:由直径和圆周上的一点构成的三角形一定是直角三角形,其中直径的边所对的角是直角,所以如果圆周上三点在同一段半圆周上,则这三点构成钝角三角形).【考点】组合图形的计数.【专题】操作、归纳计数问题.【分析】由直径和圆周上的一点构成的三角形一定是直角三角形,其中直径的边所对的角是直角,所以如果圆周上三点在同一段半圆周上,则这三点构成钝角三角形,依此按照顺序数出钝角三角形的个数即可求解.【解答】解:由图形可知:含A、B两点的钝角三角形有6个;含A、C两点的钝角三角形有5个;含A、D两点的钝角三角形有2个;含A、G两点的钝角三角形有3个;含A、H两点的钝角三角形有2个;含A、I两点的钝角三角形有1个;含B、C两点的钝角三角形有5个;含B、D两点的钝角三角形有3个;含B、E两点的钝角三角形有1个;含B、H两点的钝角三角形有2个;含B、I两点的钝角三角形有1个;含C、D两点的钝角三角形有4个;含C、E两点的钝角三角形有2个;含C、F两点的钝角三角形有1个;含D、E两点的钝角三角形有3个;含D、F两点的钝角三角形有2个;含D、G两点的钝角三角形有1个;含E、F两点的钝角三角形有3个;含E、G两点的钝角三角形有2个;含E、H两点的钝角三角形有1个;含F、G两点的钝角三角形有3个;含F、H两点的钝角三角形有2个;含F、I两点的钝角三角形有1个;含G、H两点的钝角三角形有2个;含G、I两点的钝角三角形有1个;含H、I两点的钝角三角形有1个;共有:(6+5+2+3+2+1)+(5+3+1+2+1)+(4+2+1)+(3+2+1)+(3+2+1)+(3+2+1)+(2+1)+1=19+12+7+6+6+6+3+1=60(个).答:可以画出60个不同的钝角三角形.故答案为:60个.【点评】本题考查分步计数原理,考查圆的有关问题,是一个综合题,解题的关键是对于圆上的点,怎样能组成钝角三角形.在一个圆周上有7个点,正好将圆周七等分,以这些点为顶点作三角形,可以作4.(2001•上海校级自主招生)在一个圆周上有7个点,正好将圆周七等分,以这些点为顶点作三角形,可以作_____________个等腰三角形.【考点】排列组合.【分析】构成等腰三角形分上述三种情况,看每种情况能做几个,最后把所有的作法加起来就可解决.【解答】解:构成等腰三角形分上述三种情况,每个点都做一次顶点,每种情况能作7个三角形,共可以作21个等腰三角形.故答案为:21.【点评】解决本题的关键是分情况考虑,选定顶点,看能作几个等腰三角形,再看每种三角形能作几个,最后加起来即可.5. 如图1,圆周上顺序排列着1,2,3,…,12十二个数,我们规定:相邻的四个数a1、a2、a3、a4顺序颠倒为a4、a3、a2、a1称为一次“变换”(如1、2、3、4变为4、3、2、1,又如11、12、1、2变为2、1、12、11).能否经过有限次“变换”,将12个数的顺序变为9,1,2,3,…,8,10,11,12(如图2)?请说明理由.【考点】推理与论证.【分析】5个数经过4次“变换”可将一个数提前4位,其余不变,则经过四次变化,即可得到1,2,3,4,9,5,6,7,8,10,11,12,在1,2,3,4,9这5个数中进行4四变化就可得把9提前,从而得到.【解答】解:12345→15432→34512→32154→51234.这说明经过4次“变换”可将一个数提前4位,其余不变.于是,经过4次“变换”可得:1,2,3,4,9,5,6,7,8,10,11,12.同样,再经过4次“变换”可得:9,1,2,3,4,5,6,7,8,10,11,12.【点评】本题考查了数的变化规律,关键是理解个数经过4次“变换”可将一个数提前4位,其余不变.6. 将圆周上的任意点均染成黑色或白色,对任意一种染色方法.(1)是否一定存在一个直角三角形,其顶点同色,证明你的结论;(2)证明:存在一个等腰三角形,其顶点同色.【考点】进行简单的合情推理.【专题】推理和证明.【分析】(1)若直角三角形的三个顶点在圆周上,则斜边一定为直径,我们把圆分成两个半圆,一半涂黑,一半涂白,则不存在一条直径的两个端点同色,故这样的直角三角形不是一定存在的;(2)取圆的一个内接五边形,则五个顶点中,至少有三个顶点是同色的,进而可得答案.【解答】解:(1)这样的直角三角形不是一定存在的,理由如下:把圆分成两个半圆,一半涂黑,一半涂白,则不存在一条直径的两个端点同色,此时不存在一个直角三角形,其顶点同色.证明:(2)取圆的一个内接五边形,则五个顶点中,至少有三个顶点是同色的,连接这三个顶点,可得到一个等腰三角形,故存在等腰三角形,其顶点同色.【点评】本题考查的知识点是合情推理,本题逻辑性强,证明思路比较难理解,属于中档题.7. 某工厂生产一种圆盘形玩具.在圆盘正面的圆周上均匀分布安装10个小球,其中3个为红球,7个为白球,如图所示,若两个圆盘都正面朝上,可以圆心对圆心,红球对红球,白球对白球叠放在一起,就算同一种规格.问:这类玩具一共可以有多少种不同的规格?【考点】哈密尔顿圈与哈密尔顿链.【分析】当3个红球都不相邻时,7÷3=2…余1;所以最少间隔2+1=3个白球;因此按两个红球间隔白球的数量分:最多间隔3、4、5、6、7个;分类讨论即可得出答案.【解答】解:按两个红球间隔白球的数量分类用黑点代表红球,空心点代表白球,最多间隔3个白球的有2种不同规格:最多间隔4个白球的有4种不同规格:类似地,最多间隔5个白球的有3种不同的规格,最多间隔6个白球的有2种不同规格.最多间隔7个白球的有1种规格.所以,共有不同规格:2+4+3+2+1=12(种);答:这类玩具一共可以有12种不同的规格.【点评】本题还可以这样理解:7分成3个数的和:007、016、025、034、115、124、133、223共8种,注意这是不加圆盘正面向上这个条件时的答案(即不可反扣),加上这个限制,可以认为016、025、034、124这4个都可以变化出第2种不同排列顺序来,所以是12种.。
清北学堂 2012年五一数学精品班(集训七)组合导学(组合计数 组合应用-凸图形 凸包等)

M = {( x, y ) x, y是整数, 1 ≤ x, y ≤ n} ,定义在 M 上的函数 f 具有性质:
5
北京清北学堂教育科技有限公司 电话:010‐88400806,010‐88400903 网址:
(a ) (b)
(c )
f ( x) = x a1 + x a2 + " + x an
又 g ( x) = xb1 + xb2 + " + xbn (注意,这里的 ai 与 bi 不是母函数的系数,而是指数)
( f ( x))2 − f ( x 2 )
= ( x a1 + x a2 + " + x an ) 2 − ( x 2 a1 + x 2 a2 + " + x 2 an ) = 2
即 f 2 ( x ) − g 2 ( x) = f ( x 2 ) − g ( x 2 )
④
由于 f(1)-g(1)=n-n=0,所以(x-1)|(f(x) -g(x)),从而存在自然数 h1 ,使
f ( x) − g ( x) = ( x − 1)h1 p( x), p(1) ≠ 0
因此 f ( x 2 ) − g ( x 2 ) = ( x 2 − 1)h1 p( x 2 )
f ( x) = a0 + a1 x + a2 x 2 + " + ak x k + "
联系起来,构成对应关系
{ak } ↔
f ( x)
这个 f(x)就称为{ ak }的母函数或生产函数.意思是这个数列{ ak }是由多项 f(x) 产生的. 例如:组合数列的母函数是.因为由二项式定理可得
20181122小学奥数练习卷(知识点:组合图形的计数)含答案解析

小学奥数练习卷(知识点:组合图形的计数)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共5小题)1.在8×8网格的所有方格中放入黑白两种围棋子,每个方格放一枚棋子,要求每行中的白色棋子的数目互不相同,每列中的白色棋子的数目相等,那么这个8×8网格中共有()枚黑色棋子.A.42B.32C.22D.122.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片;第二次在这个小正三角形纸片四周再放三张纸片;第三次在第二次摆好的图形四周再摆放纸片;…摆放要求是:每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合,且纸片之间除边之外,无重合(见图).第20次摆放后,该图形共用了正三角形纸片()张.A.571B.572C.573D.5743.在6×6网格的所有方格中放入围棋子,每个方格放1枚棋子,要求每行中的白色棋子的数目互不相等,每列中的白色棋子的数目都相等,那么这个6×6网格中共有()枚黑色围棋子.A.18B.14C.12D.104.在如图中,一共能数出()个含有“☆”的长方形.A.8B.10C.12D.145.如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出()个正三角形.A.6B.10C.13D.15第Ⅱ卷(非选择题)二.填空题(共34小题)6.如图,三角形中一共有个梯形.7.用长短相同的火柴棍摆成5×1997的方格网,每一个小方格的边长为一根火柴棍长(如图),共需用根火柴棍.8.在一个长方形内画三个圆,这个长方形最多可被分成部分.9.如图是一些等腰直角三角形组成的图形,图中一共有个三角形.10.如图中有个正方形.11.如图是一个左右对称的美丽图形,图中总共有个三角形.12.图中有个小正方体.13.数一数,图中共有个三角形.14.如图是历史上著名的5个柏拉图立体,它们的顶点数数分别为15.圆上的50个点A1,A2,A3,…,A50将该圆分为50段等弧,以这50个点中的某些点为顶点,一共可以得到个不同的正多边形.16.图中共有个长方形.17.如图,圆周上有12个点,将圆周12等分.以这些等分点为四个顶点的矩形共有个.18.有8个表面涂满绿漆的正方体,其棱长分别为7,9,11,…,21,若把这些正方体全部锯成棱长为1的小正方体,在这些小正方体中,有个至少是一面有漆.19.图中有个三角形,有条线段.20.如图,我们可以用13根木棍搭出图1中的两层图形,用26根小棍搭出图2中的三层图形,用43根小棍搭出图3中的四层图形,为了搭出一个五层图形,需要根小棍21.如图,在这个图形中共有个平四边形22.数一数,图中共有个三角形23.如图中,共有个锐角.24.如图中,一共有个三角形.25.图中,一共有个三角形.26.将四边形的任意一边延长,四边形其余两个顶点总在同一侧的四边形称为凸四边形,如图中共有个凸四边形.27.今天是4月4日,图4.4中共有个三角形.28.如图中有个三角形.29.数一数,图中共有个正方形.30.由35个边长为1的小正方形拼成一个7*5的长方形,其中有一格含有“☆”.图中含有“☆”的所有长方形(含正方形)共有个.31.如图是上幼儿园的小毛球写的“中国”两个字,图中一共能数出个长方形.32.如图,图中3个大三角形都是等边三角形,则图中共有个三角形.33.在平面上用长度为6厘米的牙签棒摆正方形,摆出一个长为6厘米的正方形需要4根牙签棒,摆出5个这样的正方形至少需要根牙签棒.34.图中有个长方形.35.下图“七角星”中共有个三角形.36.图中一共能数出正方形.37.图中,A、B、C、D、E是正五边形各边的中点,那么,图中共有个梯形.38.图中,A、B、C、D、E是正五边形各边的中点,那么,图中共有个梯形.39.如图由5个大小相同的正方形构成.以图中12个点为顶点的三角形共有个.三.解答题(共11小题)40.数一数,图中有多少个三角形?41.数一数,图中包含“☆”的长方形(包含正方形)有多少个?42.从图中任意选择四个点,可组成多少个不同的正方形?(不同的点组成的正方形视为不同的正方形)43.数一数,图中有多少个长方形(包含正方形)?44.数一数,图中有多少个三角形?45.如图中共有个平行四边形.46.数一数下面的图形.个长方形.47.长方形内有2017个点,连同长方形的4个顶点在内,共有2021个点,任意3个点都不在同一条直线上,以这2021个点中的某三点为顶点,可作出个互不重叠的三角形.48.平面上有5条不同的直线,这5条直线共形成n个交点,则n有多少个不同的数值?49.平面上有5条不同的直线,这5条直线共形成m个交点,则m有多少个不同的数值?50.如图,一个边长为3的正六边形被3组平行于其边的直线分割成边长为1的54个小正三角形,那么以这些小正三角形的顶点为顶点的正六边形共有多少个?参考答案与试题解析一.选择题(共5小题)1.在8×8网格的所有方格中放入黑白两种围棋子,每个方格放一枚棋子,要求每行中的白色棋子的数目互不相同,每列中的白色棋子的数目相等,那么这个8×8网格中共有()枚黑色棋子.A.42B.32C.22D.12【分析】结合题意,我们知道:每列白棋数目相等,说明白棋的数量是8的倍数;每行不相等,说明白棋每行从0、1、2、3、4、5、6、7、8中选8个数;最终组合中总数是8的倍数的只有0、1、2、3、5、6、7、8.这样便可求得白棋枚数是0+1+2+3+5+6+7+8=32枚,则黑棋的枚数就是总枚数8×8减去白棋的枚数32.【解答】解:由分析得0+1+2+3+5+6+7+8=32(枚)8×8﹣32=32(枚)故选:B.【点评】解答此题的关键是理解“每列白棋数目相等,说明白棋的数量是8的倍数;每行不相等,说明白棋每行从0、1、2、3、4、5、6、7、8中选8个数”即可.2.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片;第二次在这个小正三角形纸片四周再放三张纸片;第三次在第二次摆好的图形四周再摆放纸片;…摆放要求是:每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合,且纸片之间除边之外,无重合(见图).第20次摆放后,该图形共用了正三角形纸片()张.A.571B.572C.573D.574【分析】先找规律,第一次放1张纸片;后面每一次增加3(n﹣1)个三角形,所以第二次放1+3张纸片;第三次放1+3+6张纸片;第四次放1+3+6+9张纸片;据此规律解答即可.【解答】解:根据分析可得,第20次摆放后,该图形共用:1+3+6+9+…+3×(20﹣1)=1+3+6+9+…+57=(3+57)×(20﹣1)÷2+1=570+1=571(个)答:第20次摆放后,该图形共用了正三角形纸片571张.故选:A.【点评】本题考查了图形的计算,要几何图形的排列规律,得出后面每一次增加3(n﹣1)个三角形.3.在6×6网格的所有方格中放入围棋子,每个方格放1枚棋子,要求每行中的白色棋子的数目互不相等,每列中的白色棋子的数目都相等,那么这个6×6网格中共有()枚黑色围棋子.A.18B.14C.12D.10【分析】根据题意可知,每行的数目可以为0、1、2、3、4、5、6个,又由于每列都相等,所以总和一定是6的倍数,然后从这7个数中去掉一个数,是剩下的6个数的和是6的倍数即可解决问题,如下图(剩下的位置放黑色围棋子).【解答】解:每行的数目可以为0~6个,每列都相等,所以一定是6的倍数,0+1+2+3+4+5+6=21,如果去掉3,那么剩下的数:21﹣3=18正好是6的倍数,所以,白棋子有18个,则,黑色围棋子有:6×6﹣18=18(个)故选:A.【点评】本题解答的难点是确定,每列都相等,且总和一定是6的倍数.4.在如图中,一共能数出()个含有“☆”的长方形.A.8B.10C.12D.14【分析】下面一行中,含有五角星的有6个;加上上一行(即两行),也有6个,共有6+6=12(个);据此即可解答.【解答】解:根据分析可得,共有:6+6=12(个);答:图中,一共能数出12个含有“☆”的长方形.故选:C.【点评】要注意分类计数,做到不重不漏.5.如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出()个正三角形.A.6B.10C.13D.15【分析】连线如上图,分单个的三角形,4个三角形组成的大三角形,和最外面的最大的三角形,三类计数即可;【解答】解:单个的三角形有9个,4个三角形组成的大三角形3个,最外面的最大的三角形1个,共有:9+3+1=13(个)答:用橡皮筋可套出13个正三角形.故选:C.【点评】此题考查了组合图形的计数,应注意分类计数,以免重复,防止遗漏.对于此类题目一定要有序地查找.二.填空题(共34小题)6.如图,三角形中一共有28个梯形.【分析】根据梯形的定义,分上、下底水平的梯形和上、下底竖直的梯形分类计数,然后再相加即可求解.【解答】解:首先考虑上、下底水平的梯形的个数.(1)高为1的梯形有6+3+1=10个;(2)高为2的梯形有2+1=3个;(3)高为3的梯形有1个.因此,上、下底水平的梯形共有10+3+1=14个;同理,上、下底竖直的梯形也有14个,故图中共有梯形:2×14=28(个).故答案为:28.【点评】此题考查组合图形的计数,解决此题的关键是根据定义数清组合的梯形,注意按照一定的顺序计数,以免重复和遗漏.7.用长短相同的火柴棍摆成5×1997的方格网,每一个小方格的边长为一根火柴棍长(如图),共需用21972根火柴棍.【分析】火柴棍共有6行和1998列,分别算出多少根即可.【解答】解:(1997+1)×5+(5+1)×1997=21972故填21972.【点评】此题重在分析火柴棍的列数和行数.8.在一个长方形内画三个圆,这个长方形最多可被分成15部分.【分析】在一个长方形内画三个圆,要使这个长方形被分成的部分最多,就要使圆与圆,圆与长方形之间的交点尽量多,据此画图即可.【解答】解:画图如下:所以,这个长方形最多可被分成15部分.故答案为:15.【点评】本题考查了图形的划分,关键是明确如何使交点尽量多.9.如图是一些等腰直角三角形组成的图形,图中一共有23个三角形.【分析】由该图是一个轴对称图形可先数一侧的三角形,而上边单个三角形有6个、由2个、3个、4个、5个、6个三角形组合而成的三角形各1个,知左侧共有11个三角形,补上最大的三角形可得出图中总共有三角形11×2+1=23个.【解答】解:由于该图形是轴对称图形,所以可先数一侧的三角形,再补上最大的三角形即可,即图中共有三角形11×2+1=23个,故答案为:23.【点评】本题主要考查组合图形的计数,掌握组合图形的计数实质上就是分类数图形是关键,解决方法是:(1)合理进行分类.(2)利用排列组合的有关公式进行每一个类的数量计算.(3)将所有的类的数量进行相加.(4)仔细检查,防止遗漏.10.如图中有17个正方形.【分析】先确定如图所示基本图形中小正方形的个数,由原图中有4个这样的基本图形,且前后两个基本图形有1个重叠的小正方形可得答案.【解答】解:如图,有正方形ABOH、正方形BCDO、正方形DEFO、正方形FGHO 和正方形ACEG这5个,原图中有4个这样的基本图形,且前后两个基本图形有1个重叠的小正方形,所以原图中正方形有5×4﹣3=17个,故答案为:17.【点评】本题主要考查组合图形的计数,组合图形的计数实质上就是分类数图形,解决方法是(1)合理进行分类.(2)利用排列组合的有关公式进行每一个类的数量计算.(3)将所有的类的数量进行相加.(4)仔细检查,防止遗漏.11.如图是一个左右对称的美丽图形,图中总共有23个三角形.【分析】由该图是一个轴对称图形可先数一侧的三角形,而左侧单个三角形有6个、由2个、3个、4个、5个、6个三角形组合而成的三角形各1个,知左侧共有11个三角形,即可得出图中总共有三角形11×2+1=23个.【解答】解:由于该图是一个轴对称图形,所以可以先数一侧的三角形,所以图中总共有三角形11×2+1=23个,故答案为:23.【点评】本题主要考查组合图形的计数,掌握组合图形的计数实质上就是分类数图形是关键,解决方法是:(1)合理进行分类.(2)利用排列组合的有关公式进行每一个类的数量计算.(3)将所有的类的数量进行相加.(4)仔细检查,防止遗漏.12.图中有18个小正方体.【分析】从正面看有3层,第一层(最上层)有1个,第二层有7个,第三层有10个,然后把这三层的个数相加即可.【解答】解:1+7+10=18(个);答:图中有18个小正方体;故答案为:18.【点评】本题要结合图形的正面观测,把每一层的个数相加即可.13.数一数,图中共有15个三角形.【分析】中间横斜线上面三角形有4+3+2+1=10个,下面有2个,中间竖着的长斜线又分成了3个三角形,据此解答即可.【解答】解:(4+3+2+1)+2+3=10+2+3=15(个)答:图中共有15个三角形.故答案为:15.【点评】此题主要考查了图形计数方法的应用,根据数线段(数角)的方法进行分析解答即可.14.如图是历史上著名的5个柏拉图立体,它们的顶点数数分别为4,8,6,20,12【分析】柏拉图多面体也就是正多面体,共有图中的5个,分别是:正四面体、正六面体(正方体)、正八面体、正十二面体、正二十面体.【解答】解:正四面体的顶点数:4,正六面体(正方体)的顶点数:8,正八面体、的顶点数:6,正十二面体的顶点数:20,正二十面体的顶点数:12,故答案为:4,8,6,20,12.【点评】正多面体只有这5个,它们的性质要了解清楚.15.圆上的50个点A1,A2,A3,…,A50将该圆分为50段等弧,以这50个点中的某些点为顶点,一共可以得到18个不同的正多边形.【分析】由于题目要求是正多边形,因此正多边形的边数必须是50的约数,根据50的约数情况进行分情况加和即可.【解答】解:50=2×5×5,因此大于3的50的约数有5、10、25、50.当多边形为五边形时,可以得到50÷5=10个;当多边形为正十边形时,可以得到50÷10=5个;当多边形为正二十五边形时,可以得到50÷25=2个;当多边形为正五十边形时,可以得到50÷50=1个.共10+5+2+1=18个.故答案为:18.【点评】本题的突破口在于能想到正多边形的边数必须为50的约数,难度中等.16.图中共有7个长方形.【分析】此题采用分类的方法解答.(1)由1个图形构成的有4个;(2)由2个图形构成的有1个;(3)由3个图形构成的有1个;(4)由4个图形构成的有1个;【解答】解:(1)由1个图形构成的有4个;(2)由2个图形构成的有1个;(3)由3个图形构成的有1个;(4)由4个图形构成的有1个;答:图中共有7个长方形.故答案为:7.【点评】本题考查了对平面图形的认识,在数长方形的个数时,要有规律地进行分类.17.如图,圆周上有12个点,将圆周12等分.以这些等分点为四个顶点的矩形共有15个.【分析】12个等分点是6条直径的端点,以这些等分点为顶点的矩形,一定以其中两条直径为对角线,所以共有=15个矩形,据此解答即可.【解答】解:12个等分点是6条直径的端点,共有:==15(个)答:以这些等分点为四个顶点的矩形共有15个.故答案为:15.【点评】本题考查了图形的计数和排列组合知识的综合应用,关键是确定以这些等分点为顶点的矩形,一定以其中两条直径为对角线.18.有8个表面涂满绿漆的正方体,其棱长分别为7,9,11,…,21,若把这些正方体全部锯成棱长为1的小正方体,在这些小正方体中,有9136个至少是一面有漆.【分析】分别找到棱长为7,9,11,…,21所分成的棱长为1的小正方体至少是一面有漆的小正方体的个数,相加即可求解.【解答】解:边长为7的正方体,至少是一面有漆的棱长为1的小正方体有7×7×2+7×5×2+5×5×2=218(个);边长为9的正方体,至少是一面有漆的棱长为1的小正方体有9×9×2+9×7×2+7×7×2=386(个);边长为11的正方体,至少是一面有漆的棱长为1的小正方体有11×11×2+11×9×2+9×9×2=602(个);边长为13的正方体,至少是一面有漆的棱长为1的小正方体有13×13×2+13×11×2+11×11×2=866(个);边长为15的正方体,至少是一面有漆的棱长为1的小正方体有15×15×2+15×13×2+13×13×2=1178(个);边长为17的正方体,至少是一面有漆的棱长为1的小正方体有17×17×2+17×15×2+15×15×2=1538(个);边长为19的正方体,至少是一面有漆的棱长为1的小正方体有19×19×2+19×17×2+17×17×2=1946(个);边长为21的正方体,至少是一面有漆的棱长为1的小正方体有21×21×2+21×19×2+19×19×2=2402(个).则在这些小正方体中,有218+386+602+866+1178+1538+1946+2402=9136个至少是一面有漆.故答案为:9136.【点评】考查了组合图形的计数,本题注意不同棱长的正方体至少是一面有漆的个数为棱长×棱长×2+棱长×(棱长﹣2)×2+(棱长﹣2)×(棱长﹣2)×2.19.图中有3个三角形,有6条线段.【分析】(1)图中有3个三角形,两个小三角形和由两个小三角形组成的大三角形,共3个三角形;(2)根据线段的特点:有2个端点,有限长,进行数出即可.【解答】解:三角形:2+1=3(个);线段:(1+2)+3=6(条).答:图中有3个三角形,有6条线段.故答案为:3,6.【点评】解答此题应根据角、线段和三角形的含义进行解答.要注意按顺序计数,防止遗漏.20.如图,我们可以用13根木棍搭出图1中的两层图形,用26根小棍搭出图2中的三层图形,用43根小棍搭出图3中的四层图形,为了搭出一个五层图形,需要64根小棍【分析】比较图1和图2,多了下面5个正方形,就多了2×5+3=13根小棒;比较图2与图3,多了7个小正方形,多了2×7+3=17根小棒;照这个规律去推算.【解答】解:图4比图3多了9个小正方形,多用2×9+3=21根小棒,变成43+21=64根小棒.故填64【点评】此题的关键是找出相邻两个图形之间的变化规律,然后利用规律解题.21.如图,在这个图形中共有15个平四边形【分析】观察大正三角形的每条边上有6个平行四边形,共有6×3=18个,再去掉重复计算的3个即可.【解答】解:6×3﹣3=18﹣3=15(个)答:在这个图形中共有15个平行四边形.故答案为:15.【点评】此题主要考查图形计数方法的应用,养成按照一定顺序观察思考问题的习惯,逐步学会通过观察思考探寻事物规律的能力.22.数一数,图中共有16个三角形【分析】观察图形可知,单三角形一共有8个,两个小三角形组成的大三角形有4个;四个小三角形组成的三角形有4个,由此即可解答.【解答】解:根据分析可得,8+4+4=16(个)答:图中共有16个三角形.故答案为:16.【点评】本题关键是要按顺序计数,防止遗漏.23.如图中,共有10个锐角.【分析】图中每两条射线都可以组成锐角,如果有n条射线,则有n(n﹣1)÷2 个角,本题有5条射线,由此代入数值,进行解答即可.【解答】解:5×(5﹣1)÷2=20÷2=10(个);答:图中一共有10个锐角故答案为:10.【点评】本题考查了如何数角,结合图形可以看作握手问题,即每两条射线“握手”一次,注意数形结合的思想.24.如图中,一共有32个三角形.【分析】先把外面大正方形分成四部分,每部分有5个小三角形,共有5×4=20个,加上以正方形边长为直角边的4个,共有20+4=24个;四部分中,每相邻的两部分又交叉有2个三角形(红、蓝),共有2×4=8个;然后把上述两种情况的个数相加即可.【解答】解:根据分析可得,5×4+4+2×4=24+8=32(个)答:一共有32个三角形.故答案为:32.【点评】此题主要考查了分类计数问题,应注意先拆分再分类计数,以免重复,防止遗漏.25.图中,一共有32个三角形.【分析】先把外面大正方形分成四部分,每部分有5个小三角形,共有5×4=20个,加上以正方形边长为直角边的4个,共有20+4=24个;四部分中,每相邻的两部分又交叉有2个三角形(红、蓝),共有2×4=8个;然后把上述两种情况的个数相加即可.【解答】解:根据分析可得,5×4+4+2×4=24+8=32(个)答:一共有32个三角形.故答案为:32.【点评】此题主要考查了分类计数问题,应注意先拆分再分类计数,以免重复,防止遗漏.26.将四边形的任意一边延长,四边形其余两个顶点总在同一侧的四边形称为凸四边形,如图中共有20个凸四边形.【分析】首先在图中标注10个基本图形,再利用定义分类讨论,即可得出结论.【解答】解:首先在图中标注10个基本图形,由一个基本图形构成的凸四边形有(1)(2)(3),共3个;由两个基本图形构成的凸四边形有(1,4)(2,4)(2,5)(3,5)(6,7)(6,8),共6个;由三个基本图形构成的凸四边形有(6,7,9)(6,8,10),共2个;由四个基本图形构成的凸四边形有(1,2,4,8)(2,3,5,7)(1,8,6,9),(3,7,6,10),共4个;由五个或五个以上基本图形构成的凸四边形有ABFD,AFCD,ADCE,ABGD,ABCD,共5个,综上所述,一共有3+6+2+4+5=20个凸四边形.故答案为20.【点评】本题考查组合图形的计数问题,考查分类讨论的数学思想,正确理解题意,分类讨论是关键.27.今天是4月4日,图4.4中共有60个三角形.【分析】根据图形的特征,分两类分别计数即可.【解答】解:形如“△”的小三角形有54个;形如“”的小三角形有6个;所以,一共有54+6=60个三角形;答:图4.4中共有60个三角形.故答案为:60.【点评】此题主要考查计数方法的应用,养成按照一定顺序观察思考问题的习惯,做到不重复,不遗漏,有序计数.28.如图中有76个三角形.【分析】分三类计数,先研究一个:①以大三角形的顶点(蓝色)为顶点构成的小三角形;②交叉部分(红色)构成的小三角形;③最大的三角形4个;据此解答即可.【解答】解:①以大三角形的顶点为顶点构成的小三角形有:3×12=36(个);②交叉部分构成的小三角形有:3×12=36(个);③最大的三角形有4个;共有:36+36+4=76(个)答:图中有76个三角形.故答案为:76.【点评】此题主要考查分类计数方法的应用,要做到不重复,不遗漏,有序计数.29.数一数,图中共有23个正方形.【分析】根据方类数图形的计数原理和方法,正着放的正方形中有:较小的正方形有10个,由4个小正方形组成的是4个,同理斜着放的正方形中有:较小的正方形有7个,由4个小正方形组成的是2个,相加即可求解.【解答】解:正着放的正方形中有:10+4=14(个)斜着放的正方形中有:7+2=9(个)一共有:14+10=23(个)答:图中共有23个正方形.【点评】此题考查目的是:按照一定的顺序去观察思考问题,学会通过观察思考探寻事物的规律,通过发现的规律解决有关问题.30.由35个边长为1的小正方形拼成一个7*5的长方形,其中有一格含有“☆”.图中含有“☆”的所有长方形(含正方形)共有96个.【分析】显然含有五角星的长方形有几种情况,边长为1、2、3、4、5、6、7的长方形,根据五角星上下线的条数,和左右两边的线的数,计算出长方形的个数,然后把所有的长方形个数加起来即可.【解答】解:根据分析,五角星的上面有两条线,左面有两条线,下面有4条线,右边有6条线,所以含有☆的长方形共有:2×2×4×6=96个.故答案是:96.【点评】本题考查了组合图形的计数,本题突破点是:根据长方形是由上下两条线和左右两条线组合而成的,可以计算出长方形的个数.31.如图是上幼儿园的小毛球写的“中国”两个字,图中一共能数出25个长方形.【分析】可以向图中添加一个长方形,变成两个图,多了9个长方形,再添加一个长方形,变成第三个图,又多了3个长方形,最后添加一个长方形,变成第四个图,多了4个长方形,故不难求得长方形的个数.【解答】解:根据分析,如下图,左边第一个图中有9个长方形,添加一个长方形,变成两个图,多了9个长方形,再添加一个长方形,变成第三个图,又多了3个长方形,最后添加一个长方形,变成第四个图,多了4个长方形,故原图中共有9+9+3+4=25个长方形.故答案是:25.【点评】本题考查了组合图形的计数,本题突破点是:添加长方形法,计算出长方形的个数.32.如图,图中3个大三角形都是等边三角形,则图中共有30个三角形.【分析】观察图形,可以分为小三角形,含有两个小三角形的三角形,和大三角形,分别数出三角形的个数,再加起来.【解答】解:根据分析,小三角形的个数为:9个;含有两个小三角形的三角形的个数为:18个;大三角形的个数为:3个,故总的三角形的个数是:9+18+3=30个.【点评】本题考查了组合图形的计数,本题突破点是:分种类分别数出三角形的个数.33.在平面上用长度为6厘米的牙签棒摆正方形,摆出一个长为6厘米的正方形需要4根牙签棒,摆出5个这样的正方形至少需要15根牙签棒.【分析】要使摆出的5个正方形需要的牙签棒最少,就需要尽量多的共用邻边,据此解答即可.【解答】解:如下图排放牙签棒,需要的就最少,。
排列组合第3阶07圆周上的排列组合问题

排列组合第3阶07圆周上的排列组合问题1. 将圆周上5个点按如下规则染⾊:先任选⼀点染成红⾊,然后依逆时针⽅向,第1步转过1个间隔将到达的那个点染红,第2步转过2个间隔将到达的那个点染红,第k 步转过k 个间隔将到达的那个点染红.⼀直进⾏下去,可得到_________个红点.解:将5个点依次编号0—4,且不妨设开始染红的是0号点,则第1步染红的是1号点,第2步染红的是3号点,第3步染红的⼜是1号点.故共可得3个红点.2. 在⼀圆周上有k 个数,k ≥3.若其中任意三个相邻之数,依顺时针⽅向分别设为,,a b c ,恒有b a c αβ=+,这⾥1αβαβ+=≥0,≥0,.证明这k 个数必互相相等.任取其中⼀数,记为0a ,其余各数依顺时针⽅向分别记为121,,,k a a a -….对任意的正整数,n k n p k i =?+≥, p 是正整数, i 是整数,且01i k -≤≤,令n i a a =,按题意,对任意正整数n,有11n n n a a a αβ-+=+.若0αβ?=,结论显然成⽴.否则,有11()()n n n n a a a a βα+--=-.令1n n n b a a +=-,则1n n b b αβ-=.设100a a b a -==,则()n n b a αβ= 当n k =,有110()k k k k a b a a a a a αβ+==-=-=.由此可得0a =或1αβ=.若0a =,即0,0,1,2n b n ==…,结论显然成⽴.若有1,αβ=即,0,1,2,n b a n ==…,知数列{}n a 是以0a 为⾸项,a 为公差的等差数列,则有,00k a a a ka ==+ 即0a =.结论得证. 3. 在⼀个圆周上均匀分布10个点,以这些点为顶点,可以画出多少个不同的钝⾓三⾓形?(补充知识:由直径和圆周上的⼀点构成的三⾓形⼀定是直⾓三⾓形,其中直径的边所对的⾓是直⾓,所以如果圆周上三点在同⼀段半圆周上,则这三点构成钝⾓三⾓形).【考点】组合图形的计数.【专题】操作、归纳计数问题.【分析】由直径和圆周上的⼀点构成的三⾓形⼀定是直⾓三⾓形,其中直径的边所对的⾓是直⾓,所以如果圆周上三点在同⼀段半圆周上,则这三点构成钝⾓三⾓形,依此按照顺序数出钝⾓三⾓形的个数即可求解.【解答】解:由图形可知:含A、B两点的钝⾓三⾓形有6个;含A、C两点的钝⾓三⾓形有5个;含A、D两点的钝⾓三⾓形有2个;含A、G两点的钝⾓三⾓形有3个;含A、H两点的钝⾓三⾓形有2个;含A、I两点的钝⾓三⾓形有1个;含B、C两点的钝⾓三⾓形有5个;含B、D两点的钝⾓三⾓形有3个;含B、E两点的钝⾓三⾓形有1个;含B、H两点的钝⾓三⾓形有2个;含B、I两点的钝⾓三⾓形有1个;含C、D两点的钝⾓三⾓形有4个;含C、E两点的钝⾓三⾓形有2个;含C、F两点的钝⾓三⾓形有1个;含D、E两点的钝⾓三⾓形有3个;含D、F两点的钝⾓三⾓形有2个;含D、G两点的钝⾓三⾓形有1个;含E、F两点的钝⾓三⾓形有3个;含E、G两点的钝⾓三⾓形有2个;含E、H两点的钝⾓三⾓形有1个;含F、G两点的钝⾓三⾓形有3个;含F、H两点的钝⾓三⾓形有2个;含F、I两点的钝⾓三⾓形有1个;含G、H两点的钝⾓三⾓形有2个;含G、I两点的钝⾓三⾓形有1个;含H、I两点的钝⾓三⾓形有1个;共有:(6+5+2+3+2+1)+(5+3+1+2+1)+(4+2+1)+(3+2+1)+(3+2+1)+(3+2+1)+(2+1)+1=19+12+7+6+6+6+3+1=60(个).答:可以画出60个不同的钝⾓三⾓形.故答案为:60个.【点评】本题考查分步计数原理,考查圆的有关问题,是⼀个综合题,解题的关键是对于圆上的点,怎样能组成钝⾓三⾓形.在⼀个圆周上有7个点,正好将圆周七等分,以这些点为顶点作三⾓形,可以作4.(2001?上海校级⾃主招⽣)在⼀个圆周上有7个点,正好将圆周七等分,以这些点为顶点作三⾓形,可以作_____________个等腰三⾓形.【考点】排列组合.【分析】构成等腰三⾓形分上述三种情况,看每种情况能做⼏个,最后把所有的作法加起来就可解决.【解答】解:构成等腰三⾓形分上述三种情况,每个点都做⼀次顶点,每种情况能作7个三⾓形,共可以作21个等腰三⾓形.故答案为:21.【点评】解决本题的关键是分情况考虑,选定顶点,看能作⼏个等腰三⾓形,再看每种三⾓形能作⼏个,最后加起来即可.5. 如图1,圆周上顺序排列着1,2,3,…,12⼗⼆个数,我们规定:相邻的四个数a1、a2、a3、a4顺序颠倒为a4、a3、a2、a1称为⼀次“变换”(如1、2、3、4变为4、3、2、1,⼜如11、12、1、2变为2、1、12、11).能否经过有限次“变换”,将12个数的顺序变为9,1,2,3,…,8,10,11,12(如图2)?请说明理由.【考点】推理与论证.【分析】5个数经过4次“变换”可将⼀个数提前4位,其余不变,则经过四次变化,即可得到1,2,3,4,9,5,6,7,8,10,11,12,在1,2,3,4,9这5个数中进⾏4四变化就可得把9提前,从⽽得到.【解答】解:12345→15432→34512→32154→51234.这说明经过4次“变换”可将⼀个数提前4位,其余不变.于是,经过4次“变换”可得:1,2,3,4,9,5,6,7,8,10,11,12.同样,再经过4次“变换”可得:9,1,2,3,4,5,6,7,8,10,11,12.【点评】本题考查了数的变化规律,关键是理解个数经过4次“变换”可将⼀个数提前4位,其余不变.6. 将圆周上的任意点均染成⿊⾊或⽩⾊,对任意⼀种染⾊⽅法.(1)是否⼀定存在⼀个直⾓三⾓形,其顶点同⾊,证明你的结论;(2)证明:存在⼀个等腰三⾓形,其顶点同⾊.【考点】进⾏简单的合情推理.【专题】推理和证明.【分析】(1)若直⾓三⾓形的三个顶点在圆周上,则斜边⼀定为直径,我们把圆分成两个半圆,⼀半涂⿊,⼀半涂⽩,则不存在⼀条直径的两个端点同⾊,故这样的直⾓三⾓形不是⼀定存在的;(2)取圆的⼀个内接五边形,则五个顶点中,⾄少有三个顶点是同⾊的,进⽽可得答案.【解答】解:(1)这样的直⾓三⾓形不是⼀定存在的,理由如下:把圆分成两个半圆,⼀半涂⿊,⼀半涂⽩,则不存在⼀条直径的两个端点同⾊,此时不存在⼀个直⾓三⾓形,其顶点同⾊.证明:(2)取圆的⼀个内接五边形,则五个顶点中,⾄少有三个顶点是同⾊的,连接这三个顶点,可得到⼀个等腰三⾓形,故存在等腰三⾓形,其顶点同⾊.【点评】本题考查的知识点是合情推理,本题逻辑性强,证明思路⽐较难理解,属于中档题.7. 某⼯⼚⽣产⼀种圆盘形玩具.在圆盘正⾯的圆周上均匀分布安装10个⼩球,其中3个为红球,7个为⽩球,如图所⽰,若两个圆盘都正⾯朝上,可以圆⼼对圆⼼,红球对红球,⽩球对⽩球叠放在⼀起,就算同⼀种规格.问:这类玩具⼀共可以有多少种不同的规格?【考点】哈密尔顿圈与哈密尔顿链.【分析】当3个红球都不相邻时,7÷3=2…余1;所以最少间隔2+1=3个⽩球;因此按两个红球间隔⽩球的数量分:最多间隔3、4、5、6、7个;分类讨论即可得出答案.【解答】解:按两个红球间隔⽩球的数量分类⽤⿊点代表红球,空⼼点代表⽩球,最多间隔3个⽩球的有2种不同规格:最多间隔4个⽩球的有4种不同规格:类似地,最多间隔5个⽩球的有3种不同的规格,最多间隔6个⽩球的有2种不同规格.最多间隔7个⽩球的有1种规格.所以,共有不同规格:2+4+3+2+1=12(种);答:这类玩具⼀共可以有12种不同的规格.【点评】本题还可以这样理解:7分成3个数的和:007、016、025、034、115、124、133、223共8种,注意这是不加圆盘正⾯向上这个条件时的答案(即不可反扣),加上这个限制,可以认为016、025、034、124这4个都可以变化出第2种不同排列顺序来,所以是12种.。
2023-2024学年全国小学一年级上数学人教版单元测试(含解析)

2023-2024学年全国一年级上数学单元测试考试总分:161 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )1. 个小正方体并排摆在空地上,露在外面的面有A.个B.个C.个2. 下列算式中,得数最小的是 。
A.B.C. 3.图中共有( )条线段。
A.B.C.D.4. 把一张平行四边形卡片剪一刀,分成两个图形,下面几种情况中不可能出现的是( ).A.两个三角形B.两个梯形C.一个平行四边形和一个梯形5. 从长、宽、高分别为厘米、厘米、厘米的长方体上挖去一个棱长为厘米的正方体,剩下物体的表面积与原长方体相比,正确的描述是( )3()3911()1.92÷0.38192÷3800.192÷0.0038458105431A.变大B.变小C.不变D.无法确定6. 一个正方体的棱长总和是分米,它的每条棱长( )分米。
A.B.C.7. 个点连成线段的条数是( )条。
A.B.C.8. 个三年级的小学生,他们的体重一共大约是 千克。
A.B.C.9. 由个小正方体搭成的立体图形,从左面看到的形状是,从正面看到的形状是,这个立体图形可以是 . A.B.241262137888773()3010010006()C. D.10. 看到的立体图形中有一个面是圆形,这个立体图形可能是 。
①②③ ④A.①和②B.②和③C.③和④D.②和④卷II (非选择题)二、 填空题 (本题共计 7 小题 ,每题 3 分 ,共计21分 )11. 圆柱有________个平面,每个平面都是________形。
12. 与相邻的两个数分别是________和________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形的计数
1 数一数,在右图中共有()个三角形A.10 B.11 C.1
2 D.1
3 E.14
2 这里共有()条线段.A.三条B.四条C.五条D.六条
3 如图所示,图中三角形的个数为()A.4个B.7个C.9个D.10个
4 如图,共有()个长方形.()A.
5 B.7 C.9 D.10
5 如图中的五角星一共有()条线段A.5 B.15 C.30 D.以上都不对
6 数一数,图中一共有()条线段.A.4 B.6 C.8 D.10
7 如图,在一块木版上钉十六个钉子,每行和每列的距离都是一样的,以钉子为顶点拉上橡皮筋,组成一个
正方形,这样的正方形一共有(A)A.20个B.13个C.14个D.15个
8 图中共有()个三角形.A.25 B.27 C.29 D.36
9 平面内的8个点最多可以连成()条线段.
A.10 B.16 C.28 D.32
10 用4条直线最多能把一个圆分成的块数是()A.10 B.11 C.12
11 右图中有()个平行四边形.A.7 B.8 C.9
12 在如图中共有()个三角形.
A.18 B.19 C.20 D.21
13 在一条线段中间另有6个点,则这8个点可以构成()条线段.A.15 B.21 C.28 D.36
14 把一条细绳先对折,再把它所折成相等的三折,接着再对折,然后用剪刀在折过三次的绳中间剪一刀,那么这条绳被剪成()段.A.13 B.12 C.14 D.15
15 如图中共有()个角.A.4 B.9 C.10 D.6
16 图中有多少个长方形()A.10 B.20 C.8 D.15
17 如图中,有()A.5个B.6个C.7个
18 如图中一个有()个直角三角形.A.4 B.5 C.8
19 用哪一种方框去框下面一组数字,可以得到5种不同的结果.()
A.B.C.
20 数一数,它一共有()条线段.A.7 B.8 C.9 D.5
21 用连续的15个自然数写成一行,每相邻的4个数相加,可得到()种不同的和.
A.10 B.11 C.12 D.19
22 如图所示的立方体图形是由()个小立方体组成的.A.8 B.10 C.11 D.12
23 如图,将长度为9的线段AB分成9等份,那么图中所有线段的长度的总和是()
A.132 B.144 C.156 D.165
24 如图,在直线a上有四个点,在直线b上有三个点,以这些点为顶点,可以画出
___个三角形.
25 如图,线段AB、BC、CD、DE分别长5厘米、7厘米、3厘米、4厘米.则图中
一共有____条线段,这些线段的长度总和是_____ 厘米.
26 如图,由15个边长为1的小正方形拼成一个5×3的长方形,如图示小正方形中有“☆”.那么图
中含有“☆”的长方形(含正方形)有_______个.
27 如图,在半圆的边界周围有6个点A1、A2、A3、A4、A5、A6,其中A1、A2、A3在半圆的直径
上,问以这6个点为端点可以组成___个三角形
28 如图中,三角形的个数有____个.
29 平面上有5个点,无三点共线,以任意三点组成一个三角形,则三角形的个数应为______
30 有四个点,每三个点都不在一条直线上,过其中每两个点画直线,可以画______条直线.
31 从一点引出8条射线可组成_____ 个角.
32 如图中有______ 条线段,______ 个三角形.
33数图形.
____条线段_____个三角形_____个长方形_____个方块.
34
_____个角;______个三角形;_____条线段;_____个长方形.
35 如图所示:用每次框出三个字母,共有多少种不同的框法?需要框多少次?
36 在平面上任取4个点,四点不都在一条直线上的情况共有几种?将四点用线段分别连接,在各种情况的图中,所包含的三角形的个数分别是多少?请画图说明.
37 一条直线上共有7个点,一共有多少条不同的线段?画示意图解答.
38 如图是由22个小正方体组成的立体图形,其中共有多少个大大小小的正方体?由两个小正方体
组成的长方体有多少个?。
