第七节 旋转体的体积计算讲解
《旋转体的体积》课件

旋转体的性质
深入探讨了旋转体的几何性质,如旋 转体的表面积、质心和转动惯量等。
计算实例
通过具体的计算实例,演示了如何运 用旋转体的体积公式解决实际问题。
未来研究方向和展望
深入研究旋转体的性质
随着几何学的发展,旋转体的 性质将得到更深入的研究,如 探讨旋转体的对称性、稳定性 等。
扩展旋转体的应用领域
条件和范围。
计算中需要注意的事项
单位统一
在计算过程中,确保所有的长度单位都 是统一的,避免因单位不统一导致的误 差。
VS
精确度要求
根据问题的实际需求,合理选择计算方法 和工具,确保计算结果的精确度。
提高计算准确性的技巧和方法
01
02
03
多做练习
通过大量的练习,提高学 生的计算能力和对公式的 熟悉程度。
数学建模
在物理、化学和生物等学科中,旋转 体常被用来建立数学模型,以描述和 分析各种现象。
02
旋转体的体积计算公式
圆柱体的体积计算公式
总结词
圆柱体的体积计算公式是底面积乘以高。
详细描述
圆柱体的体积计算公式是底面积(πr^2)乘以高(h),即V=πr^2h,其中r是 底面圆的半径,h是高。
圆锥体的体积计算公式
随着科技的进步,旋转体在工 程、物理、生物等领域的应用 将更加广泛,如探讨旋转体在 流体动力学、机械工程和生物 学等领域的应用。
探索新的计算方法
随着数学和计算机技术的发展 ,将会有新的计算方法出现, 以更高效、精确地计算旋转体 的体积和其他几何量。
加强与其他学科的交叉研 究
旋转体作为几何学的重要分支 ,将与其他学科如物理学、化 学、生物学等产生更多的交叉 研究,以推动科学的发展。
旋转体体积说课艾雪微

根据旋转轴的不同,旋转体可以 分为圆柱、圆锥、圆台、球、椭 球等。
体积计算公式推导
01
02
03
圆柱体积公式推导
底面积乘以高,即$V = pi r^{2}h$。
圆锥体积公式推导
采用积分法或几何法,得 到$V = frac{1}{3}pi r^{2}h$。
圆台体积公式推导
由平行于圆锥底面的平面 截圆锥得到,其体积为$V = frac{1}{3}pi h(R^{2} + r^{2} + Rr)$。
适用场景
解题步骤
确定切片方式,计算每个薄片的面积 和厚度,相乘得到每个薄片的体积, 求和得到总体积。
适用于轴线方向形状变化较大的复杂 旋转体。
数值积分在复杂旋转体中的应用
基本原理
利用数值积分方法将复杂旋转体 的体积计算转化为离散点的求和
问题。
适用场景
适用于无法通过解析方法求解的复 杂旋转体体积问题。
高度减小
相反地,当旋转体的高度减小时,其 体积也会相应减小。这同样是由于高 度的变化对体积产生的影响。
05 实验验证与误差分析
实验设计思路及步骤介绍
设计思路
通过实际测量不同形状的旋转体,如圆柱体、圆锥体等,在液体中旋转一定圈数后液体体积的变化, 来验证旋转体体积公式的正确性。
步骤介绍
1. 准备实验器材,包括旋转体、测量液体、容器、旋转装置等;2. 将旋转体放入液体中,并固定好旋 转装置;3. 旋转一定圈数后,测量液体体积的变化;4. 重复实验多次,取平均值以减小误差。
底面半径变化对体积影响分析
底面径增大
当底面半径增大时,旋转体的体积会随之增大。这是因为底面半径决定了旋转体 底面的面积,而底面面积是影响体积的重要因素之一。
旋转体体积公式推导

旋转体体积公式推导旋转体是一种常见的几何体,其形状可以通过在平面图形绕某个轴线旋转得到。
如何求出一个旋转体的体积呢?下面,我们将通过推导旋转体体积公式来回答这个问题。
一、圆柱体的体积圆柱体是最简单的旋转体,其直径为d,高为h,其体积可以通过以下公式求出:V=πr²h其中r=d/2,代入可得:V=π(d/2)²h=πd²h/4二、圆锥体的体积圆锥体是由一个圆锥面和一个底面直径相等的圆所形成的旋转体。
其底面半径为r,高为h,其体积可以通过以下公式求出:V=1/3πr²h三、球的体积球是由绕某一条直径旋转所形成的旋转体,其体积可以通过以下公式求出:V=4/3πr³四、圆环的体积圆环是由一个圆绕其不同于圆心的轴线旋转所形成的旋转体,其外径为R,内径为r,高为h。
其体积可以通过以下公式求出:V=πh(R²-r²)五、推广到一般情况对于一般的旋转体,可以通过将其划分成无数个圆环,然后分别求出每个圆环的体积,并将这些体积累加,得到最终的旋转体体积。
当我们将每个圆环的高度取得足够小,取极限时,就可以得到以下的积分公式:V=∫2πr f(x)dx其中,f(x)为旋转曲线在x处的高度,r为旋转曲线到旋转轴线的距离,积分的区间为旋转曲线上所有的x值。
通过这个公式,我们可以求出各种复杂形状的旋转体体积,例如螺旋线、双曲线等等。
以上就是旋转体体积公式的推导过程。
通过这些公式,我们可以很方便地求出各种旋转体的体积,对于物理、数学等领域的学习和工作都非常有帮助。
求旋转体体积的两种方法

求旋转体体积的两种方法
当平面图形绕着某一直线(旋转轴)旋转时,所得到的旋转体的体积,我们可以用切片法或者圆桶法求出。
总结起来,有几种情形:
情形1:平面图形由及 x 轴围成,
利用切片法,这个图形绕 x 轴旋转所得的体积为
而它绕 y 轴所得的体积,我们利用圆桶法求得它的体积为
情形2:如果平面图形由及 y 轴围成,
那么由圆桶法,绕 x 轴旋转的体积为
而由切片法,可以得到绕 y 轴旋转所得的旋转体体积为
情形3:如果平面图形由两条曲线以及两条直线所围成,
那我们用上曲线旋转所得的体积减去下曲线旋转所得的体积,则得到绕 x 轴旋转的体积为
同样,绕 y 轴旋转所得的体积为
情形4:类似可以得到由以及
围成的图形分别绕 x 轴及 y 轴旋转所得的体积
现在我们来看几个例子。
例1:求由曲线以及两个坐标轴所围成的图形分别绕 x 轴与绕 y 轴旋转所得的旋转体的体积。
解:与求平面图形的面积一样,我们先画出区域的图形。
所以,由切片法得到绕 x 旋转所得的体积为由圆桶法得到绕 y 轴旋转所得的体积为。
旋转体体积公式绕x轴和绕y轴的公式

标题:旋转体体积公式绕x轴和绕y轴的公式概述旋转体体积公式是数学中的重要概念,它用于计算由曲线或曲面旋转产生的立体图形的体积。
在这篇文章中,我们将重点讨论旋转体体积公式绕x轴和绕y轴的具体公式及推导过程。
一、绕x轴旋转体积公式当曲线y=f(x)在x轴的区间[a,b]上绕x轴旋转一周时,所形成的旋转体的体积Vx可由以下公式计算:Vx = π∫[a,b] f(x)² dx其中,π为圆周率。
推导过程:为了推导该公式,我们可以将曲线y=f(x)绕x轴旋转一周后,得到不同x处的截面面积πf(x)²。
然后利用定积分的性质,将这些截面面积相加,即得到旋转体的体积公式。
举例说明:假设我们有曲线y=x²,要计算其在区间[0,1]上绕x轴旋转一周所形成的旋转体的体积。
根据公式,我们可以得到Vx = π∫[0,1] x^4 dx = π/5二、绕y轴旋转体积公式当曲线x=g(y)在y轴的区间[c,d]上绕y轴旋转一周时,所形成的旋转体的体积Vy可由以下公式计算:Vy = π∫[c,d] g(y)² d y推导过程:同样地,为了推导该公式,我们可以将曲线x=g(y)绕y轴旋转一周后,得到不同y处的截面面积πg(y)²。
然后利用定积分的性质,将这些截面面积相加,即得到旋转体的体积公式。
举例说明:假设我们有曲线x=y²,要计算其在区间[0,1]上绕y轴旋转一周所形成的旋转体的体积。
根据公式,我们可以得到Vy = π∫[0,1] y^4 dy = π/5总结通过本文的讨论,我们可以得出绕x轴和绕y轴旋转体积的计算公式,并了解到其推导过程。
这些公式在数学和工程领域有着广泛的应用,能够帮助我们计算由曲线旋转产生的立体图形的体积,具有重要的理论和实际意义。
为了更深入地理解旋转体体积公式绕x轴和绕y轴的推导过程,我们可以进一步探讨不同类型曲线的旋转体积公式,并应用这些公式解决实际问题。
旋转体求体积的方法

旋转体求体积的方法旋转体求体积是数学中一个重要的计算方法,它可以应用于各种实际问题的建模和解决。
首先,我们需要了解旋转体的概念。
旋转体是通过将一个曲线或者一条线段沿着某个轴线旋转一周而形成的立体图形。
常见的例子有圆锥和圆柱体。
接下来,我们介绍一种常见的方法——圆盘法。
该方法适用于当旋转体的截面是一个平行于底面的圆盘时。
以一个简单的圆柱体为例,假设它的底面半径为r,高度为h。
我们可以将圆柱体沿着垂直于底面的轴线旋转一周,形成一个立体图形。
使用圆盘法,我们可以将整个旋转体分解为无数个很小的圆盘,这些圆盘的半径随着高度的增加而变化。
每个圆盘的面积可以通过πr²计算得出,其中π是一个常数。
要计算旋转体的体积,我们需要对所有圆盘的面积进行求和。
由于每个圆盘的厚度很小,我们可以用ΔV代表一个很小的圆盘的体积。
根据圆盘的面积和厚度,可以得到ΔV = πr²Δh,其中Δh是圆盘的厚度。
接下来,我们对所有的圆盘体积进行求和,即将每个ΔV加起来。
这可以通过求极限的方法得到,即将Δh趋近于0时的极限。
最后的结果即为旋转体的体积,可以表示为V = ∫(0到h) πr²dh。
除了圆盘法,还有其他方法可以求解旋转体的体积。
例如,壳法和柱面法。
这些方法在不同的情况下有其适用性,可以根据实际问题的需要选择合适的方法。
总结起来,旋转体求体积是通过将立体图形沿着某个轴线旋转一周,并将其分解为无数个很小的圆盘,利用圆盘的面积和厚度进行求和,最后求得的体积。
通过应用不同的方法,我们可以解决各种实际问题,例如计算容器的容量、建模自然现象等。
在实际问题中,我们需要根据具体情况选择合适的方法,并进行数学推导和计算,以得到准确的解答。
希望这些内容对你理解旋转体求体积的方法有所帮助。
旋转体的体积公式参数方程

旋转体的体积公式参数方程
1. 旋转体体积公式的一般情况。
- 对于由曲线y = f(x),a≤slant x≤slant b绕x轴旋转一周所得到的旋转体体积V,其公式为V=π∫_a^b[f(x)]^2dx。
- 若曲线x = g(y),c≤slant y≤slant d绕y轴旋转一周所得到的旋转体体积V,则V=π∫_c^d[g(y)]^2dy。
2. 参数方程形式下的旋转体体积公式。
- 设曲线的参数方程为<=ft{begin{array}{l}x = x(t) y = y(t)end{array}right.,α≤slant t≤slantβ。
- 当曲线绕x轴旋转时,旋转体体积V=π∫_α^β[y(t)]^2x^′(t)dt。
这里
x^′(t)=(dx)/(dt)。
- 当曲线绕y轴旋转时,旋转体体积V = π∫_α^β[x(t)]^2y^′(t)dt,这里
y^′(t)=(dy)/(dt)。
例如,对于椭圆frac{x^2}{a^2}+frac{y^2}{b^2} = 1,其参数方程为
<=ft{begin{array}{l}x=acos t y = bsin tend{array}right.,0≤slant t≤slant2π。
- 若绕x轴旋转,则x^′(t)=-asin t,旋转体体积V=π∫_0^2π(bsin t)^2·(-asin t)dt。
- 若绕y轴旋转,则y^′(t)=bcos t,旋转体体积V=π∫_0^2π(acos t)^2·(bcos t)dt。
高数定积分旋转体体积

在高数中,旋转体是一种三维图形,可以用旋转某个二维图形围成。
旋转体的体积可以用定积分来求解。
具体来说,假设有一个二维图形 F,它位于平面 xy 上,其旋转轴为 y 轴。
如果将这个图形绕 y 轴旋转 360°得到的体积称为 V。
那么,V 可以表示为:
V = ∫F(x,y) dx
其中,F(x,y) 是围成旋转体的二维图形的面积函数。
举个例子,假设有一个圆柱体,其底面半径为 r,高为 h。
那么,这个圆柱体的体积 V 可以表示为:
V = ∫πr^2 dx = πr^2 ∫ dx
积分的上下界分别为 -h/2 和 h/2,因此:
V = πr^2 (h/2-(-h/2)) = πr^2 h
也就是说,圆柱体的体积等于底面积乘以高。
总之,旋转体的体积可以用定积分来求解,具体方法是将围成旋转体的二维图形的面积函数积分即可。
旋转体的体积【创意版】.ppt

1
0
3 y 2 dy 3
5
5 y x3, x 1, x轴
绕y轴旋转一周
1
Vy
0
3 y 2 dy 2
5
y
.,
y=x3 1
y=x3
9
1
◆练习:写出下列旋转体体积的定积分表达式
绕x轴旋转一周
V 2
1
x2 1 2 dx 22
2 1
0
2 x4dx
32 2 3 2
0
1 y x3, x 1, y 0
绕x轴旋转一周
x3, y 1, x 0
绕x轴旋转一周
y=x3 x1
1
Vx
1
dx
0
1
x6dx
6
0
7
.,
y=x3
x
1
8
◆练习:写出下列旋转体体积的定积分表达式
4 y x3, y 1, y 轴
1
绕y轴旋转一周
y
Vy
d x2dy
c
d
c
g( y) 2 dy
.,
c
x=g 5(y)
◆旋转体的体积计算公式
例2 连接坐标原点 O 及点 P( h , r) 的直线,
直线 x=h及 x轴围成一个直角三角形,将它绕
x轴旋转构成一个底半径为 r,高为 h的圆锥,
计算圆锥的体积。
y P(h,r)
解 :如图所示
直线OP的方程为 y r x ,
旋转体的定义:旋转体就是由一个平面图形饶 这平面内一条直线旋转一周而成的立体.这直 线叫做旋转轴。
可选取适当坐标系,使旋转轴为x轴或y轴
最基本的情形是曲边梯形绕x轴或y轴旋转的情形。
旋转体求体积

杨小洁
旋转体求 体积
概念
方法
应用
一、概念
旋转体是指一个平面图形绕该平面内的一条直线旋
转一周而成的立体,这条直线称为旋转体的旋转轴.如
圆柱体、圆锥体和球等都是旋转体.
这条直线称为旋转体的旋转轴.
二、方法
y f 直(x线)
x 及a, 轴x 围b成的x曲边梯形绕轴
旋转一周而成(图1),试计算它的体积.
v
sin2 xdx
1cos2x dx
0
02
2
2
1
取 横 坐 标 为 积x 分 变 量 , 积 分 区 间 为
,在
上任取小区间
,相应薄片的体积近似于以 为
底半径a ,,b 为高的扁圆a,柱b体的体积,即体积微元x,为x dx
f x
dx
于是旋转体的体积为
dV [ f (x)]2 dxVFra bibliotekb
[ a
f
(x)]2 dx
同理,由连续曲线
与直线 x y, 及 轴围
成的y曲边c梯, y形绕d轴旋转y而成的旋转体的体积为(图2)
V
d c
[
(
y
)]
2
dy
2
三、应用
求 y si,n x x以及0 轴所围x成的图形绕 轴旋转
所成立x体的体积.
解:由微元法可知:
则
dv sin2 xdx
绕x轴旋转体的体积课件

应用场景
当一个平面图形绕x轴 旋转时,可以形成圆锥 体。例如,将一个直角 三角形绕x轴旋转一周, 可以得到一个圆锥体。
计算方法
将圆锥体的底面半径和 高代入公式即可计算出 体积。
圆台体体积公式的应用
1 2 3
圆台体体积公式 V = (1/3)πh(R² + r² + Rr),其中R是上底面半 径,r是下底面半径,h是高。
详细描述
圆台体的体积计算公式为 V = (1/3) × (π × r^2 × h - π × R^2 × H),其中 r 是下 底面圆的半径,R 是上底面圆的半径,h 是圆台的高,H 是上底面到圆台顶面的高 度。这个公式适用于计算圆台体的体积。
圆柱体体积公式的推导
圆柱体体积公式
V = πr²h,其中r是底面圆的半径,h是高。
详细描述
对于一些更复杂的绕x轴旋转体,如不规则 旋转体,其体积计算需要使用更复杂的公式。 这些公式通常涉及到积分运算,需要使用微 积分的知识进行计算。在进行计算时,需要 注意旋转体的边界条件和形状,以确保计算 结果的准确性。
THANK YOU
圆台体体积公式的推导
圆台体体积公式
V = (1/3)πh(R² + r² + Rr),其中R和r分别为上底面和下底面的半径,h为高。
推导过程
将圆台体分割成无数个小的圆台体,每个小圆台体的体积为(1/3)πh(R² + r² + Rr),其中h为小圆台体 的高,R和r分别为上底面和下底面的半径。将所有小圆台体的体积相加,得到整个圆台体的体积。
绕y轴旋转体
平面曲线绕y轴旋转形成的立体图形。
旋转体体积的计算意义
实际应用
计算旋转体的体积有助于解决实际问题,如求物体的质量、 重心等。
旋转体的计算

旋转体的计算旋转体是在数学中经常出现的一个概念,它由一个曲线或者曲面绕着某个轴旋转而成。
对于旋转体的计算,我们可以通过几何方法或者积分方法进行求解。
下面将介绍一些常见的旋转体计算方法。
一、旋转体的体积计算对于一个曲线绕着x轴旋转一周所得到的旋转体,其体积可以通过以下公式进行计算:V = π * ∫[a,b] (f(x))^2 dx其中,a和b为曲线与x轴的交点,f(x)为曲线的方程。
这个公式可以通过将曲线分成无穷多个微小的圆柱体,并对其进行求和得到。
同样地,对于一个曲线绕着y轴旋转一周所得到的旋转体,其体积可以通过以下公式计算:V = π * ∫[c,d] (g(y))^2 dy其中,c和d为曲线与y轴的交点,g(y)为曲线的方程。
二、旋转体的表面积计算旋转体的表面积计算可以通过以下公式进行求解:A = 2π * ∫[a,b] f(x) * √(1 + (f'(x))^2) dx其中,a和b为曲线的范围,f(x)为曲线的方程,f'(x)为曲线的导数。
对于一个曲线绕着y轴旋转一周所得到的旋转体,其表面积可以通过以下公式进行计算:A = 2π * ∫[c,d] g(y) * √(1 + (g'(y))^2) dy其中,c和d为曲线的范围,g(y)为曲线的方程,g'(y)为曲线的导数。
三、例题演示假设有一个半径为r的圆形,我们希望计算其绕着x轴旋转一周所得到的旋转体的体积和表面积。
已知圆的方程为x^2 + y^2 = r^2。
体积的计算:V = π * ∫[-r,r] (r^2 - x^2) dx= π * [r^2 * x - (x^3)/3] |[-r,r]= π * [r^3 - (-r^3)/3]= (4/3)π * r^3表面积的计算:A = 2π * ∫[-r,r] (r * √(1 + (x/r)^2)) dx= 2π * [r^2 * ln(x + √(x^2 + r^2))] |[-r,r]= 2π * [r^2 * (ln(2r) - ln(r))]= 2π * r^2 * ln(2)结论:对于绕着x轴旋转一周的圆形,其体积为(4/3)π * r^3,表面积为2π * r^2 * ln(2)。
三角形旋转体体积

三角形旋转体体积三角形旋转体是指以一个三角形为截面,在某一条线段上旋转一周所形成的立体图形。
它的体积计算公式为:V = (1/2) * b * h * π * r,其中b为三角形的底边长,h为三角形的高,r为旋转的半径。
三角形旋转体的体积计算方法相对简单,只需要知道三角形的底边长、高和旋转半径即可。
首先,我们需要确定旋转的轴线,即旋转的线段。
然后,我们需要确定三角形的底边长和高,这两个参数决定了三角形的形状。
最后,我们需要确定旋转的半径,这个参数决定了旋转的大小。
三角形旋转体的体积计算公式中的π是一个常数,约等于3.14159。
通过将底边长、高和旋转半径代入公式,即可计算出三角形旋转体的体积。
需要注意的是,计算结果通常是一个带有π的无理数。
三角形旋转体的体积计算方法可以通过几何推导得出。
首先,我们可以将三角形旋转体分解为无数个平行于底边的圆盘形,每个圆盘形的面积可以近似看作一个矩形的面积。
然后,我们可以将这些矩形的面积相加,即可得到整个三角形旋转体的体积。
这个方法可以通过极限的思想进行推导,但是在这里我们不进行详细的数学推导。
三角形旋转体的体积计算方法可以应用在很多实际问题中。
比如,在建筑设计中,可以利用三角形旋转体的体积计算方法计算柱形的容积,从而确定柱形的材料用量。
在工程计算中,可以利用三角形旋转体的体积计算方法计算旋转部件的容积,从而确定旋转部件的设计参数。
在物理学中,可以利用三角形旋转体的体积计算方法计算旋转物体的质量,从而确定物体的物理特性。
三角形旋转体是一种常见的几何图形,它可以通过旋转三角形而得到。
三角形旋转体的体积计算方法相对简单,只需要知道三角形的底边长、高和旋转半径即可。
通过几何推导,我们可以得到三角形旋转体的体积计算公式。
这个方法可以应用在很多实际问题中,具有广泛的应用价值。
旋转体的体积计算(课堂PPT)
曲边梯形绕 y 轴旋转一周而成的立体,体积为
y
V d [ ( y)]2 dy c d x 2dy c
d
x ( y) c
o
x
3
例1. 求由曲线 y x ,直线x = 1及x轴所围成的平面图形
绕x轴旋转一周所生成的旋转体的体积.
解 如图, 选x为积分变量
y
y x
由旋转体的体积公式,得
1
Vx
(
0
x )2 dx
1
xdx
0
o
x
x2
1
22
0
4
例2. 求由曲线 x 2 4 y,直线y = 1及y轴所围成的图形
分别绕 x 轴, y 轴旋转一周所生成的旋转体的体积.
y
解 如图, 绕 x 轴旋转体的体积,
选x为积分变量
(2, 1)
1
Vx
12 2 2 ( x 2 )2 dx 04
b
左半圆弧方程为 x x2( y) b a2 y2 O A
Bx
体积微元
-a
D
dV
[ x1(
y)]2 dy
[ x2 (
y)]2 dy
[ x12 (
y)
x
2 2
(
y)]dy
环体体积为 V
a
(
a
x12
x22
)dy
a
[(b
a2 y2 )2 (b
a2 y2 )2 ]dy
a
a
y2
2 a 3
2
x3
3
x [a, a]
-a
o
a
x
由旋转体的体积公式,知:
V
a [ f ( x)]2dx
旋转体体积万能公式

旋转体体积万能公式旋转体是指由一个曲线绕某条轴线旋转一周所形成的立体图形。
计算旋转体的体积是数学中的基本问题之一,而旋转体体积万能公式则是用来计算各种不同形状的旋转体体积的通用公式。
一、圆柱体的体积计算公式圆柱体是最简单的旋转体,其体积计算公式为:V = πr²h其中,V表示圆柱体的体积,r表示底面圆的半径,h表示圆柱体的高度。
二、圆锥体的体积计算公式圆锥体是由一个直角三角形绕其斜边所形成的旋转体,其体积计算公式为:V = 1/3πr²h其中,V表示圆锥体的体积,r表示底面圆的半径,h表示圆锥体的高度。
三、球体的体积计算公式球体是由一个圆绕其直径所形成的旋转体,其体积计算公式为:V = 4/3πr³其中,V表示球体的体积,r表示球的半径。
四、圆环体的体积计算公式圆环体是由两个同心圆之间的区域绕其中一个圆的直径所形成的旋转体,其体积计算公式为:V = π(R² - r²)h其中,V表示圆环体的体积,R表示外圆的半径,r表示内圆的半径,h表示圆环体的高度。
五、其他旋转体的体积计算公式除了上述常见的旋转体,还有一些其他形状的旋转体,它们的体积计算公式如下:1. 半圆球冠的体积计算公式:V = 1/6πh(3a² + h²)其中,V表示半圆球冠的体积,a表示底面圆的半径,h表示半圆球冠的高度。
2. 椭球体的体积计算公式:V = 4/3πabc其中,V表示椭球体的体积,a、b、c分别表示椭球的三个轴长。
3. 抛物体的体积计算公式:V = 1/2πa²h其中,V表示抛物体的体积,a表示抛物线的参数,h表示抛物体的高度。
总结:旋转体体积万能公式是用来计算各种不同形状的旋转体体积的通用公式。
通过应用这些公式,我们可以准确地计算出各种旋转体的体积,为解决实际问题提供了便利。
在实际应用中,我们可以根据旋转体的形状选择合适的公式进行计算,从而得到准确的结果。
绕直线旋转所成旋转体体积的计算公式

绕绕绕绕绕绕绕绕绕绕绕绕绕绕绕绕绕
绕直线旋转所成的旋转体的体积可以用以下公式计算:
V=πr^2l
其中,V表示旋转体的体积,r表示绕直线旋转的半径,l表示旋转体的长度。
这个公式只适用于绕直线旋转所成的旋转体形状为圆柱体的情况。
如果旋转体的形状不是圆柱体,则需要使用不同的公式计算体积。
举个例子,如果要计算绕直线旋转半径为3cm,长度为10cm的旋转体的体积,则可以使用以下公式进行计算:
V=π(3cm)^2(10cm)=94.2cm^3
这样就可以得到绕直线旋转所成旋转体的体积了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
例6 一平面经过半径为 R 的圆柱体的底圆中心,
并与底面交成角? ,计算这平面截圆柱体所得立
体的体积.
解 取坐标系如图
?R
底半圆方程为
o?
y
y ? R2 ? x2
?
垂直于 x 轴的截面为直角三角形 R
x2 ? y2 ? R2
x
截面面积 A( x ) ? 1 y ? y tan ? ? 1 (R 2 ? x 2 ) tan ?
y
成的旋转体(环体)的体积
C
a
解 右半圆弧方程为 x ? x1(y) ? b? a2 ? y2
b
OA
Bx
左半圆弧方程为 x ? x2( y) ? b ? a2 ? y2
体积微元
-a
D
dV
?
? [ x1( y)]2 dy ? ? [ x2( y)]2 dy
?
?
[
x
2 1
(
y
)
?
x
2 2
(
y
)]dy
? 环旋转体的体积; 2.平行截面面积为已知的立体的体积 .
教学要求 熟练掌握应用元素法求体积的方法。
1.旋转体的体积
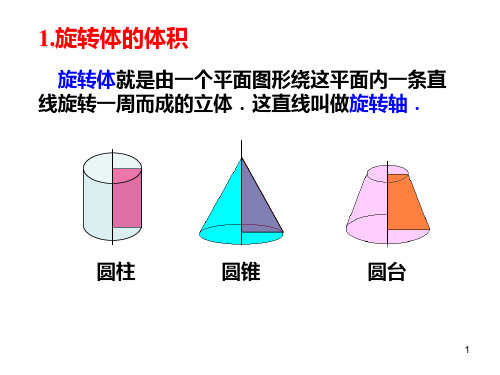
旋转体 就是由一个平面图形绕这平面内一条直 线旋转一周而成的立体.这直线叫做 旋转轴.
圆柱
圆锥
圆台
一般地,如果旋转体是由连续曲线 y ? f ( x )、直
2
2
? 立体体积
V
?
R
?? R
A( x )dx
?
1 2
R (R 2 ? x 2 ) tan ? dx
?R
? 2 R 3 tan ? . 3
小结
[ ? ? V ?
b
?
f ( x )]2 dx
?
b? y 2dx
a
a
y
d
y
y ? f (x)
o
x x ? dx
x ? ? (y)
c
x
o
x
[ ? ? V ?
d
a
(
?a
x
2 1
?
x
2 2
)dy
? ? ?
a
[(b ?
a2 ? y2 )2 ? (b ?
a 2 ? y2 )2 ]dy
?a
? ? a
? 4?b
a 2 ? y2dy ? 8b?
a a 2 ? y2 dy ? 2a 2b? 2
?a
0
2.平行截面面积为已知的立体的体积
设一立体位于 过点 x =a, x=b y 且垂直于 x 轴的两平面之间, 用垂直于 x 轴的任一平面截 此立体所得的截面积 A(x) 是 x 的已知函数,
?
x
2 3
3
? ??
x ? [? a, a]
-a
o
?
?
a
x
由旋转体的体积公式, 知:
? ? V ?
a
?
[
f
(
x
)]2 dx
?
a
?
??
a
2 3
?
x
2 3
3
??
dx
?
32 ? a3 .
?a
?a ?
?
105
??? 4
例5 求圆 ( x ? a )2 ? y 2 ? a 2 (0 ? a ? b) 绕 y 轴旋转一周所
3
同理得椭圆绕 y 轴旋转所成的旋转体的
? 体积为
V ??
b ?b
a2 b2
(b 2
?
y 2 )dy
?
4 ?a 2b.
3
练习
求摆线
? x ? a(t ? sin t)
? ?
y
?
a(1
?
cos t )
的一拱与
y
= 0所围成的
图形绕 x 轴 旋转构成旋转体的体积 .
解 绕 x 轴旋转的旋转体体积
y
? V x ?
0
绕 y轴旋转体的体积 , 选y为积分变量
? ? V y ?
1
?(
0
4 y ) 2 dy ? ?
1
4 ydy?
4?
y2 ?
1
?
2?
0
2
0
2
2
2
例4 求星形线 x 3 ? y3 ? a3 (a ? 0) 绕 x 轴旋转
构成旋转体的体.积
y
2
2
2
解 ? y3 ? a3 ? x3,
?
y2
?
? ??
a
2 3
线 x ? a 、 x ? b 及 x 轴所围成的曲边梯形绕 x 轴旋
转一周而成的立体,体积为多少?
取积分变量为 x
y
y ? f (x)
x ? [ a,b]
在[ a, b]上任取小区
o
x x ? dx
x
间[ x , x ? dx ],
取以 dx 为底的窄边梯形绕 x 轴旋转而成的薄片的体积 为体积元素,dV ? ? [ f ( x )]2 dx
?
?
( y)]2 dy?
d?x 2dy
c
c
作业:P118. 1(1)(3),2
练习
求由椭圆
x2 a2
?
y2 b2
?
1, 绕x轴旋转所成旋转体的体
积.
解
上半椭圆的方程为:
y2
?
b2 a2
(a2
?
x2)
? 由公式知:V ? ? a y2dx ?a
? ? ?
a ?a
b2 a2
(a2
?
x 2 )dx
?
4 ? ab 2 .
? ? 旋转体的体积为
V?
b
?[
f ( x )]2 dx ?
b ? y 2 dx
a
a
类似地,如果旋转体是由连续曲线
x ? ? ( y)、直线 y ? c 、 y ? d 及 y 轴所围成的
曲边梯形绕 y 轴旋转一周而成的立体,体积为
y
? V ? d ? [? ( y )]2 dy c ? ? d ? x 2 dy c
0
练习
求以抛物线 y ? 4 ? x 2及y ? 0所围成的图形为底,而垂
直于 y轴的所有截面均是高为 2的矩形的立体的体积 .
解 设截面面积为 A( y) y
A(x )
求这个立体的体积 V . 用微元法:
o a x x+dx b x
取 x 为积分变量,在区间 [a, b] 上任取一小区间
[x , x+d x] ,过其端点作垂直 x 轴的平面,
作体积微元:以A(x) 为底,dx 为高作柱体,
? 体积微元为 dV ? A( x )dx ,
从而 V ?
b
A ( x )dx .
d
x ? ? (y)
c
o
x
例1. 求由曲线 y ? x ,直线x = 1及x轴所围成的平面图形
绕x轴旋转一周所生成的旋转体的体积 .
解 如图, 选x为积分变量
y
y? x
由旋转体的体积公式 ,得
? ? V x ?
1
?(
0
x ) 2 dx
??
1
xdx
0
o
x
?
?
x2
1
?
?
2 0
2
例2. 求由曲线 x 2 ? 4 y,直线y = 1及y轴所围成的图形
分别绕 x 轴, y 轴旋转一周所生成的旋转体的体积 . y
解 如图, 绕 x 轴旋转体的体积 , (2, 1) 1
选x为积分变量
? ? V x
? ? ?1 2 ?2 ? 2 ? ( x 2 ) 2 dx 04
? ? 2? ?
16
2 0
x
4 dy
?
2?
?
? 16
x5 ?
5
2
?
o
8?
5
y2 ? 4x
x
2? a
?
y 2dx
0
o
2?a x
? ? ? 2? a2 (1 ? cos t)2 d[a(t ? sin t )] 0
? ? ? 2? a2 (1 ? cos t)2 ?a(1 ? cos t)dt 0
? ? ? a3
2?
(1 ?
3cos t
?
3 cos2 t
?
cos3 t )dt
?
5? 2a3.
