等差数列知识点总结学习资料
等差数列知识点总结

等差数列知识点总结引言等差数列是数学中常见的一个概念,它在数值模式的分析和问题解决中起到了重要的作用。
本文将对等差数列的定义、通项公式、前n项和求解等相关知识进行总结,帮助读者更好地理解和应用等差数列。
一、等差数列的定义等差数列是指一个数列中相邻两项之间的差值保持不变的数列。
它由首项 a1和公差 d 决定,可以表示为a1, a1 + d, a1 + 2d, a1 + 3d, …,其中 a1 是首项,d 是公差。
二、等差数列的通项公式等差数列的通项公式可以用来求解数列中任意一项的值。
设首项为 a1,公差为d,第 n 项的值为 an,则等差数列的通项公式可以表示为 an = a1 + (n - 1) * d。
三、等差数列的前 n 项和等差数列的前 n 项和是指数列中前 n 项的和。
根据等差数列的特点,可以通过求平均值的方式快速计算出前 n 项和的值。
设首项为 a1,公差为 d,前 n 项和为Sn,则等差数列的前 n 项和公式可以表示为 Sn = n * (a1 + an) / 2。
四、等差数列的性质总结1.等差数列的公差是相邻两项之间的固定差值,可以用来判断一个数列是否是等差数列。
2.等差数列的第 n 项可以通过通项公式求解,也可以通过逐项相加得到。
3.等差数列的前 n 项和公式可以通过求平均值的方式快速计算,可以简化问题求解的过程。
4.等差数列的性质可以应用于一些实际问题,如数值模式的预测和分析等。
五、等差数列的求解示例示例 1已知等差数列的首项 a1 = 3,公差 d = 5,求该等差数列的前 10 项和。
根据前 n 项和公式,代入已知的数值进行计算:Sn = 10 * (3 + a10) / 2= 10 * (3 + (3 + (10 - 1) * 5)) / 2= 10 * (3 + 3 + 45) / 2= 10 * 51 / 2= 255所以该等差数列的前 10 项和为 255。
示例 2已知等差数列的首项 a1 = 2,公差 d = -4,且第 5 项的值为 -18,求该等差数列的第 n 项。
(完整版)高考等差等比数列知识点总结

1高考数列知识点等差数列1.等差数列的定义:d aa n n=--1(d 为常数)(2≥n );2.等差数列通项公式:*11(1)()n a a n d dn a d n N =+-=+-∈ , 首项首项首项::1a ,公差,公差:d :d :d,末项,末项,末项::n a推广: d m n a a m n )(-+=. 从而mn a a d m n --=; 3.等差中项(1)如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即:2ba A +=或b a A +=2(2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+211()22dn a d n =+-2An Bn =+(其中(其中A A 、B 是常数,所以当是常数,所以当d d ≠0时,时,S S n 是关于是关于n n 的二次式且常数项为的二次式且常数项为00) 特别地()()()12121121212n n n n a a S n a +++++==+5.等差数列的判定方法(1) 定义法:若d a a n n=--1或d a an n =-+1(常数*∈N n )⇔ {}n a 是等差数列.是等差数列. (2) 等差中项:数列{}na 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a .(3) 数列{}n a 是等差数列⇔b kn a n +=(其中b k ,是常数)。
是常数)。
(4) 数列{}n a 是等差数列⇔2n S An Bn =+,(其中(其中A A 、B 是常数)6.等差数列的证明方法定义法:若d a a n n=--1或d a an n =-+1(常数*∈N n )⇔ {}n a 是等差数列7.等差数列的性质: (1)当公差0d ≠时,等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函的一次函 数,数,且斜率为公差d ;前n 和211(1)()222n n n d d S na d n a n -=+=+-是关于n 的二次函数且常数项为0. (2)若公差0d >,则为递增等差数列,若公差0d <,则为递减等差数列,若公差0d =,则为常数列。
(完整版)等差等比数列知识点总结

1.等差数列:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数d ,那么这个数列就叫做等差数列,这个常数d 叫做等差数列的公差,即d a a n n =--1(d 为常数)(2≥n );.2.等差中项:(1)如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即:2ba A +=或b a A +=2 (2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a3.等差数列的通项公式:一般地,如果等差数列{}n a 的首项是1a ,公差是d ,可以得到等差数列的通项公式为:()d n a a n 11-+=推广: d m n a a m n )(-+=. 从而mn a a d mn --=; 4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+211()22d n a d n =+-2An Bn =+ (其中A 、B 是常数,所以当d ≠0时,S n 是关于n 的二次式且常数项为0) 5.等差数列的判定方法(1) 定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列. (2) 等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a .(3) 数列{}n a 是等差数列⇔b kn a n +=(其中b k ,是常数)。
(4) 数列{}n a 是等差数列⇔2n S An Bn =+,(其中A 、B 是常数)。
6.等差数列的证明方法定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列.(1)当m n p q +=+时,则有q p n m a a a a +=+,特别地,当2m n p +=时,则有2m n p a a a +=.(2) 若{n a }是等差数列,则232,,n n n n n S S S S S -- ,…也成等差数列(3)设数列{}n a 是等差数列,d 为公差,奇S 是奇数项的和,偶S 是偶数项项的和,n S 是前n 项的和 1.当项数为偶数n 2时,()121135212n n n n a a S a a a a na --+=+++⋅⋅⋅+==奇 ()22246212n n n n a a S a a a a na ++=+++⋅⋅⋅+==偶 ()11=n n n n S S na na n a a nd ++-=-=-偶奇 11n n n n S na a S na a ++==奇偶2、当项数为奇数12+n 时,则21(21)(1)1n S S S n a S n a S n S S a S na S n +⎧=+=+=+⎧+⎪⎪⇒⇒=⎨⎨-==⎪⎪⎩⎩n+1n+1奇偶奇奇n+1n+1奇偶偶偶 (其中a n+1是项数为2n+1的等差数列的中间项). 1、等比数列的定义:()()*12,nn a q q n n N a -=≠≥∈0且,q 称为公比 2、通项公式:()11110,0n nn n a a a q q A B a q A B q-===⋅⋅≠⋅≠,首项:1a ;公比:q推广:n m n m n n n m m a a a q q q a --=⇔=⇔=3、等比中项:(1)如果,,a A b 成等比数列,那么A 叫做a 与b 的等差中项,即:2A ab =或A = 注意:同号的两个数才有等比中项,并且它们的等比中项有两个(两个等比中项互为相反数)(2)数列{}n a 是等比数列211n n n a a a -+⇔=⋅ 4、等比数列的前n 项和n S 公式:(1)当1q =时,1n S na = (2)当1q ≠时,()11111n n n a q a a qS qq--==-- 11''11n n n a aq A A B A B A q q=-=-⋅=---(,,','A B A B 为常数)5、等比数列的判定方法:(1)用定义:对任意的n ,都有11(0){}n n n n n na a qa q q a a a ++==≠⇔或为常数,为等比数列(2)等比中项:21111(0){}n n n n n n a a a a a a +-+-=≠⇔为等比数列 (3)通项公式:()0{}n n n a A B A B a =⋅⋅≠⇔为等比数列 6、等比数列的证明方法:依据定义:若()()*12,nn a q q n n N a -=≠≥∈0且或1{}n n n a qa a +=⇔为等比数列 7、等比数列的性质:(1)若*(,,,)m n s t m n s t N +=+∈,则n m s t a a a a ⋅=⋅。
等差数列及性质

等差数列及性质一、知识梳理:1.等差数列的定义(1)前提条件:①从第2项起.②每一项与它的前一项的差等于同一个常数.(2)结论:这个数列是等差数列.(3)相关概念:这个常数叫做等差数列的公差,常用字母d表示.2.等差中项(1)前提:三个数a,A,b成等差数列.(2)结论:A叫做a,b的等差中项.(3)满足的关系式:2A=a+b.34.等差数列通项公式的推广5.等差数列的性质(1){a n}是公差为d的等差数列,若正整数m,n,p,q满足m+n=p+q,则:a m+a n=a p+a q.特别地,当m+n=2k(m,n,k∈N*)时,a m+a n=2a k.(2)对有穷等差数列,与首末两项“等距离”的两项之和等于首末两项的和,即a1+a n =a2+a n-1=…=a k+a n-k+1=….(3)若{a n}是公差为d的等差数列,则①{c+a n}(c为任一常数)是公差为d的等差数列;②{ca n}(c为任一常数)是公差为cd的等差数列;③{a n+a n+k}(k为常数,k∈N*)是公差为2d的等差数列.(4)若{a n},{b n}分别是公差为d1,d2的等差数列,则数列{pa n+qb n}(p,q是常数)是公差为pd1+qd2的等差数列.(5).等差数列的图象由a n=d n+(a1-d),可知其图像是直线上的一些等间隔的点,其中是该直线的斜率.(6).等差数列的单调性:对于a n=d n+(a1-d),(1)当d>0时,{a n}为;(2)当d<0时,{a n}为;(3)当d=0时,{a n}为.二、题型探究:探究一:等差数列的通项公式及其应用例1.(1)已知等差数列{a n}:3,7,11,15,….①135,4m+19(m∈N*)是{a n}中的项吗?试说明理由.②若a p,a q(p,q∈N*)是数列{a n}中的项,则2a p+3a q是数列{a n}中的项吗?并说明你的理由.(2)在等差数列{a n}中,已知a5=10,a12=31,则首项a1=________,公差d=________.1.(1)若数列{a n }为等差数列,a p =q ,a q =p (p ≠q ),则a p +q =________.(2)已知等差数列{a n }中,a 15=33,a 61=217,试判断153是不是这个数列的项,如果是,是第几项?探究二:等差数列的判定例2.(1)已知函数f (x )=3xx +3,数列{x n }的通项由x n =f (x n -1)(n ≥2且x ∈N *)确定.①求证:⎩⎨⎧⎭⎬⎫1x n 是等差数列;②当x 1=12时,求x 2 015.(2)已知1b +c ,1c +a ,1a +b 成等差数列,证明:a 2,b 2,c 2也成等差数列.等差数列的判定方法有以下三种:(1)定义法:a n +1-a n =d (常数)(n ∈N *)⇔{a n }为等差数列; (2)等差中项法:2a n +1=a n +a n +2(n ∈N *)⇔{a n }为等差数列;(3)通项公式法:a n =an +b (a ,b 是常数,n ∈N *)⇔{a n }为等差数列. 但如果要证明一个数列是等差数列,则必须用定义法或等差中项法.2.(1)判断下列数列是否为等差数列:①在数列{a n }中a n =3n +2; ②在数列{a n }中a n =n 2+n .(2)已知c n =⎩⎪⎨⎪⎧1,n =1,2n -5,n ≥2,则数列{c n }________等差数列(填“是”或“不是”).(3)已知数列{a n }满足a 1=2,a n +1=2a n a n +2,则数列⎩⎨⎧⎭⎬⎫1a n 是否为等差数列?说明理由.探究三:等差中项的应用例3.一个等差数列由三个数组成,三个数的和为9,三个数的平方和为35,求这三个数.[互动探究]若将题中的三个数改为四个数成等差数列,且四个数之和为26,第二个数与第三个数之积为40,求这四个数.三个数或四个数成等差数列的设法当三个数或四个数成等差数列且和为定值时,方法一:可设出首项a1和公差d,列方程组求解.方法二:采用对称的设法,三个数时,设为a-d,a,a+d;四个数时,可设为a-3d,a-d,a+d,a+3d.3.(1)方程x2-6x+1=0的两根的等差中项为()A.1 B.2C.3 D.4(2)已知单调递增的等差数列{a n}的前三项之和为21,前三项之积为231,求数列{a n}的通项公式.探究四:等差数列性质的应用例4.在等差数列{a n}中:(1)若a5=a,a10=b,求a15;(2)若a3+a8=m,求a5+a6.(3)若a1+a2+…+a5=30,a6+a7+…+a10=80,求a11+a12+…+a15.(1)利用等差数列的通项公式列关于a1和d的方程组,求出a1和d,进而解决问题是处理等差数列问题的最基本方法.(2)巧妙地利用等差数列的性质,可以大大简化解题过程.4.(1)已知等差数列{a n }满足a 1+a 2+a 3+…+a 101=0,则有( ) A .a 1+a 101>0 B .a 2+a 101<0 C .a 3+a 99=0 D .a 51=51(2)若x ≠y ,且两个数列x ,a 1,a 2,y 和x ,b 1,b 2,b 3,y 各成等差数列,那么a 1-a 2b 1-b 2等于( )A .1 B.23C.34D.43探究五:等差数列的综合问题例5.在公差不为零的等差数列{a n }中,a 1,a 2为方程x 2-a 3x +a 4=0的根,求数列{a n }的通项公式.例6.在数列{a n }中,a 1=1,3a n a n -1+a n -a n -1=0(n ≥2,n ∈N *).(1)求证:数列⎩⎨⎧⎭⎬⎫1a n 是等差数列;(2)求数列{a n }的通项公式;(3)若λa n +1a n +1≥λ对任意n ≥2的整数恒成立,求实数λ的取值范围.5.(1)数列{a n }中,a 1=1,a 2=23,且1a n -1+1a n +1=2a n ,则a n =________.(2)已知数列{a n }满足(a n +1-a n )(a n +1+a n )=16,且a 1=1,a n >0.①求证:数列{a 2n }为等差数列; ②求a n .例7.已知等差数列{a n }的首项为a 1,公差为d ,且a 11=-26,a 51=54,求a 14的值.你能判断该数列从第几项开始为正数吗?[解] 由等差数列通项公式a n =a 1+(n -1)d ,列方程组⎩⎪⎨⎪⎧a 1+10d =-26,a 1+50d =54,解得⎩⎪⎨⎪⎧a 1=-46,d =2.∴a 14=-46+13×2=-20.∴a n =-46+(n -1)×2=2n -48. 令a n ≥0,得2n -48≥0⇒n ≥24, ∴从第25项开始,各项为正数.[错因与防范] (1)忽略了对“从第几项开始为正数”的理解,误认为n =24也满足条件.(2)由通项公式计算时,易把公式写成a n =a 1+nd ,导致结果错误.(3)等差数列通项公式中有a 1,a n ,n ,d 四个量,知三求一,一定要准确应用公式.7.(1)首项为24的等差数列,从第10项开始为负数,则公差d 的取值范围是________. (2)一个等差数列的首项为125,公差d >0,从第10项起每一项都大于1,求公差d 的范围.例8.(本题满分12分)两个等差数列5,8,11,…和3,7,11,…都有100项,那么它们共有多少相同的项?[解] 设已知的两数列的所有相同的项构成的新数列为{c n },c 1=11.2分 又等差数列5,8,11,…的通项公式为a n =3n +2,4分 等差数列3,7,11,…的通项公式为b n =4n -1.6分 所以数列{c n }为等差数列,且公差d =12,①8分 所以c n =11+(n -1)×12=12n -1.10分又a 100=302,b 100=399,c n =12n -1≤302,②得n ≤2514,可见已知两数列共有25个相同的项.12分[规范与警示] (1)解题过程中①处易出现令3n +2=4n -1,解得n =3的错误,这实际上是混淆了两个n 的取值而导致的错误,也是常犯错误,解题过程中②处易出现c n =12n -1≤399,导致错误.这是对题意不理解造成的,两个数列的公共项应以较小的为基准求解.(2)在解决数列的问题时弄清公式中各量的含义,不同的数列中同一量的意义是相同的,但是并不一定对应.如本例中项数n 在数列{a n }和数列{b n }中的意义,当项相同时,对应的序号n 不一定相同.巩固练习:1.(2015·汉口高二检测)下列说法中正确的是( )A .若a ,b ,c 成等差数列,则a 2,b 2,c 2成等差数列B .若a ,b ,c 成等差数列,则log 2a ,log 2b ,log 2c 成等差数列C .若a ,b ,c 成等差数列,则a +2,b +2,c +2成等差数列D .若a ,b ,c 成等差数列,则2a ,2b ,2c 成等差数列2.已知x ≠y ,且两个数列x ,a 1,a 2,…,a m ,y 与x ,b 1,b 2,…,b n ,y 各自都成等差数列,则a 2-a 1b 2-b 1等于( )A.m nB.m +1n +1C.n mD.n +1m +13.(2014·高考重庆卷)在等差数列{a n }中,a 1=2,a 3+a 5=10,则a 7=( ) A .5 B .8C .10 D .144.设{a n },{b n }都是等差数列,且a 1=25,b 1=75,a 2+b 2=100,则a 37+b 37=( ) A .0 B .37C .100 D .-37 5.(2014·高考辽宁卷)设等差数列{a n }的公差为d .若数列{2a 1a n }为递减数列,则( ) A .d <0B .d >0C .a 1d <0 D .a 1d >0 6.(2015·泰安高二检测)在等差数列{a n }中,a 3,a 10是方程x 2-3x -5=0的根,则a 5+a 8=________.7.(2015·河北省石家庄市月考)在等差数列{a n }中,若a 3+a 5+a 7+a 9+a 11=100,则3a 9-a 13的值为________.8.已知数列{a n }满足a 1=1,若点⎝ ⎛⎭⎪⎫a n n ,a n +1n +1在直线x -y +1=0上,则a n=________.9.已知△ABC 的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为________.10.在等差数列{a n }中,(1)已知a 5=-1,a 8=2,求a 1与d ; (2)已知a 1+a 6=12,a 4=7,求a 9.11.数列{a n }为等差数列,b n =⎝⎛⎭⎫12a n,又已知b 1+b 2+b 3=218,b 1b 2b 3=18,求{a n }的通项公式.12.已知数列{a n }满足a 1=4,a n =4-4a n -1(n >1),记b n =1a n -2.(1)求证:数列{b n }是等差数列;(2)求数列{a n }的通项公式.备选:《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共为3升,下面3节的容积共为4升,则第5节的容积为________升.巩固练习答案:1.解析:选C.因为a ,b ,c 成等差数列,则2b =a +c , 所以2b +4=a +c +4,即2(b +2)=(a +2)+(c +2), 所以a +2,b +2,c +2成等差数列.2.解析:选D.设这两个等差数列公差分别是d 1,d 2,则a 2-a 1=d 1,b 2-b 1=d 2.第一个数列共(m +2)项,∴d 1=y -x m +1;第二个数列共(n +2)项,∴d 2=y -x n +1.这样可求出a 2-a 1b 2-b 1=d 1d 2=n +1m +1. 3.解析:选B.法一:设等差数列的公差为d ,则a 3+a 5=2a 1+6d =4+6d =10,所以d =1,a 7=a 1+6d =2+6=8.法二:由等差数列的性质可得a 1+a 7=a 3+a 5=10,又a 1=2,所以a 7=8. 4.解析:选C.设c n =a n +b n ,由于{a n },{b n }都是等差数列,则{c n }也是等差数列,且c 1=a 1+b 1=25+75=100,c 2=a 2+b 2=100, ∴{c n }的公差d =c 2-c 1=0.∴c 37=100,即a 37+b 37=100.5.解析:选C.设b n =2a 1a n ,则b n +1=2a 1a n +1,由于{2a 1a n }是递减数列,则b n >b n +1,即2a 1a n >2a 1a n +1.∵y =2x 是单调增函数,∴a 1a n >a 1a n +1,∴a 1a n -a 1(a n +d )>0,∴a 1(a n -a n -d )>0,即a 1(-d )>0,∴a 1d <0.6.解析:由已知得a 3+a 10=3.又数列{a n }为等差数列,∴a 5+a 8=a 3+a 10=3. 答案:37.解析:由等差数列的性质可知,a 3+a 5+a 7+a 9+a 11=(a 3+a 11)+(a 5+a 9)+a 7=5a 7=100,∴a 7=20.∴3a 9-a 13=2a 9+a 9-a 13=(a 5+a 13)+a 9-a 13=a 5+a 9=2a 7=40.答案:408.解析:由题设可得a n n -a n +1n +1+1=0,即a n +1n +1-a n n =1,所以数列⎩⎨⎧⎭⎬⎫a n n 是以1为公差的等差数列,且首项为1,故通项公式a nn=n ,所以a n =n 2.答案:n 29.解析:由于三边长构成公差为4的等差数列,故可设三边长分别为x -4,x ,x +4. 由一个内角为120°,知其必是最长边x +4所对的角. 由余弦定理得,(x +4)2=x 2+(x -4)2-2x (x -4)·cos 120°, ∴2x 2-20x =0,∴x =0(舍去)或x =10, ∴S △ABC =12×(10-4)×10×sin 120°=15 3.答案:15 310.解:(1)∵a 5=-1,a 8=2,∴⎩⎪⎨⎪⎧a 1+4d =-1a 1+7d =2,解得⎩⎪⎨⎪⎧a 1=-5d =1. (2)设数列{a n }的公差为d .由已知得,⎩⎪⎨⎪⎧a 1+a 1+5d =12a 1+3d =7,解得⎩⎪⎨⎪⎧a 1=1d =2.∴a n =1+(n -1)×2=2n -1,∴a 9=2×9-1=17.11.解:∵b 1+b 2+b 3=⎝⎛⎭⎫12a 1+⎝⎛⎭⎫12a 2+⎝⎛⎭⎫12a 3=218,b 1b 2b 3=⎝⎛⎭⎫12a 1+a 2+a 3=18,∴a 1+a 2+a 3=3. ∵a 1,a 2,a 3成等差数列,可设a 1=a 2-d ,a 3=a 2+d ,∴a 2=1. 由⎝⎛⎭⎫121-d+12+⎝⎛⎭⎫121+d =218,得2d +2-d =174,解得d =2或d =-2. 当d =2时,a 1=1-d =-1,a n =-1+2(n -1)=2n -3;当d =-2时,a 1=1-d =3,a n =3-2(n -1)=-2n +5. 12.解:(1)证明:b n +1-b n =1a n +1-2-1a n -2=1(4-4a n)-2-1a n -2=a n 2(a n -2)-1a n -2=a n -22(a n -2)=12.又b 1=1a 1-2=12,∴数列{b n }是首项为12,公差为12的等差数列.(2)由(1)知b n =12+(n -1)×12=12n .∵b n =1a n -2,∴a n =1b n +2=2n +2.∴数列{a n }的通项公式为a n =2n+2.备选:解析:设自上而下各节的容积构成的等差数列为 a 1,a 2,a 3,a 4,a 5,a 6,a 7,a 8,a 9.则⎩⎪⎨⎪⎧a 1+a 2+a 3+a 4=4a 1+6d =3,a 7+a 8+a 9=3a 1+21d =4.解得⎩⎨⎧a 1=1322,d =766,故a 5=a 1+4d =6766. 答案:67667(1)解析:a n =24+(n -1)d ,由题意知,⎩⎪⎨⎪⎧a 10<0,a 9≥0,即⎩⎪⎨⎪⎧24+9d <0,24+8d ≥0,解得-3≤d <-83.答案:⎣⎡⎭⎫-3,-83 (2)解:设等差数列为{a n },由d >0,知a 1<a 2<…<a 9<a 10<a 11…,依题意,有⎩⎪⎨⎪⎧1<a 10<a 11<…,a 1<a 2<…<a 9≤1,即⎩⎪⎨⎪⎧a 10>1a 9≤1⇔⎩⎨⎧125+(10-1)d >1,125+(9-1)d ≤1,解得875<d ≤325,即公差d 的取值范围是⎝⎛⎦⎤875,325.。
等差数列知识点归纳总结

等差数列知识点归纳总结等差数列(ArithmeticSequence)是指一组有序的满足规定的数据,通常按公差d(即每一项与其前一项的差值)来进行排列,即形如a1,a1+d,a1+2d,a1+3d.....an-1,an的数列,其中a1是等差数列的第一项,d是等差数列的公差,而an是等差数列最后一项。
二、等差数列的性质1、如果等差数列的公差不为0,则等差数列中任意两项的差值均相等,即d=a2-a1=a3-a2=a4-a3=....an-1-an-2=an-an-1;2、如果等差数列的公差为0,则等差数列的所有数据均相等,即a1=a2=a3=...=an-1=an;3、等差数列的每一项与等差数列的第一项和项数都有关,即a3=a1+2d,a4=a1+3d......an=a1+(n-1)d;4、等差数列的和 Sn=a1+a2+a3+....an-1+an=n/2(a1+an);5、等差数列中任一项的平方和与项数有关,即a1^2+a2^2+a3^2+...+an^2=n(2a1a2+(n-1)d^2)/3;三、等差数列的特殊性质1、等差数列的四项和等差数列a1,a2,...,an中任意四项的和都是一定的,即a1+a2+a3+a4=a2+a3+a4+a5=......an-3+an-2+an-1+an;2、等差数列的两项之积等差数列a1,a2,...,an中任意两项的乘积也是一定的,即a1×a2=a2×a3=......an-1×an;3、等差数列的总和等差数列的总和Sn=a1+a2+a3+......an-1+an可表示为n/2(a1+an),即Sn=n/2(首项与末项的和);四、等差数列的运用1、求等差数列的某一项如果给出等差数列的首项和公差,通过公式a3=a1+2d,a4=a1+3d,...,an=a1+(n-1)d可以计算出第n项的值;2、求等差数列的和等差数列的和Sn=a1+a2+a3+....an-1+an=n/2(a1+an),如果给出等差数列的首项和末项,则可以通过公式求出等差数列的和;3、求等差数列的任意项之和如果要求等差数列从a1到an的和,可以通过Sn=n/2(a1+an)求解;4、求等差数列某两项之和如果要求等差数列从a1到an的和,可以通过Sn=n/2(a1+an)求解,如果要求从第m项到第n项的和,可以使用公式S(m,n)=n/2(am+an);五、等差数列的应用1、等差数列应用于等额本息贷款等额本息是指在贷款到期时,贷款本息全部偿还,每期还款数相等,比较为常见的一种贷款形式,它的特点是本金渐渐减少,利息渐渐减少,每期还款金额相等。
等差数列知识点总结和题型总结

等差数列知识点总结与题型归纳
一.等差数列知识点:
知识点 1、等差数列的定义:
①如果一个数列从第 2 项起,每一项与它的前一项的差等于同一个常数,那么
这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母 d 表示
知识点 2、等差数列的判定方法:
②定义法:对于数列an ,若 an1 an d (常数),则数列an 是等差数列
n
项和,求使得 Tn
m 20
对所有 n N 都成立的
最小正整数 m
6
关注公众号“品数学”,获取更多干货!
五、等差数列习题精选
1、等差数列{an}的前三项依次为 x , 2x 1 , 4x 2 ,则它的第 5 项为( )
A、 5x 5
B、 2x 1
C、5
D、4
2、设等差数列{an}中, a4 5, a9 17 ,则 a14 的值等于( )
1
关注公众号“品数学”,获取更多干货!
也就是: a1 an a2 an1 a3 an2
⑨若数列 an 是等差数列, Sn 是其前 n 项的和, k N * ,那么 Sk , S2k Sk ,
S3k S2k 成等差数列 如下图所示:
S3k a1 a2 a3 ak ak 1a2k a2k1a3k
11、在等差数列an 中, a2 a8 4 ,则 其前 9 项的和 S9 等于 ( )
A.18
B 27
C 36
D9
12、设等差数列{an} 的前 n 项和为 Sn ,若 S3 9 , S6 36 ,则 a7 a8 a9 ( )
A.63
B.45
C.36
D.27
13、在等差数列 an 中, a1 a2 a3 15, an an1 an2 78 , Sn 155 ,
(完整版)等差数列知识点总结及练习(精华版)

等差数列的性质总结1.等差数列的定义:(d 为常数)();d a a n n =--12≥n 2.等差数列通项公式:, 首项:,公差:d ,末项:*11(1)()n a a n d dn a d n N =+-=+-∈1a n a 推广: . 从而;d m n a a m n )(-+=mn a a d mn --=3.等差中项(1)如果,,成等差数列,那么叫做与的等差中项.即:或a A b A a b 2ba A +=b a A +=2(2)等差中项:数列是等差数列{}n a )2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a 4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+特别地,当项数为奇数时,是项数为2n+1的等差数列的中间项21n +1n a +5.等差数列的判定方法(1) 定义法:若或(常数) 是等差数列. d a a n n =--1d a a n n =-+1*∈N n ⇔{}n a (2) 等差中项:数列是等差数列. {}n a )2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a (3) 数列是等差数列(其中是常数)。
{}n a ⇔b kn a n +=b k ,(4) 数列是等差数列,(其中A 、B 是常数)。
{}n a ⇔2n S An Bn =+6.等差数列的证明方法定义法:若或(常数) 是等差数列.d a a n n =--1d a a n n =-+1*∈N n ⇔{}n a 7.提醒:等差数列的通项公式及前n 项和公式中,涉及到5个元素:,其中n a n S n n S a n d a 及、、、1称作为基本元素。
只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2.d a 、18. 等差数列的性质:(1)当公差时,0d ≠等差数列的通项公式是关于的一次函数,且斜率为公差;11(1)n a a n d dn a d =+-=+-n d 前和是关于的二次函数且常数项为0.n 211(1)(222n n n d dS na d n a n -=+=+-n (2)若公差,则为递增等差数列,若公差,则为递减等差数列,若公差,则为常数列。
等差数列知识点总结

等差数列知识清单1、等差数列定义:一般地,如果一个数列从第项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,公差通常用字母表示。
用递推公式表示为或。
根据定义,当我们看到形如:、、、、时,应能从中得到相应的等差数列。
等差数列的判定方法1. 定义法:若或(常数) 是等差数列.2.等差中项:数列是等差数列.3.数列是等差数列(其中是常数)。
4.数列是等差数列,(其中A、B是常数)。
等差数列的证明方法定义法:若或(常数) 是等差数列.例1.设S n是数列{a n}的前n项和,且S n=n2,则{a n}是()A.等比数列,但不是等差数列B.等差数列,但不是等比数列C.等差数列,而且也是等比数列D.既非等比数列又非等差数列2.等差数列通项公式:, 首项:,公差:d,末项:推广: . 从而;等差数列的通项公式是关于的一次函数,且斜率为公差;说明:等差数列(通常可称为数列)的单调性:为递增数列,为常数列, 为递减数列。
例2.等差数列{a n}中,已知a1=,a2+a5=4,a n=33,则n为( ) A.48 B.49 C.50 D.51如(1)等差数列中,,,则通项 ;(2)首项为-24的等差数列,从第10项起开始为正数,则公差的取值范围是______ ;例3.设{a n}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,则a11+a12+a13等于()A.120B.105C.90D.75例4:已知数列{a n}为等差数列,若<-1,且它们的前n项和S n有最大值,则使S n>0的n的最大值为( )A.11 B.19 C.20 D.211..已知数列{a n}的前n项和S n=n(n-40),则下列判断正确的是( )A.a19>0,a21<0B.a20>0,a21<0C.a19<0,a21>0D.a19<0,a20>02.若数列{a n}的前n项和S n=n2-10n(n=1,2,3,…),则此数列的通项公式为_______________;数列{na n}中数值最小的项是第_______项.3.等差中项(1)如果,,成等差数列,那么叫做与的等差中项.即:或. (2)等差中项:数列是等差数列.例5.“公差为0的等差数列是等比数列”;“公比为的等比数列一定是递减数列”;“a,b,c三数成等比数列的充要条件是b2=ac”;“a,b,c三数成等差数列的充要条件是2b=a+c”,以上四个命题中,正确的有()A.1个 B.2个 C.3个 D.4个1.已知1,a,b成等差数列,3,a+2,b+5成等比数列,则等差数列的公差为( )A.3或-3 B.3或-1 C.3 D.-32.在等差数列中,,则的值为( )(A)5 (B) 6 (C)8 (D)103 已知{a n}为等差数列,若a1+a5+a9=π,则cos(a2+a8)的值为________________.4、等差数列的前和的求和公式:(其中A、B是常数,所以当d≠0时,S n是关于n的二次式且常数项为0)特别地,当项数为奇数时,是项数为2n+1的等差数列的中间项(项数为奇数的等差数列的各项和等于项数乘以中间项)前和是关于的二次函数且常数项为0.例6:等差数列{a n}的前n项和记为S n,若a2+a4+a15的值是一个确定的常数,则数列{S n}中也为常数的项是( )A.S7 B.S8 C.S13 D.S15例7:设S n是等差数列{a n}的前n项和,a12=-8,S9=-9,则S16=________.1.等差数列{a n}中,S n是其前n项和,a1=-2010,-=2,则S2010的值为________.2. 设{}为等差数列,公差d = -2,为其前n项和.若,则=()A.18B.20C.22D.243 数列 中,,,前n项和,则=_,=_4已知数列 的前n项和,求数列的前项和5设等差数列{a n}的前n项和为S n,且a3+a7-a10=8,a11-a4=4,则S13等于()A.168B.156C.78D.1526.在各项均不为零的等差数列{a n}中,若a n+1-a n2+a n-1=0(n≥2),则S2n-1-4n等于…()A.-2B.0C.1D.25、等差数列的性质:(1)在等差数列中,从第2项起,每一项是它相邻二项的等差中项;(2)在等差数列中,相隔等距离的项组成的数列是等差数列, 如:,,,,……;,,,,……;(3)在等差数列中,对任意,,,;(4)在等差数列中,若,,,且,则;特别地,当时,则有,注:,(1)等差数列中,,则=____设数列是等差数列,且公差为,(Ⅰ)当项数为偶数时,(Ⅱ)当项数为奇数时,则(其中是项数为2n+1的等差数列的中间项).1 在等差数列中,S11=22,则=______2 项数为奇数的等差数列中,奇数项和为80,偶数项和为75,求此数列的中间项与项数3 .已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )A.5B.4C.3D.26、在等差数列中,有关的最值问题(1)邻项变号法① 当 、时,满足 的项数使得取最大值.② 当 、时,满足 的项数使得取最小值.(2)利用(时,是关于的二次函数)进行配方(注意应取正整数)(1)等差数列中,,,问此数列前多少项和最大?并求此最大值。
等差数列的知识点总结

等差数列的知识点总结一、概念等差数列是由一系列按照相同的公差递增或递减的数字所组成的数列。
如果一个数列 a1, a2, a3, ... , an 满足a2 - a1 = a3 - a2 = ... = an - a(n-1)那么这个数列就是等差数列,其中 a1 为首项,a2 - a1 为公差。
例如,3, 6, 9, 12, 15 就是一个等差数列,其中首项为3,公差为3。
二、性质1. 通项公式等差数列的第 n 项 a_n 可以用通项公式表示为a_n = a1 + (n-1)d其中 a1 为首项,d 为公差。
2. 数列求和等差数列的前 n 项和 Sn 可以用求和公式表示为Sn = n/2 * (a1 + an)或Sn = n/2 * (2a1 + (n-1)d)其中 a1 为首项,d 为公差,an 为第 n 项。
3. 任意三项对于等差数列中的任意三项 a_i, a_j, a_k(i < j < k),有2a_j = a_i + a_k这个性质可以用来解决很多等差数列的问题。
4. 求和公式的推导为了理解等差数列求和公式的推导,我们来考虑一个等差数列的和 S_n = a_1 + a_2 + ... + a_n。
如果我们将这个数列反向写,即 S_n = a_n + a_(n-1) + ... + a_1,那么两个数列相加得到的和是2S_n = (a_1 + a_n) + (a_2 + a_(n-1)) + ... + (a_n + a_1)由于等差数列中任意三项的性质,我们知道其中每一对括号内的和都是相等的,所以有2S_n = (a_1 + a_n) + (a_1 + a_n) + ... + (a_1 + a_n) = n * (a_1 + a_n)从而得到了等差数列求和公式。
三、应用等差数列在数学和实际生活中都有着广泛的应用。
在数学中,等差数列的求和公式可以用来解决许多数学问题,比如计算前 n 项的和。
(完整版)等差数列知识点总结

(完整版)等差数列知识点总结1. 等差数列的定义等差数列是指一个数列中,从第二项开始,每一项与它的前一项之差都相等的数列。
2. 等差数列的通项公式设等差数列的首项为 a1,公差为 d,则第 n 项的通项公式为 an = a1 + (n - 1) * d。
3. 等差数列的前 n 项和公式设等差数列的首项为 a1,末项为 an,项数为 n,公差为 d,则前 n 项的和公式为 Sn = n * (a1 + an) / 2。
4. 判断数列是否为等差数列- 检查数列中连续两项的差是否相等,即是否满足等差数列的定义。
- 可以通过计算数列的前 n 项和是否满足 Sn = n * (a1 + an) / 2 来判断。
5. 求等差数列的公差设等差数列的首项为 a1,第二项为 a2,则公差可以通过计算差值 d = a2 - a1 获得。
6. 求等差数列的项数设等差数列的首项为 a1,末项为 an,公差为 d,则项数可以通过以下公式计算:n = (an - a1 + d) / d。
7. 求等差数列的首项设等差数列的第一项为 a1,公差为 d,已知项数为 n,末项为an,则首项可以通过以下公式计算:a1 = an - (n - 1) * d。
8. 求等差数列的末项设等差数列的首项为 a1,公差为 d,已知项数为 n,末项可以通过以下公式计算:an = a1 + (n - 1) * d。
9. 等差数列的性质- 等差数列的任意三项成等差数列。
- 等差数列中的取任意几项可以组成一个等差数列。
- 等差数列的平均数等于首项与末项的平均数。
10. 应用场景等差数列的应用非常广泛,常见的应用场景包括:- 数学题中的数列问题,如求和、推导等。
- 统计学中的数据分析,如平均数、标准差等。
- 金融学中的投资计算,如等额本息还款、定期存款等。
- 工程学中的时间序列分析,如温度变化、电压波动等。
以上是等差数列的一些重要知识点总结,希望能对你有所帮助!。
等差数列知识点归纳总结

等差数列知识点归纳总结等差数列是数学中常见的一种数列形式,具有重要的应用价值。
本文将针对等差数列的定义、通项公式、求和公式以及应用进行归纳总结。
一、等差数列的定义等差数列是指数列中后一项与前一项之差始终相等的一种特殊数列。
用常数d表示公差,那么等差数列可以表示为:a₁, a₁+d, a₁+2d,a₁+3d, ...二、等差数列的通项公式等差数列通项公式是指通过已知的首项和公差,计算数列中第n项的公式。
假设首项为a₁,公差为d,则等差数列的通项公式为:an =a₁ + (n-1)d三、等差数列的求和公式等差数列求和公式是指通过已知的首项、末项和项数,计算数列所有项之和的公式。
假设首项为a₁,末项为an,项数为n,则等差数列的求和公式为:Sn = (n/2)(a₁+an)四、等差数列的性质1. 等差数列的任意三项成一等差数列。
2. 等差数列的任意两项之和与中间项的和相等。
3. 等差数列的任意相邻两项之和相等。
4. 等差数列的对称性:数列中的相等距离的项之和相等。
五、等差数列的应用等差数列广泛应用于数学、物理、经济等领域,以下是一些常见的应用场景:1. 金融贷款:假设每月还款金额等差递增,可利用等差数列求得贷款总额和还款期限。
2. 平均速度问题:假设行程中速度等差减小,可利用等差数列求得平均速度。
3. 等差数列的和与平均数关系:等差数列的和即为等差数列所有项的平均数乘以项数。
4. 数列排序问题:对于给定的一组数据,若满足等差关系,可通过等差数列的求和公式快速求得该数列的和。
六、等差数列的扩展1. 差数列:每一项与其后一项之差构成的数列。
2. 等差中项:等差数列中,若某项的前后两项之和为定值,该项称为等差数列的中项。
总结:本文对等差数列的定义、通项公式、求和公式进行了详细介绍,并归纳了其性质和应用场景。
了解等差数列的相关知识,对于解决实际问题及培养数学思维能力都具有重要的帮助。
希望读者通过本文的阅读,对等差数列有更深入的理解。
知识点归纳总结等差数列

知识点归纳总结1.等差数列2. 等比数列【例题精讲】【1】在等差数列}{n a 中,已知1684=+a a ,则该列前11项和=11S ( )A.58B.88C.143D.176答案:B【2】已知}{n a 为等差数列,若π=++951a a a ,则)cos(82a a +的值为( )A.21-B.23-C.21 D.23 答案:B【3】已知等差数列}{n a 的前n 项和为n S ,且3184=S S ,则=168S S ( ) A.81B.31 C.91 D.103 答案:C【4】已知等差数列}{n a 的前n 项和为n S ,且2211=S ,则2113a a +等于( )A.2B.4C.8D.16答案:C【5】已知等差数列}{n a 中,8,242==a a ,若13-=n a n b ,则2013b 等于( )A.2011B.2012C.2013D.2014答案:D【6】已知}{n a 为等差数列,99,105642531=++=++a a a a a a ,以n S 表示}{n a 的前n 项和,则使得n S 达到最大值的n 是( )A.21B.20C.19D.18答案:B【7】已知}{n a 为等差数列,若167-<a a ,且它们的前n 项和n S 有最大值,则使0>n S 的n 的最大值为 答案:11【8】设n S 是公差为)0(≠d d 的无穷等差数列}{n a 的前n 项和,则下列命题错误的是( )A.若0<d ,则数列}{n S 有最大项B.若数列}{n S 有最大项,则0<dC.若数列}{n S 是递增数列,则对任意*N n ∈,均有0>n S D.若对任意*N n ∈,均有0>n S ,则有数列}{n S 是递增数列答案:C【10】公比为q 的等比数列}{n a 的各项为正数,且7log ,1610122==a a a q ,则公比=q 答案:2【11】设等比数列}{n a 的前n 项和为n S ,若20103,201032011201220122013+=+=S a S a ,则公比=q ( )A.4B.41或C.2D.21或答案:A【12】在等比数列}{n a 中,已知24,21,64a a 成等比数列且6453=⋅a a ,则}{n a 的前8项和为 . 答案:85255或【13】设等比数列{}n a 的前n 项和为n S ,若633S S =,则96SS =( )A.2B.37 C.38D.3答案:B【14】已知{}n a 是首项为1的等比数列,n S 是{}n a 的前项和,且369S S =,则数列1n a ⎧⎫⎨⎬⎩⎭的前5项和为( )A.1631 B.51631或 C.5815或 D.815 答案:A【15】公比不为1的等比数列}{n a 的前n 项和为n S ,且321,,3a a a --成等差数列,若11=a ,则=4S ( ) A.20- B.0C.7D.40答案:A【16】各项都是正数的等比数列}{n a ,若132,21,a a a 成等差数列,则5443a a a a ++的值是( ) A.215+ B.215-C.251- D.215+或215- 答案:B【17】已知正项等比数列}{n a 满足12011201220134,2a a a a a a n m =⋅+=且,则)11(6nm +的最小值为 . 答案:4递推数列:数列}{n a 的任一项n a 与它前一项1-n a (或它的前几项)间关系用一个公式表示.专题:数列通项公式及求和一. 常规数列的通项与求和方法:定义法(利用等差数列、等比数列的通项与求和公式来求)1. 等差数列:<1>通项公式:*1(1)(),,n m a a n d a n m d n m N =+-=+-∈<2>求和公式:11()(1)22n n n a a n n S na d +-==+ 2. 等比数列:<1>通项公式:11,0n n mn m a a q a q q --=⋅=⋅≠<2>求和公式:11(1)(1)(1)1n n na q S a q q q =⎧⎪=-⎨≠⎪-⎩3. 一些常见的数列求和公式222221(1)(21)1236nk n n n k n =++=++++=∑2333331(1)1232nk n n kn =+⎡⎤=++++=⎢⎥⎣⎦∑【例1】已知等差数列{}n a 满足466,10a a ==. (1) 求数列{}n a 的通项公式;(2) 设等比数列{}n b 各项均为正数,其前n 项和n T ,若3232,7,n a b T T =+=求.【例2】已知{}n a 是等比数列,12,a =且134,1,a a a +成等差数列. (1) 求数列{}n a 的通项公式;(2) 若2log n n b a =,求数列{}n b 的前n 项和n S .二. 非常规数列的通项公式常用通项公式的求法有四种:求法1:累加法适用于1()n n a a f n +=+型.特点:递推公式关于相邻两项的关系且系数、幂数都相同.【例3】已知数列{}n a 满足112313nn n a a a +=+⨯+=,,求数列{}n a 的通项公式.【例4】已知数列{}n a 满足*11221,2,,2n n n a a a a a n N +++===∈ (1) 令1n n n b a a +=-,证明:{}n b 是等比数列; (2) 求{}n a 通项公式.求法2:累乘法适用于1()n n a a f n +=⋅型特点:递推公式是关于相邻两项商的关系,且商()f n 是可求数列.【例6】已知数列{}n a 满足321=a ,n n a n n a 11+=+,求n a .求法3:公式法现象:题目中出现n a 与n S 的关系式. 解决:利用1n n n a S S -=-求解.【例7】已知数列{}n a 满足:*1()n n S a n N =-∈,其中n S 为数列{}n a 的前n 项和.求n a .【同类演练】例15第一问求法4:构造法类型1:构造等比数列凡是出现关于后项和前项的一次递推形式的现象都可以构造等比. 现象1:1,(,)n n a pa q p q +=+为常数【例8】已知数列{}n a 中,111,21(2)n n a a a n -==+≥,求数列{}n a 的通项公式.【同类演练】例18第一问现象2:1(,nn n a pa q p q +=+为常数)【例9】已知数列{}n a 中,111511,()632n n n a a a ++==+,求n a .【同类演练】例17第一问现象3:1(),n n a pa f n p +=+为常数【例10】已知数列{}n a 满足21123451n n a a n n a +=+++=,,求数列{}n a 的通项公式.现象4:21,(,)n n n a pa qa p q ++=+为常数【例11】已知数列{}n a 满足*12211,3,32().n n n a a a a a n N ++===-∈求n a .类型2:构造等差数列题目中出现后项与前项分式递推形式可以构造等差. 解决办法:取倒数【例12】已知在数列{}n a 中*111,()21nn n a a a n N a +==∈+.(1) 求数列{}n a 的通项公式; (2) 若13521211,(1)(1)(1)(1)n n n nP b b b b b a -=+=++++,求证:n P >三. 非常规数列的求和常用的求和方法一般有四种: 方法1:裂项相消法把数列的通项拆成两项之差,在求和时中间项可以相互抵消,从而求得其和. 常见的拆项公式有:(1)111)1(1+-=+n n n n ;(2)1111()()n n k k n n k =-++(3))121121(21)12)(12(1+--=+-n n n n(4(5)!)!1(!n n n n -+=⋅ (6)11log log log n n n na a a a ++=- 、【例13】(2011新课标)等比数列{}n a 的各项均为正数,且212326231,9.a a a a a +==(1)求数列{}n a 的通项公式;(2)设 31323log log ......log ,n n b a a a =+++求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和【例14】等差数列{}n a 中211a =,32624a a a =+-,其前n 项和为n S .(1) 求数列{}n a 的通项公式;(2) 设数列{}n b 满足111n n b S +=-,其前n 项和为n T ,求证:*3()4n T n N <∈.【例15】已知数列{}n a 的前n 项和*1,1,(1)()n n n S a S na n n n N ==--∈. (1) 求数列{}n a 的通项公式;(2) 设12n n n b a a +=,求数列{}n b 的前前n 项和为n T .方法2:错位相减法适用于由一个等差数列和一个等比数列构成对应项之积构成的数列求和.即{}{}1122,,.n n n n n a b a b a b a b S +++等差等比求的和 解题步骤:(1)1122n n n S a b a b a b =+++,将式子两边同时乘以{}n b 的公比q ,得到n qS .(2)用n n qS S -(3)利用等比数列求和公式求解.【例16】(2011辽宁理)已知等差数列{}n a 满足2680,10a a a =+=-.(1) 求数列{}n a 的通项公式;(2) 求数列1{}2nn a -的前n 项和.【例17】已知数列{}n a 满足*1112,2()2n n n a a a n N +==-∈(1) 求证:数列{}2nn a 是等差数列;(2) 求数列{}n a 的前n 项和n S .【例18】已知数列{}n a 的前n 项和2*4()n S n n n N =+∈,数列{}n b 满足111,21n n b b b +==+.(1) 求数列{}n a ,{}n b 的通项公式;(2) 设(3)(1)4n n n a b c -+=,求数列{}n c 的前n 项和n T ..方法3:分组求和法适用于可以将数列适当拆开,分为几个等差,等比或常见的数列,先分别求和,然后在合并,形如:{},{}{}n n n n a b a b +其中为等差数列,为等比数列【例19】已知数列等差数列{}n a 满足:5269,14a a a =+=.(1) 求数列{}n a 的通项公式;(2) 若2n an n b a =+,求数列{}n b 的前n 项和n S ..方法4:倒序相加法如果一个数列{}n a ,与首末位置等“距离”的两项和相等,那么这个数列可以采用倒序来求和.一般使用于组合数列与等差数列求和.【例20】已知a xy =lg ,n n n n n y y x y x x S lg lg lg lg 221++++=-- (0>x 、0>y )求n S已知递增等比数列}{n a ,公比为q ,满足28432=++a a a ,且23+a 是42,a a 的等差中项.(1) 求数列}{n a 的通项公式;(2) 若n n n n n b b b b S a a b ++++== 32121,log ,求使5021>⋅++n n n S 成立的正整数n 的最小值.已知数列{}n a 为等差数列,n a 为正整数,其前n 项和为n S ,数列{}n b 为等比数列,且13a =,11b =,数列{}n a b 是公比为64的等比数列,2264b S =(1)求n a ,n b ;(2)求证:1211134+++<n S S S在数列}{n a 中,n n n n a n a a 21)11(,111+++==+ (1)设na b n n =,求数列}{n b 的通项公式; (2)求数列}{n a 的前n 项和nS已知数列}{n a 的前n 项和 ,3,2,1,4232=+⋅-=n a S n n n .(1) 求数列}{n a 的通项公式;(2) 设n T 为数列}4{-n S 的前n 项和,求⋅n T。
等差数列知识点总结

等差数列知识点总结等差数列是数学中常见且重要的一个概念。
在数列中,如果相邻的两项之间的差值都相等,那么这个数列就是等差数列。
等差数列有很多应用,例如在数学、物理、工程等领域中都能见到它的身影。
本文将对等差数列的定义、常见知识点以及一些定理进行总结。
1. 等差数列的定义等差数列是指数列中每一项与它的前一项之差都相等的数列。
设数列A的公差为d,首项为a₁,则数列A的通项公式为:aₙ = a₁ + (n-1) * d其中,aₙ为数列A的第n项,n为项数。
2. 前n项和公式等差数列的前n项和公式是指数列前n项的和。
设数列A的首项为a₁,公差为d,数列的前n项和为Sn,那么有如下公式:Sn = (n/2)(a₁ + aₙ)其中,n为项数,aₙ为数列A的第n项。
3. 等差数列的性质(1) 通项公式的推导:设数列A的首项为a₁,公差为d,根据等差数列的定义,可以得到递推公式:aₙ = aₙ₋₁ + d。
通过数学归纳法可以证明等差数列的通项公式为aₙ = a₁ + (n-1) * d。
(2) 首项与末项求和:等差数列的首项与末项之和等于所有项之和的一半,即a₁ + aₙ = Sn/2。
(3) 任意三项求和:对于等差数列中的任意三项aᵢ、aₙ、aₙ,其和满足如下关系:aᵢ + aₙ + aₙ = 3a〈(i+j+k)/3〉,其中,a〈(i+j+k)/3〉表示等差数列中下标为⌈(i+j+k)/3⌉的项。
(4) 项数与公差求和:对于等差数列,项数与公差的乘积等于数列中所有项的和与项数之积减去首项,即n * d = Sn - a₁。
4. 等差数列的常见定理(1) 等差中项定理:在等差数列中,任意三项构成的两个连续子列之和相等。
即对于等差数列中的任意三项aᵢ、aₙ、aₙ,有aᵢ + aₙ =2a〈(i+j)/2〉。
(2) 等差数列的均值定理:等差数列的任意k项的和与这k项的平均值之积等于这k项中间项的平方,即aᵢ + aᵢ₊₁ + ... + aₙ = (j-i+1)a〈(i+j)/2〉。
等差数列知识点总结

等差数列1. 定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
用递推公式表示为d a a n n =--1(d 为常数)(2≥n );2.等差数列通项公式:(1)*11(1)()n a a n d dn a d n N =+-=+-∈(首项:1a ,公差:d ,末项:n a )(2)d m n a a m n )(-+=. 从而mn a a d mn --=; 3.等差中项(1)如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即:2b a A +=或b a A +=2(2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a4.等差数列的前n 项和公式:1()2n n n a a s +=1(1)2n n na d -=+ 211()22d n a d n =+- 2An Bn =+(其中A 、B 是常数) (当d ≠0时,S n 是关于n 的二次式且常数项为0)5.等差数列的证明方法(1) 定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列. (2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a .(3)数列{}n a 是等差数列⇔b kn a n +=(其中b k ,是常数)。
(4)数列{}n a 是等差数列⇔2n S An Bn =+,(其中A 、B 是常数)。
注:(1)等差数列的通项公式及前n 和公式中,涉及到5个元素:1a 、d 、n 、n a 及n S ,其中1a 、d 称作为基本元素。
只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
(2)为减少运算量,要注意设元的技巧,如奇数个数成等差,可设为…,2,,,,2a d a d a a d a d --++…(公差为d );偶数个数成等差,可设为…,3,,,3a d a d a d a d --++,…(公差为2d )7.等差数列的性质:(1)当公差0d ≠时,等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函数,且斜率为公差d ;前n 和211(1)()222n n n d dS na d n a n -=+=+-是关于n 的二次函数且常数项为0.(2)若公差0d >,则为递增等差数列,若公差0d <,则为递减等差数列,若公差0d =,则为常数列。
总结等差数列知识点归纳

总结等差数列知识点归纳等差数列是数学中常见且重要的概念,它在很多领域都有着广泛的应用。
通过对等差数列的学习和理解,我们可以更好地掌握数列的性质和特点,进一步深入研究数学问题。
下面将总结等差数列的知识点,归纳为以下几个方面。
一、等差数列的定义和性质1. 等差数列的定义:等差数列是指一个数列中,从第二项开始,每一项与它的前一项的差都相等。
2. 等差数列的通项公式:设等差数列的首项为a₁,公差为d,第n项为aₙ,则等差数列的通项公式为:aₙ=a₁+(n-1)d。
3. 等差数列的前n项和公式:设等差数列的首项为a₁,公差为d,前n项和为Sₙ,则等差数列的前n项和公式为:Sₙ=(a₁+aₙ)×n/2。
二、求等差数列的项数和公差1. 已知首项和末项求项数:设等差数列的首项为a₁,末项为aₙ,项数为n,则项数n可由公式n=(aₙ-a₁)/d+1求得。
2. 已知首项和项数求末项:设等差数列的首项为a₁,公差为d,项数为n,则末项aₙ可由公式aₙ=a₁+(n-1)d求得。
3. 已知首项和公差求项数:设等差数列的首项为a₁,公差为d,末项为aₙ,则项数n可由公式n=(aₙ-a₁)/d+1求得。
4. 已知首项和末项求公差:设等差数列的首项为a₁,末项为aₙ,公差为d,则公差d可由公式d=(aₙ-a₁)/(n-1)求得。
三、常见问题实例分析1. 求等差数列的和:根据前n项和的公式Sₙ=(a₁+aₙ)×n/2,即可求得等差数列的前n项和。
2. 求等差数列中某一项的值:根据等差数列的通项公式aₙ=a₁+(n-1)d,将对应的n值代入,即可求得所需项的值。
3. 求等差数列中第一次出现满足某条件的项数:根据等差数列的通项公式aₙ=a₁+(n-1)d,代入满足条件的项的值,解方程即可求得。
四、应用领域实例展示1. 数学中的应用:等差数列广泛应用于数学中的数列求和、方程求解、数值推测等问题,帮助我们更好地理解和解决数学难题。
等差数列知识总结

1等差数列知识要点总结(务必用熟)一.概念;1、定义一般地,如果一个数列从第二项起,每一项与前一项的差是同一个常数.....,称这样的数列为等差数列,这个常数为等差数列的公差,通常用字母d 表示。
即1()n n a a d n N *+-=∈2、通项公式:①:1(1)n a a n d =+-,1a 为首项,d 为公差(二者是等差数列的基础项) 推广:②:()(,)n m a a n m d n m N *=+-∈(等差数列任意两项的关系) 可化为③:n a An B =+(关于n 的一次表达式)3、等差中项:如果在a 与b 中间插入一个数A ,使a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项,表示为:2a b A +=。
二、等差数列的性质(若数列{}n a 是公差为d 的等差数列): 1、1()1、、n m k a a a a d m n k N n m k--==∈*--;(已知任意两项,均可求公差)2、若()、、、m n p q m n p q N +=+∈*⇒m n p q a a a a +=+;(下标之和相等,对应项之和相等)3、若 ⇒ 2()、、m n k a a a m n k N +=∈*; 三、等差数列的判断:1、{}1()常数n n n a a d a +-=⇔是等差数列;(定义法)2、{}122()n n n n a a a N a ++=+∈*⇔是等差数列;(任意相邻三项都成等差数列)3、{}(,)为常数n n a kn b k b a =+⇔是等差数列;(关于n 的一次式) 四.课堂练习 1.在等差数列中,,则( ).(A )72 (B )60 (C )48 (D )36 2.在等差数列中,,,则201是该数列的( ).(A )第60项 (B )第61项 (C )第62项 (D )第63项 3.已知为等差数列,,则等于 ( ) (A ) -1 (B ) 1 (C ) 3(D )74.已知等差数列的首项.公差,则-397是该数列的第______项.5.已知等差数列中,首项,则公差6.已知等差数列中,公差,则首项7.已知等差数列中,,求的值.8..已知等差数列中,求;;;;9.已知等差数列中,求的值.10.已知等差数列中,,求.2。
等差数列知识点归纳总结

等差数列知识点归纳总结
等差数列是一种非常重要的数学概念,它广泛应用于几乎所有数学分支,包括代数、统计、优化等。
本文将介绍等差数列的基本概念、定义、性质及应用,以此对此知识点进行归纳总结。
一、等差数列的定义
等差数列是一种特殊的的数列,它的元素保持一定的差值相等,例如: 1,4,7,10...,元素之间的差值都为3.
二、等差数列的性质
(1)等差数列的前n项和
若等差数列的前n项和为Sn,公差为d,则Sn = n(a1 + an) / 2 = n(a1 + a1 + (n 1)d) / 2 = n(2a1 + (n 1)d) / 2
(2)等差数列的等比数列
如果一个数列所有元素都是正数,且满足等比数列的性质,则称这个数列为等比数列。
例如:2 ,4 ,8, 16...,元素之间的比值都为
2.
三、等差数列的应用
(1)数学问题
等差数列在解决数学问题时很有用,可以用来计算总和、平均数和对数等。
(2)统计分析
等差数列也可以用于统计分析,可以用来判断数据的变化趋势,并进行回归分析。
(3)其他
等差数列也可以在其它领域有用。
例如,它可以用来帮助用户在购物时进行折扣,并可以帮助用户在预测股票价格变化时做出正确的决策。
综上所述,等差数列是一种非常重要的数学概念,它广泛应用在几乎所有数学分支,具有明显的规律性,可以被用来解决各种数学问题,并可以用于统计分析和其他应用。
因此,掌握等差数列的相关知识是数学学习中必不可少的一部分。
等差数列知识点解读
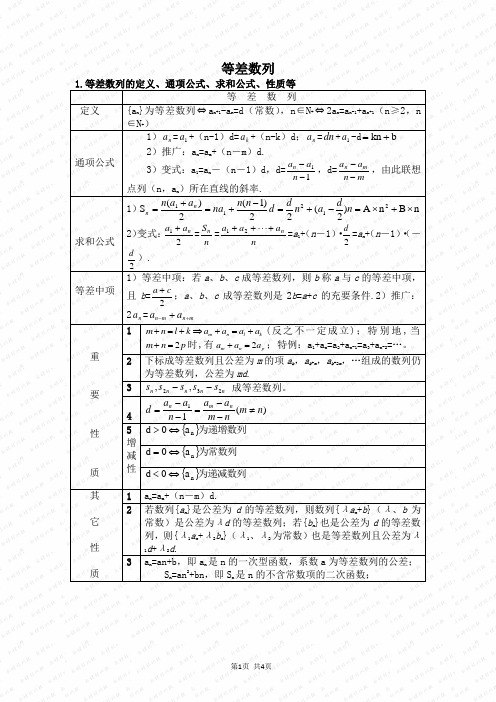
等差数列1.等差数列的定义、通项公式、求和公式、性质等等差数列定义{an }为等差数列⇔an+1-an=d(常数),n∈N+⇔2a n=a n-1+a n+1(n≥2,n∈N+)通项公式1)na=1a+(n-1)d=ka+(n-k)d;na=dn+1a-d bkn+=2)推广:an=am+(n-m)d.3)变式:a1=an-(n-1)d,d=11--naan,d=mnaamn--,由此联想点列(n,an)所在直线的斜率.求和公式1)nBnA)2(22)1(2)(S21211⨯+⨯=-+=-+=+=ndanddnnnaaannn2)变式:21naa+=nSn=naaan+⋅⋅⋅++21=a1+(n-1)·2d=an+(n-1)·(-2d).等差中项1)等差中项:若a、b、c成等差数列,则b称a与c的等差中项,且b=2ca+;a、b、c成等差数列是2b=a+c的充要条件.2)推广:2na=mnmnaa+-+重要性质1m n l km n l k a a a a+=+⇒+=+(反之不一定成立);特别地,当2m n p+=时,有2m n pa a a+=;特例:a1+a n=a2+a n-1=a3+a n-2=…。
2 下标成等差数列且公差为m的项a k,a k+m,a k+2m,…组成的数列仍为等差数列,公差为md.3nnnnnsssss232,,--成等差数列。
4)(11nmnmaanaad nmn≠--=--=5增减性{}为递增数列nad⇔>{}为常数列nad⇔={}为递减数列nad⇔<其它性质1 an=am+(n-m)d.2 若数列{a n}是公差为d的等差数列,则数列{λa n+b}(λ、b为常数)是公差为λd的等差数列;若{b n}也是公差为d的等差数列,则{λ1an+λ2bn}(λ1、λ2为常数)也是等差数列且公差为λ1d+λ2d.3 an=an+b,即an是n的一次型函数,系数a为等差数列的公差;Sn=an2+bn,即Sn是n的不含常数项的二次函数;2.等差数列的判定:{a n }为等差数列⎪⎪⎩⎪⎪⎨⎧+=+=+==-⇔+++数”)(缺常数项的“二次函的“一次函数”)(关于(定义)Bn An S n B An a a a a d a a nn n n n n n 22112 即:*),2(2(11n 1n N n n a a a d d a a a n n n n ∈≥+=⇔=-⇔-++为常数)}{ Bn An s b kn a n n +=⇔+=⇔2;3.三个数成等差可设:a ,a +d ,a +2d 或a -d ,a ,a +d ; 四个数成等差可设:a -3d ,a -d ,a +d ,a +3d .题型1 等差数列的基本运算 例1 在等差数列{a n }中,(1)已知a 15=10,a 45=90,求a 60; (2)已知S 12=84,S 20=460,求S 28;变式训练1 设{a n }为等差数列,S n 为数列{a n }的前n 项和,已知S 7=7,S 15=75,T n 为数列{nS n}的前n 项和,求T n .题型2 等差数列的判定与证明例2 已知数列{a n }满足2a n +1=a n +a n +2(n ∈N *),它的前n 项和为S n ,且a 3=5,S 6=36.求数列{a n }的通项公式;变式训练 2 在数列{a n}中,a1=1,a n+1=2a n+2n.设b n=an2n-1,证明:数列{b n}是等差数列;小结与拓展:证明数列{a n}是等差数列的两种基本方法是:1)利用定义,证明an-a n-1(n≥2)为常数;2)利用等差中项,即证明2a n=a n-1+a n+1(n≥2).题型3 等差数列的性质例 3 设等差数列{}n a的首项及公差均是正整数,前n项和为n S,且11a>,46a>,312S≤,则2010a=_ _ _.答案:4020变式训练3 在等差数列{a n}中,已知log2(a5+a9)=3,则等差数列{a n}的前13项的和S13=________.答案:52小结与拓展:解决等差(比)数列的问题时,通常考虑两类方法:①基本量法,即运用条件转化成关于a1和d(q)的方程;②巧妙运用等差(比)数列的性质(如下标和的性质、子数列的性质、和的性质).一般地,运用数列的性质,可化繁为简.题型4 等差数列的前n项和及最值问题例4 设等差数列{a n}的前n项和为S n,已知a3=12,S12>0,S13<0.(1)求公差d的取值范围;(2)指出S1,S2,S3,…,S12中哪一个最大,并说明理由.变式训练4设等差数列{}n a的前n项和为n S,若111a=-,466a a+=-,则当nS取最小值时,n等于( )A.6 B.7 C.8 D.9练习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲 数列定义及其性质一、基本概念:1、通项公式:n a ;2、前n 项和:n S3、关系:1(2)n n n a S S n -=-≥ 二、性质:1、单调性:增数列:1n n a a ->;减数列:1n n a a -<;常数列:1n n a a -=2、最值:77878789+++(0)0,00,=0,0,n n a S a a S S S a a a ⎧⎧⎪⎨⎩⎪⎪---⎧⎪⎨⎪><⎪⎪⎨⎪><⎪⎪⎪⎪⎩⎩L 最大值:减数列最小值:增数列最大值:若最大,则若或最大,则最小值:与上面相反3、前n 项积n T 有最大值: 三、几种常见数列: 1、-1,7,-13,19L 2、7,77,777,L 3、135248L ,,4、161149L ,,, 5、2468,3153563L ,,★随堂训练:1、已知数列{}n a 通项公式是231n na n =+,那么这个数列是( ) A.递增数列 B.递减数列 C.摆动数列 D.常数列2、已知数列{}n a 满足10a >,112n n a a +=,那么这个数列是( ) A.递增数列 B.递减数列 C.摆动数列 D.常数列3、已知数列{}n a 通项公式是22n a n kn =++,若对任意*n N ∈,都有1n n a a +>成立,则实数k 的取值范围是( ) 4、已知数列{}n a 通项公式是10,21n n n a T n +=+是数列{}n a 的前n 项积,即123n n T a a a a =L ,当n T 取到最大值是,n 的值为( )5、设数列{}n a 的前n 项和2n S n =,则8a 的值是( )等差数列专题一、等差数列知识点回顾与技巧点拨1.等差数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示.2.等差数列的通项公式若等差数列{a n }的首项是a 1,公差是d ,则其通项公式为a n =a 1+(n -1)d =(n -m )d =p .3.等差中项如果三个数x ,A ,y 组成等差数列,那么A 叫做x 和y 的等差中项,如果A 是x 和y 的等差中项,则A =x +y2.4.等差数列的常用性质(1)通项公式的推广:a n =a m +(n -m )d (n ,m ∈N *).(2)若{a n }为等差数列,且m +n =p +q ,则a m +a n =a p +a q (m ,n ,p ,q ∈N *).(3)若{a n }是等差数列,公差为d ,则a k ,a k +m ,a k +2m ,…(k ,m ∈N *)是公差为md 的等差数列. (4)数列S m ,S 2m -S m ,S 3m -S 2m ,…也是等差数列. (5)S 2n -1=(2n -1)a n .(6)若n 为偶数,则S 偶-S 奇=nd2;若n 为奇数,则S 奇-S 偶=a 中(中间项).5.等差数列的前n 项和公式 若已知首项a 1和末项a n ,则S n =n a 1+a n2,或等差数列{a n }的首项是a 1,公差是d ,则其前n 项和公式为S n =na 1+n n -12d .6.等差数列的前n 项和公式与函数的关系S n =d 2n 2+⎝ ⎛⎭⎪⎫a 1-d 2n ,数列{a n }是等差数列的充要条件是S n =An 2+Bn (A ,B 为常数).7.最值问题在等差数列{a n }中,a 1>0,d <0,则S n 存在最大值,若a 1<0,d >0,则S n 存在最小值.一个推导利用倒序相加法推导等差数列的前n 项和公式:S n =a 1+a 2+a 3+…+a n ,① S n =a n +a n -1+…+a 1,②①+②得:S n =n a 1+a n2.两个技巧已知三个或四个数组成等差数列的一类问题,要善于设元.(1)若奇数个数成等差数列且和为定值时,可设为…,a -2d ,a -d ,a ,a +d ,a +2d ,…. (2)若偶数个数成等差数列且和为定值时,可设为…,a -3d ,a -d ,a +d ,a +3d ,…,其余各项再依据等差数列的定义进行对称设元 . 四种方法等差数列的判断方法(1)定义法:对于n ≥2的任意自然数,验证a n -a n -1为同一常数; (2)等差中项法:验证2a n -1=a n +a n -2(n ≥3,n ∈N *)都成立; (3)通项公式法:验证a n =pn +q ; (4)前n 项和公式法:验证S n =An 2+Bn .注: 后两种方法只能用来判断是否为等差数列,而不能用来证明等差数列.基础训练:(公式的运用,定义的把握)1.已知等差数列{a n }中,a 3=9,a 9=3,则公差d 的值为( ) A .B . 1C .D . ﹣12.已知数列{a n }的通项公式是a n =2n+5,则此数列是( ) A . 以7为首项,公差为2的等差数列 B . 以7为首项,公差为5的等差数列 C . 以5为首项,公差为2的等差数列D . 不是等差数列3.在等差数列{a n }中,a 1=13,a 3=12,若a n =2,则n 等于( ) A . 23B . 24C . 25D . 264.两个数1与5的等差中项是( ) A . 1B . 3C . 2D .5.(2005•黑龙江)如果数列{a n }是等差数列,则( ) A . a 1+a 8>a 4+a 5 B . a 1+a 8=a 4+a 5C . a 1+a 8<a 4+a 5D . a 1a 8=a 4a 5考点1:等差数列的通项与前n 项和 题型1:已知等差数列的某些项,求某项【解题思路】给项求项问题,先考虑利用等差数列的性质,再考虑基本量法 【例1】已知{}n a 为等差数列,20,86015==a a ,则=75a对应练习:1、已知{}n a 为等差数列,q a p a n m ==,(k n m ,,互不相等),求k a .2、已知5个数成等差数列,它们的和为5,平方和为165,求这5个数.题型2:已知前n 项和n S 及其某项,求项数. 【解题思路】⑴利用等差数列的通项公式d n a a n )1(1-+=求出1a 及d ,代入n S 可求项数n ; ⑵利用等差数列的前4项和及后4项和求出n a a +1,代入n S 可求项数n . 【例2】已知n S 为等差数列{}n a 的前n 项和,63,6,994=-==n S a a ,求n对应练习:3、若一个等差数列的前4项和为36,后4项和为124,且所有项的和为780,求这个数列的项数n .4、已知n S 为等差数列{}n a 的前n 项和,100,7,141===n S a a ,则=n .题型3:求等差数列的前n 项和【解题思路】(1)利用n S 求出n a ,把绝对值符号去掉转化为等差数列的求和问题. (2)含绝对值符号的数列求和问题,要注意分类讨论.【例3】已知n S 为等差数列{}n a 的前n 项和,212n n S n -=.(1) 321a a a ++; ⑵求10321a a a a ++++Λ;⑶求n a a a a ++++Λ321.练习:对应练习:5、已知n S 为等差数列{}n a 的前n 项和,10,10010010==S S ,求110S .考点2 :证明数列是等差数列【名师指引】判断或证明数列是等差数列的方法有:1、定义法:d a a n n =-+1(+∈N n ,d 是常数)⇔{}n a 是等差数列;2、中项法:212+++=n n n a a a (+∈N n )⇔{}n a 是等差数列;3、通项公式法:b kn a n +=(b k ,是常数)⇔{}n a 是等差数列;4、项和公式法:Bn An S n +=2(B A ,是常数,0≠A )⇔{}n a 是等差数列.【例4】已知n S 为等差数列{}n a 的前n 项和,)(+∈=N n nS b nn .求证:数列{}n b 是等差数列.对应练习:6、设n S 为数列{}n a 的前n 项和,)(+∈=N n pna S n n ,.21a a = (1) 常数p 的值; (2) 证:数列{}n a 是等差数列.考点3 :等差数列的性质【解题思路】利用等差数列的有关性质求解.【例5】1、已知n S 为等差数列{}n a 的前n 项和,1006=a ,则=11S ;2、知n S 为等差数列{}n a 的前n 项和,)(,m n n S m S m n ≠==,则=+n m S .对应练习:7、含12+n 个项的等差数列其奇数项的和与偶数项的和之比为( ).A n n 12+ .B n n 1+ .C n n 1- .D nn 21+ 8.设n S 、n T 分别是等差数列{}n a 、{}n a 的前n 项和,327++=n n T S n n ,则=55b a .考点4: 等差数列与其它知识的综合【解题思路】1、利用n a 与n S 的关系式及等差数列的通项公式可求;2、求出n T 后,判断n T 的单调性.【例6】已知n S 为数列{}n a 的前n 项和,n n S n 211212+=;数列{}n b 满足:113=b , n n n b b b -=++122,其前9项和为.153⑴ 数列{}n a 、{}n b 的通项公式;⑵设n T 为数列{}n c 的前n 项和,)12)(112(6--=n n n b a c ,求使不等式57kT n >对+∈∀N n 都成立的最大正整数k 的值.课后练习:1.(2010广雅中学)设数列{}n a 是等差数列,且28a =-,155a =,n S 是数列{}n a 的前n 项和,则A .1011S S =B .1011S S >C .910S S =D .910S S <2.在等差数列{}n a 中,1205=a ,则=+++8642a a a a .3.数列{}n a 中,492-=n a n ,当数列{}n a 的前n 项和n S 取得最小值时,=n .4.已知等差数列{}n a 共有10项,其奇数项之和为10,偶数项之和为30,则其公差是 .5.设数列{}n a 中,112,1n n a a a n +==++,则通项n a = .对应练习:9.已知n S 为数列{}n a 的前n 项和,31=a ,)2(21≥=-n a S S n n n .⑴数列{}n a 的通项公式;⑵ 数列{}n a 中是否存在正整数k ,使得不等式1+>k ka a 对任意不小于k 的正整数都成立?若存在,求最小的正整数k,若不存在,说明理由。
