反比例函数第三课时
参评教案实际问题与反比例函数的第三课时

六、
教学反思 实际教学中经验分享: 1.上课前,通过布置预习任务,为学生提供可操作、可完成的任务。作为教师通过互联网开展教师
之间的互助,查阅了大量的资料,这节课学生学习活动所需要的相关材料和课件准备充分、适当.教师 向学生介绍一些好的网站供学生选择,鼓励并引导学生通过网络来获取信息.而课上用的资料是由学生 提供,并进行交流,学生的课堂参与度很高. 2. 我充分利用学生的预习自学,进行借助网络查找信息的指导,部分学困生是“网络高手” ,他们 可以利用互联网“做足功课” ,教师可以利用互联网开展师生在线答疑、利用网络学生之间开展同伴互 ..........................
1
/%BA%C9%BB%A8%B5%C4%C3%CE%D6%D0%D0%A1%CE%DD/blog 在充分理解新课标要求的前提下,结合搜索到的资源,确定了教学的重点和难点,确定课堂教学 形式和方法。 教学重点: 教学重点:掌握从物理问题中建构反比例函数模型. 教学难点: 教学难点:分析物理实际问题中的数量关系,正确写出函数解析式,解决实际问题,并进行归纳总 结,得出物理量关于量的方面的特性,体会数学的本原。
(4)压强公式: P =
F ,当压力 F 一定时,压强 P 是受力面积 S 的反比例函数; S
(5)欧姆定律:IR=U,当电压 U 一定时,输出电流 I 是电阻 R 的反比例函数,
(三)小结 师:大家回顾一下本节课的学习过程,想一想,本节课都有哪些收获? 师生达成共识总结: 1.反比例函数与现实生活联系非常紧密,特别是为讨论物理中的一些量之间的关系打下了良好的基 础.用数学模型的解释物理量之间的关系浅显易懂,所以我们要注重跨学科间的整合。本节课,我们归 纳了反比例函数解决物理实际问题基本模型有 5 个 2.利用构建好的数学模型、函数的思想解决这类问题.注意体会数形结合及转化的思想方法,要充 分利用函数图象的直观性,这对分析和解决实际问题很有帮助。 3.互word=%B7%B4%B1%C8%C0%FD%BA%AF%CA%FD?softid=88876
9、2反比例函数的图象与应用(第三课时)

反比例函数的图象与性质(3)教学目标:使学生对反比例函数和反比例函数的图象意义加深理解。
教学重点:反比例函数的图象 教学难点:利用反比例函数的图象解题 教学过程:二、新授:例2、如图是反比例函数2m y x-=的图象的一支。
(1) 函数图象的另一支在第几象限?试求常数m 的取值范围; (2) 点13(3,))(2,)A y C y -2、B(-1,y 和都在这个反比例函数的图象上,比较1y 、2y 、3y 的大小。
例3、如图,正比例函数y=kx 的图象与反比例函数y=60k 的图象相交于A 、B 两点,其中点A 的坐标为( 3 ,2 3 )(1)分别写出这两个函数的表达式;(2)你能求出点B 的坐标吗?你是怎样求的?与同伴进行交流; 三、随堂练习: P86~87 1、2、o hr补1、若反比例函数xk y 3-=的图象位于一、三象限内,正比例函数x k y )92(-=过二、四象限,则k 的整数值是________。
2、在同一直角坐标系内,函数y=2x 与xy 8=的交点坐标为____________。
3、如果反比例函数k y x=在每个象限内,y 随x 的增大而减小,那么它的图象分布在( )A.第一、二象限B. 第一、三象限C. 第二、三象限D. 第二、四象限4.反比例函数y=3k x+ 的图象在每个象限内的函数值y 随自变量x 的增大而增大, 那么k 的取值范围是( )A 、k ≤-3B 、k ≥-3C 、k>-3D 、k<-35.下列函数中,当x>0时,y 随x 的增大而增大的是 ( ) A 、y=2-3x B 、y=2x C 、y=-2x-1 D 、y=-12x6、已知一次函数y=kx+b 的图象经过第二、三、四象限,则反比例函数kb y x=的图象在( )A.第一、二象限; B .第三、四象限; C .第一、三象限; D .第二、四象限. 7.若0<ab ,则函数ax y =与xb y =在同一平面直角坐标系中的图象大致是( ) 四、小结 五、作业: P86 5同步导学(随堂演练)第11题。
湘教版九年级上册数学 1.2.3反比例函数y=kx(k≠0)中k的性质 课后习题重点练习课件

解:∵顶点 A 的坐标是(0,2),顶点 C 的纵坐标是 -4,∴AE=6.又∵▱ABCD 的面积是 24, ∴AD=BC=4,∴D(4,2),∴k=4×2=8, ∴反比例函数的表达式为 y=8x.
(2)AB所在直线的表达式. 解:由题意知点 B 的纵坐标为-4,且在反比例函数 y =8x的图象上.∴点 B 的横坐标为-2,∴B(-2,-4). 设 AB 所在直线的表达式为 y=k′x+b,将 A(0,2), B(-2,-4)的坐标代入,得b-=22k, ′+b=-4, 解得kb′==23,,∴AB 所在直线的表达式为 y=3x+2.
【点拨】过点 B 作 BC⊥OA 于点 C.∵点 A 的坐标是 (2,0),∴AO=2.∵△ABO 是等边三角形,∴OC= 1,∴BC= 3,∴点 B 的坐标是(1, 3).把点 B(1, 3)的坐标代入 y=kx,得 k= 3.故选 C.
【答案】C
*4.【中考·济宁】如图,点 A 的坐标是(-2,0),点 B 的 坐标是(0,6),C 为 OB 的中点,将△ ABC 绕点 B 逆 时针旋转 90°后得到△ A′BC′.若反比例函数 y=kx的图 象恰好经过 A′B 的中点 D,则 k 的值是( ) A.9 B.12 C.15 D.18
【答案】D
8.【中考·凉山州】如图,正比例函数 y=kx 与反比 例函数 y=4x的图象相交于 A,C 两点,过点 A 作 x 轴的垂线交 x 轴于点 B,连接 BC,则△ ABC 的面积等于( ) A.8 B.6 C.4 D.2
【点拨】∵点 A,C 位于反比例函数图象上且关于原 点对称,∴S△ OBA=S△ OBC.∵过双曲线上任意一点与原 点所连的线段、x 轴(或 y 轴)、和过该点向坐标轴作的 垂线所围成的直角三角形面积 S 是个定值, ∴S△OBA=12|k|.∴△ABC 的面积等于 2×12|k|=|k|=4. 【答案】C
人教版九年级数学下册26.1.2反比例函数的图象和性质(第3课时) 课件

O
x
B
SAOB SOMB SOAM 2 4 6.
(2)解法二:
y x 2,当x 0时, y 2, N(0,2).
ON 2.
1
1
SONB
ON 2
x B
2 4 4, 2
y A
N
SONA
1 ON 2
xA
1 2 2 2. 2
反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和 y=-x。对称中心是:原点
y y = —kx
y=-x
y=x
0
12
x
.如图,在y 1 (x 0)的图像上有三点A,B,C, x
经过三点分别向x轴引垂线,交x轴于A ,B ,C 三点, 111
边结OA,OB,OC,记OAA , OBB , OCC 的
(2)根据图象写出反比y例函数的值大于一次函数的值 的x的取值范围。
M(2,m)
-1 0 2
x
N(-1,-4)
(1)求反比例函数和一次函数的解析式;
解(1)∵点N(-1,-4)在反比例函数图象上
4
∴k=4,
∴y= x
y
又∵点M(2,m)在反比例函数图象上
∴m=2 ∴M(2,2)
∵点M、N都y=ax+b的图象上 M(2,m)
(1)分别求直线AB与双曲线的解析式; (2)求出点D的坐标;
(3)利用图象直接写出当x在什 么范围内取何值时,y1>y2.
5、如图,已知反比例函数 y 12 的图象与一次函数 x
y= kx+4的图象相交于P、Q两点,且P点的纵坐标
新版青岛版九年级下数学课件反比例函数第三课时
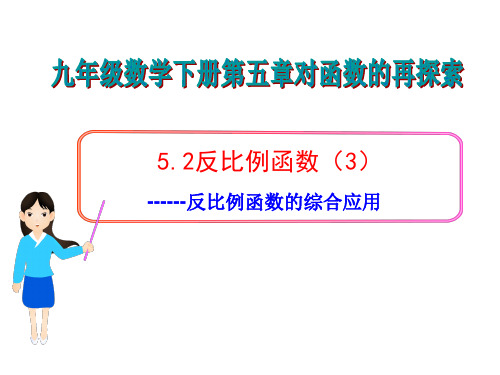
0)
图象上的一点,若矩形
AOBP的面积是6.请写出
这个反比例函数的解析式.
2.若△BPO的面积是5,那么
函数解析式又是什么呢?
B O
PA
P BO
3.如图,点P是x轴上的一个动点,过点P作x轴的 垂线PQ交双曲线于点Q,连结OQ, 当点P沿x轴正 半方向运动时,Rt△QOP面积( ).
A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定
5.2反比例函数(3)
------反比例函数的综合应用
• 解析式 • 图象
反比例函数
y
=
k x
(
k是常数,k≠0
)
双曲线
• 性质
k>0 y随x的增大而减小
k<0 y随x的增大而增大
xy=k(k≠0)
反比例函数图象上任取.理解反比例函数中k的几何性质;
典型例题:
解析:(1)由反比例函数的几何性质可知: S矩形OACB S矩形OQPR K 15
(2)以求得P(5,3),故可知 OA=3,AD=PQ=3,所以:
S矩形OADR 3 3 9
解析:
由点A可求得k=-2x3=-6; 再由 3m=-6可求得m=-2; 所以B(3,-2); 将点A,B代入到y=ax+b即可 求得a,b的值。
第一运用待定系数法求出相关的函数关系式;
再根据要求运用函数性质解决问题.
注意: 任意两个反比例函数的图象均相交.
解析:不能相交;假设相交于点A(a,b),
则应有ab=k1=k2,这与k1≠k2相矛盾。 所以不能相交。
想一想:反比例函数 y k 上那个点距离原点最近?
x
教材第22页课后练习1、2题.
反比例函数的图象与性质第三课时(导学案)

反比例函数的图象与性质一、反比例函数中的比例系数k 的几何意义矩形PMON 的面积= ; △POM 的面积= .结论是怎样推导得到的?1. 过反比例函数图象上一点P 分别作x 轴、y 轴的垂线段,如果两垂线段与两坐标轴构成的矩形面积是8,那么反比例函数的解析式是 .2.如图,A ,B 两点在双曲线4y x =上,分别经过A ,B 两点向坐标轴作垂线段,已知S 阴影=1,则S 1+S 2= .第3题图 第4题图 第5题图 3.如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB //x 轴,C ,D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 . 4.如图,点A 是反比例函数k y x =图象上的点,AB ⊥y 轴于点B ,点C 、D 在x 轴上,且BC //AD .若四边形ABCD 的面积为3,则k 值为 .5.如图,已知反比例函数1k y x =和2k y x =,AB ⊥y 轴,连接OA ,OB ,若⊥AOB 的面积等于3,则k 1- k 2= .6.如图,过反比例函数k y x=图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连结OA 、OB 、AB ,设AC 与OB 的交点为E .试探究△AOB 与梯形ACDB 的面积有何关系?7. 如图,函数2(0)y xx=>的图象经过矩形OABC的边BC的中点D,且与边AB相交于点E,则四边形ODBE的面积为.二、反比例函数与一次函数的综合应用8.已知反比例函数myx=的图象与正比例函数y kx=的图象交于A、B两点,点B的坐标为( -3,-2),则点A的坐标为.探究:下列图形中阴影部分的面积9.如图,正比例函数y=mx与反比例函数myx=的图象交于A,B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S⊥ABM =3,则k的值是 .10.如图,直线y 1=kx +b 和双曲线2m y x=相交于A ,B 两点.A 为(1,4),B 为(-4,n ). (1)求两个函数的表达式;(2)求⊥AOB 的面积; (3)在y 轴上是否存在一点P ,使得⊥P AB 的面积等于5,若存在,请求出点P 的坐标,若不存在,请说明理由;(4)观察图象,直接写出关于x 的不等式m kx b x+>的解集.11.根据图象直接写出关于x 的不等式0m kx b x+->的解集.第11题图 第12题图 12. 根据图象,直接写出 一次函数的函数值大于反比例函数的函数值时,自变量x 的取值范围.课后练习1.在同一直角坐标系中,函数y =kx -k 与y =k x(k ≠0)的图象大致是( )2.若点A (-2,-2)在反比例函数y =k x的图象上,则 (1)当2y >时,x 的取值范围是 ;(2)当2y ≥-时,x 的取值范围是 .第2题图 第3题图 3.已知双曲线6y x=-,如图所示,A (﹣1,m ),B (n ,2),则S ⊥AOB 的值为 . 4.如图所示,一次函数y =ax +b 的图象与反比例函数y =k x的图象交于M 、N 两点. (1)求反比例函数与一次函数的表达式;(2)求⊥MON 的面积;(3)根据图象,直接写出使反比例函数的值大于一次函数的值的x 的取值范围.(4)在x 轴上是否存在一点P ,使得⊥PMN 的面积等于4,若存在,请求出点P 的坐标,若不存在,请说明理由.。
17.1.2反比例函数的图像与性质(第3课时)

17.1.2反比例函数的图像与性质(3)教学目标:掌握反比例函数的图像与性质,理解反比例函数相关的面积问题. 一、复习与回忆1、 函数x k y =的图象经过点(-4,6),则下列各点中在xky =图象上的是( )A .(3,8)B .(3,-8)C .(-8,-3)D .(-4,-6)2、函数4y x=的图象的两个分支在第 象限;在每个象限y 都随x 的增大而 . 函数4y x =-的图象的两个分支在第 象限;在每个象限y 都随x 的增大而 .3、点(2,-3)在反比例函数ky x=的图象上,则k=4、若点(-2,1y )、(-1,2y )、(2,3y )在反比例函数xy 100-=的图象上,则( ) A 、1y >2y >3y B 、2y >1y >3y C 、3y >1y >2y D 、3y >2y >1y 二、学习新知:问题1:如图,点A 是反比例函数6y x =图像上一点,过点A 作AB ⊥x 轴于点B , 作AB ⊥y 轴于点C ,连接OA :⑴若A 点的横坐标为3,则ABOC S 矩形=_______;AOB S D =_______ ⑵若A 点的横坐标为a ,则ABOC S 矩形=_______;AOB S D =_______⑶思考:若点A 在函数图像上运动,矩形ABOC 和△AOB 面积会否发生变化?问题2:如图,点A 是反比例函数x y 6-=图像上一点,过点A 作AB ⊥x 轴于点B ,作AB ⊥y 轴于点C ,连结AO :⑴若A 点的横坐标为-3,则ABOC S 矩形=______;AOB S D =______; ⑵若A 点的横坐标为a ,则ABOC S 矩形=_______;AOB S D =______;⑶思考:若点A 在函数图像上运动,矩形ABOC 和△AOB 面积会否发生变化?归纳:设 ),(11y x P 是双曲线)0(≠=k xky 上任意一点,过点P 分别作x 轴,y 轴的垂线,垂足分别为A,B , 连接OA ,归纳:过双曲线上任意一点作x 轴、y 轴的垂线,与两坐标轴围成的矩形的面积为常数|k| 三、课堂练习:1、(2011•漳州)如图5,P (x ,y )是反比例函数xy 3=的图象的一个动点,PA ⊥x 轴于点A ,PB ⊥y 轴于点B ,随着自变量x 的增大,矩形OAPB 的面积( ) A 、不变B 、增大C 、减小D 、无法确定2、(2010•定西)如图6,矩形ABOC 的面积为3,函数xky =的图象过点A ,则k=( ) A 、3 B 、﹣1.5 C 、﹣3 D 、﹣63、如图7,1P ,2P ,3P 在双曲线上.过这三点分别作y 轴的垂线,得到三个三角形O A P 11∆,O A P 22∆,O A P 33∆设它们的面积分别是1S ,2S ,3S ,则( )A 、1S <2S <3SB 、2S <1S <3SC 、1S <3S <2SD 、1S =2S =3S4、(2011•江津区)已知如图8,A 是反比例函数xky =的图象上的一点,AB 丄x 轴于点B ,且△ABO 的面积是3,则k 的值是( )A 、3B 、﹣3C 、6D 、﹣621||||212111=∙=⋅=-------------∆y x S OAP O 11||||APB S x y ------------==∙=矩形则图 5图 6图7图8yxC图2图1 A yx5、(2006•茂名)已知点P 是反比例函数xky =(k≠0)的图象上任一点,过P 点分别作x 轴,y 轴的平行线,若两平行线与坐标轴围成矩形的面积为2,则k 的值为( )A 、2B 、﹣2C 、±2D 、46、(2010•牡丹江)如图9,反比例函数与正比例函数的图象相交于A 、B 两点,过点A 作AC ⊥x 轴于点C .若△ABC 的面积是4,则这个反比例函数的解析式为( )A 、xy 2=B 、x y 4=C 、xy 8=D 、xy 16=7、(2011•阜新)如图10,是函数x y 6= 与xy 3=在第一象限的图象,作一条平行于x轴的直线分别交双曲线于A 、B 两点,连接OA 、OB ,则△AOB 的面积为( ) A 、 B 、2 C 、3 D 、1四、课后作业:1、如图11,点A 在反比例函数)0(≠=k xky 的图象上,AB 垂直于x 轴,若S AOB ∆=4,那么这个反比例函数的解析式为_____________。
第三课时反比例函数的图象和性质

6 x
的图象是
_______,位于________象限,
在每个象限内y随x的增大而______。
2、若点(3,6)在反比例函数 y= (k≠0)的图象上,那么在此图象 上的点是( )
(A) (-3,6) (C) (2, -9 )
k x
(B) (2,9) (D) (3,-6 )
3、 已知反比例函数 y=
.反比例函数图象的画法——描点法:
反比例函数的图象和性质:
fx = gx = 4 x -4 x
8 10
变化趋势:无限接近X轴Y轴但不会与坐标轴相交。
6
4 y x
-15 -10 -5
4
4 y x
5 10 15
2
-2
-4
-6
-8
①
②
观察图象,分小组讨论下面两个问题: 1. 反比例函数的图象是什么形状? 2. 每个函数的图象分别位于那几个象限? 3.自左向右观察图象,判断在每一个象限内, y随x的变化如何变化?
反比例函数的图像和性质
1. 反比例函数的定义:
k 形如y= x 的函数叫做反比例函数.
其中 k为常数,k ≠0, 自变量x ≠0 2. 它的三种常见的表达形式:
k -1 ①y = (k ≠ 0)②xy = k(k ≠ 0)③y= kx (k≠0) x
3、用描点法画函数图象的一般步骤:
1.列表 2.描点
3k-2
x
,
当k<______ 时,其图象的两个分支 位于二、四象限。 4.若函数 的图象,在每一象限内y 随x的增大而增大, 则k的取值范围 是___________。
k 1 y x
4k 5、已知反比例函数 y x
湘教版数学九年级上册_课时作业:第3课时_反比例函数y=k÷x(k≠0)的图象与性质
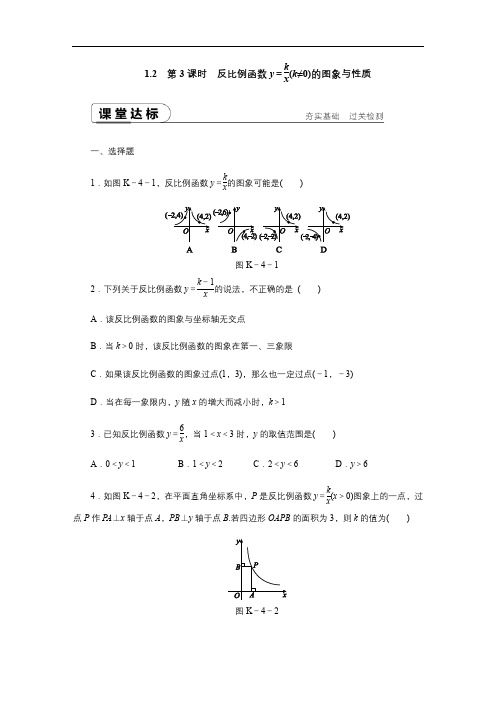
1.2 第3课时 反比例函数y =kx (k ≠0)的图象与性质一、选择题1.如图K -4-1,反比例函数y =kx的图象可能是( )图K -4-12.下列关于反比例函数y =k -1x的说法,不正确的是 ( ) A .该反比例函数的图象与坐标轴无交点B .当k >0时,该反比例函数的图象在第一、三象限C .如果该反比例函数的图象过点(1,3),那么也一定过点(-1,-3)D .当在每一象限内,y 随x 的增大而减小时,k >13.已知反比例函数y =6x ,当1<x <3时,y 的取值范围是( )A .0<y <1B .1<y <2C .2<y <6D .y >64.如图K -4-2,在平面直角坐标系中,P 是反比例函数y =kx (x >0)图象上的一点,过点P 作P A ⊥x 轴于点A ,PB ⊥y 轴于点B .若四边形OAPB 的面积为3,则k 的值为( )图K -4-2A .3B .-3 C.32 D .-325.如果k <0,那么函数y =(1-k )x 与y = kx在同一坐标系中的图象可能是( )图K -4-36.一次函数y =kx +b (k ≠0)的图象经过A (-1,-4),B (2,2)两点,P 为反比例函数y =kbx图象上一动点,O 为坐标原点,过点P 作y 轴的垂线,垂足为C ,则△PCO 的面积为( ) A .2 B .4 C .8 D .不确定二、填空题7.如图K -4-4,反比例函数y =kx 的图象经过点A (2,1).若y ≤1,则x 的取值范围是____________.图K -4-48.已知一次函数y =x +1的图象与反比例函数y =kx 的图象相交,其中有一个交点的横坐标是2,则k 的值为________.9.设函数y =3x 与y =-2x -6的图象的交点坐标为(a ,b ),则1a +2b 的值是________.10.如图K -4-5,在平面直角坐标系中,M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 与反比例函数y =8x (x >0)和y =kx(x >0)的图象分别交于点P ,Q .若S △POQ =14,则k 的值为________.图K -4-5 图K -4-611.函数y 1=x (x ≥0),y 2=4x (x >0)的图象如图K -4-6所示,由有下列结论:①两函数图象的交点A 的坐标为(2,2);②当x >2时,y 2>y 1;③当x =1时,BC =3;④当x 逐渐增大时,y 1随着x 的增大而增大,y 2随着x 的增大而减小.其中正确结论的序号是________.三、解答题12.如图K -4-7,反比例函数y 1=mx (x >0)的图象与一次函数y 2=-x +b (x >0)的图象交于点A ,B ,其中A (1,2).(1)求m ,b 的值;(2)若点B 的坐标为(2,y B ),求y B 的值,并写出y 2>y 1时,x 的取值范围.图K -4-713.如图K -4-8,一次函数y =kx +b (k ≠0)的图象与反比例函数y =ax (a ≠0)的图象在第二象限交于点A (m ,2),与x 轴交于点C (-1,0),过点A 作AB ⊥x 轴于点B ,△ABC 的面积是3.(1)求一次函数和反比例函数的表达式;(2)若直线AC 与y 轴交于点D ,求△ABD 的面积.图K -4-814.反比例函数y =kx (k 为常数,且k ≠0)的图象经过点A (1,3),B (3,m ).(1)求反比例函数的表达式及点B 的坐标;(2)在x 轴上找一点P ,使P A +PB 的值最小,求满足条件的点P 的坐标.图K -4-9新定义问题:在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“倍点”,例如点(-2,-4),(1,2),(3,6)……都是“倍点”,显然这样的“倍点”有无数多个.(1)若点M (2,a )是反比例函数y =kx 的图象上的“倍点”,求这个反比例函数的表达式.(2)对于一次函数y =3mx -1的图象上是否存在“倍点”,嘉琪说:“当m =23时,函数图象上不存在‘倍点’,当m ≠23时,函数图象上存在‘倍点’.”你认为她的说法正确吗?如果正确,请求出存在的“倍点”;如果不正确,请说明理由.详解详析[课堂达标]1.[解析] D A .∵反比例函数的图象在第一、三象限或第二、四象限,∴选项A 不符合题意.B .k =-2×6=-12,k =4×(-2)=-8.∵-12≠-8,∴选项B 不符合题意.C .k =4×2=8,k =-2×(-2)=4.∵8≠4,∴选项C 不符合题意.D .k =4×2=8,k =-2×(-4)=8.∵8=8,∴选项D 符合题意.故选D .2.[解析] B A .反比例函数的图象与坐标轴无交点,正确,不符合题意;B .当k -1>0,即k >1时,该反比例函数的图象在第一、三象限,故错误,符合题意;C .如果该反比例函数的图象过点(1,3),那么也一定过点(-1,-3),正确,不符合题意;D .当在每一象限内,y 随x 的增大而减小时,k -1>0,k >1,正确,不符合题意.故选B .3.[解析] C ∵k =6>0,∴在每个象限内,y 随x 的增大而减小.又∵当x =1时,y =6,当x =3时,y =2,∴当1<x <3时,2<y <6.故选C . 4.[答案] A 5.[答案] C6.[解析] A 将A(-1,-4),B(2,2)代入一次函数表达式,得⎩⎨⎧-k +b =-4,2k +b =2,解得⎩⎨⎧k =2,b =-2,∴反比例函数的表达式为y =-4x .∵P 为反比例函数y =kbx 图象上一动点,O 为坐标原点,过点P 作y 轴的垂线,垂足为C ,∴△PCO 的面积为12|k|=2.故选A .7.[答案] x≥2或x <0 8.[答案] 6[解析] 把x =2代入y =x +1,得y =3,∴这个交点的坐标为(2,3).把(2,3)代入y =kx ,得k =6.9.[答案] -2 10.[答案] -20[解析] ∵S △POQ =S △OMQ +S △OMP ,∴12|k|+12×|8|=14,∴|k|=20.由函数y =kx 的图象可知k<0,∴k =-20.11.[答案] ①③④[解析] ①将y 1=x(x≥0),y 2=4x(x >0)组成方程组,得⎩⎪⎨⎪⎧y =x ,y =4x ,由于x >0,解得x =2,y =2,故点A 的坐标为(2,2).②由图可知,当x >2时,y 1>y 2.③当x =1时,y 1=1,y 2=4,则BC =4-1=3.④当x 逐渐增大时,y 1随着x 的增大而增大,y 2随着x 的增大而减小.综上,正确的结论为①③④.12.解:(1)∵反比例函数y 1=m x (x>0)的图象过点A(1,2),∴2=m1,解得m =2.∵一次函数y 2=-x +b(x>0)的图象过点A(1,2),∴2=-1+b ,解得b =3. (2)将点B 的横坐标2代入y =2x ,得y B =1,∴点B 的坐标为(2,1).根据图象可得,当1<x<2时,y 2>y 1.13.解:(1)∵一次函数y =kx +b(k≠0)的图象与反比例函数y =ax (a≠0)的图象在第二象限交于点A(m ,2),与x 轴交于点C(-1,0),∴点A(a 2,2).∵△ABC 的面积是3,∴3=12·AB·BC.即3=12×2×(-1-a 2),解得a =-8,∴反比例函数的表达式为y =-8x.∴A(-4,2).把A(-4,2),C(-1,0)代入y =kx +b ,得⎩⎨⎧2=-4k +b ,0=-k +b ,解得⎩⎨⎧k =-23,b =-23,∴一次函数的表达式为y =-23x -23.(2)∵直线AC 与y 轴交于点D ,当x =0时,y =-23×0-23=-23,∴D(0,-23),∴OD =23.∴S △ABD =S △BCA +S △BCD =12·BC·(AB +OD)=12×3×(2+23)=4.14.解:(1)因为图象经过点A(1,3),所以3=k1.∴k =3,∴反比例函数的表达式为y =3x .当x =3时,m =33=1,∴点B 的坐标(3,1).(2)如图,作点B 关于x 轴的对称点C ,点C 的坐标为(3,-1).再连接AC 与x 轴交于点P ,此时PA +PB 的值最小. 设直线AC 的函数表达式为y =ax +b(a≠0).因为图象过(1,3)和(3,-1)两点,可得⎩⎨⎧a +b =3,3a +b =-1,解得⎩⎨⎧a =-2,b =5,∴y =-2x +5.当y =0时,x =2.5,∴满足条件的点P 的坐标为(2.5,0).[素养提升]解:(1)∵点M(2,a)是“倍点”, ∴a =2×2=4,∴点M 的坐标为(2,4). ∵点M(2,4)在反比例函数y =kx 的图象上,∴4=k2,解得k =8,∴反比例函数的表达式为y =8x .(2)嘉琪的说法是正确的.设函数y =3mx -1的图象上存在的“倍点”的坐标为(n ,2n), 则有2n =3mn -1.整理,得(3m -2)n =1. ①当3m -2=0时,m =23,此时不存在n 的值,使等式(3m -2)n =1成立,∴函数y =3mx -1的图象上不存在“倍点”; ②当3m -2≠0时,m≠23,由(3m -2)n =1,解得n =13m -2,那么2n =23m -2,∴当m≠23时,函数图象上存在“倍点”为(13m -2,23m -2).。
11.2+反比例函数的图像及性质(例)3课时

11.2 反比例函数的图像及性质(例)3课时一.选择题(共4小题)1.(2019•伊金霍洛旗一模)如图,在以O 为原点的直角坐标系中,矩形OABC 的两边OC 、OA 分别在x 轴、y 轴的正半轴上,反比例函数(0)ky x x=>与AB 相交于点D ,与BC 相交于点E ,若3BD AD =,且ODE ∆的面积是9,则(k = )A .92B .274C .245D .122.(2019春•姑苏区校级期末)将一次函数y x =图象向下平移b 个单位,与双曲线y =交于点A ,与x 轴交于点B ,则22(OA OB -= )A .-B .C .D 3.(2019春•姑苏区期末)如图,四边形OABC 和四边形BDEF 都是正方形,反比例函数ky x=在第一象限的图象经过点E ,若两正方形的面积差为12,则k 的值为( )A .12B .6C .12-D .84.(2019春•广陵区校级期末)如图,已知点A 是一次函数2y x =的图象与反比例函数k y x=的图象在第一象限内的交点,AB x ⊥轴于点B ,点C 在x 轴的负半轴上,且ACB OAB ∠=∠,OAB ∆的面积为4,则点C 的坐标为( )A .(8,0)-B .(6,0)-C .11(2-,0) D .9(2-,0)二.填空题(共4小题)5.(2019春•常熟市期中)点(,)P m n 是函数3y x =-和142y x =+图象的一个交点,则2mn n m +-的值为 .6.(2019•姑苏区校级模拟)6y kx =-的图象与x ,y 轴交于B 、A 两点,与ky x=的图象交于C 点,CD x ⊥轴于D 点,如果CDB ∆的面积:AOB ∆的面积1:9=,则k = .7.(2019春•吴江区期末)已知反比例函数4y x=的图象与一次函数(3)2(0)y k x k =-+>的图象在第一象限交于点P ,则点P 的横坐标a 的取值范围为 .8.(2019•富顺县三模)如图,A 是反比例函数图象上一点,过点A 作AB y ⊥轴于点B ,点C 、D 为x 轴上动点,若3CD AB =,四边形ABCD 的面积为4,则这个反比例函数的解析式为 .三.解答题(共4小题)9.(2018秋•如皋市期末)如图,一次函数28y x =-+与函数(0)k y x x=>的图象交于(,6)A m ,(,2)B n 两点,AC y ⊥轴于C ,BD x ⊥轴于D(1)求k 的值;(2)根据图象直接写出280kx x-+-<的x 的取值范围; (3)P 是线段AB 上的一点,连接PC ,PD ,若PCA ∆和PDB ∆面积相等,求点P 坐标.10.(2018•港南区二模)如图,在ABC ∆中,5AC BC ==,8AB =,AB x ⊥轴,垂足为A ,反比例函数(0)ky x x=>的图象经过点C ,交AB 于点D .(1)若OA AB =,求k 的值;(2)若BC BD =,连接OC ,求OAC ∆的面积.11.(2019春•定安县期中)已知,在平面直角坐标系xOy 中,函数4(0)y x x=>的图象与一次函数y kx k =-的图象的交点为(,2)A m . (1)求一次函数的解析式;(2)设一次函数y kx k =-的图象与y 轴交于点B ,若P 是x 轴上一点,且满足PAB ∆的面积是6,求点P 的坐标.12.(2010春•张家港市期末)如图,点P 是反比例函数11(0k y k x=>,0)x >图象上一动点,过点P 作x 轴、y 轴的垂线,分别交x 轴、y 轴于A 、B 两点,交反比例函数22(0k y k x=<且21||)k k <的图象于E 、F 两点.(1)图1中,四边形PEOF 的面积1S = (用含1k 、2k 的式子表示); (2)图2中,设P 点坐标为(2,3).①点E 的坐标是( , ),点F 的坐标是( , )(用含2k 的式子表示); ②若OEF ∆的面积为83,求反比例函数2k y x=的解析式.11.2 反比例函数的图像及性质(例)3课时参考答案与试题解析一.选择题(共4小题)1.(2019•伊金霍洛旗一模)如图,在以O 为原点的直角坐标系中,矩形OABC 的两边OC 、OA 分别在x 轴、y 轴的正半轴上,反比例函数(0)ky x x=>与AB 相交于点D ,与BC 相交于点E ,若3BD AD =,且ODE ∆的面积是9,则(k = )A .92B .274C .245D .12【分析】所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B 的横纵坐标的积即是反比例函数的比例系数. 【解答】解:四边形OCBA 是矩形, AB OC ∴=,OA BC =,设B 点的坐标为(,)a b , 3BD AD =, (4aD ∴,)b ,点D ,E 在反比例函数的图象上,∴4ab k =,(,)k E a a∴, 1113924224ODE AOD OCE BDE OCBA ab a k S S S S S ab k b a ∆∆∆∆⎛⎫=---=-⋅--⋅⋅-= ⎪⎝⎭矩形,245k ∴=, 故选:C .2.(2019春•姑苏区校级期末)将一次函数y x =图象向下平移b 个单位,与双曲线y =交于点A ,与x 轴交于点B ,则22(OA OB -= )A .-B .C .D【分析】平移后解析式是y x b =-,代入y =求出2x bx +=,y x b =-与x 轴交点B 的坐标是(,0)b ,设A 的坐标是(,)x y ,求出222222()2()OA OB x x b b x xb -=+--=-,代入求出即可.【解答】解:平移后解析式是y x b =-,代入y =得:x b -,即2x bx -,y x b =-与x 轴交点B 的坐标是(,0)b ,设A 的坐标是(,)x y , 22OA OB ∴-222x y b =+- 222()x x b b =+-- 222x xb =-22()x xb =-2==故选:B .3.(2019春•姑苏区期末)如图,四边形OABC 和四边形BDEF 都是正方形,反比例函数ky x=在第一象限的图象经过点E ,若两正方形的面积差为12,则k 的值为( )A .12B .6C .12-D .8【分析】设正方形OABC 、BDEF 的边长分别为a 和b ,则可表示出(,)D a a b -,(,)F a b a +,根据反比例函数图象上点的坐标特征得到(,)kE a b a b++,由于点E 与点D 的纵坐标相同,所以ka b a b=-+,则22a b k -=,然后利用正方形的面积公式易得12k =. 【解答】解:设正方形OABC 、BDEF 的边长分别为a 和b ,则(,)D a a b -,(,)F a b a +, 所以(,)kE a b a b++, 所以ka b a b=-+, ()()a b a b k ∴+-=, 22a b k ∴-=,两正方形的面积差为12, 12k ∴=.故选:A .4.(2019春•广陵区校级期末)如图,已知点A 是一次函数2y x =的图象与反比例函数ky x=的图象在第一象限内的交点,AB x ⊥轴于点B ,点C 在x 轴的负半轴上,且ACB OAB ∠=∠,OAB ∆的面积为4,则点C 的坐标为( )A .(8,0)-B .(6,0)-C .11(2-,0) D .9(2-,0)【分析】设2AB x =,OB x =,根据OAB ∆的面积是4求出OB 、AB 值,证AOB CAB ∆∆∽,得出比例式,代入即可求出OC ,即可得出答案.【解答】解:A 在直线2y x =上,∴设2AB x =,OB x =,OAB ∆的面积为4,∴1242x x =, 解得:2x =,4AB ∴=,2OB =,AB OB ⊥,90ABO ABO ∴∠=∠=︒, ACB OAB ∠=∠, AOB CAB ∴∆∆∽,∴AB OBBC AB =, ∴4224OC =+,6OC ∴=,即C 的坐标是(6,0)-, 故选:B .二.填空题(共4小题)5.(2019春•常熟市期中)点(,)P m n 是函数3y x =-和142y x =+图象的一个交点,则2mn n m +-的值为 5 .【分析】联立方程组,求得交点坐标,即可知道m 与n 对于的值,代入所求式子即可; 【解答】解:函数3y x =-和142y x =+相交,3142x x ∴-=+,2860x x ∴++=,4x ∴=-4x =-,点(,)P m n 是一个交点,4m ∴=-4m =-则2n =2n =,①当4m =-2n =+时,23445mn n m +-=-+;②当4m =-2n =-时,23445mn n m +-=-+;25mn n m ∴+-=;故答案为5;6.(2019•姑苏区校级模拟)6y kx =-的图象与x ,y 轴交于B 、A 两点,与ky x=的图象交于C 点,CD x ⊥轴于D 点,如果CDB ∆的面积:AOB ∆的面积1:9=,则k = 4 .【分析】由于CDB ∆的面积:AOB ∆的面积1:9=,且两三角形相似,则13DC OA =,(2kC ,2)代入直线6y kx =-求得k 值.【解答】解:由题意得:CDB ∆的面积:AOB ∆的面积1:9=,且两三角形相似,则13DC OA =,又(0,6)A -,则(2kC ,2),代入直线6y kx =-,可得:4k =. 故答案为:4.7.(2019春•吴江区期末)已知反比例函数4y x=的图象与一次函数(3)2(0)y k x k =-+>的图象在第一象限交于点P ,则点P 的横坐标a 的取值范围为 23a << .【分析】求出一次函数图象过点(3,2)根据0k >得出直线向上倾斜,求出两函数图象的交点坐标是(2,2),即可得出答案.【解答】解:当3x =时,(33)22y k =-+=, 即一次函数过点(3,2), 0k >,∴一次函数的图象向上倾斜,当一次函数的图象垂直x 轴时,即3x =,当一次函数的图象垂直y 轴时,即2y =, 即一次函数的图象和反比例函数4y x=图象的交点坐标是(2,2), 向上倾斜则在他们之间, 23a ∴<<,故答案为:23a <<.8.(2019•富顺县三模)如图,A 是反比例函数图象上一点,过点A 作AB y ⊥轴于点B ,点C 、D 为x 轴上动点,若3CD AB =,四边形ABCD 的面积为4,则这个反比例函数的解析式为 2y x=.【分析】如图,连接BD 、OA .由于同底等高的两个三角形面积相等,所以AOB ∆的面积ABD =∆的面积1=,然后根据反比例函数ky x=中k 的几何意义,知AOB ∆的面积1||2k =,从而确定k 的值,求出反比例函数的解析式. 【解答】解:设该反比例函数的解析式为(0,0)ky k x x=≠>,点(A x 、)y .AB x =,3CD AB =,四边形ABCD 的面积为4, 33BCD ABD AOB S S S ∆∆∆∴==, 1ABD AOB S S ∆∆==,∴1||12k =, 2k ∴=±;又反比例函数的图象的一支位于第一象限, 0k ∴>. 2k ∴=.∴这个反比例函数的解析式为2y x=;故答案为:2y x=.三.解答题(共4小题)9.(2018秋•如皋市期末)如图,一次函数28y x =-+与函数(0)ky x x=>的图象交于(,6)A m ,(,2)B n 两点,AC y ⊥轴于C ,BD x ⊥轴于D(1)求k 的值;(2)根据图象直接写出280kx x-+-<的x 的取值范围; (3)P 是线段AB 上的一点,连接PC ,PD ,若PCA ∆和PDB ∆面积相等,求点P 坐标.【分析】(1)根据一次函数28y x =-+的图象经过(,6)A m ,(,2)B n 两点,得到关于m 和n 的一元一次方程,解之,即可得到m 和n 的值,把点A 和点B 的坐标代入函数ky x=,解之,即可得到k 的值, (2)280k x x -+-<,即28kx x-+<,根据图象,结合点A 和点B 的坐标,即可得到答案,(3)设直线28y x =-+上点P 的坐标为(,28)x x -+.由PCA ∆和PDB ∆面积相等,得到关于x 的一元一次方程,解之即可.【解答】解:(1)一次函数28y x =-+的图象经过(,6)A m ,(,2)B n 两点, 286m ∴-+=,282n -+=,解得:1m =,3n =,函数(0ky x x=>的图象经过(,6)A m ,(,2)B n 两点,6k ∴=,(2)280kx x-+-<, 即28k x x-+<, 由图象可知:x 的取值范围为01x <<或3x >,(3)设直线28y x =-+上点P 的坐标为(,28)x x -+.由PCA ∆和PDB ∆面积相等, 11||||22A P B p AC y y BD x x ⨯⨯-=⨯⨯-,即111[6(28)]2(3)22x x ⨯⨯--+=⨯⨯-, 解得:2x =, 则284y x =-+=,∴点P 的坐标为(2,4).10.(2018•港南区二模)如图,在ABC ∆中,5AC BC ==,8AB =,AB x ⊥轴,垂足为A ,反比例函数(0)ky x x=>的图象经过点C ,交AB 于点D .(1)若OA AB =,求k 的值;(2)若BC BD =,连接OC ,求OAC ∆的面积.【分析】(1)过点C 作CE AB ⊥于点E ,CF OA ⊥于F ,则C F A E=.由8AB =,AC BC =,CE AB ⊥,可得4AE BE CF ===,可求C 点坐标,即可求k 的值.(2)设A 点坐标为(,0)m ,则C ,D 两点坐标分别为(3,4)m -,(,3)m ,由C ,D 是反比例函数(0)ky x x=>的图象上的点.可求m 的值,即可求A ,C 坐标,可得OAC ∆的面积.【解答】解:(1)过点C 作CE AB ⊥于点E ,CF OA ⊥于F ,则CF AE =8AB =,AC BC =,CE AB ⊥ 4BE AE CF ∴=== 5AC BC == 3CE ∴= 8OA AB == 5OF ∴=∴点(5,4)C点C 在ky x=图象上 20k ∴=(2)5BC BD ==,8AB = 3AD ∴=设A 点坐标为(,0)m ,则C ,D 两点坐标分别为(3,4)m -,(,3)m C ,D 在ky x=图象上 4(3)3m m ∴-= 12m ∴=(12,0)A ∴,(9,4)C ,(12,3)D 1124242AOC S ∆∴=⨯⨯=11.(2019春•定安县期中)已知,在平面直角坐标系xOy 中,函数4(0)y x x=>的图象与一次函数y kx k =-的图象的交点为(,2)A m . (1)求一次函数的解析式;(2)设一次函数y kx k =-的图象与y 轴交于点B ,若P 是x 轴上一点,且满足PAB ∆的面积是6,求点P 的坐标.【分析】(1)将A 点坐标代入4(0)y x x=>,求出m 的值为2,再将(2,2)代入y kx k =-,求出k 的值,即可得到一次函数的解析式;(2)将三角形以x 轴为分界线,分为两个三角形计算,再把它们相加. 【解答】解:(1)根据题意,将点(,2)A m 代入4y x=, 得:42m=, 解得:2m =, 即点(2,2)A ,将点(2,2)A 代入y kx k =-,得:22k k =-, 解得:2k =,∴一次函数的解析式为22y x =-;(2)如图,一次函数22y x =-与x 轴的交点为(1,0)C ,与y 轴的交点为(0,2)B -, ABP ACP BPC S S S ∆∆∆=+,∴1122622CP CP ⨯+⨯=, 解得3CP =,则P 点坐标为(4,0),(2,0)-.12.(2010春•张家港市期末)如图,点P 是反比例函数11(0k y k x=>,0)x >图象上一动点,过点P 作x 轴、y 轴的垂线,分别交x 轴、y 轴于A 、B 两点,交反比例函数22(0k y k x=<且21||)k k <的图象于E 、F 两点.(1)图1中,四边形PEOF 的面积1S = 12k k - (用含1k 、2k 的式子表示); (2)图2中,设P 点坐标为(2,3).①点E 的坐标是( , ),点F 的坐标是( , )(用含2k 的式子表示); ②若OEF ∆的面积为83,求反比例函数2k y x=的解析式.【分析】(1)根据反比例函数中比例系数k 的几何意义即可解答;(2)①根据PE x ⊥轴,PF y ⊥轴可知,P 、E 两点的横坐标相同,P 、F 两点的纵坐标相同,分别把P 点的横纵坐标代入反比例函数2k y x=即可求出E 、F 两点的坐标; ②先根据P 点的坐标求出1k 的值,再由E 、F 两点的坐标用2k 表示出PE 、PF 的长,再用2k 表示出PEF ∆的面积,把(1)的结论代入求解即可.【解答】解:(1)P 是点P 是反比例函数11(0k y k x=>,0)x >图象上一动点,1PBOA S k ∴=矩形, E 、F 分别是反比例函数22(0k y k x=<且21||)k k <的图象上两点, 21||2OBF AOE S S k ∆∆∴==, ∴四边形PEOF 的面积112OBF AOE PBOA S S S S k k ∆∆=++=+矩形,20k <,∴四边形PEOF 的面积11212OBF AOE PBOA S S S S k k k k ∆∆=++=+=-矩形.(2)①PE x ⊥轴,PF y ⊥轴可知,P 、E 两点的横坐标相同,P 、F 两点的纵坐标相同,E ∴、F 两点的坐标分别为2(2,)2k E ,2(3kF ,3);②(2,3)P 在函数1k y x=的图象上, 16k ∴=,E 、F 两点的坐标分别为2(2,)2k E ,2(3kF ,3); 232k PE ∴=-,223k PF =-, 2222(6)1(3)(2)22312PEF k k k S ∆-∴=--=, 2212(6)()12OEFk S k k ∆-∴=--222(6)(6)12k k -=--22368123k -==,20k <, 22k ∴=-.∴反比例函数2k y x =的解析式为2y x=-.考点卡片1.两点间的距离公式两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB.说明:求直角坐标系内任意两点间的距离可直接套用此公式.2.反比例函数系数k的几何意义比例系数k的几何意义在反比例函数y图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.3.反比例函数与一次函数的交点问题反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.(2)判断正比例函数y=k1x和反比例函数y在同一直角坐标系中的交点个数可总结为:①当k1与k2同号时,正比例函数y=k1x和反比例函数y在同一直角坐标系中有2个交点;②当k1与k2异号时,正比例函数y=k1x和反比例函数y在同一直角坐标系中有0个交点.4.等腰三角形的性质(1)等腰三角形的概念有两条边相等的三角形叫做等腰三角形.(2)等腰三角形的性质①等腰三角形的两腰相等②等腰三角形的两个底角相等.【简称:等边对等角】③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】(3)在①等腰;②底边上的高;③底边上的中线;④顶角平分线.以上四个元素中,从中任意取出两个元素当成条件,就可以得到另外两个元素为结论.5.正方形的性质(1)正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.(2)正方形的性质①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③正方形具有四边形、平行四边形、矩形、菱形的一切性质.④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.。
九年级数学反比例函数第3课时反比例函数的图象和性质(2)(课堂导练)课件(新版)新人教版

Page 7
,∴6=xy.
分别把点B,C的坐标代入,得
变式练习
3.已知反比例函数的图象经过P(﹣2,3).
(1)求此反比例函数的解析式; 设反比例函数的解析式为y= 把P(﹣2,3)代入y= 所以反比例函数解析式为y=﹣ ,
得k=﹣2×3=﹣6, .
Page 12
巩固提高
8.如图,已知反比例函数y= 的图象经过点A (﹣3,﹣2). (1)求反比例函数的解析式; 因为反比例函数y= 的图象
经过点A(﹣3,﹣2), 把x=﹣3,y=﹣2代入解析式 可得k=6, 所以解析式为y= .
Page 13
巩固提高
(2)若点B(1,m),C(3,n)在该函数的 图象上,试比较m与n的大小.
Page 15
,6), .
中得k=4,则反比例解析式为y=
巩固提高
(2)说出双曲线y= 所在的象限以及在每
个象限内y随x值的增大而变化的情况. ∵y= ,且k=4>0,
∴此函数的图象在第一、三象限,在每 个象限内y随x的增大而减小.
Page
16
巩固提高
10.如图,反比例函数y=
经过点A(1,3).
精典范例
例1.反比例函数y= A.y1<y2 B.y1>y2
C.y1=y2 D.不能确定
的图象经过点(﹣1,y1), A
(2,y2),则下列关系正确的是( )
Page
1
变式练习
1.点(x1,3),(x2,﹣2)在反比例函数
y=﹣ 的图象上,则下列一定正确的是( C ).
A.x1>x2 B.x1≥x2
∵k=6>0, ∴图象在一、三象限,y随x的增大而在第一象限, ∴m>n.
反比例函数第三四课时
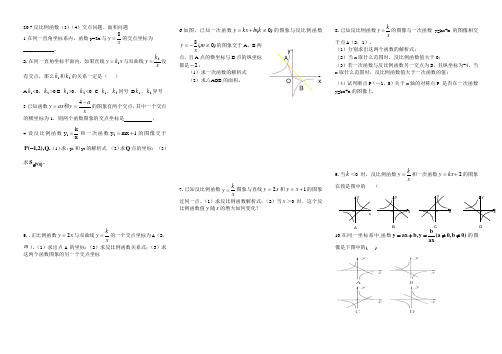
20.7反比例函数(3)(4)交点问题、面积问题 1.在同一直角坐标系内,函数y=2x 与xy 8=的交点坐标为____________。
2.在同一直角坐标平面内,如果直线x k y 1=与双曲线xk y 2=没有交点,那么1k 和2k 的关系一定是( )A 1k <0,2k >0B 1k >0,2k <0C 1k 、2k 同号D 1k 、2k 异号 3.已知函数xa y ax y -==4和的图象有两个交点,其中一个交点的横坐标为1,则两个函数图象的交点坐标是 ; 4.设反比例函数1k y x=和一次函数2y m x 1=+的图像交于.Q ),2,1(P -(1)求:y 1和y 2的解析式. (2)求Q 点的坐标; (3)求.S POQ ∆5..正比例函数x y 2=与双曲线xk y =的一个交点坐标为A (2,m )。
(1)求出点A 的坐标;(2)求反比例函数关系式;(3)求这两个函数图象的另一个交点坐标6.如图,已知一次函数)0(≠+=k b kx y 的图象与反比例函数)0(8≠-=m xy 的图象交于A ,B 两点,且A 点的横坐标与B 点的纵坐标都是2-;(1)求一次函数的解析式(2)求△AOB 的面积。
7.已知反比例函数xk y =图象与直线x y 2=和1+=x y 的图象过同一点。
(1)求反比例函数解析式;(2)当x >0时,这个反比例函数值y 随x 的增大如何变化?8.已知反比例函数k y x=的图像与一次函数y=kx+m 的图像相交于点A (2,1).(1)分别求出这两个函数的解析式;(2)当x 取什么范围时,反比例函数值大于0;(3)若一次函数与反比例函数另一交点为B ,且纵坐标为-4,当x 取什么范围时,反比例函数值大于一次函数的值;(4)试判断点P (—1,5)关于x 轴的对称点P ‘是否在一次函数y=kx+m 的图像上.9.当k <0时,反比例函数xk y =和一次函数2+=kx y 的图象在致是图中的 (10.在同一坐标系中,函数)0b ,0a (axb y ,b ax y ≠≠=+=的图像是下图中的()ABCD11.已知一次函数y=kx+b 的图象经过第二、三、四象限,则反比例函数kb y x=的图象在( )A.第一、二象限; B .第三、四象限; C .第一、三象限; D .第二、四象限. 12.若0<ab ,则函数ax y =与xb y =在同一平面直角坐标系中的图象大致是( )13.反比例函数)0k (xk y >=在第一象限内的图像如图30-2-1所示,点M 是图像上一点,MP 垂直x 轴于点P ,如果MOP ∆的面积为2,那么k 的值是( )14.如图30-2-2所示,P 是反比例函数xk y =图像上一点,过P 分别向x 轴、y 轴引垂线,若5S =阴,则解析式为 。
第三课时反比例函数的图象和性质

06
CATALOGUE
总结回顾与下节课预告
总结本节课重点内容
反比例函数概念
理解并掌握反比例函数 $y=frac{k}{x}$($k neq 0$)的
定义。
图象特征
掌握反比例函数图象为双曲线,当 $k>0$时,图象分布在第一、三象 限;当$k<0$时,图象分布在第二 、四象限。
性质分析
理解反比例函数在其定义域内的单 调性,以及函数值随自变量变化的 规律。
第三课时反比例 函数的图象和性 质
汇报人:XXX 2024-01-29
目录
• 引言 • 反比例函数图象 • 反比例函数性质 • 反比例函数在实际问题中应用 • 课堂练习与巩固提高 • 总结回顾与下节课预告
01
CATALOGUE
引言
回顾上节课内容
上节课我们学习了正比例函数的概念 、图象和性质。
正比例函数的图象是一条经过原点的 直线,且当k>0时,图象经过第一、 三象限;当k<0时,图象经过第二、 四象限。
CATALOGUE
反比例函数在实际问题中应用
物理学中反比例关系问题解决方法
利用反比例函数描述物理量之间的关系
在物理学中,有些物理量之间存在反比例关系,如电阻与电流、压力与体积等。通过构建反比例函数模型,可以 准确地描述这些物理量之间的关系。
求解物理问题中的未知量
根据已知的物理量和反比例函数关系,可以求解未知的物理量。例如,已知电阻和电流的关系,可以求解未知电 压。
案。
05
CATALOGUE
课堂练习与巩固提高
基础知识练习题
题目1
已知反比例函数 $y = frac{k}{x}$( $k neq 0$),当 $x = 2$ 时,$y = 3$,求 $k$ 的值。
沪科九年级数学上册第21章5 第3课时 反比例函数的比例系数k的几何意义与应用

O
x
下列反比例函数:
2
①y
x
1
②y
3x
10
③7y
x
3
④y
100 x
(3)若0<x1<x2,则y1<y2的函数是 ① ③ ;
(4)若x1<x2<0,则y1>y2的函数是 ② ④ ;
1
10
① k 2 0 ② k 0 ③ k
0
3
7
④k
y
O
3
0
100
k
y (k 0)
x
k>0
反比例函数
k<0
双曲线
函数图象分别位于一、三象限;
在每一个象限内,y随x的增大而减小.
函数图象分别位于二、四象限;
在每一个象限内,y随x的增大而增大.
下列反比例函数:
2
①y
x
1
②y
3x
10
③7y
x
3
④y
100 x
(1)图象位于第一、三象限的是 ② ④ ;
(3)若0<x1<x2,则y1<y2的函数是 ① ③ ;
(4)若x1<x2<0,则y1>y2的函数是 ② ④ ;
1
10
① k 2 0 ② k 0 ③ k
0
3
7
k>0
在每一个象限内,y随x的增大而减小;
k<0
在每一个象限内,y随x的增大而增大.
3
0
④k
100
下列反比例函数:
k
过反比例函数 y (k≠0)图象上一点作坐标轴的垂线,则该点、
沪科版数学九年级上册21.5反比例函数 课件(共34张PPT)

如图,是反比例函数 图象的一支.根据图象,回答下列问题:(1)图象的另一支位于哪个象限?常数m的取值范围是什么?解:因为这个反比例函数图象的一支位于第一象限,所以另一支必位于第三象限.又因为这个函数图象位于第一、三象限,所以m-5>0,解得m>5.
(2)在这个函数图象的某一支上任取点A( )和点B( ).如果 ,那么 和 有怎样的大小关系?解:∵m-5>0, ∴在这个函数图象的任一支上,y都随x的增大而减小, ∴当 时, .
当k>0时,y随x的增大而减小;当k<0时,y随x的增大而增大
练一练
1.如果反比例函数 的图象位于第二、四象限内,那么满足条件的正整数k的值是_______.2.已知直线y=kx+b 的图象经过第一、二、四象限,则函数 的图象在第________象限.3.在反比例函数 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是________.
24
(1)(3)
3.已知一次函数y=kx+b的图象如图所示,那么正比例函数y=kx和反比例函数 在同一平面直角坐标系中的图象大致是( )
C
4.已知反比例函数 (k为常数,k≠1)若点A(1,2)在这个函数的图象上,求k的值.若在这个函数图象的每一支上,y随x的增大而减小,求k的取值范围.若k=13,试判断点B(3,4),C(2,5),B点是否在这个函数的图象上,并说明理由.解:(1)代入A(1,2)得k-1=2,k=3; (2)k-1>0,k>1; (3) 代入B(3,4),C(2,5),B点在函数图象上,C点不在.
C
A
3.若函数 是反比例函数,则m的值是_____.4.在下列函数表达式中,x均表示自变量,那么哪些是y关于x的反比例函数?其相应的k的值是多少?① ;② ;③xy=2;④ ;⑤ y关于x的反比例函数有①②③;对应的k值分别为2.5,;2;7
第3课时反比例函数y=k∕x(k≠0)的图象与性质

第1章 反比例函数 1.2 反比例函数的图象与性质第3课时 反比例函数y =kx(k ≠0)的图象与性质知识点 1 反比例函数y =kx (k ≠0)的图象与性质1.反比例函数y =a 2+1x (a 是常数)的图象分布在( )A .第一、二象限B .第一、三象限C .第二、四象限D .第三、四象限2.若函数y =m +2x 的图象在其所在的每一象限内,函数值y 随自变量x 的增大而增大,则m 的取值范围是( )A .m <-2B .m <0C .m >-2D .m >03.下列关于反比例函数y =21x的三个结论:①它的图象经过点(7,3);②在其图象所在的每一个象限内,y 随x 的增大而减小;③它的图象在第二、四象限内.其中正确的是________(填序号).知识点 2 反比例函数表达式的确定4.已知反比例函数y =k x 的图象经过点(3,-4),把点(3,-4)代入y =kx ,得____________,解得k =________,所以这个反比例函数的表达式为________.5.如图1-2-6,反比例函数y =kx的图象经过点M ,则此反比例函数的表达式为( )图1-2-6A .y =-12xB .y =12xC .y =-2xD .y =2x6.已知变量x ,y 满足下面的关系,则x ,y 之间的函数表达式为( )x … -3 -2 -1 1 2 3 … y…11.53-3-1.5-1…A.y =3x B .y =-x 3C .y =-3xD .y =x 3知识点 3 反比例函数表达式中k 的几何意义图1-2-77.如图1-2-7,过反比例函数y =kx的图象上一点P (x ,y )分别作x 轴、y 轴的垂线PM ,PN ,所得的矩形PMON 的面积为3,由于矩形PMON 的面积S =PM ·PN =|y |·|x |=|xy |=3.又∵y =kx,k <0,∴k =xy =________.8.如图1-2-8,点A 是反比例函数图象上任意一点,AM ⊥x 轴,垂足为M ,O 是原点.若△AOM 的面积为3,求这个反比例函数的表达式.图1-2-8知识点 4 反比例函数与一次函数的综合9.正比例函数y =-2x 的图象与反比例函数y =-2x 的图象的交点位于( )A .第一、二象限B .第二、四象限C .第二、三象限D .第一、三象限10.函数y =x 与y =2x在同一坐标系中的大致图象是( )图1-2-9 图1-2-1011.已知一次函数y =kx +b (k ≠0)与反比例函数y =kx (k ≠0)在同一直角坐标系中的大致图象如图1-2-10所示,则k ,b 的取值范围是( )A .k >0,b >0B .k <0,b >0C .k <0,b <0D .k >0,b <012.2019·永州在同一平面直角坐标系中,函数y =x +k 与y =kx (k 为常数,k ≠0)的图象大致是( )图1-2-1113.2019·宁夏如图1-2-12,正比例函数y 1=k 1x 的图象与反比例函数y 2=k 2x 的图象相交于A ,B 两点,其中点B 的横坐标为-2,当y 1<y 2时,x 的取值范围是图1-2-12A .x <-2或x >2B .x <-2或0<x <2C .-2<x <0或0<x <2D .-2<x <0或x >214.在平面直角坐标系中,落在第一象限的等腰直角三角形的两底角的顶点坐标分别为(1,1),(5,1),它的底边与反比例函数y =kx的图象始终有交点,则k 的取值范围是________.15.如图1-2-13,一次函数y =kx +b 与反比例函数y =mx 的图象相交于A (2,3),B (-3,n )两点.(1)求一次函数与反比例函数的表达式;(2)过点B 作BC ⊥x 轴,垂足为C ,求S △ABC .图1-2-1316.2019·泸州一次函数y =kx +b (k ≠0)的图象经过点A (2,-6),且与反比例函数y =-12x的图象交于点B (a ,4).(1)求一次函数的表达式;(2)将直线AB 向上平移10个单位后得到直线l :y 1=k 1x +b 1(k 1≠0),l 与反比例函数y 2=6x的图象相交,求使y 1<y 2成立的x 的取值范围. 17.如图1-2-14,已知直线y =12x 与反比例函数y =kx (k >0)的图象交于A ,B 两点,且点A 的横坐标为4.(1)求k 的值;(2)若反比例函数y =kx(k >0)的图象上一点C 的纵坐标为8,求△AOC 的面积.图1-2-141.B2. A [解析] ∵函数y =m +2x 的图象在其所在的每一象限内,函数值y 随自变量x 的增大而增大,∴m +2<0,解得m <-2.故选A.3.①② [解析] ①∵7×3=21,∴它的图象经过点(7,3),故①正确.②∵k =21>0,∴在每一个象限内,y 随x 的增大而减小,故②正确.③它的图象应在第一、三象限,故③错误.故答案为①②.4.-4=k 3 -12 y =-12x5.C6.C [解析]设x ,y 之间的表达式为y =kx (k ≠0).把x =-3,y =1代入得k =-3, 故x ,y 之间的函数表达式为y =-3x .将其他各组数据代入,均符合. 故选C. 7.-38.解:∵点A 在反比例函数的图象上, ∴S △AOM =12|k |,∴3=12|k |,∴|k |=6.又∵反比例函数的图象经过第二象限,∴k =-6.故这个反比例函数的表达式为y =-6x.9.B [解析] ∵正比例函数y =-2x 与反比例函数y =-2x 的比例系数均为-2,-2<0,∴两函数的图象都经过第二、四象限,∴两函数的图象的交点有两个,分别位于第二、四象限.故选B.10.D11. C [解析] ∵一次函数y =kx +b (k ≠0)的图象经过第二、三、四象限,∴k <0,b <0.又∵反比例函数y =kx(k ≠0)的图象经过第二、四象限,∴k <0.综上所述,k <0,b <0.故选C. 12.B 13. B [解析] ∵正比例函数的图象和反比例函数的图象均关于原点O 对称,且点B 的横坐标为-2,∴点A 的横坐标为2.观察函数图象,发现:当x <-2或0<x <2时,一次函数的图象在反比例函数图象的下方,∴当y 1<y 2时,x 的取值范围是x <-2或0<x <2.故选B.14.1≤k ≤5 [解析] 当反比例函数y =kx 的图象经过点(1,1)时,得k =1,当反比例函数y =kx的图象经过点(5,1)时,得k =5,∴k 的取值范围是1≤k ≤5.故答案为1≤k ≤5.15.解:(1)∵点A (2,3)在函数y =mx 的图象上,∴m =6,∴反比例函数的表达式为y =6x ,∴n =6-3=-2.∵点A (2,3),B (-3,-2)在函数y =kx +b 的图象上,∴⎩⎪⎨⎪⎧3=2k +b ,-2=-3k +b ,解得⎩⎪⎨⎪⎧k =1,b =1, ∴一次函数的表达式为y =x +1.(2)设直线AB 交x 轴于点D ,则点D 的坐标为(-1,0), ∴CD =2,∴S △ABC =S △BCD +S △ACD =12×2×2+12×2×3=5.16.[解析] (1)根据点B 的纵坐标,利用反比例函数图象上点的坐标特征可求出点B 的坐标,根据点A ,B 的坐标,利用待定系数法即可求出直线AB 的函数表达式.(2)根据“上加下减”求出直线l 的表达式,联立直线l 和反比例函数的表达式组成方程组,解方程组可找出交点坐标,画出函数图象,根据两函数图象的上下位置关系即可找出使y 1<y 2成立的x 的取值范围.解:(1)∵反比例函数y =-12x 的图象过点B (a ,4),∴4=-12a,解得a =-3, ∴点B 的坐标为(-3,4).将A (2,-6),B (-3,4)的坐标代入y =kx +b ,得⎩⎪⎨⎪⎧2k +b =-6,-3k +b =4,解得⎩⎪⎨⎪⎧k =-2,b =-2, ∴一次函数的表达式为y =-2x -2.(2)将直线AB 向上平移10个单位后得到直线l :y 1=-2x +8. 联立直线l 和反比例函数的表达式组成方程组, 得⎩⎪⎨⎪⎧y =-2x +8,y =6x,解得⎩⎪⎨⎪⎧x =1,y =6或⎩⎪⎨⎪⎧x =3,y =2.∴直线l 与反比例函数图象的交点坐标为(1,6)和(3,2). 画出函数图象,如图所示.观察函数图象可知:当0<x <1或x >3时,反比例函数图象在直线l 的上方, ∴使y 1<y 2成立的x 的取值范围为0<x <1或x >3.17.解:(1)∵点A 的横坐标为4,当x =4时,y =12×4=2,∴点A 的坐标为(4,2).∵点A 是直线y =12x 与反比例函数y =kx 的图象的交点,∴k =8.(2)∵点C 在函数y =8x 的图象上,当y =8时,x =1,∴点C 的坐标为(1,8).如图,过点A 作AM ⊥x 轴,过点C 作CN ⊥y 轴,垂足分别为M ,N ,延长MA ,NC 相交于点D ,得矩形ONDM ,S 矩形ONDM =32,S △ONC =4,S △CDA =9,S △OAM =4,S △AOC =S 矩形ONDM -S △ONC -S △CDA -S △OAM =32-4-9-4=15.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18.4.3反比例函数(3课时) (设计人:刘颖----2013.3.21) 【课程目标】
【教学过程】
能力知识思维框架
探究
灵活运用
使学生进一步理解和掌握反比例函数及其图象与性质
能灵活运用函数图象和性质解决一些较综合的问题
10ˊ间的联系,
体会数形结
合及转化的
思想方法
从反比例函数
x
k
y=(k≠0)的图象
上任一点P(x,y)向x轴、y轴作垂线
段,与x轴、y轴所围成的矩形面积
k
xy
S=
=
,
例3.如图,过反比例函数
x
y
1
=(x>0)的图
象上任意两点A、B分别作x轴的垂线,垂足分别为
C、D,连接OA、OB,设△AOC和△BOD的面积分别
是S
1
、S
2
,比较它们的大小,可得()
(A)S
1
>S
2
(B)S
1
=S
2
(C)S
1
<S
2
(D)大小关系不能确定
=;当x<-2时;y的取值范围
是;当x>-2时;y的取值范围是
3.已知反比例函数y a x a
=--
()226,当
x>0时,y随x的增大而增大,求函数
关系式
4已知反比例函数y=
3m
x
-
的两点
(x
1
,y
1
),(x
2
,y
2
),当x
1
<0<x
2
时,y
1
<y
2
,则m•的取值
范围是(D)
A.m<0
B.m>0
C.m>3
D.m<3
5下列四个函数中,当x>0时,y随x的增大而减
小的是(D)
A.y=2x
B.y=x+3
C.y=-
2
x
D.y=
2
x
6.已知反比例函数
x
m
y
3
+
=经过点A(2,-m)
和B(n,2n),求:
(1)m和n的值;
(2)若图象上有两点P1(x1,y1)和P2(x2,y2),且
x
1
<0< x2,试比较y1和 y2的大小.
5ˊ
本节课学习了画反比例函数的图象和探讨了反比例
函数的性质.
1.反比例函数的图象是双曲线(hyperbola).
2.反比例函数有如下性质:
(1)当k>0时,函数的图象在第一、三象限,在每个
象限内,曲线从左向右下降,也就是在每个象限内y随x的增加而减少;
(2)当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是在每
个象限内y随x的增加而增加.
教学反思:
知识框架
知识梳理例题。
