电磁场计算题
电磁场理论习题

电磁场理论习题一1、求函数ϕ=xy+z-xyz 在点(1,1,2)处沿方向角πα=3,4πβ=,3πγ=的方向的方向导数.解:由于 M ϕ∂∂x =y -M yz = -1M y ϕ∂∂=2x y -(1,1,2)xz =0 Mzϕ∂∂=2z(1,1,2)xy -=31cos 2α=,cos 2β=,1cos 2γ=所以1cos cos cos =∂∂+∂∂+∂∂=∂∂γϕβϕαϕϕz y x lM2、 求函数ϕ=xyz 在点(5, 1, 2)处沿着点(5, 1, 2)到点(9, 4, 19)的方向的方向导数。
解:指定方向l 的方向矢量为l =(9-5) e x +(4-1)e y +(19-2)e z =4e x +3e y +17e z其单位矢量zy x z y x e e e e e e l 314731433144cos cos cos ++=++=γβα5,10,2)2,1,5(==∂∂==∂∂==∂∂MMMMMxyzxzyyzxϕϕϕ所求方向导数314123cos cos cos =•∇=∂∂+∂∂+∂∂=∂∂ l z y x lMϕγϕβϕαϕϕ3、 已知ϕ=x 2+2y 2+3z 2+xy+3x-2y-6z ,求在点(0,0,0)和点(1,1,1)处的梯度。
解:由于ϕ∇=(2x+y+3) e x +(4y+x-2)e y +(6z-6)e z所以,(0,0,0)ϕ∇=3e x -2e y -6e z(1,1,1)ϕ∇=6e x +3e y4、运用散度定理计算下列积分:2232[()(2)]x y z sxz e x y z e xy y z e ds+-++⎰⎰I=S 是z=0 和 z=(a 2-x 2-y 2)1/2所围成的半球区域的外表面。
解:设:A=xz 2e x +(x 2y-z 3)e y +(2xy+y 2z)e z 则由散度定理Ω∇⎰⎰⎰⎰⎰sA ds=Adv可得2I r dvΩΩΩ=∇==⎰⎰⎰⎰⎰⎰⎰⎰⎰222Adv (z +x +y )dv2244220sin sin aar drd d d d r dr ππππθθϕϕθθ==⎰⎰⎰⎰⎰⎰525a π=5、试求▽·A 和▽×A:(1) A=xy 2z 3e x +x 3ze y +x 2y 2e z(2)22(,,)cos sin z A z e e ρρφρφρφ=+ (3 ) 211(,,)sin sin cos r A r r e e e r r θφθφθθθ=++解:(1)▽·A=y 2z 3+0+0= y 2z 3▽×A=23232(2)(23)x yx y x e xy xy z e ∂∂∂=---∂∂∂x y z23322e e e x y z xy z x z x y(2) ▽·A=()[()]z A A A z φρρρρρφ∂∂∂++∂∂∂1 =33[(cos )(sin )]ρφρφρρφ∂∂+∂∂1=3cos ρφ▽×A=ρφρφρρρφρ∂∂∂∂∂∂z ze e e 1z A A A =221cos 0ρφρρρφρφρφ∂∂∂∂∂∂z e e e z sin=cos 2sin sin ze e e ρφρφρφρφ-+(3) ▽·A=22(sin )()1[sin ]sin r A A r A r r r r φθθθθθφ∂∂∂++∂∂∂ =2322sin cos ()()1(sin )[sin ]sin r r r r r r r θθθθθθφ∂∂∂++∂∂∂ =222212[3sin 2sin cos ]3sin cos sin r r r θθθθθθ+=+▽×A=21sin rr r r rr θφθφθθθφθ∂∂∂∂∂∂e e rsin e A A rsin A =21sin 1sin sin cos rr r r r θφθθθφθθθθ∂∂∂∂∂∂e e rsin e rsin=33cos 2cos cos sin r e e e r r θφθθθθ+-习题二1、总量为q 的电荷均匀分布于球体中,分别求球内,外的电场强度。
电磁场练习题电荷分布与电场强度计算

电磁场练习题电荷分布与电场强度计算电磁场练习题:电荷分布与电场强度计算一、电荷分布式例题考虑一个均匀带电细杆,长度为L,总电荷为Q。
假设杆的线密度为λ,即单位长度上的电荷量。
我们需要计算杆上某一点P的电场强度。
解答:我们可以将细杆分割成无数个微小长度为Δx的小元素。
设其中一段微小长度Δx上的电荷量为Δq。
由于杆是均匀带电的,每个微小电荷的电荷量应该为:Δq = λΔx根据库仑定律,电荷元素Δq在距离Δx处产生的电场强度为:ΔE = k * (Δq / r²)其中,k为库仑常数,r为Δq到点P的距离。
由于每一小段Δx上的电荷都在同一直线上,且距离P相等,我们可以将所有微小电荷元素的电场强度进行叠加,计算总的电场强度EP:EP = ∑(ΔE) = ∫(k * λΔx / r²)这里的积分表示对整个带电细杆进行累加。
考虑带电细杆在点P的两侧对称,根据几何关系,我们可以将积分区间从-L/2到L/2进行重新定义。
于是,上述电场强度的积分可以写成:EP = ∫(k * λΔx / r²) = k * λ∫(Δx / r²)对于Δx这一微小长度的杆元素,根据几何关系,可以得到:r = √(Δx² + s²)其中,s为点P到杆上微小元素Δx的垂直距离。
进一步,我们可以将Δx替换为L,从而得到:r = √(L² + s²)将以上内容整理,最终我们可以得到带电细杆在点P处的电场强度EP的表达式:EP = k * λ∫(L / (L² + s²)^(3/2))这就是求解带电细杆在点P处电场强度的公式。
在具体计算时,我们可以通过数值积分来进行求解。
二、电荷均匀球壳的电场强度计算考虑一个半径为R、带电量为Q的匀强带电球壳,我们需要计算球壳外某一点P处的电场强度。
解答:由于球壳是均匀带电的,在球壳上任意一点处ΔS的面元上的电荷量Δq应该是相等的,即Δq = Q / 4πR² * ΔS。
电磁场章习题
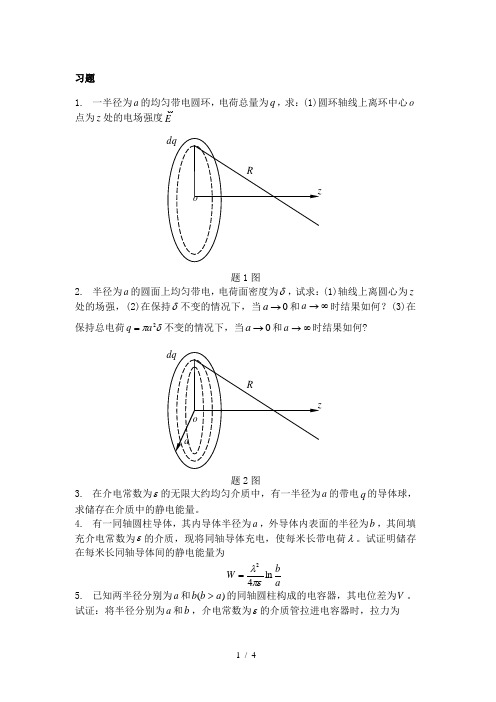
习题1. 一半径为a 的均匀带电圆环,电荷总量为q ,求:(1)圆环轴线上离环中心o点为z 处的电场强度E题1图2. 半径为a 的圆面上均匀带电,电荷面密度为δ,试求:(1)轴线上离圆心为z 处的场强,(2)在保持δ不变的情况下,当0→a 和∞→a 时结果如何?(3)在保持总电荷δπ2a q =不变的情况下,当0→a 和∞→a 时结果如何?题2图3. 在介电常数为ε的无限大约均匀介质中,有一半径为a 的带电q 的导体球,求储存在介质中的静电能量。
4. 有一同轴圆柱导体,其内导体半径为a ,外导体内表面的半径为b ,其间填充介电常数为ε的介质,现将同轴导体充电,使每米长带电荷λ。
试证明储存在每米长同轴导体间的静电能量为ab W ln 42πελ=5. 已知两半径分别为a 和)(a b b >的同轴圆柱构成的电容器,其电位差为V 。
试证:将半径分别为a 和b ,介电常数为ε的介质管拉进电容器时,拉力为ab V F ln )(20εεπ-=6. 求均匀极化介质圆球的极化电荷分布。
++--题6图 均匀极化介质7. 真空中一半径为R 的圆球空间内,分布有体密度为ρ的电荷,ρ为常量。
试求静电能量。
8. 今有一球形薄膜导体,半径为R ,其上带电荷q 。
求薄膜单位面积上所受膨胀力。
9. 在半径为a 的球体内,均匀分布着电荷,总电荷量为q ,求各点的电场E,并计算电场E的散度和旋度。
题9图 电荷的球体分布10. 已知电场强度如下式所示,求体电荷密度)(ερ电容率e 。
),(0033为常数E a a E ae E r <≤=ρρ11. 真空中有一电荷线密度为l ρ的圆环形均匀带电线,其半径为a 。
试求圆环(a) (b )轴线上任一场点P 处的电场强度。
题11图12. 半径为R 的空心球金属薄壳内,有一点电荷q ,离球小距离为b ,R b <,如图所示。
巳知球壳为个性,即壳内外表面总电荷为零。
求壳内外的电场。
电磁场与电磁波练习题

电磁场与电磁波练习题一、单项选择题(每小题1分,共15分)1、电位不相等的两个等位面()A. 可以相交B. 可以重合C. 可以相切D. 不能相交或相切2、从宏观效应看,物质对电磁场的响应包括三种现象,下列选项中错误的是()A.磁化B.极化C.色散D.传导3、电荷Q 均匀分布在半径为a 的导体球面上,当导体球以角速度ω绕通过球心的Z 轴旋转时,导体球面上的面电流密度为()A.sin 4q e a ?ωθπB.cos 4q e a ?ωθπC.2sin 4q e a ?ωθπD.33sin 4q e r aωθπ 4、下面说法错误的是()A.梯度是矢量, 其大小为最大方向导数,方向为最大方向导数所在的方向。
B.矢量场的散度是标量,若有一个矢量场的散度恒为零,则总可以把该矢量场表示为另一个矢量场的旋度。
C.梯度的散度恒为零。
D.一个标量场的性质可由其梯度来描述。
5、已知一均匀平面波以相位系数30rad/m 在空气中沿x 轴方向传播,则该平面波的频率为()A.81510π?HzB.8910?HzC.84510π?Hz D.9910?Hz6、坡印廷矢量表示()A.穿过与能量流动方向相垂直的单位面积的能量B.能流密度矢量C.时变电磁场中空间各点的电磁场能量密度D.时变电磁场中单位体积内的功率损耗7、在给定尺寸的矩形波导中,传输模式的阶数越高,相应的截止波长()A.越小B.越大C.与阶数无关D.与波的频率有关8、已知电磁波的电场强度为(,)cos()sin()x y E z t e t z e t z ωβωβ=---,则该电磁波为()A. 左旋圆极化波B. 右旋圆极化波C. 椭圆极化波D.直线极化波9、以下矢量函数中,可能表示磁感应强度的是()A. 3x y B e xy e y =+B.x y B e x e y =+C.22x y B e x e y =+D. x y B e y e x =+10、对于自由空间,其本征阻抗为()A. 0η=B.0η=C. 0η=D. 0η=11、自感和互感与回路的()无关。
【速度】电磁场30分钟计算题练习

【关键字】速度计算题练习11. 如图所示,质量为M的导体棒ab,垂直放在相距为l的平行光滑金属导轨上,导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中,左侧是水平放置、间距为d的平行金属板.R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻.(1)调节Rx=R,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v.(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量为m、带电量为+q的微粒水平射入金属板间,若它能匀速通过,求此时的Rx.(1)当Rx=R时,棒沿导轨匀速下滑时,由平衡条件安培力解得ab切割产生的感应电动势由闭合欧姆定律得回路中电流解得(2)微粒水平射入金属板间,能匀速通过,由平衡条件棒沿导轨匀速,由平衡条件金属板间电压解得2.如图所示,质量m1=,电阻R1=0.3Ω,长度l=的导体棒ab横放在U型金属框架上。
框架质量m2=,放在绝缘水平面上,与水平面间的动摩揩因数μ=0.2,相距的MM’、NN’相互平行,电阻不计且足够长。
电阻R2=0.1Ω的MN垂直于MM’。
整个装置处于竖直向上的匀强磁场中,磁感应强度B=0.5T。
垂直于ab施加F=2N的水平恒力,ab从静止开始无摩揩地运动,始终与MM’、NN’保持良好接触,当ab运动到某处时,框架开始运动。
设框架与水平面间最大静摩揩力等于滑动摩揩力,g取/s2.(1)求框架开始运动时ab速度v的大小;(2)从ab开始运动到框架开始运动的过程中,MN上产生的热量Q=0.1J,求该过程ab位移x的大小。
(1)对框架的压力① 框架受水平面的支持力②依题意,最大静摩揩力等于滑动摩揩力,则框架受到最大静摩揩力③中的感应电动势④ 中电流⑤ 受到的安培力F ⑥框架开始运动时⑦ 由上述各式代入数据解得⑧(2)闭合回路中产生的总热量⑨ 由能量守恒定律,得⑩代入数据解得3.在如图所示的竖直平面内,水平轨道CD和倾斜轨道GH与半径r=m的光滑圆弧轨道分别相切于D点和G点,GH与水平面的夹角θ=37°。
电磁场计算题

重要习题例题归纳第二章 静电场和恒定电场一、例题:1、例2.2.4(38P )半径为0r 的无限长导体柱面,单位长度上均匀分布的电荷密度为l ρ。
试计算空间中各点的电场强度。
解:作一与导体柱面同轴、半径为r 、长为l 的闭合面S ,应用高斯定律计算电场强度的通量。
当0r r <时,由于导体内无电荷,因此有0=⋅⎰→→SS d E ,故有0=→E ,导体内无电场。
当0r r>时,由于电场只在r 方向有分量,电场在两个底面无通量,因此2ερπl rl E dS E dS a a E S d E l r Sr r Sr r r r S=⋅=⋅=⋅=⋅⎰⎰⎰→→→→则有:r E l r 02περ=2、例2.2.6(39P )圆柱坐标系中,在m r2=与m r 4=之间的体积内均匀分布有电荷,其电荷密度为3/-⋅m C ρ。
利用高斯定律求各区域的电场强度。
解:由于电荷分布具有轴对称性,因此电场分布也关于z 轴对称,即电场强度在半径为r 的同轴圆柱面上,其值相等,方向在r 方向上。
现作一半径为r ,长度为L 的同轴圆柱面。
当m r20≤≤时,有02=⋅=⋅⎰→→rL E S d E r Sπ,即0=r E ;当m rm 42≤≤时,有)4(1220-=⋅=⋅⎰→→r L rL E S d E r Sπρεπ,因此,)4(220-=r rE r ερ;当m r 4≥时,有L rL E S d E r Sπρεπ0122=⋅=⋅⎰→→,即r E r 06ερ=。
3、例2.3.1(41P )真空中,电荷按体密度)1(220ar -=ρρ分布在半径为a 的球形区域内,其中0ρ为常数。
试计算球内、外的电场强度和电位函数。
解:(1)求场强:当a r >时,由高斯定律得2224επQ E r S d E S==⋅⎰→→而Q 为球面S 包围的总电荷,即球形区域内的总电荷。
300242002158)(44)(a dr a r r dr r r Q aaπρπρπρ=-==⎰⎰因此20302152r a a E rερ→→=当a r <时)53(44)(1425300020121a r r dr r r E r S d E rS -===⋅⎰⎰→→επρπρεπ因此)33(23001a r r a E r-=→→ερ (2)球电位;当a r >时,取无穷远的电位为零,得球外的电位分布为ra r d E r r03022152)(ερ=⋅=Φ⎰∞→→当a r =时,即球面上的电位为20152ερa S =Φ 当a r <时)1032(2)(24220011a r r a r d E r a rS +-=⋅+Φ=Φ⎰→→ερ4、例2.4.1(48P )圆心在原点,半径为R 的介质球,其极化强度)0(≥=→→m r a P m r 。
电磁场期末复习_计算题

②电场、磁场强度复矢量
解: ① kex3ez4, k5, ek ex0.6ez0.8
k, 53108 1.5109rad/s
c
f 7.5108Hz, 20.4m
2
k
② E H x x,,z z e 0y H 3 1 x,e z j (e 3x k4 z)(A e x/0 m .8,e z0 .6 0) 41e0 2 j (3x 0 4z)V /m
求导线产生的磁场;线圈中的感应电动势。
解: ② CH dli HeI02 co ts(A /m )
id
b a
磁感应强度为
Be
I0cost 2
(T)
SB d sd dbI0 2 c o ta sd 2 I 0 aln d dbco ts
故感应电动势为 d d tI2 0 aln d dbsi n t(V )
Jd D t r0 E m s itn 8 1 31 6 1 9 0 2 16E 0 m s itn 4 .5 1 3 0 E m si2 n 1 (6t0 )
8
电磁场与电磁波
2014复习资料
8. 在E 理z,想t介 质e x (4 εr=c 2.0 25o ,μtrs =-1))k 中(均已z 匀知平该面平波面电波场频强率度为瞬10时G值Hz为, :
8. 在E 理z,想t介 质e x (4 εr=c 20 .25o ,μtrs =-1))k ( 中已均z 知匀该平平面面波波电频场率强为度1瞬0G时H值z, 为:
③求磁场强度瞬时值④平均坡印廷矢量。
解: ③ r 120 1 80 ,
r
2 .25
Hz , t
ey
40
cos(
t-kz
4
电磁场考试试题及答案

电磁场考试试题及答案一、选择题1. 下列哪个物理量不是描述电磁场的基本量?A. 电场强度B. 磁感应强度C. 电势D. 磁化强度2. 静电场的本质特征是:A. 磁场产生于电场B. 电场产生于静电荷C. 电场与磁场相互作用D. 电场与静电荷相互作用3. 关于电磁场的能量密度,以下说法正确的是:A. 电磁场的能量密度只与电场强度有关B. 电磁场的能量密度只与磁感应强度有关C. 电磁场的能量密度与电场和磁感应强度都有关D. 电磁场的能量密度与电荷和电流有关4. 电磁波中电场和磁场的相互关系是:A. 电场和磁场以90°的相位差波动B. 电场和磁场以180°的相位差波动C. 电场和磁场处于同相位波动D. 电场和磁场没有固定的相位关系5. 有一根长直导线,通有电流,要使其产生的磁场最强,应将观察点放置在:A. 导线的外侧B. 导线的内侧C. 导线的中央D. 对称轴上二、填空题1. 电荷为2μC的点电荷在距离它10cm处的电场强度大小为______ N/C。
2. 一根长度为50cm的直导线通有5A的电流,它产生的磁感应强度大小为______ T。
三、简答题1. 什么是电磁场?它的基本特征是什么?电磁场是一种通过电荷和电流相互作用而产生的物质场。
它基于电荷和电流的特性,表现为电场和磁场的存在和相互作用。
电磁场的基本特征包括:电场与静电荷相互作用,磁场与电流相互作用,电磁场遵循麦克斯韦方程组等。
2. 电场与磁场有何区别和联系?电场是由电荷产生的一种物质场,描述电荷对其他电荷施加的作用力的特性。
而磁场则是由电流产生的一种物质场,描述电流对其他电流施加的作用力的特性。
电场和磁场之间存在密切的联系,根据麦克斯韦方程组的推导可知,变化的电场会产生磁场,而变化的磁场也会产生电场。
3. 什么是电磁波?其特点是什么?电磁波是由电场和磁场相互耦合在空间中传播的波动现象。
其特点包括:- 电磁波是横波,电场与磁场的振动方向垂直于波传播方向。
电磁场与电磁波考试试题

电磁场与电磁波考试试题一、选择题(每题 3 分,共 30 分)1、真空中的介电常数为()。
A 885×10^(-12) F/mB 4π×10^(-7) H/mC 0D 无穷大2、静电场中,电场强度的环流恒等于()。
A 电荷的代数和B 零C 电场强度的大小D 不确定3、磁场强度的单位是()。
A 安培/米B 伏特/米C 牛顿/库仑D 特斯拉4、对于时变电磁场,以下说法正确的是()。
A 电场和磁场相互独立B 电场是无旋场C 磁场是无散场D 电场和磁场没有关系5、电磁波在真空中的传播速度为()。
A 光速B 声速C 无限大D 不确定6、以下哪种波不是电磁波()。
A 可见光B 超声波C 无线电波D X 射线7、均匀平面波在理想介质中传播时,电场和磁场的相位()。
A 相同B 相反C 相差 90 度D 不确定8、电位移矢量 D 与电场强度 E 的关系为()。
A D =εEB D =ε0ECD =μH D D =μ0H9、坡印廷矢量的方向表示()。
A 电场的方向B 磁场的方向C 能量的传播方向D 电荷的运动方向10、电磁波的极化方式不包括()。
A 线极化B 圆极化C 椭圆极化D 方极化二、填空题(每题 3 分,共 30 分)1、库仑定律的表达式为________。
2、静电场的高斯定理表明,通过任意闭合曲面的电通量等于该闭合曲面所包围的________。
3、安培环路定理表明,磁场强度沿任意闭合回路的线积分等于穿过该回路所包围面积的________。
4、位移电流的定义式为________。
5、麦克斯韦方程组的四个方程分别是________、________、________、________。
6、电磁波的波长、频率和波速之间的关系为________。
7、理想导体表面的电场强度________,磁场强度________。
8、均匀平面波的电场强度和磁场强度的比值称为________。
9、线极化波可以分解为两个________极化波的合成。
第十三章电磁感应电磁场习题

第十三章电磁感应电磁场习题(一)教材外习题电磁感应习题一、选择题:1.一块铜板放在磁感应强度正在增大的磁场中时,铜板中出现涡流(感应电流),则涡流将(A)加速铜板中磁场的增加(B)减缓铜板中磁场的增加(C)对磁场不起作用(D)使铜板中磁场反向()2.在如图所示的装置中,当把原来静止的条形磁铁从螺线管中按图示情况抽出时,(A)螺线管线圈中感生电流方向如A点处箭头所示。
(B)螺线管右端感应呈S极。
(C)线框EFGH从图下方粗箭头方向看去将逆时针旋转。
(D)线框EFGH从图下方粗箭头方向看去将顺时针旋转。
()3.在无限长的载流直导线附近放置一矩形闭合线圈,开始时线圈与导线在同一平面内,且线圈中两条边与导线平行,当线圈以相同的速率作如图所示的三种不同方向的平动时,线圈中的感应电流(A)以情况Ⅰ中为最大(B)以情况Ⅱ中为最大(C)以情况Ⅲ中为最大(D)在情况Ⅰ和Ⅱ中相同()4.如图所示,一矩形金属线框,以速度v 从无场空间进入一均匀磁场中,然后又从磁场中出来,到无场空间中。
不计线圈的自感,下面哪一条图线正确地表示了线圈中的感应电流对时间的函数关系?(从线圈刚进入磁场时刻开始计时,I 以顺时针方向为正)5.如图,一矩形线框(其长边与磁场边界平行)以匀速v 自左侧无场区进入均匀磁场又穿出,进入右侧无场区,试问图(A )—(E )中哪一图象能最合适地表示线框中电流i 随时间t 的变化关系?(不计线框自感)( )6.在一个塑料圆筒上紧密地绕有两个完全相同的线圈aa '和bb ',当线圈aa '和bb '如图(1)绕制时其互感系数为M 1,如图(2)绕制时其互感系数为M 2,M 1与M 2的关系是(A )M 1 = M 2 ≠ 0 (B )M 1 = M 2 = 0(C )M 1 ≠ M 2,M 2=0(D )M 1≠M 2,M 2≠0( )7.真空中两根很长的相距为2a 的平行直导线与电源组成闭合回路如图。
电磁场考试试题及答案

电磁场考试试题及答案一、选择题(每题5分,共20分)1. 麦克斯韦方程组描述了电磁场的基本规律,下列哪一项不是麦克斯韦方程组中的方程?A. 高斯定律B. 法拉第电磁感应定律C. 欧姆定律D. 安培环路定律答案:C2. 在电磁波传播过程中,电场和磁场的相位关系是:A. 相位相同B. 相位相反C. 相位相差90度D. 相位相差180度答案:C3. 根据洛伦兹力定律,带电粒子在磁场中运动时受到的力的方向是:A. 与速度方向相同B. 与速度方向相反C. 与速度方向垂直D. 与磁场方向垂直答案:C4. 以下哪种介质的磁导率不是常数?A. 真空B. 铁C. 铜D. 空气答案:B二、填空题(每题5分,共20分)1. 根据高斯定律,通过任何闭合表面的电通量与该闭合表面所包围的总电荷量成正比,比例常数为____。
答案:\(\frac{1}{\varepsilon_0}\)2. 法拉第电磁感应定律表明,闭合回路中的感应电动势等于通过该回路的磁通量变化率的负值,其数学表达式为 \(\mathcal{E} = -\frac{d\Phi_B}{dt}\),其中 \(\Phi_B\) 表示____。
答案:磁通量3. 根据安培环路定律,磁场 \(\vec{B}\) 在闭合回路上的线积分等于该回路所包围的总电流乘以比例常数 \(\mu_0\),其数学表达式为\(\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{\text{enc}}\),其中\(I_{\text{enc}}\) 表示____。
答案:回路所包围的总电流4. 电磁波在真空中的传播速度为 \(c\),其值为 \(3 \times 10^8\) 米/秒,该速度也是光速,其物理意义是____。
答案:电磁波在真空中传播的速度三、简答题(每题15分,共40分)1. 简述电磁波的产生机制。
答案:电磁波是由变化的电场和磁场相互作用产生的。
当电场变化时,会在周围空间产生磁场;同样,变化的磁场也会在周围空间产生电场。
电磁场与电磁波试题与答案

电磁场与电磁波试题与答案电磁场与微波技术基础试题一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号。
每小题2分,共20分)1.设一个矢量场 =x x+2y y+3z z,则散度为( )A. 0B. 2C. 3D. 62.人们规定电流的方向是( )运动方向。
A.电子B.离子C.正电荷D.负电荷3.在物质中没有自由电子,称这种物质为( )A.导体B.半导体C.绝缘体D.等离子体4.静电场能量的来源是( )A.损耗B.感应C.极化D.做功5.对于各向同性介质,若介电常数为ε,则能量密度we为( )A. ?B. E2C. εE2D. εE26.电容器的大小( )A.与导体的形状有关B.与导体的形状无关C.与导体所带的电荷有关D.与导体所带的电荷无关7.电矩为的电偶极子在均匀电场中所受的作用力和库仑力矩为( )A. =0,Tq= ?B. =0, = ×C. = ?,= ×D. = ?, =08.在 =0的磁介质区域中的磁场满足下列方程( )A. × =0, ? =0B. × ≠0, ? ≠0C. × ≠0, ? =0D. × =0, ? ≠09.洛伦兹条件人为地规定的( )A.散度B.旋度C.源D.均不是10.传输线的工作状态与负载有关,当负载短路时,传输线工作在何种状态?( )A.行波B.驻波C.混合波D.都不是二、填空题(每空2分,共20分)1.两个矢量的乘法有______和______两种。
2.面电荷密度ρs( )的定义是______,用它来描述电荷在______的分布。
3.由库仑定律可知,电荷间作用力与电荷的大小成线性关系,因此电荷间的作用力可以用______原理来求。
4.矢量场的性质由它的______决定。
5.在静电场中,电位相同的点集合形成的面称为______。
6.永久磁铁所产生的磁场,称之为______。
电磁场与电磁波试题含答案

函数乘积的方法。
二、简述题 (每小题 5 分,共 20 分)
11.简述高斯通量定理,并写出其积分形式和微分形式的表达式。
12.试简述电磁场在空间是如何传播的?
13.试简述何谓边界条件。
E
q 4 0r 2
eˆr
(1)求出电力线方程;(2)画出电力线。
19.设点电荷位于金属直角劈上方,如图 1 所示,求
(1) 画出镜像电荷所在的位置
(2) 直角劈内任意一点 (x, y, z) 处的电位表达式
图1
20.设时变电磁场的电场强度和磁场强度分别为:
E E0 cos(t e )
14.什么是色散?色散将对信号产生什么影响?
三、计算题 (每小题 10 分,共 30 分)
15.标量场 x, y, z x2 y3 ez ,在点 P1,1,0处
7
(1)求出其梯度的大小
(2)求梯度的方向
16.矢量
A
eˆx
2eˆy
,B
eˆx
3eˆz
,求
(1) A B
。
9.电介质中的束缚电荷在外加
作用下,完全脱离分子的内部束缚力时,我们把这种
现象称为击穿。
10.法拉第电磁感应定律的微分形式为
。
二、简述题 (每小题 5 分,共 20 分)
11.简述恒定磁场的性质,并写出其两个基本方程。
12.试写出在理想导体表面电位所满足的边界条件。
13.试简述静电平衡状态下带电导体的性质。
(1) A B
(2) A B
17.在无源的自由空间中,电场强度复矢量的表达式为
E eˆ x 3E0 eˆ y 4E0 e jkz
高考物理电磁学计算题(三十)含答案与解析

高考物理电磁学计算题(三十)含答案与解析评卷人得分一.计算题(共40小题)1.如图,倾角为θ的斜面粗糙且绝缘,在虚平面下方区域有一垂直斜面向上的匀强电场。
一质量为m、电荷量为q的带负电的小物块(可视为质点),从斜面上A点以速度v0沿斜面匀速下滑,进入电场区域滑行距离L后停止。
求:(1)小物块与斜面间的动摩擦因数μ;(2)匀强电场场强E的大小;(3)在电场中滑行L的过程中,带电小物块电势能的变化量。
2.如图,一带正电小球质量m=0.1kg,置于光滑绝缘水平面上的A点,空间存在着斜向上与水平成37°的匀强电场。
该小球从静止开始沿水平面做匀加速直线运动,当运动到B 点时,测得其速度v B=4m/s,此时小球的位移S=4m。
重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)小球沿水平面运动的加速度大小;(2)小球对地面的压力大小;(3)小球从A点运动到B点,电势能的变化量。
3.如图1所示,半径为r的金属细圆环水平放置,环内存在竖直向上的匀强磁场,磁感应强度B随时间t的变化关系为B=kt(k>0,且为已知的常量)。
(1)已知金属环的电阻为R.根据法拉第电磁感应定律,求金属环的感应电动势E感和感应电流I;(2)麦克斯韦电磁理论认为:变化的磁场会在空间激发一种电场,这种电场与静电场不同,称为感生电场或涡旋电场。
图1所示的磁场会在空间产生如图2所示的圆形涡旋电场,涡旋电场的电场线与金属环是同心圆。
金属环中的自由电荷在涡旋电场的作用下做定向运动,形成了感应电流。
涡旋电场力F充当非静电力,其大小与涡旋电场场强E的关系满足F=qE.如果移送电荷q时非静电力所做的功为W,那么感应电动势E感=。
a.请推导证明:金属环上某点的场强大小为E=kr;b.经典物理学认为,金属的电阻源于定向运动的自由电子与金属离子(即金属原子失去电子后的剩余部分)的碰撞。
在考虑大量自由电子的统计结果时,电子与金属离子的碰撞结果可视为导体对电子有连续的阻力,其大小可表示为f=bv(b>0,且为已知的常量)。
电磁场习题

8R
6. 如图所示,一无限长载流平板宽度为a,线电流密度
(即沿x方向单位长度上的电流)为d ,求与平板共面且距
平板一边为b的任意点P的磁感强度.
解:利用无限长载流直导线的公式求解.
dx
(1) 取离P点为x宽度为dx的无限长载流细条, x
它的电流
di d dx
O
x
P
(2) 这载流长条在P点产生的磁感应强度
2R
(D) 0.
pm与 B同向
I1 I2
O
r
R
M0
2. 三条无限长直导线等距地并排安放,导线Ⅰ、Ⅱ、
Ⅲ分别载有1 A,2 A,3 A同方向的电流.由于磁相互
作用的结果,导线Ⅰ,Ⅱ,Ⅲ单位长度上分别受力F1、
F2和F3,如图所示.则F1与F2的比值是:[ ]c
(A) 7/16. (B) 5/8.
ⅠⅡ Ⅲ
L
I1 L
I1
I2
根据安培环路定理
3. 如图所示,在真空中有一半圆形闭合线圈,半径为a, 流过稳恒电流I,则圆心O处的电流元所受的安培力的
大小为_________0_I_2_d_l,方向____向__左______
4a
O处:B 0I 方向:
4a
安培力 dF Idl B
I dl
Oa I
4. 如图,半圆形线圈(半径为R)通有电流I.线圈处在与
T 2m
qB
Ra ma qp 4 1 2 Rp m p qa 1 2
Ta ma qp 4 1 2 Tp m p qa 1 2
3. 在一根通有电流I的长直导线旁,与之共面地放着一 个长、宽各为a和b的矩形线框,线框的长边与载流长 直导线平行,且二者相距为b,如图所示.在此情形中,
工程电磁场复习题(经典实用)

工程电磁场复习题(经典实用)
以下是一些经典实用的工程电磁场复习题:
1.均匀介质中,磁感应强度大小为B1的区域内有一半径为R2的导体球面,其表面电荷密度为σ。
求该球心处磁场大小。
答案:由于该导体球面没有电流,因此在球内部磁场大小都为0;而在球外,根据安培环路定理可知,该球面外的磁场大小为:B=μ0σR2/3
其中μ0为磁导率,σ为导体球面表面电荷密度,R2为导体球面半径。
2.一根长度为L、电阻为R的均匀导线被均匀分布的电荷Q沿其长度均匀分布。
求该导线的自感系数L。
答案:通过对导线进行截面上的积分可以得到:
L=μ0/4π∫(0,L)∫(0,L)q(x)q(y)/[(x-y)^2+a^2]dxdy 其中a为计算积分时引入的小量。
如果导线上的电荷分布是kΔx,则q(x)=kΔx,上式化简后即为:
L=μ0k^2L/2πln(L/a)
其中Δx趋近于0,则k趋近于无穷大。
这个积分主要考察对电势能积分的处理,注意使用ln的积分公式。
3.一根长为L的绝缘平行板电容器,其间距为d、宽度为w,其在垂直于平板的方向上受到一个均匀的电场E。
试求该电容器的电容C和存储的能量W。
答案:由于平行板电容器是一个均匀电场下的电势差系统,其电容可表示为:
C=εA/d
其中ε为介电常数,A为平行板面积,d为平板间距。
因此,该电容器的电容为:
C=εwL/d
而该电容器存储的能量可用其带电量Q表示:
W=(1/2)Q^2/C
将C代入上式,得到:
W=εwL/2E^2
上式可以用来计算存储在电容器中的能量。
大学_电磁场试题及参考答案

电磁场试题及参考答案电磁场试题一、选择题一、选择题:(每小题至少有一个选项是正确的,每小题4分,共48分)1.D2.BCD3.A4.CD5.ABC6.ABC7.D8.B9.B10.D11.B12.A二、填空题(每空3分,共30分,请把答案填写在题中横线上)13、最大、最大、零、零、零14、充电完毕、负电荷15、3:116、1.64106 1.83102三,计算题电磁场试题二、填空题17、(7分)(由法拉第电磁感应现象说明均匀变化的磁场所产生的电场是恒定的18、(7分)某雷达工作时发射的电磁波的波长=20m,每秒脉冲数n=5000个,每个脉冲持续时间t=0.02s,问电磁波的振荡频率为多少?每个光脉冲的长度L 是多少?最大的侦察距离是多少?19.(8分)一个波长范围为150~600m的无线电波段内,为避免邻台干扰,两个相邻电台频率至少应相差10kHz,求在此波段内,最多能容纳Q多少个电台.电磁场试题三、计算题(每空3分,共30分)13、LC振荡电路中,当电容器C放电完毕时,下列各物理量为(最大或零):电流i____,磁场能E磁____,电压UC___,L中电动势自____,C上电量q____。
14、如图中LC振荡电路的周期为T=210-2s。
从电流逆时针最大开始计时,当t=2.510-2s时,电容器正处于_____状态;这时电容器上极板的带电情况为_____。
15.在图所示的电路中,可变电容器的最大电容是270 pF,最小电容为30 pF,若L保持不变,则可变电容器的动片完全旋出与完全旋入时,电路可产生的振荡电流的频率之比为_____. 16.某收音机调谐电路的可变电容器动片完全旋入时,电容是390 PF,这时能接收到520kHz 的无线电电波,动片完全旋出时,电容变为39 PF,这时能收到的无线电电波的频率是______106 Hz,此收音机能收到的无线电电波中,最短的波长为______m.(取三位有效数字)电磁场试题参考答案(每小题至少有一个选项正确,每小题4分,共48分)1.根据麦克斯韦电磁理论,如下说法正确的是 ( )A.变化的电场一定产生变化的磁场B.均匀变化的电场一定产生均匀变化的磁场C.稳定的电场一定产生稳定的磁场D.振荡的电场一定产生同频率的振荡磁场2、关于LC振荡电路在振荡过程中,下列说法正确的是( )A、电流最大的时刻电压也最高B、电流增大的过程是电容器的放电过程C、电流最小的时刻电压却最高D、自感电动势最大时电容器带电量最大3. 要使LC振荡电路的周期增大一倍,可采用的办法是 ( )A.自感系数L和电容C都增大一倍B.自感系数L和电容C都减小一半C.自感系数L增大一倍,而电容C减小一半D.自感系数L减小一半,而电容C增大一倍4.在LC振荡电路的`工作过程中,下列的说法正确的是 ( )A.在一个周期内,电容器充、放电各一次B.电容器两极板间的电压最大时,线圈中的电流也最大C.电容器放电完了时,两极板间的电压为零,电路中的电流达到最大值D.振荡电路的电流变大时,电场能减少,磁场能增加5.LC回路发生电磁振荡时,振荡周期为T.若从电容器开始放电取作t=0,则 ( )A.5T/4和7T/4两个时刻,回路中电流最大,方向相反B.3T/2和2T两个时刻,电容器所带电量最大C.5T/4至3T/2时间内,回路中电流减小,电容器所带电量增加D.3T/2至7T/4时间内,磁场能向电场能转化6、下列说法正确的是 ( )A、摄像机摄像管实际上是一种将光信号转变为电信号的装置B、电视机显像管实际上是一种将电信号转变为光信号的装置C、摄像机在一秒钟内要送出25张画面D、电视机接收的画面是连续的7、由自感系数为L的线圈和可变电容器C构成收音机的调谐电路,为使收音机能接收到f1为550千赫至 f2为1650千赫范围内的所有电台的播音,则可变电容器与f1 对应的电容C1与f2对应的电容C2之比为( )A、1:3B、 3 :1C、1:9D、9:18、如图所示,L是不计电阻的电感器,C是电容器,闭合电键K,待电路达到稳定状态后,再断开电键K,LC电路中将产生电磁振荡。
电磁场计算题专项练习

电磁场计算题专项练习、电场1、(20分)如图所示,为一个实验室模拟货物传送的装置,A是一个表面绝缘质量为Ikg的小车,小车置于光滑的水平面上,在小车左端放置一质量为0.1kg 带电量为q=1× 10-2C的绝缘货柜,现将一质量为0∙9kg的货物放在货柜内.在传送途中有一水平电场,可以通过开关控制其有、无及方向.先产生一个方向水平向右,大小Eι=3×102N∕m的电场,小车和货柜开始运动,作用时间2s后,改变电场,电场大小变为E2=1 × 10N∕m,方向向左,电场作用一段时间后,关闭电场,小车正好到达目的地,货物到达小车的最右端,且小车和货物的速度恰好为零。
已知货柜与小车间的动摩擦因数尸0.1,(小车不带电,货柜及货物体积大小不计,g 取10m∕s2)求:⑴第二次电场作用的时间;⑵小车的长度;⑶小车右端到达目的地的距离.16(8分)如图所示,水平轨道与直径为d=0.8m的半圆轨道相接,半圆轨道的两端点A、B连线是一条竖直线,整个装置处于方向水平向右,大小为103V∕m的匀强电场中,一小球质量m=0.5kg,带有q=5× 10-3C电量的正电荷,在电场力作用下由静止开始运动,不计一切摩擦,g=10m∕s2(1)若它运动的起点离A为L,它恰能到达轨道最高点B,求小球在B点的速度和L的值.(2)若它运动起点离A为L=2.6m,且它运动到B点时电场消失,它继续运动直到落地,求落地点与起点的距离.6如图所示,两平行金属板 A 、B 长I = 8cm 两板间距离d = 8cm A 板比B 板电 势高300V,即卩UAB= 300VO 一带正电的粒子电量 q = 10-10C ,质量 m= 10-2Okg , 从R 点沿电场中心线垂直电场线飞入电场,初速度 v0 = 2× 106m∕s ,粒子飞出平 行板电场后经过界面MN PS 间的无电场区域后,进入固定在中心线上的 O 点的 点电荷Q 形成的电场区域(设界面PS 右边点电荷的电场分布不受界面的影响)。
电磁场与电磁波典型习题及答案(恒定磁场)
=
8 r
+ 3cotθ
≠
0 ,F
不表示磁感应强度
B。
e) ∇ ⋅ F = − ∂A + ∂A = 0 (A 为常数), J = ∇ ⋅ B = ∇ ⋅ F = 0
∂x ∂y
µ0
µ0
f) ∇ ⋅ F = 1 ∂ (r3r) + ∂2 = 6 ≠ 0 ,F 不表示磁感应强度 B。
r ∂r
∂z
4-4 无限长直线电流垂直于磁导率分别为 µ1 和 µ2 的两种介质的分界面,试求: (1) 两种介质中的磁感应强度 B1 和 B2;(2) 磁化电流分布。
B0x = 0.002 , B0 y = 0.5 , B0z = 0
即
B0 = ex 0.002 + e y 0.5
4-13 真空中有一厚度为 d 的无限大载流块,电流密度为 ez J0 ,在其中心位置有 一半径为 a 的圆柱形空腔。求腔内的磁感应强度。
解:设空腔中同时存在有密度为 ±ez J0 的电流,则可利用安培环路定律和迭加原 理求出空腔内的 B 。
+ π (r 2
− a12 )J 2 ] ⇒
B
=
eφ
⎜⎜⎝⎛
10 3
r
− 10−5 r
⎟⎟⎠⎞
当r
>
a2 时,有 B
= eφ
µ0I 2π r
=
eφ
2 ×10−5 r
4-8 已知在半径为 a 的圆柱区域内有沿轴向方向的电流,其电流密度为
J
= ex
J0r a
,其中 J0 为常数,求圆柱内外的磁感应强度。
1 r
d (r 1) = 0 dr r
在 r=0 处, 具有奇异性。以 z 轴为中心作一个圆形回路 c,由安培环路定律得
电磁场理论习题及答案6解读

1. 在3z m =的平面内,长度0.5l m =的导线沿x 轴方向排列。
当该导线以速度24x y m v e e s=+在磁感应强度22363x y z B e x z e e xz T =+-的磁场中移动时,求感应电动势。
2.长度为l 的细导体棒位于xy 平面内,其一端固定在坐标原点。
当其在恒定磁场0z B e B =中以角速度ω旋转时,求导体棒中的感应电动势。
3.试推出在线性、无耗、各向同性的非均匀媒质中的麦克斯韦方程。
4.试由麦克斯韦方程推导出电流连续性方程J tρ∂∇⋅=-∂。
5.设真空中电荷量为q 的点电荷以速度()v vc 向正z 方向匀速运动,在0t =时刻经过坐标原点,计算任一点位移电流密度(不考虑滞后效应)。
R6.已知自由空间的磁场为0cos()/y H e H t kz A m ω=-式中的0H 、ω、k 为常数,试求位移电流密度和电场强度。
7. 由麦克斯韦方程出发,试导出静电场中点电荷的电场强度和泊松方程。
8.由麦克斯韦方程组出发,导出毕奥-萨伐尔定律。
9.如图所示,同轴电缆的内导体半径1a mm =,外导体内半径4b mm =,内、外导体间为空气介质,且电场强度为 8100cos(100.5)/r E e t z V m r=- (1)求磁场强度H 的表达式 (2)求内导体表面的电流密度; (3)计算01Z m ≤≤中的位移电流。
10.试由麦克斯韦方程组中的两个旋度方程和电流连续性方程,导出麦克斯韦方程组中的两个散度方程。
11.如图所示,两种理想介质,介电常数分别为1ε和2ε,分界面上没有自由电荷。
在分界面上,静电场电力线在介质2,1中与分界面法线的夹角分别为1α和2α。
求1α和2α之间的关系。
12.写出在空气和∞=μ的理想磁介质之间分界面上的边界条件。
13.在由理想导电壁)(∞=r 限定的区域a x ≤≤0内存在一个由以下各式表示的电磁场:)cos()cos()sin()sin()()sin()sin()(000t kz axH H t kz a xa k H H t kz a xa H E z x y ωπωππωππμω-=-=-=这个电磁场满足的边界条件如何?导电壁上的电流密度的值如何?14.设电场强度和磁场强度分别为)cos()cos(00m e t H t E ψωψω+=+=证明其坡印廷矢量的平均值为)cos(2100m e av H E S ψψ-⨯=15.一个真空中存在的电磁场为0sin x E e jE kz = 0cos H e E kz ε= 其中2//k c πλω==是波长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、计算题1、如图9-3所示,一质量为m,电量为+q,重力不计的带电粒子,从A板的S点由静止开始释放,经AB加速电场加速后,穿过中间的偏转电场,再进入右侧匀强磁场区域.已知AB间的电压为U,MN极板间的电压为2U,MN 两板间的距离和板长均为L,磁场垂直纸面向里,磁感应强度为B,有理想边界.求:(1)带电粒子离开B板时速度v0的大小;(2)带电粒子离开偏转电场时v的大小与方向;(3)要使带电粒子最终垂直磁场右边界射出磁场,磁场的宽度d应为多大?2、如图所示,内壁光滑的绝缘管做在的圆环半径为R,位于竖直平面内.管的内径远小于R,以环的圆心为原点建立平面坐标系xoy,在第四象限加一竖直向下的匀强电场,其它象限加垂直环面向外的匀强磁场.一电荷量为+q、质量为m的小球在管内从b点由时静止释放,小球直径略小于管的内径,小球可视为质点.要使小球能沿绝缘管做圆周运动通过最高点a.(1)电场强度至少为多少?(2)在(1)问的情况下,要使小球继续运动,第二次通过最高点a时,小球对绝缘管恰好无压力,匀强磁场的磁感应强度多大?(重力加速度为g)3、如图所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B;在x轴下方有沿y轴负方向的匀强电场,场强为E。
一质量为m,电量为-q的粒子从坐标原点O沿着y轴正方向射出。
射出之后,第三次到达x轴时,它与点O的距离为L。
(重力不计)求(1)粒子射出时的速度v(2)粒子在磁场和电场中运动的总路程s。
4、如图所示,水平光滑绝缘轨道MN的左端有一个固定挡板,轨道所在空间存在E=4.0×102 N/C、水平向左的匀强电场.一个质量m=0.10 kg、带电荷量q=5.0×C的滑块(可视为质点),从轨道上与挡板相距x1=0.20 m的P点由静止释放,滑块在电场力作用下向左做匀加速直线运动.当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动,运动到与挡板相距x2=0.10 m的Q点,滑块第一次速度减为零.若滑块在运动过程中,电荷量始终保持不变,求:(1)滑块沿轨道向左做匀加速直线运动的加速度的大小;(2)滑块第一次与挡板碰撞过程中损失的机械能.(3)若每次碰撞损失的机械能与碰前机械能的比值为定值,求滑块运动的总路程。
5、如图所示的平面直角坐标系xOy,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿y轴正方向;在第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里,正三角形边长为L,且ab边与y轴平行。
一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。
求:(1)电场强度E的大小;(2)粒子到达a点时速度的大小和方向;(3)abc区域内磁场的磁感应强度B的最小值。
6、如图,平行金属板倾斜放置,AB长度为L,金属板与水平方向的夹角为θ,一电荷量为-q、质量为m的带电小球以水平速度v0进入电场,且做直线运动,到达B点。
离开电场后,进入如下图所示的电磁场(图中电场没有画出)区域做匀速圆周运动,并竖直向下穿出电磁场,磁感应强度为B。
试求:(1)带电小球进入电磁场区域时的速度v。
(2)带电小球在电磁场区域做匀速圆周运动的时间。
(3)重力在电磁场区域对小球所做的功。
7、在直角坐标系x O y中,第一象限内存在沿y轴负方向的有界电场,其中的两条边界分别与O x、O y重合,电场强度大小为E。
在第二象限内有垂直纸面向里的有界磁场(图中未画出),磁场边界为矩形,其中的一个边界与y轴重合,磁感应强度的大小为B。
一质量为m,电量为q的正离子,从电场中P点以某初速度沿-x方向开始运动,经过坐标(0,L)的Q点时,速度大小为,方向与-y方向成30°,经磁场偏转后能够返回电场,离子重力不计。
求:(1)正离子在P点的初速度;(2)矩形磁场的最小面积;(3)离子在返回电场前运动的最长时间。
8、如图所示,在以O为圆心,半径为R=10cm的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B=0.1T,方向垂直纸面向外。
竖直平行放置的两金属板A、K相距为d=20mm,连在如图所示的电路中,电源电动势E=91V,内阻r=1Ω定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω,S1、S2为A、K板上的两上小孔,且S1、S2跟O点在垂直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D之间的距离为H=2R。
比荷为2×105C/kg的正离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。
离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。
问:(1)请分段描述正离子自S1到荧光屏D的运动情况。
(2)如果正离子垂直打在荧光屏上,电压表的示数多大?(3)调节滑动变阻器滑片P的位置,正离子到达荧光屏的最大范围多大?9、如图所示,有3块水平放置的长薄金属板a、b 和c,a、b之间相距为L。
紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处。
板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场。
当体积为V0、密度为r、电荷量为q的带负电油滴,等间隔地以速率v0从a板上的小孔竖直向下射入,调节板间电压U ba和U bc,当U ba=U1、U bc=U2时,油滴穿过b板M孔进入细管,恰能与细管无接触地从N 孔射出。
忽略小孔和细管对电场的影响,不计空气阻力。
求:(1)油滴进入M孔时的速度v1;(2)b、c两板间的电场强度E和磁感应强度B的值;(3)当油滴从细管的N孔射出瞬间,将U ba和B立即调整到和B´,使油滴恰好不碰到a板,且沿原路与细管无接触地返回并穿过M孔,请给出和B´的结果。
10、如图所示,电源电动势为E,内电阻为r,平行板电容器两金属板水平放置,开关S是闭合的,两板间一质量为m、电量为q的油滴恰好处于静止状态,G为灵敏电流计。
则以下说法正确的A.在将滑动变阻器滑片向上移动的过程中,油滴向上加速运动,G中有从b到a的电流B.在将滑动变阻器滑片向下移动的过程中,油滴向下加速运动,G中有从b到a的电流C.在将滑动变阻器滑片向上移动的过程中,油滴仍然静止,G中有从a到b的电流D.在将S断开后,油没仍保持静止状态,G中无电流通过11、如图所示的电路中,闭合电键,灯L1、L2正常发光,由于电路出现故障,突然发现灯L1变亮,灯L2变暗,电流表的读数变小,根据分析,发生的故障可能是()A.R1断路 B.R2断路C.R3短路 D.R4短路12、在如图所示电路中,电源电动势E=6V,内阻r=1Ω,保护电阻R0=3Ω,滑动变阻器总电阻R=20Ω,闭合电键S,在滑片P从a滑到b的过程中,正确的是()A.滑动变阻器消耗的功率先减小后增大B.滑动变阻器消耗的功率先增大后减小C.滑动变阻器消耗的功率先减小后增大,再减小后增大D.滑动变阻器消耗的功率先增大后减小,再增大后减小13、电源和一个水平放置的平行板电容器、三个电阻组成如图所示的电路。
当开关S闭合后,电容器中有一个带电液滴正好处于静止状态。
现将开关S断开,则以下判断正确的是A.液滴仍保持静止状态B.液滴将向下运动C.电容器上的带电量将减为零D.电容器将有一个瞬间的充电过程14、在如图所示的电路中,皆为定值电阻,为可变电阻,电源的电动势为E,内阻为.设电流表的读数为,的读数为,电压表的读数为.当的滑触点向图中端移动时()A.变大,变小,变小 B.变大,变小,变大C.变小,变大,变大 D.变小,变大,变小参考答案一、计算题1、2、解:(1)小球恰能通过a点,小球第一次到达a点的速度为0,由动能定理有:qER﹣mgR=0…①故…②(2)设第二次到达a点的速度为vn,由动能定理有:…③到达最高点时小球对轨道恰好无压力,由牛顿第二定律有:…④联立②③④得答:(1)电场强度至少为.(2)匀强磁场的磁感应强度.3、解:粒子运动路线如图示有L=4R ①粒子初速度为v,则有 qvB=mv2/R ②由①、②式可算得 v=qBL/4m ③设粒子进入电场作减速运动的最大路程为,加速度为a, v2=2a④qE=ma ⑤粒子运动的总路程 s=2πR+2⑥由①、②、④、⑤、⑥式,得 s=πL/2+qB2L2/(16mE) ⑦4、解:(1)(2分)(2)第一次碰前在档板处的机械能为(1分)第一次碰后在档板处的机械能为(1分)滑块第一次与挡板碰撞过程中损失的机械能=(1分)(3)由(2)的结果知每碰撞损失50%的机械能,因此有路程为:=0.6m5、【知识点】带电粒子在匀强磁场中的运动;带电粒子在匀强电场中的运动.I3 K2【答案解析】(1)(2)v=v0,与x轴正方向成45°角斜向右下方(3).解析:(1)设粒子在电场中运动的时间为t,则有x = v0t = 2h y =at 2 = h qE = ma联立以上各式可得E =(2)粒子达到a点时沿负y方向的分速度为vy = at = v0所以v = = v0 方向指向第IV象限与x轴正方向成45°角(3)粒子在磁场中运动时,有qvB = m当粒子从b点射出时,磁场的磁感应强度为最小值,此时有r = L 所以B =【思路点拨】(1)粒子在电场中做类平抛运动,水平位移和竖直位移均已知,由牛顿第二定律和运动学公式,运用运动的分解法可求出场强大小E.(2)由速度的合成法求出粒子到达a点时速度大小和方向,由几何知识确定粒子经过a点时的方向.(3)三角形区域内的磁场方向垂直纸面向里,当粒子刚好与BC边相切时,磁感应强度最小,作出轨迹,由几何知识求出最小半径,由牛顿第二定律即可求出磁感应强度的最小值.该题考查了有边界电磁场的问题,在电场中的偏转,利用平抛运动的知识求解;粒子在有边界的匀强磁场中运动,利用几何关系求解运动半径和转过的圆心角是解决问题的关键.6、【命题立意】主要考查带电粒子在有界电磁场中的运动问题【思路点拨】带电粒子在电磁场中的运动是历年高考考查的热点之一。
分析问题的关键在于分析粒子在电场、磁场中运动状态,各种运动之间的速度关联如何以及画出粒子的运动轨迹。
注意粒子在边界电场、磁场中出进磁场的速度大小与方向为该题求解的突破口。
本题考查考生综合应用学科内知识分析解决物理问题的能力。
【答案】(1)(2)(3)【解析】(1)对带电小球进行受力分析,带电小球受重力mg和电场力F,F合=F sinθ,mg=F cosθ(1分)解得F合=mg tanθ(1分)根据动能定理,解得(2分)(2)带电小球进入电磁场区域后做匀速圆周运动,说明电场力和重力平衡,带电小球只在洛伦兹力作用下运动。
