反比例函数动点面积专题
2021年九年级数学中考一轮复习专项突破训练:反比例函数面积问题及K的关系(附答案)
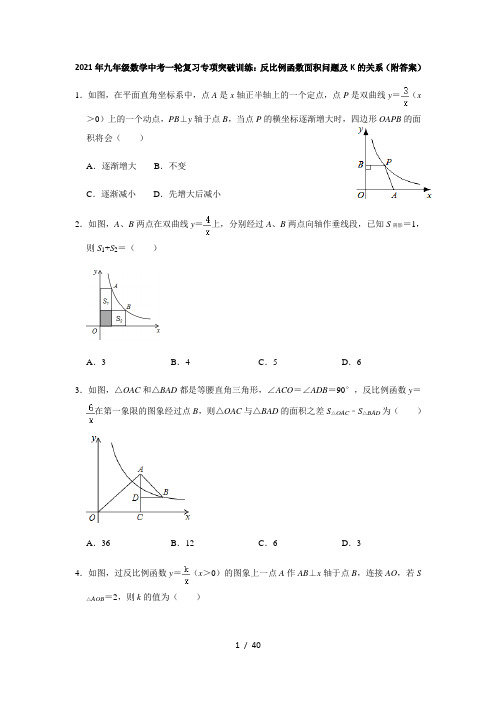
2021年九年级数学中考一轮复习专项突破训练:反比例函数面积问题及K的关系(附答案)1.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小2.如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=()A.3B.4C.5D.63.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为()A.36B.12C.6D.34.如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S=2,则k的值为()△AOBA.2B.3C.4D.55.如图,点A是反比例函数(x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为()A.1B.2C.4D.不能确定6.如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数y=经过另一条直角边AC的中点D,S△AOC=3,则k=()A.2B.4C.6D.37.如图,过点O作直线与双曲线y=(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴,y轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是()A.S1=S2B.2S1=S2C.3S1=S2D.4S1=S28.如图,直线l和双曲线(k>0)交于A、B两点,P是线段AB上的点(不与A、B 重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1,△BOD面积是S2,△POE面积是S3,则()A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S39.如图,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(k >0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD 的面积之和为,则k的值为()A.4B.3C.2D.10.如图,两个反比例函数y=和y=(其中k1>k2>0)在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形P AOB的面积为()A.k1+k2B.k1﹣k2C.k1•k2D.11.如图,在平面直角坐标系中,菱形ABCD的顶点A,B在反比例函数y=(k>0,x >0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为()A.B.C.4D.512.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为()A.8B.﹣8C.4D.﹣413.如图,P(m,m)是反比例函数y=在第一象限内的图象上一点,以P为顶点作等边△P AB,使AB落在x轴上,则△POB的面积为()A.B.3C.D.14.如图,点A(﹣2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线y =(k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是()A.﹣9B.﹣12C.﹣16D.﹣1815.如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为.16.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为.17.如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为.18.如图,已知点A,C在反比例函数y=(a>0)的图象上,点B,D在反比例函数y =(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB 与CD的距离为5,则a﹣b的值是.19.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=2,则k2﹣k1的值为.20.如图,点A,B在反比例函数y=(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是.21.如图,点A在双曲线y=上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是.22.如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E 是AB的中点,S△BEF=2,则k的值为.23.如图,A、B两点在双曲线y=上,分别经过A、B两点向坐标轴作垂线段,已知S阴=1,则S1+S2=.影24.如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为.25.如图,A.B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.26.如图,已知点A是一次函数y=x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是.27.如图,点A、B是双曲线y=上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为.28.如图,已知反比例函数y=(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=.29.如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x 轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=.30.如图,点A、点B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB 的面积等于.31.如图,已知∠AOB=90°,∠OAB=30°,反比例函数y=﹣(x<0)的图象过点B (﹣3,a),反比例函数y=(x>0)的图象过点A.(1)求a和k的值;(2)过点B作BC∥x轴,与双曲线y=交于点C.求△OAC的面积.32.如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;(2)若点C(x,y)也在反比例函数y=的图象上,当﹣3≤x≤﹣1时,求函数值y的取值范围.33.如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图象上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.(1)求k,b的值;(2)求△ACE的面积.34.如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E 是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=(x>0)的图象与边BC交于点F(1)若△OAE的面积为S1,且S1=1,求k的值;(2)若OA=2,OC=4,反比例函数y=(x>0)的图象与边AB、边BC交于点E和F,当△BEF沿EF折叠,点B恰好落在OC上,求k的值.35.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC =6.对角线AC,BD相交于点E,反比例函数(x>0)的图象经过点E,分别与AB,CD交于点F,G.(1)若OC=8,求k的值;(2)连接EG,若BF﹣BE=2,求△CEG的面积.36.在平面直角坐标系中,反比例函数y=(x>0,k>0)图象上的两点(n,3n)、(n+1,2n).(1)求n的值;(2)如图,直线l为正比例函数y=x的图象,点A在反比例函数y=(x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.37.已知反比例函数y=的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A 关于x轴对称,若△OAB的面积为6,求m的值.38.如图,点A在函数y=(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y =图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=(x>0)图象上运动时,(1)设点A横坐标为a,则点B的坐标为,点C的坐标为(用含a的字母表示);(2)△ABC的面积是否发生变化?若不变,求出△ABC的面积,若变化,请说明理由;(3)请直接写出BD与CE满足的数量关系.39.平面直角坐标系xOy中,点A、B分别在函数y1=(x>0),与y2=﹣(x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)(1)若AB∥x轴,求△OAB的面积;(2)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,当a≥3时,CD边与函数y1=(x>0)的图象有交点,请说明理由.参考答案1.解:设点P的坐标为(x,),∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,∴四边形OAPB是个直角梯形,∴四边形OAPB的面积=(PB+AO)•BO=(x+AO)•=+=+•,∵AO是定值,∴四边形OAPB的面积是个减函数,即点P的横坐标逐渐增大时四边形OAPB的面积逐渐减小.故选:C.2.解:∵点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,∴S1+S2=4+4﹣1×2=6.故选:D.3.解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a﹣b).∵点B在反比例函数y=的第一象限图象上,∴(a+b)×(a﹣b)=a2﹣b2=6.∴S△OAC﹣S△BAD=a2﹣b2=(a2﹣b2)=×6=3.故选:D.4.解:∵点A是反比例函数y=图象上一点,且AB⊥x轴于点B,∴S△AOB=|k|=2,解得:k=±4.∵反比例函数在第一象限有图象,∴k=4.故选:C.5.解:设A的坐标是(m,n),则mn=2.则AB=m,△ABC的AB边上的高等于n.则△ABC的面积=mn=1.故选:A.6.解:∵直角边AC的中点是D,S△AOC=3,∴S△CDO=S△AOC=,∵反比例函数y=经过另一条直角边AC的中点D,CD⊥x轴,∴k=2S△CDO=3,故选:D.7.解:设A点坐标为(m,﹣n),过点O的直线与双曲线y=交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,n);矩形OCBD中,易得OD=n,OC=m;则S1=mn;在Rt△EOF中,AE=AF,故A为EF中点,由中位线的性质可得OF=2n,OE=2m;则S2=OF×OE=2mn;故2S1=S2.故选:B.8.解:如右图,∵点A在y=上,∴S△AOC=k,∵点P在双曲线的上方,∴S△POE>k,∵点B在y=上,∴S△BOD=k,∴S1=S2<S3.故选:D.9.解:∵点A,B在反比例函数y=(x>0)的图象上,点A,B的横坐标分别为1,2,∴点A的坐标为(1,1),点B的坐标为(2,),∵AC∥BD∥y轴,∴点C,D的横坐标分别为1,2,∵点C,D在反比例函数y=(k>0)的图象上,∴点C的坐标为(1,k),点D的坐标为(2,),∴AC=k﹣1,BD=,∴S△OAC=(k﹣1)×1=,S△ABD=•×(2﹣1)=,∵△OAC与△ABD的面积之和为,∴,解得:k=3.故选:B.10.解:根据题意可得四边形P AOB的面积=S矩形OCPD﹣S OBD﹣S OAC,由反比例函数中k的几何意义,可知其面积为k1﹣k2.故选:B.11.解:连接AC,BD,AC与BD、x轴分别交于点E、F.由已知,A、B横坐标分别为1,4∴BE=3∵四边形ABCD为菱形,AC、BD为对角线∴S菱形ABCD=4×AE•BE=∴AE=设点B的坐标为(4,y),则A点坐标为(1,y+)∵点A、B同在y=图象上∴4y=1•(y+)∴y=∴B点坐标为(4,)∴k=5故选:D.12.解:∵AB∥x轴,∴A,B两点纵坐标相同.设A(a,h),B(b,h),则ah=k1,bh=k2.∵S△ABC=AB•y A=(a﹣b)h=(ah﹣bh)=(k1﹣k2)=4,∴k1﹣k2=8.故选:A.13.解:作PD⊥OB,∵P(m,m)是反比例函数y=在第一象限内的图象上一点,∴m=,解得:m=3,∴PD=3,∵△ABP是等边三角形,∴BD=PD=,∴S△POB=OB•PD=(OD+BD)•PD=,故选:D.14.解:∵点A(﹣2,0),B(0,1),∴OA=2,OB=1,过D作DM⊥x轴于M,则∠DMA=90°=∠AOB,∴∠DAM+∠ADM=90°,∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM+∠BAO=90°,∴∠ADM=∠BAO,∴△DMA∽△AOB,∴===2,即DM=2MA,设AM=x,则DM=2x,∵四边形OADB的面积为6,∴S梯形DMOB﹣S△DMA=6,∴(1+2x)(x+2)﹣•2x•x=6,解得:x=2,则AM=2,OM=4,DM=4,即D点的坐标为(﹣4,4),∴k=﹣4×4=﹣16,故选:C.15.解:延长BA交y轴于E,∵AB∥x轴,∴AE垂直于y轴,∵点A在双曲线上,∴四边形AEOD的面积为1,∵点B在双曲线y=上,且AB∥x轴,∴四边形BEOC的面积为3,∴矩形ABCD的面积为3﹣1=2.故答案为:2.16.解:∵点D为△OAB斜边OA的中点,且点A的坐标(﹣6,4),∴点D的坐标为(﹣3,2),把(﹣3,2)代入双曲线,可得k=﹣6,即双曲线解析式为y=﹣,∵AB⊥OB,且点A的坐标(﹣6,4),∴C点的横坐标为﹣6,代入解析式y=﹣,y=1,即点C坐标为(﹣6,1),∴AC=3,又∵OB=6,∴S△AOC=×AC×OB=9.故答案为:9.17.解:设P(0,b),∵直线AB∥x轴,∴A,B两点的纵坐标都为b,而点A在反比例函数y=﹣的图象上,∴当y=b,x=﹣,即A点坐标为(﹣,b),又∵点B在反比例函数y=的图象上,∴当y=b,x=,即B点坐标为(,b),∴AB=﹣(﹣)=,∴S△ABC=•AB•OP=••b=3.故答案为:3.18.解:如图,设CD交y轴于E,AB交y轴于F.连接OD、OC.由题意知:DE•OE=﹣b,CE•OE=a,∴a﹣b=OE(DE+CE)=OE•CD=2OE,同法:a﹣b=3•OF,∴2OE=3OF,∴OE:OF=3:2,又∵OE+OF=5,∴OE=3,OF=2,∴a﹣b=6.故答案是:6.19.解:设A(a,b),B(c,d),代入得:k1=ab,k2=cd,∵S△AOB=2,∴cd﹣ab=2,∴cd﹣ab=4,∴k2﹣k1=4,故答案为:4.20.解:过点B作直线AC的垂线交直线AC于点F,如图所示.∵△BCE的面积是△ADE的面积的2倍,E是AB的中点,∴S△ABC=2S△BCE,S△ABD=2S△ADE,∴S△ABC=2S△ABD,且△ABC和△ABD的高均为BF,∴AC=2BD,∴OD=2OC.∵CD=k,∴点A的坐标为(,3),点B的坐标为(﹣,﹣),∴AC=3,BD=,∴AB=2AC=6,AF=AC+BD=,∴CD=k===.故答案为:.21.解:∵△AOB的面积是2,∴|k|=2,∴|k|=4,解得k=±4,又∵双曲线y=的图象经过第二、四象限,∴k=﹣4,即k的值是﹣4.故答案为:﹣4.22.解:设E(a,),则B纵坐标也为,E是AB中点,所以F点横坐标为2a,代入解析式得到纵坐标:,因为BF=BC﹣FC=﹣=,所以F也为中点,S△BEF=2=,k=8.故答案是:8.23.解:∵点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,∴S1+S2=4+4﹣1×2=6.故答案为6.24.解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S▱ONMG=|k|,又∵M为矩形ABCO对角线的交点,∴S矩形ABCO=4S▱ONMG=4|k|,由于函数图象在第一象限,k>0,则++9=4k,解得:k=3.故答案是:3.25.解:过点B作BE⊥x轴于点E,∵D为OB的中点,∴CD是△OBE的中位线,即CD=BE.设A(x,),则B(2x,),CD=,AD=﹣,∵△ADO的面积为1,∴AD•OC=1,(﹣)•x=1,解得k=,故答案是:.26.解:解法一:设A(t,)、B(t,),∵△ABC是等腰直角三角形,且AB⊥x轴,∴直线BC与y轴夹角为45度角,所以根据双曲线的对称性可得,C(,t),过C作CE垂直AB于E,交y轴于D,∴AE=y C﹣y A=t﹣t=t,∵△AEC是等腰直角三角形,∴CE=AE=,则DE=t=2CE,则S△ABO=2S△ABC,∵△OAB的面积为6,∴S△ABC=3;解法二:如图,过C作CD⊥y轴于D,交AB于E,∵AB⊥x轴,∴CD⊥AB,∵△ABC是等腰直角三角形,∴BE=AE=CE,设AB=2a,则BE=AE=CE=a,设A(x,x),则B(x,x+2a),C(x+a,x+a),∵B,C在反比例函数的图象上,∴x(x+2a)=(x+a)(x+a),x=2a,∵S△OAB=AB•DE=•2a•x=6,∴ax=6,∴2a2=6,a2=3,∵S△ABC=AB•CE=•2a•a=a2=3.故答案为:3.27.解:∵点A、B是双曲线y=上的点,∴S矩形ACOG=S矩形BEOF=6,∵S阴影DGOF=2,∴S矩形ACDF+S矩形BDGE=6+6﹣2﹣2=8,故答案为:828.解:依据比例系数k的几何意义可得△AOB的面积等于|k|=1,解得k=±2,∵反比例函数y=(k为常数,k≠0)的图象在第二和第四象限,∴k=﹣2.故答案为:﹣2.29.解:∵BD⊥CD,BD=2,∴S△BCD=BD•CD=3,即CD=3,∵C(2,0),即OC=2,∴OD=OC+CD=2+3=5,∴B(5,2),代入反比例解析式得:k=10,即y=,则S△AOC=5,故答案为:530.解:延长BA交y轴于点C.S△OAC=×5=,S△OCB=×8=4,则S△OAB=S△OCB﹣S△OAC=4﹣=.故答案为:.31.解:(1)∵比例函数y=﹣(x<0)的图象过点B(﹣3,a),∴a=﹣=1,∴OE=3,BE=1,分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,∴∠BOE+∠OBE=90°,∵∠AOB=90°,∠OAB=30°,∴∠BOE+∠AOD=90°,tan30°==,∴∠OBE=∠AOD,∵∠OEB=∠ADO=90°,∴△BOE∽△OAD∴===,∴AD=•OE==3,OD=•BE==∴A(,3),∵反比例函数y=(x>0)的图象过点A,∴k=×=9;(2)由(1)可知AD=3,OD=,∵BC∥x轴,B(﹣3,1),∴C点的纵坐标为1,过点C作CF⊥x轴于F,∵点C在双曲线y=上,∴1=,解得x=9,∴C(9,1),∴CF=1,∴S△AOC=S△AOD+S梯形ADFC﹣S△COF=S梯形ADCF=(AD+CF)(OF﹣OD)=(3+1)(9﹣)=13.32.解:(1)∵△AOB的面积为2,∴k=4,∴反比例函数解析式为y=,∵A(4,m),∴m==1;(2)∵当x=﹣3时,y=﹣;当x=﹣1时,y=﹣4,又∵反比例函数y=在x<0时,y随x的增大而减小,∴当﹣3≤x≤﹣1时,y的取值范围为﹣4≤y≤﹣.33.解:(1)由已知可得AD=5,∵菱形ABCD,∴B(6,0),C(9,4),∵点D(4,4)在反比例函数y=(x>0)的图象上,∴k=16,将点C(9,4)代入y=x+b,∴b=﹣2;(2)E(0,﹣2),直线y=x﹣2与x轴交点为(3,0),∴S△AEC=2×(2+4)=6;34.解:(1)设E(a,b),则OA=b,AE=a,k=ab∵△AOE的面积为1,∴k=1,k=2;答:k的值为:2.(2)过E作ED⊥OC,垂足为D,△BEF沿EF折叠,点B恰好落在OC上的B′,∵OA=2,OC=4,点E、F在反比例函数y=的图象上,∴E(,2),F(4,),∴EB=EB′=4﹣,BF=B′F=2﹣,∴=,由△EDB∽△B′CF得:,∵DE=2,∴B′C=1,在Rt△B′FC中,由勾股定理得:12+()2=(2﹣)2,解得:k=3,答:k的值为:3.35.解:(1)∵在矩形ABCD的顶点B,AB=8,BC=6,而OC=8,∴B(2,0),A(2,8),C(8,0),∵对角线AC,BD相交于点E,∴点E为AC的中点,∴E(5,4),把E(5,4)代入y=得k=5×4=20;(2)∵AC==10,∴BE=EC=5,∵BF﹣BE=2,∴BF=7,设OB=t,则F(t,7),E(t+3,4),∵反比例函数(x>0)的图象经过点E、F,∴7t=4(t+3),解得t=4,∴k=7t=28,∴反比例函数解析式为y=,当x=10时,y==,∴G(10,),∴△CEG的面积=×3×=.36.解:(1)∵反比例函数y=(x>0,k>0)图象上的两点(n,3n)、(n+1,2n).∴n•3n=(n+1)•2n,解得n=2或n=0(舍去),∴n的值为2;(2)反比例函数解析式为y=,设B(m,m),∵OC=BC=m,∴△OBC为等腰直角三角形,∴∠OBC=45°,∵AB⊥OB,∴∠ABO=90°,∴∠ABC=45°,∴△ABD为等腰直角三角形,设BD=AD=t,则A(m+t,m﹣t),∵A(m+t,m﹣t)在反比例函数解析式为y=上,∴(m+t)(m﹣t)=12,∴m2﹣t2=12,∴S1﹣S2=m2﹣t2=×12=6.37.解:(1)根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且m﹣2>0,则m>2;(2)∵点B与点A关于x轴对称,若△OAB的面积为6,设AB交x轴于点C,∴△OAC的面积为3.设A(x,),则:△OAC的面积x•=3,解得m=8.38.解:(1)∵点A横坐标为a,点A在函数y=(x>0)图象上,∴点A纵坐标为,∵AB∥x轴,AC∥y轴,∴点B的纵坐标为:,点C的横坐标a,∴点B横坐标为:a;点C的纵坐标为:,∴B点坐标为(a,),C(a,);故答案为:(a,),C(a,);(2)∵A(a,),则C(a,),B(,),∴AB=a﹣=a,AC=﹣=,∴S△ABC=AB•AC=×a×=,即△ABC的面积不发生变化,其面积为;(3)BD=CE,如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F,∵AB∥x轴,∴△ABC∽△EFC,∴=,即=,∴EF=a,由(2)可知BG=a,∴BG=EF,∵AE∥y轴,∴∠BDG=∠FCE,在△DBG和△CFE中,∴△DBG≌△CEF(AAS),∴BD=CE.39.解:(1)A、B的横坐标分别为a、b,则点A、B的坐标分别为(a,)、(b,﹣),AB∥x轴,则,则a=﹣b,AB=a﹣b=2a,S△OAB=×2a×=3;(2)如图所示:∵a≥3,AC=2,则直线CD在y轴右侧且平行于y轴,CD一定与函数有交点,设交点为F,设点A(a,),则点C(a﹣2,),点D(a﹣2,),点F(a﹣2,)则2﹣FC=2﹣+=,∵a≥3,∴a﹣3≥0,a﹣2>0,故2﹣FC≥0,FC≤2,即点F在线段CD上,即当a≥3时,CD边与函数y1=(x>0)的图象有交点。
反比例函数动点问题

反比例函数动点问题通常涉及到一些几何和代数的知识。
以下是一个典型例题的分析:
已知A、B是反比例函数y=k/x(k>0,x≠0)的图像上的两点,当点A在第一象限时,与坐标轴围成的矩形AEOF的面积为3,则点B 与坐标轴围成的矩形的面积是()。
A. 3
B. -3
C. 6
D. 无法确定
我们可以根据题意进行推理。
由于点A在第一象限,所以矩形AEOF 的面积可以表示为|k| = 3。
同时,由于点B在反比例函数的图像上,与x轴和y轴围成一个矩形,其面积也为|k|。
但是这个矩形的面积的具体数值无法确定,因为它与点A的坐标有关。
因此,正确答案是D. 无法确定。
希望这个例子能够帮助你理解反比例函数动点问题的一般思路和方法。
如果你有更多的例题需要分析,欢迎继续提问。
反比例函数中的面积问题(共26张PPT)

课后精练
解:(1)如图,过点 D 作 DH⊥x 轴于点 H, ∵直线 AB 的解析式为 y=-2x+4,∴B 点坐标为(0,4), A 点坐标为(2,0). ∵∠OAB+∠DAH=90°,∠ADH+∠DAH=90°, ∴∠BAO=∠ADH. 又∵∠BOA=∠AHD,∴△AOB∽△DHA. ∴ADOH=ABOH=AADB=12.∴D2H=A4H=12,解得 DH=4,AH=8. ∴D(10,4),则 k=10×4=40. 故答案为:40.
③若 M 点的横坐标为 1,△OAM 为等边三角形,则 k=2+ 3;
7.如图,函数 y=kx(k 为常数,k>0)的图象与过原点的 O 的直线 相交于 A,B 两点,点 M 是第一象限内双曲线上的动点(点 M 在点 A 的左侧),直线 AM 分别交 x 轴,y 轴于 C,D 两点,连接 BM 分别 交 x 轴,y 轴于点 E,F.现有以下四个结论:
课后精练
∵D(10,4),∴D′(10,-4). 设直线 CD′的解析式为 y=ax+d, 则180a+a+dd==8- ,4,解得da==-566. , 故直线 CD′的解析式为 y=-6x+56. 当 y=0 时,x=238,故 P 点坐标为238,0. 延长 CD 交 x 轴于 Q,此时|QC-QD|的值最大, ∵CD∥AB,D(10,4),∴直线 CD 的解析式为 y=-2x+24. ∴Q(12,0).∴PQ=12-238=83. 故 P 点坐标为238,0,Q 点坐标为(12,0),线段 PQ 的长为83.
专题2 反比例函数中的面积问题
考点解读
反比例函数中的面积类问题是最能体现数形结合思想 方法的一类问题,几何中的函数问题使图形性质代数 化,函数中的几何问题使代数知识图形化,利用“数”
2021年九年级数学中考复习专题:反比例函数综合(考察坐标、取值范围、面积等)(四)

2021年九年级数学中考复习专题:反比例函数综合(考察坐标、取值范围、面积等)(四)1.如图1,在平面直角坐标系中,已知△ABC,∠ABC=90°,∠ACB=30°,顶点A 在第二象限,B,C两点在x轴的负半轴上(点C在点B的右侧),BC=2,△ACD与△ABC关于AC所在的直线对称.(1)当OC=2时,求点D的坐标;(2)若点A和点D在同一个反比例函数的图象上,求OC的长;(3)如图2,将第(2)题中的四边形ABCD向左平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=(k≠0)的图象与BA的延长线交于点P,问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.2.如图1,A(1,0)、B(0,2),双曲线y=(x>0)(1)若将线段AB绕A点顺时针旋转90°后B的对应点恰好落在双曲线y=(x>0)上①则k的值为;②将直线AB平移与双曲线y=(x>0)交于E、F,EF的中点为M(a,b),求的值;(2)将直线AB平移与双曲线y=(x>0)交于E、F,连接AE.若AB⊥AE,且EF =2AB,如图2,直接写出k的值.3.如图1,在平面直角坐标系xOy中,函数y=(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点.(1)求∠OCD的度数;(2)如图2,连接OQ、OP,当∠DOQ=∠OCD﹣∠POC时,求此时m的值;(3)如图3,点A,点B分别在x轴和y轴正半轴上的动点.再以OA、OB为邻边作矩形OAMB.若点M恰好在函数y=(m为常数,m>1,x>0)的图象上,且四边形BAPQ为平行四边形,求此时OA、OB的长度.4.如图,在四边形ABCD中,AB=BC=5,AD=DC=8,对角线BD=3+4,点B在y轴上,BD与x轴平行,点C在x轴上.(1)求∠ADC的度数.(2)点P在对角线BD上,点Q在四边形ABCD内且在点P的右边,连接AP、PQ、QC,已知AP=AQ,∠APQ=60°,设BP=m.①求CQ的长(用含m的代数式表示);②若某一反比例函数图象同时经过点A、Q,求m的值.5.已知一次函数y1=kx+n(n<0)和反比例函数y2=(m>0,x>0).(1)如图1,若n=﹣2,且函数y1、y2的图象都经过点A(3,4).①求m,k的值;②直接写出当y1>y2时x的范围;(2)如图2,过点P(1,0)作y轴的平行线l与函数y2的图象相交于点B,与反比例函数y3=(x>0)的图象相交于点C.①若k=2,直线l与函数y1的图象相交点D.当点B、C、D中的一点到另外两点的距离相等时,求m﹣n的值;②过点B作x轴的平行线与函数y1的图象相交于点E.当m﹣n的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.6.如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F 在第一象限内,OF的长度不变,且反比例函数y=经过点F.(1)如图1,当F在直线y=x上时,函数图象过点B,求线段OF的长.(2)如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.①求证:CD=2AE.②若AE+CD=DE,求k.③设点F的坐标为(a,b),当△ODE为等腰三角形时,求(a+b)2的值.7.如图,二次函数与反比例函数的图象有公共点A(﹣2,5),▱ABCD的顶点B(﹣5,p)在双曲线上,C、D两点在抛物线上(点C在y轴负半轴,点D在x轴正半轴)(1)求直线AB的表达式及C、D两点的坐标;(2)第四象限的抛物线上是否存在点E,使得四边形ACED的面积最大,若存在,求出点E的坐标和面积的最大值,不存在,说明理由.8.如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0)、D(﹣7,3),点B、C在第二象限内.(1)点B的坐标;(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.9.如图所示,在平面直角坐标系Oxy中,等腰△OAB的边OB与反比例函数y=(m >0)的图象相交于点C,其中OB=AB,点A在x轴的正半轴上,点B的坐标为(2,4),过点C作CH⊥x轴于点H.(1)已知一次函数的图象过点O,B,求该一次函数的表达式;(2)若点P是线段AB上的一点,满足OC=AP,过点P作PQ⊥x轴于点Q,连结OP,记△OPQ的面积为S△OPQ,设AQ=t,T=OH2﹣S△OPQ①用t表示T(不需要写出t的取值范围);②当T取最小值时,求m的值.10.如图,点P在曲线上,PA⊥x轴于点A,点B在y轴正半轴上,PA=PB,OA、OB的长是方程t2﹣8t+12=0的两个实数根,且OA>OB,点C是线段PB延长线上的一个动点,△ABC的外接圆⊙M与y轴的另一个交点是D.(1)填空:OA=;OB=;k=;(2)设点Q是⊙M上一动点,若圆心M在y轴上且点P、Q之间的距离达到最大值,则点Q的坐标是;(3)试问:在点C运动的过程中,BD﹣BC的值是否为定值?若是,请求出该定值;若不是,请给出合理的解释.参考答案1.解:(1)∵△ADC与△ABC关于AC所在的直线对称,∴CD=BC=2,∠ACD=∠ACB=30°,如图1,过点D作DE⊥BC于点E,∵∠DCE=60°,∴,∵OC=2,∴OE=3,∴;(2)设OC=m,则OE=m+1,OB=m+2在Rt△ABC中,∠ACB=30°,BC=2,∴,∴,∵A,D在同一反比例函数上,∴,解得:m=1,∴OC=1;(3)由(2)得:∴,∵四边形A1B1C1D1由四边形ABCD平移得到,∴,∵D1在反比例函数上,∴同理:,,∴,∴,∵x P=x A=﹣3,P在反比例函数上,∴,①若P为直角顶点,则A1P⊥DP,过点P作l1⊥y轴,过点A1作A1F⊥l1,过点D作DG⊥l1,则△A1PF∽△PDG,,解得:;②若D为直角顶点,则A1D⊥DP,过点D作l2⊥x轴,过点A1作A1H⊥l2,则△A1DH∽△DPG,,,解得:k=0(舍),综上:存在.2.解:(1)设旋转后点B的对应点为点C,过点C作CD⊥x轴于点D,如图所示∵∠BAC=90°,∴∠BAO+∠CAD=90°,∵∠BAO+∠ABO=90°,∴∠ABO=∠CAD,在△OAB和△DCA中,,∴△OAB≌△DCA(AAS),∴CD=OA=1,AD=OB=2,∴OD=OA+AD=3,∴C(3,1),把C(3,1)代入y=中,得k=3,故答案为:3;(2)直线AB表达式中的k值为﹣2,AB∥EF,则直线EF表达式中的k值为﹣2,设点E(m,n),mn=3,直线EF的表达式为:y=﹣2x+t,将点E坐标代入上式并解得,直线EF的表达式为y=﹣2x+2m+n,将直线EF表达式与反比例函数表达式联立并整理得:2x2﹣(2m+n)x+3=0,x1+x2=,x1x2=,则点F(n,),则a=(),b=(n+),===2;(3)故点E作EH⊥x轴交于点H,由(1)知:△ABO∽△EHA,∴,设EH=m,则AH=2m,则点E(2m+1,m),且k=m(2m+1)=2m2+m,直线AB表达式中的k值为﹣2,AB∥EF,则直线EF表达式中的k值为﹣2,设直线EF的表达式为:y=﹣2x+b,将点E坐标代入并求解得:b=5m+2,故直线EF的表达式为:y=﹣2x+5m+2,将上式与反比例函数表达式联立并整理得:2x2﹣(5m+2)x+3=0,用韦达定理解得:x F+x E=,则x F=,则点F(m,4m+2),则EF==2AB=2×,整理得:3m2+4m﹣4=0,解得:m=或﹣2(舍去负值),k=m(2m+1)=2m2+m=.3.解:(1)设直线PQ的解析式为y=kx+b,则有,解得,∴y=﹣x+m+1,令x=0,得到y=m+1,∴D(0,m+1),令y=0,得到x=m+1,∴C(m+1,0),∴OC=OD,∵∠COD=90°,∴∠OCD=45°.(2)如图2,过Q作QM⊥y轴于M,过P作PN⊥OC于N,过O作OH⊥CD于H,∵P(m,1)和Q(1,m),∴MQ=PN=1,OM=ON=m,∵∠OMQ=∠ONP=90°,∴△OMQ≌△ONP(SAS),∴OQ=OP,∠DOQ=∠POC,∵∠DOQ=∠OCD﹣∠POC,∠OCD=45°,∴∠DOQ=∠POC=∠QOH=∠POH=22.5°,∴MQ=QH=PH=PN=1,∵∠OCD=∠ODC=45°,∴△DMQ和△CNP都是等腰直角三角形,∴DQ=PC=,∵OC=OD=m+1,∴CD=OC=,∵CD=DQ+PQ+PC,∴=2+2,∴m=+1;(3)如图3,∵四边形BAPQ为平行四边形,∴AB∥PQ,AB=PQ,∴∠OAB=45°,∵∠AOB=90°,∴OA=OB,∴矩形OAMB是正方形,∵点M恰好在函数y=(m为常数,m>1,x>0)的图象上,∴M(,),即OA=OB=,∵AB=PQ,∴,解得:m=或(舍),∴OA=OB====.4.解:(1)连接AC交BD于点H,∵AB=BC,AD=DC,BD=BD,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,∴BH是等腰三角形ABC的高,即BH⊥AC,即BD是AC的中垂线,设HD=x,则BH=4+3﹣x,AH2=AB2﹣BH2=AD2﹣DH2,即82﹣x2=52﹣(3+4﹣x)2,解得:x=,cos∠ADB===,故∠ADB=30°BD是AC的中垂线,则∠ADB=30°=∠CDB,故∠ADC=2∠ADB=60°;(2)①连接AQ、QD、PC,∵∠APQ=60°,AP=AQ,∴△APQ为等边三角形,故∠PAQ=60°=∠PAC+∠HAQ,同理△ACD是边长为8的等边三角形,∴∠CAD=60°=∠HAQ+∠QAD,∴∠PAC=∠QAD,而AP=AQ,AD=AC,∴△ACP≌△ADQ(SAS),∵BD是AC的中垂线,故PA=PC,则△ACP为等腰三角形,∴△AQD也为等腰三角形,即AQ=QD,而AC=CD(△ACD为等边三角形),CQ=CQ,∴△ACQ≌△DCQ(SSS),故∠ACQ=∠DCQ,在△CAD中,延长CQ交AD于点K,∵AC=CD,则CK⊥AD,∴∠AKQ=90°∵∠AKQ=90°=∠AHP,∠QAK=∠PAH,PA=AQ,∴△AKQ≌△QHP(AAS),∴QK=PH,过点D作DR⊥x轴交于点R,BD∥x轴,故∠BDC=∠DCR=30°,DR=CD=8×=4=CH=OB,而BC=5,故OC=3=BH,故点C(3,0),PH=BH=BP=3﹣m=QK,在等边三角形ACD中,AD边上的高CK=CD sin∠CDA=8×sin60°=4,则CQ=CK﹣QK=4﹣3+m;②过点Q分别作x、y轴的垂线,垂足为M、N,∵AK是等边三角形CDA的高,则∠KCD=30°,而∠DCR=30°,故∠QCR=60°,QM=CQ sin∠QCM=CQ sin60°=CQ,CM=CQ,故点Q(3+CQ,CQ),点C(3,0),CH=4,故点A(3,8),反比例函数图象同时经过点A、Q,则3×8=(3+CQ)×CQ,而CQ=4﹣3+m,即m2+24m+39﹣96=0,解得:m=﹣4(不合题意值已舍去).5.解:(1)①将点A的坐标代入一次函数表达式并解得:k=2,将点A的坐标代入反比例函数得:m=3×4=12;②由图象可以看出x>3时,y1>y2;(2)①当x=1时,点D、B、C的坐标分别为(1,2+n)、(1,m)、(1,n),则BD=|2+n﹣m|,BC=m﹣n,DC=2+n﹣n=2则BD=BC或BD=DC或BC=CD,即:|2+n﹣m|=m﹣n或|2+n﹣m|=2或m﹣n=2,即:m﹣n=1或0或2或4,当m﹣n=0时,m=n与题意不符,点D不能在C的下方,即BC=CD也不存在,n+2>n,当B、D重合时,m﹣n=2成立,故m﹣n=1或4或2;②点E的横坐标为:,当点E在点B左侧时,d=BC+BE=m﹣n+(1﹣)=1+(m﹣n)(1﹣),m﹣n的值取不大于1的任意数时,d始终是一个定值,当1﹣=0时,此时k=1,从而d=1.当点E在点B右侧时,同理BC+BE=(m﹣n)(1+)﹣1,当1+=0,k=﹣1时,(不合题意舍去)故k=1,d=1.6.解:(1)∵F在直线y=x上∴设F(m,m)∵y=经过点B(2,4).∴k=8.∵F(m,m)在反比例函数的图象上,∴m2=8∴m=2(负值已舍去).∴由两点间的距离公式可知:OF==4.(2)①∵函数y=的图象经过点D,E∴OC•CD=OA•AE=k.∵OC=2,OA=4,∴CD=2AE.②由①得:CD=2AE∴可设:CD=2n,AE=n∴DE=CD+AE=3n,BD=4﹣2n,BE=2﹣n在Rt△EBD,由勾股定理得:DE2=BD2+BE2,∴9n2=(4﹣2n)2+(2﹣n)2.解得n=,∴k=4n=6﹣10.③CD=2c,AE=c当OD=DE时,22+4c2=(4﹣2c)2+(2﹣c)2,∴c=10﹣2,∴k=4c=40﹣8.(a+b)2=a2+b2+2ab=16+2k=96﹣16.当若OE=DE时,16+c2=(4﹣2c)2+(2﹣c)2,∴c=.∴k=4c=10﹣2.∴(a+b)2=a2+b2+2ab=16+2k=36﹣4.当OE=OD时,4+4c2=16+c2,解得c=2.此时点D与点E重合,故此种情况不存在.综上所述,(a+b)2的值为96﹣16或36﹣4.7.解:(1)设反比例函数的解析式为y=.∵它图象经过点A(﹣2,5)和点B(﹣5,p),∴5=,∴k=﹣10,∴反比例函数的解析式为y=﹣,∴P=﹣=2,∴点B的坐标为(﹣5,2),设直线AB的表达式为y=mx+n,则,∴,∴直线AB的表达式为y=x+7.由▱ABCD中,AB∥CD,设CD的表达式为y=x+c,∴C(0,c),D(﹣c,0),∵CD=AB,∴CD2=AB2,∴c2+c2=(﹣5+2)2+(2﹣5)2,∴c=﹣3,∴点C、D的坐标分别是(0,﹣3)、(3,0).(2)设二次函数的解析式为y=ax2+bx﹣3,,∴,∴二次函数的解析式为y=x2﹣2x﹣3,假设第四象限的抛物线上存在点E,使得△CDE的面积最大.设E(k,k2﹣2k﹣3),则F(k,k﹣3),过点E作x轴的垂线交CD于点F,则S△CDE=S△EFC+S△EFD=•EF•OD=•[(k﹣3)﹣(k2﹣2k﹣3)]=﹣(k2﹣3k)=﹣(k﹣)2+,所以,当k=时,△CDE的面积最大值为,此时点E的坐标为(,﹣).∵A(﹣2,5),C(0,﹣3),D(3,0),∴△ACD的面积为定值,∵直线AD的解析式为y=﹣x+3,∴直线AD交y轴于K(0,3),∴S△ACD=S△ACK+S△CKD=×6×2+×6×3=15,∴四边形ACED的面积的最大值为15+=.8.解:(1)过点B、D分别作BE⊥x轴、DF⊥x轴交于点E、F,∵∠DAF+∠BAE=90°,∠DAF+∠FDA=90°,∴∠FDA=∠BAE,又∠DFA=∠AEB=90°,AD=AB,∴△DFA≌△AEB(AAS),∴DF=AE=3,BE=AF=1,∴点B坐标为(﹣3,1),故答案为(﹣3,1);(2)t秒后,点D′(﹣7+2t,3)、B′(﹣3+2t,1),则k=(﹣7+2t)×3=(﹣3+2t)×1,解得:t=,则k=6,则点D′(2,3)、B′(6,1);(3)存在,理由:设:点Q(m,n),点P(0,s),mn=6,①当BD为平行四边形一条边时,图示平行四边形B′D′QP,点B′向左平移4个单位、向上平移2个单位得到点D′,同理点Q(m,n)向左平移4个单位、向上平移2个单位为(m﹣4,n+2)得到点P (0,s),即:m﹣4=0,n+2=s,mn=6,解得:m=4,n=,s=,故点Q(4,)、点P(0,);②当BD为平行四边形对角线时,图示平行四边形D′Q′B′P′,B′、D′中点坐标为(4,2),该中点也是P′Q′的中点,即:4=,=2,mm=6,解得:m=8,n=,s=,故点Q′(8,)、P′(0,);故点Q的坐标为:Q(4,)或(8,),点P的坐标为P(0,)(0,).9.解:(1)将点O、B的坐标代入一次函数表达式:y=kx得:4=2k,解得:k=2,故一次函数表达式为:y=2x,(2)①过点B作BM⊥OA,则∠OCH=∠QPA=∠OAB=∠ABM=α,则tanα=,sinα=,∵OB=AB,则OM=AM=2,则点A(4,0),设:AP=a,则OC=a,在△APQ中,sin∠APQ===sinα=,同理PQ==2t,则PA=a=t,OC=t,则点C(t,2t),T=OH2﹣S△OPQ=(OC•sinα)2﹣×(4﹣t)×2t=4t2﹣4t,②∵4>0,∴T有最小值,当t=时,T取得最小值,而点C(t,2t),故:m=t×2t=.10.解:(1)t2﹣8t+12=0,解得:t=2或6,∵OA、OB的长是方程t2﹣8t+12=0的两个实数根,且OA>OB,即OA=6,OB=2,即点A、B的坐标为(﹣6,0)、(0,2),设点P(﹣6,),由PA=PB得:36+(2+)2=()2,解得:k=﹣60,故点P(﹣6,10),故答案为:6,2,﹣60;(2)当PQ过圆心M时,点P、Q之间的距离达到最大值,tan∠ACO=,线段AB中点的坐标为(﹣3,1),则过AB的中点与直线AB垂直的直线PQ的表达式为:y=mx+n=﹣3x+n,将点(﹣3,1)的坐标代入上式并解得:n=﹣8,即点M的坐标为(0,﹣8),则圆的半径r=MB=2+8=10=MQ,过点Q作QG⊥y轴于点G,tan∠QMG=tan∠HMP===,则sin∠QMG=故GQ=MQ sin∠QMG=,MG=3,故点Q(,﹣8﹣3);故答案为:(,﹣8﹣3).(3)是定值,理由:延长PA交圆M于E,过点E作EH⊥BD于H,连接CE,DE,∵PA=PB,∴∠PAB=∠PBA,∵四边形ABCE是圆的内接四边形,∴∠PAB=∠PCE,∠PBA=∠PEC,∴∠PEC=∠PCE,∴PE=PC,∴AE=BC,∵AO⊥BD,EH⊥BD,PA⊥OA,∴四边形AOHE是矩形,∴AO=EH,AE=OH=BC,∵PA∥BD,∴=,∴,∴∠ABD=∠BDE,且∠AOB=∠EHD=90°,AO=EH,∴△AOB≌△EHD(AAS)∴OB=DH=2,∴BD﹣BC=BD﹣OH=OB+DH=4.。
专题64 反比例函数k的八种几何模型及解法(解析版)-中考数学解题大招复习讲义

模型介绍考点1一点一垂线模型【模型讲解】反比例函数图象上一点关于坐标轴的垂线、另一坐标轴上一点(含原点)围成的三角形面积等于12|k|.【示例】拓展:【例1】.如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=(x >0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会()A.越来越小B.越来越大C.不变D.先变大后变小解:如图,过点B作BC⊥PA于点C,则BC=OA,设点P(x,),=PA•BC=••x=3,则S△P AB当点A的横坐标逐渐增大时,△PAB的面积将会不变,始终等于3,故选:C.变式训练【变1-1】.如图,点A、B的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是4,则k的值为﹣.解:设OM=a,则OM=MN=NC=a,∵点A、B在反比例函数y=的图象上,AM⊥OC、BN⊥OC,∴AM=,BN=,=S△AOM+S四边形AMNB+S△BNC,∵S△AOC∴﹣×3a×=﹣k+4﹣×a×,解得k=﹣,故答案为:﹣.【变1-2】.如图,在第一象限内,点P(2,3),M(a,2)是双曲线y=(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为()A.B.C.2D.解:把P(2,3),M(a,2)代入y=得k=2×3=2a,解得k=6,a=3,设直线OM的解析式为y=mx,把M(3,2)代入得3m=2,解得m=,所以直线OM的解析式为y=x,当x=2时,y=×2=,所以C点坐标为(2,),所以△OAC的面积=×2×=.故选:B.考点2一点两垂线模型【模型讲解】反比例函数图象上一点与坐标轴的两条垂线所围成的矩形面积等于|k |.【示例】ABCD S k【例2】.双曲线与在第一象限内的图象如图所示,作一条平行于y 轴的直线分别交双曲线于A 、B 两点,连接OA 、OB ,则△AOB 的面积为()A .1B .2C .3D .4解:设直线AB 与x 轴交于点C .∵AB ∥y 轴,∴AC ⊥x 轴,BC ⊥x 轴.∵点A 在双曲线y =的图象上,∴△AOC 的面积=×10=5.∵点B 在双曲线y =的图象上,∴△COB的面积=×6=3.∴△AOB的面积=△AOC的面积﹣△COB的面积=5﹣3=2.故选:B.变式训练【变2-1】.如图,函数y=(x>0)和(x>0)的图象分别是l1和l2.设点P在l2上,PA∥y轴交l1于点A,PB∥x轴交l1于点B,△PAB的面积为.解:设点P(x,),则点B(,),A(x,),∴BP=x﹣=,AP=﹣=,==,∴S△ABP故答案为:.【变2-2】.如图,直线AB∥x轴,分别交反比例函数y=图象于A、B两点,若S△AOB=2,则k2﹣k1的值为4.解:设A(a,b),B(c,d),代入得:k1=ab,k2=cd,=2,∵S△AOB∴cd﹣ab=2,∴cd﹣ab=4,∴k2﹣k1=4,故答案为:4.【变2-3】.如图,在平面直角坐标系中,M为y轴正半轴上一点,过点M的直线l∥x轴,l分别与反比例函数y=和y=的图象交于A、B两点,若S△AOB=3,则k的值为﹣2.解:∵直线l∥x轴,∴AM⊥y轴,BM⊥y轴,=|k|,S△BOM=×4=2,∴S△AOM=3,∵S△AOB=1,∴S△AOM∴|k|=2,∵k<0,∴k=﹣2,故答案为:﹣2.考点3两曲一平行模型【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.类型1两条双曲线的k值符号相同【示例】【例3】.如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=(k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为()A.﹣8B.﹣12C.﹣24D.﹣36解:设A(x,0).∵正方形ADEF的面积为16,∴ADEF的边长为4,∴E(x﹣4,4),∵BF=2AF,∴BF=2×4=8,∴B(x,12).∵点B、E在反比例函数y=(k为常数,k≠0)的图象上,∴4(x﹣4)=12x,解得x=﹣2,∴B(﹣2,12),∴k=﹣2×12=﹣24,故选:C.变式训练【变3-1】.若正方形OABC的顶点B和正方形ADEF的顶点E都在函数的图象上.若正方形OABC的面积为1,则k的值为1;点E的坐标为(+,﹣).解:∵正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上,且正方形OABC的边长为1.∴B点坐标为:(1,1),设反比例函数的解析式为y=;∴xy=k=1,设正方形ADEF的边长为a,则E(1+a,a),代入反比例函数y=(x>0)得:1=(1+a)a,又a>0,解得:a=﹣.∴点E的坐标为:(+,﹣).【变3-2】.如图,A、B两点在双曲线y=上,分别经过A、B两点向坐标轴作垂线段,已知S=1.7,则S1+S2等于 4.6.阴影解:如图,∵A、B两点在双曲线y=上,=4,S四边形BDOC=4,∴S四边形AEOF∴S1+S2=S四边形AEOF+S四边形BDOC﹣2×S阴影,∴S1+S2=8﹣3.4=4.6故答案为:4.6.【变3-3】.如图,在反比例函数(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为1,2,3,4,….分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,则S1+S2+S3+…+S n=.(用n的代数式表示,n为正整数)解:当x=1时,P1的纵坐标为2,当x=2时,P2的纵坐标1,当x=3时,P3的纵坐标,当x=4时,P4的纵坐标,当x=5时,P5的纵坐标,…则S1=1×(2﹣1)=2﹣1;S2=1×(1﹣)=1﹣;S3=1×(﹣)=﹣;S4=1×(﹣)=﹣;…S n=﹣;S1+S2+S3+…+S n=2﹣1+1﹣+﹣+﹣+…+﹣=2﹣=.故答案为:.考点4两点一垂线模型【模型讲解】反比例函数与正比例函数图象的交点及由交点向坐标轴所作垂线围成的三角形面积等于|k|,反比例函数与一次函数图象的交点及坐标轴上任一点构成三角形的面积,等于坐标轴所分的两个三角形面积之和.【示例】【例4】.如图,正比例函数y=kx与反比例函数y=﹣相交于A,C两点,点A的横坐标为﹣4,过点A作x轴的垂线交x轴于B点,连接BC,下列结论:①k=﹣;②不等式kx<﹣的解集为﹣4<x<0或x>4;③△ABC的面积等于16.其中正确的结论个数为()A.0B.1C.2D.3解:将x=﹣4代入y=﹣得y=﹣=2,∴点A坐标为(﹣4,2),将(﹣4,2)代入y=kx得2=﹣4k,解得k=﹣,∴①正确.由反比例函数及正比例函数的对称性可得点C坐标为(4,﹣2),∴当﹣4<x<0或x>4时,kx<﹣,∴②正确.=S△AOB+S△BOC=OB•y A+OB•(﹣y C)=BO(y A﹣y C)=×(2+2)∵S△AOC=8,∴③错误.故选:C.变式训练【变4-1】.如图所示,一次函数y=kx(k<0)的图象与反比例函数y=﹣的图象交于A,B两点,过点B作BC⊥y轴于点C,连接AC,则△ABC的面积为4.解:∵BC⊥y轴于点C,=|﹣4|=2,∴S△COB∵正比例函数y=kx(k>0)与反比例函数y=﹣的图象均关于原点对称,∴OA=OB,=S△COB=2,∴S△AOC=S△AOB+S△BOC=2+2=4,∴S△ABC故答案为:4.【变4-2】.如图,过点O的直线与反比例函数y=的图象交于A、B两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为.解:∵点A反比例函数y=的图象上,过点A作AC⊥x轴于点C,=|k|=,∴S△AOC∵过点O的直线与反比例函数y=的图象交于A、B两点,∴OA=OB,=S△AOC=∴S△BOC=2S△ACO=,∴S△ABC故答案为:.【变4-3】.如图,函数y=x与y=的图象交于A、B两点,过点A作AC垂直于y轴,垂=3,则k=3.足为C,连接BC,若S△ABC解:设A(a,a)(a>0),∵函数y=x与y=的图象的中心对称性,∴B(﹣a,﹣a),=•a•2a=a2=3,∴S△ABC∴a=,∴A(,),把A(,)代入y=得k==3.故答案为:3.考点5两点两垂线模型【模型讲解】反比例函数与正比例函数图象的交点及由交点向坐标轴所作两条垂线围成的图形面积等于2|k|.【示例】【例5】.如图,正比例函数y=kx与反比例函数y=﹣的图象交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为4.解:∵点A在反比例函数y=﹣上,且AB⊥x轴,∴=2,∵A,C是反比例函数与正比例函数的交点,且CD⊥x轴,∴O是BD的中点,=2S△ABO=4.∴S△ABD故答案为:4.变式训练【变5-1】.如图,一次函数y=kx与反比例函数上的图象交于A,C两点,AB∥y轴,BC∥x轴,若△ABC的面积为4,则k=﹣2.解:设AB交x轴于点D,的面积为,由反比例函数系数的几何意义可得S△ADO由函数的对称性可得点O为AC中点,即DO为△ABC中位线,∴=,=4S△ADO=2|k|=4,∴S△ABC∵k<0,∴k=﹣2.故答案为:﹣2.【变5-2】.如图,正比例函数y=kx(k>0)与反比例函数y=的图象交于A,C两点,过点A作x轴的垂线,交x轴于点B,过点C作x轴的垂线,交x轴于点D,连接AD,BC,则四边形ABCD的面积为2.解:∵A、C是两函数图象的交点,∴A、C关于原点对称,∵CD⊥x轴,AB⊥x轴,∴OA=OC,OB=OD,=S△BOC=S△DOC=S△AOD,∴S△AOB又∵A点在反比例函数y=的图象上,=S△BOC=S△DOC=S△AOD×1=,∴S△AOB=4S△AOB=4×=2,∴S四边形ABCD故答案为:2.【变5-3】.如图,直线分别与反比例函数y=﹣和y=的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x轴交于点D,则四边形ABCD的面积是5.解:过点A作AF⊥y轴,垂足于点F;过点B作BE⊥y轴,垂足为点E.∵点P是AB中点.∴PA=PB.又∵∠APF=∠BPE,∠AFP=∠BEP=90°,∴△APF≌△BPE.=S△BPE.∴S△APF=S四边形ACOF+S四边形EODB=|﹣2|+|3|=5.∴S四边形ABCD故答案为:5.考点6反比例函数上两点和外一点模型【模型讲解】反比例函数与一次函数图象的交点和原点所围成的三角形面积,若两交点在同一分支上,用减法.【示例】方法一:S △AOB =S △COD -S △AOC -S △BOD .方法二:作AE ⊥x 轴于点E ,交OB 于点M ,BF ⊥x 轴于点F ,则S △OAM =S 四边形MEFB (划归到模型一),则S △AOB =S 直角梯形AEFB .【拓展】方法一:当BE CE 或BFFA=m 时,则S 四边形OFBE =m |k |.方法二:作EM ⊥x 轴于M ,则S △OEF =S 直角梯形EMAF (划归到上一个模型示例).【例6】.如图,一次函数y =ax +b 的图象与反比例函数y =的图象交于A ,B 两点,则S△AOB=()A.B.C.D.6解:把A(﹣4,1)代入y=的得:k=﹣4,∴反比例函数的解析式是y=﹣,∵B(1,m)代入反比例函数y=﹣得:m=﹣4,∴B的坐标是(1,﹣4),把A、B的坐标代入一次函数y=ax+b得:,解得:a=﹣1,b=﹣3,∴一次函数的解析式是y=﹣x﹣3;把x=0代入一次函数的解析式是y=﹣x﹣3得:y=﹣3,∴D(0,﹣3),=S AOD+S△BOD=×3×(1+4)=.∴S△AOB故选:A.变式训练【变6-1】.如图,直线AB经过原点O,且交反比例函数的图象于点B,A,点C在x=12,则k的值为()轴上,且.若S△BCAA.12B.﹣12C.﹣6D.6解:作AD⊥x轴于D,BE⊥x轴于E,∵点A、B在反比例函数的图象上,直线AB经过原点,∴OA=OB=AB,=12,∵,S△BCA=S△BCA=6,∴OB=BC,S△BCO∵BE⊥OC,∴OE=CE,=S△BCO=3,∴S△OBE∵BE⊥x轴于E,=|k|,∴S△OBE∴|k|=6,∵k<0,∴k=﹣6.故选:C.【变6-2】.如图,在平面直角坐标系中,反比例函数y=与直线y=交于A,B,x轴的正半轴上有一点C 使得∠ACB =90°,若△OCD 的面积为25,则k 的值为48.解:设点A 坐标为(3a ,4a ),由反比例函数图象与正比例函数图象的对称性可得点B 坐标为(﹣3a ,﹣4a ),∴OA =OB ==5a ,∵∠ACB =90°,O 为AB 中点,∴OC =OA =OB =5a ,设直线BC 解析式为y =kx +b ,将(﹣3a ,﹣4a ),(5a ,0)代入y =kx +b 得,解得,∴y =x ﹣a ,∴点D 坐标为(0,﹣a ),∴S △OCD =OC •OD =5a ×a =25,解得a =2或a =﹣2(舍),∴点A 坐标为(6,8),∴k =6×8=48.故答案为:48.【变6-3】.如图,正比例函数y =﹣x 与反比例函数y =的图象交于A ,B 两点,点C 在x 轴上,连接AC ,BC .若∠ACB =90°,△ABC 的面积为10,则该反比例函数的解析式是y =﹣.解:设点A 为(a ,﹣a ),则OA ==﹣a ,∵点C 为x 轴上一点,∠ACB =90°,且△ACB 的面积为20,∴OA =OB =OC =﹣a ,∴S △ACB =×OC ×(y A +|y B |)=×(﹣a )×(﹣a )=10,解得,a =±(舍弃正值),∴点A 为(﹣,2),∴k =﹣×2=﹣6,∴反比例函数的解析式是y =﹣,故答案为:y =﹣.考点7反比例函数上两点和原点模型【模型讲解】反比例函数与一次函数图象的交点和原点所围成的三角形面积,若两交点分别在两个分支上,用加法.【示例】方法一:S △AOB =12OD ·|x B -x A |=12OC ·|y A -y B |.方法二:S △AOB =S △AOC +S △OCD +S △OBD .方法三:作AE ⊥y 轴于点E ,BF ⊥x 轴于点F ,延长AE 与BF 相交于点N ,则S △AOB =S △ABN -S △AOE -S △OBF -S 矩形OENF .【例7】.如图,直线AB 交双曲线于A 、B ,交x 轴于点C ,B 为线段AC 的中点,过=12.则k的值为8.点B作BM⊥x轴于M,连接OA.若OM=2MC,S△OAC解:过A作AN⊥OC于N,∵BM⊥OC∴AN∥BM,∵,B为AC中点,∴MN=MC,∵OM=2MC,∴ON=MN=CM,设A的坐标是(a,b),则B(2a,b),=12.∵S△OAC∴•3a•b=12,∴ab=8,∴k=ab=8,故答案为:8.变式训练【变7-1】.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且四边形ODBE的面积为21,则k=7.解:设D点的横坐标为x,则其纵坐标为,∵BD=3AD,∴点B点的坐标为(4x,),点C的坐标为(4x,0)=21,∵S四边形ODBE﹣S△OCE﹣S△OAD=21,∴S矩形ABCD即:4x•﹣﹣=21解得:k=7.故答案为:7.【变7-2】.如图,点是直线AB与反比例函数图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.(1)求反比例函数和直线AB的解析式;(2)△ABC和△ABD的面积分别为S1,S2,求S2﹣S1.解:(1)由点A(,4)在反比例函数y=(x>0)图象上,∴n=×4=6,∴反比例函数的解析式为y=(x>0),将点B(3,m)代入y=(x>0)并解得m=2,∴B(3,2),设直线AB的表达式为y=kx+b,∴,解得,∴直线AB的表达式为y=﹣x+6;(2)由点A坐标得AC=4,则点B到AC的距离为3﹣=,∴S1==3,设AB与y轴的交点为E,则点E(0,6),如图:∴DE=6﹣1=5,由点A(,4),B(3,2)知,点A,B到DE的距离分别为,3,∴S2=S△BDE﹣S△AED=﹣=,∴S2﹣S1=﹣3=.考点8两双曲线k值符号不同模型【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.类型1两条双曲线的k值符号相同【示例】【例8】.如图,在平面直角坐标系中,函数y=kx与的图象交于A、B两点,过A作y轴的垂线,交函数的图象于点C,连接BC,则△ABC的面积为()A.2B.3C.5D.6解:∵正比例函数y=kx与反比例函数y=﹣的图象交点关于原点对称,∴设A点坐标为(x,﹣),则B点坐标为(﹣x,),C(﹣2x,﹣),=×(﹣2x﹣x)•(﹣﹣)=×(﹣3x)•(﹣)=6.∴S△ABC故选:D.变式训练【变8-1】.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=(x>0)和y=﹣(x>0)的图象交于B、A两点.若点C是y轴上任意一点,则△ABC的面积为()A.3B.6C.9D.解:设P(a,0),a>0,则A和B的横坐标都为a,将x=a代入反比例函数y=﹣中得:y=﹣,故A(a,﹣);将x=a代入反比例函数y=中得:y=,故B(a,),∴AB=AP+BP=+=,=AB•x P的横坐标=××a=,则S△ABC故选:D.【变8-2】.如图,点A和点B分别是反比例函数y=(x>0)和y=(x>0)的图象上=2,则m﹣n的值为4.的点,AB⊥x轴,点C为y轴上一点,若S△ABC解:连接AO.CO,∵AB⊥x轴,点C为y轴上一点,∴AB∥y轴,=S△ABO=2,∴S△ABC∴=2.∴=2,即m﹣n=4.故答案为:4.1.如图,Rt△ABC的顶点A在双曲线y=的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是()A.4B.﹣4C.2D.﹣2解:∵∠ACB=30°,∠AOB=60°,∴∠OAC=∠AOB﹣∠ACB=30°,∴∠OAC=∠ACO,∴OA=OC=4,在△AOB中,∠ABC=90°,∠AOB=60°,OA=4,∴∠OAB=30°,∴OB=OA=2,∴AB=OB=2,∴A点坐标为(﹣2,2),把A(﹣2,2)代入y=得k=﹣2×2=﹣4.故选:B.2.如图,平行四边形OABC的顶点B,C在第一象限,点A的坐标为(3,0),点D为边AB的中点,反比例函数y=(x>0)的图象经过C,D两点,若∠COA=α,则k的值等于()A.8sin2αB.8cos2αC.4tanαD.2tanα解:方法一:过点C作CE⊥OA于点E,过点D作DF⊥OA交OA的延长线于点F,设C点横坐标为:a,则:CE=a•tanα,∴C点坐标为:(a,a•tanα),∵平行四边形OABC中,点D为边AB的中点,∴D点纵坐标为:a•tanα,设D点横坐标为x,∵C,D都在反比例函数图象上,∴a×a•tanα=x×a•tanα,解得:x=2a,则FO=2a,∴FE=a,∵∠COE=∠DAF,∠CEO=∠DFA,∴△COE∽△DAF,∴==2,∴AF=,∴AO=OF﹣AF=a,∵点A的坐标为(3,0),∴AO=3,∴a=3,解得:a=2,∴k=a×a•tanα=2×2tanα=4tanα.方法二:∵C(a,a tanα),A(3,0),∴B(a+3,a tanα),∵D是线段AB中点,∴D(,a tanα),即D(,a tanα).∵反比例函数过C,D两点,∴k=a•a tanα=(a+6)•a tanα,解得a=2,∴k=4tanα.故选:C.3.如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,=.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是()A.2B.3C.5D.7解:设OA=3a,则OB=4a,∴A(3a,0),B(0,4a).设直线AB的解析式是y=kx+b,则根据题意得:,解得:,则直线AB的解析式是y=﹣x+4a,直线CD是∠AOB的平分线,则OD的解析式是y=x.根据题意得:,解得:则D的坐标是(,),OA的中垂线的解析式是x=,则C的坐标是(,),将C点坐标代入反比例函数y=,则k=.设OA的垂直平分线交x轴于点F,过点D作DE⊥x轴于点E,如图,则OF=CF=,OE=DE=a,∵∠DOA=45°,∴△COF和△DOE为等腰直角三角形,∴OC=OF=a,OD=OE=a,∴CD=OD﹣OC=()=(﹣)=a.∵以CD为边的正方形的面积为,∴=,则a2=,∴k=×=7.故选:D.4.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=的图象上,且OA⊥OB,cos A=,则k的值为()A.﹣3B.﹣4C.﹣D.﹣2解:过A作AE⊥x轴,过B作BF⊥x轴,∵OA⊥OB,∴∠AOB=90°,∴∠BOF+∠EOA=90°,∵∠BOF+∠FBO=90°,∴∠EOA=∠FBO,∵∠BFO=∠OEA=90°,∴△BFO∽△OEA,在Rt△AOB中,cos∠BAO==,设AB=,则OA=1,根据勾股定理得:BO=,∴OB:OA=:1,:S△OEA=2:1,∴S△BFO∵A在反比例函数y=上,=1,∴S△OEA=2,∴S△BFO则k=﹣4.故选:B.5.如图,反比例函数y=(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是()A.B.C.D.解:如图,∵点A坐标为(﹣1,1),∴k=﹣1×1=﹣1,∴反比例函数解析式为y=﹣,∵OB=AB=1,∴△OAB为等腰直角三角形,∴∠AOB=45°,∵PQ⊥OA,∴∠OPQ=45°,∵点B和点B′关于直线l对称,∴PB=PB′,BB′⊥PQ,∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,∴B′P⊥y轴,∴点B′的坐标为(﹣,t),∵PB=PB′,∴t﹣1=|﹣|=,整理得t2﹣t﹣1=0,解得t1=,t2=(不符合题意,舍去),∴t的值为.故选:A.6.如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(﹣3,2),若反比例函数y=(x>0)的图象经过点A,则k的值为()A.﹣6B.﹣3C.3D.6解:∵A与C关于OB对称,∴A的坐标是(3,2).把(3,2)代入y=得:2=,解得:k=6.故选:D.7.如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为()A.3B.6C.D.解:∵将直线y=向上平移4个单位长度后,与y轴交于点C,∴平移后直线的解析式为y=x+4,分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,x),∵OA=3BC,BC∥OA,CF∥x轴,∴△BCF∽△AOD,∴CF=OD,∵点B在直线y=x+4上,∴B(x,x+4),∵点A、B在双曲线y=上,∴3x•x=x•(x+4),解得x=1,∴k=3×1××1=.故选:D.8.如图,已知四边形ABCD是平行四边形,BC=2AB.A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数y=(k<0)的图象上,则k等于﹣12.解:设点C坐标为(a,),(k<0),点D的坐标为(x,y),∵四边形ABCD是平行四边形,∴AC与BD的中点坐标相同,∴(,)=(,),则x=a﹣1,y=,代入y=,可得:k=2a﹣2a2①;在Rt△AOB中,AB==,∴BC=2AB=2,故BC2=(0﹣a)2+(﹣2)=(2)2,整理得:a4+k2﹣4ka=16a2,将①k=2a﹣2a2,代入后化简可得:a2=4,∵a<0,∴a=﹣2,∴k=﹣4﹣8=﹣12.故答案为:﹣12.方法二:因为ABCD是平行四边形,所以点C、D是点B、A分别向左平移a,向上平移b得到的.故设点C坐标是(﹣a,2+b),点D坐标是(﹣1﹣a,b),(a>0,b>0),∴﹣a(2+b)=b(﹣1﹣a),整理得2a+ab=b+ab,解得b=2a.过点D作x轴垂线,交x轴于H点,在直角三角形ADH中,由已知易得AD=2,AH=a,DH=b=2a.AD2=AH2+DH2,即20=a2+4a2,得a=2.所以D坐标是(﹣3,4)所以k=﹣12.9.如图,点E,F在函数y=(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是2,△OEF的面积是(用含m的式子表示)解:作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,∵△OEP的面积为1,∴|k|=1,而k>0,∴k=2,∴反比例函数解析式为y=,∵EP⊥y轴,FH⊥y轴,∴EP∥FH,∴△BPE∽△BHF,∴==,即HF=mPE,设E点坐标为(t,),则F点的坐标为(tm,),+S△OFD=S△OEC+S梯形ECDF,∵S△OEF=S△OEC=1,而S△OFD=S梯形ECDF=(+)(tm﹣t)∴S△OEF=(+1)(m﹣1)=.故答案为:2,.10.如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=(k≠0)的图象经过圆心P,则k=.解:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.则有PD⊥OA,PE⊥AB.设⊙P的半径为r,∵AB=5,AC=1,=AB•PE=r,S△APC=AC•PD=r.∴S△APB∵∠AOB=90°,OA=4,AB=5,∴OB=3.=AC•OB=×1×3=.∴S△ABC=S△APB+S△APC,∵S△ABC∴=r+r.∴r=.∴PD=.∵PD⊥OA,∠AOB=90°,∴∠PDC=∠BOC=90°.∴PD∥BO.∴△PDC∽△BOC.∴=.∴PD•OC=CD•BO.∴×(4﹣1)=3CD.∴CD=.∴OD=OC﹣CD=3﹣=∴点P的坐标为(,).∵反比例函数y=(k≠0)的图象经过圆心P,∴k=×=.故答案为:.11.如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=;②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是①④(把所有正确的结论的序号都填上).解:作AE⊥y轴于E,CF⊥y轴于F,如图,∵四边形OABC是平行四边形,∴S△AOB=S△COB,∴AE=CF,∴OM=ON,∵S△AOM=|k1|=OM•AM,S△CON=|k2|=ON•CN,∴=,故①正确;∵S△AOM=|k1|,S△CON=|k2|,∴S阴影部分=S△AOM+S△CON=(|k1|+|k2|),而k1>0,k2<0,∴S阴影部分=(k1﹣k2),故②错误;当∠AOC=90°,∴四边形OABC是矩形,∴不能确定OA与OC相等,而OM=ON,∴不能判断△AOM≌△CNO,∴不能判断AM=CN,∴不能确定|k1|=|k2|,故③错误;若OABC是菱形,则OA=OC,而OM=ON,∴Rt△AOM≌Rt△CNO,∴AM=CN,∴|k1|=|k2|,∴k1=﹣k2,∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.故答案为:①④.12.如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,A n,…记点A n的横坐标为a n,若a1=2,则a2=﹣,a2013=﹣;若要将上述操作无限次地进行下去,则a1不可能取的值是0、﹣1.解:当a1=2时,B1的纵坐标为,B1的纵坐标和A2的纵坐标相同,则A2的横坐标为a2=﹣,A2的横坐标和B2的横坐标相同,则B2的纵坐标为b2=﹣,B2的纵坐标和A3的纵坐标相同,则A3的横坐标为a3=﹣,A3的横坐标和B3的横坐标相同,则B3的纵坐标为b3=﹣3,B3的纵坐标和A4的纵坐标相同,则A4的横坐标为a4=2,A4的横坐标和B4的横坐标相同,则B4的纵坐标为b4=,即当a1=2时,a2=﹣,a3=﹣,a4=2,a5=﹣,b1=,b2=﹣,b3=﹣3,b4=,b5=﹣,∵=671,∴a2013=a3=﹣;点A1不能在y轴上(此时找不到B1),即x≠0,点A1不能在x轴上(此时A2,在y轴上,找不到B2),即y=﹣x﹣1≠0,解得:x≠﹣1;综上可得a1不可取0、﹣1.故答案为:﹣;﹣;0、﹣1.13.如图,一次函数y=x+1的图象与反比例函数y=(x>0)的图象交于点A(a,3),与y轴交于点B.(1)求a,k的值;(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.解:(1)把x=a,y=3代入y=x+1得,,∴a=4,把x=4,y=3代入y=得,3=,∴k=12;(2)∵点A(4,3),D点的纵坐标是0,AD=AC,∴点C的纵坐标是3×2﹣0=6,把y=6代入y=得x=2,∴C(2,6),①如图1,作CF⊥x轴于F,交AB于E,当x=2时,y==2,∴E(2,2),∵C(2,6),∴CE=6﹣2=4,∴x A==8;②如图2,当AB是对角线时,即:四边形APBQ是平行四边形,∵A(4,3),B(0,1),点Q的纵坐标为0,∴y P=1+3﹣0=4,当y=4时,4=,∴x=3,∴P(3,4),当AB为边时,即:四边形ABQP是平行四边形(图中的▱ABQ′P′),﹣y B=y P′﹣y A得,由y Q′0﹣1=y P′﹣3,=2,∴y P′当y=2时,x==6,∴P′(6,2),综上所述:P(3,4)或(6,2).14.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数y2=的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.(1)求一次函数与反比例函数的解析式.(2)当y2>y1时,求x的取值范围.(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,∴,解得.∴一次函数的解析式为:y1=﹣x+.∵△OAP的面积为,∴•OA•y P=,∴y P=,∵点P在一次函数图象上,∴令﹣x+=.解得x=4,∴P(4,).∵点P在反比例函数y2=的图象上,∴k2=4×=2.∴一次函数的解析式为:y1=﹣x+.反比例函数的解析式为:y2=.(2)令﹣x+=,解得x=1或x=4,∴K(1,2),由图象可知,当y2>y1时,x的取值范围为:0<x<1或x>4.(3)如图,作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,∵P(4,).∴P′(4,﹣).∴PP′=1,∴直线KP′的解析式为:y=﹣x+.令y=0,解得x=.∴C(,0).=•(x C﹣x K)•PP′∴S△PKC=×(﹣1)×1=.∴当PC+KC最小时,△PKC的面积为.15.如图,一次函数y=x+1与反比例函数y=的图象相交于A(m,2),B两点,分别连接OA,OB.(1)求这个反比例函数的表达式;(2)求△AOB的面积;(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)∵一次函数y=x+1经过点A(m,2),∴m+1=2,∴m=1,∴A(1,2),∵反比例函数y=经过点(1,2),∴k=2,∴反比例函数的解析式为y=;(2)由题意,得,解得或,∴B(﹣2,﹣1),∵C(0,1),=S△AOC+S△BOC=×1×2+×1×1=1.5;∴S△AOB(3)有三种情形,如图所示,满足条件的点P的坐标为(﹣3,﹣3)或(﹣1,1)或(3,3).16.已知A(3,0)、B(0,4)是平面直角坐标系中两点,连接AB.(1)如图①,点P在线段AB上,以点P为圆心的圆与两条坐标轴都相切,求过点P 的反比例函数表达式;(2)如图②,点N是线段OB上一点,连接AN,将△AON沿AN翻折,使得点O与线段AB上的点M重合,求经过A、N两点的一次函数表达式.解:(1)作PC⊥x轴于C,PD⊥y轴于D,则四边形OCPD是矩形,∵以点P为圆心的圆与两条坐标轴都相切,∴PC=PD,∴矩形OCPD是正方形,设PD=PC=x,∵A(3,0)、B(0,4),∴OA=3,OB=4,∴BD=4﹣x,∵PD∥OA,∴△PDB∽△AOB,∴,∴,解得x=,∴P(,),设过点P的函数表达式为y=,∴k=xy==,∴y=;(2)方法一:∵将△AON沿AN翻折,使得点O与线段AB上的点M重合,∴ON=NM,MN⊥AB,由勾股定理得,AB=5,=S△AON+S△ABN,∴S△AOB∴=+,解得,ON=,∴N(0,),设直线AN的函数解析式为y=mx+,则3m+=0,∴m=﹣,∴直线AN的函数解析式为y=﹣x+.方法二:利用△BMN∽△BOA,求出BN的长度,从而得出ON的长度,。
反比例函数中及面积有关的问题

反比例函数中与面积有关的问题知识点回忆由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进展考察。
这种考察方式既能考察函数、反比例函数本身的根底知识内容,又能充分表达数形结合的思想方法,考察的题型广泛,考察方法灵活,可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的几种类型归纳如下:利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,那么两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k故S=|k|从而得结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k| 对于以下三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:结论2:在直角三角形ABO中,面积S=结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB中,面积为S=|k|类型之一k与三角形的面积k〔k>0〕经过直角三角形OAB斜边OB的中点D,与直※1、如图,双曲线y=x角边AB相交于点C.假设△OBC的面积为6,那么k=______.最正确答案过D点作DE⊥x轴,垂足为E,1k,由双曲线上点的性质,得S△AOC=S△DOE=2∵DE⊥x轴,AB⊥x轴,∴DE∥AB,∴△OAB∽△OED,又∵OB=2OD,∴S△OAB=4S△DOE=2k,由S△OAB-S△OAC=S△OBC,得2k-21k=6,解得:k=4.故答案为:4.2、如图1-ZT-1,分别过反比例函数y=x2018(x>0)的图象上任意两点A、B作x 轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S 1、S2,,比拟它们的大小,可得A.S1>S2B.S1=S2C.S1<S2D.S1、S2大小不确定。
反比例函数_---动点、面积专题(附详解)

转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;(3)若该反比例函数图象上有一点F(m,错误!未找到引用源。
)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是错误!未找到引用源。
,求代数式错误!未找到引用源。
的值.3、如图,M点是正比例函数y=kx和反比例函数错误!未找到引用源。
的图象的一个交点.(1)求这两个函数的解析式;(2)在反比例函数错误!未找到引用源。
的图象上取一点P,过点P做PA垂直于x轴,垂足为A,点Q是直线MO上一点,QB垂直于y轴,垂足为B,直线MO 上是否存在这样的点Q,使得△OBQ的面积是△OPA的面积的2倍?如果存在,请求出点Q的坐标,如果不存在,请说明理由.4、如图,已知:一次函数:y=﹣x+4的图象与反比例函数:错误!未找到引用源。
(x>0)的图象分别交于A、B两点,点M是一次函数图象在第一象限部分上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M1、M2,设矩形MM1OM2的面积为S1;点N为反比例函数图象上任意一点,过N分别向x轴、y轴作垂线,垂足分别为N1、N2,设矩形NN1ON2的面积为S2;(1)若设点M的坐标为(x,y),请写出S1关于x的函数表达式,并求x取何值时,S1的最大值;(2)观察图形,通过确定x的取值,试比较S1、S2的大小.5、如图,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P (﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB 垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ 与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由.6、如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P (﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB 垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ 与△OAP面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.。
反比例函数中的面积问题

解得 k=2 评注:第①小题中由图形所在象限可确定k>0,应用结论可直接求k值。 第②小题首先应用三角形面积的计算方法分析得出四个三角形面积相 等,列出含k的方程求k值。
例2(2008贵州省黔南州)如图,矩形ABOD的顶点A是函数 与函数 在第二象限的交点, 轴于B, 轴于D,且矩形ABOD的பைடு நூலகம்积为3. (1)求两函数的解析式. (2)求两函数的交点A、C的坐标.
图象上,∴
解得x=1从而所求面积为π 评注:对于较复杂的图形面积计算问题,先应观察图形的特征,若具有 对称特征,则应用对称关系可以简化解题过程。
四、 讨论与面积有关的综合问题 例8.(2008山东省)(1)探究新知:
如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由. (2)结论应用:
与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4. (1)试确定反比例函数的关系式; (2)求△AOC的面积.
.解:(1)∵点A(-2,4)在反比例函数图象上 ∴k=-8 ∴反比例函数解析式为y=
(2)∵B点的横坐标为-4, ∴纵坐标为y=2 ∴B(-4,2) ∵点A(-2,4)、 点B(-4,2)在直线y=kx+b上 ∴ 4=-2k+b 且2=-4k+b 解得 k=1 b=6 ∴直线AB为y=x+6 与x轴的交点坐标C(-6,0)
(3)若点P是y轴上一动点,且 , 求点P的坐标.
解:(1)由图象知k<0,由结论及已知条件得 -k=3 ∴
∴反比例函数的解析式为 ,一次函数的解析式为 (2)由 ,解得 ,
∴点A、C的坐标分别为(
,3),(3, ) (3)设点P的坐标为(0,m) 直线 与y轴的交点坐标为M(0,2) ∵
反比例函数面积问题专题

反比例函数面积问题专题【围矩形】1.如图所示,点P是反比例函数图象上一点,过点P分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是()A. B.C..D.2.反比例函数的图象如图所示,则k的值可能是()A. -1B.C. 1D. 23.如图,A、B是双曲线上的点,分别过A、B两点作x轴、y轴的垂线段.S1,S2,S3分别表示图中三个矩形的面积,若S3=1,且S1+S2=4,则k值为()A. 1B. 2C. 3D. 44.如图,在反比例函数y=(x>0)的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则S1+S2+S3=()A. 1B. 1.5C. 2D. 无法确定5.如图,两个反比例函数y=和y=(其中k1>0>k2)在第一象限内的图象是C1,第二、四象限内的图象是C2,设点P在C1上,PC⊥x轴于点M,交C2于点C,PA⊥y轴于点N,交C2于点A,AB∥PC,CB∥AP相交于点B,则四边形ODBE的面积为()A. |k1﹣k2|B.C. |k1•k2|D.6.如图,A、C是函数y=的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则()A. S1>S2B. S1<S2C. S1=S2D. 关系不能确定7.如图,过y轴上任意一点p,作x轴的平行线,与反比例函数的图象交于A点,若B为x轴上任意一点,连接AB,PB则△APB的面积为()A. 1 B. 2 C. 3 D. 48.如图,A是反比例函数图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为()A. 1 B. 2 C. -1 D. -29.反比例函数y=与y=在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为()A. B. 2 C. 3 D. 110.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=﹣和y=的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为() A. 3 B . 4 C . 5 D . 1011.双曲线y1=与y2=在第一象限内的图象如图.作一条平行于x轴的直线交y1,y2于B、A,连OA,过B作BC∥OA,交x轴于C,若四边形OABC的面积为3,则k=()A. 2B. 4 C .3 D . 512.如图,直线l和双曲线交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则()A. S1<S2<S3B. S1>S2>S3C. S1=S2>S3D. S1=S2<S313.如图是反比例函数和在第一象限内的图象,在上取点M分别作两坐标轴的垂线交于点A、B,连接OA、OB,则图中阴影部分的面积为.14.如图,直线y=kx(k>0)与双曲线y=交于A,B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=.其中正确结论的个数为()个 A. 1 B . 2 C . 3 D . 415.如图,直y=mx与双曲线y=交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是()A. 1 B. m﹣1 C. 2 D. m16.正比例函数y=x与反比例函数y=的图象相交于A、C两点.AB⊥x轴于B,CD⊥y轴于D,如图,则四边形ABCD的面积为()A. 1B.C. 2D.17.如图,A,C是函数y=(k≠0)的图象上关于原点对称的任意两点,AB,CD垂直于x轴,垂足分别为B,D,那么四边形ABCD的面积S是()A. B. 2k C. 4k D. k18.如图,反比例函数y=﹣的图象与直线y=﹣x的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为()A. 8B. 6C. 4D. 2【三角形叠梯形】19.如图,点A和B是反比例函数y=(x>0)图象上任意两点,过A,B分别作y轴的垂线,垂足为C和D,连接AB,AO,BO,△ABO的面积为8,则梯形CABD的面积为()A. 6B. 7C. 8D. 1020.如图,△ABO的顶点A和AB边的中点C都在双曲线y=(x>0)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k=()A. 2 B. 3 C. 4 D.21.如图,A、B是双曲线上任意两点,过A、B两点分别作y轴的垂线,垂足分别为C、D,连接AB,直线OB、OA分别交双曲线于点E、F,设梯形ABCD的面积和△EOF的面积分别为S1、S2,则S1与S2的大小关系是()A. S1=S2 B. S1>S2 C. S1<S2 D. 不能确定【截矩形】22.如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=(x>0)的图象于点A、B,则四边形BOAP的面积为()A. 3 B. 3.5 C. 4 D. 523.如图,双曲线y=(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为3,则k=.24.函数y=和y=在第一象限内的图象如图,点P是y=的图象上一动点,PC⊥x轴于点C,交y=的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=AP.其中所有正确结论的序号是()A. ①②③B. ②③④C. ①③④D. ①②④25.两个反比例函数和(k1>k2>0)在第一象限内的图象如图,P在C1上,作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1﹣k2③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中正确的是()【截直角三角形】26.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为()A. 20B. 18C. 16D. 1227.如图,双曲线经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.则△AOC的面积为()A. 9 B. 6 C. 4.5 D. 328.如图,已知矩形ABCO的一边OC在x轴上,一边OA在y轴上,双曲线交OB的中点于D,交BC边于E,若△OBC的面积等于4,则CE:BE的值为()A. 1:2 B . 1:3 C. 1:4 D. 无法确定29.如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值()A. 2B.C.D. 无法确定30.如图,反比例函数的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为()A. 1B. 2C. 3D. 4反比例函数【围矩形】1.解:由题意得:矩形面积等于|k|,∴|k|=4又∵反比例函数图象在二、四象限.∴k<0∴k=﹣4∴反比例函数的解析式是y=﹣.故选C.2.解:∵反比例函数在第一象限,∴k>0,∵当图象上的点的横坐标为1时,纵坐标小于1,∴k<1,故选B.3.解:∵S1+S2=4,∴S1=S2═2,∵S3=1,∴S1+S3=1+2=3,∴k=3故选C.4.解:由题意可知点P1、P2、P3、P4坐标分别为:(1,2),(2,1),(3,),(4,).∴由反比例函数的几何意义可知:S1+S2+S3=2﹣1×==1.5.故选B.5.解:∵AB∥PC,CB∥AP,∠APC=90°,∴四边形APCB是矩形.设P(x,),则A(,),C(x,),∴S矩形APCB=AP•PC=(x﹣)(﹣)=,∴四边形ODBE的面积=S矩形APCB ﹣S矩形PNOM﹣S矩形MCDP﹣S矩形AEON=﹣k1﹣|k2|﹣|k2|=.故选D.【围三角形】6.解:结合题意可得:A、C都在双曲线y=上,反比例函数系数k的几何意义有S1=S2;故选C.7.解:依题意得:△APB的面积S=|k|=×|4|=2.故选B8.解:如图,连OA,∵AB⊥x轴,∴AB∥OP,∴S△OAB=S△PAB=1,∴|k|=2×1=2,∵反比例函数图象过第二象限,∴k=﹣2.故选D.9.解:分别过A、B作x轴的垂线,垂足分别为D、E,过B作BC⊥y轴,点C为垂足,∵由反比例函数系数k的几何意义可知,S四边形OEAC=6,S△AOE=3,S△BOC=,∴S△AOB=S四边形OEAC﹣S△AOE﹣S△BOC=6﹣3﹣=.故选A.10.解:设P(a,0),a>0,则A和B的横坐标都为a,将x=a代入反比例函数y=﹣中得:y=﹣,故A(a,﹣);将x=a代入反比例函数y=中得:y=,故B(a,),∴AB=AP+BP=+=,则S△ABC=AB•x P的横坐标=××a=5.故选C11.解:由题意得:S四边形OABC=|k1|﹣|k2|=|6|﹣|k|=3;又由于反比例函数位于第一象限,k>0;k=3.故选C.12.解:结合题意可得:AB都在双曲线y=上,则有S1=S2;而AB之间,直线在双曲线上方;故S1=S2<S3故选D.13.解:∵在上取点M分别作两坐标轴的垂线交于点A、B,∴S△AOC=×5=2.5,S△BOD=×5=2.5 S矩形MDOC=3∴S阴影=S△AOC+S△BOD﹣S矩形MDOC=5﹣3=2故答案为2.【对称点】14.解:①反比例函数与正比例函数若有交点,一定是两个,且关于原点对称,所以正确;②根据A、B关于原点对称,S△ABC为即A点横纵坐标的乘积,为定值1,所以正确;③因为AO=BO,OD∥BC,所以OD为△ABC的中位线,即D是AC中点,所以正确;④在△ADO中,因为AD和y轴并不垂直,所以面积不等于k的一半,不等于,错误.故选C.15.解:由图象上的点A、B、M构成的三角形由△AMO和△BMO的组成,点A与点B关于原点中心对称,∴点A,B的纵横坐标的绝对值相等,∴△AMO和△BMO的面积相等,且为,∴点A的横纵坐标的乘积绝对值为1,又因为点A在第一象限内,所以可知反比例函数的系数k为1.故选A.16.解:根据反比例函数的对称性可知:OB=OD,AB=CD,∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2.故选C.17.解:∵A,C是函数y=(k≠0)的图象上关于原点对称的任意两点,∴若假设A点坐标为(x,y),则C点坐标为(﹣x,﹣y).∴BD=2x,AB=CD=y,∴S=S△ABD+S△CBD=BD•AB+BD•CD=2xy=2k.故四边形ABCD的面积S是2k.故选B.四边形ABCD18.解:由于点A、B在反比例函数图象上关于原点对称,则△ABC的面积=2|k|=2×4=8.故选A.【三角形叠梯形】19.解:过点B向x轴作垂线,垂足是G.由题意得:矩形BDOG的面积是|k|=3,∴S△ACO=S△BOG=.所+S梯形ABDC﹣S△ACO﹣S△BOG=8,以△AOB的面积=S矩形BDOG则梯形CABD的面积=8﹣3+3=8.故选C20.解:过点A作AM⊥OB于M,设点A坐标为(x,y),∵顶点A在双曲线y=(x>0)图象上,∴xy=k,∴S△AMO=OM•AM=xy=k,设B的坐标为(a,0),∵中点C在双曲线y=(x>0)图象上,CD⊥OB于D,∴点C坐标为(,),∴S△CDO=OD•CD=••=k,∴ay=3k,∵S△AOB=S△AOM+S△AMB =k+•(a﹣x)y =k+ay﹣xy=k+×3k﹣k =k,又∵C为AB中点,∴△AOC的面积为×k=3,∴k=4,故选C.21.解:∵直线OB、OA分别交双曲线于点E、F,∴S2=S△AOB,∵S1=S△AOC+S△AOB﹣S△BOD,而S△AOC=S△BOD=k,∴S1=S△AOB,∴S1=S2.故选A.【截矩形】22.解:∵B、A两点在反比例函数y=(x>0)的图象上,∴S△DBO=S△AOC=×2=1,∵P(2,3),∴四边形DPCO的面积为2×3=6,∴四边形BOAP的面积为6﹣1﹣1=4,故选:C.23.解:连接OE,设此反比例函数的解析式为y=(k≠0),C(c,0),则B(c,b),E(c,),设D(x,y),∵D和E都在反比例函数图象上,∴xy=k,=k,即S△AOD=S△OEC=×c×,∵梯形ODBC的面积为3,∴bc﹣×c×=3,∴bc=3,∴bc=4,∴S△AOD=S△OEC=1,∵k>0,∴k=1,解得k=2,故答案为:2.24.解:∵A、B是反比函数y=上的点,∴S△OBD=S△OAC=,故①正确;当P的横纵坐标相等时PA=PB,故②错误;=4,∵P是y=的图象上一动点,∴S矩形PDOC=S矩形PDOC﹣S△ODB﹣﹣S△OAC=4﹣﹣=3,故③正确;∴S四边形PAOB连接OP,===4,∴AC=PC,PA=PC,∴=3,∴AC=AP;故④正确;综上所述,正确的结论有①③④.故选C.25.解:①∵A、B两点都在y=上,∴△ODB与△OCA的面积都都等于,故①正确;②S矩形OCPB﹣S△AOC﹣S△DBO=|k2|﹣2×|k1|÷2=k2﹣k1,故②正确;③只有当P的横纵坐标相等时,PA=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选B.【截直角三角形】26.解:∵点A的坐标为(﹣8,6),O点坐标为(0,0),∴斜边OA的中点D的坐标为(﹣4,3),把D(﹣4,3)代入y=得k=﹣4×3=﹣12,∴反比例函数的解析式为y=﹣,∵AB⊥x轴,∴C点和横坐标为点A相同,都为﹣8,把x=﹣8代入y=﹣得y=,∴C点坐标为(﹣8,),∴AC=6﹣=,∴△AOC的面积=AC•OB=××8=18.故选B.27.解:∵OA的中点是D,双曲线y=﹣经过点D,∴k=xy=﹣3,D点坐标为:(x,y),则A点坐标为:(2x,2y),∴△BOC的面积=|k|=3.又∵△AOB的面积=×2x×2y=12,∴△AOC的面积=△AOB的面积﹣△BOC的面积=12﹣3=9.故选:A.28.解:设D点的坐标是(x,y).∵点D是线段OB的中点,∴B点的坐标是(2x,2y);∵△OBC的面积等于4,∴×2x×2y=4,即xy=﹣2,∴k=﹣2;又∵点E在双曲线上,∴点E的坐标为(2x,);∴CE:BE=:(2y﹣)=:(2×﹣)=1:3;故选B.29.解:方法1:设B点坐标为(a,b),∵OD:DB=1:2,∴D点坐标为(a,b),根据反比例函数的几何意义,∴a•b=k,∴ab=9k①,∵BC∥AO,AB⊥AO,C在反比例函数y=的图象上,∴设C点横坐标为m,则C点坐标为(m,b)将(m,b)代入y=得,m=,BC=a﹣,又因为△OBC的高为AB,所以S△OBC=(a﹣)•b=3,所以(a﹣)•b=3,(a﹣)b=6,ab﹣k=6②,把①代入②得,9k﹣k=6,解得k=.方法2:延长BC交y轴于E,过D作x轴的垂线,垂足为F.由△OAB的面积=△OBE的面积,△ODF的面积=△OCE的面积,可知,△ODF的面积=梯形DFAB=△BOC的面积=,即k=,k=.故选B.30.解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,由于函数图象在第一象限,k>0,则++6=4k,k=2.故选B.。
人教版反比例函数与面积问题

(1)求这个一次函数的解析式
(2)求△AOB的面积.
A
解
:
(2)
y
6 x
,
y x 1.
解得 xy3,2或xy3.2,
y
N M
O
x B
A (2,3)B ,(3,2) .
曲直结合
y y 4 x
⑴直线OA与双曲线的 另一交点B的坐标.
A(2, 2)
B(-2,-2)
O
C
B
D
x
⑵△BDA的面积是多少?
作x轴,y轴的垂线,垂足分别为E, F,
若设矩形OEPF和正 方形OABC不重合部 分的面积为S,写出S 关于m的函数关 系 式.
G
总结提高 一个性质:反比例函数的面积不变性
两种思想:分类讨论和数形结合
变式练习
已知:如图,反比例函数
y
6 x
与一次函数
y=kx+1的图像交于A、B两点,点A的纵坐标是3.
y
∟
P
s1
Q
∟
∟
s2
O
x
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
趁热打铁,大显身手
如图,P1、P2、P3是双曲线上的三点.过这三点分 别作y轴的垂线,得到三个三角形P1A10、P2A20、 P3A30,设它们的面积分别是S1、S2、S3,则 ( ).
A.S1<S2<S3
B.S2<S1<S3
(1)若A(2,3),求K的值 (2)在(1)的条件下,若点B的横坐标为3, y
连接OA,OB,AB,求△OAB的面积。 D A E
B
o
Cx
如图,已知,A,B是双曲线 y k (k 0) 上的两点, x
反比例函数背景下的面积问题(解析版)-2023年中考数学重难点解题大招复习讲义-函数

模型介绍一、反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k二、利用k 的几何意义进行面积转化1.如图,直线AB 与反比例函数k y x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低2.如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
【例1】.如图,反比例函数y=在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是8.过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,∴x=2时,y=3;x=6时,y=1,=S△OBD=3,故S△ACOS四边形AODB=×(3+1)×4+3=11,故△AOB的面积是:11﹣3=8.故答案为:8.变式训练【变1-1】.如图,点A在反比例函数(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,△AOB的面积为12,则k的值为()A.4B.6C.10D.12解:如图,过点A作AD⊥x轴,垂足为D,∵OC∥AD,,∴,∴,k>0,∴k=12,故选:D.【变1-2】.如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,=4,则k的值为16.若E是AB的中点,S△BEF解:设E(a,),则B纵坐标也为,∵E是AB中点,∴F点坐标为(2a,),∴BF=BC﹣FC=﹣=,=4,∵S△BEF∴a•=4,∴k=16.故答案是:16.【例2】.如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为12.解:解法一:过点A作x轴的垂线,交CB的延长线于点E,∵BC∥x轴,∴AE⊥BC,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为6,4,∴A(,6),B(,4),∴AE=2,BE=﹣=,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE===1,∴k=1,∴k=12.解法二:同理知:BE=1,设A(a,6),则B(a+1,4),∴6a=4(a+1),∴a=2,∴k=2×6=12.故答案为12.变式训练【变2-1】.如图,点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是()A.9B.8C.7D.6解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,∴A(4,3),B(2,6),作AD⊥y轴于D,BE⊥y轴于E,=S△BOE=×12=6,∴S△AOD=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,∵S△OAB=(4+2)×(6﹣3)=9,∴S△AOB故选:A.【变2-2】.如图,在直角坐标系中,O为坐标原点,函数y=与y=(a>b>0)在第一象限的图象分别为曲线C1,C2,点P为曲线C1上的任意一点,过点P作y轴的垂线交C2于点A,作x轴的垂线交C2于点B,则阴影部分的面积S△AOB=a﹣.(结果用a,b表示)解:设B(m,),A(,n),则P(m,n),∵点P为曲线C1上的任意一点,∴mn=a,=mn﹣b﹣b﹣(m﹣)(n﹣)∴阴影部分的面积S△AOB=mn﹣b﹣(mn﹣b﹣b+)=mn﹣b﹣mn+b﹣=a﹣.故答案为:a﹣.1.如图,在△ABC中,AB=AC,点A在反比例函数y=(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为()A.3B.2C.D.4解:作AE⊥BC于E,连接OA,∵AB=AC,∴CE=BE,∵OC=OB,∴OC=BC=×2CE=CE,∵AE∥OD,∴△COD∽△CEA,∴=()2=4,∵△BCD的面积等于1,OC=OB,=S△BCD=,∴S△COD=4×=1,∴S△CEA∵OC=CE,=S△CEA=,∴S△AOC=+1=,∴S△AOE=k(k>0),∵S△AOE∴k=3,故选:A.2.如图,OC交双曲线y=于点A,且OC:OA=5:3,若矩形ABCD的面积是8,且AB ∥x轴,则k的值是()A.18B.50C.12D.解:延长DA、交x轴于E,∵四边形ABCD是矩形,且AB∥x轴,∴∠CAB=∠AOE,∴DE⊥x轴,CB⊥x轴,∴∠AEO=∠ABC∴△AOE∽△CAB,∴=()2,∵矩形ABCD的面积是8,OC:OA=5:3,∴△ABC的面积为4,AC:OA=2:3,∴=()2=,=9,∴S△AOE∵双曲线y=经过点A,=|k|=9,∴S△AOE∵k>0,∴k=18,故选:A.3.如图,已知点A,B分别在反比例函数y1=﹣和y2=的图象上,若点A是线段OB 的中点,则k的值为()A.﹣8B.8C.﹣2D.﹣4解:设A(a,b),则B(2a,2b),∵点A在反比例函数y1=﹣的图象上,∴ab=﹣2;∵B点在反比例函数y2=的图象上,∴k=2a•2b=4ab=﹣8.故选:A.4.如图,点A(m,n),B(4,)在双曲线y=上,且0<m<n.若△AOB的面积为,则m+n=()A.7B.C.D.3解:∵点A(m,n),B(4,)在双曲线y=上,∴mn=4×=k,∴mn=k=6,∴双曲线为y=,∴n=,作AD⊥x轴于D,BE⊥x轴于E,=S△AOD+S梯形ADEB﹣S△BOE=S梯形ADEB,∵S△AOB∴(+)(4﹣m)=,解得m1=1,m2=﹣16,∵0<m<n.∴m=1,∴n=6,∴m+n=7,故选:A.5.如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴=3,则S△于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCDAOC为()A.2B.3C.4D.6解:在Rt△BCD中,∵×CD×BD=3,∴×CD×3=3,∴CD=2,∵C(2,0),∴OC=2,∴OD=4,∴B(4,3),∵点B是反比例函数y=(x>0)图象上的点,∴k=12,∵AC⊥x轴,==6,∴S△AOC故选:D.6.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y 轴上的动点,则△ABC的面积为()A.k1﹣k2B.(k1﹣k2)C.k2﹣k1D.(k2﹣k1)解:由题意可知,AB=﹣,AB边上的高为x,=×(﹣)•x=(k1﹣k2),∴S△ABC故选:B.7.已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=与边BC交于点D、与对角线OB交于中点E,若△OBD的面积为10,则k的值是()A.10B.5C.D.解:设E点的坐标是(x,y),∵E是OB的中点,∴B点的坐标是(2x,2y),则D点的坐标是(,2y),∵△OBD的面积为10,∴×(2x﹣)×2y=10,解得,k=,故选:D.8.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=()A.6B.9C.D.解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b)∵D、E在反比例函数的图象上,∴=k,设E的坐标为(a,y),∴ay=k∴E(a,),=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣k﹣k﹣••(b﹣)=12,∵S△ODE∴4k﹣k﹣+=12k=故选:D.9.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=8.解:∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=8÷2=4,又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,∴△AOC的面积=|k|,∴|k|=4,∵k>0,∴k=8.故答案为8.10.如图,若反比例函数y=的图象经过等边三角形POQ的顶点P,则△POQ的边长为2.解:如图,过点P作x轴的垂线于M,∵△POQ为等边三角形,∴OP=OQ,OM=QM=OQ,∵反比例函数的图象经过点P,∴设P(a,)(a>0),则OM=a,OQ=OP=2a,PM=,在Rt△OPM中,PM===a,∴=a,∴a=1(负值舍去),∴OQ=2a=2,故答案为:2.11.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x 轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.则△OAP 的面积为5.解:过P作MN⊥x轴于M,交AB于N,过A作AD⊥x轴于D,∵A(4,3),∴AD=3,OD=4,∴AO==5,∵AB=AO,∴AB=5,∵AB∥x轴,点B的横坐标是4+5=9,纵坐标是3,即点B的坐标是(9,3),设直线OB的解析式是y=ax,把B点的坐标(9,3)代入得:3=9a,解得:a=,即y=x,∵AB∥x轴,∴MN⊥AB,把A(4,3)代入y=,得k=12,即y=,解方程组得:或,∵点P在第一象限,∴点P的坐标是(6,2),∵A(4,3),AB∥x轴,P(6,2),∴MN=AD=3,PN=3﹣2=1,﹣S△APB=3﹣=5,∴△OAP的面积是S△ABO故答案为:5.12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC 面积的最小值为6.解:方法一:设A(a,),B(b,),则C(a,).将y=x+m代入y=,得x+m=,整理,得x2+mx﹣3=0,则a+b=﹣m,ab=﹣3,∴(a﹣b)2=(a+b)2﹣4ab=m2+12.=AC•BC∵S△ABC=(﹣)(a﹣b)=••(a﹣b)=(a﹣b)2=(m2+12)=m2+6,∴当m=0时,△ABC的面积有最小值6.故答案为6.方法二:因为y=x+m斜率为1,且BC∥x轴,AC∥y轴,∴∠ABC=∠BAC=45°,∴△ABC为等腰直角三角形,∴AC=BC=AB,=AC•BC=AB2,∴S△ABC当AB最小时,m=0,直线为y=x,联立方程,解得或,∴A(,),B(﹣,﹣),AB=×2=2,=×4×6=6.∴S△ABC最小故答案为:6.13.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO =AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线=6,则k的值为8.段AB于点D,连接CD,OD.若S△OCD解:根据题意设B(m,m),则A(m,0),∵点C为斜边OB的中点,∴C(,),∵反比例函数y=(k>0,x>0)的图象过点C,∴k=•=,∵∠OAB=90°,∴D的横坐标为m,∵反比例函数y=(k>0,x>0)的图象过点D,∴D的纵坐标为,作CE⊥x轴于E,=S△AOD,∵S△COES△OCD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE,S△OCD=6,∴(AD+CE)•AE=6,即(+)•(m﹣m)=6,∴m2=32,∴k==8,故答案为:8.解法二:作CE⊥OA于E,∵C为AB的中点,OA=AB,∠OAB=90°,=S△AOD=k,S△AOB=2k,∴S△OEC=k,∴S△BOD∵C为斜边OB的中点,=S△BCD=S△BOD=6,∴S△OCD∴×k=6,∴k=8.故答案为:8.14.如图,在平面直角坐标系中,▱OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD,▱OABC的面积为15,则k的值为18.解:过点D作DN⊥y轴于N,过点B作BM⊥y轴于M,设OC=a,CN=2b,MN=b,∵▱OABC的面积为15,∴BM=,∴ND=BM=,∴A,D点坐标分别为(,3b),(,a+2b),∴•3b=(a+2b),∴b=a,∴k=•3b=•3×a=18,故答案为:18.15.如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x 轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.解:连DC,如图,∵AE=3EC,△ADE的面积为3,∴△CDE的面积为1,∴△ADC的面积为4,设A点坐标为(a,b),则AB=a,OC=2AB=2a,而点D为OB的中点,∴BD=OD=b,=S△ABD+S△ADC+S△ODC,∵S梯形OBAC∴(a+2a)×b=a×b+4+×2a×b,∴ab=,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.16.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)请直接写出不等式x+b的解.解:(1)∵反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m),∴k1=8,B(﹣4,﹣2),解方程组,解得;(2)由(1)知一次函数y=k2x+b的图象与y轴的交点坐标为(0,6),=×6×4+×6×1=15;∴S△AOB(3)﹣4≤x<0或x≥1.17.如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB=,反比例函数y=的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为.(1)求反比例函数的解析式;(2)求直线EB的解析式;.(3)求S△OEB解:(1)∵A点的坐标为(a,6),AB⊥x轴,∴AB=6,∵cos∠OAB==,∴,∴OA=10,由勾股定理得:OB=8,∴A(8,6),∴D(8,),∵点D在反比例函数的图象上,∴k=8×=12,∴反比例函数的解析式为:y=;(2)设直线OA的解析式为:y=bx,∵A(8,6),∴8b=6,b=,∴直线OA的解析式为:y=x,则,x=±4,∴E(﹣4,﹣3),设直线BE的解式为:y=mx+n,把B(8,0),E(﹣4,﹣3)代入得:,解得:,∴直线BE的解式为:y=x﹣2;=OB•|y E|=×8×3=12.(3)S△OEB18.如图,直线y=x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=.(1)求反比例函数的解析式;(2)求点B的坐标;.(3)求S△OAB解:(1)∵直线y=x与反比例函数的图象交于点A(3,a),∴a=×3=4,∴点A的坐标为(3,4),∴k=3×4=12,∴反比例函数解析式y=.(2)∵点B在这个反比例函数图象上,设点B坐标为(x,),∵tanα=,∴=,解得:x=±6,∵点B在第一象限,∴x=6,∴点B的坐标为(6,2).(3)设直线OB为y=kx,(k≠0),将点B(6,2)代入得:2=6k,解得:k=,∴OB直线解析式为:y=x.过A点做AC⊥x轴,交OB于点C,如图所示:则点C坐标为(3,1),∴AC=3.S△OAB的面积=S△OAC的面积+S△ACB的面积=×|AC|×6=9.∴△OAB的面积为9.19.已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比=4.例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB (1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.=•|x A|•y B,解:(1)由题意得:S△AOB即×2×y B=4,y B=4,∴B(2,4),设反比例函数的解析式为:y=,把点B的坐标代入得:k=2×4=8,∴y=,设直线AB的解析式为:y=ax+b,把A(﹣2,0)、B(2,4)代入得:,解得:,∴y=x+2;(2)由题意得:x+2=,解得:x1=﹣4,x2=2,∴D(﹣4,﹣2),=S△OAD+S△OAB=×2×2+4=6.∴S△ODB20.如图,在平行四边形OABC中,,点A在x轴上,点D是AB 的中点,反比例函数的图象经过C,D两点.(1)求k的值;(2)求四边形OABC的面积.解:(1)过点C作CE⊥x轴于E,∵∠AOC=45°,∴OE=CE,∴OE2+CE2=OC2∵OC=2,∴OE=CE=2,∴C(2,2),∵反比例函数的图象经过点C点,∴k=2×2=4;(2)过点D作DF⊥x轴于F,∵四边形OABC是平行四边形,∴AB=OC=2,∠DAF=∠AOC=45°,又∵点D是AB的中点,∴AD=,AF=DF,∴AF2+DF2=AD2,∴AF=DF=1,∴D点的纵坐标为1,∵反比例函数的图象过点D点,∴D(4,1),∴OF=4,OA=OF﹣AF=4﹣1=3,∴平行四边形OABC的面积S=OA•CE=3×2=6.21.如图,直线y=6x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标为2.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB,求△AOB的面积.解:(1)将x=2代入y=6x,得:y=12,∴点A的坐标为(2,12),将A(2,12)代入y=,得:k=24,∴反比例函数的解析式为y=;(2)在y=中y=6时,x=4,∴点B(4,6),而A(2,12),如图,过A作AC⊥y轴,BD⊥x轴,交于点E,则OD=4,OC=12,BD=6,AC=2,AE=2,BE=6,=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE∴S△AOB=4×12﹣×2×12﹣×4×6﹣×2×6=48﹣12﹣12﹣6=18.22.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点.(1)求反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)若D(x,0)是x轴上原点左侧的一点,且满足,求x的取值范围.解:(1)∵B(2,﹣4)在反比例函数y=的图象上,∴m=﹣8,∴反比例函数的表达式为y=﹣.∵A(﹣4,n)在y=﹣的图象上,∴n=2,∴A(﹣4,2).∵y=kx+b经过A(﹣4,2)和B(2,﹣4),∴,解得∴一次函数的表达式为y=﹣x﹣2.(2)当y=﹣x﹣2=0时,解得x=﹣2.∴点C(﹣2,0),∴OC=2,=S△AOC+S△COB∴S△AOB=×2×2+×2×4=6.(3)根据函数的图象可知:若D(x,0)是x轴上原点左侧的一点,当﹣4<x<0时,满足kx+b﹣<0.23.如图,一次函数y=k1x+b的图象与反比例函数y=(x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).(1)求此一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.解:(1)∵反比例函数y=(x<0)的图象经过点A(﹣1,2),∴k2=﹣1×2=﹣2,∴反比例函数表达式为:y=﹣,∵反比例y=﹣的图象经过点B(﹣4,n),∴﹣4n=﹣2,解得n=,∴B点坐标为(﹣4,),∵直线y=k1x+b经过点A(﹣1,2),点B(﹣4,),∴,解得:,∴一次函数表达式为:y=+.(2)设直线AB与x轴的交点为C,如图1,当y=0时,x+=0,x=﹣5;∴C点坐标(﹣5,0),∴OC=5.S△AOC=•OC•|y A|=×5×2=5.S△BOC=•OC•|y B|=×5×=.S△AOB=S△AOC﹣S△BOC=5﹣=;(3)如图2,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,∵点A′和A(﹣1,2)关于x轴对称,∴点A′的坐标为(﹣1,﹣2),设直线A′B的表达式为y=ax+c,∵经过点A′(﹣1,﹣2),点B(﹣4,)∴,解得:,∴直线A′B的表达式为:y=﹣x﹣,当y=0时,则x=﹣,∴P点坐标为(﹣,0).24.如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;(2)求△OEF的面积;(3)请结合图象直接写出不等式k2x+b>0的解集.解:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),∴C点坐标为(6,4),∵A点坐标为(3,2),∴k1=3×2=6,∴反比例函数解析式为y=;把x=6代入y=得x=1,则F点的坐标为(6,1);把y=4代入y=得x=,则E点坐标为(,4),把F(6,1)、E(,4)代入y=k2x+b,得,解得,,∴直线EF的解析式为y=﹣x+5;﹣S△ODE﹣S△OBF﹣S△CEF(2)△OEF的面积=S矩形BCDO=4×6﹣×4×﹣×6×1﹣×(6﹣)×(4﹣1)=;(3)由图象得:不等式k2x+b﹣>0的解集为<x<6.25.如图,已知反比例函数y=(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P,连结OP、OQ.求△OPQ的面积.解:(1)反比例函数y=(m≠0)的图象经过点(1,4),解得m=4,故反比例函数的表达式为y=.一次函数y=﹣x+b的图象与反比例函数的图象相交于点Q(﹣4,n),所以,解得n=﹣1,b=﹣5.∴一次函数的表达式y=﹣x﹣5;(2)由,解得或.∴点P(﹣1,﹣4),在一次函数y=﹣x﹣5中,令y=0,得﹣x﹣5=0,解得x=﹣5,故点A(﹣5,0),S△OPQ=S△OP A﹣S△OAQ=×5×4−×5×1=7.5.26.如图,在平面直角坐标系中,边长为4的等边△OAB的边OB在x轴的负半轴上,反比例函数y=(x<0)的图象经过AB边的中点C,且与OA边交于点D.(1)求k的值;(2)连接OC,CD,求△OCD的面积;(3)若直线y=mx+n与直线CD平行,且与△OAB的边有交点,直接写出n的取值范围.解:(1)∵等边△OAB,∴AB=BO=AO=4,∠ABO=∠BOA=∠OAB=60°,∵点C是AB的中点,∴BC=AC=2,过点C作CM⊥OB,垂足为M,在Rt△BCM中,∠BCM=90°﹣60°=30°,BC=2,∴BM=1,CM=,∴OM=4﹣1=3,∴点C 的坐标为(﹣3,),代入y =得:k =﹣3答:k 的值为﹣3;(2)过点A 作AN ⊥OB ,垂足为N ,由题意得:AN =2CM =2,ON =OB =2,∴A (﹣2,2),设直线OA 的关系式为y =kx ,将A 的坐标代入得:k =﹣,∴直线OA 的关系式为:y =﹣x ,由题意得:,解得:舍去,,∴D (﹣,3)过D 作DE ⊥OB ,垂足为E ,S △OCD =S CMED +S △DOE ﹣S △COM =S CMED =(+3)×(3﹣)=3,答:△OCD 的面积为3.(3)①当与直线CD 平行的直线y =mx +n 过点O 时,此时y =mx +n 的n =0,②当与直线CD 平行的直线y =mx +n 经过点A 时,设直线CD 的关系式为y =ax +b ,把C 、D 坐标代入得:,解得:a =1,b =3+∴直线CD 的关系式为y =x +3+,∵y =mx +n 与直线y =x +3+平行,∴m =1,把A (﹣2,2)代入y =x +n 得:n =2+2因此:0≤n ≤2+2且n .答:n 的取值范围为:0≤n ≤2+2且n ≠3+.。
人教版反比例函数图象中的面积问题

思考
图中的这些矩形面积相等吗?
结论:
y
过双曲线上任意一点作x轴、 y轴的垂线,所得矩形的面 积S为定值,即S=|k|.
y k x
O
x
如图,已知点P(m,n)在函数y= k (k>0)
x
的图像上,PB⊥y轴,垂足为B,O’A在x轴
反比例函数图象中的面积问题
y
y
0
x
0
x
探究1 反比例函数与矩形的面积
k 已的象足知图(上 分2点像)点过 的 别上PPP 一是((分 m,点点m,那n,A,过)、么别 在n点x)Bm函轴 P,是分n,数作 则y反=别轴 yS比y向2矩=形例xO的 轴函kAxP、B数.,=垂 y_垂 轴y_|_作k_kx|_足 垂(线 _k_≠线_0.),分 垂图A,B,别
B P(m,n)
(或y轴)的垂线,所得直 O’ O
x
角三角形的面积S为定值,
即S=
1 2
|k|
.
探究3
任意正比例函数与反比例函数 图象交于A、B两点,那么
y k (k 0) x
△ABC的面积为多少呢?
y
A
C
D
图7
x
B
反比例函数与正比例函数围成的图形面积
变式:任意正比例函数与反比例函数 y= k 图像相交,
则a-b的值是多少?(中考题)
⊿AOB的面积。
图中面积相等的图形有哪些?
y
y k x
O
x
学会寻找图像中的基本构图、寻找单位面积 矩形或三角形、寻找变化中的不变量
拓展.如图,已知点A,C在反比例函数 y 的图象上,点B,D在反比例函数 y b(b
第六章反比例函数及反比例函数k的几何意义专题训练北师大版2024—2025学年九年级上册

第六章反比例函数及反比例函数k的几何意义专题训练北师大版2024—2025学年九年级上册反比例函数比例系数k的几何意义(1)意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.(2)常见的面积类型:例1.如图,点P是反比例函数y=(k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M,若△POM的面积等于3,则k的值等于()A.﹣6B.6C.﹣3D.3变式1.如图,在▱AOBC中,对角线AB、OC交于点E,双曲线经过A、E两点,若▱AOBC的面积为18,则k的值是()A.5B.6C.7D.8变式2.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1﹣k2的值为()A.8B.﹣8C.4D.﹣4变式3.如图,点P是反比例函数图象上的一点,PF⊥x轴于F点,且Rt△POF面积为4.则k的值为()A.8B.﹣8C.﹣4D.4变式4.如图,点M是反比例函数y=(x<0)图象上一点,MN⊥y 轴于点N.若P为x轴上的一个动点,则△MNP的面积为()A.2B.4C.6D.无法确定变式5.如图,点P是双曲线C:y=(x>0)上的一点,过点P作x轴的垂线交直线AB:y=x﹣2于点Q,连接OP,OQ,当点P在曲线C上运动,且点P在Q上方时,△POQ面积的最大值为()A.2B.3C.4D.6变式6.如图,已知点A为反比例函数y=(x<0)的图象上一点,过点A作AB⊥y轴,垂足为B,若△OAB的面积为3,则k的值为()A.3B.﹣3C.6D.﹣6变式7.关于x的反比例函数y=的图象如图,A、P为该图象上的点,且关于原点成中心对称.△P AB中,PB∥y轴,AB∥x轴,PB 与AB相交于点B.若△P AB的面积大于12,则关于x的方程(a ﹣1)x2﹣x+=0的根的情况是()A.2个不相等的实数根B.2个相等的实数根C.1个实数根D.无实数根变式8.如图,两个反比例函数y1=和y2=在第一象限内的图象分别是C1和C2,设点P在C1上,P A⊥x轴于点A,交C2于点B,则△POB的面积为()A.4B.2C.1D.6变式9.如图,若反比例函数的图象经过点A,AB⊥x轴于点B,C点是y轴上一点,且△ABC的面积4,则k的值为()A.﹣8B.﹣4C.4D.8变式10.如图,反比例函数的图象经过矩形OABC的边AB的中点D,若矩形OABC的面积为6,则k的值为()A.﹣3B.3C.﹣6D.6变式11.如图,点A是反比例函数的图象上的一点,过点A作AB ⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC 的面积为3,则k的值是()A.3B.﹣6C.6D.﹣3变式12.下面四个图中反比例函数的表达式均为,则阴影部分的图形的面积为3的有()A.1个B.2个C.3个D.4个变式13.如图,将一块含30°角的三角板AOB按如图所示摆放在平面直角坐标系中,∠B=60°,∠BAO=90°,△AOB的面积为4,BO与x轴的夹角为30°,若反比例函数的图象经过点A,则k的值为()A.3B.C.6D.9变式14.如图1,在△OAB中,∠AOB=45°,点B的坐标为,点A在反比例函数的图象上,设△OAB的面积为S1;如图2,在△ABC中,AB=AC,BC在x轴上,且OB:BC=1:2,点A在反比例函数的图象上,设△ABC的面积为S2,则S1+S2的值为()A.B.5C.D.变式15.如图,已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线过OB的中点E,且与边BC交于点D,若△DOE的面积为7.5,则k的值是()A.5B.10C.15D.变式16.如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为8.若点P(a,4)也在此函数的图象上,则a的值是()A.2B.﹣2C.4D.﹣4变式17.如图,在平面直角坐标系xOy中,点A、B分别在y、x 轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为()A.B.C.D.变式18.如图,在平面直角坐标系中,平行四边形ABCD与y轴分别交于E、F两点,对角线BD在x轴上,反比例函数的图象过点A并交AD于点G,连接DF.若BE:AE=1:2,AG:GD=3:2,且△FCD的面积为,则k的值是()A.B.3C.D.5变式19.如图,平面直角坐标系中,矩形OABC的边与函数y=(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于()A.4B.6C.8D.不能确定例2.如图,矩形OABC的顶点A,C分别在x轴、y轴的正半轴上,它的对角线OB与函数的图象相交于点D,且,若矩形OABC的面积为24,则k的值是.变式1.如图,已知在平面直角坐标系xOy中,点P是▱ABCO对角线OB的中点,反比例函数的图象经过点A,点P.若▱ABCO的面积为30,且y轴将▱ABCO的面积分为1:3,则k的值为.变式2.如图,在平面直角坐标系xOy中,点A,B都在反比例函数y=(x>0)的图象上,延长AB交y轴于点C,过点A作AD⊥y轴于点D,连接BD并延长,交x轴于点E,连接CE.若AB=2BC,△BCE的面积是4.5,则k的值为.变式3.如图,在平面直角坐标系xOy中,等腰Rt△OAB,∠B=90°,点A在x轴正半轴上,点B在第一象限内,反比例函数y=的图象与AB交于点C,连接OC,若BC=2AC,△OBC的面积为6,则k的值为.变式4.如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以OA,OC为边,在第一象限内作矩形OABC,且S矩形OABC=8,将矩形OABC翻折,使点B与原点O重合,折痕为MN,点C的对应点C'落在第四象限,过M点的反比例函数y=(k ≠0)的图象恰好过MN的中点,则点C'的坐标为.变式5.如图,在平面直角坐标系中,点A、C在y轴上,且,点B(﹣2,0)在x轴上,将△ABC绕点A逆时针旋转90°后得到△AB'C′,线段AB′与双曲线交于点D,连接B′C、C′C,当点D为AB′中点,且S△B'CC′=6时,则k的值是.变式6.如图,在△AOB中,OC平分∠AOB,=,反比例函数y=(k<0)图象经过点A、C两点,点B在x轴上,若△AOB的面积为9,则k的值为.变式7.如图,点A,B,C,D是菱形的四个顶点,其中点A,D在反比例函数y=(m>0,x>0)的图象上,点B,C在反比例函数y=(n<0)的图象上,且点B,C关于原点成中心对称,点A,C的横坐标相等,则的值为;过点A作AE∥x轴交反比例函数y=(n<0)的图象于点E,连结ED并延长交x轴于点F,连结OD.若S△DOF=7,则m的值为.变式8.如图,A(a,b)、B(﹣a,﹣b)是反比例函数y=的图象上的两点,分别过点A、B作y轴的平行线,与反比例函数y=的图象交于点C、D,若四边形ACBD的面积是8,则m、n之间的关系是.变式9.如图,平面直角坐标系xOy中,Rt△ABO的斜边BO在x轴正半轴上,OB=5,反比例函数y=(x>0)的图象过点A,与AB边交于点C,且AC=3BC,则a的值为,射线OA,射线OC分别交反比例函数y=(b>a>0)的图象于点D,E,连接DE,DC,若△DEC的面积为45,则b的值为.变式10.如图,点A、B在反比例函数y=(x>0)的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则k=.变式11.如图,菱形ABCD中,∠ABC=120°,顶点A,C在双曲线上,顶点B,D在双曲线上,且BD经过点O.若k1+k2=2,则菱形ABCD面积的最小值是.变式12.如图,在平面直角坐标系xOy中,正方形ABCD的顶点A、C恰好落在双曲线上,且点O在AC上,AD交x轴于点E.①当A点坐标为(1,m)时,D点的坐标为;②当CE平分∠ACD时,正方形ABCD的面积为.例3.如图,O为坐标原点,点A(﹣1,5)和点B(m,﹣1)均在反比例函数图象上(1)求m,k的值;(2)当x满足什么条件时,﹣x+4>﹣;(3)P为y轴上一点,若△ABP的面积是△ABO面积的2倍,直接写出点P的坐标.变式1.已知点A(a,ma+2)、B(b,mb+2)是反比例函数y=图象上的两个点,且a>0,b<0,m>0.(1)求证:a+b=﹣;(2)若OA2+OB2=2a2+2b2,求m的值;(3)若S△OAB=3S△OCD,求km的值.变式2.如图,双曲线y=上的一点A(m,n),其中n>m>0,过点A作AB⊥x轴于点B,连接OA.(1)已知△AOB的面积是3,求k的值;(2)将△AOB绕点A逆时针旋转90°得到△ACD,且点O的对应点C恰好落在该双曲线上,求的值.。
2021人教版中考数学小专题(三)反比例函数中k的几何意义与面积问题

交线段 AB 于点 D,连接 CD,OD,若 S△OCD=32 ,则 k 的值为(
C
)
A.3 B.52
CHale Waihona Puke 2 D.14.(2020·宿迁)如图,点 A 在反比例函数 y=kx (x>0)的图象上, 点 B 在 x 轴负半轴上,直线 AB 交 y 轴于点 C, 若ABCC =12 ,△AOB 的面积为 6,则 k 的值为__6___.
2.(2020·黔东南州)如图,点 A 是反比例函数 y=6x (x>0)上的一点,
过点 A 作 AC⊥y 轴,垂足为点 C,AC 交反比例函数 y=2x 的图象于点 B, 点 P 是 x 轴上的动点,则△PAB 的面积为( A ) A.2 B.4 C.6 D.8
3.(2020·营口)如图,在平面直角坐标系中, △OAB 的边 OA 在 x 轴正半轴上,其中∠OAB=90°,AO=AB, 点 C 为斜边 OB 的中点,反比例函数 y=kx (k>0,x>0)的图象过点 C 且
7.(2020·鄂尔多斯)如图,平面直角坐标系中,菱形 ABCD 在第一象限内, 边 BC 与 x 轴平行,A,B 两点的纵坐标分别为 6,4, 反比例函数 y=kx (x>0)的图象经过 A,B 两点, 若菱形 ABCD 的面积为 2 5 ,则 k 的值为_1_2__.
8.(2020·吉林)如图,在平面直角坐标系中,O 为坐标原点,
点 A,B 在函数 y=kx (x>0)的图象上(点 B 的横坐标大于点 A 的横坐标), 点 A 的坐标为(2,4),过点 A 作 AD⊥x 轴于点 D, 过点 B 作 BC⊥x 轴于点 C,连接 OA,AB. (1)求 k 的值; (2)若 D 为 OC 中点,求四边形 OABC 的面积.
专题训练:用反比例函数系数k的几何意义解与面积相关问题(含答案)

专训1 用反比例函数系数k 的几何意义解与面积相关问题名师点金:反比例函数的系数k 具有一定的几何意义,|k |等于反比例函数y =kx (k ≠0)图象上任意一点向两坐标轴所作垂线与坐标轴所围成的矩形的面积.在反比例函数的图象中,涉及三角形或矩形的面积时,常用系数k 的几何意义求解.反比例函数的系数k 与面积的关系1.如图,过y 轴上任意一点P ,作x 轴的平行线,分别与反比例函数y =-4x 和y =2x 的图象交于A 点和B 点,若C 为x 轴上的任意一点,连接AC ,BC ,则△ABC 的面积为( )A .3B .4C .5D .6(第1题) (第2题) (第3题)2.如图,P 是反比例函数y =kx 的图象上一点,过P 点分别向x 轴,y 轴作垂线,所得到的图中阴影部分的面积为6,则这个反比例函数的表达式为( )A .y =-6xB .y =6xC .y =-3xD .y =3x3.【2016·菏泽】如图,△OAC 和△BAD 都是等腰直角三角形,∠ACO =∠ADB =90°,反比例函数y =6x 在第一象限的图象经过点B ,则△OAC 与△BAD 的面积之差S △OAC -S △BAD为( )A .36B .12C .6D .3(第4题) (第5题) (第6题)4.如图,正比例函数y =x 与反比例函数y =1x 的图象相交于A ,B 两点,BC ⊥x 轴于点C ,则△ABC 的面积为( )A .1B .2C .3D .45.如图,函数y =-x 与函数y =-4x 的图象相交于A ,B 两点,过A ,B 两点分别作y轴的垂线,垂足分别为点C ,D ,则四边形ACBD 的面积为( )A .2B .4C .6D .86.【2016·本溪】如图,点A ,C 为反比例函数y =kx (x <0)图象上的点,过点A ,C 分别作AB ⊥x 轴,CD ⊥x 轴,垂足分别为B ,D ,连接OA ,AC ,OC ,线段OC 交AB 于点E ,点E 恰好为OC 的中点,当△AEC 的面积为32时,k 的值为( )A .4B .6C .-4D .-6已知面积求反比例函数的表达式题型1 已知三角形面积求函数表达式7.如图,在平面直角坐标系xOy 中,直线AB 与x 轴交于点A (-2,0),与反比例函数在第一象限内的图象交于点B (2,n ),连接BO ,已知S △AOB =4.(1)求该反比例函数的表达式和直线AB 对应的函数表达式; (2)若直线AB 与y 轴的交点为C ,求△OCB 的面积.(第7题)题型2 已知四边形面积求函数表达式8.如图,矩形ABOD 的顶点A 是函数y =-x -(k +1)的图象与函数y =kx 在第二象限的图象的交点,AB ⊥x 轴于B ,AD ⊥y 轴于D ,且矩形ABOD 的面积为3.(1)求两函数的表达式;(2)求两函数图象的交点A ,C 的坐标;(3)若点P 是y 轴上一动点,且S △APC =5,求点P 的坐标.(第8题)已知反比例函数表达式求图形的面积题型1 利用对称性求面积9.如图,是由四条曲线围成的广告标志,建立平面直角坐标系,双曲线对应的函数表达式分别为y =-6x ,y =6x ,现用四根钢条固定这四条曲线.这种钢条加工成矩形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共要花多少钱?(第9题)题型2 利用点的坐标及面积公式求面积10.如图,直线y =k 1x +b 与反比例函数y =k 2x (x <0)的图象相交于点A ,点B ,与x 轴交于点C ,其中点A 的坐标为(-2,4),点B 的横坐标为-4.(1)试确定反比例函数的表达式; (2)求△AOC 的面积.(第10题)题型3 利用面积关系求点的坐标11.【2016·兰州】如图,在平面直角坐标系中,OA ⊥OB ,AB ⊥x 轴于点C ,点A (3,1)在反比例函数y =kx的图象上.(1)求反比例函数y =kx的表达式;(2)在x 轴的负半轴上存在一点P ,使得S △AOP =12S △AOB ,求点P 的坐标;(3)若将△BOA 绕点B 按逆时针方向旋转60°得到△BDE ,点A ,O 的对应点分别为点E ,D .直接写出点E 的坐标,并判断点E 是否在该反比例函数的图象上,说明理由.(第11题)参考答案1.A 点拨:设△ABC 的边AB 上的高为h ,则 S △ABC =12AB ·h=12(AP +BP )·h =12(AP ·h +BP ·h ) =12(|-4|+|2|) =12×6 =3. 故选A . 2.A3.D 点拨:设△OAC 和△BAD 的直角边长分别为a ,b ,可得出B 点坐标为(a +b ,a -b ).因为点B 在反比例函数y =6x 第一象限的图象上,所以(a +b )(a -b )=a 2-b 2=6.所以S △AOC -S △BAD =12a 2-12b 2=12(a 2-b 2)=12×6=3.故选D .4.A5.D 点拨:由题意,易得出S △ODB =S △AOC =12×|-4|=2.易知OC =OD ,AC =BD ,所以S △AOC =S △ODA =S △ODB =S △OBC =2.所以四边形ACBD 的面积为S △AOC +S △ODA +S △ODB +S △OBC =8.6.C 点拨:设点C 的坐标为⎝⎛⎭⎫m ,k m ,则点E ⎝⎛⎭⎫12m ,k 2m ,A ⎝⎛⎭⎫12m ,2km ,根据三角形的面积公式可得出S △AEC =-38k =32,由此即可求出k 值.7.解:(1)如图,过点B 作BD ⊥x 轴,垂足为D . 由题易知OA =2,BD =n .∴S △AOB =12OA ·BD =12×2n =4.∴n =4.∴B 点的坐标为(2,4).∴反比例函数的表达式为y =8x.设直线AB 对应的函数表达式为y =kx +b ,由题意得⎩⎪⎨⎪⎧-2k +b =0,2k +b =4,解得⎩⎪⎨⎪⎧k =1,b =2. ∴直线AB 对应的函数表达式为y =x +2.(第7题)(2)对于y =x +2,当x =0时,y =0+2=2,∴C 点的坐标为(0,2). ∴OC =2.∴S △OCB =S △AOB -S △AOC =4-12×2×2=2.8.解:(1)由题中图象知k <0,由已知条件得|k |=3,∴k =-3. ∴反比例函数的表达式为y =-3x ,一次函数的表达式为y =-x +2. (2)由⎩⎪⎨⎪⎧y =-3x ,y =-x +2,解得⎩⎪⎨⎪⎧x 1=-1,y 1=3,⎩⎪⎨⎪⎧x 2=3,y 2=-1.∴点A ,C 的坐标分别为(-1,3),(3,-1).(3)设点P 的坐标为(0,m ),直线y =-x +2与y 轴的交点为M ,则点M 的坐标为(0,2).∵S △APC =S △AMP +S △CMP =12PM (|-1|+|3|)=5,∴PM =52,即|m -2|=52.∴m =92或m =-12.∴点P 的坐标为⎝⎛⎭⎫0,92或⎝⎛⎭⎫0,-12. 9.解:由反比例函数图象的对称性可知,两条坐标轴将矩形ABCD 分成四个全等的小矩形.因为点A 为y =6x 的图象上的一点,所以S 矩形AEOH =6.所以S 矩形ABCD =4×6=24.所以总费用为25×24=600(元).所以所需钢条一共要花600元.10.解:(1)∵点A (-2,4)在反比例函数y =k 2x 的图象上,∴k 2=-8.∴反比例函数的表达式为y =-8x.(2)∵点B 的横坐标为-4,且点B 在反比例函数y =-8x 的图象上,∴其纵坐标为2.∴点B 的坐标为(-4,2).∵点A (-2,4),B (-4,2)在直线y =k 1x +b 上,∴⎩⎪⎨⎪⎧4=-2k 1+b ,2=-4k 1+b ,解得⎩⎪⎨⎪⎧k 1=1,b =6.∴直线AB 对应的函数表达式为y =x +6.当y =0时,x =-6. ∴点C 的坐标为(-6,0). ∴S △AOC =12×6×4=12.11.解:(1)∵点A (3,1)在反比例函数y =kx 的图象上,∴k =3×1= 3.∴反比例函数的表达式为y =3x. (2)∵A (3,1),AB ⊥x 轴于点C , ∴OC =3,AC =1.由题意易得△AOC ∽△OBC , ∴OC BC =AC OC. ∴BC =OC 2AC=3.∴B 点坐标为(3,-3). ∴S △AOB =12×3×(1+3)=2 3.∴S △AOP =12S △AOB = 3.设点P 的坐标为(m ,0), ∴12×|m |×1= 3. ∴|m |=2 3.∵P 是x 轴的负半轴上的点, ∴m =-2 3.∴点P 的坐标为(-23,0). (3)点E 的坐标为(-3,-1).点E 在该反比例函数的图象上,理由如下: ∵-3×(-1)=3=k ,∴点E在该反比例函数的图象上.。
专题20反比例函数(3个知识点4种题型1种中考考法)(原卷版)-初中数学北师大版9年级上册

专题20反比例函数(3个知识点4种题型1种中考考法)【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.反比例函数的概念及表达式(重点)知识点2.反比例函数表达式的确定(重点)知识点3.根据实际问题列反比例函数的表达式(重点)【方法二】实例探索法题型1.根据反比例函数的概念求未知字母的值题型2.反比例关系的应用题型3.反比例函数关系的判断及应用题型4.应用几何图形中的数量关系建立反比例函数关系【方法三】仿真实战法考法.反比例函数的概念【方法四】成果评定法【学习目标】1.理解反比例函数的概念,会判断一个函数是不是反比例函数。
2.能结合具体问题确定反比例函数的表达式,并会确定实际问题中自变量的取值范围,求出函数值。
【知识导图】【倍速学习四种方法】【方法一】脉络梳理法知识点1.反比例函数的概念及表达式(重点)如果两个变量的每一组对应值的乘积是一个不等于零的常数,那么就说这两个变量成反比例.即xy k=,或表示为kyx=,其中k是不等于零的常数.一般地,形如kyx=(k为常数,0k≠)的函数称为反比例函数,其中x是自变量,y是函数,自变量x的取值范围是不等于0的一切实数.注意:(1)在kyx=中,自变量x是分式kx的分母,当0x=时,分式kx无意义,所以自变量x的取值范围是,函数y的取值范围是0y≠.故函数图象与x轴、y轴无交点.(2)kyx=()可以写成()的形式,自变量x的指数是-1,在解决有关自变量指数问题时应特别注意系数这一条件.(3)kyx=()也可以写成的形式,用它可以迅速地求出反比例函数的比例系数k,从而得到反比例函数的解析式.【例1】(2023春•邗江区期末)下列式子中,表示y是x的反比例函数的是()A.xy=1B.y=C.y=D.y=【变式】(2022秋•怀化期末)下列函数不是反比例函数的是()A.y=3x﹣1B.y=﹣C.xy=5D.y=知识点2.反比例函数表达式的确定(重点)待定系数法求反比例函数解析式一般步骤:【例2】(2022秋·九年级单元测试)已知y=y1-y2,y1与x成反比例,y=5;当x=1时,y=-1;求当x=-1时,y的值.知识点3.根据实际问题列反比例函数的表达式(重点)【方法二】实例探索法题型1.根据反比例函数的概念求未知字母的值一、单选题2.(2022秋•岳阳县期末)若函数y=(m+4)x|m|﹣5是反比例函数,则m的值为()A.4B.﹣4C.4或﹣4D.03.(2022秋•惠来县期末)函数y=x k﹣1是反比例函数,则k=()A.3B.2C.1D.0题型2.反比例关系的应用k15.(2023春·上海浦东新·九年级校考阶段练习)在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,16.(2022秋·河北保定·九年级校联考阶段练习)写出下列函数关系式,指出其中的正比例函数和反比例函题型4.应用几何图形中的数量关系建立反比例函数关系19.(2022春·九年级课时练习)如图,某养鸡场利用一面长为11m 的墙,其他三面用栅栏围成矩形,面积为260m ,设与墙垂直的边长为x m ,与墙平行的边长为y m .(1)直接写出y 与x 的函数关系式为______;(2)现有两种方案5x =或6x =,试选择合理的设计方案,并求此栅栏总长.20.如图,在矩形ABCD 中,点P 是BC 边上一动点,连接AP ,过点D 作DE AP ⊥于点E.设AP x =,DE y =,若6AB =,8BC =,试求y 与x 之间的函数关系式.【方法三】仿真实战法考法.反比例函数的概念1.(2023•临沂)正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为105m3,设土石方日平均运送量为V(单位:m3/天),完成运送任务所需要的时间为t(单位:天),则V与t满足()A.反比例函数关系B.正比例函数关系C.一次函数关系D.二次函数关系2.(2018•柳州)已知反比例函数的解析式为y=,则a的取值范围是()A.a≠2B.a≠﹣2C.a≠±2D.a=±2【方法四】成果评定法一、单选题A.①②B.9.(2022春·九年级课时练习)下列选项中,能写成反比例函数的是(A.人的体重和身高B.正三角形的边长和面积二、填空题18.(2021春·全国·九年级专题练习)已知反比例函数的解析式为三、解答题19.(2023秋·九年级课时练习)下列例系数.。
专题. 反比例函数(动点问题)(巩固篇)(专项练习)八年级数学下册基础知识专项讲练(苏科版)

专题11.30反比例函数(动点问题)(巩固篇)(专项练习)一、单选题1.如图,点M 是反比例函数y =4x(x <0)图象上一点,MN ⊥y 轴于点N .若P 为x 轴上的一个动点,则△MNP 的面积为()A .2B .4C .6D .无法确定2.如图,点A 是双曲线3y x =在第一象限上的一个动点,连接AO 并延长交另一分支于点B ,以AB 为边作等边△ABC ,点C 在第四象限.下列结论:①连接OC ,则AB OC ⊥;②点C 在函数()90y x x =->上运动.则()A .①对②错B .①错②对C .①②都对D .①②都错3.如图,过双曲线(0)ky x x =>上的动点A 作AB x ⊥轴于点B ,P 是直线AB 上的点,且满足2AP AB =,过点P 作x 轴的平行线交此双曲线于点C .如果APC △的面积为8,则k 的值为()A .10B .8C .16D .124.如图,矩形OABC 的顶点О与坐标原点重合,边OA ,OC 分别落在x 轴和y 轴上,点B 的坐标为()42,,点D 是边BC 上一动点,函数()0ky x x=>的图像经过点D ,且与边AB 交于点E ,连接OB 、OD .若线段OB 平分AOD ∠,则点E 的纵坐标为()A .12B .34C .1D .325.如图,A 、B 是函数y =12x上两点,P 为一动点,作PB ∥y 轴,PA ∥x 轴.若S △BOP =3.6,则S △ABP =()A .3.6B .4.8C .5.4D .66.如图,在平面直角坐标系中,A (8,0),点B 为一次函数y x =图像上的动点,以OB 为边作正方形OBCD ,当AB 最小时,点D 恰好落在反比例函数k y x =的图像上,则k =()A .-9B .-12C .-16D .-257.如图,线段AB 是直线y =x +1的一部分,其中点A 在y 轴上,点B 横坐标为2,曲线BC 是双曲线k y x=(0k ≠)的一部分,由点C 开始不断重复“A−B−C”的过程,形成一组波浪线,点P(2019,m )与Q(2025,n )均在该波浪线上,G 为x 轴上一动点,则△PQG 周长的最小值为()A .16B .6+C .6+D .98.如图,将边长为10的正三角形OAB 放置于平面直角坐标系xOy 中,C 是AB 边上的动点(不与端点A ,B 重合),作CD ⊥OB 于点D ,若点C ,D 都在双曲线y =k x上(k >0,x >0),则k 的值为()A .B .C .9D .9.如图,已知点A 是直线y=x 与反比例函数y=(k >0,x >0)的交点,B 是y=图象上的另一点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C ,过点P 作PM ⊥x 轴,PN ⊥y 轴,垂足分别为M ,N .设四边形OMPN 的面积为S ,P 点运动时间为t ,则S 关于t 的函数图象大致为()A .B .C .D .10.如图,反比例函数2y x =和正比例函数12y x =的图象交于点M ,N ,动点(),0P m 在x 轴上.若PMN 为直角三角形,则m 的值为()A .2m =5B .52m =52C .2m =±或52D .52m =±或5二、填空题11.如图,点()2,2A -在反比例函数k y x=的图象上,点M 在x 轴的正半轴上,点N 在y 轴的负半轴上,且5OM ON ==.点(),P x y 是线段MN 上一动点,过点A 和P 分别作x 轴的垂线,垂足为点D 和E ,连接OA 、OP .当OAD OPE S S < 时,x 的取值范围是________.12.如图,已知点A 是反比例函数3y x=-(0x <)的图像上的一个动点,连接OA ,若将线段OA 绕点O 顺时针旋转90°得到线段OB ,则点B 所在反比例图像的函数关系式是____.13.如图,点A 是双曲线4y x=在第一象限上的一动点,连接AO 并延长交另一分支于点B ,以AB 为斜边作等腰Rt △ABC ,点C 在第二象限,随着点A 的运动,点C 的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.14.如图,A 、B 是函数y =12x图象上两点,P 为一动点.作PB ∥y 轴.PA ∥x 轴,下列说法中:①AOP BOP ≌△△;②AOP BOP S S =;③若OA =OB ,则OP 平分∠AOB ;④若4BOP S =,则16ABP S =.正确的序号是___.15.如图,点A 为反比例函数k y x=图象上的一点,过点A 作AB ⊥y 轴于B ,点C 为x 轴上的一个动点,△ABC 的面积为3,则k 的值为________.16.如图,点A 、B 是反比例函数y 12x =图象上的两个动点,过点A 、B 分别作AC ⊥x 轴、BD ⊥x 轴,分别交反比例函数y 3x=-图象于点C 、D ,得四边形ACBD 是平行四边形.当点A 、B 不断运动时,现有以,结论:①▱ACBD 可能是菱形;②▱ACBD 不可能是矩形;③▱ACBD 可能是正方形;④▱ACBD 不可能是正方形.其中正确的是_____.(写出所有正确结论的序号)17.如图,函数112y x =+与函数(0)k y x x =>图像的交于点P ,点P 的纵坐标为4,PB x ⊥轴,垂足为点B ,点M 是函数(0)ky x x =>图像上一动点(不与P 点重合),过点M 作MD AP⊥于点D ,若45PMD ∠=︒,点M 的坐标是________.18.如图,点A 是反比例函数()280y x x=>的图象上的一动点,过点A 分别作x 轴、y 轴的平行线,与反比例函数1k y x=(0k ≠,0x >)的图象交于点B 、点C ,连接OB ,OC .若四边形OBAC 的面积为5,则k =________.三、解答题19.如图,一次函数114y k x =+与反比例函数22k y x=的图象交于点()2,A m 和()6,2B --,与y 轴交于点C .(1)1k =,2k =;(2)过点A 作AD x ⊥轴于点D ,点P 是反比例函数在第一象限的图象上一点,设直线OP与线段AD 交于点E ,当:4:1ODE ODAC S S ∆=四边形时,求点P 的坐标.(3)点M 是坐标轴上的一个动点,点N 是平面内的任意一点,当四边形ABMN 是矩形时,求出点M 的坐标.20.如图,反比例函数1k y x=的图像与一次函数2y mx n =+的图像相交于(),1A a -,()1,3B -两点.(1)求反比例函数和一次函数的解析式;(2)点P 在线段AB 上,且:1:2AOP BOP S S = ,直接写出点P 的坐标;(3)设直线AB 交y 轴于点C ,点(),0N t 是x 轴正半轴上的一个动点,过点N 作NM x ⊥轴交反比例函数1k y x=的图像于点M ,连接CN ,OM .若S 四边形COMN >3,直接写出t 的取值范围.21.如图,在平面直角坐标系中,直线y x =与反比例函数图象交于点(),A a a ,点1,22B a a ⎛⎫ ⎪⎝⎭为反比例函数()0k y x x =>图象上的点,连接OB ,AB ,且AOB S ∆为3.(1)求反比例函数的解析式;(2)点P 为y 轴上一动点,当ABP 的周长最小时,直接写出点P 的坐标.22.一次函数2y x =--的图象与反比例函数k y x=的图象相交于()3,A m -,(),3B n -两点.(1)求这个反比例函数的解析式;(2)根据图象写出使一次函数值不大于反比例函数值的x 的取值范围.(3)若动点E 在y 轴上,且6EBA S =△,求动点E 的坐标.23.如图,一次函数()110y k x b k =+≠的图象与反比例函数()220k y k x=≠的图象交于点()14A ,,()4B n -,两点.(1)求一次函数和反比例函数的表达式;(2)连接AO 并延长交双曲线于点C ,点D 为y 轴上一动点,点E 为直线AB 上一动点,连接CD ,DE ,求当CD DE +最小时点D 的坐标;24.如图,点A 在反比例函数(00)m y m x x =>>,的图像上,点A 的纵坐标为3.过点A 作x 轴的平行线交反比例函数(0)n y n m x x=>>,的图像于点C .点P 为线段AC 上一动点,过点P 作AC 的垂线,分别交反比例函数m y x =和n y x =的图像于点B ,D .(1)当416m n ==,时,①若点P 的横坐标为4(如图1),求直线AB 的函数表达式;②若点P 是AC 的中点(如图2),试判断四边形ABCD 的形状,并说明理由;(2)四边形ABCD 能否成为正方形?若能,求此时m ,n 之间的数量关系;若不能,说明理由.参考答案1.A 【分析】根据1()2MNP P M S MN y y ∆=⋅-求解.解:设点M 坐标为(,)a b ,点M 在反比例函数图象上,4ab ∴=,111()()()2222MNP P M S MN y y a b ab ∆∴=⋅-=⨯--==.故选:A .【点拨】本题考查反比例函数系数k 的几何意义,解题关键是掌握xy k =,掌握坐标系内求图形面积的方法.2.C【分析】设点A 的坐标为(a ,3a),连接OC ,则OC ⊥AB ,表示出OC ,过点C 作CD ⊥x 轴于点D ,设出点C 坐标,在Rt △OCD 中,利用勾股定理可得出x 2的值,进而得出结论.解:如图,设A (a ,3a ),点C 始终在双曲线()0k y x x=->上运动,∵点A 与点B 关于原点对称,∴OA =OB ,∵△ABC 为等边三角形,∴AB ⊥OC ,OC,∵AO =∴CO 过点C 作CD ⊥x 轴于点D ,则可得∠AOD =∠OCD (都是∠COD 的余角),设点C 的坐标为(x ,y ),则tan ∠AOD =tan ∠OCD ,即3x a a y =-,解得23a y x =-.在Rt △COD 中,CD 2+OD 2=OC 2,即2222273y x a a +=+,将23a y x =-代入,可得:2227x a =,故23a x y x ==-=,则xy =-9,即k =-9,所以,点C 在函数()90y x x=->上运动.所以,①②都对,故选:C .【点拨】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.3.D【分析】设AB =a ,则PB =3a ,从而得到B kx a =,3C k x a =,根据矩形的性质,得到PC =AD =BE =B C x x -,利用三角形面积为载体建立等式计算即可.解:设AB =a ,则PB =3a ,过点C 作CE ⊥x 轴,垂足为E ,过点A 作AD ∥x 轴,交CE 于点D ,则四边形APCD 是矩形,四边形BPCE 是矩形,∴CE =PB =3a ,∵点A 、点C 都在函数(0)k y x x =>的图像上,∴A B k x x a==,3C k x a =,根据矩形的性质,得到PC =AD =BE =B C x x -=3kk a a -,∵APC △的面积为8,∴1(2823kk a a a-⨯=,解得k =12,故选D .【点拨】本题考查了反比例函数的图像及其性质,矩形的判定和性质,三角形面积计算,熟练掌握反比例函数的性质是解题的关键.4.B【分析】先根据矩形的性质,角平分线定义得出DBO DOB ∠=∠,然后根据等腰三角形的判定得出BD OD =,在Rt COD 中根据勾股定理可求出CD ,从而求出点D 的坐标,根据待定系数法求出反比例函数解析式,最后把4x =代入求解即可.解:解∶∵OB 平分AOD ∠,∴AOB DOB ∠=∠,∵四边形ABCD 是矩形,()42B ,,∴BC OA ∥,4BC AO ==,2==OC AB ,90BCO ∠=︒,∴DBO AOB ∠=∠,∴DBO DOB ∠=∠,∴BD OD =,设BD OD a ==,则4CD BC BD a =-=-,在Rt COD 中,222CO CD OD +=,∴()22242a a -+=,解得52a =,∴32CD =,∴3,22D ⎛⎫ ⎪⎝⎭,∴3232k =⨯=,∴3y x =,当4x =时,34y =,∴点E 的纵坐标为34.故选:B .【点拨】本题考查了矩形的性质,等腰三角形的判定,勾股定理,待定系数法等知识,正确求出点D 的坐标是解题的关键.5.C【分析】延长BP ,交x 轴于点C ,由题意可设点1212,,,A a B b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则有1212,,AP a b BP OC b b a=-=-=,然后由S △BOP =3.6可进行求解问题.解:延长BP ,交x 轴于点C ,如图所示:∵PB ∥y 轴,PA ∥x 轴,∴AP BP ⊥,BC x ⊥轴,由题意可设点1212,,,A a B b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则有1212,,AP a b BP OC b b a =-=-=,∵S △BOP =3.6,∴1 3.62BP OC ⋅=,即12127.2b b a ⎛⎫-= ⎪⎝⎭,解得:25b a =,∴()111212130123 5.42225APB S AP BP a b a b a a a ⎛⎫⎛⎫=⋅=--=⨯-⨯= ⎪ ⎪⎝⎭⎝⎭ ;故选C .【点拨】本题主要考查反比例函数与几何的综合,熟练掌握反比例函数的性质及几何意义是解题的关键.6.C【分析】根据垂线段最短可得,当AB 垂直直线y x =时AB 最短,此时△AOB 是等腰直角三角形,易求OB =42D 作DE ⊥x 轴于点E ,知△DEO 为等腰直角三角形,求出DE ,OE 的长即可得到结论.解:根据垂线段最短可得,当AB 垂直直线y x =时AB 最短,∵∠AOB =45°∴∠BAO =45°∴△AOB 是等腰直角三角形,∵点A 的坐标为(8,0)∴OA =8∴42BO BA ==∵四边形OBCD 是正方形,∴90DO BO DOB ==∠=︒∴45DOC BOC ∠=∠=︒过点D 作DE ⊥x 轴于点E ,∴45ODE DOE ∠=∠=︒∴△DEO 为等腰直角三角形,∴4DE OE ==∵点D 在第二象限,∴D (-4,4)又点D 在反比例函数k y x=的图像上∴(4)416k =-⨯=-故选:C .【点拨】本题考查了最短路径问题、待定系数法求函数解析式、正方形的性质等知识,解答此题的关键是正确求出点D 的坐标.7.B【分析】由点B 在直线y=x+1上,点B 横坐标为2,可求纵坐标,确定点B 的坐标,进而求出反比例函数的关系式,再确定点C 的坐标,由点C 开始不断重复“A-B-C”的过程,可以推断点P (2019,m )与Q (2025,n )具体所在的位置,再依据对称,求线段的和最小的方法求出答案.解:当x=2时,y=x+1=2+1=3,∴B (2,3)∵B (2,3)在双曲线k y x =上,∴k=6把x=6代入6y x=得:y=1,∴C (6,1)∵2019÷6=336……3,2025÷6=337……3,∴点P 落在第337个“A-B-C”的P 处,而点Q 落在第338个“A-B-C”的Q 处,示意如图:把3x =代入6,y x =2,y ∴=∴P (2019,2),Q (2025,2),PQG 周长的最小,PQ=6定值,∴只要GP+GQ 最小即可,过Q 作QH x ⊥轴,使Q,H 关于x 轴对称,连接HP 交x 轴于,G ()2025,2,H ∴-6,4,PQ QH ∴==由勾股定理得:PH =∴PQG 周长的最小值为PQ+GP+GQ=6PH PQ +=+故选B .【点拨】考查反比例函数、一次函数的图象和性质,轴对称性质的应用,根据规律推断出点P 、Q 的位置,找出点G 的位置,依据勾股定理求出线段的长,是解决问题的关键.8.D【分析】根据等边三角形的性质表示出D ,C 点坐标,进而利用反比例函数图象上点的坐标特征得出答案.解:过点D 作DE ⊥x 轴于点E ,过C 作CF ⊥x 轴于点F ,如图所示.可得:∠ODE =30°,∠BCD =30°,设OE =a ,则OD =2a ,DE a ,∴BD =OB ﹣OD =10﹣2a ,BC =2BD =20﹣4a ,AC =AB ﹣BC =4a ﹣10,∴AF =12AC =2a ﹣5,CF AF 2a ﹣5),OF =OA ﹣AF =15﹣2a ,∴点D (a a ),点C [15﹣2a 2a ﹣5)].∵点C 、D 都在双曲线y =k x 上(k >0,x >0),∴a a =(15﹣2a )2a ﹣5),解得:a =3或a =5.当a =5时,DO =OB ,AC =AB ,点C 、D 与点B 重合,不符合题意,∴a =5舍去.∴点D (3,∴k =故选D .【点拨】本题考查了反比例函数图象上点的坐标特征以及等边三角形的性质,解题的关键是找出点D 、C 的坐标.9.B解:设点P 的运动速度为v ,①由于点A 在直线y=x 上,故点P 在OA 上时,四边形OMPN 为正方形,四边形OMPN 的面积S=(vt )2,②点P 在反比例函数图象AB 时,由反比例函数系数几何意义,四边形OMPN 的面积S=k ;③点P 在BC 段时,设点P 到点C 的总路程为a ,则四边形OMPN 的面积=OC•(a ﹣vt )=﹣2OC v ⋅t+2OC a ⋅,只有B 选项图形符合.故选B .考点:动点问题的函数图象.10.D 【分析】联立方程组212y x y x ⎧=⎪⎪⎨⎪=⎪⎩并求解,得到(2,1),(2,1)M N --,由两点间距离公式求出,,PM PN MN 的长,再分90,90,90PMN PNM MPN ∠=︒∠=︒∠=︒三种情况依据勾股定理列出方程求解即可解:联立方程组得212y x y x ⎧=⎪⎪⎨⎪=⎪⎩,解得,21x y =-⎧⎨=-⎩或21x y =⎧⎨=⎩,(2,1),(2,1)M N ∴--∵(),0P m ∴[][]2222(2)0(1)45,PN m m m =--+--=++222(22)(11)20,MN =--+--=2222(2)(01)45,PM m m m =-+-=-+①若90PNM ∠=︒时,则有222PN MN PM +=,22452045m m m m ∴+++=-+,5,2m \=-②若90MPN ∠=︒时,则有222PM PN MN +=,22454520.m m m m ∴-++++=,m ∴=③若90PMN ∠=︒时,则有222PM MN PN +=,22452045m m m m ∴-++=++,52m ∴=;综上所述,m 的值为52±或故选:D .【点拨】本题考查了一次函数与反比例函数的交点问题,正确进行分类讨论是解题的关键.11.14x <<【分析】先求出反比例函数的解析式,再求出线段MN 的解析式,最后联立两个解析式求出B 和C 两个点的坐标,再根据k 的几何意义,确定P 点位置,即可得到相应的x 的取值范围.解:∵点()2,2A -∴()224k =⨯-=-,所以反比例函数的解析式为:4y x=-,因为5OM ON ==,∴()()5,0,0,5M N -,设线段MN 解析式为:()05y px q x =+≤≤,∴505p q q +=⎧⎨=-⎩,∴15p q =⎧⎨=-⎩,∴线段MN 解析式为:()505y x x =-≤≤,联立以上两个解析式得:54y x y x =-⎧⎪⎨=-⎪⎩,解得:14x y =⎧⎨=-⎩或41x y =⎧⎨=-⎩,经检验,符合题意;由图可知,两个函数的图像交点分别为点B 和点C ,∴()1,4B -,()4,1C -,∵OAD OPE S S < ,∴P 点应位于B 和C 两点之间,∴14x <<,故答案为:14x <<.【点拨】本题涉及到了动点问题,考查了反比例函数的图像与性质、k 的几何意义、待定系数法等内容,解决本题的关键是牢记反比例函数的图像与性质,理解k 的几何意义,以及能联立两个函数的解析式求交点坐标等,本题蕴含了数形结合的思想方法等.12.3y x=【分析】如图,设A (m ,n ),过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,得到AC =n ,OC =-m ,根据反比例函数图象上点的坐标特征可得3=-mn ,根据平角的定义及角的和差关系可得∠OAC =∠BOD ,根据旋转的性质可得OB =OA ,利用AAS 可证明△ACO ≌△ODB ,根据全等三角形的性质得到AC =OD =n ,CO =BD =-m ,可得点B 坐标,利用待定系数法即可得答案.解:如图,设A (m ,n ),过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,∵点A 是反比例函数3y x=-(0x <)的图像上的一个动点,∴3=-mn ,AC =n ,OC =-m ,∵将线段OA 绕点O 顺时针旋转90°得到线段OB ,∴∠AOB =90°,OA =OB ,∴∠OAC +∠AOC =∠BOD +∠AOC =90°,∴∠OAC =∠BOD ,在△ACO 和△ODB 中,ACO BDO OAC BOD OA OB ∠=⎧⎪∠=∠⎨⎪=⎩,∴△ACO ≌△ODB ,∴AC =OD =n ,CO =BD =-m ,∴B (n ,-m ),设过点B 的反比例函数的解析式为k y x=,∴3k mn =-=,∴点B 所在反比例图像的函数关系式为3y x =,故答案为:3y x=【点拨】本题考查了坐标与图形变化-旋转,反比例函数图形上点的坐标特征,待定系数法求反比例函数的解析式,全等三角形的判定和性质,正确的作出辅助线是解题的关键.13.y =-4x【分析】连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,如图,设A 点坐标为4,a a骣琪琪桫,再证明△COD ≌△OAE (AAS ),表示C 点坐标为4,a a骣琪-琪桫,从而可得答案.解:连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,如图,设A 点坐标为4,a a骣琪琪桫,∵A 点、B 点是正比例函数图象与双曲线4y x =的交点,∴点A 与点B 关于原点对称,∴OA =OB∵△ABC 为等腰直角三角形,∴OC =OA ,OC ⊥OA ,∴∠DOC +∠AOE =90°,∵∠DOC +∠DCO =90°,∴∠DCO =∠AOE ,∵在△COD 和△OAE 中CDO OEA DCO EOA CO OAìÐ=ÐïïÐ=Ðíï=ïî∴△COD ≌△OAE (AAS ),∴OD =AE =4a,CD =OE =a ,∴C 点坐标为4,a a骣琪-琪桫,∵44a a -=-g ,∴点C 在反比例函数4y x =-图象上.故答案为:4y x=-【点拨】本题考查的是等腰直角三角形的性质,三角形全等的判定与性质,反比例函数的图象与性质,利用三角形的全等确定C 的坐标是解本题的关键.14.②③##③②【分析】由点P 是动点,可判断出①错误,设出点P 的坐标,求出AP 、BP 的长,再利用三角形面积公式计算即可判断出②;利用角平分线定理的逆定理可判断③;先求出矩形OMPN 的面积为4,进而得出mn =4,最后用三角形的面积公式解答即可.解:∵点P 是动点,∴BP 与AP 不一定相等,∴BOP △与AOP 不一定全等,故①不正确;设P (m ,n ),∵BP ∥y 轴,∴B (m ,12m ),A (12n ,n )∴AP =|12n-m |∴S △AOP =12·|12n-m |n =12|12-mn |同理:S △BOP =12·|12m -n |m =12|12-mn |∴S △AOP =S △BOP ;故②正确;如图1,过点P 作PF ⊥OA 于F ,PE ⊥OB 于E ,∴BOP S =12OB ·PE ,AOP S =12OA ·PF∵BOP AOP S S = ,∴OB ·PE =OA ·PF∵OA =OB ,∴PE =PF ,∵PE ⊥OB ,PF ⊥OA∴OP 是∠AOB 的平分线,故③正确;如图2,延长BP 交x 轴于N ,延长AP 交轴于M ,∵AM ⊥y 轴,BN ⊥x 轴,∴四边形OMPN 是矩形,∵点A ,B 在双曲线y =12x 上,∴6AMO ONB S S == ,∵4BOP S = ,∴2PMO PNO S S == ,∴S 矩形OMPN =4,∴mn =4,∴m =4n ∴12|3|2||BP n n n n m=-=-=,8||12AP m n n =-=∴1182||822||APBS AP BP n n ∆=⨯=⨯⨯=故④不正确;故答案为②③.【点拨】本题属于反比例函数与几何综合题,主要考查了反比例函数的性质、三角形面积公式、角平分线定理逆定理、矩形的判定和性质等知识点,正确作出辅助线并灵活应用所学知识是解答本题的关键.15.6【分析】连接OA ,可得S △ABO =S △ABC =3,根据反比例函数k 的几何意义,可求出k 的值.解:连接OA ,∵AB ⊥y 轴,∴AB ∥x 轴,∴S △ABO =S △ABC =3,即:12|k |=3,∴k =6或k =-6,∵在第二象限,∴k =-6,故答案为:-6.【点拨】考查反比例函数的图象和性质,理解反比例函数k 的几何意义以及同底等高的三角形的面积相等,是解决问题的前提.16.①②④【分析】设A(a,12a),B(b,12b),则C(a,-3a),D(b,-3b),由平行四边形的性质AC=BD列出方程求得a、b的关系,进而得B、C的坐标,根据坐标可以判断BC不与x轴平行,从而判断AC与BD垂直,进而判断③错误;②④正确;根据随着|a|不断变小,AC越来越大,BC越来越小,可以判断AC有可能与BC相等,进而判断①的正误.解:设A(a,12a),B(b,12b),则C(a,-3a),D(b,-3b),∵AC=BD,∴-15a=15b,∴a=-b,∴yC=-3a=3b≠yB=12b,∴BC不与x轴平行,∴AC与BC不可能垂直,∴▱ACBD不可能是矩形,▱ACBD不可能是正方形.故③错误;②④正确;∵随着|a|不断变小,AC越来越大,BC越来越小,∴AC有可能与BC相等,故①正确;故答案为①②④.【点拨】本题主要考查了反比例函数的图象与性质,平行四边形的性质,菱形的判定,矩形、正方形的判定,解题的关键是由平行四边形的对边相等,得出a、b的关系.17.(12,2)【分析】过点D作GH⊥PB,交BP的延长线于G,作MH⊥HG于H,证得△PGD≅△DHM(AAS),得PG=DH,DG=MH,设D(m,112m ),表示出点M的坐标,从而得出m的方程,解方程即可.解:过点D作GH⊥PB,交BP的延长线于G,作MH⊥HG于H,如图所示,∵△PMD 是等腰直角三角形,∴PD =DM ,∵∠PDG +∠MDH =90°,∠PDG +∠DPG =90°,∴∠DPG =∠MDH ,∵∠G =∠H ,∴△PGD ≅△DHM (AAS),∴PG =DH ,DG =MH ,∵点P 的纵坐标为4,∴将y =4代入112y x =+,得x =6,∴P 点坐标为(6,4),将P (6,4),代入(0)k y x x =>,得:k =24,∴反比例函数解析式为:24(0)y x x=>设D (m ,112m +),∴DG =m -6,PG =132m -,∴MH =m -6,DH =132m -,∴M (332m -,172m -),∵点M 在反比例24y x=的图象上,∴31372422m m ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭ ,解得16m =,210m =,当m =6时,M (6,4)(舍去),当m =10时,M (12,2),故答案为:(12,2).【点拨】本题是反比例函数与一次函数图象的交点问题,主要考查了函数图象上点的坐标的特征,等腰直角三角形的性质,全等三角形的判定与性质,构造全等三角形表示出点M 的坐标是解题的关键.18.3【分析】延长,AB AC 分别交y 轴,x 轴于点,E D ,易得四边形OBAC 的面积等于8k -,即可得解.解:延长,AB AC 分别交y 轴,x 轴于点,E D ,∵AB x 轴,AC y 轴,则:四边形AEOD 为矩形,,OBE ODC 为直角三角形,∵点A 在反比例函数()280y x x=>的图象上,点B 、点C 在反比例函数1k y x =(0k ≠,0x >)上,∴8AEOD S =矩形,2OBE ODC k S S ==,∴四边形OBAC 的面积85OBE ODC AEOD S S S k =--=-= 矩形,∴3k =;故答案为:3.【点拨】本题考查一直图形面积求k 值.熟练掌握k 值的几何意义,是解题的关键.19.(1)1,12;(2)⎝;(3)()0,8-或()8,0-.【分析】(1)根据点B 的坐标,利用待定系数法即可求出1k 、2k 的值;(2)根据一次函数图象上点的坐标特征求出点A 、C 的坐标,根据梯形的面积公式求出ODAC S 四边形的值,进而即可得出ODE S ∆的值,结合三角形的面积公式即可得出点E 的坐标,利用待定系数法即可求出直线OP 的解析式,再联立直线OP 与双曲线的解析式成方程组,通过解方程组求出点P 的坐标;(3)过点B 作直线12M M AB ⊥交x 轴于点2M 交y 轴于点1M ,作出符合题意的图形,利用待定系数法求出直线12M M 的解析式,再求出1M 、2M 的坐标即可.(1)解:将点()6,2B --代入114y k x =+,1264k -=-+,解得:11k =,故一次函数的解析式为;14y x =+,将点()6,2B --代入22k y x =,226k -=-,解得:212k =,故反比例函数的解析式为12y x =;故答案为:1,12(2)解:依照题意,画出图形,如图所示.当2x =时,246m =+=,∴点A 的坐标为()2,6;当0x =时,14044y x =+=+=,∴点C 的坐标为()0,4,∵()114621022()ODAC S OC AD OD =+⋅=⨯+⨯=四边形,:4:1ODE ODAC S S ∆=四边形,∴111210224ODE S OD DE DE =⋅=⨯=⨯ ,∴52DE =,即点E 的坐标为52,2⎛⎫ ⎪⎝⎭,设直线OP 的解析式为y kx =,将点52,2E ⎛⎫ ⎪⎝⎭代入y kx =,得522k =,解得:54k =,∴直线OP 的解析式为54y x =,联立得1254y x y x ⎧=⎪⎪⎨⎪=⎪⎩,解得:11x y ⎧⎪⎨⎪⎩22x y ⎧=⎪⎨⎪=⎩,∵点P 在第一象限,∴点P的坐标为⎝;(3)解:过点B 作直线12M M AB ⊥交x 轴于点2M 交y 轴于点1M ,依照题意画出图形,如图所示.则1290CBM CBM ∠=∠=︒时,四边形11ABM N 与22ABM N 是满足题意的矩形,∵直线AB 的解析式为4y x =+,∴可设直线12M M 的解析式为y x b =-+,把点()6,2B --代入y x b =-+得到26b -=+,解得8b =-,直线12M M 的解析式为8y x =--,当0x =时,8088y x =--=-=-,当0y =时,08x =--,解得8x =-,∴()10,8M -,()28,0M -,故点M 的坐标为()0,8-或()8,0-.【点拨】本题考查了待定系数法求出一次函数及反比例函数解析式、一次函数图象上点的坐标特征、梯形(三角形)的面积公式、矩形的性质,解题的关键是根据题意画出图形,作出辅助线.20.(1)反比例函数的解析式为3y x-=,一次函数解析式为2y x =-+;(2)点P 的坐标为(53,13);(3)t >32【分析】(1)将点B ,点A 坐标代入反比例函数的解析式,可求a 和k 的值,利用待定系数法可求一次函数解析式;(2)连接OA ,OB ,OP ,求得OC 的长,根据AOB AOC BOC S S S =+ ,:1:2AOP BOP S S = ,求得BOP BOC POC S S S =+ 进而求得点P 的坐标;(3)先求出点C 坐标,由面积关系可求解.解:(1)∵反比例函数k y x=的图像与一次函数y mx n =+的图像相交于(),1A a -,()1,3B -两点,∴()131k a =-⨯=⨯-,∴3,3k a =-=,∴点()3,1A -,∴反比例函数的解析式为3y x-=,由题意可得:313m n m n =-+⎧⎨-=+⎩,解得:12m n =-⎧⎨=⎩,∴一次函数解析式为2y x =-+;(2)连接OA ,OB ,OP ,令0x =代入22y x =-+,解得22y =,∴一次函数与y 轴的交点C 坐标为()0,2,∴2OC =,∵点P 在线段AB 上,∴设点P 为(),2m m -+,∵点A ()3,1-,点B ()1,3-,∴4AOB AOC BOC S S S =+= ,∵:1:2AOP BOP S S = ,∴2833BOP AOB S S == ,∵1BOP BOC POC S S S m =+=+ ,∴813m +=,解得53m =,∴123m -+=,∴点P 的坐标为51,33⎛⎫ ⎪⎝⎭;(3)∵直线AB 交y 轴于点C ,∴点C ()0,2,∴31222OMN OCN COMN S S S t =+=+⨯⨯ 四边形,∵3COMN S >四边形,∴312322t +⨯⨯>,∴32t >.【点评】本题考查了反比例函数与一次函数的交点问题,利用待定系数法求解析式,反比例函数的性质等知识,求出两个解析式是解题的关键.21.(1)4y x =;(2)100,3P ⎛⎫ ⎪⎝⎭.【分析】(1)先求出直线OA 的解析式为y x =,直线OB 的解析式为4y x =,过点A作AC x ∥轴,交OB 于C ,在求出1,4C a a ⎛⎫ ⎪⎝⎭,进而得出1344AC a a a =-=,根据21313324244AOB AOC ABC S S S a a a a a =+=⨯⨯+⨯⨯= ,再根据面积即可得出a 的值,求出()2,2A ,即可得出答案;(2)根据(1)可得:()2,2A ,()1,4B ,由于点D 与点A 关于y 轴对称,可知当PA PB +的值最小,即B ,P ,D 三点在同一直线上时ABP 的周长最小,求出直线BD 的解析式为21033y x =+,即可得出答案.(1)解:∵设直线OA 的解析式为1y k x =,将(),A a a 代入,得出:11k =,∴直线OA 的解析式为y x =,设直线OB 的解析式为2y k x =,将1,22B a a ⎛⎫ ⎪⎝⎭代入,得出:24k =,∴直线OB 的解析式为4y x =,过点A 作AC x ∥轴,交OB 于C ,∵(),A a a ,∴点C 的纵坐标为a ,∵点C 在直线OB 上,∴点c 的横坐标为:14a ,∴1,4C a a ⎛⎫ ⎪⎝⎭,∴1344AC a a a =-=,∴21313324244AOB AOC ABC S S S a a a a a =+=⨯⨯+⨯⨯= ,∴2334a =,解得:12a =,22a =-(舍去),∴()2,2A ,∴224k =⨯=,∴反比例函数的解析式为:4y x=;(2)解:根据(1)可得:()2,2A ,()1,4B ,∵点D 与点A 关于y 轴对称,∴PA PD =,∴AB PA PB AB PD PB ++=++,∵AB 为定值,∴当PA PB +的值最小,即B ,P ,D 三点在同一直线上时ABP 的周长最小,∴()2,2D -,设直线BD 的解析式为y ax b =+,将()1,4B ,()2,2D -,代入得:422a b a b +=⎧⎨-+=⎩,解得:23103a b ⎧=⎪⎪⎨⎪=⎪⎩,∴直线BD 的解析式为21033y x =+,当0x =时,103y =,∴100,3P ⎛⎫ ⎪⎝⎭.【点拨】本题考查反比例函数与一次函数,轴对称的性质,正确得出反比例函数解析式是解题的关键.22.(1)3y x=-;(2)-<3≤0x 或1x ≥;(3)()0,5-或()0,1【分析】(1)将点A 坐标代入直线表达式,求出m ,得到具体坐标,再将点A 坐标代入反比例函数表达式,求出k 值可;(2)求出点B 坐标,结合图像可得结果;(3)设点E 坐标为()0,a ,求出直线AB 与y 轴交点F 的坐标,再根据6EBA S =△,列出方程,解之可得.(1)解:将()3,A m -代入2y x =--得:()321m =---=,∴()3,1A -,代入k y x=中,得:()313k =-⨯=-,∴3y x=-;(2)将(),3B n -代入2y x =--中,得32n -=--,解得:1n =,∴()1,3B -,由图像可知:当一次函数图像在反比例函数图像下方时,对应的x 为-<3≤0x 或1x >,∴使一次函数值不大于反比例函数值的x 的取值范围是-<3≤0x 或1x ≥.(3)设点E 坐标为()0,a ,直线AB 与y 轴交于点F ,在2y x =--中,令0x =,则=2y -,∴()0,2F -,∵6EBA S =△,∴()162B A EF x x ⨯⨯-=,即12462a ⨯--⨯=,解得:5a =-或1a =,∴点E 的坐标为()0,5-或()0,1.【点拨】本题考查了一次函数与反比例函数交点问题,用待定系数法确定反比例函数的解析式;要能够熟练掌握待定系数法,学会表示交点形成的三角形面积是解题的关键.23.(1)一次函数解析式为3y x =+,反比例函数解析式为4y x=;(2)()03D -,【分析】(1)先把点A 坐标代入反比例函数解析式中求出反比例函数解析式,进而求出点B 的坐标,再把A 、B 的坐标代入一次函数解析式中求出一次函数解析式即可;(2)设直线AB 与x 轴,y 轴分别交于N ,M ,作点C 关于y 轴的对称点H ,连接CH 交y 轴于G ,连接HD ,推出当H D E 、、三点共线且HD AB ⊥时,HD DE +最小,即CD DE +最小;求出()()3003N M -,,,,进而证明45OMN ONM ∠=∠=︒,即可退出45GHD GDH =︒=∠∠,得到DG HG =;由对称性可知()14C --,,则()14H -,,由此求出3OD =,则()03D -,.(1)解:把()14A ,代入到反比例函数()220k y k x=≠中得:241k =,∴24k =,∴反比例函数解析式为4y x =,把()4B n -,代入到()4B n -,4y x=中得:414n ==--,∴()41B --,;把()14A ,,()41B --,代入到一次函数()110y k x b k =+≠中得:11441k b k b +=⎧⎨-+=-⎩,∴113k b =⎧⎨=⎩,∴一次函数解析式为3y x =+;(2)解:设直线AB 与x 轴,y 轴分别交于N ,M ,作点C 关于y 轴的对称点H ,连接CH 交y 轴于G ,连接HD ,∴CD HD =,∴CD DE HD DE +=+,∴当H D E 、、三点共线且HD AB ⊥时,HD DE +最小,即CD DE +最小;在3y x =+中,令0x =,则3y =,令0y =,则3x =-,∴()()3003N M -,,,,∴3OM ON ==,∴45OMN ONM ∠=∠=︒,∴45GDH EDM ==︒∠∠,∴45GHD GDH =︒=∠∠,∴DG HG =;由对称性可知()14C --,,∴()14H -,,∴41OG DG HG ===,,∴3OD =,∴()03D -,.【点拨】本题主要考查了一次函数与反比例函数综合,轴对称最短路径问题,等腰直角三角形的性质与判定,正确作出辅助线确定当H D E 、、三点共线且HD AB ⊥时,HD DE+最小,即CD DE +最小是解题的关键.24.(1)①直线AB 的解析式为344y x =-+;②四边形ABCD 是菱形,理由见分析;(2)四边形ABCD 能成为正方形,9m n +=.【分析】(1)①先确定出点A ,B 坐标,再利用待定系数法即可得出结论;②先确定出点D 坐标,进而确定出点P 坐标,进而求出PD PB ,,即可得出结论;(2)先确定出33m A ⎛⎫ ⎪⎝⎭,,33n C ⎛⎫ ⎪⎝⎭,进而求出点P 的坐标,再求出B ,D 坐标,最后用BD AC =,即可得出结论.(1)解:①∵4m =,∴反比例函数为4y x=,当4x =时,1y =,∴()41B ,,当3y =时,∴43x =,∴43x =,∴433A ⎛⎫ ⎪⎝⎭,设直线AB 的解析式为y kx b =+,∴43341k b k b ⎧+=⎪⎨⎪+=⎩,解得344k b ⎧=-⎪⎨⎪=⎩,∴直线AB 的解析式为344y x =-+;②四边形ABCD 是菱形,理由如下:由①知,433A ⎛⎫ ⎪⎝⎭,∵AC x ∥轴,∴1633C ⎛⎫ ⎪⎝⎭,,∵点P 是线段AC 的中点,∴1033P ⎛⎫ ⎪⎝⎭,,当103x =时,由4y x =得,65y =,由16y x =得,245y =,∴56359PB =-=,355249PD =-=,∴PB PD =,∵PA PC =,∴四边形ABCD 为平行四边形,∵BD AC ⊥,∴四边形ABCD 是菱形;(2)解:四边形ABCD 能是正方形,理由:当四边形ABCD 是正方形,记AC BD ,的交点为P ,P 为AC 的中点,∴BD AC =,当3y =时,由m y x =得,3m x =,由n y x=得,3n x =,∴33m A ⎛⎫ ⎪⎝⎭,,33n C ⎛⎫ ⎪⎝⎭,∴36m n P +⎛⎫ ⎪⎝⎭,∴66m n m B m n +⎛⎫ +⎝⎭,,66m n n D m n +⎛⎫ ⎪+⎝⎭,,∵BD AC =,∴6633n m n m m n m n -=-++,∴18m n +=.【点拨】此题是反比例函数综合题,主要考查了待定系数法,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD 是平行四边形是解本题的关键.。
反比例函数专题一、k的几何意义解与面积相关问题

∴点A,C的坐标分别为(-1,3),(3,-1).
专题训练
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标. 解:设点P的坐标为(0,m),直线y=-x+2与y轴的交点
为M,则M的坐标为(0,2).
∵S△APC=S△AMP+S△CMP=
1 2
×PM×(|-1|+|3|)=5,
∴PM= 5 ,即|m-2|= 5 .∴m= 9 或m=- 1 .
解:
由
ìïïïíïïïî
y y
= =
- x+ 6, x
7,
得
祆 镲 镲 眄 镲 镲 铑xy11
= =
1, x2 6,y2
= =
6, 1.
∴点D的坐标为(6,1).
当x=2时,反比例函数图象上的点为(2,3),
直线上的点为(2,5),此时可得整点为(2,4);
当x=3时,反比例函数图象上的点为(3,2),
a 的图象上, x
∴a=3×2=6,∴反比例函数的表达式为y=
6
.
x
∵B(3,2),∴EF=2.∵BD⊥y轴,OC=CA,
∴AE=EF= 1 AF,∴AF=4,∴点A的纵坐标为4.
2 ∵点A在反比例函数y=
6 的图象上,
∴点将AA的( 横3 坐, 4标),为B(332,,2∴)的xA坐( 32标,代4)入. y=kx+b,得
专题训练
题型2 利用对称性求面积 7.如图是由四条曲线围成的广告标志,建立平面直角坐
标=系6x ,.现双用曲四线根对钢应条的固函定数这解四析条式曲分线别,为这y=种-钢条6x ,加y工 成矩形产品按面积计算,每单位面积25元,请你帮助 工人师傅计算一下,所需钢条一共花多少钱?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数 ---动点、面积专题(附详解)一、解答题(共7小题)1、已知反比例函数y=的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是2,设Q点的纵坐标为n,求n﹣2n+9的值..1,1)2、已知:反比例函数经过点B((1)求该反比例函数解析式;(2)连接OB,再把点A(2,0)与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;(3)若该反比例函数图象上有一点F(m,)(其中m>0),在线段OF 上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OE的面积,求代数的值y=kx和反比例函数的图象的一个交点.3、如图,M点是正比例函数(1)求这两个函数的解析式;轴,垂足x做PA垂直于P(2)在反比例函数的图象上取一点,过点P为A,点Q是直线MO上一点,QB垂直于y轴,垂足为B,直线MO 上是否存在这样的点Q,使得△OBQ的面积是△OPA的面积的2倍?如果存在,请求出点Q的坐标,如果不存在,请说明理由.4、如图,已知:一次函数:y=﹣x+4的图象与反比例函数:(x>0)的图象分别交于A、B两点,点M是一次函数图象在第一象限部分上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M、M,设矩形MMOM的面积为2112S;点N为反比例函数图象上任意一点,过N分别向x轴、y轴作垂线,垂足分1别为N、N,设矩形NNON的面积为S;21221(1)若设点M的坐标为(x,y),请写出S关于x的函数表达式,并求x取何1值时,S的最大值;1(2)观察图形,通过确定x的取值,试比较S、S的大小.21、如图,已知正比例函数和反比例函数的图象都经过(,,(,)为双曲线上的一点为坐标平面上一动点P垂直轴Q垂直轴,垂足分别)写出正比例函数和反比例函数的关系式)当在直M上运动时,直M上是否存在这样的,使得OBQ面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由.OAP与△.6、如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ 为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.7、如图,点P(a,b)和点Q(c,d)是反比例函数y=图象上第一象限内的两个动点(a<b,a≠c),且始终有OP=OQ.(1)求证:a=d,b=c;(2)P是点P关于y轴的对称点,Q是点Q关于x轴的对称点,连接PQ分别1111交OP、OQ于点M、N.①求证:PQ∥PQ;11.②求四边形PQNM的面积S能否等于?若能,求出点P的坐标;若不能,请说明理由.反比例动点与面答案与评分标一、解答题(共7小题)1、已知反比例函数y=的图象经过点A(﹣.)1,(1)试确定此反比例函数的解析式;是否在此反比例函B.判断点OB30°得到线段点顺时针旋转O绕OA是坐标原点,将线段O)点2(.数的图象上,并说明理由;(3)已知点P(m,m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x2轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n﹣2n+9的值.考点:反比例函数综合题;待定系数法求反比例函数解析式;旋转的性质。
专题:综合题。
,1),运用待定系数法即可求出此反比例函数1)由于反比例函数y=的图象经过点A(﹣分析:(的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m,m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后2n+9的值.的值代入,即可求出n﹣2将所求的代数式变形,把mn;,∴反比例函数的解析式为,解得1)由题意得1=k=﹣y=﹣解答:解:(C2()过点A作x轴的垂线交x轴于点.在Rt△AOC中,OC=, AC=1,=2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段∴OA=OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB?sin∠BOD=,OD=OB=1,∴B点坐标为(﹣1,),的图象上.y=﹣﹣y=)在反比例函数,1(﹣B,∴点y=中,得代入﹣将x=1,0<m的图象上,其中﹣y=)在反比例函数m+6,m(P,∵点﹣xy=得﹣y=)由3(.2).m,n=﹣,∴m+2m+1=0,∵PQ⊥x轴,∴Q点的坐标为(∴m(m+6)2222+n=0,,∴mn=﹣1,∴mn+2mn0∵△OQM的面积是,∴OM?QM=,∵m<22n+9=8.﹣∴n﹣22n=﹣1,∴n点评:本题综合考查了运用待定系数法求反比例函数的解析式,旋转的性质,三角函数的定义,求代数式的值等知识,尤其是在最后一问中,没有必要求出n 的具体值,而是将mn=﹣1作为一个整体代入,有一定的技巧性,使计算简便.2、已知:反比例函数经过点B(1,1).(1)求该反比例函数解析式;135°得到按顺时针方向旋转绕点O,0)与点B连接,将△OAB,再把点(2)连接OBA(2P是否在此双曲线上,并说明理由;的坐标,试判断点△OA′B′,写出A′B′的中点PEOF上任取一点E,设)((3)若该反比例函数图象上有一点Fm,)(其中m>0,在线段点的纵坐标为n,过F点作FM⊥x轴于点M求,代数式,连接EM,使△OEM的面积是的值.考:反比例函数综合题分析:(1)函数式y=,且过(1,1)点,代入可确定k的值,从而求出函数式.′′′′中点的坐标,可判和B的坐标,从而求出ABA(2)因为△OAB是等腰直角三角形,旋转后求出断是否在双曲线线上.在反比例函数图象F的面积是,△OEM的关系式,因为m和n,从而可求出0M=mEH=n3()因为,上,代入函数式,可求出结果.分)1(解:解答:)反比例函数解析式:1(;(2)∵已知B(1,1),A(2,0)∴△OAB是等腰直角三角形∵顺时针方向旋转135°,′,﹣)∴中点P为(﹣,﹣).),A(﹣∴B′(0,﹣(2分))?(﹣)=1(3分)∴点∵(﹣P在此双曲线上.(4分)(5分)0M=m (3)∵EH=n,∴S=,∴m===△OEM)在函数图象上 6=1.(分)又∵F(m,∴22﹣2=.代入上式,得(,∴nm=将+7分)+﹣=1,∴n=的值,进而确定函点评:本题考查反比例函数的综合应用,关键是知道用已知点确定反比例函数式k数式,以及反比例函数上的点,和由这点做顶点的三角形的面积的关系.的图象的一个交点.y=kxM3、如图,点是正比例函数和反比例函数)求这两个函数的解析式;(1MOQAxPA做垂直于轴,垂足为,点是直线PP)在反比例函数(2的图象上取一点,过点上一点,QB垂直于y轴,垂足为B,直线MO上是否存在这样的点Q,使得△OBQ的面积是△OPA的面积的2倍?如果存在,请求出点Q的坐标,如果不存在,请说明理由.考:反比例函数综合题分析:(1)从图象上可看到正比例函数y=kx和反比例函数y=都过(1,2)点,从而可求出函数式.(2)P是反比例函数上的一点,过点P做PA垂直于x轴,垂足为A,所以△OPA的面积是m,点Q是直线MO上一点,QB垂直于y轴,垂足为B,Q点的坐标为(x,kx),所以根据△OBQ的面积是倍可列方程求解.2的面积的△OPA.解答:解:(1)∵y=kx过(﹣1,2)点,∴k=﹣2,∴y=﹣2x.∵y=过(﹣1,2)点,∴m=﹣2.∴y=﹣;(2)∵△OPA的面积是m=1,Q点的坐标为(x,﹣2x),∴?|x|?|﹣2x|=2,x=±,.,﹣2)Q点的坐标为(﹣,2),或(因为在第二象限所以点评:本题考查反比例函数的综合运用,关键能够熟练确定函数式,并能够掌握由函数图象上的点作为顶点的三角形面积和函数坐标之间的关系.4、如图,已知:一次函数:y=﹣x+4的图象与反比例函数:(x>0)的图象分别交于A、B两点,点M是一次函数图象在第一象限部分上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M、M,设矩形MMOM的面积为S;点N为反比例函数图象上任意一点,过N分别向x轴、y轴作12121垂线,垂足分别为N、N,设矩形NNON的面积为S;22211(1)若设点M的坐标为(x,y),请写出S关于x的函数表达式,并求x取何值时,S的最大值;11(2)观察图形,通过确定x 的取值,试比较S、S的大小.21考:反比例函数综合题;一次函数的图象专:计算题分析:(1)已知M点坐标,根据M点在一次函数:y=﹣x+4的图象上,代入把M点纵坐标用x表示出来,从而表示出矩形MMOM的面积为S;(2)观察图形S、S,观察反比例函数在一次函数上方还是21121下方,从而比较其大小.解答:解:(1)∵M的坐标为(x,y),M点在还函数y=﹣x+4的图象上,∴y=﹣x+4,22;时,,当)﹣﹣(x=x+4=xy=x∴S(﹣)﹣+4x=x2+4x=2S=4最大值11.(2)设N(x,y),点N在反比例函数:图象上,1122,∴S=x×y=2,由S=S可得:﹣x+4x=2,即x﹣4x﹣2=0,∴21121通过观察图象可得:当时,S=S,当或时,S<S,2211.>时,当SS21点评:此题考查一次函数和反比例函数的性质及应用,学会通过图象比较面积的大小,比较简单.5、如图,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由.考点:反比例函数综合题。
