高一立体几何平行垂直解答题精选

合集下载

立体几何线面平行垂直、面面平行垂直专题练习(高三党必做)

立体几何线面平行垂直、面面平行垂直专题一、解答题（本大题共27小题，共324.0分）1.如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．（1）证明：MN∥平面PAB；（2）求直线AN与平面PMN所成角的正弦值．2.如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝AD，∠BAD＝∠ABC＝90°，E是PD的中点．BC＝12(1)证明：直线CE∥平面PAB；(2)点M在棱PC上，且直线BM与底面ABCD所成角为45°，求二面角M-AB-D的余弦值．3.如图，在三棱柱ABC-A1B1C1中，BB1⊥平面ABC，∠BAC=90°，AC=AB=AA1，E是BC的中点．（1）求证：AE⊥B1C；（2）求异面直线AE与A1C所成的角的大小；（3）若G为C1C中点，求二面角C-AG-E的正切值．4.如图所示，在四棱锥P-ABCD中，底面四边形ABCD是菱形，AC∩BD=O，△PAC是边长为2的等边三角形，PB=PD=√6，AP=4AF．（Ⅰ）求证：PO⊥底面ABCD；（Ⅱ）求直线CP与平面BDF所成角的大小；（Ⅲ）在线段PB上是否存在一点M，使得CM∥平面BDF如果存在，求BM的值，如果不存在，请说明理BP由．5.如图，在直三棱柱ABC-A1B l C1中，AC=BC=√2，∠ACB=90°．AA1=2，D为AB的中点．（Ⅰ）求证：AC⊥BC1；（Ⅱ）求证：AC1∥平面B1CD：（Ⅲ）求异面直线AC1与B1C所成角的余弦值．6.如图，正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面AQC1所成角的正弦值．7.如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=√6，AB=4．（1）求证：M为PB的中点；（2）求二面角B-PD-A的大小；（3）求直线MC与平面BDP所成角的正弦值．8.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．（1）证明：PB∥平面AEC；（2）设AP=1，AD=√3，三棱锥P-ABD的体积V=√3，求A到平面PBC的距4离．9.如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．（Ⅰ）证明：BE⊥DC；（Ⅱ）求直线BE与平面PBD所成角的正弦值；（Ⅲ）若F为棱PC上一点，满足BF⊥AC，求二面角F-AB-P的余弦值．10.如图，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．11.如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．（I）求证：EM⊥AD；（II）求证：MN∥平面ADE；（III）求点A到平面BCE的距离．12.已知几何体ABCDEF中，AB∥CD，AD⊥DC，EA⊥平面ABCD，FC∥EA，AB=AD=EA=1，CD=CF=2．（Ⅰ）求证：平面EBD⊥平面BCF；（Ⅱ）求点B到平面ECD的距离．13.如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD=2，E、F分别为CD、PB的中点．（1）求证：EF∥平面PAD；（2）求证：平面AEF⊥平面PAB；（3）设AB=√2AD，求直线AC与平面AEF所成角θ的正弦值．14.如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ADC=45∘，AD=AC=2，O为AC的中点，PO⊥平面ABCD且PO=6，M为BD的中点．(1)证明：AD⊥平面PAC；(2)求直线AM与平面ABCD所成角的正切值．15.如图，正三棱柱ABC-A1B1C1中，AB=2，AA1=√2，点D为A1C1的中点．（I）求证：BC1∥平面AB1D；（II）求证：A1C⊥平面AB1D；（Ⅲ）求异面直线AD与BC1所成角的大小．16.如图，P-ABD和Q-BCD为两个全等的正棱锥，且A，B，C，D四点共面，其中AB=1，∠APB=90°．（Ⅰ）求证：BD⊥平面APQ；（Ⅱ）求直线PB与平面PDQ所成角的正弦值．17.如图，在三棱柱ABC-A1B1C1中，平面A1ACC1⊥底面ABC，AB=BC=2，∠ACB=30°，∠C1CB=60°，BC1⊥A1C，E为AC的中点，侧棱CC1=2．（1）求证：A1C⊥平面C1EB；（2）求直线CC1与平面ABC所成角的余弦值．18.如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，AB=6，BC=2√3，AC=2√6，D为线段AB上的点，且AD=2DB，PD⊥AC．（1）求证：PD⊥平面ABC；，求点B到平面PAC的距离．（2）若∠PAB=π419.如图，三棱柱ABC-A1B1C1中，A1A⊥平面ABC，△ABC为正三角形，D是BC边的中点，AA1=AB=1．（1）求证：平面ADB1⊥平面BB1C1C；（2）求点B到平面ADB1的距离．20.如图，在三棱锥P-ABC中，点D，E，F分别为棱PC，AC，AB的中点，已知PA⊥平面ABC，AB⊥BC，且AB=BC．（1）求证：平面BED⊥平面PAC；（2）求二面角F-DE-B的大小；（3）若PA=6，DF=5，求PC与平面PAB所成角的正切值．21.如图,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD＝CD＝1,DB=2√2.(1)证明PA∥平面BDE;(2)证明AC⊥平面PBD;(3)求直线BC与平面PBD所成的角的正切值.22.如图所示，在四棱台ABCD-A1B1C1D1中，AA1⊥底面ABCD，四边形ABCD为菱形，∠BAD=120°，AB=AA1=2A1B1=2．（Ⅰ）若M为CD中点，求证：AM⊥平面AA1B1B；（Ⅱ）求直线DD1与平面A1BD所成角的正弦值．=√2.23.如图，在直三棱柱ABC−A1B1C1中，∠ACB=90°，E为A1C1的中点，CC1C1E（Ⅰ）证明：CE⊥平面AB1C1；（Ⅱ）若AA1=√6，∠BAC=30°，求点E到平面AB1C的距离．24.如图，在四棱锥E-ABCD中，底面ABCD是边长为√2的正方形，平面AEC⊥平面CDE，∠AEC=90°，F为DE中点，且DE=1．（Ⅰ）求证：BE∥平面ACF；（Ⅱ）求证：CD⊥DE；（Ⅲ）求FC与平面ABCD所成角的正弦值．25.已知：平行四边形ABCD中，∠DAB=45°，AB=√2AD=2√2，平面AED⊥平面ABCD，△AED为等边三角形，EF∥AB，EF=√2，M为线段BC的中点．（1）求证：直线MF∥平面BED；（2）求证：平面BED⊥平面EAD；（3）求直线BF与平面BED所成角的正弦值．26.如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=√2，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AC=√2，AB=BC=1，E为AD中点．（Ⅰ）求证：PE⊥平面ABCD；（Ⅱ）求异面直线PB与CD所成角的余弦值；（Ⅲ）求平面PAB与平面PCD所成的二面角．27.如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（1）证明：AB1⊥平面A1B1C1；（2）求直线AC1与平面ABB1所成的角的正弦值．答案和解析1.【答案】（1）证明：法一、如图，取PB 中点G ，连接AG ，NG ，∵N 为PC 的中点， ∴NG ∥BC ，且NG =12BC ，又AM =23AD =2，BC =4，且AD ∥BC ， ∴AM ∥BC ，且AM =12BC ，则NG ∥AM ，且NG =AM ，∴四边形AMNG 为平行四边形，则NM ∥AG ， ∵AG ⊂平面PAB ，NM ⊄平面PAB ， ∴MN ∥平面PAB ；法二、在△PAC 中，过N 作NE ⊥AC ，垂足为E ，连接ME ，在△ABC 中，由已知AB =AC =3，BC =4，得cos ∠ACB =42+32−322×4×3=23，∵AD ∥BC ，∴cos ∠EAM =23，则sin ∠EAM =√53，在△EAM 中，∵AM =23AD =2，AE =12AC =32，由余弦定理得：EM =√AE 2+AM 2−2AE ⋅AM ⋅cos∠EAM =√94+4−2×32×2×23=32，∴cos ∠AEM =(32)2+(32)2−42×32×32=19，而在△ABC 中，cos ∠BAC =32+32−422×3×3=19，∴cos ∠AEM =cos ∠BAC ，即∠AEM =∠BAC ， ∴AB ∥EM ，则EM ∥平面PAB ．由PA ⊥底面ABCD ，得PA ⊥AC ，又NE ⊥AC ， ∴NE ∥PA ，则NE ∥平面PAB ． ∵NE ∩EM =E ，∴平面NEM ∥平面PAB ，则MN ∥平面PAB ；（2）解：在△AMC 中，由AM =2，AC =3，cos ∠MAC =23，得CM 2=AC 2+AM 2-2AC •AM •cos ∠MAC =9+4−2×3×2×23=5．∴AM 2+MC 2=AC 2，则AM ⊥MC ， ∵PA ⊥底面ABCD ，PA ⊂平面PAD ，∴平面ABCD ⊥平面PAD ，且平面ABCD ∩平面PAD =AD ， ∴CM ⊥平面PAD ，则平面PNM ⊥平面PAD ．在平面PAD 内，过A 作AF ⊥PM ，交PM 于F ，连接NF ，则∠ANF 为直线AN 与平面PMN 所成角．在Rt△PAC中，由N是PC的中点，得AN=12PC=12√PA2+PC2=52，在Rt△PAM中，由PA•AM=PM•AF，得AF=PA⋅AMPM =√42+22=4√55，∴sin∠ANF=AFAN =4√5552=8√525．∴直线AN与平面PMN所成角的正弦值为8√525．【解析】本题考查直线与平面平行的判定，考查直线与平面所成角的求法，考查数学转化思想方法，考查了空间想象能力和计算能力，是中档题．（1）法一、取PB中点G，连接AG，NG，由三角形的中位线定理可得NG∥BC，且NG=12BC，再由已知得AM∥BC，且AM=12BC，得到NG∥AM，且NG=AM，说明四边形AMNG为平行四边形，可得NM∥AG，由线面平行的判定得到MN∥平面PAB；法二、证明MN∥平面PAB，转化为证明平面NEM∥平面PAB，在△PAC中，过N作NE⊥AC，垂足为E，连接ME，由已知PA⊥底面ABCD，可得PA∥NE，通过求解直角三角形得到ME∥AB，由面面平行的判定可得平面NEM∥平面PAB，则结论得证；（2）由勾股定理得CM⊥AD，进一步得到平面PNM⊥平面PAD，在平面PAD内，过A作AF⊥PM，交PM于F，连接NF，则∠ANF为直线AN与平面PMN所成角．然后求解直角三角形可得直线AN与平面PMN所成角的正弦值．2.【答案】（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF∥AD，EF=12AD，AB=BC=12AD，∠BAD=∠ABC=90°，∴BC∥AD，EF∥BC,EF=BC,∴四边形BCEF是平行四边形，可得CE∥BF，BF⊂平面PAB，CE⊄平面PAB，∴直线CE∥平面PAB;（2）解:如图所示，取AD中点O，连接PO，CO，由于△PAD为正三角形，则PO⊥AD，因为侧面PAD为等边三角形且垂直于底面ABCD，平面PAD∩平面ABCD=AD，所以PO⊥平面ABCD，所以PO⊥CO. 因为AO=AB=BC=12AD，且∠BAD=∠ABC= 90∘，所以四边形ABCO是矩形，所以CO⊥AD，以O为原点，OC为x轴，OD为y轴，OP为z轴建立空间直角坐标系,不妨设AB=BC=12AD=1，则OA=OD=AB=CO=1.又因为△POC为直角三角形，|OC|=√33|OP|，所以∠PCO=60∘.作MN⊥CO，垂足为N，连接BN，因为PO ⊥CO ，所以MN //PO ，且PO ⊥平面ABCD ，所以MN ⊥平面ABCD ，所以∠MBN 即为直线BM 与平面ABCD 所成的角, 设CN =t ，因为∠PCO =60∘，所以MN =√3t ，BN =√BC 2+CN 2=√t 2+1. 因为∠MBN =45∘，所以MN =BN ，即√3t =√t 2+1，解得t =√22，所以ON =1−√22，MN =√62，所以A (0,−1,0)，B (1,−1,0)，M (1−√22,0,√62)，D (0,1,0)，则AB ⃗⃗⃗⃗⃗ =(1,0,0)，AD⃗⃗⃗⃗⃗⃗ =(0,2,0)，AM ⃗⃗⃗⃗⃗⃗ =(1−√22,1,√62). 设平面MAB 和平面DAB 的法向量分别为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1)，n 2⃗⃗⃗⃗ =(x 2,y 2,z 2), 则{AB ⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0AM ⃗⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0，即{x 1=0(1−√22)x 1+y 1+√62z 1=0，可取z 1=−2，则n 1⃗⃗⃗⃗ =(0,√6,−2), 同理可得n 2⃗⃗⃗⃗ =(0,0,1)，所以.因为二面角M -AB -D 是锐角，所以其余弦值为√105.【解析】本题考查直线与平面平行的判定定理的应用，空间向量求二面角夹角，考查空间想象能力以及计算能力，属于中档题．（1）取PA 的中点F ，连接EF ，BF ，通过证明CE ∥BF ，利用直线与平面平行的判定定理证明即可．（2）取AD 中点O ，连接PO ，CO ，作MN ⊥CO ，垂足为N ，以O 为原点，OC 为x 轴，OD 为y 轴，OP 为z 轴建立空间直角坐标系，即可求出二面角M -AB -D 的余弦值．3.【答案】证明：（1）因为BB 1⊥面ABC ，AE ⊂面ABC ，所以AE ⊥BB 1,由AB =AC ，E 为BC 的中点得到AE ⊥BC , ∵BC ∩BB 1=B ，BC 、BB 1⊂面BB 1C 1C ， ∴AE ⊥面BB 1C 1C ，,∴AE ⊥B 1C ；解：（2）取B 1C 1的中点E 1，连A 1E 1，E 1C ，则AE ∥A 1E 1， ∴∠E 1A 1C 是异面直线AE 与A 1C 所成的角，设AC =AB =AA 1=2，则由∠BAC =90°，可得A 1E 1=AE =√2，A 1C =2√2，E 1C 1=EC =12BC =√2，∴E 1C =√E 1C 12+C 1C 2=√6，∵在△E 1A 1C 中，cos ∠E 1A 1C =2+8−62⋅√2⋅2√2=12，所以异面直线AE 与A 1C 所成的角为π3；（3）连接AG ，设P 是AC 的中点，过点P 作PQ ⊥AG 于Q ，连EP ，EQ ，则EP ⊥AC ，又∵平面ABC ⊥平面ACC 1A 1,平面ABC ∩平面ACC 1A 1=AC ∴EP ⊥平面ACC 1A 1，而PQ ⊥AG ∴EQ ⊥AG ．∴∠PQE 是二面角C -AG -E 的平面角，由(2)假设知：EP =1，AP =1， Rt △ACG ∽Rt △AQP ，PQ =CG·AP AG=1√5，故tan ∠PQE =PEPQ =√5，所以二面角C -AG -E 的平面角正切值是√5.【解析】本题考查异面直线的夹角，线线垂直的判定，属于中档题，熟练掌握线面垂直，线线垂直与面面垂直之间的转化及异面直线夹角及二面角的定义，是解答本题的关键，属于较难题.（1）由BB 1⊥面ABC 及线面垂直的性质可得AE ⊥BB 1，由AC =AB ，E 是BC 的中点，及等腰三角形三线合一，可得AE ⊥BC ，结合线面垂直的判定定理可证得AE ⊥面BB 1C 1C ，进而由线面垂直的性质得到AE ⊥B 1C ；（2）取B 1C 1的中点E 1，连A 1E 1，E 1C ，根据异面直线夹角定义可得，∠E 1A 1C 是异面直线A 与A 1C 所成的角，设AC =AB =AA 1=2，解三角形E 1A 1C 可得答案．（3）连接AG ，设P 是AC 的中点，过点P 作PQ ⊥AG 于Q ，连EP ，EQ ，则EP ⊥AC ，由直三棱锥的侧面与底面垂直，结合面面垂直的性质定理，可得EP ⊥平面ACC 1A 1，进而由二面角的定义可得∠PQE 是二面角C -AG -E 的平面角．4.【答案】（Ⅰ）证明：因为底面ABCD 是菱形，AC ∩BD =O ，所以O 为AC ，BD 中点．-------------------------------------（1分）又因为PA =PC ，PB =PD ，所以PO ⊥AC ，PO ⊥BD ，---------------------------------------（3分）所以PO ⊥底面ABCD ．----------------------------------------（4分）（Ⅱ）解：由底面ABCD 是菱形可得AC ⊥BD ，又由（Ⅰ）可知PO ⊥AC ，PO ⊥BD ．如图，以O 为原点建立空间直角坐标系O -xyz ．由△PAC 是边长为2的等边三角形，PB =PD =√6，可得PO =√3，OB =OD =√3．所以A(1，0，0)，C(−1，0，0)，B(0，√3，0)，P(0，0，√3)．---------------------------------------（5分）所以CP ⃗⃗⃗⃗⃗ =(1，0，√3)，AP ⃗⃗⃗⃗⃗ =(−1，0，√3)．由已知可得OF ⃗⃗⃗⃗⃗ =OA⃗⃗⃗⃗⃗ +14AP ⃗⃗⃗⃗⃗ =(34，0，√34)-----------------------------------------（6分）设平面BDF 的法向量为n −=（x ，y ，z ），则{√3y =034x +√34z =0令x =1，则z =−√3，所以n ⃗ =（1，0，-√3）．----------------------------------------（8分）因为cos ＜CP ⃗⃗⃗⃗⃗ ，n ⃗ ＞=CP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗|CP ⃗⃗⃗⃗⃗ ||n ⃗⃗ |=-12，----------------------------------------（9分）所以直线CP 与平面BDF 所成角的正弦值为12，所以直线CP 与平面BDF 所成角的大小为30°．-----------------------------------------（10分）（Ⅲ）解：设BMBP =λ（0≤λ≤1），则CM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +λBP ⃗⃗⃗⃗⃗ =(1，√3(1−λ)，√3λ)．---------------------------------（11分）若使CM ∥平面BDF ，需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ，---------------------（12分）解得λ=13∈[0，1]，----------------------------------------（13分）所以在线段PB 上存在一点M ，使得CM ∥平面BDF ．此时BM BP =13．-----------------------------------（14分）【解析】（Ⅰ）证明PO ⊥底面ABCD ，只需证明PO ⊥AC ，PO ⊥BD ；（Ⅱ）建立空间直角坐标系，求出直线CP 的方向向量，平面BDF 的法向量，利用向量的夹角公式可求直线CP 与平面BDF 所成角的大小；（Ⅲ）设BMBP =λ（0≤λ≤1），若使CM ∥平面BDF ，需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ，即可得出结论．本题考查线面垂直，考查线面平行，考查线面角，考查向量知识的运用，正确求出向量的坐标是关键．5.【答案】解：（I ）证明：∵CC 1⊥平面ABC ，AC ⊂平面ABC ，∠ACB =90°， ∴CC 1⊥AC ，AC ⊥BC ，又BC ∩CC 1=C ，∴AC ⊥平面BCC 1，BC 1⊂平面BCC 1， ∴AC ⊥BC 1．（II ）证明：如图，设CB 1∩C 1B =E ，连接DE ， ∵D 为AB 的中点，E 为C 1B 的中点，∴DE ∥AC 1， ∵DE ⊂平面B 1CD ，AC 1⊄平面B 1CD ， ∴AC 1∥平面B 1CD ．（III ）解：由DE ∥AC 1，∠CED 为AC 1与B 1C 所成的角，在△CDE 中，DE =12AC 1=12√AC 2+CC 12=√62， CE =12B 1C =12√BC 2+BB 12=√62，CD =12AB =12√AC 2+BC 2=1，cos ∠CED =CE 2+DE 2−CD 22×CE×DE=32+32−12×√62×√62=23，∴异面直线AC 1与B 1C 所成角的余弦值为23．【解析】本题考查线线垂直的判定、线面平行的判定、异面直线及其所成的角．（I ）先证线面垂直，再由线面垂直证明线线垂直即可；（II ）作平行线，由线线平行证明线面平行即可；（III ）先证明∠CED 为异面直线所成的角，再在三角形中利用余弦定理计算即可． 6.【答案】解：如图，在正三棱柱ABC -A 1B 1C 1中，设AC ，A 1C 1的中点分别为O ，O 1，则，OB ⊥OC ，OO 1⊥OC ，OO 1⊥OB ，故以{OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ ，OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底，建立空间直角坐标系O -xyz ，∵AB =AA 1=2，A （0，-1，0），B （√3，0，0）， C （0，1，0），A 1（0，-1，2），B 1（√3，0，2），C 1（0，1，2）．（1）点P 为A 1B 1的中点．∴P(√32，−12，2)，∴BP ⃗⃗⃗⃗⃗ =(−√32，−12，2)，AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2)． |cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=|−1+4|√5×2√2=3√1020．∴异面直线BP 与AC 1所成角的余弦值为：3√1020；（2）∵Q 为BC 的中点．∴Q （√32，12，0）∴AQ ⃗⃗⃗⃗⃗ =(√32，32，0)，AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2)，设平面AQC 1的一个法向量为n⃗ =（x ，y ，z ），由{AQ ⃗⃗⃗⃗⃗ ·n ⃗ =√32x +32y =0AC 1⃗⃗⃗⃗⃗⃗⃗ ·n⃗ =2y +2z =0，可取n⃗ =（√3，-1，1），设直线CC 1与平面AQC 1所成角的正弦值为θ， sinθ=|cos|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n⃗ |=2√5×2=√55， ∴直线CC 1与平面AQC 1所成角的正弦值为√55．【解析】本题考查了向量法求空间角，属于中档题．设AC ，A 1C 1的中点分别为O ，O 1，以{OB ⃗⃗⃗⃗⃗⃗ ，OC ⃗⃗⃗⃗⃗ ，OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底，建立空间直角坐标系O -xyz ，（1）由|cos ＜BP ⃗⃗⃗⃗⃗ ，AC 1⃗⃗⃗⃗⃗⃗⃗ ＞|=|BP ⃗⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |可得异面直线BP 与AC 1所成角的余弦值；（2）求得平面AQC 1的一个法向量为n⃗ ，设直线CC 1与平面AQC 1所成角的正弦值为θ，可得sinθ=|cos ＜CC 1⃗⃗⃗⃗⃗⃗⃗ ，n⃗ ＞|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |，即可得直线CC 1与平面AQC 1所成角的正弦值．7.【答案】（1）证明：如图，设AC ∩BD =O ，∵ABCD 为正方形，∴O 为BD 的中点，连接OM ，∵PD ∥平面MAC ，PD ⊂平面PBD ，平面PBD ∩平面AMC =OM ， ∴PD ∥OM ，则BOBD =BM BP，即M 为PB 的中点；（2）解：取AD 中点G ， ∵PA =PD ，∴PG ⊥AD ，∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD =AD ， ∴PG ⊥平面ABCD ，则PG ⊥AD ，连接OG ，则PG ⊥OG ，由G 是AD 的中点，O 是AC 的中点，可得OG ∥DC ，则OG ⊥AD ．以G 为坐标原点，分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系，由PA =PD =√6，AB =4，得D （2，0，0），A （-2，0，0），P （0，0，√2），C （2，4，0），B （-2，4，0），M （-1，2，√22），DP ⃗⃗⃗⃗⃗ =(−2，0，√2)，DB⃗⃗⃗⃗⃗⃗ =(−4，4，0)．设平面PBD 的一个法向量为m ⃗⃗⃗ =(x ，y ，z)，则由{m ⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0，得{−2x +√2z =0−4x +4y =0，取z =√2，得m ⃗⃗⃗ =(1，1，√2)．取平面PAD 的一个法向量为n ⃗ =(0，1，0)．∴cos ＜m ⃗⃗⃗ ，n ⃗ ＞=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ ||n ⃗⃗ |=12×1=12． ∴二面角B -PD -A 的大小为60°；（3）解：CM ⃗⃗⃗⃗⃗⃗ =(−3，−2，√22)，平面BDP 的一个法向量为m ⃗⃗⃗ =(1，1，√2)．∴直线MC 与平面BDP 所成角的正弦值为|cos ＜CM ⃗⃗⃗⃗⃗⃗ ，m ⃗⃗⃗ ＞|=|CM ⃗⃗⃗⃗⃗⃗⋅m ⃗⃗⃗|CM ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||=|−2√9+4+12×1|=2√69．【解析】本题考查线面角与面面角的求法，训练了利用空间向量求空间角，属中档题．（1）设AC ∩BD =O ，则O 为BD 的中点，连接OM ，利用线面平行的性质证明OM ∥PD ，再由平行线截线段成比例可得M 为PB 的中点；（2）取AD 中点G ，可得PG ⊥AD ，再由面面垂直的性质可得PG ⊥平面ABCD ，则PG ⊥AD ，连接OG ，则PG ⊥OG ，再证明OG ⊥AD ．以G 为坐标原点，分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系，求出平面PBD 与平面PAD 的一个法向量，由两法向量所成角的大小可得二面角B -PD -A 的大小；（3）求出CM⃗⃗⃗⃗⃗⃗ 的坐标，由CM ⃗⃗⃗⃗⃗⃗ 与平面PBD 的法向量所成角的余弦值的绝对值可得直线MC 与平面BDP 所成角的正弦值．8.【答案】解：（Ⅰ）证明：设BD 与AC 的交点为O ，连结EO ， ∵ABCD 是矩形， ∴O 为BD 的中点 ∵E 为PD 的中点， ∴EO ∥PB ．EO ⊂平面AEC ，PB ⊄平面AEC ∴PB ∥平面AEC ；（Ⅱ）∵AP =1，AD =√3，三棱锥P -ABD 的体积V =√34，∴V =16PA ⋅AB ⋅AD =√36AB =√34，∴AB =32，PB =√1+(32)2=√132．作AH ⊥PB 交PB 于H ，由题意可知BC ⊥平面PAB ， ∴BC ⊥AH ，故AH ⊥平面PBC ．又在三角形PAB 中，由射影定理可得：AH =PA⋅AB PB=3√1313A 到平面PBC 的距离3√1313．【解析】本题考查直线与平面垂直，点到平面的距离的求法，考查空间想象能力以及计算能力．（Ⅰ）设BD 与AC 的交点为O ，连结EO ，通过直线与平面平行的判定定理证明PB ∥平面AEC ；（Ⅱ）通过AP =1，AD =√3，三棱锥P -ABD 的体积V =√34，求出AB ，作AH ⊥PB 角PB于H ，说明AH 就是A 到平面PBC 的距离．通过解三角形求解即可． 9.【答案】证明：（I ）∵PA ⊥底面ABCD ，AD ⊥AB ，以A 为坐标原点，建立如图所示的空间直角坐标系，∵AD =DC =AP =2，AB =1，点E 为棱PC 的中点． ∴B （1，0，0），C （2，2，0），D （0，2，0）， P （0，0，2），E （1，1，1）∴BE⃗⃗⃗⃗⃗ =（0，1，1），DC ⃗⃗⃗⃗⃗ =（2，0，0） ∵BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0， ∴BE ⊥DC ；（Ⅱ）∵BD ⃗⃗⃗⃗⃗⃗ =（-1，2，0），PB ⃗⃗⃗⃗⃗ =（1，0，-2），设平面PBD 的法向量m⃗⃗⃗ =（x ，y ，z ），由{m ⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =0，得{−x +2y =0x −2z =0，令y =1，则m⃗⃗⃗ =（2，1，1），则直线BE 与平面PBD 所成角θ满足： sinθ=m⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |⋅|BE ⃗⃗⃗⃗⃗⃗ |=2√6×√2=√33，故直线BE 与平面PBD 所成角的正弦值为√33．（Ⅲ）∵BC⃗⃗⃗⃗⃗ =（1，2，0），CP ⃗⃗⃗⃗⃗ =（-2，-2，2），AC ⃗⃗⃗⃗⃗ =（2，2，0），由F 点在棱PC 上，设CF⃗⃗⃗⃗⃗ =λCP ⃗⃗⃗⃗⃗ =（-2λ，-2λ，2λ）（0≤λ≤1），故BF ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CF⃗⃗⃗⃗⃗ =（1-2λ，2-2λ，2λ）（0≤λ≤1），由BF ⊥AC ，得BF ⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =2（1-2λ）+2（2-2λ）=0，解得λ=34，即BF ⃗⃗⃗⃗⃗ =（-12，12，32），设平面FBA 的法向量为n ⃗ =（a ，b ，c ），由{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BF ⃗⃗⃗⃗⃗ =0，得{a =0−12a +12b +32c =0令c =1，则n⃗ =（0，-3，1），取平面ABP 的法向量i =（0，1，0），则二面角F -AB -P 的平面角α满足： cosα=|i ⋅n ⃗⃗ ||i|⋅|n ⃗⃗ |=3√10=3√1010，故二面角F -AB -P 的余弦值为：3√1010【解析】本题考查的知识点是空间二面角的平面角，建立空间直角坐标系，将二面角问题转化为向量夹角问题，是解答的关键．（I ）以A 为坐标原点，建立空间直角坐标系，求出BE ，DC 的方向向量，根据BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0，可得BE ⊥DC ；（II ）求出平面PBD 的一个法向量，代入向量夹角公式，可得直线BE 与平面PBD 所成角的正弦值；（Ⅲ）根据BF ⊥AC ，求出向量BF ⃗⃗⃗⃗⃗ 的坐标，进而求出平面FAB 和平面ABP 的法向量，代入向量夹角公式，可得二面角F -AB -P 的余弦值． 10.【答案】证明：（Ⅰ）取AD 的中点F ，连接EF ，CF ，∵E 为PD 的中点，∴EF ∥PA ，EF ∥平面PAB ，在四边形ABCD 中，BC ∥AD ，AD =2DC =2CB ，F 为中点，∴四边形CBAF 为平行四边形，故CF ∥AB ，CF ∥平面PAB ，∵CF ∩EF =F ，EF ∥平面PAB ，CF ∥平面PAB ， ∴平面EFC ∥平面ABP ， ∵EC ⊂平面EFC ， ∴EC ∥平面PAB ．解：（Ⅱ）连接BF ，过F 作FM ⊥PB 于M ，连接PF ， ∵PA =PD ，∴PF ⊥AD ，∵DF ∥BC ，DF =BC ，CD ⊥AD ，∴四边形BCDF 为矩形，∴BF ⊥AD ，又AD ∥BC ，故PF ⊥BC ，BF ⊥BC ，又BF ∩PF =F ,BF 、PF ⊂平面PBF ，BC ⊄平面PBF ， ∴BC ⊥平面PBF ，∴BC ⊥PB ，设DC =CB =1，由PC =AD =2DC =2CB ，得AD =PC =2， ∴PB =√PC 2−BC 2=√4−1=√3， BF =PF =1，∴MF =√12−(√32)2=12，又BC ⊥平面PBF ，∴BC ⊥MF ，又PB ∩BC =B ,PB 、BC ⊂平面PBC ，MF ⊄平面PBC ， ∴MF ⊥平面PBC ，即点F 到平面PBC 的距离为12，∵MF =12，D 到平面PBC 的距离应该和MF 平行且相等，均为12， E 为PD 中点，E 到平面PBC 的垂足也为所在线段的中点，即中位线， ∴E 到平面PBC 的距离为14，在△PCD 中,PC =2,CD =1,PD =√2，,故由余弦定理得CE =√2，设直线CE 与平面PBC 所成角为θ，则sinθ=14CE=√28．【解析】本题考查线面平行的证明，考查线面角的正弦值的求法，考查空间中线线、能力，考查数形结合思想、化归与转化思想，属于中档题．（Ⅰ）取AD的中点F，连结EF，CF，推导出EF∥PA，CF∥AB，从而平面EFC∥平面ABP，由此能证明EC∥平面PAB．（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，推导出四边形BCDF为矩形，从而BF⊥AD，进而AD⊥平面PBF，由AD∥BC，得BC⊥PB，再求出BC⊥MF，由此能求出sinθ．11.【答案】证明：（Ⅰ）∵EA=EB，M是AB的中点，∴EM⊥AB，∵平面ABE⊥平面ABCD，平面ABE∩平面ABCD=AB，EM⊂平面ABE，∴EM⊥平面ABCD，∵AD⊂平面ABCD，∴EM⊥AD；（Ⅱ）取DE的中点F，连接AF，NF，∵N是CE的中点，∴NF=//12CD，∵M是AB的中点，∴AM=//12CD，∴NF=//AM，∴四边形AMNF是平行四边形，∴MN∥AF，∵MN⊄平面ADE，AF⊂平面ADE，∴MN∥平面ADE；解：（III）设点A到平面BCE的距离为d，由（I）知ME⊥平面ABC，BC=BE=2，MC=ME=√3，则CE=√6，BN=√BE2−EN2=√102，∴S△BCE=12CE⋅BN=√152，S△ABC=12BA×BC×sin60°=√3，∵V A-BCE=V E-ABC，即13S△BCE×d=13S△ABC×ME，解得d=2√155，故点A到平面BCE的距离为2√155．【解析】本题考查线线垂直、线面平行的证明，考查点到平面的距离的求法，涉及到力、数据处理能力，考查数形结合思想，是中档题．（Ⅰ）推导出EM ⊥AB ，从而EM ⊥平面ABCD ，由此能证明EM ⊥AD ；（Ⅱ）取DE 的中点F ，连接AF ，NF ，推导出四边形AMNF 是平行四边形，从而MN ∥AF ，由此能证明MN ∥平面ADE ；（III ）设点A 到平面BCE 的距离为d ，由V A -BCE =V E -ABC ，能求出点A 到平面BCE 的距离．12.【答案】（I ）证明：∵AB ∥CD ，AD ⊥DC ，AB =AD =1，CD =2，∴BD =BC =√2， ∴BD 2+BC 2=CD 2， ∴BD ⊥BC ，∵EA ⊥平面ABCD ，BD ⊂平面ABCD ， ∴EA ⊥BD ，∵EA ∥FC ， ∴FC ⊥BD ，又BC ⊂平面BCF ，FC ⊂平面BCF ，BC ∩CF =C ， ∴BD ⊥平面FBC ，又BD ⊂平面BDE ，∴平面BDE ⊥平面BCF ．（II ）解：过A 作AM ⊥DE ，垂足为M ， ∵EA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴EA ⊥CD ，又CD ⊥AD ，EA ∩AD =A ， ∴CD ⊥平面EAD ，又AM ⊂平面EAD ， ∴AM ⊥CD ，又AM ⊥DE ，DE ∩CD =D ， ∴AM ⊥平面CDE ，∵AD =AE =1，EA ⊥AD ，∴AM =√22，即A 到平面CDE 的距离为√22，∵AB ∥CD ，CD ⊂平面CDE ，AB ⊄平面CDE ， ∴AB ∥平面CDE ，∴B 到平面CDE 的距离为√22．【解析】（I ）先计算BD ，BC ，利用勾股定理的逆定理证明BD ⊥BC ，再利用EA ⊥平面ABCD 得出AE ⊥BD ，从而有CF ⊥BD ，故而推出BD ⊥平面FBC ，于是平面EBD ⊥平面BCF ；（II ）证明AB ∥平面CDE ，于是B 到平面CDE 的距离等于A 到平面CDE 的距离，过A 作AM ⊥DE ，证明AM ⊥平面CDE ，于是AM 的长即为B 到平面CDE 的距离．本题考查了线面垂直、面面垂直的判定与性质，空间距离的计算，属于中档题． 13.【答案】证明：方法一：（1）取PA 中点G ，连结DG 、FG ． ∵F 是PB 的中点， ∴GF ∥AB 且GF =12AB ，又底面ABCD 为矩形，E 是DC 中点， ∴DE ∥AB 且DE =12AB∴GF ∥DE 且GF =DE ，∴EF ∥DG∵DG ⊂平面PAD ，EF ⊄平面PAD ， ∴EF ∥平面PAD ．（2）∵PD ⊥底面ABCD ，AB ⊂面ABCD ∴PD ⊥AB又底面ABCD 为矩形 ∴AD ⊥AB 又PD ∩AD =D ∴AB ⊥平面PAD ∵DG ⊂平面PAD ∴AB ⊥DG∵AD =PD ，G 为AP 中点 ∴DG ⊥AP又AB ∩AP =A ， ∴DG ⊥平面PAB又由（1）知EF ∥DG ∴EF ⊥平面PAB ，又EF ⊂面AEF ∴平面AEF ⊥平面PAB ．证法二：（1）以D 为坐标原点，DA 、DC 、DP 所在直线分别为x 轴、y 轴、z 轴，建立如图所示空间直角坐标系．设AB =a ． ∵AD =PD =2，∴A （2，0，0），B （2，a ，0），C （0，a ，0），P （0，0，2）， ∵E 、F 分别为CD ，PB 的中点 ∴E （0，a2，0），F （1，a2，0）．∴EF ⃗⃗⃗⃗⃗ =(1，0，1)， ∵DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ =（0，0，2）+（2，0，0）=（2，0，2）， ∴EF ⃗⃗⃗⃗⃗ =12（DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ ）=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ，故EF ⃗⃗⃗⃗⃗ 、DP ⃗⃗⃗⃗⃗ 、DA ⃗⃗⃗⃗⃗ 共面，又EF ⊄平面PAD ∴EF ∥平面PAD ．（2）由（1）知EF ⃗⃗⃗⃗⃗ =(1，0，1)，AB ⃗⃗⃗⃗⃗ =(0，a ，0)，AP⃗⃗⃗⃗⃗ =(−2，0，2)． ∴EF ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =0，EF ⃗⃗⃗⃗⃗ •AP ⃗⃗⃗⃗⃗ =-2+0+2=0， ∴EF ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ，EF ⃗⃗⃗⃗⃗ ⊥AP ⃗⃗⃗⃗⃗ ，又AB ∩AP =A ，∴EF ⊥平面PAB ，又EF ⊂平面AEF ，∴平面AEF ⊥平面PAB ，（3）AB =2√2由（1）知，∴AE ⃗⃗⃗⃗⃗ =（-2，√2，0），EF⃗⃗⃗⃗⃗ =（1，0，1）设平面AEF 的法向量n ⃗ =(x ，y ，z)，则{n⃗ ⋅AE ⃗⃗⃗⃗⃗ =0n ⃗ ⋅EF ⃗⃗⃗⃗⃗ =0即−2x +√2y =0令x =1，则y =√2，z =-1， ∴n⃗ =（1，√2，-1），又AC⃗⃗⃗⃗⃗ =（-2，2√2，0）， ∴cos ＜AC⃗⃗⃗⃗⃗ ，n ⃗ ＞=−2+4+02√12=√36， ∴sinθ=|cos ＜AC⃗⃗⃗⃗⃗ ，n ⃗ ＞|=√36．【解析】方法一；（1）取PA 中点G ，连结DG 、FG ，要证明EF ∥平面PAD ，我们可以证明EF 与平面PAD 中的直线AD 平行，根据E 、F 分别是PB 、PC 的中点，利用中位线定理结合线面平行的判定定理，即可得到答案．（2）根据线面垂直的和面面垂直的判断定理即可证明．方法二：（1）求出直线EF 所在的向量，得到EF ⃗⃗⃗⃗⃗ =12（DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ ）=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ，即可证明EF ∥平面PAD ．（2）再求出平面内两条相交直线所在的向量，然后利用向量的数量积为0，根据线面垂直的判定定理得到线面垂直，即可证明平面AEF ⊥平面PAB（3）求出平面的法向量以及直线所在的向量，再利用向量的有关运算求出两个向量的夹角，进而转化为线面角，即可解决问题．本题考查了本题考查的知识点是直线与平面平行的判定，面面垂直，直线与平面所成的角，解决此类问题的关键是熟练掌握几何体的结构特征，进而得到空间中点、线、面的位置关系，利于建立空间之间坐标系，利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题，属于中档题．14.【答案】解：（1）证明：∵PO ⊥平面ABCD ，且AD ⊂平面ABCD ， ∴PO ⊥AD ， ∵∠ADC =45°且AD =AC =2， ∴∠ACD =45°， ∴∠DAC =90°， ∴AD ⊥AC ，∵AC ⊂平面PAC ，PO ⊂平面PAC ，且AC ∩PO =O ， ∴由直线和平面垂直的判定定理知AD ⊥平面PAC ．（2）解：取DO 中点N ，连接MN ，AN ，由PO ⊥平面ABCD ，得MN ⊥平面ABCD ， ∴∠MAN 是直线AM 与平面ABCD 所成的角， ∵M 为PD 的中点， ∴MN ∥PO ，且MN =12PO =3， AN =12DO =√52，在Rt △ANM 中，tan ∠MAN =MNAN =3√52=6√55，即直线AM 与平面ABCD 所成角的正切值为6√55．【解析】（1）由PO ⊥平面ABCD ，得PO ⊥AD ，由∠ADC =45°，AD =AC ，得AD ⊥AC ，从而证明AD ⊥平面PAC ．（2）取DO 中点N ，连接MN ，AN ，由M 为PD 的中点，知MN ∥PO ，由PO ⊥平面出直线AM 与平面ABCD 所成角的正切值．本题考查直线与平面垂直的证明，考查直线与平面所成角的正切值的求法．解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题． 15.【答案】证明：（I ）在三棱柱ABC -A 1B 1C 1中，连接A 1B ，交AB 1于O 点，连接OD∵在△A 1BC 1中，A 1D =DC 1，A 1O =OB ， ∴OD ∥BC 1，又∵OD ⊂平面AB 1D ，BC 1⊄平面AB 1D ； ∴BC 1∥平面AB 1D ；（II ）在三棱柱ABC -A 1B 1C 1中，A 1A ⊥平面A 1B 1C 1； ∵B 1D ⊂平面A 1B 1C 1； ∴A 1A ⊥B 1D在△A 1B 1C 1中，D 为A 1C 1的中点 ∴B 1D ⊥A 1C 1又∵A 1A ∩A 1C 1=A 1，A 1A ，A 1C 1⊂平面AA 1C 1C ， ∴B 1D ⊥平面AA 1C 1C ，又∵A 1C ⊂平面AA 1C 1C ， ∴B 1D ⊥A 1C又∵A 1D AA 1=AA1AC =√22∴∠DA 1A =∠A 1AC =90°∴△DA 1A ∽△A 1AC ，∠ADA 1=∠CA 1A∵∠DA 1C +∠CA 1A =90° ∴∠DA 1C +∠ADA 1=90°∴A 1C ⊥AD又∵B 1D ∩AD =D ，B 1D ，AD ⊂平面AB 1D ； ∴A 1C ⊥平面AB 1D ；解：（III ）由（I ）得，OD ∥BC 1，故AD 与BC 1所成的角即为∠ADO在△ADO 中，AD =√3，OD =12BC 1=√62，AO =12A 1B =√62，∵AD 2=OD 2+AO 2，OD =AO∴△ADO 为等腰直角三角形故∠ADO =45°即异面直线AD 与BC 1所成角等于45°【解析】（I ）连接A 1B ，交AB 1于O 点，连接OD ，由平行四边形性质及三角形中位线定理可得OD ∥BC 1，进而由线面平行的判定定理得到BC 1∥平面AB 1D ；（II ）由直棱柱的几何特征可得A 1A ⊥B 1D ，由等边三角形三线合一可得B 1D ⊥A 1C 1，进而由线面垂直的判定定理得到B 1D ⊥平面AA 1C 1C ，再由三角形相似得到A 1C ⊥AD 后，可证得A 1C ⊥平面AB 1D ．（III ）由（I ）中OD ∥BC 1，可得异面直线AD 与BC 1所成角即∠ADO ，解△ADO 可得答案．本题考查的知识点是直线与平面垂直的判定，异面直线及其所成的角，直线与平面平行的判定，（I ）的关键是证得OD ∥BC 1，（II ）的关键是熟练掌握线面垂直与线线垂直之间的转化，（III ）的关键是得到异面直线AD 与BC 1所成角即∠ADO ．16.【答案】（Ⅰ）证明：由P -ABD ，Q -BCD 是相同正三棱锥，且∠APB =90°，分别过P 、Q 作PE ⊥平面ABD ，QF ⊥平面BCD ，垂足分别为E 、F ，则E 、F 分别为底面正三角形ABD 与BCD 的中心．连接EF 交BD 于G ，则G 为BD 的中点，连接PG 、QG ，则PG ⊥BD ，QG ⊥BD ，又PG ∩QG =G ，∴BD ⊥平面PQG ，则BD ⊥PQ ，再由正三棱锥的性质可得PA ⊥BD ，又PQ ∩PA =P ，∴BD ⊥平面APQ ；（Ⅱ）∵正三棱锥的底面边长为1，且∠APB =90°，∴PQ =EF =2EG =2×13AG =2×13×√32=√33， PE =√(√22)2−(√33)2=√66，则V B−PQD =13×12×√33×√66×1=√236．△PDQ 底边PQ 上的高为√(√22)2−(√36)2=√156，∴S △PDQ =12×√33×√156=√512．设B 到平面PQD 的距离为h ，则13×√512ℎ=√236，得h =√105．∴直线PB 与平面PDQ 所成角的正弦值为√105√22=2√55．【解析】（Ⅰ）由题意分别过P 、Q 作PE ⊥平面ABD ，QF ⊥平面BCD ，可得E 、F 分别为底面正三角形ABD 与BCD 的中心．连接EF 交BD 于G ，可得PG ⊥BD ，QG ⊥BD ，由线面垂直的判定及性质可得BD ⊥PQ ，再由正三棱锥的性质可得PA ⊥BD ，则BD ⊥平面APQ ；（Ⅱ）由已知求得PQ ，PE 的长，求得四面体B -PQD 的体积，利用等积法求出B 到平面PQD 的距离，则直线PB 与平面PDQ 所成角的正弦值可求．本题考查直线与平面所成的角，考查线面垂直的判定，考查空间想象能力和思维能力，训练了利用等积法求多面体的体积，是中档题． 17.【答案】（1）证明：如图：∵AB =BC ，E 为AC 的中点，∴BE ⊥AC ，∵平面A 1ACC 1⊥平面ABC ，平面A 1ACC 1∩平面ABC =AC ， ∴BE ⊥平面A 1ACC 1，∵A 1C ⊂平面A 1ACC 1，∴BE ⊥A 1C ．（2）解：∵面A1ACC1⊥面ABC，∴C1在面ABC上的射影H在AC上，∴∠C1CA为直线C1C与面ABC所成的角．过H作HM⊥BC于M，连C1M，在Rt△C1CM中，CM=CC1cos∠C1CM=2cos60°=1．在Rt△CMH中，CH=CMcos∠ACB =2√33．∴在Rt△C1CH中，cos∠C1CH=CHCC1=23√32=√33．∴直线C1C与面ABC所成的角的余弦值为√33.【解析】（1）证明BE⊥平面A1ACC1，可得BE⊥A1C，即可证明：A1C⊥平面C1EB；（2）判断∠C1CA为直线C1C与面ABC所成的角．过H作HM⊥BC于M，连C1M，即可求直线CC1与平面ABC所成角的余弦值．本题考查线面垂直的判定与性质，考查线面角，考查学生分析解决问题的能力，属于中档题．18.【答案】证明：（1）连接CD，据题知AD=4，BD=2，∵AC2+BC2=AB2，∴∠ACB=90°，∴cos∠ABC=2√36=√33，∴CD2=4+12−2×2×2√3cos∠ABC=8，∴CD=2√2，∴CD2+AD2=AC2，∴CD⊥AB，又∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，CD⊂平面ABC,∴CD⊥平面PAB，∵PD⊂平面PAB，∴CD⊥PD，∵PD⊥AC，CD∩AC=C，CD、AC⊂平面ABC,∴PD⊥平面ABC．解：（2）∵∠PAB=π4，∴PD=AD=4，∴PA=4√2，在Rt△PCD中，PC=√PD2+CD2=2√6，∴△PAC是等腰三角形，∴S△PAC=8√2，设点B到平面PAC的距离为d，由V B-PAC=V P-ABC，得13S△PAC×d=13S△ABC×PD，∴d==3，故点B到平面PAC的距离为3．【解析】本题考查线面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．（1）连接CD，推导出CD⊥AB，CD⊥PD，由此能证明PD⊥平面ABC．（2）设点B到平面PAC的距离为d，由V B-PAC=V P-ABC，能求出点B到平面PAC的距离．19.【答案】解：（1）证明：∵ABC-A1B1C1中，A1A⊥平面ABC，又BB 1⊂平面BB 1C 1C ， ∴平面BB 1C 1C ⊥平面ABC ，∵△ABC 为正三角形，D 为BC 的中点， ∴AD ⊥BC ，又平面BB 1C 1C ∩平面ABC =BC ， ∴AD ⊥平面BB 1C 1C ，又AD ⊂平面ADB 1，∴平面ADB 1⊥平面BB 1C 1C ；（2）由（1）可得△ADB 1为直角三角形，又AD =√32，B 1D =√52，∴S △ADB 1=12×AD ×B 1D =√158，又S △ADB =12S △ABC =√38，设点B 到平面ADB 1的距离为d ，则V B−ADB 1=V B 1−ADB ， ∴13S △ADB 1⋅d =13S △ADB ⋅BB 1， ∴点B 到平面ADB 1的距离d =S △ADB ⋅BB 1S △ADB 1=√3√15=√55．【解析】本题考查面面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题.（1）推导出BB 1⊥平面ABC ，从而平面BB 1C 1C ⊥平面ABC ，推导出AD ⊥BC ，从而AD ⊥平面BB 1C 1C ，由此能证明平面ADB 1⊥平面BB 1C 1C ；（2）设点B 到平面ADB 1的距离为d ，由V B−ADB 1=V B 1−ADB ，能求出点B 到平面ADB 1的距离.20.【答案】证明：（1）∵PA ⊥平面ABC ，BE ⊂平面ABC ， ∴PA ⊥BE ．∵AB =BC ，E 为AC 的中点， ∴BE ⊥AC ，又PA ⊂平面PAC ，AC ⊂平面PAC ，PA ∩AC =A ， ∴BE ⊥平面PAC ，又BE ⊂平面BED ， ∴平面BED ⊥平面PAC ．（2）∵D ，E 是PC ，AC 的中点， ∴DE ∥PA ，又PA ⊥平面ABC ，∴DE ⊥平面ABC ，∵EF ⊂平面ABC ，BE ⊂平面ABC ， ∴DE ⊥EF ，DE ⊥BE ．∴∠FEB 为二面角F -DE -B 的平面角．∵E ，F 分别是AC ，AB 的中点，AB =AC ， ∴EF =12BC =12AB =BF ，EF ∥BC ．又AB ⊥BC ，∴BF ⊥EF ，∴△BEF 为等腰直角三角形，∴∠FEB =45°． ∴二面角F -DE -B 为45°．∴PA⊥BC，又BC⊥AB，PA⊂平面PAB，AB⊂平面PAB，PA∩AB=A，∴BC⊥平面PAB．∴∠CPB为直线PC与平面PAB所成的角．∵PA=6，∴DE=12PA=3，又DF=5，∴EF=√DF2−DE2=4．∴AB=BC=8．∴PB=√PA2+AB2=10．∴tan∠CPB=BCPB =4 5．【解析】（1）通过证明BE⊥平面PAC得出平面BED⊥平面PAC；（2）由DE∥PA得出DE⊥平面ABC，故DE⊥EF，DE⊥BE，于是∠FEB为所求二面角的平面角，根据△BEF为等腰直角三角形得出二面角的度数；（3）证明BC⊥平面PAB得出∠CPB为所求角，利用勾股定理得出BC，PB，即可得出tan∠CPB．本题考查了线面垂直，面面垂直的判定，空间角的计算，做出空间角是解题关键，属于中档题．21.【答案】解：（1）证明：设AC∩BD=H，连接EH，在△ADC中，因为AD=CD，且DB平分∠ADC，所以H为AC的中点，又有题设，E为PC的中点，故EH∥PA，又HE⊂平面BDE，PA⊄平面BDE，所以PA∥平面BDE（2）证明：因为PD⊥平面ABCD，AC⊂平面ABCD，所以PD⊥AC由（1）知，BD⊥AC，PD∩BD=D，故AC⊥平面PBD（3）由AC⊥平面PBD可知，BH为BC在平面PBD内的射影，所以∠CBH为直线与平面PBD所成的角．由AD⊥CD，AD=CD=1，DB=2√2，可得DH=CH=√22，BH=3√22在Rt△BHC中，tan∠CBH=CHBH =13，所以直线BC与平面PBD所成的角的正切值为13．【解析】（1）欲证PA∥平面BDE，根据直线与平面平行的判定定理可知只需证PA与平面BDE内一直线平行，设AC∩BD=H，连接EH，根据中位线定理可知EH∥PA，而又HE⊂平面BDE，PA⊄平面BDE，满足定理所需条件；（2）欲证AC⊥平面PBD，根据直线与平面垂直的判定定理可知只需证AC与平面PBD内两相交直线垂直，而PD⊥AC，BD⊥AC，PD∩BD=D，满足定理所需条件；（3）由AC⊥平面PBD可知，BH为BC在平面PBD内的射影，则∠CBH为直线与平面PBD所成的角，在Rt△BHC中，求出此角即可．本小题主要考查直线与平面平行．直线和平面垂直．直线和平面所成的角等基础知识，考查空间想象能力、运算能力和推理能力．。

高一立体几何平行垂直证明基础练习

高一立体几何平行垂直证明基础练习高一垂直证明基础练习专项1、点线面位置关系判定问题解题方法与技巧：在判定点线面的位置关系时，通常有两个切入点（1）集合：点、线点、面的位置关系从集合的从属关系来判定；线、面都是点集，所以在考虑线面关系时从集合与集合的包含关系或者集合与集合的交、并、补关系来判定；（2）几何：把集合与几何关系结合来判定线线，线面，面面关系例1、设是三个不重合的平面，l是直线，给出下列命题①若，则；②若l上两点到的距离相等，则；③若④若其中正确的命题是（）A．①②B．②③C．②④D．③④解析：①由面面垂直关系已知不成立，可能垂直也可能相交平行。

错误；②由点到面距离易知直线还可能和平面相交；③因为所以在平面β内一定有一直线垂直α所以正确④根据平行关系易知正确答案选D练习1、设，是两条不同的直线，是一个平面，则下列命题正确的是（）（A）若，，则（B）若，，则（C）若，，则（D）若，，则练习2、给定下列四个命题：（）①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；.④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中，为真命题的是A．①和②B．②和③C．③和④D．②和④练习3.（2009浙江卷文）设是两个不同的平面，是一条直线，以下命题正确的是（）A．若，则B．若，则C．若，则D．若，则练习4．顺次连接空间四边形各边中点所成的四边形必定是（）A、平行四边形B、菱形C、正方形D、梯形练习题答案：练习1：B；练习2：D；练习3：C；练习4：A；2、空间中线面的平行垂直证明例1：如图：四棱锥—中，底面是平行四边形，为侧棱的中点，证明：∥平面解析：证明PC平行于面EBD，只需在面EBD内找一条直线和已知直线平行即可E为中点，首先考虑构造等腰三角形中位线，取AC中点O连接EO即可证明：取AC的中点O,连接EO，例2：三棱柱—中，为的中点，为的中点，为的中点，证明：平面∥平面解析：面面平行的证明定理，证明两平面内两组相交直线平行，即把面面平行问题转化为线线平行问题，按解决线线平行的思路即可解决问题证明：连接BC1,EF分别为BC、B1C1、BB1、CC1的中点，例3：如图：四棱锥—中，⊥平面，底面是矩形，，为的中点，⊥，证明：⊥解析：线线垂直的证明分同平面直线垂直证明和异平面垂直证明，在处理异平面垂直证明问题时，优先考虑证明一直线垂直于另一直线所在平面，转化为线面垂直证明问题即证明PD垂直于面BEF即可证明：点例4：如图：四棱锥—中，⊥平面，底面是矩形，证明：平面⊥平面练习1：如图：四棱锥—中，底面是平行四边形，为侧棱的中点，证明：∥平面练习2：如图：三棱柱—中，为的中点，证明：∥平面练习3：如图：三棱柱—中，为的中点，证明：∥平面练习4：如图：四棱锥—中，底面是平行四边形，、分别为、的中点，证明：∥平面练习5：如图：三棱柱—中，、分别为、的中点，证明：∥平面练习6：如图：四棱锥—中，底面是平行四边形，、分别为、的中点，证明：∥平面练习7：如图：三棱柱—中，为的中点，为的中点，证明：∥平面练习8：如图：四棱锥—中，⊥平面，底面是梯形，∥，，，，为的中点，证明：⊥练习9：如图：直三棱柱—中，，，、分别为、的中点，为的中点，证明：⊥练习10：如图：四棱锥—中，⊥平面，⊥，，，⊥，⊥，为的中点，证明：⊥练习11：如图：四棱锥—中，底面是矩形，平面⊥平面，证明：平面⊥平面练习12：如图：五面体中，是正方形，⊥平面，∥，，证明：平面⊥平面练习13：如图：四棱锥—中，⊥平面，是菱形，，为的中点，证明：平面⊥平面练习14：如图：四棱锥—中，平面⊥平面，，，证明：平面⊥平面。

立体几何解答题训练(平行)

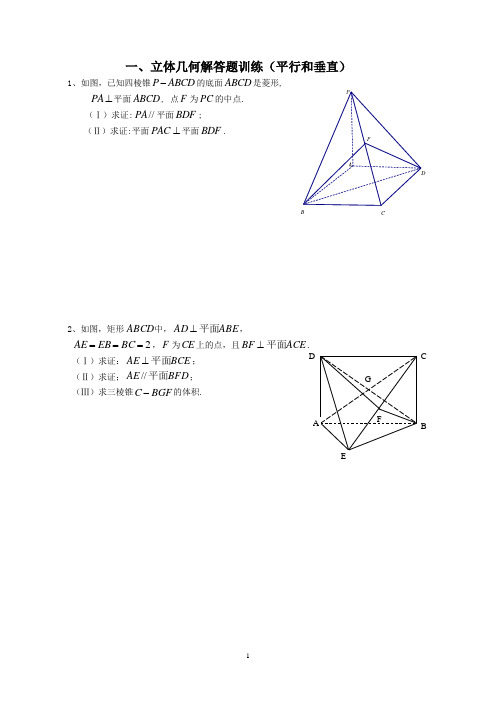
一、立体几何解答题训练（平行和垂直）1、如图，已知四棱锥P ABCD -的底面ABCD 是菱形,PA ⊥平面ABCD , 点F 为PC 的中点. （Ⅰ）求证://PA 平面BDF ; （Ⅱ）求证:平面PAC ⊥平面BDF .2、如图，矩形ABCD 中，ABE AD 平面⊥，2===BC EB AE ，F 为CE 上的点，且ACE BF 平面⊥（Ⅰ）求证：BCE AE 平面⊥；（Ⅱ）求证；BFD AE 平面//；（Ⅲ）求三棱锥BGF C -的体积.AFPDCBBC3、如图所示，四棱锥P-ABCD 底面是直角梯形，,,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD ，E 为PC 的中点。

PA ＝AD ＝AB ＝1。

（1）证明：PAD EB 平面；（2）证明：BE PDC ⊥平面；（3）求三棱锥B-PDC 的体积V 。

4．如图，已知棱柱1111D C B A ABCD -的底面是菱形，且⊥1AA 面ABCD ，60=∠DAB ，1AA AD =，F 为棱1AA 的中点，M 为线段1BD 的中点，（1）求证：//MF 面ABCD ；（2）求证：⊥MF 面11B BDD ；AB CDA 1B 1C 1D 1FM5、如图3所示，在直三棱柱111ABC A B C -中，90ACB ∠=，2AB =， 1BC =，1AA =（Ⅰ）证明：1AC ⊥平面11AB C ；（Ⅱ）若D 是棱1CC 的中点，在棱AB 上是否存在一点E ，使DE 平面11AB C ？证明你的结论．6、如图，四棱锥P －ABCD 的底面为矩形，侧面P AD 是正三角形，且侧面P AD ⊥底面ABCD ， E 是侧棱PD 上一点，且PB ∥平面EAC .（1）求证：E 是PD 的中点；（2）求证：AE ⊥平面PCD .E A BC D PA BCPD7、如图所示，在棱长为2的正方体1111ABCD A B C D -中，E 、F 分别为1DD 、DB 的中点．（Ⅰ）求证：EF //平面11ABC D ；（Ⅱ）求证：1EF B C ⊥；（Ⅲ）求三棱锥EFC B V -1的体积．8.如图4，在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，AB DC ∥，PAD △是等边三角形，已知24BD AD ==，2AB DC == （1）求证：BD ⊥平面PAD ；（2）求三棱锥A PCD -的体积．CDBFE D 1C 1B 1A A 1DC 1A 1B 1CBA9. 如图5,在三棱柱111-ABC A B C 中，侧棱1AA ⊥底面ABC ,,⊥AB BC D 为AC 的中点, 12A A AB ==,3BC =. （1）求证：1//AB 平面1BC D ； (2) 求四棱锥11-B AAC D 的体积.10．如图，已知三棱锥A —BPC 中，AP ⊥PC ， AC ⊥BC ，M 为AB 中点，D 为PB 中点，且△PMB 为正三角形。

高中数学高考总复习立体几何各种平行与垂直的判断习题及详解

高中数学高考总复习立体几何各种平行与垂直的判断习题及详解一、选择题1．设b 、c 表示两条不重合的直线，α、β表示两个不同的平面，则下列命题是真命题的是( )A.⎭⎪⎬⎪⎫b ⊂αc ∥α⇒b ∥c B.⎭⎪⎬⎪⎫b ⊂αb ∥c ⇒c ∥α C.⎭⎪⎬⎪⎫c ∥αc ⊥β⇒α⊥βD.⎭⎪⎬⎪⎫c ∥αα⊥β⇒c ⊥β [答案] C[解析] 选项A 中的条件不能确定b ∥c ；选项B 中条件的描述也包含着直线c 在平面α内，故不正确；选项D 中的条件也包含着c ⊂β，c 与β斜交或c ∥β，故不正确．[点评] 线线、线面、面面平行或垂直的性质定理和判定定理是解决空间图形位置关系推理的重要依据，在推理中容易把平面几何中的一些结论引用到立体几何中造成错误．对空间中位置关系的考虑不周，也是造成判断错误的因素，所以做这类题目应当考虑全面．2．定点A 和B 都在平面α内，定点P ∉α，PB ⊥α，C 是α内异于A 和B 的动点，且PC ⊥AC .那么，动点C 在平面α内的轨迹是( )A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点 [答案] B[解析] 连接BC ，∵PB ⊥α，∴AC ⊥PB . 又∵PC ⊥AC ，∴AC ⊥BC .∴C 在以AB 为直径的圆上．故选B. 3．设α、β、γ为平面，给出下列条件： ①a 、b 为异面直线，a ⊂α，b ⊂β，a ∥β，b ∥α； ②α内不共线的三点到β的距离相等； ③α⊥γ，β⊥γ.其中能使α∥β成立的条件的个数是( ) A ．0 B ．1 C ．2D ．3[答案] B[解析]对于②，三个点不一定在同侧；对于③，面面的垂直关系不具有传递性．对于①，过b作平面γ∩α＝b′，则b∥b′，∵a与b异面，∴a与b′相交，容易证明b′∥β，又∵a∥β，∴α∥β，故只有①正确．4．a、b、c是三条直线，α、β是两个平面，b⊂α，c⊄α，则下列命题不成立的是() A．若α∥β，c⊥α，则c⊥βB．“若b⊥β，则α⊥β”的逆命题C．若a是c在α内的射影，b⊥a，则b⊥cD．“若b∥c，则c∥α”的逆否命题[答案] B[解析]一条直线垂直于两个平行平面中的一个，则垂直于另一个，故A正确；若c∥α，∵a是c在α内的射影，∴c∥a，∵b⊥a，∴b⊥c；若c与α相交，则c与a相交，由线面垂直的性质与判定定理知，若b⊥a，则b⊥c，故C正确；∵b⊂α，c⊄α，b∥c，∴c∥α，因此原命题“若b∥c，则c∥α”为真，从而其逆否命题也为真，故D正确．如图，α⊥β，α∩β＝l，b⊂α，b与l不垂直，则b与β不垂直，∴B不成立．5．(文)(2010·天津河东区)已知直线a⊂平面α，直线AO⊥α，垂足为O，P A∩α＝P，若条件p：直线OP不垂直于直线a，条件q：直线AP不垂直于直线a，则条件p是条件q的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件[答案] C故OP⊥a⇔AP⊥a，从而p⇔q.(理)(2010·河南新乡调研)设α、β、γ为平面，l、m、n为直线，则m⊥β的一个充分条件为()A．α⊥β，α∩β＝l，m⊥lB．n⊥α，n⊥β，m⊥αC．α∩γ＝m，α⊥γ，β⊥γD．α⊥γ，β⊥γ，m⊥α[答案] B[解析]如图①知A错；如图②知C错；如图③在正方体中，两侧面α与β相交于l，都与底面γ垂直，γ内的直线m⊥α，但m与β不垂直，故D错．6．如图，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB 沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下列命题正确的是()A．平面ABD⊥平面ABCB．平面ADC⊥平面BDCC．平面ABC⊥平面BDCD．平面ADC⊥平面ABC[答案] D[解析]∵在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，∴BD ⊥CD.又平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，故CD⊥平面ABD，则CD⊥AB.又AD⊥AB，故AB⊥平面ADC.∴平面ABC⊥平面ADC.7．(文)(2010·重庆文)到两互相垂直的异面直线的距离相等的点()A．只有1个B．恰有3个C ．恰有4个D ．有无穷多个[答案] D[解析] 过两条互相垂直的异面直线的公垂线段中点且与两条直线都成45°角的直线上所有点到两条直线的距离都相等，故选D.(理)(2010·全国Ⅱ理)与正方体ABCD －A 1B 1C 1D 1的三条棱AB 、CC 1、A 1D 1所在直线的距离相等的点( )A ．有且只有1个B ．有且只有2个C ．有且只有3个D ．有无数个[答案] D[解析] 如图连结B 1D ，可知B 1D 上的点到AB 、CC 1、A 1D 1的距离均相等，故选D.8．(文)平行四边形ABCD 的对角线交点为O ，点P 在平面ABCD 之外，且P A ＝PC ，PD ＝PB ，则PO 与平面ABCD 的关系是( )A ．斜交B ．平行C ．垂直D ．无法确定[答案] C[解析] ∵P A ＝PC ，∴PO ⊥AC ，∵PB ＝PD ，∴PO ⊥BD ，∵AC ∩BD ＝O ，∴PO ⊥平面ABCD .(理)棱长都为2的直平行六面体(底面为平行四边形的棱柱)ABCD －A 1B 1C 1D 1中，∠BAD ＝60°，则对角线A 1C 与侧面DCC 1D 1所成角的正弦值为( )A.12B.22C.34D.38 [答案] C[解析] 如图所示，过点A 1作直线A 1M ⊥D 1C 1，交D 1C 1延长线于点M ，连结MC ，A 1C ，则可得A 1M ⊥面DD 1C 1C ，∠A 1CM 就是直线A 1C 与面DD 1C 1C 所成的角．∵所有棱长均为2，∠A 1D 1C 1＝120°，∴A 1M ＝A 1D 1sin60°＝3，又A 1C ＝AC 12＋CC 12＝(23)2＋22＝4， ∴sin ∠A 1CM ＝A 1M A 1C ＝34，故应选C.[点评] 求直线与平面所成角时，一般要先观察分析是否可以找(或作)出直线上一点到平面的垂线，若能找出则可以将线面角归结到一个直角三角形中求解．若不容易找出线面角，则可以考虑能否进行转化或借助于空间向量求解，请再练习下题：(2010·全国Ⅰ文)正方体ABCD －A 1B 1C 1D 1中BB 1与平面ACD 1所成角的余弦值为( ) A.23B.33C.23D.63[答案] D[解析] 解法1：设BD 与AC 交于点O ，连结D 1O ，∵BB 1∥DD 1，∴DD 1与平面ACD 1所成的角就是BB 1与平面ACD 1成的角．∵AC ⊥BD ，AC ⊥DD 1，DD 1∩BD ＝D ，∴AC ⊥平面DD 1B ，平面DD 1B ∩平面ACD 1＝OD 1，∴OD 1是DD 1在平面ACD 1内的射影，故∠DD 1O 为直线DD 1与平面ACD 1所成的角，设正方体的棱长为1，则DD 1＝1，DO ＝22，D 1O ＝62，∴cos ∠DD 1O ＝DD 1D 1O ＝63，∴BB 1与平面ACD 1所成角的余弦值为63. 解法2：因为BB 1∥DD 1，所以BB 1与平面ACD 1所成角和DD 1与平面ACD 1所成角相等，设DO ⊥平面ACD 1，由等体积法得VD －ACD 1＝VD 1－ACD ，即13S △ACD 1·DO ＝13S △ACD ·DD 1.设DD 1＝a ，则S △ACD 1＝12AC ·AD 1sin60°＝12×(2a )2×32＝32a 2，S △ACD ＝12AD ·CD ＝12a 2.所以DO ＝S △ACD ·DD 1S △ACD 1＝a 33a 2＝33a ，设DD 1与平面ACD 1所成角为θ，则sin θ＝DO DD 1＝33，所以cos θ＝63.解法3：建立如图所示空间直角坐标系D －xyz ，设边长为1，BB 1→＝(0,0,1)，平面ACD 1的一个法向量n ＝(1,1,1)，∴cos 〈BB 1→，n 〉＝13·1＝33，∴BB 1与面ACD 1所成角的余弦值为63. 9．(文)(2010·鞍山一中模拟)已知直线l ⊥平面α，直线m ⊂平面β，给出下列命题： ①α∥β⇒l ⊥m ；②α⊥β⇒l ∥m ；③l ∥m ⇒α⊥β；④l ⊥m ⇒α⊥β，其中正确的是( ) A ．①②③ B ．②③④ C ．②④ D ．①③ [答案] D∵m ⊂β，∴此时推不出l ∥m ，故②错，排除A ，故选D. (理)若平面α与平面β相交，直线m ⊥α，则( ) A ．β内必存在直线与m 平行，且存在直线与m 垂直 B ．β内不一定存在直线与m 平行，不一定存在直线与m 垂直 C ．β内不一定存在直线与m 平行，但必存在直线与m 垂直 D ．β内必存在直线与m 平行，不一定存在直线与m 垂直 [答案] C[解析] 若β内存在直线与m 平行，则必有β⊥α，但α与β不一定垂直，故否定A 、D ；在β内必存在与m 在β内射影垂直的直线，从而此线必与m 垂直，否定B ，故选C.10．(文)(2010·芜湖十二中)已知两条不同的直线m 、n ，两个不同的平面α、β，则下列命题中的真命题是( )A ．若m ⊥α，n ⊥β，α⊥β，则m ⊥nB ．若m ∥α，n ∥β，α∥β，则m ∥nC ．若m ⊥α，n ∥β，α⊥β，则m ⊥nD ．若m ∥α，n ⊥β，α⊥β，则m ∥n[答案] A[解析]如图(1)，m⊥α，n⊥α满足n∥β，但m∥n，故C错；如图(2)知B错；如图(3)正方体中，m∥α，n⊥β，α⊥β，知D错．(理)(2010·浙江金华十校模考)设a，b为两条直线，α，β为两个平面，下列四个命题中真命题是()A．若a，b与α所成角相等，则a∥bB．若a∥α，b∥β，α⊥β，则a⊥bC．若a⊂α，b⊂β，a⊥b，则α⊥βD．若a⊥α，b⊥β，α⊥β，则a⊥b[答案] D[解析]正四棱锥P－ABCD中，P A、PC与底面ABCD所成角相等，但P A与PC相交，∴A错；如图(1)正方体中，a∥b∥c，满足a∥α，b∥β，α⊥β，故B错；图(2)正方体中，上、下底面为β、α，a、b为棱，满足a⊂α，b⊂β，a⊥b，但α∥β，故C错；二、填空题11．对于四面体ABCD，给出下列四个命题：①若AB＝AC，BD＝CD，则BC⊥AD；②若AB＝CD，AC＝BD，则BC⊥AD；③若AB ⊥AC ，BD ⊥CD ，则BC ⊥AD ； ④若AB ⊥CD ，AC ⊥BD ，则BC ⊥AD .其中真命题的序号是________．(把你认为正确命题的序号都填上) [答案] ①④[解析] 本题考查四面体的性质，取BC 的中点E ，则BC ⊥AE ，BC ⊥DE ，∴BC ⊥面ADE ，∴BC ⊥AD ，故①正确．设O 为A 在面BCD 上的射影，依题意OB ⊥CD ，OC ⊥BD ，∴O 为垂心，∴OD ⊥BC ，∴BC ⊥AD ，故④正确，②③易排除，故答案为①④.12．(文)P 为△ABC 所在平面外一点，P A 、PB 、PC 与平面ABC 所成角均相等，又P A 与BC 垂直，那么△ABC 形状可以是________．①正三角形 ②等腰三角形 ③非等腰三角形 ④等腰直角三角形(将你认为正确的序号全填上) [答案] ①②④[解析] 设点P 在底面ABC 上的射影为O ，由P A 、PB 、PC 与平面ABC 所成角均相等，得OA ＝OB ＝OC ，即点O 为△ABC 的外心，又由P A ⊥BC ，得OA ⊥BC ，即AO 为△ABC 中BC 边上的高线，∴AB ＝AC ，即△ABC 必为等腰三角形，故应填①②④.(理)如图将边长为1的正方形纸板ABCD 沿对角线AC 折起，使平面ACB ⊥平面ACD ，然后放在桌面上，使点B 、C 、D 落在桌面，这时点A 到桌面的距离为________．[答案]63[解析] 取AC 中点O ，∵OB ⊥AC ，OD ⊥AC ，OB ∩OD ＝O ，∴AC ⊥平面BOD ，∴∠BOD ＝90°.又∵BO ＝OD ＝22，∴BD ＝1，S △BOD ＝14， ∴V A －BCD ＝13S △BOD ·AC ＝212，设A 到桌面距离为h ，V A －BCD ＝13S △BCD ·h ＝13×34×h ＝212，∴h ＝63，即A 到桌面距离为63. 13．(2010·安徽淮北一中)已知四棱锥P －ABCD 的底面ABCD 是矩形，P A ⊥底面ABCD ，点E 、F 分别是棱PC 、PD 的中点，则①棱AB 与PD 所在的直线垂直； ②平面PBC 与平面ABCD 垂直； ③△PCD 的面积大于△P AB 的面积；④直线AE与直线BF是异面直线．以上结论正确的是________．(写出所有正确结论的编号)[答案]①③[解析]由条件可得AB⊥平面P AD，所以AB⊥PD，故①正确；∵P A⊥平面ABCD，∴平面P AB、平面P AD都与平面ABCD垂直，故平面PBC不可能与平面ABCD垂直，②错；S△PCD＝12CD·PD，S△P AB＝12AB·P A，由AB＝CD，PD>P A知③正确；由E、F分别是棱PC、PD的中点可得EF∥CD，又AB∥CD，所以EF∥AB，故AE与BF共面，故④错．14．(文)(2010·河北唐山)如图，在直四棱柱ABCD－A1B1C1D1中，∠ADC＝90°，且AA1＝AD＝DC＝2，M∈平面ABCD，当D1M⊥平面A1C1D时，DM＝________.[答案]2 2[解析]∵DA＝DC＝DD1且DA、DC、DD1两两垂直，故当点M使四边形ADCM为正方形时，D1M⊥平面A1C1D，∴DM＝2 2.(理)(2010·安徽巢湖市质检)已知正方体ABCD－A1B1C1D1的棱长为1，E，F，G分别是AB，BC，B1C1的中点．下列命题正确的是________(写出所有正确命题的编号)．①以正方体的顶点为顶点的三棱锥的四个面最多只有三个面是直角三角形；②P在直线FG上运动时，AP⊥DE；③Q在直线BC1上运动时，三棱锥A－D1QC的体积不变；④M是正方体的面A1B1C1D1内到点D和C1距离相等的点，则M点的轨迹是一条线段．[答案]②③④[解析]三棱锥A1－ABC的四个面都是Rt△，故①错；F在FG上运动时，PF⊥平面ABCD，∴PF⊥DE，又在正方体ABCD中，E、F为AB、BC中点，∴AF⊥DE，∴DE⊥平面P AF，∴DE⊥P A，故②真；VA－D1QC＝VQ－AD1C，∵BC1∥AD1，∴BC1∥平面AD1C，∴无论点Q在BC1上怎样运动，Q到平面AD1C距离都相等，故③真；到点D和C1距离相等的点在经过线段C1D的中点与DC1垂直的平面α上，故点M为平面α与正方体的面A1B1C1D1相交线段上的点，这条线段即A1D1.三、解答题15．(文)(2010·江苏，16)如图，四棱锥P －ABCD 中，PD ⊥平面ABCD ，PD ＝DC ＝BC ＝1，AB ＝2，AB ∥DC ，∠BCD ＝90°(1)求证：PC ⊥BC(2)求点A 到平面PBC 的距离．[解析] (1)∵PD ⊥平面ABCD ，BC ⊂平面ABCD ，∴PD ⊥BC . 由∠BCD ＝90°知，BC ⊥DC ， ∵PD ∩DC ＝D ，∴BC ⊥平面PDC ， ∴BC ⊥PC .(2)设点A 到平面PBC 的距离为h ， ∵AB ∥DC ，∠BCD ＝90°，∴∠ABC ＝90°， ∵AB ＝2，BC ＝1，∴S △ABC ＝12AB ·BC ＝1，∵PD ⊥平面ABCD ，PD ＝1， ∴V P －ABC ＝13S △ABC ·PD ＝13，∵PD ⊥平面ABCD ，∴PD ⊥DC ， ∵PD ＝DC ＝1，∴PC ＝2， ∵PC ⊥BC ，BC ＝1， ∴S △PBC ＝12PC ·BC ＝22，∵V A －PBC ＝V P －ABC ， ∴13S △PBC ·h ＝13，∴h ＝2， ∴点A 到平面PBC 的距离为 2.(理)如图，已知三棱锥A －BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 的中点，D 为PB 中点，且△PMB 为正三角形．(1)求证：DM ∥平面APC ； (2)求证：平面ABC ⊥平面APC ；(3)若BC ＝4，AB ＝20，求三棱锥D －BCM 的体积．[解析] (1)∵M 为AB 中点，D 为PB 中点，∴DM ∥AP ，又DM ⊄平面APC ，AP ⊂平面APC .∴DM ∥平面APC .(2)∵△PMB 为正三角形，且D 为PB 中点，∴MD ⊥PB ，又由(1)知MD ∥AP ，∴AP ⊥PB又已知AP ⊥PC ，∴AP ⊥平面PBC ，∴AP ⊥BC ，又∵AC ⊥BC∴BC ⊥平面APC∴平面ABC ⊥平面APC .(3)∵AB ＝20，∴MP ＝10，∴PB ＝10又BC ＝4，PC ＝100－16＝221∴S △BDC ＝12S △PBC ＝14PC ·BC ＝14×4×221 ＝221又MD ＝12AP ＝12202－102＝5 3 ∴V D －BCM ＝V M －BCD ＝13S △BDC ·DM ＝13×221×5 3 ＝107.16．(文)如图，已知在直四棱柱ABCD －A1B 1C 1D 1中，AD ⊥DC ，AB ∥DC ，DC ＝DD 1＝2AD ＝2AB ＝2.(1)求证：DB ⊥平面B 1BCC 1；(2)设E 是DC 上一点，试确定E 的位置，使得D 1E ∥平面A 1BD ，并说明理由．[解析] (1)证明：∵AB ∥DC ，AD ⊥DC ，∴AB ⊥AD ，在Rt △ABD 中，AB ＝AD ＝1，∴BD ＝2，易求BC ＝2，又∵CD ＝2，∴BD ⊥BC .又BD ⊥BB 1，B 1B ∩BC ＝B ，∴BD ⊥平面B 1BCC 1.(2)DC 的中点即为E 点．∵DE ∥AB ，DE ＝AB ，∴四边形ABED 是平行四边形．∴AD 綊BE .又AD 綊A 1D 1，∴BE 綊A 1D 1，∴四边形A 1D 1EB 是平行四边形．∴D 1E ∥A 1B .∵D 1E ⊄平面A 1BD ，A 1B ⊂平面A 1BD .∴D 1E ∥平面A 1BD .(理)在三棱锥P －ABC 中，△P AC 和△PBC 是边长为2的等边三角形，AB ＝2，O 是AB 中点．(1)在棱P A 上求一点M ，使得OM ∥平面PBC ；(2)求证：平面P AB ⊥平面ABC ；(3)求二面角P －BC －A 的余弦值．[解析] (1)当M 为棱P A 的中点时，OM ∥平面PBC .证明如下：∵M 、O 分别为P A 、AB 中点，∴OM ∥PB又PB ⊂平面PBC ，OM ⊄平面PBC∴OM ∥平面PBC .(2)连结OC 、OP∵AC ＝CB ＝2，O 是AB 中点，AB ＝2，∴OC ⊥AB ，OC ＝1.同理，PO ⊥AB ，PO ＝1.又PC ＝2，∴PC 2＝OC 2＋PO 2＝2，∴∠POC ＝90°，∴PO ⊥OC .∵PO ⊥OC ，PO ⊥AB ，AB ∩OC ＝O ，∴PO ⊥平面ABC .∵PO ⊂平面P AB ，∴平面P AB ⊥平面ABC .(3)如图，建立空间直角坐标系O －xyz .则B (1,0,0)，C (0,1,0)，P (0,0,1)，∴BC →＝(－1,1,0)，PB →＝(1,0，－1)．由(2)知OP →＝(0,0,1)是平面ABC 的一个法向量．设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·BC →＝0n ·PB →＝0⇒⎩⎪⎨⎪⎧－x ＋y ＝0x －z ＝0，令z ＝1，则x ＝1，y ＝1，∴n ＝(1,1,1)．∴cos 〈OP →，n 〉＝OP →·n |OP →|·|n |＝11×3＝33. ∵二面角P －BC －A 的平面角为锐角，∴所求二面角P －BC －A 的余弦值为33. 17．(文)如图，在△BCD 中，∠BCD ＝90°，BC ＝CD ＝1，AB ⊥平面BCD ，∠ADB ＝60°，E 、F 分别是AC 、AD 上的动点，且AE AC ＝AF AD ＝λ(0<λ<1)．(1)判断EF 与平面ABC 的位置关系并给予证明；(2)是否存在λ，使得平面BEF ⊥平面ACD ，如果存在，求出λ的值，如果不存在，说明理由．[分析] (1)EF 与平面ABC 相交于点E ，故其关系只能是垂直或斜交，由条件AE AC ＝AF AD＝λ易知，EF ∥CD ，由∠BCD ＝90°及AB ⊥平面BCD ，易证CD ⊥平面ABC .(2)∵EF ∥CD ，故问题相当于过点B 作一个平面与ACD 垂直，这样的平面一定存在，故只须计算出λ即可，由条件不难得到BE ⊥CD ，故只须BE ⊥AC .[解析] (1)EF ⊥平面ABC .证明：因为AB ⊥平面BCD ，所以AB ⊥CD ，又在△BCD 中，∠BCD ＝90°，所以BC ⊥CD ，又AB ∩BC ＝B ，所以CD ⊥平面ABC ，又在△ACD 中，E 、F 分别是AC 、AD 上的动点，且AEAC ＝AF AD＝λ(0<λ<1)，∴EF ∥CD ，∴EF ⊥平面ABC .(2)∵CD ⊥平面ABC ，BE ⊂平面ABC ，∴BE ⊥CD ，在Rt △ABD 中，∠ADB ＝60°，∴AB ＝BD tan60°＝6，则AC ＝AB 2＋BC 2＝7，当BE ⊥AC 时，BE ＝AB ×BC AC ＝67，AE ＝AB 2－BE 2＝367，则AE AC ＝3677＝67，即λ＝AE AC ＝67时，BE ⊥AC ，又BE ⊥CD ，AC ∩CD ＝C ，∴BE ⊥平面ACD ，∵BE ⊂平面BEF ，∴平面BEF ⊥平面ACD . 所以存在λ，且当λ＝67时，平面BEF ⊥平面ACD . [点评] 高考整体降低了对立体几何的考查要求，故线线、线面、面面的位置关系成了主要的考查点，其中平行、垂直的证明题与探索题是重点，同时也要注意由三视图与几何体的结合进行表面积与体积的计算等问题．(理)已知四棱锥P－ABCD 的三视图如下图所示，E 是侧棱PC 上的动点．(1)求四棱锥P －ABCD 的体积；(2)是否不论点E 在何位置，都有BD ⊥AE ？证明你的结论；(3)若点E 为PC 的中点，求二面角D －AE －B 的大小．[解析] (1)由三视图可知，四棱锥P －ABCD 的底面是边长为1的正方形，侧棱PC ⊥底面ABCD ，且PC ＝2.∴V P －ABCD ＝13S 正方形ABCD ·PC ＝13×12×2＝23，即四棱锥P－ABCD 的体积为23.(2)不论点E 在何位置，都有BD ⊥AE .证明如下：连结AC ，∵ABCD 是正方形，∴BD ⊥AC .∵PC ⊥底面ABCD ，且BD ⊂平面ABCD ，∴BD ⊥PC .又∵AC ∩PC ＝C ，∴BD ⊥平面P AC .∵不论点E 在何位置，都有AE ⊂平面P AC .∴不论点E 在何位置，都有BD ⊥AE .(3)解法1：在平面DAE 内过点D 作DF ⊥AE 于F ，连结BF .∵AD ＝AB ＝1，DE ＝BE ＝12＋12＝2，AE ＝AE ＝3，∴Rt △ADE ≌Rt △ABE ，从而△ADF ≌△ABF ，∴BF ⊥AE .∴∠DFB 为二面角D －AE －B 的平面角．在Rt △ADE 中，DF ＝AD ·DE AE ＝1×23＝63， ∴BF ＝63. 又BD ＝2，在△DFB 中，由余弦定理得cos ∠DFB ＝DF 2＋BF 2－BD 22DF ·BF ＝－12， ∴∠DFB ＝2π3，即二面角D －AE －B 的大小为2π3. 解法2：如图，以点C 为原点，CD ，CB ，CP 所在的直线分别为x ，y ，z 轴建立空间直角坐标系．则D (1,0,0)，A (1,1,0)，B (0,1,0)，E (0,0,1)，从而DA →＝(0,1,0)，DE →＝(－1,0,1)，BA→＝(1,0,0)，BE →＝(0，－1,1)．设平面ADE 和平面ABE 的法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)，由⎩⎪⎨⎪⎧ n 1·DA →＝0n 1·DE →＝0⇒⎩⎪⎨⎪⎧ y 1＝0－x 1＋z 1＝0，取n 1＝(1,0,1)．由⎩⎪⎨⎪⎧ n 2·BA →＝0n 2·BE →＝0⇒⎩⎪⎨⎪⎧x 2＝0－y 2＋z 2＝0，取n 2＝(0，－1，－1)．设二面角D －AE －B 的平面角为θ，则cos θ＝n 1·n 2|n 1|·|n 2|＝－12·2＝－12， ∴θ＝2π3，即二面角D －AE －B 的大小为2π3.。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

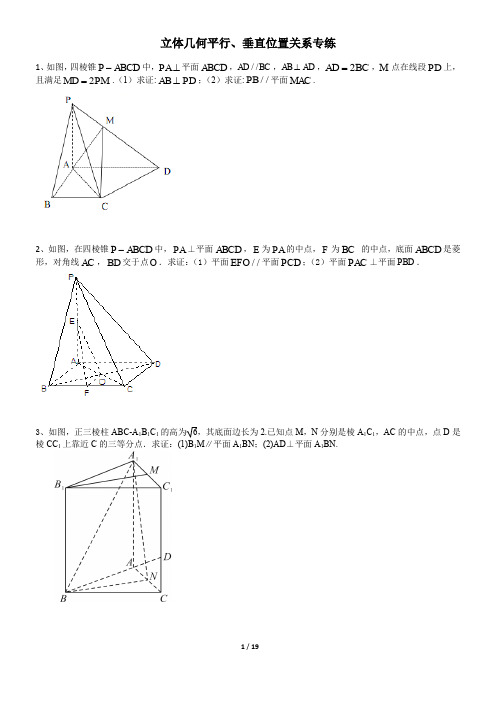
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ，又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点，所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ，所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

专题20立体几何中的平行与垂直问题(解析版)

专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨：证明直线与平面的平行与垂直问题，一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

直线与平面的平行有两种方法：一是在面内找线；二是通过面面平行转化。

直线与平面垂直关键是找两条相交直线例1、（2019南通、泰州、扬州一调）如图，在四棱锥PABCD中，M, N分别为棱PA, PD的中点.已知侧面PAD丄底面ABCD,底面ABCD是矩形，DA=DP.求证：（1）MN〃平面PBC；MD丄平面PAB.【证明】（1）在四棱锥P-ABCD中，M, N分别为棱PA, PD的中点，所以MN〃AD.（2分）又底面ABCD是矩形，所以BC〃AD.所以MN〃BC.（4分）又BC U平面PBC，MN Q平面PBC，所以MN〃平面PBC. （6分）（2）因为底面ABCD是矩形，所以AB丄AD.又侧面PAD丄底面ABCD，侧面PAD n底面ABCD=AD, AB U底面ABCD，所以AB丄侧面PAD.（8分）又MD U侧面PAD，所以AB丄MD.（10分）因为DA=DP,又M为AP的中点，从而MD丄PA. （12分）又PA，AB在平面PAB内，PA n AB=A，所以MD丄平面PAB.（14分）例2、（2019扬州期末）如图所示，在三棱柱ABCA1B1C1中，四边形AA1B1B为矩形，平面AA1B1B丄平面ABC,点E，F分别是侧面AA1B1B，BB1C1C对角线的交点.（1）求证：EF〃平面ABC；（2）求证：BB］丄AC.规范解答（1）在三棱柱ABCA1B1C1中，四边形AA1B1B,四边形BB1C1C均为平行四边形，E, F分别是侧面AA1B1B, BB1C1C对角线的交点，所以E, F分别是AB1，CB1的中点，所以EF〃AC.（4分）因为EF Q平面ABC, AC U平面ABC，所以EF〃平面ABC.（8分）（2）因为四边形AA1B1B为矩形，所以BB1丄AB.因为平面AA1B1B丄平面ABC,且平面AA1B1B n平面ABC=AB, BB1U平面AA1B1B, 所以BB1丄平面ABC.（12分）因为AC U平面ABC，所以BB1丄AC.（14分）例3、（2019南京、盐城二模）如图，在三棱柱ABCA1B1C1中，AB=AC, A1C丄BC］, AB］丄BC1，D, E 分别是AB1和BC的中点.求证：（1）DE〃平面ACC1A1；（2）AE丄平面BCC1B1.A _________ c,规范解答⑴连结A1B，在三棱柱ABCA1B1C1中，AA1#BB1且AA1=BB1，所以四边形AA1B1B是平行四边形．又因为D是AB1的中点，所以D也是BA1的中点.（2分）在厶BA1C中，D和E分别是BA1和BC的中点，所以DE〃A］C.又因为DE G平面ACC1A1，A1C U平面ACC1A1，所以DE〃平面ACC1A1.（6分）（2）由（1）知DE〃A］C，因为A1C丄BC” 所以BC］丄DE.（8 分）又因为BC］丄AB1，AB1H DE=D，AB1，DE U平面ADE，所以BC1丄平面ADE.又因为AE U平在ADE,所以AE丄BC1.（10分）在厶ABC中，AB=AC，E是BC的中点，所以AE丄BC.（12分）因为AE丄BC1，AE丄BC，BC1H BC=B，BC1，BC U平面BCC1B1，所以AE丄平面BCC1B1. （14 分）例4、（2019苏锡常镇调研）如图，三棱锥DABC中，已知AC丄BC，AC丄DC，BC=DC，E，F 分别为BD，CD 的中点．求证：（1）EF〃平面ABC；（2）BD丄平面ACE.所以EF 〃平面ABC.（6分）（2）因为AC丄BC，AC丄DC，BC H DC = C，BC，DC U平面BCD所以AC丄平面BCD，（8分）因为BD U平面BCD，所以AC丄BD，（10分）因为DC=BC，E为BD的中点，所以CE丄BD，（12分）因为AC n CE = C, AC，CE U平面ACE，所以BD丄平面ACE.（14分）例5、（2019苏州三市、苏北四市二调）如图，在直三棱柱ABCA1B1C1中，侧面BCC1B1为正方形，A1B1 丄B1C1•设A1C与AC1交于点D, B1C与BC1交于点E.求证：（1） DE〃平面ABB1A1；（2） BC］丄平面A1B1C.规范解答（1）因为三棱柱ABCA1B1C1为直三棱柱，所以侧面ACC1A1为平行四边形．又A1C 与AC1 交于点D,所以D为AC]的中点，同理，E为BC]的中点•所以DE〃AB.（3分）又AB U平面ABB]A], DE G平面ABB]A], 所以DE〃平面ABB]A].（6分）（2）因为三棱柱ABCA]B]C]为直三棱柱，所以BB]丄平面A]B]C]. 又因为A]B]U平面A]B]C],所以BB]丄A]B i.（8分）又A]B]丄B]C], BB], B]C] U 平面BCC]B], BB]n B]C1=B1，所以A]B]丄平面BCC]B].（10 分）又因为BC]U平面BCC]B1，所以A]B丄BC].（12分）又因为侧面BCC]B1为正方形，所以BC]丄BQ.又A1B1n B1C=B1，A1B1，B1C U平面A1B1C, 所以BC1丄平面A1B1C.（14分）例6、（2017苏北四市一模）如图，在正三棱柱ABCA1B1C1中，已知D, E分别为BC, B1C1的中点，点F 在棱CC1上，且EF丄CD.求证：（1）直线A1E〃平面ADC1；⑴证法1连结ED,因为D, E分别为BC, B1C1的中点，所以B&/BD且B1E=BD, 所以四边形BBDE是平行四边形，（2分）所以BB/DE且BB1=DE. 又BB]〃AA]且BB]=AA], 所以AA/DE且AA1=DE, 所以四边形AA]ED是平行四边形，所以A]E〃AD.（4分）又因为AE G平面ADC, AD U平面ADC，所以直线AE〃平面ADC.（7分）1 1 1畀 ------ 1B证法2连结ED,连结A1C, EC分别交AC” DC1于点M, N,连结MM,则因为D, E分别为BC,B1C1的中点，所以C1E^CD且C、E=CD,所以四边形C1EDC是平行四边形，所以N是CE的中点.（2分）因为A1ACC1为平行四边形，所以M是A1C的中点，（4分）所以MN//A\E.又因为A]E G平面ADC，MN U平面ADC，，所以直线Af〃平面ADC、.（7分）（2）在正三棱柱ABCA1B1C1中，BB]丄平面ABC.又AD U平面ABC，所以AD丄BB、.又A ABC是正三角形，且D为BC的中点，所以AD丄BC.（9分）又BB，，BC U 平面BBCC，，BB1A BC=B，所以AD丄平面B,BCC,，又EF U平面BBCC，所以AD丄EF.（11分）又EF丄CD，CD，AD U平面ADC,，C,D A AD=D，所以直线EF丄平面ADC,.（14分）题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题，一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

高一立体几何解答题训练

高一立体几何解答题训练（线面平行、垂直，面面平行垂直）1.如图，四面体ABCD中，AD⊥平面BCD，E、F分别为AD、AC的中点，BC⊥CD 求证：（1）EF//平面BCD（2）BC⊥平面ACDB2.如图，三棱锥A-BCD被一平面所截，截面EFGH是一个矩形（1）求证（1）CD//平面EFGH（2）求异面直线AB与CD所成的角B3.在四棱锥P-ABCD中，△PBC为正三角形，AB⊥平面PBC，AB//CD,AB=1/2CD,，E为PD中点，（1）求证：AE//平面PBC；（2）求证：AE⊥平面PDCCBAD4. 已知正方形ABCD ，E 、F 分别为AB 、CD 的中点，将△ADE 以DE 处折起，如图所示，证明：BF//平面ADECEB DFEA5. 如图，P 为△ABC 所在平面外一点，PA ⊥平面ABC ，∠ABC=90°，AE ⊥PB 于E ，AF⊥PC 于F ，求证：（1）BC ⊥平面PAB ；（2）AE ⊥平面PBC ；（3）PC ⊥平面AEFAP6. 如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点，求证：（1）PA//平面BDE ；（2）平面PAC ⊥平面BDE ；（3）若棱长都为2，求棱锥的体积。

PCA7. 如图，在边长为a 的棱形ABCD 中，∠ABC=60°，PC ⊥面ABCD ，E 、F 分别是PA 、AB 的中点。

（1）求证：EF//平面PBC（2）求E 到平面PBC 的距离FDA8. 如图，已知正四棱柱ABCD-A 1B 1C 1D 1的底面边长为3，侧棱长为4，连接A 1B ，过A做AF ⊥A 1B 垂足为F ，且AF 的延长线交B 1B 于E （1）求证：D 1B ⊥平面AEC （2）求三棱锥B-AEC 的体积C 1A C。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

高中数学高考总复习立体几何平行与垂直的判断习题及详解

高中数学高考总复习立体几何平行与垂直的判断习题及详解一、选择题1．(文)(09·福建)设m，n是平面α内的两条不同直线；l1，l2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是()A．m∥β且l1∥αB．m∥l1且n∥l2C．m∥β且n∥βD．m∥β且n∥l2[答案] B[解析]如图(1)，α∩β＝l，m∥l，l1∥l，满足m∥β且l1∥α，故排除A；如图(2)，α∩β＝l，m∥n∥l，满足m∥β，n∥β，故排除C.在图(2)中，m∥n∥l∥l2满足m∥β，n∥l2，故排除D，故选B.[点评]∵l1与l2相交，m∥l1，n∥l2，∴m与n相交，由面面平行的判定定理可知α∥β；但当m、n⊂α，l1，l2⊂β，l1与l2相交，α∥β时，如图(3)，得不出m∥l1且n∥l2.(理)设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是()A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β[答案] C[解析]对于A，如图正方体α、β分别为平面ABCD与平面ADD1A1，a、b分别为直线B1B和C1C.a与b也可能平行，对于B，∵a⊥α，α∥β，∴a⊥β，又b⊥β，∴a∥b，对于D，a与b也可能平行，故选C.2．(2010·郑州检测)已知α，β，γ是三个不同的平面，命题“α∥β，且α⊥γ⇒β⊥γ”是真命题．如果把α，β，γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题有()A．0个B．1个C．2个D．3个[答案] C[解析]依题意得，命题“a∥b，且a⊥γ⇒b⊥γ”是真命题(由“若两条平行线中的一条与一个平面垂直，则另一条也与这个平面垂直”可知)；命题“a∥β，且a⊥c⇒β⊥c”是假命题(直线c可能位于平面β内，此时结论不成立)；命题“α∥b，且α⊥c⇒b⊥c”是真命题(因为α∥b，因此在平面α内必存在直线b1∥b；又α⊥c，因此c∥b1，c⊥b)．综上所述，其中真命题共有2个，选C.3．(2010·东北三校模拟)正方体ABCD －A 1B 1C 1D 1中，M ，N ，P 分别为A 1B 1，CD ，B 1C 1的中点，则下列命题正确的是( )A ．AM 与PC 是异面直线B ．AM ⊥PC C ．AM ∥平面BC 1ND ．四边形AMC 1N 为正方形 [答案] C[解析] 连接MP ，AC ，A 1C 1，AM ，C 1N ，由题易知MP ∥A 1C 1∥AC ，且MP ＝12AC ，所以AM 与PC 是相交直线，假设AM ⊥PC ，∵BC ⊥平面ABB 1A 1，∴BC ⊥AM ，∴AM ⊥平面BCC 1B 1，又AB ⊥平面BCC 1B 1矛盾，∴AM 与PC 不垂直．因为AM ∥C 1N ，C 1N ⊂平面BC 1N ，所以AM ∥平面BC 1N .又易得四边形AMC 1N 为菱形而不是正方形，故选C.4．(文)对两条不相交的空间直线a 与b ，必存在平面α，使得( ) A ．a ⊂α，b ⊂α B ．a ⊂α，b ∥α C ．a ⊥α，b ⊥αD ．a ⊂α，b ⊥α[答案] B[解析] a 、b 异面时，A 错，C 错；若D 正确，则必有a ⊥b ，故排除A 、C 、D ，选B.(理)设a 、b 为两条直线，α、β为两个平面．下列四个命题中，正确的命题是( ) A ．若a 、b 与α所成的角相等，则a ∥b B ．若a ∥α，b ∥β，α∥β，则a ∥b C ．若a ⊂α，b ⊂β，a ∥b ，则α∥β D ．若a ⊥α，b ⊥β，α⊥β，则a ⊥b [答案] D[解析] 若直线a 、b 与α成等角，则a 、b 平行、相交或异面；对选项B ，如a ∥α，b ∥β，α∥β，则a 、b 平行、相交或异面；对选项C ，若a ⊂α，b ⊂β，a ∥b ，则α、β平行或相交；对选项D ，由⎭⎪⎬⎪⎫a ⊥αβ⊥α⇒a ∥β或a ⊂β，无论哪种情形，由b ⊥β都有b ⊥a .，故选D. 5．一个正方体纸盒展开后如图，在原正方体纸盒中有下列结论：①AB ⊥EF ②AB 与CM 成60°③EF 与MN 是异面直线④MN ∥CD 其中正确的是( )A．①②B．③④C．②③D．①③[答案] D[解析]本题考查学生的空间想象能力，将其还原成正方体如图所示，AB⊥EF，EF与MN是异面直线，AB∥CM，MN⊥CD.只有①③正确，故选D.6．(文)(2010·山东潍坊)已知m、n是两条不同的直线，α、β、γ是三个不同的平面，则下列命题正确的是()A．若α⊥γ，α⊥β，则γ∥βB．若m∥n，m⊂α，n⊂β，则α∥βC．若m∥n，m∥α，则n∥αD．若m∥n，m⊥α，n⊥β，则α∥β[答案] D[解析]对于选项A，两平面β、γ同垂直于平面α，平面β与平面γ可能平行，也可能相交；对于选项B，平面α、β可能平行，也可能相交；对于选项C，直线n可能与平面α平行，也可能在平面α内；对于选项D，∵m∥n，m⊥α，∴n⊥α，又n⊥β，∴α∥β，故选D.(理)(2010·曲师大附中)已知两个不同的平面α，β和两条不重合的直线a，b，则下列四个命题中为真命题的是()A．若a∥b，b⊂α，则a∥αB．若α⊥β，α∩β＝b，a⊥b，则a⊥βC．若a⊂α，b⊂α，a∥β，b∥β，则α∥βD．若α∥β，a⊄α，a⊄β，a∥α，则a∥β[答案] D[解析]选项A中，直线a可能在平面α内；选项B中，直线a可能在平面β内；选项C 中，直线a ，b 为相交直线时命题才成立．7．(2010·江苏南通)在正方体ABCD －A 1B 1C 1D 1中，P 、Q 分别是棱AA 1、CC 1的中点，则过点B 、P 、Q 的截面是( )A ．邻边不等的平行四边形B ．菱形但不是正方形C ．邻边不等的矩形D ．正方形 [答案] B[解析] 设正方体棱长为1，连结D 1P ，D 1Q ，则易得PB ＝PQ ＝D 1P ＝D 1Q ＝52，取D 1D 的中点M ，则D 1P 綊AM 綊BQ ，故截面为四边形PBQD 1，它是一个菱形，又PQ ＝AC ＝2，∴∠PBQ 不是直角，故选B.8．(文)(2010·山东日照、聊城模考)已知直线l 、m ，平面α、β，且l ⊥α，m ⊂β，给出下列四个命题：①若α∥β，则l ⊥m ；②若l ⊥m ，则α∥β；③若α⊥β，则l ∥m ；④若l ∥m ，则α⊥β；其中真命题是( ) A ．①② B ．①③ C ．①④D ．②④[答案] C [解析][点评] 如图，α∩β＝m ，则l ⊥m ，故(2)假；在上述图形中，当α⊥β时，知③假．(理)(2010·福建福州市)对于平面α和共面的直线m ，n ，下列命题是真命题的是( ) A ．若m ，n 与α所成的角相等，则m ∥n B ．若m ∥α，n ∥α，则m ∥nC．若m⊥α，m⊥n，则n∥αD．若m⊂α，n∥α，则m∥n[答案] D[解析]正三棱锥P－ABC的侧棱P A、PB与底面成角相等，但P A与PB相交应排除A；若m∥α，n∥α，则m与n平行、相交或异面，应排除B；若m⊥α，m⊥n，则n∥α或n⊂α，应排除C.∵m、n共面，设经过m、n的平面为β，∵m⊂α，∴α∩β＝m，∵n∥α，∴n∥m，故D正确．9．(文)(2010·北京顺义一中月考)已知l是直线，α、β是两个不同平面，下列命题中的真命题是()A．若l∥α，l∥β，则α∥βB．若α⊥β，l∥α，则l⊥βC．若l⊥α，l∥β，则α⊥βD．若l∥α，α∥β，则l∥β[答案] C[解析]如图在正方体ABCD－A1B1C1D1中，取平面ABD1A1为α，平面ABCD为β，B1C1为l，则排除A、B；又取平面ADD1A1为α，平面BCC1B1为β，B1C1为l，排除D.(理)(2010·广东罗湖区调研)已知相异直线a，b和不重合平面α，β，则a∥b的一个充分条件是()A．a∥α，b∥αB．a∥α，b∥β，α∥βC．a⊥α，b⊥β，α∥βD．α⊥β，a⊥α，b∥β[答案] C[解析]a∥α，b∥α时，a与b可相交可异面也可平行，故A错；a∥α，b∥β，α∥β时，a与b可异面，故B错；由α⊥β，a⊥α得，a∥β或a⊂β，又b∥β，此时a与b可平行也可异面，排除D.10．(2010·日照实验高中)如图，正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2，AB ＝1，M ，N 分别在AD 1，BC 上移动，且始终保持MN ∥平面DCC 1D 1，设BN ＝x ，MN ＝y ，则函数y ＝f (x )的图象大致是( )[答案] C[解析] 过M 作ME ⊥AD 于E ，连接EN ，则平面MEN ∥平面DCC 1D 1，所以BN ＝AE ＝x (0≤x <1)，ME ＝2x ，MN 2＝ME 2＋EN 2，则y 2＝4x 2＋1，y 2－4x 2＝1(0≤x <1，y >0)，图象应是焦点在y 轴上的双曲线的一部分．故选C.二、填空题11．(文)如图，在正四棱柱ABCD －A 1B 1C 1D 1中，E 、F 、G 、H 分别是棱CC 1、C 1D 1、D 1D 、DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 满足条件________时，有MN ∥平面B 1BDD 1.[答案] M ∈线段FH[解析] 因为HN ∥BD ，HF ∥DD 1，所以平面NHF ∥平面B 1BDD 1，又平面NHF ∩平面EFGH ＝FH .故线段FH 上任意点M 与N 相连，有MN ∥平面B 1BDD 1，故填M ∈线段FH .(理)(2010·南充市模拟)已知两异面直线a ，b 所成的角为π3，直线l 分别与a ，b 所成的角都是θ，则θ的取值范围是________．[答案] [π6，π2]12．在四面体ABCD 中，M 、N 分别是△ACD 、△BCD 的重心，则四面体的四个面中与MN 平行的是________．[答案] 面ABC 和面ABD[解析] 连结AM 并延长交CD 于点E ，∵M 为△ACD 的重心，∴E 为CD 的中点，又N 为△BCD 的重心，∴B 、N 、E 三点共线，由EM MA ＝EN NB ＝12得MN ∥AB ，因此MN ∥平面ABC ，MN ∥平面ABD .13．如图是一正方体的表面展开图，B 、N 、Q 都是所在棱的中点，则在原正方体中， ①AB 与CD 相交；②MN ∥PQ ；③AB ∥PE ；④MN 与CD 异面；⑤MN ∥平面PQC . 其中真命题的序号是________．[答案] ①②④⑤[解析] 将正方体还原后如图，则N 与B 重合，A 与C 重合，E 与D 重合，∴①、②、④、⑤为真命题．14．如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为a ，点P 是棱AD 上一点，且AP ＝a3，过B 1，D 1，P 的平面交底面ABCD 于PQ ，Q 在直线CD 上，则PQ ＝________.[答案]223a [解析] ∵B 1D 1∥平面ABCD ，平面B 1D 1P ∩平面ABCD ＝PQ ，∴B 1D 1∥PQ ，又B 1D 1∥BD ，∴BD ∥PQ ，设PQ ∩AB ＝M ，∵AB ∥CD ，∴△APM ∽△DPQ ，∴PQ PM ＝PDAP＝2，即PQ ＝2PM ，又△APM ∽△ADP ，∴PM BD ＝AP AD ＝13，∴PM ＝13BD ，又BD ＝2a ，∴PQ ＝223a .三、解答题15．(文)(2010·南京调研)如图，在四棱锥E －ABCD 中，四边形ABCD 为平行四边形，BE ＝EC ，AE ⊥BE ，M 为CE 上一点，且BM ⊥平面ACE .(1)求证：AE ⊥BC ；(2)如果点N 为线段AB 的中点，求证：MN ∥平面ADE .[解析] (1)因为BM ⊥平面ACE ，AE ⊂平面ACE ，所以BM ⊥AE .因为AE ⊥BE ，且BE ∩BM ＝B ，BE 、BM ⊂平面EBC ，所以AE ⊥平面EBC . 因为BC ⊂平面EBC ，所以AE ⊥BC . (2)解法1：取DE 中点H ，连接MH 、AH .因为BM ⊥平面ACE ，EC ⊂平面ACE ，所以BM ⊥EC . 因为BE ＝BC ，所以M 为CE 的中点．所以MH 为△EDC 的中位线，所以MH 綊12DC .因为四边形ABCD 为平行四边形，所以DC 綊AB . 故MH 綊12AB .因为N 为AB 的中点，所以MH 綊AN .所以四边形ANMH 为平行四边形，所以MN ∥AH . 因为MN ⊄平面ADE ，AH ⊂平面ADE ，所以MN ∥平面ADE .解法2：取EB 的中点F ，连接MF 、NF .因为BM ⊥平面ACE ，EC ⊂平面ACE ，所以BM ⊥EC . 因为BE ＝BC ，所以M 为CE 的中点，所以MF ∥BC .因为N 为AB 的中点，所以NF ∥AE ，因为四边形ABCD 为平行四边形，所以AD ∥BC .所以MF ∥AD .因为NF 、MF ⊄平面ADE ，AD 、AE ⊂平面ADE ，所以NF ∥平面ADE ，MF ∥平面ADE . 因为MF ∩NF ＝F ，MF 、NF ⊂平面MNF ，所以平面MNF ∥平面ADE .因为MN ⊂平面MNF ，所以MN ∥平面ADE .(理)(2010·厦门市质检)如图所示的几何体中，△ABC 为正三角形，AE 和CD 都垂直于平面ABC ，且AE ＝AB ＝2，CD ＝1，F 为BE 的中点．(1)若点G 在AB 上，试确定G 点位置，使FG ∥平面ADE ，并加以证明；(2)在(1)的条件下，求三棱锥D －ABF 的体积． [解析] (1)当G 是AB 的中点时，GF ∥平面ADE . ∵G 是AB 的中点，F 是BE 的中点， ∴GF ∥AE ，又GF ⊄平面ADE ，AE ⊂平面ADE ， ∴GF ∥平面ADE . (2)连接CG ，由(1)可知： GF ∥AE ，且GF ＝12AE .又AE ⊥平面ABC ，CD ⊥平面ABC ，∴CD ∥AE ，又CD ＝12AE ，∴GF ∥CD ，GF ＝CD ，∴四边形CDFG 为平行四边形， ∴DF ∥CG ，且DF ＝CG .又∵AE ⊥平面ABC ，CG ⊂平面ABC ，∴AE ⊥CG . ∵△ABC 为正三角形，G 为AB 的中点， ∴CG ⊥AB ，又AB ∩AE ＝A ，∴CG ⊥平面ABE . 又CG ∥DF ，且CG ＝DF ，∴DF 为三棱锥D －ABF 的高，且DF ＝ 3. 又AE ⊥平面ABC ，AB ⊂平面ABC ，∴AE ⊥AB . ∵在Rt △ABE 中，AB ＝AE ＝2，F 为BE 的中点，∴S △ABF ＝12S △ABE ＝12×12×2×2＝1.∴V D －ABF ＝13S △ABF ·DF ＝13×1×3＝33，∴三棱锥D －ABF 的体积为33. 16．(文)(2010·安徽合肥质检)如图，PO ⊥平面ABCD ，点O 在AB 上，EA ∥PO ，四边形ABCD 为直角梯形，BC ⊥AB ，BC ＝CD ＝BO ＝PO ，EA ＝AO ＝12CD .(1)求证：BC ⊥平面ABPE ；(2)直线PE 上是否存在点M ，使DM ∥平面PBC ，若存在，求出点M ；若不存在，说明理由．[解析] (1)∵PO ⊥平面ABCD ， BC ⊂平面ABCD ，∴BC ⊥PO ，又BC ⊥AB ，AB ∩PO ＝O ，AB ⊂平面ABP ，PO ⊂平面ABP ，∴BC ⊥平面ABP ，又EA ∥PO ，AO ⊂平面ABP ， ∴EA ⊂平面ABP ，∴BC ⊥平面ABPE . (2)点E 即为所求的点，即点M 与点E 重合．取PO 的中点N ，连结EN 并延长交PB 于F ， ∵EA ＝1，PO ＝2，∴NO ＝1，又EA 与PO 都与平面ABCD 垂直，∴EF ∥AB ， ∴F 为PB 的中点，∴NF ＝12OB ＝1，∴EF ＝2，又CD ＝2，EF ∥AB ∥CD ，∴四边形DCFE 为平行四边形，∴DE ∥CF ， ∵CF ⊂平面PBC ，DE ⊄平面PBC ， ∴DE ∥平面PBC .∴当M 与E 重合时即可．(理)在长方体ABCD －A 1B 1C 1D 1中，O 为底面正方形的中心，过A 1、C 1、B 三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD －A 1C 1D 1及其三视图．(1)求证：D1O∥平面A1BC1；(2)是否存在过点A1与直线DC1垂直的平面A1PQ，与线段BC1交于点P，与线段CC1交于点Q？若存在，求出线段PQ的长；若不存在，请说明理由．[分析]要证D1O∥平面A1BC1，∵O为DB的中点，∴取A1C1中点E，只须证D1E綊OB，或利用长方体为正四棱柱的特性，证明平面ACD1∥平面A1C1B，假设存在平面A1PQ ⊥DC1，利用正四棱柱中，BC⊥平面DCC1D1，故有BC⊥DC1，从而平面A1PQ与平面BCC1的交线PQ⊥DC1，故只须在面DCC1D1的边CC1上寻找点Q，使D1Q⊥DC1即可．[解析](1)连接AC，AD1，D1C，易知点O在AC上．D1、四边形A1D1CB均为平行四边根据长方体的性质得四边形ABC Array 1形，∴AD1∥BC1，A1B∥D1C，又∵AD1⊄平面A1C1B，BC1⊂平面A1C1B，∴AD1∥平面A1C1B，同理D1C∥平面A1BC1，又∵D1C∩AD1＝D1，∴根据面面平行的判定定理知平面ACD1∥平面A1BC1.∵D1O⊂平面ACD1，∴D1O∥平面A1BC1.(2)假设存在过点A1与直线DC1垂直的平面A1PQ，与线段BC1交于点P，与线段CC1交于点Q.D，过点D1作C1D的垂线交C1C于点Q，过点Q作PQ连接C Array 1∥BC交BC1于点P，连接A1P，A1Q.∵C1D⊥D1Q，C1D⊥A1D1，D1Q∩A1D1＝D1，∴C1D⊥平面A1D1Q.∵A1Q⊂平面A1D1Q，∴C1D⊥A1Q.∵PQ∥BC∥A1D1，∴C1D⊥PQ，∵A1Q∩PQ＝Q，∴C1D⊥平面A1PQ.∴存在过点A1与直线DC1垂直的平面A1PQ，与线段BC1交于点P，与线段CC1交于点Q.在矩形CDD 1C 1中，∵Rt △D 1C 1Q ∽Rt △C 1CD ，∴C 1Q CD ＝D 1C 1C 1C ，结合三视图得C 1Q 2＝24，∴C 1Q ＝1. ∵PQ ∥BC ，∴PQ BC ＝C 1Q CC 1＝14，∴PQ ＝14BC ＝12. 17．(文)(2010·东北师大附中)如图所示，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为DD 1、DB 的中点．(1)求证：EF ∥平面ABC 1D 1；(2)求证：EF ⊥B 1C ；(3)求三棱锥B 1－EFC 的体积．[解析] (1)证明：连结BD 1，在△DD 1B 中，E 、F 分别为D 1D ，DB 的中点，则EF ∥D 1B ，又EF ⊄平面ABC 1D 1，D 1B ⊂平面ABC 1D 1，∴EF ∥平面ABC 1D 1.(2)证明：∵B 1C ⊥AB ，B 1C ⊥BC 1，AB ∩BC 1＝B ，∴B 1C ⊥平面ABC 1D 1，又BD 1⊂平面ABC 1D 1，∴B 1C ⊥BD 1，又EF ∥BD 1，∴EF ⊥B 1C .(3)解：∵CF ⊥BD ，CF ⊥BB 1，∴CF ⊥平面BDD 1B 1，即CF ⊥平面EFB 1，且CF ＝BF ＝ 2∵EF ＝12BD 1＝3，B 1F ＝BF 2＋BB 12＝(2)2＋22＝6，B 1E ＝B 1D 12＋D 1E 2＝12＋(22)2＝3，∴EF 2＋B 1F 2＝B 1E 2，即∠EFB 1＝90°，∴VB 1－EFC ＝VC －B 1EF ＝13·S △B 1EF ·CF ＝13×12·EF ·B 1F ·CF ＝13×12×3×6×2＝1. (理)(2010·河北唐山)如图，在四棱锥V －ABCD 中，底面ABCD 是矩形，侧棱VA ⊥底面ABCD ，E 、F 、G 分别为VA 、VB 、BC 的中点．(1)求证：平面EFG ∥平面VCD ；(2)当二面角V －BC －A 、V －DC －A 依次为45°、30°时，求直线VB 与平面EFG 所成的角．[解析] (1)∵E 、F 、G 分别为VA 、VB 、BC 的中点，∴EF ∥AB ，FG ∥VC ，又ABCD 是矩形，∴AB ∥CD ，∴EF ∥CD ，又∵EF ⊄平面VCD ，FG ⊄平面VCD ，∴EF ∥平面VCD ，FG ∥平面VCD ，又EF ∩FG ＝F ，∴平面EFG ∥平面VCD .(2)∵VA ⊥平面ABCD ，CD ⊥AD ，∴CD ⊥VD .则∠VDA 为二面角V －DC －A 的平面角，∴∠VDA ＝30°.同理∠VBA ＝45°.作AH ⊥VD ，垂足为H ，由上可知CD ⊥平面VAD ，则AH ⊥平面VCD .∵AB ∥平面VCD ，∴AH 即为B 到平面VCD 的距离．由(1)知，平面EFG ∥平面VCD ，则直线VB 与平面EFG 所成的角等于直线VB 与平面VCD 所成的角，记这个角为θ.∵AH ＝VA sin60°＝32VA ，VB ＝2VA ，∴sin θ＝AH VB ＝64，故直线VB 与平面EFG 所成的角是arcsin64.。

立体几何最典型的平行与垂直题型归纳(带答案)(1)

专题:立体几何最典型的平行与垂直题型归纳1．四面体ABCD 中，△ ABC 是正三角形，△ ACD 是直角三角形，∠ ABD ＝∠ CBD，AB＝BD ，则四面体的四个表面中互相垂直的平面有（）对．2．如图，在四棱锥P﹣ABCD 中，PA⊥底面ABCD ，四边形ABCD 为长方形，AD＝2AB，点E、F 分别是线段PD、PC 的中点．（Ⅰ）证明：EF∥平面PAB；（Ⅱ）在线段AD 上是否存在一点O，使得BO⊥平面PAC，若存在，请指出点O 的位置，⊥底面ABCD ，且PA＝AD＝2，AB＝BC＝1，M 为PD 的中点．Ⅰ）求证：CM ∥平面PAB；Ⅱ）求证：CD ⊥平面PAC．AD ∥BC ，∠ BAD ＝90°，PA4．如图，△ ABC 为正三角形，AE 和CD 都垂直于平而ABC，F 是BE 中点，AE＝AB＝2，CD＝1．1）求证：DF ∥平面ABC；2）求证：AF ⊥DE；3）求异面直线AF 与BC 所成角的余弦值．5．如图，在四棱锥A﹣BCDE 中，平面ABC⊥平面BCDE ，∠ CDE ＝∠ BED ＝90°，AB＝CD＝2，DE＝BE＝1，AC＝．（1）证明：D E⊥平面ACD ；2）求棱锥C﹣ABD 的体积．6．如图，在四棱锥P﹣ABCD 中，底面ABCD 是矩形，PA⊥平面ABCD，PA＝AD＝2，AB ＝1，M 为线段PD 的中点．I）求证：BM ⊥PDII ）求直线CM 与PB 所成角的余弦值．7．如图，在正三棱柱ABC﹣A1B1C1 中，所有棱长都等于2．（1）当点M 是BC 的中点时，求异面直线AB1和MC1所成角的余弦值；专题 :立体几何最容易错的最难的平行与垂直问题汇编1．如图，在三棱柱 ABC ﹣A 1B 1C 1中，侧棱垂直于底面，∠ ACB ＝90°， 2AC ＝AA 1，D ，M 分别是棱 AA 1， BC 的中点．证明：2）若∠ ABC ＝120°，AE ⊥EC ，AB ＝2，求点 G 到平面 AED 的距离．3．如图，在四棱锥 P ﹣ ABCD 中，平面 PAD ⊥平面 ABCD ，PA ⊥PD ，PA ＝PD ，AB ⊥AD ， AB ＝1，AD ＝2，AC ＝CD ＝．（ 1）求证： PD ⊥平面 PAB ；1）证明：平面 PAB ⊥平面 PAD；AB ∥CD ，且∠ BAP ＝∠ CDP ＝90BE ⊥平面 ABCD ．1）证明：平面 AEC ⊥平面 BED ．2）若 PA ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥 P ﹣ABCD 的体积为，求该四棱 1）证明： AC ⊥BD ；（2）已知△ ACD 是直角三角形， AB ＝BD ，若 E 为棱 BD 上与 D6．如图，在四棱锥 A ﹣EFCB 中，△ AEF 为等边三角形，平面 AEF ⊥平面 EFCB ，EF ＝ 2，四边形 EFCB 是高为的等腰梯形， EF ∥BC ，O 为 EF 的中点．AD ＝CD ．求 O 到平面 ABC 的距离．专题:立体几何最典型的平行与垂直题型归纳1．四面体ABCD 中，△ ABC 是正三角形，△ ACD 是直角三角形，∠ ABD ＝∠ CBD，AB＝BD ，则四面体的四个表面中互相垂直的平面有（）对．A ．0 B．1 C． 2 D． 3【解答】解：取AC 的中点E，连接BE，DE，∵∠ ABD＝∠ CBD ，∴ BD 在平面ABC 上的射影在直线BE 上，∵△ ACD 是直角三角形，∴∠ ADC＝90°，设 AB ＝ 2，则 BE ＝，DE ＝ AC ＝1，BD ＝2，2 2 2∴DE 2+BE 2＝ BD 2，即 DE ⊥BE ，又 BE ⊥ AC ，DE ∩AC ＝E ，∴ BE ⊥平面 ACD ，∴平面 ABC ⊥平面 ACD ．∵ D 在平面 ABC 上的射影为 E ， B 在平面 ACD 上的射影为 E ，∴平面 ABD 与平面 ABC 不垂直，平面 BCD 与平面 ABC 不垂直，平面 ABD 与平面 ACD 不垂直，平面 BCD 与平面 ACD 不垂直，过A 作 AF ⊥BD ，垂足为 F ，连接 CF ，由△ ABD ≌△ CBD 可得 CF ⊥BD ，故而∠ AFC 为二面角 A ﹣BD ﹣C 的平面角， ∵ AD ＝＝， ∴ cos ∠ ABD ∴ CF ＝ AF ＝∴ cos ∠ AFC ＝∴∠ AFC ≠ 90°，∴平面 ABD 与平面 BCD 不垂直．F 分别是线段 PD 、PC 的中点．证明： EF ∥平面 PAB ；BO ⊥平面 PAC ，若存在，请指出点 O 的位置，并证明 BO ⊥平面 PAC ；若不存在，请说明理由．2．如图，在四棱锥 P ﹣ABCD 中， PA ⊥底面 ABCD ，四边形 ABCD 为长方形， AD ＝ 2AB ，在线段 AD 上是否存在一点 O ，使得，∴ sin ∠ ABD＝∵EF ∥CD ，∴ EF ∥AB ，∴ EF ∥平面 PAB ． ⋯（6 分）此时点 O 为线段 AD 的四等分点，满足，⋯（ 8 分） ∵长方形ABCD 中，∴△ ABO ∽△ ADC ， ∴∠ ABO+∠CAB ＝∠ DAC + ∠CAB ＝90°，∴AC ⊥BO ，（10 分）又∵ PA ⊥底面 ABCD ，BO? 底面ABCD ， ∴PA ⊥BO ， ∵PA ∩AC ＝A ，PA 、AC? 平面 PACABCD 为长方形，∴CD ∥AB ，∠ BAO ＝∠ ADC ＝ 90°，四边形 ABCD 为直角梯形， AD∥BC ，∠ BAD＝，PA 又∵ EF? 平面 PAB ， AB? 平面 PAB ，Ⅱ）在线段 AD 上存在一点 O ，使得 BO ⊥平面 PAC ，⊥底面ABCD ，且PA＝AD＝2，AB＝BC＝1，M为PD 的中点．（Ⅰ）求证：CM ∥平面PAB；（Ⅱ）求证：CD ⊥平面PAC．解答】证明：（I ）取PA 的中点E，连接ME 、BE，∵ ME ∥AD，ME AD，∴ ME ∥BC，ME＝BC，∴四边形BCME 为平行四边形，∴ BE∥CM ，∵BE? 平面PAB，CM?平面PAB，∴ CM∥平面PAB；（II ）在梯形ABCD 中，AB＝BC＝1，AD＝2，∠ BAD＝90° 过C作CH⊥AD于H，∴AC ＝CD＝2 2 2∵AC2+CD2＝AD2，∴ CD⊥AC又∵ PA⊥平面ABCD ，CD ?平面ABCD，∴ CD⊥PA∵PA∩AC＝A，∴CD ⊥平面PAC4．如图，在三棱柱ABC﹣A1B1C1中，AB＝AC，A1在底面ABC的射影为BC的中点，D是B1C1 的中点，证明：A1D⊥平面A1BC．解答】证明：设 E 为 BC 的中点，连接 A 1E ， DE ，AE ，由题意得 A 1E ⊥平面 ABC ，∴ A 1E ⊥AE ．∵ AB ＝ AC ， AE ⊥BC ，∴ AE ⊥平面 A 1BC ．由 D ，E 分别为 B 1C 1，BC 的中点，得 DE ∥B 1B 且 DE ＝B 1B ，从而 DE ∥A 1A 且 DE ＝A 1A ，∴四边形 A 1AED 为平行四边形，∴ A 1D ∥AE ．5．如图，△ ABC 为正三角形， AE 和 CD 都垂直于平而 ABC ，F 是 BE 中点， AE ＝AB ＝ 2，CD ＝ 1．（1）求证： DF ∥平面 ABC ；（2）求证： AF ⊥DE ；（3）求异面直线 AF 与 BC 所成角的余弦值．【解答】（1）证明：取 AC 中点 O ，过 O 作平面 ABC 的垂线交 DE连结 OB ，则 OG ⊥OB ， OG ⊥ OC ，∵△ ABC 是正三角形， O 是 AC 中点，∴ OB ⊥ OC ，以 O 为原点， OB 、OC 、OG 所在直线分别为 x 、y 、z轴，建立空间直角坐标系，又∵ AE ⊥平面 A 1BC ， ∴ A 1D ⊥平面 A 1BC∵F 是 BE 中点， AE ＝AB ＝ 2，CD ＝1，＝（﹣ ， 1， 0），＝（ 0，0， 1），∵CD ⊥平面 ABC ，∴ ＝（0，0，1）是平面 ABC 的一个法向量，又 DF? 平面 ABC ，∴ DF ∥平面 ABC ．2）证明：∵ ＝（），＝（ 0，﹣2，1），∴ ＝ 0﹣ 1+1＝0，∴AF ⊥DE ．（3）解：∵ ＝（），＝（﹣ ，1， 0），设 AF 、 BC 所成角为 θ，cos θ＝ ∴异面直线 AF 与 BC 所成角的余弦值6．如图，在四棱锥 P ﹣ABCD 中，底面 ABCD 是矩形， PA ⊥平面 ABCD ，PA ＝AD ＝2，AB ＝ 1，M 为线段 PD 的中点．（ I ）求证： BM ⊥PD（ II ）求直线 CM 与 PB 所成角的余弦值．∴ ＝（，0），＝（），＝（0，﹣ 2，1），∵ ＝， ∴，D （0，1，1），E （0，﹣1，∴A （0，﹣ 1，0），B（| | ＝【解答】（ I ）证明：连接 BD ，∵四棱锥 P ﹣ABCD 中，底面 ABCD 是矩形， PA ⊥平面 ABCD ，PA ＝AD ＝2，AB ＝1， ∴PB ＝BD ＝∵ M 为线段 PD 的中点，∴BM ⊥PD（II ）解：连接 AC ，与 BD 交于 O ，连接 OM ，则∵ M 为线段 PD 的中点，∴MO ∥PB∴直线 CM 与 PB 所成角的余弦值为7．如图，在正三棱柱 ABC ﹣A 1B 1C 1 中，所有棱长都等于 2．（ 1）当点 M 是 BC 的中点时，① 求异面直线 AB 1和 MC 1 所成角的余弦值；② 求二面角 M ﹣AB 1﹣C 的正弦值；（2）当点 M 在线段 BC 上（包括两个端点）运动时，求直线 MC 1与平面 AB 1C 所成角的∴∠ CMO （或其补角）为直线 CM 与 PB 所成角，在△ MOC中， ∴ cos ∠ CMO＝CM ＝＝，．．解答】解：（1）取 AC 的中点为 O ，建立空间直角坐标系 O ﹣ xyz ，则，C （ 0，1，0），当 M 是 BC 的中点时，则． ①，设异面直线 AB 1 和 MC 1 所成角为 θ，则＝＝．＝＝．② ，，，，令 x ＝ 2，∴ ，∴ ．设二面角 M ﹣ AB 1﹣ C 的平面角为 θ，则＝．所以．（ 2）当 M 在 BC 上运动时，设．设平面 MAB 1的一个法向量为，则．∴ 设平面 AB 1C 的一个法向量为，令，则 y ＝﹣ 1，z ＝﹣ 1，∴，，则正弦值的取值范围．设M（x，y，z），∴，∴ ，则，∴ ．设直线MC1 与平面AB1C 所成的角为θ ，则设，设t＝λ+1 ∈[1，2]，所以，t∈[1，2]．设，∴∵ ，∴ ，∴∴直线MC 1与平面AB1C 所成的角的正弦值的取值范围为6．如图，在四棱锥 A ﹣BCDE 中，平面 ABC ⊥平面 BCDE ，∠ CDE ＝∠ BED ＝90°， AB ＝CD ＝ 2，DE ＝BE ＝1，AC ＝．（ 1）证明： DE ⊥平面 ACD ；（ 2）求棱锥 C ﹣ ABD 的体积．【解答】解：（ 1）在直角梯形 BCDE 中，∵DE ＝ BE ＝ 1， CD ＝ 2，∴ BC ＝＝，又 AB ＝2， AC ＝，∴ AB 2＝AC 2+BC 2，即 AC ⊥ BC ，又平面 ABC ⊥平面 BCDE ，平面 ABC ∩平面 BCDE ＝BC ，AC? 平面 ABC ，∴AC ⊥平面 BCDE ，又 DE? 平面 BCDE ，∴AC ⊥ DE ，又 DE ⊥DC ，AC ∩CD ＝C ，∴ DE ⊥平面 ACD ．1．如图，在三棱柱 ABC ﹣A 1B 1C 1中，侧棱垂直于底面，∠ ACB ＝90°， 2AC ＝AA 1，D ，M分别是棱 AA 1， BC 的中点．证明：S △BCD ?AC ＝V C ﹣ABD ＝V A ﹣BCD ＝1)AM∥平面BDC12)DC1⊥平面BDC ．∴AD ∥ MN ，且 AD ＝ MN ；∴四边形 ADNM 为平行四边形，∴DN ∥AM ；又 DN? 平面 BDC 1，AM? 平面 BDC 1，∴ AM ∥平面 BDC 1⋯（ 6 分）（ 2）由已知 BC ⊥CC 1，BC ⊥AC ，又 CC 1∩ AC ＝ C ，∴ BC ⊥平面 ACC 1A 1，又 DC 1? 平面 ACC 1A 1，∴ DC 1⊥BC ；由已知得∠ A 1DC 1＝∠ ADC ＝45°，∴∠ CDC 1＝ 90°，∴DC 1⊥DC ；又 DC ∩BC ＝C ，∴ DC 1⊥平面 BDC ．⋯（ 12分）【解答】证明：（ 1）如图所示，取 BC 1 的中点 N ，连接 DN ，MN ．则 MN ∥ CC 1，且 M N ＝ CC 1；又 AD ∥CC 1，且 ADV ＝，2．如图，四边形 ABCD 为菱形， G 为 AC 与 BD 的交点， BE ⊥平面 ABCD ．（ 1）证明：平面 AEC ⊥平面 BED ．因为 BE ⊥平面 ABCD ， AC? 平面 ABCD ，所以 AC ⊥BE ，⋯（ 2 分）又因为 DB ∩BE ＝B ，所以 AC ⊥平面 BED ．⋯（ 3分）又 AC? 平面 AEC ，所以平面 AEC ⊥平面 BED ．⋯（ 5 分）2）取 AD 中点为 M ，连接 EM ．因为∠ ABC ＝ 120°．，AB ＝2，所以 AB ＝DB ＝ 2，AG ＝，DG ＝ 1，因为 AE ⊥EC ，所以 EG ＝＝，所以 BE ＝，⋯（ 6 分）所以 AE ＝DE ＝，又所以 AD 中点为 M ，所以 EM ⊥AD 且 EM ＝．设点 G 到平面 AED 的距离为为 h ，则三棱锥 E ﹣ADG 的体积为求点 G 到平面 AED 的距离．为菱形，所以 AC ⊥BD ，⋯（ 1 分）即，解得 h ＝．PAD ⊥平面 ABCD ，PA ⊥PD ，PA ＝PD ，AB ⊥AD ，ABCD ，且平面 PAD ∩平面 ABCD ＝AD ，AB ⊥AD ，AB? 平面 ABCD ，∴ AB ⊥平面 PAD ，∵PD? 平面 PAD ，∴AB ⊥PD ，又 PD ⊥PA ，且 PA ∩AB ＝A ，∴ PD ⊥平面 PAB ；（ 2）解：取 AD 中点 O ，连接 PO ，则 PO ⊥ AD ，又平面 PAD ⊥平面 ABCD ， ∴PO ⊥平面 ABCD ，∵PA ⊥PD ，PA ＝PD ，AD ＝2，∴ PO ＝1．10 分）所以点 G 到平面 AED 的距离为AB ＝1，AD ＝2，AC ＝CD ＝．1）求证： PD ⊥平面PAB ；在△ ACD 中，由 AD ＝2，AC ＝CD ＝，可得．4．如图，在四棱锥 P ﹣ABCD 中， AB ∥CD ，且∠ BAP ＝∠ CDP ＝901）证明：平面 PAB ⊥平面 PAD ；P ﹣ABCD 中，∠ BAP ＝∠ CDP ＝ 90°，∴AB ⊥PA ，CD ⊥PD ，又 AB ∥ CD ，∴ AB ⊥PD ，∵PA ∩PD ＝P ，∴ AB ⊥平面 PAD ，∵AB? 平面 PAB ，∴平面 PAB ⊥平面 PAD ．解：（2）设 PA ＝PD ＝AB ＝DC ＝a ，取 AD 中点O ，连结 PO ，∵PA ＝PD ＝AB ＝DC ，∠ APD ＝90°，平面 PAB ⊥平面 PAD ，∵四棱锥 P ﹣ABCD 的体积为由 AB ⊥平面 PAD ，得 AB ⊥ AD ，∴V P ﹣ABCD ＝2）若 PA ＝PD ＝ AB ＝ DC ，∠ APD ＝90°，且四棱锥 P ﹣ ABCD 的体积为求该四棱 ∴ PO ⊥底面ABCD ， O P＝＝＝＝，解得 a ＝2，∴ PA ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝2 ，PO ＝， ∴ PB ＝ PC ＝＝2 ，∴该四棱锥的侧面积：S 侧＝ S △PAD +S △PAB +S △PDC +S △PBC＝+1）证明： AC ⊥ BD ；2）已知△ ACD 是直角三角形， AB ＝ BD ，若 E 为棱 BD 上与 D 不重合的点， ∵△ ABC 是正三角形， AD ＝CD ，∴DO ⊥AC ，BO ⊥AC ，∵DO ∩BO ＝O ，∴ AC ⊥平面 BDO ，∵BD? 平面 BDO ，∴AC ⊥BD ．解：（2）法一：连结 OE ，由（ 1）知 AC ⊥平面 OBD ， ∵OE? 平面 OBD ，∴ OE ⊥ AC ，设 AD ＝ CD ＝，则 OC ＝ OA ＝ 1， EC ＝ EA ，2 2 2 ∵AE ⊥CE ，AC ＝2，∴ EC 2+EA 2＝AC 2，∴ EC ＝ EA ＝＝ CD ，∴E 是线段 AC 垂直平分线上的点，∴ EC ＝EA ＝CD ＝，由余弦定理得：AE ⊥＝ 6+2 ．AD ＝CD ．∵BE＜＜BD＝2，∴BE＝1，∴ BE＝ED ，∵四面体ABCE 与四面体ACDE 的高都是点 A 到平面BCD 的高h，∵ BE＝ED ，∴ S△DCE＝S△BCE，∴四面体ABCE 与四面体ACDE 的体积比为1．法二：设AD＝CD＝，则AC＝AB＝BC＝BD＝2，AO＝CO＝DO＝1，∴ BO＝＝，∴ BO2+DO2＝BD2，∴ BO⊥DO，以O 为原点，OA 为x 轴，OB 为y 轴，OD 为z 轴，建立空间直角坐标系，则C（﹣1，0，0），D（0，0，1），B（0，，0），A（1，0，0），设E（a，b，c），，（0≤λ≤1），则（a，b，c﹣1）＝λ（0，，﹣1），解得E（0，，1﹣λ），∴ ＝（1，），＝（﹣ 1 ，），∵AE⊥EC，∴＝﹣1+3λ2+ （1﹣λ）2＝0，由λ∈[0 ，1]，解得，∴ DE＝BE，∵四面体ABCE 与四面体ACDE 的高都是点 A 到平面BCD 的高h，∵DE＝BE，∴ S△DCE＝S△BCE，∴四面体ABCE 与四面体ACDE 的体积比为1．AEF⊥平面EFCB，EF＝2，四边形EFCB 是高为的等腰梯形，EF∥BC，O 为EF 的中点．1）求证：AO⊥CF；O 为EF 的中点，所以AO⊥ EF ⋯（ 1 分）又因为平面AEF⊥平面EFCB，AO? 平面AEF，平面AEF ∩平面EFCB ＝EF ，所以AO ⊥平面EFCB，⋯（ 4 分）又CF? 平面EFCB ，所以AO⊥ CF ⋯（ 5 分）（2）解：取BC 的中点G，连接OG．由题设知，OG⊥BC ⋯（ 6 分）由（1）知AO⊥平面EFCB ，又BC? 平面EFCB ，所以OA⊥BC，因为OG∩OA＝O，所以BC⊥平面AOG⋯（8 分）过O 作OH⊥AG，垂足为H，则BC⊥ OH ，因为AG∩BC＝G，所以OH⊥平面ABC．⋯（10 分）因为，所以，即O 到平面ABC 的距离为．（另外用等体积法亦可）⋯（12 分）10．直三棱柱ABC﹣A1B1C1 中，若∠ BAC＝90°，AB＝AC＝AA1，则异面直线BA1 与B1C 所成角的余弦值为（A．0 B．C．。

微专题12 立体几何中的平行与垂直问题答案

微专题12例题1证法1如图1，在四棱锥PABCD 中，取线段PD 的中点M ，连接FM ，AM.因为F 为PC 的中点，所以FM ∥CD ，且FM ＝12CD.因为四边形ABCD 为矩形，E 为AB 的中点，所以EA ∥CD ，且EA ＝12CD.所以FM ∥EA ，且FM ＝EA.所以四边形AEFM 为平行四边形．所以EF ∥AM. 又AM 平面PAD ，EF 平面PAD ，所以EF ∥平面PAD.证法2如图2，在四棱锥PABCD 中，连接CE 并延长交DA 的延长线于点N ，连接PN.因为四边形ABCD 为矩形，所以AD ∥BC.所以∠BCE ＝∠ANE ，∠CBE ＝∠NAE.又AE ＝EB ，所以△CEB ≌△NEA.所以CE ＝NE. 又F 为PC 的中点，所以EF ∥NP.又NP 平面PAD ，EF 平面PAD ，所以EF ∥平面PAD. 证法3如图3，在四棱锥PABCD 中，取CD 的中点Q ，连接FQ ，EQ.在矩形ABCD 中，E 为AB 的中点，所以AE ＝DQ ，且AE ∥DQ.所以四边形AEQD 为平行四边形，所以EQ ∥AD. 又AD 平面PAD ，EQ 平面PAD,所以EQ ∥平面PAD.因为Q ，F 分别为CD ，CP 的中点，所以FQ ∥PD.又PD 平面PAD ，FQ 平面PAD ，所以FQ ∥平面PAD. 又FQ ，EQ 平面EQF ，FQ ∩EQ ＝Q ，所以平面EQF ∥平面PAD.因为EF 平面EQF ，所以EF ∥平面PAD.(2)在四棱锥PABCD 中，设AC ，DE 相交于点G(如图4)．在矩形ABCD 中，因为AB ＝2BC ，E 为AB 的中点．所以DA AE ＝CDDA＝2，又∠DAE ＝∠CDA ，所以△DAE ∽△CDA ，所以∠ADE ＝∠DCA.又∠ADE ＋∠CDE ＝∠ADC ＝90°，所以∠DCA ＋∠CDE ＝90°.由△DGC 的内角和为180°，得∠DGC ＝90°. 即DE ⊥AC.因为点P 在平面ABCD 内的正投影O 在直线AC 上，所以PO ⊥平面ABCD.因为DE 平面ABCD ，所以PO ⊥DE. 因为PO ∩AC ＝O ，PO ，AC 平面PAC ，所以DE ⊥平面PAC ，又DE 平面PDE ，所以平面PAC ⊥平面PDE.变式联想变式1证明：(1)因为E ，F 分别是A 1D 1，B 1C 1的中点，所以EF ∥A 1B 1，在正方体ABCDA 1B 1C 1D 1中，A 1B 1∥AB ，所以EF ∥AB.又EF 平面ABHG ，AB平面ABHG ，所以EF ∥平面ABHG.(2)在正方体ABCDA 1B 1C 1D 1中，CD ⊥平面BB 1C 1C ，又BH 平面BB 1C 1C ，所以BH ⊥CD.① 设BH ∩CF ＝P ，△BCH ≌△CC 1F ，所以∠HBC ＝∠FCC 1，因为∠HBC ＋∠PHC ＝90°，所以∠FCC 1＋∠PHC ＝90°.所以∠HPC ＝90°，即BH ⊥CF.②由①②，又DC ∩CF ＝C ，DC ，CF 平面CFED ，所以BH ⊥平面CFED. 又BH 平面ABHG ，所以平面ABHG ⊥平面CFED.变式2证明：(1)如图，连接MN ，正三棱柱ABCA 1B 1C 1中，AA 1∥CC 1且AA 1＝CC 1，则四边形AA 1C 1C 是平行四边形，因为点M ，N 分别是棱A 1C 1，AC 的中点，所以MN ∥AA 1且MN ＝AA 1，又正三棱柱ABCA 1B 1C 1中AA 1∥BB 1且AA 1＝BB 1，所以MN ∥BB 1且MN ＝BB 1，所以四边形MNBB 1是平行四边形，所以B 1M ∥BN ，又B 1M 平面A 1BN ，BN 平面A 1BN ，所以B 1M ∥平面A 1BN.(2)正三棱柱ABCA 1B 1C 1中，AA 1⊥平面ABC ， BN 平面ABC ，所以BN ⊥AA 1，在正△ABC 中，N 是AB 的中点，所以BN ⊥AC ，又AA 1，AC 平面AA 1C 1C ，AA 1∩AC ＝A ，所以BN ⊥平面AA 1C 1C ，又AD 平面AA 1C 1C ，所以AD ⊥BN ，由题意得，AA 1＝6，AC ＝2，AN ＝1，CD ＝63，所以AA 1AC ＝ANCD＝32，又∠A 1AN ＝∠ACD ＝π2，所以△A 1AN 与△ACD 相似，则∠AA 1N ＝∠CAD ，所以∠ANA 1＋∠CAD ＝∠ANA 1＋∠AA 1N ＝π2，则AD ⊥A 1N ，又BN ∩A 1N ＝N ，BN ，A 1N平面A 1BN ，所以AD ⊥平面A 1BN. 说明：变式1和2都通过“计算”来证明垂直，复习时应注意长度，角度等量的“计算”的运用来实现位置关系的求证．串讲激活串讲1解析：(1)因为BC ⊥平面PAB ，AD 平面PAB ，所以BC ⊥AD.因为PA ＝AB ，D 为PB 的中点，所以AD ⊥PB.因为PB ∩BC ＝B ，所以AD ⊥平面PBC.(2)连接DC ，交PE 于点G ，连接FG.因为AD ∥平面PEF ，AD 平面ADC ，平面ADC ∩平面PEF ＝FG ，所以AD ∥FG.因为D 为PB 的中点，E 为BC 的中点，连接DE ，则DE 为△BPC 的中位线，△DEG ∽△CPG.所以DG GC ＝DE PC ＝12.所以AF FC ＝DG GC ＝12.串讲2解析：(1)在三棱台ABCDEF 中，AC ∥DF ，又AC 平面ACE ，DF 平面ACE ，所以DF ∥平面ACE ，又DF 平面DEF ，平面ACE ∩平面DEF ＝a ，所以DF ∥a.(2)线段BE 上存在点G ，且BG ＝13BE ，使得平面DFG ⊥平面CDE.证明如下：如图所示，取CE 的中点O ，连接FO 并延长交BE 于点G ，连接GD ，因为CF ＝EF ，所以GF ⊥CE.在三棱台ABCDEF 中，因为AB ⊥BC ，所以DE ⊥EF ，因为CF ⊥平面DEF ，DE 平面DEF ，所以CF ⊥DE ，又CF ∩EF ＝F ，所以DE ⊥平面CBEF ，GF 平面CBEF ，所以DE ⊥GF.因为GF ⊥CE ，DE ⊥GF ，CE ∩DE ＝E ，CE 平面CDE ，DE 平面CDE ，所以GF ⊥平面CDE ，又GF 平面DFG ，所以平面DFG ⊥平面CDE ，此时，侧面BCFE 的平面图如图所示，延长FG ，交CB 的延长线于点H ，因为O 是CE 的中点，EF ＝CF ＝2BC ，由平面几何知识可证得△HOC ≌△FOE ，所以HB ＝BC ＝12EF ，由△HGB ∽△FGE ，可知BG GE ＝12，即BG ＝13BE.新题在线(1)证法1取CE 中点F ，连接FB ，MF.因为M 为DE 的中点，F 为CE 的中点，所以MF ∥CD 且MF ＝12CD.又因为在矩形ABCD 中，N 为AB 的中点，所以BN ∥CD 且BN ＝12CD ，所以MF ∥BN 且MF ＝BN ，所以四边形BNMF 为平行四边形，所以MN ∥BF. 又MN 平面BEC ，BF 平面BEC ，所以MN ∥平面BEC.证法2取AE 中点G ，连接MG ，GN.因为G 为AE 的中点，M 为DE 的中点，所以MG ∥AD. 又因为在矩形ABCD 中，BC ∥AD ，所以MG ∥BC. 又因为MG 平面BEC ，BC 平面BEC ，所以MG ∥平面BEC.因为G为AE的中点，N为AB的中点，所以GN∥BE.又因为GN平面BEC，BE平面BEC，所以GN∥平面BEC.又因为MG∩GN＝G，MG，GN平面GMN，所以平面GMN∥平面BEC.又因为MN平面GMN，所以MN∥平面BEC.(2)因为四边形ABCD为矩形，所以BC⊥AB.因为平面ABCD⊥平面ABE，平面ABCD∩平面ABE＝AB，BC平面ABCD，且BC⊥AB，所以BC⊥平面ABE.因为AH平面ABE，所以BC⊥AH.因为AB＝AE，H为BE的中点，所以BE⊥AH.因为BC∩BE＝B，BC平面BEC，BE平面BEC，所以AH⊥平面BEC.又因为CE平面BEC，所以AH⊥CE.。

高一立体几何平行垂直解答题精选

高一立体几何平行垂直解答题精选1.空间四边形SABC中, SO⊥平面ABC, O为△ABC的重心。

求证:(1) AB⊥平面SOC。

(2) 平面SOC⊥平面SAB。

2.如图所示, 在正三棱柱ABC-A₁B₁C₁中,E, M分别为BB₁,A₁C的中点,求证:(1) EM⊥平面A A₁C₁C。

(2) 平面 A₁EC⊥平面AA₁C₁C。

3.如图,矩形ABCD中,AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.(1)求证:AE⊥平面BCE。

(2)求证:AE∥平面BPD.4.设P,Q 是边长为a的正方体 AC₁的面AA₁D₁D₁面 A₁B₁C₁D₁的中心,如图。

(1) 证明 PQ∥平面 AA₁B₁B₁(2) 求线段 PQ的长.5.如图,在四棱锥PABCD 中,PD ⊥面ABCD,AB ∥DC,AB ⊥AD,BC=5. DC=3, AD=4,∠PAD=60°,(1) 当主视图方向与向量 AD ⃗⃗⃗⃗⃗ 的方向相同时，画出四 PBC.7.如图,PA ⊥矩形ABCD 所在平面,M,N 分别是AB,PC 的中点。

6. 已知直四棱柱ABCD-A ₁B ₁C ₁D ₁的底面是菱形,且∠DAB=60°,AD=AA。

F 为棱 BB,的中点，M 为线段 AC ，的中点. 求证: (1)直线MF∥平面ABCD ₁ (2) 平面 AFC ₁⊥平面ACC ₁A ₂(1)求证: MN∥平面PAD 。

(2) 求证: MN⊥CD。

(3)若二面角P-DC-A-45°,求证: MN⊥平面PDC.8.如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC -90°. AB=BC=BB1=2. M, N 分别是AB, A1C 的中点.(1)求证: MN∥平面BCC1B1; (2)求证: MN⊥平面 AIBIC: (3)求三棱锥M-AIBIC 的体积.。

立体几何中线面平行的经典方法+经典题(附详细解答)

DB A 1高中立体几何证明平行的专题(基本方法)立体几何中证明线面平行或面面平行都可转化为线线平行，而证明线线平行一般有以下的一些方法： (1)通过“平移”。

(2)利用三角形中位线的性质。

(3)利用平行四边形的性质。

(4)利用对应线段成比例。

(5)利用面面平行，等等。

(1) 通过“平移”再利用平行四边形的性质1．如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分别为棱AB 、 PD 的中点．求证：AF ∥平面PCE ；分析：取PC 的中点G ，连EG.，FG ，则易证AEGF 是平行四边形2、如图，已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝1＋3，过A 作AE ⊥CD ，垂足为E ，G 、F 分别为AD 、CE 的中点，现将△ADE 沿AE 折叠，使得DE ⊥EC. （Ⅰ）求证：BC ⊥面CDE ；（Ⅱ）求证：FG ∥面BCD ；分析：取DB 的中点H ，连GH,HC 则易证FGHC 是平行四边形3、已知直三棱柱ABC －A 1B 1C 1中，D, E, F 分别为AA 1, CC 1, AB 的中点， M 为BE 的中点, AC ⊥BE. 求证：（Ⅰ）C 1D ⊥BC ；（Ⅱ）C 1D ∥平面B 1FM. 分析：连EA ，易证C 1EAD 是平行四边形，于是MF//EA（第1题图）4、如图所示, 四棱锥P -ABCD 底面是直角梯形,,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面;分析:：取PD 的中点F ，连EF,AF 则易证ABEF 是平行四边形(2) 利用三角形中位线的性质5、如图，已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点，求证：AM ∥平面EFG 。

分析：连MD 交GF 于H ，易证EH 是△AMD 的中位线6、如图，ABCD 是正方形，O 是正方形的中心，E 是PC 的中点。

高一平行与垂直的综合应用知识点+例题+练习含答案

1.证明方法(1)证明平行关系的方法：①证明线线平行的常用方法a.利用平行公理，即证明两直线同时和第三条直线平行；b.利用平行四边形进行转换；c.利用三角形中位线定理证明；d.利用线面平行、面面平行的性质定理证明.②证明线面平行的常用方法a.利用线面平行的判定定理，把证明线面平行转化为证线线平行；b.利用面面平行的性质定理，把证明线面平行转化为证面面平行.③证明面面平行的方法证明面面平行，依据判定定理，只要找到一个面内两条相交直线与另一个平面平行即可，从而将证面面平行转化为证线面平行，再转化为证线线平行.(2)证明空间中垂直关系的方法：①证明线线垂直的常用方法a.利用特殊平面图形的性质，如利用直角三角形、矩形、菱形、等腰三角形等得到线线垂直；b.利用勾股定理逆定理；c.利用线面垂直的性质，即要证线线垂直，只需证明一线垂直于另一线所在平面即可.②证明线面垂直的常用方法a.利用线面垂直的判定定理，把线面垂直的判定转化为证明线线垂直；b.利用面面垂直的性质定理，把证明线面垂直转化为证面面垂直；c.利用常见结论，如两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面.③证明面面垂直的方法证明面面垂直常用面面垂直的判定定理，即证明一个面过另一个面的一条垂线，将证明面面垂直转化为证明线面垂直，一般先从现有直线中寻找，若图中不存在这样的直线，则借助中点、高线或添加辅助线解决. 2.应特别注意的几个易错点定理图形语言易错点等角定理⎭⎪⎬⎪⎫∠AOB 和∠A ′O ′B ′中OA ∥O ′A ′，OB ∥O ′B ′且方向相同⇒∠AOB＝∠A ′O ′B ′易忽略“方向相同” 线面平行的判定定理 ⎭⎪⎬⎪⎫a ⊄α，b ⊂αa ∥b ⇒a ∥α易丢掉“a ⊄α”或“b⊂α” 线面平行的性质定理⎭⎪⎬⎪⎫a ∥α，a ⊂βα∩β＝b ⇒a ∥b易忽略“α∩β＝b ”直线和平面垂直的判定定理 ⎭⎪⎬⎪⎫l ⊥a ，l ⊥b a ⊂α，b ⊂αa ∩b ＝O⇒l ⊥α易忽略“a ∩b ＝O ”两个平面垂直的性质定理 ⎭⎪⎬⎪⎫α⊥βα∩β＝c a ⊂α，a ⊥c ⇒a ⊥β易忽略“a ⊂α”面面平行的判定定理⎭⎪⎬⎪⎫a ∥α，b ∥αa ⊂β，b ⊂βa ∩b ＝O ⇒α∥β易忽略“a ∩b ＝O ”面面平行的判定定理的推论 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⊂α，b ⊂αa ∩b ＝Oc ⊂β，d ⊂βc ∩d ＝O ′a ∥c ，b ∥d ⇒α∥β易忽略“a ∩b ＝O ”或“c ∩d ＝O ′”【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)若平面外一条直线上有两个点到平面的距离相等，则直线与平面平行.( × )(2)若直线a∥α，P∈α，则过点P且平行于a的直线有无数条.(×)(3)若a⊥b，b⊥c，则a∥c.(×)(4)α，β，γ为三个不同平面，α∥β，β∥γ⇒α∥γ.(√)(5)若α⊥γ，β⊥γ，且α∩β＝l，则l⊥γ.(√)(6)α⊥β，a⊥β，b⊥α⇒a∥b.(×)1.(教材改编)如图，已知平面α，β，且α∩β＝AB，PC⊥α，垂足为C，PD⊥β，垂足为D，则直线AB与CD的位置关系是________.答案AB⊥CD解析∵PC⊥α，∴PC⊥AB，又∵PD⊥β，∴PD⊥AB，∴AB⊥平面PCD，∴AB⊥CD.2.已知正方体ABCD—A1B1C1D1中，E，F，G分别为B1C1，A1D1，A1B1的中点，则平面EBD 与平面FGA的位置关系为________.答案平行3.如图所示，边长为a的正△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED 绕DE旋转过程中的一个图形，下列命题中错误的是________.①动点A′在平面ABC上的射影在线段AF上；②恒有平面A′GF⊥平面BCED；③三棱锥A′—FED的体积有最大值；④异面直线A′E与BD不可能互相垂直.答案④解析由题意知，DE⊥平面A′FG，又DE⊂平面ABC，所以平面A′FG⊥平面ABC，且它们的交线是AF ，过A ′作A ′H ⊥AF ，则A ′H ⊥平面ABC ，所以A ′在平面ABC 上的射影一定在线段AF 上，且平面A ′GF ⊥平面BCED ，故①②均正确；三棱锥A ′—EFD 的体积可以表示为V ＝13S △EFD ·A ′H ，当平面A ′DE ⊥平面ABC 时，A ′H 最大，故三棱锥A ′—EFD 的体积有最大值，故③正确；连结CD ，EH ，当CD ∥EH 时，BD ⊥EH ，又知EH 是A ′E 在平面ABC 内的射影，所以BD ⊥A ′E ，因此异面直线A ′E 与BD 可能垂直，故④错误.4.已知点P 是等腰三角形ABC 所在平面外一点，且P A ⊥平面ABC ，P A ＝8，在△ABC 中，底边BC ＝6，AB ＝5，则P 到BC 的距离为________. 答案 4 5解析取BC 的中点D ，连结AD ，PD .∵AD ⊥BC ，P A ⊥BC ，且AD ∩P A ＝A ，∴BC ⊥平面P AD ，∴BC ⊥PD ， ∴在Rt △P AD 中，PD ＝82＋42＝4 5.5.(教材改编)如图，在三棱锥V —ABC 中，∠VAB ＝∠VAC ＝∠ABC ＝90°，则平面VBA 与平面VBC 的位置关系为_____________________________________________________.答案垂直解析 ∵∠VAB ＝∠VAC ＝∠ABC ＝90°， ∴BC ⊥AB ，VA ⊥AC ，VA ⊥AB ，由⎭⎪⎬⎪⎫VA ⊥AB VA ⊥AC ⇒VA ⊥平面ABC ， ∴VA ⊥BC ，由⎭⎪⎬⎪⎫VA ⊥BC AB ⊥BC ⇒BC ⊥平面VAB ∴BC ⊥AB ，又BC ⊂平面VBC ， ∴平面VBC ⊥平面VBA.题型一线、面平行垂直关系的判定例1 (1)如图所示，在直棱柱ABC —A 1B 1C 1中，若D 是AB 的中点，则AC 1与平面CDB 1的关系为________.①AC 1∥平面CDB 1； ②AC 1在平面CDB 1中； ③AC 1与平面CDB 1相交； ④无法判断关系.(2)已知m ，n 为直线，α，β为平面，给出下列命题：①⎩⎪⎨⎪⎧ m ⊥α，m ⊥n ⇒n ∥α；②⎩⎪⎨⎪⎧m ⊥β，n ⊥β⇒m ∥n ； ③⎩⎪⎨⎪⎧m ⊥α，m ⊥β⇒α∥β；④⎩⎪⎨⎪⎧m ⊂α，n ⊂β，α∥β⇒m ∥n .其中正确的命题是________. 答案 (1)① (2)②③解析 (1)连结BC 1，BC 1与CB 1交于E 点，(如图)连结DE ，则DE ∥AC 1，又DE ⊂平面CDB 1，AC 1⊄平面CDB 1， ∴AC 1∥平面CDB 1.(2)对于①，n 可能在α内；对于④，m 与n 可能异面.易知②，③是真命题. 思维升华对线面平行、垂直关系的判定：(1)易忽视判定定理与性质定理的条件，如易忽视线面平行的判定定理中直线在平面外这一条件；(2)结合题意构造或绘制图形，结合图形作出判断；(3)可举反例否定结论或用反证法判断结论是否正确.(1)在正方形SG1G2G3中，E，F分别为G1G2，G2G3的中点.现在沿SE，SF及EF 把这个正方形折成一个四面体，使点G1，G2，G3重合，记为点G，则SG与平面EFG的位置关系为________.答案垂直解析翻折后SG⊥EG，SG⊥FG，从而SG⊥平面EFG.(2)已知三个平面α，β，γ.若α∥β，α∩γ＝a，β∩γ＝b，且直线c⊂β，c∥b.①判断c与α的位置关系，并说明理由；②判断c与a的位置关系，并说明理由.解①c∥α，∵α∥β，∴α与β没有公共点.又∵c⊂β，∴c与α无公共点，故c∥α.②c∥a.∵α∥β，∴α与β没有公共点.又α∩γ＝a，β∩γ＝b，∴a⊂α，b⊂β，且a，b⊂γ，∴a∥b.又c∥b，∴a∥c.题型二平行与垂直关系的证明命题点1线面平行的证明例2在正方体ABCD—A1B1C1D1中，E，F分别为棱BC，C1D1的中点.求证：EF∥平面BB1D1D. 证明如图所示，连结AC交BD于点O，连结OE，则OE∥DC，OE＝12DC.∵DC∥D1C1，DC＝D1C1，F为D1C1的中点，∴OE∥D1F，OE＝D1F，∴四边形D1FEO为平行四边形，∴EF∥D1O.又∵EF ⊄平面BB1D1D，D1O⊂平面BB1D1D，∴EF∥平面BB1D1D.命题点2面面平行的证明例3如图所示，已知正方体ABCD—A1B1C1D1.(1)求证：平面A1BD∥平面B1D1C.(2)若E，F分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD.证明(1)∵B1B∥DD1，B1B＝D1D，∴四边形BB1D1D是平行四边形，∴B1D1∥BD，又BD⊂平面A1BD，B1D1⊂平面B1D1C，∴BD∥平面B1D1C.同理A1D∥平面B1D1C，又∵A1D∩BD＝D，A1D，BD⊂平面A1BD，∴平面A1BD∥平面B1D1C.(2)由BD∥B1D1，得BD∥平面EB1D1.如图所示，取BB1的中点G，连结AG，GF，易得AE∥B1G，又∵AE＝B1G，∴四边形AEB1G是平行四边形，∴B1E∥AG.同理GF ∥AD .又∵GF ＝AD ， ∴四边形ADFG 是平行四边形，∴AG ∥DF ，∴B 1E ∥DF ，∴DF ∥平面EB 1D 1. 又∵BD ∩DF ＝D ， ∴平面EB 1D 1∥平面FBD . 命题点3 直线与平面垂直的证明例4 如图，在多面体ABCDEF 中，四边形ABCD 是菱形，AC 、BD 相交于点O ，EF ∥AB ，AB ＝2EF ，平面BCF ⊥平面ABCD ，BF ＝CF ，点G 为BC 的中点.(1)求证：OG ∥平面EFCD ； (2)求证：AC ⊥平面ODE .证明 (1)∵四边形ABCD 是菱形，AC ∩BD ＝O ， ∴点O 是BD 的中点，∵点G 为BC 的中点，∴OG ∥CD ，又∵OG ⊄平面EFCD ，CD ⊂平面EFCD ， ∴OG ∥平面EFCD .(2)∵BF ＝CF ，点G 为BC 的中点，∴FG ⊥BC . ∵平面BCF ⊥平面ABCD ，平面BCF ∩平面ABCD ＝BC ， FG ⊂平面BCF ，FG ⊥BC ， ∴FG ⊥平面ABCD .∵AC ⊂平面ABCD ，∴FG ⊥AC ，∵OG ∥AB ，OG ＝12AB ，EF ∥AB ，EF ＝12AB ，∴OG ∥EF ，OG ＝EF ，∴四边形EFGO为平行四边形，∴FG∥EO.∵FG⊥AC，FG∥EO，∴AC⊥EO.∵四边形ABCD是菱形，∴AC⊥DO，∵EO∩DO＝O，EO、DO在平面ODE内，∴AC⊥平面ODE.命题点4面面垂直的证明例5如图所示，在正三棱柱ABC—A1B1C1中，E为BB1的中点，求证：截面A1CE⊥侧面ACC1A1.证明如图所示，取A1C的中点F，AC的中点G，连结FG，EF，BG，则FG∥AA1，且GF＝12AA1.因为BE＝EB1，A1B1＝CB，∠A1B1E＝∠CBE＝90°，所以△A1B1E≌△CBE，所以A1E＝CE.因为F为A1C的中点，所以EF⊥A1C.又FG∥AA1∥BE，GF＝12AA1＝BE，且BE⊥BG，所以四边形BEFG是矩形，所以EF⊥FG.因为A1C∩FG＝F，所以EF ⊥侧面ACC 1A 1. 又因为EF ⊂平面A 1CE ，所以截面A 1CE ⊥侧面ACC 1A 1. 命题点5 平行、垂直的综合证明例6 如图，四边形ABCD 是正方形，DE ⊥平面ABCD .(1)求证：AC ⊥平面BDE ；(2)若AF ∥DE ，DE ＝3AF ，点M 在线段BD 上，且BM ＝13BD ，求证：AM ∥平面BEF .证明 (1)因为DE ⊥平面ABCD ，所以DE ⊥AC .因为四边形ABCD 是正方形，所以AC ⊥BD .又BD ∩DE ＝D ，从而AC ⊥平面BDE .(2)如图，延长EF ，DA 交于点G .因为AF ∥DE ，DE ＝3AF ，所以GA GD ＝AF DE ＝13.因为BM ＝13BD ，所以BM BD ＝13，所以BM BD ＝GA GD ＝13，所以AM ∥GB .又AM ⊄平面BEF ，GB ⊂平面BEF ，所以AM ∥平面BEF .思维升华 (1)空间线面的位置关系的判定方法①证明直线与平面平行，设法在平面内找到一条直线与已知直线平行，解答时合理利用中位线性质、线面平行的性质，或构造平行四边形，寻求比例关系确定两直线平行.②证明直线与平面垂直，主要途径是找到一条直线与平面内的两条相交直线垂直.解题时注意分析观察几何图形，寻求隐含条件.(2)空间面面的位置关系的判定方法①证明面面平行，需要证明线面平行，要证明线面平行需证明线线平行，将“面面平行”问题转化为“线线平行”问题.②证明面面垂直，将“面面垂直”问题转化为“线面垂直”问题，再将“线面垂直”问题转化为“线线垂直”问题.如图，四边形AA1C1C为矩形，四边形CC1B1B为菱形，且平面CC1B1B⊥平面AA1C1C，D，E分别为边A1B1，C1C的中点.求证：(1)BC1⊥平面AB1C；(2)DE∥平面AB1C.证明(1)∵四边形AA1C1C为矩形，∴AC⊥C1C.又平面CC1B1B⊥平面AA1C1C，平面CC1B1B∩平面AA1C1C＝CC1，∴AC⊥平面CC1B1B.∵BC1⊂平面CC1B1B，∴AC⊥BC1.又四边形CC1B1B为菱形，∴B1C⊥BC1.∵B1C∩AC＝C，∴BC1⊥平面AB1C.(2)取AA1的中点F，连结DF，EF.∵四边形AA1C1C为矩形，E，F分别为C1C，AA1的中点，∴EF∥AC.∵EF⊄平面AB1C，AC⊂平面AB1C，∴EF ∥平面AB 1C .∵D ，F 分别为边A 1B 1，AA 1的中点，∴DF ∥AB 1. ∵DF ⊄平面AB 1C ，AB 1⊂平面AB 1C ， ∴DF ∥平面AB 1C .∵EF ∩DF ＝F ，EF ⊂平面DEF ，DF ⊂平面DEF ， ∴平面DEF ∥平面AB 1C .∵DE ⊂平面DEF ，∴DE ∥平面AB 1C .题型三平行与垂直的应用例7 (2015·安徽)如图，三棱锥P -ABC 中，P A ⊥平面ABC ，P A ＝1，AB ＝1，AC ＝2，∠BAC ＝60°.(1)求三棱锥P -ABC 的体积；(2)证明：在线段PC 上存在点M ，使得AC ⊥BM ，并求PMMC的值.(1)解由题设AB ＝1，AC ＝2，∠BAC ＝60°，可得S △ABC ＝12·AB ·AC ·sin 60°＝32.由P A ⊥平面ABC ，可知P A 是三棱锥P -ABC 的高，又P A ＝1. 所以三棱锥P -ABC 的体积V ＝13·S △ABC ·P A ＝36.(2)证明在平面ABC 内，过点B 作BN ⊥AC ，垂足为N ，在平面P AC 内，过点N 作MN ∥P A 交PC 于点M ，连结BM .由P A ⊥平面ABC 知P A ⊥AC ，所以MN ⊥AC .由于BN ∩MN ＝N ，故AC ⊥平面MBN ，又BM ⊂平面MBN ，所以AC ⊥BM .在Rt △BAN 中，AN ＝AB ·cos ∠BAC ＝12，从而NC ＝AC －AN ＝32，由MN ∥P A ，得PM MC ＝ANNC＝13.思维升华(1)利用平行关系可以转移点到面的距离，从而求几何体体积或解决关于距离的最值问题.(2)对于存在性问题的证明与探索有三种途径：途径一：先猜后证，即先观察与尝试给出条件再证明；途径二：先通过命题成立的必要条件探索出命题成立的条件，再证明充分性.途径三：将几何问题转化为代数问题，探索出命题成立的条件.如图，在四棱锥P—ABCD中，底面ABCD是矩形，P A⊥平面ABCD，P A＝AD ＝1，AB＝3，点F是PD的中点，点E是边DC上的任意一点.(1)当点E为DC边的中点时，判断EF与平面P AC的位置关系，并加以证明；(2)证明：无论点E在边DC的何处，都有AF⊥EF；(3)求三棱锥B—AFE的体积.(1)解当点E为DC边的中点时，EF与平面P AC平行.证明如下：在△PDC中，E，F分别为DC，PD的中点，∴EF∥PC，又EF⊄平面P AC，而PC⊂平面P AC，∴EF∥平面P AC.(2)证明∵P A⊥平面ABCD，CD⊂平面ABCD，∴P A⊥CD.∵四边形ABCD是矩形，∴CD⊥AD.∵AD∩AP＝A，∴CD⊥平面P AD.又AF⊂平面P AD，∴AF⊥CD.∵P A＝AD，点F是PD的中点，∴AF⊥PD.又CD∩PD＝D，∴AF⊥平面PCD.∵EF⊂平面PCD，∴AF⊥EF.即无论点E 在边DC 的何处，都有AF ⊥EF .(3)解作FG ∥P A 交AD 于G ，则FG ⊥平面ABCD ，且FG ＝12，又S △ABE ＝32，∴V B —AEF ＝V F —AEB ＝13S △ABE ·FG ＝312.∴三棱锥B —AFE 的体积为312.6.立体几何平行、垂直的证明问题典例 (14分)(2014·北京)如图，在三棱柱ABC －A 1B 1C 1中，侧棱垂直于底面，AB ⊥BC ，AA 1＝AC ＝2，BC ＝1，E ，F 分别是A 1C 1，BC 的中点.(1)求证：平面ABE ⊥平面B 1BCC 1； (2)求证：C 1F ∥平面ABE ； (3)求三棱锥E －ABC 的体积. 规范解答(1)证明在三棱柱ABC －A 1B 1C 1中，BB 1⊥底面ABC ，所以BB 1⊥AB .[1分] 又因为AB ⊥BC ，所以AB ⊥平面B 1BCC 1，[2分] 又AB ⊂平面ABE ，所以平面ABE ⊥平面B 1BCC 1.[3分](2)证明取AB 的中点G ，连结EG ，FG .[4分]因为E ，F 分别是A 1C 1，BC 的中点，所以FG ∥AC ，且FG ＝12AC .[6分]因为AC ∥A 1C 1，且AC ＝A 1C 1，所以FG ∥EC 1，且FG ＝EC 1，所以四边形FGEC 1为平行四边形. 所以C 1F ∥EG .[8分]又因为EG ⊂平面ABE ，C 1F ⊄平面ABE ，所以C 1F ∥平面ABE .[10分](3)解因为AA 1＝AC ＝2，BC ＝1，AB ⊥BC ，所以AB ＝AC 2－BC 2＝ 3.[12分]所以三棱锥E －ABC 的体积 V ＝13S △ABC ·AA 1＝13×12×3×1×2＝33.[14分]证明线面平行问题(一)第一步：作(找)出所证线面平行中的平面内的一条直线. 第二步：证明线线平行.第三步：根据线面平行的判定定理证明线面平行. 第四步：反思回顾.检测关键点及答题规范. 证明线面平行问题(二)第一步：在多面体中作出要证线面平行中的线所在的平面.第二步：利用线面平行的判定定理证明所作平面内的两条相交直线分别与所证平面平行；第三步：证明所作平面与所证平面平行. 第四步：转化为线面平行. 第五步：反思回顾，检查答题规范. 证明面面垂直问题第一步：根据已知条件确定一个平面内的一条直线垂直于另一个平面内的一条直线. 第二步：结合已知条件证明确定的这条直线垂直于另一平面内的两条相交直线.第三步：得出确定的这条直线垂直于另一平面.第四步：转化为面面垂直.第五步：反思回顾，检查答题规范.温馨提醒(1)证线面平行的方法：①利用判定定理，关键是找平面内与已知直线平行的直线.可先直观判断平面内是否已有，若没有，则需作出该直线，常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.②若要借助于面面平行来证明线面平行，则先要确定一个平面经过该直线且与已知平面平行，此目标平面的寻找方法是经过线段的端点作该平面的平行线.(2)证明两个平面垂直，通常是通过证明线线垂直→线面垂直→面面垂直来实现，因此，在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化.[方法与技巧]1.在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，其转化关系为在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”.2.空间中直线与直线垂直、直线与平面垂直、平面与平面垂直三者之间可以相互转化，每一种垂直的判定都是从某种垂直开始转向另一种垂直最终达到目的，其转化关系为在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决.[失误与防范]1.在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.2.线面平行关系证明的难点在于辅助面和辅助线的添加，在添加辅助线、辅助面时一定要以某一性质定理为依据，绝不能主观臆断.3.在用线面垂直的判定定理证明线面垂直时，考生易忽视说明平面内的两条直线相交，而导致被扣分，这一点在证明中要注意.口诀：线不在多，重在相交.4.面面垂直的性质定理在立体几何中是一个极为关键的定理，这个定理的主要作用是作一个平面的垂线，在一些垂直关系的证明中，很多情况都要借助这个定理作出平面的垂线.注意定理使用的条件，在推理论证时要把定理所需要的条件列举完整，同时要注意推理论证的层次性，确定先证明什么、后证明什么.A组专项基础训练(时间：45分钟)1.设α，β为两个不重合的平面，l，m，n为两两不重合的直线，给出下列四个命题：①若α∥β，l⊂α，则l∥β；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；③若l∥α，l⊥β，则α⊥β；④若m，n是异面直线，m∥α，n∥α，且l⊥m，l⊥n，则l⊥α.其中真命题的序号是________.答案①③④解析①由α∥β，l⊂α知，l与β无公共点，故l∥β.②当m⊂α，n⊂α，m与n相交，m∥β，n∥β时，α∥β.③由l∥α知，α内存在l′，使得l′∥l.因为l⊥β，所以l′⊥β，故α⊥β.④易知α内存在m′，n′，使得m′∥m，n′∥n，且m′，n′相交，由l⊥m，l⊥n知，l⊥m′且l⊥n′，故l⊥α.2.已知平面α，β，直线m，n，给出下列命题：①若m∥α，n∥β，m∥n，则α∥β；②若α∥β，m∥α，n∥β，则m∥n；③若m⊥α，n⊥β，m⊥n，则α⊥β；④若α⊥β，m⊥α，n⊥β，则m⊥n.其中是真命题的是________.(填写所有真命题的序号)答案③④解析对于①，平面α与β可能相交，故①错；对于②，若α∥β，m∥α，n∥β，则直线m 与n可能平行，可能相交，也可能异面，故②错；对于③，由面面垂直的判定可知③正确；对于④，由面面垂直的性质可知m⊥n，故④正确.因此真命题的序号为③④.3.在四棱锥P—ABCD中，P A⊥底面ABCD，底面各边都相等，M是PC上一动点，当M满足是________时，平面MBD⊥平面ABCD.答案PC的中点解析当M 是PC 中点时，连结AC ，BD 交于O ，由题意知，O 是AC 的中点，连结MO ，则MO ∥P A .∵P A ⊥平面ABCD ，∴MO ⊥平面ABCD ，MO ⊂平面MBD ，∴平面MBD ⊥平面ABCD . 4.如图，ABCD 是空间四边形，E ，F ，G ，H 分别是四边上的点，且它们共面，并且AC ∥平面EFGH ，BD ∥平面EFGH ，AC ＝m ，BD ＝n ，当EFGH 是菱形时，AE ∶EB ＝________.答案m n解析设AE ＝a ，EB ＝b ，由题意知，EF ∥AC ，得EF ＝bm a ＋b ，同理EH ＝ana ＋b.因为EF ＝EH ，所以bm a ＋b ＝an a ＋b，所以a b ＝mn .5.如图，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，底面是以∠ABC 为直角的等腰直角三角形，AC ＝2a ，BB 1＝3a ，D 是A 1C 1的中点，点F 在线段AA 1上，当AF ＝________时，CF ⊥平面B 1DF .答案 a 或2a解析由题意易知，B 1D ⊥平面ACC 1A 1，所以B 1D ⊥CF .要使CF ⊥平面B 1DF ，只需CF ⊥DF 即可. 令CF ⊥DF ，设AF ＝x ，则A 1F ＝3a －x . 易知Rt △CAF ∽Rt △F A 1D ，得AC AF ＝A 1F A 1D ，即2a x ＝3a －x a ，整理得x 2－3ax ＋2a 2＝0，解得x ＝a 或x ＝2a .6.如图，四棱锥P —ABCD 的底面ABCD 是平行四边形，平面PBD ⊥平面ABCD ，PB ＝PD ，P A ⊥PC ，CD ⊥PC ，O ，M 分别是BD ，PC 的中点，连结OM .求证：(1)OM ∥平面P AD ； (2)OM ⊥平面PCD .证明 (1)连结AC .因为四边形ABCD 是平行四边形，所以O 为AC 的中点.在△P AC 中，因为O ，M 分别是AC ，PC 的中点，所以OM ∥P A . 因为OM ⊄平面P AD ，P A ⊂平面P AD ，所以OM ∥平面P AD .(2)连结PO .因为O 是BD 的中点，PB ＝PD ，所以PO ⊥BD .因为平面PBD ⊥平面ABCD ，平面PBD ∩平面ABCD ＝BD ，PO ⊂平面PBD ，所以PO ⊥平面ABCD ，从而PO ⊥CD . 因为CD ⊥PC ，PC ∩PO ＝P ， PC ⊂平面P AC ，PO ⊂平面P AC ，所以CD ⊥平面P AC .因为OM ⊂平面P AC ，所以CD ⊥OM .因为P A⊥PC，OM∥P A，所以OM⊥PC.因为CD⊂平面PCD，PC⊂平面PCD，CD∩PC＝C，所以OM⊥平面PCD.7.如图所示，在正方体ABCD－A1B1C1D1中，E是棱DD1的中点.(1)证明：平面ADC1B1⊥平面A1BE；(2)在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论.(1)证明如图，因为ABCD－A1B1C1D1为正方体，所以B1C1⊥面ABB1A1.因为A1B⊂面ABB1A1，所以B1C1⊥A1B.又因为A1B⊥AB1，B1C1∩AB1＝B1，所以A1B⊥面ADC1B1.因为A1B⊂面A1BE，所以平面ADC1B1⊥平面A1BE.(2)解当点F为C1D1中点时，可使B1F∥平面A1BE.证明如下：易知：EF∥C1D，且EF＝12C1D.设AB1∩A1B＝O，则B1O∥C1D且B1O＝12C1D，所以EF∥B1O且EF＝B1O，所以四边形B1OEF为平行四边形.所以B1F∥OE.又因为B1F⊄面A1BE，OE⊂面A1BE.8.如图所示，在正方体ABCD—A1B1C1D1中，E，F分别是棱DD1，C1D1的中点.(1)证明：平面ADC1B1⊥平面A1BE；(2)证明：B1F∥平面A1BE；(3)若正方体棱长为1，求四面体A1—B1BE的体积.(1)证明如图，连结AB1.因为ABCD—A1B1C1D1为正方体，所以B1C1⊥平面ABB1A1.因为A1B ⊂平面ABB1A1，所以B1C1⊥A1B.因为A1B⊥AB1，B1C1∩AB1＝B1，所以A1B⊥平面ADC1B1.因为A1B⊂平面A1BE，所以平面ADC1B1⊥平面A1BE.(2)证明如图，连结EF，DC1，OE，B1F.由已知条件得EF∥C1D，且EF＝12C1D.设AB1∩A1B＝O，则B1O∥C1D且B1O＝12C1D，所以EF∥B1O且EF＝B1O，所以四边形B1OEF为平行四边形，所以B1F∥OE.因为B1F⊄平面A1BE，OE⊂平面A1BE，(3)解 VA 1—B 1BE ＝VE —A 1B 1B ＝13S △A 1B 1B ·B 1C 1＝16. B 组专项能力提升(时间：25分钟)9.在正四面体P —ABC 中，D ，E ，F 分别是AB ，BC ，CA 的中点，给出下面三个结论： ①BC ∥平面PDF ；②DF ⊥平面P AE ；③平面PDF ⊥平面ABC .其中不成立．．．的结论是________.(填写所有不成立的结论的序号) 答案 ③解析如图，由题知BC ∥DF ，∴BC ∥平面PDF .∵四面体P —ABC 为正四面体，∴BC ⊥P A ，AE ⊥BC ，BC ⊥平面P AE ，∴DF ⊥平面P AE ，∴平面P AE ⊥平面ABC ，∴①和②成立.设此正四面体的棱长为1，则P A ＝1，AM ＝34，PM 2＝PD 2－DM 2＝⎝⎛⎭⎫322－⎝⎛⎭⎫142＝1116，∴P A 2≠AM 2＋PM 2，故③不成立.10.如图，过四棱柱ABCD —A 1B 1C 1D 1的木块上底面内的一点P 和下底面的对角线BD 将木块锯开，得到截面BDEF .(1)请在木块的上表面作出过点P 的锯线EF ，并说明理由；(2)若该四棱柱的底面为菱形，四边形BB1D1D是矩形，试证明：平面BDEF⊥平面ACC1A1.(1)解在上底面内过点P作B1D1的平行线分别交A1D1，A1B1于E，F两点，则EF为所作的锯线.在四棱柱ABCD—A1B1C1D1中，侧棱B1B∥D1D，B1B＝D1D，所以四边形BB1D1D是平行四边形，B1D1∥BD.又EF∥B1D1，所以EF∥BD，故EF为截面BDEF与平面A1B1C1D1的交线，故EF为所作锯线.如图所示.(2)证明由于四边形BB1D1D是矩形，所以BD⊥B1B.又A1A∥B1B，所以BD⊥A1A.又四棱柱的底面为菱形，所以BD⊥AC.因为AC∩A1A＝A，所以BD⊥平面A1C1CA.因为BD⊂平面BDEF，所以平面BDEF⊥平面A1C1CA.11.如图，P A垂直于矩形ABCD所在的平面，AD＝P A＝2，CD＝22，E，F分别是AB，PD 的中点.(1)求证：AF∥平面PCE；(2)求证：平面PCE⊥平面PCD；(3)求四面体PECF的体积.(1)证明设G为PC的中点，连结FG，EG.∵F 为PD 的中点，E 为AB 的中点，∴FG 綊12CD ，AE 綊12CD ，∴FG 綊AE ， ∴四边形AEGF 为平行四边形，∴AF ∥GE . ∵GE ⊂平面PEC ，AF ⊄平面PEC ， ∴AF ∥平面PCE .(2)证明 ∵P A ＝AD ＝2，∴AF ⊥PD .又∵P A ⊥平面ABCD ，CD ⊂平面ABCD ， ∴P A ⊥CD .∵AD ⊥CD ，P A ∩AD ＝A ，∴CD ⊥平面P AD .∵AF ⊂平面P AD ，∴AF ⊥CD .∵PD ∩CD ＝D ，∴AF ⊥平面PCD ，∴GE ⊥平面PCD .∵GE ⊂平面PEC ，∴平面PCE ⊥平面PCD .(3)解由(2)知GE ⊥平面PCD ，所以EG 为四面体PEFC 的高，又EG ＝AF ＝2，CD ＝22，S △PCF ＝12PF ·CD ＝2，所以四面体PEFC 的体积V ＝13S △PCF ·EG ＝223.。

专题08 立体几何中的平行与垂直问题(解析版)

专题08立体几何中的平行与垂直问题【考点预测】1.证明空间中直线、平面的平行关系（1）证明直线与平面平行的常用方法：①利用定义，证明直线a 与平面α没有公共点，一般结合反证法证明；②利用线面平行的判定定理，即线线平行⇒线面平行.辅助线的作法为：平面外直线的端点进平面，同向进面，得平行四边形的对边，不同向进面，延长交于一点得平行于第三边的线段；③利用面面平行的性质定理，把面面平行转化成线面平行；（2）证明面面平行的常用方法：①利用面面平行的定义，此法一般与反证法结合；②利用面面平行的判定定理；③利用两个平面垂直于同一条直线；④证明两个平面同时平行于第三个平面.（3）证明线线平行的常用方法：①利用直线和平面平行的判定定理；②利用平行公理；2.证明空间中直线、平面的垂直关系（1）证明线线垂直的方法①等腰三角形底边上的中线是高；②勾股定理逆定理；③菱形对角线互相垂直；④直径所对的圆周角是直角；⑤向量的数量积为零；⑥线面垂直的性质（）；⑦平行线垂直直线的传递性（∥）.（2）证明线面垂直的方法①线面垂直的定义；②线面垂直的判定（）； ③面面垂直的性质（）；平行线垂直平面的传递性（∥）；⑤面面垂直的性质（）. （3）证明面面垂直的方法①面面垂直的定义；②面面垂直的判定定理（）.,a b a b αα⊥⊂⇒⊥,a c a ⊥b b c ⇒⊥,,,,a b a c c b bc P a ααα⊥⊥⊂⊂=⇒⊥,,,b a b a a αβαβαβ⊥=⊥⊂⇒⊥,a b α⊥a b α⇒⊥,,l l αγβγαβγ⊥⊥=⇒⊥,a a βααβ⊥⊂⇒⊥【典型例题】例1．（2022·全国·高一课时练习）下列命题：①垂直于同一条直线的两个平面互相平行；②垂直于同一个平面的两条直线互相平行；③一条直线在平面内，另一条直线与这个平面垂直，则这两条直线互相垂直．其中正确的个数是（）A ．0B ．1C ．2D ．3【答案】D【解析】【分析】①应用反证法：AB α⊥于A ，AB β⊥于B ，假设,αβ不平行，利用线面垂直的性质及三角形的内角和得到矛盾，即可判断；②③根据线面垂直的性质判断即可.【详解】①如下图，若AB α⊥于A ，AB β⊥于B ，假设,αβ不平行，则,αβ相交，，令l αβ=，在l 任找一点C ，连接,AC BC ，则,,A B C 为三角形，由,AC BC αβ⊂⊂，则AB AC ⊥，AB BC ⊥，即90BAC ABC ∠=∠=︒，显然,,A B C 不能构成三角形，与假设矛盾，所以,αβ平行，正确.②由线面垂直的性质定理知：垂直于同一个平面的两条直线互相平行，正确；③由线面垂直的性质知：一条直线与平面垂直，则垂直于平面内所有直线，正确；故选：D例2．（2022·河南开封·高一期中）已知直线a ，b ，平面,αβ，则下列命题中正确的是（）A ．,a αβα⊥⊂，则a β⊥B ．//,//a αβα，则a β∥C ．//,a b ββ⊂，则//a bD ．a 与b 互为异面直线，//,//,//,//a a b b αβαβ，则//αβ【答案】D【解析】【分析】根据空间中直线与直线、直线与平面、平面与平面的位置关系判断即可.【详解】A 选项中，只有直线a 与两平面的交线垂直的时候结论才成立；B 选项中，还有可能a β⊂；C 选项中，两直线a ，b 平行或异面；D 选项中，过直线a 上一点做//b b '，则相交直线a ，b '确定一个平面，设为γ，易得//γα且//γβ，所以//αβ；故选：D ．（多选题）例3．（2022·河南开封·高一期中）如图，在棱长均相等的正四棱锥P ABCD -中，M 、N 分别为侧棱PA 、PB 的中点，O 是底面四边形ABCD 对角线的交点，下列结论正确的有（）A ．//PC 平面OMNB ．平面//PCD 平面OMNC ．OM PA ⊥D ．PD ⊥平面OMN【答案】ABC【解析】【分析】 A 选项，由中位线证明线线平行，推导出线面平行；B 选项，在A 选项的基础上证明面面平行；从而推导出D 错误；由勾股定理的逆定理得到PA PC ⊥，从而得到OM PA ⊥.【详解】因为O 为底面四边形ABCD 对角线的交点，所以O 为AC 的中点，由M 是PA 的中点，可得∥PC MO ，因为PC ⊄在平面OMN ，OM ⊂平面OMN ，所以//PC 平面OMN ，A 正确；同理可推得//PD 平面OMN ，⋂=，而PC PD PPCD平面OMN，B正确；所以平面//因为PD⊂平面PCD，故PD不可能垂直平面OMN，D错误；设该正四棱锥的棱长为a，则,2PA PC a AC a，===⊥，所以PA PCPC MO，因为∥⊥，C正确.所以OM PA故选ABC．例4．（2022·全国·高一课时练习）如图，三棱台DEFABC中，AB＝2DE，G，H分别为AC，BC的中点．(1)求证：BD∥平面FGH；(2)若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH．【答案】(1)证明见解析(2)证明见解析【解析】【分析】（1）由已知，连接DG，CD与FG交与点M，先证明四边形CFDG是平行四边形，从而得到DM＝MC．结合BH＝HC，可证明MH∥BD，再使用线面平行的判定定理即可证明；（2）先证明四边形EFCH是平行四边形，从而得到CF∥HE．因为CF⊥BC，所以HE⊥BC，再证明GH∥AB，因为AB⊥BC，所以GH⊥BC，从而利用线面垂直的判定定理证明BC⊥平面EGH，再使用面面垂直的判定定理即可完成证明.(1)如图所示，连接DG ，设CD ∩GF ＝M ，连接MH ．在三棱台DEF ABC 中，AB ＝2DE ，所以AC ＝2DF ．因为G 是AC 的中点，所以DF ∥GC ，且DF ＝GC ，所以四边形CFDG 是平行四边形，所以DM ＝MC ．因为BH ＝HC ，所以MH ∥BD ．又BD ⊄平面FGH ，MH ⊂平面FGH ，所以BD ∥平面FGH ．(2)因为G ，H 分别为AC ，BC 的中点，所以GH ∥AB ．因为AB ⊥BC ，所以GH ⊥BC ．又H 为BC 的中点，所以EF ∥HC ，EF ＝HC ，所以四边形EFCH 是平行四边形，所以CF ∥HE ．因为CF ⊥BC ，所以HE ⊥BC ．又HE ，GH ⊂平面EGH ，HE ∩GH ＝H ，所以BC ⊥平面EGH ．又BC ⊂平面BCD ，所以平面BCD ⊥平面EGH ．例5．（2022·全国·高一期中）在正方体1111ABCD A B C D -中，M 、N 分别是AB 、AD 的中点，E 、F 、P 分别是11B C 、1BB 、1DD 的中点.(1)证明：MN ∥平面11BDD B ；(2)证明：1CA MN ⊥；(3)请判断直线EF 与平面MNP 位置关系（不需说明理由）.【答案】(1)证明见详解；(2)证明见详解；(3)EF ⊂平面MNP ．【解析】【分析】（1）因为MN BD ∥，根据线面平行判定即可证明；（2）先证MN ⊥平面1A AC ，根据线面垂直性质即可证明线线垂直；（3）连接11C D 中点G 如图所示即可判断结果．(1)∵MN BD ∥，MN ⊂面11BDD B ，BD ⊂平面11BDD B ，∴MN ∥平面11BDD B ；(2)1AA ⊥平面ABCD ，MN ⊂平面ABCD ，∴1AA MN ⊥∵AC BD ⊥，MN BD ∥∴AC MN ⊥．又∵1AA AC A =，∴MN ⊥平面1A AC ，∴1CA MN ⊥．(3) EF ⊂平面MNP例6．（2022·河南开封·高一期中）在条件①AC BC ⊥；②1AB AC =；③平面1AB C ⊥平面11BB C C 中任选一个，补充到下面的问题中，并给出问题解答．问题：如图，在直三棱柱111ABC A B C -中，1BC CC =，且________，求证：11BC AB ⊥．【答案】证明见解析【解析】【分析】选条件①：将证明11BC AB ⊥转化为证明1BC ⊥平面1AB C ，再根据线面垂直的判定定理分析所需条件，将所需条件不断转化为线线垂直、线面垂直，结合已知可证；选择②：设11BC B C M ⋂=，连接AM ，利用等腰三角形的性质可证1BC ⊥平面1AB C ，然后可证；选择③：根据面面垂直的性质定理可证1BC ⊥平面1AB C ，然后可证.【详解】（情况一）补充条件①AC BC ⊥．证明：在直棱柱111ABC A B C -中，1BB ⊥平面ABC ，因为AC ⊂平面ABC ，所以1BB AC ⊥．因为1,⊥=AC BC BC BB B ，BC ⊂平面11BB C C ，1BB ⊂平面11BB C C所以AC ⊥平面11BB C C ．因为1BC ⊂平面11BB C C ，所以1AC BC ⊥，因为1BC CC =，所以四边形11BB C C 为菱形，所以11B C BC ⊥．因为1AC B C C ⋂=，AC ⊂平面1AB C ，1B C ⊂平面1AB C所以1BC ⊥平面1AB C ．因为1AB ⊂平面1AB C ，所以11BC AB ⊥．（情况二）补充条件②1AB AC =．证明：设11BC B C M ⋂=，连接AM ．因为1AB AC =，M 为1BC 的中点，所以1AM BC ⊥．因为1BC CC =，所以四边形11BB C C 为菱形，所以11B C BC ⊥．因为AM ⊂平面11,AB C B C ⊂平面11,=AB C AMB C M ，所以1BC ⊥平面1AB C ．因为1AB ⊂平面1AB C ，所以11BC AB ⊥，（情况三）补充条件③平面1AB C ⊥平面11BB C C ．证明：在棱柱111ABC A B C -中，因为1BC CC =，所以四边形11BB C C 为菱形，所以11B C BC ⊥．因为平面1AB C ⊥平面11BB C C ，平面1AB C平面1111,=⊂BB C C B C BC 平面11BB C C ，所以1BC ⊥平面1AB C ．因为1AB ⊂平面1AB C ，所以11BC AB ⊥．例7．（2022·全国·高一课时练习）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，,E F 分别为,AD PB 的中点．(1)求证：PE BC ⊥；(2)求证：平面PAB ⊥平面PCD ；【答案】(1)证明见解析(2)证明见解析【解析】【分析】（1）根据等腰三角形的性质得到PE AD ⊥，再根据//BC AD 可得PE BC ⊥；（2）根据面面垂直的性质定理得到AB ⊥平面PAD ，进一步得到AB PD ⊥，再根据线面垂直的判定定理得到PD ⊥平面PAB ，最后根据面面垂直的判定定理可证平面PAB ⊥平面PCD .(1)因为PA PD =，E 为AD 的中点，所以PE AD ⊥.因为底面ABCD 为矩形，所以//BC AD ，所以PE BC ⊥.(2)因为底面ABCD 为矩形，所以AB AD ⊥.又因为平面PAD ⊥平面ABCD ，所以AB ⊥平面PAD ，所以AB PD ⊥.又因为PA PD ⊥，PA AB A =，所以PD ⊥平面PAB .因为PD⊂平面PCD，所以平面PAB⊥平面PCD.例8．（2022·山西·大同一中高一阶段练习）如图，在四面体P ABD中，AD⊥平面P AB，PB ⊥P A(1)求证：PB⊥平面APD；(2)若AG⊥PD，G为垂足，求证：AG⊥BD．【答案】(1)证明见解析；(2)证明见解析.【解析】【分析】（1）由线面垂直的性质有AD PB⊥，再根据线面垂直的判定证结论.（2）由（1）及面面垂直的判定可得面PBD⊥面APD，再由面面垂直的性质有AG⊥面PBD，根据线面垂直的性质即可证结论.(1)由AD⊥平面P AB，PB⊂面PAB，则AD PB⊥，又PB⊥P A，PA AD A⋂=，则PB⊥平面APD；(2)由（1）及PB⊂面PBD，则面PBD⊥面APD，=，AG⊥PD，AG⊂面APD，又面PBD面APD PD所以AG⊥面PBD，而BD⊂面PBD，所以AG⊥BD．【过关测试】一、单选题1．（2022·江苏·海安县实验中学高一期中）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）．A．B．C．D．【答案】A【解析】【分析】根据线面平行的判定定理，结合图形逐一分析各个选项，即可得答案.【详解】⋂=，连接QO，对于A：如图所示，连接BC、DE，设BC DE O∕∕，因为Q、O分别为所在棱的中点，所以AB QOMNQ Q，即直线QO与平面MNQ不平行，又QO⋂平面=所以直线AB与平面MNQ不平行，故A符合题意；对于B：如图所示，取DG的中点E，连接CB、AD、EQ、NE，则////MQ CB MN AC ，，且AC CB C MNMQ M ==，，所以平面//ACBD 平面MNQE ，又AB 平面ACBD ，AB ⊄平面MNQ ，所以AB ∕∕平面MNQ ，故B 不符合题意.对于C ：如图所示，连接DC ，则//AB DC ，因为M 、Q 为所在棱的中点，所以//MQ DC ，又MQ 平面MNQ ，DC ⊄平面MNQ ，所以//DC 平面MNQ ，所以//AB 平面MNQ ，故C 不符合题意；对于D ：如图所示，连接DC ，//AB DC ，因为Q 、N 为所在棱的中点，所以NQ CD ∕∕，所以//AB NQ ，又NQ ⊂平面MNQ ，AB ⊄平面MNQ ，所以AB ∕∕平面MNQ ，故D 不符合题意.故选：A.2．（2022·广东·海珠外国语实验中学高一期中）已知平面α平面l β=，直线//,//a a αβ，则直线a 与l 的位置关系是（） A ．平行或异面 B ．相交 C ．平行 D ．异面【答案】C【解析】【分析】过a 作平面m γα=、n ηβ=，由线面平行的性质得//m a 、//n a ，即//m n ，根据线面平行判定及性质有//m l ，最后由平行公理的推论判断直线a 与l 的位置关系.【详解】过a 作平面m γα=，//a α，则//m a ，过a 作平面n ηβ=，//a β，则//n a所以//m n ，m β⊄，n β⊂，则//m β，而m α⊂，平面α平面l β=，则//m l ，综上，//a l .故选：C3．（2022·广东·广州市第四十一中学高一阶段练习）已知直线m 、n 和平面αβ、，下列命题正确的是（）A ．若,m n n α∥∥，则m αB ．若,,m n m n ααβ⊂∥∥、，则αβ∥C ．若,,m n αβαβ⊂⊂∥，则m n ∥D ．若α∥,m ββ⊂，则m α 【答案】D【解析】【分析】本题考查平行关系的理解，常见错误有对平行线传递性的误解以及平行相关定义、定理的条件结论理解错误．【详解】A 中，可知m 与n 的位置关系：平行或相交或异面，A 不正确；B 中，根据面面平行的判定定理，前提m 与n 必须相交，B 不正确；C 中，可知m 与n 的位置关系：平行或异面，C 不正确；D 中，若α∥β，则平面α内任一条直线均平行平面β，D 正确．故选：D ．4．（2022·江苏省太湖高级中学高一期中）已知,m n 是两条不同的直线，,αβ是两个不同的平面，则下列命题正确的是（）A ．若m ∥α，n ⊂α，则m ∥nB ．若m ∥n ，m α⊄, n ⊂α则m ∥αC ．若m ∥α, n ∥α，m β⊂，n β⊂，则α∥βD ．若m ∥α，n ∥β， α∥β，则m ∥n【答案】B【解析】【分析】利用直线和平面平行的判定定理和直线与平面平行的性质定理即可求解.【详解】对于选项A ,由直线和平面的性质定理可知，直线m 只能和过这条直线的任意平面与平面α的交线平行，则直线m 和n 不一定平行，则A 不正确；对于选项B ，利用直线与平面平行的判定定理可知选项B 正确；对于选项C ，平面α和平面β可能相交，则选项C 不正确，对于选项D ，直线m 和直线n 可能相交或异面，则D 不正确；故选：B .5．（2022·全国·高一课时练习）下列说法中正确的是（）①过平面外一点有且只有一条直线和已知平面垂直；②过直线外一点有且只有一个平面和已知直线垂直；③过平面外一点可作无数条直线与已知平面平行；④过直线外一点只可作一条直线与已知直线垂直．A ．①②③B ．①③④C ．②③D ．②③④ 【答案】A【解析】【分析】根据空间中线面的关系，可以求解.【详解】由线面垂直的性质及线面平行的性质知①②③正确；④错，过直线外一点作平面与直线垂直，则平面内过这一点的所有直线都与该直线垂直．故选:A6．（2022·全国·高一课时练习）在正方体ABCD A 1B 1C 1D 1中，点P 是线段BC 1上任意一点，则下列结论中正确的是（）A ．AD 1⊥DPB ．AP ⊥B 1C C ．AC 1⊥DPD ．A 1P ⊥B 1C【答案】B【解析】【分析】由正方体的性质有B 1C ⊥BC 1，B 1C ⊥AB ，再根据线面垂直的性质判断B ，根据正方体性质判断A 、C 、D.【详解】在正方体ABCD A 1B 1C 1D 1中，DP 与1BC 不垂直，而11//AD BC ，即DP 与1AD 也不垂直，A 错误；因为B 1C ⊥BC 1，B 1C ⊥AB ，BC 1∩AB ＝B ，所以B 1C ⊥平面ABC 1D 1，因为点P 是线段BC 1上任意一点，即AP 面ABC 1D 1，所以AP ⊥B 1C ，B 正确；若E 为AB 中点，则1//AC PE ，而DP 与PE 不垂直，则1AC 不与DP 垂直，C 错误；由下图知：结合正方体性质知，1A P 与1B C 不垂直，D 错误.故选：B7．（2022·全国·高一课时练习）如图，正四面体ABCD 中，E ，F 分别是线段AC 的三等分点，P 是线段AB 的中点，G 是直线BD 上的动点，则（）A ．存在点G ，使PG ⊥EF 成立B ．存在点G ，使FG ⊥EP 成立C ．不存在点G ，使平面EFG ⊥平面ACD 成立D ．不存在点G ，使平面EFG ⊥平面ABD 成立【答案】C【解析】【分析】A 选项假设PG ⊥EF ，证得AC ⊥面ABD ，与题设矛盾即可判断；B 选项由PE BF ∥求出异面直线,PE FG 的夹角小于2π即可判断；C 选项取CD 中点N ，过B 作BH AN ⊥于H ，先证BH ⊥面ACD ，再由BH 与面EFG 相交即可判断；D 选项直接证明当G 与BD 中点M 重合时，面ABD ⊥面EFG 即可.【详解】在A 中，取BD 中点M ，连接,AM CM ，易得,AM BD CM BD ⊥⊥，,AM CM ⊂面ACM ，AM CM M ⋂=，故BD ⊥面ACM ，又AC ⊂面ACM ，故BD AC ⊥，若PG ⊥EF ，,PG BD ⊂面ABD ，PG BD G ⋂=，则AC ⊥面ABD ，显然不成立，故不存在点G ，使PG ⊥EF 成立，故A 错误；在B 中，连接,BF DF ，易得PE BF ∥，故BFG ∠或其补角即为异面直线,PE FG 的夹角，不妨设3AB =，在ABF 中，由余弦定理2222cos 3BF AB AF AB AF π=+-⋅⋅，即22213223272BF =+-⨯⨯⨯=，解得7BF 7DF =在BFD △中，222779cos 0227BF DF BD BFD BF DF +-+-∠==>⋅⨯，则2BFD π∠<，显然2BFG BFD π∠<∠<，故不存在点G ，使FG ⊥EP 成立，故B 错误；在C 中，取CD 中点N ，连接,AN BN ，过B 作BH AN ⊥于H ，易得,BN CD AN CD ⊥⊥，,AN BN ⊂面ABN ，AN BN N =，故CD ⊥面ABN ，又BH ⊂面ABN ，故CD BH ⊥，又,AN CD ⊂面ABN ，AN CD N ⋂=，故BH ⊥面ACD ，若平面EFG ⊥平面ACD ，则BH ⊂面EFG 或BH 面EFG ，显然BH 与面EFG 相交，故不存在点G ，使平面EFG ⊥平面ACD 成立，故C 正确；在D 中，当G 与BD 中点M 重合时，由A 选项知有BD ⊥面ACM ，即BD ⊥面EFG ，又BD ⊂面ABD ，故面ABD ⊥面EFG ，故存在点G ，使平面EFG ⊥平面ABD 成立，故D 错误．故选：C ．8．（2022·内蒙古·呼和浩特市教育教学研究中心高一期末）如图，在三棱锥P ABC -中，不能证明⊥AP BC 的条件是（）A ．BC ⊥平面APCB ．AP PC ⊥，AP PB ⊥ C ．PC BC ⊥，平面APC ⊥平面BPCD ．BC PC ⊥，AB BC ⊥【答案】D【解析】【分析】 A 选项利用线面垂直（BC ⊥平面APC ）可推出线线垂直（⊥AP BC ），B 选项利用两组线线垂直（AP PC ⊥，AP PB ⊥）推出线面垂直（AP ⊥平面BPC ），再推出线垂直（⊥AP BC ），C 选项利用面面垂直的性质定理可推出⊥AP BC ，D 选项不能证明出⊥AP BC .【详解】BC ⊥平面APC ，AP ⊂平面APC ，BC AP ∴⊥ ，故A 选项可以证明，因此不选.AP PC ⊥，AP PB ⊥，,,PC PB P PC PB ⋂=⊂平面BPC ，AP ∴⊥平面BPC ，BC ⊂平面BPC ，BC AP ∴⊥.故B 选项可以证明，因此不选.平面APC ⊥平面BPC ，平面APC 平面=BPC PC ，PC BC ⊥，由面面垂直的性质定理知BC ⊥平面APC .AP ⊂平面APC ，BC AP ∴⊥，故C 选项可以证明，因此不选.由D 选项BC PC ⊥，AB BC ⊥并不能推出⊥AP BC .故选：D.二、多选题9．（2022·江苏·盐城中学高一期中）如图，正方体1111ABCD A B C D -的棱长为1，点P 是11B CD 内部（不包括边界）的动点，若11AP B D ⊥，则线段AP 长度的可能取值为（）A ．1110B 23C ．65D 5 【答案】BC【解析】【分析】利用线面垂直得线线垂直，从而确定点P 的轨迹，再根据平面几何的知识求距离的最大、最小值，判断选项即可.【详解】取11B D 中点O ，在正方体1111ABCD A B C D -中，11AB AD =，O 是11B D 的中点，11B D AO ∴⊥，同理11B D OC ⊥，11B D ∴⊥面AOC ，又点P 是11B CD 内部（不包括边界）的动点，11AP B D ⊥P ∴一定在线段OC 上运动在AOC △中，6AO CO ==2AC = 故cos OCA ∠=132AC OC =26sin 1cos OCA OCA ∠=-∠，故A 到OC 的距离23sin d AC OCA =⋅∠=232AP ≤故选BC ．10．（2022·广东·广州市白云中学高一期中）在三棱锥P ABC -中，从顶点P 向底面作垂线，垂足是H ，给出以下命题中正确的是（）A ．若,PA BC PB AC ⊥⊥，则H 是ABC 的垂心B ．若,,PA PB PC 两两互相垂直，则H 是ABC 的垂心C ．若PA PB PC ==，则H 是ABC 的外心D ．若H 是AC 的中点，则PA PB PC ==【答案】ABC【解析】【分析】作出图形，结合选项逐项分析即可求出答案.【详解】由题意知PH ⊥平面ABC ，且BC ⊂平面ABC ，所以PH BC ⊥，又因为PA BC ⊥，且PA PH P =，所以BC ⊥平面PAH ，又AH ⊂平面PAH ，因此BC AH ⊥；同理AC BH ⊥，所以H 是ABC 的垂心，故A 正确；由题意知PH ⊥平面ABC ，且BC ⊂平面ABC ，所以PH BC ⊥，又因为PA PC ⊥，PA PB ⊥，且PC PB P =，所以PA ⊥平面PBC ，又因为BC ⊂平面PBC ，所以PA BC ⊥，且PA PH P =，所以BC ⊥平面PAH ，又AH ⊂平面PAH ，因此BC AH ⊥；同理AC BH ⊥，所以H 是ABC 的垂心，故B 正确；PH ⊥平面ABC ，且BC ⊂平面ABC ，AB 平面ABC ，AC ⊂平面ABC ，所以,,⊥⊥⊥PH AB PH AC PH BC ，又因为PA PB PC ==，所以≅≅Rt PAH Rt PBH Rt PCH ，因此AH BH CH ==，所以H 是ABC 的外心，故C 正确；由题意知PH ⊥平面ABC ，且AC ⊂平面ABC ，所以PH AC ⊥，又H 是AC 的中点，所以PA PC =，当12BH AC =时，有PA PB PC ==，当12≠BH AC ，PA PC PB =≠，故D 不一定成立；故选：ABC.11．（2022·云南师大附中高一期中）已知m ，n 是互不重合的直线，α，β是互不重合的平面，下列四个命题中正确的是（） A ．若m α⊂，n ⊂α，m n P =，//m β，//n β，则//αβB ．若m α⊥，m n ⊥，//αβ，则//n βC ．若//m α，//m β，n αβ=，则//m nD ．若m α⊥，m β⊂，则αβ⊥【答案】ACD【解析】【分析】A 根据面面平行的判定判断；B 由线面、面面位置关系，结合平面的基本性质判断；C 过m 作平面l γα⋂=，由线面平行性质及平行公理的推论判断；D 由面面垂直的判定判断.【详解】A ：由//m β，//n β且,m n α⊂，m n P =，根据面面平行的判定知：//αβ，正确；B ：m α⊥，m n ⊥，//αβ，则//n β或n β⊂，错误；C ：过m 作平面l γα⋂=，而//m α，则//m l ，又//m β则l β//，n αβ=，故//l n ，所以//m n ，正确；D ：由m α⊥，m β⊂，根据面面垂直的判定知：αβ⊥，正确.故选：ACD12．（2022·河北省唐县第一中学高一期中）如图，在直四棱柱1111ABCD A B C D -中，BC CD ⊥，AB CD ∥，3BC =12AA AB AD ===，点P ，Q ，R 分别在棱1BB ，1CC ，1DD 上，若A ，P ，Q ，R 四点共面，则下列结论正确的是（）A ．任意点P ，都有AP QR ∥B ．存在点P ，使得四边形APQR 为平行四边形C ．存在点P ，使得BC ∥平面APQRD ．存在点P ，使得△APR 为等腰直角三角形【答案】AC【解析】【分析】根据面面平行的性质，结合假设法逐一判断即可.【详解】对于A ：由直四棱柱1111ABCD A B C D -，//AB CD ，所以平面11//ABB A 平面11DCC D ，又因为平面APQR ⋂平面11ABB A AP =，平面APQR ⋂平面11DCC D QR =，所以//AP QR ，故A 正确；对于B ：若四边形APQR 为平行四边形，则//AR QP ，而AD 与BC 不平行，即平面11ADD A 与平面11BCC B 不平行，所以平面APQR ⋂平面11BCC B PQ =，平面APQR ⋂平面11ADD A AR =，直线PQ 与直线AR 不平行，与//AR QP 矛盾，所以四边形APQR 不可能是平行四边形，故B 不正确；对于C ：当BP CQ =时，R 为D 时，满足//BC 平面APQR ，故C 正确.对于D ：假设存在点P ，使得APR △为等腰直角三角形，令BP x =，过点D 作DE AB ⊥，则3DE BC ==DR 上取一点M 使得DM BP x ==，连接,BD PM ，则四边形BDMP 为矩形，所以2MP BD ==，则()2224PR PM MR DR x =+=+- 2224AP PB AB x +=+2224AR DR AD DR =+=+显然,AR PR AP PR ≠≠，若由AP AR =，则BP DR x ==且//BP DR ⇒四边形BPDR 为平行四边BPDR ，所以2222228282RP BC CD AP BP x +=++D 错误；故选：AC.【点睛】关键点睛：运用假设法进行求解是解题的关键.三、填空题13．（2022·广东·广州市白云中学高一期中）正四棱锥S ABCD -的底面边长为a ，侧棱长为2a ，点P ，Q 分别在BD 和SC 上，并且:1:2=BP PD ，//PQ 平面SAD ，则线段PQ 的长为__________． 66a 【解析】【分析】过P 作//PM BC ，交CD 于M ，连结QM ，即可证明平面//PQM 平面SAD ，根据面面平行的性质得到//MQ SD ，再分别求出PM 、QM ，利用余弦定理求出cos ADS ∠，由此利用余弦定理能求出线段PQ 的长．【详解】解：如图，过P 作//PM BC ，交CD 于M ，连结QM ，正四棱锥S ABCD -的底面边长为a ，侧棱长为2a ，点P ，Q 分别在BD 和SC 上， :1:2=BP PD ，//PQ 平面SAD ，因为//PM BC ，//AD BC ，所以//PM AD ，PM ⊄平面SAD ，AD ⊂平面SAD ，所以//PM 平面SAD ，又PM PQ P =，,PM PQ ⊂平面PQM ，所以平面//PQM 平面SAD ，平面PQM平面SDC MQ =，平面SDC 平面SAD SD =， //MQ SD ∴，2233PM BC a ∴==， //QM SD ∴，1233QM SD a ∴==， //SD QM ，//AD MP ，PMQ ADS ∴∠=∠，222222441cos 2224AD SD SA a a a ADS AD SD a a +-+-∠===⨯⨯⨯⨯， 22222244162cos 299492233a PQ PM QM PM QM PMQ a a a a =+-⋅⋅∠=+-⨯⨯⨯=， 6PQ ∴=． ∴线段PQ 6．6 14．（2022·广东·海珠外国语实验中学高一期中）如图，长方体1111ABCD A B C D -的底面ABCD 是正方形.其侧面展开图是边长为4的正方形，E 、F 分别是侧棱11,AA CC 上的动点，点P 在棱1AA 上，且1AP =，若//EF 平面PBD ，则EF 的长=___________.6【解析】【分析】连接AC 与BD 交于点O ，取PQ =AP =1，连接QC ，得到//OP QC ，再由//EF 平面PBD ，利用线面平行的性质得到//EF OP ，进而得到//EF QC 求解.【详解】解：因为长方体1111ABCD A B C D -的底面ABCD 是正方形，其侧面展开图是边长为4的正方形，所以底面边长为1AD =，高为14AA =，如图所示：连接AC 与BD 交于点O ，取PQ =AP =1，连接QC ，则//OP QC ，因为//EF 平面PBD ，且EF ⊂平面1A ACC ，平面11A ACC ⋂平面BPD OP =，所以//EF OP ，则//EF QC ，又//QE CF ，所以四边形QEFC 是平行四边形，所以26EF QC OP ===615．（2022·浙江浙江·高一期中）在棱长为1的正方体1111ABCD A B C D -中，Q 为线段AD 的中点，P 为正方体内部及其表面上的一动点，且1PQ BD ⊥，则满足条件的所有点P 构成的平面图形的的周长等于________.【答案】32【解析】【分析】分别取111111,,,,CD CC B C A B A A 的中点E ，N ，M ，G ，F ，易证AC ⊥平面11D DBB ，则1AC BD ⊥，从而1QE BD ⊥，同理1QF BD ⊥，由线面垂直判定定理得到1BD ⊥平面ENMGFG ，进而得到所有点P 构成的平面图形为正六边形ENMGFG 求解.【详解】如图所示：分别取111111,,,,CD CC B C A B A A 的中点E ，N ，M ，G ，F ，则//QE AC ，易知AC BD ⊥，1AC DD ⊥，又1DD BD D =，所以AC ⊥平面11D DBB ，则1AC BD ⊥，所以1QE BD ⊥，同理 1QF BD ⊥，又1QE QF Q ⋂=，所以1BD ⊥平面ENMGFG ，即所有点P 构成的平面图形为正六边形ENMGFG ，因为正方体的棱长为1，所以正六边形ENMGFG 2，所以正六边形ENMGFG 2632= 故答案为：3216．（2022·全国·高一专题练习）如图，在直三棱柱ABC A 1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E ，要使AB 1⊥平面C 1DF ，则线段B 1F 的长为________．【答案】12##0.5【解析】【分析】根据线面垂直得到线线垂直，根据三角形面积求出DE 3求出线段B 1F 的长.【详解】设B 1F ＝x ，因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF .由已知可得A 1B 1＝2，设Rt △AA 1B 1斜边AB 1上的高为h ，则DE ＝12h . 又11AB A S =122＝221222+ ，所以h 23DE 3 在Rt △DB 1E 中，B 1E 2223623⎛⎫⎛⎫-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 在Rt △DB 1F 中，由面积相等得：2216212222x x ⎛⎫+= ⎪ ⎪⎝⎭，解得：x ＝12.即线段B 1F 的长为12.故答案为：12四、解答题17．（2022·江苏·无锡市第一中学高一期中）如图，三棱柱111ABC A B C -的侧棱与底面垂直，AC BC ⊥，点D 是AB 的中点.(1)求证1AC B C ⊥；(2)求证：1//AC 平面1CDB .【答案】(1)证明见解析(2)证明见解析【解析】【分析】（1）由侧棱与底面垂直可得1CC AC ⊥，结合AC BC ⊥，可得AC ⊥平面11BCC B ，即可得证；（2）连接1C B ，设1CB 与1C B 的交点为E ，连接DE ，则E 为1BC 中点，利用中位线的性质可知1//DE AC ，进而即可证明结论.(1)证明：在三棱柱111ABC A B C -中，因为1CC ⊥平面ABC ，AC ⊂平面ABC ，所以1CC AC ⊥，又AC BC ⊥，1CC AC C =，1CC ，BC ⊂平面11BCC B ，所以AC ⊥平面11BCC B ，又1B C ⊂平面11BCC B ，所以1AC B C ⊥.(2)证明：连接1C B ，设1CB 与1C B 的交点为E ，连接DE ，则E 为1BC 中点，因为点D 是AB 的中点，所以1//DE AC ，因为DE ⊂平面1CDB ，1AC ⊄平面1CDB ，所以1//AC 平面1CDB .18．（2022·广东·广州六中高一期中）如图，在四棱锥P ABCD -中，//AB CD ，AB AD ⊥，2CD AB =，平面PAD ⊥底面ABCD ，E 和F 分别是CD 和PC 的中点，求证：(1)//BE 平面PAD ；(2)CD ⊥平面BEF ．【答案】(1)证明见解析(2)证明见解析【解析】【分析】(1)根据线面平行的判定定理证明//BE 平面PAD ；(2)先根据平面与平面垂直的性质定理证明AB ⊥平面PAD ，再根据线面垂直的判定定理证明CD ⊥平面BEF ．(1)因为E 是CD 的中点，2CD AB =，所以AB DE =，因为//AB CD ，所以//AB DE ，所以四边形ABED 为平行四边形，所以//BE AD ，BE ⊄平面PAD ，AD ⊂平面PAD ，所以//BE 平面PAD ；(2)因为平面PAD ⊥底面ABCD ，平面PAD 底面ABCD AD =，AB AD ⊥，AB 底面ABCD ，所以AB ⊥平面PAD ，又//AB CD ，所以CD ⊥平面PAD ，,AD PD ⊂平面PAD ，所以，CD AD ⊥，CD PD ⊥，因为//BE AD ，所以CD BE ⊥，因为E 和F 分别是CD 和PC 的中点，所以//EF DP ，又CD PD ⊥，所以CD EF ⊥，BE EF E =，,BE EF ⊂平面BEF ，所以CD ⊥平面BEF ．19．（2022·山西·大同一中高一阶段练习）如图，等腰梯形ABCD 中，AD ＝DC ＝BC ＝2，AB ＝4，E 为AB 的中点，将△ADE 沿DE 折起、得到四锥P －DEBC ，F 为PC 的中点，M 为EB 的中点(1)证明：FM //平面PDE ；(2)证明：DE ⊥PC ；(3)当四棱锥P －DEBC 的体积最大时，求三棱锥E －DCF 的体积．【答案】(1)证明见解析；(2)证明见解析；(3)12.【解析】【分析】（1）连接CM 并延长与DE 延长线交于G ，在△CPG 中//FM PG ，根据线面平行的判定即可证结论.（2）H 为DE 中点，连接,PH CH ，易得DEBC 为平行四边形、△PDE 为等边三角形且60EDC ∠=︒，进而可得PH DE ⊥、CH DE ⊥，再根据线面垂直的判定、性质证明结论. （3）首先确定四棱锥P －DEBC 的体积最大时面PDE ⊥面DEBC ，再确定P －DEBC 的体高，并求得F 到面DEBC 的距离，由E DCF F DEC V V --=及棱锥的体积公式求体积.(1)连接CM 并延长与DE 延长线交于G ，则G 在面PDE 内，M 为EB 的中点，则M 为CG 中点，在△CPG 中//FM PG ，又PG ⊂面PDE ，FM ⊄面PDE ，所以FM //平面PDE .(2)若H 为DE 中点，连接,PH CH ，由题设//CD EB 且2CD EB ==，即DEBC 为平行四边形，则2DE BC ==，所以△PDE 为等边三角形，故PH DE ⊥，又ABCD 为等腰梯形，则60EBC ∠=︒ 所以60EDC ∠=︒，又1DH =，2CD =，易知：CH DE ⊥，又PHCH H =，则DE ⊥面PHC ，PC ⊂面PHC ，故DE ⊥PC . (3)当四棱锥P －DEBC 的体积最大时，面PDE ⊥面DEBC ，则△PDE 的高PH 即为四棱锥P －DEBC 的体高，又F 为PC 的中点，所以F 到面DEBC 的距离32PH h ==，由（2）易知DEBC 为边长为2的菱形，又132DEC DEBC S S =1132E DCF F DEC DEC V V hS --===. 20．（2022·湖南·长沙市南雅中学高一期中）已知正方体1111-ABCD A B C D ．(1)求证：AD1//平面1C BD ；(2)求证：1AD ⊥平面1A DC ．【答案】(1)证明见解析；(2)证明见解析.【解析】【分析】（1）根据给定条件，证明11//AD BC ，再利用线面平行的判定推理作答.（2）利用线面垂直的性质证明1CD AD ⊥，再利用线面垂直的判定推理作答.(1)在正方体1111ABCD A B C D -中，1111////C D A B AB ，1111C D A B AB ==，则有四边形11ABC D 是平行四边形，有11//AD BC ，而1BC ⊂平面1C BD ，1AD ⊄平面1C BD ，所以1//AD 平面1C BD ．(2)在正方体1111ABCD A B C D -中，CD ⊥平面11A ADD ，1AD ⊂平面11A ADD ，则1CD AD ⊥，在正方形11A ADD 中，11A D AD ⊥，又1A D CD D =，1,A D CD ⊂平而1A DC ，所以1AD ⊥平而1A DC ．21．（2022·云南昆明·高一期中）如图，四棱柱1111ABCD A B C D -中，底面ABCD 是菱形，60ABC ∠=︒，1AA ⊥平面ABCD ，E 为1AA 中点，12AA AB ==.(1)求证：1AC ∥平面11B D E ；(2)求三棱锥11A B D E -的体积；(3)在1AC 上是否存在点M ，满足1AC ⊥平面11MB D ？若存在，求出AM 的长；若不存在，说明理由.【答案】(1)证明见解析 3(3)32【解析】【分析】（1）连11A C 交11B D 于点F ，连EF ，由中位线定理以及线面平行的判定证明即可；（2）过1B 作111⊥B H D A 的延长线于点H ，由线面垂直的判定证明1B H ⊥平面11AA D D ，最后由1111113AED B AED V S B H =⋅三棱锥-△得出体积；（3）由线面垂直的性质证明111AC B D ，作1⊥FM AC ，垂足为M ，由线面垂直的判定证明1AC ⊥平面11MB D ，最后得出AM 的长.(1)证明：连11A C 交11B D 于点F ，连EF ，∵1111D C B A 是菱形，∴F 是11A C 中点，∵E 是1AA 中点，∴1∥EF AC ，∵EF ⊂平面11B D E ，1AC ⊄平面11B D E ，∴1AC ∥平面11B D E .(2)解：过1B 作111⊥B H D A 的延长线于点H ，由1AA ⊥底面ABCD 知1AA ⊥平面1111D C B A ，则11⊥AA B H ，又1111=⋂AA A A ，1B H ⊥平面11AA D D .由11160∠=∠=︒A B C ABC 知1160︒∠=A H B ，又112A B =，则13B H =1111111113123332AED A B D E B AED V V S B H --==⋅=⨯⨯⨯=三棱锥三棱锥 (3)解：∵1AA ⊥平面ABCD ，平面1111∥A B C D 平面ABCD ，∴1AA ⊥平面1111D C B A ，∵11B D ⊂平面1111D C B A ，∴111⊥B D AA ，∵菱形1111D C B A 中1111B D A C ⊥，1111A C AA A =，11A C ，1AA ⊂平面11AA C ，∴11B D ⊥平面11AA C ，又1AC ⊂平面11AA C ，∴111AC B D ，过F 在11Rt AAC △中，作1⊥FM AC ，垂足为M ，则由11⋂=M B F D F ，FM ，11B D ⊂平面11MB D 知1AC ⊥平面11MB D ，∴存在M 满足条件，在11Rt AAC △中，1112AA AC ==，122AC =F 是11A C 中点， ∴12==C M FM 23222==AM 22．（2022·江苏·盐城中学高一期中）如图，四棱锥P －ABCD 中，底面ABCD 为菱形，P A ⊥底面ABCD ，P A ＝2，3PC =E 是线段PC 上的一点，()R PE EC λλ=∈．(1)试确定实数λ，使//PA 平面BED ，并给出证明；(2)当2λ=时，证明：PC ⊥平面BED ．【答案】(1)1λ=，证明见解析。

垂直关系立体几何高一数学总结练习含答案解析A

§6垂直关系1.直线与平面垂直的概念(1)定义:如果一条直线和一个平面内的①直线都②,那么称这条直线和这个平面垂直.(2)画法:通常把表示直线的线段画成和表示平面的平行四边形的③垂直,如下图所示.2.平面与平面垂直的概念(1)相关概念a.半平面:一个平面内的一条直线把这个平面分成④,其中的⑤都叫作半平面.b.二面角:从一条直线出发的⑥所组成的图形叫作二面角,⑦叫作二面角的棱,⑧叫作二面角的面.c.二面角的记法以直线AB为棱,半平面α、β为面的二面角(如下图所示)记作:二面角⑨.d.二面角的平面角以二面角的棱上⑩为端点,在两个半平面内分别作的两条射线,这两条射线所成的角叫作二面角的平面角.e.直二面角:的二面角叫作直二面角.(2)平面与平面垂直a.定义:两个平面相交,如果所成的二面角是,就说这两个平面互相垂直.b.画法:把表示直立平面的平行四边形的竖边画成和表示水平平面的平行四边形的横边垂直.3.直线与平面垂直的判定定理(1)文字语言:如果一条直线和一个平面内的垂直,那么该直线与此平面垂直.(2)符号语言:若直线a⫋平面α,直线b⫋平面α,,则l⊥α.(如下图所示)4.平面与平面垂直的判定定理(1)文字语言:如果一个平面经过另一个平面的,那么这两个平面互相垂直,可简记为“线面垂直,则面面垂直”.(2)符号语言:若直线AB⫋平面β,AB⊥平面α,则β⊥α.如下图所示.5.直线与平面垂直的性质定理(1)文字语言:如果两条直线同时垂直于一个,那么这两条直线平行.(2)符号语言:若a⊥α,b⊥α,则a∥b.如图所示.6.平面与平面垂直的性质定理(1)文字语言:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即“面面垂直,则线面垂直”.(2)符号语言:若α⊥β,α∩β=MN,BC⫋α,BC⊥MN,则BC⊥β.如下图所示.知识清单①所有②垂直③一条边④两部分⑤每一部分⑥两个半平面⑦这条直线⑧每个半平面⑨α-AB-β⑩任一点垂直于棱平面角是直角直角两条相交直线直线l⊥a,l⊥b,a∩b=A一条垂线平面基础过关一、选择题1.C 过直线l的平面都与α垂直.2.A ①③符合要求.3.D 结合图形,可知选D.4.B 若a与b垂直,则这样的平面有1个;若a与b不垂直,则不存在.5.C ∵M为AB的中点,∠ACB=90°,∴BM=AM=CM,又PM⊥平面ABC,AB,MC⫋平面ABC,∴AB⊥PM,MC⊥PM,从而可知Rt△PMB≌Rt△PMA≌Rt△PMC,故PA=PB=PC.6.D D中直线b有可能在平面α内.7.B 在平面α内垂直于直线a的射影的无数条直线都与直线a垂直.8.D 连接BE、DE,则易知AC⊥DE,AC⊥BE,∴AC⊥平面BDE,又AC⫋平面ABC,∴平面ABC⊥平面BED.9.A 解本题时容易误认为折叠后SD与DG互相垂直,而错选B或D.因为四边形SG1G2G3是正方形,所以SG1⊥G1E,SG3⊥G3F,EG2⊥FG2,当正方形折成四面体之后上述三个垂直关系仍保持不变,因此,在四面体SEFG中,SG⊥GE,SG⊥GF,所以SG⊥△EFG所在平面,故选A.二、填空题10.答案 3解析由PA⊥平面ABC知,平面PAB⊥平面ABC,平面PAC⊥平面ABC;又易知BC⊥平面PAB,所以平面PBC⊥平面PAB,故满足条件的共3对.11.答案①②④解析画出图形,由判定定理得①②④正确.12.答案①③④⇒②或②③④⇒①解析由题意构造四个命题:(1)①②③⇒④;(2)①②④⇒③;(3)①③④⇒②;(4)②③④⇒①.易知(1)(2)错误,(3)(4)正确.三、解答题13.证明如下图所示,连接MO,A 1C 1.在正方体ABCD-A 1B 1C 1D 1中, ∵DB⊥AA 1,DB⊥AC,AA 1∩AC=A, ∴DB⊥平面ACC 1A 1. ∵A 1O ⫋平面ACC 1A 1, ∴A 1O⊥DB. 在矩形ACC 1A 1中, ∵tan∠AA 1O=√22, tan∠MOC=√22, ∴∠AA 1O=∠MOC. ∴∠A 1OA+∠MOC=90°. ∴A 1O⊥OM.又OM∩DB=O, ∴A 1O⊥平面MBD.14.证明 (1)∵底面ABCD 为菱形,∠BAD=120°,∴∠ABC=60°. 取BC 的中点E,连接AE 、PE 、AC, 易证△ABC 为正三角形, ∴AE⊥BC,∵PB=PC,∴PE⊥BC, 又PE∩AE=E, ∴BC⊥平面APE, 又AP ⫋平面APE, ∴BC⊥AP.同理可证:DC⊥AP,又DC∩BC=C, ∴AP⊥平面ABCD, 又AP ⫋平面PAB,∴平面PAB⊥平面ABCD.(2)由(1)知AP⊥平面ABCD.又AP⫋平面PAD,∴平面PAD⊥平面ABCD.15.证明∵四边形ABCD是正方形,∴BD⊥AC.∵A'A⊥平面ABCD,且BD⫋平面ABCD,∴A'A⊥BD.又∵AC∩A'A=A,∴BD⊥平面ACC'A'.又∵BD⫋平面A'BD,∴平面ACC'A'⊥平面A'BD.16.证明∵PA⊥平面ABC,BC⫋平面ABC,∴PA⊥BC.又∵AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.∵BC⫋平面PBC,∴平面PBC⊥平面PAB.又∵平面PBC∩平面PAB=PB,AE⊥PB,∴AE⊥平面PBC,又∵PC⫋平面PBC,∴AE⊥PC.17.解析(1)证明:由已知得DE⊥AE,∵DE⊥EC,AE∩EC=E,∴DE⊥平面ABCE,又∵BC⫋平面ABCE,∴DE⊥BC.又BC⊥CE,DE∩CE=E,∴BC⊥平面DCE.(2)证明:取AB中点H,连接GH,FH.则GH∥BD,FH∥BC,则易得GH∥平面BCD, FH∥平面BCD.则易得平面FHG∥平面BCD, ∴GF∥平面BCD.(3)经分析可知,R 点满足3AR=RE 时,平面BDR⊥平面BDC. 理由:取BD 的中点Q,连接DR,BR,CR,CQ,RQ. 容易计算得CD=2,BR=√52,CR=√132,DR=√212,CQ=√2. 在△BDR 中,BR=√52,DR=√212,DB=2√2,可得RQ=√52.则在△CRQ 中,CQ 2+RQ 2=CR 2, ∴CQ⊥RQ.又在△CBD 中,CD=CB,Q 为BD 的中点,∴CQ⊥BD.∴CQ⊥平面BDR,∴平面BDC⊥平面BDR.一、选择题1.已知l⊥α,则过l 与α垂直的平面( ) A.有1个 B.有2个 C.有无数个 D.不存在2.如果一条直线垂直于一个平面内的下列不同情况,能保证该直线与平面垂直的是( ) ①三角形的两边 ②梯形的两边 ③圆的两条直径 ④正六边形的两条边 A.①③ B.② C.②④ D.①②④3.若平面α⊥平面β,平面β⊥平面γ,则( ) A.α∥γ B.α⊥γ C.α与γ相交但不垂直D.以上都有可能4.若两直线a 与b 异面,则过a 且与b 垂直的平面( ) A.有且只有1个B.可能有1个,也可能不存在C.有无数多个D.一定不存在5.如图所示,已知△ABC为直角三角形,其中∠ACB=90°,M为AB的中点,连接PM,CM,PM垂直于△ABC所在平面,那么( )A.PA=PB>PCB.PA=PB<PCC.PA=PB=PCD.PA≠PB≠PC6.已知直线a、b与平面α,则下列四个命题中不正确的是( )A.如果a⊥α,b⊥α,那么a∥bB.如果a⊥α,a∥b,那么b⊥αC.如果a⊥α,b∥α,那么a⊥bD.如果a⊥α,a⊥b,那么b∥α7.若直线a与平面α不垂直,那么在平面α内与直线a垂直的直线( )A.只有一条B.有无数条C.是平面内的所有直线D.不存在8.在空间四边形ABCD中,AB=BC,AD=CD,E为对角线AC的中点,则下列判断正确的是( )A.平面ABD⊥平面BDCB.平面ABC⊥平面ABDC.平面ABC⊥平面ADCD.平面ABC⊥平面BED9.如图(1),在正方形SG1G2G3中,E,F分别是G1G2和G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,如图(2),那么,在四面体SEFG中必有( )A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面二、填空题10.如下图所示,PA⊥平面ABC,∠ABC=90°,则图中互相垂直的平面的对数为.11.在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论:①BC∥平面PDF;②DF⊥平面PAE;③平面PDF⊥平面ABC;④平面PAE⊥平面PBC.其中正确结论的序号是.12.已知α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题.三、解答题13.如下图所示,在正方体ABCD-A1B1C1D1中,M为棱CC1的中点,AC交BD于点O,求证:A1O⊥平面MBD.14.如下图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=120°,且PB=PC=PD. 求证:(1)平面PAB⊥平面ABCD;(2)平面PAD⊥平面ABCD.15.如图,在正方体ABCD-A'B'C'D'中,证明:平面ACC'A'⊥平面A'BD.16.如图,在Rt△ABC中,∠B=90°,PA⊥平面ABC,过点A作AE⊥PB于点E.求证:AE⊥PC.17.如下图所示,已知在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+√3,过点A作AE⊥CD,垂足为E,G、F分别为AD、CE的中点,现将△ADE沿AE折叠,使得DE⊥EC.(1)求证:BC⊥平面CDE;(2)求证:FG∥平面BCD;(3)在线段AE上找一点R,使得平面BDR⊥平面DCB,并说明理由.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017.12.181.已知直三棱柱ABC-ABiG，点N在AC上且CN=3AN,点M , P, Q分别是AA i , A1B1, BC的中点.求证：直(1)求证：OM //平面AA1D1D ；(2)求证：OM 丄BC1.4.如图，AB为圆O的直径，点E,F在圆O上，且AB//EF，矩形ABCD所在的平面和圆O所在的平面垂直，且AD =EF =AF =1, AB =2.高一立体几何平行、精选2.如图，在正方形ABC D ABCD中，E, 面AFC平行的平面？若存在，请作出并证明;F, M分别是棱B C，BB，0 D的中点，是否存在过点E，M且与平若不存在，请说明理由.3.在正方体ABCD—ABC1D1中，M，O分别是A1B, BD的中点.(1) 求证：平面AFC丄平面CBF ；(2) 在线段CF上是否存在了点M，使得0M //平面ADF ?并说明理由.5•已知：正三棱柱ABC-AB1C1中，AA =3，AB=2，N为棱AB的中点.(1)求证：AGP平面NBQ .(2 )求证：平面CNB,丄平面ABBA .(3 )求四棱锥G -ANB,A的体积.6.已知△ BCD中,/ BCD=90°, BC=CD=1 AB丄平面BCD / ADB=60°, E、F 分别是AC AD 上的动点，且AEAC(1)(2)7 .如图，在菱形ABCD中，N A B C 6 0 , A 与BD相交于点O , AE丄平面ABCD,CF //AE, AB =AE =2.AF=一=A(0 WA <1).AD求证：不论几为何值，总有平面BEFI平面ABC 当入为何值时，平面BEFI平面ACD ?&(I )求证：BD 丄平面ACFE ;(II )当直线F0与平面ABCD 所成的角的余弦值为如时，求证：EF 丄BE ；10(III )在(II )的条件下，求异面直线 OF 与DE 所成的余弦值.8•如图，四棱锥 P -ABCD 中，AD // BC ，AD =2BC =4，AB =2j 3，Z BAD =90°，M ,0 分别为CD 和AC 的中点，P0丄平面ABCD .(1)求证：平面PBM 丄平面PAC ；一 PN(2)是否存在线段 PM 上一点N ，使用ON II 平面PAB ，若存在，求——的值；如果不存在，说明理由PMPAD 是正三角形，且与底面 ABCD 垂直，底面ABCD 是边长为2(1) EN // 平面 PDC ； (2) BC 丄平面PEB ； (3) 平面PBC 丄平面ADMN .1 丄平面 PAB ， AD // BC ，BC = CD = — AD ，E ，F 分别为2线段AD ，PD 的中点.(l) 求证：CE 〃平面PAB ; (n)求证：PD 丄平面CEF ； (m) 写出三棱锥D -CEF 与三棱锥11.如图，点P 是菱形ABCD 所在平面外一点，N BAD =60°, P PCD 是等边三角形，AB = 2 , PA =2J 29.如图，在四棱锥P — ABCD 中，侧面的菱形，NBAD =60： N 是PB 的中点, 过A, D,N 三点的平面交 PC 于M , E 为AD 的中点，求证:10.如图，四棱锥P-ABCD 中，PD P -ABD 的体积之比.(结论不要求证明)JJM是PC的中点.(I)求证：PA P平面BDM ；(n)求证：平面PAC丄平面BDM ；(川)求直线BC与平面BDM的所成角的大小.12.在四棱锥A-BCDE中，底面BCDE为菱形，侧面ABE为等边三角形，且侧面ABE丄底面BCDE , O , F分别为BE , DE的中点.(I)求证：AO丄CD .(n)求证：平面AOF丄平面ACE .(川)侧棱AC上是否存在点P，使得BP P平面AOF ?若存在，求出13 .在四棱锥P- ABCD中，侧面PCD丄底面ABCD , PD丄CD ,梯形，AB//CD，乂ADC =90"，AB =AD = PD =1，CD =2 .述明理由.AP——的值；若不存在，请说明理由PCE为PC中点，底面ABCD是直角(1) 求证:(2) 求证:BE//平面PAD ；BC丄平面PBD ；(3)在线段PC上是否存在一点Q，使得二面角Q - BD - P为45°?若存在，求PQPC的值；若不存在，请1.见解析【解析】试题分析：根据题目给出的P, Q分别是AB i, BC的中点，想到取别交BM BN于点E, F,根据题目给出的线段的长及线段之间的关系证出GE GF i汇=二=-，从而得到EF// PQ然后利用线面平行的判定即可得证;3所以EF/ PQ 又EF?平面BMN PC?平面BMN所以PQ/平面BMN.由正方体的特征及N为BB的中点，可知平面AFC与直线DD相交，且交点为a与平面A i FCG平行，注意到EM/ BD // FG则平面a必与CC相交于点N,1为棱CD，B C的中点，易知CN： C C=—.于是平面EMt满足要求.4试题解析：如图，设N是棱C i C上的一点，且C i N =4C i C时，平面EMN过点E，M且与平面A i FC平行.证明如下：设H为棱C i C的中点，连接B i H , D i H.•••C i N=AC I C，•- C i N = 2C i H.又E为B i C i的中点,••• EN // B i H.又CF // B i H ,••• EN // CF.试题解析: 如图，取AB中点G,连接PG, QG分别交BM BN于点E，F，贝U E,F分别为BM BN的中点.而GE/1 1 1— AM，GE= —AM，GF// — AN，GF=—AN,且CN=3AN 所以2 2 2 2GFEP =3AN=1，所以GEFQ NC 3 EPGF iFQ=3 9参考答案AB的中点G连接PG QG后分EP FQ2 .详见解析.【解析】试题分析：DD的中点结合M E又 EN ?平面 A I FC , CF ?平面 A i FC , ••• EN //平面 A I FC .同理 MN // D 1H ，D 1 H // A 1F ， ••• MN // A I F .又 MN ?平面 A I F C , A I F ?平面 A I FC , • MN //平面 A I FC . 又 EN nMN = N , •••平面 EMN //平面 A 1 F C .点睛：本题考查线面平行的判定定理和面面平行的判定定理的综合应用，属于中档题.直线和平面平行的判定定理:平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；平面与平面平行的判定定理：个平面内的两条相交直线与另一个平面分别平行，则这两个平面平行.3. (1)见解析(2)见解析【解析】试题分析：(1)连接AD ，AD 1，由M , O 分别是AB ，BD 的中点可证OM // AD ，即可证明OM //平面AA 1D 1D ； (2)由D 1C 1 // AB 且D J G = AB 可证DC 1BA 为平行四边形，即可证 AD 1 // BG , 再根据AD 丄可证明OM 丄BC 1.试题解析:(1)连接AD , AD 1，因为M , O 分别是A,B , BD 的中点, 所以 OM // AD ，且 AD U 平面 AA 1D 1D , 所以OM //平面AA 1D 1D(2)由题意D 1C 1 // AB 且D 1C^ AB ，所以DC 1BA 为平行四边形，所以 AD 1 // BC 1 , 由(I) OM // AD ，且 AD 丄 AU ，所以 OM 丄 BGCl4. ( 1)证明见解析；(2)存在，见解析;【解析】试题分析：(1 )要证明平面AFC丄平面CBF，只需证AF丄平面CBF，则只需证AF丄CB ,AF丄BF ,再根据题目条件分别证明即可；(2)首先猜测存在CF的中点M满足OM //平面ADF，作辅助线，通过OM / /AN，由线面平行的判定定理，证明OM //平面ADF 。

试题解析：解：(1)因为平面ABCD丄平面ABEF,CB丄AB , 平面ABCD C平面ABEF = AB，所以CB丄平面ABEF，因为AF U平面ABEF，所以AF丄CB ,又AB为圆O的直径，所以AF丄BF ,因为CB C BF = B，所以AF丄平面CBF，因为AF U平面AFC，所以平面AFC丄平面CBF .(2)如图，取CF的中点M,DF的中点NA，连接N,MN,OM ,1则MN//CD，M^2CD，又AO//CD, A^-CD，所以MN //AO,MN =AO，所以四边形MNAO为平行四边形，所以OM //AN，又AN U平面DAF ,OM 0平面DAF ,【解析】试题分析:丄AB，从而只要再证CN与平面ABBA内另一条直线垂直即可,这可由正棱柱的侧棱与底面垂直得到，从而得线面垂直，于是有面面垂直;心ABG中，边A Bl的高就是四棱锥的高，再求得四边形(1)要证线面平行, 就是要证线线平行, 考虑过直线AG的平面AGB与平面CB1N的交线ON (其中O是BC i与B,C的交点)，而由中位线定理易得AG / /ON，从而得线面平行;所以OM //平面DAF，即存在一点M为CF的中点，使得OM //平面DAF .5. (1 )见解析；(2)见解析；(3)"2(2 )由于心ABC是正三角形，因此有CN(3 )要求四棱锥的体积，由正三棱柱的性质知ANBiA的面积，即可得体积.试题解析:(1)证明：连接BG，交BC于0点，连接NO , •••在PABC1中, N，0分别是AB，BC i中点,•- NO PAG,••• NO U 平面NCR ,AC i 2 平面NCB i ,••• AG P平面NCR ,(2 )证明：•••在等边PABC中,N是棱AB中点，••• CN 丄AB ,又•••在正三棱柱中，BB1丄平面ABC ,CN u 平面ABC ,•- BB i 丄CN ,••• ABC BR =B点,(3)作GD丄A,B1于D点,•- GD是四棱锥G -ANBA高, 1h = —AB tan602^AB ,BBi u平面ABBA ,•••CN丄平面ABBA ,•/ CN 匸平面CNB1,•••平面CNB丄平面ABBA -底面积S =3天2 -亠3咒12=921 3^/3V c^ANB1A^ = —Sh = ----------------------3 2【点睛】（1）证明平面和平面垂直的方法：①面面垂直的定义；②面面垂直的判定定理.（2）已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直.66. （1）见解析（2）入=-【解析】（1）证明：••• AB丄平面BCD, ••• AB丄CD.•/ CD丄BC,且ABA BC= B,A CD丄平面ABC.AE AF•••——=——=入⑥X< 1），AC AD•••不论入为何值，恒有EF// CD.••• EF丄平面ABC, EF U 平面BEF.•••不论入为何值恒有平面BEF丄平面ABC.⑵解：由（1）知，BE丄EF,v平面BEFI平面ACD,；BE丄平面ACD.：BE丄AC.••• BC= CD= 1，/ BCD= 90° / ADB= 60°二BD= 72，AB= 72tan60 °= 76.■ -AC- J AB2 + Bc2= 77.【解析】试题分析：（I ）要证BD与平面ACFE垂直，只要证BD与平面ACFE内两条相交直线垂直即可，这由已知线面垂直可得一个，又由菱形对角线垂直又得一个，由此可证；（II ）由已知线面垂直得FC丄平面ACFE，从而知N FOC为直线FO与平面ACFE所成的角，从而可得FC,FO ,然后计算出三线段EF,BE,BF的长，由勾股定理逆定理可得垂直；（III ）取BE中点M，则有MO //DE，从而可得异面直线所成的角，再解相应三角形可得. 试题解析：(I ) BD丄平面ACFEi BD丄Ag菱形ABCD由AB2= AEAC,得AE=6 AE■-入=AC6故当L—时，平面BEF丄平面7ACD7. （I ）见解析；（II ）见解析; (III ) 一45BD丄AEu AE丄平面ABCD(II ) FC丄平面ABCD =直线FC与平面ABCD所成的角FOC = codFOC =5°而且RtAFOC10中，CO =1= FO = Ji0,FC =3，过E 作EN //AC 交FC 于点N= RUFNE 中EF = J5, R馆FCB 中FB=丽,RtAEAB中EB =5/8= EF2+EB2=FB2= EF 丄EB ；1(III )取BE边的中点M，连接MO,= MO //DE且MO = 2 DE = N FOM为所求的角或其补角,2 2 2FM=J EF2+EM2=V7二RtAFOM 中c。

高一立体几何平行垂直解答题精选

立体几何线面平行垂直、面面平行垂直专题练习(高三党必做)

高一立体几何平行垂直证明基础练习

立体几何解答题训练(平行)

高中数学高考总复习立体几何各种平行与垂直的判断习题及详解

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

专题20立体几何中的平行与垂直问题(解析版)

高一立体几何解答题训练

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

高中数学高考总复习立体几何平行与垂直的判断习题及详解

立体几何最典型的平行与垂直题型归纳(带答案)(1)

微专题12 立体几何中的平行与垂直问题答案

高一立体几何平行垂直解答题精选

立体几何中线面平行的经典方法+经典题(附详细解答)

高一 平行与垂直的综合应用知识点+例题+练习 含答案

专题08 立体几何中的平行与垂直问题(解析版)

垂直关系立体几何高一数学总结练习含答案解析A

高一平行与垂直的综合应用知识点+例题+练习含答案