电路分析基础(张永瑞)第三版 第六章课后部分习题
电路分析基础(张永瑞)

(2.1-7)
(2.1-7)式即是图2.1-2 所示电路以支路电流为未知量的足够的
相互独立的方程组之一,它完整地描述了该电路中各支路电
流和支路电压之间的相互约束关系。应用克莱姆法则求解
(2.1-7)式。系数行列式Δ和各未知量所对应的行列式Δj(j=1, 2, 3)分别为
例 2.1-2 图 2.1-4 所示电路为电桥电路,AB支路为电 源支路,CD支路为桥路,试用支路电流法求电流ig, 并讨 论电桥平衡条件。
图 2.1-4 例 2.1-2 用图
解 设各支路电流参考方向和回路的巡行方向如图中 所标。该电路有 6 条支路、4 个节点,以支路电流为未知 量,应建立 3 个独立节点的KCL方程,3个独立回路的 KVL方程。根据元件VAR 和 KCL、KVL列出以下方程组:
图 2.1-2 支路电流法分析用图
根据KCL,对节点 a 和 b 分别建立电流方程。设流出 节点的电流取正号,则有
节点 a
i1 i2 i3 0
(2.1-2)
节点 b
i1 i2 i3 0
根据KVL,按图中所标巡行方向(或称绕行方向)对回路Ⅰ、 Ⅱ、Ⅲ 分别列写KVL方程(注意:在列写方程中,若遇到电阻, 两端电压就应用欧姆定律表示为电阻与电流乘积),得
u1 = R1i1
如果电路中的受控源的控制量就是某一支路电流, 那么方程组中方程个数可以不增加, 由列写出的前 3 个 基本方程稍加整理即可求解。如果受控源的控制量是另 外的变量, 那么需对含受控源电路先按前面讲述的步骤 一、 二去列写基本方程(列写的过程中把受控源先作为独 立源一样看待),然后再加一个控制量用未知电流表示的 辅助方程,这一点应特别注意。
归纳、明确支路电流法分析电路的步骤。
《电路分析基础(第三版)》(沈元隆刘栋编著)第6章详解

这是复数方程,同时提供振幅之间和 相位之间的两个关系,即: (1)
U=RI (2) u =i。
时域模型图
相量模型图
2 电容元件伏安关系的相量形式
电容电压电流关系为
i(t ) C du
dt
当u(t)=Umcos(t+u )时
i(t)
Im
cos(ωt
6
6
10cos(100 t 5 ) 10cos(100 t )
62
3
所以 Fm =10, = /3rad, =100rad/s, f =/2=50Hz
7-1-2 正弦量间的相位差
正弦稳态电路中,各电压电流都是 频率相同的正弦量,常常需要将这些正 弦量的相位进行比较。两个正弦电压电
分析正弦稳态的有效方法——相量法。
7-1 正 弦 量
7-1-1 正弦量的三要素
正弦量——按正弦规律随时间变化的 物理量。
函数式表示:f(t)= Fm cos(ωt+ )
Fm——振幅;
ω——角频率;rad/s ωt+ ——相位;弧度(rad)或度();
——初相位。| |
f——频率;赫(Hz) ω=2f
注意:
1 流出节点的电流取”+”号,流入 节点的电流取”-”号。
2 流出任一节点的全部支路电流振 幅(或有效值)的代数和并不一定等于 零。即,一般情况下:
n
Ikm 0
k 1
n
Ik 0
k 1
例5 已知 i1(t) 10 2 cos(ωt 60)A , i2(t) 5 2 sintA
试求电流i(t)及其有效值相量。
W I 2RT T i 2(t )Rdt 0
《电路分析基础》第2版-习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) 50W;(2) 300 V、25V,200V、75 V;(3) R2=12.5Ω,R3=100Ω,R4=37.5Ω1-2 V A=8.5V,V m=6.5V,V B=0.5V,V C=−12V,V D=−19V,V p=−21.5V,U AB=8V,U BC=12.5,U DA=−27.5V1-3 电源(产生功率):A、B元件;负载(吸收功率):C、D元件;电路满足功率平衡条件。
1-4 (1) V A=100V,V B=99V,V C=97V,V D=7V,V E=5V,V F=1V,U AF=99V,U CE=92V,U BE=94V,U BF=98V,U CA=−3 V;(2) V C=90V,V B=92V,V A=93V,V E=−2V,V F=−6V,V G=−7V,U AF=99V,U CE=92V,U BE=94V,U BF=98V,U CA=−3 V1-5 I≈0.18A ,6度,2.7元1-6 I=4A,I1=11A,I2=19A1-7 (a) U=6V,(b) U=24 V,(c) R=5Ω,(d) I=23.5A1-8 (1) i6=−1A;(2) u4=10V,u6=3 V;(3) P1=−2W发出,P2 =6W吸收,P3 =16W吸收,P4=−10W发出,P5=−7W发出,P6=−3W发出1-9 I=1A,U S=134V,R≈7.8Ω1-10 S断开:U AB=−4.8V,U AO=−12V,U BO=−7.2V;S闭合:U AB=−12V,U AO=−12V,U BO=0V 1-11 支路3,节点2,网孔2,回路31-12 节点电流方程:(A) I1 +I3−I6=0,(B)I6−I5−I7=0,(C)I5 +I4−I3=0回路电压方程:①I6 R6+ U S5 +I5 R5−U S3 +I3 R3=0,②−I5 R5−U S5+ I7R7−U S4=0,③−I3 R3+ U S3 + U S4 + I1 R2+ I1 R1=01-13 U AB=11V,I2=0.5A,I3=4.5A,R3≈2.4Ω1-14 V A=60V,V C=140V,V D=90V,U AC=−80V,U AD=−30V,U CD=50V1-15I1=−2A,I2=3A,I3=−5A,I4=7A,I5=2A第2章习题参考答案2-1 2.4 Ω,5 A2-2 (1) 4 V,2 V,1 V;(2) 40 mA,20 mA,10 mA2-3 1.5 Ω,2 A,1/3 A2-4 6 Ω,36 Ω2-5 2 A,1 A2-6 1 A2-7 2 A2-8 1 A2-9 I1 = −1.4 A,I2 = 1.6 A,I3 = 0.2 A2-10 I1 = 0 A,I2 = −3 A,P1 = 0 W,P2 = −18 W2-11 I1 = −1 mA,I2 = −2 mA,E3 = 10 V2-12 I1 = 6 A,I2 = −3 A,I3 = 3 A2-13 I1 =2 A,I2 = 1A,I3 = 1 A,I4 =2 A,I5 = 1 A2-14 V a = 12 V ,I1 = −1 A,I2 = 2 A2-15 V a = 6 V,I1 = 1.5 A,I2 = −1 A,I3 = 0.5 A2-16 V a = 15 V,I1 = −1 A,I2 = 2 A,I3 = 3 A2-17 I1 = −1 A,I2 = 2 A2-18 I1 = 1.5 A,I2 = −1 A,I3 = 0.5 A2-19 I1 = 0.8 A,I2 = −0.75 A,I3 = 2 A,I4 = −2.75 A,I5 = 1.55 A2-20 I3 = 0.5 A2-21 U0 = 2 V,R0 = 4 Ω,I0 = 0.1 A2-22 I5 = −1 A2-23 (1) I5 = 0 A,U ab = 0 V;(2) I5 = 1 A,U ab = 11 V2-24 I L = 2 A2-25 I S =11 A,R0 = 2 Ω2-26 18 Ω,−2 Ω,12 Ω2-27 U=5 V2-28 I =1 A2-29 U=5 V2-30 I =1 A2-31 10 V,180 Ω2-32 U0 = 9 V,R0 = 6 Ω,U=15 V第3章习题参考答案3-1 50Hz,314rad/s,0.02s,141V,100V,120°3-2 200V,141.4V3-3 u=14.1sin (314t−60°) V3-4 (1) ψu1−ψu=120°;(2) ψ1=−90°,ψ2=−210°,ψu1−ψu2=120°(不变)3-5 (1)150290VU=∠︒,25020VU=︒;(2) u3ωt+45°)V,u4ωt+135°)V3-6 (1) i1=14.1 sin (ωt+72°)A;(2) u2=300 sin (ωt-60°)V3-7 错误:(1) ,(3),(4),(5)3-8 (1) R;(2) L;(3) C;(4) R3-9 i=2.82 sin (10t−30°) A,Q≈40 var3-10 u=44.9sin (314t−135°) V,Q=3.18 var3-11 (1) I=20A;(2) P=4.4kW3-12 (1)I≈1.4A, 1.430AI≈∠-︒;(3)Q≈308 var,P=0W;(4) i≈0.98 sin (628t−30°) A3-13 (1)I=9.67A,9.67150AI=∠︒,i=13.7 sin (314t+150°) A;(3)Q=2127.4 var,P=0W;(4)I C=0A3-14 (1)C =20.3μF ;(2) I L =0.25A ,I C =16A第4章 习题参考答案4-1 (a) 536.87Z =∠︒Ω,0.236.87S Y =∠-︒;(b) 45Z =-︒Ω,45S Y =︒ 4-2 Y =(0.06-j0.08) S ,R ≈16.67 Ω,X L =12.5 Ω,L ≈0.04 H 4-3 R 600V U =∠︒,L 8090V U =∠︒,S 10053.13V U =∠︒ 4-4 2036.87I =∠-︒4-545Z =︒Ω,10A I =∠︒,R 1000V U =∠︒,L 12590V U =∠︒,C 2590V U =∠-︒ 4-645S Y =︒,420V U =∠︒,R 20A I =∠︒,L 0.2290A I =∠-︒,C 1.2290A I =∠︒4-7 10245A I =∠︒,S 10090V U =∠︒ 4-8 (a) 30 V ;(b) 2.24 A 4-9 (a) 10 V ;(b) 10 A 4-10 (a) 10 V ;(b) 10 V 4-11 U =14.1 V4-12 U L1 =15 V ,U C2 =8 V ,U S =15.65 V4-13 U X1 =100 V ,U 2 =600 V ,X 1=10 Ω,X 2=20 Ω,X 3=30 Ω4-14 45Z =︒Ω,245A I =∠-︒,120A I =∠︒,2290A I =∠-︒,ab 0V U =4-15 (1)A I =,RC Z =,Z =Ω;(2)10R =Ω,C 10X =Ω 4-16 P = 774.4 W ,Q = 580.8 var ,S = 968 V·A 4-17 I 1 = 5 A ,I 2 = 4 A4-18 I 1 = 1 A ,I 2 = 2 A ,526.565A I =∠︒,26.565V A 44.72S =∠-︒⋅4-19 10Z =Ω,190A I =∠︒,R252135V U =∠︒,10W P = 4-20 ω0 =5×106 rad/s ,ρ = 1000 Ω,Q = 100,I = 2 mA ,U R =20 mV ,U L = U C = 2 V 4-21 ω0 =104 rad/s ,ρ = 100 Ω,Q = 100,U = 10 V ,I R = 1 mA ,I L = I C = 100 mA 4-22 L 1 = 1 H ,L 2 ≈ 0.33 H第5章 习题参考答案5-3 M = 35.5 mH5-4 ω01 =1000 rad/s ,ω02 =2236 rad/s 5-5 Z 1 = j31.4 Ω,Z 2 = j6.28 Ω 5-6 Z r = 3+7.5 Ω 5-7 M = 130 mH 5-8 2245A I =∠︒ 5-9 U 1 = 44.8 V5-10 M 12 = 20 mH ,I 1 = 4 A 5-11 U 2 = 220 V ,I 1 = 4 A 5-12 n = 1.95-13 N 2 = 254匝,N 3 = 72匝 5-14 n = 10,P 2 = 31.25 mW第6章 习题参考答案6-1 (1) A 相灯泡电压为零,B 、C 相各位为220V6-3 I L = I p = 4.4 A ,U p = 220 V ,U L = 380 V ,P = 2.3 kW 6-4 (2) I p = 7.62 A ,I L = 13.2 A6-5 A 、C 相各为2.2A ,B 相为3.8A 6-6 U L = 404 V6-7 A N 20247U ''=∠-︒V6-8 cos φ = 0.961,Q = 5.75 kvar 6-9 33.428.4Z =∠︒Ω6-10 (1) I p = 11.26 A ,Z = 19.53∠42.3° Ω; (2) I p = I l = 11.26 A ,P = 5.5 kW 6-11 U l = 391 V6-12 A t 53.13)A i ω=-︒B t 173.13)A i ω=-︒C t 66.87)A i ω=+︒6-13 U V = 160 V6-14 (1) 负载以三角形方式接入三相电源(2) AB 3.8215A I =-︒,BC 3.82135A I =-︒,CA 3.82105A I =︒A 3.8645A I =∠-︒,B 3.86165A I =∠-︒,C 3.8675A I =∠︒6-15 L = 110 mH ,C = 91.9 mF第7章 习题参考答案7-1 P = 240 W ,Q = 360 var 7-2 P = 10.84 W7-3 (1)() 4.7sin(100)3sin3A i t t t ωω=+︒+ (2) I ≈3.94 A ,U ≈58.84 V ,P ≈93.02 W7-4 m12π()sin(arctan )V 2MU L u t t zRωωω=+-,z =7-5 直流电源中有交流,交流电源中无直流7-6 U 1=54.3 V ,R = 1 Ω,L = 11.4 mH ;约为8%,(L ’ = 12.33 mH )7-7 使总阻抗或总导纳为实数(虚部为0)的条件为12X R R R ==7-8 19.39μF C =,275.13μF C = 7-9 L 1 = 1 H ,L 2 = 66.7 mH 7-10 C 1 = 10 μF ,C 2 = 1.25 μF第8章 习题参考答案8-6 i L (0+)=1.5mA ,u L (0+)=−15V8-7 i 1(0+)=4A ,i 2(0+)=1A ,u L (0+)=2V ,i 1(∞)=3A ,i 2(∞)=0,u L (∞)=0 8-8 i 1(0+)=75mA ,i 2(0+)=75mA ,i 3(0+)=0,u L1(0+)=0,u L2(0+)=2.25V8-9 6110C ()2e Ati t -⨯= 8-10 4L ()6e V t u t -=8-11 6110C ()10(1e )V t u t -⨯=-,6110C ()5e A t i t -⨯= *8-12 500C ()115e sin(86660)V t u t -=+︒ 8-13 10L ()12e V t u t -=,10L ()2(1e )A t i t -=- 8-14 21R S ()eV t R Cu t U -=-,3R S (3)e V u U τ-=-8-15 (1) τ=0.1s ,(2) 10C ()10e V t u t -=,(3) t =0.1s 8-16 510C ()109e V t u t -=-8-17 10L ()5e A t i t -=8-18 (a)00()1()1(2)f t t t t t =---;(b)00000()1()1()[1()1(2)]1()21()1(2)f t t t t t t t t t t t t t =------=-⨯-+- 8-19 0.50.5(1)C ()[5(1e )1()5(1e )1(-1)]V t t u t t t ---=--- 8-20 u o 为三角波,峰值为±0.05V*8-21 临界阻尼R ,欠阻尼R ,过阻尼R *8-22 12666L ()[(1e )1()(1e)1(1)2(1e)1(2)]t t ti t t t t -----=-+-----。
电力系统分析基础习题答案-第五张第六章.docx

电力系统分析部分习题答案(参考)稳态部分第四章复杂电力系统的潮流计算4-1-3解:(1)不考虑非标准变比时:(因为对称,所以只求上三角元素)V| I =1/Z16 = l/(jO.l) = -jiO Y12 = Y|3 = Y14= Y15 = 0.0 Y16 = Y61 = -1/Z I6 =jioY22 = 1/Z24 = l/(i°」)= -j!0 Y23 = Y25 = Y26 =0.0 Y24 =-l/Z24 = jioY33 = I/Z35 = l/(jo.l) = -jio Y34 = Y36 = 0.0 Y35 = -I/Z35 =jioY44 = 1/Z24 + 1/Z45 + 1/Z46 = l/(j().l) + l/(j().2) + l/(j0.2) = -j20 Y45 = -1/Z45 = j5 = -1/Z46 = j5 Y55 = 1 / Z35 +1 / Z45 + 1 / Z56 + y 50 = 1 /(j0.1) + 1 /(j0・2) +1/00.1) + j0.2 = -j24.8 Y56 =-l/Z56 =jlO V66 = 1 / Z l6 + i / Z46 +1 / Z56 + y60 = 1 /(j0.1) + 1 /(.jO. 1) + 1 /(j0.2) = -J24.8-jio 0-jiojiojio所以:Y = 0 0-jio 0 jio 00jl() 0 -j2() j5 j500 jl() j5 -J24.8 jl()jio 0 0 j5 jio -J24.8(2)当考虑非标准变比时,只有变压器两侧的节点的白导纳和这两个节点Zl'可的互导纳有变化。
y I6=l/(Z l6*k) = l/(j0.1*l.l) = -j9.09y l0 =(1 ・k)/(Z|6 *k2) = 0.1 心0.1 *1.1*0」)=j0.8265 y61()=(k-l)/(Z16*k ) = 0」心0.1*1.!) = -j0.909Y16 = Y61=-y16=j9.09 ¥^=^24.8Y| ] = -j9.09 4- j().826 = -8.264第五章电力系统的有功功率和频率调整5- 1-2解:/i] =aF (/ap G1 =O .24-O .OO 2PGI均未超出发电厂的出力范围,为最优分配方案。
电子测量技术基础课后习题答案_1_8章张永瑞(第三版)

电子测量技术基础课后习题答案_1_8章张永瑞(第三版)一1.1 解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2 叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3 解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4 叙述电子测量的主要容。
答:电子测量容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等:(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
《电路理论基础》(第三版 陈希有)习题答案第六章

答案6.22解:对图(a)电路做戴维南等效,如图(b)所示。
OC U inZ (b)i j 1/(j )Z L C ωω=+ (1)SOC j I U Cω=(2) 由图(b)可知,当i 0Z =时,电阻两端电压U 与电阻R 无关,始终等于OC (0)U R ≠。
由式(1)解得1/100rad/s ω== 将式(3)代入式(2)得OC 1100A 1090V j100rad/s 0.01FU U ==∠︒⨯=∠-︒⨯90V u t ω=-()答案6.23解:先对图(a)电路ab 端左侧电路作戴维南等效,如图(b)所示。
U iZ (b)令32000rad/s 210H 4L X L ω-==⨯⨯=Ω得等效阻抗i 4j48//8//j42(1j)4j4Z Ω⨯Ω=ΩΩΩ==+ΩΩ+Ω由OCi 1j U i Z R Cω=++知,欲使电流i 有效值为最大,电容的量值须使回路阻抗虚部为零,即:012]j 1Im[=-=++CC R Z i ωω 等效后电路如图(b)所示。
解得1250μF 2C ω==答案6.24解:应用分压公式,输出电压o U 可表示为o n1n 2U U U =-i i 1j 12j U C U R Cωω=-⨯+ i i i j 121j 2(j 1)U U CR U CR CR ωωω-=-=++ 当 0=R , o U 超前于i U 180;当 1R Cω=,o U 超前于i U ︒90;当 ∞→R , o U 与i U 同相位。
即当R 由零变到无穷时,o U 超前于i U 相位差从180到0变化。
答案6.25解:图示电路负载等效导纳为22221j j()j ()()R LY C C R L R L R L ωωωωωω=+=+-+++ (1) 22222222222)()(21)()(C L R LC L R L C L R R Yωωωωωωω++-=⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎥⎦⎤⎢⎢⎣⎡+= (2) 由式(2)可见:当)2/(12LC =ω时,Y C ω=与R 无关,电流有效值CU U Y I ω==不随R 改变。
电工技术第6章(李中发版)课后习题及详细解答

第6章一阶动态电路分析6.1 如图6.3所示电路,在开关S断开前已处于稳态,试求开关S断开后瞬间电压u C和电流i C、i1、i2的初始值。
分析先在时的等效电路中求,因为时电路已处于稳态,电路中各处的电流和电压都是常数,电容中的电流,所以这时电容C可看作开路。
然后在时的等效电路中求、和,这时电容C可用电压为的恒压源代替。
解画出时的等效电路,如图6.4(a)所示。
根据分压公式,得时电容两端的电压为:(V)根据换路定理,时电容两端的电压为:(V)在瞬间,电容C可用电压为V的恒压源代替,由此可画出时的等效电路,如图6.4(b)所示。
由于4Ω电阻支路已断开,故时的电流i2为:(A)根据欧姆定律,得时的电流i1为:(A)根据KCL,得时的电流i C为:(A)图6.3 习题6.1的图图6.4 习题6.1解答用图6.2 如图6.5所示电路,在开关S闭合前已处于稳态,试求开关S闭合后瞬间电压u L和电流i L、i1、i2的初始值。
分析先在时的等效电路中求,因为时电路已处于稳态,电路中各处的电流和电压都是常数,电感两端的电压,所以这时电感L可看作短路。
然后在时的等效电路中求、和,这时电感L可用电流为的恒流源代替。
解画出时的等效电路,如图6.6(a)所示。
根据欧姆定律,得时电感中的电流为:(A)根据换路定理,时电感中的电流为:(A)图6.5 习题6.2的图图6.6 习题6.2解答用图在瞬间,电感可用电流为A的恒流源代替,由此可画出时的等效电路,如图6.6(b)所示。
根据欧姆定律,得时电感两端的电压为:(V)根据分流公式,得时的电流i1和i2分别为:(A)6.3 如图6.7所示电路,在开关S闭合前已处于稳态,试求开关S闭合后瞬间电压u C、u L和电流i L、i C、i的初始值。
分析先在时的等效电路中求和,因为时电路已处于稳态,电路中各处的电流和电压都是常数,电容中的电流,电感两端的电压,所以这时电容C可看作开路,电感L可看作短路。
电路分析基础(第四版)张永瑞答案第6章

42
第6 章
电路频率响应
(2) 当发生串联谐振时回路中电流有效值
U s 100 I0 10 A r 10
UC0=QUs=100×100×10-6=10 mV
43
第6 章
电路频率响应
6.9 一个rLC串联谐振电路如题6.9图所示, 已知该电 路的谐振角频率ω0=10 000 rad/s, 通频带BW=100 rad/s, r=10
第6 章
电路频率响应
第6章 电路频率响应
6.1 题6.1图所示的简单RC并联电路在电子线路中常 用来产生晶体管放大器的自给偏压。 图中电流 I 看成是
激励, 电压 U 看成是响应。 试求该一阶网络的网络函数
H(jω)、截止角频率ωc,并画出它的幅频特性和相频特性。
1
第6 章
电路频率响应
题6.1图
2
最高调谐频率为
f0max 1 1 1692 kHz 6 12 2 LCmin 2 3.14 295 10 30 10
f=(1692~530)kHz
38
第6 章
电路频率响应
6.8 在图示的rLC串联谐振电路中, 已知r=10 Ω, 回路
的品质因数Q=100, 谐振频率f0=1000 kHz。
UC 8 Q 80 U s 0.1
1 r r 25 12 Q2 f 0 10
r′=25-r=25-20=5 Ω
33
第6 章
电路频率响应 Gx=1.25×10-6 S
将r′与C的串联化为并联,
所以并接Yx前、 后电路的通频带分别为
f 0 106 BW 104 Hz Q 100
G1G2 jC (G1 G2 g m )
电路分析基础第6章习题答案 ppt课件
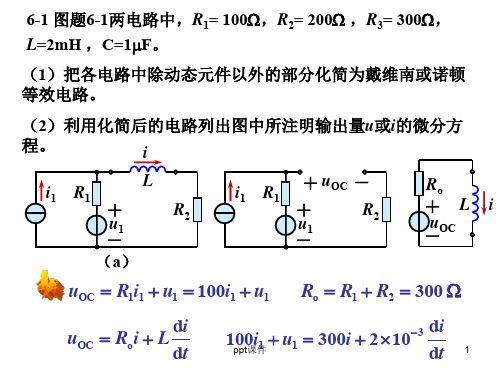
7
dt
6-4 图题6-4所示电路中,各电源均在 t =0时开始作用于电路,
求 i (t),已知电容电压初始值为零。
i(t)
i(t)
4k +
1V -
1mA
4k
+
6k
+
uOC
2F
1V-
-
1mA 6k
把除电容元件以外的电路进行戴维南变换
(1 4k
1 6k
)uOC
10 3
1 4k
uOC 3 V
+
4
u
i1(t)
-
18
6-9 电路如图题6-8所示,电压源于 t =0 时开始作用于电路,试 求i (t),t≥0。
-10i1(t)+
4A 4 2H i1(t) i(t)
14
+
2H
-56V i(t)
时间常数为: 2 1 s
14 7
稳态时 i() 56 4 A 14
t
i(t) i()(1 e ) 4(1 e 7t ) V t≥0
4
103
ppt课件
(0.5
0.75e
208.3t
)
mA
t≥0
9
6-5 电路如图题6-5所示,开关在 t =0时闭合,求t=15s时ua及
各支路电流。 设电容的初始储能为零
+200V 60k 40k
6k 1000pF
+ ua uC -
-300V
时间常数为: RoC (60k // 40k 6k)109 3105 s
1.5 1.25 1.2 16
6-8 电路如图题6-7所示,电压源于 t =0 时开始作用于电路,试
电路分析教程(第三版)答案 燕庆明

《电路分析教程(第3版)》第2章习题解析2-1 求图示电路(a)中的电流i和(b)中的i1和i2。
题2-1图解根据图(a)中电流参考方向,由KCL,有i = (2 – 8 )A= – 6A对图(b),有i1 = (5 – 4) mA = 1mAi2 = i1 + 2 = 3mA2-2 图示电路由5个元件组成。
其中u1 = 9V,u2 = 5V,u3 = -4V,u4 = 6V,u5 = 10V,i1 = 1A,i2 = 2A,i3 = -1A。
试求:(1)各元件消耗的功率;(2)全电路消耗功率为多少?说明什么规律?题2-2图解 (1)根据所标示的电流、电压的参考方向,有P 1 = u 1 i 1 = 9 × 1 W= 9WP 2 = u 2 ( - i 1) = 5 × ( -1 )W = -5WP 3 = u 3 i 2 = ( -4 ) × 2W = -8WP 4 = u 4 i 3 = 6 × ( -1 ) W= -6WP 5 = u 5 ( - i 3) = 10 × 1W = 10W(2)全电路消耗的功率为P = P 1 + P 2 + P 3 + P 4 + P 5 = 0该结果表明,在电路中有的元件产生功率,有的元件消耗功率,但整个电路的功率守恒。
2-3 如图示电路,(1)求图(a)中电压u AB ;(2)在图(b)中,若u AB = 6V ,求电流i 。
题2-3图解 对于图(a),由KVL ,得u AB =( 8 + 3 × 1 - 6 + 2 × 1)V = 7V 对于图(b),因为u AB = 6i - 3 + 4i + 5 = 6V故i = 0.4A2-4 如图示电路,已知u = 6V ,求各电阻上的电压。
题2-4图解 设电阻R 1、R 2和R 3上的电压分别为u 1、u 2和u 3,由分压公式得u 1 = 3211R R R R ++·u = 122× 6 V= 1Vu 2 =3212R R R R ++·u = 124× 6 V= 2V u 3 = 3213R R R R ++·u = 126× 6V = 3V2-5 某收音机的电源用干电池供电,其电压为6V ,设内阻为1Ω。
电路分析基础第四版课后习题第六章第七章答案

uOC
=1 1.2 − 0.4α
, iSC
= 10mA , Rab
=
uOC iSC
=
250 3−α
Ω
微分方程为
duC dt
+ (12 − 4α ) ×103uC
= 104
6-6 电路如图题 6-6 所示。(1)t = 0 时 S1 闭合( S2 不闭合),求 i, t ≥ 0 ;(2)t = 0 时 S2 闭
,τ
=
L R
=
2s
iL (t)
=
4.5 1.5
(1 −
e−0.5t
)A
=
3(1 −
e−0.5t
)A
,t
≥0
(2)
S2
闭合(
S1 不闭合),断开电感,得戴维南等效电路,其中 uOC
=
6 6+
2
×12
=
8V
,
Ro
=
2Ω // 6Ω
= 1.5Ω
,τ
=
L R
= 1.5s
iL (t)
=
8 2
(1 −
−1t
e 1.5 )A
电感分别视为短路和开路,冲激电流全部流过电容,故电容电压为
∫ uc
(0+
)
=
1 C
0+δ (t)dt = 1
0−
C
由于它是有限值,所以电感的电流不会发生跃变, iL (0+ ) = iL (0− ) = 0 。
综上所述,冲激电压作用于 RLC 串联电路时,仅在换路瞬间电感的电流才会发生跃变, 而电容的电压不会发生跃变;冲激电流作用于 RLC 并联电路,仅在换路瞬间电容的电压发生 跃变,而电感电流不发生跃变。
电力系统暂态分析(第三版)习题答案

电力系统暂态分析(第三版)习题答案本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March第一章电力系统分析基础知识1-2-1 对例1-2,取,,用准确和近似计算法计算参数标幺值。
解:①准确计算法:选取第二段为基本段,取,,则其余两段的电压基准值分别为:电流基准值:各元件的电抗标幺值分别为:发电机:变压器:输电线路:变压器:电抗器:电缆线路:电源电动势标幺值:②近似算法:取,各段电压电流基准值分别为:,,,各元件电抗标幺值:发电机:变压器:输电线路:变压器:电抗器:电缆线路:电源电动势标幺值:发电机:变压器:输电线路:变压器:电抗器:电缆线路:电源电动势标幺值:1-3-1 在例1-4中,若母线的三相电压为:在空载情况下点突然三相短路,设突然三相短路时。
试计算:(1)每条电缆中流过的短路电流交流分量幅值;(2)每条电缆三相短路电流表达式;(3)三相中哪一相的瞬时电流最大,并计算其近似值;(4)为多少度时,a相的最大瞬时电流即为冲击电流。
解:(1)由例题可知:一条线路的电抗,电阻,阻抗,衰减时间常数三相短路时流过的短路电流交流分量的幅值等于:(2)短路前线路空载,故所以(3)对于abc相:,,,可以看出c相跟接近于,即更与时间轴平行,所以c相的瞬时值最大。
(4)若a相瞬时值电流为冲击电流,则满足,即。
第二章同步发电机突然三相短路分析2-2-1 一发电机、变压器组的高压侧断路器处于断开状态,发电机空载运行,其端电压为额定电压。
试计算变压器高压侧突然三相短路后短路电流交流分量初始值。
发电机:,,,,,变压器:,,解:取基准值,电流基准值则变压器电抗标幺值发电机次暂态电抗标幺值次暂态电流标幺值有名值2-3-1 例2-1的发电机在短路前处于额定运行状态。
(1)分别用,和计算短路电流交流分量,和;(2)计算稳态短路电流。
解:(1),短路前的电动势:所以有:(2)第三章电力系统三相短路电流的实用计算第四章对称分量法即电力系统元件的各序参数和等值电路4-1-1 若有三相不对称电流流入一用电设备,试问:(1)改用电设备在什么情况下,三相电流中零序电流为零(2)当零序电流为零时,用电设备端口三相电压中有无零序电压答:(1)①负载中性点不接地;②三相电压对称;③负载中性点接地,且三相负载不对称时,端口三相电压对称。
电路分析基础(张永瑞)第三版-课后习题答案
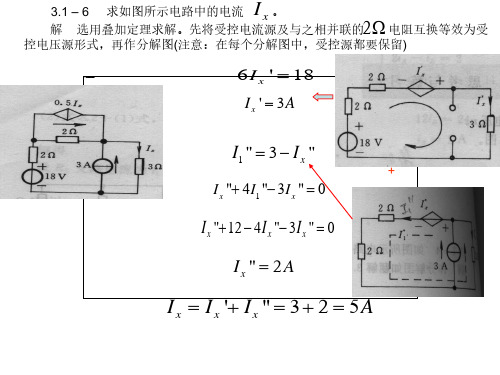
Vc、Vd
Vd 6V,Va U oc
1 1 1 1 1 ( ) U V 6 0 oc c 3 4 12 3 12 1 U ( 1 1 )V 1 6 12 oc c 3 3 3 3
2U oc Vc 1.5 U oc 2Vc 42
10 4 7 A 11 2 2 3 1 A 3 6 3
画出戴维南等效电源接上电阻
R0 (1 1) // 2 3 // 6 3
U ab
当
Rx 6 Rx U oc R0 Rz 3 Rx
Rx 3 时,电压 U ab
9
时,电压
63 3V 33
3.1 – 6 求如图所示电路中的电流 x。 解 选用叠加定理求解。先将受控电流源及与之相并联的2 电阻互换等效为受 控电压源形式,再作分解图(注意:在每个分解图中,受控源都要保留)
I
6 I x ' 18
即 解得
Ix ' 3A
I1 " 3 I x "
+
所以
I x " 4 I1 " 3I x " 0
所以等效电源内阻
R0
由最大功率传输定理可知,当
U 10 I
(b)
外加电源法求R0
RL R0 10
时其上可获得最大功率。此时
pL max
2 U oc 40 2 40W 4 R0 4 10
Vd 6 I1 0.5 A 12 12 Vc 21 I2 7A 3 3
由KCL求得
I sc I1 I 2 0.5 7 7.5 A
R0 U oc 15 2 I sc 7.5
《参考习题答案》PPT课件

题6—4 图
6
高频电子线路习题参考答案
解6-4
iLa i1 i2 0
iLb i1 i2 gD K (ct )(uc u ) gD K (ct )(uc u )
gD K (ct )(uc u )
gD
4
cos ct
4 3
cos
16
高频电子线路习题参考答案
6-7 在图示桥式调制电路中,各二极管的特性一致,均为自 原点出发、斜率为gD的直线,并工作在受u2控制的开关 状态。若设RL>>RD(RD=1/gD),试分析电路分别工作 在振幅调制和混频时u1、u2各应为什么信号,并写出uo 的表示式。
解6-7 当u2的正半周,二极管全部导 通,电桥平衡,输出为零。 当u2的负半周,二极管全部截 止,,输出为电阻分压。 所以输出电压为:
1 2
2
cos ct
2 3
cos
3c t
2 5
cos 5ct
.....
cos
t
因此,与(1)相比,输出信号也中包含了的基频分量和c 、
c 频率分量,但多了c的奇次谐波与的组合频率
(2n+1)c 分量
12
高频电子线路习题参考答案
在考虑负载的反作用时
i1
rD
1 R
RL
K (ct )uD1
1
U Ee
cos
t
cos
ct
1.3 1
0.563cos104 t
cos107
t
uo (t ) EC ioRL 10 6.5 1 0.563cos104 t cos107 t(V )
(2)
电路分析基础第三版课后答案

电路分析基础第三版课后答案【篇一:《电路分析基础》作业参考解答】txt>第一章(p26-31)1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a)(a)解:标注电压如图(a)所示。
由kvl有u?15?5?2?5v 故电压源的功率为p1??15?2??30w(发出)电流源的功率为p2?2?u?2?5?10w(吸收)电阻的功率为p3?5?22?5?4?20w(吸收)(b)解:标注电流如图(b)所示。
(b)由欧姆定律及kcl有i2?15?3a,i1?i2?2?3?2?1a5故电压源的功率为p1??15?i1??15?1??15w(发出)电流源的功率为p2??15?2??30w(发出)电阻的功率为p3?5?i2?5?32?5?9?45w(吸收)1-8 试求题1-8图中各电路的电压u,并分别讨论其功率平衡。
(b)解:标注电流如图(b)所示。
由kcl有i?6?2?4a 故u?2?i?2?4?8v2由于电流源的功率为p1??6?u??6?8??48w电阻的功率为p2?2?i2?2?42?32w外电路的功率为p3?2?u?2?8?16w且pk?13kp1p2p34832160所以电路的功率是平衡的,及电路发出的功率之和等于吸收功率之和。
(b)1-10 电路如题1-10图所示,试求:(1)图(a)中,i1与uab;解:如下图(a)所示。
因为(a)i?10?2?0.9i15所以i1?2?20?2.222a0.99uab?4(i1?i)?4??20?2??8?0.889v991-19 试求题1-19图所示电路中控制量i1及电压u0。
解:如图题1-19图所示。
由kvl及kcl有1000i1u020u0i1600i1u060005000整理得1000i1u0203000i1u00解得i1?5?10?3a?5ma,u0?15v。
题1-19图补充题:u1. 如图1所示电路,已知 i ?a , ab ? 16 v ,求电阻r。
精品文档-电路分析基础(第四版)张永瑞-第6章

12 N112
(6.1-1a)
21 N 2 21
(6.1-1b)
第六章 互感与理想变压器
图 6.1-1耦合电感元 件
第六章 互感与理想变压器
仿照自感系数定义,我们定义互感系数为
M 21
21
i1
(6.1-2a)
M 12
12
i2
(6.1-2b)
(6.1-2a)式表明穿越第二个线圈的互磁链与激发该互磁链的第一
第六章 互感与理想变压器
图6.1-5 互感线圈的同名端
第六章 互感与理想变压器
如果像图6.1-6所示那样,设i1仍是从a端流入,i2不是从c 端流入,而是从c端流出,就认为(判定)磁通相消。由图6.1-6 可见,两互感线圈上电压与其上电流参考方向关联, 所以
u1
L1
di1 dt
M
di2 dt
(6.1-9a)
第六章 互感与理想变压器
所以
u1
d 1
dt
L1
di1 dt
M
di2 dt
u2
d 2
dt
L2
di2 dt
M
di1 dt
(6.1-7a) (6.1-7b)
由上述分析可见,具有互感的两线圈上的电压,在设其参考 方向与线圈上电流参考方向关联的条件下,它等于自感压降与互 感压降的代数和, 磁通相助取加号,磁通相消取减号。
L2
di dt
M
di dt
( L1
L2
2M
)
di dt
Lab
di dt
式中
Lab L1 L2 2M
(6.2-1) (6.2-2)
称为两互感线圈顺接串联时的等效电感。 由(6.2-1)式画出的等 效电路如图6.2-1(b)所示。
