长正方体体积
实用文档之长方体正方体体积

实用文档之"长方体与正方体体积"知识点:1、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh长=体积÷宽÷高 a=V÷b÷h宽=体积÷长÷高b=V÷a÷h高=体积÷长÷宽 h= V÷a÷b2.正方体的体积=棱长×棱长×棱长V=a×a×a=a3读作“a的立方”表示3个a相乘,(即a·a·a)长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高用字母表示:V=S h(横截面积相当于底面积,长相当于高)。
3、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
固体一般就用体积单位,计量液体的体积,如水、油等。
常用的容积单位有升和毫升也可以写成L和ml。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升(1 L = 1 dm3 1 ml = 1 cm3)注意:1、长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
2、*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:V 物体 =V 现在-V 原来也可以 V 物体 =S ×(h 现在- h 原来)V 物体 = S ×h 升高3、【体积单位换算】 大单位 小单位 小单位 大单位 进率: 1立方米=1000立方分米=1000000立方厘米 (立方相邻单位进率1000)1立方分米=1000立方厘米=1升=1000毫升1立方厘米=1毫升1平方米=100平方分米=10000平方厘米1平方千米=100公顷=1000000平方米注意:长方体与正方体关系把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
长方体、正方体的体积和容积
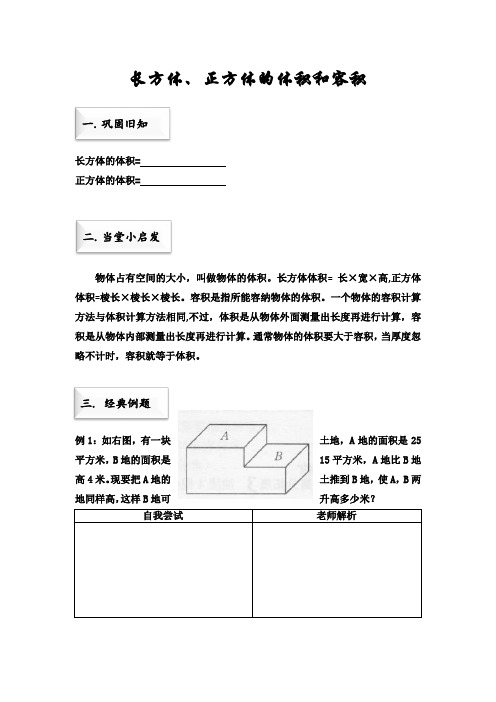
长方体、正方体的体积和容积一.巩固旧知长方体的体积=正方体的体积=二.当堂小启发物体占有空间的大小,叫做物体的体积。
长方体体积= 长×宽×高,正方体体积=棱长×棱长×棱长。
容积是指所能容纳物体的体积。
一个物体的容积计算方法与体积计算方法相同,不过,体积是从物体外面测量出长度再进行计算,容积是从物体内部测量出长度再进行计算。
通常物体的体积要大于容积,当厚度忽略不计时,容积就等于体积。
三. 经典例题例1:如右图,有一块土地,A地的面积是25平方米,B地的面积是15平方米,A地比B地高4米。
现要把A地的土推到B地,使A,B两地同样高,这样B地可升高多少米?自我尝试老师解析如下图,有一堆土,甲处比乙处高50厘米,现在要把这堆土推平整,使甲处和乙处一样高,要从甲处取多少厘米厚的土填在乙处?例2: 一块长方形铁皮长24厘米,四角剪去边长3厘米的正方形后,然后通过折叠、焊接,做成一个无盖的长方体铁盒,铁盒的容积是486立方厘米。
求原来长方形铁皮的面积。
自我尝试老师解析一张长方形的铁皮,长是8分米,宽是5分米,四角剪去边长10厘米的正方形后,然后通过折叠、焊接,做成一个无盖的长方体铁盒,这个铁盒的容积是多少立方分米?(铁皮厚度不计)小试牛刀小试牛刀例3:木工师傅用2厘米厚的木板做成一只有盖的长方体报箱,从外面量长64厘米,宽34厘米,高39厘米,这只报箱的容积是多少?自我尝试老师解析小试牛刀一正方体木箱,从外面量得棱长52厘米,箱壁厚1厘米,求木箱容积。
四. 举一反三1、一根方钢长5米,它的横截面是一个边长2厘米的正方形,已知1立方分米钢重7.8千克,一吨这样的钢材约有多少根?(保留整数)2、底面是正方形的长方体,所有棱长之和是80厘米,已知高10厘米,求体积。
3、长方体棱长之和是60分米,长是7分米,高是3分米,求长方体体积。
4、在一个棱长为3厘米的大立方体的顶部中央挖去一个棱长为1厘米的小立方体,求这个立方体的表面积和体积。
长方体正方体的体积计算公式

长方体正方体的体积计算公式咱们在数学的世界里啊,经常会碰到各种各样的图形,其中长方体和正方体那可是相当重要的角色。
先来说说长方体,这玩意儿就像是一个长长的盒子。
那怎么算出它的体积呢?其实很简单,就是用长乘以宽再乘以高。
比如说,有一个长方体的盒子,长是 5 厘米,宽是 3 厘米,高是 2 厘米,那它的体积就是 5×3×2 = 30 立方厘米。
我记得有一次,我在课堂上讲这个知识点的时候,有个小家伙瞪着大眼睛,一脸迷茫地问我:“老师,为啥要这么算啊?”我当时就笑了,然后从讲台上拿起一个长方体的粉笔盒,问大家:“你们看,这个粉笔盒就像一个长方体,如果我们把它一层一层地摆小方块,长的方向能摆 5 个,宽的方向能摆 3 个,高的方向能摆 2 层,那一共不就是 30 个小方块嘛,这 30 个小方块组成的空间大小,不就是这个长方体的体积嘛!”听我这么一说,小家伙们恍然大悟,脸上露出了开心的笑容。
再说说正方体,正方体其实就是一种特殊的长方体,它的长、宽、高都相等。
所以计算它的体积就更简单啦,直接边长乘边长再乘边长。
比如一个正方体的棱长是 4 厘米,那它的体积就是 4×4×4 = 64 立方厘米。
咱们在生活中也经常能看到长方体和正方体的身影。
像家里的冰箱,基本上就是一个长方体,咱们买冰箱的时候,不就得考虑它的体积大小,看看能不能放得下咱们想要放的东西嘛。
还有小朋友玩的魔方,那就是一个正方体,通过计算它的体积,咱们能大概知道它用了多少材料做成的。
总之,长方体和正方体的体积计算公式虽然简单,但用处可大着呢!大家可得好好掌握,以后在解决实际问题的时候就能派上大用场啦!。
长正方体的体积计算方法
推导长正方体的体积计算方法 年级 备课教师 使用教师
知识与技能目标:使学生理解长方体和正方体体积公式的推导。
教学目标 方法与过程目标:能运用公式进行长方体和正方体体积的计算。
情感态度与价值观目标:培养学生空间和空间想象能力。
教学重点 长正方体体积公式的推导。 教学难点 运用公式计算。 教学时间 环 节
2、一根长方体木料,长 5 厘米,横截面的面积是 0.06 平方厘米。这根木料的体积是多少? 理解横截面积的含义,体会长方体不同放置,说法各不 相同。 出示另一种计算方法:长方体体积=横截面积×长 3、家具厂订购 500 根方木,每根方木横截面的面积是 24 平方分米,长 3 米。这根木料一共是多少平方米? 理解面积单位和长度单位要一致。但不可能相同。 5、练一练 :用方程法。 (1) 、一块长方体的木板,体积是 90 立方分米。这块木 板的长是 60 分米,宽是 3 分米。这块木板的厚度是多少 分米? (2) 、一根长方体水泥柱,体积是 1 立方米,高是 4 米, 它的底面积是多少? (选择方法解答)
(3) 、观察:每排个数、排数、层数与体积有什么关 系? 板书:体积=每排个数排数排数×层数 每排个数、排数、层数相当于长方体的什么?
新 课 个小正方体,长正好是几厘米;摆几排,宽正好是几厘
米;摆几层,高也正好是几厘米。 (4)如何计算长方体的体积? 板书:长方体体积=长×宽×高 字母公式:V=abh 练习: 1、一个长方体,长 7 厘米,宽 4 厘米,高 3 厘米,它 的面积是多少? 2、导出正方体体积公式: 根据长方体和正方体的关系,你能想出正方体的体积怎 样计算吗?
教学难点 教学时间 环 节
体积单位的进率的化聚。 课时 教学准备 教学过程 个性化设计
长方体正方体的棱长总和体积表面积的公式

长方体正方体的棱长总和体积表面积的公式
长方体体积=长×宽×高
长方体表面积=(长×宽+长×高+宽×高)×2'
长方体棱长和=(长+宽+高)×4
正方体体积=棱长×棱长×棱长
正方体表面积=棱长×棱长×6
正方体棱长和=棱长×12
扩展资料:
长方体是底面是长方形的直棱柱。
正方体是特殊的长方体,正方体是六个面都是正方形的长方体。
长方体的每一个矩形都叫做长方体的面,面与面相交的线叫做长方体的棱,三条棱相交的点叫做长方体的顶点。
长方体六个面面积的和,叫作长方体的表面积。
长方体的体积是对长方体的一种度量,长方体的体积等于长、宽、高之积。
表面积
因为相对的2个面面积相等,所以先算上下两个面,再算前后两个面,最后算左右两个面。
设一个长方体的长、宽、高分别为a、b、c,则它的表面积为S = (ab+bc+ca)×2,也等于2ab+2bc+2ca,还等于2(ab+bc+ca)。
公式:长方体的表面积=长×宽×2+宽×高×2+长×高×2,或:长方体的表面积=(长×宽+宽×高+长×高)×2。
体积
长方体的体积=长×宽×高。
设一个长方体的长、宽、高分别为a、b、c,则它的体积:
因为长方体也属于棱柱的一种,所以棱柱的体积计算公式它也同样适用。
长方体体积=底面积×高,即
(S是底面积)。
长方体和正方体的体积复习

【知识点3】 体积单位及体积单位的互化 体积单位:立方厘米、立方分米和立米 1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm3 体积单位的互化: 把高级单位化成低级单位,用高级单位数乘 以进率;------大化小,乘了好
把低级单位聚成高级单位,用低级单位数 除以进率。-----------小化大,除了吧
五年级(下册)
【知识点1】 体积的概念和计算公式
体积:物体所占空间的大小叫做物体的体积。 长方体的体积= 长×宽×高 用字母表示:V=abh 正方体的体积= 棱长×棱长×棱长 用字母表示:V=a3
【知识点2】长方体和正方体的体积统一公式:
长方体或正方体的体积=底面积×高 用字母表示:V=Sh
长方体体积公式的推导过程: 你是如何推导出长方体的体积公式的?再说说你 在推导时用了什么数学方法? 答:我是用体积1立方厘米的小正方体摆不同的长 方体,并把摆成的不同形状的长方体的长、宽、 高的数据与各个长方体所含小正方体的个数作比 较,通过比较,观察发现长方体所含小正方体的 个数就是长方体的体积,它与它的长×宽×高的 积正好相等,从而推导出长方体的体积=长×宽× 高如果用V表示长方体的体积,用a、b、h分别表 示长方体的长、宽、高,那么长方体的体积公式 可以写成V=abh,我在推导时采用了实验、观察、 比较、归纳、推理等方法。
4.有一个底面积是正方形的长方体,高是20厘 米,侧面展开正好是一个正方形。求这个长方 体的体积。
5.家具厂订购500根方木,每根方木横截 面的面积是24平方分米,长是3米,这些 木料一共是多少方?
同学们,通过这节课的学 习你有怎样的收获呢?
1.正方体的棱长扩大到原来的6倍,体积也扩大到原 来的6倍。( ) 2.如果将一块长方体的橡皮泥捏成一个正方体,我 们看到它的形状变发,但是它所占的空间的大小没变。 ( ) 3.一个物体的体积是1立方分米,这个物体的形状 一定是正方体。( ) 4.1立方米比1平方米大。( ) 5.长方体和正方体的体积都等于底面积乘以高。 ( ) 6.一个长方体的体积扩大2倍,它的长、宽、高都 扩大2倍。( )
长方体正方体表面积和体积公式

长方体正方体表面积和体积公式
长方体和正方体是几何学中常见的几何体,它们的表面积和体积是通过一些简单的公式来计算的。
首先来看长方体。
长方体是一种有六个矩形面的立体图形,其中每个面都是相对的两个相等的矩形。
我们可以使用以下公式来计算长方体的表面积和体积。
长方体的表面积等于所有面的面积之和。
假设长方体的长、宽、高分别为L、W、H,则长方体的表面积S可以用下面的公式表示:
S = 2LW + 2LH + 2WH
长方体的体积等于底面积乘以高。
长方体的体积V可以用下面的公式表示:
V = LWH
接下来我们来看正方体。
正方体是一种特殊的长方体,它的六个面都是正方形。
正方体的边长为a。
正方体的表面积和体积公式与长方体类似。
正方体的表面积等于所有面的面积之和。
正方体的表面积S可以用下面的公式表示:
S = 6a^2
正方体的体积等于边长的立方。
正方体的体积V可以用下面的公式表示:
V = a^3
长方体和正方体的表面积和体积公式是非常有用的,它们可以帮助我们计算这些几何体的重要属性。
无论是在日常生活中还是在工程领域,我们都经常需要使用这些公式来解决问题。
希望通过这篇文章的介绍,读者能更好地理解长方体和正方体的表面积和体积公式,并能灵活应用它们解决实际问题。
长方体正方体的表面积和体积公式

建筑安全网 建筑安全网价格
OO4Ov8ZD4P1S
)平方厘米。
10、一个长方体长4分米,宽3分米,高2分米,它的表面积是(
)平方分米。
11、正方体的棱长之和是60分米,它的表面积是(
)平方分米。
二、判断题
1、把两个完全一样的正方体拼成一个长方体,体积和表面积都不变。( )
2、长方体的长、宽、高分别是3 cm、4 cm和4 cm,其中有两个相对的面是正方形。(
5、用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、 宽7厘米的长方体框架,它的高应该是多少厘米?
6、天天游泳池,长25米,宽10米,深1.6米,在游泳池的四周和池底砌瓷砖,如果瓷砖的边长 是1分米的正方形,那么至少需要这种瓷砖多少块?
7、一盒饼干长20厘米,宽15厘米,高30厘米,现在要在它的四周贴上商标纸,如果商标纸的 接头处是4厘米,这张商标纸的面积是多少平方厘米?
c=πd =2πr Ѕ=πr S=ch
S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch 圆柱的体积=底面积×高 V=Sh
V=πr h=π(d÷2) h=π(C÷2÷π) h 圆锥的体积=底面积×高÷3
V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷3
A. 增加了
B .减少了
C. 没有变
10、如果把一个棱长是10厘米的正方体切成两个完全相同的长方体,这两个长方体的表面积
之和比原来的正方体表面积(
)。
A. 增加了
B. 减少了
C .没有变化
长方体正方体体积计算

长方体正方体体积计算在我们的日常生活和学习中,经常会遇到与长方体和正方体体积计算相关的问题。
无论是在建筑设计、包装物品,还是在数学学习中,理解和掌握它们的体积计算方法都非常重要。
首先,让我们来认识一下长方体和正方体。
长方体是一种有六个面的立体图形,每个面都是长方形(有可能有两个相对的面是正方形),相对的面面积相等。
而正方体则是一种特殊的长方体,它的六个面都是完全相同的正方形。
那么,如何计算长方体的体积呢?我们知道,长方体的体积等于长乘以宽乘以高。
假设一个长方体的长为 5 厘米,宽为 3 厘米,高为 2厘米,那么它的体积就是 5×3×2 = 30 立方厘米。
这就好比是用一个个1 立方厘米的小正方体去填充这个长方体,长的方向能放 5 个,宽的方向能放 3 个,高的方向能放2 层,所以总的小正方体个数就是 30 个,也就是长方体的体积是 30 立方厘米。
再来看正方体,由于正方体的六个面都相等,所以它的体积计算就相对简单一些,正方体的体积等于棱长的立方。
比如说,一个正方体的棱长是 4 厘米,那么它的体积就是 4×4×4 = 64 立方厘米。
理解了体积的计算方法,我们来看看它们在实际生活中的应用。
比如,要建造一个长方体形状的水池,我们需要知道它的体积来确定能容纳多少水。
如果水池的长是 10 米,宽是 5 米,深是 2 米,那么水池的体积就是 10×5×2 = 100 立方米,也就是说这个水池能容纳 100 立方米的水。
在包装物品时,也经常会用到体积的计算。
假设要包装一个长方体形状的礼物,礼物盒的长、宽、高分别是30 厘米、20 厘米、10 厘米,那么我们就可以通过计算体积来选择合适大小的包装纸。
这个礼物盒的体积就是 30×20×10 = 6000 立方厘米。
除了实际应用,在数学学习中,长方体和正方体体积的计算也是很多问题的基础。
长方体、正方体体积的计算方法

长方体、正方体体积的计算方法知识点回顾1、长方体正方体的特征:⑴长方体有 6 个面,都是长方形,也可能有两个相对的面是正方形,相对的面的面积相等;长方体有12 条棱,相对的棱长度相等;长方体有8 个顶点。
⑵正方体有 6 个面,6 个面的面积相等;正方体有12 条棱,12 条棱长度相等;正方体有8 个顶点。
⑶长方体和正方体两个面相交的线叫做棱,三条棱相交的点叫做顶点。
长方体相交于同一顶点的三条棱的长度,分别叫做它的长、宽、高。
⑷正方体是长、宽、高都相等的长方体。
正方体是特殊的长方体。
⑸长方体(或正方体) 6 个面的总面积,叫做它的表面积。
⑹长方体的表面积=(长×宽+长×高+宽×高)× 2 用字母表示S=2(ab+ah+bh)或长方体的表面积=长×宽×2+长×高×2+宽×高×2 用字母表示S=2ab+2ah+2bh2正方体的表面积=棱长×棱长×6 用字母表示S=6a⑺解决有关长方体和正方体表面积的实际问题时,我们要注意有时只求长方体、正方体的4 个面(如:烟囱、通风管等)或 5 个面。
本节内容⑻物体所占空间的大小叫做物体的体积。
容器所能容纳物体的体积,叫做这个容器的容积。
3)、立方分米(dm3)、立方米(m3)。
常用的容积单⑼常用的体积单位有立方厘米(cm位有升(L)、毫升(ml)。
⑽1 立方米=1000 立方分米 1 立方分米=1000 立方厘米1 立方分米=1 升 1 立方厘米=1 毫升相邻体积单位的进率是1000。
⑾长方体的体积=长×宽×高V=abh长方体的长=体积÷宽÷高3⑿正方体的体积=棱长×棱长×棱长V= a⒀长方体(或正方体)的体积=底面积×高V=sh长方形的高=体积÷底面积长方体的体积=横截面积×长长方体的长=体积÷横截面积⒁长方体的棱长和=(长+宽+高)× 4 C=4(a+b+h)长方体的棱长和=长×4+宽×4+高×4 C=4a+4b+4h长方体的高=棱长和÷4-长-宽正方体的棱长和=棱长×12 C=12a正方体的棱长=棱长和÷12例题1.填空(1)( )叫做物体的体积。
长方体正方体所有公式

长方体正方体所有公式
1.长方体表面积公式:S=2(ab+ac+bc),其中a、b、c分别为长方体的三条边长。
2. 长方体体积公式:V = abc,其中a、b、c分别为长方体的三条边长。
3. 长方体对角线长公式:d = √(a + b + c),其中a、b、c分别为长方体的三条边长。
4. 长方体的空间对角线长公式:D = √(a + b + c),其中a、
b、c分别为长方体的三条边长。
正方体公式:
1. 正方体表面积公式:S = 6a,其中a为正方体的边长。
2. 正方体体积公式:V = a,其中a为正方体的边长。
3. 正方体对角线长公式:d = √3a,其中a为正方体的边长。
4. 正方体的空间对角线长公式:D = a√3,其中a为正方体的边长。
以上就是长方体和正方体的所有公式,希望对您有所帮助。
- 1 -。
长方体正方体体积问题

长方体正方体体积问题长方体和正方体是常见的几何体形状,它们的体积是我们在数学中常常遇到的问题。
本文将围绕长方体和正方体的体积展开讨论,介绍它们的定义、计算方法以及实际应用。
一、长方体的体积长方体是一种有六个面的立体,它的六个面都是矩形。
我们可以用三个边长来描述一个长方体,分别为长、宽和高,用L、W和H表示。
长方体的体积是指长方体所占据的三维空间的大小,用V表示。
计算长方体的体积非常简单,只需要将长方体的长、宽和高相乘即可,即V = L × W × H。
例如,如果一个长方体的长为5cm,宽为3cm,高为2cm,那么它的体积就是5cm × 3cm × 2cm = 30cm³。
长方体的体积可以用立方厘米、立方米等单位来表示,具体使用哪种单位要根据实际情况来定。
在计算体积时,要确保所使用的长度单位一致,以避免计算结果的错误。
长方体的体积在日常生活中有许多实际应用。
比如,在装箱运输时,我们需要计算物体的体积以确定所需的包装箱尺寸;在建筑设计中,需要计算房间的体积以确定空调、采暖等设备的容量。
二、正方体的体积正方体是一种特殊的长方体,它的六个面都是正方形。
正方体的边长用a表示,正方体的体积用V表示。
正方体的体积计算方法与长方体类似,只需要将正方体的边长相乘三次即可,即V = a × a × a,也可以简写为V = a³。
例如,如果一个正方体的边长为4cm,那么它的体积就是4cm × 4cm × 4cm = 64cm³。
与长方体类似,正方体的体积也可以用不同的单位来表示,具体使用哪种单位要根据实际情况来确定。
在计算体积时,要注意所使用的长度单位的一致性,以免计算结果出现错误。
正方体的体积在几何学和物理学中有广泛的应用。
例如,在立方体的几何问题中,我们可以通过计算体积来解决相关的计算问题;在物理学中,正方体的体积可以用来计算物体的质量密度等。
长方体正方体体积

长方体正方体体积 Prepared on 24 November 2020长方体与正方体体积知识点:1、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh长=体积÷宽÷高 a=V÷b÷h宽=体积÷长÷高b=V÷a÷h高=体积÷长÷宽 h= V÷a÷b2.正方体的体积=棱长×棱长×棱长V=a×a×a= a3读作“a的立方”表示3个a相乘,(即a·a·a)长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高用字母表示:V=S h(横截面积相当于底面积,长相当于高)。
3、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
固体一般就用体积单位,计量液体的体积,如水、油等。
常用的容积单位有升和毫升也可以写成L和ml。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升(1 L = 1 dm3 1 ml = 1 cm3)注意:1、长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
2、*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:V 物体 =V 现在-V 原来也可以 V 物体 =S ×(h 现在- h 原来)V 物体 = S ×h 升高3、【体积单位换算】 大单位 小单位 小单位 大单位 进率: 1立方米=1000立方分米=1000000立方厘米 (立方相邻单位进率1000)1立方分米=1000立方厘米=1升=1000毫升1立方厘米=1毫升1平方米=100平方分米=10000平方厘米1平方千米=100公顷=1000000平方米注意:长方体与正方体关系把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
长正方体体积公式

长正方体体积公式
长正方体是一种立体几何体,它有三个不同的边长,分别为长、宽、高。
长正方体的体积是指其所占空间的大小,可以用一个简单的公式进行计算。
长正方体的体积公式为:V=lwh
其中,V表示长正方体的体积,l表示长,w表示宽,h表示高。
将长、宽、高代入公式中,即可计算出长正方体的体积。
需要注意的是,当长正方体的三条边长都为整数时,其体积也是一个整数。
此外,长正方体也可以被视为一个立方体的变形,因为它们都是由6个正方形面组成的。
但是,立方体的三条边长是相等的,而长正方体却不一定相等。
在实际生活中,长正方体广泛应用于建筑、家具、货物包装等方面。
对于建筑和家具而言,计算长正方体体积可以帮助设计师更好地规划空间和材料,确保建筑和家具的稳定性和美观性。
对于货物包装而言,计算长正方体体积可以帮助物流公司更好地评估运输成本和效率,确保货物能够安全、高效地运输到目的地。
总之,长正方体体积公式是一个简单而实用的公式,可以在数学、工程、物流等领域中得到广泛应用。
- 1 -。
正方体长方体的体积公式

正方体长方体的体积公式正方体长方体的体积公式正方体和长方体是我们在日常生活中经常遇见的几何图形,它们在建筑、制造、装饰等领域中都发挥着重要的作用。
正方体和长方体的体积计算是几何学中的基本问题之一,本文将详细介绍正方体长方体的体积公式并给出实例说明。
正方体的体积公式:正方体是一种六个面都相等且互成直角的立方体,它的体积公式为:V = a³其中,a表示正方体的边长,V表示正方体的体积。
正方体的体积是边长的三次方,也可以理解为在三维空间中由六个面所包围的立体空间的大小。
通过计算正方体的体积可以帮助我们明确建筑物、器具等的空间大小,从而更合理地规划设计和利用空间。
例如,一台电视机的外包装为一个立方体,长宽高分别为50cm,40cm,30cm,我们可以通过正方体的体积公式计算它的容积:V = a³ = 50cm × 40cm × 30cm = 60000cm³因此,这台电视机外包装的容积为60000cm³。
长方体的体积公式:长方体是一种六个面都为矩形的立方体,它的体积公式为:V = l × w × h其中,l、w、h分别表示长方体的长度、宽度、高度,V表示长方体的体积。
长方体的体积可以看做底面积与高的乘积,也可以理解为在三维空间中由六个面所包围的立体空间的大小。
与正方体不同的是,长方体的体积需要分别计算长度、宽度和高度,因此在计算长方体的体积时需要注意各个参数的单位是否一致。
例如,一根木棒的形状为长方体,长度为2m,宽度为10cm,厚度为20cm,我们可以通过长方体的体积公式计算它的容积:V = l × w × h = 2m × 0.1m × 0.2m = 0.04m³因此,这根木棒的容积为0.04m³。
应用举例:作为几何学中的基础知识,正方体和长方体的体积公式在我们的日常生活中有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体和正方体的体积
浦东新区林苑小学高圆教学内容:九年制义务教育课本数学五年级第二学期P40,41。
教学目标:
1、理解长方体、正方体体积计算公式的推导过程。
2、掌握长方体、正方体体积计算公式,正确计算长方体、正方体的体积。
3、经历动手操作,观察分析,归纳概括,进一步构建体积的空间观念。
4、能运用长方体和正方体的体积计算公式解决生活实际问题。
教学重点:
长方体、正方体的体积计算。
教学难点:
长方体、正方体的体积计算公式的推导过程。
教学过程:
一、引入
1、激发学生学习数学的兴趣和需要。
哪个物体的体积小?(直接比较)
哪个礼盒的体积大?(不能直接比较)
板书:长方体的体积
2、猜想:长方体体积的大小可能与长方体的什么有关系呢?
板书:长、宽、高
二、小组合作,探究新知
1、探究一
学生动手操作:用12个体积是1 cm3的小正方体搭成一个长方体。
探究二
1)把数据填入表格。
2)想一想所拼成的长方体的长、宽、高与体积有什么联系?
2、反馈交流
教师提问:这些长方体有什么共同点?不同点?
为什么形状不同而体积相等呢?
观察这些从实际操作中得出的数据,结合拼摆成的图形,想一想这些数据与长方体的体积有没有关系?是什么关系?(长方体的体积等于它的长、宽、高的乘积)板书:长方体的体积=长×宽×高
3、质疑:刚才所得出的公式是否适用于任何一个长方体的体积计算?
验证长方体的体积=长×宽×高
板书:V=abh
4、小结:通过刚才的探究学习,我们知道长方体的体积和它的什么有关系?
5、应用:红星小学需要建造一个长方体的领操台,它的长为8米,宽为5米,高为2米,这个领操台的体积是多少立方米?(口答练习,媒体演示)
6、练习:利用公式计算下列长方体的体积
三、正方体体积
1、(演示课件)此时的长方体的长,宽,高分别是4cm,是什么图形?
2、讨论正方体体积公式.
板书:正方体体积=棱长×棱长×棱长。
V=a×a×a=a3
3、a3的意义
4、练习:利用公式计算下列正方体的体积
四、课堂总结
我们通过猜想、探究、质疑和验证的方法推导出了长方体、正方体的体积计算公式,请大家回忆一下推导的过程。
五、解决实际问题
1、计算比较两个长方体模型体积大小
2、课件演示:解决实际问题。
3、(机动)动脑筋:把1立方分米的正方体礼盒装入一个长方体打包盒,打包盒里面长为4分米,宽为3分米,高为2.5分米。
盒子里最多能装几个礼盒?
板书设计:
长方体、正方体的体积
长方体的体积=长×宽×高
v=abh
正方体的体积=棱长×棱长×棱长
v=a×a ×a =a3。
