计算物理随机游走
随机游走离散型随机变量的随机漫步模型

随机游走离散型随机变量的随机漫步模型随机游走是一种描述随机变量在一条离散路径上从一个状态跳转到另一个状态的模型。
在该模型中,随机变量在每次转移时根据一定的概率进行状态的跳转,使得其在状态空间中进行“随机漫步”。
本文将介绍随机游走的概念、离散型随机变量以及随机漫步模型的基本原理。
一、随机游走的概念随机游走(Random Walk)是一种数学模型,用于描述在离散路径上随机变量的运动轨迹。
在随机游走过程中,随机变量从当前状态跳转到下一个状态的概率是随机的,并且其转移规律通常遵循一定的概率分布。
随机游走常用于模拟各种现实中的问题,如股票价格的变化、传染病的传播等。
二、离散型随机变量离散型随机变量(Discrete Random Variable)指的是在一定的取值范围内,可能取到有限个或可列个数值的随机变量。
与连续型随机变量不同,离散型随机变量的取值仅限于某些特定的数值。
常见的离散型随机变量包括二项分布、泊松分布等。
三、随机漫步模型随机漫步模型(Random Walk Model)是一种描述随机变量以随机方式在状态空间中移动的数学模型。
在随机漫步模型中,随机变量在每次转移时根据一定的概率进行状态的跳转,使得其在状态空间中进行随机的移动。
具体的转移规律通常由转移概率矩阵来描述。
在离散型随机变量的随机漫步模型中,随机变量的状态空间是有限个或可列个状态。
随机漫步模型可以用一个状态转移矩阵来表示,矩阵的元素表示从一个状态转移到另一个状态的概率。
通过迭代计算,可以得到随机变量在每个状态下的概率分布,从而对其进行建模和分析。
随机漫步模型在实际应用中具有广泛的意义。
例如,在金融领域中,可以利用随机漫步模型来预测股票价格的变化趋势;在物理学领域中,可以使用随机漫步模型来模拟原子或分子的扩散过程等。
总结:随机游走离散型随机变量的随机漫步模型是一种描述随机变量在离散路径上随机跳转的数学模型。
通过随机漫步模型,我们可以对离散型随机变量的状态进行建模和分析,为实际问题的解决提供参考。
计算物理 随机游走

n
x n = ( p − q )n = 0
i = 1, i = j
∑s s
i
n
j
+
i j i =1, j =1, i ≠ j
6
∑s s
n
x n = ∑ si
i =1
2 x n = ∑ si ⋅ ∑ s j = i =1 j =1 n n
n
xn = 0
( s1 + s2 ) ⋅ ( s1 + s2 )
正方形格点划分 等步长h 等步长
其中, 是在区域D的正则内点 上的函数q(x,y)的值。 的正则内点0上的函数 的值。 其中,q0是在区域 的正则内点 上的函数 的值
13
1 φ0 = (φ1 + φ2 + φ3 + φ4 − h2 q0 ) 4
其中, 可以解释为概率 即有: 可以解释为概率。 其中,1/4可以解释为概率。即有:
右边分布积分再代入边界条件:p( ±∞ , t ) = 0
+ ∞ ∂ p( x , t ) ∂ p( x , t ) ∂ p( x , t ) D∫ x dx = Dx dx = 0 − D∫ 2 −∞ −∞ ∂ x ∂x − ∞ ∂x +∞ 2
9
+∞
∂ x =0 ∂t
由于在t=0时 粒子在原点处, 由于在 时 , 粒子在原点处 , 从而粒子 位置的平均值是不随时间变化的。 位置的平均值是不随时间变化的。
x2 =
2 k BT
α
t + c1e
−α t
m
+ c2
x
2
=
2 k BT
α
t = 2 Dt
D为扩散系数。 为扩散系数。 为扩散系数
彭芳麟计算物理基础课后答案
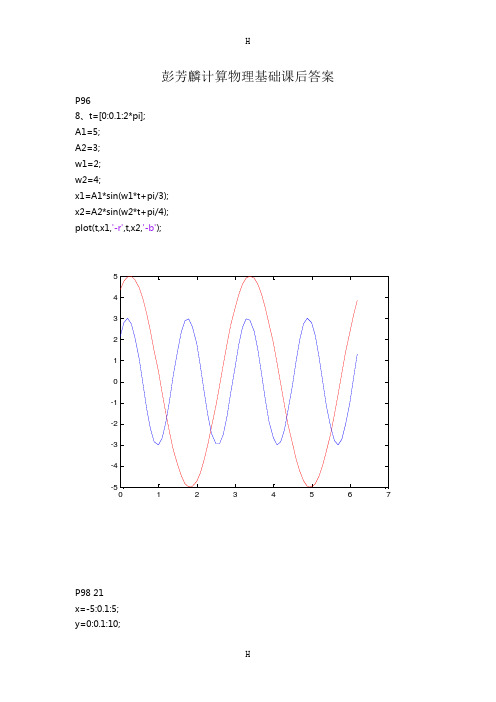
彭芳麟计算物理基础课后答案P968、t=[0:0.1:2*pi]; A1=5; A2=3; w1=2; w2=4;x1=A1*sin(w1*t+pi/3); x2=A2*sin(w2*t+pi/4); plot(t,x1,'-r',t,x2,'-b');1234567-5-4-3-2-1012345P98 21 x=-5:0.1:5; y=0:0.1:10;[X,Y]=meshgrid(x,y); z=X.^2.*Y + sqrt(Y)./X; mesh(X,Y,z);-2024-22P97 20 subplot(1,2,1);[X0,Y0,Z0]=sphere(20); X=2*X0;Y=3*Y0; Z=4*Z0+1; surf(X,Y,Z); axis equal subplot(1,2,2) t=-1:0.1:1;[X,Y,Z]=cylinder(1+t.^2,20);%形成旋转曲面 surf(X,Y,Z); P195 1x=[-1.0 -0.75 -0.50 -0.25 0 0.25 0.50 0.75 1.00];y=[-0.2209 0.3295 0.8826 1.4392 2.0003 2.5645 3.1334 3.7061 4.2836];a=polyfit(x,y,1);a= 2.2516 2.0131y=2.2516x+2.0131P151 3syms vvp=1578;f=int(4/pi^(1/2)*v^2/vp^3*exp(-v^2/vp^2),v,0,Inf);VF=vpa(f);1. 解:依题,取a 5,c 1,m 16, x0 1xn 1 (5xn 1)(mod16),x0 1,x伪随机数:n n162. 解:依题,取a 137,c 187,m 256,x0 1xn 1 (137xn 187)(mod 256),x0 1,xn 2 (137xn 1 187)(mod 256),x x x伪随机数:n n ,n 1 n 1 ,n 2 n 2256 256 2563. 解:引入二维随机均匀分布向量(x,) 表示针在桌上的位置,s 1 1x [0, ], f (x ) ;[0, ], f () .1 22 s / 2 0 2 / 2 0其中,s 为线间的距离,l 为针长度,x 为线中点到最近平行线的距离,为针与线平行线间的夹角。
耦合的公式(二)

耦合的公式(二)耦合的公式在物理学和工程学中,耦合是指两个或多个系统之间相互影响或相互依赖的现象。
在数学建模中,我们可以使用耦合的公式来描述这种相互影响或依赖关系。
下面是一些常见的耦合公式及其解释说明。
1. 费马的小定理费马的小定理是数论中的一个重要定理,它描述了素数与模运算之间的关系。
该定理可以表示为以下公式:a^{p-1} \equiv 1 \pmod{p}其中,a是一个整数,p是一个素数。
例如,我们要判断一个数是否为素数,可以使用费马的小定理。
如果对于给定的数a,我们选择一个素数p,计算a^{p-1}对p取余,如果结果等于1,则a可能是素数,否则不是素数。
2. 随机游走随机游走是一种随机过程,描述了在随机因素的影响下,物体在空间中的连续移动。
其中一个经典的随机游走模型是随机行走模型,可以用以下公式表示:x_t = x_{t-1} + \epsilon_t其中,x_t表示在时间t的位置,x_{t-1}表示在时间t-1的位置,_t表示在时间t的随机步长。
例如,我们可以用随机游走模型来模拟股票价格的变动。
每个时间点的股票价格可以通过上一个时间点的价格加上一个随机的步长来计算。
3. 麦克斯韦方程组麦克斯韦方程组是电磁学中的一组基本方程,描述了电场和磁场之间的耦合关系。
其中一个麦克斯韦方程可以表示为以下公式:\nabla \times \mathbf{E} = -\frac{\partial \mathbf {B}}{\partial t}其中,表示电场,表示磁场,,表示对时间的偏导数。
这个方程描述了磁场随时间变化的规律与电场的旋度之间的关系。
4. 生态系统模型生态系统模型是用于描述生物群落、能量流动和物质循环等生态系统过程的数学模型。
一个常见的生态系统模型是Lotka-Volterra方程,可以表示为以下公式:\frac{dN_1}{dt} = r_1N_1 - \alpha_1N_1N_2\frac{dN_2}{dt} = -r_2N_2 + \alpha_2N_1N_2其中,N_1和N_2表示两个物种的数量,r_1和r_2表示它们的自然增长率,_1和_2表示相互作用的强度。
原子物理学中的量子随机行走

原子物理学中的量子随机行走量子随机行走(Quantum Random Walk),是原子物理学中研究的重要课题之一。
它通过模拟单个粒子在离散空间中随机移动的过程,揭示了微观世界中非经典的行为特征。
量子随机行走的基本概念可以从经典随机行走开始理解。
在经典随机行走中,一个粒子在平面上进行二维随机移动,每一步只能向上、下、左或右移动。
经过多次随机选择方向并移动一步,粒子的位置会随着时间的推移逐渐扩散,形成一个随机分布。
而在量子随机行走中,粒子不再是经典粒子,而是由量子态描述的,具有波粒二象性。
它既可以表现为粒子的离散位置,也可以表现为波函数的连续分布。
在量子随机行走中,粒子的行为会受到“硬币”操作的影响。
这里的“硬币”是指量子系统的一个自由度,它的状态可以是0或1,分别代表右移或左移的方向。
在每一步移动之前,粒子都会与这个“硬币”进行相互作用,并根据测量结果决定下一步移动的方向。
而这个“硬币”操作通常由一系列基本的量子逻辑门实现,比如Hadamard门或CNOT门等。
值得注意的是,量子随机行走和经典随机行走之间存在很大差异。
经典随机行走是完全随机的,而量子随机行走则会在某些情况下表现出非经典的行为。
例如,当“硬币”处于纠缠态时,粒子的位置分布会出现干涉现象,形成一种周期性的特征。
这种干涉效应与经典随机行走的扩散过程形成鲜明对比,展现了量子行走的独特之处。
量子随机行走不仅在理论物理中具有重要意义,而且在实验方面也有广泛的应用。
通过实验可以观测到量子随机行走的多种行为特征,如扩散速率、干涉现象等。
这些实验结果不仅丰富了对量子行为的理解,也有助于开发新的量子技术。
量子随机行走的研究还涉及到许多其他领域,比如量子算法、量子通信以及量子传感等。
在量子算法中,量子随机行走可以用于设计一些特定问题的高效算法,如搜索和优化问题。
而在量子通信和传感中,量子随机行走可以用于实现更安全和高效的通信和传感方案。
实际上,量子随机行走已经成为量子信息领域的一个重要研究方向,吸引了越来越多的科学家的关注和研究。
计算物理学练习题及参考解答

如图第一项限中单位正方形内投点在圆内的概率即为单位圆面积的四分之一。
2 数学方程: 4 dx1 dx2 (1 x12 x2 )
1
0
1
0
算法框图: 产生随机点 (ξ, η) M 个; 统计其中满足条件 2 2 1 的点的个数 N; 计算π值 4 N / M 。 Matlab 程序:P=4/100000*length(find(sum(rand(2,100000).^2)<1))
F ( x ) pi 。
xi x
在区间[0,1]上取均匀分布的随机数ξ,判断满足下式的 j 值:
F ( x j 1 ) F ( x j )
则抽样值η为 x j ,η分布符合分布函数 F(x)的要求为。 25、试述连续分布的随机变量的变换抽样法。 答:设连续型随机变量η的分布密度函数为 f ( x ) 。要对满足分布密度函数 f(x)的随机变量η 抽样较难时 可考虑通过其它已知函数的抽样来得到。考虑变换
!输出 avu,du1,du2,del 100 open(12,file='out.dat') write(12,1000) Nt,Ng,Nf,Ns,dx,avu,du1,du2,del close(12)
5
1000 format(4i10,5f15.4) end 计算距离的函数子程序 function dist(x,y,z) dist=sqrt(x*x+y*y+z*z) return end ! 计算权重的函数子程序 subroutine weight(x,f) dimension x(6) r1=dist(x(1),x(2),x(3)) r2=dist(x(4),x(5),x(6)) f=exp(-3.375*(r1+r2)) return end ! 梅氏游动一步的子程序 subroutine walk(RND,dx,x) dimension x(6),x0(6) call weight(x,f0) do 10 i=1,6 x0(i)=x(i) call random(RND) ! 存旧 10 x(i)=x(i)+dx*(RND-0.5) ! 生新 call weight(x,f) call random(RND) if(f.ge.f0*RND) goto 30 !游动 do 20 i=1,6 20 x(i)=x0(i) !不动 30 return End 29.有限差分法 答:微分方程和积分微分方程数值解的方法。基本思想是把连续的定解区域用有限个离散点构成的网格来 代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数 来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件 就近似地代之以代数方程组,即有限差分方程组 ,解此方程组就可以得到原问题在离散点上的近似解。 然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。 30.采用有限差分法求解微分方程时可以用直接法、随机游走法和迭代求解法。其中迭代法被广泛采用, 有直接迭代法、高斯-赛德尔迭代法和超松弛迭代法。 !
闪电的随机游走模型

423社会科学闪电的随机游走模型吕源淇(南京市江宁区汤山作厂,江苏 南京 210000)摘 要:本文对一个兴趣性的问题,即闪电的模型,进行了一些简单初步的探索。
我们分成两部分的来介绍。
第一部分,我们阐述模型的基础,也是概率模型或者说随机游走,因为闪电的形成是由于某处的空气作为介质被“击穿”,从而产生电流,接着在空气中传导,然后不断重复上述过程。
因此只有在电势差足够大的地方才可能产生击穿空气,进而产生电流。
所以我们考虑用电势差的大小来代表击穿的概率。
接着在第二部分,我们通过求解一组偏微分方程,即麦克斯韦方程组,来精确求出上述的概率值。
关键词:闪电模型;随机游走;偏微分方程数值解 一、闪电的随机游走模型首先,我们考虑对二维空间进行电势的初值设定,不妨设最上端(云层)的电势为1,而地面的电势为0,然后采用线性插值对空间的每一点赋值。
接着,假设t 时刻,之前产生的电流到达了点(ii,jj),此处的电势记为φii,jj 那么此时刻电流有三个方向可以走即前,前左,前右,概率大小由电势差决定即:由于概率是[0,1]之间的实数,因此归一化得:用计算机随机模拟得到下面的“闪电”:二、闪电的微分方程模型(一)建立模型直接用到的物理知识我们考虑麦克斯韦方程组电场部分的两个方程,它们可以归结为一个方程即:这个二阶偏微分方程描述了电势随空间的变化规律,通过给定边值和初值条件,利用该方程就能够求解全空间的电势分布。
(二)模型的建立我们的模型有以下假定:(1)假定空间中每一点均无电荷(于是ρ=0)。
(2)假定初始时刻大地与天空形成一个平行板电容器(于是初始空间电势是线性分布的)。
(3)假定闪电传播只受到空间各点电势的影响。
在上述假设的基础上,我们把方程(1)用差分形式表示,得:其中h x 表示把X 轴等分为n 分后每一份的长度,由于我们考虑的是,因此进一步简化为从上式可以看到在点(j,i)的电势是其四个邻接点的电势的算术平均。
马文淦《计算物理学》习题

第 6 页,共 7 页
H 0 ( x ) = 1, H1 ( x ) = x , = H n +1 ( x ) 2 x H n ( x ) − 2n H n −1 ( x ). (7)Mathematica 语言编写一个从某点出发求多元函数的局部极小或极大 值的程序包。 (8)用 Mathematica 语言编写一个程序包,它能实现平面图形的(a)平 移, (b)旋转, (c)对 x 坐标轴的反射。
第三章、Monte Carlo 方法的若干应用(习题)
(1)利用 Monte Carlo 方法计算三维、四维、五维和六维空间的单位半径 球的体积。 (2)利用分布密度函数 f ( x ) = A e − x 做重要抽样来求积分,并分析误差与 投点数的关系。
I =∫
+∞ 0
x 5/2 e − x d x.
∑
j =1
l
1 π4 ≥ ξ , 1 j4 90
然后置 x = −
1 ln(xxxx 2 3 4 5 ) ,其中 ξi 为 [0,1] 区间均匀分布的伪随机数。 L (11)对正则高斯分布抽样: ( x − µ )2 1 = p( x ) d x exp − d x. 2 σ 2 σ 2p (12)Gamma 函数的一般形式为 = f ( x) d x an x n −1 e − ax d x ( x ≥ 0) ( n − 1)!
第四章、有, 数值求解正方形场域 ( 0 ≤ x ≤ 1,
的拉普拉斯方程:
∇2ϕ ( x, y ) = 0; ( x,0) ϕ = ( x,1) 0, ϕ= (0, y ) ϕ= (1, y ) 1. ϕ=
(2)用有限差分法发展一个程序,数值求解极坐标下的泊松方程:
分数阶布朗运动

分数阶布朗运动分数阶布朗运动,又称为分数阶随机游走或分数阶随机过程,是一类重要的随机过程模型。
与传统的布朗运动相比,分数阶布朗运动在时间上不再是连续的,而是具有非整数阶的时间导数。
这种非整数阶导数的引入使得分数阶布朗运动具有了更广泛的应用领域和更丰富的动力学行为。
分数阶布朗运动的定义是在分数阶微分方程的框架下进行建模和分析的。
分数阶微分方程是一种一般化的微分方程,其导数的阶数可以是任意实数,包括整数和分数。
在分数阶布朗运动中,时间导数的阶数被认为是一个分数,这就使得运动的时间步长变得更加灵活和多样化。
分数阶布朗运动在金融学、物理学、生物学等多个领域都有重要的应用。
在金融学中,分数阶布朗运动被用来描述股票价格、汇率等金融产品的价格变动。
与传统的布朗运动相比,分数阶布朗运动可以更好地捕捉到金融市场中的长尾分布和时间相关性。
在物理学中,分数阶布朗运动被用来描述粒子在非平衡系统中的扩散行为。
与传统的布朗运动相比,分数阶布朗运动可以更好地描述具有记忆效应和非马尔可夫性质的扩散过程。
在生物学中,分数阶布朗运动被用来描述细胞内分子的运动。
与传统的布朗运动相比,分数阶布朗运动可以更好地描述细胞内复杂环境中的扩散行为。
分数阶布朗运动的性质与传统的布朗运动有很大的不同。
首先,分数阶布朗运动的路径是不连续的,即存在无穷多个分割点,使得运动在不同的时间段内具有不同的行为。
其次,分数阶布朗运动的路径可以是非马尔可夫的,即过去的状态不仅仅取决于当前的状态,还取决于过去的状态。
最后,分数阶布朗运动的路径可以是非平稳的,即其统计性质随时间的演化而变化。
分数阶布朗运动的建模和分析是一个相对较新的领域,目前仍存在许多未解决的问题和挑战。
例如,如何求解分数阶微分方程的解析解和数值解,如何计算分数阶布朗运动的统计性质,以及如何利用分数阶布朗运动进行系统建模和控制等。
这些问题的解决将进一步推动分数阶布朗运动的理论发展和应用研究。
分数阶布朗运动是一种重要的随机过程模型,具有广泛的应用领域和丰富的动力学行为。
量子计算技术中的量子随机游走

量子计算技术中的量子随机游走随着科技的不断发展,量子计算技术逐渐成为了一个备受关注的领域。
其中,量子随机游走技术备受瞩目,被认为是未来量子计算机的重要组成部分之一。
那么,什么是量子随机游走技术?它背后的原理又是什么呢?量子随机游走是指,由量子系统进行的一种特殊的计算过程。
在量子随机游走中,一个量子粒子将被放置在一个走廊中,而该走廊由多个节点组成。
通过“量子掷币”,量子粒子将在不同节点中进行随机跳跃。
在这个过程中,粒子将会与其他量子粒子进行干涉,从而得到一些与经典物理难以比拟的结果。
这些结果将被采用来完成一些复杂的计算任务,例如图像处理等。
要理解量子随机游走的原理,首先必须了解量子叠加原理。
量子叠加原理指的是,当一个量子系统处于两个或多个可能状态的叠加态时,该系统将具有这些状态的所有特性。
例如,在一个叠加态粒子系统中,粒子将同时具有“自旋上”和“自旋下”的特性,而这些特性都可以被同时使用。
基于量子叠加原理,量子随机游走利用量子粒子的叠加状态完成随机跳跃。
在量子掷币时,量子系统将同时处于“正面”和“反面”的叠加态中。
这意味着,量子粒子将以等概率的方式跳到任何一个节点中。
然而,在跳跃时,量子粒子也将和其他量子粒子进行干涉,从而会生成一些不同于经典物理的结果。
这些结果将被采用来计算复杂的问题,例如搜索、排序和图像处理等。
当前,量子随机游走技术尚处于研究阶段。
尽管有一些实验已经证实了这种技术的巨大潜力,但要将它转化为实用技术仍然需要时间和资金的大量投入。
在未来,量子随机游走技术有望成为一种重要的量子计算机技术,带来革命性的改变。
在结论中,量子随机游走技术作为量子计算技术中的一项重要内容,它背后的原理是量子叠加原理。
这种技术可以用来计算复杂问题,例如搜索、排序和图像处理等。
虽然目前尚处于研究阶段,但它有着巨大的潜力,是未来量子计算机的一个重要组成部分。
未来,量子随机游走技术有望为我们带来巨大的改变。
随机游走算法,转移概率-概述说明以及解释

随机游走算法,转移概率-概述说明以及解释1.引言1.1 概述:随机游走算法是一种基于概率的算法,用于模拟随机的行为和变化过程。
它可以描述在一个有限的状态空间中,通过按照一定的规则进行状态转移,从而模拟随机选择下的状态变化。
这一算法在许多领域中有着广泛的应用,包括计算机科学、物理学、生物学、金融等。
随机游走算法的核心思想是通过定义转移概率来描述状态之间的转移规则。
在一个随机游走过程中,每个状态都有一定的概率转移到其他状态,而这些概率可以根据实际情况进行确定。
通过迭代计算,随机游走算法可以模拟出状态的分布情况,进而提供对系统行为的理解和预测。
随机游走算法具有很多重要的特性和优点。
首先,它是一种非常灵活的模型,可以适用于各种不同的问题和场景。
其次,随机游走算法能够捕捉到系统中的随机变动和不确定性,从而可以更好地解释和预测实际情况。
此外,随机游走算法具有较快的收敛速度和较低的计算复杂度,使得它成为许多算法和模型的重要基础。
然而,随机游走算法也存在一些限制和缺点。
首先,它需要事先确定好状态空间和转移概率,这对于复杂系统可能是一个挑战。
其次,随机游走算法对初始状态的选择非常敏感,不同的初始状态可能会导致完全不同的结果。
此外,随机游走算法在处理长时间序列或具有周期性特征的问题时可能存在某些局限性。
综上所述,随机游走算法是一种重要且广泛应用的算法,能够在各个领域中提供对系统行为的建模和预测。
虽然它具有一些限制和缺点,但通过进一步研究和改进,随机游走算法有望在未来的发展中发挥更大的作用。
在接下来的章节中,我们将详细介绍随机游走算法的基本概念、应用领域以及优缺点,并对其重要性和未来发展进行总结和展望。
1.2 文章结构文章结构部分的内容可以包含以下内容:文章结构部分主要介绍了整篇文章的组织结构和各个部分的主要内容,将读者引导到整个文章的框架。
2. 文章结构本文分为引言、正文和结论三个主要部分。
2.1 引言部分引言部分主要对随机游走算法进行了概述,介绍了其基本概念以及本文的目的。
量子随机行走与原子粒子的移动行为

量子随机行走与原子粒子的移动行为量子随机行走是一种基于量子力学的行为模式,它模拟了粒子在空间中的移动。
在经典物理中,我们通常使用随机游走来描述粒子的移动。
然而,量子随机行走却展现出了一些非经典的特性,这使得它成为了一个备受关注的研究课题。
在经典随机游走中,粒子在每个时间步长中都会随机地向左或向右移动一步。
而在量子随机行走中,粒子的移动是由量子力学规律所决定的。
具体来说,量子随机行走是由一个带有两个状态的量子比特(qubit)和一个带有两个操作的量子门(quantum gate)组成的。
在量子随机行走中,粒子的移动受到两个因素的影响:粒子的位置和粒子的状态。
粒子的位置可以用一个整数来表示,而粒子的状态则可以用一个二进制数(0或1)来表示。
在每个时间步长中,粒子会根据当前的位置和状态进行移动。
具体来说,粒子会根据其状态在位置上进行“跳跃”,并在每个位置上进行“旋转”。
在量子随机行走中,粒子的移动是通过量子门来实现的。
量子门是一种能够对量子比特进行操作的装置,它可以将一个量子比特的状态转换为另一个状态。
在量子随机行走中,粒子的移动是通过对量子比特的状态进行操作来实现的。
具体来说,粒子会在每个位置上进行一个旋转操作,然后根据旋转后的状态在位置上进行一个跳跃操作。
量子随机行走与原子粒子的移动行为之间存在着一定的联系。
原子粒子在空间中的移动可以通过量子随机行走来模拟。
在实际的物理实验中,科学家们通过操控原子粒子的状态和位置,成功地实现了量子随机行走。
这些实验结果表明,量子随机行走可以用来描述原子粒子在空间中的移动行为。
量子随机行走在物理学领域中有着广泛的应用。
例如,在材料科学中,科学家们可以利用量子随机行走来研究材料中的电子输运行为。
在计算机科学中,量子随机行走也被用来设计新的量子算法。
此外,量子随机行走还被应用于网络搜索、图像处理等领域。
总结起来,量子随机行走是一种基于量子力学的行为模式,它模拟了粒子在空间中的移动。
马文淦_计算物理_习题

3、投针法计算圆周率数值,画出流程图,编写程序 方法 1 投针 10^1 次,pi 的蒙卡模拟值为 2.500000000000000 投针 10^2 次,pi 的蒙卡模拟值为 2.777777777777778 投针 10^3 次,pi 的蒙卡模拟值为 2.985074626865672 投针 10^4 次,pi 的蒙卡模拟值为 3.133813851457223 投针 10^5 次,pi 的蒙卡模拟值为 3.142875102143441 投针 10^6 次,pi 的蒙卡模拟值为 3.143418467583497 投针 10^7 次,pi 的蒙卡模拟值为 3.142216400044368 //本程序在 Visual C++ 6.0 下编译通过 #include<stdio.h> #include<math.h> #include<windows.h> void main() { int xi10, xi20; double delta1,delta2; double I; double pi; int n; double N; FILE *fp; fp = fopen("3.txt","w"); for (n = 1; n <= 7; n++) { I = 0; srand(time(0)); for (N = pow(10, n); N > 0 ; N--) { xi10 = rand(); xi20 = rand(); delta1 = (double)(xi10 % 32767) / 32767.0 / 2.0; delta2 = (double)(xi20 % 32767) / 32767.0 / 2.0 * 3.1415926; if (delta1 < (sin(delta2) / 2.0)) { I = I + 1; }
量子随机游走的原理与实验操作指南

量子随机游走的原理与实验操作指南随机游走是一种数学和物理领域常见的模型,用于描述一随机过程在空间上的随机漫步。
随机游走的应用已经扩展到各个领域,包括金融、社会科学和生物学等。
随着量子计算的发展,量子随机游走成为了一个备受关注的研究领域,它在量子信息和量子计算方面具有潜在的应用。
量子随机游走是指在量子力学框架下进行的随机游走过程。
与经典随机游走不同,量子随机游走利用了量子叠加和量子纠缠的特性,使得游走结果具有量子性质。
量子随机游走在某些情况下能够表现出经典随机游走无法达到的优势,如更快的搜索速度和更好的定位精度。
在量子随机游走的理论中,一个量子粒子被放置在一个由节点构成的图中,该图可以是平面上的格点图或是一般的无向图。
粒子可以从一个节点跳到相邻节点,并在每个节点上执行一个量子操作。
在经典随机游走中,粒子跳到相邻节点的概率是均匀的;而在量子随机游走中,粒子在每个节点跳到相邻节点的概率由量子操作的幺正矩阵决定。
量子随机游走的原理基于量子叠加和量子相位干涉效应。
在游走的初态中,量子粒子处于所有可能的位置的叠加态,然后通过量子操作的幺正矩阵,粒子会在不同节点之间产生干涉,导致概率幅的相对相位发生变化,最终影响粒子在图中的分布。
通过适当设计的幺正矩阵,可以使得粒子的分布呈现出特定的行为,如扩散、局域化或者扩散与局域化的交替。
进行量子随机游走的实验操作需要一系列步骤和实验装置。
首先,需要准备实验装置,包括一台用于制备和操作量子态的量子计算机,并搭建一个由量子比特构成的网络图。
将量子比特配置到所需的初态,通常是制备一个等概率分布的叠加态。
其次,需要设计并实施适当的量子操作来实现量子随机游走。
这些操作可以采用量子逻辑门、单量子比特门和受控门等量子操作来实现。
在每个节点上的量子操作要根据具体的应用需求进行选择。
实验过程中要保持量子系统的纯度,控制好解相-非相干和弛豫等噪声。
物理实验中,通常会使用量子纠缠技术来延长量子态的寿命,并对量子态进行测量。
计算物理随机游走

通过分子动力学模拟,可以研究不同成分、结构对材料性能的影 响,为新材料的设计和开发提供理论指导。
材料制备工艺优化
分子动力学模拟可用于优化材料的制备工艺,提高材料的性能和 稳定性。
量子计算在处理大规模数据中的潜力
量子计算原理
大规模数据处理
量子计算可应用于处理大规模数据,通过量子叠加 和量子纠缠等特性,实现高效的数据分析和挖掘。
随机游走具有马尔可夫性质,即下一步的状态仅 与当前状态有关,与历史状态无关。
03 路径依赖性
尽管每一步是随机的,但长期行为可能呈现出一 定的规律性,如扩散现象。
一维、二维及三维随机游走
一维随机游走
01
粒子在一条直线上进行左右随机移动,位置随时间变化形成一
维随机序列。
二维随机游走
02
粒子在平面上进行上下左右随机移动,位置变化构成二维随机
用
布朗运动与扩散现象
01
02
03
布朗运动
悬浮在液体或气体中的微 粒受到周围分子的无规则 碰撞而产生的无规则运动。
扩散现象
物质分子从高浓度区域向 低浓度区域转移的过程, 其速率与浓度梯度和扩散 系数有关。
随机游走模型
描述布朗运动和扩散现象 的常用模型,通过模拟大 量粒子的随机运动来揭示 宏观规律。
化学反应动力学过程模拟
01
化学反应速率
描述化学反应快慢的物理量,与反应物浓度、温度等因素有关。
02
随机游走模型在化学反应中的应用
通过模拟反应物分子的随机运动,可以研究反应速率、反应机理等动力
学过程。
03
Monte Carlo模拟
一种基于随机数的计算方法,可用于模拟复杂的化学反应过程。
量子随机行走与量子游走算法

量子随机行走与量子游走算法量子随机行走(Quantum Random Walk)是一种基于量子力学原理的随机行走模型,它在量子计算和量子信息领域引起了广泛的兴趣。
量子随机行走的基本思想是将经典随机行走的概念与量子叠加态相结合,通过量子叠加态的干涉效应来实现更高效的搜索和优化算法。
量子随机行走的研究不仅对于理解量子计算的基本原理有着重要意义,还有着广泛的应用前景。
量子随机行走的基本模型可以用一个二维的格子表示,其中每个格子代表一个状态,而行走者则在不同的状态之间移动。
在经典随机行走中,行走者在每个时间步骤中以一定的概率向左或向右移动。
而在量子随机行走中,行走者的状态是一个量子叠加态,可以同时处于多个位置上。
行走者在每个时间步骤中通过量子门操作实现状态的转移,从而实现量子随机行走。
量子随机行走的一个重要应用是在搜索算法中,特别是在无序数据库搜索问题中。
传统的搜索算法需要遍历整个数据库来找到目标元素,而量子随机行走算法可以通过量子叠加态的干涉效应,在较少的步骤中找到目标元素。
这是因为量子随机行走可以在多个位置上同时进行搜索,并通过干涉效应增强目标元素的概率幅值,从而实现更高效的搜索。
除了搜索算法,量子随机行走还可以应用于优化问题。
优化问题是在给定约束条件下,寻找使目标函数取得最小或最大值的变量取值。
量子随机行走算法可以通过量子叠加态的干涉效应,在搜索空间中同时搜索多个解,并通过干涉效应增强优化目标的概率幅值,从而实现更高效的优化。
量子随机行走的实现可以通过量子电路和量子算法来实现。
量子电路是一种将量子比特之间的相互作用通过量子门操作来实现的物理系统。
量子算法是一种通过量子叠加态和干涉效应来实现更高效计算的算法。
量子随机行走的实现需要设计合适的量子电路和量子算法,并通过量子比特的干涉效应来实现量子随机行走的目标。
近年来,随着量子计算技术的不断发展,量子随机行走在理论和实验研究中取得了一系列重要进展。
研究人员通过实验验证了量子随机行走的基本原理,并在搜索算法和优化问题中实现了一些重要的应用。
数值模拟在物理实验中的应用方法简介

数值模拟在物理实验中的应用方法简介物理实验一直是科学研究的重要手段之一,它可以通过实际观察和测量来验证理论模型,并为理论模型提供数据支持。
然而,传统的物理实验有其局限性,比如实验成本高、实验过程复杂、有时难以精确控制等。
而数值模拟则可以克服这些困难,成为一种重要的物理实验辅助工具。
数值模拟是利用计算机模拟物理实验过程和结果的方法。
它基于物理方程和数值计算方法,通过将实验对象所遵循的物理规律以数学形式表达出来,并使用数值计算方法求解相应的数学模型,从而得到模拟结果。
下面将介绍数值模拟在物理实验中的几种常用方法。
第一种方法是有限元法(Finite Element Method,FEM)。
有限元法是一种将实际物体离散化为有限数量的元素,再分别对每个元素进行计算和模拟的方法。
它适用于复杂的三维物体模拟,如机械结构的强度和振动分析。
有限元法可以将物理模型划分为许多小的有限元,通过求解每个元素的位移、应力和应变等物理量的方程,最终得到整个物体的力学性能和应力分布。
有限元法具有计算精度高、适用范围广等优点,因此在工程领域得到了广泛应用。
第二种方法是蒙特卡罗方法(Monte Carlo method)。
蒙特卡罗方法是一种基于随机数统计的数值计算方法,它模拟了随机现象的特性,如粒子碰撞、随机游走等。
蒙特卡罗方法常用于模拟粒子的输运过程,比如在核能领域用于计算辐射剂量分布。
蒙特卡罗方法通过生成大量的随机数来模拟概率过程,通过统计随机数的频率分布,从而得到物理系统的统计特性。
第三种方法是计算流体力学(Computational Fluid Dynamics,CFD)。
计算流体力学是研究流体动力学和传热传质问题的数值模拟方法。
它基于质量、动量和能量守恒方程,通过将流体领域离散化为网格单元,再通过数值计算和迭代求解,模拟流体的运动和传热传质过程。
计算流体力学广泛应用于气体、液体以及其他复杂流体体系的模拟,比如风洞实验、气动优化设计等。
高斯分布与随机游走

工高作斯详分情布与随机游走
从这个几何图来看,我们可以很直观的看到随机游走一段时间之后呢,大多数蚂蚁居然都 挤在了 中心区域, 遵循越靠近中心,密度越大,越往边界密度越小的规律 这个规律其实最早是由法国数学家棣莫弗发现的
工高作斯详分情布与随机游走
我们来复盘一下他的思路,蚂蚁每次的爬行 都会在X轴和y轴上留下投影
工高作斯详分情布与随机游走
树上的每一个点都是 一次选择,我们能很 清楚地看到蚂蚁的行 进路线 最右边的终点呢,表 示了蚂蚁在几步之后 离中心点的距离
工高作斯详分情布与随机游走
把通往最右边的这一 列终点的路线数量排 列出来,它们的数量 分布大致上如下 这个式子,这就是大 名鼎鼎的二项分布,
工高作斯详分情布与随机游走
这类问题被称为随机游走问题, 是概率论和随机过程里很重要的 一个课题
工随作机详游情行,爬行 完全随机,一段时间 后拍一张定格照,然 这张定格照上画几个 圆圈
我们发现越靠近中心 原点的地方,蚂蚁的 密度就越大,如果我 们增加一个维度,
工随作机详游情走到中心
也就是把蚂蚁的密度 看成是高度的话,它 们的分布 在大致上类似于这么 一个几何形状
高斯分布与随 机游走
工高作斯详分情布与随机游走
目录
工高作斯详分情布与随机游走
数学家高斯将一个铁丝网格挂到了空中,放 一群观察爬行。对于蚂蚁来说,在网格的任 意一个交点处都会面临上下左右四个选择 假把这只蚂蚁放在网格的正中心,过一段时 间再去看它是出现在网格的边界处?还是中 心处?
工随作机详游情走到中心
工- 作详情
20XX 感谢聆听 批评指导 THANK YOU TO LISTEN TO CRITICISM GUIDANCE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 d2 1 d 2 2 2 xFx x ( mx ) mx 2 2 dt 2 dt
2
1 d2 1 d 2 2 2 xFx x ( mx ) mx 2 2 dt 2 dt
对颗粒总数进行平均:
涨落力平局值为零
2 k BT mx
1 d2 1 d 2 2 2 xFx mx mx x 2 2 dt 2 dt d2 2 d 2 2 k BT x x 2 dt m dt m
x ( 0) 0
p( x , t ) D 2 p( x , t ) t 2 x (t ) 2 D t
x(t ) x(0) 0
╳
x2,再积分。
x 2 ( t ) 2 Dt
该结果与Brown 运动方程完全一致,说明Brown 运动
或RW 模型的随机行走就是描述了扩散的物理过程。
等步长h
其中,q0是在区域D的正则内点0上的函数q(x,y)的值。
12
1 0 (1 2 3 4 h2q0 ) 4
其中,1/4可以解释为概率。即有:
一 Brown运动
1827 年 植 物 学 家 Brown 观 察到水中的花粉等颗粒可以不 停的作无规则运动。
由于 Brown 颗粒的质量远较液体的分子大,我们将颗 粒看成是一个巨分子,它不停地受到周围环境中液体分子 的碰撞,这种碰撞的频率为每秒1019次,因此我们观察到的 Brown 颗粒的运动是大量碰撞的涨落的结果,它是一种完 全无规则的随机运动。
由于指数项的幂系数 非常大,α/m≈107秒-1,当 时 间 t=10-6 秒时指数项可 以忽略。 将起始点放在原点,c2=0
x x
2
2 k BT
t c1e
t
m
c2
2
2 k BT
t 2 Dt
D为扩散系数。
3
二 醉汉行走问题 x
O s i 1
Person 在1905 年发表于《Nature》的论文中提出的: “一个人从θ点出发,沿直线走了l 码,然后他转了 一个角度后由沿第二条直线走了l 码,他重复了n 次这样 的过程。我想求出 n 次过程后此人位于离开起始点 r 到 r+dr 距离内的概率”
9
pro=0.5 do i=1,nwalk x=0.0d0 do j=1,nstep call randomnum() if (rand .lt. pro) then x=x+1.0 else x=x-1.0 end if write(10,'(I15,F15.6)')j,x sumx(j)=sumx(j)+x sumx2(j)=sumx2(j)+x*x end do end do do i=1,nstep write(11,'(I15,2F15.6)') $ i,sumx(i)/dble(nwalk),sumx2(i)/dble(nwalk) end do
Байду номын сангаас
i j i 1, j 1, i j n
i 1, i j
s s
i
n
j
s s
x
2 n
s n
i 1 2 i
n
x
2
2 k BT
t 2 Dt
1 D 2
6
三 扩散的物理
扩散是由于粒子浓度梯度的存在▽ρ形成粒子往低浓 度区域迁移的趋势,单位时间内通过某一方向垂直截面
的粒子数即为粒子流密度:
J D
由粒子数守恒的Liouvill连续性方程:
J 0 t
p( x , t ) D 2 p( x , t ) t
p(x,t)dx为粒子在t时刻存在于x-x+dx之间的概率:
( x, t ) 0 p( x, t )
7
任意函数的平均值可以表示为:
1
在描述Brown 运动时,我们 将影响系统在相空间中轨迹的随 机力应用于决定性运动方程,也 就是把液体分子的自由度凝缩为
仅用随机力代表。
1907 年 由 Langevin 提 出 的 Brown 运动方程:
Fx x m x
f v为阻力
Fx为涨落力
2 d 1 d 2 2 ( xx ) x 2 x x x x dt 2 dt 2
i 1, i j
s s
i
n
j
i j i 1, j 1, i j
5
s s
n
x n si
i 1
2 xn si s j i 1 j 1 n n
n
xn 0
( s1 s2 ) ( s1 s2 ) s1 s1 s1 s2 s2 s1 s2 s2
f ( x, y )
f ( x, t ) p( x, t )dx
p( x , t ) D 2 p( x , t ) t
╳
x,再积分。
p( x , t ) xp( x , t )dx x =0 x t dx t t
10
11
四 蒙特卡罗方法求解泊松方程
若泊松方程及其边界条件为
2 2 2 2 q( x , y ) y x F ( s )
Γ为求解区域D的边界, s为边界Γ上的点。
1 0 (1 2 3 4 h2q0 ) 4
正方形格点划分
4
醉汉的步长为1 向右行走的一步的几率为p=0.5
O
x
向左走一步的几率为q=1-p=0.5
向右走了nR步,向左走了nL
s i 1
s 1
2 i
总共走了n=nR+nL步
x n si
i 1
2 xn si s j i 1 j 1 n n
n
xn ( p q)n 0
右边分布积分再代入边界条件:p( , t ) 0
p( x , t ) p( x , t ) p( x , t ) D x dx Dx D dx 0 2 x x x 2
8
x 0 t
由于在 t=0时,粒子在原点处,从而粒子 位置的平均值是不随时间变化的。
