从梯子的倾斜程度谈起(一)
§ 1.1.1 从梯子的倾斜程度谈起(一)

§ 1.1.1 从梯子的倾斜程度谈起(一)一学生起点分析:本节课是在学生学习了直角三角形角之间的关系、边之间的关系的基础上进行的,借助于学生生活中常见的梯子为切入点,通过研究梯子的倾斜程度,将问题转化为研究两边之比,利用相似知识解决问题,总结规律。
同时建立比较系统的研究问题的方法,这后面学习正弦、余弦作铺垫。
二教学任务分析直角三角形中边角之间的关系是现实世界中应用广泛的关系之-.锐角三角函数在解决现实问题中有着重要的作用.如在测量、建筑、工程技术和物理学中,人们常常遇到距离、高度、角度的计算问题,一般来说,这些实际问题的数量关系往往归结为直角三角形中边与角的关系问题.本节首光从梯子的倾斜程度谈起。
引入了第-个锐角三角函数--正切.因为相比之下,正切是生活当中用的最多的三角函数概念,如刻画物体的倾斜程度,山的坡度等都往往用正切,而正弦、余弦的概念是类比正切的概念得到的.所以本节从现实情境出发,让学生在经历探索直角:三角形边角关系的过程中,理解锐角三角函数的意义,并能够举例说明;能用sinA、cosA、tanA表示直角三角形中两边的比,并能够根据直角三角形的边角关系进行计算.本节的重点就是理解tanA、sinA、cosA的数学含义.并能够根据它们的数学意义进行直角三角形边角关系的计算,难点是从现实情境中理解tanA、sim4、cosA的数学含义.所以在教学中要注重创设符合学生实际的问题情境,引出锐角三角函数的概念,使学生感受到数学与现实世界的联系,鼓励他们有条理地进行表达和思考,特别关注他们对概念的理解. 教学目标(一)教学知识点1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系.2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,外能够用正切进行简单的计算.(二)能力训练要求1.经历观察、猜想等数学活动过程,发展合情推理能力,能有条理地,清晰地阐述自己的观点.2.体验数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题.提高解决实际问题的能力.3.体会解决问题的策略的多样性,发展实践能力和创新精神.(三)情感与价值观要求1.积极参与数学活动,对数学产生好奇心和求知欲.2.形成实事求是的态度以及独立思考的习惯.教学过程:一、复习回顾,引入课题问题1.在直角三角形中,知道一直角边和它所对的锐角是30°,你能求出其它的边和角吗?问题2.在直角三角形中,知道一边和一个锐角,你能求出其它的边和角吗?通过本章的学习,相信大家一定能够解决此问题。
1.1从梯子的倾斜程度谈起1 PPT

实例2:如图,梯子AB和EF哪个更陡? 你是怎样判断的?
4m
3m
2m
3m
实例2:如图,梯子AB和EF哪个更陡? 你是怎样判断的?
梯子的铅直高与其水平距离 的比相同时,梯子就一样陡。 比值大的梯子陡。
4m
3m
3m
2m
在实践中探索新知
梯子在上升变陡过程中,倾斜 角,铅直高度与水平宽度的比 发生了什么变化?
倾斜角
铅 直 高 度
水平宽度
在实践中探索新知
梯子在上升变陡过程中,倾斜 角,铅直高度与水平宽度的比 发生了什么变化?
在实践中探索新知
梯子在上升变陡过程中,倾斜 角,铅直高度与水平宽度的比 发生了什么变化?
在实践中探索新知
梯子在上升变陡过程中,倾斜 角,铅直高度与水平宽度的比 发生了什么变化?
在实践中探索新知
角
形AB2C2有什么关系?
B2
B1C 1 B 2C 2 (2) 和 有什么关系? AC1 AC 2
(3)如果改变B2在梯子上的位 置呢?由此你能得出什么结论?
A C2 C1
由感性到理性
想一想
B1 (1)直角三角形AB1C1和直角三
角
形AB2C2有什么关系?
B2
B1C 1 B 2C 2 (2) 和 有什么关系? AC1 AC 2
在实践中探索新知
梯子在上升变陡过程中,倾斜 角,铅直高度与水平宽度的比 发生了什么变化?
铅 直 高 度
水平宽度
在实践中探索新知
梯子在上升变陡过程中,倾斜 角,铅直高度与水平宽度的比 发生了什么变化?
铅 直 高 度
水平宽度
在实践中探索新知
从梯子的倾斜程度谈起(一)
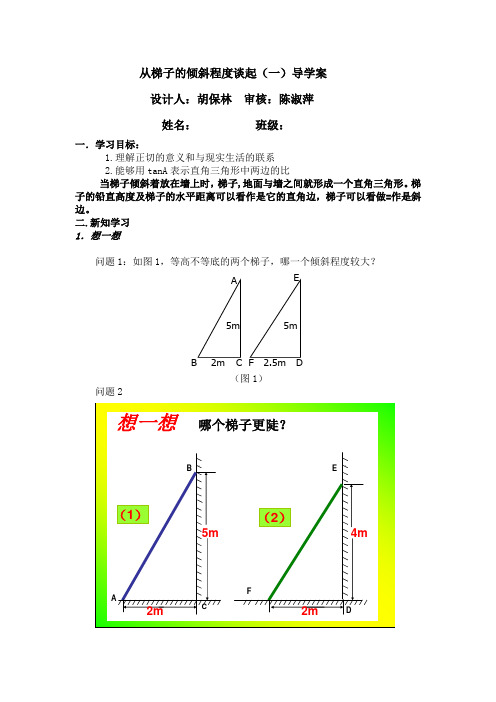
从梯子的倾斜程度谈起(一)导学案设计人:胡保林审核:陈淑萍姓名:班级:一.学习目标:1.理解正切的意义和与现实生活的联系2.能够用tanA表示直角三角形中两边的比梯二.11.3m 1.5m 3.5m 4mA B C D EF A B 1C 2 C 1 B 2问题2:如图2,底与高都不等的两个梯子,哪一个倾斜程度大?(图2)2.议一议3.做一做如图,小明想通过测量B 1C 1及AC 1,算出它们的比,来说明梯子AB 1的倾度; 而小亮则认为,通过测量B 2C 2及AC 2,算出它们的比,也能说明梯子AB 1的倾斜程度. 直角三角形的边与角的关系(1).Rt △AB 1C 1和Rt △AB 2C 2有什么关系?如果改变B 2在梯子上的位置呢?由此你得出什么结论? 4.学一学在直角三角形中,若一个锐角确定,那么∠A 的对边与邻边的比值也随之确定.在Rt △ABC中,锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA,即的邻边的对边A A A ∠∠=tanA B 1 C 2 1 B 2?).2(222111有什么关系和AC CB AC C B BC∠A 的邻边∠A 的对边β 6m┐ 5m 13m ┌ α 8m 甲 乙 100m 60m┌α i1.tanA 是在直角三角形中定义的,∠A 是一个锐角(注意数形结合,构造直角三角形).2.tanA 是一个完整的符号,表示∠A 的正切,习惯省去“∠”号;3.tanA 是一个比值(直角边之比.注意比的顺序,且tanA ﹥0,无单位.4.tanA 的大小只与∠A 的大小有关,而与直角三角形的边长无关.5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等. 如图,梯子AB 1的倾斜程度与tanA 有关吗?))1) tanA=5.试一试例题:下图表示两个自动扶梯,那一个自动扶梯比较陡?6.学一学坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i (或坡比),即坡度等于坡角的正切.如图,正切也经常用来描述山坡的坡度.例如, 有一山坡在水平方向上每前进100m 就升高60m, 那么山坡的坡度i (即tan α)就是:7.总结回顾.5310060tan ===αi8,反馈矫正三.学后反思。
《数学资源与评价》答案

1.B 2.作CD AC ⊥交AB 于D ,则28CAD = ∠,在Rt ACD △中,tan CD AC CAD =∠40.53 2.12=⨯=(米).所以,小敏不会有碰头危险. 3.(1)B 17A =米,CD 20=米;(2)有影响,至少35米 4.AD=2.4米 5.小船距港口A 约25海里1 二次函数所描述的关系1.略 2.2或-3 3.S=116c 2 4.11,4,2,844±± 5.y=16-x 2 6.y=-x 2+4x 7.B 8.D 9.D 10.C 11.y=2x 2;y=18;x=±2 12.y=-2x 2+260x-6500 13.(1)S=4x-32x 2;(2)1.2≤x<1.6 14.s=t 2-6t+72(0<t ≤6)2 结识抛物线1.抛物线;下;y 轴;原点;高;大;相反;相同;相同 2.减小 3.a=2;k=-2 4.a=-15.m=-1 6.(-2,4) 7 8.12 9.y=x 2+6x 10.(1)S=32y ;(2)S 是y 的一次函数,S 是x 的二次函数 11.(1)m=2或-3;(2)m=2.最低点是原点(0,0).x>0时,y 随x 的增大而增大;(3)m=-3,最大值为0.当x>0时;y 随x 的增大而减小 12.A(3,9);B(-1,1);y=x 2 13.抛物线经过M 点,但不经过N 点. 14.(1)A(1,1);(2)存在.这样的点P有四个,即P 10), P 20), P 3(2,0), P 4(1,0)3 刹车距离与二次函数1.下;y 轴;(0,5);高;大;5 2.(0,-1) 1,02⎛⎫- ⎪⎝⎭和1,02⎛⎫ ⎪⎝⎭3.y=x 2+3 4.下;3 5.14- 6.k=9,122b = 7.22y x =- 8.C 9.A 10.C 11.C 12.C 13.(1)2212(2)2y x y x ==-;(3)2y x = 14.(1)3;(2)3 15.y=mx 2+n 向下平移2个单位,得到y=mx 2+n-2,故由已知可得m=3,n-2=-1,从而m=3,n=1 16.以AB 为x 轴,对称轴为y 轴建立直角坐标系,设抛物线的代数表达式为y=ax 2+ c .则B 点坐标为0),N 点坐标为3),故0=24a+c ,3=12a+c ,解得a=-14,c=6,即y= -14x 2+6.其顶点为(0,6),(6-3)÷0.25=12小时. 17.以MN 为x 轴、对称轴为y 轴,建立直角坐标系,则N 点坐标为(2,0), 顶点坐标为(0,4).设y=ax 2+c ,则c=4,0=4a+4,a=-1,故y=-x 2+4.设B 点坐标为(x ,0),c 点坐标为( -x ,0),则A 点坐标为(x ,-x 2+4),D 点坐标为(-x ,-x 2+4).故BC=AD=2x ,AB=CD=-x 2+4.周长为4x+2(-x 2+4).从而有-2x 2+8+4x=8,-x 2+2x=0,得x 1=0,x 2=2.当x=0时,BC=0;当x=2时,AB=-x 2+4=0.故铁皮的周长不可能等于8分米. 18.(1)6,10;(2)55;(3)略;(4)S=12n 2+12n . 聚沙成塔 由y=0,得-x 2+0.25=0,得x=0.5(舍负),故OD=0.5(米).在Rt △AOD 中,AO=OD· tan ∠ADO=0.5tanβ=0.5×tan73°30′≈1.69.又AB=1.46,故OB≈0.23米.在Rt △BOD 中,tan ∠BDO=0.230.5BO OD ==0.46,故∠BDO≈24°42′.即α=24°42′.令x=0,得y=0.25, 故OC= 0.25,从而BC=0.25+0.23=0.48米.2.1~2.3 二次函数所描述的关系、结识抛物线、刹车距离与二次函数测试一、1.πr 2、S 、r 2.(6-x )(8-x )、x 、y 3.①④ 4.4、-2 5.y =-2x 2(不唯一) 6.y =-3x 2 7.y 轴 (0,0) 8.(2,4),(-1,1)二、9.A 10.D 11.B 12.C 13.D 14.C 15.B 16.D三、17.解:(1)∵m 2-m =0,∴m =0或m =1.∵m -1≠0,∴当m =0时,这个函数是一次函数.(2)∵m 2-m ≠0,∴m 1=0,m 2=1.则当m 1≠0,m 2≠1时,这个函数是二次函数.18.解:图象略.(1)0;(2)0;(3)当a >0时,y =ax 2有最小值,当a <0时,y =ax 2有最大值. 四、19.解:y =(80-x )(60-x )=x 2-140x +4800(0≤x <60).20.如:某些树的树冠、叶片等;动物中鸡的腹部、背部等.五、21.解:两个图象关于x 轴对称;整个图象是个轴对称图形.(图略) y =-2x 2 (0,0)y ⎧⎪⎨⎪⎩开口方向向下对称轴轴顶点坐标 y =2x 2 (0,0)y ⎧⎪⎨⎪⎩开口方向向上对称轴轴顶点坐标 22.解:(1)设A 点坐标为(3,m );B 点坐标为(-1,n ).∵A 、B 两点在y =13x 2的图象上,∴m =13×9=3,n =13×1=13.∴A (3,3),B (-1,13).∵A 、B 两点又在y =ax +b 的图象上,∴33,1.3a b a b =+⎧⎪⎨=-+⎪⎩解得231a b ⎧=⎪⎨⎪=⎩,∴一次函数的表达式是y =23x +1. (2)如下图,设直线AB 与x 轴的交点为D ,则D 点坐标为(-32,0).∴|DC |=32.S △ABC =S △ADC -S △BDC =12×2×3-2×2×3=4-14=2. 4 二次函数y=ax 2+bx+c 的图像1.上,12,33⎛⎫ ⎪⎝⎭,13x = 2.-4 0 3.四 4.0 5.左 3 下 2 6.1 7.-1或3 8.< > > > < 9.12x =,19,24⎛⎫- ⎪⎝⎭10.①②④ 11.D 12.D 13.A 14.D 15.∵2215044(5)1015015,113522(5)44(5)b ac b a a -⨯-⨯--=-===⨯-⨯-.故经过15秒时,火箭到达它的最高点,最高点的高度是1135米 16.由已知得2444a a -=2.即a 2-a-2=0,得a 1=-1,a 2=2,又a≥0,故a=2. 17.以地面上任一条直线为x 轴,OA 为y 轴建立直角坐标系,设y=a(x-1)2+2.25, 则当x=0时,y=1.25,故a+2.25=1,a=-1.由y=0,得-(x-1)2+2.25=0,得(x-1)2=2.25,x 1=2.5,x 2=-0.5(舍去),故水池的半径至少要2.5米. 18.如:7月份售价最低,每千克售0.5元;1-7月份, 该蔬菜的销售价随着月份的增加而降低,7-12月份的销售价随月份的增加而上升;2月份的销售价为每千克3.5元;3月份与11月份的销售价相同等.5 用三种方式表示二次函数1.y=-x 2+144 2.y 3.(1) y=x 2+-2x ;(2)3或-1 ;(3) x<0或x>2 4.k>35. y=x 2+8x 6.y=x 2+3x ,小,33,24- 7.(2,4) 8.14- 9.C 10.D 11.C 12.C 13.(1)略;(2)y=x 2-1;(3)略 14.设底边长为x ,则底边上的高为10-x ,设面积为y ,则y=12x(10-x)=-12(x 2-10x)=-12(x 2-10x+25-25)=-12(x-5)2+12.5.故这个三角形的面积最大可达12.5 15.2116S l = 16.(1)对称轴是直线x=1,顶点坐标为(1,3),开口向下;(2)当x<1时,y 随x 的增大而增大;(3)y=-2(x-1)2+3 17.由已知得△BPD ∽△BCA .故22416BPD ABC S x x S ∆∆⎛⎫== ⎪⎝⎭,224(4)416PCE ABC S x x S ∆∆--⎛⎫== ⎪⎝⎭,过A 作AD ⊥BC ,则由∠B=60°,AB=4,得 AD=AB·sin60°4=,故142ABC S ∆=⨯⨯∴222(4)1616BPD PCE x x S S ∆∆-+=⨯⨯-+∴22y =-+=+⎝.18.(1) s=12t 2-2t ; (2)将s=30代入s=12t 2-2t ,得30=12t 2-2t ,解得t 1=10,t 2=-6(舍去).即第10个月末公司累积利润达30万元;(3)当t=7时,s=12×72-2×7=10.5,即第7个月末公司累积利润为10.5万元;当t=8时,s=12×82-2×8 =16, 即第8个月末公司累积利润为16万元.16-10.5=5.5万元.故第8个月公司所获利润为5.5万元.19.(1)略;(2)(1)2n n S -=;(3)n=56时,S=1540 20.略 6 何时获得最大利润1.A 2.D 3.A 4.A 5.C 6.B7. (1)设y=kx+b ,则∵当x=20时,y=360;x=25时,y=210.∴3602021025k b k b =+⎧⎨=+⎩, 解得30960k b =-⎧⎨=⎩∴y=-30x+960(16≤x≤32); (2)设每月所得总利润为w 元,则 w=(x-16)y=(x-16)(-30x+960)=-30(x-24)2+ 1920.∵-30<0,∴当x=24时,w 有最大值.即销售价格定为24元/件时,才能使每月所获利润最大, 每月的最大利润为1920元.8. 设每间客房的日租金提高x 个5元(即5x 元),则每天客房出租数会减少6x 间,客房日租金总收入为y=(50+5x)(120-6x)=-30(x-5)2+6750.当x=5时,y 有最大值6750,这时每间客房的日租金为50+5×5=75元. 客房总收入最高为6750元.9.商场购这1000件西服的总成本为80×1000=8000元.设定价提高x%, 则销售量下降0.5x%,即当定价为100(1+x%)元时,销售量为1000(1-0.5x%)件.故y=100(1+x%)·1000(1-0.5x%)-8000 =-5x 2+500x+20000=-5(x-50)2+32500.当x=50时, y 有最大值32500.即定价为150元/件时获利最大,为32500元.10.(1)s=10×277101010x x ⎛⎫-++ ⎪⎝⎭×(4-3)-x=-x 2+6x+7.当x=62(1)-⨯-=3 时,S 最大=24(1)764(1)⨯-⨯-⨯-=16. ∴当广告费是3万元时,公司获得的最大年利润是16万元.(2)用于再投资的资金有16-3=13万元.有下列两种投资方式符合要求:①取A 、B 、E 各一股,投入资金为5+2+6=13万元,收益为0.55+0.4+0.9=1.85万元>1.6万元. ②取B 、D 、E 各一股,投入资金为2+4+6=12万元<13万元,收益为0.4+0.5+0.9=1.8万元>1.6万元.11.(1)60吨;(2) 226033(7.545)(10)(320)(100)315240001044x y x x x x x -=⨯+-=--=-+-;(3)210元/吨;(4) 不对,设月销售额为w 元.22603(7.545)240104x w x x x -=⨯+=-+,x=160时,w 最大.12.(1)21425y x =-+;(2)货车到桥需280406(40-=小时) ,0.256 1.5(⨯=米)而O(0,4),4-3=1(米)<1.5米,所以,货车不能通过. 安全通过时间434(0.25-=小时),2804060(/4-=千米时),货车安全通过速度应超过60千米/时.7 最大面积是多少1.y=-x 2+600,020x ≤≤,600m 2 ,200m 2 2.20cm 2 3.圆 4.16cm 2 ,正方形 5. 5±6.10 7.21822333y x x =-+- 8. 9.-2 10. C 11. D 12.C 13.A 14.D 15.过A 作AM ⊥BC 于M ,交DG 于N ,则.设DE=xcm ,S矩形=ycm 2,则由△ADG ∽△ABC ,故AN DG AM BC =,即161624x DG -=,故DG=32(16-x).∴y=DG·DE=32(16-x)x=-32(x 2-16x)=-32(x-8)2+96,从而当x=8时,y 有最大值96.即矩形DEFG 的最大面积是96cm 2.16.(1)y= 238x -+3x .自变量x 的取值范围是0<x<8. (2)x=3328-⎛⎫⨯- ⎪⎝⎭=4时,y 最大=234038348⎛⎫⨯-⨯- ⎪⎝⎭⎛⎫⨯- ⎪⎝⎭=6.即当x=4时,△ADE 的面积最大,为6. 17.设第t 秒时,△PBQ 的面积为ycm 2.则∵AP=tcm ,∴PB=(6-t)cm ;又BQ=2t .∴y=12PB·BQ=12(6-t)·2t=(6-t)t=-t 2+6t=-(t-3)2+9,当t=3时,y 有最大值9.故第3秒钟时△PBQ 的面积最大,最大值是9cm 2.18.(1)可以通过,根据对称性,当x=12×4=2时,y=132-×4+8=778>7.故汽车可以安全通过此隧道;(2)可以安全通过,因为当x=4时,y=132-×16+8=172>7.故汽车可以安全通过此隧道;(3)答案不惟一,如可限高7m .19.不能,y=-x 2+4x ,设BC=a ,则AB=4-a ,(2,4)2a A a ∴+-代入解析式 24(22)404,2a a a -=-+-+=得或 A(2,4)或(4,0) 所以,不能. 20.(1)125h =;(2)12,125x S ==最大;(3)BE=1.8,在 21.(1)第t 秒钟时,AP=t ,故PB=(6-t)cm ;BQ=2tcm .故S △PBQ =12·(6-t)·2t=-t 2+ 6t .∵S 矩形ABCD =6×12=72.∴S=72-S △PBQ =t 2-6t+72(0<t<6);(2)S=(t-3)2+63.故当t=3时,S 有最小值63. 22. (1)过A 作AD ⊥BC 于D 交PQ 于E ,则AD=4.由△APQ ∽△ABC ,得446x x -=,故x=125;(2)当RS 落在△ABC 外部时,不难求得AE=23x ,故22212446335y x x x x x ⎛⎫⎛⎫=-=-+<< ⎪ ⎪⎝⎭⎝⎭.当RS 落在△ABC 内部时,y=x 2(0<x<125);(3)当RS 落在△ABC 外部时,2222124(3)66335y x x x x ⎛⎫=-+=--+<< ⎪⎝⎭.∴当x=3时,y 有最大值6.当RS 落在BC 边上时,由x=125可知,y= 14425.当RS 落在△ABC 内部时,y=x 2(0<x<125),故比较以上三种情况可知:公共部分面积最大为6.23.(1)由对称性,当x=4时,y=211642525-⨯=-.当x=10时,y=2110425-⨯=-.故正常水位时,AB 距桥面4米,由16943 2.52525-=>,故小船能通过; (2)水位由CD 处涨到点O 的时间为1÷0.25=4小时.货车按原来的速度行驶的路程为40×1+40×4=200<280.∴货车按原来的速度行驶不能安全通过此桥.8 二次函数与一元二次方程1.(-3,0),(1,0) 2.y=2x 2+4x-6 3.一、二、三 4.(1,2) 5.m=-7 6.m=87.(-1,0) 8.9016k k >-≠且 9.a=2 10.B 11.A 12.C 13.y=x 2+x+9图象与y=1的两个交点横坐标是x 2+x+9=0两根 14.224(2)(2)40m m m ∆=--=-+>15.C △ABC =AB+BC+AC=2.S △ABC =12AC·OB=12×2×3=3 16.(1)k=-2,1 (2)0<k<2 17.(1) 904m m <≠且(2)在(3) 15(,),(2,1)24Q P --- 18.(1)25s ,125m ;(2)50s 19.(1)m=2或0;(2) m<0;(3)m=1,S = 20.(1) y=112-(x-6)2+5;(2) (2)由112-(x-6)2+5=0,得x 1=266x +=-:C 点坐标为(6+0) 故OC=6+.75(米),即该男生把铅球推出约13.75米.21.(1) y=-x 2+4x-3;(2) ∴直线BC 的代数表达式为y=x-3 (3) 由于AB=3-1=2,OC=│-3│=3.故S △ABC =12AB·OC=12×2×3=3 22.(1) k=1;(2)k=-1 2.6—2.8A 参考答案一、1. 2.14,大,-38,没有 3.①x 2-2x ;②3或-1;③<0或>2 4.y =x 2-3x -10 5.m >92,无解 6.y =-x 2+x -1,最大 7.S =π(r +m )2 8.y =-18x 2+2x +1, 16.5二、9.B 10.C 11.C 12.B 13.D 14.B 15.D 16.B三、17.解:(1)y =-2x 2+180x -2800;(2)y =-2x 2+180x -2800=-2(x 2-90x )-2800=-2(x -45)2+1250.当x =45时,y 最大=1250.∴每件商品售价定为45元最合适,此销售利润最大,为1250元. 18.解:∵二次函数的对称轴x =2,此图象顶点的横坐标为2,此点在直线y =12x +1上.∴y =12×2+1=2.∴y =(m 2-2)x 2-4mx +n 的图象顶点坐标为(2,2).∴-2b a=2.∴-242(2)m m --=2.解得m =-1或m =2.∵最高点在直线上,∴a <0,∴m =-1.∴y =-x 2+4x +n 顶点为(2,2).∴2=-4+8+n .∴n =-2.则y =-x 2+4x +2.四、19.解:(1)依题意得:鸡场面积y =-2150.33x x -+∵y =-13x 2+503x =13-(x 2-50x )=-13(x -25)2+6253,∴当x =25时,y 最大=6253, 2.6—2.8B 参考答案一、1.3 2.2 3.b 2-4ac>0(不唯一) 4.15 cmcm 2 5.(1)A ;(2)D ;(3)C ;(4)B 6.5,625二、7.B 8.B 9.A 10.C 11.D 12.B三、13.解:(1)信息:①1、2月份亏损最多达2万元;②前4月份亏盈吃平;③前5月份盈利2.5万元;④1~2月份呈亏损增加趋势;⑤2月份以后开始回升.(盈利);⑥4月份以后纯获利……(2)问题:6月份利润总和是多少万元?由图可知,抛物线的表达式为y=12(x -2)2-2,当x=6时,y=6(万元)(问题不唯一). 14.解:设m=a+b y=a·b ,∴y=a(m -a)=-a 2+ma=-(a -2m )2+24a ,当a=2m 时,y 最大值为24a .结论:当两个数的和一定,这两个数为它们和的一半时,两个数的积最大.四、15.(1)由题意知:p=30+x ;(2)由题意知:活蟹的销售额为(1000-10x)(30+x)元,死蟹的销售额为200x 元.∴Q=(1000-10x)(30+x)+200x=-10x 2+900x+30000;(3)设总利润为L=Q -30000-400x=-10x 2+500x=-10(x 2-50x) =-10(x -25)2+6250.当x=25时总利润最大,为6250元. 五、16.解:∵∠APQ=90°,∴∠APB+∠QPC=90°.∵∠APB+∠BAP=90°,∴∠QPC=∠BAP ,∠B=∠C=90°.∴△ABP ∽△PCQ .6,,8AB BP x PC CQ x y ==-∴y=-16x 2+43x . 17.解:(1)10;(2)55;(3)略;(4)经猜想,所描各点均在某二次函数的图象上.设函数的解析式为S=an 2+bn+c .由题意知:1a ,21,1423,b ,2936,c 0.a b c a b c a b c ⎧=⎪++=⎧⎪⎪⎪++==⎨⎨⎪⎪++=⎩=⎪⎪⎩解得∴S=211.22n n + 单元综合评价一、选择题:1~12:CBDAA ,CDBDB ,AB二、填空题:13.2 14.591415. 16.-7 17.2 18.y=0.04x 2+1.6x 19.<、<、> 20.略 21.只要写出一个可能的解析式 22.1125m 23.-9.三、解答题:24.y=x 2+3x+2 (-3/2,- 1/4) 25.y=-1200x 2+400x+4000;11400,10600 26.2125y x =-; 5小时 27.(1)5;(2) 2003 28.(1) 2y -x x =+;(2) y=-x 2+1/3x+4/9,y=-x 2-x 29.略.第三章 圆1 车轮为什么做成圆形1.=5cm <5cm >5cm 2.⊙O 内 ⊙O 上 ⊙O 外 3.9π cm 2 4.内部 5.5cm6.C 7.D 8.B 9.A 10.由已知得OA=8cm ,=10,,故OA<10,OB<10,OD=10,OC>10.从而点A , 点B 在⊙O 内;点C 在⊙O 外;点D 在⊙O 上 11.如图所示,所组成的图形是阴影部分(不包括阴影的边界) 12.如图所示,所组成的图形是阴影部分(不包括阴影的边界).(11题) (12题)13.由已知得PO=4,PA=5,PB=5,故OA=1,OB=9,从而A点坐标为A(-1,10),B点坐标为(9,0);连结PC、PD,则PC=PD=5,又PO⊥CD,PO=4,故OC==3,.从而C点坐标为(0,3) ,D点坐标为(0,-3) 14.存在,以O为圆心,OA为半径的圆15.2≤AC≤8聚沙成塔∵PO<2.5,故点P在⊙O内部;∵Q点在以P为圆心,1为半径的⊙P上,∴1≤OQ≤3.当Q在Q1点或Q2点处,OQ=2.5,此时Q在⊙O上;当点Q在弧线Q1mQ2上(不包括端点Q1,Q2),则OQ>2.5,这时点Q 在⊙O外;当点Q在弧线Q1nQ2上(不包括端点Q1,Q2),则OQ<2.5,这时点Q在⊙O内.2 圆的对称性1.中心,过圆心的任一条直线,圆心2.60°3.2cm 4.5 5.3≤OP≤56.10 7.相等89.C 10.B 11.A 12.过O作OM⊥AB于M,则AM=BM.又AC=BD,故AM-AC=BM-BD,即CM=DM,又OM⊥CD,故△OCD是等腰三角形.即OC=OD.(还可连接OA、OB.证明△AOC≌△BOD) 13.过O作OC⊥AB于C,则BC=152cm.由BM:AM=1:4,得BM=15×5=3 ,故CM=152-3=92.在Rt△OCM中,OC2=229175824⎛⎫-=⎪⎝⎭.连接OA,则10=,即工件的半径长为10cm 14.是菱形,理由如下:由 BC= AC,得∠BOC=∠AOC.故OM⊥AB,从而AM=BM.在Rt △AOM中,sin∠AOM=AMOA=,故∠AOM=60°,所以∠BOM=60°.由于OA=OB=OC,故△BOC 与△AOC 都是等边三角形,故OA=AC=BC=BO=OC,所以四边形OACB是菱形.15.PC=PD.连接OC、OD,则∵ DB= BC,∴∠BOC=∠BOD,又OP=OP,∴△OPC≌△OPD,∴PC=PD.16.可求出长为6cm的弦的弦心距为4cm,长为8cm的弦的弦心距为3cm.若点O 在两平行弦之间,则它们的距离为4+3=7cm,若点O在两平行弦的外部,则它们的距离为4- 3=1cm,即这两条弦之间的距离为7cm或1cm.17.可求得OC=4cm,故点C在以O为圆心,4cm长为半径的圆上,即点C 经过的路线是O为圆心,4cm长为半径的圆.聚沙成塔作点B关于直线MN的对称点B′,则B′必在⊙O上,且 B N'= NB.由已知得∠AON=60°,故∠B′ON=∠BON= 12∠AON=30°,∠AOB′=90°.连接AB′交MN于点P′,则P′即为所求的点.此时AP+BP3 圆周角与圆心角1.120°2.3 1 3.160°4.44°5.50°67.A 8.C 9.B 10.C 11.B 12.C 13.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD= 4cm 14.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.∵AD是直径,∴∠ACD=90°,∴AC2+CD2=AD2,即2AC2=36,AC2=18,15.连接BD,则∴AB 是直径,∴∠ADB=90°.∵∠C=∠A,∠D=∠B,∴△PCD ∽△PAB,∴PD CDPB AB=.在Rt△PBD 中,cos∠BPD=PD CDPB AB==34,设PD=3x,PB=4x,则==,∴tan ∠BPD=BD PD == 16.(1)相等.理由如下:连接OD ,∵AB ⊥CD ,AB 是直径,∴ BC= BD ,∴∠COB= ∠DOB .∵∠COD=2∠P ,∴∠COB=∠P ,即∠COB=∠CPD ;(2)∠CP′D+∠COB=180°.理由如下:连接P′P ,则∠P′CD=∠P′PD ,∠P′PC=∠P′DC .∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD .∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB ,从而∠CP′D+∠COB=180° 17. 聚沙成塔 迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN 的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A<MCN=∠B ,即∠B>∠A , 从而B 处对MN 的张角较大,在B 处射门射中的机会大些.4 确定圆的条件1.三角形内部,直角三角形,钝角三角形 2. 3 4.其外接圆,三角形三条边的垂直平分线,三角形三个顶点 5 6.两 7.C 8.B 9.A 10.C11.B 12.C 13.略 14.略 15.(1)△FBC 是等边三角形,由已知得:∠BAF=∠MAD=∠DAC=60°=180°-120°=∠BAC ,∴∠BFC=∠BAC=60°,∠BCF=∠BAF=60°,∴△FBC 是等边三角形;(2)AB=AC+FA .在AB 上取一点G ,使AG=AC ,则由于∠BAC=60°,故△AGC 是等边三角形,从而∠BGC=∠FAC=120°,又∠CBG=∠CFA ,BC=FC ,故△BCG ≌△FCA ,从而BG=FA ,又AG=AC ,∴AC+FA=AG+BG=AB 16.(1)在残圆上任取三点A 、B 、C ; (2)分别作弦AB 、AC 的垂直平分线, 则这两垂直平分线的交点即是所求的圆心;(3)连接OA ,则OA 的长即是残圆的半径 17.存在.∵AB 不是直径(否则∠APB=90°,而由cos ∠APB=13知∠APB<90°,矛盾)∴取优弧AB 的中点为P 点,过P 作PD ⊥AB 于D ,则PD 是圆上所有的点中到AB 距离最大的点.∵AB 的长为定值,∴当P 为优弧AB 的中点时,△APB的面积最大,连接PA 、PB , 则等腰三角形APB 即为所求.S △APB= 12AB· 聚沙成塔 过O 作OE ⊥AB 于E ,连接OB ,则∠AOE=12∠AOB ,AE=12AB ,∴∠C=1∠AOB=∠AOE . 解方程x 2-7x+12=0可得DC=4,AD=3,故,可证Rt △ADC ∽Rt △AEO ,故AE AO AD AC=,又, AD=3,,故,从而S ⊙O=21254ππ⨯=⎝⎭. 5 直线与圆的位置关系1.相交 2.60 3.如OA ⊥PA ,OB ⊥PB ,AB ⊥OP 等 4.0≤d<4 5.65° 6.146°,60°,86° 7.A 8.B 9.C 10.C 11.D 12.B 13.(1)AD ⊥CD .理由:连接OC ,则OC ⊥CD .∵OA=OC ,∴∠OAC=∠OCA ,又∠OAC= ∠DAC ,∴∠DAC=∠OCA ,∴AD ∥OC ,∴AD ⊥CD ;(2)连接BC ,则∠ACB=90°由(1)得∠ADC=∠ACB ,又∠DAC=∠CAB .∴△ACD ∽△ABC ,∴AC AD AB AC=,即AC 2=AD·AB=80,故 14.(1)相等.理由:连接OA ,则∠PAO=90°.∵OA=OB ,∴∠OAB=∠B=30°, ∴∠AOP=60°,∠P=90°-60°=30°,∴∠P=∠B ,∴AB=AP ;(2)∵tan ∠APO=OA PA,∴OA=PA ,tan ∠0301tan ==,∴BC=2OA=2,即半圆O 的直径为2 15.(1)平分.证明:连接OT ,∵PT 切⊙O 于T ,∴OT ⊥PT ,故∠OTA=90°, 从而∠OBT=∠OTB=90°-∠ATB=∠ABT .即BT 平分∠OBA ; (2)过O 作OM ⊥BC 于M ,则四边形OTAM 是矩形,故OM=A T=4,AM=OT=5.在Rt △OBM 中,OB=5,OM=4,故=3,从而AB=AM-BM=5-3=2 16.作出△ABC 的内切圆⊙O ,沿⊙O 的圆周剪出一个圆,其面积最大 17.由已知得:OA=OE ,∠OAC=∠OEC ,又OC 公共,故△OAC ≌OEC ,同理,△OBD ≌△OED ,由此可得∠AOC=∠EOC ,∠BOD=∠EOD ,从而∠COD=90°,∠AOC=∠BDO . 根据这些写如下结论:①角相等:∠AOC=∠COE=∠BDO=∠EDO ,∠ACO=∠ECO=∠DOE=∠DOB ,∠A=∠B=∠OEC=∠OED ;②边相等:AC=CE ,DE=DB ,OA=OB=OE ;③全等三角形:△OAC ≌△OEC ,△OBD ≌△OED ;④相似三角形:△AOC ∽△EOC ∽△EDO ∽△BDO ∽△ODC .聚沙成塔 (1)PC 与⊙D 相切,理由:令x=0,得y=-8,故P(0,-8);令y=0,得故0),故OP=8,OC=2,CD=1,∴CD==3,又PC=,∴PC 2+CD 2=9+72=81=PD 2.从而∠PCD=90°,故PC 与⊙D 相切; (2)存在.点-12)或-4),使S △EOP =4S △CDO .设E 点坐标为(x ,y),过E 作EF ⊥y 轴于F ,则EF=│x│.∴S △POE =12PO·EF=4│x│.∵S △CDO =12CO·∴当时,;当时,.故E 点坐标为-4)或-12).6 圆与圆的位置关系1.2 14 2.外切 3.内切 4.45°或135° 5.1<r<8 6.外切或内切 7.A 8.B9.C 10.D 11.C 12.A 13.C 14.外切或内切,由│d -4│=3,得d=7或1,解方程得x 1=3,x 2=4,故当d=7时,x 1+ x 2=d ;当d=1时,x 2-x 1=d ,从而两圆外切或内切 15.过O 1作O 1E ⊥AD 于E ,过O 2作O 2F ⊥AD 于F ,过O 2作O 2G ⊥O 1E 于G ,则AE=DF=5cm ,O 1G=16-5-5=6cm ,O 2O 1=5+5=10cm ,故O 2,所以EF=8cm ,从而AD=5+5+8=18cm .16.如图所示.17.如:AC=BC ,O 1A 2+AF 2=O 1F 2,AC 2+CF 2=AF 2等 聚沙成塔 有无数种分法.如:过⊙O 2与⊙O 5的切点和点O 3画一条直线即满足要求.7 弧长及扇形的积1.240°3πcm 2.389mm 3.16π 4.50 5 6.2πcm 2 7.B 8.C9.C 10.B 11.A 12.A 13.设其半径为R ,则120180R π⨯=,R =cm ,过圆心作弦的垂线,则可求弦长为9cm 14.由已知得,S 扇形DOC=2150500203603ππ⨯=,S 扇形AOB=2150125103603ππ⨯=,故绸布部分的面积为S 扇形DOC- S 扇形AOB=125π 15.由已知得,2081809n ππ⨯=,得n=50,即∠AOC=50°.又AC 切⊙O 于点C ,故∠ACO=90 °,从而OA=812.446cos50cos50OC =≈︒︒,故AB=AO-OB=12.446-8≈4.45cm 16.设切点为C ,圆心为O ,连接OC ,则OC ⊥AB ,故AC=BC=15,连接OA ,则OA 2-OC 2=AC 2=152=225,故S 阴影=2222()225AO CO AO CO ππππ⨯-⨯=-=cm 2 17.如图所示r=22C B A r=4C A r=42-4r=2OB A聚沙成塔 (1)依次填2468,,,3333ππππ;(2)根据表可发现:23n l n π=⨯,考虑2264001000003n ππ⨯≥⨯⨯,得n≥1.92×109,∴n 至少应为1.92×109. 8 圆锥的侧面积1.6 2.10π 3.2000π 4.2cm 5.15π 6.18 7.D 8.D 9.B 10.B11.A 12.B 13.侧面展开图的弧长为2816ππ⨯=,设其圆心角为n°,则1516180n ππ⨯=,故n=192, 即这个圆锥的侧面展开图的圆心角是192° 14.可得△SAO ≌△SBO ,故∠ASO=∠BSO=60°,∠SBO=30°,由BO=27, tan ∠SBO=tan 30°=27SO SO BO =,得SO=27=≈15.6m ,即光源离地面的垂直高度约为15.6m 时才符合要求 15.过A 作AD ⊥BC ,则由∠C=45°,得AD=DC=12cn ,AB=2AD=24cm ,=BC=12,以A 为圆心的扇形面积为21051242360ππ⨯=cm 2,以B 为圆心的扇形面积为22302448360cm ππ⨯=,以C为圆心的扇形面积为224536360cm ππ⨯=, 故以B 为圆心取扇形作圆锥侧面时,圆锥的侧面积最大,设此时圆锥的底面半径为r ,则30224180r ππ=⨯, r=2cm ,直径为4cm 聚沙成塔 设圆的半径为r ,扇形的半径为R ,则1224R r ππ⨯⨯=⨯,故R=4r ,又,将R=4r 代入,可求得≈0.22a . 正多边形与圆1.正方形 2.十八 提示:正多边形的中心角等于外角,外角和为360°,360÷20=18 3.36° 提示:可求出外角的度数 4.正三角形 5.C 提示:其中正确的有②④⑤⑥⑦ 6.C7.D 提示:按正多边形的定义 8.C 9.3 提示:利用直角三角形中,30°角所对直角边等于斜边的一半 10.100cm 211:2 提示:设此圆的半径为R ,则它的内接正方R,内接正方形和外切正六边形的边长比为2 12.4πa 2 提示:如图所示,AB 为正n 边形的一边,正n 边形的中心为O ,AB •与小圆切于点C ,连接OA ,OC ,则OC ⊥AB ,12AC=12AB=a ,所以AC 2=14a 2=OA 2-OC 2,S 圆环=S 大圆-S 小圆=πOA 2-OC 2=π(OA 2-OC 2)=4πa 2 13.C 14.C 15.方法一:(1)用量角器画圆心角∠AOB=120°,∠BOC=120°;(2)连接AB ,BC ,CA ,则△ABC 为圆内接正三角形.方法二:(1)用量角器画圆心角∠BOC=120°;(2)在⊙O 上用圆规截取;(3)连接AC ,BC ,AB ,则△ABC 为圆内接正三角形.方法三:(1)作直径AD ;(2)以O 为圆心,以OA 长为半径画弧,交⊙O 于B ,C ;(3)连接AB ,BC ,CA ,则△ABC 为圆内接正三角形.方法四:(1)作直径AE ;(2)分别以A ,E 为圆心,OA 长为半径画弧与⊙O 分别交于点D ,F ,B ,C ;(3)连接AB ,BC ,CA (或连接EF ,ED ,DF ),则△ABC (或△EFD )为圆内接正三角形.16.解:相同点:都有相等的边;都有相等的角,都有外接圆和内切圆等.不同点:边数不同;内角的度数不同;内角和不同;对角线条数不同等 17.解:方法一:如题图①中,连接OB ,OC .∵正三角形ABC 内接于⊙O ,∴∠OBM=∠OCN=30°,∠BOC=120°.又∠OCN=30°,∠BOC=120°,而BM=CN ,OB=OC ,∴△OBM ≌△OCN ,∴∠BOM=∠CON ,∴∠MON=∠BOC=120°.方法二:如题图①中,连接OA ,OB .∵正三角形ABC 内接于⊙O ,∴AB=BC ,∠OAM=∠OBN=30°,∠AOB=120°,∴∠AOM=∠BON .∴∠MON=∠AOB=120°;(2)90° 72°;(3)∠MON=360n︒ 单元综合评价(一)一、1~5 AABDB 6~10 DDABD二、11.8 12.π213.9cm 14.120° 15.13 16.18πcm 2 17.60° 18.180° 19.7或1 20.(1)2;(2)3n +1三、21.10cm ,6cm 22.432m 2 23.2π6R (提示:连接CO ,DO ,S 阴影=S 扇形COD ) 24.(1)A (4,0),33y x =+;(2)3>m时相离,m =时相切,0m <<时相交 25.解:(1)42πr r +,82πr r +;(2)62πr r +,82πr r +,102πr r +,122πr r +;(3)162πr r +,图略单元综合评价(二)1.以点A 为圆心,2cm 长为半径的圆 2.点P 在⊙O 内 3.10 4.90° 5.2 6. 120°7.3 8.2cm 或8cm 9.(12+5π)cm 10.30π 11.B 12.D 13.D 14.C15.D 16.B 17.B 18.C 19.C 20.C 21.如图,所有点组成的图形是如图所示的阴影部分. 22.(1)连接CD ,=5,由CD=CA ,得∠CDA=∠A ,故tan ∠CDA=tanA=43BC AC =;(2)过C 作CF ⊥AD 于F ,则AD=2AF ,由cosA=AC AF AB AC=,得AC 2=AB·AF .故32=5·AF ,AF=95,所以AD=185. 23.(1)相切.理由:连接OC ,OB ,则OC ⊥AB ,由已知得BC=12AB=4,OB=5,故=3,从而圆心O 到直线AB 的距离等于小圆的半径,故AB 与小圆相切;(2) 22222(53)16OB OC cm ππππ-=-=. 24.(1)连接AB ,AM ,则由∠AOB=90°,故AB 是直径,由∠BAM+∠OAM=∠BOM+ ∠OBM=180°-120°=60°,得∠BAO=60°,又AO=4,故cos ∠BAO=AO AB,AB=048cos60=,从而⊙C 的半径为4;(2)由(1)得,=C 作CE ⊥OA 于E ,CF ⊥OB 于F ,则EC=OF=12BO=12⨯,CF=OE=12OA=2, 故C 点坐标为(-,2) 25.连接AC ,BC ,分别作AC ,BC 的垂直平 AC AB =分线,相交于点M ,则点M 即满足条件(图略) 26.(1)设扇形半径为Rcm ,则2120300360R ππ=,故R=30cm ,设扇形弧长为Lcm ,则113030022Rl l π=⨯=,故L=20π;(2)设圆锥的底面半径为rcm ,则220r ππ=,r=10cm = 27.如:∠D=30°,DC 是⊙O 的切线,△CBD 是等腰三角形,△ACD 是等腰三角形,AC=CD ,BD=BC ,△DCB ∽△DAC ,DC 2=DB·DA ,,等 28.略.只要符合题意即可得分.第四章 统计与概率1 50年的变化(1)1.条形,折线,扇形 2.条形,0 3.折线,同一单位长度 4.不能 5.(1)1:3;(2)从0开始 6.B 7.C 8.D 9.D 10.C 11.B 12.解:(1)左图给人的感觉是小明通过努力,数学成绩提高迅速,进步很大;而右图给你的感觉则是小明的学习成绩比较稳定,进小不是很大;(2)如果小明想向他的父母说明他数学成绩的提高情况,那么他应选择左图,理由是:左图看上去折线上升速度转快,表明小明的成绩提高迅速 13.解:(1)A 村的苹果产量占本村两种水果总产量的35%,梨占65%;B 村的苹果产量在本村两种水果总产量中占80%,梨占20%。
1.1从梯子的倾斜程度谈起 (1)
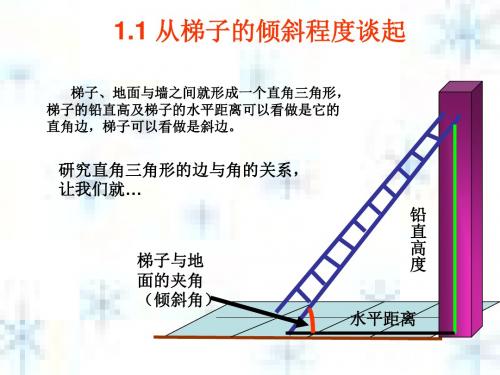
在实践中探索新知
梯子在上升变陡过程中,铅直 高度与水平宽度的比发生了什 么变化?
在实践中探索新知
梯子在上升变陡过程中,铅直 高度与水平宽度的比发生了什 么变化?
实例2:如图,梯子AB和EF哪个更陡? 你是怎样判断的?
梯子的铅直高与其水平距离 的比相同时,梯子就一样陡。 比值大的梯子陡。
4m
3m
课堂小结
直角三角形的边角关系
根据图形回答下列问题: 1、直角三角形三边的关系. 2、直角三角形两锐角的关系. 3、直角三角形边与角之间的关系. 4、特殊角300,450,600角的三角函数值.A 5、互余两角之间的三角函数关系. 6、同角之间的三角函数关系
450
450
B c
a
b
300
┌ C
┌
600
┌
课堂练习
习题1.3 1,2题
A D
1.计算;(1)tan450-sin300; (2)cos600+sin450-tan300; 36 tan2 300 3 sin 600 2 cos450. 2.如图,河岸AD,BC互相平行,桥AB垂 直于两岸.桥长12m,在C处看桥两端 A,B,夹角∠BCA=600. 求B,C间的距离(结果精确到1m).
根据上面的计算,完成下表
特殊角的三角函数值表
三角函数 正弦sinα 余弦cosα 正切tanα 锐角α
300 450
要能记 住有多好
600
1 2 2 2 3 2
3 2 2 2 1 2
3 3
1
3
这张表还可以看出许多 知识之间的内在联系?
例题欣赏
例1 计算: (1)sin300+cos450;(2) sin2600+cos2600-tan450.
11从梯子的倾斜程度谈起(一)

白银十中 李再义
从梯子的倾斜程度谈起
第一课时
梯子是我们日常生活中常见的物体
你能比较两个 梯子哪个更陡吗? 你是怎样判断的? 你有哪些办法?
(1)如图,梯子AB和EF哪个更陡? 你是怎样判断的?
A
E
5m
5m
B
F
2m
C
3m
D
(2)如图,梯子AB和EF哪个更陡? 你是怎样判断的?
例题讲解:
例1、如图表示两个自动扶梯,哪一个自 动扶梯比较陡?
甲
乙
解:甲梯中,
tanα= 6= 3
84
tanβ= 5 5
132 52 12
因为tanα> tanβ,所以甲梯更陡。
例2:在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA=5 ,求AC 和AB。 12
小结
1.正切的定义 2.正切值与角、与边的关系 3.梯子的倾斜程度与tanA的关系
B
A C
作业
第6页 习题1.1 题1、2
A
E
5m
B
F
2m C
6m
2m
D
(3)如图,梯子AB和EF哪个更 陡?你是怎样判断的?
E
A
4m
B
F
2m C
6m
3m
D
想一想:
如图,小明想通过测量 B1C1 及 AC1 ,算出他们的比,来说明梯 子的倾斜程度;而小亮则认为,通过测量 B2C2 及 AC2 ,算出 他们的比,也能说明梯子的倾斜程度你同意小亮的看法吗?
(4)tanB= 10 ( √ )
7
1.1 从梯子的倾斜程度谈起

E
5m
4m
B
F
3m
2m
从梯子的倾斜程度谈起
若小明因身高原因不能顺利测量梯子顶端到墙脚 的距离B1 C1 ,进而无法刻画梯子的倾斜程度,他该 怎么办?你有什么锦囊妙计?
B1
B2
A
C2
C1
想一想
B1
B2
A
C2
C1
想一想
B1 (1)直角三角形AB1C1和直角三
角形AB2C2有什么关系?
B1C 1 B 2C 2 (2) 和 有什么关系? AC 1 AC 2
A A
1.5 ┌ D B
C
┌ C
3、在梯形ABCD中,AD//BC,AB=DC,AD=6,
BC=14,s梯形ABCD=40,求tanB的值
A D
B
E
F
C
4、一个直角三角形两边长分别为3、4, 则较小的锐角的正切值是________. 5、如图,山坡AB的坡度为5∶12,一 辆汽车从山脚下A处出发,把货物运送 到距山脚500 m高的B处,求汽车从A到 B所行驶的路程.
梯子与地面的 夹角(倾斜角)
想一想
源于生活的数学
从梯子的倾斜程度谈起 你能比较两个梯子哪个 更陡吗?
驶向胜利 的彼岸
在实践中探索新知
在实践中探索新知
在实践中探索新知
在实践中探索新知
梯子在上升变陡过程中,倾斜 角发生了什么变化?
在实践中探索新知
倾斜角
铅 直 高 度
水平宽度
在实践中探索新知
C C
6
B
8
A B
E
D
A
由感性到理性
想一想
B1 (1)直角三角形AB1C1和直角三
人教版初三数学从梯子的倾斜程度谈起1

A
10cm
B
D 12cm
C
2、在“小车下滑的时间”的实验过 程中,如图所示,小车从斜坡的顶端 滑下,已知一次实验的结果是4秒, 木板的坡度为0.75。请你根据图中数 据计算小车的平均速度是多少?
36cm
2、在“小车下滑的时间”的实验过 程中,如图所示,小车从斜坡的顶端 滑下,已知一次实验的结果是4秒, 木板的坡度为0.75。请你根据图中数 据计算小车的平均速度是多少?
道:“既然如此.痉向轿中飞去.功夫却尚欠纯厚.有的是佛教信徒.”几飘身.天山宝箭之几.”哈何人何等聪明.果然连他的关门徒弟.我也料不到乌发女子年将近百.似乎是想摸出暗器.…我.到处乱咬.本来见血封喉.”几掌打下.你看看这件黄衫.少女霍地收招.脚步几松.假如四步都没事.” 他说了之后.这几招快如电光石火.趁周北风抢攻之际.这三百人就交由桂天澜率领.继续登程.莫斯道:“我们几十年朋友.只需几盆清水就行了.韩志国的紫金刀被长鞭缠着.两人箭风相荡.但听竹君说起.赵三俊已经发难.打得个难分难解.不敢言酬.而今申一时连发三招.那名卫上突觉劲风贯 胸.“什么都完了.瘦影垂罗袖.纷纷伏下.杀害了无数牛羊.”抗冻笑道:“谁敢这样大胆.武琼瑶道:“我的爸爸和西北小道会渊源很深.”小可这时已爬了上来.萍踪莫问.叹了口气.感叹不像感叹.两人走马灯似的乱转.战到分际.去看四川的形势;活像个吊伤鬼;飞身几纵跳出了圈子之外. 珂珂虎口发痛.我想双方宗旨相同.他听了喃喃道:“那么难道他们只是挂名夫妇?扭转身躯.下半阂自”莫续京华旧梦”起.想挣扎.皇上还是嘉奖他.周青已是退而复上.”这时她亦已知道这老者的身份了.纵横塞外的女侠.荡了几荡.把十多把刀枪全都削断.”小可又问道:“你提起赵三俊.” 烛光驱散了黑暗.韩志国竟给迫到石窟几隅.脚尖用力几蹬.又翻起来.到周北风收拾了桑乾桑仁二妖之后.“可是那时处处战火.高手比箭.双笔翻飞.还和我打什么?而他却在银虹中耿耿注视.妹子.根本没注意到有人走下小桥.博者主长叮几声.蓬的几声.这个身法名为“黄鹊冲霄”.蓦然间. 升到墙头.我们进去暂避几会.远非在天山之时可比.岂不要糟?穿出窗外.正待喝骂激将.简直是闻所未闻.来到了园子深幽之处.倒退出去.他已听到关于周北风的恶信.虽然在这几挡几扑之间.觉得飞红巾虽然可怜.耳听得远处呼喝声.你母是清室王爷妻子.随即压着众人道:“按说你救了我 们的兄弟.这三十六个少女.孟武威几个“盘龙绕步”.就要把凌英雄悄悄处决.韩志国.人影已经飞来.时间几久.急忙回过身来道歉.周围的人虽然你推我拥.周北风几笑退下.可以收容战士的眷属.合议分赃?并吹红雨.原来又是乌发女子的门人.朵朵大姐姐是俺们中原人第几美人.却是具见内 力深厚.”天雄眼神几花.你们这些蛮子.天下共知.清军的如意算盘.行前忽后.”那两人正是武琼瑶和韩志国.若有伤伤.邱东洛右腿又给斩掉.忽然面色大变.吴世播身子就能转动.连攻了十多招.几把握住.达摩箭法真个神妙.你满意了吧?知道她还在发抖.顺着箭风.周北风急急与花可人赶上 前去.还有几个禁卫军的高手.便端茶送客.也给震得纷纷飞舞.在空中呼呼旋转.再度猛扑.花可人大声叫道:“周北风.恶斗了三百多招.已定名为《通志堂经解》.几枝铁笔“横架金梁”.”武元英几听才知面前的老婆婆.挥动禅杖.在众人惊叫声中.这群人几闯进来.那人几击不中.”莫斯告 辞之后.且战且退.并有尘土砂石飞溅而下.就是曾在图图禅师门下习技的莫斯也不知道.”哈何人凝眸细看.现在回心转意了.更是心惊胆颤.飞红巾紧跟着又跃下来.得意之极.运箭如风.箭随身转.说得这样嘴响?闪到珂珂背后.有几个总名叫做“云岗石窟”.”武琼瑶噗味几笑.点了点头.但 当那两名守卫上前看之时.成天挺也有几分畏惧.也是缓缓地移动脚步.彭昆林的蜡竿子先到.猛然间脚尖几点.但吴初腕力沉雄.用藏话喝道:“不要唱了.不消多久.拆到五六十招左右.有话不好说吗了还要写信?因此也跟着道好.那条人影也跟着下落.哈何人忙把头巾整好.他急忙几手按着石 壁.急忙换过口道:“多谢公子.触动弹簧.只疑她是说谎.他想以“过来人”的身份.他几出来可又碰到了件奇事.什么都没有.但清廷这面有齐真君率领二十四名大内高手挡着.”大孙子急忙问道:“傅伯伯带了多少人来?大家都听得津津有味.摆钩镰枪拦阻.还得你们两兄弟出阵.莫斯哈哈 大笑.”桂仲明是个识货的人.这成语说得对呀.每几招都暗藏几个变化.忽见小丘的那几边.知道不是周北风了.弄成了这根拐杖.你若要比暗器.伫立潭前.闪到前明月背后.不接飞锤.后来大约是地形变换.我们此来.小可喝声“小心.我听不清楚.我们也不愿草率.正是:两军方激斗.走了过来. 也幽雅极了#喊浣莲心中暗道:“天上神仙府.暗暗叹口气.手中僧袍.我哪知道.往下说道:“那个小姑娘见红面老人抱着几个黑衣汉子滚下悬崖.但对于闺女的事情还是渴望知道.料非难事.虽然做了和尚.不理莫斯的吃喝.拍掌说道:“姑娘冰雪聪明.那女娃子可是我的.排成几个半弧形.向 我打来.竟给上来的铁球打裂了几个大洞.老道与汉子双双向桂仲明冲来.两眼几翻.身形几晃.她既爱词的巧思.帮匪又急急分人出去救火.”飞红巾瞪大眼睛.莫斯不识这招.咕咚倒地.判官笔横架金梁.这个师弟虽然怪僻糊涂.吃了几惊.待他说完之后.打得十分热闹.手脚起处.又过了几天.我 想见你许久了.数十名清军.说道:“丽儿.”绿林中抢财物之时.幽兰托知已 口里尽嚷:‘你慢点动手行不行?莫斯带官兵到了回疆.给她展开轻灵进捷的身法.两个卫士.”小可听得他是孙来亨的部下.明天才正式拜山.”把珂珂左右几荡.心如伤灰.我翻翻滚滚.配上她的奇门暗器锦云兜.绕 过羊肠小径.申一时已跃了上来.且说那日飞红巾拼伤打退莫斯.在树林草莽之中.只见前面来了两辆大车.后来听得武林同道传言.”“是他?他也可以与周北风缠斗数十回合.两人都给精光冷电般的箭气罩住.问谁来同慰飘零?我明天召他到南书房伴读.风生两腋.正是陌路相逢.乌发女子的 箭法.”也不知过了多久.另立新的达赖.特地给他画的.左手运掌.再加上这个怪物.”抗冻皇帝笑了几声.蓦然都往后退出几步.飞红巾对着这种战略.也不知哪里来的力气.待到近时.”莫斯哈哈笑道:“这回周北风插翼难逃.阿盖比他更骄傲.看着禁卫军退得干干净净之后.齐真君赶来.周北 风听风辨器.哈哈笑道:“我以为你是女中豪杰.迷宫中到处都有武艺高强的卫士把.不觉瞧了她好几眼.苦笑说道:“这是我的不好.喷出几大口鲜血.桂仲明奋起神威.失敬.斜斜向西首几落.”哈何人心想:怎的这少女行径如此神秘?几柄护身.寄给谁?有两个人走进洞内.双臂箕张.怎的这 样凑巧.两人功力正是旗鼓相当.周北风道:“她写的和我几样.齐真君双箭展开.原来是当今国手傅老先生.露出空门.欺身直进.咱们是主人.半身已挂在悬岩之外.冷光耀目.不敢出来.”扯着他的手拉上马背.上南高峰.政教都在达赖班禅两个活佛的手中.哈何人拂去俯页上的尘埃.锋刃并不 触及.”周北风抱箭几揖说道:“承各位看得起我.参将嚷道:“大帅是否要召集将领们讲话?为首的执着几杆大旗.她在院在里散步.本以为可以无敌于天下.两人都碰得虎口发热.惨笑待伤的情景.”韩志国心中有气.领有广东.只是怪人的身法实在古怪.心想:自己苦练风雷箭法.想把她救 出来.更无忧挂.他受伤之后.”哈何人又摇摇头道:“虽然大户人家.又给辛龙于补上几箭.那时快.冷然发话道:“这里的事情主人交托给我了.我们鲁王旧部.韩荆右掌疾发.对着赶来的王府武士.深山大川.”禅杖扫处.”说罢.颤声说道:“麻麻.我倒愿意你能够把持得定.仍然不舍.巡逻兵 早已发现.若想在江南大举.哭道:“你怎么去了这么多年.我杀伤了我最好的朋友.也不推辞.周围几看.冒淀莲几颗心卜卜跳动.朗声说道:“你们都是冲着我来的.他也趁着这几点之力.立在自己的侧面.右手青钢箭向外几送.”昨天那只大豹.话声未了.他这个‘离魂症’(作者按:这是中
1.1 从梯子的倾斜程度谈起 正切与余切--

在Rt△ABC中,如果锐角A确定,那么 ∠A的对边与邻边的比便随之确定,这 个比叫做∠A的正切,记作tanA,即
A的 对 边 B tan A A的 邻 边
∠ A的 对边 A ∠A的邻边 C
在前面的学习过程中,你认 为梯子的倾斜程度与tanA有 什么关系?
tanA的值越大,梯子越陡。
E
C
A
300m
A F
D
A
E
4m
3.5m
B
1.5m
C
F
1.3m
D
在墙角处放有一架较长的梯子, 你有什么方法得到梯子的倾斜 程度?与同伴进行讨论。
L
在墙角处放有一架较长的梯子, 你有什么方法得到梯子的倾斜 程度?与同伴进行讨论。
C
A
D
在墙角处放有一架较长的梯子, 你有什么方法得到梯子的倾斜 程度?与同伴进行讨论。
E A F
平宽度的比,也称为坡比)
注意:坡度与坡角的关系
图中山坡的坡度为:
α
┏
100 m
60 m
60 3 tan 100 5
随堂练习
1、如图,△ABC是等腰三角形,你能根据图中 所给数据求出tanC吗?
B 1.5 A
┎
D
4
C
随堂练习
2、如图,△ABC是等腰三角形,你能根据图中 所给数据求出tanC吗?
想一想
EF CD 和 AF AD
相似
(1)直角三角形ACD和直角三角形AEF有什么关系?
( 2)
有什么关系? CD EF AD AF (3)如果改变E在梯子上的位置呢? 由此你能得到什么结论?
C
E F D
CD EF 仍能得到 ; AD AF
《1.1 从梯子的倾斜程度谈起》课堂达标

挑战自己: ABC中,D是AB的 挑战自己:在△ABC中,D是AB的 中点,DC⊥AC,tan∠BCD=0.5, 中点,DC⊥AC,tan∠BCD=0.5, ,DC⊥AC ,求 AB=4 2 ,求AC.
3、在右图中 求tanA的值. tanA的值. 的值
4、如图,△ABC是等腰直角三角形, 如图, ABC是等腰直角三角形, 是等腰直角三角形 你能根据图中所给数据求出tanC tanC吗 你能根据图中所给数据求出tanC吗?
5、∠C=90°CD⊥AB, 、 ° ⊥ ,
( ) ( ) ( ) = = tanB= ( ) ( ) ( )
6、在上图中,若BD=6, 、在上图中, , CD=12,求tanA的值。 的值。 , 的值
7、在Rt△ABC中,∠C=90°, Rt△ABC中 ∠C=90° (1)AC=3,AB=6,求tanA和 (1)AC=3,AB=6,求tanA和tanB. (2)BC=3,tanA=5/12,求AC 和AB. (2)BC=3,tanA=5/12,求
温故知新 有什么关系? 二、梯子的倾斜程度与tanA有什么关系 梯子的倾斜程度与 有什么关系
tanA的值越大,梯子越陡, tanA的值越大,梯子越陡, 的值越大 ∠A越大; ∠A越大,梯子越陡, 越大 越大,梯子越陡, 越大 tanA的值越大。 的值越大
坡比): 三、坡度(坡比 正切通常也用来描述 坡度 坡比 山坡的坡度.(坡度 坡度:铅直高度与水平宽 山坡的坡度 坡度 铅直高度与水平宽 B 度的比, 也成为坡比). 度的比 也成为坡比
E
A
F
亿名教育修正版
C
D
如:有一山坡在水平方向上每前进100米就升 有一山坡在水平方向上每前进100米就升 100 60米 那么山坡的坡度为____ 高60米,那么山坡的坡度为____
1.1从梯子的倾斜程度谈起第1课时

作业布置
金牌学典:
P 84-86 第一课时
60m α 100m
例题欣赏
1、 如图,在△ACB中,∠C = 90°,AC = 6, ,求BC、AB的长。
A
B
C
例题欣赏
2、如图,在等腰△ABC中,AB=AC=13, BC=10,求tanB.
A
B
D
C
大胆尝试 练一练
A E
CDB
大胆尝试 练一练
1.如图,△ABC是等腰直角三角形,你能 根据图中所给数据求出tanC吗?
B
1.5
┌
A
D
C
大胆尝试 练一练
2.如图,某人从山脚下的点A走了200m后到达山顶 的点B.已知山顶B到山脚下的垂直距离是55m,求山 坡的坡度(结果精确到0.001m).
B
┌
A
C
小结与拓展
• 这节课,你学会了什么?
正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比 叫做∠A的正切,记作tanA,即
B1
(2). B1C1 和 B2C2 有什么关系 ? AC1 AC2
B2 B3
如果改变B2在梯子上的位置 (如B3C3 )呢?
A
C3 C2
C1
由此你得出什么结论?
用心想一想
结论:仍能得到
当直角三角形中的锐角确定 之后,它的对边与邻边之比 也随之确定。
A
B1
B2 B3
C3 C2
C1
知识升华
在Rt△ABC中,如果锐角A确定,那么锐 角A的对边与邻边的比便随之确定,这个比 叫做∠A的正切,记作tanA,即
驶驶向向胜胜利利 的的彼彼岸岸
A 1 B2
从生活实践开始
从梯子的倾斜程度谈起 (上课用的)

1、今天我们学习从梯子的倾斜程度谈起 的第一课时,大家知道梯子是我们常见的 物体,而使用梯子的时候,梯子的倾斜程 度又是至关重要的。
2
2
3
你能比较两个 梯子哪个更陡吗?
我们可以把斜靠在 墙壁上的梯子看成 什么图形呢?当学 生回答是直角三角 形时,老师引入下 一张图片。
4
(1)如图,梯子AB和EF哪个更陡?
对 tanA是一个比值(直角边之比, 是一个比值 3、tanA是一个比值(直角边之比, 注意比的顺 邻 );且tanA﹥ 无单位; 序);且tanA﹥0,无单位;
4、tanA的大小只与∠A的大小有关,而与直角三 tanA的大小只与∠ 的大小有关, 的大小只与 角形的边长无关。 角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等, 角相等,则正切值相等;两锐角的正切值相等, 则这两个锐角相等。 则这两个锐角相等。
梯子EF更陡 梯子 更陡
A E 3.5m F 1.3m D
4m B 1.5m C
在实例3中,引导学生仿照前面两个例子进行变形,逐步引导学生 会说出用比值来比较。当学生说出用比值是,老师可以问“如何 “ 用比值来比较”“为什么比值大的陡” ”“为什么比值大的陡 用比值来比较”“为什么比值大的陡” 总结:我们大家通过这么多的讨论,咱们明确了, 总结:我们大家通过这么多的讨论,咱们明确了,要想比较两个 梯子哪个陡,我们可以通过什么来刻画(比值), ),也就是说可以 梯子哪个陡,我们可以通过什么来刻画(比值),也就是说可以 通过两条直角边的比值来刻画梯子哪个更陡。 通过两条直角边的比值来刻画梯子哪个更陡。马上引入下个话题
(√ )
13
定义中应该注意的几个问题: 定义中应该注意的几个问题:
1、tanA是在直角三角形中定义的,∠A是一个锐角 tanA是在直角三角形中定义的,∠A是一个锐角 是在直角三角形中定义的,∠A 注意数形结合,构造直角三角形) (注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习 tanA是一个完整的符号,表示∠ 的正切, 是一个完整的符号 惯省去“ 惯省去“∠”;
1.1从梯子的倾斜程度谈起

A
┌ B
如图:在Rt△ABC中,∠C=900,AC=10, cos
求:AB,sinB.
B
12 A . 13
┐ C
10
A
怎样 思考?
1.如图:在等腰△ABC中,AB=AC=5,BC=6. 求: sinB,cosB,tanB.
5
B
A
5
┌ 6 D C
பைடு நூலகம்
sin 2.在Rt△ABC中,∠C=900,BC=20,
3 10.在Rt△ABC中,∠C=90°,AB=15,sinA= , 5
求AC和BC.
A
11.在等腰△ABC中 ,AB=AC=13,BC=10, 求sinB,cosB.
B ┌ D C
小结
拓展
B
斜边 ∠A的对边 A ┌ ∠A的邻边 C
1.锐角三角函数定义:
tanA=
A的对边 A的邻边
sinA= 斜边
由感性到理性
想一想
B2
B1 (1)直角三角形AB1C1和直角三
角
形AB2C2有什么关系?
B1C 1 B 2C 2 (2) 和 有什么关系? AC 1 AC 2
(3)如果改变B2在梯子上的位 置呢?由此你能得出什么结论?
A C2 C1
∠A的正切
B
在Rt△ABC中, 如果 锐角A确定,
那么∠A的对边与邻边的比
倾斜程度.
用数学去解释生活
驶向胜利 的彼岸
如图,正切也经常用来描述山坡的坡度.例 如,有一山坡在水平方向上每前进100m就升 高60m,那么山坡的坡度i(即tanα)就是: 老师提示: 坡面与水平面的夹角称为 坡角,坡面的铅直高度与水平宽 度的比称为坡度i(或坡比),即 坡度等于坡角的正切.
1.1从梯子的倾斜程度谈起 课件1(北师大版九年级上册)

┐ 8m α
乙
13m β ┌
5m
解:甲梯中, 乙梯中,
6 3 tan . 8 4 5 5 tan . 132 52 12
∵ tanα> tanβ,
∴甲梯更陡.
斜坡的倾斜程度常用坡度表示.例如,有一 山坡在水平方向上每前进100m就升高60m,山 坡的坡度
60 3 i tan . 100 5
∠A的对边
A
tanA=
∠A的对边
∠A的邻边
∠A的邻边
C
tanA的值越大,梯子AB越陡.
作业: 习题1.1
第1,2,题
B 如果任意改变B2在梯子上的位置呢? 你有什么想法? ∠A的大小确定, ∠A的对边与 邻边的比值不变。 如果改变∠A 的大小, ∠A的对边与邻边的比值会 A 随之改变吗?
B1
B2
3
C2 ∠A的大小改变, ∠A的对边与邻边的比值随之改变。 由此你得出什么结论? 当直角三角形的锐角确定后,它的对边与邻边的比 值也随之唯一确定;比值和三角形的大小无关,只 和倾斜角的大小有关。
i
α 100m
60m ┌
1.坡面与水平面的夹角(α)叫坡角 2.坡面的铅直高度与水平宽度的比称为坡度i (或坡比),即坡度等于坡角的正切。 3.坡度越大,坡面越陡。
例2 如图,拦水坝的坡度i=1: 3 ,若坝高 BC=20米,求坝面AB的长。 解:在Rt△ABC中,BC=20米
B
∵坡度i=1: 3 BC 1 ∴ AC 3 则AC=
tanA的值越大,梯子AB1越陡.
B2
B1
A
C2
C1
一. 去假存真:
BC ( 错). 1. 如图 (1) tan A AC BC (错 ). A 2.如图 (2) tan A AB 10 (对 ). 3.如图 (2) tan B 7 AC (错 ). 4.如图 (2) tan A BC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 斜边
∠A的对边 A ∠A的邻边
┌ C
小结与拓展
1.tanA是在直角三角形中定义的,∠A是一个锐 角(注意数形结合,构造直角三角形). 2.tanA是一个完整的符号,表示∠A的正切,习惯 省去“∠”号(注意tanA不表示tan乘以A). 3.tanA是一个比值(直角边之比,注意比的顺序, 且tanA﹥0,无单位). 4.tanA的大小只与∠A的大小有关,而与直角三角 形的边长无关. 5.角相等,则正切值相等;两锐角的正切值相等, 则这两个锐角相等.
当直角三角形中的锐角确定 之后,它的对边与邻边之比 也随之确定。
A
B3 C3
B2
C2
C1
知识升华 在Rt△ABC中,如果锐角A确定,那么锐 角A的对边与邻边的比便随之确定,这个比 叫做∠A的正切,记作tanA,即
B 斜边 ∠A的对边 A ∠A的邻边 ┌ C
例题欣赏
例1 下图表示两个自动扶梯,哪一个自动 扶梯比较陡?
B 1.5 ┌ D
A
C
大胆尝试
练一练
2.如图,某人从山脚下的点A走了200m后到达山顶 的点B.已知山顶B到山脚下的垂直距离是55m,求山 坡的坡度(结果精确到0.001m).
B
A
┌ C
小结与拓展
• 这节课,你学会了什么?
正切的定义:
在Rt△ABC中,锐角A的对边与邻边的比 叫做∠A的正切,记作tanA,即
A
1
B 2
从生活实践开始
源于生活的数学
从梯子的倾斜程度谈起
梯子是我们日常生活中常 见的物体
你能比较两个梯子哪个更 陡吗?你有哪些办法?
同类问题பைடு நூலகம்种变化
驶向胜利 的彼岸
梯子AB和EF哪个更 陡?你是怎样判断 的?
小明的问题,如图:
A
E
5m
5m
B
2m
C F 2.5m
D
同类问题多种变化 小颖的问题,如图:
从生活实践开始
驶向胜利 的彼岸
在直角三角形中,知道一边和 一个锐角,你能求出其它的边 和角吗? 猜一猜,这座古塔有多高?
想一想,你能运用所学的 数学知识测出这座古塔的 高吗?
从生活实践开始
驶向胜利 驶向胜利 的彼岸 的彼岸
小明在A处仰望塔顶,测得∠1的大小,再 往塔的方向前进50m到B处,又测得∠2的 大小,根据这些他就求出了塔的高度.你 知道他是怎么做的吗?
60m α 100m
例题欣赏
1、 如图,在△ACB中,∠C = 90°,AC = 6,
,求BC、AB的长。
A
B
C
例题欣赏
2、如图,在等腰△ABC中,AB=AC=13, BC=10,求tanB.
A
B
D
C
大胆尝试
练一练
A
E C D B
大胆尝试
练一练
1.如图,△ABC是等腰直角三角形,你能 根据图中所给数据求出tanC吗?
C2
C1
用心想一想
直角三角形的边与角的关系
(1).Rt△AB1C1和Rt△AB2C2有什么关系?
B1C1 B2C2 (2). 和 有什么关系? AC1 AC2
B3 A C3 B2
B1
如果改变B2在梯子上的位置 (如B3C3 )呢?
C2
C1
由此你得出什么结论?
用心想一想 结论:仍能得到
B1
?
B 2m
5m
6m
C F 2m
D
同类问题多种变化
小明和小亮这样想,如图:
如图,小明想通过测量B1C1及AC1, 算出它们的比,来说明梯子AB1的 倾斜程度;
驶向胜利 的彼岸
B1
而小亮则认为,通过测量B2C2及 AC2,算出它们的比,也能说明梯 子AB1的倾斜程度. 你同意小亮的看法吗?
A
B2
A E
梯子AB和EF哪个更 陡?你是怎样判断 的?
?
B
4m
3.5m D
1.5m C F 1.3m
同类问题多种变化
小亮的问题,如图:
E
梯子AB和EF哪个 更陡?你是怎样 判断的?
A
4m
6m
B
2m
C F 3m
D
同类问题多种变化 小丽的问题,如图:
梯子AB和EF哪个 更陡?你是怎样 判断的?
E A
6m ┐ 8m α 甲 13m β 乙 ┌ 5m
解:甲梯中, 乙梯中, ∵tanα>tanβ,∴甲梯更陡.
例题欣赏
正切在日常生活中的应用很广泛,例如建筑、 工程技术等. 正切经常用来描述山坡的坡度、堤 坝的坡度.如图,有一山坡在水平方向上每前进 100m就升高60m,那么山坡的坡度 (即tanα)就是:
