小学三年级奥数讲解.竖式数字谜
小学三年级奥数讲解.竖式数字谜之欧阳术创编

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
三年级巧解竖式谜

三年级巧解竖式谜一、竖式谜的概念。
竖式谜是一种数学谜题,通常是给出一个不完整的竖式(加法竖式、减法竖式等),其中一些数字被用符号(如□、△等)或者空白代替,要求我们根据竖式的运算规则以及已知数字,推理出被隐藏的数字。
二、解题方法与技巧。
1. 从个位开始分析。
- 在加法竖式中,例如:- begin{array}{r} □3 + 2□ hline 59 end{array}- 先看个位,因为3 + □ = 9,所以这个□里的数字是9 - 3=6。
- 再看十位,□+2 = 5,由于个位相加没有进位(如果进位,十位相加结果会大于5),所以这个□里的数字是5 - 2 = 3。
- 在减法竖式中,例如:- begin{array}{r} 7□ - □5 hline 34 end{array}- 先看个位,□ - 5 = 4,那么□ = 4 + 5 = 9。
- 再看十位,7-□ = 3,所以□ = 7 - 3 = 4。
2. 考虑进位与退位情况。
- 加法进位:- 例如:begin{array}{r} □8 + 4□ hline □3 end{array}- 个位8+□结果个位是3,这说明8+□ = 13,□ = 13 - 8 = 5,并且向十位进1。
- 十位□+4 + 1=□(这里十位结果是一个两位数,设为□),假设十位结果是73中的7,那么□+4 + 1 = 7,□ = 7- 4 - 1=2。
- 减法退位:- 例如:begin{array}{r} □0 - 3□ hline 41 end{array}- 个位0-□ = 1,这是不够减的情况,需要从十位借1当10,所以10-□ = 1,□ = 9。
- 十位□ - 1-3 = 4,□ = 4 + 3+1 = 8。
3. 根据数字范围和数位关系推理。
- 例如:在一个三位数加两位数的竖式中,和是四位数。
- begin{array}{r} □□□ + □□ hline1□□□ end{array}- 由于和是四位数,最小的四位数是1000,所以第一个加数的百位至少是9。
三年级奥数--竖式数字谜

1.右边竖式中的每个汉字代表不同的数字,这些汉字各代表哪些数字?少()年()早()立()志()向()有()何()惧()2.右式中不同的汉字代表1~9中不同的数字,当算式成立时,“中国”这两个汉字所代表的两位数最大是________。
3.右面的算式里,每个方框代表一个数字。
问:这6个方框中的数字的总和是________。
4.下边是一道题的乘法算式,请问:A、B、C、D、E分别代表什么数字?5.右边残缺算式中已知3个4,那么补全后它的乘积是___________。
6.解算式谜: (下列竖式中的每个汉字、字母各代表不同的数字 )巧()解()趣()题()妙()趣()横()生()7.下面算式均由1,2,……9九个数字组成,请填空使算式成立。
1.在下面算式的□内,填上适当的数字,使算式成立.2.在下面算式的□内,填上适当的数字,使算式成立.3.在下面算式的□内,填上适当的数字,使算式成立.4.在下面算式的□内,填上适当的数字,使算式成立.5.右面竖式“春夏秋冬四季”分别代表什么数字?春=()夏=()秋=()冬=()四=()季=()年=()奥数基础-竖式数字谜(3)1.在下面算式的□内,填上适当的数字,使算式成立.2.右面的算式里,每个方框代表一个数字,问这六个方框中的数字的总和是____。
3.在下面算式的□内,填上适当的数字,使算式成立.3、(1)“争当小雏鹰”分别代表什么数字?(2)下式中“优”代表什么数字?争=()当=()小=()雏=()鹰=()学=()习=()再=()优=()4.右面竖式中的每个不同汉字代表0~9中不同的数码,求出它们使得竖式成立的值。
巧=()解=()数=()字=()谜=()。
小学三年级奥数讲解.竖式数字谜

竖式数字谜之巴公井开创作第1部份:加、减法竖式数字谜这一部份主要讲加、减法竖式的数字谜问题.解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”.关键是通过综合观察、分析,找出解题的“突破口”.题目分歧,分析的方法分歧,其“突破口”也就分歧.这需要通过不竭的“学”和“练”,逐步积累知识和经验,总结提高解题能力.例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数肯定是 4.即5+?=9.从和的百位数与十位数是18,可判定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的.从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可判定:□加上个位进上来的1是5,去失落进上来的1应是4.百位上2+□=6,可知:□=4,去失落进上来的1,□=3.例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比力难解的.可是认真分析一下减法算式各部份的数位,即可以找到突破口.被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此.那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,标明被减数的最高位就是“1”.这样,就可以判定被减数是1000.知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1.十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数年夜的.那么,?-8=9,可知被减数十位上是7.再看百位,因为被减数是四位数.相减后,成了三位数,差的百位数又是9,从而判定,被减数的百位上是0,千位上肯定是1了.例5:下面的算式,加数的数字都被墨水污染了.你能知道被污染的四个数字的和吗?解:和的个位数是9,可知加数的个位数字相加没有进位.即两个数字和是9.和的百位与十位上的数是18,即是两个加数十位数字的和.所以,被污染的四个数字的和是:18+9=27.例6:下面算式中的数字都被遮盖住了,求竖式中被遮盖住的几个数字的和.解:这是一道三个三位数的加法.从和的前两位是29,可判定三个加数的百位必需是9,因为三个9的和才是27,多出的部份即是进位造成的.同理,可判定加数的三个十位数字的和,也必需是9,多出的2(29-27),是个位进位造成的.而和的个位数是1,判定三个加数的个位数字和是21.因此,被遮盖的数,数字和是:27+27+21=75针对练习1.在□里填上适当的数.□8□+□6□3□□1 2 8□+9 1□□□6 3□□+□7 8□0 2 6□□5—□□7□2 6□—□7 99□6□0 0□—6 0□91□4 92.在下面的算式内,各填上一个合适的数字,使等式成立.□□□—8 56 3 73.在下面的算式内,各填上一个合适的数字,使等式成立.□□□—□8 5□□□—□8 7□□□—2□55 4 87 3 78 3 74.在下面的算式内,各填上一个合适的数字,使等式成立.□2—2□2 44 9□—□□71 7 5□2□—□□85 3 65.在方格中填上0—9十个数字,不能重复,使等式成立,你能做到吗?□□4+2 8□□□□3第2部份:乘、除法竖式数字谜掌握好乘、除法的基本运算规则(第2讲的公式(3)(4)及推演出的变形式子)是解乘、除法竖式谜的基础.根据题目结构形式,通过综合观察、分析,找出“突破口”是解题的关键.例1:在乘法竖式的□中填入合适的数字,使竖式成立.例2:在右边乘法竖式的□里填入合适的数字,使竖式成立.3□7×□2□9□例3:在左下边除法竖式的□中填入适当的数,使竖式成立.例4:在右边除法竖式的□中填入合适的数字,使竖式成立.针对练习1.在下列各竖式的□里填上合适的数:2.在右式中,“我”、“爱”、“数”、“学”分别代表什么数时,乘法竖式成立?3.“我”、“们”、“爱”、“祖”、“国”各代表一个分歧的数字,它们各即是几多时,右边的乘法竖式成立?4.在下列各除法竖式的□里填上合适的数,使竖式成立:5.在下式的□里填上合适的数.第2部份:乘、除法竖式数字谜掌握好乘、除法的基本运算规则(第2讲的公式(3)(4)及推演出的变形式子)是解乘、除法竖式谜的基础.根据题目结构形式,通过综合观察、分析,找出“突破口”是解题的关键.例1:在乘法竖式的□中填入合适的数字,使竖式成立.例2:在右边乘法竖式的□里填入合适的数字,使竖式成立.3□7×□2□9□例3:在左下边除法竖式的□中填入适当的数,使竖式成立.例4:在右边除法竖式的□中填入合适的数字,使竖式成立.针对练习1.在下列各竖式的□里填上合适的数:2.在右式中,“我”、“爱”、“数”、“学”分别代表什么数时,乘法竖式成立?3.“我”、“们”、“爱”、“祖”、“国”各代表一个分歧的数字,它们各即是几多时,右边的乘法竖式成立?4.在下列各除法竖式的□里填上合适的数,使竖式成立:时间:二O二一年七月二十九日。
小学三年级奥数讲解竖式数字谜

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三1 / 8 位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
三年级奥数乘除竖式谜

三年级奥数乘除竖式谜在三年级的数学学习中,乘法和除法是一个非常重要的知识点。
为了帮助学生更好地掌握乘法和除法,并提高他们的计算能力,老师们常常会给学生出一些有趣的谜题和问题。
本文将介绍一些有趣的三年级奥数乘除竖式谜,帮助学生巩固乘除竖式的计算方法。
第一题:陆婷有24颗苹果,她把这些苹果平均分给4个小朋友,请问每个小朋友得到几颗苹果?解答:这是一个除法的问题。
我们可以用竖式来解决这个问题。
24 ÷ 4 = 6答案是每个小朋友得到6颗苹果。
第二题:汤姆家有32个饼干,他想平均分给8个小朋友,请问每个小朋友得到几个饼干?解答:同样是一个除法的问题。
32 ÷ 8 = 4答案是每个小朋友得到4个饼干。
第三题:一箱苹果有48个,小明想平均分给6个人,请问每个人得到几个苹果?解答:这次我们来看一个有余数的除法问题。
48 ÷ 6 = 8(余数0)答案是每个人得到8个苹果,没有剩下的。
第四题:妈妈做了一大桶果汁,里面有60升,她想平均分给5个朋友,请问每个朋友得到几升果汁?解答:同样是一个除法问题。
60 ÷ 5 = 12答案是每个朋友得到12升果汁。
第五题:小明购买了一捆铅笔,一共有36支,他想平均分给9个同学,请问每个同学得到几支铅笔?解答:继续用除法来解决这个问题。
36 ÷ 9 = 4答案是每个同学得到4支铅笔。
通过上面这些例子,我们可以看到除法可以帮助我们解决一些分享物品的问题。
而乘法则可以帮助我们解决一些组合问题。
下面我们来看一些乘法谜题。
第一题:一袋子里有5个橙子,每个橙子上都有3个小鼠咬了一口,请问一共有几个小鼠咬了橙子?解答:这是一个乘法的问题。
5 × 3 = 15答案是一共有15只小鼠咬了橙子。
第二题:一包饼干有8块,一盒饮料有6瓶,请问一共有多少个饼干和饮料?解答:再来看一个乘法问题。
8 × 6 = 48答案是一共有48个饼干和饮料。
小学三年级奥数讲解竖式数字谜

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
小学三年级奥数讲解.竖式数字谜

竖式数字谜之蔡仲巾千创作第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目分歧,分析的方法分歧,其“突破口”也就分歧。
这需要通过不竭的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数肯定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,即可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,标明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
(完整)小学三年级奥数讲解.竖式数字谜

(完整)小学三年级奥数讲解.竖式数字谜竖式数字谜第1部分:加、减法竖式数字谜这一部分要紧说加、减法竖式的数字谜咨询题。
解加、减法数字谜咨询题的基本功,在于掌握好上一说中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是经过综合观看、分析,找出解题的“突破口”。
题目别同,分析的办法别同,其“突破口”也就别同。
这需要经过别断的“学”和“练”,逐步积存知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数基本上两位数,从第一具加数个位是5与和的个位数是9,能够判断第二个加数的个位数必然是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数基本上9,如此,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只懂其中两个加数的个位分不是7、5,而和的个位却是8,确信是进位造成的。
从7+5+?=□8,可推断另一具加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:那个减法算式,只告知了减数是1,被减数、减数都别懂!全式应有八个数字,其中七个基本上未知数,初看是比较难解的。
然而仔细分析一下减法算式各部分的数位,便能够找到突破口。
被减数有四位,减去1后,差却成了三位数,惟独相减时延续退位,才会这样。
这么,啥数减去1需要向高位借数呢?惟独“0”!而最高位退1后成了0,表明被减数的最高位算是“1”。
如此,就能够断定被减数是1000。
懂了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
这么,?-8=9,可知被减数十位上是7。
三年级奥数基础教程竖式数字谜小学

三年级奥数基础教程竖式数字(shùzì)谜小学这一讲主要讲加、减法竖式的数字(shùzì)谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算(yùn suàn)规则(1)(2)及其推演(tuīyǎn)的变形规则,另外(lìnɡ wài)还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1 在右边的竖式中,A,B,C,D各代表什么数字?解:显然,C=5,D=1(因两个数字之和只能进一位)。
由于A+4+1即A+5的个位数为3,且必进一位(因为4>3),所以A+5=13,从而A=13-5=8。
同理,由7+B+1=12,即B+8=12,得到B=12-8=4。
故所求的A=8,B=4,C=5,D=1。
例2 求下面各竖式中两个加数的各个数位上的数字之和:分析与解:(1)由于和的个位数字是9,两个加数的个位数字之和不大于9+9=18,所以两个加数的个位上的两个方框里的数字之和只能是9。
(这是“突破口”)再由两个加数的个位数之和未进位,因而两个加数的十位数字之和就是14。
故这两个加数的四个数字之和是9+14=23。
(2)由于和的最高两位数是19,而任何两个一位数相加的和都不超过18,因此,两个加数的个位数相加后必进一位。
(这是“突破口”,与(1)不同) 这样,两个加数的个位数字相加之和是15,十位数字相加之和是18。
所求的两个加数的四个数字之和是15+18=33。
注意:(1)(2)两题虽然题型相同,但两题的“突破口”不同。
(1)是从和的个位着手分析,(2)是从和的最高两位着手分析。
例3 在下面的竖式中,A,B,C,D,E各代表什么数?分析与解:解减法竖式数字谜,与解加法竖式数字谜的分析方法一样,所不同的是“减法”。
三年级奥数_第14讲巧解竖式数字谜
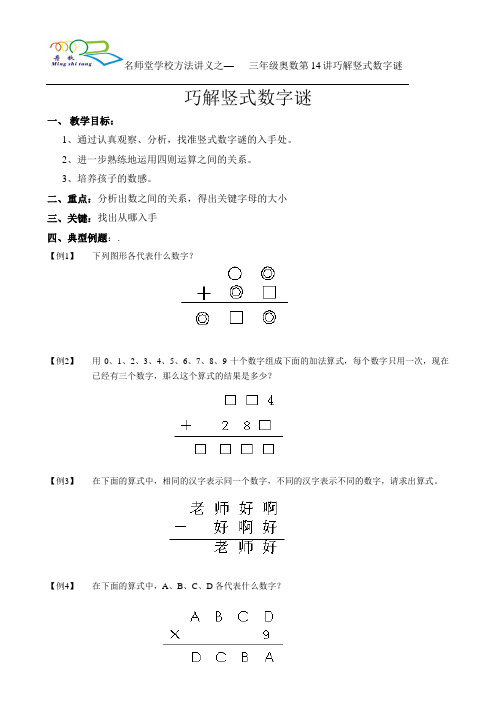
巧解竖式数字谜一、教学目标:1、通过认真观察、分析,找准竖式数字谜的入手处。
2、进一步熟练地运用四则运算之间的关系。
3、培养孩子的数感。
二、重点:分析出数之间的关系,得出关键字母的大小三、关键:找出从哪入手四、典型例题:.【例1】下列图形各代表什么数字?【例2】用0、1、2、3、4、5、6、7、8、9十个数字组成下面的加法算式,每个数字只用一次,现在已经有三个数字,那么这个算式的结果是多少?【例3】在下面的算式中,相同的汉字表示同一个数字,不同的汉字表示不同的数字,请求出算式。
【例4】在下面的算式中,A、B、C、D各代表什么数字?【例5】□里填哪些数字,可以使这道除法算式成为一道完整的算式?五、挑战自我1、下面算式中,相同的汉字表示同一个数字,不同的汉字表示不同的数字,试确定算式中的各汉字所代表的数字。
2、在2、3、4、5、6这五个数中挑选四个,填在方框里,使下面的算式的结果是888。
3、在下面的算式中,相同的汉字表示同一个数字,不同的汉字表示不同的数字,它们各代表多少时,算式才成立?4、在下面的减法算式的空格内,各填入一个合适的数字,使算式成立。
5、下面算式中,相同的汉字表示同一个数字,不同的汉字表示不同的数字,当它们各代表多少时算式成立?6、下面算式中,“数学兴趣班”代表多少?7、下面算式中,相同的汉字表示同一个数字,不同的汉字表示不同的数字,当它们各代表多少时算式成立?8、在□里填上适当的数,使等式成立。
9、在下面的□内填入合适的数,使算式成立。
10、每个字母代表0~9中的不同数字,要使那么E×F =().11、下面的算式中,每个方格代表一个数字,问:这6个方格中的数字的总和是多少?(第三届华罗庚金杯初赛试题)12、在下面的乘法算式中,A、B、C、D表示不同的数字,ABC是一个三位数,求三位数ABC(美国小学数学奥林匹克试题)13、在下边的除法算式中,适合条件的商是多少?(“从小爱数学”小少年数学邀请赛试题)。
小学三年级奥数 竖式数字迷 知识点与习题

第3讲竖式数字谜(一)这一讲主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1在右边的竖式中,A,B,C,D各代表什么数字?解:显然,C=5,D=1(因两个数字之和只能进一位)。
由于A+4+1即A+5的个位数为3,且必进一位(因为4>3),所以A+5=13,从而A=13-5=8。
同理,由7+B+1=12,即B+8=12,得到B=12-8=4。
故所求的A=8,B=4,C=5,D=1。
例2求下面各竖式中两个加数的各个数位上的数字之和:分析与解:(1)由于和的个位数字是9,两个加数的个位数字之和不大于9+9=18,所以两个加数的个位上的两个方框里的数字之和只能是9。
(这是“突破口”) 再由两个加数的个位数之和未进位,因而两个加数的十位数字之和就是14。
故这两个加数的四个数字之和是9+14=23。
(2)由于和的最高两位数是19,而任何两个一位数相加的和都不超过18,因此,两个加数的个位数相加后必进一位。
(这是“突破口”,与(1)不同) 这样,两个加数的个位数字相加之和是15,十位数字相加之和是18。
所求的两个加数的四个数字之和是15+18=33。
注意:(1)(2)两题虽然题型相同,但两题的“突破口”不同。
(1)是从和的个位着手分析,(2)是从和的最高两位着手分析。
例3在下面的竖式中,A,B,C,D,E各代表什么数?分析与解:解减法竖式数字谜,与解加法竖式数字谜的分析方法一样,所不同的是“减法”。
首先,从个位减起(因已知差的个位是5)。
4<5,要使差的个位为5,必须退位,于是,由14-D=5知,D=14-5=9。
(这是“突破口”)再考察十位数字相减:由B-1-0<9知,也要在百位上退位,于是有10+B-1-0=9,从而B=0。
小学三年级奥数讲解.竖式数字谜之欧阳德创编

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
小学三年级奥数讲解竖式数字谜

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
小学三年级奥数讲解竖式数字谜

小学三年级奥数讲解竖式数字谜Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
欢迎阅读竖式数字谜
第1部分:加、减法竖式数字谜
这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还
解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
相减后,成了三位数,差的百位数又是9,从而断定,被减数的百位上是0,千位上必定是1了。
例5:下面的算式,加数的数字都被墨水污染了。
你能知道被污染的四个数字的和吗?
解:和的个位数是9,可知加数的个位数字相加没有进位。
即两个数字和是9。
和的百位与十位上的数是18,便是两个加数十位数字的和。
所以,被污染的四
个数字的和是:18+9=27。
例6:下面算式中的数字都被遮盖住了,求竖式中被遮盖住的几个数字的和。
解:这是一道三个三位数的加法。
从和的前两位是29,可断定三个加数的百位必须是9,因为三个9的和才是27,多出的部分便是进位造成的。
同理,可断定加数的三个十位数字的和,也必须是9,多出的2(29-27),是个位进位造成的。
而和的个位数是1,断定三个加数的个位数字和是21。
因此,被遮盖的数,数字和是:27+27+21=75
针对练习
—2□
2 4 —□□7
1 7 5
—□□8
5 3 6
5.在方格中填上0—9十个数字,不能重复,使等式成立,你能做到吗?
□□4
+2 8□
□□□3
第2部分:乘、除法竖式数字谜
掌握好乘、除法的基本运算规则(第2讲的公式(3)(4)及推演出的变形式子)是解乘、除法竖式谜的基础。
根据题目结构形式,通过综合观察、分析,找出“突破口”是解题的关键。
例1:在乘法竖式的□中填入合适的数字,使竖式成立。
例2:在右边乘法竖式的□里填入合适的数字,使竖式成立。
3□7
例1:在乘法竖式的□中填入合适的数字,使竖式成立。
例2:在右边乘法竖式的□里填入合适的数字,使竖式成立。
3□7
×□
2□9□
例3:在左下边除法竖式的□中填入适当的数,使竖式成立。
例4:在右边除法竖式的□中填入合适的数字,使竖式成立。
