三角函数的图像和性质 测试题及解析
三角函数的图象和性质练习题及答案

1y三角函数图像与性质练习题(一)一.选择题 〔每题5分,共100分〕1.将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=-⎪⎝⎭平移,平移后的图象如下图,那么平移后的图象所对应函数的解析式是( ) A.sin()6y x π=+B.sin()6y x π=-C.sin(2)3y x π=+D.sin(2)3y x π=- 2. 为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数R x x y ∈=,sin 2的图像上所有的点( )A.向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍〔纵坐标不变〕B.向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍〔纵坐标不变〕C.向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍〔纵坐标不变〕 D.向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍〔纵坐标不变〕3. 函数()2sin (0)f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-,那么ω的最小值等于( )A.23B.32C.2D.3 4.函数y =sin(2x +3π)的图象可由函数y =sin2x 的图象经过平移而得到,这一平移过程可以是( ) A.向左平移6πB.向右平移6πC.向左平移12π D.向右平移12π 5. 要得到函数y =sin (2x -)6π的图像,只需将函数y =cos 2x 的图像( )A.向右平移6π个单位 B.向右平移3π个单位 C. 向左平移6π个单位 D. 向左平移3π个单位 6. 为了得到函数y =sin (2x-4π)+1的图象,只需将函数y =sin 2x 的图象〔〕平移得到A.按向量a=(-8π,1)B. 按向量a=(8π,1)C.按向量a=(-4π,1)D. 按向量a=(4π,1) 7.假设函数()sin ()f x x ωϕ=+的图象如图,那么ωϕ和的取值是( )A.1ω=,3πϕ= B.1ω=,3πϕ=-C.12ω=,6πϕ= D.12ω=,6πϕ=- 8. 函数πsin 23y x ⎛⎫=-⎪⎝⎭在区间ππ2⎡⎤-⎢⎥⎣⎦,的简图是( )9. 函数sin(2)cos(2)63y x x ππ=+++的最小正周期和最大值分别为( ) A.,1π B.,2π C.2,1π D. 2,2π 10. 函数()sin()(0)3f x x πϖϖ=+>的最小正周期为π,那么该函数的图象( )A.关于点(,0)3π对称 B.关于直线4x π=对称 C.关于点(,0)4π对称 D.关于直线3x π=对称11.函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的局部图象如图,那么( ) A.4,2πϕπω==B.6,3πϕπω==C.4,4πϕπω== D.45,4πϕπω==12. 要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=-⎪3⎝⎭的图象( ) yx11-2π- 3π- O6ππyx11- 2π- 3π- O 6ππ yx1 1-2π-3πO 6π-πy xπ2π- 6π-1O 1-3π A.B. C. D.A.向右平移π6个单位 B.向右平移π3个单位 C.向左平移π3个单位 D.向左平移π6个单位 13. 设函数()x f ()φω+=x sin ⎪⎭⎫ ⎝⎛<<>20,0πφω.假设将()x f 的图象沿x 轴向右平移61个单位长度,得到的图象经过坐标原点;假设将()x f 的图象上所有的点的横坐标缩短到原来的21倍〔纵坐标不变〕, 得到的图象经过点⎪⎭⎫⎝⎛1,61. 那么( ) A.6,πφπω== B.3,2πφπω== C.8,43πφπω== D. 适合条件的φω,不存在 14. 设函数)()0(1)6sin()(x f x x f '>-+=的导数ωπω的最大值为3,那么f (x )的图象的一条对称轴的方程是( ) A.9π=x B.6π=x C.3π=x D.2π=x三角函数图像与性质练习题答案三角函数的图象和性质练习题(二)一、选择题1.函数sin(2)(0)y x ϕϕπ=+≤≤是R 上的偶函数,那么ϕ的值是〔 〕A.0B.4πC.2πD.π2. 将函数x y 4sin =的图象向左平移12π个单位,得到)4sin(ϕ+=x y 的图象,那么ϕ等于A .12π-B .3π-C .3πD .12π 3.假设,24παπ<<那么〔 〕 (45<a<90)A .αααtan cos sin >>B .αααsin tan cos >>C .αααcos tan sin >>D .αααcos sin tan >>1 2 3 4 5 6 7 8 9 10 C C B A B B C A A A 11 12 13 14 CAAA4.函数23cos()56y x π=-的最小正周期是〔 〕A .52πB .25π C .π2 D .π5 5.在函数x y sin =、x y sin =、2sin(2)3y x π=+、2cos(2)3y x π=+中, 最小正周期为π的函数的个数为〔〕. A .1个B .2个 C .3个 D .4个6.x x x f 32cos 32sin)(+=的图象中相邻的两条对称轴间距离为 〔 〕 A .3π B .π34 C .π23 D .π677. 函数)252sin(π+=x y 的一条对称轴方程〔 〕A .2π-=xB .4π-=xC .8π=xD .=x π458. 使x y ωsin =〔ω>0〕在区间[0,1]至少出现2次最大值,那么ω的最小值为〔 〕 A .π25B .π45C .πD .π23二、填空题1.关于x 的函数()cos()f x x α=+有以下命题: ①对任意α,()f x 都是非奇非偶函数; ②不存在α,使()f x 既是奇函数,又是偶函数;③存在α,使()f x 是偶函数;④对任意α,()f x 都不是奇函数.其中一个假命题的序号是,因为当α=时,该命题的结论不成立.2.函数xxy cos 2cos 2-+=的最大值为________.3.假设函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,那么自然数k 的值为______. 4.满足23sin =x 的x 的集合为_________________________________. 5.假设)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2,那么ϖ=________.三、解答题1.比拟大小〔1〕00150sin ,110sin ;〔2〕00200tan ,220tan 2. (1) 求函数1sin 1log 2-=xy 的定义域. 〔2〕设()sin(cos ),(0)f x x x π=≤≤,求()f x 的最大值与最小值. 3.)33sin(32)(πω+=x x f 〔ω>0〕〔1〕假设f (x +θ)是周期为2π的偶函数,求ω及θ值; ω= 1/3 ,θ= . 〔2〕f (x )在〔0,3π〕上是增函数,求ω最大值 "三角函数的图象和性质练习题二"参考答案一、选择题 1.C [解析]:当2πϕ=时,sin(2)cos 22y x x π=+=,而cos 2y x =是偶函数2.C [解析]:函数x y 4sin =的图象向左平移12π个单位,得到)12(4sin π+=x y 的图象,故3πϕ=3.D [解析]:tan 1,cos sin 1,ααα><<αααcos sin tan >>4.D [解析]:2525T ππ== 5.C [解析]:由x y sin =的图象知,它是非周期函数6.C [解析]: ∵x x x f 32cos 32sin)(+==)432sin(2π+x∴图象的对称轴为πππk x +=+2432,即)(2383Z k k x ∈+=ππ故相邻的两条对称轴间距离为π237.A [解析]:当2π-=x 时 )252sin(π+=x y 取得最小值-1,应选A8.A [解析]:要使x y ωsin =〔ω>0〕在区间[0,1]至少出现2次最大值 只需要最小正周期⋅45ωπ2≤1,故πω25≥ 二、填空题1、①0[解析]:此时()cos f x x =为偶函数2、3[解析]:2cos 4cos 2412cos 2cos 2cos x x y x x x++-===----3、2,3或[解析]:,12,,2,32T k k N k kkππππ=<<<<∈⇒=而或4、|2,2,33x x k k k Z ππππ⎧⎫=++∈⎨⎬⎩⎭或 5、34[解析]:[0,],0,0,3333x x x ππωππω∈≤≤≤≤< 三、解答题1.解:〔1〕0sin110sin 70,sin150sin 30,sin 70sin 30,sin110sin150==>∴>而 〔2〕0tan 220tan 40,tan 200tan 20,tan 40tan 20,tan 220tan 200==>∴>而 2.解:〔1〕221111log 10,log 1,2,0sin sin sin sin 2x x x x -≥≥≥<≤ 22,6k x k πππ<≤+或522,6k x k k Z ππππ+≤<+∈5(2,2][2,2),()66k k k k k Z ππππππ++∈为所求.〔2〕0,1cos 1x x π≤≤-≤≤当时,而[11]-,是()sin f t t =的递增区间 当cos 1x =-时,min ()sin(1)sin1f x =-=-; 当cos 1x =时,max ()sin1f x =. 4.解:(1) 因为f (x +θ)=)333sin(32πθω++x又f (x +θ)是周期为2π的偶函数, 故∈+==k k 6,31ππθω Z(2) 因为f (x )在〔0,3π〕上是增函数,故ω最大值为61三角函数的图象专项练习一.选择题1.为了得到函数)62sin(π-=x y 的图象,可以将函数y=cos2x 的图象 ( )A .向右平移6π个单位长度B. 向右平移3π个单位长度 C. 向左平移6π个单位长度 D. 向左平移3π个单位长度2.以下函数中振幅为2,周期为π,初相为6π的函数为 ()A .y=2sin(2x+3π) B. y=2sin(2x+6π) C .y=2sin(21x+3π) D. y=2sin(21x+6π) 3.三角方程2sin(2π-x)=1的解集为 ( ) A .{x│x=2kπ+3π,k∈Z}B .{x│x=2kπ+35π,k∈Z}.C .{x│x=2kπ±3π,k∈Z}D .{x│x=kπ+(-1)K ,k∈Z}.4.假设函数f(x)=sin(ωx+ϕ)的图象〔局部〕如下图,那么ω,ϕ的取值是 ( )A .3,1πϕω==B.3,1πϕω-==C .6,21πϕω==D.6,21πϕω-==5.函数y=tan(2x+φ)的图象过点(0,12π),那么φ的值可以是 ( ) A. -6π B. 6π C.12π- D.12π6.设函数y=2sin(2x+Φ)的图象为C ,那么以下判断不正确的选项是〔 〕A .过点(,2)3π的C 唯一 B.过点(,0)6π-的C 不唯一C .C 在长度为2π的闭区间上至多有2个最高点D .C 在长度为π的闭区间上一定有一个最高点,一个最低点 7.方程)4cos(lg π-=x x 的解的个数为〔 〕A .0B .无数个C .不超过3D .大于38.假设函数y=f(x)的图像上每点的纵坐标保持不变,横坐标伸长到原2倍,然后再将整个图像沿x 轴向左平移2π个单位,沿y 轴向下平移1个单位,得到函数1sin 2y x =的图像,那么y=f(x)是 ( )A .1sin(2)122y x π=++B.1sin(2)122y x π=-+ C .1sin(2)124y x π=-+ D.11sin()1224y x π=++9.()sin()2f x x π=+,()cos()2g x x π=-,那么f(x)的图像 ( )A .与g(x)的图像一样 B.与g(x)的图像关于y 轴对称C .向左平移2π个单位,得g(x)的图像 D.向右平移2π个单位,得g(x)的图像 10.函数f(x)=sin(2x+2π)图像中一条对称轴方程不可能为( )A.x=4πB. x=2πC. x=πD. x=23π11.函数y=2与y=2sinx ,x ∈3[,]22ππ-所围成的图形的面积为 ( ) A .πB.2πC.3πD.4π12.设y=f(t)是某港口水的深度y 〔米〕关于时间t 〔时〕的函数,其中240≤≤t .下表是该港口某一天从0时至24时记录的时间t 与水深y 的关系:经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asina(ωt+ϕ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )A.]24,0[,6sin312∈+=t t y πB.]24,0[),6sin(312∈++=t t y ππC.]24,0[,12sin 312∈+=t t y πD.]24,0[),212sin(312t t y ππ++=二.填空题 13.函数y=5sin(3x −2π)的频率是______________。
三角函数的图象与性质经典例题含答案

1、(1)(2008浙江卷5)在同一平面直角坐标系中,函数 的图象和直线 的交点个数是(D)
(A)0(B)1(C)2(D)4
(2)、函数 单调增区间是(A)
A[2kπ- ,2kπ+ ](k∈Z)B.[2kπ+ ,2kπ+ ](k∈Z)
C.[2kπ-π,2kπ](k∈Z)D.[2kπ,2kπ+π](k∈Z)
2.(1)已知f(x)的定义域为[0,1],则f(cosx)的定义域是[2kπ- ,2kπ+ ]
(2)函数y=|sin(2x+ )|的最小正周期是
三.典例解析
例1、求函数)y= sin( - )的单调递增区间:
例2、(2008北京卷).已知函数 ( )的最小正周期为 .
(Ⅰ)求 的值;(Ⅱ)求函数 在区间 上的取值范围.
8、(2008湖南卷)函数 在区间 上的最大值是(C)
A.1B. C. D.1+
9、函数y= 的最大值是(B)
A. -1B. +1C.1- D.-1-
10、(2001上海春)关于x的函数f(x)=sin(x+ )有以下命题:
①对任意的 ,f(x)都是非奇非偶函数;
②不存在 ,使f(x)既是奇函数,又是偶函数;
①图象 关于直线 对称;②图象 关于点 对称;
③函数 在区间 内是增函数;
④由 的图角向右平移 个单位长度可以得到图象 .
6.函数 的图象向右平移 ( )个单位,得到的图象关于直线 对称,则 的最小值全国卷II)函数y=sin2xcos2x的最小正周期是(D)
(A)2π(B)4π(C)(D)
化简完是
三角函数的图象与性质
一.要点精讲
1.正弦函数、余弦函数、正切函数的图像
高三数学三角函数的图象与性质试题答案及解析

高三数学三角函数的图象与性质试题答案及解析1.将函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象关于对称,则ω的最小值是( )A.6B.C.D.【答案】D【解析】将f(x)=sinωx的图象向左平移个单位,所得图象关于x=,说明原图象关于x=-对称,于是f(-)=sin(-)=±1,故(k∈Z),ω=3k+(k∈Z),由于ω>0,故当k=0时取得最小值.选D考点:三角函数的图象与性质2.已知函数的最大值是2,且.(1)求的值;(2)已知锐角的三个内角分别为,,,若,求的值.【答案】(1);(2)【解析】(1)先由辅助角公式将化为一个的三角函数,利用最大值为2求出A,再利用列出关于的方程,解出的值;(2)由(1)可得的解析式,由可求得和,再由同角三角函数基本关系式求出,将2C代入将用C表示出来,利用三角形内角和定理及诱导公式,将化为A,B的函数,再利用两角和与差的三角公式,化为A,B的三角函数,即可求出.试题解析:(1)∵函数的最大值是2,,∴ 2分∵又∵,∴ 4分(2)由(1)可知 6分,∴ 8分∵∴, 10分∴12分考点: 辅助角公式;三角函数图像与性质;诱导公式;两角和与差的三角公式;运算求解能力3.函数的部分图象如图所示,则的值分别是()A.B.C.D.【答案】A【解析】由图知在时取到最大值,且最小正周期满足,故,,∴,∵,∴,∴,∴,∴.【考点】由三角函数图象确定函数解析式.4.设则A.B.C.D.【答案】C.【解析】故选C.【考点】1.三角函数基本关系式(商关系);2. 三角函数的单调性.5.设函数.(1)求函数f(x)的最大值和最小正周期。
(2)设A、B、C为⊿ABC的三个内角,若,,且C为锐角,求.【答案】(1);(2)【解析】(1)利用领个角的和的余弦公式、二倍角化简整理得,由可求得函数的最大值,根据求出函数的最小正周期;(2)将代入,再利用倍角公式求得,从而得到角,由,根据,求得,由结合诱导公式、两个角的和的正弦公式求出结论.(1).∴当,即(k∈Z)时,,(4分)f(x)的最小正周期,故函数f(x)的最大值为,最小正周期为π.(6分)(2)由,即,解得.又C为锐角,∴.(8分)∵,∴.∴.(12分)【考点】三角函数的和差公式、二倍角公式.6.(12分)(2011•广东)已知函数f(x)=2sin(x﹣),x∈R.(1)求f(0)的值;(2)设α,β∈,f(3)=,f(3β+)=.求sin(α+β)的值.【答案】(1)﹣1(2)【解析】(1)把x=0代入函数解析式求解.(2)根据题意可分别求得sinα和sinβ的值,进而利用同角三角函数基本关系求得cosα和cosβ的值,最后利用正弦的两角和公式求得答案.解:(1)f(0)=2sin(﹣)=﹣1(2)f(3)=2sinα=,f(3β+)=2sinβ=.∴sinα=,sinβ=∵α,β∈,∴cosα==,cosβ==∴sin(α+β)=sinαcosβ+cosαsinβ=点评:本题主要考查了两角和与差的正弦函数.考查了对三角函数基础公式的熟练记忆.7.已知命题:函数是最小正周期为的周期函数,命题:函数在上单调递减,则下列命题为真命题的是()A.B.C.D.【答案】D【解析】函数的最小正周期为,故命题为真命题;结合正切函数图象可知,正切函数在区间上是增函数,因此函数在区间上是增函数,故命题为假命题,因此命题、、为假命题,为真命题,故选D.【考点】1.三角函数的基本性质;2.复合命题8.(2013•湖北)将函数的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是()A.B.C.D.【答案】B【解析】y=cosx+sinx=2(cosx+sinx)=2sin(x+),∴图象向左平移m(m>0)个单位长度得到y=2sin[(x+m)+]=2sin(x+m+),∵所得的图象关于y轴对称,∴m+=kπ+(k∈Z),则m的最小值为.故选B9.已知函数,.(1)求函数的最小正周期;(2)若函数有零点,求实数的取值范围.【答案】(1);(2)实数的取值范围是.【解析】(1)求函数的最小正周期,需对函数化简,把它化为一个角的一个三角函数,利用来求,因此本题的关键是化简,由形式,需对三角函数降次,因此利用二倍角公式将函数化为,由,即可得,即可求出周期;(2)若函数有零点,即,有解,移项得,因此,方程有解,只要在函数的值域范围即可,因此只需求出即可.(1) 4分6分∴周期 7分(2)令,即, 8分则, 9分因为, 11分所以, 12分所以,若有零点,则实数的取值范围是. 13分【考点】三角恒等变化,三角函数的周期,值域.10.已知向量,设函数.(1)求f(x)的最小正周期;(2)求f(x)在[0,]上的最大值和最小值.【答案】(1)π(2)最大值是1,最小值是-【解析】(1)f(x)=a·b=(cosx,-)·(sinx,cos2x)=cosxsinx-cos2x=sin2x-cos2x=sin(2x-)f(x)的最小正周期为T=π,(2)∵0≤x≤,∴-≤2x-≤.由正弦函数的性质知,sin(2x-)∈[-,1]当2x-=,即x=时,f(x)取得最大值1.当2x-=-,即x=0时,f(0)=-,因此, f(x)在[0,]上的最大值是1,最小值是-.11.已知函数f(x)=(2cos2x-1)sin2x+cos4x(1)求f(x)的最小正周期及最大值。
高考数学:三角函数的图像和性质问题(解析版)

【高考地位】近几年高考降低了对三角变换的考查要求,而加强了对三角函数的图象与性质的考查,因为函数的性质是研究函数的一个重要内容,是学习高等数学和应用技术学科的基础,又是解决生产实际问题的工具,因此三角函数的性质是高考的重点和难点。
要充分运用数形结合的思想,把图象与性质结合起来,同时也要能利用函数的性质来描绘函数的图象,这样既有利于掌握函数的图象与性质,又能熟练地运用数形结合的思想方法。
在高考各种题型均有出现如选择题、填空题和解答题,其试题难度属中档题.【方法点评】类型一求三角函数的单调区间使用情景:一般三角函数类型解题模板:第一步先将函数式化为基本三角函数的标准式,要特别注意参数A, 的正负;第二步利用三角函数的辅助角公式一般将其化为同名函数,且在同一单调区间;第三步运用三角函数的图像与性质确定其单调区间.例1 函数cos( 2 )y x 的单调递增区间是()4A.[k π+,kπ+8 58π] B .[k π-38π,kπ+8]C.[2k π+,2kπ+8 58π] D .[2k π-38π,2kπ+8] (以上k∈Z)【答案】 B.考点:三角函数单调性.【点评】本题解题的关键是将 2x作为一个整体,利用余弦函数的图像将函数y cos( 2x)的单调44递增区间转化为2x 在区间2k ,2k 上递减的.4【变式演练1】已知函数 f (x) sin( 2 x )( 0), 直线x x1,x x2 是y f (x) 图像的任意两条对称6轴,且x1 x 的最小值为2 2.求函数 f (x) 的单调增区间;【答案】[ k , k ], k Z .3 6【解析】试题分析:根据两条对称轴之间的最小距离求周期,根据周期求,根据公式求此函数的单调递增区间.试题解析:由题意得T , 则1, f (x) sin(2 x ). 由2k 2x 2k , 解得6 2 6 23 k , Z. 故 f ( x) 的单调增区间是k k ], k Z x k k [ .,6 3 6考点:1.y A sin x 的单调性;【变式演练2】已知函数sin( )+ ( 0 0 )f x A x B A ,,的一系列对应值如下表:2x6 3 5643116 [73176y 2 4 2 4 (1)根据表格提供的数据求函数 f x 的解析式;(2)求函数 f x 的单调递增区间和对称中心;【答案】(1) f x 3sin x 1(2)352k ,2k (k Z)(k + ,1)(k Z).6 6 3(2)当2 2 ( )k x k k Z,即2 3 25x k ,k k Z时,函数f x 单调递2 2 ( )6 6增.令= ( x k k Z),所以函数 f x 的对称中心为+ 1 ( x k k Z),得= + ( k k Z)(,).3 33考点:1.三角函数解析式及基本性质;2.数形结合法[ 来源:Z*xx*]类型二由y A sin( x ) 的图象求其函数式使用情景:一般函数y A s in( x ) 求其函数式解题模板:第一步观察所给的图像及其图像特征如振幅、周期、与x轴交点坐标等;第二步利用特殊点代入函数解析式计算得出参数A, , 中一个或两个或三个;第三步要从图象的升降情况找准第一个零点的位置,并进一步地确定参数;第四步得出结论.例2 已知函数y A sin( x ) y A s in( x )( 0, , x R) 的图象如图所示,则该函数的2解析式是()(A)y 4 sin( x ) (B)y 4 s in( x )8 4 8 4(C)y 4 s in( x ) (D)y 4 sin( x )8 4 8 4【答案】 D考点:y Asin x 的图像【点评】本题的解题步骤是:首先根据已知图像与x轴的交点坐标可得其周期为T ,进而可得的大小;然后观察图像知其振幅 A 的大小;最后将图像与x 轴的交点坐标代入函数的解析式即可得到的大小.【变式演练3】已知函数 f x A sin x (其中 A 0, 0, )的部分图象如图所示,则f x2的解析式为()6A.2sinf x x B.f x2sin2x36C.2sin2f x x D.f x2sin4x6【答案】B【解析】考点:由y A s in(x)的部分图像确定解析式。
三角函数图像与性质练习题及答案

三角函数图像与性质练习题及答案(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--三角函数的图像与性质练习题一 选择题1.把函数=sin y x 的图像上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图像向左平移4π个单位,这时对应于这个图像的解析式是( )A .cos 2y x =B .sin 2y x =-C .sin(2)4y x π=-D .sin(2)4y x π=+2.函数cos(4)3y x π=+图象的两条相邻对称轴间的距离为( )A .π8B .π4C .π2D .π3.函数21cos ()xf x -=( )A .在ππ(,)22-上递增B .在π(,0]2-上递增,在π(0,)2上递减C .在ππ(,)22-上递减D .在π(,0]2-上递减,在π(0,)2上递增4.下列四个函数中,最小正周期为π,且图象关于直线12x π=对称的是( )A .sin()23xy π=+B .sin()23x y π=- C .sin(2)3y x π=+D .sin(2)3y x π=-5.函数231sin 232y x x =+的最小正周期等于( )A .πB .2πC .4πD .4π6.“φ=π”是“曲线y=sin(2x +φ)过坐标原点的”( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件xy O π2π 1-1 7.函数2sin()y x ωϕ=+在一个周期内的图象如图所示,则此函数的解析式可能是( )A .2sin(2)4y x π=-B .2sin(2)4y x π=+C .32sin()8y x π=+D .72sin()216x y π=+ 8.(北京市东城区普通校2013届高三3月联考数学(理)试题 )已知函数sin()y A x ωϕ=+的图象如图所示,则该函数的解析式可能..是 ( ) 第6题图( )A .41sin(2)55y x =+B .31sin(2)25y x =+C .441sin()555y x =-D .441sin()555y x =+9.(2013·湖北)将函数y =3cos x +sin x (x ∈R ) 的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )10.函数y =sin 2x +sin x -1的值域为 ( ) A .[-1,1]B .[-54,-1]C .[-54,1]D .[-1,54]11.已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b 的值为( ) A .-1B .3C .-1或3D .-3二 填空题12.函数y =lg sin 2x +9-x 2的定义域为________________.13.已知函数π()sin(2)6f x x =+,其中π[,]6x a ∈-.当3a π=时,()f x 的值域是______;若()f x 的值域是1[,1]2-,则a 的取值范围是______.14.定义一种运算,令,且,则函数的最大值是______15.(北京北师特学校203届高三第二次月考理科数学)把函数x y 2sin =的图象沿 x 轴向左平移6π个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数)(x f y =图象,对于函数)(x f y =有以下四个判断: ①该函数的解析式为)6sin(2x 2y π+=; ②该函数图象关于点)0,3(π对称; ③该函数在]6,0[π上是增函数;④函数a x f y +=)(在]2,0[π上的最小值为3,则32=a .其中,正确判断的序号是________________________16.设函数f (x )=3sin(π2x +π4),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________. 三 解答题17. 已知函数2()cos cos f x x x x a =++.(Ⅰ)求()f x 的最小正周期及单调递减区间;(Ⅱ)若()f x 在区间[,]63ππ-上的最大值与最小值的和为32,求a 的值.18. 已知函数()()0,,sin 2162cos 62cos 2>∈-+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛-=ωωπωπωR x x x x x f 的最小正周期为π. (I)求ω的值;(II)求函数()x f 在区间⎥⎦⎤⎢⎣⎡-3,4ππ上的最大值和最小值.19. 已知函数,2cos 26sin 6sin )(2x x x x f ωπωπω-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+= 其中 R x ∈,0>ω.(1)求函数)(x f 的值域;(2)若函数)(x f 的图象与直线1-=y 的两个相邻交点间的距离为2π,求函数)(x f 的单调增区间. 20. 已知函数()()21cos 22sin sin cos 3+-=x x x x x f .(I)求⎪⎭⎫⎝⎛3πf 的值; (II)求函数()x f 的最小正周期及单调递减区间. 21. 已知向量()()3cos ,0,0,sin a x b x ==,记函数()()23sin 2f x a b x =++.求:(I)函数()f x 的最小值及取得小值时x 的集合; (II)函数()f x 的单调递增区间.22. 函数()sin()(0,0,||)2f x A x A ωϕωϕπ=+>><部分图象如图所示.(Ⅰ)求函数()f x 的解析式,并写出其单调递增区间;(Ⅱ)设函数()()2cos 2g x f x x =+,求函数()g x 在区间[,]64ππ-上的最大值和最小值. 答案1. A 【解析】把函数=sin y x 的图像上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,得到=sin 2y x 的图象,再把图像向左平移4π个单位,得到=sin 2()sin(2)cos 242y x x x ππ+=+=,所以选A.4 C32π6πo2x2-y5. A【解析】11cos 2=sin 2222x y x +-1=sin 2cos 2sin(2)223x x x π+=+,所以函数的周期222T πππω===,选A. 6. A ϕπ=时,sin(2)sin 2y x x π=+=-,过原点,便是函数过原点的时候ϕ可以取其他值,故选A 答案.7. 【答案】B解:由图象可知52882T πππ=-=,所以函数的周期T π=,又2T ππω==,所以2ω=。
专题五 三角函数的图像与性质(基础题型)含详解

专题五三角函数的图像与性质(基础题型)一.选择题(共14小题)1.若关于x的方程2sin(2x+)=m在[0,]上有两个不等实根,则m的取值范围是()A.(1,)B.[0,2]C.[1,2)D.[1,]2.三角函数y=sin 是()A.周期为4π的奇函数B.周期为的奇函数C.周期为π的偶函数D.周期为2π的偶函数3.函数y=sin(﹣2x)的单调递减区间是()A.[﹣kπ+,﹣kπ+],k∈Z B.[2kπ﹣,2kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ﹣,kπ+],k∈Z4.已知函数f(x)=sin(2x﹣)(x∈R)下列结论错误的是()A.函数f(x)的最小正周期为πB.函数f(x)是偶函数C.函数f(x)的图象关于直线x=对称D.函数f(x)在区间上是增函数5.已知函数f(x)=|sinx|,下列结论中错误的是()A.f(x)既偶函数,又是周期函数.B.f(x)的最大值为C.y=f(x)的图象关于直线x=对称D.y=f(x)的图象关于直线x=π对称6.函数的图象的对称轴方程为()A.B.C.D.7.y=cos(x+1)图象上相邻的最高点和最低点之间的距离是()A.B.πC.2D.8.方程cosx=lgx的实根的个数是()A.1B.2C.3D.无数9.函数y=sin(2x+)是()A.周期为π的奇函数B.周期为π的偶函数C.周期为的奇函数D.周期为的偶函数10.函数y=2tan(3x﹣)的一个对称中心是()A.(,0)B.(,0)C.(﹣,0)D.(﹣,0)11.函数f(x)=tan(2x﹣)的单调递增区间是()A.[﹣,+](k∈Z)B.(﹣,+)(k∈Z)C.(kπ+,kπ+)(k∈Z)D.[kπ﹣,kπ+](k∈Z)12.为了得到函数y=2sin(2x+)的图象,可以将函数y=2sin2x图象()A.向右平移个长度单位B.向左平移个长度单位C.向右平移个长度单位D.向左平移个长度单位13.将函数y=sin2x的图象向左平移个单位长度,所得图象的函数解析式为()A.y=sin(2x+)B.y=sin(2x﹣)C.y=sin(2x+)D.y=sin(2x﹣)14.为了得到函数的图象,只需把函数y=sin3x的图象()A.向左平移B.向左平移C.向右平移D.向右平移二.填空题(共6小题)15.函数y=3cos(2x+)的最小正周期为.16.在,则函数y=tanx的值域为.17.函数的最小正周期是.18.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象如图所示,则函数的解析式为f(x)=.19.函数f(x)=Asin(ω+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+…+f(2016)=.20.如图是的图象,则其解析式为.三.解答题(共4小题)21.求函数y=tan(x+)的定义域、周期和单调区间.22.已知函数f(x)=tan(x﹣).(1)求函数f(x)的定义域;(2)求函数f(x)的单调区间;(3)求函数f(x)的对称中心.23.已知函数f(x)=2sin(2x﹣)(x∈R).(1)求函数f(x)的最小正周期及单调递增区间;(2)当x∈[,]时,求f(x)的最大值和最小值.24.求下列函数的单调区间:(1)f(x)=sin(x+),x∈[0,π];(2)f(x)=|tanx|;(3)f(x)=cos(2x﹣),x∈[﹣,].专题五三角函数的图像与性质(基础题型)参考答案与试题解析一.选择题(共14小题)1.若关于x的方程2sin(2x+)=m在[0,]上有两个不等实根,则m的取值范围是()A.(1,)B.[0,2]C.[1,2)D.[1,]【分析】把方程2sin(2x+)=m化为sin(2x+)=,画出函数f(x)=sin (2x+)在x∈[0,]上的图象,结合图象求出方程有两个不等实根时m 的取值范围.【解答】解:方程2sin(2x+)=m可化为sin(2x+)=,当x∈[0,]时,2x+∈[,],画出函数y=f(x)=sin(2x+)在x∈[0,]上的图象如图所示;根据方程2sin(2x+)=m在[0,]上有两个不等实根,得≤<11≤m<2∴m的取值范围是[1,2).故选:C.【点评】本题主要考查方程根的存在性以及个数判断以及正弦函数的图象应用问题,体现了转化、数形结合的数学思想.2.三角函数y=sin是( )A .周期为4π的奇函数B .周期为的奇函数C .周期为π的偶函数D .周期为2π的偶函数【分析】由条件利用正弦函数的奇偶性和周期性,可得结论.【解答】解:三角函数y=sin是奇函数,它的周期为=4π,故选:A .【点评】本题主要考查正弦函数的奇偶性和周期性,属于基础题.3.函数y=sin (﹣2x )的单调递减区间是( )A .[﹣kπ+,﹣kπ+],k ∈ZB .[2kπ﹣,2kπ+],k ∈ZC .[kπ﹣,kπ+],k ∈ZD .[kπ﹣,kπ+],k ∈Z【分析】利用诱导公式可得本题即求函数y=sin (2x ﹣)的单调递增区间.令 2kπ﹣≤2x ﹣≤2kπ+,求得x 的范围,可得函数y=sin (﹣2x )的单调递减区间.【解答】解:函数y=sin (﹣2x )=﹣sin (2x ﹣)的单调递减区间,即函数y=sin (2x ﹣)的单调递增区间.令 2kπ﹣≤2x ﹣≤2kπ+,求得 kπ﹣≤x ≤kπ+,k ∈z ,故函数y=sin (2x ﹣)的单调递增区间,即函数y=sin (﹣2x )的单调递减区间为[kπ﹣,kπ+],k ∈Z ,故选:D.【点评】本题主要考查诱导公式、正弦函数的增区间,体现了转化的数学思想,属于基础题.4.已知函数f(x)=sin(2x﹣)(x∈R)下列结论错误的是()A.函数f(x)的最小正周期为πB.函数f(x)是偶函数C.函数f(x)的图象关于直线x=对称D.函数f(x)在区间上是增函数【分析】由条件利用诱导公式,余弦函数的周期性、奇偶性、单调性以及图象的对称性,判断各个选项是否正确,从而得出结论.【解答】解:函数f(x)=sin(2x﹣)=﹣cos2x,故它的最小正周期为π,故A满足条件;显然,它是偶函数,故B正确;当x=时,求得函数值y=0,不是最值,故f(x)的图象不关于直线x=对称,故C错误;在区间上,f(x)=﹣cos2x是增函数,故D正确,故选:C.【点评】本题主要考查诱导公式,余弦函数的图象和性质,属于基础题.5.已知函数f(x)=|sinx|,下列结论中错误的是()A.f(x)既偶函数,又是周期函数.B.f(x)的最大值为C.y=f(x)的图象关于直线x=对称D.y=f(x)的图象关于直线x=π对称【分析】由条件利用正弦函数的值域,可得结论.【解答】解:根据函数f (x )=|sinx |的最大值为1,可得B 不正确, 故选:B .【点评】本题主要考查正弦函数的值域,属于基础题. 6.函数的图象的对称轴方程为( )A .B .C .D .【分析】根据余弦函数的性质即可求解对称轴方程 【解答】解:函数,令,k ∈Z可得:πx=,即,k ∈Z .故选:C .【点评】本题考查了余弦函数的图象及性质,对称轴方程的求法.属于基础题.7.y=cos (x +1)图象上相邻的最高点和最低点之间的距离是( ) A .B .πC .2D .【分析】y=cos (x +1)的周期是2π,最大值为1,最小值为﹣1,即可求出y=cos (x +1)图象上相邻的最高点和最低点之间的距离.【解答】解:y=cos (x +1)的周期是2π,最大值为1,最小值为﹣1,∴y=cos (x +1)图象上相邻的最高点和最低点之间的距离是=,故选:A .【点评】本题考查了函数y=Acos (ωx +φ)的图象与性质的应用问题,是基础题.8.方程cosx=lgx的实根的个数是()A.1B.2C.3D.无数【分析】本题即求函数y=cosx的图象和y=lgx的图象的交点个数,数形结合可得结论.【解答】解:方程cosx=lgx的实根的个数,即函数y=cosx的图象和y=lgx的图象的交点个数,数形结合可得函数y=cosx的图象和y=lgx的图象的交点个数为3,故选:C.【点评】本题主要考查方程根的存在性以及个数判断,余弦函数、对数函数的图象特征,体现了转化、数形结合的数学思想,属于基础题.9.函数y=sin(2x+)是()A.周期为π的奇函数B.周期为π的偶函数C.周期为的奇函数D.周期为的偶函数【分析】由条件利用诱导公式以及余弦函数的周期性和奇偶性,可得结论.【解答】解:由于函数y=sin(2x+)=sin(2x+)=cos2x,故此函数是周期为=π的偶函数,故选:B.【点评】本题主要考查诱导公式以及余弦函数的周期性和奇偶性,属于基础题.10.函数y=2tan(3x﹣)的一个对称中心是()A.(,0)B.(,0)C.(﹣,0)D.(﹣,0)【分析】对称中心就是函数图象与x轴的交点或函数图象的渐近线和x轴的交点,令3x﹣=,k∈z,解得x=+,k∈z,故对称中心为(+,0 ),从而得到答案.【解答】解:∵函数y=2tan(3x﹣),令3x﹣=,k∈z,可得x=+,k∈z,故对称中心为(+,0 ),令k=﹣2,可得一个对称中心是(﹣,0),故选:C.【点评】本题考查正切函数的对称中心的求法,得到3x﹣=,k∈z 是解题的关键,属于基础题.11.函数f(x)=tan(2x﹣)的单调递增区间是()A.[﹣,+](k∈Z)B.(﹣,+)(k∈Z)C.(kπ+,kπ+)(k∈Z)D.[kπ﹣,kπ+](k∈Z)【分析】由正切函数的单调性的性质即可得到结论.【解答】解:由<2x﹣,即﹣<x<+,(k∈Z),故函数的单调性增区间为(﹣,+)(k∈Z),故选:B.【点评】本题主要考查正切函数的单调性的求解,利用正切函数的图象和性质是解决本题的关键.12.为了得到函数y=2sin(2x+)的图象,可以将函数y=2sin2x图象()A.向右平移个长度单位B.向左平移个长度单位C.向右平移个长度单位D.向左平移个长度单位【分析】根据三角函数的图象平移关系进行判断即可.【解答】解:由y=2sin(2x+)=2sin2(x+),可以将函数y=2sin2x图象向左平移个长度单位即可,故选:D.【点评】本题主要考查三角函数图象关系的判断,结合平移关系是解决本题的关键.13.将函数y=sin2x的图象向左平移个单位长度,所得图象的函数解析式为()A.y=sin(2x+)B.y=sin(2x﹣)C.y=sin(2x+)D.y=sin(2x﹣)【分析】直接利用函数图象的平移变换得答案.【解答】解:将函数y=sin2x的图象向左平移个单位长度,所得图象的函数解析式为y=sin2(x+)=sin(2x+).故选:A.【点评】本题考查y=Asin(ωx+φ)型函数图象的平移,是基础题.14.为了得到函数的图象,只需把函数y=sin3x的图象()A.向左平移B.向左平移C.向右平移D.向右平移【分析】由题意利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.【解答】解:把函数y=sin3x的图象向右平移个单位,可得函数的图象,故选:D.【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.二.填空题(共6小题)15.函数y=3cos(2x+)的最小正周期为π.【分析】根据余弦函数y=Acos(ωx+φ)的最小正周期为T=,求出即可.【解答】解:函数y=3cos(2x+)的最小正周期为T===π.故答案为:π.【点评】本题考查了余弦函数y=Acos(ωx+φ)的图象与性质的应用问题,是基础题目.16.在,则函数y=tanx的值域为[﹣1,1] .【分析】根据正切函数的图象与性质,求出x∈[﹣,]时函数y=tanx的值域即可.【解答】解:∵,∴﹣1≤tanx≤1,∴函数y=tanx的值域为[﹣1,1].故答案为:[﹣1,1].【点评】本题考查了正切函数的图象与性质的应用问题,是基础题目.17.函数的最小正周期是2.【分析】由已知中函数的解析为,我们可以求出对应ω值,代入T=,即可得到函数的最小正周期.【解答】解:∵函数∴ω=∴T==2故答案为:2【点评】本题考查的知识点是正切函数的周期性,其中根据函数的解析式求出ω值,是解答本题的关键,在解答过程中易将正切型函数的周期误认为而产生错解.18.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象如图所示,则函数的解析式为f(x)=.【分析】由题意求出A,T,利用周期公式求出ω,利用当x=时取得最大值3,求出φ,得到函数的解析式,即可.【解答】解:由题意可知A=3,T=2()=4π,ω==,当x=时取得最大值3,所以3=3sin(+φ),sin()=1,,∵,所以φ=,函数f(x)的解析式:f(x)=.故答案为:.【点评】本题是基础题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,注意函数的周期的求法,考查计算能力,常考题型.19.函数f(x)=Asin(ω+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+…+f(2016)=0.【分析】由函数的图象的顶点坐标求出A,由周期求出ω,可得函数的解析式,再利用利用正弦函数的周期性求得要求式子的值.【解答】解:由题意和图象可得A=2,T=6,则T=8,则ω=,∴f(0)+f(1)+f(2)+f(3)+…+f(8)=0,∴f(0)+f(1)+f(2)+f(3)+…+f(2016)=252×0=0,故答案为:0.【点评】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,利用正弦函数的周期性求函数的值,属于基础题.20.如图是的图象,则其解析式为.【分析】由图象可得A值,结合周期公式可得ω,代点可得φ值,可得解析式.【解答】解:由图象可得A=2,周期T=﹣(﹣)=2π,由周期公式可得ω=1,∴y=2sin(x+φ),代点(﹣,0)可得0=2sin(﹣+φ),结合0<φ<可得φ=故答案为:【点评】本题考查正弦函数的图象和性质,属基础题.三.解答题(共4小题)21.求函数y=tan(x+)的定义域、周期和单调区间.【分析】利用正切函数的定义域,求出函数的定义域,通过正切函数的周期公式求出周期,结合正切函数的单调增区间求出函数的单调增区间.【解答】解:由,解得.∴定义域.周期函数,周期.由,解得∴函数的单调递增区间为.【点评】本题是基础题,考查正切函数的基本知识,单调性、周期性、定义域,考查计算能力.22.已知函数f(x)=tan(x﹣).(1)求函数f(x)的定义域;(2)求函数f(x)的单调区间;(3)求函数f(x)的对称中心.【分析】(1)由题意利用正切函数的定义域可得x﹣≠kπ+,求得x的范围,可得函数的定义域.(2)根据题意利用正切函数的单调则区间可得kπ﹣<x﹣<kπ+,由此求得x的范围,得到f(x)的增区间.(3)利用正切函数的图象的对称性,求得函数f(x)的对称中心.【解答】解:(1)对于函数f(x)=tan(x﹣),令x﹣≠kπ+,求得x≠kπ+,k∈Z,故函数的定义域为{x|x≠kπ+,k∈Z}.(2)令kπ﹣<x﹣<kπ+,求得π﹣<x<kπ+,可得函数的增区间为(π﹣,kπ+),k∈Z.(3)令x﹣≠,求得x≠+,k∈Z,故函数的对称中心为(+,0),k∈Z.【点评】本题主要考查正切函数的定义域、单调区间、以及图象的对称性,属于基础题.23.已知函数f(x)=2sin(2x﹣)(x∈R).(1)求函数f(x)的最小正周期及单调递增区间;(2)当x∈[,]时,求f(x)的最大值和最小值.【分析】(1)根据正弦型函数求出f(x)的最小正周期和单调递增区间;(2)求出x∈[,]时2sin(2x﹣)的取值范围,即得f(x)的最大、最小值.【解答】解:(1)函数f(x)=2sin(2x﹣),∴函数f(x)的最小正周期为T==π;令2kπ﹣≤2x﹣≤2kπ+,k∈Z;解得kπ﹣≤x≤kπ+,k∈Z;∴f(x)单调递增区间是[kπ﹣,kπ+],k∈Z;(2)当x∈[,]时,2x﹣∈[,],∴sin(2x﹣)∈[﹣,1],∴2sin(2x﹣)∈[﹣,2],∴f(x)的最大值是2,最小值是﹣.【点评】本题考查了正弦型函数的图象与性质的应用问题,是基础题.24.求下列函数的单调区间:(1)f(x)=sin(x+),x∈[0,π];(2)f(x)=|tanx|;(3)f(x)=cos(2x﹣),x∈[﹣,].【分析】(1)直接利用整体思想求出正弦型函数的单调区间.(2)直接利用整体思想求出正切型函数的单调区间.(3)直接利用整体思想求出余弦型函数的单调区间.【解答】解:(1)f(x)=sin(x+),x∈[0,π];令:(k∈Z),解得:(k∈Z),由于:x∈[0,π];则:函数的递增区间为:[0,]令:(k∈Z),解得:(k∈Z),由于:x∈[0,π];则:函数的递减区间为:[](2)f(x)=|tanx|;由于y=tanx的单调增区间为:(k∈Z),所以:函数的单调增区间为:(k)(k∈Z),函数的单调减区间为:(k∈Z),(3)f(x)=cos(2x﹣),x∈[﹣,].令:,(k∈Z),解得:,(k∈Z),当k=0时,函数的单调增区间为:[].令:,(k∈Z),解得:,(k∈Z),故函数的单调减区间为:[﹣,﹣]和[].【点评】本题考查的知识要点:三角函数的性质单调性的应用.。
三角函数的图像与性质-拔高难度-习题

三角函数的图像与性质一、选择题(共12小题;共60分)1. 有下列说法:①作正弦函数的图象时,单位圆的半径长与 []_________________的图象关于点对称;③的图象关于直线成轴对称;④正弦函数()__________________ᗒ_ᗔ_ᗘ_ᡄ_ᡄ_ᡄ_ᡄ_ᡄA. B. C. D.2. 已知函数,则下列结论正确的是A. 的最小正周期是B. 在上单调递增C. 的图象关于对称D. 的图象关于点对称3. 已知函数,则下列结论中,正确的是A. 是奇函数B. 不是周期函数C. 定义域是D. 值域是4. 若函数在区间上单调递增,在区间上单调递减,则A. B. C. D.5. 已知函数,下面结论错误的是A. 函数的最小正周期为B. 函数在区间上是增函数C. 函数的图象关于直线对称D. 函数是奇函数6. 如图所示,对单摆施加一个作用力后单摆从某点开始来回摆动,离开平衡位置(/)_D_Dd__________-ðϨϨ____,单摆摆动时从最右边到最左边的距离为A. 厘米B. 厘米C. 厘米D. 厘米7. 函数)的图象是A. B.C. D.8. 已知和是函数的图象的两条相邻的对称轴,则A. B. C. D.9. 函数 (/内的图象是A. B.C. D.10. 已知函数,其部分图象如图所示,点(/)√D_,, ()的解析式可以是A. B.C. D.11. 函数在一个周期内的图象是A. B.C. D.12. 设,且,下列不等式中成立的是①;②;③;④.A. ①②B. ③④C. ①④D. ②③二、填空题(共5小题;共25分)13. 如果函数是定义在上的偶函数,其在上的图象如图所示,那么不等式D_Dd__________ĬĝϨϨ_14. 锐角三角形的内角分别是 D_Dd___①②③15. 已知,,的值为.16. 已知函数,则下面结论错误的是.(填序号)①函数的最小正周期为②函数在区间上是增函数;③函数的图象关于直线 (④函数是奇函数.17. 函数的最大值为,最小值为.三、解答题(共5小题;共65分)18. 求下列函数的最小正周期:(1);(2).19. 已知函数(1)当 ()D_的单调递减区间;(2)当时,在上的值域为,求20. 若的图象的一个对称中心为且,求 D21. 在锐角三角形 (){22. 已知函数(1)画出的图象,并写出其单调区间、最大值、最小值.(2)判断是否为周期函数,如果是,求出最小正周期.答案第一部分1. D 【解析】由正弦函数图象可明确判断出①②③④均正确.2. D3. D 【解析】因为,且在上是减函数,在上是增函数,所以函数的值域为.4. C 【解析】因为当时,函数是增函数,当时,函数为减函数,即当时,函数为增函数,当时,函数为减函数,所以,所以.5. D6. A 【解析】因为,所以,从最左边到平衡位置需要的时间为秒.由得从最右边到最左边的距离为厘米.7. D 【解析】利用排除法.由于时,无意义,故排除A,B,又因为时,有,,所以排除C.8. A 【解析】因为直线和是函数的图象的相邻的两条对称轴,所以,即,,又,所以,所以,因为直线是函数图象的对称轴,所以,所以,因为,所以,检验知此时直线也为函数图象的对称轴.9. D10. A【解析】由已知可得,设其周期为,则:,,,由于,可得:,可得:,整理可得:,解得:,,由于,可得:,所以,,,解得:,,所以,当时,,函数的解析式是.11. A 【解析】由,知,所以的周期为,排除B,D.令,得,所以,若,则,即图象过点.12. B 【解析】设点,点,由于函数的图象在上是上凸型的,而表示线段中点的纵坐标,故有,故①不正确;由于函数的图象在上是上凸型的,表示线段中点的纵坐标,故有,故②不正确;由于函数的图象在上是上凹型的,表示线段中点的纵坐标,故有,故③正确;由于函数的图象在上是上凹型的,故有,故④正确.第二部分13.【解析】当时,当时.由的图象知在上.因为为偶函数,也是偶函数,所以为偶函数,所以的解集为.14. ①②③【解析】故①成立.函数在区间上是减函数.因为所以,故②成立.在锐角三角形中,因为,所以,则有,即,同理,故③成立.15.【解析】构造函数,则在上是奇函数,由已知,,得,即.因为在上单调递增,且,所以,所以.16. ④【解析】因为,所以,故①正确;因为在上是减函数,则在上是增函数,故②正确;由图象知的图象关于直线对称,故③正确;为偶函数,故④不正确.17. ,【解析】由题知,而,所以函数的最大值为,最小值为.素材来源于网络,林老师编辑整理第三部分18. (1)因为,即,所以所求函数的最小正周期是.另解:.(2)因为,所以所求函数的最小正周期是.另解.19. (1)当时,.因为的单调递减区间为,所以当.即时,是减函数,所以的单调递减区间是.(2),因为,所以,所以.又因为,所以,所以.因为的值域是,所以,且,解得,.20. 因为的对称中心为,所以,把代入,得,又因为,所以当时,;当时,,所以或.21. 因为为锐角三角形,所以,所以,因为在上是增函数,所以,同理可得,,所以.22. (1)图中实线为的图象.由图可知,函数的单调递增区间为,,单调递减区间为,,,.(2)由(1)知为周期函数,最小正周期.。
三角函数的图像与性质专项训练(解析版)

三角函数的图像与性质专项训练一、单选题1.(23-24高一上·浙江宁波·期末)为了得到πsin 53y x ⎛⎫=+ ⎪⎝⎭的图象,只要将函数sin 5y x =的图象()A .向左平移π15个单位长度B .向右平移π15个单位长度C .向右平移π3个单位长度D .向左平移π3个单位长度2.(23-24高一上·浙江丽水·期末)已知函数()()2sin f x x ωϕ=+的图象向左平移π6个单位长度后得到函数π2sin 23y x ⎛⎫=+ ⎪⎝⎭的图象,则ϕ的一个可能值是()A .0B .π12C .π6D .π33.(23-24高一下·浙江杭州·期末)为了得到函数()sin2f x x =的图象,可以把()cos2g x x =的图象()A .向左平移π2个单位长度B .向右平移π2个单位长度C .向左平移π4个单位长度D .向右平移π4个单位长度4.(23-24高一上·浙江宁波·期末)已知函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭.若π8f x ⎛⎫- ⎪⎝⎭为奇函数,π8f x ⎛⎫+ ⎪⎝⎭为偶函数,且()f x 在π0,6⎛⎫⎪⎝⎭上没有最小值,则ω的最大值是()A .2B .6C .10D .145.(23-24高一上·浙江湖州·期末)我们知道,每一个音都是由纯音合成的,纯音的数学模型是sin y A x ω=.已知某音是由3个不同的纯音合成,其函数为()11sin sin 2sin 323f x x x x =++,则()A .π3f ⎛⎫=⎪⎝⎭B .()f x 的最大值为116C .()f x 的最小正周期为2π3D .()f x 在π0,6⎛⎫⎪上是增函数6.(23-24高一上·浙江杭州·期末)已知函数()*2sin 6f x x ωω⎛⎫=+∈ ⎪⎝⎭N 有一条对称轴为23x =,当ω取最小值时,关于x 的方程()f x a =在区间,63ππ⎡⎤-⎢⎥⎣⎦上恰有两个不相等的实根,则实数a 的取值范围是()A .(2,1)--B .[1,1)-6⎣7.(23-24高一下·浙江丽水·期末)已知函数1()2sin(32f x x x π=ω-ω>∈,R),若()f x 的图象的任意一条对称轴与x 轴交点的横坐标均不属于区间(3π,4π),则ω的取值范围是()A .1287(,[]2396B .1171729(,][,]2241824C .52811[,][,]93912D .11171723[,][]182418248.(23-24高一下·浙江杭州·期末)已知函数()()sin ,0f x x ωω=>,将()f x 图象上所有点向左平移π6个单位长度得到函数()y g x =的图象,若函数()g x 在区间π0,6⎡⎤⎢⎥⎣⎦上单调递增,则ω的取值范围为()A .(]0,4B .(]0,2C .30,2⎛⎤⎥⎝⎦D .(]0,1【答案】C【详解】因为函数()()sin ,0f x x ωω=>,二、多选题9.(23-24高一上·浙江台州·期末)已知函数()ππsin cos sin cos 44f x x x x x ⎛⎫⎛⎫=+++ ⎪ ⎝⎭⎝⎭,则()A .函数()f x 的最小正周期为2πB .点π,08⎛⎫- ⎪⎝⎭是函数()f x 图象的一个对称中心C .函数()f x 在区间π5π,88⎡⎤⎢⎥上单调递减D .函数()f x 的最大值为110.(23-24高一上·浙江湖州·期末)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,现有一个筒车按逆时针方向匀速转动.每分钟转动5圈,如图,将该筒车抽象为圆O ,筒车上的盛水桶抽象为圆O 上的点P ,已知圆O 的半径为4m ,圆心O 距离水面2m ,且当圆O 上点P 从水中浮现时(图中点0P )开始计算时间,点P 的高度()h t 随时间t (单位秒)变化时满足函数模型()()sin h t A t b ωϕ=++,则下列说法正确的是()A .函数()h t 的初相为π6B .1秒时,函数()h t 的相位为0故选:BC .11.(23-24高一上·浙江丽水·期末)已知函数π()tan(2)6f x x =-,则()A .()f x 的最小正周期是π2B .()f x 的定义域是π{|π,Z}3x x k k ≠+∈C .()f x 的图象关于点π(,0)12对称D .()f x 在ππ(,)32上单调递增三、填空题12.(23-24高一上·浙江金华·期末)函数()π2π200cos 30063f n n ⎛⎫=++ ⎪⎝⎭({}1,2,3,,12n ∈⋅⋅⋅为月份),近似表示某地每年各个月份从事旅游服务工作的人数,游客流量越大所需服务工作的人数越多,则可以推断,当n =时,游客流量最大.13.(23-24高一上·浙江湖州·期末)已知()3sin 4f x x ϕ⎛⎫=+ ⎪⎝⎭,其中0,2ϕ⎛⎫∈ ⎪⎝⎭,且ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,若函数()f x 在区间2π,3θ⎛⎫⎪上有且只有三个零点,则θ的范围为.14.(23-24高一上·浙江温州·期末)已知函数()π2sin (0)6f x x ωω⎛⎫=+> ⎪⎝⎭,对x ∀∈R 都有()π3f x f ⎛⎫⎪⎝⎭≤,且在,163⎛⎫ ⎪⎝⎭上单调,则ω的取值集合为四、解答题15.(23-24高一下·浙江丽水·期末)已知函数22()sin2f x x x x =.(1)求函数()f x 的最小正周期及单调递减区间;(2)将函数()f x 的图象上每个点的纵坐标缩短到原来的12,横坐标也缩短到原来的12,得到函数()g x 的图象,若函数()y g x m =-在区间π0,4⎡⎤⎢⎥内有两个零点,求实数m 的取值范围.16.(23-24高一下·浙江衢州·期末)已知函数()cos2f x x x =+.(1)求函数()f x 的最小正周期和对称中心;(2)求函数()f x 在π0,2⎡⎤⎢⎥上的值域.17.(23-24高一上·浙江杭州·期末)已知函数22()sin 2sin cos 3cos ,R f x x x x x x =++∈.求:(1)函数()f x 的最小值及取得最小值的自变量x 的集合;(2)函数()f x 的单调增区间.18.(23-24高一下·浙江杭州·期末)已知实数0a <,设函数22()cos sin2f x x a x a =+-,且()64f =-.(1)求实数a ,并写出()f x 的单调递减区间;(2)若0x 为函数()f x 的一个零点,求0cos2x .19.(23-24高一上·浙江嘉兴·期末)已知函数()24cos 2f x x x a x =--.(1)若1a =-,求函数()f x 在[]0,2上的值域;(2)若关于x 的方程()4f x a =-恰有三个不等实根123,,x x x ,且123x x x <<,求()()131278f x f x x --的最大值,并求出此时实数a 的值.,。
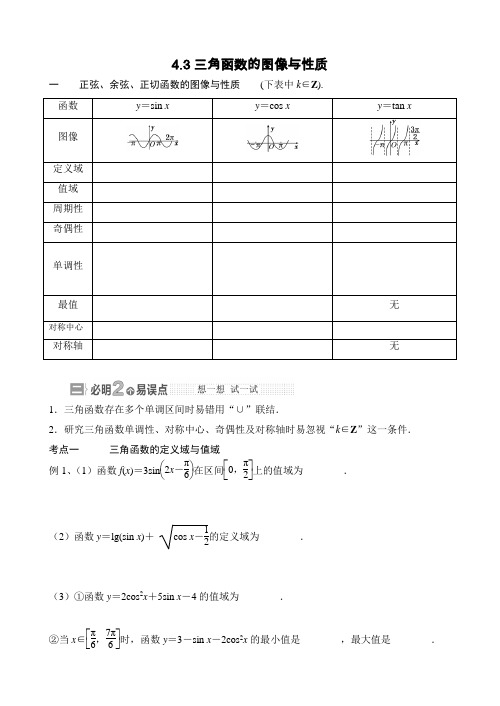
三角函数的图像和性质 测试题及解析

三角函数的图象与性质函数y =A sin(ωx +φ)的图象(时间:80分钟 满分:100分)一、选择题(每小题5分,共40分) 1.函数y =sin ⎝ ⎛⎭⎪⎫4x +32π的周期是( ). A .2π B .π C.π2 D .π4 解析 T =2π4=π2. 答案 C2.函数y =cos ⎝ ⎛⎭⎪⎫x +π2(x ∈R )是( ).A .奇函数B .偶函数C .非奇非偶函数D .无法确定 解析 ∵y =cos ⎝ ⎛⎭⎪⎫x +π2=-sin x ,∴此函数为奇函数.答案 A3.函数y =cos x 图象上各点的纵坐标不变,把横坐标变为原来的2倍,得到图象的解析式为y =cos ωx ,则ω的值为( ).A .2B .12C .4D .14解析 由已知y =cos x 的图象经变换后得到y =cos 12x 的图象,所以ω=12. 答案 B4.函数y =-x sin x 的部分图象是( ).解析 考虑函数的奇偶性并取特殊值.函数y =-x sin x 是偶函数,当x ∈⎝ ⎛⎭⎪⎫0,π2时,y <0. 答案 C5.在下列区间上函数y =sin ⎝ ⎛⎭⎪⎫x +π4为增函数的是( ).A.⎣⎢⎡⎦⎥⎤-π2,π2 B .⎣⎢⎡⎦⎥⎤-3π4,π4 C .[-π,0] D .⎣⎢⎡⎦⎥⎤-π4,3π4 解析 由2k π-π2≤x +π4≤2k π+π2(k ∈Z )得2k π-3π4≤x ≤2k π+π4(k ∈Z ),当k =0时,-3π4≤x ≤π4,故选B. 答案 B6.已知简谐运动f (x )=2sin ⎝ ⎛⎭⎪⎫π3x +φ⎝ ⎛⎭⎪⎫|φ|<π2的图象经过点(0,1),则该简谐运动的最小正周期T 和初相φ分别为( ).A .T =6,φ=π6B .T =6,φ=π3C .T =6π,φ=π6D .T =6π,φ=π3 解析 将(0,1)点代入f (x )可得sin φ=12. ∵|φ|<π2,∴φ=π6,T =2ππ 3=6.答案 A7.已知函数y =A sin(ωx +φ)+B 的一部分图象如图所示,如果A >0,ω>0,|φ|<π2,则( ).A .A =4B .ω=1C .φ=π6 D .B =4 解析 由图象可知,A =2,14T =5π12-π6=π4,T =π, ω=2.∵2×π6+φ=π2,∴φ=π6,故选C. 答案 C8.若函数f (x )=3sin(ωx +φ)对任意的x 都有f ⎝ ⎛⎭⎪⎫π3+x =f ⎝ ⎛⎭⎪⎫π3-x ,则f ⎝ ⎛⎭⎪⎫π3等于( ).A .3或0B .-3或0C .0D .-3或3 解析 ∵f ⎝ ⎛⎭⎪⎫π3+x =f ⎝ ⎛⎭⎪⎫π3-x ,∴f (x )关于直线x =π3对称, ∴f ⎝ ⎛⎭⎪⎫π3应取得最大值或最小值. 答案 D二、填空题(每小题5分,共20分)9.函数y =cos x 在区间[-π,a ]上为增函数,则a 的取值范围是________. 解析 ∵y =cos x 在[-π,0]上为增函数,又在[-π,a ]上递增,∴[-π,a ]⊆[-π,0],∴a ≤0. 又∵a >-π,∴-π<a ≤0. 答案 (-π,0]10.函数y =tan x ,x ∈⎣⎢⎡⎦⎥⎤0,π4的值域是________.解析 ∵y =tan x 在⎣⎢⎡⎦⎥⎤0,π4上单调递增,∴0≤tan x ≤1,即y ∈[0,1]. 答案 [0,1]11.已知函数y =2sin(ωx +φ)(ω>0)在一个周期内当x =π12时,有最大值2,当x =7π12时有最小值-2,则ω=________.解析 由题意知T =2×⎝ ⎛⎭⎪⎫7π12-π12=π.∴ω=2πT =2.答案 212.函数y =6sin ⎝ ⎛⎭⎪⎫14x -π6的初相是________,图象最高点的坐标是________.解析 初相为-π6,当14x -π6=π2+2k π,即x =8π3+8k π(k ∈Z )时,函数取得最大值6. 答案 -π6⎝ ⎛⎭⎪⎫8π3+8k π,6(k ∈Z ) 三、解答题(每小题10分,共40分)13.用“五点法”作出函数y =2sin ⎝ ⎛⎭⎪⎫x -π3+3的图象,并指出它的周期、频率、相位、初相、最值及单调区间. 解 (1)列表:x -π3 0 π2 π 3π2 2π x π3 5π6 4π3 11π6 7π3 y35313(2)描点、作图(如图所示).将函数在一个周期内的图象向左、向右两边扩展,得y =2sin ⎝ ⎛⎭⎪⎫x -π3+3的图象.由图象知,周期T =2π,频率f =1T =12π,相位为x -π3,初相为-π3,最大值为5,最小值为1,函数的单调递减区间为⎣⎢⎡⎦⎥⎤5π6+2k π,11π6+2k π,k ∈Z ,单调递增区间为⎣⎢⎡⎦⎥⎤-π6+2k π,5π6+2k π,k ∈Z . 14.求函数y =-2tan ⎝ ⎛⎭⎪⎫3x +π3的定义域、值域,并指出它的周期、奇偶性和单调性.解 由3x +π3≠π2+k π,得x ≠π18+k π3(k ∈Z ),∴函数y =-2tan ⎝ ⎛⎭⎪⎫3x +π3的定义域为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠π18+k π3(k ∈Z ).它的值域为R ,周期为T =π3,它既不是奇函数,也不是偶函数.由-π2+k π<3x +π3<π2+k π(k ∈Z ),得-5π18+k π3<x <π18+k π3(k ∈Z ),所以函数y =-2tan ⎝ ⎛⎭⎪⎫3x +π3在区间⎝ ⎛⎭⎪⎫-5π18+k π3,π18+k π3(k ∈Z )上单调递减. 15.设函数f (x )=sin ⎝ ⎛⎭⎪⎫12x +φ⎝ ⎛⎭⎪⎫0<φ<π2,y =f (x )图象的一条对称轴是直线x =π4.(1)求φ;(2)求函数y =f (x )的单调增区间.解 (1)∵x =π4是y =f (x )的图象的一条对称轴, ∴sin ⎝ ⎛⎭⎪⎫12×π4+φ=±1,∴π8+φ=k π±π2,k ∈Z ,∵0<φ<π2,∴φ=3π8.(2)由(1)知φ=3π8,因此y =sin ⎝ ⎛⎭⎪⎫12x +3π8.由题意得:2k π-π2≤12x +38π≤2k π+π2,k ∈Z , 即4k π-74π≤x ≤4k π+π4,k ∈Z ,∴函数的单调增区间为⎣⎢⎡⎦⎥⎤4k π-74π,4k π+π4,k ∈Z .16.已知函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|<π2的图象在y 轴上的截距为1,它在y 轴右侧的第一个最大值点和最小值点分别为(x 0,2)和(x 0+3π,-2). (1)求f (x )的解析式;(2)将y =f (x )图象上所有点的横坐标缩短到原来的13,然后再将所得到的图象向x 轴正方向平移π3个单位长度,得到函数y =g (x )的图象,写出g (x )的解析式,并作出在长度为一个周期上的图象.解 (1)由已知,易得A =2,T 2=(x 0+3π)-x 0=3π,解得T =6π,∴ω=13. 把(0,1)代入解析式y =2sin ⎝ ⎛⎭⎪⎫x 3+φ,得2sin φ=1.又|φ|<π2,解得φ=π6. ∴y =2sin ⎝ ⎛⎭⎪⎫x 3+π6.(2)压缩后的函数解析式为y =2sin ⎝ ⎛⎭⎪⎫x +π6,再平移得g (x )=2sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫x -π3+π6=2sin ⎝ ⎛⎭⎪⎫x -π6.列表:x π6 2π3 7π6 5π3 13π6 x -π6 0 π2 π 3π2 2π 2sin ⎝ ⎛⎭⎪⎫x -π62-2图象如图:。
2024_2025学年高三数学新高考一轮复习专题三角函数的图像和性质1含解析

三角函数的图像和性质学校:___________姓名:___________班级:___________考号:___________一、单选题(本大题共6小题,共30.0分。
在每小题列出的选项中,选出符合题目的一项)1.函数的定义域为A. B.C. D.2.函数的定义域是()A. (0,]B. (0,)C. [0,]D. (0,]3.已知f(x)=cos x(cos x +sin x)在区间[-,m]上的最大值是,则实数m的最小值是()A. B. C. D.4.若f(x )=(x -)在区间[-a,a]上单调递增,则实数a的最大值为()A. B. C. D.5.已知函数f(x)=sin(ωx +)(ω>0)在区间[-,]上单调递增,则ω的取值范围为( )A. (0,]B. (0,]C. [,]D. [,2]6.函数f(x )=(4x +)+的零点个数为()A. 2B. 3C. 4D. 5二、多选题(本大题共2小题,共10.0分。
在每小题有多项符合题目要求)7.函数f(x)=A (x +)(A >0,>0,||<)的部分图象如图所示,则()1A. f(x)的图象的最小正周期为B. f(x)的图象的对称轴方程为x=+2k(k Z)C. f(x)的图象的对称中心为(+2k,0)(k Z)D. f(x)的单调递增区间为[4k-,4k+](k Z)8.已知函数,现给出下列四个命题,其中正确的是()A. 函数的最小正周期为B. 函数的最大值为1C. 函数在上单调递增D. 将函数的图象向左平移个单位长度,得到的函数解析式为三、填空题(本大题共2小题,共10.0分)9.已知函数f(x)=sin(2x+φ)(0≤φ<π)关于直线对称,则f(0)= .10.筒车是我国古代独创的一种水利浇灌工具,因其经济又环保,至今还在农业生产中得到应用,明朝科学家徐光启在农政全书中用图画1描绘了筒车的工作原理.假定在水流稳定的状况下,简车上的每一个盛水筒都做匀速圆周运动.如图2,将筒车抽象为一个几何图形圆,筒车的半径为4m,筒车转轮的中心O到水面的距离为2m,筒车每分钟沿逆时针方向转动4圈.规定:盛水筒M对应的点P从水中出现即时的位置时起先计算时间,且以水轮的圆心O为坐标原点,过点O的水平直线为x轴建立平面直角坐标系设盛水筒M从点运动到点P时所经过的时间为单位:,且此时点P距离水面的高度为单位:,则h 与t的函数关系式为,点P第一次到达最高点须要的时间为四、解答题(本大题共2小题,共24.0分。
三角函数图像和性质练习题(附答案)

三角函数的图像与性质一、选择题1.已知函数f(x)=2sin ϖx(ϖ>0)在区间[3π-,4π]上的最小值是-2,则ϖ的最小值等于( )A.32B.23C.2D.32.若函数cos(3y x πω=+(0)ω>的图象相邻两条对称轴间距离为2π,则ω等于.A .12B .12C .2D .43.将函数sin()6y x x R π=+∈的图象上所有的点向左平行移动4π个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为A .5sin(2)()12y x x R π=+∈ B .5sin()()212x y x R π=+∈C .sin()212x y x R π=-∈ D .5sin()224x y x R π=+∈4.函数262cos(-+=πx y 的图像F 按向量a 平移到F /,F /的解析式y=f(x),当y=f(x)为奇函数时,向量a 可以等于A.)2,6(-πB.)2,6(πC.)2,6(--πD.)2,6(π-5.将函数sin yx =的图象向左平移(02)ϕϕπ≤≤个单位后,得到函数sin(6y x π=-的图象,则ϕ等于()A .6πB .76πC .116πD .56π 6.函数x x y 2cos 32sin -= 66(ππ≤≤-x 的值域为A. []2,2-B. []0,2-C. []2,0 D. ]0,3[-7.将函数的图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的解析式是 ( )A .B . C. D.8.函数f(θ ) = 的最大值和最小值分别是( )sin θ -1cos θ -2 (A) 最大值 和最小值0(B) 最大值不存在和最小值 4334(C) 最大值 -和最小值0 (D) 最大值不存在和最小值-43349.ααcos sin +=t 且αα33cos sin+<0,则t 的取值范围是( )A. [)0,2-B. []2,2-C. ()(]2,10,1 -D. ()()+∞-,30,3 10.把函数)(x f y =的图象沿着直线0=+y x 的方向向右下方平移22个单位,得到函数x y 3sin =的图象,则A 、2)23sin(--=x yB 、2)63sin(--=x yC 、2)23sin(++=x yD 、2)63sin(++=x y 二、填空题11.设函数).0)(3cos()(πϕϕ<<+=x x f 若)()(x f x f '+是奇函数,则ϕ=.12.方程2cos()14x π-=在区间(0,)π内的解是.13.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间14.已知x R ∈,则函数()max sin ,cos f x x x ⎧=⎨⎩的最大值与最小值的和等于 。
(完整版)三角函数的图象与性质练习题及答案

三角函数的图象与性质练习题一、选择题1.函数f (x )=sin x cos x 的最小值是( ) A .-1B .-12C.12D .12.如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎫4π3,0中心对称,那么|φ|的最小值为 ( ) A.π6B.π4C.π3D.π23.已知函数y =sin πx3在区间[0,t ]上至少取得2次最大值,则正整数t 的最小值是 ( ) A .6B .7C .8D .94.已知在函数f (x )=3sin πxR 图象上,相邻的一个最大值点与一个最小值点恰好在x 2+y 2=R 2上,则f (x )的最小正周期为 ( ) A .1B .2C .3D .45.已知a 是实数,则函数f (x )=1+a sin ax 的图象不可能是 `( D )6.给出下列命题:①函数y =cos ⎝⎛⎭⎫23x +π2是奇函数; ②存在实数α,使得sin α+cos α=32; ③若α、β是第一象限角且α<β,则tan α<tan β; ④x =π8是函数y =sin ⎝⎛⎭⎫2x +5π4的一条对称轴方程; ⑤函数y =sin ⎝⎛⎭⎫2x +π3的图象关于点⎝⎛⎭⎫π12,0成中心对称图形. 其中正确的序号为( )A .①③B .②④C .①④D .④⑤7.将函数y =sin 2x 的图象向左平移π4个单位,再向上平移1个单位,所得图象的函数解析式是 ( )A .y=2cos 2xB .y =2sin 2xC .y =1+sin(2x +π4) D .y =cos 2x8.将函数y =sin ⎝⎛⎭⎫2x +π4的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移π4个单位,所得到的图象解析式是 ( )A .f (x )=sin xB .f (x )=cos xC .f (x )=sin 4xD .f (x )=cos 4x9.若函数y =A sin(ωx +φ)+m 的最大值为4,最小值为0,最小正周期为π2,直线x =π3是其图象的一条对称轴,则它的解析式是 ( ) A .y =4sin ⎝⎛⎭⎫4x +π6B .y =2sin ⎝⎛⎭⎫2x +π3+2 C .y =2sin ⎝⎛⎭⎫4x +π3+2D .y =2sin ⎝⎛⎭⎫4x +π6+2 10.若将函数y =tan ⎝⎛⎭⎫ωx +π4(ω>0)的图象向右平移π6个单位长度后,与函数y =tan ⎝⎛⎭⎫ωx +π6的图象重合,则ω的最小值为 ( ) A.16B.14C.13D.1211.电流强度I (安)随时间t (秒)变化的函数 I =A sin(ωt +φ)(A >0,ω>0,0<φ<2π)的图象如右图所示, 则当t =1001秒时,电流强度是( )A .-5安B .5安C .53安D .10安12.已知函数f (x )=sin(ωx +π4)(x ∈R ,ω>0)的最小正周期为π,为了得到函数g (x )=cos ωx 的图象,只要将y =f (x )的图象( )A .向左平移π8个单位长度B .向右平移π8个单位长度C .向左平移π4个单位长度D .向右平移π4个单位长度二、填空题(每小题6分,共18分)13.函数y =12sin ⎝⎛⎭⎫π4-23x 的单调递增区间为______________. 14.已知f (x )=sin ⎝⎛⎭⎫ωx +π3 (ω>0),f ⎝⎛⎭⎫π6=f ⎝⎛⎭⎫π3,且f (x )在区间⎝⎛⎭⎫π6,π3上有最小值,无最大值,则ω=________. 15.关于函数f (x )=4sin ⎝⎛⎭⎫2x +π3(x ∈R ),有下列命题: ①由f (x 1)=f (x 2)=0可得x 1-x 2必是π的整数倍; ②y =f (x )的表达式可改写为y =4cos ⎝⎛⎭⎫2x -π6; ③y =f (x )的图象关于点⎝⎛⎭⎫-π6,0对称; ④y =f (x )的图象关于直线x =-π6对称.其中正确的命题的序号是________.(把你认为正确的命题序号都填上)16.若动直线x =a 与函数f (x )=sin x 和g (x )=cos x 的图象分别交于M 、N 两点,则|MN |的最大值为________. 三、解答题(共40分)17.设函数f (x )=sin ()2x +φ (-π<φ<0),y =f (x )图象的一条对称轴是直线x =π8.(1)求φ; (2)求函数y =f (x )的单调增区间.18.已知函数f (x )=2cos 2ωx +2sin ωx cos ωx +1 (x ∈R ,ω>0)的最小正周期是π2.(1)求ω的值; (2)求函数f (x )的最大值,并且求使f (x )取得最大值的x 的集合.19.设函数f (x )=cos ωx (3sin ωx +cos ωx ),其中0<ω<2. (1)若f (x )的周期为π,求当-π6≤x ≤π3时f (x )的值域;(2)若函数f (x )的图象的一条对称轴为x =π3,求ω的值.20.已知函数f (x )=A sin(ωx +φ)+ b (ω>0,|φ|<2π)的图象的一部分如图所示: (1)求f (x )的表达式; (2)试写出f (x )的对称轴方程.21.函数y =A sin(ωx +φ) (A >0,ω>0,|φ|<π2)的一段图象如图所示.(1)求函数y =f (x )的解析式;(2)将函数y =f (x )的图象向右平移π4个单位,得到y =g (x )的图象,求直线y =6与函数y =f (x )+g (x )的图象在(0,π)内所有交点的坐标.22.已知函数f (x )=A sin(ωx +φ) (A >0,ω>0,|φ|<π2,x ∈R )的图象的一部分如图所示.(1)求函数f (x )的解析式;(2)当x ∈⎣⎡⎦⎤-6,-23时,求函数y =f (x )+f (x +2)的最大值与最小值及相应的x 的值.三角函数的图象与性质练习题及答案一、选择题1.函数f (x )=sin x cos x 的最小值是( B ) A .-1B .-12C.12D .12.如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎫4π3,0中心对称,那么|φ|的最小值为 ( A ) A.π6B.π4C.π3D.π23.已知函数y =sin πx3在区间[0,t ]上至少取得2次最大值,则正整数t 的最小值是 ( C ) A .6B .7C .8D .94.已知在函数f (x )=3sin πxR 图象上,相邻的一个最大值点与一个最小值点恰好在x 2+y 2=R 2上,则f (x )的最小正周期为 ( D ) A .1B .2C .3D .45.已知a 是实数,则函数f (x )=1+a sin ax 的图象不可能是 `( D )6.给出下列命题:①函数y =cos ⎝⎛⎭⎫23x +π2是奇函数; ②存在实数α,使得sin α+cos α=32; ③若α、β是第一象限角且α<β,则tan α<tan β; ④x =π8是函数y =sin ⎝⎛⎭⎫2x +5π4的一条对称轴方程; ⑤函数y =sin ⎝⎛⎭⎫2x +π3的图象关于点⎝⎛⎭⎫π12,0成中心对称图形. 其中正确的序号为( C )A .①③B .②④C .①④D .④⑤7.将函数y =sin 2x 的图象向左平移π4个单位,再向上平移1个单位,所得图象的函数解析式是 ( A )A .y =2cos 2xB .y =2sin 2xC .y =1+sin(2x +π4) D .y =cos 2x8.将函数y =sin ⎝⎛⎭⎫2x +π4的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移π4个单位,所得到的图象解析式是 ( A )A .f (x )=sin xB .f (x )=cos xC .f (x )=sin 4xD .f (x )=cos 4x9.若函数y =A sin(ωx +φ)+m 的最大值为4,最小值为0,最小正周期为π2,直线x =π3是其图象的一条对称轴,则它的解析式是 ( D ) A .y =4sin ⎝⎛⎭⎫4x +π6B .y =2sin ⎝⎛⎭⎫2x +π3+2 C .y =2sin ⎝⎛⎭⎫4x +π3+2D .y =2sin ⎝⎛⎭⎫4x +π6+2 10.若将函数y =tan ⎝⎛⎭⎫ωx +π4(ω>0)的图象向右平移π6个单位长度后,与函数y =tan ⎝⎛⎭⎫ωx +π6的图象重合,则ω的最小值为 ( D ) A.16B.14C.13D.1211.电流强度I (安)随时间t (秒)变化的函数 I =A sin(ωt +φ)(A >0,ω>0,0<φ<2π)的图象如右图所示, 则当t =1001秒时,电流强度是( A )A .-5安B .5安C .53安D .10安12.已知函数f (x )=sin(ωx +π4)(x ∈R ,ω>0)的最小正周期为π,为了得到函数g (x )=cos ωx 的图象,只要将y =f (x )的图象( A )A .向左平移π8个单位长度B .向右平移π8个单位长度C .向左平移π4个单位长度D .向右平移π4个单位长度二、填空题(每小题6分,共18分)13.函数y =12sin ⎝⎛⎭⎫π4-23x 的单调递增区间为______________.⎣⎡⎦⎤98π+3k π,21π8+3k π (k ∈Z ) 14.已知f (x )=sin ⎝⎛⎭⎫ωx +π3 (ω>0),f ⎝⎛⎭⎫π6=f ⎝⎛⎭⎫π3,且f (x )在区间⎝⎛⎭⎫π6,π3上有最小值,无最大值,则ω=________. 31415.关于函数f (x )=4sin ⎝⎛⎭⎫2x +π3(x ∈R ),有下列命题: ①由f (x 1)=f (x 2)=0可得x 1-x 2必是π的整数倍; ②y =f (x )的表达式可改写为y =4cos ⎝⎛⎭⎫2x -π6; ③y =f (x )的图象关于点⎝⎛⎭⎫-π6,0对称; ④y =f (x )的图象关于直线x =-π6对称.其中正确的命题的序号是________.(把你认为正确的命题序号都填上) ②③16.若动直线x =a 与函数f (x )=sin x 和g (x )=cos x 的图象分别交于M 、N 两点,则|MN |的最大值为________. 2 三、解答题(共40分)17.设函数f (x )=sin ()2x +φ (-π<φ<0),y =f (x )图象的一条对称轴是直线x =π8.(1)求φ; (2)求函数y =f (x )的单调增区间. 解 (1)令2×π8+φ=k π+π2,k ∈Z ,∴φ=k π+π4,又-π<φ<0,则-54<k <-14,∴k =-1, 则φ=-3π4.(2)由(1)得:f (x )=sin ⎝⎛⎭⎫2x -3π4, 令-π2+2k π≤2x -3π4≤π2+2k π, 可解得π8+k π≤x ≤5π8+k π,k ∈Z ,因此y =f (x )的单调增区间为⎣⎡⎦⎤π8+k π,5π8+k π,k ∈Z . 18.已知函数f (x )=2cos 2ωx +2sin ωx cos ωx +1 (x ∈R ,ω>0)的最小正周期是π2.(1)求ω的值; (2)求函数f (x )的最大值,并且求使f (x )取得最大值的x 的集合. 解 (1)f (x )=21+cos 2ωx2+sin 2ωx +1=sin 2ωx +cos 2ωx +2=2⎝⎛⎭⎫sin 2ωx cos π4+cos 2ωx sin π4+2 =2sin ⎝⎛⎭⎫2ωx +π4+2. 由题设,函数f (x )的最小正周期是π2,可得2π2ω=π2, 所以ω=2.(2)由(1)知,f (x )=2sin ⎝⎛⎭⎫4x +π4+2. 当4x +π4=π2+2k π,即x =π16+k π2(k ∈Z )时,sin ⎝⎛⎭⎫4x +π4取得最大值1,所以函数f (x )的最大值是2+2, 此时x 的集合为⎩⎨⎧⎭⎬⎫x |x =π16+k π2,k ∈Z .19.设函数f (x )=cos ωx (3sin ωx +cos ωx ),其中0<ω<2. (1)若f (x )的周期为π,求当-π6≤x ≤π3时f (x )的值域;(2)若函数f (x )的图象的一条对称轴为x =π3,求ω的值.解 f (x )=32sin 2ωx +12cos 2ωx +12=sin ⎝⎛⎭⎫2ωx +π6+12. (1)因为T =π,所以ω=1. ∴f (x )=sin ⎝⎛⎭⎫2x +π6+12, 当-π6≤x ≤π3时,2x +π6∈⎣⎡⎦⎤-π6,5π6, 所以f (x )的值域为⎣⎡⎦⎤0,32. (2)因为f (x )的图象的一条对称轴为x =π3,所以2ω⎝⎛⎭⎫π3+π6=k π+π2(k ∈Z ), ω=32k +12 (k ∈Z ), 又0<ω<2,所以-13<k <1,又k ∈Z ,所以k =0,ω=12.20.已知函数f (x )=A sin(ωx +φ)+ b (ω>0,|φ|<2π)的图象的一部分如图所示: (1)求f (x )的表达式; (2)试写出f (x )的对称轴方程. 解 (1)由图象可知,函数的最大值M =3,最小值m =-1, 则A =,1213,22)1(3=-==--b , 又π)6π32(2=-=πT ,∴2ππ2π2===T ω,∴f (x )=2sin(2x +φ)+1, 将x =6π,y =3代入上式,得1)3π(=+ϕ ∴π22π3πk +=+ϕ,k ∈Z , 即φ=6π+2k π,k ∈Z ,∴φ=6π, ∴f (x )=2sin )6π2(+x +1. (2)由2x +6π=2π+k π,得x =6π+21k π,k ∈Z , ∴f (x )=2sin )6π2(+x +1的对称轴方程为 216π+=x k π,k ∈Z. 21.函数y =A sin(ωx +φ) (A >0,ω>0,|φ|<π2)的一段图象如图所示.(1)求函数y =f (x )的解析式;(2)将函数y =f (x )的图象向右平移π4个单位,得到y =g (x )的图象,求直线y =6与函数y =f (x )+g (x )的图象在(0,π)内所有交点的坐标.解 (1)由题图知A =2,T =π,于是ω=2πT=2,将y =2sin 2x 的图象向左平移π12个单位长度,得y =2sin(2x +φ)的图象.于是φ=2×π12=π6, ∴f (x )=2sin ⎝⎛⎭⎫2x +π6. (2)依题意得g (x )=2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4+π6=-2cos ⎝⎛⎭⎫2x +π6. 故y =f (x )+g (x )=2sin ⎝⎛⎭⎫2x +π6-2cos ⎝⎛⎭⎫2x +π6 =22sin ⎝⎛⎭⎫2x -π12. 由22sin ⎝⎛⎭⎫2x -π12=6,得sin ⎝⎛⎭⎫2x -π12=32. ∵0<x <π,∴-π12<2x -π12<2π-π12. ∴2x -π12=π3或2x -π12=2π3,∴x =524π或x =38π, ∴所求交点坐标为⎝⎛⎭⎫5π24,6或⎝⎛⎭⎫3π8,6. 22.已知函数f (x )=A sin(ωx +φ) (A >0,ω>0,|φ|<π2,x ∈R )的图象的一部分如图所示.(1)求函数f (x )的解析式;(2)当x ∈⎣⎡⎦⎤-6,-23时,求函数y =f (x )+f (x +2)的最大值与最小值及相应的x 的值. 解 (1)由图象知A =2,T =8, ∵T =2πω=8,∴ω=π4.又图象过点(-1,0),∴2sin ⎝⎛⎭⎫-π4+φ=0. ∵|φ|<π2,∴φ=π4. ∴f (x )=2sin ⎝⎛⎭⎫π4x +π4.(2)y =f (x )+f (x +2)=2sin ⎝⎛⎭⎫π4x +π4+2sin ⎝⎛⎭⎫π4x +π2+π4=22sin ⎝⎛⎭⎫π4x +π2=22cos π4x . ∵x ∈⎣⎡⎦⎤-6,-23,∴-3π2≤π4x ≤-π6. ∴当π4x =-π6,即x =-23时,y =f (x )+f (x +2)取得最大值6;π4x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2 2.当。
高考复习:三角函数的图像与性质(含参考答案与解析方法)
4.3三角函数的图像与性质一 正弦、余弦、正切函数的图像与性质 (下表中k ∈Z ).1.三角函数存在多个单调区间时易错用“∪”联结.2.研究三角函数单调性、对称中心、奇偶性及对称轴时易忽视“k ∈Z ”这一条件. 考点一 三角函数的定义域与值域例1、(1)函数f (x )=3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域为________.(2)函数y =lg(sin x )+ cos x -12的定义域为________.(3)①函数y =2cos 2x +5sin x -4的值域为________.②当x ∈⎣⎡⎦⎤π6,7π6时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________.考点二 三角函数的单调性例2、函数y =2sin ⎝⎛⎭⎫x -π4的单调递减区间为 _____________.变式训练1 (1)函数y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫x -π4的单调递减区间为_____________; (2)函数y =sin ⎝⎛⎭⎫-2x +π3的单调递减区间为_______________.考点三 三角函数的对称性与奇偶性例3、(2013·扬州期末)已知函数f (x )=-2sin 2x +23sin x · cos x +1.(1)求f (x )的最小正周期及对称中心;(2)当x ∈⎣⎡⎦⎤-π6,π3时,求f (x )的最大值和最小值.例4 (1)若函数y =3sin(2x +φ)(0<φ<π)的图像关于点⎝⎛⎭⎫π3,0中心对称,则φ=________.(2) 已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π3的一条对称轴为x =π3,一个对称中心为点⎝⎛⎭⎫π12,0,则ω的最小值为______.(3)设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图像如图所示,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则f ⎝⎛⎭⎫16的值为______.冲刺高考:1、已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是________.2、已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b 的值为________.3、(2014·北京)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________. 课堂练习1、 函数y =lg sin 2x +9-x 2的定义域为________________.2、 函数y =sin x -cos x 的定义域是________.3、 函数f (x )=2sin ⎝⎛⎭⎫x -π4,x ∈[-π,0]的单调增区间为________.4、若函数f (x )=2sin ωx (ω>0)在⎣⎡⎤-2π3,2π3上单调递增,则ω的最大值为______.5、将函数y =3cos x +sin x (x ∈R ) 的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是________.4.3三角函数的图像与性质(作业)1、已知函数f (x )=-2sin(2x +φ)(|φ|<π),若f (π8)=-2,则f (x )的单调递减区间是________.2、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是________.3、给出下列四个命题,其中不正确的命题为______.(填序号) ①若cos α=cos β,则α-β=2k π,k ∈Z ;②函数y =2cos ⎝⎛⎭⎫2x +π3的图象关于x =π12中心对称;③函数y =cos(sin x )(x ∈R )为偶函数;④若α、β均为第一象限角,且α>β,则sin α>sin β ⑤函数y =sin|x |是周期函数,且周期为2π.4、 函数y =cos 2x +sin 2x ,x ∈R 的值域是________.5、 函数y =cos(π4-2x )的单调减区间为________.6、设函数f (x )=3sin(π2x +π4),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________.7、已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)=________.8、已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间.9、设函数f (x )=sin(πx 4-π6)-2cos 2πx8+1.(1)求f (x )的最小正周期.(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时,y =g (x )的最大值.4.3三角函数的图像与性质一 正弦、余弦、正切函数的图像与性质(下表中k ∈Z ).1.三角函数存在多个单调区间时易错用“∪”联结.2.研究三角函数单调性、对称中心、奇偶性及对称轴时易忽视“k ∈Z ”这一条件. 考点一 三角函数的定义域与值域例1 (1)函数f (x )=3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域为________. 解析:当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6,sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-12,1, 故3sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-32,3, 即此时函数f (x )的值域是⎣⎡⎦⎤-32,3. (2) (2014·湛江调研)函数y =lg(sin x )+ cos x -12的定义域为________.解析:要使函数有意义必须有⎩⎪⎨⎪⎧ sin x >0,cos x -12≥0,即⎩⎪⎨⎪⎧sin x >0,cos x ≥12, 解得⎩⎪⎨⎪⎧2k π<x <π+2k π,-π3+2k π≤x ≤π3+2k π(k ∈Z ), ∴2k π<x ≤π3+2k π,k ∈Z ,∴函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π<x ≤π3+2k π,k ∈Z .(3)①函数y =2cos 2x +5sin x -4的值域为________.②当x ∈⎣⎡⎦⎤π6,7π6时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________. 解析:①y =2cos 2x +5sin x -4=2(1-sin 2x )+5sin x -4=-2sin 2x +5sin x -2 =-2(sin x -54)2+98. 故当sin x =1时,y max =1,当sin x =-1时,y min =-9,故y =2cos 2x +5sin x -4的值域为[-9,1]. ②∵x ∈⎣⎡⎦⎤π6,7π6,∴sin x ∈⎣⎡⎦⎤-12,1. 又y =3-sin x -2cos 2x =3-sin x -2(1-sin 2x )= 2⎝⎛⎭⎫sin x -142+78. ∴当sin x =14时,y min =78, 当sin x =-12或sin x =1时,y max =2.答案:(1)[-9,1] (2)78 2[类题通法]1.三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图像来求解.2.三角函数值域的不同求法 (1)利用sin x 和cos x 的值域直接求;(2)把所给的三角函数式变换成y =A sin(ωx +φ)的形式求值域; (3)把sin x 或cos x 看作一个整体,转换成二次函数求值域; (4)利用sin x ±cos x 和sin x cos x 的关系转换成二次函数求值域. 考点二 三角函数的单调性例2、求函数y =2sin ⎝⎛⎭⎫x -π4的单调递减区间 [解] 由2k π+π2≤x -π4≤2k π+3π2,k ∈Z ,得2k π+3π4≤x ≤2k π+7π4,k ∈Z .故函数y =2sin ⎝⎛⎭⎫x -π4的单调减区间为 ⎣⎡⎦⎤2k π+3π4,2k π+7π4(k ∈Z ). 变式训练1 (1)求函数y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫x -π4的单调递减区间;(2)求函数y =sin ⎝⎛⎭⎫-2x +π3的单调递减区间 解 (1)画出函数y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫x -π4的图像,易知其单调递减区间为⎣⎡⎦⎤k π+3π4,k π+5π4(k ∈Z ). (2) y =-sin ⎝⎛⎭⎫2x -π3, 它的减区间是y =sin ⎝⎛⎭⎫2x -π3的增区间. 由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故所给函数的减区间为⎣⎡⎦⎤k π-π12,k π+5π12,k ∈Z ; 例3、求函数y =sin ⎝⎛⎭⎫π3+4x +cos ⎝⎛⎭⎫4x -π6的周期、单调区间及最大、最小值. 解 ∵⎝⎛⎭⎫π3+4x +⎝⎛⎭⎫π6-4x =π2, ∴cos ⎝⎛⎭⎫4x -π6=cos ⎝⎛⎭⎫π6-4x =cos ⎣⎡⎦⎤π2-⎝⎛⎭⎫π3+4x =sin ⎝⎛⎭⎫π3+4x . ∴y =2sin ⎝⎛⎭⎫4x +π3,周期T =2π4=π2. 当-π2+2k π≤4x +π3≤π2+2k π (k ∈Z )时,函数单调递增,∴函数的递增区间为⎣⎡⎤-5π24+k π2,π24+k π2 (k ∈Z ). 当π2+2k π≤4x +π3≤3π2+2k π (k ∈Z )时,函数单调递减, ∴函数的递减区间为⎣⎡⎦⎤π24+k π2,7π24+k π2(k ∈Z ).当x =π24+k π2 (k ∈Z )时,y max =2; 当x =-5π24+k π2 (k ∈Z )时,y min =-2.考点三 三角函数的对称性与奇偶性例4、(2013·扬州期末)已知函数f (x )=-2sin 2x +23sin x · cos x +1.(1)求f (x )的最小正周期及对称中心;(2)当x ∈⎣⎡⎦⎤-π6,π3时,求f (x )的最大值和最小值. 解:(1)f (x )= 3 sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6, 所以f (x )的最小正周期为T =2π2=π.令 sin ⎝⎛⎭⎫2x +π6=0,得x =k π2-π12(k ∈Z ), 所以f (x )的对称中心为⎝⎛⎭⎫k π2-π12,0(k ∈Z ). (2)因为x ∈⎣⎡⎦⎤-π6,π3,所以-π6≤2x +π6≤5π6, 所以-12≤sin ⎝⎛⎭⎫2x +π6≤1,所以-1≤f (x )≤2. 所以当x =-π6时,f (x )的最小值为-1;当x =π6时,f (x )的最大值为2.例5 (1)若函数y =3sin(2x +φ)(0<φ<π)的图像关于点⎝⎛⎭⎫π3,0中心对称,则φ=________.解析:由题意得3sin ⎝⎛⎭⎫23π+φ=0,所以23π+φ=k π(k ∈Z ).又因为0<φ<π,所以φ=π3. (2) 已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π3的一条对称轴为x =π3,一个对称中心为点⎝⎛⎭⎫π12,0,则ω的最小值为______.解析:由题意知π3-π12≥T 4,T =2πω≤π,ω≥2.(3)设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图像如图所示,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则f ⎝⎛⎭⎫16的值为______.解析:由题意知,点M 到x 轴的距离是12,根据题意可设f (x )=12cos ωx ,又由题图知12·2πω=1,所以ω=π,所以f (x )=12cos πx ,故f ⎝⎛⎭⎫16=12cos π6=34. [类题通法]1.若f (x )=A sin(ωx +φ)为偶函数,则当x =0时,f (x )取得最大或最小值. 若f (x )=A sin(ωx +φ)为奇函数,则当x =0时,f (x )=0.2.对于函数y =A sin(ωx +φ),其对称轴一定经过图像的最高点或最低点,对称中心一定是函数的零点,因此在判断直线x =x 0或点(x 0,0)是否是函数的对称轴或对称中心时,可通过检验f (x 0)的值进行判断.三角函数的单调性、对称性、周期性例6、(1)已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是________.(2)已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b的值为________.(3)(2014·北京)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________. 思维点拨 (1)(π2,π)为函数f (x )某个单调减区间的子集;(2)由f (x +π4)=f (-x )可得函数的对称轴,应用函数在对称轴处的性质求解即可;(3)利用正弦型函数图象的对称性求周期. 解析 (1)由π2<x <π得π2ω+π4<ωx +π4<πω+π4,由题意知(π2ω+π4,πω+π4)⊆[π2,3π2], ∴⎩⎨⎧π2ω+π4≥π2,πω+π4≤3π2,∴12≤ω≤54. (2)由f (x +π4)=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3.(3)∵f (x )在⎣⎡⎦⎤π6,π2上具有单调性, ∴T 2≥π2-π6, ∴T ≥2π3. ∵f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3, ∴f (x )的一条对称轴为x =π2+2π32=7π12. 又∵f ⎝⎛⎭⎫π2=-f ⎝⎛⎭⎫π6, ∴f (x )的一个对称中心的横坐标为π2+π62=π3. ∴14T =7π12-π3=π4, ∴T =π. 答案 (1)[12,54] (2)-1或3 (3)π温馨提醒 (1)对于已知函数的单调区间的某一部分确定参数ω的范围的问题:首先,明确已知的单调区间应为函数的单调区间的子集;其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解.(2)函数y =A sin(ωx +φ)+b 的图象与其对称轴的交点是最值点. 课堂练习1、函数y =lg sin 2x +9-x 2的定义域为________________.解析 由⎩⎪⎨⎪⎧ sin 2x >0,9-x 2≥0,得⎩⎪⎨⎪⎧2k π<2x <2k π+π,k ∈Z ,-3≤x ≤3.∴-3≤x <-π2或0<x <π2. ∴函数y =lg sin 2x +9-x 2的定义域为 {x |-3≤x <-π2或0<x <π2}.2、函数y =sin x -cos x 的定义域是________. 解析 要使函数有意义,必须有sin x -cos x ≥0,即sin x ≥cos x ,同一坐标系中作出y =sin x ,y =cos x ,x ∈[0,2π]的图象如图所示.结合图象及正、余弦函数的周期是2π知, 函数的定义域为{x |2k π+π4≤x ≤2k π+5π4,k ∈Z }.3、函数f (x )=2sin ⎝⎛⎭⎫x -π4,x ∈[-π,0]的单调增区间为________. 解析:当x -π4∈⎣⎡⎦⎤2k π-π2,2k π+π2,k ∈Z 时,是f (x )的单调增区间. 又因为x ∈[-π,0],故取k =0得x ∈⎣⎡⎦⎤-π4,0 4、若函数f (x )=2sin ωx (ω>0)在⎣⎡⎦⎤-2π3,2π3上单调递增,则ω的最大值为______. 解析:依题意可知12×T ≥2×2π3,即12×2πω≥2×2π3,解得ω≤34,从而ω的最大值为34.5、将函数y =3cos x +sin x (x ∈R ) 的图象向左平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是________.解析 y =3cos x +sin x =2sin(x +π3)向左平移m 个单位长度后得到y =2sin(x +π3+m ),它关于y 轴对称可得 sin(π3+m )=±1, ∴π3+m =k π+π2,k ∈Z ,∴m =k π+π6,k ∈Z , ∵m >0,∴m 的最小值为π6.4.3三角函数的图像与性质(作业)1、已知函数f (x )=-2sin(2x +φ)(|φ|<π),若f (π8)=-2,则f (x )的单调递减区间是________.解析 由f (π8)=-2得f (π8)=-2sin(2×π8+φ)=-2sin(π4+φ)=-2,所以sin(π4+φ)=1.因为|φ|<π, 所以φ=π4. 由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,解得 k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递减区间为[k π-3π8,k π+π8](k ∈Z ).2、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是________.解析 根据题意平移后函数的解析式为 y =sin ω⎝⎛⎭⎫x -π4, 将⎝⎛⎭⎫3π4,0代入得sin ωπ2=0,则ω=2k ,k ∈Z ,且ω>0, 故ω的最小值为2. 3、给出下列四个命题,其中不正确的命题为______.(填序号) ①若cos α=cos β,则α-β=2k π,k ∈Z ;②函数y =2cos ⎝⎛⎭⎫2x +π3的图象关于x =π12中心对称; ③函数y =cos(sin x )(x ∈R )为偶函数;④若α、β均为第一象限角,且α>β,则sin α>sin β⑤函数y =sin|x |是周期函数,且周期为2π. 答案 ①④⑤解析 命题①:若α=-β,则cos α=cos β,假命题;命题②:x =π12,cos ⎝⎛⎭⎫2x +π3=cos π2=0,故x =π12是y =2cos ⎝⎛⎭⎫2x +π3的对称中心;命题⑤:函数y =sin|x |不是周期函数. 4、函数y =cos 2x +sin 2x ,x ∈R 的值域是________. 解析 y =cos 2x +sin 2x =cos 2x +1-cos 2x 2=1+cos 2x2.∵cos 2x ∈[-1,1],∴y ∈[0,1].5、函数y =cos(π4-2x )的单调减区间为________.解析 由y =cos(π4-2x )=cos(2x -π4)得2k π≤2x -π4≤2k π+π(k ∈Z ),故k π+π8≤x ≤k π+5π8(k ∈Z ). 所以函数的单调减区间为[k π+π8,k π+5π8](k ∈Z ).6、设函数f (x )=3sin(π2x +π4),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________. 解析 f (x )=3sin(π2x +π4)的周期T =2π×2π=4,f (x 1),f (x 2)应分别为函数f (x )的最小值和最大值, 故|x 1-x 2|的最小值为T2=2.7、已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)=________.解析 由题中图象可知,此正切函数的半周期等于3π8-π8=π4,即最小正周期为π2, 所以ω=2.由题意可知,图象过定点(3π8,0),所以0=A tan(2×3π8+φ), 即3π4+φ=k π(k ∈Z ), 所以φ=k π-3π4(k ∈Z ),又|φ|<π2,所以φ=π4. 又图象过定点(0,1),所以A =1.综上可知,f (x )=tan(2x +π4), 故有f (π24)=tan(2×π24+π4)=tan π3= 3.8、已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1. (1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈⎣⎡⎦⎤0,π2,∴2x +π6∈⎣⎡⎦⎤π6,7π6. ∴sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, ∴-2a sin ⎝⎛⎭⎫2x +π6∈[-2a ,a ]. ∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1, ∴b =-5,3a +b =1,因此a =2,b =-5. (2)由(1)得,f (x )=-4sin ⎝⎛⎭⎫2x +π6-1, g (x )=f ⎝⎛⎭⎫x +π2=-4sin ⎝⎛⎭⎫2x +7π6-1=4sin ⎝⎛⎭⎫2x +π6-1, 又由lg g (x )>0,得g (x )>1,∴4sin ⎝⎛⎭⎫2x +π6-1>1,∴sin ⎝⎛⎭⎫2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π6,k ∈Z ,其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z ,∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时,g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z .9、设函数f (x )=sin(πx 4-π6)-2cos 2πx8+1.(1)求f (x )的最小正周期.(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时,y =g (x )的最大值.解 (1)f (x )=sin πx 4cos π6-cos πx 4sin π6-cos πx 4=32sin πx 4-32cos πx 4=3sin(πx 4-π3), 故f (x )的最小正周期为T =2ππ4=8.(2)方法一 在y =g (x )的图象上任取一点(x ,g (x )), 它关于x =1的对称点(2-x ,g (x )).由题设条件,知点(2-x ,g (x ))在y =f (x )的图象上,从而g (x )=f (2-x )=3sin[π4(2-x )-π3]=3sin[π2-πx 4-π3]=3cos(πx 4+π3).当0≤x ≤43时,π3≤πx 4+π3≤2π3,因此y =g (x )在区间[0,43]上的最大值为g (x )max =3cos π3=32.方法二 区间[0,43]关于x =1的对称区间为[23,2],且y =g (x )与y =f (x )的图象关于直线x =1对称, 故y =g (x )在[0,43]上的最大值为y =f (x )在[23,2]上的最大值.由(1)知f (x )=3sin(πx 4-π3),当23≤x ≤2时,-π6≤πx 4-π3≤π6. 因此y =g (x )在[0,43]上的最大值为g (x )max =3sin π6=32.。
近三年三角函数的图像和性质高考真题和答案

近三年三角函数的图像和性质高考真题和答案一、填空题1.(2020·全国卷Ⅲ)关于函数f (x )=sin x +1sin x 有如下四个命题:①f (x )的图象关于y 轴对称;②f (x )的图象关于原点对称;③f (x )的图象关于直线x =π2对称;④f (x )的最小值为2.其中所有真命题的序号是________.2.(2019·全国卷Ⅰ)函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +3π2-3cos x 的最小值为________. 3.(2019·北京高考)函数f (x )=sin 22x 的最小正周期是________.二、选择题1.(2019·全国卷Ⅱ)若x 1=π4,x 2=3π4是函数f (x )=sin ωx (ω>0)两个相邻的极值点,则ω=( )A .2 B.32 C .1 D.122.(2019·全国卷Ⅰ)关于函数f (x )=sin|x |+|sin x |有下述四个结论:①f (x )是偶函数;②f (x )在区间⎝ ⎛⎭⎪⎫π2,π单调递增;③f (x )在[-π,π]有4个零点;④f (x )的最大值为2.其中所有正确结论的编号是( )A .①②④B .②④C .①④D .①③3.(2018·全国卷Ⅰ)已知函数f (x )=2cos 2x -sin 2x +2,则( )A .f (x )的最小正周期为π,最大值为3B .f (x )的最小正周期为π,最大值为4C .f (x )的最小正周期为2π,最大值为3D .f (x )的最小正周期为2π,最大值为44.(2018·全国卷Ⅲ)函数f (x )=tan x 1+tan 2x的最小正周期为( ) A.π4 B.π2 C .π D .2π三、大题 1.(2019·浙江高考)设函数f (x )=sin x ,x ∈R .(1)已知θ∈[0,2π),函数f (x +θ)是偶函数,求θ的值;(2)求函数y =⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π122+⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π42的值域.2.(2018·北京高考)已知函数f (x )=sin 2x +3sin x cos x .(1)求f (x )的最小正周期;(2)若f (x )在区间⎣⎢⎡⎦⎥⎤-π3,m 上的最大值为32,求m 的最小值.3.(2017·浙江高考)已知函数f (x )=sin 2x -cos 2x -23sin x cos x (x ∈R ).(1)求f ⎝ ⎛⎭⎪⎫2π3的值; (2)求f (x )的最小正周期及单调递增区间.参考答案填空1.②③2.-43. π2选择BACBC大题1.解:(1)因为f (x +θ)=sin(x +θ)是偶函数,所以对任意实数x 都有sin(x +θ)=sin(-x +θ), 即sin x cos θ+cos x sin θ=-sin x cos θ+cos x sin θ, 故2sin x cos θ=0,所以cos θ=0.又θ∈[0,2π),因此θ=π2或θ=3π2.(2)y =⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π122+⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π42 =sin 2⎝ ⎛⎭⎪⎫x +π12+sin 2⎝ ⎛⎭⎪⎫x +π4 =1-cos ⎝ ⎛⎭⎪⎫2x +π62+1-cos ⎝ ⎛⎭⎪⎫2x +π22=1-12⎝ ⎛⎭⎪⎫32cos2x -32sin2x =1-32cos ⎝ ⎛⎭⎪⎫2x +π3. 因此所求函数的值域是⎣⎢⎡⎦⎥⎤1-32,1+32. 2.解:(1)f (x )=12-12cos2x +32sin2x =sin ⎝ ⎛⎭⎪⎫2x -π6+12. 所以f (x )的最小正周期为T =2π2=π.(2)由(1)知f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6+12.由题意知-π3≤x ≤m ,所以-5π6≤2x -π6≤2m -π6.要使f (x )在⎣⎢⎡⎦⎥⎤-π3,m 上的最大值为32,即需sin ⎝ ⎛⎭⎪⎫2x -π6在⎣⎢⎡⎦⎥⎤-π3,m 上的最大值为1.所以2m -π6≥π2,即m ≥π3.所以m 的最小值为π3. 3.解:(1)由sin 2π3=32,cos 2π3=-12,得f ⎝ ⎛⎭⎪⎫2π3=⎝ ⎛⎭⎪⎫322-⎝ ⎛⎭⎪⎫-122-23×32×⎝ ⎛⎭⎪⎫-12=2. (2)由cos2x =cos 2x -sin 2x 与sin2x =2sin x cos x 得f (x )=-cos2x -3sin2x =-2sin ⎝ ⎛⎭⎪⎫2x +π6. 所以f (x )的最小正周期是π.由正弦函数的性质得π2+2k π≤2x +π6≤3π2+2k π,k ∈Z ,解得π6+k π≤x ≤2π3+k π,k ∈Z .所以f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤π6+k π,2π3+k π(k ∈Z ).。
专题05 三角函数的图象及性质(原卷版)

专题05三角函数的图象及性质一、单选题1.(2022·江苏海安·高三期末)函数()cos()6f x x πω=+的部分图象如图,则下列选项中是其一条对称轴的是( )A .724x π= B .38x π= C .512x π=D .1124x π=【答案】C 【分析】由给定解析式及图象确定ω值的表达式,再逐项分析判断作答. 【详解】 依题意,点2(,0)3π是函数()cos()6f x x πω=+的图象对称中心,且2π3在函数()f x 的一个单调增区间内,则22,Z 362k k πππωπ+=-∈,即31k ω=-,Z k ∈, 令函数()f x 周期为T ,由图象知2233243T T ππ⎧<⎪⎪⎨⎪>⎪⎩,即有8493T ππ<<,而2T πω=,则有3924ω<<, 因此,393124k <-<,解得513612k <<,而Z k ∈,则1k =,2ω=,()cos(2)6f x x π=+, 由2,Z 6x n n ππ+=∈得函数()f x 图象的对称轴:,Z 212n x n ππ=-∈, 当0n =时,12x π=-,当1n =时,512x π=,当2n =时,1112π=x ,即选项A ,B ,D 不满足,选项C 满足.故选:C2.(2022·江苏海安·高三期末)通信卫星与经济发展、军事国防等密切关联,它在地球静止轨道上运行,地球静止轨道位于地球赤道所在平面,轨道高度为h km (轨道高度是指卫星到地球表面的距离).将地球看作是一个球(球心为O ,半径为r km ),地球上一点A 的纬度是指OA 与赤道平面所成角的度数,点A 处的水平面是指过点A 且与OA 垂直的平面,在点A 处放置一个仰角为θ的地面接收天线(仰角是天线对准卫星时,天线与水平面的夹角),若点A 的纬度为北纬30,则tan θ=( )A2rr h + B2rr h + C2hr h+ D2hr h+ 【答案】A 【分析】根据题意作出图形,由三角形的边角关系以及正弦定理结合同角三角函数基本关系、两角差的正弦公式即可求解. 【详解】如图:30AOB ∠=,CAD θ∠=,BC h =, 在Rt AOD 中3tan 303AD OA =⋅=,2cos303OA OD ==,所以BD OD OB r =-=-=,CD BC BD h =-=, 因为180903060ADO ∠=--=,所以18060120ADC ∠=-=,18012060ACD θθ∠=--=-,在ACD △中,由正弦定理可得:sin sin CD ADCAD ACD =∠∠即()33sin sin 60h θθ=-,所以1sin sin 2h θθθ⎛⎫-=⎪ ⎪⎝⎭⎝⎭, sin 2r hθθ+=,所以sin 2tan cos rr hθθθ==+, 故选:A.3.(2022·江苏如东·高三期末)正弦信号是频率成分最为单一的一种信号,因为这种信号的波形是数学上的正弦函数而得名,很多复杂的信号都可以通过多个正弦信号叠加得到,因而正弦信号在实际中作为典型信号或测试信号获得广泛应用.已知某个信号的波形可以表示为f (x )=sin x +sin2x +sin3x .则( ) A .f (x )的最大值为3 B .π是f (x )的一个周期 C .f (x )的图像关于(π,0)对称 D .f (x )在区间0,2π⎛⎫⎪⎝⎭上单调递增【答案】C 【分析】由函数解析式判断各选项中的性质可得. 【详解】sin y x =取最大值1时,22x k ππ=+,k Z ∈,sin 2y x =取最大值1时,,4x k k Z ππ=+∈,sin3y x =取最大值1时,2,36k x k Z ππ=+∈,三者不可能同时取得,因此sin sin 2sin 33y x x x =++<,A 错; ()sin()sin(22)sin(33)sin sin 2sin3f x x x x x x x ππππ+=+++++=-+-与()f x 不可能恒相等,π不可能是周期,B 错;()()()()()2sin 2πsin 42sin 63sin sin 2sin3f x x x x x x x f x πππ-=-+-+-=---=-,所以()f x 的图象关于点(,0)π对称,C 正确; 函数图象是连续的,而3sin sin sin0222f ππππ⎛⎫=++= ⎪⎝⎭,()sin sin sin ()66322f f πππππ=++=>,因此()f x 在(0,)2π上不可能递增,D 错误. 故选:C .4.(2022·江苏如皋·高三期末)已知1sin 32πα⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫+ ⎪⎝⎭的值为( )A .12B .12-C D 【答案】B 【分析】利用诱导公式及二倍角的正弦公式即可求解. 【详解】1sin 32πα⎛⎫+= ⎪⎝⎭2sin 2sin 2cos 212sin 63233πππππαααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴+=+-=-+=--+ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦22112sin 121322πα⎛⎫⎛⎫=+-=⨯-=- ⎪ ⎪⎝⎭⎝⎭,故选:B5.(2022·江苏常州·高三期末)函数()sin 2tan f x x x =+的最小正周期是( )A .π4B .π2C .πD .2π【答案】C 【分析】分别判断函数sin 2y x =和tan y x =的最小正周期,从而可得出答案. 【详解】解:因为函数sin 2y x =的最小正周期为22ππ=,函数tan y x =的最小正周期为π, 且()()()()πsin2πtan πsin 22πtan sin2tan f x x x x x x x +=+++=++=+, πT ∴=.故选:C.6.(2022·广东揭阳·高三期末)已知函数()3sin 23f x x π⎛⎫=+ ⎪⎝⎭,则该函数的增区间为( )A .()2,222k k k ππππ⎡⎤-++∈⎢⎥⎣⎦ZB .()52,266k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z C .()5,1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z D .()7,1212k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z 【答案】C 【分析】利用整体代换法和复合函数的单调性求函数的增区间. 【详解】 令222232k x k πππππ-+≤+≤+,解得5,1212k x k k ππππ-+≤≤+∈Z ,所以函数的增区间是()5,1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z . 故选:C.7.(2022·广东潮州·高三期末)己知1cos 3x =,则sin(2)2x π+=( )A .79-B .79C .89-D .89【答案】A 【分析】利用诱导公式和二倍角公式化简计算. 【详解】解:217sin(2)cos 22cos 121299x x x π+==-=⨯-=-.故选:A8.(2022·广东东莞·高三期末)若π(0,)2α∈,212tan cos αα=,则tan α=( )A .12B .1C .2D 【答案】B 【分析】根据22sin cos 1αα+=,和sin tan cos ααα=,即可得到22tan tan 1αα=+,进而求出结果. 【详解】因为0,2πα⎛⎫∈ ⎪⎝⎭,所以cos 0α≠,所以222221sin cos tan 1cos cos ααααα+==+, 所以22tan tan 1αα=+,即()2tan 10α-=,所以tan 1α=, 故选:B.9.(2022·广东东莞·高三期末)已知函数()sin f x x =,()x x g x e e -=+,则下列结论正确的是( ) A .()()f x g x 是偶函数 B .|()|()f x g x 是奇函数 C .()|()|f x g x 是奇函数 D .|()()|f x g x 是奇函数【答案】C 【分析】先以偶函数定义去判断选项A 的正误,再以奇函数的定义去判断选项B 、C 、D 的正误.选项A: ()()(e e )sin x x f x g x x -=+()()(e e )sin()(e e )sin ()()x x x x f x g x x x f x g x ----=+-=-+=-,是奇函数,判断错误;选项B: sin (e e )|())|(x xf x xg x -=+sin()(e e )sin (e e )|()|()()()x x x x f x g x f x x x g x ----=-++==,是偶函数,判断错误;选项C: ()|()|e e sin x xg x f x x -=+e e sin()e ()|()|()e sin ()x x x x x xf xg x f x g x --+-+=---==-, 是奇函数,判断正确;选项D: (e |()()e s |)in x xf xg x x -+=(e e )sin()(e e )si |()()||()n ()|x x x x x f x g x f x x g x --+---==+, 是偶函数,判断错误. 故选:C10.(2022·广东罗湖·高三期末)已知3sin 35πα⎛⎫+=- ⎪⎝⎭,则cos 6πα⎛⎫-= ⎪⎝⎭( )A .45B .45-C .35D .35【答案】D 【分析】利用三角函数诱导公式将所求式子转化后即可得出结论. 【详解】3sin 35πα⎛⎫+=- ⎪⎝⎭,3cos cos sin 63235ππππααα⎛⎫⎛⎫⎛⎫∴-=+-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:D.11.(2022·广东佛山·高三期末)已知1sin ,,0222ππαα⎛⎫⎛⎫+=∈- ⎪ ⎪⎝⎭⎝⎭,则tan α等于( )A .BC .D 【答案】A利用诱导公式求出cos α,再用平方关系求出sin α即可计算作答. 【详解】因1sin 22πα⎛⎫+= ⎪⎝⎭,则1cos 2α=,而,02πα⎛⎫∈- ⎪⎝⎭,于是得sin α=所以sin tan cos ααα== 故选:A12.(2022·湖南常德·高三期末)已知函数()()sin f x A x =+ωϕ(0A >,0>ω,2πϕ<)的部分图象如图所示,则下列四个结论中正确的是( )A .若,02x ⎡⎤∈-⎢⎥⎣⎦π,则函数f (x )的值域为11,2⎡⎤-⎢⎥⎣⎦B .点,03π⎛-⎫⎪⎝⎭是函数f (x )图象的一个对称中心C .函数f (x )在区间,02π⎡⎤-⎢⎥⎣⎦上是增函数D .函数f (x )的图象可以由函数cos 2y x =的图象向右平移12π个单位长度得到 【答案】A 【分析】结合五点法求得函数解析式,然后利用正弦函数性质确定单调性、对称中心、函数值域及三角函数图象变换判断即得. 【详解】由题图及五点作图法得1A =,512πωϕπ⋅+=,2332πωϕπ⋅+=, 则2ω=,6π=ϕ,故()sin 26f x x π⎛⎫+ ⎝=⎪⎭.由,02x ⎡⎤∈-⎢⎥⎣⎦π,得52,666x πππ⎡⎤+∈-⎢⎥⎣⎦,故()1sin 21,62f x x π⎛⎫⎡⎤=+∈- ⎪⎢⎥⎝⎭⎣⎦,函数f (x )在区间,02π⎡⎤-⎢⎥⎣⎦上不是增函数,故A 正确,C 错误;∵当3x π=-时,262x ππ+=-,所以点,03π⎛-⎫⎪⎝⎭不是函数f (x )图象的一个对称中心,故B 错误;由cos 2sin 22y x x π⎛⎫==+ ⎪⎝⎭,将函数cos 2y x =的图象向右平移12π个单位长度得到sin 2122y x ππ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦sin 23x π⎛⎫=+ ⎪⎝⎭的图象,故D 错误.故选:A .13.(2022·湖南娄底·高三期末)将函数()()cos 04f x x πωω⎛⎫=+> ⎪⎝⎭的图象向右平移4π个单位长度后得到函数()g x 的图象,若()g x 在5,44ππ⎛⎫⎪⎝⎭上单调递减,则ω的最大值为( )A .14B .34C .12D .1【答案】B 【分析】求得()cos 44g x x ωππω⎛⎫=-+ ⎪⎝⎭,由5,44x ππ⎛⎫∈ ⎪⎝⎭可求得4444x πωπππωωπ<-+<+,结合函数()g x 的单调性可得出关于ω的不等式,由此可得出ω的最大值. 【详解】将()f x 的图象向右平移4π个单位长度后得到()cos 44g x x ωππω⎛⎫=-+ ⎪⎝⎭的图象. 因为5,44x ππ⎛⎫∈ ⎪⎝⎭,所以4444x πωπππωωπ<-+<+, 因为()g x 在5,44ππ⎛⎫⎪⎝⎭上单调递减,所以4πωππ+≤,304ω<≤,所以ω的最大值为34.故选:B.14.(2022·湖北武昌·高三期末)已知函数()y g x =的图象与函数sin 2y x =的图象关于直线x π=对称,将()g x 的图象向右平移3π个单位长度后得到函数()y f x =的图象,则函数()y f x =在0,2x π⎡⎤∈⎢⎥⎣⎦时的值域为( )A .⎡⎢⎣⎦ B .1⎡-⎢⎣⎦C .1⎡⎤⎢⎥⎣⎦D .[]01,【答案】C 【分析】由对称性先求出()g x 的解析式,再由平移得出()y f x =的解析式,再由正弦函数的性质得出其值域. 【详解】设(),x y 为()g x 的图像上一点,则点(),x y 关于直线x π=对称的点为()2,x y π- 由题意点()2,x y π-在函数sin 2y x =的图象上,则()sin 22sin 2y x x π=-=-所以()sin 2g x x =-,则()2sin 2sin 233f x x x ππ⎛⎫⎛⎫=--=--⎪ ⎪⎝⎭⎝⎭当0,2x π⎡⎤∈⎢⎥⎣⎦时,223323,x πππ⎡⎤-∈⎢⎥⎣⎦-,则2sin 23x π⎡⎛⎫-∈-⎢ ⎪⎝⎭⎣⎦所以()1f x ≤≤ 故选:C15.(2022·湖北江岸·高三期末)计算)tan 70cos10201︒︒︒-=( )A .1B .﹣1C .12D .12-【答案】B 【分析】根据诱导公式、三角恒等变换、二倍角公式可得结果,尽可能地化简为同角的三角函数值 【详解】)))()tan 70cos10201cot 20cos10201cos 20cos101sin 20cos 20cos10sin 20cos1020cos 20sin 20cos102sin10sin 20sin 20sin 201︒︒︒-=︒︒︒-︒⎫=︒⎪︒⎭︒=︒︒⎝⎭︒=︒-︒︒︒=-︒︒-︒=︒=-故选:B16.(2022·湖北江岸·高三期末)下列四个函数中,以π为最小正周期,其在,2ππ⎛⎫⎪⎝⎭上单调递减的是( )A .sin y x =B .sin y x =C .cos 2y x =D .sin 2y x =【答案】A 【分析】对于A ,sin y x =符合题中要求,对于B, sin y x =不是周期函数,对于C ,D ,sin 2y x =,cos 2y x =在,2ππ⎛⎫⎪⎝⎭上都不是单调函数,由此可判断正确答案. 【详解】sin y x =的最小正周期为π,在,2ππ⎛⎫⎪⎝⎭上单调递减,符合题意,故A 正确;sin y x =不是周期函数,故B 错误;cos 2y x =中,,2x ππ⎛⎫∈ ⎪⎝⎭,则2π,2πx,故cos 2y x =中在,2x ππ⎛⎫∈ ⎪⎝⎭时不是单调函数,故C 错误;sin 2y x =,,2x ππ⎛⎫∈ ⎪⎝⎭,则2π,2πx,故sin 2y x =中在,2x ππ⎛⎫∈ ⎪⎝⎭时不是单调函数,故D 错误,故选:A.17.(2022·湖北襄阳·高三期末)已知tan 226θπ⎛⎫-= ⎪⎝⎭,则cos 3πθ⎛⎫-= ⎪⎝⎭( )A .35B .35 C .45D .45-【答案】B 【分析】利用倍角公式可得cos 3πθ⎛⎫- ⎪⎝⎭22cos sin 2626θπθπ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭,再利用弦化切,即求.【详解】∵tan 226θπ⎛⎫-= ⎪⎝⎭,∴cos 3πθ⎛⎫-= ⎪⎝⎭22cos 2cos sin 262626θπθπθπ⎛⎫⎛⎫⎛⎫-=--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222cos sin 2626cos sin 2626θπθπθπθπ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭221tan 1426141tan 26θπθπ⎛⎫-- ⎪-⎝⎭==+⎛⎫+- ⎪⎝⎭35=-.18.(2022·湖北省鄂州高中高三期末)已知tan 2θ=-,则sin sin cos θθθ=+( )A .2B .12-C .12D .2-【答案】A 【分析】以齐次式法去求值即可解决. 【详解】sin sin tan 2cos 2sin cos sin cos tan 121cos cos θθθθθθθθθθθ-====++-++ 故选:A19.(2022·湖北·高三期末)若点55sin ,cos 66M ππ⎛⎫ ⎪⎝⎭在角α的终边上,则cos2=α( )A .12-B .12C. D【答案】A 【分析】先将点55sin ,cos 66M ππ⎛⎫ ⎪⎝⎭化简,得1,2M ⎛ ⎝⎭,结合同角三角函数先求出cos α,再结合二倍角公式求出cos2α即可【详解】 由55sin ,cos66M ππ⎛⎫⎪⎝⎭得1,2M ⎛ ⎝⎭, 则1cos 2α=,21cos22cos 12αα=-=-.故选:A.20.(2022·山东省淄博实验中学高三期末)已知函数()() 2sin 10,2f x x πωϕωϕ⎛⎫=++>< ⎪⎝⎭,()1f α=-,()3f β=,若αβ-的最小值为32π,且的图像关于点,14π⎛⎫ ⎪⎝⎭对称,则函数()f x 的所有对称轴中,离原点最近的对称轴方程是( ) A .34x π=-B .2x π=-C .12x π=D .4x π=【分析】根据题意分别求出ω与ϕ,即求出()f x 的解析式,再求出()f x 的对称轴,找到离原点最近的对称轴方程即可. 【详解】由()1f α=-,()3f β=,αβ-的最小值为32π知, 3T π=,223T πω==, ()22sin 13f x x ϕ⎛⎫∴=++ ⎪⎝⎭.()f x 的图像关于点,14π⎛⎫⎪⎝⎭对称, 2()2sin()11sin()04346f πππϕϕ∴=⨯++=⇒+=2πϕ<6πϕ∴=-.()22sin 136f x x π⎛⎫∴=-+ ⎪⎝⎭.()f x 的对称轴为2=,362x k k z πππ-+∈.3,2x k k z ππ⇒=+∈.当1k =-时,2x π=-是离原点最近的对称轴方程. 故选:B.21.(2022·山东青岛·高三期末)已知角α的终边上一点P 的坐标为55sin ,cos 66ππ⎛⎫⎪⎝⎭,则角α的最小正值为( ) A .6πB .23π C .76π D .53π 【答案】D 【分析】先根据角α终边上点的坐标判断出角α的终边所在象限,然后根据三角函数的定义即可求出角α的最小正值. 【详解】 因为5sin06π>,5cos 06π<,所以角α的终边在第四象限, 根据三角函数的定义,可知5sin cos6πα==, 故角α的最小正值为5233ππαπ=-=. 故选:D .22.(2022·山东枣庄·高三期末)已知圆锥的侧面展开图是一个半径为3,圆心角为120°的扇形,则该圆锥的体积为( ).A.2πB .CD .π【答案】C 【分析】设此圆锥的底面半径为r ,高为h ,母线长为l ,根据底面圆周长等于展开扇形的弧长,建立关系式解出r ,再根据勾股定理,即可求出此圆锥高,进而求得体积. 【详解】设此圆的底面半径为r ,高为h ,母线长为l , ∵圆锥的侧面展开图是一个半径为3,圆心角为23π的扇形, ∴3l =,又2223r l πππ=⨯=,解得1r =,因此,此圆锥的高h =圆锥的体积为21133V r h ππ==⨯ 故选:C .23.(2022·山东枣庄·高三期末)已知30.4tan 1,tan0.1,a b c πππ⎛⎫=+-== ⎪⎝⎭,则( ).A .b c a <<B .c a b <<C .a c b <<D .a b c <<【答案】D 【分析】 由3010.12ππ<-<<,得到3tan(1)tan0.1π-<,令()tan f x x x =-,利用导数求得()f x 在(0,1)上单调递增,得到()0f x >,得出tan ,(0,1)x x x >∈,进而得到b c < ,即可求解. 【详解】因为3010.12ππ<-<<,且tan y x =在(0,)2π为单调递增函数, 所以33tan(1)tan(1)tan0.1πππ+-=-<,即a b <,令()tan ,(0,1)f x x x x =-∈,可得()211cos f x x'=-, 当(0,1)x ∈时,21cos y x=单调递减,所以()f x '在(0,1)单调递增,且()00f '=, 所以()0f x '>在(0,1)上恒成立,所以()f x 在(0,1)上单调递增,且()00f =, 所以()0f x >,即tan 0x x ->,即tan ,(0,1)x x x >∈,所以0.1tan0.1>, 又因为0.40.1c π=>,所以a b c <<.故选:D.24.(2022·山东枣庄·高三期末)已知sin 6πα⎛⎫-= ⎪⎝⎭,则4cos 23πα⎛⎫-= ⎪⎝⎭( ). A .59- B .59 C .13- D .13【答案】A 【分析】利用三角恒等变换公式化简求值得解. 【详解】解:2cos 2cos(2)cos(2)[12sin ()]3336πππππαααα⎛⎫-+-=--=--=--- ⎪⎝⎭25(12)99=--⋅=-.故选:A25.(2022·山东枣庄·高三期末)θ为第三或第四象限角的充要条件是( ). A .sin 0<θ B .cos 0<θC .sin tan 0θθ<D .cos tan 0θθ<【答案】D 【分析】第三或第四象限角,不含终边在y 轴负半轴. 【详解】对于A :第三或第四象限角,以及终边在y 轴负半轴,故A 错误; 对于B :第二或第三象限角,以及终边在x 轴负半轴,故B 错误; 对于C :第二或第三象限角,故C 错误; 对于D :第三或第四象限角,故D 正确.故选:D26.(2022·山东莱西·高三期末)要得到cos 34y x π⎛⎫=- ⎪⎝⎭的图象,只需将sin3y x =的图象( )A .向左平行移动4π个单位长度 B .向右平行移动12π个单位长度 C .向右平行移动712π个单位长度D .向左平行移动512π个单位长度 【答案】C 【分析】首先利用诱导公式统一函数名,即3sin 3cos 32y x x π⎛⎫==+⎪⎝⎭,然后根据平移变换即可求解. 【详解】解:因为函数37sin3cos 3cos 32124y x x x πππ⎡⎤⎛⎫⎛⎫==+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以要得到cos 34y x π⎛⎫=- ⎪⎝⎭的图象,只需将sin3y x =的图象向右平行移动712π个单位长度,故选:C.27.(2022·山东青岛·高三期末)已知04παβ<<<,则下列大小关系中正确的是( )A .cos cos (sin )(sin )αβαα>B .sin sin log cos log cos αααβ>C .sin sin (cos )(cos )αβαβ>D .sin cos (cos )(sin )ββαα< 【答案】C 【分析】A.构造函数()sin xy α=,利用其单调性比较大小; B.构造函数sin log y x α=,利用其单调性比较大小;C.构造函数()cos xy α=及函数sin y x β=,利用其单调性比较大小;D.将sin cos (cos )(sin )ββαα<转化为cos tan log sin αβα>,判断cos tan ,log sin αβα的大小关系即可. 【详解】04παβ<<<,则0sin cos 1αα<<<,且cos cos αβ>,sin sin αβ<A.因为函数()sin xy α=在R 上单调递减,故cos cos sin sin αβαα<,A 错误;B.因为函数sin log y x α=在()0,∞+上单调递减,故sin sin log cos log cos αααβ<,B 错误;C.因为函数()cos xy α=在R 上单调递减,函数sin y x β=在()0,∞+上单调递增,sin sin sin (cos )(cos )(cos )αββααβ>>,C 正确;D.sin cos sin ln (cos )(sin )(cos )cos ln(sin )ββαααβαβ⇔<<cos ln(sin )tan log sin cos (c sin l s )n o αααβαββ⇔>⇔> 04πβ<<,0tan 1β∴<<又cos cos log sin log cos 1αααα>=,cos tan log sin αβα∴<,D 错误; 故选:C.28.(2022·山东德州·高三期末)若函数()cos f x x x ωω-,0>ω,x ∈R ,又()12f x =,()20f x =,且12x x -的最小值为3π8,则ω的值为( )A .43B .83C .4D .163【答案】A 【分析】利用辅助角公式化简函数()y f x =的解析式,由12x x -的最小值为函数()y f x =的最小正周期的14,可求得函数()y f x =的最小正周期,进而可求得正数ω的值. 【详解】()()cos 2sin 06πωωωω⎛⎫=-=-> ⎪⎝⎭f x x x x ,所以()22sin 26πω⎛⎫-≤=-≤ ⎪⎝⎭f x x ,因为12x x -的最小值为函数()y f x =的最小正周期的14,所以,函数()y f x =的最小正周期为33482ππ=⨯=T , 因此,222433ππωπ⨯===T . 故选:A29.(2022·山东济南·高三期末)已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,则( )A .()2sin 32f x x π⎛⎫=+ ⎪⎝⎭B .()2sin 23f x x π⎛⎫=- ⎪⎝⎭C .()2sin 6f x x π⎛⎫=+ ⎪⎝⎭D .()12sin 26f x x π⎛⎫=- ⎪⎝⎭【答案】A 【分析】由函数()()sin f x A x ωϕ=+的部分图象,即可求出,,A ωϕ的值,即可求出结果. 【详解】由图象可知,327=4126πππω⎛⎫⨯-- ⎪⎝⎭,所以2ω=, 又()f x 过点7,212π⎛⎫- ⎪⎝⎭,所以2A =,且772sin 221212f ππϕ⎛⎫⎛⎫=⨯+=- ⎪⎪⎝⎭⎝⎭即7sin 16πϕ⎛⎫+=-⎪⎝⎭,所以73=2,62k k ππϕπ++∈Z ,即=2,3k k πϕπ+∈Z , 又2πϕ<,所以=3πϕ,所以()2sin 32f x x π⎛⎫=+ ⎪⎝⎭.故选:A.30.(2022·山东临沂·高三期末)已知πsin (,π)2αα=∈,则cos()6πα-=( )A .-1B .0C .12D 【答案】B 【分析】先根据πsin (,π)2αα=∈求出2π3α=,进而求出πcos()6α-∵πsin (,π)2αα=∈,∴2π3α=,故ππcos()cos 0.62α-== 故选:B31.(2022·河北深州市中学高三期末)函数()2sin 1x f x x x =++在,22ππ⎡⎤-⎢⎥⎣⎦上的图象为( ) A . B .C .D .【答案】D 【分析】利用函数的奇偶性排除部分选项,再由函数的值域判断. 【详解】∵()()f x f x -=,∴()f x 为偶函数,故排除A ,B .∵sin 1x ≤,211x x ++≥,∴()1f x <,故排除C , 故选:D .32.(2022·河北深州市中学高三期末)235cos sinsin 242412πππ=( )A .116BC .18D【分析】利用诱导公式及二倍角的正弦公式计算可得; 【详解】 解:235cos sinsin cos sin sin 2424122424212ππππππππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭ 111cossincossin cos sin 24241221212468ππππππ====. 故选:C33.(2022·河北唐山·高三期末)为了得到函数sin 2y x =的图像,只需把函数sin 22y x π⎛⎫=+ ⎪⎝⎭的图像( )A .向左平移2π个单位 B .向右平移2π个单位 C .向左平移4π个单位 D .向右移4π个单位 【答案】D 【分析】先对函数sin 22y x π⎛⎫=+ ⎪⎝⎭的解析式进行整理,再结合三角函数的平移规律即可得到结论.【详解】因为:sin 2sin 224y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭.所以:函数sin 22y x π⎛⎫=+ ⎪⎝⎭的图象向右平移4π个单位,可得到函数sin 2y x =的图象. 故选:D.34.(2022·河北保定·高三期末)已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭,则( )A .()f x 的最小正周期为2πB .()510log 42f <<C .()f x 的图象关于点,03π⎛-⎫⎪⎝⎭对称D .()451log log 23f f ⎛⎫< ⎪⎝⎭【答案】D根据三角函数的周期性定义和三角函数的对称性的概念,即可判断选项A ,C 是否正确;当02x π<<时,易得1()f x ⎤⎥⎝⎦∈,再根据50log 412π<<<,即可判断B 是否正确;由函数sin y x =的单调性,可知()f x 在,36ππ⎛⎫- ⎪⎝⎭上单调递增,再根据4511log log 232613ππ-<<<<-<,由单调性新即可判断D 是否正确. 【详解】因为函数()()sin =sin =sin =333f x x x x f x πππππ⎡⎤⎛⎫⎛⎫⎛⎫+=++-++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以()f x 的最小正周期为π,故A 错误; 当02x π<<时,5,336x πππ⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭,所以1sin ,132x π⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦,所以()1,12f x ⎛⎤∈ ⎥⎝⎦,而50log 412π<<<,所以()51log 412f <<,故B 错误; 若()f x 的图象关于点,03π⎛-⎫⎪⎝⎭对称,则()23f x f x π⎛⎫-=-- ⎪⎝⎭, 又22sin =sin 3333f x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,()sin =sin =sin 333f x x x x πππ⎛⎫⎛⎫⎛⎫--=--+----- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以()23f x f x π⎛⎫-≠-- ⎪⎝⎭,故C 错误;由于函数sin y x =的图象是将函数sin y x =在x 轴下方的图象翻折到x 轴上方,所以可知sin y x =在,,2k k k πππ⎛⎫+∈⎪⎝⎭Z 上单调递增, 令,32k x k k ππππ<+<+∈Z ,所以()f x 在区间,,36k k k ππππ⎛⎫-++∈ ⎪⎝⎭Z 上单调递增,所以()f x 在,36ππ⎛⎫- ⎪⎝⎭上单调递增,又44511log 3log log 123263ππ<-=<<<<--,所以()451log log 23f f ⎛⎫< ⎪⎝⎭,故D 正确.故选:D.35.(2022·山东淄博·高三期末)cos102cos102sin10-=( )ABCD .2【答案】A 【分析】利用二倍角的正弦公式以及两角差的正弦公式化简可得结果. 【详解】()cos102sin 3010cos10cos104sin10cos10cos102sin 202cos102sin102sin102sin102sin10-----===()cos10cos103sin1032sin10--==.故选:A.36.(2022·湖北·恩施土家族苗族高中高三期末)已知11tan ,tan ,37αβ==-且,(0,)αβπ∈,则2αβ-=( )A .4πB .4π-C .34π-D .34π-或4π 【答案】C 【分析】根据给定条件利用三角恒等变换求出tan 2()αβ-的值,再判断2αβ-的范围即可得解. 【详解】因11tan ,tan 37αβ==-,则22122tan 33tan 211tan 41()3ααα⨯===--, 31()tan 2tan 47tan(2)1311tan 2tan 1()47αβαβαβ----===++⨯-, 因,(0,)αβπ∈,tan 0,tan 0αβ><,则0,22ππαβπ<<<<,又tan 20α>,有022πα<<,于是得20παβ-<-<,因此,324παβ-=-, 所以324παβ-=-. 故选:C37.(2022·湖南常德·高三期末)若1tan 5α=,则cos2α的值为( ) A .1213-B .126-C .1213D .2526【答案】C 【分析】根据二倍角公式以及商数关系即可求出. 【详解】2222222211cos sin 1tan 125cos 2cos sin 1tan 13115ααααααα⎛⎫- ⎪--⎝⎭====++⎛⎫+ ⎪⎝⎭. 故选:C .38.(2022·江苏扬州·高三期末)已知ππsin 136αα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭,则cos2=α( )A.B .12CD【答案】B 【分析】化简已知条件,求得sin α,进而求得cos2α. 【详解】由题意可知,11sin cos 122αααα⎫-=⎪⎪⎭, 即2sin 1α=,解得1sin 2α=, 所以2211cos 212sin 1222αα⎛⎫=-=-⨯= ⎪⎝⎭.故选:B二、多选题39.(2022·江苏扬州·高三期末)已知函数()cos f x x x ωω+(ω>0),下列说法中正确的有( )A .若ω=1,则f (x )在(0,)2π上是单调增函数B .若()()66f x f x ππ+=-,则正整数ω的最小值为2C .若ω=2,则把函数y =f (x )的图象向右平移6π个单位长度,所得到的图象关于原点对称 D .若f (x )在(0,)π上有且仅有3个零点,则1723<66ω≤ 【答案】BD 【分析】化简函数f (x )的表达式,再逐一分析各个选项中的条件,计算判断作答. 【详解】依题意,()2sin()6f x x πω=+,对于A ,1ω=,()2sin()6f x x π=+,当(0,)2x π∈时,有2(,)663x πππ+∈,因sin y x =在2(,)63ππ上不单调,所以()2sin()6f x x π=+在(0,)2π上不单调,A 不正确;对于B ,因()()66f x f x ππ+=-,则6x π=是函数()f x 图象的一条对称轴,,Z 662k k πππωπ+=+∈,整理得62k ω=+,而0>ω,即有N k *∈,min 2ω=,B 正确;对于C ,2ω=,()2sin(2)6f x x π=+,依题意,函数()2sin[2()]2sin(2)6666y f x x x ππππ=-=-+=-,这个函数不是奇函数,其图象关于原点不对称,C 不正确; 对于D ,当(0,)x π∈时,(,)666x πππωωπ+∈+,依题意,3<46ππωππ+≤,解得1723<66ω≤,D 正确.故选:BD40.(2022·江苏通州·高三期末)已知函数()3sin 2f x A x ϕ⎛⎫=+ ⎪⎝⎭(A >0,0<φ<π)的图象如图所示,则( )A .π4ϕ=B .π6f x ⎛⎫- ⎪⎝⎭是偶函数C .当ππ,3x ⎡⎤∈--⎢⎥⎣⎦时,f (x )的最大值为1D .若()()()12122f x f x x x ⋅=≠,则12x x +的最小值为π【答案】AC 【分析】根据图象求得,A ϕ,根据三角函数的奇偶性、最值等知识对选项逐一分析,从而确定正确选项. 【详解】由图可知()35π5π3πsin 12ππ264240π0πk k Z ϕϕϕϕϕ⎧⎛⎫⎧⨯+=-+=+⎪⎪ ⎪⇒∈⇒=⎝⎭⎨⎨⎪⎪<<<<⎩⎩,A 选项正确. ()3πsin 24f x A x ⎛⎫=+ ⎪⎝⎭,()π0sin14f A A ==⇒= 所以()3π24f x x ⎛⎫=+ ⎪⎝⎭.π3ππ362642f x x x ⎡⎤⎛⎫⎛⎫-=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦为奇函数,B 选项错误.π33π53πππ,π,π32224244x x x -≤≤--≤≤--≤+≤-,3π3π1sin 124224x x ⎛⎫⎛⎫-≤+≤+≤ ⎪ ⎪⎝⎭⎝⎭,C 选项正确.()3π24f x x ⎛⎫⎡=+∈ ⎪⎣⎝⎭, 若()()()12122f x f x x x ⋅=≠,则11223ππ3ππ2π,2π242242x k x k +=++=+,12,Z k k ∈,11224π4ππ,π3636x k x k =+=+,12,Z k k ∈, 12124π4πππ3636x x k k +=+++()124ππ33k k =++, 当120k k +=时,12x x +取得最小值为π3,D 选项错误.故选:AC41.(2022·江苏宿迁·高三期末)将函数()()sin f x A x ωϕ=+的图象向左平移6π个单位长度后得到()y g x =的图象如图,则( )A .()f x 为奇函数B .()f x 在区间,62ππ⎛⎫⎪⎝⎭上单调递增C .方程()1f x =在()0,2π内有4个实数根D .()f x 的解析式可以是()2sin 23f x x π⎛⎫=- ⎪⎝⎭【答案】BC 【分析】利用图象可求得函数()g x 的解析式,利用函数图象平移可求得函数()f x 的解析式,可判断D 选项;计算()0f 可判断A 选项;利用正弦型函数的单调性可判断B 选项;当()0,2x π∈时,求出方程()1f x =对应的223x π-可能取值,可判断C 选项. 【详解】由图可知,函数()g x 的最小正周期为453123T πππ⎛⎫=+=⎪⎝⎭,22Tπω∴==,()max 2A g x ==, 所以,()()2sin 2g x x ϕ=+,则552sin 2126g ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,可得5sin 16⎛⎫+= ⎪⎝⎭πϕ, 所以,()52Z 62k k ππϕπ+=+∈,得()2Z 3k k πϕπ=-∈, 因为2πϕ<,则3πϕ=-,所以,()2sin 23g x x π⎛⎫=- ⎪⎝⎭,将函数()g x 的图象向右平移6π个单位可得到函数()f x 的图象,故()22sin 22sin 2633f x x x πππ⎡⎤⎛⎫⎛⎫=--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.对于A 选项,因为()202sin 03f π⎛⎫=-≠ ⎪⎝⎭,故函数()f x 不是奇函数,A 错;对于B 选项,当63x ππ<<时,22033x ππ-<-<,故函数()f x 在区间,62ππ⎛⎫⎪⎝⎭上单调递增,B 对;对于C 选项,由()22sin 213f x x π⎛⎫=-= ⎪⎝⎭,可得21sin 232x π⎛⎫-= ⎪⎝⎭, 当()0,2x π∈时,22102333x πππ-<-<,所以,2513172,,,36666x πππππ⎧⎫-∈⎨⎬⎩⎭,C 对; 对于D 选项,()22sin 22sin 233f x x x ππ⎛⎫⎛⎫=-≠- ⎪ ⎪⎝⎭⎝⎭,D 错.故选:BC.42.(2022·江苏如皋·高三期末)已知函数2cos sin cos 1()()f x x x x =+-,则下列说法正确的是( )A .5()()8f x f π≥B .()()88f x f x ππ+=-C .()()088f x f x ππ++-=D .()1)(2f f >【答案】ABD 【分析】根据给定条件利用二倍角公式、辅助角公式化简函数()f x ,再逐项分析判断作答. 【详解】依题意,2()2sin cos 2cos 1sin 2cos2)4f x x x x x x x π=+-=++,对于A ,553())8842f ππππ=⨯+==min ()f x = 即R x ∀∈,5()()8f x f π≥,A 正确;对于B ,()sin(2)282f x x x ππ+=+=,()2)82f x x ππ-=-2x =,即()()88f x f x ππ+=-,B 正确;对于C ,取8x π=,()()()(0)20884f x f x f f πππ++-=+=≠,C 不正确;对于D ,因3244πππ<+<,34224πππ<+<,则10))2((f f >>,D 正确. 故选:ABD43.(2022·广东潮州·高三期末)已知函数()sin cos (*)n n f x x x n N =+∈,则( ) A .对任意正奇数n ,f (x )为奇函数B .当n =3时,f (x )在[0,2π]上的最小值为2C .当n =4时,f (x )的单调递增区间是[,]()4Z k k k πππ-+∈D .对任意正整数n ,f (x )的图象都关于直线4x π=对称【答案】BD 【分析】通过判断(0)f 的值,判断A 的正误;利用函数的导数判断函数的单调性,求解最大值,判断B 的正误;求出函数的单调增区间判断C 的正误;判断()()2f x f x π-=,判断D 的正误.【详解】解:对于A ,取1n =,则()sin cos f x x x =+,从而(0)10f =≠,此时()f x 不是奇函数,则A 错误; 对于B ,当3n =时,22()3sin cos 3cos sin 3sin cos (sin cos )f x x x x x x x x x '=-=-,当x [0,)4π∈时,()0f x '<;当(,]42x ππ∈时,()0f x '>.所以()f x 在[0,)4π上单调递减,在(,]42ππ上单调递增,所以()f x 的最小值为33()4f π=+=B 正确;对于C ,当4n =时,4422222211cos413()sin cos (sin cos )2sin cos 1sin 21cos42444x f x x x x x x x x x -=+=+-=-=-=+, 令242k x k πππ-+≤≤,则4,442k k x k Z πππ-+≤≤∈, 所以()f x 的递增区间为[,]()422k k k Z πππ-+∈,则C 错误;对于D ,因为()sin ()cos ()cos sin ()222n n n n f x x x x x f x πππ-=-+-=+=,所以()f x 的图象关于直线4x π=对称,则D 正确; 故选:BD.44.(2022·广东东莞·高三期末)已知函数()sin cos f x a x b x =+,若()0f x ∈R 都有()3f x f π⎛⎫≤ ⎪⎝⎭,则下列结论正确的是( )A .()s 3f x x π⎛⎫=+ ⎪⎝⎭B .()6πf x x ⎛⎫=+ ⎪⎝⎭C .()f x 的图象向左平移 6π个单位后,图象关于原点对称D .()f x 的图象向右平移2 3π个单位后,图象关于y 轴对称 【答案】BD 【分析】先根据条件()0f =b 值,根据()3f x f π⎛⎫≤ ⎪⎝⎭可知3f π⎛⎫⎪⎝⎭为函数最大值,据此列出关于a 的方程,求出a 值,得到函数f(x)的解析式,结合辅助角公式和诱导公式,可判断A 、B 的正误,再根据三角函数图象的变换规律,可判断B 、D 的正误. 【详解】()sin cos ,(0)f x a x b x f =+=,b ∴=,又对任意x ∈R 都有()3f x f π⎛⎫≤ ⎪⎝⎭,则()3f π为()f x 的最大值,()3f π∴== ,整理得:2(3)0a -= ,则3a = ,所以()3sin ))63f x x x x x ππ==+=- ,因此A 选项错误,B 正确;()f x 的图象向左平移6π个单位后得到的图象对应的函数解析式为:()))663g x x x πππ=++=+ ,该函数图象不关于原点对称,故C 错误;()f x 的图象向右平移23π个单位后,得到函数2())63x x x ππϕ=+-=- 的图象, 该图象关于y 轴对称,故D 正确, 故选:BD45.(2022·广东汕尾·高三期末)设函数1,0()cos ,0x xx f x e x x -⎧>⎪=⎨⎪≤⎩,下列四个结论中正确的是( )A .函数()f x 在区间[),1π-上单调递增B .函数()y f x x =-有且只有两个零点C .函数()f x 的值域是[]1,1-D .对任意两个不相等正实数12,x x ,若12()()f x f x =,则122x x +> 【答案】CD 【分析】利用导数判断0x >时,()y f x =的单调性,根据单调性可求值域,然后结合0x ≤时,()cos f x x =,从而可判断选项A ,C ;首先利用导数判断0x ≤时,()()cos g x f x x x x =-=-的零点个数;然后再利用单调性判断0x >时,()1()ex x g x f x x x -=-=-的零点个数,从而可判断选项B ;不妨设1201x x <<<,根据题意把要证明122x x +>,转化为证明()()112f x f x ->;然后构造函数112()(01)ee x xxxx x ϕ---=-<<,利用导数判断函数的单调性即可证明,从而判断选项D. 【详解】 当0x >时,1()e x x f x -=,所以()11211e e 1()e e x x x x x x f x -----='-=,所以当01x <<时,()0,()f x y f x '>=在(0,1)单调递增, 当1x >时,()0,()f x y f x '<=在(1,)+∞单调递减, 故0x >时,0()(1)1f x f <≤=,又当0x ≤时,()cos f x x =,所以(0)1f =,1()1f x -≤≤, 所以函数()f x 在[,0),(0,1)π-单调递增,所以A 错误,C 正确; 当0x ≤时,令()()cos g x f x x x x =-=-,则()sin 10g x x =-'-≤, 所以()cos g x x x =-在(,0]-∞单调递减,所以当0x ≤时,()(0)1g x g ≥=, 所以函数()y f x x =-在(,0]-∞上没有零点; 当0x >时,()1()ex x g x f x x x -=-=-,所以只需求函数11()1e x h x -=-在(0,)+∞上零点个数,又因为11()1ex h x -=-在(0,)+∞上单调递减,且111(1)10e h -=-=, 所以函数()y f x x =-在(0,)+∞上只有一个零点. 所以函数()y f x x =-有且仅有一个零点,所以B 错误;当0x >时,若()()12f x f x =,因为函数()f x 在(0,1)单调递增,在()1,+∞单调递减, 所以不妨设1201x x <<<,则1122x <-<,所以要证122x x +>,只需证122x x -<,即只需证()()122f x f x ->, 又因为()()12f x f x =,所以只需证()()112f x f x ->.因为()()111111111112111222x x x x x x x x f x f x ee e e ---------=-=-, 所以令函数112()(01)ee x xx xx x ϕ---=-<<, 则()22111(1)e e 11()0e e e xx x x x x x x ϕ--+----=-'=>,所以112()e e x xx xx ϕ---=-在(0,1)单调递增,所以1111121()(1)0e e x ϕϕ---<=-=, 即112()0(01)ee x xxxx x ϕ---=-<<<恒成立,所以1()0x ϕ<, 即()()11111111220x x x x f x f x e e -----=-<,所以()()112f x f x ->, 从而122x x +>成立. 所以选项D 正确. 故选:CD.46.(2022·广东清远·高三期末)将函数1cos (0)6⎛⎫=+> ⎪⎝⎭y x πωω图象上所有的点向右平移6π个单位长度后,得到函数2cos(2)||2⎛⎫=+< ⎪⎝⎭y x πϕϕ的图象,若函数12()f x y y =+,则( )A .()f x 的最小值是B .()f x 的图象关于直线4x π=对称C .()f x 的最小正周期是πD .()f x 的单调递增区间是,()2k k k πππ⎡⎤-∈⎢⎥⎣⎦Z【答案】ACD 【分析】根据题意先求出2y ,进而求出()f x ,然后通过两角和与差的余弦公式进行化简,最后结合三角函数值的图象和性质求得答案. 【详解】由题意知,12cos 2,cos 2cos 26666⎡⎤⎛⎫⎛⎫⎛⎫=+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦y x y x x ππππ,则11()cos 2cos 2cos 2sin 2cos 2sin 26622f x x x x x x x ππ⎛⎫⎛⎫=++-=⋅+⋅ ⎪ ⎪⎝⎭⎝⎭2x =,()f x 的最小值是π,故A ,C 正确;令2()x k k π=∈Z ,得()2k x k π=∈Z ,若24k ππ=,则12=∉Z k ,故B 错误;令222()-≤≤∈Z k x k k πππ,得()2-≤≤∈Z k x k k πππ,即()f x 的单调递增区间是,()2k k k πππ⎡⎤-∈⎢⎥⎣⎦Z ,故D 正确. 故选:ACD.47.(2022·广东汕尾·高三期末)以下关于函数()sin 22f x x x =的命题,正确的是( ) A .函数()y f x =的最小正周期为πB .点,012π⎛⎫⎪⎝⎭是函数()y f x =图象的一个对称中心C .直线3x π=的函数()y f x =图象的一条对称轴D .将函数()y f x =的图象向右平移6π个单位后得到的函数的图象关于原点对称 【答案】AD 【分析】整理可得2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,代入周期公式,可判断A 的正误,根据212f π⎛⎫= ⎪⎝⎭可判断B 的正误,根据03f π⎛⎫= ⎪⎝⎭可判断C 的正误,求得平移后的解析式,可判断D 的正误,即可得答案. 【详解】由题意得()sin 222sin 23f x x x x π⎛⎫=+=+ ⎪⎝⎭,所以最小正周期22T ππ==,所以A 对. 2sin 2212123πππf ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,所以直线12x π=是函数()f x 图象的一条对称轴,所以B 错.2sin 20333πππf ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,所以点,03π⎛⎫ ⎪⎝⎭是函数()f x 图象的一个对称中心,所以C 错.将函数2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移6π个单位后得到的图象对应的函数为2sin 22sin 263y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,是奇函数,所以D 对.故选:AD .48.(2022·广东·铁一中学高三期末)将函数()()πcos 02f x x ωω⎛⎫=-> ⎪⎝⎭的图象向右平移π2个单位长度后得到函数()g x 的图象,且()01g =-,则下列说法正确的是( ) A .()g x 为奇函数 B .π02g ⎛⎫-= ⎪⎝⎭。
高考数学专题《三角函数的图象与性质》习题含答案解析

专题5.3 三角函数的图象与性质1.(2021·北京市大兴区精华培训学校高三三模)下列函数中,既是奇函数又以π为最小正周期的函数是()A .cos 2y x =B .sin2y x=C .sin cos y x x=+D .tan 2y x=【答案】B 【解析】由三角函数的奇偶性和周期性判断即可得出答案.【详解】解:A 选项:cos 2y x =是周期为π的偶函数,故A 不正确;B 选项:sin2y x =是周期为π的奇函数,故B 正确;C选项:sin cos 4y x x x π⎛⎫=+=+ ⎪⎝⎭,周期为2π且非奇非偶函数,故C 不正确;D 选项:tan 2y x =是周期为2π的奇函数,故D 不正确.故选:B.2.(2021·海南高三其他模拟)下列函数中,既是偶函数又存在零点的是( )A .ln y x =B .21y x =+C .sin y x=D .cos y x=【答案】D 【解析】根据题意,依次分析选项中函数的奇偶性以及是否存在零点,综合即可得答案.【详解】解:根据题意,依次分析选项:对于A ,y lnx =,为对数函数,不是奇函数,不符合题意,对于B ,21y x =+,为二次函数,是偶函数,但不存在零点,不符合题意,对于C ,sin y x =,为正弦函数,是奇函数,不符合题意,对于D ,cos y x =,为余弦函数,既是偶函数又存在零点,符合题意,故选:D .练基础3.(2021·浙江高三其他模拟)函数y =sin tan x e xx在[-2,2]上的图像可能是( )A .B .C .D .【答案】B 【解析】利用同角三角函数的商数关系并注意利用正切函数的性质求得函数的定义域,可以化简得到()cos ,2x k f x e x x k Z π⎛⎫=≠∈ ⎪⎝⎭,考察当x 趋近于0时,函数的变化趋势,可以排除A,考察端点值的正负可以评出CD.【详解】()sin cos ,tan 2x x e x k f x e x x k Z x π⎛⎫==≠∈ ⎪⎝⎭,当x 趋近于0时,函数值趋近于0cos 01e =,故排除A;()22cos 20f e =<,故排除CD,故选:B4.(2021·全国高三其他模拟(理))函数y =tan(3x +6π)的一个对称中心是( )A .(0,0)B .(6π,0)C .(49π,0)D .以上选项都不对【答案】C 【解析】根据正切函数y =tan x 图象的对称中心是(2k π,0)求出函数y =tan(3x +6π)图象的对称中心,即可得到选项.【详解】解:因为正切函数y =tan x 图象的对称中心是(2k π,0),k ∈Z ;令3x +6π=2k π,解得618k x ππ=-,k ∈Z ;所以函数y =tan(3x +6π)的图象的对称中心为(618k ππ-,0),k ∈Z ;当k =3时,C 正确,故选:C.5.(2019年高考全国Ⅱ卷文)若x 1=,x 2=是函数f (x )=(>0)两个相邻的极值点,则=( )A .2B .C .1D .【答案】A【解析】由题意知,的周期,解得.故选A .6.(2021·临川一中实验学校高三其他模拟(文))若函数cos (0)y x ωω=>的图象在区间,24ππ⎛⎫- ⎪⎝⎭上只有一个对称中心,则ω的取范围为( )A .12ω<≤B .ω1≤<2C .13ω<≤D .13ω≤<【答案】A 【解析】根据题意可得422πππω≤<,即可求出.【详解】4π43πsin x ωωω3212()sin f x x ω=232()44T ωπππ==-=π2ω=由题可知,cos (0)y x ωω=>在,42ππ⎡⎫⎪⎢⎣⎭上只有一个零点,又2x πω=,2x πω=,所以422πππω≤<,即12ω<≤.故选:A.7.(2019年高考北京卷文)设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的( ) A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】时,,为偶函数;为偶函数时,对任意的恒成立,即,,得对任意的恒成立,从而.从而“”是“为偶函数”的充分必要条件,故选C.8.(2021·青海西宁市·高三二模(文))函数()cos 218f x x π⎛⎫=-- ⎪⎝⎭图象的一个对称中心为( )A .,14π⎛⎫-- ⎪⎝⎭B .,14π⎛⎫-⎪⎝⎭C .,116π⎛⎫-- ⎪⎝⎭D .3,116π⎛⎫-- ⎪⎝⎭【答案】D 【解析】根据余弦函数的对称中心整体代换求解即可.【详解】令2()82x k k πππ-=+∈Z ,可得5()216k x k ππ=+∈Z .所以当1k =-时,316x π=-,故3,116π⎛⎫-- ⎪⎝⎭满足条件,当0k =时,516x π=,故5,116π⎛⎫-⎪⎝⎭满足条件;故选:D0b =()cos sin cos f x x b x x =+=()f x ()f x ()=()f x f x -x ()cos()sin()cos sin f x x b x x b x -=-+-=-cos sin cos sin x b x x b x +=-sin 0b x =x 0b =0b =()f x9.(2021·全国高一专题练习)设函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭,则下列结论错误的是( )A .()f x 的最小正周期为2πB .()f x 的图象关于直线23x π=对称C .()f x 在,2ππ⎛⎫⎪⎝⎭单调递减D .()f x 的一个零点为6x π=【答案】C 【解析】根据解析式结合余弦函数的性质依次判断每个选项的正误即可.【详解】函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭,()f x ∴的最小正周期为2π,故A 正确;22(cos 1333f πππ⎛⎫=+=- ⎪⎝⎭,∴()f x 的图象关于直线23x π=对称,故B 正确;当x ∈,2ππ⎛⎫⎪⎝⎭时,54,363πππx ⎛⎫+∈ ⎪⎝⎭,()f x 没有单调性,故C 错误;()cos 0663f πππ⎛⎫=+= ⎪⎝⎭,∴()f x 的一个零点为6x π=,故D 正确.综上,错误的选项为C.故选:C.10.(2017·全国高考真题(理))函数f (x )=s in 2x +3cosx ―34(x ∈0,__________.【答案】1【解析】化简三角函数的解析式,则f (x )=1―cos 2x+3cos x ―34=―cos 2x +3cos x +14= ―(cos x ―32)2+1,由x ∈[0,π2]可得cos x ∈[0,1],当cos x =32时,函数f (x )取得最大值1.练提升1.(2021·河南高二月考(文))已知函数()()sin 0,02f x x πωϕωϕ⎛⎫=+ ⎪⎝⎭><<的相邻的两个零点之间的距离是6π,且直线18x π=是()f x 图象的一条对称轴,则12f π⎛⎫=⎪⎝⎭( )A.B .12-C .12D【答案】D 【解析】由相邻两个零点的距离确定周期求出6ω=,再由对称轴确定6π=ϕ,代入12x π=可求出结果.【详解】解:因为相邻的两个零点之间的距离是6π,所以26T π=,23T ππω==,所以6ω=,又sin 6sin 118183f πππϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+=±⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,且02πϕ<<,则6π=ϕ,所以()sin 66f x x π⎛⎫=+ ⎪⎝⎭,则sin 612126f πππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭.故选:D.2.(2020·山东潍坊�高一期末)若函数的最小正周期为,则( )A .B .C .D .【答案】C 【解析】由题意,函数的最小正周期为,可得,解得,即,()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭π(2)(0)5f f f π⎛⎫>>-⎪⎝⎭(0)(2)5f f f π⎛⎫>>-⎪⎝⎭(0)(2)5f f f π⎛⎫>-> ⎪⎝⎭(0)(2)5f f f π⎛⎫->> ⎪⎝⎭()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭πwππ=1w =()tan()4f x x π=+令,即,当时,,即函数在上单调递增,又由,又由,所以.故选:C.3.(2021·广东佛山市·高三二模)设()0,θπ∈,则“6πθ<”是“1sin 2θ<”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A 【解析】由条件即06πθ<<,由06πθ<<,得1sin 2θ<;反之不成立,可举反例.再由充分必要条件的判定得答案.【详解】由()0,θπ∈,则6πθ<,即06πθ<<所以当06πθ<<时,由正弦函数sin y x =的单调性可得1sin sin62πθ<=,即由6πθ<可以得到1sin 2θ<.反之不成立,例如当56πθπ<<时,也有1sin 2θ<成立,但6πθ<不成立.故“6πθ<”是“1sin 2θ<”的充分不必要条件故选:A4.(2021·四川省华蓥中学高三其他模拟(理))已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的最,242k x k k Z πππππ-+<+<+∈3,44k x k k Z ππππ-+<<+∈1k =544x ππ<<()f x 5(,)44ππ4(0)(),()()()555f f f f f πππππ=-=-+=425ππ>>(0)(2)5f f f π⎛⎫>-> ⎪⎝⎭大值为2,其图象相邻两条对称轴之间的距离为2π且()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称,则下列判断不正确的是()A .要得到函数()f x 的图象,只需将2cos 2y x =的图象向右平移12π个单位B .函数()f x 的图象关于直线712x π=对称C .,126x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()f x D .函数()f x 在5,612ππ⎡⎤⎢⎥⎣⎦上单调递减【答案】C 【解析】根据最大值为2,可得A ,根据正弦型函数的周期性,可求得ω,根据对称性,可求得ϕ,即可得()f x 解析式,根据正弦型函数的单调性、值域的求法,逐一分析选项,即可得答案.【详解】由题意得A =2,因为其图象相邻两条对称轴之间的距离为2π,所以22Tπ=,可得2T ππω==,所以2ω=,所以()2sin(2)f x x ϕ=+,因为,06π⎛⎫-⎪⎝⎭为对称中心,所以2,6k k Z πϕπ⎛⎫⨯-+=∈ ⎪⎝⎭,因为||2ϕπ<,令k =0,可得3πϕ=,所以2n 2)3(si f x x π⎛⎫=+⎪⎝⎭.对于A :将2cos 2y x =的图象向右平移12π个单位,可得2cos 22cos 22cos 22sin 22sin 21266263y x x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-=-=-=--=+ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,故A 正确;对于B :令2,32x k k Z πππ+=+∈,解得,212k x k Z ππ=+∈,令k =1,可得712x π=,所以函数()f x 的图象关于直线712x π=对称,故B 正确;对于C :因为,126x ππ⎡⎤∈-⎢⎥⎣⎦,所以22,363x πππ⎡⎤+∈⎢⎥⎣⎦,所以当236x ππ+=时,min ()2sin16f x π==,故C 错误;对于D :令3222,232k x k k Z πππππ+≤+≤+∈,解得7,1212k x k k Z ππππ+≤≤+∈,令k =0,可得一个单调减区间为7,1212ππ⎡⎤⎢⎥⎣⎦,因为57,,6121212ππππ⎡⎤⎡⎤⊂⎢⎥⎢⎥⎣⎦⎣⎦,所以函数()f x 在5,612ππ⎡⎤⎢⎥⎣⎦上单调递减,故D 正确.故选:C5.(2021·玉林市第十一中学高三其他模拟(文))已知函数()sin (0)f x x ωω=>的图象向右平移4π个单位长度得y =g (x )的图象,若函数g (x )的图象与直线y =在,22ππ⎡⎤-⎢⎥⎣⎦上恰有两个交点,则a 的取值范围是( )A .[416,)39B .1620,[)99C .[208,93D .[8,4)3【答案】B 【解析】由函数的平移可得()sin 4g x x πωω⎛⎫=- ⎪⎝⎭,结合三角函数的图象与性质可得ω满足的不等式,即可得解.【详解】由题意,()sin sin 44g x x x ππωωω⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,当,22x ππ⎡⎤∈-⎢⎥⎣⎦时,3,444x πωπωπωω⎡⎤-∈-⎢⎥⎣⎦,因为函数g (x )的图象与直线y =在,22ππ⎡⎤-⎢⎥⎣⎦上恰有两个交点,则3542,2433122,2433k k k k πωπππππωππππ⎧⎛⎤-∈-+-+ ⎪⎥⎪⎝⎦⎨⎡⎫⎪∈++⎪⎢⎪⎣⎭⎩或3412,2433272,2433k k k k πωπππππωππππ⎧⎛⎤-∈-++ ⎪⎥⎪⎝⎦⎨⎡⎫⎪∈++⎪⎢⎪⎣⎭⎩,k Z ∈,又0>ω,所以1620,99ω⎡∈⎫⎪⎢⎣⎭.故选:B.6.(2020·北京四中高三其他模拟)函数tan 42y x ππ⎛⎫=- ⎪⎝⎭ 的部分图象如图所示,则 ()OA OB AB +⋅=( )A .6B .5C .4D .3【答案】A 【解析】根据正切函数的图象求出A 、B 两点的坐标,再求出向量的坐标,根据向量数量积的坐标运算求出结果.【详解】由图象得,令tan 42y x ππ⎛⎫=- ⎪⎝⎭=0,即42x ππ-=kπ,k Z∈k =0时解得x =2,令tan 42y x ππ⎛⎫=-⎪⎝⎭=1,即424x πππ-=,解得x =3,∴A (2,0),B (3,1),∴()()()2,0,3,1,1,1OA OB AB ===,∴()()()5,11,1516OA OB AB +⋅=⋅=+=.故选:A .7.(2020·全国高三其他模拟(文))若函数()(0)xf x n nπ=>图象上的相邻一个最高点和一个最低点恰好都在圆222:O x y n +=上,则()1f =( )A B .C .-D .【答案】A 【解析】首先由题意判断该正弦型函数的大概图象及相邻最高点和最低点与圆的交点情况.从而解得n 的取值,再代入1x =求解.【详解】解:设两交点坐标分别为()11,x y ,()22,x y ,则1y =,2y =-又函数()(0)xf x n nπ=>为奇函数,∴12x x =-,当22xnx n ππ=⇒=时,函数取得最大值,∴12n x =-,22nx =,由题,函数()(0)xf x n nπ=>图象上的相邻一个最高点和一个最低点恰好都在圆22: O x y n +=上,∴22242n n n ⎛⎫+=⇒= ⎪⎝⎭,则(1)4f π==.故选:A.8.【多选题】(2021·全国高三其他模拟)已知函数()2sin(),(0,0)f x x ωϕωϕπ=+><<图象的一条对称轴为23x π=,4⎛⎫= ⎪⎝⎭f π,且()f x 在2,43ππ⎛⎫ ⎪⎝⎭内单调递减,则以下说法正确的是( )A .7,012π⎛⎫-⎪⎝⎭是其中一个对称中心B .145ω=C .()f x 在5,012π⎛⎫- ⎪⎝⎭单増D .16f π⎛⎫-=- ⎪⎝⎭【答案】AD 【解析】先根据条件求解函数的解析式,然后根据选项验证可得答案.【详解】∵f (x )关23x π=对称,4⎛⎫= ⎪⎝⎭f π,f (x )在2,43ππ⎛⎫ ⎪⎝⎭单调递减,232232,22643k k ωπωϕπππππϕωϕπ⎧=+=+⎧⎪⎪⎪∴∴⎨⎨=⎪⎪+=+⎩⎪⎩,B 错误;()2sin 2,6f x x π⎛⎫=+ ⎪⎝⎭令2,6x k k ππ+=∈Z ,可得,,122k x k ππ=-+∈Z 当1k =-时,7,12x π=-即()f x 关于7,012π⎛⎫- ⎪⎝⎭对称,A 正确;令222,262k x k πππππ-+<+<+得,312k x k ππππ-+<<+∴()f x 在,312ππ⎡⎤-⎢⎥⎣⎦单调递増,即C 错误;2sin 2sin 16366f ππππ⎛⎫⎛⎫⎛⎫-=-+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,D 正确,故选:AD.9.【多选题】(2021·重庆市蜀都中学校高三月考)已知函数()f x 满足x R ∀∈,有()(6)f x f x =-,且(2)(2)f x f x +=-,当[1,1]x ∈-时,)()lnf x x =-,则下列说法正确的是( )A .(2021)0f =B .(2020,2022)x ∈时,()f x 单调递增C .()f x 关于点(1010,0)对称D .(1,11)x ∈-时,方程()sin 2f x x π⎛⎫=⎪⎝⎭的所有根的和为30【答案】CD 【解析】利用已知条件可知()f x 在[1,1]x ∈-上为奇函数且单调递减,关于21x k =+、(2,0)k ,k Z ∈对称,且周期为4,即可判断各选项的正误.【详解】由题设知:()))()f x x x f x -===-=-,故()f x 在[1,1]x ∈-上为奇函数且单调递减,又(2)(4)(2)f x f x f x +=-=-,即关于21x k =+、(2,0)k ,k Z ∈对称,且最小周期为4,A :(2021)(50541)(1)1)0f f f =⨯+==-≠,错误;B :(2020,2022)x ∈等价于(0,2)x ∈,由上易知:(0,1)上递减,(1,2)上递增,故()f x 不单调,错误;C :由上知:()f x 关于(2,0)k 对称且k Z ∈,所以()f x 关于(1010,0)对称,正确;D :由题意,只需确定()f x 与sin 2xy π=在(1,11)x ∈-的交点,判断交点横坐标的对称情况即可求和,如下图示,∴共有6个交点且关于5x =对称,则16253410x x x x x x +=+=+=,∴所有根的和为30,正确.故选:CD10.(2021·浙江杭州市·杭州高级中学高三其他模拟)设函数sin 3xy π=在[,1]t t +上的最大值为()M t ,最小值为()N t ,则()()M t N t -在3722t ≤≤上最大值为________.【答案】1【解析】依题意可得函数在39,22⎡⎤⎢⎥⎣⎦上单调递减,则39[,1],22t t ⎡⎤+⊆⎢⎥⎣⎦,所以()()cos 36t M t N t ππ⎛⎫-=-+⎪⎝⎭,即可求出函数的最大值;【详解】解:函数sin3xy π=的周期为6,函数sin3xy π=在39,22⎡⎤⎢⎥⎣⎦上单调递减,当3722t ≤≤时,39[,1],22t t ⎡⎤+⊆⎢⎥⎣⎦(1)()()sinsin2cos sin cos 3336636tt t t M t N t πππππππ+⎛⎫⎛⎫⎛⎫-=-=+-=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为3722t ≤≤,所以243363t ππππ≤+≤,所以11cos 362t ππ⎛⎫-≤+≤-⎪⎝⎭所以1()()12M t N t ≤-≤当52t =时取最大值1故答案为:11.(2021·全国高考真题(理))已知命题:,sin 1p x x ∃∈<R ﹔命题:q x ∀∈R ﹐||e 1x ≥,则下列命题中为真命题的是( )A .p q ∧B .p q⌝∧C .p q∧⌝D .()p q ⌝∨【答案】A 【解析】由正弦函数的有界性确定命题p 的真假性,由指数函数的知识确定命题q 的真假性,由此确定正确选项.【详解】由于1sin 1x -≤≤,所以命题p 为真命题;由于0x ≥,所以||e 1x ≥,所以命题q 为真命题;所以p q ∧为真命题,p q ⌝∧、p q ∧⌝、()p q ⌝∨为假命题.故选:A .2.(2021·全国高考真题)下列区间中,函数()7sin 6f x x π⎛⎫=-⎪⎝⎭单调递增的区间是( )练真题A .0,2π⎛⎫⎪⎝⎭B .,2ππ⎛⎫⎪⎝⎭C .3,2ππ⎛⎫ ⎪⎝⎭D .3,22ππ⎛⎫ ⎪⎝⎭【答案】A 【解析】解不等式()22262k x k k Z πππππ-<-<+∈,利用赋值法可得出结论.【详解】因为函数sin y x =的单调递增区间为()22,22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭,对于函数()7sin 6f x x π⎛⎫=- ⎪⎝⎭,由()22262k x k k Z πππππ-<-<+∈,解得()22233k x k k Z ππππ-<<+∈,取0k =,可得函数()f x 的一个单调递增区间为2,33ππ⎛⎫-⎪⎝⎭,则20,,233πππ⎛⎫⎛⎫⊆- ⎪ ⎪⎝⎭⎝⎭,2,,233ππππ⎛⎫⎛⎫⊄- ⎪ ⎪⎝⎭⎝⎭,A 选项满足条件,B 不满足条件;取1k =,可得函数()f x 的一个单调递增区间为58,33ππ⎛⎫⎪⎝⎭,32,,233ππππ⎛⎫⎛⎫⊄- ⎪ ⎪⎝⎭⎝⎭且358,,233ππππ⎛⎫⎛⎫⊄ ⎪ ⎪⎝⎭⎝⎭,358,2,233ππππ⎛⎫⎛⎫⊄ ⎪⎪⎝⎭⎝⎭,CD 选项均不满足条件.故选:A.3.(2019年高考全国Ⅰ卷文)函数f (x )=在的图象大致为( )A .B .C .D .【答案】D2sin cos ++x xx x[,]-ππ【解析】由,得是奇函数,其图象关于原点对称,排除A .又,排除B ,C ,故选D .4.(2020·全国高考真题(理))设函数()cos π(6f x x ω=+在[π,π]-的图像大致如下图,则f (x )的最小正周期为( )A .10π9B .7π6C .4π3D .3π2【答案】C 【解析】由图可得:函数图象过点4,09π⎛⎫-⎪⎝⎭,将它代入函数()f x 可得:4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭又4,09π⎛⎫-⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点,所以4962πππω-⋅+=-,解得:32ω=所以函数()f x 的最小正周期为224332T πππω===故选:C22sin()()sin ()()cos()()cos x x x xf x f x x x x x -+----===--+-+()f x 22π1π42π2(1,π2π()2f ++==>2π(π)01πf =>-+5.(2020·全国高考真题(理))关于函数f (x )=1sin sin x x+有如下四个命题:①f (x )的图像关于y 轴对称.②f (x )的图像关于原点对称.③f (x )的图像关于直线x =2π对称.④f (x )的最小值为2.其中所有真命题的序号是__________.【答案】②③【解析】对于命题①,152622f π⎛⎫=+=⎪⎝⎭,152622f π⎛⎫-=--=- ⎪⎝⎭,则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭,所以,函数()f x 的图象不关于y 轴对称,命题①错误;对于命题②,函数()f x 的定义域为{},x x k k Z π≠∈,定义域关于原点对称,()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭,所以,函数()f x 的图象关于原点对称,命题②正确;对于命题③,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭ ,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭,则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,所以,函数()f x 的图象关于直线2x π=对称,命题③正确;对于命题④,当0x π-<<时,sin 0x <,则()1sin 02sin f x x x=+<<,命题④错误.故答案为:②③.6.(2018·北京高考真题(理))设函数f (x )=cos(ωx ―π6)(ω>0),若f (x )≤f (π4)对任意的实数x 都成立,则ω的最小值为__________.【答案】23【解析】因为f (x )≤f (π4)对任意的实数x 都成立,所以f (π4)取最大值,所以π4ω―π6=2k π(k ∈Z ),∴ω=8k +23(k∈Z ),因为ω>0,所以当k =0时,ω取最小值为23.。
高二数学三角函数的图象与性质试题答案及解析

高二数学三角函数的图象与性质试题答案及解析1.已知,x,y R.(1)若,求的最小值;(2)设,求的取值范围.【答案】(1);(2)。
【解析】(1)利用“乘1法”(即任何数乘以1等于其本身)把变形为,然后,利用基本不等式求最值。
(2)利用转化与化归思想,利用把中的二元转化为一元,既得,这是一个关于的二次函数,即问题转化为二次函数给定区间上的最值问题,注意对称轴与给定区间的关系。
试题解析:(1).当且仅当,时等号成立. 8分(2)由,得.由,,得.,当时,;当时,.所以,的取值范围是. 16分【考点】(1)转化与化归思想的应用;(2)利用基本不等式求最值,注意条件:一正、二定、三相等,(3)与三角函数有关的二次函数给定区间上的最值问题,注意对称轴与给定区间的关系。
2.已知函数(其中,,)的部分图象如图所示,则函数的解析式是 .【答案】.【解析】由图像,得,;代入得,令,得,所以函数的解析式为.【考点】三角函数的图像与性质.3.函数(其中,)的图象如图所示,为了得到的图象,只需将的图象()A.向右平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向左平移个单位长度【答案】C【解析】由函数图象可知,,即,所以,又过,代入得,因为,所以,即有,从而,此时为了得到的图象,只需将的图象向右平移个单位长度,故选择C.【考点】三角函数的图象、性质及图象变换.4.若对可导函数,当时恒有,若已知是一锐角三角形的两个内角,且,记则下列不等式正确的是()A.B.C.D.【答案】C【解析】由于当时恒有,所以,故知函数F(x)在[0,1]上是减函数;又因为已知是一锐角三角形的两个内角,且,所以,因此有,故选C.【考点】1.函数的导数;2.三角函数的性质.5.已知函数满足,其图像与直线y=0的某两个交点的横坐标分别为、,的最小值为,则().A.B.C.D.【答案】D【解析】函数满足,即是奇函数,,即;因为其图像与直线y=0的某两个交点的横坐标分别为、,的最小值为,所以,即,.【考点】三角函数的图像与性质.6.将函数y=cos2x的图象向右平移个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为().A.y=sinx B.y=-cos4x C.y=sin4x D.y=cosx【答案】A.【解析】.【考点】函数图像的平移伸缩变换,诱导公式.7.函数的图象沿x轴向左平移个单位后,得到一个偶函数的图象,则φ的一个可能的值为().A.B.C.D.【答案】A.【解析】可知,即,而此函数为偶函数,则令,得,取,得,故选A.(此题也可由选项分别代入表达式进行排除.)【考点】图像的平移,偶函数的概念,诱导公式.8.函数的一个单调递增区间为 ( )A.B.C.D.【答案】D【解析】由余弦函数的图象:知应选D.【考点】余弦函数的单调性9.函数f(x)=Asin(ωx+)(ω>0)的图像与x轴交点的横坐标构成一个公差为的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图像()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【答案】A【解析】由题设知,又因为,而,所以所以,=,因为所以,要得到的图象,只需将的图象向左平移个单位.故选A.【考点】1、三解函数的图象与性质;2、三角函数的图象变换;3、诱导公式.10.下列函数中,最小正周期为π的偶函数是()A.B.C.y=sin2x+cos2x D.y=【答案】D【解析】,是最小正周期为π的奇函数;,,是最小正周期为的偶函数;,,最小正周期为,非奇非偶函数.,则函数是最小正周期为π的偶函数.【考点】1.诱导公式;2.函数的奇偶性;3.函数的周期.11.函数的最小正周期是()A.B.C.D.【答案】D【解析】,所以最小正期为.【考点】1.函数的周期;2.倍角公式.12.函数的值域为()A.B.C.D.【答案】B【解析】【考点】三角函数化简及性质点评:三角函数化简时常会用到关系式,其中由共同决定,结合的范围是求出值域13.函数(,,是常数,,)的部分图象如下图所示,则的值是【答案】【解析】依题意,,所以,令,则,故,所以.【考点】由y="A" sin(ωx+φ)的部分图象确定其解析式.点评:本题主要考查由函数y="A" sin(ωx+∅)的部分图象求函数的解析式,属于中档题.14.函数在点处的切线方程是( )A.B.C.D.【答案】D【解析】因为,所以,切线的斜率为-2,切线方程为,故选D。
(完整word版)三角函数图像与性质试题及配套答案

xO y1 2 3三角函数测试题一、选择题1、函数)32sin(2π+=x y 的图象( )A .关于原点对称B .关于点(-6π,0)对称C .关于y 轴对称D .关于直线x=6π对称 2、函数sin(),2y x x R π=+∈是 ( )A .[,]22ππ-上是增函数 B .[0,]π上是减函数C .[,0]π-上是减函数D .[,]ππ-上是减函数 3、如图,曲线对应的函数是 ( ) A .y=|sin x | B .y=sin |x |C .y=-sin |x |D .y=-|sin x |4.下列函数中,最小正周期为π,且图象关于直线3x π=对称的( ). A 。
)62sin(+=x y B.sin()26x y π=+ C.sin(2)6y x π=- D.sin(2)3y x π=-5.函数)sin(ϕω+=x y 的部分图象如右图,则ω,ϕ可以取的一组值是( )。
A 。
,24ωϕππ== B.,36ωϕππ==C.5,44ωϕππ==D.,44ωϕππ==6。
要得到3sin(2)4y x π=+的图象,只需将x y 2sin 3=的图象( ).A.向左平移4π个单位B.向右平移4π个单位C 。
向左平移8π个单位 D.向右平移8π个单位7。
设tan()2απ+=,则sin()cos()sin()cos()αααα-π+π-=π+-π+( ).A.3 B 。
13C 。
1D 。
1- 8。
A 为三角形ABC 的一个内角,若12sin cos 25A A +=,则这个三角形的形状为( ).A. 锐角三角形B. 钝角三角形C. 等腰直角三角形D. 等腰三角形9.定义在R 上的函数)(x f 既是偶函数又是周期函数,若)(x f 的最小正周期是π,且当[0,]2x π∈时,x x f sin )(=,则5()3f π的值为( ).A.21-B.23 C.23-D 。
2110.函数2cos 1y x =+的定义域是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的图象与性质
函数y =A sin(ωx +φ)的图象
(时间:80分钟 满分:100分)
一、选择题(每小题5分,共40分) 1.函数y =sin ⎝ ⎛
⎭
⎪⎫4x +32π的周期是( ).
A .2π
B .π C.π2 D .π
4 解析 T =2π4=π
2. 答案 C
2.函数y =cos ⎝ ⎛⎭
⎪⎫
x +π2(x ∈R )是( ).
A .奇函数
B .偶函数
C .非奇非偶函数
D .无法确定 解析 ∵y =cos ⎝ ⎛⎭⎪⎫
x +π2=-sin x ,∴此函数为奇函数.
答案 A
3.函数y =cos x 图象上各点的纵坐标不变,把横坐标变为原来的2倍,得到图象的解析式为y =cos ωx ,则ω的值为( ).
A .2
B .12
C .4
D .1
4
解析 由已知y =cos x 的图象经变换后得到y =cos 12x 的图象,所以ω=1
2. 答案 B
4.函数y =-x sin x 的部分图象是( ).
解析 考虑函数的奇偶性并取特殊值.函数y =-x sin x 是偶函数,当x ∈⎝ ⎛
⎭⎪⎫0,π2时,y <0. 答案 C
5.在下列区间上函数y =sin ⎝ ⎛⎭
⎪⎫
x +π4为增函数的是( ).
A.⎣⎢⎡⎦⎥⎤-π2,π2 B .⎣⎢⎡⎦⎥⎤-3π4,π4 C .[-π,0] D .⎣⎢⎡⎦⎥⎤
-π4,3π4 解析 由2k π-π2≤x +π4≤2k π+π2(k ∈Z )得2k π-3π4≤x ≤2k π+π
4(k ∈Z ),当k =0时,-3π4≤x ≤π
4,故选B. 答案 B
6.已知简谐运动f (x )=2sin ⎝ ⎛⎭⎪⎫π3x +φ⎝ ⎛
⎭⎪⎫|φ|<π2的图象经过点(0,1),则该简谐运动的最
小正周期T 和初相φ分别为( ).
A .T =6,φ=π6
B .T =6,φ=π3
C .T =6π,φ=π6
D .T =6π,φ=π
3 解析 将(0,1)点代入f (x )可得sin φ=1
2. ∵|φ|<π2,∴φ=π6,T =2π π 3
=6.
答案 A
7.已知函数y =A sin(ωx +φ)+B 的一部分图象如图所示,如果A >0,ω>0,|φ|<π
2,
A .A =4
B .ω=1
C .φ=π
6 D .B =4 解析 由图象可知,A =2,14T =5π12-π6=π
4,T =π, ω=2.∵2×π6+φ=π2,∴φ=π
6,故选C. 答案 C
8.若函数f (x )=3sin(ωx +φ)对任意的x 都有f ⎝ ⎛⎭⎪⎫π3+x =f ⎝ ⎛⎭⎪⎫π3-x ,则f ⎝ ⎛⎭⎪⎫
π3等于( ).
A .3或0
B .-3或0
C .0
D .-3或3 解析 ∵f ⎝ ⎛⎭⎪⎫π3+x =f ⎝ ⎛⎭⎪⎫
π3-x ,
∴f (x )关于直线x =π
3对称, ∴f ⎝ ⎛⎭⎪⎫
π3应取得最大值或最小值. 答案 D
二、填空题(每小题5分,共20分)
9.函数y =cos x 在区间[-π,a ]上为增函数,则a 的取值范围是________. 解析 ∵y =cos x 在[-π,0]上为增函数,
又在[-π,a ]上递增,∴[-π,a ]⊆[-π,0],∴a ≤0. 又∵a >-π,∴-π<a ≤0. 答案 (-π,0]
10.函数y =tan x ,x ∈⎣⎢⎡
⎦⎥⎤0,π4的值域是________.
解析 ∵y =tan x 在⎣⎢⎡⎦⎥⎤0,π4上单调递增, ∴0≤tan x ≤1,即y ∈[0,1].
11.已知函数y =2sin(ωx +φ)(ω>0)在一个周期内当x =π
12时,有最大值2,当x =7π
12时有最小值-2,则ω=________.
解析 由题意知T =2×⎝ ⎛⎭⎪⎫
7π12-π12=π.∴ω=2πT =2.
答案 2
12.函数y =6sin ⎝ ⎛⎭⎪⎫
14x -π6的初相是________,图象最高点的坐标是________.
解析 初相为-π6,当14x -π6=π2+2k π,即x =8π
3+8k π(k ∈Z )时,函数取得最大值6. 答案 -π
6
⎝ ⎛⎭
⎪⎫
8π3+8k π,6(k ∈Z ) 三、解答题(每小题10分,共40分)
13.用“五点法”作出函数y =2sin ⎝ ⎛⎭⎪⎫
x -π3+3的图象,并指出它的周期、频率、
相位、初相、最值及单调区间. 解 (1)列表:
(2)将函数在一个周期内的图象向左、向右两边扩展,得y =2sin ⎝ ⎛⎭⎪⎫
x -π3+3的图
象.
由图象知,周期T =2π,频率f =1T =1
2π,
相位为x -π3,初相为-π
3
,最大值为5,最小值为1,
函数的单调递减区间为⎣⎢⎡⎦⎥⎤
5π6+2k π,11π6+2k π,k ∈Z ,单调递增区间为
⎣⎢⎡⎦
⎥⎤
-π6+2k π,5π6+2k π,k ∈Z . 14.求函数y =-2tan ⎝ ⎛
⎭⎪⎫3x +π3的定义域、值域,并指出它的周期、奇偶性和单调
性.
解 由3x +π3≠π2+k π,得x ≠π18+k π3(k ∈Z ),∴函数y =-2tan ⎝ ⎛
⎭
⎪⎫3x +π3的定义
域为⎩⎨⎧
x ⎪⎪⎪⎭
⎬⎫x ≠π18+k π
3(k ∈Z ).它的值域为R ,周期为T =π
3,它既不是奇函数,
也不是偶函数.由-π2+k π<3x +π3<π2+k π(k ∈Z ),得-5π18+k π3<x <π18+k π
3(k ∈Z ),所以函数y =-2tan ⎝ ⎛⎭⎪⎫3x +π3在区间⎝ ⎛⎭⎪⎫-5π18+k π3,π18+k π3(k ∈Z )上单调递减. 15.设函数f (x )=sin ⎝ ⎛⎭⎪⎫12x +φ⎝ ⎛
⎭⎪⎫0<φ<π2,y =f (x )图象的一条对称轴是直线x =π4.
(1)求φ;
(2)求函数y =f (x )的单调增区间.
解 (1)∵x =π
4是y =f (x )的图象的一条对称轴, ∴sin ⎝ ⎛⎭⎪⎫
12×π4+φ=±1,∴π8+φ=k π±π2,k ∈Z ,
∵0<φ<π2,∴φ=3π8.
(2)由(1)知φ=3π8,因此y =sin ⎝ ⎛⎭⎪⎫
12x +3π8.
由题意得:2k π-π2≤12x +38π≤2k π+π
2,k ∈Z , 即4k π-74π≤x ≤4k π+π
4,k ∈Z ,
∴函数的单调增区间为⎣⎢⎡
⎦
⎥⎤4k π-74π,4k π+π4,k ∈Z .
16.已知函数f (x )=A sin(ωx +φ)⎝ ⎛
⎭⎪⎫A >0,ω>0,|φ|<π2的图象在y 轴上的截距为1,它在y 轴右侧的第一个最大值点和最小值点分别为(x 0,2)和(x 0+3π,-2). (1)求f (x )的解析式;
(2)将y =f (x )图象上所有点的横坐标缩短到原来的1
3,然后再将所得到的图象向x 轴正方向平移π
3个单位长度,得到函数y =g (x )的图象,写出g (x )的解析式,并作出在长度为一个周期上的图象.
解 (1)由已知,易得A =2,T 2=(x 0+3π)-x 0=3π,解得T =6π,∴ω=13. 把(0,1)代入解析式y =2sin ⎝ ⎛⎭⎪⎫
x 3+φ,得2sin φ=1.
又|φ|<π2,解得φ=π
6. ∴y =2sin ⎝ ⎛⎭
⎪⎫
x 3+π6.
(2)压缩后的函数解析式为y =2sin ⎝ ⎛⎭⎪⎫
x +π6,再平移得g (x )=2sin ⎣⎢⎡⎦⎥⎤⎝
⎛⎭⎪⎫x -π3+π6=2sin ⎝ ⎛⎭⎪⎫
x -π6.
列表:。
