(完整版)概率论第四章答案
概率论与数理统计》课后习题答案第四章

习题4.11.设10个零件中有3个不合格. 现任取一个使用,若取到不合格品,则丢弃重新抽取一个,试求取到合格品之前取出的不合格品数X 的数学期望.解 可得X 的概率分布为0123~77711030120120X ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为7771()012310301201204531208E X =⨯+⨯+⨯+⨯==2..某人有n 把外形相似的钥匙,其中只有1把能打开房门,但他不知道是哪一把,只好逐把试开.求此人直至将门打开所需的试开次数X 的数学期望.解 可得X 的概率分布为12~111n X nn n ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为111()121(1)122E X n n n nn n n n =⨯+⨯++⨯++==3.设5次重复独立试验中每次试验的成功率为0.9,若记失败次数为X ,求X 的数学期望。
解 由题意~(5,0.1)X B ,则X 的数学期望为 ()50.10.E X =⨯= 4.设某地每年因交通事故死亡的人数服从泊松分布.据统计,在一年中因交通事故死亡一人的概率是死亡两人的概率的21,求该地每年因交通事故死亡的平均人数。
解 设该地每年因交通事故死亡的人数为X ,由题意X 服从泊松分布() (0)P λλ>.因1{1}{2}2P X P X === 即121 41!22!ee λλλλλ--=⇒= 于是X 的数学期望为()4E X λ== 所以地每年因交通事故死亡的平均人数为4人。
5.设随机变量X 在区间(1,7)上服从均匀分布,求2{()}P X E X <. 解 因X 在区间(1,7)上服从均匀分布,故X 的数学期望为17()42E X +== 于是22{()}{4}1 {22}6P X E X P X P X <=<=<-<<=6.设连续型随机变量X 的概率密度为01() (,0)0 b ax x p x a b ⎧<<=>⎨⎩其它又知()0.75E X =,求,a b 的值解 由密度函数的性质可得()1p x dx +∞-∞=⎰即1111b aax dx b =⇒=+⎰又由()0.75E X =,可得1()0.75b xp x dx x ax dx +∞-∞=⋅=⎰⎰即0.752ab =+ 求解110.752ab a b ⎧=⎪⎪+⎨⎪=⎪+⎩可得 3,2a b ==.7.设随机变量X 的概率密度为0<1()2 120 x x p x x x <⎧⎪=-≤<⎨⎪⎩其它求数学期望()E X解1201331221()() (2) ()133E X xp x dxx xdx x x dx x x x +∞-∞==⋅+⋅-=+-=⎰⎰⎰8.设随机变量X 的概率分布为X -2 -1 0 1 P 0.2 0.3 0.1 0.4 求 (1)(21)E X -;(2)2()E X .解 (1) (21)2()1E X E X -=- 其中()20.210.3010.40.3E X =-⨯-⨯++⨯=-则(21)2()12(0.3)1 1.6E X E X -=-=⨯--=-(2)22222()0.2(2)0.3(1)0.100.41 1.5E X =⨯-+⨯-+⨯+⨯=9.假设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作。
概率论与数理统计第四章课后习题及参考答案

概率论与数理统计第四章课后习题及参考答案1.在下列句子中随机地取一个单词,以X 表示取到的单词包含的字母的个数,试写出X 的分布律,并求)(X E .Have a good time解:本题的随机试验属于古典概型.所给句子共4个单词,其中有一个单词含一个字母,有3个单词含4个字母,则X 的所有可能取值为1,4,有41)1(==X P ,43)4(==X P ,从而413434411)(=⋅+⋅=X E .2.在上述句子的13个字母中随机地取一个字母,以Y 表示取到的字母所在的单词所含的字母数,写出Y 的分布律,并求)(Y E .解:本题的随机试验属于古典概型.Y 的所有可能取值为1,4,样本空间Ω由13个字母组成,即共有13个样本点,则131)1(==Y P ,1312)4(==Y P ,从而1349131241311)(=⋅+⋅=Y E .3.一批产品有一、二、三等品及废品4种,所占比例分别为60%,20%,10%和10%,各级产品的出厂价分别为6元、8.4元、4元和2元,求产品的平均出厂价.解:设产品的出厂价为X (元),则X 的所有可能取值为6,8.4,4,2,由题设可知X 的分布律为X 68.442P6.02.01.01.0则16.51.021.042.08.46.06)(=⨯+⨯+⨯+⨯=X E (元).4.设随机变量X 具有分布:51)(==k X P ,5,4,3,2,1=k ,求)(X E ,)(2X E 及2)2(+X E .解:3)54321(51)(=++++=X E ,11)54321(51)(222222=++++=X E ,274)(4)()44()2(222=++=++=+X E X E X X E X E .5.设离散型随机变量X 的分布列为k k kk X P 21)!2)1((=-=, ,2,1=k ,问X 是否有数学期望.解:因为∑∑∞=∞==⋅-111212)1(k k k k kkk 发散,所以X 的数学期望不存在.6.设随机变量X 具有密度函数⎪⎩⎪⎨⎧≤≤-=其他.,0,22,cos 2)(2πππx x x f 求)(X E 及)(X D .解:因为x x 2cos 在]2,2[ππ-上为奇函数,所以0d cos 2d )()(222=⋅==⎰⎰-∞+∞-πππx x x x x f x X E ,2112d cos 2d )()(2222222-=⋅==⎰⎰-∞+∞-ππππx x x x x f x X E ,故2112)]([)()(222-=-=πX E X E X D .7.设随机变量X 具有密度函数⎪⎩⎪⎨⎧<<-≤<=其他.,0,21,2,10,)(x x x x x f 求)(X E 及)(X D .解:1d )2(d d )()(2112=-+==⎰⎰⎰∞+∞-x x x x x x x f x X E ,67d )2(d d )()(2121322=-+==⎰⎰⎰∞+∞-x x x x x x x f x X E ,61)]([)()(22=-=X E X E X D .8.设随机变量X 在)21,21(-上服从均匀分布,求)sin(X Y π=的数学期望与方差.解:由题可知X 的密度函数为⎪⎩⎪⎨⎧<<-=其他.,0,2121,1)(x x f 则0d 1sin d )(sin )][sin()(2121=⋅===⎰⎰-∞+∞-x x x x f x X E Y E πππ,21d 1sin d )(sin )]([sin )(21212222=⋅===⎰⎰-∞+∞-x x x x f x X E Y E πππ,21)]([)()(22=-=Y E Y E Y D .9.某正方形场地,按照航空测量的数据,它的边长的数学期望为350m ,又知航空测量的误差随机变量X 的分布列为X (m)30-20-10-0102030P05.008.016.042.016.008.005.0而场地边长随机变量Y 等于边长的数学期望与测量误差之和,即X Y +=350,求场地面积的数学期望.解:设场地面积为S ,则2Y S =,16.01042.0016.0)10(08.0)20(05.030)(⨯+⨯+⨯-+⨯-+⨯-=X E 005.03008.020=⨯+⨯+,16.01042.0016.0)10(08.0)20(05.0)30()(222222⨯+⨯+⨯-+⨯-+⨯-=X E 18605.03008.02022=⨯+⨯+,故)350700(])350[()()(2222++=+==X X E X E Y E S E 122686350)(700)(22=++=X E X E .10.A ,B 两台机床同时加工零件,每生产一批较大的产品时,出次品的概率如下表所示:A 机床次品数X 0123概率P7.02.006.004.0B 机床次品数X 0123概率P8.006.004.010.0问哪一台机床加工质量较好.解:44.004.0306.022.017.00)(=⨯+⨯+⨯+⨯=X E ,8.004.0306.022.017.00)(22222=⨯+⨯+⨯+⨯=X E ,6064.0)]([)()(22=-=X E X E X D ,44.010.0304.0206.018.00)(=⨯+⨯+⨯+⨯=Y E ,12.110.0304.0206.018.00)(22222=⨯+⨯+⨯+⨯=Y E ,9264.0)]([)()(22=-=Y E Y E Y D ,)()(Y E X E =,但)()(Y D X D <,故A 机床加工质量较好.11.设随机变量X 与Y 相互独立,且方差存在,试证:22)]()[()()]([)()()(Y E X D Y D X E Y D X D XY D ++=,由此得出)()()(Y D X D XY D ≥.证:22)]([])[()(XY E XY E XY D -=222)]()([)(Y E X E Y X E -=2222)]([)]([)()(Y E X E Y E X E -=2222)]([)]([})]([)(}{)]([)({Y E X E Y E Y D X E X D -++=22)]()[()()]([)()(Y E X D Y D X E Y D X D ++=.因为)(X D ,)(Y D ,2)]([X E ,2)]([Y E 非负,所以)()()(Y D X D XY D ≥.12.已知随机变量X 的密度函数为⎩⎨⎧≤≤++=其他.,010,)(2x c bx x a x f又已知5.0)(=X E ,15.0)(=X D ,求a ,b ,c .解:c b a x c bx x a x x f ++=++==⎰⎰∞+∞-2131d )(d )(1102,c b a x c bx x a x x x f x X E 213141d )(d )()(5.0102++=++===⎰⎰∞+∞-,⎰⎰++-=-==∞+∞-1222d )()5.0(d )()]([)(15.0xc bx x a x x x f X E x X D 41314151-++=c b a ,解之得12=a ,12-=b ,3=c .13.设),(Y X 的分布律为(1)求)(X E 及)(Y E ;(2)设XYZ =,求)(Z E ;(3)设2)(Y X Z -=,求)(Z E .解:(1)2)13.00(3)1.001.0(2)1.01.02.0(1)(=++⨯+++⨯+++⨯=X E ,0)1.01.01.0(1)3.001.0(0)01.02.0()1()(=++⨯+++⨯+++⨯-=Y E ,(2)1.01)3.001.0(00)31(1.021(2.01)(⨯+++⨯+⨯-+⨯-+⨯-=Z E 1511.0311.021-=⨯+⨯+,(3)1.0)01(0)]1(3[1.0)]1(2[2.0)]1(1[)(2222⨯-+⨯--+⨯--+⨯--=Z E 51.0)13(1.0)12(1.0)11(3.0)03(0)02(22222=⨯-+⨯-+⨯-+⨯-+⨯-+.14.设随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤+=其他.,0,10,20,3),(y x yx y x f求)(X E ,)(Y E ,)(Y X E +及)(22Y X E +.解:⎰⎰∞+∞-∞+∞-=y x y x f x X E d d ),()(911d d 31020=+⋅=⎰⎰y x y x x ,⎰⎰∞+∞-∞+∞-=y x y x yf Y E d d ),()(95d d 31020=+⋅=⎰⎰y x y x y ,⎰⎰∞+∞-∞+∞-+=+y x y x f y x Y X E d d ),()()(916d d 3)(1020=+⋅+=⎰⎰y x y x y x ,⎰⎰∞+∞-∞+∞-+=+y x y x f y x Y X E d d ),()()(2222613d d 3)(102022=+⋅+=⎰⎰y x y x y x .15.),(Y X 在区域}1,0,0|),{(≤+≥≥=y x y x y x D 上服从均匀分布,求)(X E ,)23(Y X E -及)(XY E .解:由题可知),(Y X 的联合密度函数为⎩⎨⎧≤≤-≤≤=其他.,0,10,10,2),(y y x y x f ⎰⎰∞+∞-∞+∞-=y x y x f x X E d d ),()(31d d 21010==⎰⎰-yy x x ,⎰⎰∞+∞-∞+∞--=-y x y x f y x Y X E d d ),()23()23(31d d )23(21010=-=⎰⎰-yy x y x ,⎰⎰∞+∞-∞+∞-=y x y x xyf XY E d d ),()(121d d 21010==⎰⎰-y y x xy .16.设二维随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧>+≤+=.1,0,1,1),(2222y x y x y x f π证明:随机变量X 与Y 不相关,也不相互独立.证:⎰⎰⎰⎰⋅=⋅=∞+∞-∞+∞-πθθππ201d d cos 1d d 1)(r r r y x x X E ,同理,0)(=Y E ,⎰⎰⎰⎰⋅⋅=⋅=∞+∞-∞+∞-πθθθππ201d d sin cos 1d d 1)(r r r r y x xy XY E ,0)()()(),cov(=-=Y E X E XY E Y X ,故随机变量X 与Y 不相关.当11≤≤-x 时,ππ21112d 1d ),()(22x y y y x f x f x x X -===⎰⎰---∞+∞-,其他,0)(=x f X ,故⎪⎩⎪⎨⎧≤≤--=其他.,0,11,12)(2x x x f X π同理,⎪⎩⎪⎨⎧≤≤--=其他.,0,11,12)(2y y y f Y π易得)()(),(y f x f y x f Y X ≠,故随机变量X 与Y 不相互独立.17.设随机变量1X ,2X 的概率密度分别为⎩⎨⎧≤>=-.0,0,0,e 2)(21x x x f x ,⎩⎨⎧≤>=-.0,0,0,e 4)(42y y y f y 试用数学期望的性质求:(1))(21X X E +及)32(221X X E -;(2)又设1X ,2X 相互独立,求)(21X X E .解:由题可知1X ~)2(E ,2X ~)4(E ,则21)(1=X E ,41)(2=X E ,161)(2=X D ,81)]([)()(22222=+=X E X D X E .(1)43)()()(2121=+=+X E X E X X E ,85)(3)(2)32(221221=-=-X E X E X X E .(2)81)()()(2121==X E X E X X E .18.(1)设1X ,2X ,3X 及4X 独立同在)1,0(上服从均匀分布,求)51(41∑=k k kX D ;(2)已知随机变量X ,Y 的方差分别为25和36,相关系数为4.0,求Y X U 23+=的方差.解:(1)由题易得121)(=i X D ,)51(41∑=k k kX D )(5141∑==k kkX D )](4)(3)(2)([514321X D X D X D X D +++=21)4321(121512222=+++⋅=.(2)由已知25)(=X D ,36)(=Y D ,4.0)()(),cov(==Y D X D Y X XY ρ,得12),cov(=Y X ,)2,3cov(2)2()3()23()(Y X Y D X D Y X D U D ++=+=513),cov(232)(2)(322=⋅⋅++=Y X Y D X D .19.一民航送客车载有20位旅客自机场开出,旅客有10个车站可以下车,如果到达一个车站没有旅客下车就不停车,以X 表示停车的次数,求)(X E (设每位旅客在各个车站下车是等可能的,并设各旅客是否下车相互独立).解:引入随机变量⎩⎨⎧=站无人下车.,在第站有人下车;,在第i i X i 01,10,,2,1 =i .易知1021X X X X +++= .按题意,任一旅客在第i 站不下车的概率为9.0,因此20位旅客都不在第i 站下车的概率为209.0,在第i 站有人下车的概率为209.01-,也就是209.0)0(==i X P ,209.01)1(-==i X P ,10,,2,1 =i .由此209.01)(-=i X E ,10,,2,1 =i .进而)()()()()(10211021X E X E X E X X X E X E +++=+++= 784.8)9.01(1020=-=(次).20.将n 只球(1~n 号)随机地放进n 只盒子(1~n 号)中去,一只盒子装一只球.若一只球装入与球同号的盒子中,称为一个配对,记X 为总的配对数,求)(X E .解:引入随机变量⎩⎨⎧=号盒子.号球未放入第第号盒子号球放入第第i i i i X i ,0,,1,n i ,,2,1 =,则n X X X X +++= 21,显然n X P i 1)1(==,则nX P i 11)0(-==,n i ,,2,1 =,从而nX E i 1)(=,n i ,,2,1 =,于是1)()()()()(2121=+++=+++=n n X E X E X E X X X E X E .21.设随机变量),(Y X 的分布律为试验证X 和Y 是不相关的,但X 和Y 不是相互独立的.证:0)25.00(2)025.0(1)025.0()1()25.00(2)(=+⨯++⨯++⨯-++⨯-=X E ,5)25.00025.0(4)025.025.00(1)(=+++⨯++++⨯=Y E ,0)4(25.0)8(0225.0125.0)1(02)(⨯-+⨯-+⨯+⨯+⨯-+⨯-=XY E 025.0804=⨯+⨯+,所以0)()()(),cov(=-=Y E X E XY E Y X ,故X 与Y 不相关.易知25.025.00)2(=+=-=X P ,5.0025.025.00)1(=+++==Y P ,0)1,2(==-=Y X P ,有)1()2()1,2(=-=≠=-=Y P X P Y X P ,故X 与Y 不相互独立.22.设二维随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤+=其他.,0,10,10,),(y x y x y x f 求)(X E ,)(Y E ,)(X D ,)(Y D ,)(XY E ,),cov(Y X 及XY ρ.解:127d d )(d d ),()(1010=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,125d d )(d d ),()(1010222=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,14411)]([)()(22=-=X E X E X D ,由轮换对称性,得127)(=Y E ,14411)(=Y D ,31d d )(d d ),()(1010=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x xy y x y x xyf XY E ,1441)()()(),cov(-=-=Y E X E XY E Y X ,111)()(),cov(-==Y D X D Y X XY ρ.23.设X ~),(2σμN ,Y ~),(2σμN ,且X ,Y 相互独立.求Y X Z βα+=1和Y X Z βα-=2的相关系数(α,β是不为0的常数).解:由题可知μ==)()(Y E X E ,2)()(σ==Y D X D ,则2222)]([)()(σμ+=+=X E X D X E ,2222)]([)()(σμ+=+=Y E Y D Y E ,μβαβα)()()(1+=+=Y X E Z E ,μβαβα)()()(2-=-=Y X E Z E ,222221)()()()()(σβαβαβα+=+=+=Y D X D Y X D Z D ,222222)()()()()(σβαβαβα+=+=-=Y D X D Y X D Z D ,)()])([()(222221Y X E Y X Y X E Z Z E βαβαβα-=-+=))(()()(22222222σμβαβα+-=-=Y E X E ,222212121)()()()(),cov(σβα-=-=Z E Z E Z Z E Z Z ,22222121)()(),cov(21βαβαρ+-==Z D Z D Z Z Z Z .24.设),(Y X 的联合概率密度为⎩⎨⎧≤≤≤≤--=.,0,10,10,2),(其他y x y x y x f (1)求),cov(Y X ,XY ρ和)32(Y X D -;11(2)X 与Y 是否独立?解:(1)125d d )2(d d ),()(1010=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,41d d )2(d d ),()(1010222=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,61d d )2(d d ),()(1010=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x xy y x y x xyf XY E ,14411)]([)()(22=-=X E X E X D ,由轮换对称性,125)(=Y E ,14411)(=Y D ,1441)()()(),cov(-=-=Y E X E XY E Y X ,111)()(),cov(-==Y D X D Y X XY ρ,)3,2cov(2)3()2()32(Y X Y D X D Y X D -+-+=-144155),cov(12)(3)(222=-+=Y X Y D X D .(2)当10≤≤x 时,x y y x y y x f x f X -=--==⎰⎰∞+∞-23d )2(d ),()(10,其他,0)(=x f X ,故⎪⎩⎪⎨⎧≤≤-=其他.,0,10,23)(x x x f X 同理,⎪⎩⎪⎨⎧≤≤-=其他.,0,10,23)(y y y f Y 因为)()(),(y f x f y x f Y X ≠,故X 与Y 不相互独立.。
概率论第四章 习题答案

1 ⎛2⎞ 1 DX = EX − ( EX ) = − ⎜ ⎟ = . 2 ⎝ 3 ⎠ 18 1 2 DZ = 4 DX = 4 × = . 18 9
【解毕】
9.在一次拍卖中,两人竞买一幅名画,拍卖以暗标的形式进行,并以最高价成交.设两人 的出价相互独立且均服从(1,2)上的均匀分布,求这幅画的期望成交价. 解:设两人的出价分别为随机变量 X , Y ,则这幅画的期望成交价为 Z = max { X , Y } 由题意知, X 与Y 独立,且 X ∼ U (1, 2); Y ∼ U (1, 2) 先求 Z 的分布函数 当 1 < z < 2 时, F ( z ) = P ( Z £ z ) = P (max { X , Y } £ z ) = P ( X £ z ,Y £ z )
= P( X £ z ) P (Y £ z ) = ( z -1)2
当 z £ 1 时, F ( z ) = 0 ;当 z ³ 2 时, F ( z ) = 1 于是 Z 的密度函数为 f ( z ) = ï í
ì2( z -1),1 < z < 2 ï ï 0, 其它 ï î 5 3
EZ = ò
+¥
3 X .求: ( 1)常数 a, b, c; (2) Ee . 4
【解】 (1)由概率密度的性质知,有
+∞ 2 4
1=
又因为
−∞
∫
f ( x )dx = ∫ axdx + ∫ ( cx + b )dx = 2a + 6c + 2b.
0 2
+∞
2
4
2 = EX =
−∞
∫ xf ( x )dx = ∫ xiaxdx + ∫ x ( cx + b )dx
《概率论与数理统计》第04章习题解答

第四章 正态分布1、解:(0,1)ZN(1){ 1.24}(1.24)0.8925P Z ∴≤=Φ={1.24 2.37}(2.37)(1.24)0.99110.89250.0986P Z <≤=Φ-Φ==-= {2.37 1.24}( 1.24)( 2.37)(1.24)(2.37)0.89250.99110.0986P Z -<≤-=Φ--Φ-=-Φ+Φ=-+=(2){}0.9147()0.9147 1.37{}0.05261()0.0526()0.9474 1.62P Z a a a P Z b b b b ≤=∴Φ==≥=-Φ=Φ==,,得,,,得2、解:(3,16)XN8343{48}()()(1.25)(0.25)0.89440.59870.295744P X --∴<≤=Φ-Φ=Φ-Φ=-= 5303{05}()()(0.5)(0.75)44(0.5)1(0.75)0.691510.77340.4649P X --<≤=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= 31(25,36){25}0.95442(3,4){}0.95X N C P X C X N C P X C -≤=>≥、()设,试确定,使;()设,试确定,使解:(1)(25,36){25}0.9544X N P X C -≤=,{2525}0.9544P C X C ∴-≤≤+=25252525()()0.954466()()2()10.9544666()0.9772,21266C C C C CC CC +---Φ-Φ=-Φ-Φ=Φ-=Φ=∴==即, (2)(3,4){}0.95XN P X C >≥,331()0.95()0.952231.6450.292C CCC ---Φ≥Φ≥-≥≤-即,,4、解:(1)2(3315,575)XN4390.2533152584.753315{2584.754390.25}()()575575(1.87)( 1.27)(1.87)1(1.27)0.969310.89800.8673P X --∴≤≤=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= (2)27193315{2719}()( 1.04)1(1.04)10.85080.1492575P X -≤=Φ=Φ-=-Φ=-=(25,0.1492)YB ∴4440{4}(0.1492)(10.1492)0.6664ii i i P Y C -=∴≤=-=∑5、解:(6.4,2.3)X N{}{}1()81(1.055)10.85540.14462.3(85}0.17615 6.451(0.923)(0.923)0.82121()2.3P X P X X P X -Φ>-Φ-∴>>======->-Φ-Φ-Φ6、解:(1)2(11.9,(0.2))XN12.311.911.711.9{11.712.3}()()(2)(1)(2)1(1)0.20.20.977210.84130.8185P X --∴<<=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= 设A ={两只电阻器的电阻值都在欧和欧之间} 则2()(0.8185)0.6699P A ==(2)设X , Y 分别是两只电阻器的电阻值,则22(11.9,(0.2))(11.9,(0.2))X N Y N ,,且X , Y 相互独立[]22212.411.9{(12.4)(12.4)}1{12.4}{12.4)}1()0.21(2.5)1(0.9938)0.0124P X Y P X P Y -⎡⎤∴>>=-≤⋅≤=-Φ⎢⎥⎣⎦=-Φ=-=7、一工厂生产的某种元件的寿命X (以小时计)服从均值160μ=,均方差为的正态分布,若要求{120200}0.80P X <<≥,允许最大为多少解:因为2(160,)XN σ由2001601201600.80{120200}()()P X σσ--≤<<=Φ-Φ从而 40402()10.80()0.9σσΦ-≥Φ≥,即,查表得401.282σ≥,故σ≤8、解:(1)2(90,(0.5))XN8990{89}()(2)1(2)10.97720.02280.5P X -∴<=Φ=Φ-=-Φ=-= (2)设2(,(0.5))X N d由808080{80}0.991()0.99()0.99 2.330.50.50.5d d d P X ---≥≥∴-Φ≥Φ≥≥,,,即 从而d ≥ 9、解:22~(150,3),~(100,4)X Y X N Y N 与相互独立,且则(1)2221~(150(100,3)4)(250,5)W X Y N N =+++=()222222~2150100,(2)314(200,52)W X Y N N =+-⨯+-⨯+⨯=-22325~(125,)(125,(2.5))22X Y W N N +== (2)242.6250{242.6}()( 1.48)1(1.48)10.93060.06945P X Y -+<=Φ=Φ-=-Φ=-= 12551255125522212551251255125()1()(2)1(2)2.5 2.522(2)220.97720.0456X Y X Y X Y P P P ⎧+⎫++⎧⎫⎧⎫->=<-+>+⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭--+-=Φ+-Φ=Φ-+-Φ=-Φ=-⨯=10、解:(1)22~(10,(0.2)),~(10.5,(0.2))X N Y N X Y ,且与相互独立22~(0.5,2(0.2))(0.5,(0.282))X Y N N ∴--⨯=-0(0.5){0}()(1.77)0.96160.282P X Y ---<=Φ=Φ=(2)22~(10,(0.2)),~(10.5,)X N Y N X Y σ设,且与相互独立222~(0.5,2(0.2))(0.5,(0.2))X Y N N σ∴--⨯=-+0.90{0}P X Y ≤-<=Φ=Φ由1.28≥,故σ≤11、设某地区女子的身高(以m 计)2(1.63,(0.025))WN ,男子身高(以m 计)2(1.73,(0.05))MN ,设各人身高相互独立。
概率论第四、五章课后习题答案

第四章 随机变量的数字特征2.某产品的次品率为0.1,检验员每天检验4次,每次随机地取10件产品进行检验,如发现其中的次品数多于1,就去调整设备。
以X 表示一天中调整设备的次数,试求E (X )。
(设诸产品是否为次品是相互独立的。
)解:先求检验一次,决定需要调整设备的概率。
设抽检出次品件数为Y ,则Y ~b (10,0.1).记需调整设备一次的概率为p ,则2639.01.09.01109.01}1{}0{1)1(910=⨯⨯⎪⎪⎭⎫ ⎝⎛--==-=-=>=Y P Y P Y P p 又因各次检验结果相互独立,故)2639.0,4(~b X X 的分布律为于是0556.12639.0444)1(43)1(62)1(41)(43223=⨯==⨯+-⨯+-⨯+-⨯=p pp p p p p p X E以后将会知道若X ~b (n ,p ),则np X E =)(.6.(1)设随机变量X 的分布律为求)53(),(),(22+XE X E X E(2)设)(~λπX ,求)11(+X E解:(1)E (X )=(-2)⨯0.4+0⨯0.3+2⨯0.3=-0.2 由关于随机变量函数的数学期望的定理,知E (X 2)=(-2)2⨯0.4+02⨯0.3+22⨯0.3=2.8E (3X 2+5)=[3⨯ (-2)2+5]⨯0.4+[3⨯ 02+5]⨯0.3+[3⨯22+5]⨯0.3=13.4如利用数学期望的性质,则有E (3X 2+5)=3E (X 2)+5=3⨯2.8+5=13.4(2)因)(~λπX ,故!}{k ek X P k λλ-==)1(1)1()1!(!)!1()!1(}{11)11(1100λλλλλλλλλλλλλλλλ--∞=-∞=-∞=+-∞=-∞=-=-=-==+=+==+=+∑∑∑∑∑eeej ej ek ek ek X P k X E j jj jk k k k k7. (1)设随机变量X 的概率密度为⎩⎨⎧≤>=-0,00,)(x x e x f x求(I)Y =2X ;(II) Y =e -2X 的数学期望(2)设随机变量n X X X ,,2,1 相互独立,且都服从(0,1)上的均匀分布,(I)求},,max{2,1n X X X U =的数学期望;(II)求},,min{2,1n X X X V =的数学期望。
概率论第四章习题解答(全)

(0.9)10 (0.9)9 3486 0.3874 0.7361
则需要调整设备的概率
P{Y 1} 1 P{Y } 1 0.7361 0.2639
(3)求一天中调整设备的次数 X 的分布律 由于 X 取值为 0,1,2,3,4。 p 0.2369 ,则 X B (4, 0.2369) 于是
个随机变量,其概率密度为
1 x, 0 x 1500, 15002 1 f ( x) ( x 3000),1500 x 3000, 2 1500 0, 其它
求 E( X ) 解 按连续型随机变量的数学期望的定义有
0 1500
E ( X ) xf ( x)dx xf ( x)dx
X p
2
3
4
9
1 8
5 8
1 8
1 8
所以
1 5 1 1 15 E( X ) 2 3 4 9 。 8 8 8 8 4
(2)因为 Y 的取值为 2,3,4,9 当 Y 2 时,包含的字母为“O”,“N”,故
P{Y 2}
1 C2 1 ; 30 15
当 Y 3 时,包含的 3 个字母的单词共有 5 个,故
P (Ck ) P ( Ak | A1 A2 Ak 1 ) P ( Ak 1 | A1 A2 Ak 2 ) P ( A2 | A1 ) P ( A1 )
而
P{ X 1} P ( A1 )
1 2
1 1 P{ X 2} P ( A1 A2 ) P ( A2 | A1 ) P ( A1 ) 3 2 1 2 1 1 1 P ( A2 | A1 A2 ) P ( A2 | A1 ) P ( A1 ) , 4 3 2 4 3 一般地,若当 X k 时,盒中共有 k 1 只球,其中只有一只白球,故 P ( X k ) P ( A1 A2 Ak 1 Ak ) P ( Ak | A1 A2 Ak 1 ) P ( Ak 1 | A1 A2 Ak 2 ) P ( A2 | A1 ) P ( A1 ) 1 k 1 k 2 1 2 1 1 1 k 1 k k 1 4 3 2 k k
概率论与数理统计第四章习题参考答案

=
⎡ E⎢
1
⎢⎣ n −1
n i =1
(Xi
−
⎤ X )2 ⎥
⎥⎦
=
1 n −1
⎡ E⎢
⎢⎣
n i =1
X
2 i
−
nX
2⎤ ⎥ ⎥⎦
=
1 n −1
⎡n ⎢ ⎢⎣ i=1
E
(
X
2 i
)
−
nE( X
2⎤ )⎥ ⎥⎦
∑[ ] [ ] =
1 n −1
⎧ ⎨ ⎩
n i =1
D(X i ) + E 2 (X i )
X −µ 3/2
<
⎫ 1.96⎬
=
0.95
⎭
故,正态总体均值 µ 的 95%的置信区间为 (X − 2.94, X + 2.94)
代入样本值得正态总体均值 µ 的 95%的置信区间为(-2.565,3.315)。
(2)当σ 未知时,由 T = X − µ ~ t(n − 1) 即T = X − µ ~ t(3) ,所以
n
−a n
=0 =0
无解。由此不能求得
a,
b
的极大似然估计量。
⎩ ∂b
b−a
解:X
的概率密度为
f
(x)
=
⎪⎧ ⎨b
1 −
a
,
a
≤
x
≤
b
,
⎪⎩ 0, 其它
似然函数为 L(a, b) = 1 , θ1 ≤ xi ≤ θ 2 ,i = 1,2,L, n , (b − a)n
对于给定的样本值 (x1 , x2 ,L, xn )
−
n
D(
概率论第四章习题答案

概率论第四章习题答案概率论是数学中的一个重要分支,它研究了随机现象的规律性和不确定性。
在概率论的学习过程中,习题是不可或缺的一部分,通过解答习题可以加深对概率论知识的理解和运用。
本文将针对概率论第四章的习题进行解答,以帮助读者更好地掌握这一章节的内容。
第一题:某班级有30名学生,其中有10名男生和20名女生。
从中随机选取2名学生,求选出的两名学生都是男生的概率。
解答:首先,计算总的样本空间。
从30名学生中选取2名学生,共有C(30, 2)= 435种可能的选法。
然后,计算选出的两名学生都是男生的样本空间。
从10名男生中选取2名学生,共有C(10, 2) = 45种可能的选法。
所以,选出的两名学生都是男生的概率为P = 45/435 = 1/9。
第二题:某班级有30名学生,其中有10名男生和20名女生。
从中随机选取4名学生,求选出的学生中至少有1名男生的概率。
解答:首先,计算总的样本空间。
从30名学生中选取4名学生,共有C(30, 4)= 27,405种可能的选法。
然后,计算选出的学生中全是女生的样本空间。
从20名女生中选取4名学生,共有C(20, 4) = 4,845种可能的选法。
所以,选出的学生中至少有1名男生的概率为P = 1 - 4,845/27,405 =22,560/27,405 ≈ 0.822。
第三题:某班级有30名学生,其中有10名男生和20名女生。
从中随机选取6名学生,求选出的学生中至少有3名男生的概率。
解答:首先,计算总的样本空间。
从30名学生中选取6名学生,共有C(30, 6) = 593,775种可能的选法。
然后,计算选出的学生中全是女生或者只有1名男生或者只有2名男生的样本空间。
从20名女生中选取6名学生,共有C(20, 6) = 38,760种可能的选法。
从10名男生中选取1名学生,共有C(10, 1) = 10种可能的选法。
从10名男生中选取2名学生,共有C(10, 2) = 45种可能的选法。
概率论第四章习题解答
X9
EX 9
9
9
8 9
20
2024年8月31日7时4分
P104 练习4.2 题1 SD 1
1,1
f XY
x,
y
1 0
0 x 1, x y x 其它
yx
DZ D2X 1 4DX
EX xf x, ydxdy
0D
y x 1
1 0
x x
xdy
dx
1 2x2dx 2
P113 习题四 一 填空题 7 X与Y相互独立
f
X
x
2x
0
0
x 其它
1,fY
y
x y t
FT t PT t P X Y t fXY x, y dxdy
x yt
1当t 0时:FT t 0dxdy 0
0
x yt
2 当0 t时:FT
t
t
dx
tx 25e5x5 ydy
0
0
1 e5t 5te5t
t,0
x
FT
t
1
e5t
0
5te5t
t0 t0
33
2 EX 2
xi2 pij
i1 j1
20.1 30.3 30.1 2
33
3 EY 2
yi2 pij
12 0.212 0.112 0.1 22 0.1
22 0.132 0.332 0.1 4.8
i1 j1
12 0.2 12 0.1 12 0.1
12 0.1 12 0.1 0.6
2024年8月31日7时4分
P100 练习4.1 题12
2
f XY
x,
y
x
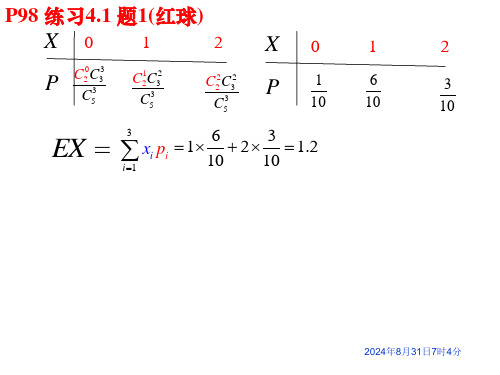
(完整版)概率论第四章答案

习题4-11. 设随机变量X求()E X ;E (2-3 X );2()E X ;2(35)E X +.解 由定义和数学期望的性质知2.03.023.004.0)2()(-=⨯+⨯+⨯-=X E ; (23)23()23(0.2) 2.6E X E X -=-=-⨯-=; 8.23.023.004.0)2()(2222=⨯+⨯+⨯-=X E ; 4.1358.235)(3)53(22=+⨯=+=+X E X E . 2. 设随机变量X 的概率密度为,0,()0,0.xe xf x x -⎧>⎪=⎨⎪⎩≤求Xe Z X Y 22-==和的数学期望.解()(2)2()22x E Y E X E X x x ∞-====⎰e d ,2201()()3Xx x E Z E ee e dx ∞---==⋅=⎰. 3. 游客乘电梯从底层到电视塔顶观光, 电梯于每个整点的第5分钟、第25分钟和第55分钟从底层起行. 假设一游客在早八点的第X 分钟到达底层侯梯处, 且X 在区间[0, 60]上服从均匀分布. 求该游客等候电梯时间的数学期望. 解已知X 在[0,60]上服从均匀分布, 其概率密度为1,060,()600,.x f x =⎧⎪⎨⎪⎩≤≤其它记Y 为游客等候电梯的时间,则5,05,25,525,()55,2555,65,5560.X X X X Y g X X X X X -<-<==-<-<⎧⎪⎪⎨⎪⎪⎩≤≤≤≤因此, 6001()[()]()()()60E Y E g X g x f x dx g x dx ∞-∞===⎰⎰()5255560525551(5)(25)(55)(65)60x dx x dx x dx x dx =-+-+-+-⎰⎰⎰⎰=11.67(分钟)..14. 某保险公司规定, 如果在一年内顾客的投保事件A 发生, 该公司就赔偿顾客a 元. 若一年内事件A 发生的概率为p , 为使该公司受益的期望值等于a 的10%, 该公司应该要求顾客交多少保险费?解 设保险公司要求顾客交保费c 元. 引入随机变量⎩⎨⎧=.A ,0,A 1不发生事件发生事件,X 则{1},{0}1P X p P X p ====-. 保险公司的受益值1,,0.c a X Y c X -=⎧=⎨=⎩, 于是 ()(){1}{0}E Y c a P X c P X ap c =-⨯=+⨯==-+. 据题意有10%ap c a -+=⨯, 因此应要求顾客角保费(0.1)c p a =+.习题4-21. 选择题(1) 已知(1,(3))E D X X =-= 则2[3(2)]()E X-=.(A) 9. (B) 6. (C) 30. (D) 36. 解22[3(2)]3(44)E X E X X -=-+23[()4()4]E X E X =-+23{()[()]4()4}D X E X E X =+-+ 3(3144)36=⨯+++=.可见,应选(D).(2) 设~(,),(6,( 3.6))B n p E D X X X ==, 则有( ).(A)10, 0.6n p ==. (B) 20, 0.3n p ==. (C) 15, 0.4n p ==. (D) 12, 0.5n p ==.解 因为~(,),B n p X 所以E (X )=n p,D (X )=np (1-p ), 得到np =6, np (1-p )=3.6 . 解之,n=15 , p =0.4 . 可见,应选(C).(3) 设X 与Y 相互独立,且都服从2(,)N μσ, 则有( ).(A) ()()()E X Y E X E Y -=+. (B) ()2E X Y μ-=.(C)()()()D X Y D X D Y -=-. (D) 2()2D X Y σ-=.解 注意到0)()()(=-=-Y E X E Y XE .由于X 与Y 相互独立,所以22)()()(σ=+=-Y D X D Y X D . 选(D).(4) 在下列结论中, 错误的是( ).(A) 若~(,),().X B n p E X np =则(B) 若()~1,1X U -,则()0D X =. (C) 若X 服从泊松分布, 则()()D X E X =.(D) 若2~(,),X N μσ 则~(0,1)X N μσ-.解)1,1(~-U X , 则3112212)()(22==-=a b X D . 选(B). 2. 已知X , Y 独立, E (X )= E (Y )=2, E (X 2)= E (Y 2)=5, 求E (3X -2Y ),D (3X -2Y ).解 由数学期望和方差的性质有E (3X -2Y )= 3E (X )-2 E (Y )=3×2-2×2=2,(32)9()4()D X Y D X D Y -=+})]([)({4})]([)({92222Y E Y E X E X E -⨯+-⨯=13)45(4)45(9=-⨯+-⨯=.3. 设随机变量X 1, X 2, X 3相互独立, 其中X 1服从区间[0, 6]上的均匀分布,22~0,2X N (), 3~3X P (), 记12323Y X X X =-+, 求E (Y )和D (Y ) .解 由题设知21122(60)()3,()3,()0,()4,12E X D X E X D X -=====3321111(),()39E X D X λλ====.由期望的性质可得123123()(23)()2()3()13203 4.3E Y E X X X E X E X E X =-+=-+=-⨯+⨯=又123,,X X X 相互独立, 所以123123()(23)()4()9()1344920.9D Y D X X X D X D X D X =-+=++=+⨯+⨯=4. 设两个随机变量X 和Y 相互独立, 且都服从均值为0, 方差为12的正态分布, 求||X Y -的的期望和方差.解 记UX Y =-. 由于11~(0,),~(0,)22X N Y N , 所以()()()0,E U E X E Y =-= ()()()1D U D X D Y =+=.由此~(0,1)U N . 进而2222220 (||)(||)||x x xE X Y E U x dx xe dx e+∞---+∞+∞-∞-====⎰2222(||)()()[()]101E U E U D U E U==+=+=.故而2222 (||)(||)(||)[(||)]11D X Y D UE U E Uπ-==-=-=-.5. 设随机变量]2,1[~-UX, 随机变量⎪⎩⎪⎨⎧<-=>=.0,1,0,0,0,1XXXY求期望()E Y和方差)(YD.解因为X的概率密度为1,12,()30,.Xxf x-=⎧⎪⎨⎪⎩≤≤其它于是Y的分布率为00--11{1}{0}31()d d3XP Y P X f x x x∞=-=<===⎰⎰,{0}{0}0P Y P X====,+2002{1}{0}31()d d3XP Y P X f x x x∞==>===⎰⎰.因此121()1001333E Y=-⨯+⨯+⨯=,222212()(1)001133E Y=-⨯+⨯+⨯=.故有2218()()[()]199D YE Y E Y=-=-=.6. 设随机变量U在区间[-2, 2]上服从均匀分布, 随机变量1,1,1, 1.UXU--=>-⎧⎨⎩若≤若1,1,1, 1.UYU-=>⎧⎨⎩若≤若求E(X+Y), D(X+Y).解(1) 随机变量(X, Y)的可能取值为(-1,-1),(-1,1),(1,-1),(1,1).{1,1}{P X Y P U =-=-=≤1,U -≤-1-211}{1}41d 4P U x =-==⋅⎰≤, {1,1}{P X Y P U =-==≤1,U -1}0>=, {1,1}{1P X Y P U ==-=>-,U ≤1111}21d 4x -==⋅⎰, 211{1,1}{1,1}41d 4P X Y P U U x ===>->==⋅⎰.于是得X 和Y 的联合密度分布为(2) Y X +和)(Y X +的概率分布分别为由此可见22()044E X Y +=-+=;2()[()]2D X Y E X Y +=+=.习题4-31. 选择题(1) 在下列结论中, ( )不是随机变量X 与Y 不相关的充分必要条件(A) E (XY )=E (X )E (Y ). (B) D (X +Y )=D (X )+D (Y ). (C) Cov(X ,Y )=0. (D) X 与 Y 相互独立.解 X 与 Y 相互独立是随机变量X 与Y 不相关的充分条件,而非必要条件. 选(D).(2) 设随机变量X 和Y 都服从正态分布, 且它们不相关, 则下列结论中不正确的是( ).(A) X 与Y 一定独立. (B) (X , Y )服从二维正态分布. (C) X 与Y 未必独立. (D) X +Y 服从一维正态分布.解 对于正态分布不相关和独立是等价的. 选(A).(3) 设(X , Y )服从二元正态分布, 则下列说法中错误的是( ).(A) (X , Y )的边缘分布仍然是正态分布.(B) X 与Y 相互独立等价于X 与Y 不相关. (C) (X , Y )是二维连续型随机变量.(D)由(X , Y )的边缘分布可完全确定(X , Y )的联合分布. 解 仅仅由(X , Y )的边缘分布不能完全确定(X , Y )的联合分布. 选(D)2 设D (X )=4, D (Y )=6, ρXY =0.6, 求D (3X -2Y ) .解(32)9()4()12Cov(,)D X Y D X D Y X Y -=+-)()(126449Y D X D XY ⨯⨯-⨯+⨯=ρ727.24626.0122436≈⨯⨯⨯-+=.3. 设随机变量X , Y 的相关系数为5.0, ,0)()(==Y E X E 22()()2E X E Y ==,求2[()]E XY +.解222[()]()2()()42[Cov(,)()()]E X Y E X E XY E Y X Y E X E Y +=++=++42420.526.ρ=+=+⨯⨯=4. 设随机变量(X , Y )若E (XY )=0.8, 求常数a ,b 解 首先由∑∑∞=∞==111i j ijp得4.0=+b a . 其次由0.8()100.420110.2210.22E XY a b b ==⨯⨯+⨯⨯+⨯⨯+⨯⨯=+ 得3.0=b . 进而1.0=a . 由此可得边缘分布律于是 , . 故 Cov(,)()()()0.8 1.40.50.1X Y E XY E X E Y =-=-⨯=.5. 已知随机变量(,)~(0.5,4;0.1,9;0)X Y N , Z =2X -Y , 试求方差D (Z ), 协方差Cov(,)X Z , 相关系数ρXZ .解 由于X ,Y 的相关系数为零, 所以X 和Y 相互独立(因X 和Y 服从正态分布). 因此25944)()(4)2()(=+⨯=+=-=Y D X D Y X D Z D ,Cov(,)Cov(,2)2Cov(,)Cov(,)2()08X Z X X Y X X X Y D X =-=-=-=.因此80.825XZ ρ===⨯. 6. 设随机变量(X , Y )服从二维正态分布: 2~(1,3)X N , 2~(0,4)Y N ; X 与Y 的相关系数1,232XYX YZ ρ=-=+. 求: (1) E (Z ), D (Z ); (2) X 与Z 的相关系数ρXZ ; (3)问X 与Z 是否相互独立?为什么?解 (1) 由于)3,1(~2N X , )4,0(~2N Y , 所以16)(,0)(,9)(,1)(====Y D Y E X D X E ,而1Cov(,)3462XY X Y ρ==-⨯⨯=-.因此 31021131)(21)(31)23()(=⨯+⨯=+=+=Y E X E Y X E Z E ,1111()()()()2Cov(,)329432X Y D Z D D X D Y X Y =+=++111916Cov(,)943X Y =⨯+⨯+3)6(3141=-⨯++=.(2) 由于1111Cov(,)Cov(,)()Cov(,)9(6)0,323232XY X Z X D X X Y =+=+=⨯+⨯-= 所以0XZ ρ==.(3) 由0=XZ ρ知X 与Z 不相关, 又X 与Z 均服从正态分布, 故知X 与Z 相互独立.7.证明: 对随机变量(X , Y ), E (XY )=E (X )E (Y )或者D (X ±Y )=D (X )+D (Y )的充要条件是X与Y 不相关.证 首先我们来证明)()()(Y E X E XY E =和()()()D X Y D X D Y ±=+是等价的.事实上, 注意到()()()2Cov(,)D X Y D X D Y X Y ±=+±.因此()()()D X Y D X D Y ±=+Cov(,)0()()()X Y E XY E X E Y ⇔=⇔=.其次证明必要性. 假设E (XY )=E (X )E (Y ), 则Cov(,)()()()0X Y E XY E X E Y =-=.进而0XYρ==, 即X 与Y 不相关.最后证明充分性. 假设X 与Y 不相关, 即0=XYρ, 则Cov(,)0X Y =. 由此知)()()(Y E X E XY E =.总习题四1. 设X 和Y 是相互独立且服从同一分布的两个随机变量, 已知X 的分布律为1{},1,2,33P X i i ===. 又设max{,},min{,}U X Y V X Y ==.(1) 写出二维随机变量(U , V )的分布律; (2) 求()E U .解 (1) 下面实际计算一下{1,3}P UV ==.注意到max{,},min{,}U X Y V X Y ==, 因此{1,3}{1,3}{3,1}P U V P X Y P X Y =====+=={1}{3}{3}{1}P X P Y P X P Y ===+==9231313131=⨯+⨯=.(2) 由(,)U V 的分布律可得关于U 的边缘分布律所以13522()1239999E U =⨯+⨯+⨯=. 2. 从学校乘汽车到火车站的途中有3个交通岗. 假设在各个交通岗遇到红灯的事件是相互独立的, 并且概率是25. 设X 为途中遇到红灯的次数, 求随机变量X 的分布律、分布函数和数学期望.解 令X 表示途中遇到红灯的次数, 由题设知2~(3,)XB . 即X 的分布律为从而3127543686(){}01231251251251255k E X kP X k ====⨯+⨯+⨯+⨯=∑. 3. 设随机变量),(Y X 的概率密度为212,01,(,)0,.y y x f x y ⎧⎪=⎨⎪⎩≤≤≤其它求22(),(),(),()E X E Y E XY E X Y +.解 112404()(,)1245xE X xf x y dxdy dx x y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰. 11240003()(,)1235xE X yf x y dxdy dx y y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰.112500031()(,)12362x E XY xyf x y dxdy dx xy y dy x dx ∞∞-∞-∞==⋅===⎰⎰⎰⎰⎰.122222220()()(,)()12xE X Y x y f x y dxdy dx x y y dy ∞∞-∞-∞+=+=+⋅⎰⎰⎰⎰155012423216(4)5653015x x dx =+=+==⎰. 4. 设随机变量(X ,Y )的概率密度为1sin(),0,0,222(,)0,.≤≤≤≤其它ππx y x y f x y ⎧+⎪=⎨⎪⎩求E (X ),D (X ),E (Y ),D (Y ),E (XY )和 Cov(X ,Y ).解22001()(,)sin()24E X xf x y dxdy x x y dxdy πππ+∞+∞-∞-∞==+=⎰⎰⎰⎰.22222200()(,)1sin() 2.282E X x f x y dxdyx x y dxdy ππππ+∞+∞-∞-∞==+=+-⎰⎰⎰⎰于是有2216)]([)()(222-+=-=ππX E X E X D . 利用对称性,有2216)(,4)(2-+==πππY D Y E .又()(,)E XY xyf x y dxdy +∞+∞-∞-∞=⎰⎰22001sin()2xy x y dxdy ππ=+⎰⎰220022001sin()21[sin cos cos sin ]2xdx y x y dyxdx y x y x y dyππππ=+=+⎰⎰⎰⎰12-=π.所以协方差2Cov(,)()()()1216X Y E XY E X E Y ππ=-=--.5. 设随机变量X 与Y 独立, 同服从正态分布1(0,)2N , 求(1)();()E X Y D X Y --;(2) (max{,});(min{,})E X Y E X Y .解 (1) 记Y X -=ξ.由于)21,0(~),21,0(~N Y N X ,所以,0)()()(=-=Y E X E E ξ 1)()()(=+=Y D X D D ξ.由此)1,0(~N ξ. 所以2222(||)(||)||x x E X Y E x dx xedx ξ+∞+∞---∞-==⎰22x e+∞-==101)]([)()()|(|2222=+=+==ξξξξE D E E .故而ππξξξ2121|)](|[)|(||)(||)(|222-=⎪⎪⎭⎫ ⎝⎛-=-==-E E D Y X D .(2) 注意到2||)(),max(Y X Y X Y X -++=, 2||),min(Y X Y X Y X --+=.所以ππ21221|]}[|)()({21)],[max(==-++=Y X E Y E X E Y X E ,ππ21221|]}[|)()({21)],[min(-=-=--+=Y X E Y E X E Y X E .6. 设随机变量),(Y X 的联合概率密度为,02,02,8(,)0,.x yx y f x y +⎧⎪=⎨⎪⎩≤≤≤≤其它求: E (X ), E (Y ), Cov(X ,Y ), ρXY , D (X+Y ).解 注意到),(y x f 只在区域2≤≤0,2≤≤0:y x G 上不为零, 所以()(,)8Gx yE X xf x y dxdy x x y ∞∞-∞-∞+==⎰⎰⎰⎰d d222000117()(1)846dx x x y dy x x dx =+=+=⎰⎰⎰,22()(,)E Xx f x y dxdy ∞∞-∞-∞=⎰⎰222232000115()()843dx x x y dy x x dx =+=+=⎰⎰⎰, 因而 36116735)]([)()(2222=-=-=X E X E X D .又()(,)E XY xyf x y dxdy ∞∞-∞-∞=⎰⎰22220001144()()8433dx xy x y dy x x dx =+=+=⎰⎰⎰. 由对称性知2275()(),()()63E Y E X E Y E X ====, 3611)()(==X D Y D . 这样,4491Cov(,)()()()33636X Y E XY E X E Y =-=-=-, 111XY ρ==-,5()()()2Cov(,)9D X Y D X D Y X Y +=++=.7. 设A , B 为随机事件, 且111(),(|),(|)432P A P B A P A B ===, 令 10A X A =⎧⎨⎩,发生,,不发生, 10B Y B =⎧⎨⎩,发生,,不发生.求: (1) 二维随机变量(X , Y )的概率分布; (2) X 与Y 的相关系数XY ρ.解 由1()(|)3()P AB P B A P A ==得1111()()33412P AB P A ==⨯=, 进而由1(|)2P A B = ()()P AB P B =得1()2()6P B P AB ==. 在此基础上可以求得(1)1{1,1}()12P X Y P AB ====,111{0,1}()()()61212P X Y P AB P B P AB ====-=-=,111{1,0}()()()4126P X Y P AB P A P AB ====-=-=,{0,0}()1()1[()()()]P X Y P AB P A B P A P B P AB ====-=-+-U 11121[]46123=-+-=.故(X , Y )的概率分布为(2) 由(1)因此211(),(),44E X E X ==22113()()[()]41616D XE X E X =-=-=, 22211115(),(),()()[()]6663636E Y E Y D Y E Y E Y ===-=-=. 又由(X , Y )的分布律可得21111()00011011312121212E XY =⨯⨯+⨯⨯+⨯⨯+⨯⨯=. 故11115XYρ-⨯===.。
概率论习题及解答-第四章特征函数

的一个新分割, 且
∑n ∑ m
ξ +η =
(xi + yj )1AiBj .
i=1 j=1
所以由数学期望的定义和概率的有限可加性得
∑n ∑ m
∑n ∑ m
∑n ∑ m
E(ξ + η) =
(xi + yj)P(AiBj) =
xiP(AiBj) +
yj P(AiBj )
i=1 j=1
i=1 j=1
i=1 j=1
概率论习题解答
李勇 张余辉
May 30, 2018
1 第四章 数字特征与特征函数
§4.1.4 练习题
练习4.1.1 设 ξ 和 η 均为简单随机变量, 试证明 E(ξ + η) = E(ξ) + E(η).
证明: 不妨假设
∑n ξ = xi1Ai ,
i=1
∑ m η = yj 1Bj ,
j=1
其中 {Ai} 和 {Bj} 均为样本空间的分割. 记 Cij = AiBj, 则 {Cij : 1 i n, 1 j m} 构成样本空间
解: 记 ξ = min{ξ1, ξ2, · · · , ξn}, η = max{ξ1, ξ2, · · · , ξn}, 则 (ξ, η) 的联合密度函数
p(ξ,η)(x, y) = n(n − 1)(y − x)n−2, 0 < x < y < 1,
所以 ξ 和 η 的边缘密度函数分别为 ∫∞
∑n
∑ m
= xiP(Ai) + yjP(Bj) = E(ξ) + E(η).
i=1
j=1
练习4.1.2 假设简单随机变量 ξ 和 η 相互独立, 试证明
概率论第4章习题参考解答

概率论第4章习题参考解答 1. 若每次射击中靶的概率为0.7, 求射击10炮, 命中3炮的概率, 至少命中3炮的概率, 最可能命中几炮. 解: 设ξ为射击10炮命中的炮数, 则ξ~B (10,0.7), 命中3炮的概率为 =⨯⨯==733103.07.0}3{C P ξ0.0090至少命中3炮的概率, 为1减去命中不到3炮的概率, 为=⨯⨯-=<-=≥∑=-2010103.07.01}3{1}3{i i i i C P P ξξ0.9984因np +p =10×0.7+0.7=7.7不是整数, 因此最可能命中[7.7]=7炮. 2. 在一定条件下生产某种产品的废品率为0.01, 求生产10件产品中废品数不超过2个的概率. 解: 设ξ为10件产品中的废品数, 则ξ~B (10,0.01), 则废品数不超过2个的概率为=⨯⨯=≤∑=-20101099.001.0}2{i i i iC P ξ0.99993. 某车间有20部同型号机床, 每部机床开动的概率为0.8, 若假定各机床是否开动彼此独立, 每部机床开动时所消耗的电能为15个单位, 求这个车间消耗电能不少于270个单位的概率. 解: 设每时刻机床开动的数目为ξ, 则ξ~B (20,0.8), 假设这个车间消耗的电能为η个单位, 则η=15ξ, 因此2061.02.08.0}18{}15270{}27015{}270{20182020=⨯⨯==≥=≥=≥=≥∑=-i i i iC P P P P ξξξη4. 从一批废品率为0.1的产品中, 重复抽取20个进行检查, 求这20个产品中废品率不大于0.15的概率. 解: 设这20个产品中的废品数为ξ, 则ξ~B (20,0.1), 假设这20个产品中的废品率为η, 则η=ξ/20. 因此∑=-⨯⨯=≤=≤=≤320209.01.0}3{}15.020{}15.0{i i i iC P P P ξξη=0.8675. 生产某种产品的废品率为0.1, 抽取20件产品, 初步检查已发现有2件废品, 问这20件中, 废品不少于3件的概率. 解: 设ξ为这20件产品中的废品数, 则ξ~B (20,0.1), 又通过检查已经知道ξ定不少于2件的条件, 则要求的是条件概率}2{}23{}2|3{≥≥⋂≥=≥≥ξξξξξP P P因事件}3{}2{≥⊃≥ξξ, 因此2}23{≥=≥⋂≥ξξξ因此5312.06083.02852.019.01.0209.019.01.01}{1}2{1}{}2{1}{}2{}{}{}{}2{}3{}2|3{192018222010202202202202203=-=⨯⨯--⨯⨯-==-=-===-===-=====≥≥=≥≥∑∑∑∑∑∑======C i P P i P P i P P i P i P i P P P P i i i i i i ξξξξξξξξξξξξξ6. 抛掷4颗骰子, ξ为出现1点的骰子数目, 求ξ的概率分布, 分布函数, 以及出现1点的骰子数目的最可能值. 解: 因掷一次骰子出现一点的概率为1/6, 则ξ~B (4,1/6), 因此有⎪⎪⎩⎪⎪⎨⎧≥<≤⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛<==⎪⎭⎫ ⎝⎛⨯⨯==∑≤--4140656100)(),4,3,2,1,0(6561}{4444x x C x x F k C k P x k kk k kk kξ或者算出具体的值如下所示:ξ0 1 2 3 4 P0.48230.38580.11570.01540.0008⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<≤<≤<=41439992.0329838.0218681.0104823.000)(x x x x x x x F从分布表可以看出最可能值为0, 或者np +p =(4/6)+1/6=5/6小于1且不为整数, 因此最可能值为[5/6]=0. 7. 事件A 在每次试验中出现的概率为0.3, 进行19次独立试验, 求(1)出现次数的平均值和标准差; (2)最可能出现的次数. 解: 设19次试验中事件A 出现次数为ξ, 则ξ~B (19,0.3), 因此 (1)ξ的数学期望为E ξ=np =19×0.3=5.7 方差为Dξ=np (1-p )=19×0.3×0.7=3.99标准差为997.199.3===ξσξD(2)因np +p =5.7+0.3=6为整数, 因此最可能值为5和6. 8. 已知随机变量ξ服从二项分布, E ξ=12, D ξ=8, 求p 和n . 解: 由E ξ=np =12 (1) 和D ξ=np (1-p )=8 (2) 由(1)得n =12/p , 代入到(2)得 12(1-p )=8, 解出p =(12-8)/12=1/3=0.3333 代回到(1)式得n =12/p =12×3=36 9. 某柜台上有4个售货员, 并预备了两个台秤, 若每个售货员在一小时内平均有15分钟时间使用台秤, 求一天10小时内, 平均有多少时间台秤不够用. 解: 每个时刻构成一n =4的贝努里试验, 且p =15/60=0.25, 因此, 设ξ为每个时刻要用秤的售货员数, 则ξ~B (4, 0.25), 当ξ>2时, 台秤不够用. 因此每时刻台秤不够用的概率为=+⨯⨯=>433425.075.025.0)2(C P ξ0.0508因此10个小时内平均有0.0508×10=0.508个小时台秤不够用. 10. 已知试验的成功率为p , 进行4重贝努里试验, 计算在没有全部失败的情况下, 试验成功不止一次的概率. 解: 设ξ为4次试验中的成功数, 则ξ~B (4,p ), 事件"没有全部失败"即事件{ξ>0}, 而事件"试验成功不止一次"即事件{ξ>1}, 因此要求的是条件概率P {ξ>1|ξ>0}, 又因事件{ξ>1}被事件{ξ>0}包含, 因此这两个事件的交仍然是{ξ>1}, 因此434141}0{1}1{}0{1}0{}1{}0|1{q pq q P P P P P P ---===-=-=-=>>=>>ξξξξξξξ其中q =1-p 11. ξ服从参数为2,p 的二项分布, 已知P (ξ≥1)=5/9, 那么成功率为p 的4重贝努里试验中至少有一次成功的概率是多少?解: 因ξ~B (2,p ), 则必有9/5)1(1)0(1)1(2=--==-=≥p P P ξξ, 解得3/13/213/219/49/51)1(2=-==-=-=-p p p 则假设η为成功率为1/3的4重贝努里试验的成功次数, η~B (4,1/3), 则802.081161321)1(1)0(1)1(44=-=⎪⎭⎫⎝⎛-=--==-=≥p P P ηη12. 一批产品20个中有5个废品, 任意抽取4个, 求废品数不多于2个的概率解: 设ξ为抽取4个中的废品数, 则ξ服从超几何分布, 且有==≤∑=-204204155}2{i i i C C C P ξ0.968 13. 如果产品是大批的, 从中抽取的数目不大时, 则废品数的分布可以近似用二项分布公式计算. 试将下例用两个公式计算, 并比较其结果. 产品的废品率为0.1, 从1000个产品中任意抽取3个, 求废品数为1的概率. 解: 设任抽3个中的废品数为ξ, 则ξ服从超几何分布, 废品数为0.1×1000=100 ===3100029001100}1{C C C P ξ0.2435 而如果用二项分布近似计算, n =3, p =0.1, ξ~B (3,0.1)=⨯⨯≈=2139.01.0}1{C P ξ0.2430近似误差为0.0005, 是非常准确的.14. 从一副朴克牌(52张)中发出5张, 求其中黑桃张数的概率分布. 解: 设ξ为发出的5张中黑桃的张数, 则ξ服从超几何分布, 则)5,4,3,2,1,0(}{5525135213===--i C C C i P i i ξ则按上式计算出概率分布如下表所示:ξ0 1 2 3 4 5 P0.22150.41140.27430.08150.01070.000515. 从大批发芽率为0.8的种子中, 任取10粒, 求发芽粒数不小于8粒的概率. 解: 设ξ为10粒种子中发芽的粒数, 则ξ服从超几何分布, 但可以用二项分布近似, 其中p =0.8, n =10, 则∑=-⨯⨯=≥10810102.08.0}8{i i i iC P ξ=0.677816. 一批产品的废品率为0.001, 用普哇松分布公式求800件产品中废品为2件的概率, 以及不超过2件的概率. 解: 设ξ为800件产品中的废品数, 则ξ服从超几何分布, 可以用二项分布近似, 则ξ~B (800, 0.001), 而因为试验次数很大废品率则很小, 可以用普阿松分布近似, 参数为 λ=np =800×0.001=0.89526.0!8.0}2{1438.028.0}2{28.08.02=≈≤=≈=∑=--i i e i P e P ξξ 17. 某种产品表面上的疵点数服从普哇松分布, 平均一件上有0.8个疵点, 若规定疵点数不超过1个为一等品, 价值10元, 疵点数大于1不多于4为二等品, 价值8元, 4个以上为废品, 求产品为废品的概率以及产品的平均价值. 解: 设ξ为产品表面上的疵点数, 则ξ服从普哇松分布, λ=0.8, 设η为产品的价值, 是ξ的函数. 则产品为废品的概率为0014.0!8.01}4{1}4{48.0=-=≤-=>∑=-i i e i P P ξξ==≤==∑=-18.0!8.0}1{}10{i i e i P P ξη0.8088==≤<==∑=-428.0!8.0}41{}8{i i e i P P ξη0.1898则产品的平均价值为Eη = 10×P {η=10}+8×P {η=8}=10×0.8088+8×0.1898=9.6064(元) 18. 一个合订本共100页, 平均每页上有两个印刷错误, 假定每页上印刷错误的数目服从普哇松分布, 计算该合订本中各页的印刷错误都不超过4个的概率. 解: 设ξ为每页上的印刷错误数目, 则ξ服从普哇松分布, λ=2, 则1页印刷错误都不超过4个的概率为 ==≤∑=-402!2}4{i i e i P ξ0.9473而100页上的印刷错误都不超过4个的概率为[]=≤100}4{ξP 0.00445419. 某型号电子管的“寿命”ξ服从指数分布, 如果它的平均寿命E ξ=1000小时, 写出ξ的概率密度, 并计算P (1000<ξ≤1200). 解: 因Eξ=1000=1/λ, 其概率密度为⎪⎩⎪⎨⎧≤>=-0010001)(1000x x ex xϕ0667.0)12001000(2.111000120010001000=-=-=≤<----e e ee P ξ20. ξ~N (0,1), Φ0(x )是它的分布函数, φ0(x )是它的概率密度, Φ0(0), φ0(0), P (ξ=0)各是什么值? 解: 因有 20221)(x ex -=πϕ, ⎰∞--=Φxt dt ex 20221)(π, 因此φ0(x )为偶函数, 由对称性可知Φ0(0)=0.5, 并有πϕ21)0(0=,因ξ为连续型随机变量, 取任何值的概率都为0, 即P (ξ=0)=0.21. 求出19题中的电子管在使用500小时没坏的条件下, 还可以继续使用100小时而不坏的概率?解: 要求的概率为P (ξ>600|ξ>500), 因此905.0}500{}600{}500|600{1.010005001000600===>>=>>---e e eP P P ξξξξ22. 若ξ服从具有n 个自由度的χ2-分布, 证明ξ的概率密度为⎪⎪⎩⎪⎪⎨⎧<≥⎪⎭⎫ ⎝⎛Γ=---022)(21212x x e n x x x nn ϕ称此分为为具有n 个自由度的χ-分布 证: 设ξη=, 则因ξ的概率密度函数为⎪⎪⎩⎪⎪⎨⎧≤>⎪⎭⎫ ⎝⎛Γ=--0221)(2122x x e x n x xn nξϕη的分布函数为)0()()()()()(22>=≤=≤=≤=x x F x P x P x P x F ξηξξη对两边求导得)0(22222)(2)(2121222222>⎪⎭⎫ ⎝⎛Γ=⎪⎭⎫ ⎝⎛Γ==-----x en x en x xx x x x n n x n n ξηϕϕ23. ξ~N (0,1), 求P {ξ≥0}, P {|ξ|<3}, P {0<ξ≤5}, P {ξ>3}, P {-1<ξ<3} 解: 根据ξ的对称性质及查表得: P {ξ≥0}=1-Φ0(0)=0.5 P {|ξ|<3}=2Φ0(3)-1=2×0.99865-1=0.9973 P {0<ξ≤5}=Φ0(5)-0.5=0.5P {ξ>3}=1-Φ0(3)=1-0.99865=0.00135P {-1<ξ<3}=Φ0(3)-Φ0(-1)=Φ0(3)+Φ0(1)-1=0.99865+0.8413-1=0.83995 24. ξ~N (μ,σ2), 为什么说事件"|ξ-μ|<2σ"在一次试验中几乎必然出现?解: 因为)1,0(~N σμξ- 19545.0197725.021)2(2}2{}2|{|0≈=-⨯=-Φ=<-=<-σμξσμξP P因此在一次试验中几乎必然出现.25. ξ~N (10,22), 求P (10<ξ<13), P (ξ>13), P (|ξ-10|<2). 解: 因为)1,0(~210N -ξ6826.018413.021)1(2}1210{}2|10{|0.0668193319.01)5.1(1}5.1210{}13{43319.05.093319.0)0()5.1(}5.12100{}1310{0000=-⨯=-Φ=<-=<-=-=Φ-=>-=>=-=Φ-Φ=<-<=<<ξξξξξξP P P P P P26. 若上题中已知P {|ξ-10|<c }=0.95, P {ξ<d }=0.0668, 分别求c 和d .解: 因为)1,0(~210N -ξ, 则有95.01)2(2}2210{}|10{|0=-Φ=<-=<-cc P c P ξξ 解得975.0295.01)2(0=+=Φc, 查表得,96.12=c得c =3.92 再由5.00668.0)210(}210210{}{0<=-Φ=-<-=<d d P d P ξξ知,0210<-d 因此0668.0)210(1)210(00=-Φ-=-Φd d即9332.00668.01)210(0=-=-Φd ,查表得5.1210=-d , 解得7310=-=d27. 若ξ~N (μ,σ2), 对于P {μ-kσ<ξ<μ+kσ}=0.90, 或0.95, 或0.99, 分别查表找出相应的k值.解: 先求P {μ-kσ<ξ<μ+kσ}=0.90对应的k 值. 因)1,0(~N σμξ-, 因此 90.01)(2}{}{0=-Φ=<-=+<<-k k P k k P σμξσμξσμ 即95.0290.01)(0=+=Φk , 查表得k =1.64 同理, 由975.0295.01)(0=+=Φk , 查表得k =1.96 由995.0299.01)(0=+=Φk , 查表得k =2.57 28. 某批产品长度按N (50, 0.252)分布, 求产品长度在49.5cm 和50.5cm 之间的概率, 长度小于49.2cm 的概率.解: 设ξ为产品长度, 则ξ~N (50, 0.252), 且有)1,0(~25.050N -ξ, 则9545.0197725.021)2(2}225.050{}225.0502{}5.505.49{0=-⨯=-Φ=<-=<-<-=<<ξξξP P P0006871.09993129.01)2.3(1)2.3(}25.0502.4925.050{}2.49{00=-=Φ-=-Φ=-<-=<ξξP P29. ξi ~N (0,1)(i =1,2,3), 并且ξ1,ξ2,ξ3相互独立, ∑==3131i i ξξ,∑=-=312)(i i ξξη, 求),cov(,),,cov(1ηξηξξE解: 此题要用到, 两个独立的服从正态分布的随机变量相加后得到的随机变量仍然服从正态分布. 因此, 因为3131,031=⎪⎭⎫ ⎝⎛==∑=i i D D E ξξξ, 则)31,0(~N ξ313131)()cov(2131111==⎪⎭⎫ ⎝⎛==∑=ξξξξξξξE E E i i32313121)cov(2)2()(22222=+⨯-=+-=+-=-ξξξξξξξξξξE E E E i i i i i因此2323)()(312312=⨯=-=⎪⎭⎫ ⎝⎛-=∑∑==i i i i E E E ξξξξη ξξ-i 也服从正态分布, 且有03131)]([),cov(2=-=-=-=-ξξξξξξξξξE E E i i i即ξ与ξξ-i 不相关, 而因为它们服从正态分布, 因此也就是ξ与ξξ-i 相互独立,则ξ与2)(ξξ-i 也相互独立, 则ξ与η中的加和中的每一项相互独立, 当然也与η相互独立, 因此有0),cov(=ηξ, 因为相互独立的随机变量一定不相关.30. (ξ,η)有联合概率密度22)(21,2122ηξζπ+=+-y x e , 求ζ的概率密度.解: 由联合概率密度看出, ξ与η相互独立服从标准正态分布, 则有 ξ2与η2也相互独立且服从自由度为1的χ2-分布, 即ξ2~χ2(1), η2~χ2(1), 因此ζ=ξ2+η2~χ2(2), 即它的概率密度为⎪⎩⎪⎨⎧<>=-00212x x exζϕ即ζ服从λ=1/2的指数分布.。
概率论第四章部分习题解答

2
2
x2
=
2 2π σ
∫
E (Y ) =
).
m 1 np Φ npq
6
m 2 np p (m 1 ≤ Y n ≤ m 2 ) ≈ Φ npq
五,练习题
1. 设 ~ N(0,1),求下列概率: X 求下列概率:
(1) P( X ≤ 1.5);
(2) P( X > 2.5);
(3) P(| X |< 1.68); (4) P(0.36 ≤ X ≤ 0.64)
E (Y 2 ) =
2
2
∫ 2π
+∞
0
x e dx = (2n - 1)!!
2
x 2n - 2
2
( 2 n 1 )! ! , n 为奇数 ∴ DY = E (Y ) - [ E (Y )] = ( 2 n 1 )! ! [( n 1 )! ! ] 2 , n 为偶数
∴ E (XY ) = E ( X
(4) P ( 0.36 ≤ X ≤ 0.64) = Φ(0.64) Φ( 0.36)
= Φ(0.64) + Φ(0.36) 1 = 0.7389 + 0.6406 1= 0.3795
7
2. 设 ~ N(1,22 ),求下列概率: X 求下列概率:
(1) P( X < 2.2); (3) P(| X |< 3.5);
概率论与数理统计课后答案第4章

概率论与数理统计课后答案第第4章大数定律与中心极限定理4.1设D(x)为退化分布:讨论下列分布函数列的极限是否仍是分布函数?1 1 卄亠(1){D(x n)}; (2){D(x )};(3){D(x 0},其中n =1,2;n n解:(1) (2)不是;(3)是。
4.2设分布函数F n(x)如下定义:‘0x 兰-nl /、x + nF n (x)=」---- 一n c x 兰n2n1 x > n问F(x) =lim F n(x)是分布函数吗?n_)pC解:不是。
4.3设分布函数列{ F n(x)}弱收敛于分布函数F(x),且F(x)为连续函数,则{F n(x)}在(」:,::)上一致收敛于F(x)。
证:对任意的;.0,取M充分大,使有1 —F(x) ::;, —x _ M; F(x) ::;,—x^ -M对上述取定的M,因为F(x)在[-M,M]上一致连续,故可取它的k分点:捲- -M :: X2 :…X k4 ::X k = M ,使有F(X j .J - F(xJ ::;,1 一i ::k ,再令x° - - ::, X k 1 =::,则有F(X i J —FW) :::;,0 G ::k 1(1)这时存在N,使得当n • N时有| F n(X i) —F(X i)|::;,0 叮牛 1(2)成立,对任意的X •(-::,::),必存在某个i(0 _i 一k),使得x・(X i,X i 1),由(2) 知当n •N时有F n (X)— F n (X i i ) ::: F(X j .J ;F n (X)_ F n (X i ) . F(X i )-;(4) 由( 1), (3), (4)可得F n (x) -F(x)::: F(X i 1)-F(x) , F(X i i )-F(X i ); :::2;,F n (x) - F (x) F (X i ) - F (x) - ; _ F (X i ) - F (X i .1)- ; -2 ;,即有F n (x )-F (x ) 名成立,结论得证4.5设随机变量序列「鳥同时依概率收敛于随机变量 •与,证明这时必有P (二)二1。
概率论第四章课后习题答案

习题四1.设)2,5(~2N X ,求下列概率(1))52(≤≤X P ;(2))2(≤X P ;(3))3(>X P ;(4))93(≤≤-X P .解:(1))0255.1()25525252()52(≤-≤-=-≤-≤-=≤≤X P X P X P 4332.019332.05.01)5.1()0()5.1()0(=-+=-Φ+Φ=-Φ-Φ=(2))25225252()22()2(-≤-≤--=≤≤-=≤X P X P X P )5.3()5.1()5.1255.3(-Φ--Φ=-≤-≤-=X P 0666.09332.099977.0)5.1()5.3(=-=Φ-Φ=(3)8413.0)1()1(1)125()25325()3(=Φ=-Φ-=->-=->-=>X P X P X P (4))2254()25925253()93(≤-≤-=-≤-≤--=≤≤-X P X P X P 9772.01999968.09772.01)4()2()4()2(=-+=-Φ+Φ=-Φ-Φ=2.已知某次测试的成绩),73(~2σN X ,95分以上的同学占2.28%.求 (1)介于80分与90分之间的同学的比例; (2)小于60分的同学的比例.解:因0228.0%28.2)7395(1)739573()95(==-Φ-=->-=>σσσX P X P即9772.0)22(=Φσ,查表得222=σ,则11=σ,故).11,73(~2N X(1))11171173117()1173901173117380()9080(<-<=-<-<-=<<X P X P X P 2005.07389.09394.0)64.0()55.1(=-=Φ-Φ=(2))18.1()11131173()1173601173()60(-Φ=-<-=-<-=<X P X P X P 119.0881.01)18.1(1=-=Φ-=3.已知随机变量),2(~2σN X ,且44.0)13(=≤-X P ,求)22(≥-X P .解:因)24222()42()13(σσσ-≤-≤-=≤≤=≤-X P X P X P44.0)0()2(=Φ-Φ=σ即94.0)0(44.0)2(=Φ+=Φσ,则12.094.022)2(22)22()22(=⨯-=Φ-=≥-=≥-σσσX P X P4. 已知随机变量),(~2σμN X ,且)1()3()1(-Φ=≥=-<X P X P 求σμ,.解:依题有)1()1()1()1(-Φ=--Φ=--<-=-<σμσμσμX P X P)1()3()3(1)3()3(-Φ=--Φ=-Φ-=-≥-=≥σμσμσμσμX P X P由此可得,⎪⎩⎪⎨⎧=-=+1311σμσμ,解得.2,1==σμ6.设随机变量)1,0(~N X ,求)(2X E .解:因1)(,0)(==X D X E ,则.1)]([)()(22=+=X E X D X E 11.一加法器同时收到48个噪声电压(1,2,,48)i X i =,设它们是相互独立的随机变量,且都在区间[0,10]上服从均匀分布,记481i i X X ==∑,求(180)P X >.解:依题可知,32512)010()(,52100)(22=-===+==i i X D X E σμ,由独立同分布中心极限定理得48481(180)(180)ii i Xn P X P X P μ=->=>=>∑∑11(3)(3)0.99865=-Φ=-Φ-=Φ=12. 一部件包括100个部分,每部分的长度是一个随机变量,它们相互独立,且服从同一分布,其数学期望为2mm ,均方差为0.05mm.规定总长度200mm 误差在1mm 内算合格品,试求产品合格的概率.解:设随机变量i X 表示“第i 个部分的长度”,1,2,,100.i =则12100,,,X X X 相互独立,05.0)(,2)(====i i X D X E σμ且1001ii X X ==∑表示“该部件的总长度”, 由独立同分布中心极限定理得(0.1)21P X n P μ-<=<=Φ- 2(2)120.977210.9554=Φ-=⨯-=13. 掷硬币900次,试求: (1)至少出现正面480次的概率;(2)出现正面在420次到480次之间的概率.解:设随机变量X 表示“掷900次硬币中出现正面的次数”,则15)1(,450),21,900(~=-=p np np B X ,由棣莫弗—拉普拉斯中心极限定理得(1)0228.09772.01)2(1)1545048015450()480(=-=Φ-≈-≥-=≥X P X P (2)9544.019772.021)2(2)153015450()480420(=-⨯=-Φ≈<-=<<X P X P 14. 一船舶在某海区航行,已知每遭受一次波浪的冲击,纵摇角大于 3的概率31=p ,若船舶遭受了90000次波浪冲击,问其中有30500~29500次纵摇角度大于 3的概率是多少?解:设随机变量X 表示“在90000次波浪冲击中纵摇角大于 3的次数”,则2100)1(,30000),31,90000(~=-=p np np B X ,由棣莫弗—拉普拉斯中心极限定理得1)54.3(2)2100500210030000()3050029500(-Φ≈<-=<<X P X P9996.019998.02=-⨯=16.设有30个电子器件3021,,,D D D ,它们的使用情况如下:1D 损坏,2D 接着使用;2D 损坏,3D 接着使用等等.设器件i D 的使用寿命服从参数1.0=λ(单位:1-h )的指数分布.令T 为30个器件使用的总时数,问T 超过350h 的概率是多少?解:设随机变量i T 表示“第i 个电子器件的使用寿命”,.30,,2,1 =i 依题可知,3021,,,T T T 相互独立,1001)(,101)(),1.0(~22======λσλμi i i T D T E e T ,且∑==301i i T T ,由独立同分布中心极限定理得)30101030350(1)350()350()350(301301⨯-Φ-≈->-=>=>∑∑==σμσμn n n n TP T P T P i ii i。
概率第四章答案

习题四1.设随机变量X 的分布律为X -1 0 1 2 P1/8 1/2 1/8 1/4求E (X ),E (X 2),E (2X +3). 【解】(1) 11111()(1)012;82842E X =-⨯+⨯+⨯+⨯= (2) 2222211115()(1)012;82844E X =-⨯+⨯+⨯+⨯=(3) 1(23)2()32342E X E X +=+=⨯+=2.已知100个产品中有10个次品,求任意取出的5个产品中的次品数的数学期望、方差. 【解】设任取出的5个产品中的次品数为X ,则X 的分布律为 X 0 12345P5905100C 0.583C = 1410905100C C 0.340C = 2310905100C C 0.070C = 3210905100C C 0.007C = 4110905100C C 0C = 5105100C 0C = 故 ()0.58300.34010.07020.00730405E X =⨯+⨯+⨯+⨯+⨯+⨯ 0.501,= 52()[()]iii D X x E X P ==-∑222(00.501)0.583(10.501)0.340(50.501)00.432.=-⨯+-⨯++-⨯=3.设随机变量X 的分布律为X -1 0 1 Pp 1 p 2 p 3且已知E (X )=0.1,E (X 2)=0.9,求P 1,P 2,P 3. 【解】因1231P P P ++=……①,又12331()(1)010.1E X P P P P P =-++=-=……②,222212313()(1)010.9E X P P P P P =-⋅+⋅+⋅=+=……③由①②③联立解得1230.4,0.1,0.5.P P P ===4.袋中有N 只球,其中的白球数X 为一随机变量,已知E (X )=n ,问从袋中任取1球为白球的概率是多少?【解】记A ={从袋中任取1球为白球},则(){|}{}Nk P A P A X k P X k ===∑全概率公式1{}{}1().NNk k k P X k kP X k N Nn E X N N========∑∑5.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤≤-<≤.,0,21,2,10,其他x x x x求E (X ),D (X ). 【解】1221()()d d (2)d E X xf x x x x x x x +∞-∞==+-⎰⎰⎰21332011 1.33x x x ⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎣⎦⎣⎦122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰ 故 221()()[()].6D XE X E X =-=6.设随机变量X ,Y ,Z 相互独立,且E (X )=5,E (Y )=11,E (Z )=8,求下列随机变量的数学期望.(1) U =2X +3Y +1; (2) V =YZ -4X .【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++ 25311144.=⨯+⨯+=(2) [][4][]4()E V E YZ X E YZ E X =-=- ,()()4()Y Z E Y E Z E X ⋅-因独立1184568.=⨯-⨯= 7.设随机变量X ,Y 相互独立,且E (X )=E (Y )=3,D (X )=12,D (Y )=16,求E (3X -2Y ),D (2X -3Y ). 【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=⨯-⨯=(2) 22(23)2()(3)412916192.D X Y D X DY -=+-=⨯+⨯= 8.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<.,0,0,10,其他x y x k试确定常数k ,并求E (XY ). 【解】因1001(,)d d d d 1,2x f x y x y x k y k +∞+∞-∞-∞===⎰⎰⎰⎰故k =210()(,)d d d 2d 0.25xE XY xyf x y x y x x y y +∞+∞-∞-∞===⎰⎰⎰⎰.9.设X ,Y 是相互独立的随机变量,其概率密度分别为f X (x )=⎩⎨⎧≤≤;,0,10,2其他x x f Y (y )=(5)e ,5,0,.y y --⎧>⎨⎩其他求E (XY ).【解】方法一:先求X 与Y 的均值 12()2d ,3E X x x x ==⎰ 5(5)5()e d 5e d e d 51 6.z y y z z E Y y yz z z +∞+∞+∞=-----=+=+=⎰⎰⎰令由X 与Y 的独立性,得2()()()6 4.3E XY E X E Y ==⨯=方法二:利用随机变量函数的均值公式.因X 与Y 独立,故联合密度为(5)2e ,01,5,(,)()()0,,y X Y x x y f x y f x f y --⎧≤≤>==⎨⎩其他 于是11(5)2(5)552()2ed d 2de d 6 4.3y y E XY xy x x y x x y y +∞+∞----=⋅==⨯=⎰⎰⎰⎰10.设随机变量X ,Y 的概率密度分别为f X (x )=⎩⎨⎧≤>-;0,0,0,22x x x e f Y (y )=⎩⎨⎧≤>-.0,0,0,44y y y e 求(1) E (X +Y );(2) E (2X -3Y 2). 【解】22-200E()()d =2e d [e ]+e d x x x X X xf x x x x x x +∞+∞+∞--+∞-∞=⋅=-⎰⎰⎰201e d .2x x +∞-==⎰401()()d =4e dy .4y Y E Y yf y y y +∞+∞--∞=⋅=⎰⎰22242021()()d 4e d .48y Y E Y y f y y y y +∞+∞--∞==⋅==⎰⎰从而(1)113()()().244E X Y E X E Y +=+=+=(2)22115(23)2()3()23288E X Y E X E Y -=-=⨯-⨯= 11.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧<≥-.0,0,0,22x x cx xke求(1) 系数c ;(2) E (X );(3) D (X ).【解】(1) 由222()d ed 12k x cf x x cx x k+∞+∞--∞===⎰⎰得22c k =. (2) 2220()()d()2e d k x E X xf x x x k x x +∞+∞--∞==⋅⎰⎰22220π2e d .2k x k x x k+∞-==⎰(3) 22222221()()d()2e.k x E X x f x x x k x k +∞+∞--∞==⋅⎰⎰故 222221π4π()()[()].24D X E X E X k k k⎛⎫-=-=-= ⎪ ⎪⎝⎭ 12.袋中有12个零件,其中9个合格品,3个废品.安装机器时,从袋中一个一个地取出(取出后不放回),设在取出合格品之前已取出的废品数为随机变量X ,求E (X )和D (X ). 【解】设随机变量X 表示在取得合格品以前已取出的废品数,则X 的可能取值为0,1,2,3.为求其分布律,下面求取这些可能值的概率,易知9{0}0.750,12P X === 39{1}0.204,1211P X ==⨯= 329{2}0.041,121110P X ==⨯⨯= 3219{3}0.005.1211109P X ==⨯⨯⨯=于是,得到X 的概率分布表如下: X 0 1 2 3 P0.7500.2040.0410.005由此可得()00.75010.20420.04130.0050.301.E X =⨯+⨯+⨯+⨯=22222222()075010.20420.04130.0050.413()()[()]0.413(0.301)0.322.E X D X E X E X =⨯+⨯+⨯+⨯==-=-=13.一工厂生产某种设备的寿命X (以年计)服从指数分布,概率密度为f (x )=⎪⎩⎪⎨⎧≤>-.0,0,0,414x x xe为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备,工厂获利100元,而调换一台则损失200元,试求工厂出售一台设备赢利的数学期望. 【解】厂方出售一台设备净盈利Y 只有两个值:100元和 -200元/41/411{100}{1}e d e 4x P Y P X x +∞--==≥==⎰1/4{200}{1}1e.P Y P X -=-=<=-故1/41/41/4()100e(200)(1e )300e 20033.64E Y ---=⨯+-⨯-=-= (元).14.设X 1,X 2,…,X n 是相互独立的随机变量,且有E (X i )=μ,D (X i )=σ2,i =1,2,…,n ,记∑==n i i S X n X 12,1,S 2=∑=--n i i X X n 12)(11. (1) 验证)(X E =μ,)(X D =n2σ;(2) 验证S 2=)(11122∑=--ni i X n X n ; (3) 验证E (S 2)=σ2.【证】(1) 1111111()()().n nn i i i i i i E X E X E X E X nu u n n n n ===⎛⎫===== ⎪⎝⎭∑∑∑22111111()()n nni i i ii i i D X D X D X X DXn nn ===⎛⎫== ⎪⎝⎭∑∑∑之间相互独立2221.n n nσσ==(2) 因222221111()(2)2nnnniii ii i i i i XX X X X X X nX X X ====-=+-=+-∑∑∑∑2222112nnii i i X nX X nX X nX ===+-=-∑∑故22211()1ni i S X nX n ==--∑. (3) 因2(),()i i E X u D X σ==,故2222()()().i i i E X D X EX u σ=+=+同理因2(),()E X u D X nσ==,故222()E X u nσ=+.从而222221111()()[()()]11n ni i i i E s E X nX E X nE X n n ==⎡⎤=-=-⎢⎥--⎣⎦∑∑221222221[()()]11().1ni i E X nE X n n u n u n n σσσ==--⎡⎤⎛⎫=+-+=⎢⎥ ⎪-⎝⎭⎣⎦∑15.对随机变量X 和Y ,已知D (X )=2,D (Y )=3,Cov(X ,Y )= -1,计算:Cov (3X -2Y +1,X +4Y -3). 【解】Cov(321,43)3()10Cov(,)8()X Y X Y D X X Y D Y -++-=+- 3210(1)8328=⨯+⨯--⨯=- (因常数与任一随机变量独立,故Cov(X ,3)=Cov(Y ,3)=0,其余类似). 16.设二维随机变量(X ,Y )的概率密度为f (x ,y )=221,1,π0,.x y ⎧+≤⎪⎨⎪⎩其他试验证X 和Y 是不相关的,但X 和Y 不是相互独立的. 【解】设22{(,)|1}D x y x y =+≤.2211()(,)d d d d πx y E X xf x y x y x x y +∞+∞-∞-∞+≤==⎰⎰⎰⎰ 2π1001=cos d d 0.πr r r θθ=⎰⎰同理E (Y )=0. 而 Cov(,)[()][()](,)d d X Y x E x y E Y f x y x y +∞+∞-∞-∞=--⎰⎰222π1200111d d sin cos d d 0ππx y xy x y r r r θθθ+≤===⎰⎰⎰⎰, 由此得0XY ρ=,故X 与Y 不相关. 下面讨论独立性,当|x |≤1时,2212112()1.ππx X x f x y x --- 当|y |≤1时,2212112()1ππy Y y f y x y ----显然()()(,).X Y f x f y f x y ≠故X和Y不是相互独立的.17.设随机变量(X,Y)的分布律为-1 0 1-1 0 1 1/8 1/8 1/8 1/8 0 1/8 1/8 1/8 1/8验证X和Y是不相关的,但X和Y不是相互独立的.【解】联合分布表中含有零元素,X与Y显然不独立,由联合分布律易求得X,Y及XY的分布律,其分布律如下表X -1 0 1P 382838Y -1 0 1P 382838XY -1 0 1P 284828由期望定义易得E(X)=E(Y)=E(XY)=0.从而E(XY)=E(X)·E(Y),再由相关系数性质知ρXY=0, 即X与Y的相关系数为0,从而X和Y是不相关的.又331{1}{1}{1,1}888P X P Y P X Y =-=-=⨯≠==-=-从而X与Y不是相互独立的.18.设二维随机变量(X,Y)在以(0,0),(0,1),(1,0)为顶点的三角形区域上服从均匀分布,求Cov(X,Y),ρXY.【解】如图,S D=12,故(X,Y)的概率密度为题18图2,(,),(,)0,x y Df x y∈⎧=⎨⎩其他.XY()(,)d d DE X xf x y x y =⎰⎰1101d 2d 3xx x y -==⎰⎰22()(,)d d DE X x f x y x y =⎰⎰11201d 2d 6xx x y -==⎰⎰从而222111()()[()].6318D XE X E X ⎛⎫=-=-= ⎪⎝⎭同理11(),().318E Y D Y == 而 1101()(,)d d 2d d d 2d .12xDDE XY xyf x y x y xy x y x xy y -====⎰⎰⎰⎰⎰⎰所以1111Cov(,)()()()123336X Y E XY E X E Y =-=-⨯=-. 从而1Cov(,)12)()XY X Y D Y ρ-===-19.设(X ,Y )的概率密度为f (x ,y )=1ππsin(),0,0,2220.x y x y ,⎧+≤≤≤≤⎪⎨⎪⎩其他求协方差Cov (X ,Y )和相关系数ρXY . 【解】π/2π/21π()(,)d d d sin()d .24E X xf x y x y x xx y y +∞+∞-∞-∞==+=⎰⎰⎰⎰ππ2222201ππ()d sin()d 2.282E X x x x y y =+=+-⎰⎰从而222ππ()()[()] 2.162D XE X E X =-=+-同理 2πππ(),() 2.4162E Y D Y ==+- 又 π/2π/2π()d sin()d d 1,2E XY x xy x y x y =+=-⎰⎰故 2ππππ4Cov(,)()()()1.2444X Y E XY E X E Y -⎛⎫⎛⎫=-=--⨯=- ⎪ ⎪⎝⎭⎝⎭222222π4Cov(,)(π4)π8π164.πππ8π32π8π32)()2162XY X Y D Y ρ-⎛⎫- ⎪--+⎝⎭===-=-+-+-+- 20.已知二维随机变量(X ,Y )的协方差矩阵为⎥⎦⎤⎢⎣⎡4111,试求Z 1=X -2Y 和Z 2=2X -Y 的相关系数.【解】由已知知:D (X )=1,D (Y )=4,Cov(X ,Y )=1.从而12()(2)()4()4Cov(,)1444113,()(2)4()()4Cov(,)414414,D Z D X Y D X D Y X Y D Z D X Y D X D Y X Y =-=+-=+⨯-⨯==-=+-=⨯+-⨯=12Cov(,)Cov(2,2)Z Z X Y X Y =--2Cov(,)4Cov(,)Cov(,)2Cov(,)2()5Cov(,)2()215124 5.X X Y X X YY Y D X XY D Y =--+=-+=⨯-⨯+⨯=故12Z Z ρ===21.对于两个随机变量V ,W ,若E (V 2),E (W 2)存在,证明:[E (VW )]2≤E (V 2)E (W 2).这一不等式称为柯西许瓦兹(Couchy -Schwarz )不等式. 【证】令2(){[]},.g t E V tW t R =+∈显然22220()[()][2]g t E V tW E V tVW t W ≤=+=++222[]2[][],.E V t E VW t E W t R =++∀∈可见此关于t 的二次式非负,故其判别式Δ≤0, 即2220[2()]4()()E VW E W E V ≥∆=- 2224{[()]()()}.E VW E V E W =-故222[()]()()}.E VW E V E W ≤22.假设一设备开机后无故障工作的时间X 服从参数λ=1/5的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y 的分布函数F (y ).【解】设Y 表示每次开机后无故障的工作时间,由题设知设备首次发生故障的等待时间X ~E (λ),E (X )=1λ=5. 依题意Y =min(X ,2).对于y <0,f (y )=P {Y ≤y }=0. 对于y ≥2,F (y )=P (X ≤y )=1.对于0≤y <2,当x ≥0时,在(0,x )内无故障的概率分布为 P {X ≤x }=1 -e -λx ,所以F (y )=P {Y ≤y }=P {min(X ,2)≤y }=P {X ≤y }=1 -e -y/5.23.已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品.从甲箱中任取3件产品放乙箱后,求:(1)乙箱中次品件数Z 的数学期望;(2)从乙箱中任取一件产品是次品的概率. 【解】(1) Z 的可能取值为0,1,2,3,Z 的概率分布为33336C C {}C k kP Z k -==, 0,1,2,3.k =因此,()0123.202020202E Z =⨯+⨯+⨯+⨯=(2) 设A 表示事件“从乙箱中任取出一件产品是次品”,根据全概率公式有30(){}{|}k P A P Z k P A Z k ====∑191921310.202062062064=⨯+⨯+⨯+⨯= 24.假设由自动线加工的某种零件的内径X (毫米)服从正态分布N (μ,1),内径小于10或大于12为不合格品,其余为合格品.销售每件合格品获利,销售每件不合格品亏损,已知销售利润T (单位:元)与销售零件的内径X 有如下关系T =⎪⎩⎪⎨⎧>-≤≤<-.12,5,1210,20,10,1X X X 若若若 问:平均直径μ取何值时,销售一个零件的平均利润最大?【解】(){10}20{1012}5{12}E T P X P X P X =-<+≤≤->{10}20{1012}5{12}(10)20[(12)(10)]5[1(12)]25(12)21(10) 5.P X u u P u X u u P X u u u u u u u u =--<-+-≤-≤--->-=-Φ-+Φ--Φ---Φ-=Φ--Φ--故2/2d ()25(12)(1)21(10)(1)0(()),d x E T u u x u ϕϕϕ-=-⨯---⨯-= 令这里得 22(12)/2(10)/225e 21eu u ----=两边取对数有2211ln 25(12)ln 21(10).22u u --=--解得 125111ln 11ln1.1910.91282212u =-=-≈(毫米)由此可得,当u =10.9毫米时,平均利润最大.25.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤≤.,0,0,2cos 21其他πx x 对X 独立地重复观察4次,用Y 表示观察值大于π/3的次数,求Y 2的数学期望.(2002研考)【解】令 π1,,3(1,2,3,4)π0,3i X Y i ⎧>⎪⎪==⎨⎪≤⎪⎩X .则41~(4,)i i Y Y B p ==∑.因为ππ{}1{}33p P X P X =>=-≤及π/30π11{}cos d 3222x P X x ≤==⎰,所以111(),(),()42,242i i E Y D Y E Y ===⨯=2211()41()()22D YE Y EY =⨯⨯==-,从而222()()[()]12 5.E Y D Y E Y =+=+=26.两台同样的自动记录仪,每台无故障工作的时间T i (i =1,2)服从参数为5的指数分布,首先开动其中一台,当其发生故障时停用而另一台自动开启.试求两台记录仪无故障工作的总时间T =T 1+T 2的概率密度f T (t ),数学期望E (T )及方差D (T ). 【解】由题意知:55e ,0,()0,0t i t f t t -⎧≥=⎨<⎩.因T 1,T 2独立,所以f T (t )=f 1(t )*f 2(t ).当t <0时,f T (t )=0;当t ≥0时,利用卷积公式得55()5120()()()d 5e 5e d 25e tx t x t T f t f x f t x x x t +∞-----∞=-==⎰⎰故得525e ,0,()0,0.t T t t f t t -⎧≥=⎨<⎩ 由于T i ~E (5),故知E (T i )=15,D (T i )=125(i =1,2)因此,有E (T )=E (T 1+T 2)=25.又因T 1,T 2独立,所以D (T )=D (T 1+T 2)=225. 27.设两个随机变量X ,Y 相互独立,且都服从均值为0,方差为1/2的正态分布,求随机变量|X -Y |的方差.【解】设Z =X -Y ,由于22~0,,~0,,22X N Y N ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭且X 和Y 相互独立,故Z ~N (0,1).因22()()(||)[(||)]D X Y D Z E Z E Z -==-22()[()],E Z E Z =-而22/2()()1,(||)||e d 2πz E Z D Z E Z z z +∞--∞===⎰ 2/202e d π2πz z z +∞-==所以 2(||)1πD X Y -=-. 28.某流水生产线上每个产品不合格的概率为p (0<p <1),各产品合格与否相互独立,当出现一个不合格产品时,即停机检修.设开机后第一次停机时已生产了的产品个数为X ,求E (X )和D (X ).【解】记q =1 -p ,X 的概率分布为P {X =i }=q i -1p ,i =1,2,…,故12111()().1(1)i ii i q p E X iq p p q p q q p ∞∞-=='⎛⎫'===== ⎪--⎝⎭∑∑ 又221211121()()i i i i i i E X i qp i i q p iq p ∞∞∞---=====-+∑∑∑2232211()12112.(1)ii q pq q pq p q p pq q p q p p p∞=''⎛⎫''=+=+⎪-⎝⎭+-=+==-∑所以 22222211()()[()].p pD XE X E X p p p--=-=-=题29图29.设随机变量X 和Y 的联合分布在点(0,1),(1,0)及(1,1)为顶点的三角形区域上服从均匀分布.(如图),试求随机变量U =X +Y 的方差. 【解】D (U )=D (X +Y )=D (X )+D (Y )+2Cov(X ,Y )=D (X )+D (Y )+2[E (XY ) -E (X )·E (Y )]. 由条件知X 和Y 的联合密度为2,(,),(,)0,0.x y G f x y t ∈⎧=⎨<⎩ {(,)|01,01,1}.G x y x y x y =≤≤≤≤+≥ 从而11()(,)d 2d 2.X xf x f x y y y x +∞-∞-===⎰⎰因此11122300031()()d 2d ,()2d ,22X E X xf x x x x E X x x =====⎰⎰⎰22141()()[()].2918D XE X E X =-=-=同理可得 31(),().218E Y D Y ==1115()2d d 2d d ,12xGE XY xy x y x x y y -===⎰⎰⎰⎰541Cov(,)()()(),12936X Y E XY E X E Y =-=-=- 于是 1121()().18183618D U D X Y =+=+-=30.设随机变量U 在区间[ -2,2]上服从均匀分布,随机变量X =1,1,1,1,U U -≤-⎧⎨>-⎩ Y =1,1,1, 1.U U -≤⎧⎨>⎩若试求(1)X 和Y 的联合概率分布;(2)D (X +Y ).【解】(1) 为求X 和Y 的联合概率分布,就要计算(X ,Y )的4个可能取值( -1, -1),( -1,1),(1, -1)及(1,1)的概率.P {x = -1,Y = -1}=P {U ≤ -1,U ≤1}112d d 1{1}444x x P U ---∞-=≤-===⎰⎰P {X = -1,Y =1}=P {U ≤ -1,U >1}=P {∅}=0, P {X =1,Y = -1}=P {U > -1,U ≤1}11d 1{11}44x P U -=-<≤==⎰21d 1{1,1}{1,1}{1}44x P X Y P U U P U ===>->=>=⎰. 故得X 与Y 的联合概率分布为(1,1)(1,1)(1,1)(1,1)(,)~1110424X Y ----⎡⎤⎢⎥⎢⎥⎣⎦. (2) 因22()[()][()]D X Y E X Y E X Y +=+-+,而X +Y 及(X +Y )2的概率分布相应为202~111424X Y -⎡⎤⎢⎥+⎢⎥⎣⎦, 24()~1122X Y ⎡⎤⎢⎥+⎢⎥⎣⎦. 从而11()(2)20,44E X Y +=-⨯+⨯= 211[()]042,22E X Y +=⨯+⨯=所以22()[()][()] 2.D X Y E X Y E X Y +=+-+= 31.设随机变量X 的概率密度为f (x )=x-e 21,( -∞<x <+∞) (1) 求E (X )及D (X );(2) 求Cov(X ,|X |),并问X 与|X |是否不相关? (3) 问X 与|X |是否相互独立,为什么?【解】(1)||1()e d 0.2x E X xx +∞--∞==⎰ 2||201()(0)e d 0e d 2.2x x D X x x x x +∞+∞---∞=-==⎰⎰(2) Cov(,|)(||)()(||)(||)X X E X X E X E X E X X =-= ||1||e d 0,2x x x x +∞--∞==⎰所以X 与|X |互不相关.(3) 为判断|X |与X 的独立性,需依定义构造适当事件后再作出判断,为此,对定义域-∞<x <+∞中的子区间(0,+∞)上给出任意点x 0,则有0000{}{||}{}.x X x X x X x -<<=<⊂<所以000{||}{} 1.P X x P X x <<<<<故由00000{,||}{||}{||}{}P X x X x P X x P X x P X x <<=<><<得出X 与|X |不相互独立.32.已知随机变量X 和Y 分别服从正态分布N (1,32)和N (0,42),且X 与Y 的相关系数ρXY = -1/2,设Z =23YX +. (1) 求Z 的数学期望E (Z )和方差D (Z ); (2) 求X 与Z 的相关系数ρXZ ;(3) 问X 与Z 是否相互独立,为什么? 【解】(1) 1().323X Y E Z E ⎛⎫=+=⎪⎝⎭ ()2Cov ,3232XY X Y D Z D D ⎛⎫⎛⎫⎛⎫=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11119162Cov(,),9432X Y =⨯+⨯+⨯⨯ 而1Cov(,))()3462XY X Y D Y ρ⎛⎫==-⨯⨯=- ⎪⎝⎭所以 1()146 3.3D Z =+-⨯= (2) 因()()11Cov(,)Cov ,Cov ,Cov ,3232X Y X Z X X X X Y ⎛⎫=+=+ ⎪⎝⎭ 119()(6)3=0,323D X =+⨯-=- 所以 Cov(,)0.)()XZ X Z D Z ρ==(3) 由0XZ ρ==,得X 与Z 不相关.又因1~,3,~(1,9)3Z N X N ⎛⎫ ⎪⎝⎭,所以X 与Z 也相互独立.33.将一枚硬币重复掷n 次,以X 和Y 表示正面向上和反面向上的次数.试求X 和Y 的相关系数XY ρ.【解】由条件知X +Y =n ,则有D (X +Y )=D (n )=0.再由X ~B (n ,p ),Y ~B (n ,q ),且p =q =12, 从而有 ()()4nD X npq D Y ===所以 0()()()2()()XY D X Y D X D Y D X D Y ρ=+=++2,24XY n nρ=+ 故XY ρ= -1. 34.设随机变量X 和Y 的联合概率分布为-1 0 10 10.07 0.18 0.15 0.08 0.32 0.20试求X 和Y 的相关系数ρ.【解】由已知知E (X )=0.6,E (Y )=0.2,而XY 的概率分布为YX -1 0 1 P 0.080.720.2所以E (XY )= -0.08+0.2=0.12Cov(X ,Y )=E (XY ) -E (X )·E (Y )=0.12 -0.6×0.2=0从而 XY ρ=035.对于任意两事件A 和B ,0<P (A )<1,0<P (B )<1,则称ρ=())()()()()()(B P A P B P A P B P A P AB P ⋅-为事件A 和B 的相关系数.试证:(1) 事件A 和B 独立的充分必要条件是ρ=0; (2) |ρ|≤1. 【证】(1)由ρ的定义知,ρ=0当且仅当P (AB ) -P (A )·P (B )=0.而这恰好是两事件A 、B 独立的定义,即ρ=0是A 和B 独立的充分必要条件. (2) 引入随机变量X 与Y 为1,,0,A X A ⎧⎪=⎨⎪⎩若发生若发生; 1,,0,B Y B ⎧⎪=⎨⎪⎩若发生若发生.由条件知,X 和Y 都服从0 -1分布,即01~1()()X P A P A ⎧⎨-⎩ 01~1()()Y P B P B ⎧⎨-⎩从而有E (X )=P (A ),E (Y )=P (B ),D (X )=P (A )·P (A ),D (Y )=P (B )·P (B ),Cov(X ,Y )=P (AB ) -P (A )·P (B )所以,事件A 和B 的相关系数就是随机变量X 和Y 的相关系数.于是由二元随机变量相关系数的基本性质可得|ρ|≤1. 36. 设随机变量X 的概率密度为YXf X (x )=⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-.,0,20,41,01,21其他x x令Y =X 2,F (x ,y )为二维随机变量(X ,Y )的分布函数,求:(1) Y 的概率密度f Y (y ); (2) Cov(X ,Y );(3)1(,4)2F -. 解: (1) Y 的分布函数为2(){}{}Y F y P Y y P X y =≤=≤.当y ≤0时, ()0Y F y =,()0Y f y =; 当0<y <1时,(){{0}{0Y F y P X P X P X =≤≤=≤<+≤≤=,()Y f y =;当1≤y <4时,1(){10}{02Y F y P X P X =-≤<+≤≤=()Y f y =;当y ≥4时,()1Y F y =,()0Y f y =. 故Y 的概率密度为1,()04,0,.Y y f y y <<=≤<⎪⎩其他(2) 0210111()()d d d 244+X E X =xf x x x x x x ∞∞=+=⎰⎰⎰--, 02222210115()()()d d d )246+X E Y =E X =x f x x x x x x ∞∞=+=⎰⎰⎰--, 02233310117()()()d d d 248+X E XY =E Y =x f x x x x x x ∞∞=+=⎰⎰⎰--, 故 Cov(X,Y ) =2()()()3E XY E X E Y =⋅-.(3) 2111(,4){,4}{,4}222F P X Y P X X -=≤-≤=≤-≤11{,22}{2}22P X X P X =≤--≤≤=-≤≤-11{1}24P X =-≤≤-=.37. 设随机变量X 服从参数为1的泊松分布,求P{X=E(X 2)}.解:因为其分布律为P{x=k}=1!e k -,k=0,1,2,…,12211011121111()!(1)!(1)!11(2)!(1)!() 2.k k k k k e k k E X k e e k k k e k k e e e -∞∞∞--===∞∞-==--+===--⎛⎫=+ ⎪--⎝⎭=+=∑∑∑∑∑所以211{()}{2}.2!2P x E X P X e e --=====所以。
《概率论与数理统计》习题及答案第四章

《概率论与数理统计》习题及答案第 四 章1.一个袋子中装有四个球,它们上面分别标有数字1,2,2,3,今从袋中任取一球后不放回,再从袋中任取一球,以,X Y 分别表示第一次,第二次取出的球上的标号,求(,)X Y 的分布列.解(,)X Y 的分布列为其中(1,1)(1)(1|1)0P X Y P X P Y X =======余者类推。
2.将一枚硬币连掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值,试写出(,)X Y 的分布列及边缘分布列。
解一枚硬币连掷三次相当于三重贝努里试验,故1~(3,).2X B 331()(),0,1,2,32k P X k C k ===,于是(,)X Y 的分布列和边缘分布为01013818i p ⋅其中(0,1)(0)(1|0)0P X Y P X P Y X =======,13313(1,1)(1)(1|1)()128P X Y P X P Y X C =======⨯=,余者类推。
3.设(,)X Y 的概率密度为又(1){(,)|1,3}D x y x y =<<;(2){(,)|3}D x y x y =+<。
求{(,)}P X Y D ∈ 解(1)1321{(,)}(6)8P x y D x y dxdxy ∈=--⎰=321(6)8x x y dxdy --- =)落在圆222()x y r r R +≤<内的概率. 解(1)22223201(R x y R CR dxdy C R C r drd ππθ+≤==-⎰⎰⎰⎰333233R R C R C πππ⎡⎤=-=⎢⎥⎣⎦, ∴33C R π=.(2)设222{(,)|}D x y x y r =+≤,所求概率为322323232133r r r Rr R R R πππ⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦. 5.已知随机变量X 和Y 的联合概率密度为 求X 和Y 的联合分布函数.解1设(,)X Y 的分布函数为(,)F x y ,则解2由联合密度可见,,X Y 独立,边缘密度分别为 边缘分布函数分别为(),()X Y F x F y ,则 设(,)X Y 的分布函数为(,)F x y ,则6.设二维随机变量(,)X Y 在区域:0D x <<求边缘概率密度。
概率论与数理统计课后习题答案 第四章

(2) 令
,求 Y 的概率密度 fY(y).
解:
(1)
(2)
由 Y=2X-1 得
, X’=
=
七、 设二维随机变量(X,Y)的概率密度为
其他
求: (1)E(X+Y); (2)E(XY); (3)
.
解:
(1)
(2)
(3)
八、 设随机变量 X 的分布律为
X
-1
0
1
P
记 Y=X2,求: (1)D(X), D(Y); 解:
ρ
ρ
ρ
ρ
5. 证明 D(X-Y)=D(X)+D(Y)-2Cov(X,Y). 证:
6. 设(X,Y)的协方差矩阵为 解:
,求 X 与 Y 的相关系数 ρxy.
ρ
自测题 4
一、 选择题
1. 设随机变量 X 服从参数为 0.5 的指数分布,则下列各项中正确的是 B .
A. E(X)=0.5, D(X)=0.25
2. 设二维随机变量(X,Y)的概率密度为
求 Cov(X,Y). 解:
其他
3. 设二维随机变量(X,Y)的概率密度为
求 X 与 Y 的相关系数 ρxy. 解:
其他
运用分部积分法. 服从λ =1 的指数分布
所以 ρ
4. 设二维随机变量(X,Y)服从二维正态分布,且 E(X)=0, E(Y)=0, D(X)=16, D(Y)=25, Cov(X,Y)=12,求(X,Y)的联合概 率密度函数 f(x,y). 解:
解: Cov(X,Y)=0
2. 设随机变量 X 的分布律为 3 .
X
-1
0
1
2
P
0.1 0.2 0.3 0.4
概率论与数理统计习题解答(第4章)

第4章习题答案三、解答题1. 设随机变量X求)(X E ,)(2X E ,)53(+X E .解:E (X ) =∑∞=1i ixp= ()2-4.0⨯+03.0⨯+23.0⨯= -0.2E (X 2) =∑∞=12i i p x= 44.0⨯+ 03.0⨯+ 43.0⨯= 2.8E (3 X +5) =3 E (X ) +5 =3()2.0-⨯+5 = 4.42. 同时掷八颗骰子,求八颗骰子所掷出的点数和的数学期望. 解:记掷1颗骰子所掷出的点数为X i ,则X i 的分布律为6,,2,1,6/1}{ ===i i X P记掷8颗骰子所掷出的点数为X ,同时掷8颗骰子,相当于作了8次独立重复的试验, E (X i ) =1/6×(1+2+3+4+5+6)=21/6 E (X ) =8×21/3=283. 某图书馆的读者借阅甲种图书的概率为p 1,借阅乙种图书的概率为p 2,设每人借阅甲乙图书的行为相互独立,读者之间的行为也是相互独立的. (1) 某天恰有n 个读者,求借阅甲种图书的人数的数学期望.(2) 某天恰有n 个读者,求甲乙两种图书至少借阅一种的人数的数学期望. 解:(1) 设借阅甲种图书的人数为X ,则X~B (n , p 1),所以E (X )= n p 1 (2) 设甲乙两种图书至少借阅一种的人数为Y , 则Y ~B (n , p ),记A ={借甲种图书}, B ={借乙种图书},则p ={A ∪ B }= p 1+ p 2 - p 1 p 2 所以E (Y )= n (p 1+ p 2 - p 1 p 2 )4. 将n 个考生的的录取通知书分别装入n 个信封,在每个信封上任意写上一个考生的姓名、地址发出,用X 表示n 个考生中收到自己通知书的人数,求E (X ).解:依题意,X~B (n ,1/n ),所以E (X ) =1.5. 设)(~λP X ,且}6{}5{===X P X P ,求E (X ).解:由题意知X ~P (λ),则X 的分布律P{}k X ==λλ-e k k!,k = 1,2,...又P {}5=X =P {}6=X , 所以λλλλ--=e e!6!565解得 6=λ,所以E (X ) = 6.6. 设随机变量X 的分布律为,,4,3,2,1,6}{22 --===k kk X P π问X 的数学期望是否存在?解:因为级数∑∑∑∞=+∞=+∞=+-=-=⨯-11212112211)1(6)6)1(()6)1((k k k k k k kk k k πππ, 而 ∑∞=11k k 发散,所以X 的数学期望不存在.7. 某城市一天的用电量X (十万度计)是一个随机变量,其概率密度为⎪⎩⎪⎨⎧>=-.0,0,91)(3/其它x xe x f x 求一天的平均耗电量.解:E (X ) =⎰⎰⎰∞-∞-∞∞-==03/203/9191)(dx e x dx xe xdx x f x x x =6.8. 设某种家电的寿命X (以年计)是一个随机变量,其分布函数为⎪⎩⎪⎨⎧>-=.0,5,251)(2其它x x x F求这种家电的平均寿命E (X ).解:由题意知,随机变量X 的概率密度为)()(x F x f '=当x >5时,=)(x f 3350252xx =⨯--,当x ≤5时,=)(x f 0. E (X ) =10|5050)(5-53=-==∞++∞∞+∞⎰⎰xdx x x dx x xf 所以这种家电的平均寿命E (X )=10年.9. 在制作某种食品时,面粉所占的比例X 的概率密度为⎩⎨⎧<<-=.0,10,)1(42)(5其它x x x x f 求X 的数学期望E (X ).解:E (X ) =dx x x dx x xf ⎰⎰+∞∞-=-152)1(42)(=1/410. 设随机变量X 的概率密度如下,求E (X ).⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<-≤≤-+=.010,)1(2301)1(23)(22其它,,,,x x x x x f解:0)1(1023)1(0123)()(22=-++-=+∞∞-=⎰⎰⎰dx x x dx x x dx x xf X E .111. 设),4(~p B X ,求数学期望)2(sinX E π. 解:X 的分布律为k n kk n p p C k X P --==)1(}{, k = 0,1,2,3,4,X 取值为0,1,2,3,4时,2sinX π相应的取值为0,1,0,-1,0,所以)21)(1(4)1(1)1(1)2(sin13343114p p p p p C p p C XE --=-⨯--⨯=π12. 设风速V 在(0,a )上服从均匀分布,飞机机翼受到的正压力W 是V 的函数:2kV W =,(k > 0,常数),求W 的数学期望.解:V 的分布律为⎪⎩⎪⎨⎧<<=其它 ,00 ,1)(a v a v f ,所以 ===+∞∞-=⎰⎰aa v a k dv a kv dx v f kv W E 03022|)31(1)()(231ka13. 设随机变量(X ,求E (X ),E (Y ),E (X – Y ).解:E (X )=0×(3/28+9/28+3/28)+1×(3/14+3/14+0)+ 2×(1/28+0+0)= 7/14=1/2 E (Y )=0×(3/28+3/14+1/28)+1×(9/28+3/14+0)+ 2×(3/28+0+0)=21/28=3/4 E (X -Y ) = E (X )- E (Y )=1/2-3/4= -1/4.14. 设随机变量(X ,Y )具有概率密度⎩⎨⎧≤+≤≤≤≤=其它,01,10,10,24),(y x y x xy y x f ,求E (X ),E (Y ),E (XY )解:E (X )=⎰⎰⎰⎰-=⋅11022424xDydydx x xydxdy x dx x x ⎰-⋅=1022)1(2124dx x x x ⎰+-=10432)2412(52)51264(1543=+-=x x x.152)34524638()1(31242424)(5/22424)(1654311010322210102=-+-=-⋅==⋅===⋅=⎰⎰⎰⎰⎰⎰⎰⎰⎰--x x x x dx x x dydx y xxydxdy xy XY E xdxdy y xydxdy y Y E DxDy15.所得利润(以元计)为)12(1000X Y -=,求E (Y ),D (Y ).解: E (Y) = E [1000(12-X )]=1000E [(12-X )]=1000×[(12-10)×0.2+(12-11)]×0.3+(12-12)×0.3+(12-13)×0.1+(12-14)×0.1] = 400E (Y 2) = E [10002(12-X )2]=10002E [(12-X )2]=10002[(12-10)2×0.2+(12-11)2×0.3+(12-12)2×0.3+(12-13)2×0.1 +(12-14)2×0.1]=1.6×106D (Y )=E (Y 2)-[E (Y )]2=1.6×106- 4002=1.44×10616. 设随机变量X 服从几何分布 ,其分布律为,,2,1,)1(}{1 =-==-k p p k X P k 其中0 < p < 1是常数,求E (X ),D (X ).解:令q=1- p ,则∑∑∑∑∞=∞=-∞=-∞==⨯=⨯==⨯=111111)()}{()(k kk k k k k dqdq p qk p p qk k X P k X Ep q dq d p q dq d p k k /1)11(0∑∞==-==∑∑∑∑∞=-∞=-∞=-∞=⨯+⨯-=⨯==⨯=1111112122])1([)()}{()(k k k k k k k q k qk k p p qk k X P k X Ep qk k pq k k /1)1(12+⨯-=∑∞=-p qdq d pq p q dqd pq k k kk /1)(/1012222∑∑∞=∞=+=+=p p q p q pq p q dq d pq /1/2/1)1(2/1)11(2322+=+-=+-= D (X ) = E (X 2)- E (X ) =2q /p 2+1/p -1/p 2 = (1-p )/p 217. 设随机变量X 的概率密度为⎪⎩⎪⎨⎧<-=其它,01||,11)(2x x x f π,试求E (X ),D (X ).解:E (X )=011)(112=-=⎰⎰-∞∞-dx xxdx x f x πD (X )=E (X 2)=⎰⎰⎰--∈-∞∞-=-=2/2/2]2/,2/[11222cos sin sin 11)(ππππππdt tt tx dx xxdx x f x t2122cos 122/0=-=⎰ππdt t 18. 设随机变量(X ,Y )具有D (X ) = 9,D (Y ) = 4,6/1-=XY ρ,求)(Y X D +,)43(+-Y X D . 解:因为)()(),(Y D X D Y X Cov XY =ρ,所以)()(),(Y D X D Y X Cov XY ρ==-1/6×3×2=-1,11249),(2)()()(=-+=++=+Y X Cov Y D X D Y X D51)1(6369)3,(2)(9)()43(=--+=-++=+-Y X Cov Y D X D Y X D19. 在题13中求Cov (X ,Y ),ρXY . 解:E (X ) =1/2, E (Y ) =3/4, E (XY )=0×(3/28+9/28+3/28+3/14+1/28)+1×3/14+2×0+4×0=3/14, E (X 2)= 02×(3/28+9/28+3/28)+12×(3/14+3/14+0)+ 22×(1/28+0+0)=4/7, E (Y 2)= 02×(3/28+3/14+1/28)+12×(9/28+3/14+0)+ 22×(3/28+0+0)=27/28, D (X )= E (X 2) -[E (X )]2 = 4/7-(1/2)2= 9/28, D (Y )= E (Y 2)- [E (Y )]2=27/28-(3/4)2= 45/112, Cov (X ,Y )= E (XY )- E (X ) E (Y ) =3/14- (1/2) ×(3/4)= -9/56, ρXY = Cov (X ,Y ) /()(X D )(Y D )=-9/56 ÷ (28/9112/45)= -5/520. 在题14中求Cov (X ,Y ),ρXY ,D (X + Y ).解:52)()(==Y E X E ,,)(152=XY E 752)()()(),(-=-=Y E X E XY E Y X Cov )(5124)(2101032Y E dydx y x X E x ===⎰⎰-[])(25125451)()()(22Y D X E X E X D ==-=-= 752),(2)()()(32)()(),(=++=+-==Y X Cov Y D X D Y X D Y D X D Y X Cov XYρ21. 设二维随机变量(X , Y )的概率密度为⎪⎩⎪⎨⎧≤+=.0,1,1),(22其它y x y x f π试验证X 和Y 是不相关的,但X 和Y 不是相互独立的.解:0/12/)(112111122=-==⎰⎰⎰-----dx x x dydx x X E x xππOx2x20/)(111122==⎰⎰----x x dydx y Y E π 0/)(111122==⎰⎰----x x dydx xy XY E π,所以Cov (X ,Y )=0,ρXY =0,即X 和Y 是不相关.⎪⎩⎪⎨⎧<<--=⎪⎩⎪⎨⎧<<-==⎰⎰---∞+∞-其他,,其他,01112011,/1),()(21122x x x dy dy y x f x f x x X ππ ⎪⎩⎪⎨⎧<<--=⎪⎩⎪⎨⎧<<-==⎰⎰---∞+∞-其他,,其他,01112011,/1),()(21122y y y dx dx y x f y f y y Y ππ 当x 2 + y 2≤1时,f ( x,y )≠f X ( x ) f Y (y ),所以X 和Y 不是相互独立的22. 设随机变量(X , Y )的概率密度为⎩⎨⎧<<<=.010,2||,2/1),(其它x x y y x f 验证X 和Y 是不相关的,但X 和Y 不是相互独立的.解:由于f ( x,y )的非零区域为D : 0 < x < 1, | y |< 2x32221102212====⎰⎰⎰⎰⎰-dx x xdydx dxdy y x xf X E xx D ),()(,0211022⎰⎰⎰⎰-===xx Dydydx dxdy y x yf Y E ),()(,0211022⎰⎰⎰⎰-===xx Dxydydx dxdy y x xyf XY E ),()(,所以Cov (X ,Y )=0,从而0)()(),(==y D x D y x Cov xy ρ,因此X 与Y 不相关 .⎪⎩⎪⎨⎧<<===⎰⎰-∞∞-其他,010,221),()(22Xx x dy dy y x f x x x f⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤-=<<-+===⎰⎰⎰-∞+∞-其他,020,421202,42121),()(1212Y y y dx y y dx dx y x f y y y f所以,当0<x <1, -2<y<2时,)()(),(y f x f y x f Y X ≠,所以X 和Y 不是相互独立的 .⎪⎩⎪⎨⎧≤>>=⎩⎨⎧≥<<--==-0,00,0,1)(,0),()(y y e y f Y x Y mx xY Y x n mY Y Q Q y Y θθθ的密度函数为[]()()()取最大值时,当又则令)(n ln 0n m )(d n ln,n 0)(1)()(d )()()()(1.1.)()(.)()( 20000000Q E n m x e dx Q E n m x n m e n e n m n e n m dx Q E nxn m e n m m xenx nxe e n m xe n m m xe nxe dy n m e ye n m m xde de nx yde n m dye m x dy e y x n m y dy Yf Y Q Q E x xxx x x x x y x xyx y x y x y x y x y y x x y x y Y +-=∴<+-=+-=∴+==-+=-⎪⎭⎫ ⎝⎛-+-=-+++-=+-++-+-=-+⎥⎥⎦⎤⎢⎢⎣⎡+-+=-++-=+--==---------∞+----∞+---∞+--∞∞-⎰⎰⎰⎰⎰⎰⎰θθθθθθθθθθθθθθθθθθθθθθθθθθθ四、应用题.1. 某公司计划开发一种新产品市场,并试图确定该产品的产量,他们估计出售一件产品可获利m 元,而积压一件产品导致n 元的损失,再者,他们预测销售量Y (件)服从参数θ的解:设生产x 件产品时,获利Q 为销售量Y 的函数2. 设卖报人每日的潜在卖报数为X 服从参数为λ的泊松分布,如果每日卖出一份报可获报酬m 元,卖不掉而退回则每日赔偿n 元,若每日卖报人买进r 份报,求其期望所得及最佳卖报数。
概率论与数理统计答案第四章

概率论与数理统计答案第四章第四章 大数定律与中心极限定理4.1 设)(x D 为退化分布:⎩⎨⎧≤>=0001)(x x x D讨论下列分布函数列的极限是否仍是分布函数?,2,1},01({)3()};1({)2()};({)1(=-++n n x D n x D n x D 其中解:(1)(2)不是;(3)是。
4.2 设分布函数)(x F n 如下定义:⎪⎩⎪⎨⎧>≤<-+-≤=nx nx n n nx n x x F n 120)(问)(lim )(x F x F n n ∞→=是分布函数吗?解:不是。
4.3设分布函数列)}({x F n 弱收敛于分布函数)(x F ,且)(x F 为连续函数,则)}({x F n 在),(∞-∞上一致收敛于)(x F 。
证:对任意的0>ε,取M 充分大,使有M x x F M x x F -≤∀<≥∀<-,)(;,)(1εε对上述取定的M ,因为)(x F 在],[M M -上一致连续,故可取它的k 分点:Mx x x M x k k =<<<<-=-121 ,使有ki x F x F i i <≤<-+1,)()(1ε,再令∞=-∞=+10,k x x ,则有10,)()(1+<≤<-+k i x F x F i i ε (1)这时存在N ,使得当N n >时有10,|)()(|+≤≤<-k i x F x F i i n ε (2)成立,对任意的),(∞-∞∈x ,必存在某个)0(k i i ≤≤,使得),(1+∈i i x x x ,由(2)知当N n >时有ε+<≤++)()()(11i i n n x F x F x F (3)ε->≥)()()(i i n n x F x F x F (4)由(1),(3),(4)可得εεε2)()()()()()(11<+-≤+-<-++i i i n x F x F x F x F x F x F , εεε2)()()()()()(1->--≥-->-+i i i n x F x F x F x F x F x F ,即有ε2)()(<-x F x F n 成立,结论得证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题4-11. 设随机变量X求()E X ;E (2-3 X );2()E X ;2(35)E X +.解 由定义和数学期望的性质知2.03.023.004.0)2()(-=⨯+⨯+⨯-=X E ; (23)23()23(0.2) 2.6E X E X -=-=-⨯-=; 8.23.023.004.0)2()(2222=⨯+⨯+⨯-=X E ; 4.1358.235)(3)53(22=+⨯=+=+X E X E . 2. 设随机变量X 的概率密度为,0,()0,0.xe xf x x -⎧>⎪=⎨⎪⎩≤求Xe Z X Y 22-==和的数学期望.解()(2)2()22x E Y E X E X x x ∞-====⎰e d ,2201()()3Xx x E Z E ee e dx ∞---==⋅=⎰. 3. 游客乘电梯从底层到电视塔顶观光, 电梯于每个整点的第5分钟、第25分钟和第55分钟从底层起行. 假设一游客在早八点的第X 分钟到达底层侯梯处, 且X 在区间[0, 60]上服从均匀分布. 求该游客等候电梯时间的数学期望. 解已知X 在[0,60]上服从均匀分布, 其概率密度为1,060,()600,.x f x =⎧⎪⎨⎪⎩≤≤其它记Y 为游客等候电梯的时间,则5,05,25,525,()55,2555,65,5560.X X X X Y g X X X X X -<-<==-<-<⎧⎪⎪⎨⎪⎪⎩≤≤≤≤因此, 6001()[()]()()()60E Y E g X g x f x dx g x dx ∞-∞===⎰⎰()5255560525551(5)(25)(55)(65)60x dx x dx x dx x dx =-+-+-+-⎰⎰⎰⎰=11.67(分钟)..14. 某保险公司规定, 如果在一年内顾客的投保事件A 发生, 该公司就赔偿顾客a 元. 若一年内事件A 发生的概率为p , 为使该公司受益的期望值等于a 的10%, 该公司应该要求顾客交多少保险费?解 设保险公司要求顾客交保费c 元. 引入随机变量⎩⎨⎧=.A ,0,A 1不发生事件发生事件,X 则{1},{0}1P X p P X p ====-. 保险公司的受益值1,,0.c a X Y c X -=⎧=⎨=⎩, 于是 ()(){1}{0}E Y c a P X c P X ap c =-⨯=+⨯==-+. 据题意有10%ap c a -+=⨯, 因此应要求顾客角保费(0.1)c p a =+.习题4-21. 选择题(1) 已知(1,(3))E D X X =-= 则2[3(2)]()E X-=.(A) 9. (B) 6. (C) 30. (D) 36. 解22[3(2)]3(44)E X E X X -=-+23[()4()4]E X E X =-+23{()[()]4()4}D X E X E X =+-+ 3(3144)36=⨯+++=.可见,应选(D).(2) 设~(,),(6,( 3.6))B n p E D X X X ==, 则有( ).(A)10, 0.6n p ==. (B) 20, 0.3n p ==. (C) 15, 0.4n p ==. (D) 12, 0.5n p ==.解 因为~(,),B n p X 所以E (X )=n p,D (X )=np (1-p ), 得到np =6, np (1-p )=3.6 . 解之,n=15 , p =0.4 . 可见,应选(C).(3) 设X 与Y 相互独立,且都服从2(,)N μσ, 则有( ).(A) ()()()E X Y E X E Y -=+. (B) ()2E X Y μ-=.(C)()()()D X Y D X D Y -=-. (D) 2()2D X Y σ-=.解 注意到0)()()(=-=-Y E X E Y XE .由于X 与Y 相互独立,所以22)()()(σ=+=-Y D X D Y X D . 选(D).(4) 在下列结论中, 错误的是( ).(A) 若~(,),().X B n p E X np =则(B) 若()~1,1X U -,则()0D X =. (C) 若X 服从泊松分布, 则()()D X E X =.(D) 若2~(,),X N μσ 则~(0,1)X N μσ-.解)1,1(~-U X , 则3112212)()(22==-=a b X D . 选(B). 2. 已知X , Y 独立, E (X )= E (Y )=2, E (X 2)= E (Y 2)=5, 求E (3X -2Y ),D (3X -2Y ).解 由数学期望和方差的性质有E (3X -2Y )= 3E (X )-2 E (Y )=3×2-2×2=2,(32)9()4()D X Y D X D Y -=+})]([)({4})]([)({92222Y E Y E X E X E -⨯+-⨯=13)45(4)45(9=-⨯+-⨯=.3. 设随机变量X 1, X 2, X 3相互独立, 其中X 1服从区间[0, 6]上的均匀分布,22~0,2X N (), 3~3X P (), 记12323Y X X X =-+, 求E (Y )和D (Y ) .解 由题设知21122(60)()3,()3,()0,()4,12E X D X E X D X -=====3321111(),()39E X D X λλ====.由期望的性质可得123123()(23)()2()3()13203 4.3E Y E X X X E X E X E X =-+=-+=-⨯+⨯=又123,,X X X 相互独立, 所以123123()(23)()4()9()1344920.9D Y D X X X D X D X D X =-+=++=+⨯+⨯=4. 设两个随机变量X 和Y 相互独立, 且都服从均值为0, 方差为12的正态分布, 求||X Y -的的期望和方差.解 记UX Y =-. 由于11~(0,),~(0,)22X N Y N , 所以()()()0,E U E X E Y =-= ()()()1D U D X D Y =+=.由此~(0,1)U N . 进而2222220 (||)(||)||x x xE X Y E U x dx xe dx e+∞---+∞+∞-∞-====⎰2222(||)()()[()]101E U E U D U E U==+=+=.故而2222 (||)(||)(||)[(||)]11D X Y D UE U E Uπ-==-=-=-.5. 设随机变量]2,1[~-UX, 随机变量⎪⎩⎪⎨⎧<-=>=.0,1,0,0,0,1XXXY求期望()E Y和方差)(YD.解因为X的概率密度为1,12,()30,.Xxf x-=⎧⎪⎨⎪⎩≤≤其它于是Y的分布率为00--11{1}{0}31()d d3XP Y P X f x x x∞=-=<===⎰⎰,{0}{0}0P Y P X====,+2002{1}{0}31()d d3XP Y P X f x x x∞==>===⎰⎰.因此121()1001333E Y=-⨯+⨯+⨯=,222212()(1)001133E Y=-⨯+⨯+⨯=.故有2218()()[()]199D YE Y E Y=-=-=.6. 设随机变量U在区间[-2, 2]上服从均匀分布, 随机变量1,1,1, 1.UXU--=>-⎧⎨⎩若≤若1,1,1, 1.UYU-=>⎧⎨⎩若≤若求E(X+Y), D(X+Y).解(1) 随机变量(X, Y)的可能取值为(-1,-1),(-1,1),(1,-1),(1,1).{1,1}{P X Y P U =-=-=≤1,U -≤-1-211}{1}41d 4P U x =-==⋅⎰≤, {1,1}{P X Y P U =-==≤1,U -1}0>=, {1,1}{1P X Y P U ==-=>-,U ≤1111}21d 4x -==⋅⎰, 211{1,1}{1,1}41d 4P X Y P U U x ===>->==⋅⎰.于是得X 和Y 的联合密度分布为(2) Y X +和)(Y X +的概率分布分别为由此可见22()044E X Y +=-+=;2()[()]2D X Y E X Y +=+=.习题4-31. 选择题(1) 在下列结论中, ( )不是随机变量X 与Y 不相关的充分必要条件(A) E (XY )=E (X )E (Y ). (B) D (X +Y )=D (X )+D (Y ). (C) Cov(X ,Y )=0. (D) X 与 Y 相互独立.解 X 与 Y 相互独立是随机变量X 与Y 不相关的充分条件,而非必要条件. 选(D).(2) 设随机变量X 和Y 都服从正态分布, 且它们不相关, 则下列结论中不正确的是( ).(A) X 与Y 一定独立. (B) (X , Y )服从二维正态分布. (C) X 与Y 未必独立. (D) X +Y 服从一维正态分布.解 对于正态分布不相关和独立是等价的. 选(A).(3) 设(X , Y )服从二元正态分布, 则下列说法中错误的是( ).(A) (X , Y )的边缘分布仍然是正态分布.(B) X 与Y 相互独立等价于X 与Y 不相关. (C) (X , Y )是二维连续型随机变量.(D)由(X , Y )的边缘分布可完全确定(X , Y )的联合分布. 解 仅仅由(X , Y )的边缘分布不能完全确定(X , Y )的联合分布. 选(D)2 设D (X )=4, D (Y )=6, ρXY =0.6, 求D (3X -2Y ) .解(32)9()4()12Cov(,)D X Y D X D Y X Y -=+-)()(126449Y D X D XY ⨯⨯-⨯+⨯=ρ727.24626.0122436≈⨯⨯⨯-+=.3. 设随机变量X , Y 的相关系数为5.0, ,0)()(==Y E X E 22()()2E X E Y ==,求2[()]E XY +.解222[()]()2()()42[Cov(,)()()]E X Y E X E XY E Y X Y E X E Y +=++=++42420.526.ρ=+=+⨯⨯=4. 设随机变量(X , Y )若E (XY )=0.8, 求常数a ,b 解 首先由∑∑∞=∞==111i j ijp得4.0=+b a . 其次由0.8()100.420110.2210.22E XY a b b ==⨯⨯+⨯⨯+⨯⨯+⨯⨯=+ 得3.0=b . 进而1.0=a . 由此可得边缘分布律于是 , . 故 Cov(,)()()()0.8 1.40.50.1X Y E XY E X E Y =-=-⨯=.5. 已知随机变量(,)~(0.5,4;0.1,9;0)X Y N , Z =2X -Y , 试求方差D (Z ), 协方差Cov(,)X Z , 相关系数ρXZ .解 由于X ,Y 的相关系数为零, 所以X 和Y 相互独立(因X 和Y 服从正态分布). 因此25944)()(4)2()(=+⨯=+=-=Y D X D Y X D Z D ,Cov(,)Cov(,2)2Cov(,)Cov(,)2()08X Z X X Y X X X Y D X =-=-=-=.因此80.825XZ ρ===⨯. 6. 设随机变量(X , Y )服从二维正态分布: 2~(1,3)X N , 2~(0,4)Y N ; X 与Y 的相关系数1,232XYX YZ ρ=-=+. 求: (1) E (Z ), D (Z ); (2) X 与Z 的相关系数ρXZ ; (3)问X 与Z 是否相互独立?为什么?解 (1) 由于)3,1(~2N X , )4,0(~2N Y , 所以16)(,0)(,9)(,1)(====Y D Y E X D X E ,而1Cov(,)3462XY X Y ρ==-⨯⨯=-.因此 31021131)(21)(31)23()(=⨯+⨯=+=+=Y E X E Y X E Z E ,1111()()()()2Cov(,)329432X Y D Z D D X D Y X Y =+=++111916Cov(,)943X Y =⨯+⨯+3)6(3141=-⨯++=.(2) 由于1111Cov(,)Cov(,)()Cov(,)9(6)0,323232XY X Z X D X X Y =+=+=⨯+⨯-= 所以0XZ ρ==.(3) 由0=XZ ρ知X 与Z 不相关, 又X 与Z 均服从正态分布, 故知X 与Z 相互独立.7.证明: 对随机变量(X , Y ), E (XY )=E (X )E (Y )或者D (X ±Y )=D (X )+D (Y )的充要条件是X与Y 不相关.证 首先我们来证明)()()(Y E X E XY E =和()()()D X Y D X D Y ±=+是等价的.事实上, 注意到()()()2Cov(,)D X Y D X D Y X Y ±=+±.因此()()()D X Y D X D Y ±=+Cov(,)0()()()X Y E XY E X E Y ⇔=⇔=.其次证明必要性. 假设E (XY )=E (X )E (Y ), 则Cov(,)()()()0X Y E XY E X E Y =-=.进而0XYρ==, 即X 与Y 不相关.最后证明充分性. 假设X 与Y 不相关, 即0=XYρ, 则Cov(,)0X Y =. 由此知)()()(Y E X E XY E =.总习题四1. 设X 和Y 是相互独立且服从同一分布的两个随机变量, 已知X 的分布律为1{},1,2,33P X i i ===. 又设max{,},min{,}U X Y V X Y ==.(1) 写出二维随机变量(U , V )的分布律; (2) 求()E U .解 (1) 下面实际计算一下{1,3}P UV ==.注意到max{,},min{,}U X Y V X Y ==, 因此{1,3}{1,3}{3,1}P U V P X Y P X Y =====+=={1}{3}{3}{1}P X P Y P X P Y ===+==9231313131=⨯+⨯=.(2) 由(,)U V 的分布律可得关于U 的边缘分布律所以13522()1239999E U =⨯+⨯+⨯=. 2. 从学校乘汽车到火车站的途中有3个交通岗. 假设在各个交通岗遇到红灯的事件是相互独立的, 并且概率是25. 设X 为途中遇到红灯的次数, 求随机变量X 的分布律、分布函数和数学期望.解 令X 表示途中遇到红灯的次数, 由题设知2~(3,)XB . 即X 的分布律为从而3127543686(){}01231251251251255k E X kP X k ====⨯+⨯+⨯+⨯=∑. 3. 设随机变量),(Y X 的概率密度为212,01,(,)0,.y y x f x y ⎧⎪=⎨⎪⎩≤≤≤其它求22(),(),(),()E X E Y E XY E X Y +.解 112404()(,)1245xE X xf x y dxdy dx x y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰. 11240003()(,)1235xE X yf x y dxdy dx y y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰.112500031()(,)12362x E XY xyf x y dxdy dx xy y dy x dx ∞∞-∞-∞==⋅===⎰⎰⎰⎰⎰.122222220()()(,)()12xE X Y x y f x y dxdy dx x y y dy ∞∞-∞-∞+=+=+⋅⎰⎰⎰⎰155012423216(4)5653015x x dx =+=+==⎰. 4. 设随机变量(X ,Y )的概率密度为1sin(),0,0,222(,)0,.≤≤≤≤其它ππx y x y f x y ⎧+⎪=⎨⎪⎩求E (X ),D (X ),E (Y ),D (Y ),E (XY )和 Cov(X ,Y ).解22001()(,)sin()24E X xf x y dxdy x x y dxdy πππ+∞+∞-∞-∞==+=⎰⎰⎰⎰.22222200()(,)1sin() 2.282E X x f x y dxdyx x y dxdy ππππ+∞+∞-∞-∞==+=+-⎰⎰⎰⎰于是有2216)]([)()(222-+=-=ππX E X E X D . 利用对称性,有2216)(,4)(2-+==πππY D Y E .又()(,)E XY xyf x y dxdy +∞+∞-∞-∞=⎰⎰22001sin()2xy x y dxdy ππ=+⎰⎰220022001sin()21[sin cos cos sin ]2xdx y x y dyxdx y x y x y dyππππ=+=+⎰⎰⎰⎰12-=π.所以协方差2Cov(,)()()()1216X Y E XY E X E Y ππ=-=--.5. 设随机变量X 与Y 独立, 同服从正态分布1(0,)2N , 求(1)();()E X Y D X Y --;(2) (max{,});(min{,})E X Y E X Y .解 (1) 记Y X -=ξ.由于)21,0(~),21,0(~N Y N X ,所以,0)()()(=-=Y E X E E ξ 1)()()(=+=Y D X D D ξ.由此)1,0(~N ξ. 所以2222(||)(||)||x x E X Y E x dx xedx ξ+∞+∞---∞-==⎰22x e+∞-==101)]([)()()|(|2222=+=+==ξξξξE D E E .故而ππξξξ2121|)](|[)|(||)(||)(|222-=⎪⎪⎭⎫ ⎝⎛-=-==-E E D Y X D .(2) 注意到2||)(),max(Y X Y X Y X -++=, 2||),min(Y X Y X Y X --+=.所以ππ21221|]}[|)()({21)],[max(==-++=Y X E Y E X E Y X E ,ππ21221|]}[|)()({21)],[min(-=-=--+=Y X E Y E X E Y X E .6. 设随机变量),(Y X 的联合概率密度为,02,02,8(,)0,.x yx y f x y +⎧⎪=⎨⎪⎩≤≤≤≤其它求: E (X ), E (Y ), Cov(X ,Y ), ρXY , D (X+Y ).解 注意到),(y x f 只在区域2≤≤0,2≤≤0:y x G 上不为零, 所以()(,)8Gx yE X xf x y dxdy x x y ∞∞-∞-∞+==⎰⎰⎰⎰d d222000117()(1)846dx x x y dy x x dx =+=+=⎰⎰⎰,22()(,)E Xx f x y dxdy ∞∞-∞-∞=⎰⎰222232000115()()843dx x x y dy x x dx =+=+=⎰⎰⎰, 因而 36116735)]([)()(2222=-=-=X E X E X D .又()(,)E XY xyf x y dxdy ∞∞-∞-∞=⎰⎰22220001144()()8433dx xy x y dy x x dx =+=+=⎰⎰⎰. 由对称性知2275()(),()()63E Y E X E Y E X ====, 3611)()(==X D Y D . 这样,4491Cov(,)()()()33636X Y E XY E X E Y =-=-=-, 111XY ρ==-,5()()()2Cov(,)9D X Y D X D Y X Y +=++=.7. 设A , B 为随机事件, 且111(),(|),(|)432P A P B A P A B ===, 令 10A X A =⎧⎨⎩,发生,,不发生, 10B Y B =⎧⎨⎩,发生,,不发生.求: (1) 二维随机变量(X , Y )的概率分布; (2) X 与Y 的相关系数XY ρ.解 由1()(|)3()P AB P B A P A ==得1111()()33412P AB P A ==⨯=, 进而由1(|)2P A B = ()()P AB P B =得1()2()6P B P AB ==. 在此基础上可以求得(1)1{1,1}()12P X Y P AB ====,111{0,1}()()()61212P X Y P AB P B P AB ====-=-=,111{1,0}()()()4126P X Y P AB P A P AB ====-=-=,{0,0}()1()1[()()()]P X Y P AB P A B P A P B P AB ====-=-+-U 11121[]46123=-+-=.故(X , Y )的概率分布为(2) 由(1)因此211(),(),44E X E X ==22113()()[()]41616D XE X E X =-=-=, 22211115(),(),()()[()]6663636E Y E Y D Y E Y E Y ===-=-=. 又由(X , Y )的分布律可得21111()00011011312121212E XY =⨯⨯+⨯⨯+⨯⨯+⨯⨯=. 故11115XYρ-⨯===.。
