高中物理微积分应用(完美)
高中物理微积分应用(完美)

高中物理中微积分思想伟大的科学家牛顿,有很多伟大的成就,建立了经典物理理论,比如:牛顿三大定律,万有引力定律等;另外,在数学上也有伟大的成就,创立了微积分。
微积分(Calculus )是研究函数的微分、积分以及有关概念和应用的数学分支。
微积分是建立在实数、函数和极限的基础上的。
微积分最重要的思想就是用"微元"与"无限逼近",好像一个事物始终在变化你很难研究,但通过微元分割成一小块一小块,那就可以认为是常量处理,最终加起来就行。
微积分学是微分学和积分学的总称。
它是一种数学思想,‘无限细分’就是微分,‘无限求和’就是积分。
无限就是极限,极限的思想是微积分的基础,它是用一种运动的思想看待问题。
微积分堪称是人类智慧最伟大的成就之一。
在高中物理中,微积分思想多次发挥了作用。
1、解决变速直线运动位移问题匀速直线运动,位移和速度之间的关系x=vt ;但变速直线运动,那么物体的位移如何求解呢?例1、汽车以10m/s 的速度行驶,到某处需要减速停车,设汽车以等减速2m/s 2刹车,问从开始刹车到停车,汽车走了多少公里?【解析】 现在我们知道,根据匀减速直线运动速度位移公式at v v +=0 2021at t v x +=就可以求得汽车走了0.025公里。
但是,高中所谓的的匀变速直线运动的位移公式是怎么来的,其实就是应用了微积分思想:把物体运动的时间无限细分。
在每一份时间微元内,速度的变化量很小,可以忽略这种微小变化,认为物体在做匀速直线运动,因此根据已有知识位移可求;接下来把所有时间内的位移相加,即“无限求和”,则总的位移就可以知道。
现在我们明白,物体在变速直线运动时候的位移等于速度时间图像与时间轴所围图形的“面积”,即2021at t v x +=。
【微积分解】汽车在减速运动这段时间内速度随时间变化的关系t at v v 2100-=+=,从开始刹车到停车的时间t=5s ,所以汽车由刹车到停车行驶的位移kmt t t a t v dt at v dt t v x 025.0)10()2()()(50252050050=-=+=+==⎰⎰小结:此题是一个简单的匀变速直线运动求位移问题。
微积分在物理中的应用举例

微积分在物理中的应用举例
微积分,作为数学中的重要分支,不仅仅是一种抽象的理论,而在现实世界中有着广泛的应用。
特别是在物理学领域,微积分的应用更是无处不在。
本文将通过几个具体的例子来说明微积分在物理中的应用。
运动学中的微积分应用
在研究物体的运动时,我们需要对其位置、速度和加速度进行分析。
而微积分正是运动学中经常使用的工具之一。
例如,对于一个运动的物体,我们可以通过微积分来求解其在不同时刻的位置,速度和加速度之间的关系。
通过对这些关系进行分析,可以更好地理解物体的运动规律。
力学中的微积分应用
在力学中,微积分可被用来分析受力物体的运动。
例如,通过对牛顿第二定律的微积分分析,我们可以得出物体在不同时间下的轨迹和速度变化。
此外,微积分还可以帮助我们计算物体受力时的加速度,从而更好地理解物体的受力情况。
热力学中的微积分应用
在研究热力学问题时,微积分同样扮演着重要角色。
例如,通过微积分可以分析热传导过程中物体温度的变化规律。
此外,微积分还可以用来解决热力学系统中的复杂方程,从而帮助我们更好地理解热力学系统的特性。
结论
通过以上几个例子,我们可以看到微积分在物理学中的重要性和广泛应用。
无论是运动学、力学还是热力学,微积分都扮演着至关重要的角色,帮助我们更好地理解和解决物理学中的问题。
因此,微积分的学习和应用对于物理学研究具有重要意义。
微积分在物理中的应用举例

微积分在物理中的应用举例微积分是一门研究变化的数学学科,它在物理学中有着广泛的应用。
物理学家们利用微积分的工具和概念描述自然现象、建立模型、解决问题。
下面将通过几个具体的例子来说明微积分在物理学中的应用。
1. 运动学中的速度与加速度在物理学中,我们经常需要描述物体的运动状态,包括速度和加速度。
速度是位置随时间的变化率,而加速度则是速度随时间的变化率。
这些概念可以通过微积分来表达和计算。
例如,一个物体的位移可以表示为速度关于时间的积分,而速度则可以表示为加速度关于时间的积分。
微积分使得我们能够准确描述和分析物体的运动规律。
2. 牛顿第二定律牛顿第二定律是描述力和物体运动之间关系的基本定律,它可以用微积分来推导和解释。
根据牛顿第二定律,物体的加速度与作用在物体上的合力成正比,通过微积分可以将这个关系表达为一个微分方程。
通过对微分方程的求解,我们可以得到物体在不同情况下的运动方程,从而预测物体的运动轨迹和速度变化。
3. 电场力和电势能在电动力学中,微积分也广泛应用于描述电场力和电势能。
电场力是描述电荷之间相互作用的力,而电势能则是电场力做功的能量。
微积分可以帮助我们计算电场力和电势能之间的关系,以及在不同电场分布下的电势能变化。
这种分析对于研究电路中电荷流动、电场能量转换等现象非常重要。
总结微积分在物理学中的应用是十分广泛的,它为物理学提供了强大的工具和方法。
通过微积分,我们可以更深入地理解自然现象,推导和解释物理原理,建立物理模型并做出预测。
以上是仅仅是几个微积分在物理学中应用的例子,实际上微积分在物理学中的应用远不止这些,它在整个物理学研究中都扮演着重要的角色。
微积分在高中物理中的应用

121微积分在高中物理中的应用邓圭恩微积分是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支。
它是数学的一个基础学科。
微积分是指求函数曲线的切线斜率、求函数图形的面积、求图形的体积的一种方法和过程,在高中物理概念、物理定律都包涵微积分的思想。
本文分析了微积分在高中物理的一些具体应用,目的是理解微积分思想的同时也能熟练地运用微积分来解决物理中的问题。
数学作为物理学中的重要工具,它即能准确而又简洁地表达物理概念和规律,也能为物理提供思维语言和方法。
运用数学方法解决物理问题是高中阶段学习目标之一,高中生掌握求导和积分的思想及方法,是为物理学习提供了即方便实用又强大的工具。
1微积分在高中动力学中的应用 1.1利用微积分解决变速运动问题在高中阶段,变速运动问题往往是许多同学的难点,很多变速运动问题的模型都很难建立,对许多同学甚至是教师的思维能力都是一个很大的考验。
但微积分知识和思想能帮助大家用更简洁普适的模型来解决这方面的问题,比如对于下面这一道题:例2:狐狸沿半径R 的圆轨道以恒定速率v 奔跑,在狐狸出发的同时,猎犬从圆心O 出发以相同的速率v 追击过程中,圆心、猎犬和狐狸始终连成一直线。
(1)建立相应坐标系,求出猎犬运动的轨道方程,并画出轨道曲线。
(2)判断猎犬能否追上狐狸。
这道题是一道经典的物理竞赛题,现在也是被选入许多高校的自招理论试题,其经典解法有很多,但绝大多数都复杂冗长,很多同学并不能很好的理解。
而如果我们选用微积分的方法,就会得到很容易为大家所接受,也较容易的解法了。
取圆心O 为坐标原点,从O 到狐狸的初始位置设置极轴,建立极坐标系。
我们先得到猎犬切向、径向加速度、速度与猎犬所在的r、θ的关系狐狸的圆运动角速度为:Rv dt d ==ωθ当狐狸在θ角位置时,圆心O、猎犬D 及狐狸F 共线,如图所示故猎犬的横向速度为猎犬的径向与切向速度为:r Rv dt d rv ==θθ,vRr v v v r 22221-=-=θ 径向与切向加速度为:R r R v v dtd r dt d dt dr r a 122222-⋅==+⋅=ωθθθv r a R r dt dr dr dv r dt dv dt d r d r d r r r 22222222)(-=-⋅=-=-=ωωθθ 由r R v v r d dr r22-==θθ积分:⎰⎰=-θθθ022d r R dr r 可得猎犬的轨道方程为: θ=Rr arcsin 即θsin R r =猎犬的轨道曲线如图中虚线所示。
微积分在高中物理教学及高考中的应用

微积分在高中物理教学及高考中的应用
微积分是一门重要的数学课程,在高中物理教学及高考中有重要的应用。
首先,在高中物理教学中,微积分可以帮助学生理解物理学的深层次的概念和原理。
例如,在力学和弹性中,知道力和位移之间的关系,学生需要用到微积分,例如需要用到曲率来计算曲线上力的变化情况,或者用梯度和位移之间的关系来分析影响力的改变等。
此外,散度和积分也在物理学中有实际的应用,例如在电动力学中,学生可以运用微积分的知识确定电流的变化情况。
其次,在高考中,微积分也是非常重要的科目之一,它不但是数学竞赛中的重要科目,而且也在高考的多项科目中得到了普遍的应用。
例如,在物理学中,考生可以利用提高后的微积分知识分析曲线上的力、磁力场和重力场等问题;在电动力学中,考生可以运用微积分知识计算电势和电压;在力学中,考生可以利用微积分知识求出运动弹性曲线;在热力学中,考生可以利用梯度来分析热力学问题;而在化学中,考生可以利用积分来分析反应的反应速率等。
总之,在高考中,微积分的应用是不可分割的部分。
最后,微积分在高中物理教学及高考中的应用,不仅可以扩大学生们在物理学和化学中的知识面,而且可以提高学生的数学水平,从而增强学生的理解和解决问题的能力。
因此,在高中物理教学及高考中,加强对微积分的学习和学术研究是非常有必要的。
综上所述,在高中物理教学及高考中,微积分有着重要的应用,它可以帮助学生更深入地理解物理学和化学中的问题,同时提高学生
的数学水平,从而增强学生的理解和解决问题的能力。
因此,加强对微积分的学习及学术研究,有助于提高高中物理教学及高考中的教学水平。
微积分在高中物理中的应用

微积分在高中物理中的应用一、非匀变速直线运动的位移计算一小球以速度v 做直线运动,其速度随时间变化规律为22+-=t v ,求小球在0—1s 内的位移。
由题意可知,小球的速度并不是均匀变化的,无法运用匀变速直线运动的公式计算位移,现在尝试运用微积分的思想来解决问题。
试想,将[0,1]这段时间分为n 个时间段:[0,n 1],[n 1,n 2],…,[nn 1-,1] 每个时间段的长度为 nn t t t t t i i 101=-=-=∆- 当Δt 很小时,在[t 1-i ,t i ]上,v(t)的变化很小,可以认为物体近似的以速度v(t 1-i )做匀速运动,在这一段时间上物体的位移t t v x i i ∆≈∆-)(1在[0,1]上物体的总位移∑∑=-=∆=∆=n i i n i it t v x x 111)(∑=-⎪⎭⎫ ⎝⎛+⋅=n i i n n t x 12121- ()[]()()22111131-26121n 1-2121n 1-2111110-3222322+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=+--=+-+⋯++=+⋅⎪⎭⎫ ⎝⎛--⋯-⋅⎪⎭⎫ ⎝⎛-⋅=n n n n n n nn n n n n 所以,n 越大即t ∆越小时,时间段[0,1]分得越细,∑=∆n i i x 1与x 的近似程度就越好,当∞→n 时,两者之差趋向于零,即3522111131-lim lim 11=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=∆=∞→=-∞→∑x n n x tv x n ni i n 所以,小球在0—1s 内的位移为35m 由此可以看出利用微积分思想可以解决非匀速直线运动的位移问题。
此过程比较麻烦,也可以直接使用牛顿—莱布尼茨公式。
二、变力作功在弹簧的弹性限度内,将其从平衡位置拉到距平衡位置l m 处,已知弹簧劲度系数为k ,求此过程中拉力F 所做的功W 。
在弹性限度内,拉力F 与弹簧拉伸长度成正比()kx x F =所以 20202121kl kx dx kx W ll ===⎰ 拉力F 所做的功为221kl三、交变电流有效值的计算求正弦式交变电流t I i m ωsin =的有效值解: 设电流的有效值为I ,则i W Rt I =2将t I i m ωsin =等号两边同时平方得到t I i m ω222sin =Rt I Q 2=令 T t =所以在半个周期内TRI W t t RI W dt t RI W dt t I R W dt t I R W m i T m i T m i Tmi Tm i 2202202202222412sin 412122cos 2122cos 1sin =⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=-==⎰⎰⎰ωωωωω所以 TR I W Rt I m i 2241==2221m I I =2mI I = 正弦式交流电的有效值为2mI I =。
微积分在物理学中的应用

微积分在物理学中的应用微积分是数学的一个重要分支,它研究函数的变化和变化率,是物理学中不可或缺的工具。
微积分的应用范围广泛,尤其在物理学中,它发挥着重要的作用。
本文将介绍微积分在物理学中的几个重要应用。
一、速度和加速度的计算在物理学中,速度和加速度是描述物体运动的重要概念。
微积分可以帮助我们计算速度和加速度。
假设一个物体在时间t内的位移为s(t),那么速度v(t)可以通过求位移函数的导数来计算,即v(t) =ds(t)/dt。
同样地,加速度a(t)可以通过求速度函数的导数来计算,即a(t) = dv(t)/dt。
微积分的求导运算可以帮助我们精确地计算速度和加速度,从而更好地理解物体的运动规律。
二、曲线的长度和曲率的计算在物理学中,我们经常需要计算曲线的长度和曲率。
微积分可以帮助我们解决这些问题。
对于一条曲线C,我们可以将其分割成无数个小线段,然后计算每个小线段的长度,再将这些长度相加,就可以得到曲线的长度。
这个过程可以通过微积分中的积分运算来实现。
同样地,曲率描述了曲线的弯曲程度,可以通过微积分中的导数运算来计算。
微积分的这些运算使得我们能够准确地计算曲线的长度和曲率,从而更好地理解曲线的性质。
三、力和功的计算在物理学中,力和功是描述物体受力和做功的重要概念。
微积分可以帮助我们计算力和功。
假设一个物体在位移s下受到力F的作用,那么力可以通过求位移函数的导数来计算,即 F = dW(s)/ds。
同样地,功可以通过力和位移的乘积来计算,即W = ∫Fds。
微积分的这些运算使得我们能够准确地计算力和功,从而更好地理解物体受力和做功的过程。
四、体积和质量的计算在物理学中,体积和质量是描述物体性质的重要概念。
微积分可以帮助我们计算体积和质量。
对于一个具有复杂形状的物体,我们可以将其分割成无数个小体积,然后计算每个小体积的大小,再将这些大小相加,就可以得到物体的体积。
同样地,质量可以通过微积分中的积分运算来计算。
高中物理微积分应用(完美)

Q0→Q1
q ③根据电容电量公式Q=CU,有Q1=CU=CRi ,那么q= Q0- CRi ; ④联立上式,有i=== - CR ⑤进行公式变形,令x= - ,则有i= - CR= 同学们思考一下,i应该是什么函数,才能满足i= ?,或者说什么函数 的导数等于函数本身? 我们观察到,只有y=Cex形式的函数才满足i= 关系,C为待定常数。 故可以知道,i = Cex = Ce-t/CR 当t=0 时,U0= , i0= = ;而把t=0 代人,得i = Ce-t/CR=C;故C=
我们解决物理问题。
导数
㈠ 物理量的变化率
我们经常对物理量函数关系的图像处理,比如v-t图像,求其斜率可
以得出加速度a,求其面积可以得出位移s,而斜率和面积是几何意义上
的微积分。我们知道,过v-t图像中某个点作出切线,其斜率即a=.
t
v
下面我们从代数上考察物理量的变化率:
【例】若某质点做直线运动,其位移与时间的函数关系为上s=3t+2t2,
①(△t+C)=C
②C·△t=0 ③f(△t)=f(0)
④ f(t+△t)=f(t)
⑤=1
『附录』常用等价无穷小关系()
① ;② ;③ ;④ ;⑤
㈢ 导数
前面我们用了极限“”的表示方法,那么物理量y的变化率的瞬时值z
可以写成:
z=,并简记为z=,称为物理量y函数对时间变量t的导数。物理上经常
用某物理量的变化率来定义或求解另一物理量,如v=、a=、i=、ε=N
小结:此题是一个简单的匀变速直线运动求位移问题。对一般的变速直 线运动,只要结合物理知识求速度关于时间的函数,画出v-t图像, 找“面积”就可以。或者,利用定积分就可解决.
微积分在物理的应用

微积分在物理的应用微积分是数学中的一个重要分支,它在物理学中有着广泛的应用。
物理学领域中的微积分主要涉及到有关运动、力学、能量、功等方面的计算。
以下将分步骤阐述微积分在物理学中的应用。
第一步,微积分在运动学中的应用。
运动学是研究物体运动状态及其规律的一门学科。
微积分可以帮助我们求出物体运动过程中的速度、加速度、位移等参数。
当需要知道物体在某一时刻的速度时,可以通过微积分的导数计算。
同样地,当需要知道物体在某一时刻的加速度时,可以通过微积分的二阶导数计算。
微积分也可以用于求解物体的位移,这是通过将速度对时间积分得到的。
第二步,微积分在力学中的应用。
力学是研究物体在受外力作用下运动、平衡和变形规律的一门学科。
微积分可以帮助我们计算物体在不同受力状态下的运动轨迹,从而分析出受力过程。
在求解物体受力的过程中,可以通过微积分的积分方式得到物体的总受力。
同时,微积分也可以计算出物体所受的重力、弹力、张力等,从而提供更加精确的计算。
第三步,微积分在能量中的应用。
能量是指物体进行运动和发生变形时所具有的能力。
微积分可以帮助我们计算物体在不同状态下的能量变化量。
当物体在运动过程中所进行的功时,可以通过微积分的积分方式计算出功率。
当需要知道物体在某个瞬间的能量时,积分可以帮助得出更加精确的计算结果。
综上所述,微积分在物理学中的应用非常广泛,主要通过计算物体的运动、力学和能量等方面。
在进行微积分计算时,必须基于正确的公式和理论基础,从而得出准确的结果。
对于学习微积分的人来说,需要认真掌握微积分的基本知识和技能,以便于在物理学中应用。
微积分思想在高中物理中的典型应用

微积分思想在高中物理中的典型应用任孝有 任雅群(北京市通州区潞河中学 北京 101100)(收稿日期:2019-04-16)摘要:微积分思想是现代物理学中的重要思想,它将复杂变化的物理过程转化为定量可解,对学生物理思维和数学思维的提升十分有益.本文结合高中物理中的典型习题,实际说明了如何运用微积分思想解决物理问题.关键词:微积分 图像面积 物理方程 对如图1所示的匀加速直线运动过程,将其运动过程分为n个运动间隔,如图2所示,每个间隔的时间为Δti,每个间隔的最小速度为vi(i=1,2,…,n),则每个间隔的位移近似为xi=viΔti,全程的总位移近似为X=x1+x2+x3+…=∑xi,在几何上体现为如图2所示的Δti上的矩形面积和,此时的X小于真实总位移.增大n从而减小Δti,vi更加接近全程的真实速度,则xi更加接近对应过程的真实位移,X也更加接近真实总位移,矩形面积和也更加接近梯形面积;令n趋近于无穷,则xi和X趋近于真实值,即对n取极限后,矩形面积和等于梯形面积,也就是图线与横纵轴所围成图形的面积,为真实的位移.因此直接求得梯形面积,就可算出对应的变速运动的位移.其他物理过程同理.图1 匀加速直线运动v-t图像图2 匀加速直线运动分割当然,如果vi表示的是每个间隔的最大速度,取和后X大于真实值,但取极限后,X转化为真实值,仍旧体现为图线与横纵轴所围成图形的面积.分割,化变为恒获得物理意义;求和,获得宏观近似值;取极限,获得精确值.以上过程是一种连续后的跳跃,突变.也就是说,在数学图像中,如果横纵轴两个物理量的乘积是个新物理量,而且这个物理量是个过程量,那么图像与横纵轴所围的面积就反映着这个过程量的具体数值.但如果是个状态量则对应的是矩形面积,不可累加,如图3所示电源的U-I图像.櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆櫆 (mg)2+(qE)槡2mg=vMvN(12)设M和N离开电场的动能分别为Ek1和Ek2,由题设条件可得Ek1=1.5Ek2.即 12mv2M=1.5×12mv2N(13)联立式(12)、(13)可得 E=mg槡2q(14)点评:在这道题中运用了运动的合成与分解、平均速度、动量定理、相似比等方法.巧妙的分别在水平方向和竖直方向来进行分析研究,一切问题迎刃而解.图3 U-I图像1 数学图像的面积先微分再积分【例1】电容器充电后就储存了能量,某同学研究电容器储存的能量E与电容器的电容C,电荷量Q及电容器两极间电压U之间的关系.他从等效的思想出发,认为电容器储存的能量等于把电荷从一个极板搬运到另一个极板过程中克服电场力所做的功.为此他做出电容器两极间的电压u随电荷量q变化的图像如图4所示.请按照他的想法,推导电容器储存的能量.图4 u-q图像解析:电容器两极板间电压为u′时,从一个极板搬运Δq的电荷量到另一极板,克服电场力所做的功近似为W=Δqu′,图像上体现为Δq上方小矩形的面积,类似于v-t图像,图线与横轴所围的面积表示的就是充电过程中克服电场力做功即最终储存的电能E=12qU=12CU2=12q2C小结:克服电场力做功的过程就是其他形式的能转化为电容器储存的能量的过程.【例2】利用图像分析问题是物理学中常用的方法,其中的斜率、面积通常具有明确的物理意义.(1)小明以6m/s的初速度将足球水平踢出,足球在草坪上滚动直到停下来的全过程中的速度-时间图像如图5所示.图5中图线与坐标轴所围的面积等于12个小方格的面积.求足球滚动了多远才停下来?解析:图5中图线与坐标轴所围的面积即为足球滚动距离,每个小格代表的距离为1m,所以足球滚动了12m才停下来.图5 足球在草坪滚动时的v-t图像(2)用如图6所示的电路研究电容器的放电过程,其中电压传感器相当于一个理想电压表,可以显示电阻箱两端电压随时间的变化关系.实验时将电阻箱R的阻值调至2 000Ω,将开关S拨到a端,电源向电容器充电,待电路稳定后,将电压传感器打开,再将开关S拨到b端,电容器通过电阻箱放电.以S拨到b端时为t=0时刻,电压传感器测得的电压U随时间t变化图像如图7所示.忽略导线及开关的电阻,且不考虑电路的辐射问题.求电容器所带电荷量的最大值.图6 研究电容器放电过程电路图图7 电阻箱两端U-t图像解析:U-t图像面积无物理意义,但改造成UR t图像即I-t图像,面积即最大电荷.在电容器放电过程中的极短时间内有ΔQ=IΔt根据欧姆定律有I=URU t图线与t轴所围面积除以电阻R即为电容器所带电荷量的最大值,由图可知该面积等于12个小方格的面积.因此电容器所带电荷量的最大值Q=6×10-3 C小结:非规则图形如何求总面积?数格!对于不是整格的,将不足半格与超过半格凑成一个整格,但不好凑怎么办?舍去不足半个的,只数超过半个的就可以!不能恰好凑成一个呢?数格子也是一种测量方法,有误差不可避免!可以将格子分得尽可能小,以减小误差.计算时,注意横纵轴的物理单位.这种思想在“用油膜法估测分子大小”的实验中得到很好的体现.【例3】摩天大楼中一部直通高层的客运电梯,行程超过百米.电梯的简化模型如8所示.考虑安全、舒适、省时等因索,电梯的加速度a随时间t变化.已知电梯在t=0时由静止开始上升,a-t图像如图9所示.类比是一种常用的研究方法.对于直线运动,教科书中讲解了由v-t图像求位移的方法.请你借鉴此方法,对比加速度和速度的定义,根据图9所示a-t图像,求电梯在第1s内的速度改变量Δv1和第2s末的速率v2.图8 电梯简化模型图9 电梯a-t图像解析:Δv1=12×1×1m/s=0.5m/sv2=Δv2=12(1+2)×1m/s=1.5m/s小结:面积是速度的变化量而不是速度,清楚乘积的物理意义才能正确解决问题.【例4】如图10所示,弹簧的一端固定,另一端连接一个物块,弹簧质量不计.物块(可视为质点)的质量为m,在水平桌面上沿x轴运动.以弹簧原长时物块的位置为坐标原点O,当弹簧的伸长量为x时,物块所受弹簧弹力大小F=κx,κ为常量.请画出F随x变化的示意图,并根据F-x图像求物块沿x轴从O点运动到位置x的过程中弹力所做的功.图10 例4情境图解析:根据胡克定律F=κx,可以画出F-x图像如图11所示,有W=-12κx2图11 F-x图像小结:弹簧弹力的功写成-κx·x则是以末状态的力充当了全程的力,忽视了弹簧弹力是变力的特点.【例5】如图12所示的匀强磁场内有一光滑水平轨道,在外力作用下,金属杆从O点由静止开始向右做匀加速运动.加速度大小为a,磁感应强度大小为B,光滑轨道宽L,左侧电阻阻值为R,不计其他电阻.求在从静止开始的一段时间t内安培力的冲量大小.图12 例5情境图解析:根据题意有F安=BILI=BLvRv=at联立以上3式F安=B2 L2 aRt画出安培力的冲量与时间关系的F安-t图像,如图13所示,由图像面积可得安培力的冲量I安=12tB2 L2 aRt=B2 L2 a2Rt2图13 F安-t图像小结:可否不画图,直接根据安培力的平均值F安=0+B2 L2 atR2计算冲量?不可以,因为需要体现F安与时间t是线性关系.2 物理方程的先微分再积分【例6】如图14所示,空间有一个范围足够大的匀强磁场,磁感应强度为B,一个质量为m,电荷量为+q的带电小圆环套在一根固定的绝缘竖直细杆上,杆足够长,环与杆的动摩擦因数为μ.现使圆环以初速度v0向上运动,经时间t圆环回到出发位置.不计空气阻力.已知重力加速度为g.求当圆环回到出发位置时速度v的大小.图14 例6情境图解析:在圆环运动的过程中,圆环受向下的重力mg,水平方向的洛伦兹力qvB,细杆的弹力N和摩擦力f,其中f一直与运动方向相反,且摩擦力的大小f=μN=μqvB圆环从开始向上运动到回到出发位置的过程中,取竖直向上为正方向,根据动量定理有If-mgt=-mv-mv0而If=-∑f上it上i+∑f下it下i=-∑μqv上iBt上i+∑μqv下iBt下i=-μqB∑v上it上i+μqB∑v下it下i=μqB(x下-x上)=0所以v=gt-v0小结:需要对上下两个过程分别使用微积分,因为向上运动的距离与返回运动的距离相等,最终求得滑动摩擦力的冲量为零.【例7】如图15所示,在竖直向下的磁感应强度为B的匀强磁场中,两根足够长的平行光滑金属轨道MN和PQ固定在水平面内,相距为L.一质量为m的导体棒ab垂直于MN和PQ放在轨道上,与轨道接触良好.轨道和导体棒的电阻均不计.若轨道左端M与P间接一电容器,电容器的电容为C,导体棒在水平向右恒力F的作用下从静止开始运动.求导体棒运动过程中加速度的大小.图15 例7情境图解析:导体棒ab向右加速运动,在极短时间Δt内,导体棒的速度变化Δv,根据加速度的定义a=ΔvΔt导体棒产生的电动势变化ΔE=BLΔv电容器增加的电荷Δq=CΔE=CBLΔv根据电流的定义I=ΔqΔt解得I=CBLa导体棒ab受到的安培力F安=BIL=B2 L2 Ca根据牛顿第二定律F-F安=ma解得a=Fm+CB2 L2小结:加速度是恒定的吗?不清楚!为了求出加速度,分割后看成是匀变速运动,此处也是化变为恒,是化变加速为匀加速,即变化的a转化为恒定的a.从最终结果看出,a与时间无关,也就是说各段的a相同,即全程是匀加速直线运动.上什么山唱什么歌,具体问题要具体分析.【例8】在磁感应强度为B,方向如图16所示的匀强磁场中,两根平行且光滑的金属轨道MN和PQ固定在水平面内,相距为L,电阻不计.轨道端点M和P间接有阻值为R的电阻.一个长为L,质量为m,阻值为r的金属导体棒ab垂直于MN和PQ放在轨道上,与轨道接触良好.给导体棒ab瞬时速度v0,求:金属棒ab向前运动的最大距离x.图16 例8情境图解析:以金属棒为研究对象,在很短的一段时间Δt内根据动量定理 BiLΔt=mΔvi(1)在某时刻根据全电路欧姆定律i=BLviR+r(2)由式(1)、(2)得 BBLviR+rLΔt=mΔvi(3)ab经时间t停下来,对式(3)在时间t内求和 ∑BBLviR+rLΔt=∑mΔvi BBLR+rL∑viΔt=m∑Δvi BBLR+rLx=mv0(4)解得x=mv0(R+r)B2 L2小结:安培力的冲量,用式(4)左侧计算出的结果是真实值还是近似值?式(1)左侧的匀速如何对应于右侧的变速?下面简要说明为什么是近似值.对于在一极短时间Δt内,初速度为vi的匀减速直线运动过程,结合F安-t图像,如图17所示,安培力的冲量IFi=12B2 L2viR+r+B2 L2(vi-aΔt)R+r[]Δt=B2 L22(R+r)(2viΔt-aΔt 2)图17 Δt时间内F安-t图像因为Δt为一极短时间,Δt 2相对于Δt来说可以忽略不计,所以IFi=B2 L2R+rviΔt=B2 L2R+rxi同样ab经时间t停下来,对上式在时间t内求和IF=B2 L2R+rx与式(4)左侧一致,因此近似在Δt 2的忽略上.物理结果是存在误差的,但这个误差是极小的,可以满足实际的需要.微积分思想与整体法和隔离法是一脉相承的,只是操作时,先分析可研究的局部,再获得整体,适当的练习有益于学生尤其是高三学生物理思维的提升.参考文献1 程守洙,江之永.普通物理学.北京:高等教育出版社.20162 匡继昌.微积分和无穷小量的哲学思考.数学教育学报,2007,16(2)。
微积分在物理学中的应用

微积分在物理学中的应用微积分是数学的一个重要分支,它在物理学中有着广泛的应用。
物理学研究的是自然界中的各种现象和规律,而微积分则为我们提供了一种强大的工具,帮助我们理解和描述这些现象和规律。
本文将探讨微积分在物理学中的应用,并且通过几个具体例子来说明其重要性。
首先,微积分在物理学中的一个重要应用是对物体的运动进行描述和分析。
牛顿运动定律是经典力学的基础,而微积分则是对运动进行建模和求解的数学工具。
例如,当我们研究一个物体在一维直线上的运动时,我们可以通过微积分的方法求解物体的位移、速度和加速度之间的关系。
通过对位移-时间曲线进行微分,我们可以得到速度-时间曲线;通过对速度-时间曲线进行微分,我们可以得到加速度-时间曲线。
这样,我们就可以通过微积分来分析物体在不同时间点的位置、速度和加速度等信息。
其次,微积分在物理学中的另一个重要应用是对物体的力学性质进行研究。
力学是物理学的一个分支,研究物体的运动和相互作用。
微积分可以帮助我们理解和描述物体受力的变化和作用力的大小。
例如,当我们研究一个物体在重力场中的运动时,我们可以通过微积分的方法求解物体所受的重力和空气阻力之间的平衡关系。
通过对受力-时间曲线进行积分,我们可以得到物体的动能和势能之间的关系。
这样,我们就可以通过微积分来分析物体在不同位置和时间点的受力情况。
此外,微积分还在热力学和电磁学等领域中有着重要的应用。
热力学研究的是热能的传递和转化,而微积分可以帮助我们理解和描述热能的变化和流动。
例如,当我们研究一个物体的温度随时间的变化时,我们可以通过微积分的方法求解物体所受的热量和热容之间的关系。
通过对温度-时间曲线进行积分,我们可以得到物体的热能和热功之间的关系。
这样,我们就可以通过微积分来分析物体在不同温度和时间点的热力学性质。
在电磁学中,微积分也起着重要的作用。
电磁学研究的是电荷和电磁场之间的相互作用,而微积分可以帮助我们理解和描述电荷和电场的变化和分布。
微积分在物理 中的简单应用
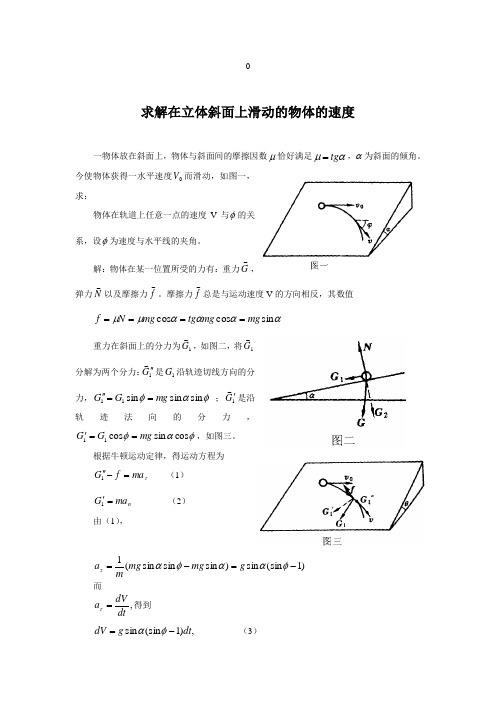
求解在立体斜面上滑动的物体的速度一物体放在斜面上,物体与斜面间的摩擦因数μ恰好满足αμtg =,α为斜面的倾角。
今使物体获得一水平速度0V 而滑动,如图一,求:物体在轨道上任意一点的速度V 与φ的关系,设φ为速度与水平线的夹角。
解:物体在某一位置所受的力有:重力G ,弹力N 以及摩擦力f 。
摩擦力f总是与运动速度V 的方向相反,其数值 ααααμμsin cos cos mg mg tg mg N f ====重力在斜面上的分力为1G ,如图二,将1G 分解为两个分力:1G''是1G 沿轨迹切线方向的分力,φαφsin sin sin 11mg G G =='' ;1G '是沿轨迹法向的分力,φαφcos sin cos 11mg G G ==',如图三。
根据牛顿运动定律,得运动方程为τma f G =-''1 (1)n ma G ='1(2) 由(1),)1(sin sin )sin sin sin (1-=-=φααφατg mg mg ma 而 ,dt dV a =τ得到 ,)1(sin sin dt g dV -=φα (3)式中φ是t 的函数,但是这个函数是个未知函数,因此还不能对上式积分,要设法在φ与t 中消去一个变量,才能积分,注意到 φφd d ds V V dS dt 1== (4)而φd ds表示曲线在该点的曲率半径ρ,根据(2)式,ρφα2cos sin V m mg = (5)由式(3)(4)(5),可得到,)sec (φφφd tg V dV-=φφφφd tg V dV V V ⎰⎰-=00)sec (,积分,得到)sin 1ln()ln(sec cos ln ln 0φφφφ+-=+--=tg V V,.sin 10φ+=V V运用积分法求解链条的速度及其时间一条匀质的金属链条,质量为m ,挂在一个光滑的钉子上,一边长度为1L ,另一边长度为,2L 而且120L L <<,如图一。
微积分在物理中的应用

微积分在物理中的应用微积分在物理中的应用真的是个让人啧啧称奇的话题,听起来像是高大上的东西,其实跟我们的日常生活息息相关。
想想看,咱们平常开车、骑自行车,甚至是扔个飞盘,背后都有微积分的影子。
你有没有想过,为什么汽车能在不同的速度下稳稳地前进?这背后可少不了微积分的帮忙,真是让人感慨万分。
咱们先说说速度这个事。
开车的时候,车速总是在变化,有时候加速,有时候减速。
你可能觉得这只是踩刹车和油门的问题,这里就藏着微积分的奥秘。
想象一下,假设你在某个时刻开得飞快,这时你就需要知道你的速度到底有多快。
这就需要用到瞬时速度的概念,简单来说,就是在某一瞬间你车速的变化率。
通过微积分,你可以很容易地计算出这些变化,让你在开车的时候更得心应手,避免不必要的麻烦。
再说说抛物运动,大家应该都玩过投篮吧?投篮的时候,篮球的轨迹可是个优美的抛物线。
这就是微积分的又一场精彩演出。
想象一下,你把篮球投出去,微积分就能告诉你篮球从你手中飞出去到落地的每一个瞬间。
在这个过程中,重力不断影响着篮球的速度和方向。
微积分帮助你计算出每一时刻篮球的高度、速度,甚至能算出它落地的具体位置。
哇,简直像是给篮球加了一个隐形的导航仪。
再来聊聊功和能量,听起来高深,其实不然。
想象你在滑雪,雪坡越陡,越滑越快,对吧?这其中的能量转化就是个微积分的游戏。
你从高处滑下来的时候,势能转化为动能,速度越快,能量也越多。
这些变化可以用微积分来描述,让你明白能量是如何在不同状态之间转换的。
每一次滑行,都是在和微积分跳舞,恰到好处。
还有热力学,嘿嘿,听起来很复杂,其实也不难。
比如说,热量的传递,想象你手里拿着一杯热咖啡,渐渐变凉的过程,背后也是微积分在默默工作。
微积分能够帮助我们计算热量是如何从咖啡传递到空气中的。
每一秒钟,温度的变化就像在和时间赛跑,微积分就像一个专门记录的时钟,让我们能清晰地看到这个过程。
对了,咱们还得提提流体力学,大家都知道水流动得可快了。
微积分思想在高中物理中的应用

微积分思想在高中物理中的应用
高中物理中的微积分思想的应用可以有很多,大概有下面几个方面,都属于微积分思想的重要应用。
首先,在力学中,物理学家使用微积分的思想来探究任何物体的
运动情况,主要是通过计算加速度、速度和位置,也就是计算物体运
动的函数来求解。
例如,如何分析一个物体自由落体运动的轨迹和速度,就要用到微积分思想。
其次,牛顿第二定律中又引入了微积分思想,牛顿第二定律可以
用F=ma表示,其中F代表力,m代表质量,a代表加速度。
加速度的
变化就是微积分中的导数概念,用微积分的思想,可以很容易地计算
出速度的变化。
此外,在动能定理中也用到了微积分思想,动能定理可以用来计
算物体的动能,例如可以用它来计算物体下落时的动能和势能的大小,也可以用来求解物体的动量变化。
总之,微积分思想在高中物理学中应用十分广泛,不仅仅可以用
来计算物体的运动轨迹,还可以用来求解力学中的力和动量,对物理
学学习有着不可或缺的作用。
利用微积分解决物理问题

利用微积分解决物理问题微积分是数学中的一门重要工具,被广泛应用于各个领域,尤其在物理学中有着重要的作用。
利用微积分的方法可以解决许多与物理相关的问题,本文将通过介绍几个具体的例子,来说明微积分在物理问题中的应用。
1. 物体的运动分析假设有一个物体在直线上做匀速运动,我们想知道在任意一时刻物体的位置。
根据微积分的思想,我们可以通过对速度函数进行积分,得到物体在不同时间的位置函数。
如果物体的速度函数是$v(t)$,其中$t$表示时间,那么物体的位置函数可表示为$s(t)=\int v(t)dt$。
通过计算速度函数积分的结果,我们可以准确地描述物体的位置随时间的变化规律。
2. 弹簧振子的运动弹簧振子是物理学中常见的系统之一。
我们可以用微积分来分析弹簧振子的运动情况。
假设有一个弹簧振子,其位移函数为$x(t)$,其中$t$表示时间。
根据牛顿第二定律,我们可以得到$x(t)$满足的微分方程$m\frac{d^2x}{dt^2}+kx=0$,其中$m$是质量,$k$是弹簧的劲度系数。
通过求解这个微分方程,我们可以得到弹簧振子的位移随时间的变化规律。
3. 计算物体的质量在一些实验中,我们需要知道物体的质量。
我们可以利用微积分中积分的思想来解决这个问题。
假设我们测得一个物体在不同时间下的速度函数为$v(t)$,我们可以通过对速度函数进行积分,来得到物体在不同时间下的位移函数$x(t)$。
假设物体在时间$t_1$到$t_2$之间的位移为$\Delta x$,那么根据牛顿第二定律,物体所受合外力的大小等于物体质量乘以加速度,即$F=ma$。
根据牛顿第二定律可以得到力函数$F(t)$和加速度函数$a(t)$之间的关系$F(t)=ma(t)$。
利用最终的位移函数$x(t)$,我们可以求解出物体所受外力的大小。
4. 计算物体的密度物体的密度是物理学中的一个重要概念,用以描述物体单位体积内的质量。
对于一个具有均匀密度的物体,通过微积分的方法可以计算出其密度。
高中数学微积分微积分在实际问题中的应用

高中数学微积分微积分在实际问题中的应用微积分作为数学的一个重要分支,是研究变化和积分的学科。
它在实际问题中的应用非常广泛,从物理到经济,从工程到生物等各个领域都可以看到微积分的身影。
本文将介绍微积分在实际问题中的应用,并举例说明其重要性。
一、速度和加速度在物理学中,速度和加速度是描述物体运动的重要参数。
微积分可以应用于求解速度和加速度的问题。
以匀速直线运动为例,如果我们已知物体的位移函数s(t),我们可以通过求解其导数来得到速度函数v(t),即v(t) = ds(t)/dt。
类似地,我们可以通过求解速度函数的导数得到加速度函数a(t),即a(t) = dv(t)/dt。
这种应用可以帮助我们更好地理解和描述物体的运动情况。
二、函数的极值在数学中,函数的极值是函数中的一个重要特点。
微积分可以应用于求解函数的极值问题。
对于一个函数f(x),要求其极大值或极小值,我们可以通过求解函数的导数f'(x) = 0来得到。
解这个方程的解析解或数值解,就可以找到函数的极值点。
这种应用可以在优化问题、经济学、物理学等领域中发挥重要作用。
三、曲线的弧长在几何学中,曲线的弧长是描述曲线长度的一个重要概念。
微积分可以应用于求解曲线的弧长问题。
对于一个曲线C,我们可以将其划分成无限小的线段,然后对每个线段求长,并对所有线段的长度求和,即可得到曲线的总弧长。
这个求和过程实际上就是对曲线的积分运算。
这种应用可以在计算几何学、物理学等领域中使用。
四、变化率和斜率在实际问题中,变化率和斜率是有重要意义的。
微积分可以应用于求解变化率和斜率的问题。
对于一个函数f(x),我们可以通过求解其导数f'(x)来得到该函数的变化率和斜率。
例如,在经济学中,利润函数的变化率可以帮助我们了解企业的盈利状况;在物理学中,速度函数的斜率可以描述物体的运动状态。
这些应用帮助我们更好地理解和分析实际问题。
五、积分和面积在几何学中,积分可以应用于求解曲线下面积的问题。
(完整)微积分在物理 中的简单应用(DOC)
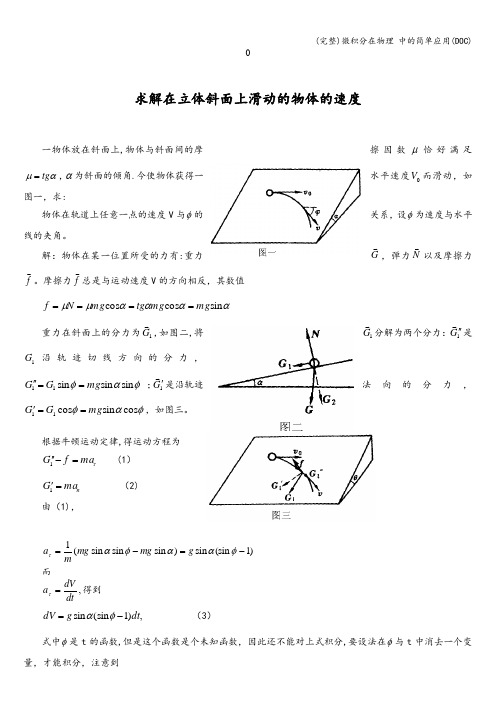
求解在立体斜面上滑动的物体的速度擦因数μ恰好满足一物体放在斜面上,物体与斜面间的摩αμtg =,α为斜面的倾角.今使物体获得一水平速度0V 而滑动,如图一,求:物体在轨道上任意一点的速度V 与φ的关系,设φ为速度与水平线的夹角。
G ,弹力N以及摩擦力解:物体在某一位置所受的力有:重力f 。
摩擦力f 总是与运动速度V 的方向相反,其数值ααααμμsin cos cos mg mg tg mg N f ====重力在斜面上的分力为1G,如图二,将1G 分解为两个分力:1G ''是1G 沿轨迹切线方向的分力,φαφsin sin sin 11mg G G =='' ;1G'是沿轨迹法向的分力,φαφcos sin cos 11mg G G ==',如图三。
根据牛顿运动定律,得运动方程为τma f G =-''1(1) n ma G ='1(2) 由(1),)1(sin sin )sin sin sin (1-=-=φααφατg mg mg m a 而,dtdVa =τ得到 ,)1(sin sin dt g dV -=φα (3)式中φ是t 的函数,但是这个函数是个未知函数,因此还不能对上式积分,要设法在φ与t 中消去一个变量,才能积分,注意到φφd d ds V V dS dt 1==(4) 而φd ds表示曲线在该点的曲率半径ρ,根据(2)式,ρφα2cos sin V mmg = (5)由式(3)(4)(5),可得到 ,)sec (φφφd tg V dV-= φφφφd tg V dV V V ⎰⎰-=00)sec (, 积分,得到)sin 1ln()ln(sec cos ln lnφφφφ+-=+--=tg V V, .sin 10φ+=V V运用积分法求解链条的速度及其时间子上,一边长度为1L ,另一条匀质的金属链条,质量为m,挂在一个光滑的钉一边长度为,2L 而且120L L <<,如图一。
微积分在物理的应用

微积分在物理的应用
微积分是数学中的一个分支,它主要研究连续变化的量和它们的变化率。
这种数学工具在物理中有广泛的应用,尤其在描述物理系统的动态时非常有用。
微积分可以帮助我们计算速度、加速度和力的变化率。
例如,当一个物体在运动时,我们可以用微积分来计算它的速度和加速度。
同样,在描述天体运动时,我们可以用微积分来计算天体的位置和速度。
微积分也可以帮助我们理解能量和功的概念。
当物体受到力时,它会进行功。
我们可以用微积分来计算这些功。
在电学和磁学中,微积分也有着重要的应用。
例如,我们可以用微积分来计算电场和磁场的变化。
总之,微积分是物理学中不可或缺的数学工具。
它可以帮助我们更好地理解物理系统的动态和变化。
- 1 -。
高中数学中的微积分知识有哪些实际应用

高中数学中的微积分知识有哪些实际应用在高中数学的学习中,微积分是一个重要且具有挑战性的部分。
它不仅仅是理论上的知识,更在实际生活中有着广泛而多样的应用。
首先,微积分在物理学中的应用极为显著。
比如在研究物体的运动时,我们常常需要用到微积分的概念。
假设一个物体在直线上做变速运动,其速度随时间变化的函数为v(t),那么通过对速度函数进行积分,就可以得到物体在一段时间内的位移。
反过来,如果已知物体的位移函数 s(t),对其求导就能得到速度函数。
这为我们精确分析物体的运动状态提供了强大的工具。
再看电学中的电流问题。
电流强度 i(t)随时间变化,通过对电流函数进行积分,可以求出在一段时间内通过电路某横截面的电荷量。
同样,对电荷量函数求导可以得到电流强度。
在力学中,计算变力做功也是微积分的用武之地。
当力的大小或方向随位置变化时,传统的力学公式不再适用。
此时,我们可以将路径分成许多小段,在每一小段上力近似看作恒力,求出每小段的功,然后通过积分将这些小段的功累加起来,就能得到变力所做的总功。
其次,微积分在经济学领域也发挥着重要作用。
在成本和收益的分析中,边际成本和边际收益是关键的概念。
边际成本是指每增加一单位产量所增加的成本,边际收益则是每增加一单位产量所增加的收益。
通过对成本函数和收益函数求导,可以得到边际成本函数和边际收益函数。
企业在决策生产数量时,往往会根据边际成本等于边际收益的原则来确定最优产量,以实现利润最大化。
在金融学中,现值和终值的计算也离不开微积分。
比如,要计算一笔未来的资金在当前的价值(现值),或者计算当前的一笔资金在未来的价值(终值),都需要用到微积分中的连续复利公式。
再者,微积分在生物学中也有应用。
比如在研究种群增长模型时,常见的逻辑斯蒂增长模型就涉及到微积分的知识。
通过对模型中的函数进行分析和求解,可以预测种群数量的变化趋势,为保护生态平衡和制定合理的资源管理策略提供依据。
在医学领域,药物在体内的代谢过程也可以用微积分来描述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们解决物理问题。
导数
㈠ 物理量的变化率
我们经常对物理量函数关系的图像处理,比如v-t图像,求其斜率可
以得出加速度a,求其面积可以得出位移s,而斜率和面积是几何意义上
的微积分。我们知道,过v-t图像中某个点作出切线,其斜率即a=.
t
v
下面我们从代数上考察物理量的变化率:
【例】若某质点做直线运动,其位移与时间的函数关系为上s=3t+2t2,
式:
⑴ 导数的四则运算
①=±
③=
②=·v + u·
⑵ 常见函数的导数
①=0(C为常数); ④=-sint;
②=ntn-1 (n为实数); ⑤=et;
③=cost;
⑶ 复合函数的导数
在数学上,把u=u(v(t))称为复合函数,即以函数v(t)为u(x)的自
变量。
=·
复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以
L(弧长)=α(弧度)x r(半径) (弧度制)
又因为车在A、B两点以速率v作圆周运动,所以:
综合以上各式得: F= 圆周运动向心力公式 故摩擦力对车所做的功: 【微积分解】物体在轨道上受到的摩擦力,从最低点运动到最高点摩擦 力所做的功为 小结:这题是一个复杂的变力做功问题,利用公式直接求功是难以办到
小结:此题是一个简单的匀变速直线运动求位移问题。对一般的变速直 线运动,只要结合物理知识求速度关于时间的函数,画出v-t图像, 找“面积”就可以。或者,利用定积分就可解决.
2、解决变力做功问题
v 恒力做功,我们可以利用公式直接求出;但对于变力做功,我们如
何求解呢? 例2:如图所示,质量为m的物体以恒定速率v沿半径为R的竖直圆轨道 运动,已知物体与竖直圆轨道间的摩擦因数为,求物体从轨道最低点运 动到最高点的过程中,摩擦力做了多少功。
但是,高中所谓的的匀变速直线运动的位移公式是怎么来的,其实 就是应用了微积分思想:把物体运动的时间无限细分。在每一份时间微 元内,速度的变化量很小,可以忽略这种微小变化,认为物体在做匀速 直线运动,因此根据已有知识位移可求;接下来把所有时间内的位移相 加,即“无限求和”,则总的位移就可以知道。现在我们明白,物体在变 速直线运动时候的位移等于速度时间图像与时间轴所围图形的“面积”, 即。 【微积分解】汽车在减速运动这段时间内速度随时间变化的关系,从开 始刹车到停车的时间t=5s, 所以汽车由刹车到停车行驶的位移
①求出t时刻的速度v ②写出合力F与位移x的关系 ③验证简谐运动中质点的机械能守恒。
【练】2、某矩形线框面积为S,匝数为N,处于磁感应强度为B的匀强 磁场中,如图所示,线框绕PQ轴以角速度ω匀速转动,从水平位置开 始计时,在t时刻:①写出磁通量Ф的表达式②求出线框产生的感应电 动势ε P Q θ 三:微分和积分 ㈠ 简单问题 【例】电容器是一种存储电荷的元件,它的基本工作方式为充电和放 电,我们先考察电容器放电时的情况。某电容为C的电容器,其已充 电的电量为Q0,若让该电容与另一个阻值为R的的电阻串联起来,该 电容器将会放电,其释放的电能转化电阻的焦耳热(内能)。试讨 论,放电时流过电阻R的电流随时间t 的变化关系如何? 分析:①根据电荷守恒定律,当通过电阻R的电量为q时,电容器的电量
一场源点荷为Q,在距Q为r的A点有一点电荷为q,此A处电势φ=kQ/r
【例】问均匀带电的立方体角上一点的电势是中心的几倍。
分析:
①根据对称性,可知立方体的八个角点电势相等;将原立方体等分为八
个等大的小立方体,原立方体的中心正位于八个小立方体角点位置;而
根据电势叠加原理,其电势即为八个小立方体角点位置的电势之和,即
第三次,我们把时间段平均分为4段,每段时间△t=;
…………
第N次,我们把时间段平均分为N+1段,每段时间△t=;
…………
一直这样进行下去,我们知道,△t越来越小,虽然它不为零,但永
远逼近零,我们称它为无穷小,记为△t→0。或者,用数学形式表示
为 △t=0。其中“”表示极限,意思是△t的极限值为0。常规计算:
1、解决变速直线运动位移问题 匀速直线运动,位移和速度之间的关系x=vt;但变速直线运动,那
么物体的位移如何求解呢? 例1、汽车以10m/s的速度行驶,到某处需要减速停车,设汽车以等减速 2m/s2刹车,问从开始刹车到停车,汽车走了多少公里? 【解析】 现在我们知道,根据匀减速直线运动速度位移公式 就可以求 得汽车走了0.025公里。 a=-2m/s2
㈡ 无穷小 当△t取很小时,可以用V=求瞬时速度,也可用i=求瞬时电流,用
ε=求瞬时感应电动势。下面,我们来理解△t: △t是很小的不为零的正数,它小到什么程度呢?可以说,对于我们
任意给定一个不为零的正数ε,都比△t大,即:ε>△t 。或者从动态 的角度来看,给定一段时间t,我们进行如下操作:
第一次,我们把时间段平均分为2段,每段时间△t=; 第二次,我们把时间段平均分为3段,每段时间△t=;
大立方体的中心点电势:U1=8U2=2 Ckρa2
;即U0=U1
【小结】我们发现,对于一个物理问题,其所求的物理量总是与其他已
知物理量相关联,或者用数学语言来说,所求的物理量就是其他物理量
(或者说是变量)的函数。如果我们能够把这个函数关系写出来,或者
将其函数图像画出来,那么定量或定性地理解物理量的变化情况,帮助
【解析】物体沿竖直圆轨道从最低点匀速率运动到最高点的过程中,在 不同位置与圆环间的正压力不同,故而摩擦力为一変力,本题不能简单 的用来求。
.
x y O
mg mg NA NB B A
可由圆轨道的对称性,在圆轨道水平直径上、下各取两对称位置A和 B,设OA、OB与水平直径的夹角为θ。在的足够短圆弧上,△S可看作 直线,且摩擦力可视为恒力,则在A、B两点附近的△S内,摩擦力所做 的功之和可表示为:
等,甚至不限于对时间求导,如F=、Ex=、ρ=等。
这个dt(也可以是dx、dv、dm等)其实相当于微元法中的时间微元
△t,当然每次这样用来求物理量变化率的瞬时值太繁琐了,毕竟微元
法只是草创时期的微积分。
如果能把常见导数计算的基本规律弄懂,那么我们可以简单快速地
求解物理量变化率的瞬时值(导数)了。同学们可以课后推导以下公
变形为i= - CR,即以上解法中的微分方程。
微分与导数有什么关系呢?对某自变量为时间t的函数F(t),它的
极其微小的变化,我们记它为微分dF,它与时间微分dt满足关系式:
dF=dt,其中为F对t的导数。
下面是常见的微分公式与微分运算法则:
在△t的时间内,通过电阻R的电量为△q。虽然电流随时间发生变
化,但在很短的时间△t内,可以认为电流几乎不变,当成恒定电流处
理,故有△q= i△t 。对电容有Q=CU=CiR,△Q=CR△i;由电量守
恒,△Q= -△q ,故-i△t=CR△i,然后把“△”形式改写成微积
分语言的“d”形式,就有-idt=CRdi (dt和di称之为微分),数学
中间变量对自变量的导数——称为链式法则。
在简谐振动中,在单位时间内物体完成全振动的次数叫频率,用f表
示,频率的2π倍叫角频率,即ω =2πf
【练】1、某弹簧振子在X轴上做直线运动,其位移x与时间t的关系为 x=Asinωt,即,质点在坐标原点附近往复运动,最大位移为A(A称 为振幅),周期为(ω称为角频率),物理上把这种运动叫简谐运 动。请完成以下几问:
所以,流过电阻R的电流随时间t 的变化关系为:i = e-t/CR 【练】对于上例电容器放电问题,试讨论,放电时电容器的电量Q随 时间t 的变化关系如何?
㈡微分 1、从上面式子可以看出,理论上虽然我们说是要经过无穷长的时间电 容才放完电,电流为零,但实际上只需要电流减少足够小时,电流计就 检测不到有电流了。 2、对于i= - CR或i= ,我们称之为微分方程,最直观的解决方法是观 察有哪些函数满足该微分方程的函数关系,当然,我们要注意比如上题 中的t=0 之类的初始条件。 3、一般来说,微积分可以帮助同学们深刻理解物理概念和公式,但微 元法可以帮助同学们更细致地明了物理过程。下面我们用微元法的方式 来处理这个问题。
高中物理中微积分思想 伟大的科学家牛顿,有很多伟大的成就,建立了经典物理理论,比 如:牛顿三大定律,万有引力定律等;另外,在数学上也有伟大的成 就,创立了微积分。 微积分(Calculus)是研究函数的微分、积分以及有关概念和应用的 数学分支。微积分是建立在实数、函数和极限的基础上的。微积分最重 要的思想就是用"微元"与"无限逼近",好像一个事物始终在变化你很难 研究,但通过微元分割成一小块一小块,那就可以认为是常量处理,最 终加起来就行。 微积分学是微分学和积分学的总称。 它是一种数学思想,‘无限细 分’就是微分,‘无限求和’就是积分。无限就是极限,极限的思想是微积 分的基础,它是用一种运动的思想看待问题。微积分堪称是人类智慧最 伟大的成就之一。在高中物理中,微积分思想多次发挥了作用。
①(△t+C)=C
②C·△t=0 ③f(△t)=f(0)
பைடு நூலகம்
④ f(t+△t)=f(t)
⑤=1
『附录』常用等价无穷小关系()
① ;② ;③ ;④ ;⑤
㈢ 导数
前面我们用了极限“”的表示方法,那么物理量y的变化率的瞬时值z
可以写成:
z=,并简记为z=,称为物理量y函数对时间变量t的导数。物理上经常
用某物理量的变化率来定义或求解另一物理量,如v=、a=、i=、ε=N
的。利用微积分思想,把物体的运动无限细分,在每一份位移微元内, 力的变化量很小,可以忽略这种微小变化,认为物体在恒力作用下的运 动;接下来把所有位移内的功相加,即“无限求和”,则总的功就可以知 道。
在高中物理中还有很多例子,比如我们讲过的瞬时速度,瞬时加速 度、感应电动势、引力势能等都用到了微积分思想,所有这些例子都有 它的共性。作为大学知识在高中的应用,虽然微积分高中不要求,但他 的思想无不贯穿整个高中物理。“微积分思想”丰富了我们处理问题的手 段,拓展了我们的思维。我们在学习的时候,要学会这种研究问题的思 想方法,只有这样,在紧张的学习中,我们才能做到事半功倍。
