数轴相反数课件
合集下载
《相反数》(上课)课件PPT1

⑤互为相反数的两个数一定不相等;× 8是 的相反数, 的相反数是-(+3),
【例题2】下列判断不正确的有( )
⑥任何一个正数的相反数都是负数;
⑦除零以外的数都有相反数;×
二、填空
1._5_2_的相反数是-52;_-_1_的相反数是1.
2. a的相反数是_-_a_; -m是_m__的相反数; +(-b)的相反数是_b__;-(+c)是__c_的相反数.
4.-a=a,说明某个数的相反数是本身,该数是 0,0的相反数是0. 5.若a、b互为相反数,则a=-b/b=-a,或a+b=0, a÷b=-1.
【例题1】填空题 A=-5,B=+3,C=+1
(2)相反数成对出现。
(3)数轴上表示相反数的两个对应点,分别位于 原点两侧,它们到原点距离相等。
1.-5.8是 5.8 的相反数, 3 的相反数是-(+3), 在横线上填上“>”“≥”或“<”“≤”
②互为相反数的数在数轴上的点一定在原点的两边;
④符号不同的两个数是相反数;
0的相反数是0
+6.82的相反数是-6.82
【例题2】下列判断不正确的有( C )
①互为相反数的两个数一定不相等;
②互为相反数的数在数轴上的点一定在原点的两边;
③所有的有理数都有相反数;
④相反数是符号相反的两个数.
A.1个
B.2个
③ –0.5的相反数是2; × 2、观察所画的数轴及表示的点回答下列问题:
②互为相反数的数在数轴上的点一定在原点的两边; 若-a=a,表示的什么含义?a的值为? ② –6和8互为相反数;
④符号不同的两个数是相反数; × +(-b)的相反数是___;-(+c)是___的相反数.
【例题2】下列判断不正确的有( )
⑥任何一个正数的相反数都是负数;
⑦除零以外的数都有相反数;×
二、填空
1._5_2_的相反数是-52;_-_1_的相反数是1.
2. a的相反数是_-_a_; -m是_m__的相反数; +(-b)的相反数是_b__;-(+c)是__c_的相反数.
4.-a=a,说明某个数的相反数是本身,该数是 0,0的相反数是0. 5.若a、b互为相反数,则a=-b/b=-a,或a+b=0, a÷b=-1.
【例题1】填空题 A=-5,B=+3,C=+1
(2)相反数成对出现。
(3)数轴上表示相反数的两个对应点,分别位于 原点两侧,它们到原点距离相等。
1.-5.8是 5.8 的相反数, 3 的相反数是-(+3), 在横线上填上“>”“≥”或“<”“≤”
②互为相反数的数在数轴上的点一定在原点的两边;
④符号不同的两个数是相反数;
0的相反数是0
+6.82的相反数是-6.82
【例题2】下列判断不正确的有( C )
①互为相反数的两个数一定不相等;
②互为相反数的数在数轴上的点一定在原点的两边;
③所有的有理数都有相反数;
④相反数是符号相反的两个数.
A.1个
B.2个
③ –0.5的相反数是2; × 2、观察所画的数轴及表示的点回答下列问题:
②互为相反数的数在数轴上的点一定在原点的两边; 若-a=a,表示的什么含义?a的值为? ② –6和8互为相反数;
④符号不同的两个数是相反数; × +(-b)的相反数是___;-(+c)是___的相反数.
数轴和相反数ppt课件
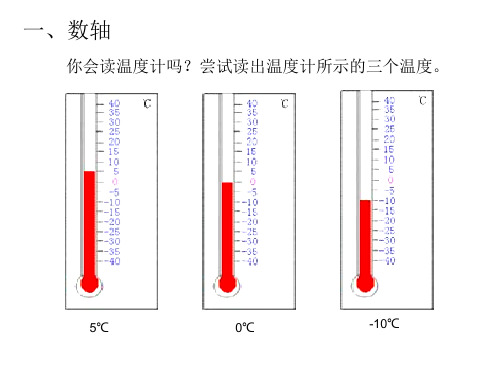
需注意的是:在同一数轴中单位长度应保持一致。
例1.下图中表示数轴正确的是( D )
例2.下列4个数中,在-2到0之间的数是( A )
A.-1
B.1
C.-3
D.3
方法总结:先看数轴三要素是否齐全,再看单位长度是否一致,数字的 标注是否符合规定。
综上所述,也可将数轴定义为规定了原点、正方向、单位长度的直线。
例6.下列说法正确的是( D )
A.3是相反数
B.-3是相反数
C.3和-2互为相反数
D.3与-3互为相反数
例7.一个数的相反数仍是它本身,这个数是(C )
A. 1
B. -1
C. 0
D.正数
2.相反数的几何意义: 动手实践:借助于数轴表示以下几组数,说出你的发现;
4和-4,
3和-3,
1
1
1 2 和-1 2 ,
2.数轴的三要素:
1)原点:在数轴上表示数0的点叫做原点。实际问题中应取 适当的点作为原点。
2)正方向:通常规定数轴从原点向右(或向上)为正方向。
3)单位长度:一般地,从原点向右,每隔一个单位长度取 一个点以此表示数a,2a,3a,...,从原点向左,每隔一 个单位长度取一个点,依次表示-a,-2a,-3a,....(a>0)。
会学到无理数,数轴上的点还能表示无理数 2)有理数与数轴上的点是一一对应的
例3.在数轴上画出下列各点:
1 (1)-100,0,200,400;(2)-3 2 ,-2,0 ,+2.5,+3;
(1)
-1-0100 0 0
200200 400
400
(2)
例4.下列语句中,说法正确的个数是( B )
(1)数轴上的点只表示整数; (2)数轴是一条直线; (3)数轴上的一个点只能表示一个数; (4)数轴上找不到既比表示正数,又不表示负数的点; (5)数轴上的点表示的数都是有理数;
例1.下图中表示数轴正确的是( D )
例2.下列4个数中,在-2到0之间的数是( A )
A.-1
B.1
C.-3
D.3
方法总结:先看数轴三要素是否齐全,再看单位长度是否一致,数字的 标注是否符合规定。
综上所述,也可将数轴定义为规定了原点、正方向、单位长度的直线。
例6.下列说法正确的是( D )
A.3是相反数
B.-3是相反数
C.3和-2互为相反数
D.3与-3互为相反数
例7.一个数的相反数仍是它本身,这个数是(C )
A. 1
B. -1
C. 0
D.正数
2.相反数的几何意义: 动手实践:借助于数轴表示以下几组数,说出你的发现;
4和-4,
3和-3,
1
1
1 2 和-1 2 ,
2.数轴的三要素:
1)原点:在数轴上表示数0的点叫做原点。实际问题中应取 适当的点作为原点。
2)正方向:通常规定数轴从原点向右(或向上)为正方向。
3)单位长度:一般地,从原点向右,每隔一个单位长度取 一个点以此表示数a,2a,3a,...,从原点向左,每隔一 个单位长度取一个点,依次表示-a,-2a,-3a,....(a>0)。
会学到无理数,数轴上的点还能表示无理数 2)有理数与数轴上的点是一一对应的
例3.在数轴上画出下列各点:
1 (1)-100,0,200,400;(2)-3 2 ,-2,0 ,+2.5,+3;
(1)
-1-0100 0 0
200200 400
400
(2)
例4.下列语句中,说法正确的个数是( B )
(1)数轴上的点只表示整数; (2)数轴是一条直线; (3)数轴上的一个点只能表示一个数; (4)数轴上找不到既比表示正数,又不表示负数的点; (5)数轴上的点表示的数都是有理数;
相反数_课件

反数、( ×) (2)一个数得相反数一定就是负数、( × )
(3)零得相反数就是零、(√ )
(4)-8就是相反数、(× )
我来做一做:
(1)分别写出下列各数的相反数:
+11.2, -7, 3 , - 3 1 ;
2
(2)指出下列各数是哪个数的相反数:
1
3.1415926 , -0 , -10 .
解: (1)+11、2得相反数就是-11、2 , (2) 3、1415926就是- 3、1415926得相反数,
好 看谁掌握得最 :
(1)下列说法正确得就是 ( D)
(A) (B)
2 3
与
3 2
-( 1
3
互为相反数
)与+(
)互13 为相反数
(C)5与-(-5)互为相反数
(D) 1 与-0、125互为相反数
8
好 看谁掌握得最 :
(2)下列结论正确得就是 ( C) (A) 0没有相反数 (B) 符号不同得两个数就是相反数 (C) 一个数得相反数得相反数就是她本身 (D) 互为相反数得两个数中,一个就是正 数,一个就是负数
只有符号不同得两个数称互为相反数、 规定: 零得相反数就是零 、
画出一条数轴,并在数轴上找出以下点 -2、5与+2、5,+1与-1,+3与-3
、
-2、
0
5
、
+2、5
、、
-1 0 +1
、
、
-3
0
+3
每一对数在数轴上得对应点位于原点得两侧,且到原 点得距离相等、
我来 辨一辨:
(1)只要符号不同得两个数就称互为相
-7表示_7_得相反数; -(-7) 表示___-7得相反数、
(3)零得相反数就是零、(√ )
(4)-8就是相反数、(× )
我来做一做:
(1)分别写出下列各数的相反数:
+11.2, -7, 3 , - 3 1 ;
2
(2)指出下列各数是哪个数的相反数:
1
3.1415926 , -0 , -10 .
解: (1)+11、2得相反数就是-11、2 , (2) 3、1415926就是- 3、1415926得相反数,
好 看谁掌握得最 :
(1)下列说法正确得就是 ( D)
(A) (B)
2 3
与
3 2
-( 1
3
互为相反数
)与+(
)互13 为相反数
(C)5与-(-5)互为相反数
(D) 1 与-0、125互为相反数
8
好 看谁掌握得最 :
(2)下列结论正确得就是 ( C) (A) 0没有相反数 (B) 符号不同得两个数就是相反数 (C) 一个数得相反数得相反数就是她本身 (D) 互为相反数得两个数中,一个就是正 数,一个就是负数
只有符号不同得两个数称互为相反数、 规定: 零得相反数就是零 、
画出一条数轴,并在数轴上找出以下点 -2、5与+2、5,+1与-1,+3与-3
、
-2、
0
5
、
+2、5
、、
-1 0 +1
、
、
-3
0
+3
每一对数在数轴上得对应点位于原点得两侧,且到原 点得距离相等、
我来 辨一辨:
(1)只要符号不同得两个数就称互为相
-7表示_7_得相反数; -(-7) 表示___-7得相反数、
相反数 课件(共20张PPT) 2024-2025学年数学沪科版(2024)七年级上册

(5) 相反数等于它本身的数只有0 ( √ );
(6) 符号不同的两个数互为相反数( × ).
2
2
0
0
2
习题4
化简下列各式的符号,并回答问题:
①−(−2)=______;②+(−15)=______;③−[−(−4)]=_____;
−15
−4
2
④−[−(+3.5)]=_____
3.5 ;⑤−{−[−(−5)]}=_______.
个数的相反数,如2与−2互为相反数,即2的相反数是−2,−2的相反数是2.
特别规定:0的相反数是0.
一般地,数a的相反数是-a,这里a表示任意一个数,即它可以是正数、负数或者0.
2
2
0
0
2
在数轴上,−2与+2,−4和+4所对应的点位于原点两侧,且与
原点的距离相等.
想一想:数轴上表示相反数的两个点和原点有什么关系?
2
2
0
0
2
典型例题
例2
化简下列各数:
(1)−(+10);
(2)+(−0.15);
(3)+(+3);
(4)−(−12);
(5)+[−(−1.1)] ; (6)−[+(−7)].
解:(1)−(+10)=−10;
(2)+(−0.15)=−0.15;
(3)+(+3)=3;
(4)−(−12)=12;
(5)+[−(−1.1)]=+(+1.1)=1.1;
0
2
−3 −2 −1
0
1
2
3
4
1.2 第1课时 数轴课件 (共20张PPT)沪科版(2024)数学七年级上册

C
A
B
数轴
应用
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
画法
一画:
二定:
三选:
四统一:
画直线
定原点
选正方向
统一单位长度
定义
单位长度
原点
正方向
1.在数轴上,原点及原点右边的点表示的数是( )A. 正数 B. 负数C. 非正数 D. 非负数
画数轴注意事项:
用数轴上的点表示有理数
数轴上能表示分数或小数吗?
比如你能表示 1.5 吗?
例1 说出图所示的数轴上 A,B,C,D 各点表示的数.
解:点 C 在原点表示 0,
点 A 在原点左边与原点距离 2 个单位长度,故表示 -2.
同理,点 B 表示 -3.5.
点 D 在原点右边与原点距离 2 个单位长度,故表示 2.
C
4.有理数 a,b,c 在数轴上的位置如图所示,则 ( )A. a,b,c 均是正数 B. a,b,c 均是负数C. a,b 是正数,c 是负数 D. a,b 是负数,c 是正数
D
5. 画出数轴并表示下列有理数:
解:如下图所示.
6. 在数轴上,老师不小心把一滴墨水滴在画好的数轴上,如图所示,试根据图中标出的数值判断被墨水盖住的整数,并把它写出来.
2.在数轴上表示 -3 的点与表示 4 的点之间的距离是( )A. 7 B. -7C. 1 D. -1
D
A
3. 下列说法中,正确的是 ( )A. 数轴是一条规定了原点、正方向和单位长度的射线B. 离原点近的点所表示的有理数较小C. 数轴上的点可以表示任意有理数D. 原点在数轴的正中间
e7d195523061f1c0c2b73831c94a3edc981f60e396d3e182073EE1468018468A7F192AE5E5CD515B6C3125F8AF6E4EE646174E8CF0B46FD19828DCE8CDA3B3A044A74F0E769C5FA8CB87AB6FC303C8BA3785FAC64AF5424764E128FECAE4CC72932BB65C8C121A0F41C1707D94688ED66335DC6AE12288BF2055523C0C26863D2CD4AC454A29EEC183CEF0375334B579
A
B
数轴
应用
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
画法
一画:
二定:
三选:
四统一:
画直线
定原点
选正方向
统一单位长度
定义
单位长度
原点
正方向
1.在数轴上,原点及原点右边的点表示的数是( )A. 正数 B. 负数C. 非正数 D. 非负数
画数轴注意事项:
用数轴上的点表示有理数
数轴上能表示分数或小数吗?
比如你能表示 1.5 吗?
例1 说出图所示的数轴上 A,B,C,D 各点表示的数.
解:点 C 在原点表示 0,
点 A 在原点左边与原点距离 2 个单位长度,故表示 -2.
同理,点 B 表示 -3.5.
点 D 在原点右边与原点距离 2 个单位长度,故表示 2.
C
4.有理数 a,b,c 在数轴上的位置如图所示,则 ( )A. a,b,c 均是正数 B. a,b,c 均是负数C. a,b 是正数,c 是负数 D. a,b 是负数,c 是正数
D
5. 画出数轴并表示下列有理数:
解:如下图所示.
6. 在数轴上,老师不小心把一滴墨水滴在画好的数轴上,如图所示,试根据图中标出的数值判断被墨水盖住的整数,并把它写出来.
2.在数轴上表示 -3 的点与表示 4 的点之间的距离是( )A. 7 B. -7C. 1 D. -1
D
A
3. 下列说法中,正确的是 ( )A. 数轴是一条规定了原点、正方向和单位长度的射线B. 离原点近的点所表示的有理数较小C. 数轴上的点可以表示任意有理数D. 原点在数轴的正中间
e7d195523061f1c0c2b73831c94a3edc981f60e396d3e182073EE1468018468A7F192AE5E5CD515B6C3125F8AF6E4EE646174E8CF0B46FD19828DCE8CDA3B3A044A74F0E769C5FA8CB87AB6FC303C8BA3785FAC64AF5424764E128FECAE4CC72932BB65C8C121A0F41C1707D94688ED66335DC6AE12288BF2055523C0C26863D2CD4AC454A29EEC183CEF0375334B579
《相反数》ppt课件

设a是一个正数,数轴上与原点的距离等于a(a为正数) 的点有几个?这些点表示的数有什么关系?
如果a是一个正数,数轴上与原点的距离是a的点有两 个,它们分别在原点左右两侧,表示-a和a,我们说这 两个点关于原点对称.
新知探究 知识点1 相反数
相反数:只有符号不同的两个数互为相反数. 特别地,
0的相反数是0.
A.5或-5
B.2.5或-2.5 C.5或-2.5 D.- 5或2.5
一个数到它的相反数的距离 是这个数到原点距离的2倍.
2.点A在数轴上,将点A先向左移动10个单位长度,再 向右移动4个单位长度到点B,此时点B所表示的数与点 A原来所表示的数互为相反数,求点A原来表示的数是 多少? 解:将点A先向左移动10个单位长度,再向右移动4个 单位长度到点B,相当于点A向左移动了6个单位长度, 即AB的长度是6.因为点A,B表示的数互为相反数,所 以A,B两点与原点的距离都是3,所以点A表示的数是3.
数轴上一个数到它的相反数的距离是这个数到 原点距离的2倍.
除了符号不同之外,其他部分完
全相同,不能理解为只要符号不 同的两个数就互为相反数.例如, +5和-2虽然符号不同,但不能说 它们互为相反数.
相反数的求法 (1) 求一个数的相反数,只需改变这个数前面的符号, 即可得到这个数的相反数. (2) 求一个数的相反数就是在这个数的前面加上“-”号, 即a的相反数是-a,其实只是改变这个数的符号.
3.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是 相反数为它本身的数,计算3a+4b+5c的值. 解:因为-[-(-5)]=-5,所以a=-(-5)=5. 因为最小的正整数是1,b比最小的正整数大4, 所以b=1+4=5. 因为c是相反数为它本身的数,所以c=0. 所以3a+4b+5c=3×5+4×5+5×0=35.
相反数-完整版PPT课件

达标训练 1.下列说法中正确的个数为 ①符号不相同的两个数互为相反数;②一个数的相反数一定是负数; ③两个互为相反数的和等于0; ④若两个数互为相反数,则这两个数一定一正一负. A.1个 B2个 C.3个 D.4个
-8 的相反数是___8__,7 的相反数是___-_7__
深入思考
数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示互为相反数的两个数的点,分别
位于原点的____左__右,
相等
对称
典例分析
例1 判断正误:
(1)-5是5的相反数( √);
(2)5是-5的相反数( )√ ;
(3)2与1 互为相1反数( );
典例分析
1 -4是____的相4 反数,-(4)=___ ; -4
1 2 是____1_的相反5 数,
5
1 5
1 ___5__;
3 –-71是____的-7相1 反数,--71=____; 71
4--100是____的-1相00反数,--100=_____ 100
中考链接 1(2009 遂宁)5的相反数是 2(2009 杭州) 如果ab=0,那么a,b两个实数一定是 A都等于0 B一正一负 C互为相反数 D互为倒数 ,n互为相反数,则5m5n-5= .
思考: 1在数轴上,点M表示-4,点N与M点的距离为3,则点N表示什么数? 2如图,数轴上点A,B表示的数分别为-a和b,比较-a与b的大小关系
B
A
b
-a
动动脑
数轴上与原点距离是 3 的点有_____两个,这些 点表示的数是________3_,__-;3 与原点的距离是 5 的点有_____两个,这些点表 示的数是_______5_,__-_5_
-8 的相反数是___8__,7 的相反数是___-_7__
深入思考
数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示互为相反数的两个数的点,分别
位于原点的____左__右,
相等
对称
典例分析
例1 判断正误:
(1)-5是5的相反数( √);
(2)5是-5的相反数( )√ ;
(3)2与1 互为相1反数( );
典例分析
1 -4是____的相4 反数,-(4)=___ ; -4
1 2 是____1_的相反5 数,
5
1 5
1 ___5__;
3 –-71是____的-7相1 反数,--71=____; 71
4--100是____的-1相00反数,--100=_____ 100
中考链接 1(2009 遂宁)5的相反数是 2(2009 杭州) 如果ab=0,那么a,b两个实数一定是 A都等于0 B一正一负 C互为相反数 D互为倒数 ,n互为相反数,则5m5n-5= .
思考: 1在数轴上,点M表示-4,点N与M点的距离为3,则点N表示什么数? 2如图,数轴上点A,B表示的数分别为-a和b,比较-a与b的大小关系
B
A
b
-a
动动脑
数轴上与原点距离是 3 的点有_____两个,这些 点表示的数是________3_,__-;3 与原点的距离是 5 的点有_____两个,这些点表 示的数是_______5_,__-_5_
人教版八年级数学上册课件:专题课堂1 数轴、相反数、绝对值 (共15张PPT)

C
解:如图:
初中数学
6.已知数轴上点A表示-5,点B,C表示互为相反数的两个数,且点C与点 A之间的距离为2,求点B,C表示的数. 解:因为数轴上点A表示-5,点C与点A之间的距离为2,所以数轴上点 C表示-3或-7.因为点B,C表示互为相反数的两个数,所以数轴上点B 表示3或7,所以点B,C表示的数分别是3,-3或7,-7
解:(1) (2)由(1)中数轴可知超市D距货场A 2千米 (3)货车一共行驶了2+ 1.5+5.5+2=11(千米)
初中数学
8.根据|x|≥0这条性质,解答下列问题: (1)当x取何值时,|x-2|有最小值?这个最小值是多少? (2)当x取何值时,3-|x-2|有最大值?这个最大值是多少? 解:(1)x=2时,最小值为0 (2)x=2时,最大值为3
初中数学
解:(1)因为点B所表示的数是-3,所以与点B的距离是3个单位长度的点所 表示的数是-6或0 (2)点C所表示的数是4,向左移动6个单位长度到达点D,则点D表示的数是 -2 (3)把点A向右移动2个单位,点C向左移动7个单位(答案不唯一,将其中两个 点移到第三个点的位置即可)
初中数学
2.小敏家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记 为A,B,C,D,学校位于小敏家西150 m,邮局位于小敏家东100 m, 图书馆位于小敏家西400 m. (1)用数轴表示A,B,C,D的位置; (2)一天小敏从家里先去邮局寄信后,以50 m/min的速度往图书馆方向 走了约8 min,试问这时小敏约在什么位置?距图书馆和学校各约多少米?
解:分两种情况讨论:①当点 C 在原点与点 B 之间时,有 OC=14OB =6;②当点 C 在原点的左边时,|OC|=21|OB|=21×24=12.故点 C 对应的数为 6 或-12
解:如图:
初中数学
6.已知数轴上点A表示-5,点B,C表示互为相反数的两个数,且点C与点 A之间的距离为2,求点B,C表示的数. 解:因为数轴上点A表示-5,点C与点A之间的距离为2,所以数轴上点 C表示-3或-7.因为点B,C表示互为相反数的两个数,所以数轴上点B 表示3或7,所以点B,C表示的数分别是3,-3或7,-7
解:(1) (2)由(1)中数轴可知超市D距货场A 2千米 (3)货车一共行驶了2+ 1.5+5.5+2=11(千米)
初中数学
8.根据|x|≥0这条性质,解答下列问题: (1)当x取何值时,|x-2|有最小值?这个最小值是多少? (2)当x取何值时,3-|x-2|有最大值?这个最大值是多少? 解:(1)x=2时,最小值为0 (2)x=2时,最大值为3
初中数学
解:(1)因为点B所表示的数是-3,所以与点B的距离是3个单位长度的点所 表示的数是-6或0 (2)点C所表示的数是4,向左移动6个单位长度到达点D,则点D表示的数是 -2 (3)把点A向右移动2个单位,点C向左移动7个单位(答案不唯一,将其中两个 点移到第三个点的位置即可)
初中数学
2.小敏家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记 为A,B,C,D,学校位于小敏家西150 m,邮局位于小敏家东100 m, 图书馆位于小敏家西400 m. (1)用数轴表示A,B,C,D的位置; (2)一天小敏从家里先去邮局寄信后,以50 m/min的速度往图书馆方向 走了约8 min,试问这时小敏约在什么位置?距图书馆和学校各约多少米?
解:分两种情况讨论:①当点 C 在原点与点 B 之间时,有 OC=14OB =6;②当点 C 在原点的左边时,|OC|=21|OB|=21×24=12.故点 C 对应的数为 6 或-12
【数学课件】相反数ppt课件

(3)-3是3的相反数;
(4)-3与+3互为相反数; (5)+3是-3的相反数; (6)一个数的相反数不可能是它本身; (7) 符号相反的两个数叫做互为相反数;
(8)互为相反数的两个数不一定一个是正数,一个是负数;
(9)相反数和我们以前学过的倒数是一样的.
【例题】
【例2】化简: -(-2.5),-(+3),+(-0.7), 解:-(-2.5)=2.5
好好学习,天天向上。
14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金
15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
观察这两个数,有什么相同和不同? 符号不同
5
数字相同
5
一般地,设a是一个正数,数轴上与原点的距离是 a的点有两个,它们分别在原点左右,表示a和-a,我 们就说这两点关于原点对称.
-5 -a
-2
0
2
a 5
像2和-2,5和-5这样,只有正负号不同的两个数称互为 相反数.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 8
[解析] 3 8 =2是有理数,cos45°=是无理数.故无理数有 cos45°共三个.
,π,
第1讲┃ 归类示例
对无理数的判定,不能只被表面形式迷惑, 而应从最后结果去判断.一般来说,用根号表示 的数不一定就是无理数,如 是有理数, 用三角函数符号表示的数也不一定就是无理数, 如sin30°、tan45°也不是无理数,一个数是不 是无理数关键在于不同形式表示的数的最终结果 是不是无限不循环小数.
第1讲┃ 归类示例
(1)求一个数的相反数,直接在这个数的前面加上负 号,有时需要化简得出. (2)一个负数的绝对值等于它的相反数.反过来,一 个数的绝对值等于它的相反数,则这个数是非正数. (3)解绝对值和数轴的有关问题时常用到字母表示数 的思想、分类讨论思想和数形结合思想.
第1讲┃ 归类示例 ► 类型之三 科学记数法 命题角度: 用科学记数法表示数. 例3 [2012·绵阳] 绵阳市统计局发布2012年一季 度全市完成GDP共317亿元,居全省第二位,将这一数 据用科学计数法表示为( B ) A.31.7×109元 C.3.17×1011元 B.3.17×1010元 D.31.7×1010元
代数比较 规则
几何比较 规则
第2讲┃ 考点聚焦
考点3 比较实数大小的常用方法
设a, b是任意两实数,则a-b>0⇔a>b;a- b<0⇔a<b;a-b=0⇔a=b 设a, b是两正实数,则 a/b >1⇔a>b; a/b =1⇔a=b; a/b <1⇔a<b 设a, b是两负实数,则|a|>|b|⇔a<b;|a|= |b|⇔a=b;|a|<|b|⇔a>b 除此之外,还有平方法、倒数法等方法
第2讲┃ 归类示例
[解析] 解法一:采用“特殊值法”来解,令 x 1 1 1 1 2 = ,则 x = , =2,∴ >x>x2. 2 4 x x 解法二: 可用“差值比较法”来解, ∵当 0<x<1 时,1-x>0, x-1<0, x+1>0, ∴x-x2=x(1-x)>0, 2 x -1 (x+1)(x-1) 1 2 ∴x>x . 又 x - = = <0, x x x 1 1 2 ∴x< , ∴x <x< . x x
第1讲┃ 归类示例
► 类型之四 创新应用 命题角度: 1.探究数字规律; 2.探究图形与数字的变化关系. 例4 [2012·恩施] 观察数表:
23 根据表中数的排列规律,则B+D=______
第1讲┃ 归类示例
[解析] 仔细观察每一条虚线或与虚线平行的直线上 的数字,从左至右相加等于最后一个数字, ∴1+4+3=B,1+7+D+10+1=34, ∴B=8,D=15,∴B+D=8+15=23.
一个近似数四舍五入到哪一位,那么就说这个近似数精确到哪 近似 一位.对于带计数单位的近似数,由近似数的位数和后面的 数 单位共同确定.如3.618万,数字8实际上是十位上的数字, 即数
非负数 的概念 常见的 非负数 非负数的 性质
正数和零叫做非负数 /a/,a2,√a(a≥0,a可代表一个数或一个 式)
图 1-1
第1讲┃ 回归教材
解:从图中可以看出,OO′的长就是这个圆的周长π , 所以O′的坐标是π . [点析] 用画图的方法可以将一个无理数用数轴上的点 表示出来.事实上每一个无理数都可以用数轴上的一个点 表示出来.
第1讲┃ 回归教材
中考变式
1.[2012·泰州] 如图1-2,数轴上的点P表示的数是-1,
将点P向右移动3个单位长度得到点P′,则点P′表示的数是 ________ . 2
图1-2
第1讲┃ 回归教材
2.[2011·贵阳] 如图1-3,矩形OABC的边OA长为2, 边 AB 长为1,OA 在数轴上,以原点 O 为圆心,对角线 OB 的长为半径画弧,交正半轴于一点,则这个点表示的实数是 ( D ) A . 2.5 B . 2 √2 C.√3 D.√5
第2讲┃ 归类示例
变式题 如图2-1,若A是实数a在数轴上对 应的点,则关于a、-a、1的大小关系表示正确的是 ( A )
图2-1 A.a<1<-a B.a<-a<1 C.1<-a<a D.-a<a<1 [解析] 互为相反数所表示的点关于原点对称,所以a, -a 所表示的点关于原点对称,故a<1<-a.
第1讲┃ 归类示例 ► 类型之二 实数的有关概念
命题角度: 1.数轴、相反数、倒数等概念; 2.绝对值的概念及计算. 例2 填空题: 0 (1)相反数等于它本身的数是_________ ; ±1 (2)倒数等于它本身的数是_____________ ; 0或1 (3)平方等于它本身的数是_____________ ; (4)平方根等于它本身的数是______________ ; 0 (5)绝对值等于它本身的数是__________________ . 非负数
第1讲┃ 归类示例
此类实数规律性的问题的特点是给定一列 数或等式或图形,要求适当地进行计算,必要 的观察,猜想,归纳,验证,利用从特殊到一 般的数学思想,分析特点,探索规律,总结结 论.
第1讲┃ 回归教材
回归教材
硬币在数轴上滚动得到的启示
教材母题 人教版八上P83探究 如图1-1,直径为1个单位长度的圆从原点沿数轴 向右滚动一周,圆上的一点由原点到达点O′,点O′的 坐标是多少?
第2讲┃ 归类示例
► 类型之四 探索实数中的规律 命题角度: 1. 探究实数运算规律; 1 1 1 第 1 个等式:a1= = ×1- ; 2. 实数运算中阅读理解问题. 3 1×3 2
1 1 1 1 第 2 个等式:a2= = × - ; 3×5 2 3 5 例4 [2012·广东] 观察下列 等式: 1 1 1 1 第 3 个等式:a3= = × - ; 5×7 2 5 7 1 1 1 1 第 4 个等式:a4= = × - ; 7×9 2 7 9 …
第1讲┃ 考点聚焦
2.按正负分类: 正整数 正有理数 正分数 正实数 正无理数 零 实数 负整数 负有理数 负实数 负分数 负无理数
第1讲┃ 考点聚焦 考点2 实数的有关概念 名称 数轴 定义 原点 、 规定了_______ 正方向、________ 单位长度的 _______ 直线 符号 不同的两个 只有______ 数互为相反数 乘积 为1的两个数 ________ 互为倒数 性质 数轴上的点与实数一 一对应 若a、b互为相反数, 则有a+b=0,|a|= |b|.0的相反数是0 0没有倒数,倒数等于 本身的数是1或-1
有理数的一切运算性质的运算律 都适用于实数运算 先算乘方、开方,再算乘除,最 后算加减,有括号的要先算括号 内的,若没有括号,在同一级运 算中,要从左至右依次进行运算
(1)零指数、负整数指 数的意义,防止以下 错误:①3-2= ; ② 2 a -2 = (2)遇 到绝对值一般要先去 掉绝对值符号,再进 行计算;(3)无论何种 运算,都要注意先定 符号后运算
第2讲┃ 归类示例
两个实数的大小比较方法有: (1) 正数大于零, 负数小于零; (2) 利用数轴; (3) 差值比较法; (4) 商 值比较法; (5) 倒数法; (6) 取特殊值法, (7) 计算器 比较法等.
第2讲┃ 归类示例 ► 类型之三 实数与数轴
命题角度: 1.实数与数轴上的点一一对应关系; 2.数轴与相反数、倒数、绝对值等概念结合; 3.数轴与实数大小比较、实数运算结合; 4.利用数轴进行代数式的化简. 例3 [2012·聊城]在如图2-2所示的数轴上,点B与 点C关于点A对称,A、B两点对应的实数分别是√3和-1, 则点C所对应的实数是( D )
相反数
倒数
第1讲┃ 考点聚焦
名称 定义 性质
a(a>0) 0(a=0) |a|= -a(a<0)
绝对 数轴上表示数a的点与原点的________, 距离 值 记作 |a|
数法
设这个数为m,①当 |m|≥10时,n等于 把一个数写成________ 原数的整数位数减1; a×10n 的形式.(其中 1≤|a|<10.n为整数),这种记数法 ②当|m|≤1时,|n| 叫科学记数法 等于原数左起第一 个非零数字前所有 零的个数
第2讲┃ 归类示例 ► 类型之二 实数的大小比较
命题角度: 1.利用实数的比较大小法则比较大小; 2.实数的大小比较常用方法. 1 2 例 2 当 0<x<1 时,x ,x, 的大小顺序是( C ) x 1 1 2 2 A. <x<x B. <x <x x x 1 2 2 1 C.x <x< D.x<x < x x
差值比较法
商值比较法 绝对值比较 法 其他方法
第2讲┃ 归类示例
归类示例
► 类型之一 实数的运算 命题角度: 1.实数的加减乘除乘方开方运算; 2.实数的运算在实际生活中的应用. 例1 [2012·丽水] 计算:
第2讲┃ 归类示例
第2讲┃ 归类示例
(1)在进行实数的混合运算时,首先要明确与 实数有关的概念、性质、运算法则和运算律,要弄 清按怎样的运算顺序进行.中考中常常把绝对值、 锐角三角函数、二次根式结合在一起考查. (2)要注意零指数幂和负指数幂的意义.负指数 幂的运算: (a≠0,且p是正整数),零指数幂 的运算: =1(a≠0).
图 2- 2
A.1+√3 B.2+√3 C.2√3-1 D.2√3+1
第2讲┃ 归类示例
[解析] 设点 C 所对应的实数是x, 则有x-√3=√3-(-1),解得x=2√3+1.
第2讲┃ 归类示例
(1)互为相反数所表示的点关于原点对称; (2)绝对值相等的数所表示的点到原点的距离相等; (3)实数与数轴上的点一一对应,故而常将实数及表示实 数的字母在数轴上表示出来,然后结合相反数、绝对值及数 轴上数的符号特征等相关知识来解决实数的有关问题.
[解析] 3 8 =2是有理数,cos45°=是无理数.故无理数有 cos45°共三个.
,π,
第1讲┃ 归类示例
对无理数的判定,不能只被表面形式迷惑, 而应从最后结果去判断.一般来说,用根号表示 的数不一定就是无理数,如 是有理数, 用三角函数符号表示的数也不一定就是无理数, 如sin30°、tan45°也不是无理数,一个数是不 是无理数关键在于不同形式表示的数的最终结果 是不是无限不循环小数.
第1讲┃ 归类示例
(1)求一个数的相反数,直接在这个数的前面加上负 号,有时需要化简得出. (2)一个负数的绝对值等于它的相反数.反过来,一 个数的绝对值等于它的相反数,则这个数是非正数. (3)解绝对值和数轴的有关问题时常用到字母表示数 的思想、分类讨论思想和数形结合思想.
第1讲┃ 归类示例 ► 类型之三 科学记数法 命题角度: 用科学记数法表示数. 例3 [2012·绵阳] 绵阳市统计局发布2012年一季 度全市完成GDP共317亿元,居全省第二位,将这一数 据用科学计数法表示为( B ) A.31.7×109元 C.3.17×1011元 B.3.17×1010元 D.31.7×1010元
代数比较 规则
几何比较 规则
第2讲┃ 考点聚焦
考点3 比较实数大小的常用方法
设a, b是任意两实数,则a-b>0⇔a>b;a- b<0⇔a<b;a-b=0⇔a=b 设a, b是两正实数,则 a/b >1⇔a>b; a/b =1⇔a=b; a/b <1⇔a<b 设a, b是两负实数,则|a|>|b|⇔a<b;|a|= |b|⇔a=b;|a|<|b|⇔a>b 除此之外,还有平方法、倒数法等方法
第2讲┃ 归类示例
[解析] 解法一:采用“特殊值法”来解,令 x 1 1 1 1 2 = ,则 x = , =2,∴ >x>x2. 2 4 x x 解法二: 可用“差值比较法”来解, ∵当 0<x<1 时,1-x>0, x-1<0, x+1>0, ∴x-x2=x(1-x)>0, 2 x -1 (x+1)(x-1) 1 2 ∴x>x . 又 x - = = <0, x x x 1 1 2 ∴x< , ∴x <x< . x x
第1讲┃ 归类示例
► 类型之四 创新应用 命题角度: 1.探究数字规律; 2.探究图形与数字的变化关系. 例4 [2012·恩施] 观察数表:
23 根据表中数的排列规律,则B+D=______
第1讲┃ 归类示例
[解析] 仔细观察每一条虚线或与虚线平行的直线上 的数字,从左至右相加等于最后一个数字, ∴1+4+3=B,1+7+D+10+1=34, ∴B=8,D=15,∴B+D=8+15=23.
一个近似数四舍五入到哪一位,那么就说这个近似数精确到哪 近似 一位.对于带计数单位的近似数,由近似数的位数和后面的 数 单位共同确定.如3.618万,数字8实际上是十位上的数字, 即数
非负数 的概念 常见的 非负数 非负数的 性质
正数和零叫做非负数 /a/,a2,√a(a≥0,a可代表一个数或一个 式)
图 1-1
第1讲┃ 回归教材
解:从图中可以看出,OO′的长就是这个圆的周长π , 所以O′的坐标是π . [点析] 用画图的方法可以将一个无理数用数轴上的点 表示出来.事实上每一个无理数都可以用数轴上的一个点 表示出来.
第1讲┃ 回归教材
中考变式
1.[2012·泰州] 如图1-2,数轴上的点P表示的数是-1,
将点P向右移动3个单位长度得到点P′,则点P′表示的数是 ________ . 2
图1-2
第1讲┃ 回归教材
2.[2011·贵阳] 如图1-3,矩形OABC的边OA长为2, 边 AB 长为1,OA 在数轴上,以原点 O 为圆心,对角线 OB 的长为半径画弧,交正半轴于一点,则这个点表示的实数是 ( D ) A . 2.5 B . 2 √2 C.√3 D.√5
第2讲┃ 归类示例
变式题 如图2-1,若A是实数a在数轴上对 应的点,则关于a、-a、1的大小关系表示正确的是 ( A )
图2-1 A.a<1<-a B.a<-a<1 C.1<-a<a D.-a<a<1 [解析] 互为相反数所表示的点关于原点对称,所以a, -a 所表示的点关于原点对称,故a<1<-a.
第1讲┃ 归类示例 ► 类型之二 实数的有关概念
命题角度: 1.数轴、相反数、倒数等概念; 2.绝对值的概念及计算. 例2 填空题: 0 (1)相反数等于它本身的数是_________ ; ±1 (2)倒数等于它本身的数是_____________ ; 0或1 (3)平方等于它本身的数是_____________ ; (4)平方根等于它本身的数是______________ ; 0 (5)绝对值等于它本身的数是__________________ . 非负数
第1讲┃ 归类示例
此类实数规律性的问题的特点是给定一列 数或等式或图形,要求适当地进行计算,必要 的观察,猜想,归纳,验证,利用从特殊到一 般的数学思想,分析特点,探索规律,总结结 论.
第1讲┃ 回归教材
回归教材
硬币在数轴上滚动得到的启示
教材母题 人教版八上P83探究 如图1-1,直径为1个单位长度的圆从原点沿数轴 向右滚动一周,圆上的一点由原点到达点O′,点O′的 坐标是多少?
第2讲┃ 归类示例
► 类型之四 探索实数中的规律 命题角度: 1. 探究实数运算规律; 1 1 1 第 1 个等式:a1= = ×1- ; 2. 实数运算中阅读理解问题. 3 1×3 2
1 1 1 1 第 2 个等式:a2= = × - ; 3×5 2 3 5 例4 [2012·广东] 观察下列 等式: 1 1 1 1 第 3 个等式:a3= = × - ; 5×7 2 5 7 1 1 1 1 第 4 个等式:a4= = × - ; 7×9 2 7 9 …
第1讲┃ 考点聚焦
2.按正负分类: 正整数 正有理数 正分数 正实数 正无理数 零 实数 负整数 负有理数 负实数 负分数 负无理数
第1讲┃ 考点聚焦 考点2 实数的有关概念 名称 数轴 定义 原点 、 规定了_______ 正方向、________ 单位长度的 _______ 直线 符号 不同的两个 只有______ 数互为相反数 乘积 为1的两个数 ________ 互为倒数 性质 数轴上的点与实数一 一对应 若a、b互为相反数, 则有a+b=0,|a|= |b|.0的相反数是0 0没有倒数,倒数等于 本身的数是1或-1
有理数的一切运算性质的运算律 都适用于实数运算 先算乘方、开方,再算乘除,最 后算加减,有括号的要先算括号 内的,若没有括号,在同一级运 算中,要从左至右依次进行运算
(1)零指数、负整数指 数的意义,防止以下 错误:①3-2= ; ② 2 a -2 = (2)遇 到绝对值一般要先去 掉绝对值符号,再进 行计算;(3)无论何种 运算,都要注意先定 符号后运算
第2讲┃ 归类示例
两个实数的大小比较方法有: (1) 正数大于零, 负数小于零; (2) 利用数轴; (3) 差值比较法; (4) 商 值比较法; (5) 倒数法; (6) 取特殊值法, (7) 计算器 比较法等.
第2讲┃ 归类示例 ► 类型之三 实数与数轴
命题角度: 1.实数与数轴上的点一一对应关系; 2.数轴与相反数、倒数、绝对值等概念结合; 3.数轴与实数大小比较、实数运算结合; 4.利用数轴进行代数式的化简. 例3 [2012·聊城]在如图2-2所示的数轴上,点B与 点C关于点A对称,A、B两点对应的实数分别是√3和-1, 则点C所对应的实数是( D )
相反数
倒数
第1讲┃ 考点聚焦
名称 定义 性质
a(a>0) 0(a=0) |a|= -a(a<0)
绝对 数轴上表示数a的点与原点的________, 距离 值 记作 |a|
数法
设这个数为m,①当 |m|≥10时,n等于 把一个数写成________ 原数的整数位数减1; a×10n 的形式.(其中 1≤|a|<10.n为整数),这种记数法 ②当|m|≤1时,|n| 叫科学记数法 等于原数左起第一 个非零数字前所有 零的个数
第2讲┃ 归类示例 ► 类型之二 实数的大小比较
命题角度: 1.利用实数的比较大小法则比较大小; 2.实数的大小比较常用方法. 1 2 例 2 当 0<x<1 时,x ,x, 的大小顺序是( C ) x 1 1 2 2 A. <x<x B. <x <x x x 1 2 2 1 C.x <x< D.x<x < x x
差值比较法
商值比较法 绝对值比较 法 其他方法
第2讲┃ 归类示例
归类示例
► 类型之一 实数的运算 命题角度: 1.实数的加减乘除乘方开方运算; 2.实数的运算在实际生活中的应用. 例1 [2012·丽水] 计算:
第2讲┃ 归类示例
第2讲┃ 归类示例
(1)在进行实数的混合运算时,首先要明确与 实数有关的概念、性质、运算法则和运算律,要弄 清按怎样的运算顺序进行.中考中常常把绝对值、 锐角三角函数、二次根式结合在一起考查. (2)要注意零指数幂和负指数幂的意义.负指数 幂的运算: (a≠0,且p是正整数),零指数幂 的运算: =1(a≠0).
图 2- 2
A.1+√3 B.2+√3 C.2√3-1 D.2√3+1
第2讲┃ 归类示例
[解析] 设点 C 所对应的实数是x, 则有x-√3=√3-(-1),解得x=2√3+1.
第2讲┃ 归类示例
(1)互为相反数所表示的点关于原点对称; (2)绝对值相等的数所表示的点到原点的距离相等; (3)实数与数轴上的点一一对应,故而常将实数及表示实 数的字母在数轴上表示出来,然后结合相反数、绝对值及数 轴上数的符号特征等相关知识来解决实数的有关问题.
